Predictive coding and stochastic resonance as fundamental principles of auditory phantom perception

Abstract

Mechanistic insight is achieved only when experiments are employed to test formal or computational models. Furthermore, in analogy to lesion studies, phantom perception may serve as a vehicle to understand the fundamental processing principles underlying healthy auditory perception. With a special focus on tinnitus—as the prime example of auditory phantom perception—we review recent work at the intersection of artificial intelligence, psychology and neuroscience. In particular, we discuss why everyone with tinnitus suffers from (at least hidden) hearing loss, but not everyone with hearing loss suffers from tinnitus.

We argue that intrinsic neural noise is generated and amplified along the auditory pathway as a compensatory mechanism to restore normal hearing based on adaptive stochastic resonance. The neural noise increase can then be misinterpreted as auditory input and perceived as tinnitus. This mechanism can be formalized in the Bayesian brain framework, where the percept (posterior) assimilates a prior prediction (brain’s expectations) and likelihood (bottom-up neural signal). A higher mean and lower variance (i.e. enhanced precision) of the likelihood shifts the posterior, evincing a misinterpretation of sensory evidence, which may be further confounded by plastic changes in the brain that underwrite prior predictions. Hence, two fundamental processing principles provide the most explanatory power for the emergence of auditory phantom perceptions: predictive coding as a top-down and adaptive stochastic resonance as a complementary bottom-up mechanism.

We conclude that both principles also play a crucial role in healthy auditory perception. Finally, in the context of neuroscience-inspired artificial intelligence, both processing principles may serve to improve contemporary machine learning techniques.

How is information processed in the brain during auditory phantom perception? Schilling et al. review recent work at the intersection of artificial intelligence, psychology and neuroscience and bring together disparate frameworks—stochastic resonance and predictive coding—to offer an explanation for the emergence of tinnitus.

Introduction

The ultimate goal of neuroscience is to gain a mechanistic understanding of how information is processed in the brain. Since the early beginnings of the scientific study of the brain, lesions or more broadly anatomical damages and their physiological effects have provided pivotal insights into brain function. Analogously, phantom perception may serve as a vehicle to understand the fundamental processing principles underlying normal perception. The prime example of an auditory phantom perception is tinnitus, which is believed to be caused by anatomical damage along the auditory pathway. Here we provide a mechanistic explanation of how tinnitus emerges in the brain: namely, how the neural and mental processes underlying perception, cognition and behaviour contribute to and are affected by the development of tinnitus. These insights may not only point to strategies how tinnitus may be reversed or at least mitigated, but also how auditory perception is implemented in the brain in general.

While there is broad agreement in the auditory neuroscience community on these goals, there is far less agreement on the way to achieve them. There is still a popular belief among neuroscientific and psychological tinnitus researchers that we are largely data-driven. In other words, generating large, multi-modal and complex datasets—analysed with advanced data science methods—are believed to lead to fundamental insights into how tinnitus emerges. Indeed, in the last decades we have assembled a broad database, which has inspired models that make quantitative predictions. These predictions scaffold new experimental paradigms that aim to unravel the mechanisms of tinnitus perception. In the following, we summarize some of the main findings in tinnitus research, over the last decades, and then turn to strategic questions about how to leverage these advances, from the perspective of formal modelling.

Some universal correlations between hearing loss, tinnitus and neural hyperactivity in the auditory system have been found in both animal and human studies. These reproducible findings can be considered as the common denominator of tinnitus research and could offer the minimal starting point for theoretical considerations. Tinnitus is a phenomenon arising somewhere along the auditory pathway, but not in the inner ear.¹ Thus, it can be shown that the spontaneous activity of neurons along the auditory pathway is increased after hearing loss,^2–4 whereas the damaged cochlea transmits less information to the higher auditory nuclei.^5,6 However, it has been argued that not all alterations in neural activity in animal models, which were caused by an acoustic trauma, are necessarily related to tinnitus.^1,7 Although there exist some behavioural tests to check for the putative presence of a tinnitus percept based on conditioning^8,9 or startle responses,^10–12 the reliability of these paradigms remains controversial.^7,13 Thus, studies on human subjects complement these findings. In several recent studies, it was shown that the tinnitus pitch lies within the frequency range of the hearing loss and thus it is an obvious assumption that tinnitus can be regarded as a within frequency channel phenomenon.^14–17 Potentially, it is sufficient to assume that the mechanisms causing tinnitus occur in each impaired frequency channel individually and that crosstalk between the different frequency channels along the tonotopic map is not crucial to explain the basic principles behind tinnitus development.¹⁸

This assumption is supported by recent findings e.g. by Dalligna and coworkers,¹⁴ who report that the tinnitus is directly centred at the frequency of the largest hearing loss. For the sake of completeness, it should be mentioned that other studies on tinnitus and its relation to hearing loss found a special emphasis of the edges of the impaired frequency range on the tinnitus pitch.^19-21 However, recently, Keppler and coworkers¹⁵ contradicted these findings and stated that there is no correlation between tinnitus frequency and the edges of the impaired frequency ranges.

Indeed, the above neural correlates of tinnitus and hearing loss are just a small distillation of all studies that aspire to unravel mechanisms that underpin tinnitus, but these findings are robust and constitute the basis of most theoretical and computational models of tinnitus. In the 1990s the first computational models of tinnitus emerged. These models considered decreased lateral inhibition—due to deficient auditory input (i.e. cochlear damage)—as the main cause of tinnitus. Gerken²² created a feed-forward brainstem model and suggested the inferior colliculus to be the crucial structure for tinnitus development. Kral and Majernik,²³ as well as Langner and Wallhäuser-Franke²⁴ pursued computational models, based on decreased lateral inhibition. Bruce and coworkers²⁵ developed these models further and implemented lateral inhibition in a spiking recurrent neural network. In a subsequent step, the principles were implemented in a model of the auditory cortex based on spiking neurons.²⁶

Besides lateral inhibition, homeostatic plasticity²⁷ and central gain changes are hypothesized to be the cause for tinnitus emergence and manifestation. These hypotheses are based on the idea that incoming neuronal signals are amplified, in order to compensate the decreased input from the damaged cochlea. Thus, Parra and Pearlmutter²⁸ implemented that principle in an ‘abstract’ model, where they simply defined several frequency channels with a certain input. The output was scaled with the average, which means that a decreased input leads to a higher scaling or amplification factor, respectively. However, they did not consider a plausible neural implementation of their mathematical model. Schaette and Kempter^29-31 further developed several computational models, investigating the effects of central gain increase on tinnitus emergence. Finally, Chrostowski and coworkers³² developed a cortex model to investigate central gain changes in the cortex (for detailed review on computational tinnitus models see Schaette and Kempter¹).

In 2013, Zeng³³ introduced a model that argues that tinnitus is not caused by increased central gain, which means a multiplicative amplification of the signal, but by increased central noise, which means an additive neural noise, that is intrinsically generated. The idea of an additional intrinsic or extrinsic noise as an explanation for tinnitus has gained some popularity in recent years e.g. Koops and Eggermont.³⁴ However, Zeng raised the question why the brain should increase central noise levels. This question was addressed in 2016 by Krauss and coworkers,¹⁸ who showed that internally generated neural noise could partially restore hearing ability after hearing loss through the effect of stochastic resonance.^35-37 Stochastic resonance is a phenomenon in which the addition of noise to a non-linear system can improve its sensitivity to weak signals. It occurs when a system—which is normally unable to detect weak signals—features an optimal level of noise that lifts the weak signals above the detection threshold. This is because the noise serves to ‘jiggle’ the system, making it easier for weak signals to cross a response threshold. However, the effect only works in a narrow range, as the noise amplitude has to be tuned to an optimal level. Noise amplitudes that are too low would not lift the subthreshold signal above the detection threshold. Conversely, noise amplitudes that are too high would significantly worsen the signal-to-noise ratio up to a level at which the signal disappears completely in the noise. Stochastic resonance has been observed in a variety of physical, biological and neural systems, (for overview cf. Koops and Eggermont³⁴ and Krauss et al.³⁵).

The idea behind the stochastic resonance model of auditory phantom perception (Erlangen model of tinnitus development) is that a subthreshold signal—from an impaired cochlea—is lifted stochastically above the detection threshold by adding uncorrelated neural noise. In earlier studies it has been shown that human hearing may be enhanced beyond the absolute threshold of hearing by adding acoustic white noise to a subthreshold acoustic stimulus.³⁸ The Erlangen model hypothesizes that this mechanism is also implemented in the dorsal cochlear nucleus (DCN) and that—instead of acoustic white noise—internally generated neural noise is added to the cochlea output, to lift it above the detection threshold.³⁷ Recently, several studies have provided evidence that cross-modal stochastic resonance is a universal principle for enhancing sensory perception.^36,39,40

This stochastic resonance hypothesis is further supported by the finding that, on average, hearing thresholds are better in patients suffering from hearing loss with tinnitus compared to a control group of patients suffering from hearing loss but without tinnitus.^19,41,42 Along the same line, the stochastic resonance effect as add-on to the central noise model may explain the Zwicker tone illusion,^43-45 i.e. the perception of a phantom sound, which occurs after stimulation with notched noise, and why auditory sensitivity for frequencies adjacent to the Zwicker tone are improved beyond the absolute threshold of hearing during Zwicker tone perception.⁴⁶ Furthermore, recently, a crucial prediction of the stochastic resonance model of tinnitus development was confirmed experimentally by using brainstem audiometry⁴⁷ and assessing behavioural signs of tinnitus¹⁰ in an animal model: simulated transient hearing loss improves auditory thresholds and leads, as a side effect, to the perception of tinnitus.⁴⁸ Both the model from Zeng and the model from Krauss et al.,³⁵ are not based on a particular or specified neural network architecture. However, in 2020, Schilling and coworkers developed a hybrid model based on a biophysically realistic model of the cochlea and the DCN combined with a deep neural network representing all further processing stages along the auditory pathway. In this model, intrinsically generated noise could indeed significantly increase speech perception via SR.⁴⁹ Recently, a similar hybrid neural network model has led to further insights into the mechanisms of impaired speech recognition caused by hearing loss.⁵⁰

In parallel to the intrinsic neural noise models from Zeng and Krauss and colleagues, Sedley and coworkers developed a conceptual model, which describes tinnitus as arising from a prediction error of the brain.^51,52 This model is based on the idea that the brain is a Bayesian prediction machine, trying to minimize prediction errors or free energy,^53,54 a principle also known as predictive coding. According to the theoretical framework of predictive coding, the brain’s main function is to generate and test predictions about incoming sensory information. In particular, the brain is constantly generating hypotheses or predictions about what is happening in the environment, based on past experiences, and then comparing these predictions with incoming sensory data. The ensuing prediction error is then thought to drive representations about states of affairs generating sensations towards better predictions; thereby resolving prediction errors.

This predictive coding model of tinnitus addresses the issue of whether or not an individual perceives tinnitus as an interplay between existing auditory predictions (which, by default, do not feature tinnitus) and spontaneous activity (i.e. noise) in the central auditory pathway (considered a ‘tinnitus precursor’). Whether the posterior (i.e. percept) crosses the threshold for perception depends on both of these factors, including their mean values (e.g. firing rate) and their precision. More recently, by using a hierarchical Gaussian filter, a computational instantiation of this model has been able to explain phenomenology in individual tinnitus subjects and predict their residual inhibition characteristics.⁵⁵ Despite the fact that in recent years tinnitus research converged to the three main models described above (central noise, central gain, predictive coding), it has to be stated that there exist several further computational simulations and approaches trying to explain and characterize tinnitus development based e.g. on information theoretical considerations (see Dotan and Shriki⁵⁶ and Gault et al.⁵⁷).

Besides the computational models that rest upon a mathematical formulation, there exist several phenomenological models, such as the thalamo-cortical dysrhythmia model,^58,59 the thalamic low-threshold calcium spike model,⁶⁰ the fronto-striatal gating hypothesis^61,62 and the overlapping subnetwork theory.^63,64 Finally, there exists another Bayesian brain/predictive coding model of tinnitus, which is somewhat the polar opposite to what Sedley and Friston were arguing for. There, tinnitus is not believed to arise from spontaneous noise increase, which higher predictions go on to accept, but on the contrary that tinnitus arises from reduced input to the auditory cortex, leading it to ‘make up’ or ‘fill in’ an auditory percept from auditory memory.⁶⁵ However, this assumption contradicts the findings that spontaneous neural activity is increased along the entire auditory pathway starting from the DCN after hearing loss.^2-4

As there exist various models of tinnitus development, which are far too numerous to be treated in detail in this study, criteria are needed to define which models are apt to understand tinnitus development. In their review paper, Schaette and Kempter¹ define three major criteria for the quality of a model: first—and in line with Popper’s ideas⁶⁶—a model should be falsifiable, which means there should be experimental paradigms, which could be used to test a certain candidate model. Second, a model should make quantitative predictions, as opposed to purely qualitative, often vague, predictions, cf. also Lazebnik.⁶⁷ Third, a model should be as simple as possible, i.e. contain the smallest number of parameters and assumptions as possible, a principle called Ockham’s razor.⁶⁸ Hence, if two models explain experimental data equally well, the simpler one has to be considered the better one.

With the huge progress of artificial intelligence (AI) during the last decade, which is mainly due to increased computing power, a new discipline has been founded, called Cognitive Computational Neuroscience (CCN) as an integrative endeavour at the intersection of AI, cognitive science and neuroscience.^69,70

Here, we first discuss the opportunities and limitations of this new research agenda. In particular, we present key thought experiments that highlight the major challenges on the road towards a CCN of tinnitus. In the light of these considerations, we subsequently review current models of tinnitus and assess their explanatory power. Finally, we present an integration of those models that we consider most promising and point towards a unified theory of tinnitus development.

Three challenges ahead

The challenge of developing a common formal language

In 2002, Yuri Lazebnik compared the biologists’ endeavour—of trying to understand the building blocks and processes of living cells—with the problems that engineers typically deal with. In his opinion paper ‘Can a biologist fix a radio?—Or, what I learned while studying apoptosis’, Lazebnik argued that many fields of biomedical research at some point reach

‘a stage at which models, that seemed so complete, fall apart, predictions that were considered so obvious are found to be wrong, and attempts to develop wonder drugs largely fail. This stage is characterized by a sense of frustration at the complexity of the process'.⁶⁷

Subsequently, Lazebnik⁶⁷ discussed a number of intriguing analogies between the physical and life sciences. In particular, he identified formal language as the most important difference between the two. Lazebnik argues that biologists and engineers use quite different languages for describing phenomena. On the one hand, biologists draw box-and-arrow diagrams, which are—even if a certain diagram makes overall sense—difficult to translate into quantitative assumptions, and hence limits its predictive or investigative value.

Indeed, these thoughts fit to the criterion for a ‘good model’ as pointed out by Schaette and Kempter,¹ i.e. that a model should make quantitative predictions. However, on the other hand a model should be as simple as possible and understandable, which means that it is important to find a compromise between too fine-grained and too coarse-grained descriptions of the system to be explained (see Marr’s levels of analysis in Fig. 1A, based on Marr and Poggio⁷¹).

Figure 1.

Marr’s levels of analysis. (A) The scheme illustrates how measurement methods (such as MEG, EEG etc.), neuroscientific disciplines, as well as theoretical models can be structured in three different levels of analysis (according to Marr and Poggio⁷¹). (B) Tinnitus models in the light of the three levels of analysis. The grey bars illustrate how the different models cover the different levels of analysis (implementational, algorithmic, computational). The central noise model and the stochastic resonance model can be unified (1). The stochastic resonance model is at the algorithmic level as there exists a neural network model,³⁸ which could reproduce the stochastic resonance effect in tinnitus context. The exact molecular mechanism, such as the specific neurotransmitter, are unknown and therefore it is not at the implementational level. The mathematical formulation of the predictive coding model cannot be fully translated to a neural network model and therefore it is at the computational model. A neural network implementation of the predictive coding model would be algorithmic. Homeostatic plasticity is a collection of the molecular and thus implementational mechanisms behind the central gain model (2).

Lazebnik also remarks that scientific assumptions and conversations are often ‘vague’ and ‘avoid clear, quantifiable predictions’. A freely adapted example drawn from Lazebnik’s paper⁶⁷ would be a statement like

‘an imbalance of excitatory and inhibitory neural activity after hearing-loss appears to cause an overall neural hyperactivity, which in turn seems to be correlated with the perception of tinnitus^'.

Descriptions of electrophysiological findings are an important starting point for hypothesis generation, but they are no more than a first step. Description needs to be complemented with explanation and prediction (compare also the four main goals of psychology as described in Holt et al.⁷²). Furthermore, Lazebnik urges a more formal common language for biological sciences, in particular a language that has the precision and expressivity found in engineering, physics or computer science. Any engineer trained in electronics for instance, is able to unambiguously understand a diagram describing a radio or any other electronic device. Thus, engineers can discuss a radio using terms that are common ground in the community. Furthermore, this commonality enables engineers to identify familiar functional architectures or motifs; even in a diagram of a completely novel device. Finally, due to the mathematical underpinnings of the language used in engineering, it is perfectly suited for quantitative analyses and computational modelling. For instance, a description of a certain radio includes all key parameters of each component like the capacity of a capacitor, but not irrelevant parameters—that do not ‘matter’—like its colour, shape or size.

We emphasize that this does not mean that anatomical descriptions are useless in order to understand brain function, especially since there is a close correlation between structure and function in the brain. However, also in neurobiology there exist both kinds of detail: those that are crucial for understanding neural processing, and those that are not relevant variables.

Lazebnik concludes that ‘the absence of such language is the flaw of biological research that causes David’s paradox’, i.e. the paradoxical phenomenon frequently observed in biology and neuroscience that ‘the more facts we learn the less we understand the process we study’.⁶⁷

Some conclusions for tinnitus research can be drawn from Lazebniks’ thoughts on a more formal approach in biological sciences. The ‘central gain’ and ‘homeostatic plasticity’ theory on tinnitus emergence is a good example how the communication on tinnitus research can be improved. For example, Roberts stated in 2018 that the increase of central gain is ‘increase of input output functions by forms of homeostatic plasticity’, which means that homeostatic plasticity is necessarily connected to central gain adaptations.⁷³ In contrast to that, Schaette and Kempter¹ state that central gain changes can occur within seconds and thus are not necessarily caused by homeostatic plasticity. Only on longer timescales, both effects can be regarded as ‘functionally equivalent’.¹ Indeed, tinnitus research would profit from a unified terminology for the different concepts, in the best case, a mathematical formulation.

The challenge of developing a unified mechanistic theory

In 2014, Joshua Brown built on Lazebnik’s ideas and published the opinion article ‘The tale of the neuroscientists and the computer: why mechanistic theory matters'.⁷⁴ In this thought experiment, a group of neuroscientists finds an alien computer and tries to figure out its function.

First, the MEG/EEG researcher tried to investigate the computer. She found that every time ‘when the hard disk was assessed, the disk controller showed higher voltages on average, and especially more power in the higher frequency bands’.⁷⁴

Subsequently, the cognitive neuroscientist, i.e. the functional MRI researcher argued that MEG/EEG has insufficient spatial resolution to see what is going on inside the computer. He carried out a large number of experiments, the results of which can be summarized with the realization that during certain tasks, certain regions seem to be more activated and that none of these components could be understood properly in isolation. Thus, the researcher analysed the interactions of these components, showing that there is a vast variety of different task-specific networks in the computer.

Finally, the electrophysiologist noted, critically, that his colleagues may have found coarse-grained patterns of activity, but it is still unclear what the individual circuits are doing. He starts to implant microelectrode arrays into the computer and probes individual circuit points by measuring voltage fluctuations. With careful observation, the electrophysiologist identifies units responding stochastically when certain inputs are presented, and that nearby units seem to process similar inputs. Furthermore, each unit seems to have characteristic tuning properties.

Brown’s tale ends with the conclusion that even though they performed a multitude of different empirical investigations, yielding a broad range of interesting results, it is still highly questionable whether ‘the neuroscientists really understood how the computer works'. ⁷⁴

This provocative thought experiment speaks to some ideas that are relevant for tinnitus research.

In 2021, four leading scientists in tinnitus research discussed different tinnitus models at the Annual-Mid-Winter Meeting of the Association for Otolaryngology and diagnosed a ‘lack of consistency of concepts about the neural correlate of tinnitus’.⁷⁵ Thus, a clearly defined theoretical framework is needed, which helps empirical groups to develop experimental paradigms suited to confirm or falsify different candidate models. To achieve that, inter-disciplinary teams or at least an inter-disciplinary approach is needed.⁷⁶

The challenge of developing appropriate analysis methods

In 2017 Jonas and Kording implemented the thought experiment of Brown in an experimental study. In their study ‘Could a neuroscientist understand a microprocessor?’⁷⁷ the authors address this question by emulating a classical microprocessor, the MOS 6502, which was implemented as the central processing unit (CPU) in the Apple I, the Commodore 64, and the Atari Video Game System, in the 1970s and 1980s. In contrast to contemporary CPUs, like Intel’s i9-9900K, that consist of more than three billion transistors, the MOS 6502 only consisted of 3510 transistors. It served as a ‘model organism’ in the mentioned study, and performed three different ‘behaviors’, i.e. three classical video games (Donkey Kong, Space Invaders and Pitfall).

The idea behind this approach is that the microprocessor, as an artificial information processing system, has three decisive advantages compared to natural nervous systems. First, it is fully understood at all levels of description and complexity, from its gross architecture and the overall data flow, through logical gate primitives, to the dynamics of single transistors. Second, its internal state is fully accessible without any restrictions to temporal or spatial resolution. And third, it offers the ability to perform arbitrary invasive experiments on it, which are impossible in living systems due to ethical or technical reasons. Using this framework, the authors applied a wide range of popular data analysis methods from neuroscience to investigate the structural and dynamical properties of the microprocessor. The methods used included—but were not restricted to—Granger causality for analysing task-specific functional connectivity, time-frequency analysis as a hallmark of MEG/EEG research, spike pattern statistics, dimensionality reduction, lesioning and tuning curve analysis.

The authors concluded that although each of the applied methods yielded results strikingly similar to what is known from neuroscientific or psychological studies, none of them could actually elucidate how the microprocessor works, or more broadly speaking, was appropriate to gain a mechanistic understanding of the investigated system.

Of course, there are potential criticisms of this study; for example, the brain is no computer and thus the drawn parallels are insufficient. Nevertheless, the idea to use a known model system to check for the validity of the evaluation procedures and common methods is a seminal principle. In 2009 Bennett and coworkers⁷⁸ performed an even stranger experiment, when they used standard functional MRI and statistics techniques to analyse the brain activity of a dead salmon, and indeed found a blood oxygenation level-dependent (BOLD) signal due to stimulation. At first glance, this experiment seemed to be at least useless if not even funny, but it was a wake-up call and indeed changed the way functional MRI data are evaluated. Nowadays there exist strict rules how to correct for multiple testing in functional MRI research, to prevent pseudo-effects being a result of wrong statistical testing.^78,79 In computational neuroscience and AI research, newly developed methods are always applied to standard datasets such as the MNIST (Modified National Institute of Standards and Technology) database consisting of 60 000 images of hand-written digits^80,81 or artificially generated datasets with known properties, e.g. Schilling et al.,^47,82 Zenke and Vogels⁸³ and Krauss et al.⁸⁴ The principle of using fully known—even trivial systems—to test the validity of tools, methods or even theories could be an important approach in tinnitus research. Even in computational modelling, simply implementing a system in all details without an underlying theory, which serves as a solid base, will not lead to a real understanding. Indeed, theory needs computational modelling, but the statement is also true the other way around.⁸⁵ Therefore, it is crucial that computational models meet a basic standard—they should be capable of accurately explaining well established and simple phenomena. This serves as a basis to verify their validity before drawing more complex conclusions.

Towards a cognitive computational neuroscience of tinnitus

What does it mean to understand a system?

If popular analysis methods fail to deliver mechanistic understanding, what are the alternative approaches? Most obviously, narrative hypotheses about the structure and function of the system under investigation will help. Instead of simply describing data features with correlations, coherence, Granger causality etc.—in the hope of learning something about the functioning of the system under investigation—it would be much more effective to have a concrete hypothesis about the structure or function architecture of the system and then search for empirical evidence for that and alternative hypotheses.

Note that this does not exclude explorative analysis of existing data, in order to generate new hypotheses. However, as we pointed out in a previous publication,⁸⁶ to avoid statistical errors due to ‘HARKing’ (‘hypothesizing after results are known’ is defined as generating scientific statements exclusively based on the analysis of huge datasets without previous hypotheses^87,88 and to guarantee consistency of the results, it is necessary to apply e.g. resampling techniques such as subsampling.⁴⁷ Alternatively, the well established machine learning practice of cross-validation: i.e. splitting the dataset into multiple parts before the beginning of the evaluation can be used. There, one data part is used for generating new hypotheses and another part for subsequently statistically testing these hypotheses. Accumulation of such data-driven knowledge may finally lead to a new theory.

Ideally, the verbally defined (narrative) hypotheses to be experimentally tested would be derived from such an underlying theory. As Kurt Lewin, the father of modern experimental psychology, pointed out: ‘There is nothing so practical as a good theory'.⁸⁹ If we had theorized that the microprocessor from the thought experiment above performs arithmetic calculations, we could have, e.g. derived the hypothesis that there must be something like 1-bit adders, and could have searched for them specifically.

Conversely, Allan Newell, one of the fathers of artificial intelligence, stated that ‘You can‘t play 20 questions with nature and win'.⁹⁰ This suggests that testing one narrative hypothesis after another will never lead to a mechanistic understanding. Therefore, this raises the fundamental question of what it actually means to ‘understand’ a system.

Yuri Lazebnik argued that understanding of a system is achieved when one could fix a broken implementation:

‘Understanding of a particular region or part of a system would occur when one could describe so accurately the inputs, the transformation, and the outputs that one brain region could be replaced with an entirely synthetic component’.⁶⁷

In engineering terms, this understanding can be simply described as y = f (x), where x is the input, y is the output and f is the transformation.

According to David Marr, one can seek to understand a system at (at least) three complementary levels of analysis.⁷¹ He distinguished the computational, the algorithmic and the implementational level of analysis (Fig. 1A). The computational level is the most coarse-grained level of analysis. It asks what computational problem is the system seeking to solve, that results in the observed phenomena; in our context, phantom perceptions like tinnitus. This level of analysis is addressed by the fields of psychology and cognitive neuroscience. In contrast, the implementational level represents the most fine-grained description of a system. Here, the system’s concrete physical layout is analysed. In computer science and engineering, this corresponds to the exact hardware architecture and the individual software realization, with a particular programming language. In the brain, where there exists no clear distinction between software and hardware (or wetware), this level of description corresponds to the structural design of ion channels, synapses, neurons, local circuits and larger systems, and the physiological processes these components are subject to. This level of analysis can be considered as the hallmark of physiology and neurobiology. Finally, the algorithmic level takes an intermediate position between the previously described levels. It is about which algorithms—that are physically realized at the implementational level—the system employs to manipulate its internal representations, in order to solve the tasks and problems identified at the computational level. In computer science, the algorithmic level would be described independently of a specific programming language by abstract pseudocode.

Indeed, there are ways of moving between the different levels of description, afforded by ‘cognitive computational models’⁹¹ and ‘cognitive computational neuroscience’.⁹² Thus, in both fields, cognitive processes are simulated or recapitulated in silico, however, cognitive computational neuroscience uses—in contrast to ‘cognitive computational models’—neural networks as basis of the simulations. Therefore, cognitive computational neuroscience gives us an idea how processing might work algorithmically in the brain. Note that the similar terms (cognitive computational neuroscience and cognitive computational models) reflect the long—and not always straight-forward—history of science of mind. Indeed, very recently the term cognitive computational neuroscience is more and more replaced by the term neuroAI.^93,94

We argue that analysis at the algorithmic level is most crucial to understand auditory phantom perceptions like tinnitus or Zwicker tone. Only by knowing the algorithms that underlie normal auditory perception, we will gain a detailed understanding of what exactly happens under certain pathological conditions such as hearing loss, and which processes eventually cause the development of tinnitus, so that we can mitigate or reverse these processes.

Which discipline addresses this level of analysis in tinnitus research? Computational neuroscience comes to mind immediately. However, in ‘good old-fashioned’ computational neuroscience, great efforts have been made to model the physiological and biophysical processes at the level of single neurons, dendrites, axons, synapses or even ion channels, leading to increasingly complex computational models. These models, mostly based on systems of coupled differential equations, can mimic experimental data in great detail. Perhaps the most popular among these models is the famous Hodgkin-Huxley model,⁹⁵ which reproduces the temporal course of the membrane potential of a single neuron with impressive accuracy. These types of models are of great importance to deepen our understanding of fundamental physiological processes. However, in our opinion, they also must be considered as belonging to the implementational level of analysis, since they merely describe the physical realization of the algorithms, rather than the algorithms themselves.

In the following section, we will discuss emerging research directions that speak to the algorithmic level of analysis in the context of tinnitus research.

The integration of artificial intelligence in tinnitus research

As we argued above, hypothesis testing alone does not lead to a mechanistic understanding. Instead, it needs to be complemented by the construction of task-pointing computational models, since only synthesis in a computer simulation can reveal the interaction of proposed components entailed by a mechanistic explanation, i.e. which algorithms are realized, and whether they can account for the perceptual, cognitive or behavioural function in question. As Nobel laureate and theoretical physicist Richard Feynman pointed out: ‘What I cannot create, I do not understand'.

Along these lines, one may consider extending the four goals of psychology, i.e. to describe, explain, predict and change cognition and behaviour,⁷² by adding a fifth one: to build synthetic cognition and behaviour. This is in the tradition of ‘Walter’s tortoises’,^96-99 one major attempt to build synthetic cognition and behaviour using analogue electronics. This approach could be revisited in the 21st century, using artificial deep neural networks.

As pointed out in previous publications,^69,100-103 these computational models can be based on constructs from AI, for example deep learning.^104,105 A related development in AI rests upon the explicit use of generative models, leading to formulations of action and perception, in terms of predictive coding and active inference. Examples of their application to auditory processing and hallucinations range from examining the role of certain oscillatory frequencies in message passing, through to simulations of active listening and speech perception.^106-112

Artificial deep neural networks are designed to solve problems clearly defined at the computational level of analysis, in our case auditory perception tasks like, e.g. speech recognition. These models are precisely defined at an algorithmic level, which is completely independent from any individual programming language or specific software library, i.e. the implementational level of analysis. Hence, these algorithms could, at least in principle, also be realized in the brain as biological neural networks. Once we have built such models and algorithms in computer simulations, we can subsequently compare their dynamics and internal representations with brain—and behavioural—data in order to reject or adjust putative models, thereby successively increasing biological fidelity.⁶⁹ Vice versa, the ensuing models may also serve to generate new testable hypotheses about cognitive and neural processing in auditory neuroscience.

As mentioned above, this research approach—combining AI, cognitive science and neuroscience—has been coined as CCN.⁶⁹ Furthermore, besides the advantages discussed above, this approach furnishes the opportunity for in silico testing of new, putative treatment interventions for conditions like tinnitus, prior to in vivo experiments. In this way, CCN may even serve to reduce the number of animal experiments.

However, we note that CCN of auditory perception is not only beneficial for neuroscience. As noted in Hassabis et al.,¹¹³ understanding biological brains could play a vital role in building intelligent machines, and that current advances in AI have been inspired by the study of neural computation in humans and animals. Thus, CCN of auditory perception may contribute to the development of neuroscience-inspired AI systems in the domain of natural language processing.¹¹⁴ Finally, neuroscience may even serve to investigate machine behaviour,¹¹⁵ i.e. illuminate the black box of deep learning.^116,117 However, so far, most AI research does not even attempt to mimic or understand the brain or biology in general.

In other neuroscientific strands, such as research on spatial navigation, the fusion of classical neuroscience and AI has already led to major breakthroughs and still promises further advances in the future.¹¹⁸ For example, Stachenfeld and colleagues developed a mathematical framework for the function of place and grid cells in the entorhinal-hippocampal system based on predictive coding.^119,120 On the other hand, researchers from Google DeepMind developed artificial agents based on Long-Short-Term-Memory (LSTM)^121,122 neurons, in which place and grid cells emerged automatically.¹²³ In another AI model, Gerum and coworkers¹²⁴ showed that spatial navigation in a maze could be achieved by very small neural networks, which are trained with an evolutionary algorithm and are evolutionary pruned.

Towards a unified model of tinnitus development

The hierarchy of the different tinnitus models

In the following section, we describe a path towards a CCN of tinnitus research. Thus, in a first step we have to go back to Labzebnik⁶⁷ and find a way to communicate efficiently and formally about various tinnitus models. Extant tinnitus models can be sorted by the different levels of analysis according to Marr and Poggio.⁷¹ This means that each model can be assigned to one or more of the three categories (Fig. 1B): implementational level (molecular mechanisms, synapses etc.), algorithmic level (how neural signals are translated to information processing) and computational level (what are the basic mathematical imperatives for processing; see also ‘What does it mean to understand a system?’).

The three levels of analysis can be easily illustrated with the Lateral Inhibition Model of tinnitus, which describes tinnitus as a result of decreased lateral inhibition^23,125 due to decreased cochlear input; e.g. caused by a noised-induced cochlear synaptopathy.⁶ Thus, the lateral inhibition model explains tinnitus on all different levels of description. The implementational level (see Marr’s level of analysis in Fig. 1A), which corresponds to the molecular mechanisms of lateral inhibition, is nearly fully understood. For example, in the DCN cartwheel cells release glycine to inhibit fusiform cells, which are excitatory.^126-128 The computational role of inhibition is to narrow the input range of the fusiform cells.¹²⁸ To provide such contrast enhancement via lateral inhibition, neurons surrounding a certain excitatory neuron, which receives auditory input, are inhibited. This wiring scheme ‘sharpens’ the tuning curves of neurons along the auditory pathway. The wiring scheme corresponds to the algorithmic level of analysis. The computational level of description is the mathematical description of decreased lateral inhibition. Thus, hearing loss leads to decreased input from the cochlea, which causes a decreased firing rate of the inhibitory neurons and thus to disinhibition of subsequent excitatory neurons. These properties can be easily written down in simple mathematical formulas. This means that the underlying mechanisms of the lateral inhibition model of tinnitus are fully understood from specific neurotransmitter processes to an abstract mathematical formulation. This is the goal of cognitive computational neuroscience. However, the fact that the model explains tinnitus manifestation on all scales does not say anything about the correctness of the model’s predictions. Indeed, a good model should be understood on all scales (implementational to computational), but it must also fit experimental observations, which is not the case in the Lateral Inhibition Model. Other models trying to explain tinnitus do not provide full explanatory power.

The thalamic bursting theory—which proposes that bursting neurons in the thalamus cause tinnitus—has a valid explanation for the origin of the spike bursts (low threshold calcium spikes, for details see Jeanmonod et al.⁶⁰). However, it remains elusive, in terms of how these bursts cause tinnitus. Other top-down models—such as the predictive coding model,⁵² based on the Bayesian Brain theory—provide a valid mathematical description of the proposed mechanisms, but do not provide a full explanation of how the Bayesian statistics can be implemented in a neural network and thus in the brain.¹²⁹ However, there exist some first approaches toward neural networks for Bayesian inference which will ultimately prove possible, but are still not fully developed.^130-132 Other tinnitus models describe macro-phenomena such as the thalamo-cortical dysrhythmia,⁵⁹ or describe tinnitus as a result of overlapping neural circuits.⁶³ Those models are phenomenological, but do not provide a mathematical description and thus are difficult to falsify or test in silico.

A critical role of stochastic resonance and central noise

In the following paragraph we provide an in-depth discussion of central noise and central gain, as possible causes for tinnitus, and consider how to adjudicate between—or combine—these two theories. To discuss these two models and their relationship, it is necessary to introduce a proper nomenclature. Thus, in the following we refer to the mathematical description of Zeng, who describes central gain as a linear amplification factor g, which increases the input signal I (s = subjectively perceived loudness respectively evoked neural activity; cf. Chrostowski et al.³²). Central noise N is a further additive term^33,133 (Eq. 1).

$$s=\mathit{g}\cdot I+\mathit{N}$$ (1)

Central gain increase is a collective term summarizing all mechanisms that lead to an increased amplification of the input signal (I) along the auditory pathway (for an extensive review, see Auerbach et al.¹³⁴). Therefore, the term central gain increase can refer to a decrease in inhibitory synaptic responses, an increase in excitatory synaptic responses, as well as enhanced intrinsic neuronal excitability.¹³⁴ All of these mechanisms cause a multiplicative amplification of the input signal (amplification factor: g). To sharpen the scientific language, it is necessary to distinguish between the observable effect (central gain increase) and the underlying neuronal principles (e.g. homeostatic plasticity^27,134). Central gain increase could be caused by homeostatic plasticity, which means that the average spike rate of affected neurons—after a decrease of neuronal input due to a hearing loss—is kept constant by plastic changes of the system (e.g. enhanced intrinsic excitability, synaptic scaling, meta-plasticity¹³⁴). Central gain and homeostatic plasticity are often used as synonyms in the context of tinnitus models, although they describe the problem on different levels.

The central noise model—in contrast to the central gain model—describes tinnitus as a consequence of increased spontaneous activity, which is added to the input signal (additive term, N).³³ In analogy to the relation of central gain and homeostatic plasticity, the underlying principle of the central noise model is stochastic resonance.^135-137 The original central noise model of Zeng from 2013 was exclusively based on psychophysical considerations and measurements, which means that the term s in Eq. 1 was meant to be the subjectively perceived loudness.³³ Furthermore, the original model makes no statements on the nature of the central noise, or on higher brain functions such as thalamic gating or predictive coding etc., and thus provides no explanation what the neuronal signal looks like and why an addition of noise causes an ongoing conscious percept.

The novelty of the stochastic resonance model is based on the idea that the abstract concept of an additive central noise can be interpreted as real intrinsically generated neural noise, which increases hearing ability by exploiting the stochastic resonance effect. Thus, the term s in Eq. 1 is re-interpreted as actual neural activity.

We categorized the stochastic resonance model^18,35,37 as an algorithmic level model on Marr’s scale (Fig. 1), which means that the calculations (Eq. 1 and the calculation of the autocorrelation function, cf. below) necessary to leverage the stochastic resonance effect should be linked to the neural substrate of the auditory pathway. This corresponds to the implementational level according to Marr. The stochastic resonance model (Fig. 2) is based on the idea that the auditory system continuously optimizes sensitivity via a feedback loop, which adapts the amplitude of the additive noise (central noise) to maximize information transmission. The information transmission is quantified via the autocorrelation of the signal.^18,35 Thus, one might call the inverse autocorrelation function the cost-function to be minimized. However, to calculate the autocorrelation of the signal, so-called neuronal delay lines are needed, which are prominent in two brain regions the cerebellum and the DCN.¹³⁸ The mechanism behind the auto-correlation calculation based on delay lines is based on the fact that the signal transmission is slowed down by the delay line through inter-neurons or unmyelinated nerve fibres.⁴² Thus, the delayed signal is then compared to the same signal at a later time point, which was not delayed. The delay serves the purpose to generate a time shift (in mathematical formulation of auto-correlation function commonly termed as lag-time τ), which allows us to compare one signal stream at several time points with itself.^139,140

Figure 2.

Stochastic resonance model of tinnitus induction. In the healthy auditory system, the input signal (A) can pass the detection threshold resulting in a supra-threshold signal as output (B). In case of hearing loss, the input signal remains below the threshold (C), resulting in zero output. However, if the optimum amount neural noise (D) is added to the weak signal, then signal plus noise can pass the threshold again (E), making a previously undetectable signal, detectable again (F). The optimum amount of noise depends on the momentary statistics of the input signal and is continuously adjusted via a feedback loop. This processing principle is called adaptive stochastic resonance.

Another strong argument for the validity of the stochastic resonance model is the fact that otherwise there is no plausible explanation for the cross-modal input from the somatosensory system to the DCN,^141,142 except the notion that the somatosensory system serves as the noise-generator of the stochastic resonance feedback loop.¹⁸ It is common knowledge that—for the stochastic resonance effect—the exact spectral composition of noise is irrelevant.^92,143 This suggests spontaneously firing neurons in the somatosensory system are sufficient to trigger the stochastic resonance effect. In summary, the theoretical construct of an information transmission maximizing feedback can be mapped onto certain neuronal structures, with an architecture that is sufficient to perform the requisite calculations.

The whole stochastic resonance model is an intra-frequency channel model, which means that cross-talk between different frequency channels is not necessary to explain the emergence of tinnitus. As already described above, tinnitus is highly related to frequency channels, which are impaired by e.g. synaptopathy in the cochlea and a resulting (hidden) hearing loss.¹⁴ Frequencies are represented tonotopical along the whole auditory pathway up to the auditory cortex.¹⁴⁴ Thus, it seems plausible that the amplitude of the neural noise added to each frequency channel of the DCN is tuned individually. Such a channel-wise optimization of the noise amplitude is the simplest explanation according to Occam’s razor and provides a plausible explanation for the fact that the tinnitus pitch is highly correlated to impaired frequency channels.³⁷

Tinnitus as a result of multiplicative central gain or additive central noise?

Central gain increase and central noise increase cannot be fully decoupled, for example, an increased excitability of neurons along the auditory pathway caused by homeostatic plasticity automatically leads to an amplification of neural noise. The fact that the additive neural noise (central noise) is amplified (central gain) along the auditory pathway is a direct consequence of the neuroanatomy of the auditory system. As the neural noise is already added in the DCN¹⁸ being the first processing stage of the auditory pathway, multiplicative amplification (central gain) has necessarily an effect on the noise.¹⁴⁵

Thus, Eq. 1 could be altered so that the amplification factor also has an effect on the central noise:

$$\mathit{s}=\mathit{g}\cdot (\mathit{I}+\mathit{N})$$ (2)

As described above, the homeostatic plasticity mechanisms mediating central gain increase have been implicated in tinnitus generation,¹⁴⁶ however, these mechanisms are simply too slow to explain acute tinnitus phenomena after a noise trauma caused by a sudden loud stimulus.¹⁴⁷

In contrast, neural circuits operating on faster time scales can explain acute tinnitus: namely, tinnitus is caused by a subcortical feedback loop adapting neural noise input into the auditory system.³⁵ As described above and illustrated in Fig. 2 we suggest that stochastic resonance plays a critical role in not only generating tinnitus but also restoring hearing to a certain degree.^18,34,36

To illustrate this role, we interpret Eq. 2 in a classical signal detection task, in which the neural signal(s) has to reach a threshold for the input signal I to be detected.

In cases of hearing loss, the input I is effectively reduced. Therefore, to reach the same neural threshold, one could increase either the central noise N, or the central gain g, or both. Because increasing gain results in a squared increase in variance,¹³³ which increases the difficulty of signal detection, it is not the most economical means of compensating for hearing loss in cognitive neural computation (e.g. Occam’s razor). Instead, it makes sense to add internal neural noise to lift weak input signals above the sensory threshold by means of stochastic resonance.^135-137 In traditional stochastic resonance, a non-linear device such as hard thresholding and periodic signals, are needed.¹³⁶ Recently, it has been shown that autocorrelation can serve as an estimator for the information content of the signal, even if it is non-periodic.³⁵

The critical role of stochastic resonance is supported by broad empirical evidence: first, additional intrinsic neural noise^18,41 as well as external acoustic noise³⁸ can improve pure-tone hearing thresholds by ∼5 dB. However, this 5 dB threshold decrease (i.e. improvement) does not explain why this mechanism is evolutionary advantageous, as the cost of a potentially annoying and morbid tinnitus perception may be high. In a computational model, it has been shown that frequency-specific intrinsic neural noise has the potential to significantly improve speech recognition by a far larger amount (up to a factor of 2).⁴⁹ This improvement in speech comprehension and the perception of complex sounds—which could also be important for orienting animals as warning sounds—could be an explanation for the emergence of this mechanism in our auditory system during evolution. Furthermore, a significantly improved speech perception could have major positive effects and might contribute to a decreased cognitive decline in elderly people.^148,149

In recent studies, the fact that different modalities exploit stochastic resonance to improve the signal has been proven.^40,150 It seems that stochastic resonance and especially cross-modal stochastic resonance is a universal principle of sensory processing.³⁶

Second, central noise is needed to stabilize a biological system. Zeng showed that ‘mathematically, the loudness at threshold is infinite when the internal noise is zero (c = 0), and vice versa. This is a fundamental argument for why the brain has or needs internal noise because infinite loudness is clearly biologically unacceptable’.¹⁵¹

Third, as described above, the central noise model based on the stochastic resonance mechanism provides a mechanistic explanation for the purpose of the somatosensory projections to auditory nuclei such as the DCN.^142,152,153 In fact, very recently, Koops and Eggermont argued that ‘increased and uncorrelated noise, potentially the result from a noise source outside of the auditory pathway’³⁴ might play a major role in tinnitus development. Potentially, this somatosensory input is nothing else than intrinsically generated neural noise, which is modulated in the DCN to leverage stochastic resonance in the auditory system. This theory accords with the finding that tinnitus can be modulated by somatosensory input like, e.g. jaw movement.^154-156 Furthermore, tinnitus development can be prevented^157-160 or suppressed^158-160 by the presentation of external acoustic noise, which works best when the noise spectrum covers the impaired frequencies and the tinnitus pitch.^158-160 In a recent study, a novel approach was developed combining somatosensory stimulation with auditory stimulation, to modulate the tinnitus loudness.¹⁶¹ Finally, it has been demonstrated that electrotactile stimulation of the fingertips enhances cochlear implant speech recognition in noise,¹⁶² Mandarin tone recognition¹⁶³ and melody recognition.¹⁶⁴ While the authors did not make any mention of stochastic resonance or internal noise, it is a reasonable assertion that the observed effect might have acted via cross-modal stochastic resonance.³⁶

These arguments suggest that tinnitus is indeed caused by additive neural noise (central noise) instead of a multiplicative gain. Central gain induced tinnitus would be characterized by increased evoked activity along the auditory pathway in tinnitus patients. Thus, auditory brainstem responses should have higher amplitudes in tinnitus patients compared to control patients. However, an increased evoked activity in tinnitus was refuted in several recent human patient as well as in animal studies.^165-168 Increased evoked neural activity is related to hypersensitivity against mild sounds, the so-called hyperacusis. Thus, increased central gain is potentially a better fit to explain hyperacusis rather than tinnitus.^167,168

Hyperacusis could be one missing key to disentangle central noise and central gain adaptations of the auditory system.

As described above, central gain and central noise cannot be fully disambiguated (Eq. 2) as both auditory input and added neural noise is amplified via homeostatic plasticity along the auditory pathway. Therefore, tinnitus severity should correlate with amplification along the auditory pathway, which means that tinnitus severity should be highly correlated with the hyperacusis severity. This correlation was found in 2020 by Cederroth and coworkers.¹⁶⁹ In summary, the three findings that first tinnitus patients without hyperacusis show no increase in evoked activity,^165,167 second hyperacusis patients show increased evoked activity¹⁶⁷ and third tinnitus severity correlates with hyperacusis,¹⁶⁹ are a strong indication for the theory described above. To put the theory in a nutshell: central noise increase causes tinnitus, central gain increase causes hyperacusis, and central gain increase does not just cause hyperacusis but also amplifies the neural noise perceived as tinnitus.

Tinnitus and the Bayesian brain

The combined central gain and the central noise model provides a sophisticated and mathematically well developed explanation for the tinnitus-related neural hyperactivity in the brainstem. However, these theories do not explain why this hyperactivity is transmitted through the thalamus and induces a conscious experience. Indeed, there exist several mechanisms in the brain that are supposed to prevent ongoing neural activity to be transmitted to the cortex¹⁷⁰ and becoming a conscious and disturbing auditory percept. Up to now it is unclear why these mechanisms fail to do so. Furthermore, the stochastic resonance model does not make predictions on tinnitus heterogeneity. In particular, tinnitus is probably always caused by hearing loss, but hearing loss does not necessarily lead to tinnitus.¹⁷¹ Additionally, the stochastic resonance model predicts that hearing aids should at least milden tinnitus, due to a downregulation of added neural noise in the DCN control circuit. However, while this is true for some patients, hearing aids do not milden tinnitus in all patients,¹⁷² and this heterogeneity is not covered by the stochastic resonance model.

In the following, we provide an explanation of how and why the added central noise bypasses the filter mechanism of the brain and how this might also deliver solution approaches to the problem of tinnitus heterogeneity.

The only model with a solid mathematical background dealing with these issues is the sensory precision model from Sedley et al.,⁵² which is based on the algorithmic formulation of predictive coding within the computational ‘Bayesian brain’ hypothesis.^{53,65,129,173-175} Bayesian formulations of predictive processing are based on the Bayes theorem (Eq. 3)^176,177 that describes, mathematically, how to update beliefs in the light of new incoming information. Furthermore, this account also proposes a solution to other paradoxical evidence from the tinnitus literature, including that certain types of brain activity linked to perception (gamma oscillations) can show both positive and negative correlations with perceived tinnitus loudness, depending on how tinnitus loudness is manipulated.¹⁷⁸

$$p(x|o)\propto p(o|x)p(x)$$ (3)

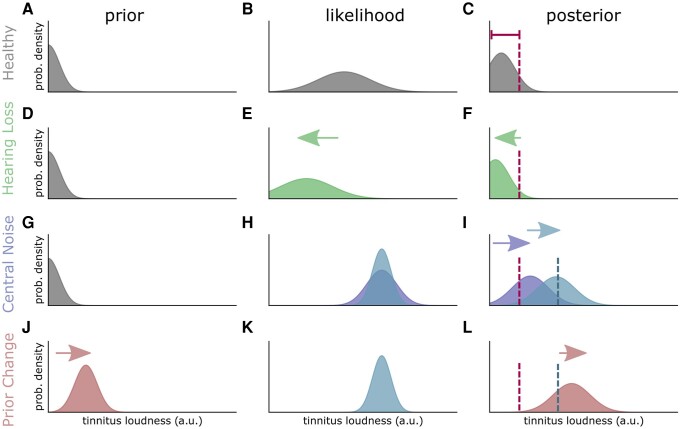
Here, o corresponds to observations (e.g. sensorineural responses) and x to their inferred causes (e.g. auditory loudness). In this context, the brain is continuously updating its posterior belief distribution p(x|o) about actual sound intensity x, given auditory afferents or observations o. This update is achieved by combining the prior expectations p(x) (Fig. 3A), descending from the higher regions of the processing hierarchy, with sensory input—reporting the likelihood or sensory evidence—ascending from below [p(o|x), Fig. 3B]. ‘Likelihood’ refers to the probability that the pattern of sensory input indicates a particular underlying sensory event or cause. In the healthy system (no hearing loss, Fig. 3A–C) the default prediction (prior, Fig. 3A) would be that there is no auditory input. In silence, the likelihood is a broad distribution with a low mean (Fig. 3B), as there is exclusively spontaneous activity. This spontaneous activity has been termed a ‘tinnitus precursor’, which usually has a low precision and is therefore not interpreted as auditory input. Reducing sensory precision is also called sensory attenuation. However, if the precision of the tinnitus precursor increases (or, sensory attenuation is insufficient) then the posterior shifts to the perception of a sound, and tinnitus occurs.

Figure 3.

Predictive coding model of tinnitus induction. The posterior (represents the percept) is the product of the likelihood (bottom-up neuronal signal) and the prior (top-down prediction of the auditory input). The predictive coding hypothesis of tinnitus development is formalized in the Bayesian brain framework. The brain predicts the likelihood of the occurrence of a certain auditory input loudness [p(x), x: model] in one certain frequency channel. The prior (prediction) is based on the experiences on how often certain auditory stimuli occurs and has nothing to do with the present neuronal signal coming from the cochlea. In the healthy case the prior distribution has a low mean (standard auditory input is zero, A). The likelihood p(o|x) (B) represents the bottom-up signal, respectively, the measurements of the sensor (cochlea and brainstem). The posterior is the probability that under the condition of one particular neuronal signal (spike rate) a certain stimulus loudness is the cause of that neural activity. In the healthy case, the low spontaneous activity (B) is most probably the consequence of the absence of an auditory input. The effect that low spontaneous activity (with low precision) is assumed to be the consequence of no auditory input is called sensory attenuation (C, left side of the dashed curve). Decreased cochlear input due to hearing loss (D) shifts the likelihood (E) and consequently the posterior (F) to lower values, which means that a hearing loss does not directly cause tinnitus. Central noise (G) increases the spontaneous activity and thus increases the mean of the likelihood (H, dark blue distribution). The product of p(x) and p(o|x) is shifted to higher values (I, dark blue). Potentially, the precision of the likelihood is also increased (lower variance) through the central noise effect (H, cyan distribution), which further shifts the posterior to higher values (I, cyan), as the mean of the product of the probabilities is weighted with the precision. The increased neuronal activity is interpreted as auditory input, which means that there is a tinnitus percept. This effect can be amplified, as the continuous change of neural activity (through central gain and central noise) leads to continuous miss predictions. The prediction error between prior [p(x)] and likelihood [p(o|x)] is decreased by adapting the prior (J). Therefore, tinnitus becomes the standard prediction, which further manifests the phantom percept (L). The effect might be the correlate of chronic manifestation of tinnitus.

The occurrence of an external sound (evoked response) shifts the likelihood to higher values and the precision of the likelihood rises, as neuronal activity encoding a certain loudness level is generated, with a high precision. Therefore, the posterior belief is—although the prior predicts no input—that there is an auditory input, as precise sensory evidence shifts the posterior to higher values.

Starting from this configuration, the predictive coding model of tinnitus development can be structured in three main steps: (i) hearing loss (Fig. 3D); (ii) compensation of hearing loss through stochastic resonance and central gain; and (iii) increased precision of this spontaneous central noise (tinnitus precursor). A fourth step is thought to result in tinnitus becoming chronic, which is adjustment of auditory priors (shifting away from ‘silence’ as the default, to expecting a tinnitus-like sound); this allows the tinnitus precursor to be perceived even at relatively low precision levels, as it shows some concordance with auditory priors. The first step is hearing loss, which means that there is loss of precise input from the cochlea. Thus, the activity of the neurons along the auditory pathway is attenuated, which means that the likelihood becomes less precise in relation to the posterior (Fig. 3E). Thus, the posterior is shifted to lower values (Fig. 3F), and things are perceived as quieter or silent. This means that hearing loss and predictive coding alone are not sufficient to explain tinnitus. In a next step, the decreased input through hearing loss is compensated by adding neural noise by means of stochastic resonance (Fig. 3G). This means that the mean of the likelihood [p(o|x) in Eq. 4, Fig. 3H, dark blue distribution] is increased as neural activity (N in Eq. 2) is added to auditory input through the mechanism of stochastic resonance. This effect is further increased by the central gain amplification along the auditory pathway (g in Eq. 2, likelihood Fig. 3H, cyan distribution), further amplifying tinnitus loudness (posterior belief: Fig. 3I). There are good reasons to assume that the precision of the neuronal signal is increased through subcortical phenomena: as described above, internal neural noise is not comparable with the pressure fluctuations (white uncorrelated acoustic noise) used to lift subthreshold auditory signal above the detection threshold, as shown be Zeng and coworkers.³⁸ Thus, noise increase might entail the addition of regular spike trains. Therefore, as the stochastic resonance feedback loop optimizes for a certain noise amplitude with low variance the precision of the likelihood might be increased (note that stochastic resonance is not limited to any particular noise^92,143). Nevertheless, it is not obvious that central noise increases the sensory precision. The addition of regular spike trains or patterns to the cochlear signal might cause the system to run in an attractor. The number of possible neural states is limited as the neural noise causes a continuous activity and makes low-activity states very unlikely. This is in line with the therapeutic approaches of Tass and Popovych,¹⁷⁹ who tried to get out of this neuronal attractor by presenting acoustic stimuli. An amplification through central gain in contrast to an additive noise might have the opposite effect, as a multiplicative term would increase the number of possible neural activity patterns. This fact indicates that central noise is a better complement to the predictive coding model of tinnitus development. It is an upcoming challenge and important milestone to unravel the exact neuronal patterns that fulfil the properties described above.

Besides the fact that the increased spontaneous activity through central noise and central gain mechanisms changes the likelihood, it also leads to continuous prediction errors. Therefore, the final part of the model is an update of the prior (Fig. 3J). Thus, the prior is shifted to higher input loudness values to minimize the error between likelihood and predictions (Fig. 3K). Physiologically, any accompanying increase in the precision of these priors is usually associated with an increase in the postsynaptic gain or excitability of neuronal populations reporting prediction errors (usually superficial pyramidal cells in the cortex). See Benrimoh et al.,¹⁰⁷ Bastos et al.,¹⁷³ Adams et al.,¹⁸⁰ Friston et al.,¹⁸¹ Kanai et al.,¹⁸² Shipp¹⁸³ and Sterzer et al.¹⁸⁴ for a predictive coding account of neuronal message passing and the role of precision weighted prediction errors in hallucinatory phenomena.

In short, the result is that the presence of auditory input becomes the new default prediction and shifts the posterior to higher values (Fig. 3L). This final step could be the correlate of tinnitus and might explain why—in some patients—the restoration of hearing through, e.g. hearing aids does not cure tinnitus.

An important question is why divergent behaviour should occur in optimally functioning systems such as those involved in stochastic resonance and predictive coding; i.e. why should similar conditions, such as hearing loss, result in accepting central noise as a percept in some cases but not others. To address this, we must consider that what is ‘optimal’ varies according to the hierarchical level concerned, and the situational context. With regard to hierarchical level, accepting central noise as a percept reduces prediction error at the lower hierarchical level where the noise is generated, but (at least initially) results in the introduction of a prediction error at higher hierarchical levels by introducing an unexpected percept. Thus, the balance of priority between hierarchical levels may help to explain the emergence (or non-emergence) of tinnitus in different instances. Regarding wider context, we consider here stress as one example; in certain stressful situations, one is hypervigilant to a broad range of sensory inputs, particularly those which might indicate potential threats, which can include novel or previously unanticipated ones. Such stress can be considered a relative shift of precision away from sensory priors, towards sensory likelihoods. This might explain the initial onset of tinnitus during stress, which has been reported.¹⁸⁵ However, once default sensory priors have adjusted to accept tinnitus, the conflict between hierarchical levels disappears, as low-level likelihood and high-level prediction become concordant.

Conclusion and outlook

In conclusion, the combination of the process theory of central noise increase and adaptive stochastic resonance—as a bottom-up mechanism—together with the computational model of predictive coding—as a complementary top-down mechanism—provides an integrated explanation of tinnitus emergence. Here, bottom-up refers to the overall information flow, i.e. modification of signals originating from lower brain structures, like the cochlear nucleus and primary auditory cortex. It is important to note that this does not imply that the predictive coding framework is solely top-down or that the stochastic resonance model is solely bottom-up.

Furthermore, the models provide a mathematical framework, which can be used to make quantitative predictions that can be tested through novel experimental paradigms, e.g. for the calculation of the autocorrelation function, specific neuronal delay-lines are needed. As the neuroanatomy along the auditory pathway is mostly known, one could calculate how long specific delay lines are and if they fit this hypothesis. Furthermore, one can look specifically for the noise generator—most probably in the somatosensory system—and characterize, e.g. the spectral composition of its output. Independent of these predictions, since both stochastic resonance and predictive coding as universal processing mechanisms are ubiquitous in the brain, we speculate that the presented integrative framework may extend to the perception of other sensory modalities and even beyond to certain aspects of cognition and behaviour in general.

A current challenge is a network theory of predictive coding, which explains how these computations are implemented in the brain.¹²⁹ Several studies have attempted to place predictive coding in the larger context of Bayesian belief updating in the brain.^{173,181,183,186-188} Furthermore, to unravel the exact characteristics of the neural noise necessary to significantly decrease sensory precision, is an important challenge that needs to be addressed in future studies.

Our integrated model of auditory (phantom) perception demonstrates that the fusion of computational neuroscience, AI and experimental neuroscience leads to innovative ideas and paves the way for further advances in neuroscience and AI research. For instance, novel evaluation techniques for neurophysiological data based on AI and Bayesian statistics were recently established,^189-192 the role of noise in neural networks and other biological information processing systems was considered^193-196 and the benefit and application of noise and randomness in machine learning approaches was further investigated.^49,197,198 On the one hand, the fusion of these complementary fields may evince the neural mechanisms of tinnitus (CCN⁶⁹) and information processing principles that underwrite functional brain architectures. On the other hand, neuroscience-inspired AI¹¹³ may accelerate research in machine learning. We hope that the four major steps towards a CCN of tinnitus, i.e. (i) finding an exact language; (ii) developing a mechanistic theory; (iii) testing the methods in fully specified test systems; and (iv) merging AI with computational and experimental neuroscience, will afford novel opportunities in tinnitus research.

Funding

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation): grant KR5148/2-1 (project number 436456810) to PK, grant KR5148/3-1 (project number 510395418) to P.K., grant GRK2839 (project number 468527017) to P.K., grant SCHI 1482/3-1 (project number 451810794) to A.S., grant TZ100/2-1 (project number 510395418) to K.T. Additionally, P.K. was supported by the Emerging Talents Initiative (ETI) of the University Erlangen-Nuremberg (grant 2019/2-Phil-01), and K.F. is supported by funding for the Wellcome Centre for Human Neuroimaging (Ref: 205103/Z/16/Z) and a Canada-UK Artificial Intelligence Initiative (Ref: ES/T01279X/1). Furthermore, the research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (ERC Grant No. 810316 to A.M.).

A.M.: ERC Grant No. 810316. A.S.: DFG grant SCHI 1482/3-1 (project number 451810794). K.F.: Wellcome Centre for Human Neuroimaging (Ref: 205103/Z/16/Z); Canada-UK Artificial Intelligence Initiative (Ref: ES/T01279X/1). K.T.: DFG grant TZ100/2-1 (project number 510395418). P.K.: DFG grant KR5148/2-1 (project number 436456810); DFG grant KR5148/3-1 (project number 510395418); DFG grant GRK2839 (project number 468527017); Emerging Talents Initiative (ETI) of the University Erlangen-Nürnberg (grant 2019/2-Phil-01).

Competing interests

The authors report no competing interests.