Intent-to-treat (ITT) effects are typically the parameter of interest in randomized clinical trials (RCTs) (1–5). But ITT estimands have drawbacks, particularly when adherence is low. Thus, complementing estimates of ITT effects with estimates of per-protocol effects—the effect of receiving the assigned protocol through the duration of the study—is often useful (6–8).
For example, the ITT estimate from the Feeding America Intervention Trial for Health—Diabetes Mellitus (FAITH-DM) did not find that the intervention reduced hemoglobin A1c (HbA1c) at 6 months (difference in HbA1c between intervention and comparison group = 0.24%; 95% confidence interval (CI): –0.09, 0.58) (9). However, as with many interventions meant for low-income populations, the same conditions that prompted intervention made adherence difficult. Thus, presenting only ITT estimates does not address whether the intervention works as intended when adhered to, or whether refinements to overcome additional barriers may be useful (10). Estimates of per-protocol effects can help answer this question. Here, we provide an example of estimating time-fixed per-protocol effects and compare several different estimators, including doubly robust estimators, which have seldom been used in this setting.
METHODS
The FAITH-DM trial
The FAITH-DM trial has been described (Clinicaltrials.gov: NCT02569060) (9). Briefly, FAITH-DM was a 6-month RCT conducted in 3 Feeding America food banks (with 27 affiliated food pantries), located in Oakland, California; Detroit, Michigan; and Houston, Texas. The goal was to determine whether supplying self-management support and diabetes-appropriate food through food pantries would improve glycemic control in those with type 2 diabetes mellitus (T2DM). Between October 2015 and September 2016, 568 food pantry clients were enrolled and randomized 1-to-1 to receive the intervention or usual care. The primary outcome was HbA1c ascertained at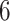 
months after enrollment. Institutional review board approval for this analysis was provided by the University of California, San Francisco, Human Research Protection Program.
Per-protocol effects
Full and partial intervention engagement was defined a priori for both arms (see Web Appendix 1, available at https://doi.org/10.1093/aje/kwad156) (9). To estimate the time-fixed per-protocol effect for full engagement, we account for variation in participant engagement level and informative loss to follow-up (7, 11). The parameter of interest was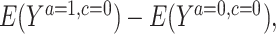 
where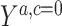 
is the potential HbA1c in treatment arm 
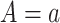under no censoring (details provided in Web Appendix 1).
Identification of the parameter of interest from observed data requires 3 standard assumptions: causal consistency (11, 12), conditional exchangeability (13), and positivity (14). Here, the parameter of interest might not be identified due to violation of conditional exchangeability because we had to restrict covariates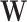 
due to positivity violations (15). Further evaluation of identification assumptions can be found in Web Appendix 1, Web Tables 1 and 2, and Web Figures 1–4.
Estimation
We estimated the per-protocol effects using g-computation (16, 17), inverse probability weighting (IPW) (11), augmented IPW (AIPW) (18), and targeted maximum likelihood estimation (TMLE) (19). For each approach we specified models for the outcome-covariate mechanism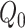 
(g-computation), intervention mechanism 
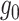(IPW), or both (AIPW, TMLE). Estimators were fitted separately, stratified by intervention arm (Web Appendix 1). Missing outcome data were accounted for through estimation methods, and missing baseline covariate data, 
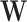, were imputed using multiple imputation with chained equations (see Web Appendix 1), using the “mice” package (20).
All analyses were performed using R, version 4.0.3 (R Foundation for Statistical Computing, Vienna, Austria; see Web Appendix 2 for code).
RESULTS
Participant characteristics
The mean age of the 568 trial participants was 54.8 years, and the mean baseline HbA1c was 9.75% (Web Table 3). Most participants were female (67.6%), identified as Hispanic/Latino or non-Hispanic Black/African American race or ethnicity (83.8%), and were food insecure (68.7%). Forty-five (16%) participants in the intervention arm had full engagement, 29 (10%) participants had partial engagement, 149 (52%) had low engagement, and 62 (22%) were lost to follow-up. In the usual care arm, 224 (79%) participants were fully engaged and 59 (21%) participants were lost to follow-up. Those who were fully engaged in the intervention were more likely to be older, of male sex, of Hispanic or Latino ethnicity, and have less education (Web Table 4). Web Tables 3–5 and Web Figure 5 present additional results.
Full engagement
Had all participants been fully engaged and retained in follow-up, the mean HbA1c level at 6 months in the intervention arm, as estimated by TMLE, would have been 8.63%, (95% CI: 8.12, 9.14) (Table 1). The mean 6-month HbA1c estimate for the control arm was 8.99% (95% CI: 8.73, 9.26). This translated to a TMLE per-protocol average treatment effect estimate of −0.37% (95% CI: −0.94, 0.21), a point estimate that favors the intervention. Results were similar across the 4 estimators. The treatment effect estimate was closest to the null for the IPW estimator (−0.26%, 95% CI: −0.86, 0.33), and IPW had the largest bootstrapped standard error. Bootstrapped standard errors were smallest for AIPW.
Table 1.
Estimates of 6-Month Hemoglobin A1c According to Trial Arm and Average Treatment Effect Using 4 Different Estimators in the Feeding American Intervention Trial for Health—Diabetes Mellitus (Detroit, Michigan; Houston, Texas; and Oakland, California), 2015–2016a
| Estimator | Mean (SE b ) HbA1c, Intervention | 95% CI | Mean (SE b ) HbA1c, Control | 95% CI | ATE (SE b ) | 95% CI |
|---|---|---|---|---|---|---|
| Intent-to-treatc | 9.12 | 8.88 | 0.24 (0.17) | −0.09, 0.58 | ||
| Per-protocol, full engagementd,e | ||||||
| G-computation | 8.60 (0.26) | 8.09, 9.11 | 9.02 (0.13) | 8.76, 9.28 | −0.42 (0.29) | −0.98, 0.14 |
| IPW | 8.61 (0.27) | 8.09, 9.14 | 8.98 (0.14) | 8.71, 9.25 | −0.26 (0.31) | −0.86, 0.33 |
| AIPW | 8.50 (0.25) | 8.00, 8.99 | 8.86 (0.13) | 8.60, 9.12 | −0.37 (0.28) | −0.91, 0.18 |
| TMLE | 8.63 (0.26) | 8.12, 9.14 | 8.99 (0.14) | 8.73, 9.26 | −0.37 (0.29) | −0.94, 0.21 |
| Per-protocol, partial/full engagementd | ||||||
| G-computation | 8.82 (0.18) | 8.46, 9.17 | 9.02 (0.13) | 8.76, 9.28 | −0.20 (0.21) | −0.62, 0.22 |
| IPW | 8.86 (0.19) | 8.49, 9.23 | 8.98 (0.14) | 8.71, 9.25 | −0.01 (0.24) | −0.49, 0.46 |
| AIPW | 8.69 (0.17) | 8.35, 9.03 | 8.83 (0.13) | 8.57, 9.10 | −0.14 (0.21) | −0.54, 0.26 |
| TMLE | 8.84 (0.18) | 8.49, 9.20 | 8.99 (0.14) | 8.73, 9.26 | −0.15 (0.22) | −0.58, 0.28 |
Abbreviations: AIPW, augmented inverse probability weighting; ATE, average treatment effect; CI, confidence interval; HbA1c, hemoglobin A1c; IPW, inverse probability weighting; SE, standard error; TMLE, targeted maximum likelihood estimation.
a Results with and without weight truncation to 25 were equivalent to the second decimal, and therefore only one set of results across estimators and engagement is presented.
b SEs obtained using nonparametric bootstrap over B = 3, 000 nonparametric bootstrap estimates, each with M = 50 imputations.
c Estimates obtained from Seligman et al. (9).
d Models adjusted for sex, baseline HbA1c, food security, depression, age, race/ethnicity (3 categories with “other” set to missing), and education.
e Note n = 11 bootstrap resamples missing due to model nonconvergence within that sample for per-protocol, full engagement estimates only.
Full or partial engagement
The TMLE-estimated mean 6-month HbA1c in the intervention arm, had everyone been at least partially engaged and not lost to follow-up, was 8.84% (95% CI: 8.49, 9.20). In the control arm, the TMLE-estimated mean 6-month HbA1c was 8.99% (95% CI: 8.73, 9.26). Thus, the TMLE per-protocol average treatment effect estimate was −0.15% (95% CI: −0.58, 0.28), again favoring the intervention. Estimates of the mean 6-month HbA1c in each trial arm were similar across the 4 estimators.
Across the 3 analyses (ITT vs. per-protocol with partial/full engagement vs. per-protocol with full engagement), the standard errors increased (0.17 vs. 0.22 vs. 0.29), and were the highest for the full-engagement per-protocol effect, which was expected due to progressively decreasing effective sample sizes. This trend is observed in the width of the 95% CIs in Figure 1 (and in the distribution of estimates from the bootstrap resamples, Web Figures 3 and 4).
Figure 1.
Comparisons of the intent-to-treat and per-protocol effects, estimated using targeted maximum likelihood estimation, under 2 definitions of trial engagement in the Feeding America Intervention Trial for Health—Diabetes Mellitus (Detroit, Michigan; Houston, Texas; and Oakland, California), 2015–2016. HbA1c, hemoglobin A1c.
DISCUSSION
We illustrated how to estimate per-protocol treatment effects for 2 different a priori levels of engagement/adherence compared with ITT, using 4 different estimators (g-computation, IPW, AIPW, and TMLE) in the Feeding America Intervention Trial for Health—Diabetes Mellitus. Secondary subgroup analyses of the FAITH-DM trial showed that those in the intervention arm who fully engaged in the trial had lower 6-month HbA1c levels than those who were not fully engaged (8.60% vs. 9.24%; P = 0.02) (9). These types of “per-protocol” subgroup analyses, restricted to those who fully engage in the intervention, are subject to possible collider-stratification bias because they condition on participant engagement, a postrandomization variable (21). The per-protocol analyses we present here appropriately account for this issue. We observed a dose-response trend (Figure 1) in the relationship between the ITT and per-protocol effects under different levels of engagement (partial/full engagement vs. full engagement only), although confidence intervals crossed the null for all 3 estimates. The increase in standard error for the per-protocol analyses compared with the ITT analysis illustrates an important trade-off in precision one makes when estimating per-protocol effects, especially when protocol adherence is low.
The primary limitation of this study is the low proportion of individuals who met the definition for full engagement in the intervention arm. This led to small numbers of individuals in the analysis for the intervention, which could have an impact on the ability to identify the parameter of interest due to trade-offs between satisfying the positivity and conditional exchangeability assumptions. For example, we could not adjust for study site in our analyses because only 1 participant in the intervention arm in Houston was fully engaged (Web Table 4). Thus, our estimates may be biased due to unmeasured confounding between engagement and the outcome. The small sample sizes also precluded use of machine learning algorithms with the doubly robust estimators. While machine learning allows for flexible estimation of nuisance functions, which could reduce bias in the estimate, the trade-off for such flexibility would further increase variance for already imprecise estimates (22, 23).
While there are likely time-varying relationships between HbA1c, covariates such as food insecurity and depressive symptoms, and engagement in the study, this trial did not collect time-varying data in a manner that would allow for analyses that include time-varying confounding. However, these methods have been extended to such settings (24, 25).
The FAITH-DM trial was a behavioral health intervention that had prespecified definitions for trial engagement, which allowed us to estimate per-protocol effects for both full and full/partial engagement. If investigators anticipate that study participants may experience barriers to adherence, prespecifying such definitions is useful. Few existing analyses have compared the g-computation, IPW, AIPW, and TMLE estimators for the per-protocol effect, and few existing per-protocol analyses have been conducted in behavioral health interventions. We demonstrate here that these estimators provide similar estimates of the per-protocol average treatment effect, though AIPW and TMLE may be preferred due to double robustness (18, 19, 24). Results are consistent with previous studies comparing these estimators showing that the doubly robust methods tended to have lower standard errors compared with IPW, although it is surprising here that the AIPW standard errors tended to be more precise than g-computation across all analyses (22, 24, 26, 27).
The results of this study help to show why per-protocol results are useful complements to ITT results. Together, they can help distinguish between 2 scenarios: one in which an intervention has little effect and one in which the intervention is effective only if adhered to. This distinction has important implications, as interventions found to be ineffective in ITT analyses are often not pursued (28). Without complementary information, investigators may erroneously conclude that “the intervention doesn’t work” rather than “there are barriers to address.” Given the complexity of addressing health-related social needs such as food insecurity, we believe that rigorously estimated per-protocol effects should be more commonly used components in the analysis plans of health-related social needs interventions.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by the National Heart, Lung, and Blood Institute (grant T32HL129982 to C.X.L.), National Institute of Allergy and Infectious Diseases (grant R01AI157758 to S.R.C.), and National Institute of Diabetes and Digestive and Kidney Diseases (grants 2P30DK092924 to H.K.S. and K23DK109200 to S.A.B.). Funding for the parent trial was provided by Feeding America, the Laura and John Arnold Foundation, the Urban Institute via a Robert Wood Johnson Foundation grant, and the National Institute of Diabetes and Digestive and Kidney Diseases under award P30DK092924.
The manual of operations, including detailed protocol and study forms, can be accessed at Open Science Framework (https://osf.io/re9hw/). Data described in the manuscript will be made available upon request to qualified parties pending application and approval. Analytical code is available in Web Appendix 2.
The views expressed in this article are those of the authors and do not reflect those of the National Institutes of Health.
H.K.S. receives funding from Feeding America and serves as Feeding America’s Senior Medical Advisor. S.A.B. reports grants from NIH and personal fees from the Aspen Institute, and S.A.B. and H.K.S. report personal fees from the Gretchen Swanson Center for Nutrition, outside of the submitted work. The other authors report no conflicts.
Contributor Information
Catherine X Li, Department of Epidemiology, Gillings School of Global Public Health, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States; School of Medicine, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States.
Stephen R Cole, Department of Epidemiology, Gillings School of Global Public Health, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States.
Hilary K Seligman, Division of General Internal Medicine, University of California San Francisco, San Francisco, California, United States; Center for Vulnerable Populations, University of California San Francisco, San Francisco, California, United States.
Seth A Berkowitz, Cecil G. Sheps Center for Health Services Research, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States; Division of General Medicine and Clinical Epidemiology, Department of Medicine, School of Medicine, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States.
REFERENCES
- 1. Friedman LM, Furberg CD, DeMets D, et al., eds. Fundamentals of Clinical Trials. 5th ed. Cham, Switzerland: Springer International Publishing; 2015. [Google Scholar]
- 2. DeMets DL, Cook T. Challenges of non–intention-to-treat analyses. JAMA. 2019;321(2):145–146. [DOI] [PubMed] [Google Scholar]
- 3. Peto R, Collins R, Gray R. Large-scale randomized evidence: large, simple trials and overviews of trials. Ann N Y Acad Sci. 1993;703(1):314–340. [DOI] [PubMed] [Google Scholar]
- 4. Gupta SK. Intention-to-treat concept: a review. Perspect Clin Res. 2011;2(3):109–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Greenland S. Randomization, statistics, and causal inference. Epidemiology. 1990;1(6):421–429. [DOI] [PubMed] [Google Scholar]
- 6. Hernán MA, Robins JM. Per-protocol analyses of pragmatic trials. N Engl J Med. 2017;377(14):1391–1398. [DOI] [PubMed] [Google Scholar]
- 7. Robins JM, Finkelstein DM. Correcting for noncompliance and dependent censoring in an AIDS clinical trial with inverse probability of censoring weighted (IPCW) log-rank tests. Biometrics. 2000;56(3):779–788. [DOI] [PubMed] [Google Scholar]
- 8. Cain LE, Cole SR. Inverse probability-of-censoring weights for the correction of time-varying noncompliance in the effect of randomized highly active antiretroviral therapy on incident AIDS or death. Stat Med. 2009;28(12):1725–1738. [DOI] [PubMed] [Google Scholar]
- 9. Seligman HK, Smith M, Rosenmoss S, et al. Comprehensive diabetes self-management support from food banks: a randomized controlled trial. Am J Public Health. 2018;108(9):1227–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Murray EJ, Swanson SA, Hernán MA. Guidelines for estimating causal effects in pragmatic randomized trials [preprint]. arXiv. 2019. 10.48550/arXiv.1911.06030. Accessed May 14, 2020. [DOI] [Google Scholar]
- 11. Robins JM, Hernán MÁ, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. [DOI] [PubMed] [Google Scholar]
- 12. Cole SR, Frangakis CE. The consistency statement in causal inference: a definition or an assumption? Epidemiology. 2009;20(1):3–5. [DOI] [PubMed] [Google Scholar]
- 13. Hernán MA, Robins JM. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Westreich D, Cole SR. Invited commentary: positivity in practice. Am J Epidemiol. 2010;171(6):674–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Petersen ML, Porter KE, Gruber S, et al. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. 2012;21(1):31–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Snowden JM, Rose S, Mortimer KM. Implementation of g-computation on a simulated data set: demonstration of a causal inference technique. Am J Epidemiol. 2011;173(7):731–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ahern J, Hubbard A, Galea S. Estimating the effects of potential public health interventions on population disease burden: a step-by-step illustration of causal inference methods. Am J Epidemiol. 2009;169(9):1140–1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Funk MJ, Westreich D, Wiesen C, et al. Doubly robust estimation of causal effects. Am J Epidemiol. 2011;173(7):761–767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Gruber S, Laan M. Targeted Maximum Likelihood Estimation: A Gentle Introduction. Berkeley, CA: UC Berkeley Division of Biostatistics; 2009. (Working Paper Series, Working Paper 252). https://biostats.bepress.com/ucbbiostat/paper252. Accessed May 29, 2020. [Google Scholar]
- 20. Buuren S, Groothuis-Oudshoorn K. mice: multivariate imputation by chained equations in R. J Stat Softw. 2011;45(1):1–67. [Google Scholar]
- 21. Rosenbaum PR. The consequences of adjustment for a concomitant variable that has been affected by the treatment. J R Stat Soc Ser Gen. 1984;147(5):656–666. [Google Scholar]
- 22. Zivich PN, Breskin A. Machine learning for causal inference: on the use of cross-fit estimators. Epidemiology. 2021;32(3):393–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Keil AP, Edwards JK. You are smarter than you think: (super) machine learning in context. Eur J Epidemiol. 2018;33(5):437–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61(4):962–973. [DOI] [PubMed] [Google Scholar]
- 25. Laan MJ, Rose S, eds. Targeted Learning in Data Science: Causal Inference for Complex Longitudinal Studies. 1st ed. Cham, Switzerland: Springer International Publishing; 2018. [Google Scholar]
- 26. Li H, Rosete S, Coyle J, et al. Evaluating the robustness of targeted maximum likelihood estimators via realistic simulations in nutrition intervention trials [preprint]. arXiv. 2021. 10.48550/arXiv.2109.14048. Accessed May 17, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Balzer L, Ahern J, Galea S, et al. Estimating effects with rare outcomes and high dimensional covariates: knowledge is power. Epidemiol Methods. 2016;5(1):1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Deaton A, Cartwright N. Understanding and misunderstanding randomized controlled trials. Soc Sci Med. 2018;210:2–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.