Methanediol from cloud-processed formaldehyde is only a minor source of atmospheric formic acid

Significance

Formaldehyde processing by liquid clouds was recently claimed to be a large source of formic acid explaining the well-documented underprediction of formic acid observations by models. This mechanism involves formaldehyde conversion into methanediol in clouds and gas-phase oxidation of methanediol into formic acid. We use high-level theoretical means to characterize the reaction generating formic acid in this mechanism, and we provide a detailed assessment of the relevant aqueous processes and of their atmospheric consequences, backed by numerical simulations. We estimate that formaldehyde cloud-processing accounts for less than 10% of the source required to close the global budget of formic acid.

Abstract

Atmospheric formic acid is severely underpredicted by models. A recent study proposed that this discrepancy can be resolved by abundant formic acid production from the reaction (1) between hydroxyl radical and methanediol derived from in-cloud formaldehyde processing and provided a chamber-experiment-derived rate constant, k₁ = 7.5 × 10⁻¹² cm³ s⁻¹. High-level accuracy coupled cluster calculations in combination with E,J-resolved two-dimensional master equation analyses yield k₁ = (2.4 ± 0.5) × 10⁻¹² cm³ s⁻¹ for relevant atmospheric conditions (T = 260–310 K and P = 0–1 atm). We attribute this significant discrepancy to HCOOH formation from other molecules in the chamber experiments. More importantly, we show that reversible aqueous processes result indirectly in the equilibration on a 10 min. time scale of the gas-phase reaction $\mathrm{HCHO}+{\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{HOCH}}_2\mathrm{OH}$ (2) with a HOCH₂OH to HCHO ratio of only ca. 2%. Although HOCH₂OH outgassing upon cloud evaporation typically increases this ratio by a factor of 1.5–5, as determined by numerical simulations, its in-cloud reprocessing is shown using a global model to strongly limit the gas-phase sink and the resulting production of formic acid. Based on the combined findings in this work, we derive a range of 1.2–8.5 Tg/y for the global HCOOH production from cloud-derived HOCH₂OH reacting with OH. The best estimate, 3.3 Tg/y, is about 30 times less than recently reported. The theoretical equilibrium constant K_eq (2) determined in this work also allows us to estimate the Henry’s law constant of methanediol (8.1 × 10⁵ M atm⁻¹ at 280 K).

Formic acid contributes significantly to precipitation acidity in remote areas (1–3) and facilitates the nucleation of cloud droplets (4). Nevertheless, the origin and sources of atmospheric formic acid present a longstanding enigma in atmospheric chemistry. While known sources account for some 30–60 Teragrams per year (Tg/y) with the largest contribution attributed to the photochemical degradation of (mainly biogenic) volatile organic compounds (VOC) (5–8) and at most 15 Tg/y to direct emissions (5, 7, 8), the known global sink is estimated at well over 100 Tg/y (5–8), at least double the known source strength. Moreover, several proposed chemical mechanisms for formic acid production from abundant biogenic VOC such as isoprene and other terpenoids (5, 7, 8) remain largely unsupported. On the other hand, abundant production of the related formaldehyde from the photochemical degradation of isoprene and other volatile organic compounds is well established (8–11). However, formic acid is not a known product of the gas-phase oxidation of formaldehyde.

Recently, Franco et al. (12) proposed a novel mechanism for abundant gas-phase formic acid production from formaldehyde processed in (liquid) clouds to methanediol (HOCH₂OH) as suggested earlier (2, 13), though considered by Franco et al. to be outgassed to a larger extent than previously thought (2, 13–15). In essence, Franco et al. (12) propose that HOCH₂OH reacts in the gas phase with the hydroxyl radical (OH) rapidly enough to compete with its dehydration (reverting to HCHO), so as to lead mainly to HO^•CHOH radicals and for a minor fraction to HOCH₂O^• radicals,

$$\begin{array}{c}{\mathrm{HOCH}}_2\mathrm{OH}+\mathrm{OH}\to {\mathrm{HO}}^{•}\mathrm{CHOH}+{\mathrm{H}}_2\mathrm{O},\hfill \end{array}$$ [1a]

$$\begin{array}{c}{\mathrm{HOCH}}_2\mathrm{OH}+\mathrm{OH}\to {\mathrm{HOCH}}_2{\mathrm{O}}^{{}^{•}}+{\mathrm{H}}_2\mathrm{O},\hfill \end{array}$$ [1b]

which both quickly yield HCOOH by reaction with molecular oxygen. Based on an approximate measurement of the rate constant of reaction (1) and using a chemistry-climate model, Franco et al. (12) estimate that the proposed gas-phase oxidation of methanediol produces as much as four times more formic acid than all other known chemical processes combined, and claim to reconcile—in this way—model predictions and measurements of formic acid abundance.

Franco et al. (12) reported two experimental and one theoretical determinations of the rate constant of the reaction (1) between methanediol and hydroxyl radical (k₁) at 298 K. The first (i), k_1,fit = 7.5 × 10⁻¹² [range: (1 − 10) × 10⁻¹²] cm³ s^–1, was based on the temporal behavior of HOCH₂OH and HCOOH in smog chamber experiments (SAPHIR, Jülich). The concentrations over time of OH—the source of which could be switched on and off—and HCHO were also measured. The second (ii), k_1,reac = (20 ± 13) × 10⁻¹² cm³ s⁻¹ was derived from accompanying OH reactivity determinations by assuming that the difference between the measured total OH reactivity and the sum of calculated individual contributions of measured species was due entirely to reaction (1). From the same chamber experiments, an overall rate constant k₂ = (8.5 ± 1) × 10⁻⁵ s⁻¹ at ca. 298 K was also derived for the dehydration reaction of gas-phase methanediol, without considering the reverse reaction,

$${\mathrm{HOCH}}_2\mathrm{OH}\rightleftharpoons \mathrm{HCHO}+{\mathrm{H}}_2\mathrm{O},$$ [2]

that competes with reaction (1). In their work, the reverse reaction was not considered and they attributed the high apparent k₂ to a chamber wall reaction. Third (iii), Franco et al. (12) presented a quantum-chemical and theoretical-kinetics determination of the rate constant of reaction (1), $k_{1,\text{theor}}=\left(8.8-9.4\right)\times {10}^{-13}{\mathrm{cm}}^3{\mathrm{s}}^{-1}$ for the relevant temperature range 260–300 K, using the CCSD(T)/CBS(DTQ)//IRCMax(CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVQZ) computational level in combination with multiconformer transition state theory kinetics.

If the Franco et al. (12) mechanism is correct, their findings would be of tremendous importance for our understanding of the biogeochemical cycling of oxygenated organic species. For this reason, it is vital to examine the hypotheses and parameterizations behind this assessment. The most important parameter is the rate constant of reaction (1). The lower theoretical value (see iii) computed by Franco et al. (12) implies a lifetime with respect to reaction (1) of ca. 10 d at an average [OH] of 1 × 10⁶ cm⁻³. With such a rate, reaction (1) would have to compete—and could even be outrun—by (wet + dry) deposition. For compounds with similar Henry’s law constants [HLC for methanediol = 7 × 10⁴ M atm⁻¹ at 300 K (16)], such as methylglyoxal, acetic, and formic acid, model studies estimate global lifetimes ranging between 2 and 4 d due to (wet + dry) deposition (5, 17, 18). Accordingly, to assess the importance of the mechanism of Franco et al. (12), the uncertainty range of k₁ = (1 − 33) × 10⁻¹² cm³ s^–1 needs to be considerably reduced. Therefore, the prime objective for this work is the accurate theoretical determination of k₁ over a wide enough temperature range, using the most accurate quantum chemical and kinetics methodologies currently available.

A second process of interest is the dehydration of methanediol (2). Literature data on the transition-state energy for the reaction ${\mathrm{HOCH}}_2\mathrm{OH}+2{\mathrm{H}}_2\mathrm{O}\to \mathrm{HCHO}+3{\mathrm{H}}_2\mathrm{O}$ (19) imply that the gas-phase methanediol reaction with water dimer:

$${\mathrm{HOCH}}_2\mathrm{OH}+{\left({\mathrm{H}}_2\mathrm{O}\right)}_2\to \mathrm{HCHO}+{\left({\mathrm{H}}_2\mathrm{O}\right)}_3,$$ [3]

results at 298 K and near-100% relative humidity in a ${\mathrm{CH}}_2{\left(\mathrm{OH}\right)}_2\to \mathrm{HCHO}$   conversion rate approaching 10⁻⁴ s⁻¹, suggesting that the overall conversion (2) observed by Franco et al. (12) might be due to (3). Moreover, the data above suggest that reaction (3) could compete with reaction (1) in clouds. The possible consequences of a fast reaction (3) prompt a higher-level theoretical investigation of that reaction, which is a secondary aim of this work. More importantly, the possibility of an indirect establishment of an equilibrated reaction (2) in clouds will be addressed. Third, in high-concentration formalin solutions such as those used in the Franco et al. (12) chamber experiments, methanediol is known to polymerize to poly-(oxymethylene)glycols HO(CH₂O)_nH (20, 21), and oligomers such as HOCH₂OCH₂OH and HOCH₂OCH₂OCH₂OH may be outgassed together with HOCH₂OH, followed by reaction with OH possibly resulting also in HCOOH:

$$\begin{array}{c}{\mathrm{HOCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+\mathrm{OH}\to {\mathrm{H}}_2\mathrm{O}\hfill \\ +\mathrm{radical}\left(\mathrm{s}\right)\to \cdots \to \mathrm{HCOOH},\end{array}$$ [4]

$$\begin{array}{c}{\mathrm{HOCH}}_2{\mathrm{OCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+\mathrm{OH}\to {\mathrm{H}}_2\mathrm{O}\hfill \\ +\mathrm{radical}\left(\mathrm{s}\right)\to \cdots \to \mathrm{HCOOH}.\end{array}$$ [5]

The neglect of such processes in ref. 12 might explain why their experimentally derived value (k_1,fit = 7.5 × 10⁻¹²) is much higher than their k_1,theor of ca. 1 × 10⁻¹² cm³ s^–1. Therefore, the possible contribution of these processes to HCOOH production in the Franco et al. (12) experiment will also be examined and quantified in this work.

Finally, we will address the questions of the Henry’s Law constant of HOCH₂OH as well as the extent of HOCH₂OH versus HCHO outgassing from cloud droplets under typical cloud conditions, as their magnitudes are crucial parameters in the production of atmospheric formic acid by reaction of resulting gas-phase methanediol with hydroxyl radicals.

Results and Discussion

Mechanism of Reaction (1) between HOCH₂OH and OH.

Fig. 1 depicts the relevant portion of the mechanism of reaction (1), as obtained by high-level mHEAT-345(Q) (22) and amHEAT-345(Q) (22) computations, and fully validated against Active Thermochemical Tables (ATcT) reaction enthalpies (23, 24). As seen in Fig. 1, the association of hydroxyl radical (^•OH) and methanediol (MD) leads first to the formation of a vibrationally excited prereaction complex (PRC†). The PRC is a van der Waals complex, which contains two hydrogen bonds, with a binding energy of 4.89 kcal mol^–1. When it is formed, PRC can either redissociate back to the initial reactants, a barrierless process via a loose, variational TS0 (not shown in Fig. 1) or undergo a further H-abstraction steps to yield products. There are two distinct H-abstraction pathways. In the first (i), ^•OH abstracts a hydrogen atom from the central carbon via TS1 to produce HO^•CHOH and H₂O; starting from the PRC, this step must overcome an amHEAT-calculated energy barrier of 4.71 kcal mol^–1, such that TS1 is submerged by –0.18 kcal mol^–1. In pathway (ii), ^•OH abstracts the hydrogen atom of the –OH group via TS2 leading to ^•OCH₂OH and H₂O, over an amHEAT barrier of 8.02 kcal mol^–1, about 3.3 kcal mol^–1 higher than TS1. However, as seen in Fig. 1, the PRC geometry is more favorable for pathway (ii) such that its barrier—with reaction-coordinate frequency for TS2 of 2117i cm^–1—is much narrower than that of pathway (i) with imaginary TS1 frequency of 1013i cm^–1. Therefore, quantum mechanical tunneling effects through TS2 should be substantially more important than through TS1, especially at low temperatures. So, interestingly, while TS1 is energetically favored, due to tunneling effects pathway (ii) through TS2 dominates at very low temperatures (SI Appendix, Fig. S1). As a result, the kinetics analysis must consider the competition of these two reaction pathways.

Fig. 1.

Unscaled potential energy (in kcal mol^–1) surface for the OH + HOCH₂OH reaction calculated using mHEAT-345(Q) (in black) and amHEAT-345(Q) (in blue) methods. The benchmark ATcT values (in red) are also included for comparison.

The relevant abstraction reactions were recently computed by Franco et al. (12) at the CCSD(T)/CBS(aD,aT,aQ) level of theory using M06-2X/aug-cc-pVQZ geometries. Their reaction mechanism looks similar to that characterized in this work, e.g., their TS2 energy of +3.03 kcal mol^–1 is in excellent agreement with our amHEAT result of +3.13 kcal mol^–1. However, there is a more significant difference of ca. 1 kcal mol^–1 for TS1, which kinetically controls the reaction under atmospheric conditions. The largest difference, –0.59 kcal mol^–1, comes from the zero-point energies (ZPE) and different TS geometries. Our treatment of ZPE fully included anharmonic effects, crucial for hindered rotors, calculated at the CCSD(T)/aug-cc-pVTZ level of theory while Franco et al. (12) used a harmonic ZPE. Scheme 1 shows the optimized geometry of TS1 in this work and those reported by Franco et al. (12) As compared to the CCSD(T)/aug-cc-pVTZ geometry in this study, the M06-2X calculation produces an earlier TS, while the IRCMax yields a later transition structure, as expected. The second important difference of –0.34 kcal mol^–1 comes from the inclusion of higher-order correction using the CCSDT (–0.17 kcal mol^–1) and CCSDT(Q) (–0.17 kcal mol^–1) corrections in this study, which were not considered in the work of Franco et al. (12).

Scheme 1.

Comparison of the CCSD(T)/aug-cc-pVTZ optimized geometry for TS1 in this study with those obtained by Franco et al. (12) using the M06-2X/aug-cc-pVQZ and the IRCMax(CCSD(T)/aVTZ//M06-2X) levels of theory.

Rate Coefficient of Reaction (1).

Low harmonic vibrational frequencies that correspond to large amplitude motions—two for HOCH₂OH and one for each TS1 and TS2 (SI Appendix)—may be incorrectly described with the VPT2 approach. Hence, before solving the 2DME for rate coefficients, it is important to treat hindered (internal) rotors of key stationary points appropriately. In this work, we consider these vibrations separately from the remaining motions and treat them as noncoupled one-dimensional hindered internal rotors (1DHR) using the Multiwell software package (25). We computed the torsional potentials (SI Appendix, Figs. S2–S7) and solved the 1D Schrödinger equation to obtain a full set of eigenvalues of each 1DHR (SI Appendix) (25, 26). For each 1DHR, direct state counting was used to compute the sum of (anharmonic) quantum states; these are then combined with those of the remaining motions to obtain the overall sum of ro-vibrational quantum states. It should be mentioned that the 1DHR treatments also change the ZPE of MD, TS1, and TS2, by an amount of +0.01, −0.09, and −0.19 kcal mol⁻¹, respectively. As a result, the calculated relative energies given in Fig. 1 are adjusted by the same amounts.

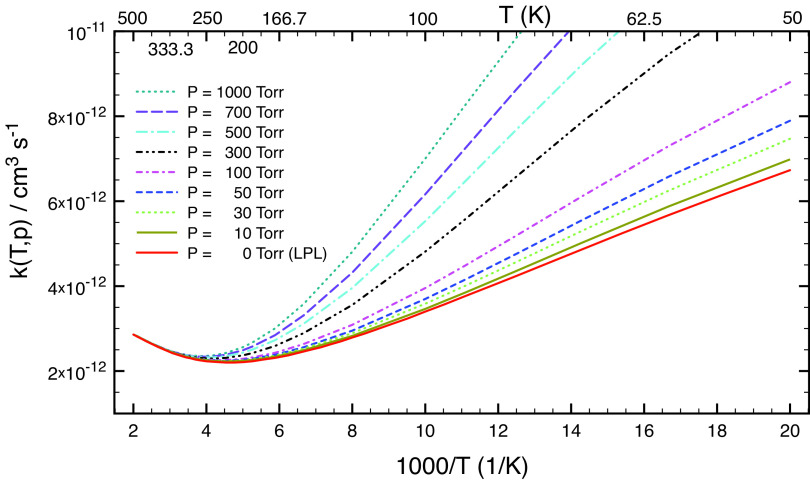
The rate coefficients calculated as a function of both temperature and pressure (i.e. falloff curves) are displayed in Fig. 2 and SI Appendix, Fig. S8. As seen in Fig. 2, the calculated rate coefficients increase with pressure, as expected. Importantly, when temperature is greater than ca. 250 K, the calculated k(T) becomes less sensitive to pressure. Under atmospheric conditions (T ≥ 200 K and P ≤ 1 atm) considered in this work, the calculated k₁(T) is nearly pressure-independent, as shown in SI Appendix, Fig. S8. k₁(T) is adequately approximated by the low-pressure limit (LPL) where rate coefficients can be computed from first principles using SI Appendix, Eq. S9. However, the change of k(T,P) with temperature is rather complicated, as seen in Fig. 2. Starting from very low temperatures, k first decreases rather sharply but flattens considerably around 220 K to increase slowly again at higher temperatures (Fig. 2). This characteristic concave curve can also be found for other analogous reactions (26–30) and is due to the characteristics of the two competing H-abstraction pathways. At low temperatures (T ≤ 220 K), the enthalpy for the submerged TS1 and the tunneling effects for TS2 control the kinetics, resulting in k(T,P) decreasing as the temperature increases. At higher temperatures (T ≥ 220 K), entropy ultimately becomes dominant while tunneling effects lose importance, leading to k(T,P) increasing with temperature.

Fig. 2.

Rate coefficient of reaction (1) as a function of temperature at various pressures.

Fig. 2 and SI Appendix, Fig. S8 show that under tropospheric conditions (200 K ≤ T ≤ 320 K, and P ≤ 1 atm), the calculated rate coefficients are practically at the LPL and vary only marginally (within 10%) from 2.3 × 10⁻¹² cm³ s⁻¹ at 200 K to 2.5 × 10⁻¹² cm³ s⁻¹ at 350 K. It should be noted that the high-level computed rate constant of this work for reaction (1), k₁(298 K) = (2.4 ± 0.5) × 10⁻¹² cm³ s⁻¹, is about three times smaller than the best-fit k₁ value of 7.5 × 10⁻¹² cm³ s⁻¹ reported by Franco et al. (12). A likely explanation for this difference is discussed below. At the same time, our k₁(298 K) is about 2.5 times larger than the theoretical value k_1,theor = 0.94 × 10⁻¹² cm³ s⁻¹ of Franco et al. (12), due to their energy barrier for TS1 being ca. 1 kcal mol^–1 too high (see above), though this is somewhat offset by their TST calculation giving the high-pressure limit rate constant, which is quite far from being reached at atmospheric pressures.

It is interesting to examine the role of the reaction pathway that corresponds to TS2. SI Appendix, Fig. S9 displays the calculated yields of product ^•OCH₂OH as a function of both temperature (50−400 K) and pressure (1 − 1000 Torr). This shows that the yield of ^•OCH₂OH increases with pressure but decreases significantly with temperature. This result can be expected because TS2 lies higher than TS1 and the tunneling effects via TS2 become relatively more important at lower temperatures and higher pressures. Recently, we have found that the tunneling effects can cause a fall-off curve for the reaction of ^•OH and HNO₃ (28). At 298 K, the calculated yield of ^•OCH₂OH is ca. 5%, in excellent agreement with that found by Franco et al. (12). So, one can conclude that the formation of ^•OCH₂OH is minor in the lower troposphere and under combustion conditions but can become very important in the interstellar medium (ISM) environments.

HO(CH₂O)_nH Oligomers as Additional Formic Acid Sources in the Conditions of the Franco et al. (12) Experiments.

The likely reason for the large discrepancy between the best experimental rate coefficient k_1,fit = 7.5 × 10^–12 cm³ s^–1 of Franco et al. (12) and our theoretical rate coefficient k₁(298 K, 1 atm) = 2.4 × 10^–12 cm³ s^–1 is that there are other important, but overlooked sources of HCOOH in the experiments of Franco et al. (12). In these experiments, methanediol was introduced in the simulation chamber by dispersing a highly concentrated formalin solution of ca. 36.5%, of which ca. 1 µL of solution was injected as a fine mist and evaporated in a heated flow of dry synthetic air that was rapidly mixed with the humidified synthetic air in the chamber. In formalin (i.e., aqueous solutions of formaldehyde), the main component HOCH₂OH (methanediol MD, or methylene glycol) is present in equilibrium with its HO(CH₂O)_nH oligomers, i.e., HOCH₂OCH₂OH (dimethylene glycol, DMG), HOCH₂OCH₂OCH₂OH (trimethylene glycol, TMG), etc., leaving only traces of molecular formaldehyde HCHO (20, 21, 31, 32):

$${\mathrm{HOCH}}_2\mathrm{OH}+{\mathrm{HOCH}}_2\mathrm{OH}\rightleftharpoons {\mathrm{HOCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+{\mathrm{H}}_2\mathrm{O},$$ [6]

$$\begin{array}{c}{\mathrm{HOCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+{\mathrm{HOCH}}_2\mathrm{OH}\hfill \\ \rightleftharpoons {\mathrm{HOCH}}_2{\mathrm{OCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+{\mathrm{H}}_2\mathrm{O}.\end{array}$$ [7]

The equilibrium constants K₆, K₇, etc. in aqueous solution have been determined by several groups and are well established for the first two oligomers (21, 31–33); rates of forward and reverse reactions have also been measured (33).

As detailed in SI Appendix, we argue that together with MD, gas-phase DMG and TMG were also present in the Franco et al. (12) experiments in a molar ratio of approximately 3.8:2.5:1.0, nearly identical to their aqueous-phase ratio due to the very fast spray volatilization and sharp decrease in concentrations upon injection in the chamber. Furthermore, gas-phase DMG and TMG are both shown in SI Appendix to react with OH even faster than MD resulting in additional HCOOH production in these experiments:

$$\begin{array}{c}{\mathrm{HOCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+\mathrm{OH}\to {\mathrm{H}}_2\mathrm{O}\hfill \\ +{\mathrm{HOC}}^{{}^{•}}{\mathrm{HOCH}}_2\mathrm{OH}{/}^{•}{\mathrm{OCH}}_2{\mathrm{OCH}}_2\mathrm{OH}\to \mathrm{HCOOH},\end{array}$$ [8]

$$\begin{array}{c}{\mathrm{HOCH}}_2{\mathrm{OCH}}_2{\mathrm{OCH}}_2\mathrm{OH}+\mathrm{OH}\to {\mathrm{H}}_2\mathrm{O}\hfill \\ +{\mathrm{HOCH}}_2{\mathrm{OC}}^{{}^{•}}{\mathrm{HOCH}}_2\mathrm{OH}\to \mathrm{HCOOH},\end{array}$$ [9]

with relative rate constants in the ratio: $k_1:k_8:k_9=1:1.8:3.3$  . As a result, the apparent rate constant k_1,app, derived under the assumption of Franco et al. (12) that all HCOOH is formed only in reaction (1), is given by:

$$\begin{array}{c}{k}_{1,\mathrm{app}}=(k_1\left[\mathrm{MD}\right]\left[\mathrm{OH}\right]+k_8\left[\mathrm{DMG}\right]\left[\mathrm{OH}\right]\hfill \\ +k_9\left[\mathrm{TMG}\right]\left[\mathrm{OH}\right])/\left[\mathrm{MD}\right]\left[\mathrm{OH}\right]\approx 3.0 k_1,\end{array}$$ [10]

This result (k_1,app = ca. 3 k₁) coincides with the discrepancy between the best-fit k_1,fit of Franco et al. (12), determined under the assumption of (1) as the only HCOOH source, and the theoretical k_1,theor obtained in this work. Also, the much larger k_1,reac = (20 ± 13) × 10⁻¹² cm³ s⁻¹ of Franco et al., compared to our k_1,theor = 2.4 × 10⁻¹² cm³ s⁻¹, can be ascribed in part to OH-removal by reactions (8) and (9) and also by reaction with HO₂^• resulting from the products.

At this point, it should be stressed that aqueous-phase DMG and TMG are entirely negligible at the very low concentrations of HCHO/MD in atmospheric clouds. For example, with 1 ppb MD at 280 K and 800 hPa, i.e., [MD] = 2.3 × 10¹⁰ cm⁻³, and with k₆ < 10⁻²³ cm³ s⁻¹ adapted from the aqueous phase value (33), it takes >2.5 × 10¹⁰ s (≈0.8 millennium) to convert just 1% of the initial MD into DMG.

Note that the possible water-dimer-catalyzed dehydration of HOCH₂OH (reaction 3, see above), as well as decompositions of HOCH₂OCH₂OH and HOCH₂OCH₂OCH₂OH, including those catalyzed by water, were also investigated in this work and all found to be negligible under the conditions of the experiments of Franco et al. (12) and those in clouds. Details on these reactions are given in SI Appendix. The result for HOCH₂OH supports the view of Franco et al. (12) that the relatively high apparent rate constant for dehydration of HOCH₂OH derived from their chamber experiments (see above) must be ascribed to a reaction on the walls and has therefore no meaning for atmospheric processes.

Fast, Indirect Establishment of Gas-Phase Equilibrium HOCH₂ OH ⇌ HCHO + H₂O in Clouds; Intrinsic Henry’s Law Coefficients of HCHO and HOCH₂OH.

It is shown in this subsection that the gas phase equilibrium (2) is established quickly and closely, though indirectly, in typical liquid tropospheric clouds. Therefore, because of its importance in the context of this paper, the equilibrium constant K_eq(T) is first (re-)determined independently, based on newly evaluated ATcT thermochemical data, using quantum statistical methods:

$$K_{\mathrm{eq}}\left(T\right)=\frac{Q_{\mathrm{HCHO}}\bullet Q_{{\mathrm{H}}_2\mathrm{O}}}{Q_{{\mathrm{HOCH}}_2\mathrm{OH}}}\times e^{-\mathrm{\Delta }{H}_r(0 K)/RT},$$ [11]

In this equation, $\mathrm{\Delta }{H}_r\left(0 K\right)=8.18\pm 0.15 \mathrm{kcal} {\mathrm{mol}}^{-1}$ i is the reaction enthalpy at 0 K taken from the most recent version of ATcT (23) and precisely equal to the quantum theoretical amHEAT value found in this work. Q_i is the complete partition function of a chemical species i. Experimental fundamental frequencies and rotational constants of H₂O and HCHO are used to compute their ro-vibrational partition functions. Experimental ro-vibrational data (34) for HOCH₂OH are not available, so high-level (accurate) theoretical results (35) reported recently are used. The calculated K_eq(2) values as a function of temperature are given in SI Appendix, Table S1. Of interest below, $K_{\mathrm{eq}}\left(2\right)\left(280 \mathrm{K}\right)=1.39\times {10}^{19} {\mathrm{cm}}^{-3}$ and $K_{\mathrm{eq}}\left(2\right)\left(300 \mathrm{K}\right)=4.41\times {10}^{19} {\mathrm{cm}}^{-3}$ . Given the conservative error estimate of 0.15 kcal/mol on the reaction enthalpy, the uncertainty of K_eq(2)(280 K) is estimated at a factor ≈1.3.

The equilibrium (2) cannot be established directly in the gas phase in clouds, as the forward and the reverse reactions face much too high barriers (19, 36, 37); even the reactions catalyzed by one water molecule (19) and by a water-dimer (see above) are negligibly slow. Nevertheless, we show here that this gas-phase equilibrium is quickly established in clouds, though indirectly, as a result of four separate in-cloud processes/reactions. The four reactions are the following, in logical order: (i) transfer of gas-phase HCHO towards and into cloud droplets and its reverse; (ii) aqueous-phase hydration of HCHO to form MD and its reverse; (iii) transfer of MD from the liquid to the gas phase and its reverse; (iv) transfer of H₂O vapor to the aqueous phase and its reverse:

$${\mathrm{HCHO}}_{\mathrm{g}}\rightleftharpoons {\mathrm{HCHO}}_{\mathrm{aq}},$$ [12]

$${\mathrm{HCHO}}_{\mathrm{aq}}+{{\mathrm{H}}_2\mathrm{O}}_{\mathrm{l}}\rightleftharpoons {{\mathrm{HOCH}}_2\mathrm{OH}}_{\mathrm{aq}},$$ [13]

$${{\mathrm{HOCH}}_2\mathrm{OH}}_{\mathrm{aq}}\rightleftharpoons {{\mathrm{HOCH}}_2\mathrm{OH}}_{\mathrm{g}},$$ [14]

$${{\mathrm{H}}_2\mathrm{O}}_{\mathrm{g}}\rightleftharpoons {{\mathrm{H}}_2\mathrm{O}}_{\mathrm{l}},$$ [15]

The sum of these four processes is indeed HCHO_g + H2O_g ⇌ HOCH₂OHg, i.e., the reverse gas-phase reaction (2). They are represented in the schematic Fig. 3, together with their forward and reverse rates as well as the resulting relative molar loads at equilibrium in the aqueous and gas phases for typical cloud conditions (liquid water content L = 2 × 10⁻⁷ m³ m⁻³ and T = 280 K) derived in this work (SI Appendix). Our aim in this section is to show that the equilibria are sufficiently rapid to allow equilibration of overall reaction (2) within the lifetime of typical clouds.

Fig. 3.

In-cloud processes relating gas-phase and aqueous-phase HCHO and MD (methanediol), and atmospheric fate of the released methanediol. The rates (in black) and the relative molar loads at equilibrium (in red) are calculated for typical cloud conditions of temperature (T), liquid volume fraction (L), and droplet radius (r). The gas-to-aqueous rates and aqueous molar loads are proportional to L, whereas the ratios MD_g/HCHO_g and MD_aq/HCHO_aq are L-independent.

The equilibrium ratio ${\left[\mathrm{H}\mathrm{O}\mathrm{C}{\mathrm{H}}_2\mathrm{O}\mathrm{H}\right]}_{\mathrm{aq}}/{\left[\mathrm{H}\mathrm{C}\mathrm{H}\mathrm{O}\right]}_{\mathrm{aq}}$   of the aqueous-phase reaction (13) has most recently been determined to be 2,200 at 298 K by Rivlin et al. (33). Combining this with its T-dependence of Winkelman et al. (37) yields a ratio of 5,000 at 280 K, the typical cloud temperature. Given the forward rate of 0.002 s⁻¹ at 280 K (36, 37), the reverse rate is 10 s⁻¹. For reactions (12), (14), and (15), we derive in SI Appendix the rates of transfer from the gas to the aqueous phase (k_g-a) and from the aqueous to gas phase (k_a-g) for typical cloud conditions (Fig. 3). In addition, SI Appendix provides a discussion of the uncertainties of the underlying parameters, e.g., the coefficients of accommodation by water, as well as resulting uncertainties in the derived relaxation times and other parameters.

The individual k_g-a and k_a-g of reactions (12)–(14) as well as the relevant molar loads in the gas and aqueous phase are shown in Fig. 3. The reverse rate k_a-g of reaction (12) is so fast (~11,200 s⁻¹) that this reaction is quasiinstantaneously equilibrated, and the molar load of HCHO_aq, relative to HCHO_g, is only about 1.38 × 10⁻⁵. As a result, the formation of HOCH₂OH_aq in reaction (13) can be considered to occur directly by reaction of HCHO_g with H₂O_l with an effective rate $k_{\mathrm{fwd}}\left(13\right)\times \frac{k_{\mathrm{g}-\mathrm{a}}\left(12\right)}{k_{\mathrm{a}-\mathrm{g}}\left(12\right)}=$  $1.38\times {10}^{-4} {\mathrm{s}}^{-1}$ , and the reverse reaction can be considered to occur directly from HOCH₂OH_g at an effective rate $\begin{array}{c}\frac{k_{\mathrm{rev}\left(13\right) }- k_{\mathrm{g}-\mathrm{a}}\left(14\right)}{\left[k_{\mathrm{g}-\mathrm{a}}\left(14\right) + k_{\mathrm{l}-\mathrm{a}}\left(14\right)\right]}=1.58\times {10}^{-3} {\mathrm{s}}^{-1}\hfill \end{array}$ . Therefore, the relaxation time for the overall reaction ${\mathrm{HCHO}}_{\mathrm{g}}+{{\mathrm{H}}_2\mathrm{O}}_{\mathrm{g}}\rightleftharpoons {{\mathrm{HOCH}}_2\mathrm{OH}}_{\mathrm{g}}$ is given by $\begin{array}{c}1/\left\{k_{\mathrm{fwd}}\left(13\right)\times \frac{k_{\mathrm{g}-\mathrm{a}}\left(12\right)}{k_{\mathrm{l}-\mathrm{a}}\left(12\right)}+k_{\mathrm{rev}}\left(13\right)\times k_{\mathrm{g}-\mathrm{a}}\left(14\right)/\right.\left[k_{\mathrm{g}-\mathrm{a}}\left(14\right)\right.\hfill \end{array}$$\begin{array}{c}\left.\left.+k_{\mathrm{a}-\mathrm{g}}\left(14\right)\right]\right\}\hfill \end{array}$ , which for L = 2 × 10⁻⁷ and 280 K gives 580 s, with an uncertainty of ca. 50%. The above verifies that the overall gas-phase equilibrium ${\left\{{\left[\mathrm{HCHO}\right]}_{\mathrm{g}}/{\left[{\mathrm{HOCH}}_2\mathrm{OH}\right]}_{\mathrm{g}}\right\}}_{\mathrm{eq}}$ is rapidly established and maintained in typical clouds. Given the equilibrium constant K_eq(2) = 1.39 × 10¹⁹ cm⁻³ at 280 K, accurately determined above, and the equilibrium concentration [H₂O]_g = 2.57 × 10¹⁷ cm⁻³ at 280 K and 100% RH, we evaluate the ratio ${\left\{{\left[\text{HCHO}\right]}_{\mathrm{g}}/{\left[{\text{HOCH}}_2\mathrm{OH}\right]}_{\mathrm{g}}\right\}}_{\mathrm{eq}}={\mathrm{K}}_{\mathrm{eq}}\left(2\right)/{\left[{\mathrm{H}}_2\mathrm{O}\right]}_{\mathrm{g},\mathrm{eq}}$ in typical clouds at 54, with an uncertainty of a factor 1.3.

Furthermore, as also detailed in SI Appendix, we derive in this work the intrinsic Henry Law Constant (HLC) of HCHO—characterizing equilibrium (12)—at 3.0 M atm⁻¹, and the intrinsic HLC of MD for equilibrium (14) at 8.1 × 10⁵ M atm⁻¹, both at 280 K. Most interestingly, from the k_a-g values for (12) and (14) (Fig. 3), it follows that the water-to-air transfer rate k_a-g is ca. 1.75 × 10⁵ times faster for HCHO than for HOCH₂OH. The much lower affinity of formaldehyde to liquid water can be readily ascribed to the different numbers of strong hydrogen bonds that HCHO and HOCH₂OH can make in water, i.e., 1 versus up to 4.

Release and Fate of HOCH₂OH After Cloud Evaporation.

When clouds evaporate, they release more gas-phase MD than is present at equilibrium in the cloud, because a fraction of the aqueous MD is transferred to the gas phase. That fraction is only weakly dependent on liquid water content and is primarily controlled by the rate of change of liquid water content when cloud droplets appear and disappear, as shown by numerical simulations detailed in SI Appendix, Fig. S18 and Table S8. The fraction ranges between 0.3 for long-lived clouds (for a 1-h liquid water disappearance time) to ca. 0.7 for short-lived clouds. The resulting yield of gas-phase MD due to in-cloud processing of HCHO ranges between 3 and 10% in a broad range of conditions (SI Appendix, Table S8), i.e., between 1.5 and 5 times the in-cloud equilibrium ratio. Using these results, we parametrize the postevaporation MD/HCHO ratio as function of liquid water content, temperature, and a cloud characteristic time, namely the cloud contact time T_c (average time that an air parcel spends within a cloud), as detailed in SI Appendix.

In order to estimate the fate and impact of HOCH₂OH in the atmosphere, we implement the above parametrization in a global chemistry-transport model (8). The conversion rate of HCHO into MD is calculated as the yield of MD per cloud event, multiplied by the frequency of such events, obtained from cloud fractions from a global meteorological reanalysis (38) in combination with the assumed cloud contact time T_c (SI Appendix). Given the importance, high variability and high uncertainty of this parameter, we conduct simulations for a broad range of values between 0.25 and 4 h, with T_c = 2 h as reference case.

Besides reaction with OH, dry deposition, and wet scavenging, all explicitly represented in the model, in-cloud reprocessing is a major sink of MD, as the average time between subsequent cloud encounters (1–2 d) is similar to or even lower than the MD lifetime (~2 d) with respect to reaction with OH and deposition (SI Appendix). In order to account for this effect, and acknowledging the fact that the postevaporation MD/HCHO ratio is essentially independent on the initial concentration of MD prior to cloud droplet formation (SI Appendix, Fig. S19), we ignore in-cloud processing as a direct MD sink in the model, but we replace the in-cloud HCHO conversion rate by a net conversion rate accounting for the presence of previously formed MD (SI Appendix). This approach is possible only because the ratio of MD to HCHO atmospheric concentrations is most often lower than the postevaporation ratio (SI Appendix, Fig. S21 B and C), such that the net in-cloud formation rate is generally positive. In this way, in case of high cloudiness and frequent in-cloud processing of both HCHO and MD, the ratio of their concentration approaches the postevaporation ratio defined above.

Estimate of the Global Production of Formic Acid by the Reaction of In-Cloud, HCHO-Derived HOCH₂OH with OH (1).

Adopting T_c = 2 h, in-cloud MD processing reduces the net MD production by more than a factor 2 according to the global model simulations, with stronger effects at high latitudes where volume cloud fractions are largest (SI Appendix, Fig. S21 and Table S9). Deposition and the photochemical sink represent ca. 40 and 60% of the total MD sink (excluding in-cloud processing), respectively. The global production of HCOOH by the title reaction (1) amounts to 3.3 Tg/y, with an estimated range of 1.24–8.5 Tg/y, based on sensitivity simulations varying the relevant parameters within their expected uncertainties (SI Appendix, Table S9). By far, the largest source of uncertainty is the cloud contact time T_c, which determines the frequency of in-cloud processing, and the Henry’s law constants. However, we argue that the maximum HCOOH production (8.5 Tg/y) calculated at the lower end of the considered range of T_c represents an asymptote, due to the effect of in-cloud reprocessing, and that shorter values would not affect the range mentioned above. Uncertainties in the other considered parameters k₁, K_eq(2), and K_eq(13) have a comparatively much lower impact (~10% each), thanks to the high-accuracy determinations from this work. It is worth noting that the best estimate of global HCOOH production (3.2 Tg/y) is very close to the production (3.8 Tg/y) that would be obtained by assuming a constant [MD]/[HCHO] ratio in the atmosphere, equal to the in-cloud equilibrium ratio determined above (1/54).

The effect of the additional HCOOH source is highest (>20%) at high latitudes as well as in the summer Hemisphere above the boundary layer (SI Appendix, Fig. S22). Its impact is low near the surface over the continents (few %), but it reaches up to 50% over remote oceanic areas (Fig. 4 and SI Appendix, Fig. S23). The impact on HCHO is close to negligible.

Fig. 4.

Model-calculated impact of in-cloud HCHO processing on the tropospheric vertical column of HCOOH (in %) for (A) January and (B) July. Results shown for run B (best estimate, see SI Appendix).

Conclusions and Atmospheric Implications

Our analysis of the reaction between OH radicals and methanediol, derived in clouds from HCHO, has resulted in several crucial insights and results leading to the conclusion that this reaction is only a minor source of atmospheric formic acid. The reaction enthalpies of MD + OH (1) calculated from benchmark thermochemical ATcT heats of formation and from the amHEAT protocol values agree within 0.05 kcal mol⁻¹. The combination of high-accuracy coupled cluster calculations using the amHEAT protocol and an E,J-resolved two-dimensional master equation approach allowed us to determine the currently highest-level theoretical rate coefficient k₁(MD + OH) at 2.4 × 10⁻¹² cm³ s⁻¹ for relevant atmospheric conditions (T = 260–310 K and P = 0–1 atm). This value is three times lower than the best-fit value of 7.5 × 10⁻¹² cm³ s⁻¹ recently derived by Franco et al. from simulation chamber experiments (12); quantitative argumentation is provided above that other, overlooked sources of formic acid in the experiments account for twice more HCOOH than the reaction MD + OH. The rate constant determined in this work implies an average atmospheric lifetime of 4.8 d at [OH] = 1.0 × 10⁶ cm^–3 with respect to reaction (1) such that reaction (1) should be outrun by the combined MD sink due to deposition and reuptake by clouds.

Of prime importance, it is shown in this work that the gas-phase equilibrium ${\text{HOCH}}_2\mathrm{OH}\rightleftharpoons \text{HCHO}+{\mathrm{H}}_2\mathrm{O}$ is quickly established indirectly in liquid clouds, on a 10-min. time scale, by four reversible reactions, resulting in an in-cloud ratio ${\left\{{\left[\text{HCHO}\right]}_{\mathrm{g}}/{\left[{\text{HOCH}}_2\mathrm{OH}\right]}_{\mathrm{g}}\right\}}_{\mathrm{eq}}$ of ca. 50 at 280 K based on the theoretical K_eq(T) determined in this work. Although between typically 1.5 and 5 times higher amounts of gaseous HOCH₂OH are evaluated to be released directly when clouds evaporate, global modeling shows that HOCH₂OH cannot accumulate to high levels in the atmosphere, due to its reprocessing by clouds. The combined new findings of this work allow an estimate of global atmospheric formic acid production from the reaction of (in-cloud, HCHO-derived) HOCH₂OH with OH of only 3.3 Tg/y (range 1.2–8.5 Tg/y), i.e., about 14–50 times less than the range (46–153 Tg/y) estimated by Franco et al. (12).

Materials and Methods

The theoretical methodologies are detailed in SI Appendix. For the principally investigated HOCH₂OH + OH reaction, the lowest-lying doublet state potential energy surface was constructed using the high-accuracy amHEAT-345(Q) composite Coupled Cluster method (22), with an expected uncertainty of ca. 0.2 kcal mol^–1; the calculated reaction enthalpies were validated within 0.1 kcal mol^–1 against newly derived benchmark ATcT values (23). The thermal rate coefficient k₁(HOCH₂OH + OH) as a function of temperature and pressure was computed using E,J-resolved two-dimensional master equation (2DME) techniques (39–47). The equilibrium constant of ${\text{HOCH}}_2\mathrm{OH}\rightleftharpoons \text{HCHO}+{\mathrm{H}}_2\mathrm{O}$   was theoretically derived using the most recent ATcT reaction enthalpy (23) and partition functions based on experimental (34) or recently published high-accuracy theoretical ro-vibrational data (35). Theoretical energy barriers and rate coefficients or rate ratios for other reactions were obtained using appropriate levels of coupled cluster methods (22) and (2-TS) transition state theory models (27, 30), detailed in SI Appendix.

Box model simulations were performed using the Kinetic PreProcessor (KPP) package (48), and global modeling of tropospheric composition was made using the MAGRITTE (Model of Atmospheric composition at Global and Regional scales using Inversion Techniques for Trace gas Emissions) (8), with modifications described in SI Appendix.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.