Abstract
Machine learning has found unique applications in nuclear medicine from photon detection to quantitative image reconstruction. While there have been impressive strides in detector development for time-of-flight positron emission tomography, most detectors still make use of simple signal processing methods to extract the time and position information from the detector signals. Now with the availability of fast waveform digitizers, machine learning techniques have been applied to estimate the position and arrival time of high-energy photons. In quantitative image reconstruction, machine learning has been used to estimate various corrections factors, including scattered events and attenuation images, as well as to reduce statistical noise in reconstructed images. Here machine learning either provides a faster alternative to an existing time-consuming computation, such as in the case of scatter estimation, or creates a data-driven approach to map an implicitly defined function, such as in the case of estimating the attenuation map for PET/MR scans. In this article, we will review the abovementioned applications of machine learning in nuclear medicine.
Keywords: Positron emission tomography, machine learning, deep learning, image reconstruction, timing resolution, attenuation correction, scatter correction, denoising
I. Introduction
NUCLEAR medicine uses radioactive tracers to study biochemical processes in human and animals. It has wide applications in clinical practice and biomedical research. Depending on the radioisotope that is used, the emitted photons are either detected by single photon emission computed tomography (SPECT) or positron emission tomography (PET) scanners. Here we focus on PET, although similar techniques are also applicable to SPECT. In PET, positron emitters, such as 11C and 18F, are used to tag molecules of interest. After being injected into a subject, the radiotracer decays and emits a positron, which annihilates with an electron nearby producing two 511 keV photons traveling in opposite directions. By detecting the two photons, PET can identify the line of response (LOR) that contains the positron annihilation. The total number of coincidence photons recorded in each LOR (after accounting for various corrections) is proportional to the line integral of the radiotracer distribution. Therefore, PET data can be reconstructed by the inverse of Radon transform, such as the filtered backprojection algorithm.
In the past two decades, PET instrumentation has seen tremendous development. The latest PET scanners are capable of measuring the time of flight difference of the two photons with ~200 ps time resolution (corresponding to a location uncertainty of 3 cm) and thus limits the location of the annihilation site to a short line segment. This substantially reduces the uncertainty in PET measurements and correspondingly the noise amplification during image reconstruction. With the introduction of PET/CT scanners and more recently PET/MR scanners, functional images from PET are accompanied by high-resolution anatomical images from CT or MRI, which not only improves the clinical workflow, but also increases the diagnostic accuracy. During the same period, model-based iterative image reconstruction has also been developed to improve image quality and has become main-stream in PET applications.
Now, machine learning offers a new wave of opportunities for PET imaging. Machine learning has been applied to quantitative image reconstruction to estimate various correction factors and to reduce radiation dose. The development of high-speed electronics allows direct acquisition of digital waveforms from PET detectors and thus provides opportunities of using machine learning to estimate the position, energy, and arrival time of annihilation photons. It is worth noting that machine learning approaches neither solve the inverse problem, nor a minimization (maximum likelihood) problem, but rather provide results via a functional mapping. The accuracy of the mapping highly depends on the complexity of the machine learning model, how representative of the training data are, and the effectiveness of the training procedure. In this article, we will provide a review of the machine learning applications in PET detectors and in quantitative image reconstruction. Section II provides some basic background information on PET scanners for readers who are not familiar with PET. Section III reviews machine learning applications in PET detectors with a focus on the estimation of position and arrival time of incident photons. Section IV reviews machine learning applications in quantitative image reconstruction, including the estimation of attenuation map from MRI image, estimation of scatter events, image denoising, and image reconstruction. Section V provides a summary and future outlook.
II. An Introduction to PET Scanners
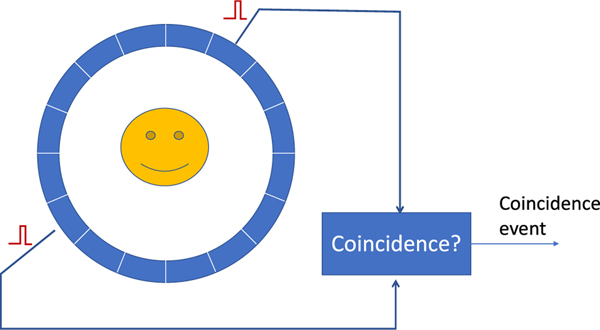
PET uses a ring of detectors to detect annihilation photons produced from positron annihilations (Fig. 1). Two photons detected within a predefined coincidence timing window (about 2–6 ns depending on the size of the field of view and time of flight capabilities of the scanner) are considered to be from the same positron annihilation and form a coincidence event. PET detectors usually consist of scintillation crystals that convert 511 keV photons into visible light and photosensors such as a photomultiplier tube (PMT) or silicon photomultiplier (SiPM), that convert visible light into an electronic signal. To obtain good spatial resolution, the scintillation crystals are often cut into small elements. However, to improve the signal-to-noise ratio of PET data, the scintillation crystals need to be sufficiently thick in the radial direction in order to efficiently stop and detect the photons. Therefore, the scintillators are usually long fingerlike crystals for high spatial resolution and high stopping power detectors. The bulky size of the scintillation crystals that are required to detect sufficient numbers of 511 keV photons is one of the fundamental reasons that PET detectors have lower spatial resolution than CT detectors, which are designed to detect photons with energies ranging from 10’s to ~150 keV
Fig. 1.
A PET scanner uses a ring of detectors to detect 511 keV annihilation photons. A coincidence event is formed when a pair of photons are recorded within a predefined coincidence timing window.
Besides identifying the position of annihilation photons, the timing resolution of PET detectors plays a critical role in identifying correct annihilation photon pairs. Because PET detectors are operated independently, the number of random coincidences (coincidences formed by detecting two photons from two independent positron annihilations) between any two detectors is proportional to the event rate on each of the two detectors and the width of the coincidence timing window. Thus, the better the timing resolution is, the tighter the coincidence timing window can be set to reduce random coincidences. Early commercial PET scanners using bismuth germanate (BGO) crystals had a timing resolution of around 2 ns (FWHM1), while the latest PET scanners have achieved a timing resolution approaching 200 ps (FWHM) using lutetium oxyorthosilicate (LSO) crystals [1]. Although the coincidence timing window cannot be less than the time for light to travel across the object, better timing resolution can more accurately pinpoint the annihilation site along the LOR joining the two detectors. Such time-of-flight (TOF) information can be used to reduce uncertainty in the data and thus reduce the variance in the reconstructed PET images [2].
Another type of undesired background events are scattered photons. A scatter event is formed when one or both 511 keV photons undergo Compton scatter and deviate from the original path before reaching the PET detectors. Scatter events do not carry accurate position information of the positron annihilation and reduce the contrast of PET images. The physics of photon scattering in tissue is well understood. The angular distribution of scattered photons is given by the Klein–Nishina formula and the energy ratio before and after scattering is given by
where is the energy of the incident photon and is the photon energy after scatter. For 511keV photons, the above equation reduces to
Clearly an ideal detector with perfect energy resolution can reject scattered events. Modern PET scanners have an energy resolution of around 10% (at 511 keV), which allows efficient rejection of large angle scatter, but there are still a significant number of scattered events being recorded that need to be corrected for during image reconstruction. A typical clinical PET scan has, very roughly, a 1:1:1 ratio between true coincidences, scattered events, and random events.
In addition to reducing image contrast, Compton scattering causes photon loss along the original LOR in the form of photon attenuation. Because two coincidence photons are attenuated independently along opposite directions of the same LOR, the overall attenuation effect is independent of the positron annihilation position in the LOR and thus can be easily measured using an external source. The ability to accurately correct for photon attenuation makes PET a fully quantitative imaging modality. For standalone PET scanners, attenuation factors are measured using a rotating positron source outside the patient. With the introduction of PET/CT scanners, the attenuation map is typically computed from CT images using bilinear scaling with consideration of the x-ray energy. The conversion formula for the attenuation coefficient at voxel is [3]
where is the Hounsfield units (HU) units of voxel in the CT image. , and Threshold are values depending on the energy of the x-ray and are given in [3]. The attenuation factors can then be calculated by
where denotes the interaction length of LOR with voxel .
Recently, PET/MR scanners have been introduced. Compared with x-ray CT, MRI does not involve any ionizing radiation and also provides better soft tissue contrast. In addition, MR images acquired simultaneously with PET scan can also aid in motion correction and partial volume correction for PET imaging. However, MR images are unrelated to photon attenuation and there is no simple expression that can convert an MR image to the corresponding attenuation map. This is one of the areas where machine learning has been extensively studied to find the unknown transformation between an MR image and the attenuation map of a patient.
All the aforementioned corrections aim at reducing bias in quantitation PET imaging. Another aspect to improve the quantitative accuracy is to reduce the noise in PET images. One solution is to improve the photon detection efficiency of PET scanners by using more scintillation crystals and better geometric coverage. As an example, the EXPLORER consortium has recently built a 2-m long PET scanner that increase the photon detection efficiency by nearly 40-fold for total-body imaging [4, 5]. Another avenue to reduce noise is through image reconstruction and image processing. Model-based iterative image reconstruction methods with regularization have been developed and adopted by manufacturers [6]. Machine learning also finds natural applications in this area given its success in natural image denoising. In the following sections, we will discuss machine learning applications in PET detector and image reconstruction in detail.
III. MACHINE LEARNING IN PET DETECTORS
The role of the detectors used in a PET system is, first and most importantly, to absorb the high energy 511 keV annihilation photons with high efficiency (> 90% total absorption), and second to provide accurate measures of (1) the detection time ( picoseconds), (2) the energy deposited by the absorbed photon ( at 511 keV), and (3) the location where the 511 keV photon was absorbed in the detector ( for clinical scanners, ~ 1 mm for preclinical scanners). These are all critical parameters that largely influence the performance of the PET system, including sensitivity, spatial resolution, time-of-flight reconstruction, and scatter and random coincidence rejection.
The vast majority of detectors used in PET imaging systems are based on scintillation detection, where the 511 keV photon is absorbed in a high-density scintillating crystal (e.g. L(Y)SO, BGO, LaBr3, etc.) that produces a short burst of light with a rise time of a few nanoseconds or less, and a decay time of approximately 10 – 1000 ns depending on the scintillator composition. The scintillation light propagates through the scintillator crystal and is collected by a fast photodetector (i.e. SiPM, PMT). Dedicated front-end electronics are used to digitize and decode the photodetector signals, including computing the total charge collected by each photodetector, the arrival time of the scintillation light estimated from the rising edge of the signal, and in some cases measuring quantities related to the pulse shape such as the exponential rise and decay times. Many PET systems make use of dedicated ASICs and FPGA logic for decoding the photodetector signals into discrete values [7, 8].
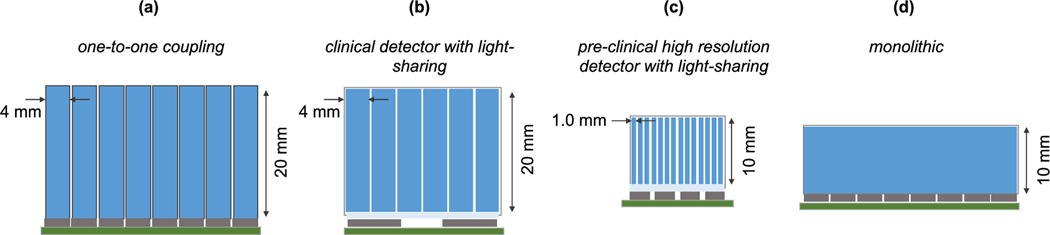
There are three common scintillator detector designs used in PET, all of which have been employed in commercial and research PET systems (Figure 2). First and most intuitive is the 1:1 coupling configuration, where long fingerlike scintillator crystals (e.g. typical for modern clinical PET systems) are coupled to individual photodetector elements (e.g. SiPMs) (Figure 2a) [9]. This approach provides good light collection and trivial estimation of the position-ofinteraction, but since the crystal size is limited by the size of the photodetector, achieving detector spatial resolution better than ~4 mm is challenging. A way to overcome this is through optical multiplexing, where the light exiting the back of the scintillator crystals is allowed to spread through a light guide and is collected by multiple photodetectors (Figure 2b) [10]. In this way, the light exiting each crystal acts as a point source forming a cone-like distribution of light on the photodetector arrangement, which can be relatively easily discriminated from the adjacent crystals using analytical methods such as center-of-gravity to parameterize the light distribution [11]. This optical multiplexing approach reduces the number of photodetectors needed to resolve a large crystal array, even up to ~40-fold reduction [12], and allows the use of much small scintillator crystals for superior spatial resolution compared to what is realistically achieved with 1:1 coupling (Figure 2c). However, the use of light sharing across multiple photodetectors typically results in light losses that degrades energy and timing resolution, and may limit the ability to resolve edge crystals in the array. Lastly, instead of pixelated crystals, a continuous monolithic scintillator crystal (e.g. ) can be used and read-out with an array of photodetector elements coupled to one crystal face (Figure 2d) [13, 14]. Similar to the light sharing approach, monolithic detectors rely on measuring the spatial distribution of the collected scintillation light to estimate the position-of-interaction, but with the ability for arbitrary localization precision. This approach presents a number of potential advantages, such as higher sensitivity and intrinsic measurement of the depth-of-interaction in the scintillator for better spatial resolution capabilities, however, the relationship between position-of-interaction and the measured light distribution can be highly non-linear mainly at the crystal edges, making position estimation difficult especially for thick (i.e. ~20 mm) monolithic crystals. Additionally, these detectors typically require complicated and time-consuming calibration procedures that present challenges in scaling to a complete PET system compared to pixelated detectors.
Fig. 2.
Common designs of detectors used in modern PET systems. The drawing dimensions indicate typical values and are not indicative of all available technology.
It is understood from this that the spatial and temporal properties of the scintillation light collected by the photodetectors carries all the information describing the 511 keV photon’s position-, energy-, and time-of-interaction in the detector. Unfortunately, the number of scintillation photons produced in response to the 511 keV photon absorption (i.e. the scintillator conversion efficiency) is generally quite low; with L(Y)SO for example, the most commonly used scintillator in PET, approximately 30,000 photons are produced in the visible wavelength range [15], of which approximately 10 – 30% are ultimately converted by the photodetector after losses in the crystal and the photodetector conversion efficiency. Therefore, the choice of signal processing and estimation algorithms used to extract these parameters from the photodetector signals represents a crucial component of the detector performance and that of the PET system. It is not surprising, given the statistics-limited nature of scintillation combined with the multiple random processes involved in photon detection and light transport in the crystal, that machine learning methods have been pursued for many of the signal processing and estimation tasks used in PET detectors.
A. Position :
The most prevalent use of machine learning in PET detectors has been in estimating the position-of-interaction of the 511 keV photon in the detector. In nearly all detectors used in PET imaging systems, (that is, excluding semiconductor detectors such as CZT or TlBr), the spatial distribution of the scintillation light as collected by the assembly of photodetectors is used to determine the location where the photon was absorbed in the detector. Solving this inverse problem then requires fitting the function that maps the scintillation light distribution to the position-of-interaction, but this is often challenging given the quanta-limited nature of scintillation detection and non-linear light distributions near the edges of the detector. Additionally, effects such as the random number and isotropic directionality of the emitted scintillation light, the possibility for multiple reflections of the scintillation light inside the detector volume, and the relatively high likelihood of one or more Compton interactions of the 511 keV photon in the scintillator volume before photoelectric absorption, make the task of solving the inverse problem a difficult statistical task and well-suited for machine learning techniques.
In general, with PET scintillation detectors, the total charge collected by each photodetector for a photon interaction approximates the number of scintillation photons collected by the photodetector, and the vector or matrix containing the set of photodetector outputs is used for position discrimination. For practical considerations related to minimizing the number of readout channels from each detector, the photodetector signals are sometimes multiplexed, for instance row-column summing of the photodetector array outputs. In either case, the discretized detector readout is well-suited and readily used as the input for several machine learning algorithms [16], including library approaches such as -nearest neighbors (NN) [17], regression methods such as support vector machines (SVM) [18], or neural network approaches such as multilayer perceptron (MLP) or convolutional neural networks (CNN) [19]. The overall aim of these machine learning methods is to achieve superior localizing performance compared to conventionally used linear methods such as center-of-gravity calculation. In the following sections, we review some of the detectors and machine learning positioning algorithms that have been described in the literature.
1). Monolithic Detectors:
The main challenge in monolithic detectors is solving the inverse problem that maps the light distribution to the position-of-interaction in the presence of limited-statistics noise and the highly non-linear behavior near the edges of the crystal, a problem well suited for machine learning methods. Common to all supervised machine learning techniques for monolithic detectors is the requirement for labeled training data needed to train the algorithm (i.e. fitting the function that maps the measured light distribution to position-of-interaction). This process typically requires irradiating the detector with a pencil-beam 511 keV photon source, but more efficient data acquisition methods in combination with data clustering techniques have been recently developed as discussed in the following section.
a). Positioning estimation:
One of the earliest applications of machine learning in PET detectors involved the use of artificial neural networks to estimate 2D (i.e. without depth-of-interaction) or 3D position-of-interaction in 10 – 20 mm thick L(Y)SO or BGO monolithic crystals read out by an arrangement of SiPMs, APDs, or PMTs [16, 20–24]. In these detectors, the charge collected by each photodetector is input to a feed-forward multilayer artificial neural network consisting of an input layer containing the set of input nodes that each receive one photodetector signal, followed by one or more fully connected hidden layers and their activation functions (e.g. sigmoid, tanh, or rectified linear), and lastly the output, which can be a regression or classification output that represents the 2D or 3D position-of-interaction in the crystal volume. Training data were mainly acquired using pencil-beam irradiation at several irradiation angles with respect to the front surface of the crystal, and the neuron weights were obtained by either error back-propagation Levenberg-Marquardt or algebraic training, yielding overall similar performance. However, Levenberg-Marquardt is often preferred due to its simple architecture that is more readily suitable for FPGA implementation. Compared to other estimators such as center-of-gravity or fitting methods, the neural network-based approaches, in general, resulted in superior detector spatial resolution, mainly due to reduced positioning bias at the edges of the detector where linear estimation methods such as Anger logic fail to accurately decode the non-linear light distribution.
A similar approach using a gradient tree boosting algorithm [25] has also been described for 3D positioning in monolithic detectors [26, 27]. The choice of algorithm here was influenced by practical considerations relating to implementing the positioning algorithm into the system electronics. Gradient tree boosting algorithms rely only on binary decision operations, making them a relatively straightforward and a computationally relaxed algorithm for fast event processing and satisfying the memory restrictions of FPGAs.
Lastly, Peng et al have developed a quasi-monolithic detector employing a stack of thin scintillator slabs read-out on their lateral sides with SiPMs [28]. The main purpose of using a stack of thin monolithic crystals is for unambiguous depth-of-interaction determination along with identifying inter-crystal scatter occurring in different crystal layers for improved spatial resolution and sensitivity. A CNN approach is used, where the map populated by the charge collected from each of the SiPMs is used as the input array to the convolutional layer, followed by a classification output that maps the light distribution to a 2D position-of-interaction in each layer. The CNN approach may be useful here when considering Compton interactions across two or more crystal layers, such that the CNN can receive the matrix of the photodetector outputs from all layers simultaneously in order to identify the correct photon trajectory.
Aside from neural networks, lazy-learning machine learning algorithms such as -nearest neighbors have been investigated for monolithic PET detectors [29–31]. Here, the photodetector outputs are stored for a large number of events acquired with the spatially defined calibration source, then a test event is assigned to the position-of-interaction that contains the most events that are similar to the test event (i.e. minimizing Euclidean distance between the photodetector outputs). The library methods can achieve good performance similar to neural network methods, but do not require a training operation to fit the light distribution mapping function, instead the function is determined purely empirically. However, these library approaches necessitate storing a large number of library signals, and for each test event, comparing with a large number of signals stored in the library. This is, of course, computationally intensive and challenging from a data storage perspective for online data processing.
b). Calibration:
Training the machine learning algorithms described previously requires the acquisition of events from a 511 keV source with known beam geometry [32, 33]. The relationship between the interaction position and the spatial distribution of light is typically obtained using a dedicated calibration data acquisition that uses a pencil beam or fanbeam source of 511 keV photons to control the interaction location in the scintillator. For 3D position estimation capabilities, additional oblique or side-on irradiation is generally required, further complicating the calibration procedures.
One limitation in this method of obtaining training data is the uncertainty in the true or first interaction location in the scintillator, limited by the high probability of Compton scattering in the scintillator prior to total photoelectric absorption. Obtaining ground-truth training data via Monte Carlo simulations may be possible to unambiguously determine all positions-of-interaction, however resolving the mismatch between the simulations and the true experimental conditions is likely challenging.
2). Pixelated Detectors:
With pixelated scintillation PET detectors, analytical linear estimation techniques such as Anger logic in combination with a pre-defined look-up-table are adequate for positioning, and therefore there has been very few investigations into the use of machine learning or other statistical estimators for estimating the crystal-of-interaction. In fact, the absence of a requirement for a complicated estimation method with these detectors likely contributes to the prevalent use of this detector design in commercial systems.
However, machine learning can still play an important role in improving the positioning accuracy of these common detectors, primarily in the identification of inter-crystal scatter events [34]. Inter-crystal scatter is the process by which the 511 keV photon first undergoes Compton scattering in one or multiple locations in the monolithic scintillator volume, or different crystal elements in a pixelated detector, before undergoing photoelectric absorption at a different location or crystal element. In pixelated detectors, the described scattering-photoelectric cascade may also occur within a single crystal (intra-crystal scatter). Although intra-crystal scatter does not lead to crystal misidentification, the resulting ambiguity in the depth-of-interaction degrades spatial resolution, and also often degrades energy resolution when using long scintillator crystals. Depending on the amount of energy deposited in each detector element (i.e. scattering angle), the position-of-interaction can be misidentified away from the true line-of-response vector. Additionally, inter-crystal scatter often results in a loss of detection sensitivity: by depositing energy in multiple crystals, the event may be rejected by the energy window for the crystal to which the event is assigned, even if the full 511 keV was deposited throughout the interaction chain. The main challenge in correctly identifying and positioning inter-crystal scatter events is the very low light output generated from the low angle Compton scattering events and, making the determination of the correct 511 keV photon trajectory in the crystal difficult.
A method to identify inter-crystal scatter events using SVM was described for a multi-layer DOI detector [35]. The SVM method is used to distinguish multiple peaks in the measured light distribution indicative of inter-crystal scatter, from single peaks that represent purely photoelectric absorption. The SVM method achieves the best identification performance compared to peak searching and principal component analysis methods. The main benefit of SVM compared to neural network-based methods, aside from the algorithm simplicity and absence of an often time-consuming network training step, is that SVM regression always finds the global minimum whereas training multilayer neural networks is more susceptible to stopping at a local minimum [18]. However, the study used only simulated data, making obtaining the training data labels trivial; doing so experimentally remains challenging.
A neural network approach for identifying and including characterized inter-crystal coincidences in the reconstruction was proposed by Michaud et al for the LabPET scanner [36]. During the pre-processing step, the coincidence sorter identifies triplet coincidences that likely arise from inter-crystal scatter based on the measured energies and hit positions in the detectors. Using Monte Carlo simulated training data, a feed-forward artificial neural network is trained to identify the most probably line-of-response from the triplets and preserve the true coincidences. This method showed highly promising results, most importantly providing a 54% increase in sensitivity with measured data generated from the LabPET research PET scanner.
B. Timing
One of the most strongly impacted measures from the low light output in a PET detector is the time-of-interaction estimate, since only the first few scintillation photons contribute meaningfully to the timing estimate, placing greater pressure on the signal processing algorithm used to extract the timing information from the photodetector signals. The precision in estimating the time-of-interaction is defined as the timing resolution, and determines the time-of-flight (TOF) capabilities and random coincidence rejection of the scanner. Similar to position estimation, numerous physical processes contribute to timing uncertainty that presents difficulty for the use of analytical models used for timing discrimination. These include the generation of scintillation light, variable light propagation in the scintillator crystal that is influenced by the detector design and fabrication methods, timing jitter introduced by the electrical conversion and charge amplification in the photodetector, and random noise sources such as dark noise, optical cross-talk and after-pulsing.
In nearly all PET detectors, the time-of-interaction is estimated using simple linear methods that measure the time at which the photodetector signal crosses a pre-defined threshold [37]. However, these methods condense all the potentially useful timing information contained in the detector waveforms into a single linear estimator, not likely an optimal use of the information contained in photodetector signals. Since the time-varying photodetector signal carries all the information that describes the time-of-interaction in the scintillator, the timing discrimination algorithm should ideally be based on digitizing the rising edge of the signals and extracting features in the photodetector signals that describe the time-of-interaction using a non-linear statistical estimator, a task well suited for a variety of machine learning algorithms. A second motivator for the use of supervised machine learning algorithms for PET timing estimation comes from a practical standpoint; unlike other estimation tasks encountered in radiation detection (e.g. position estimation), it is trivial to experimentally obtain ground-truth labeled training data for TOF-PET. Since the two 511 keV annihilation photons are produced at the same time, the time-of-flight difference between the photons is determined exactly by the speed of light and the difference in distance from the annihilation site to each of the detectors in which the photons interact. Ground-truth TOF-labeled training data can thus be easily obtained by moving a point source of radiation over a small distance range between a pair of detectors, a range of known time-of-flight differences can be achieved.
One of the earliest investigations of machine learning timing discrimination was described by Leroux et al [38], who used a multilayer artificial neural network to estimate the time-of-interaction from the digitized photodetector waveforms. Two detectors were compared, an LSO-APD detector and a BGO-APD detector, both tested in coincidence with a fast reference detector used to trigger the waveform digitizer. However, the neural network timing discriminator provided negligible improved in timing resolution compared to digital constant fraction discrimination, possibly because of the low sampling rate used in the study (100 MHz).
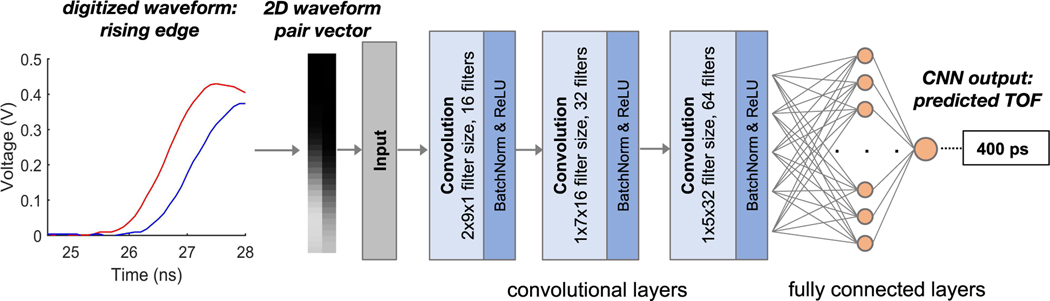
We recently developed a technique to estimate the time-of-flight difference for a coincident 511 keV event directly from the digitized waveforms of two LYSO – PMT detectors using CNNs (Figure 3) [39]. The main motivation for using CNNs here is their ability to learn complex representations of the input data with minimal human engineering [40], and thus is suitable for estimating the time-of-interaction from the waveforms that are confounded by several complex random processes. Due to the convolution operations applied in the hidden layers CNNs also benefit from translational invariance, meaning the output is not biased by the exact alignment or synchronization of the waveforms with respect to the digital sampling period. However, careful pre-processing and training setup must be ensured to avoid over-fitting or fitting to local minima rather than the global minimum.
Fig. 3.
Schematic outline of a representative CNN used to estimate PET time--of--flight from digitized waveforms. Only the rising edge of the signal is shown on the left plot.
For each coincident event the digitized waveforms are stored as a 2D vector, where the first dimension is the number of detector channels (two in this case, but there is likely no limitation in adding more channels, for example waveforms from multiple photodetectors common in PET block detectors). The second dimension represents the length of the digitized waveform. Since essentially all the timing information is contained in the first few nanoseconds of the waveforms, it is not necessary to store the entire waveform for TOF estimation, the rising edge is sufficient. Ground-truth labeled training data was acquired by stepping a 68Ge point source +/− 7.5 cm about the midpoint between the detectors in 5 mm increments.
Timing resolution obtained with the test dataset was compared for CNN timing estimation vs. leading edge and constant fraction discrimination implemented on the digitized signals in post-processing. We found a significant improvement in coincidence timing resolution with CNNs vs. two conventional methods, 20% (231 ps vs. 185 ps) for leading edge and 23% (242 ps vs. 185 ps) for CFD. We recently extended CNN TOF estimation to detectors comprised of 20 mm long BGO crystals coupled to SiPMs, a configuration that has been previously investigated for TOF-PET by exploiting the prompt Cerenkov emissions in the BGO crystal for improved timing compared to the slow scintillation light [41, 42]. We found a similar improvement in timing resolution, achieving a coincidence timing resolution of 371 ps FWHM and 1136 ps FWTM.
A similar method to extract the time-of-interaction directly from the detector waveforms was proposed with a library approach [43]. A waveform library is generated for a range of time-of-flight values between coincident detectors in the J-PET system, then the time-of-flight for a test event is assigned based on the most similar library waveforms. Again, this library approach is attractive due to its implementation simplicity and excellent correspondence between the test and library waveforms, but is challenging to implement due to high computational demands of comparing the test waveforms with a large number of library waveforms.
C. Summary
Table I summarizes the challenges and machine learning methods used in PET detectors. An important technology development that has enabled some of the described machine learning signal processing algorithms, especially for timing estimation, has been fast, affordable waveform digitizers [44]. It is expected that these technologies may be incorporated into the system electronics of PET scanners in the future to facilitate the use of machine learning or other statistical estimators for position and timing estimation [45, 46]. Another technology needed for realistic implementation of machine learning methods in PET detectors is their deployment in the front-end electronics (i.e. FPGA) to avoid the pitfalls associated with storage and offline processing of the raw digitized waveforms from each of the photodetectors, which is especially challenging at high event rates. Fortunately, several of the machine learning methodologies described here were already implemented in FPGAs and showed possibility for high event rate data processing [26, 38, 47].
TABLE I.
Challenges and machine learning methods in PET detector
| Position (x,y,z) | |||||
|---|---|---|---|---|---|
| Monolithic detectors: | |||||
| Challenge: Determine position-of-interaction in the scintillator from the distribution of scintillation light measured by the photodetectors | |||||
| Algorithm: Train a machine learning model to map the charge collected by each photodetector (input) to position-of-interaction (output). Training data acquired with a narrow beam of photons or with simulated data. | |||||
| Estimate position (2D and 3D) with artificial neural network (ANN) [16, 20–24]. | Estimate position with gradient tree boosting algorithm [25–27]. | Estimate 2D position in quasi-monolithic detector with convolutional neural network (CNN) [28]. | Estimate position using a library of reference signals and k nearest neighbors (k-NN) [29–31]. | ||
| Pixelated detectors: | |||||
| Challenge: Determine and recover inter-crystal scattering (photon interacts in two or more crystals) | |||||
| Algorithm: Train a machine learning model to map the charge collected bv each photodetector (input) or charge to position-of-interaction (output). Training data acquired with a narrow beam of photons or with simulated data. | |||||
| Identify inter-crystal scatter in multi-layer DOI detector with support vector machine (SVM) [35]. | Identify trues from triplet coincidences caused by inter-crystal scatter using artifical neural network (ANN) [36]. | ||||
| Timing (TOF) | |||||
| Challenge: Determine time-of-flight with ~hundreds psec precision from noisy photodetector signals. | |||||
| Algorithm: Train a machine learning model to estimate timing from digitized detector waveforms. Training data acquired experimentally with known source-to-detector distances. | |||||
| Use ANN to estimate timing pick-off from digitized waveforms [38]. | Use CNN to estimate time-of-flight directly from set of coincidence waveforms [39]. | Estimate time-of-flight from library of digitized waveforms and k-NN algorithm [43]. | |||
One challenge facing the practical use of machine learning methods for PET detector signal processing is the need for more efficient and scalable calibration methods. The pencil-beam methods are extremely time consuming (sometimes up to several days for a single detector), and require a dedicated experimental setup with robotic stages. Recently, there have been several methods proposed for improving the practical acquisition of training data for monolithic detectors [26, 32, 48–50]. For monolithic detectors, these approaches have focused on simplifying or accelerating the training data acquisition, such as using fan-beam or even uniform irradiation instead of pencil-beam irradiation. These accelerated data acquisition techniques are then accompanied by unsupervised data clustering techniques such as -means or self-organizing maps to obtain the training dataset. Spatial resolution is generally maintained with these methods, indicating that good quality training data can be produced with the data clustering methods.
For timing estimation with CNNs or another similar approach, one concern and possible limitation is the need to acquire training data over a range of time-of-flight differences. In our initial work with CNN TOF estimation, a stepped point source was used to vary the TOF. The practical difficulties in scaling this data acquisition to a larger system containing more than two detector modules can easily be appreciated. It would be highly desirable to be able to acquire labeled training data using a stationary point source or some other practical method. We postulate that it is possible to obtain pseudo-ground-truth labeled TOF training data by shifting the digitized waveform pairs either forward or backward in time relative to one another using digital post-processing techniques. In this way, we can obtain training data with arbitrary TOF labels. This method was recently validated [51], demonstrating that nearly identical timing resolution can be obtained with training data acquired with digital TOF offsets compared to using a stepped point source. The further development of practical methods for acquiring the training data needed for machine learning algorithms represents a crucial component in translating these methods to the system-level.
In the future, we envision the use of machine learning signal processing algorithms that simultaneously estimate position-, energy-, and time-of-interaction directly from the set of photodetector waveforms. This would not only provide a convenient all-in-one estimator, but likely also provide overall better detector performance. Although position, energy, and time-of-interaction are treated as independent parameters in the detector signal processing, they are in fact not physically independent. Most evident is the dependence of the timing estimate on the position-of-interaction and energy deposited by the photon; the position-of-interaction in the scintillator influences the propagation time of the scintillation light to each photodetector, while the energy deposited by the 511 keV photon determines the number of scintillation photons and therefore the early photon flux that limits and potentially biases the timing estimate. Neural network methods using CNNs have already shown to be successful for timing discrimination using digitized waveforms, and it appears plausible that this method could be adapted to include the waveforms from multiple photodetectors in the CNN input, from which the CNN is able to estimate the position-of-interaction.
IV. MACHINE LEARNING IN QUANTITATIVE IMAGE RECONSTRUCTION
For PET imaging, the measured emission sinogram data can be modeled as a collection of independent Poisson random variables and its mean is related to the tracer distribution image through an affine transform [52]
| (3.1) |
where is the detection probability matrix, and are diagonal matrices containing the LOR efficiency factors and attenuation factors (AFs), respectively, is the expectation of scattered events, and denotes the expectation of random events. is the number of LORs and is the number of image voxels. For quantitative image reconstruction, all the components in (3.1) need to be estimated either before the image reconstruction or during the reconstruction process. Among them, the detection probability matrix is usually pre-computed based on the scanner geometry and detector properties. The element, , denoting the probability of a photon pair produced in voxel reaching detector pair , can be computed either analytically using ray-tracing techniques [53], or by Monte Carlo simulations [52] or real point source measurements [54]. The LOR efficiency factors model the effect of imperfect detector sensitivities and are often estimated using calibration scans of sources with known activity distribution [55]. The expectation of random events can be estimated from either the single-event rates or delayed window measurements [56]. In contrast, the estimation of the attenuation factors and the expectation of scatter events are more challenging, at least in some cases, and will be discussed in more detail below. Furthermore, even with everything estimated properly, the reconstructed PET images still suffer high noise due to limited number of detected coincidence photons counts, as well as the ill-posedness of the detection probability matrix . Machine learning has provided new ways to tackle these problems encountered in PET image reconstruction. A range of studies have demonstrated its feasibility and advantages over traditional methods. Below we will review the development of machine learning methods for attenuation correction, scatter correction, noise reduction, and also integration of deep learning methods in iterative image reconstruction [57–59].
A. Attenuation correction
Correction for the object attenuation of annihilation photons is essential for accurate estimation of radiotracer concentration using PET because on average less than 10% annihilation photon pairs can escape from an adult human body without attenuation. In PET/CT, the attenuation map can be easily obtained from the CT image using a bilinear scaling transform. However, this is not the case in PET/MR scanners because the MR signal is not directly related to the photon attenuation coefficients, and there is no simple transform that can convert a MR image into the attenuation map directly.
To address this issue, many methods have been proposed to generate pseudo-CT images from MR images based on T1-weighted, Dixon, ultra-short echo time (UTE) or zero echo time (ZTE) sequences. One commonly used approach relies on an atlas generated from existing patient CT and MR image pairs [60–63]. A pseudo CT is created by non-rigidly registering the atlas to the patient MR image. With the availability of time-of-flight information, joint estimation of the emission and attenuation images is also achievable [64–68]. Another approach is based on image segmentation: the MR image is segmented into different tissue classes with the corresponding attenuation coefficients assigned to produce the attenuation map [69–76]. Various machine learning methods have also been proposed, including fuzzy-mean clustering [77], random forest [78], and Gaussian mixture regression [79]. For more details about these methods, readers are referred to previous review papers specifically about MR-based AC [80–84].
One major challenge in generating the attenuation map from an MR image is the differentiation between bone and air regions which have similar intensities in most MR sequences but vastly different attenuation coefficients for high-energy photons. Misclassification between bone and air can introduce large errors in PET images, affecting the quantification accuracy and resulting in misdiagnosis. One susceptible region is the nasal sinuses due to the proximity of bone and air regions. Bone-air misclassification can result in considerable quantification errors in the frontal lobe. This can cause inaccurate diagnosis for frontotemporal dementia. Another region is the mastoid part of the temporal bone, the mastoid process, which is also mixed with bone and air. Inaccuracy of bone prediction for this region can change the apparent cerebellar uptake, which can affect tracer kinetic analysis of the entire brain, because the cerebellum is often adopted as the reference region in kinetic modeling [85]. In addition to bone-air misclassification for the brain, bone-fat mis-classification in pelvic regions can also cause large errors in, or near, bone regions [86, 87].
| (3.2) |
where the first item denotes the pixel-to-pixel difference between the ground truth , , and the network generated , , and the last three items represent the gradient difference between and along the , and directions, respectively. and are used to adjust the strength of pixel-intensity and pixel-gradient differences. The norm is preferred over the norm to preserve more edge details, because in CT images the bone region is often thin, and the contrast is high. The network structures employed in most of these CNN approaches are based on the U-net structure [97], due to its excellent performance for synthetic image generation as first demonstrated in [88]. In [89], the segmented region labels were employed as training labels so that the pseudo-CT generation is translated to the MR tissue classification problem. In [90], both Dixon and ZTE images were used as the network input. In order to efficiently exploiting the input information, the convolution modules in deeper layers of the U-net were replaced by group-convolution modules, similar to the modules used in ResNeXt [98]. In [90, 94], multiple-contrast MR images were used as the network input. Apart from employing MR images as the network input, simultaneously reconstructed emission and attenuation images from TOF PET data have also been used [93, 96]. Furthermore, there have been studies trying to train a CNN to directly map reconstructed images without attenuation correction to images with attenuation correction [99–101]. In these cases, no additional anatomical image was utilized. One advantage of deep neural networks is the ability to incorporate information from multiple sources without any preprocessing. However, finding an efficient network structure for the optimal information integration is worth further investigation.
Beyond CNNs, several studies have exploited generative adversarial networks (GANs) [102–104] for pseudo-CT generation. In GAN, there are two networks trained simultaneously [105], one is the generative network and the other is the discriminative network . The generative network takes the MR image as the network input and outputs the pseudoCT image. The discriminative network then determines whether the pseudo-CT generated from is fake (0) or real (1), and outputs a value between 0 and 1. During the training phase, the generative network tries to generate the pseudoCT image close to the real CT image, and the discriminative network attempts to distinguish the pseudo-CT image from the real CT image. The whole process can be expressed as an alternating minimax optimization of the discriminative loss defined as
| (3.3) |
Directly training GANs based on the discriminative loss defined in (3.3) is not easy [106] and several papers have thus combined the discriminative loss with the pixel-intensity and pixel-gradient loss to improve the pseudo-CT image quality [107–109]. In [102], a combination of the discriminative loss and the pixel-to-pixel loss defined in (3.2) is used. The improvement of adding the discriminative loss compared with using the pixel-to-pixel loss has been demonstrated. In [104], apart from the GAN for pseudo-CT image generation, another GAN for CT image segmentation was introduced to constrain the shape of the generated pseudo-CT. One requirement of combining the pixel-to-pixel loss or the segmentation-based loss with the discriminative loss is that the MR and CT images should be well registered. This is easy for brain regions, where rigid registration is sufficient. For other organs, such as the head and neck region and the lung region, accurate registration is more difficult. One solution to avoid the requirement of co-registration is using the cycle-consistency adversary network (Cycle-GAN), which was originally proposed for the style transfer using un-paired training data [110]. It has been demonstrated that pseudo-CT images can be generated for the brain regions based on T1-weighted MR images using a Cycle-GAN [103]. Currently the GAN-related approaches have only been applied to the brain [102–104] and pelvic regions [102]. More work in other body parts, such as the abdominal or head and neck regions, where registration errors are relatively large and GAN approaches could potentially have a greater impact, is still to be conducted.
B. Scatter correction
Compared with the estimation of random events, estimation of scatter within the patient is far more complex and time-consuming because scatter events depend on both the emission activity distribution and attenuation map. Usually an initial image reconstruction without scatter correction is performed to provide the emission activity distribution for scatter estimation. Then another image reconstruction is performed with the estimated scatter distribution. The procedure can be repeated several times for a more accurate scatter correction.
For the estimation of the scatter mean , Monte Carlo simulation-based photon tracking is considered to be the gold standard, but it is very time-consuming to generate enough number of counts to reduce noise in the estimate. The 3D single scatter simulation (SSS) approach is widely adopted in commercial scanners due to its fast computational time [111, 112]. However, SSS assumes only one scatter for each scattered event and there is still room for improvement when multiple scatters are considered. In theory, all the information required for scatter estimation is contained in the emission data and attenuation factors (AF). The latter determines the attenuation map and jointly they determine the emission image. Therefore, machine learning provides a suitable tool to find the mapping from the emission data and attenuation factors to the expectation of the scatter events.
Fig. 4 shows an example set of 2D sinograms from a patient PET scan, including the emission sinogram, the log of attenuation correction factor (), and the scatter mean estimated using 3D SSS. The scatter mean sinogram is spatially smooth, and the distribution pattern is correlated with the emission data and log(ACF). Machine learning approaches can be used to learn the scatter-mean image, by training a mapping function with the emission data events and log(ACF) as the input. Once the mapping is learned during training, the inference process will take less time compared with current scatter estimation process. In addition, the Monte-Carlo-simulated scatter means can be employed as training labels, which is much easier to be obtained compared to other medical imaging tasks as no extra patient datasets are needed. The predicted results can be better than the SSS approach as the learning process takes multiple scatters into consideration. However, the prediction can also fail if the testing data do not lie in the same space as the training data, due to abnormal activity distribution or new organ structures.
Fig. 4.
A set of 2D sinograms extracted from a 3D PET dataset of a patient scan, (a) The emission sinogram, (b) the log(ACF) sinogram, and (c) the estimated scatter sinogram based on the 3D SSS model. The vertical axis is the radial distance ranging from −35 cm to +35 cm and the horizontal axis is the projection angle ranging from 0 to 180 degree. The radiotracer is 18F-FDG.
Currently there are several on-going efforts trying to use deep learning to estimate the scatter mean following some success in scatter prediction for x-ray CT [113, 114] . A U-net structure was used [97]. The emission sinogram, AF and log(ACF) were employed as the network input and the training label comes from the scatter mean estimated by the SSS approach. The training loss function was constructed based on the Poisson distribution assumption of the scatter events. The trained network can predict the scatter mean reasonably well for the brain region, with a normalized mean absolute error rate (NMAE2) of 4.17% compared to the SSS method [115]. For the prostate region, due to the influence of high uptake from the bladder as well as field-of-view limitations, the NMAE error can be as high as 14.11%. The advantage of the deep learning method is the computation speed: less than 30s for the CNN predication compared to 3.5 min for the SSS computation, for a whole-body PET scan with 5 bed positions. The computational advantage will be even greater if the CNN is used to predict the Monte-Carlo-based multiple scatter estimation. Apart from employing deep learning to predict the scatter mean, it is also feasible to estimate essential components of the scatter model. For example, a 1D Gaussian kernel can be applied to convolve the scatter mean estimated from SSS to approximate the multiple scatter estimation [116]. This convolution kernel can be replaced by a neural network to predict multiple scatter profiles from single scatter profiles as shown in [117]. The network input is the single scatter profile and the network output is the multiple scatter profile.
In addition to predicting scatter mean in the raw data space, the work in [99] proposed a joint correction of attenuation and scatter in the image space using a CNN. The network input was the uncorrected image (without attenuation and scatter corrections (NASC)), the label was the attenuation and scatter corrected image, and the L2 norm between the network output and the training label was chosen as the training objective function. The mean SUV differences (mean ±SD) compared with the CT-based attenuation and scatter correction were 4.0 ± 15.4%. The large variation of the CNN result was due to an outlier in the test subjects with a mean difference of 48.5 ± 10.4%. Another test subject also showed relatively large differences (–13.5%) for the tumor uptake. The existence of outliers highlights some potential pitfalls of deep learning-based methods. Part of the reason is that as the theory has shown, TOF PET data only determines the attenuation factors up to a constant, which means TOF PET data alone are not sufficient to determine both the emission activity image and attenuation map that are required for scatter estimation. Therefore, it may not be totally surprising that a deep CNN cannot perform perfect attenuation and scatter correction from NASC PET images. It also indicates that domain specific knowledge is still helpful in the era of deep learning.
Currently the potential of deep learning in scatter correction is still being explored. There is no large patient study performed to demonstrate the robustness of the deep learning approach for scatter estimation, so further evaluation is needed.
C. Noise reduction (denoising)
Due to limited counts detected and various physical degradation factors, PET images have a higher noise level3 compared to CT and MR images. Noise can reduce lesion detectability and introduce quantification errors, leading to inaccurate diagnosis/staging of diseases. In addition, for longitudinal studies or scans of pediatric populations, it is desirable to reduce the dose level of PET scans, which would further increase the noise level. The high noise level also prevents PET images from being reconstructed at its highest spatial resolution because post-reconstruction filtering is often required to reduce noise. Therefore, reducing image noise can allow PET images to be reconstructed at a higher spatial resolution, which will be beneficial for many PET applications, such as cancer detection and staging, and identification of Tau deposition pattern for tracking the progression of the Alzheimer’s disease.
Traditional methods for PET image denoising includes non-local mean method [118, 119], HYPR filter [120] and guided image filter [121]. Sparse representation approaches, such as dictionary learning, have been shown to improve PET image quality [122, 123]. Apart from dictionary learning, the prediction of high-quality image from low-quality image can also be treated as a regression problem, and the random forest regression method has also been investigated [124]. With the availability of PET/CT and PET/MR scanners, anatomical priors can be utilized for PET image denoising [125]. Also, the prior PET scans of the same patient can be used to reduce noise in follow-up PET scans [126, 127].
In recent years, deep learning methods have shown great potential for low-level image processing tasks, such as super resolution [128, 129] and denoising applications [130]. These methods have also been applied to static PET image denoising and demonstrated better performance than traditional denoising approaches for various tracers and tasks [131–143]. For deep learning methods, most networks were trained with shorter-scan PET images as the input and longer-scan PET images as the label. Anatomical priors from MR/CT images can be used as additional network-input channels to improve PET image quality [131, 132, 135, 137, 138]. In [135] multicontrast MR images were employed as the network input. Again, this is one advantage of deep learning approaches as no user-defined weighting between low-quality PET and anatomical prior images is needed. Since PET images are intrinsically 3D, 3D convolutional operations have been proposed for PET images [133, 136]. To reduce the trainable parameters and memory usage, 2D convolution has also been adopted by supplying multiple neighboring axial slices as additional network-input channels to utilize the axial information and reduce artefacts [132, 134]. In addition to CNNs, GANs were also investigated [133, 141, 143]. Apart from the commonly used metrics to evaluate image quality shown in most of the studies, e.g. structural similarity index (SSIM), peak signal-to-noise ratio (PSNR), contrast-to-noise ratio (CNR), and contrast recovery coefficient (CRC) vs. standard deviation (STD), clinical image quality scores and amyloid status rated by radiologists were reported in [135]. Apart from denoising in the image domain, applications of CNN to pre-processing steps in the sinogram domain have also been explored, such as sinogram super-resolution [144] and gap filling [145].
One reason for the success of deep learning in computer vision is the availability of large amounts of training data. For medical imaging, acquiring a large number of training pairs is not an easy task. With the developments of realistic phantoms, such as BrainWeb [146] and XCAT [147], and advanced physics modeling approaches, data augmentation using simulated datasets is possible. In [134], phantom data were first exploited to initialize the network, and real datasets were employed to fine-tune the last several layers of the network. The benefits of this data augmentation approach are shown in Fig. 5. Recently the deep image prior framework [148] shows that the noisy image itself can be treated as the training label and intrinsic structures of the noisy image can be learned through network parameter optimization. No high-quality PET training labels are needed in this process. Following this framework, in [136], the MR or CT image from PET/CT or PET/MR scans was used as the network input and the noisy PET image itself was employed as the training label to perform image denoising.
Fig. 5.
Sagittal view of the clinical lung test data set using different denoising methods. Spine regions in the sagittal view are zoomed in for easier visual comparison. First column: EM image smoothed by Gaussian denoising; second column: EM images smoothed by NLM denoising; third column: EM image denoised by CNN trained from simulated phantom; fourth column: EM image denoised by CNN from real data only; fifth column: EM image denoised by CNN with fine-tuning. Permission to reuse this figure obtained from Gong et al 2018.
One unique feature of PET is its intrinsic dynamic-imaging ability, by which tracer pharmacokinetic parameters and corresponding physiologic information can be derived [149]. In dynamic imaging, the collected coincidence data are divided into various frames in time. Based on specific kinetic models [150], parametric images, reflecting metabolism rate, receptor binding or perfusion rate, can be derived. Compared to static PET imaging with the same scanning time, the image quality of parametric images can be much worse for compartmental models due to the ill-posedness of the fitting procedure. There are two ways that a CNN can be applied to improve dynamic PET imaging. The first approach is to use a neural network to denoise dynamic PET images before the kinetic fitting step, by processing either one frame at a time [139] or all frames together [151, 152]. The frame-by-frame approach is similar the static PET image denoising, but the variation in tracer distribution and noise level among the dynamic PET frames requires special handling. In contrast, processing all the frames together can exploit both spatial and temporal information. The second approach is to train a network to map dynamic PET images to corresponding parametric images directly. Such direct mapping is especially useful for PET data with missing time points. For example, in [153] dynamic PET images from a partial scan, along with MR images providing cerebral blood flow (CBF) and structure information, were used to predict binding potential (BP) images derived from the full 60-min scan. The use of a CNN avoids the difficulty of providing an explicit model between the MR information and the binding potential. The BP image generated by the network shows better image quality than those derived based on the simplified reference tissue model with partial data. However, such approaches are difficult to implement to improve the image quality of parametric images derived from the full 60-min scan, because of the lack of even longer dynamic PET scans. To address this issue, a modified deep image prior framework, which included the kinetic modeling in the training function, was applied to parametric image estimation based on the Logan plot [154]. The network input is the CT prior image and the network output is the parametric image. The network was trained during the parametric image estimation and no high-quality reference image was required in this approach.
In summary, various studies have applied deep learning approaches to static and dynamic PET image denoising and show better performance than state-of-the-art methods. Currently most of the experiments are based on using 18F-FDG as the tracer, with some studies on 18F-Florbetaben for amyloid imaging [135], 11C-UCB-J for synaptic density imaging [139], and 68Ga-PRGD2 for lung cancer studies [136]. Obviously, patterns of tumor uptake in oncology studies is totally different from amyloid imaging in dementia studies. Whether a network trained using existing tracers can be applied to PET scans of a new tracer is unclear and deserves more study [155]. In addition, recurrent neural networks (RNNs) can also be considered for dynamic PET imaging to utilize the temporal information. Another important topic for dynamic imaging is the estimation of the blood input function (radiotracer activity in the arterial blood as a function of time). Whether we can use the deep learning approach to determine the blood input function based on partial data needs further experimental validation.
D. Image reconstruction
Apart from image denoising, machine learning methods have also been incorporated in PET image reconstruction. Here we only cover deep neural network-based image reconstruction methods. For other machine learning approaches, readers are referred to another review article in this issue dedicated to image reconstruction [156].
Most existing studies focus on the penalized likelihood reconstruction framework where the unknown PET image is estimated by
| (3.4) |
is the log-likelihood function and is a penalty function with being the hyperparameter. A neural network can be used either inside the penalty function or replace it altogether. Because of the additional constraint from the log-likelihood function , the reconstruction approach is expected to be more robust to the mismatches between the training and testing data than the denoising approach.
One class of methods use pre-trained denoising networks. In [157], a denoising CNN was pre-trained and the penalty function was constructed as the L2-norm difference between and the network output. To make the network robust to different noise levels, a local linear fitting procedure, similar to the guided image filter [158], was performed during each iteration to make the network output match the intermediate penalized reconstruction result. The effect of the local linear fitting procedure is similar to fine-tuning the last spatial-variant layer of the neural network during each iteration. Another approach is using a pre-trained network to represent the PET image and performing a constrained maximum likelihood estimation
| (3.5) |
where denotes the pre-trained network and is an arbitrary input [58]. This is an extension of the linear representation using the kernel method [159]. Compared with the kernel method, a deep neural network has a stronger representation power and can take advantage of the inter-subject prior information in the training data. During the image reconstruction process, the network parameters were fixed and the network input was updated. This method was further extended in [160], where a self-attention GAN structure [161] was used and an additional constraint on the network input was added to stabilize the reconstruction process. The network representation-based reconstruction framework is similar to the multi-layer convolutional sparse coding (CSC) framework [162], where the filter parameters were fixed and the coefficients were updated.
In an effort to avoid pre-training a network with a large number of training images, Gong et al applied the deep image prior framework [148] to PET reconstruction [57]. Through representing the PET image by a neural network, the image reconstruction process was transferred to a network training process. The training label is the PET sinogram and the training objective function was the log-likelihood function of the sinogram data. The network was trained from scratch during the image reconstruction process without using any other training images. This unsupervised learning framework has also been extended to the direct parametric PET reconstruction [163, 164], where acquiring high-quality training data is more difficult.
Another class of methods use the novel scheme of unrolling the iterative updates and replacing the regularization operation by a neural network [165, 166]. Compared to traditional network training, the data-consistency module is involved in the training process. During inference, it is similar to the traditional iterative image reconstruction. This unrolled neural network approach has been widely used in MR community as the forward and backward projections can be easily performed via fast Fourier transform (FFT). For PET, the forward and backward projections are computationally intensive, and the total training time is much longer than that for a denoising network. In addition, clinical PET data are routinely acquired and reconstructed in the fully 3D mode, making the GPU memory a limiting factor when there are multiple unrolling modules. More efforts are needed to advance the application of unrolled neural networks to PET image reconstruction.
Finally, there are also efforts on training a deep network to perform the end-to-end mapping from the sinogram data to the PET image, where the iterative reconstruction process is not needed and the inference process is fast [167]. As no PET physical models are involved in this mapping, a network with a larger transforming capability is needed in order to learn the mapping, thus requiring more training data.
V. SUMMARY AND OUTLOOK
We have seen a dramatic increase in the applications of machine learning in PET imaging in the last couple years. As discussed in this review, machine learning has found applications in both the front-end detector electronics and back-end image processing aspects of PET imaging. With the availability of digitized waveforms from each of the photodetectors and increasing hardware computing power, we expect to see more machine learning based solutions to improve the accuracy and sensitivity of photon detection in PET detectors as well as to reduce bias and variance in quantitative PET image reconstruction.
With an increasing variety of machine learning methods being proposed, one area that requires more attention is task-based evaluation. Some initial work has been performed [168], but more studies using large clinical datasets are needed. This is more critical for deep learning-based methods than for traditional methods because deep learning-based methods are less interpretable, and their generalizability is not guaranteed. One revealing example is given in [167], where a deep neural network trained to perform PET image reconstruction at one count level failed completely when the count level was changed. Such a dramatic breakdown was not seen with traditional iterative reconstruction algorithms. While this specific problem might be solved by including more diverse training data, it underscores the importance of critically evaluated deep learning-based methods using a large dataset. For example, in most existing studies, the images employed during network training are from normal anatomy. For abnormal structures, such as broken skulls, which are common among traumatic brain injury (TBI) patients, or brain regions after surgery, the robustness of network predictions of these special situations requires further investigation. In practice, the conditions under which a deep learning method has been evaluated and verified need to be specified more clearly than that for the traditional methods and care has to be taken to make sure those conditions are satisfied to avoid unexpected results with potentially large ramifications for a given patient..
Acknowledgments
This work was supported in part by the U.S. National Institutes of Health under Grants R01 EB000194 and R03 EB027268.
Biographies
 Kuang Gong received his B.S. degree in Information Science and Electronic Engineering (ISEE) from Zhejiang University in 2011, M.S. degree in Statistics and Ph.D. degree in Biomedical Engineering from UC Davis, in 2015 and 2018, respectively. He is currently a Research Fellow in the Department of Radiology, Massachusetts General Hospital, Harvard Medical School. His research interests include image reconstruction methods, medical imaging physics, as well as machine learning applications in medical imaging.
Kuang Gong received his B.S. degree in Information Science and Electronic Engineering (ISEE) from Zhejiang University in 2011, M.S. degree in Statistics and Ph.D. degree in Biomedical Engineering from UC Davis, in 2015 and 2018, respectively. He is currently a Research Fellow in the Department of Radiology, Massachusetts General Hospital, Harvard Medical School. His research interests include image reconstruction methods, medical imaging physics, as well as machine learning applications in medical imaging.
 Eric Berg received his B.S. (2012) in Physics and Astronomy from University of Manitoba, Canada, and his Ph.D. (2016) in Biomedical Engineering from University of California, Davis. Since 2016, Eric has held a postdoctoral scholar position at University of California, Davis. His research includes the development of machine learning methods for signal analysis in PET detectors, in particular time-of-flight detectors, along with instrumentation and software development for new total-body PET systems.
Eric Berg received his B.S. (2012) in Physics and Astronomy from University of Manitoba, Canada, and his Ph.D. (2016) in Biomedical Engineering from University of California, Davis. Since 2016, Eric has held a postdoctoral scholar position at University of California, Davis. His research includes the development of machine learning methods for signal analysis in PET detectors, in particular time-of-flight detectors, along with instrumentation and software development for new total-body PET systems.
 Simon R. Cherry received his BSc (Hons) in physics with astronomy from University College London in 1986 and his PhD in medical physics from the Institute of Cancer Research, University of London, in 1989. After a postdoctoral fellowship at the University of California, Los Angeles (UCLA), he joined the faculty in the UCLA Department of Molecular and Medical Pharmacology in 1993. In 2001, Dr. Cherry joined UC Davis as a professor in the Department of Biomedical Engineering and he is now a Distinguished Professor. He served as chair of the Department of Biomedical Engineering at UC Davis from 2007 to 2009. Dr. Cherry is an elected fellow of six professional societies, including the Institute for Electronic and Electrical Engineers (IEEE) and the Biomedical Engineering Society (BMES). He is editor-in-chief of the journal Physics in Medicine and Biology. Dr. Cherry received the Academy of Molecular Imaging Distinguished Basic Scientist Award (2007), the Society for Molecular Imaging Achievement Award (2011) and the IEEE Marie Sklodowska-Curie Award (2016). In 2016, he was elected member of the National Academy of Engineering, and in 2017 he was elected to the National Academy of Inventors. Dr. Cherry has authored more than two hundred peer-reviewed journal articles, review articles and book chapters in the field of biomedical imaging. He is also lead author of the widely used textbook Physics in Nuclear Medicine.
Simon R. Cherry received his BSc (Hons) in physics with astronomy from University College London in 1986 and his PhD in medical physics from the Institute of Cancer Research, University of London, in 1989. After a postdoctoral fellowship at the University of California, Los Angeles (UCLA), he joined the faculty in the UCLA Department of Molecular and Medical Pharmacology in 1993. In 2001, Dr. Cherry joined UC Davis as a professor in the Department of Biomedical Engineering and he is now a Distinguished Professor. He served as chair of the Department of Biomedical Engineering at UC Davis from 2007 to 2009. Dr. Cherry is an elected fellow of six professional societies, including the Institute for Electronic and Electrical Engineers (IEEE) and the Biomedical Engineering Society (BMES). He is editor-in-chief of the journal Physics in Medicine and Biology. Dr. Cherry received the Academy of Molecular Imaging Distinguished Basic Scientist Award (2007), the Society for Molecular Imaging Achievement Award (2011) and the IEEE Marie Sklodowska-Curie Award (2016). In 2016, he was elected member of the National Academy of Engineering, and in 2017 he was elected to the National Academy of Inventors. Dr. Cherry has authored more than two hundred peer-reviewed journal articles, review articles and book chapters in the field of biomedical imaging. He is also lead author of the widely used textbook Physics in Nuclear Medicine.
 Jinyi Qi received his B.S. degree in Electrical Engineering in 1993 from Tsinghua University, Beijing, China, and his Ph.D. degree in Electrical Engineering in 1998 from the University of Southern California. He is now a Professor in the Department of Biomedical Engineering at UC Davis, where he served as the Interim Department Chair from 2015 to 2016. Dr. Qi has been an Associate Editor of IEEE Transactions on Medical Imaging since 2006 and is an elected Fellow of AIMBE and IEEE. His research interests include statistical image reconstruction, medical image processing, image quality evaluation, and imaging system optimization.
Jinyi Qi received his B.S. degree in Electrical Engineering in 1993 from Tsinghua University, Beijing, China, and his Ph.D. degree in Electrical Engineering in 1998 from the University of Southern California. He is now a Professor in the Department of Biomedical Engineering at UC Davis, where he served as the Interim Department Chair from 2015 to 2016. Dr. Qi has been an Associate Editor of IEEE Transactions on Medical Imaging since 2006 and is an elected Fellow of AIMBE and IEEE. His research interests include statistical image reconstruction, medical image processing, image quality evaluation, and imaging system optimization.
Footnotes
FWHM: full width at half maximum
, where is the network output and is the training label estimated based on .
Distribution of PET image noise is neither Gaussian nor Poisson. Only the measured data for each detector bin follow a Poisson distribution.
Contributor Information
Kuang Gong, Department of Biomedical Engineering, University of California, Davis, CA, USA and is now with Massachusetts General Hospital, Boston, MA, USA.
Eric Berg, Department of Biomedical Engineering, University of California, Davis, CA, USA.
Simon R. Cherry, Department of Biomedical Engineering and Department of Radiology, University of California, Davis, CA, USA
Jinyi Qi, Department of Biomedical Engineering, University of California, Davis, CA, USA.
REFERENCES
- [1].van Sluis JJ, et al. , Performance characteristics of the digital Biograph Vision PET/CT system. J Nucl Med, 2019. [DOI] [PubMed] [Google Scholar]
- [2].Budinger TF, Time-of-flight positron emission tomography: status relative to conventional PET. J Nucl Med, 1983. 24(1): p. 73–8. [PubMed] [Google Scholar]
- [3].Carney JPJ, et al. , Method for transforming CT images for attenuation correction in PET/CT imaging. Medical Physics, 2006. 33(4): p. 976–983. [DOI] [PubMed] [Google Scholar]
- [4].Zhang X, et al. , Quantitative image reconstruction for total-body PET imaging using the 2-meter long EXPLORER scanner. Phys Med Biol, 2017. 62(6): p. 2465–2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Cherry SR, et al. , Total-Body PET: Maximizing Sensitivity to Create New Opportunities for Clinical Research and Patient Care. J Nucl Med, 2018. 59(1): p. 3–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Ahn S, et al. , Quantitative comparison of OSEM and penalized likelihood image reconstruction using relative difference penalties for clinical PET. Physics in Medicine & Biology, 2015. 60(15): p. 5733. [DOI] [PubMed] [Google Scholar]
- [7].Anghinolfi F, et al. , NINO: an ultra-fast and low-power front-end amplifier/discriminator ASIC designed for the multigap resistive plate chamber. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2004. 533(1): p. 183–187. [Google Scholar]
- [8].Rolo M, et al. , TOFPET ASIC for PET applications. Journal of Instrumentation, 2013. 8(02): p. C02050. [Google Scholar]
- [9].Miller M, et al. , Characterization of the Vereos digital photon counting PET system. Journal of Nuclear Medicine, 2015. 56(supplement 3): p. 434. [Google Scholar]
- [10].Casey M.and Nutt R, A multicrystal two dimensional BGO detector system for positron emission tomography. IEEE Transactions on Nuclear Science, 1986. 1(33): p. 460–463. [Google Scholar]
- [11].Anger HO, Scintillation camera. Review of scientific instruments, 1958. 29(1): p. 27–33. [Google Scholar]
- [12].Jakoby BW, et al. , Physical and clinical performance of the mCT time-of-flight PET/CT scanner. Physics in Medicine and Biology, 2011. 56(8): p. 2375–89. [DOI] [PubMed] [Google Scholar]
- [13].Joung J, Miyaoka RS, and Lewellen TK, cMiCE: a high resolution animal PET using continuous LSO with a statistics based positioning scheme. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2002. 489(1): p. 584–598. [Google Scholar]
- [14].Schaart DR, et al. , A novel, SiPM-array-based, monolithic scintillator detector for PET. Physics in medicine and biology, 2009. 54(11): p. 3501–12. [DOI] [PubMed] [Google Scholar]
- [15].Melcher C.and Schweitzer J, Cerium-doped lutetium oxyorthosilicate: a fast, efficient new scintillator. IEEE Transactions on Nuclear Science, 1992. 39(4): p. 502–505. [Google Scholar]
- [16].Bruyndonckx P, et al. , Evaluation of machine learning algorithms for localization of photons in undivided scintillator blocks for PET detectors. IEEE Transactions on Nuclear Science, 2008. 55(3): p. 918–924. [Google Scholar]
- [17].Cover T.and Hart P, Nearest neighbor pattern classification. IEEE transactions on information theory, 1967. 13(1): p. 21–27. [Google Scholar]
- [18].Burges CJ, A tutorial on support vector machines for pattern recognition. Data mining and knowledge discovery, 1998. 2(2): p. 121–167. [Google Scholar]
- [19].Krizhevsky A, Sutskever I, and Hinton GE. Imagenet classification with deep convolutional neural networks. in Advances in neural information processing systems. 2012. [Google Scholar]
- [20].Bruyndonckx P, et al. , Neural network-based position estimators for PET detectors using monolithic LSO blocks. IEEE Transactions on Nuclear Science, 2004. 51(5): p. 2520–2525. [Google Scholar]
- [21].Tavernier S, et al. , A high-resolution PET detector based on continuous scintillators. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2005. 537(1): p. 321–325. [Google Scholar]
- [22].De Acilu PG, et al. , Study and optimization of positioning algorithms for monolithic PET detectors blocks. Journal of Instrumentation, 2012. 7(06): p. C06010. [Google Scholar]
- [23].Bronstein AM, et al. , Optimal nonlinear line-of-flight estimation in positron emission tomography. IEEE Transactions on Nuclear science, 2003. 50(3): p. 421–426. [Google Scholar]
- [24].Wang Y, et al. , 3D position estimation using an artificial neural network for a continuous scintillator PET detector. Physics in Medicine & Biology, 2013. 58(5): p. 1375. [DOI] [PubMed] [Google Scholar]
- [25].Friedman JH, Stochastic gradient boosting. Computational Statistics & Data Analysis, 2002. 38(4): p. 367–378. [Google Scholar]
- [26].Müller F, et al. , Gradient Tree Boosting-based Positioning Method for Monolithic Scintillator Crystals in Positron Emission Tomography. IEEE Transactions on Radiation and Plasma Medical Sciences, 2018. [Google Scholar]
- [27].Müller F, et al. , A novel DOI Positioning Algorithm for Monolithic Scintillator Crystals in PET based on Gradient Tree Boosting. IEEE Transactions on Radiation and Plasma Medical Sciences, 2018. [Google Scholar]
- [28].Peng P, et al. , Compton PET: a simulation study for a PET module with novel geometry and machine learning for position decoding. Biomedical Physics & Engineering Express, 2018. 5(1): p. 015018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Marcinkowski R, et al. , Sub-millimetre DOI detector based on monolithic LYSO and digital SiPM for a dedicated small-animal PET system. Physics in medicine and biology, 2016. 61(5): p. 2196. [DOI] [PubMed] [Google Scholar]
- [30].Maas MC, et al. , Experimental characterization of monolithic-crystal small animal PET detectors read out by APD arrays. IEEE transactions on nuclear science, 2006. 53(3): p. 1071–1077. [Google Scholar]
- [31].Maas MC, et al. , Monolithic scintillator PET detectors with intrinsic depth-of-interaction correction. Physics in Medicine and Biology, 2009. 54(7): p. 1893. [DOI] [PubMed] [Google Scholar]
- [32].Borghi G, et al. , Experimental validation of an efficient fan-beam calibration procedure for-nearest neighbor position estimation in monolithic scintillator detectors. IEEE Transactions on Nuclear Science, 2015. 62(1): p. 57–67. [Google Scholar]
- [33].Bruyndonckx P, et al. , Investigation of an in situ position calibration method for continuous crystal-based PET detectors. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2007. 571(1–2): p. 304–307. [Google Scholar]
- [34].Rafecas M, et al. , Inter-crystal scatter in a dual layer, high resolution LSO-APD positron emission tomograph. Physics in Medicine & Biology, 2003. 48(7): p. 821. [DOI] [PubMed] [Google Scholar]
- [35].Yoshida E, et al. , Inter-crystal scatter identification for a depth-sensitive detector using support vector machine for small animal positron emission tomography. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2007. 571(1–2): p. 243–246. [Google Scholar]
- [36].Michaud J-B, et al. , Sensitivity increase through a neural network method for LOR recovery of ICS triple coincidences in high-resolution pixelated-detectors PET scanners. IEEE Trans. Nucl. Sci, 2015. 62(1): p. 82–94. [Google Scholar]
- [37].Monzo J, et al. , Digital signal processing techniques to improve time resolution in positron emission tomography. IEEE Transactions on Nuclear Science, 2011. 58(4): p. 1613–1620. [Google Scholar]
- [38].Leroux J-D, et al. , Time discrimination techniques using artificial neural networks for positron emission tomography. IEEE Transactions on Nuclear Science, 2009. 56(3): p. 588–595. [Google Scholar]
- [39].Berg E.and Cherry SR, Using convolutional neural networks to estimate time-of-flight from PET detector waveforms. Physics in medicine and biology, 2017. 63(2): p. 02LT01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].LeCun Y, Bengio Y, and Hinton G, Deep learning. Nature, 2015. 521(7553): p. 436–444. [DOI] [PubMed] [Google Scholar]
- [41].Brunner S.and Schaart D, BGO as a hybrid scintillator/Cherenkov radiator for cost-effective time-of-flight PET. Physics in medicine and biology, 2017. 62(11): p. 4421–4439. [DOI] [PubMed] [Google Scholar]
- [42].Kwon SI, et al. , Bismuth germanate coupled to near ultraviolet silicon photomultipliers for time-of-flight PET. Physics in medicine and biology, 2016. 61(18): p. L38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Moskal P, et al. , A novel method for the line-of-response and time-of-flight reconstruction in TOF-PET detectors based on a library of synchronized model signals. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2015. 775: p. 54–62. [Google Scholar]
- [44].Ritt S.Design and performance of the 6 GHz waveform digitizing chip DRS4. in Nuclear Science Symposium Conference Record, 2008. NSS’08. IEEE. 2008. IEEE. [Google Scholar]
- [45].Yeom JY, et al. , Readout electronics and data acquisition of a positron emission tomography time-of-flight detector module with waveform digitizer. IEEE Transactions on Nuclear Science, 2013. 60(5): p. 3735–3741. [Google Scholar]
- [46].Ashmanskas W, et al. , Waveform-sampling electronics for a whole-body time-of-flight PET scanner. IEEE transactions on nuclear science, 2014. 61(3): p. 1174–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Yonggang W, et al. , FPGA based electronics for PET detector modules with neural network position estimators. IEEE Transactions on Nuclear Science, 2011. 58(1): p. 34–42. [Google Scholar]
- [48].van Dam HT, et al. , Improved nearest neighbor methods for gamma photon interaction position determination in monolithic scintillator PET detectors. IEEE Transactions on Nuclear Science, 2011. 58(5): p. 2139–2147. [Google Scholar]
- [49].Borghi G, Tabacchini V, and Schaart DR, Towards monolithic scintillator based TOF-PET systems: practical methods for detector calibration and operation. Phys. Med. Biol, 2016. 61(13): p. 4904–4928. [DOI] [PubMed] [Google Scholar]
- [50].España S, et al. , Fast calibration of SPECT monolithic scintillation detectors using un-collimated sources. Physics in Medicine & Biology, 2013. 58(14): p. 4807. [DOI] [PubMed] [Google Scholar]
- [51].Berg E, Kwon SI, and Cherry SR, Improving time-of-flight performance of BGO-SiPM detectors using convolutional neural networks, in IEEE Nuclear Science Symposium and Medical Imaging Conference. 2018: Sydney, NSW, Australia. [Google Scholar]
- [52].Qi J, et al. , High-resolution 3D Bayesian image reconstruction using the microPET small-animal scanner. Physics in Medicine & Biology, 1998. 43(4): p. 1001–1001. [DOI] [PubMed] [Google Scholar]
- [53].Siddon RL, Fast calculation of the exact radiological path for a three-dimensional CT array. Medical Physics, 1985. 12(2): p. 252–255. [DOI] [PubMed] [Google Scholar]
- [54].Gong K, et al. , Sinogram blurring matrix estimation from point sources measurements with rank-one approximation for fully 3-D PET. IEEE transactions on medical imaging, 2017. 36(10): p. 2179–2188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Badawi RD and Marsden PK, Developments in component-based normalization for 3D PET. Physics in Medicine & Biology, 1999. 44(2): p. 571-571. [DOI] [PubMed] [Google Scholar]
- [56].Brasse D, et al. , Correction methods for random coincidences in fully 3D whole-body PET: impact on data and image quality. Journal of nuclear medicine, 2005. 46(5): p. 859–867. [PubMed] [Google Scholar]
- [57].Gong K, et al. , PET Image Reconstruction Using Deep Image Prior. IEEE Transactions on Medical Imaging, 2018: p. 1-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Gong K, et al. , Iterative PET image reconstruction using convolutional neural network representation. IEEE transactions on medical imaging, 2018. 38(3): p. 675–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Kim K, et al. , Penalized PET Reconstruction Using Deep Learning Prior and Local Linear Fitting. IEEE Transactions on Medical Imaging, 2018. 37(6): p. 1478–1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Wollenweber SD, et al. , Evaluation of an atlas-based PET head attenuation correction using PET/CT & MR patient data. IEEE Transactions on Nuclear Science, 2013. 60(5): p. 3383–3390. [Google Scholar]
- [61].Burgos N, et al. , Attenuation correction synthesis for hybrid PET-MR scanners: application to brain studies. IEEE Transactions on Medical Imaging, 2014. 33(12): p. 2332–2341. [DOI] [PubMed] [Google Scholar]
- [62].Izquierdo-Garcia D, et al. , An SPM8-based approach for attenuation correction combining segmentation and nonrigid template formation: application to simultaneous PET/MR brain imaging. Journal of Nuclear Medicine, 2014. 55(11): p. 1825–1830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Yang J, et al. , Quantitative evaluation of atlas-based attenuation correction for brain PET in an integrated time-of-flight PET/MR imaging system. Radiology, 2017: p. 161603-161603. [DOI] [PubMed] [Google Scholar]
- [64].Defrise M, Rezaei A, and Nuyts J, Time-of-flight PET data determine the attenuation sinogram up to a constant. Physics in Medicine & Biology, 2012. 57(4): p. 885-885. [DOI] [PubMed] [Google Scholar]
- [65].Rezaei A, et al. , Simultaneous reconstruction of activity and attenuation in time-of-flight PET. IEEE Transactions on Medical Imaging, 2012. 31(12): p. 2224–2233. [DOI] [PubMed] [Google Scholar]
- [66].Mehranian A.and Zaidi H, Joint estimation of activity and attenuation in whole-body TOF PET/MRI using constrained Gaussian mixture models. IEEE Transactions on Medical Imaging, 2015. 34(9): p. 18081821. [DOI] [PubMed] [Google Scholar]
- [67].Li Q, et al. , Joint estimation of activity image and attenuation sinogram using time-of-flight positron emission tomography data consistency condition filtering. Journal of Medical Imaging, 2017. 4(2): p. 023502–023502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Ahn S, et al. , Joint estimation of activity and attenuation for PET using pragmatic MR-based prior: application to clinical TOF PET/MR whole-body data for FDG and non-FDG tracers. Physics in Medicine & Biology, 2018. 63(4): p. 45006-45006. [DOI] [PubMed] [Google Scholar]
- [69].Martinez-Möller A, et al. , Tissue classification as a potential approach for attenuation correction in whole-body PET/MRI: evaluation with PET/CT data. Journal of Nuclear Medicine, 2009. 50(4): p. 520–526. [DOI] [PubMed] [Google Scholar]
- [70].Keereman V, et al. , MRI-based attenuation correction for PET/MRI using ultrashort echo time sequences. Journal of Nuclear Medicine, 2010. 51(5): p. 812–818. [DOI] [PubMed] [Google Scholar]
- [71].Berker Y, et al. , MRI-based attenuation correction for hybrid PET/MRI systems: a 4-class tissue segmentation technique using a combined ultrashort-echo-time/Dixon MRI sequence. Journal of Nuclear Medicine, 2012. 53(5): p. 796–804. [DOI] [PubMed] [Google Scholar]
- [72].Ladefoged CN, et al. , Region specific optimization of continuous linear attenuation coefficients based on UTE (RESOLUTE): application to PET/MR brain imaging. Physics in Medicine & Biology, 2015. 60(20): p. 8047-8047. [DOI] [PubMed] [Google Scholar]
- [73].Sekine T, et al. , Clinical evaluation of zero-echo-time attenuation correction for brain 18F-FDG PET/MRI: comparison with atlas attenuation correction. Journal of Nuclear Medicine, 2016. 57(12): p. 1927–1932. [DOI] [PubMed] [Google Scholar]
- [74].Leynes AP, et al. , Hybrid ZTE/Dixon MR-based attenuation correction for quantitative uptake estimation of pelvic lesions in PET/MRI. Medical Physics, 2017. 44(3): p. 902–913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Khalifé M, et al. , Subject-specific bone attenuation correction for brain PET/MR: can ZTE-MRI substitute CT scan accurately? Physics in Medicine & Biology, 2017. 62(19): p. 7814-7814. [DOI] [PubMed] [Google Scholar]
- [76].Yang J, et al. , Evaluation of sinus/edge corrected ZTE-based attenuation correction in brain PET/MRI. Journal of Nuclear Medicine, 2017: p. jnumed-116. [Google Scholar]
- [77].Zaidi H, et al. , Fuzzy clustering-based segmented attenuation correction in whole-body PET imaging. Physics in Medicine & Biology, 2002. 47(7): p. 1143-1143. [DOI] [PubMed] [Google Scholar]
- [78].Huynh T, et al. , Estimating CT image from MRI data using structured random forest and auto-context model. IEEE Transactions on Medical Imaging, 2016. 35(1): p. 174–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Johansson A, Karlsson M, and Nyholm T, CT substitute derived from MRI sequences with ultrashort echo time. Medical physics, 2011. 38(5): p. 2708–2714. [DOI] [PubMed] [Google Scholar]
- [80].Wagenknecht G, et al. , MRI for attenuation correction in PET: methods and challenges. Magnetic resonance materials in physics, biology and medicine, 2013. 26(1): p. 99–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Bezrukov I, et al. MR-based PET attenuation correction for PET/MR imaging. in Seminars in nuclear medicine. 2013. Elsevier. [DOI] [PubMed] [Google Scholar]
- [82].Keereman V, et al. , Challenges and current methods for attenuation correction in PET/MR. Magnetic Resonance Materials in Physics, Biology and Medicine, 2013. 26(1): p. 81–98. [DOI] [PubMed] [Google Scholar]
- [83].Mehranian A, Arabi H, and Zaidi H, Vision 20/20: Magnetic resonance imaging-guided attenuation correction in PET/MRI: Challenges, solutions, and opportunities. Medical physics, 2016. 43(3): p. 1130–1155. [DOI] [PubMed] [Google Scholar]
- [84].Hofmann M, et al. , Towards quantitative PET/MRI: a review of MR-based attenuation correction techniques. European journal of nuclear medicine and molecular imaging, 2009. 36(1): p. 93–104. [DOI] [PubMed] [Google Scholar]
- [85].Lammertsma AA and Hume SP, Simplified reference tissue model for PET receptor studies. Neuroimage, 1996. 4(3): p. 153–158. [DOI] [PubMed] [Google Scholar]
- [86].Samarin A, et al. , PET/MR imaging of bone lesions–implications for PET quantification from imperfect attenuation correction. European journal of nuclear medicine and molecular imaging, 2012. 39(7): p. 1154–1160. [DOI] [PubMed] [Google Scholar]
- [87].Ouyang J, et al. , Bias atlases for segmentation-based PET attenuation correction using PET-CT and MR. IEEE transactions on nuclear science, 2013. 60(5): p. 3373–3382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Han X, MR-based synthetic CT generation using a deep convolutional neural network method. Medical Physics, 2017. 44(4): p. 1408–1419. [DOI] [PubMed] [Google Scholar]
- [89].Liu F, et al. , Deep Learning MR Imaging–based Attenuation Correction for PET/MR Imaging. Radiology, 2017: p. 170700-170700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Gong K, et al. , Attenuation correction for brain PET imaging using deep neural network based on Dixon and ZTE MR images. Physics in Medicine & Biology, 2018. 63(12): p. 125011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Ladefoged CN, et al. , Deep learning based attenuation correction of PET/MRI in pediatric brain tumor patients: Evaluation in a clinical setting. Frontiers in neuroscience, 2018. 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Spuhler KD, et al. , Synthesis of Patient-Specific Transmission Data for PET Attenuation Correction for PET/MRI Neuroimaging Using a Convolutional Neural Network. Journal of Nuclear Medicine, 2019. 60(4): p. 555–560. [DOI] [PubMed] [Google Scholar]
- [93].Hwang D, et al. , Improving the accuracy of simultaneously reconstructed activity and attenuation maps using deep learning. Journal of Nuclear Medicine, 2018. 59(10): p. 1624–1629. [DOI] [PubMed] [Google Scholar]
- [94].Leynes AP, et al. , Zero-echo-time and Dixon deep pseudo-CT (ZeDD CT): direct generation of pseudo-CT images for pelvic PET/MRI attenuation correction using deep convolutional neural networks with multiparametric MRI. Journal of Nuclear Medicine, 2018. 59(5): p. 852–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Torrado-Carvajal A, et al. , Dixon-VIBE deep learning (DIVIDE) pseudo-CT synthesis for pelvis PET/MR attenuation correction. Journal of Nuclear Medicine, 2019. 60(3): p. 429–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Hwang D, et al. , Generation of PET attenuation map for whole-body time-of-flight 18F-FDG PET/MRI using a deep neural network trained with simultaneously reconstructed activity and attenuation maps. Journal of Nuclear Medicine, 2019: p. jnumed. 118.219493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Ronneberger O, Fischer P, and Brox T. U-net: Convolutional networks for biomedical image segmentation. in International Conference on Medical Image Computing and Computer-Assisted Intervention. [Google Scholar]
- [98].Xie S, et al. Aggregated Residual Transformations for Deep Neural Networks. in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR). [Google Scholar]
- [99].Yang J, et al. , Joint correction of attenuation and scatter in image space using deep convolutional neural networks for dedicated brain 18 F-FDG PET. Physics in medicine & biology, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Shiri I, et al. , Direct attenuation correction of brain PET images using only emission data via a deep convolutional encoder-decoder (Deep-DAC). European radiology, 2019: p. 1–13. [DOI] [PubMed] [Google Scholar]
- [101].Van Hemmen H, et al. , A deep learning-based approach for direct whole-body PET attenuation correction. Journal of Nuclear Medicine, 2019. 60(supplement 1): p. 569. [Google Scholar]
- [102].Nie D, et al. , Medical image synthesis with context-aware generative adversarial networks. Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, 2017: p. 417–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].Wolterink JM, et al. Deep MR to CT synthesis using unpaired data. in International Workshop on Simulation and Synthesis in Medical Imaging. 2017. Springer. [Google Scholar]
- [104].Arabi H, et al. , Novel adversarial semantic structure deep learning for MRI-guided attenuation correction in brain PET/MRI. European journal of nuclear medicine and molecular imaging, 2019: p. 1–14. [DOI] [PubMed] [Google Scholar]
- [105].Goodfellow I, et al. Generative adversarial nets. in Advances in neural information processing systems. 2014. [Google Scholar]
- [106].Arjovsky M, Chintala S, and Bottou L, Wasserstein gan. arXiv preprint arXiv:.07875, 2017. [Google Scholar]
- [107].Isola P, et al. Image-to-image translation with conditional adversarial networks. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2017. [Google Scholar]
- [108].Wolterink JM, et al. , Generative adversarial networks for noise reduction in low-dose CT. IEEE transactions on medical imaging, 2017. 36(12): p. 2536–2545. [DOI] [PubMed] [Google Scholar]
- [109].Yang Q, et al. , Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE transactions on medical imaging, 2018. 37(6): p. 1348–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Zhu J-Y, et al. , Unpaired image-to-image translation using cycle-consistent adversarial networks. arXiv preprint arXiv:1703.10593, 2017. [Google Scholar]
- [111].Watson CC, New, faster, image-based scatter correction for 3D PET. Nuclear Science, IEEE Transactions on, 2000. 47(4): p. 1587–1594. [Google Scholar]
- [112].Watson CC, Newport D, and Casey ME, A single scatter simulation technique for scatter correction in 3D PET, in Three-dimensional image reconstruction in radiology and nuclear medicine. 1996, Springer: Dordrecht. p. 255–268. [Google Scholar]
- [113].Maier J, et al. , Real-time scatter estimation for medical CT using the deep scatter estimation: Method and robustness analysis with respect to different anatomies, dose levels, tube voltages, and data truncation. Medical physics, 2019. 46(1): p. 238–249. [DOI] [PubMed] [Google Scholar]
- [114].Xu S, et al. Deep residual learning in CT physics: scatter correction for spectral CT. in 2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). 2017. IEEE. [Google Scholar]
- [115].Berker Y, Joscha M, and Kachelries M. Deep scatter estimation in PET: fast scatter correction using a convolutional neural network. in IEEE Nuclear Science Symposium and Medical Imaging Conference 2018. [Google Scholar]
- [116].Qian H, Manjeshwar R, and Thielemans K. A comparative study of multiple scatter estimations in 3D PET. in IEEE Nuclear Science Symposuim & Medical Imaging Conference. 2010. [Google Scholar]
- [117].Qian H, Rui X, and Ahn S. Deep Learning Models for PET Scatter Estimations. in IEEE Nuclear Science Symposium and Medical Imaging Conference2017. [Google Scholar]
- [118].Chan C, et al. , Postreconstruction nonlocal means filtering of whole-body PET with an anatomical prior. IEEE Transactions on Medical Imaging, 2014. 33(3): p. 636–650. [DOI] [PubMed] [Google Scholar]
- [119].Dutta J, Leahy RM, and Li Q, Non-local means denoising of dynamic PET images. PloS one, 2013. 8(12): p. e81390-e81390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].Christian BT, et al. , Dynamic PET denoising with HYPR processing. Journal of Nuclear Medicine, 2010. 51(7): p. 1147–1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Yan J, Lim JC-S, and Townsend DW, MRI-guided brain PET image filtering and partial volume correction. Physics in medicine & biology, 2015. 60(3): p. 961-961. [DOI] [PubMed] [Google Scholar]
- [122].Wang Y, et al. , Semisupervised tripled dictionary learning for standard-dose PET image prediction using low-dose PET and multimodal MRI. IEEE Transactions on Biomedical Engineering, 2017. 64(3): p. 569–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [123].Li T, et al. , Low-count PET image restoration using sparse representation. Nuclear Instruments Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2018. 888: p. 222–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [124].Kang J, et al. , Prediction of standard-dose brain PET image by using MRI and low-dose brain [18F] FDG PET images. Medical physics, 2015. 42(9): p. 5301–5309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Bai B, Li Q, and Leahy RM, Magnetic resonance-guided positron emission tomography image reconstruction. Semin Nucl Med, 2013. 43(1): p. 30–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Ellis S.and Reader AJ, Simultaneous maximum a posteriori longitudinal PET image reconstruction. Phys Med Biol, 2017. 62(17): p. 6963–6979. [DOI] [PubMed] [Google Scholar]
- [127].Ellis S.and Reader AJ, Penalized maximum likelihood simultaneous longitudinal PET image reconstruction with difference-image priors. Med Phys, 2018. 45(7): p. 3001–3018. [DOI] [PubMed] [Google Scholar]
- [128].Dong C, et al. , Image super-resolution using deep convolutional networks. IEEE transactions on pattern analysis and machine intelligence, 2016. 38(2): p. 295–307. [DOI] [PubMed] [Google Scholar]
- [129].Ledig C, et al. Photo-realistic single image super-resolution using a generative adversarial network. in Proceedings of the IEEE conference on computer vision and pattern recognition. 2017. [Google Scholar]
- [130].Zhang K, et al. , Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing, 2017. 26(7): p. 3142–3155. [DOI] [PubMed] [Google Scholar]
- [131].Xiang L, et al. , Deep auto-context convolutional neural networks for standard-dose PET image estimation from low-dose PET/MRI. Neurocomputing, 2017. 267: p. 406–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132].Xu J, et al. , 200x Low-dose PET reconstruction using deep learning. arXiv preprint arXiv:1712.04119, 2017. [Google Scholar]
- [133].Wang Y, et al. , 3D conditional generative adversarial networks for high-quality PET image estimation at low dose. NeuroImage, 2018. 174: p. 550–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [134].Gong K, et al. , PET image denoising using a deep neural network through fine tuning. IEEE Transactions on Radiation and Plasma Medical Sciences, 2018. 3(2): p. 153–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [135].Chen KT, et al. , Ultra–Low-Dose 18F-Florbetaben Amyloid PET Imaging Using Deep Learning with Multi-Contrast MRI Inputs. Radiology, 2018: p. 180940-180940. [Google Scholar]
- [136].Cui J, et al. CT-guided PET Image Denoising using Deep Neural Network without Prior Training Data. in IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). 2018. Sydney: IEEE. [Google Scholar]
- [137].da Luis CO and Reader AJ. Deep Learning for Suppression of Resolution-Recovery Artefacts in MLEM PET Image Reconstruction. in 2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). 2017. IEEE. [Google Scholar]
- [138].Liu C-C and Qi J, Higher SNR PET image prediction using a deep learning model and MRI image. Physics in Medicine & Biology, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139].Yang B, et al. , Brain PET dose reduction using a shallow artificial neural network. Journal of Nuclear Medicine, 2018. 59(supplement 1): p. 99a-99a. [Google Scholar]
- [140].Kaplan S.and Zhu Y-M, Full-Dose PET Image Estimation from Low-Dose PET Image Using Deep Learning: a Pilot Study. Journal of digital imaging, 2018: p. 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [141].Ouyang J, et al. , Ultra-low-dose PET Reconstruction using Generative Adversarial Network with Feature Matching and Task-Specific Perceptual Loss. Medical physics, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142].Yang B, Ying L, and Tang J, Artificial neural network enhanced Bayesian PET image reconstruction. IEEE transactions on medical imaging, 2018. 37(6): p. 1297–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143].Song T-A, et al. , Super-resolution PET imaging using convolutional neural networks. arXiv preprint arXiv:.03645, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [144].Hong X, et al. , Enhancing the image quality via transferred deep residual learning of coarse PET sinograms. IEEE transactions on medical imaging, 2018. 37(10): p. 2322–2332. [DOI] [PubMed] [Google Scholar]
- [145].Shiri I, Sheikhzadeh P, and Ay MR, Deep-Fill: Deep Learning Based Sinogram Domain Gap Filling in Positron Emission Tomography. arXiv preprint arXiv:.07168, 2019. [Google Scholar]
- [146].Cocosco CA, et al. , Brainweb: Online interface to a 3D MRI simulated brain database. NeuroImage, 1997. [Google Scholar]
- [147].Segars WP, et al. , 4D XCAT phantom for multimodality imaging research. Medical Physics, 2010. 37(9): p. 4902–4915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [148].Ulyanov D, Vedaldi A, and Lempitsky V, Deep Image Prior. arXiv preprint arXiv:1711.10925, 2017. [Google Scholar]
- [149].Wang G.and Qi J, Direct estimation of kinetic parametric images for dynamic PET. Theranostics, 2013. 3(10): p. 802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150].Carson RE, Tracer kinetic modeling in PET, in Positron Emission Tomography. 2005, Springer. p. 127–159. [Google Scholar]
- [151].Cui J, et al. , Deep reconstruction model for dynamic PET images. PloS one, 2017. 12(9): p. e0184667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [152].Klyuzhin IS, et al. Use of a 4 D Deep Autoencoder to Denoise Dynamic PET Data. in IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). 2018. [Google Scholar]
- [153].Scott CJ, et al. Short Acquisition Time PET/MR Pharmacokinetic Modelling Using CNNs. in International Conference on Medical Image Computing and Computer-Assisted Intervention. 2018. Springer. [Google Scholar]
- [154].Cui J, et al. CT-guided PET parametric image reconstruction using deep neural network without prior training data. in Medical Imaging 2019: Physics of Medical Imaging. 2019. International Society for Optics and Photonics. [Google Scholar]
- [155].Liu H, et al. , Noise reduction with cross-tracer transfer deep learning for low-dose oncological PET. Journal of Nuclear Medicine, 2019. 60(supplement 1): p. 108. [Google Scholar]
- [156].Fessler J, Ravishankar S, and Ye JC, Image reconstruction using sparsity, data-adaptive methods and machine learning-Proceeding of IEEE, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [157].Kim K, et al. , Penalized PET Reconstruction Using Deep Learning Prior and Local Linear Fitting. IEEE transactions on medical imaging, 2018. 37(6): p. 1478–1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].He K, Sun J, and Tang X, Guided image filtering. IEEE transactions on pattern analysis and machine intelligence, 2012. 35(6): p. 1397–1409. [DOI] [PubMed] [Google Scholar]
- [159].Wang G.and Qi J, PET image reconstruction using kernel method. IEEE Transactions on Medical Imaging, 2015. 34(1): p. 61–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [160].Xie Z, et al. Generative adversarial networks based regularized image reconstruction for PET. in 15th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. 2019. International Society for Optics and Photonics. [Google Scholar]
- [161].Zhang H, et al. , Self-attention generative adversarial networks. arXiv preprint arXiv:.08318, 2018. [Google Scholar]
- [162].Sulam J, et al. , Multilayer convolutional sparse modeling: Pursuit and dictionary learning. IEEE Transactions on Signal Processing, 2018. 66(15): p. 4090–4104. [Google Scholar]
- [163].Gong K, et al. Direct patlak reconstruction from dynamic PET using unsupervised deep learning. in 15th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. 2019. International Society for Optics and Photonics. [Google Scholar]
- [164].Hashimoto F, Ote K, and Tsukada H, Dynamic PET Image Denoising Using Deep Convolutional Neural Network Without Training Datasets. Journal of Nuclear Medicine, 2019. 60(supplement 1): p. 242. [Google Scholar]
- [165].Lim H, et al. , Improved low-count quantitative PET reconstruction with a variational neural network. arXiv preprint arXiv:.02327, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [166].Gong K, et al. MAPEM-Net: an unrolled neural network for Fully 3D PET image reconstruction. in 15th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. 2019. International Society for Optics and Photonics. [Google Scholar]
- [167].Ida Häggström, et al. , DeepPET: A deep encoder-decoder network for directly solving the PET reconstruction inverse problem, in arXiv:1804.07851. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [168].Juan Ramon A, et al. , Initial Investigation of Low-Dose SPECT-MPI via Deep Learning, in IEEE Medical Imaging Conference. 2018. [Google Scholar]