The transitivity of the Hardy–Weinberg law

Abstract

The Hardy–Weinberg law is shown to be transitive in the sense that a multi-allelic polymorphism that is in equilibrium will retain its equilibrium status if any allele together with its corresponding genotypes is deleted from the population. Similarly, the transitivity principle also applies if alleles are joined, which leads to the summation of allele frequencies and their corresponding genotype frequencies. These basic polymorphism properties are intuitive, but they have apparently not been formalized or investigated. This article provides a straightforward proof of the transitivity principle, and its usefulness in genetic data analysis is explored, using high-quality autosomal microsatellite databases from the US National Institute of Standards and Technology. We address the reduction of multi-allelic polymorphisms to variants with fewer alleles, two in the limit. Equilibrium test results obtained with the original and reduced polymorphisms are generally observed to be coherent, in particular when results obtained with length-based and sequence-based microsatellites are compared. We exploit the transitivity principle in order to identify disequilibrium-related alleles, and show its usefulness for detecting population substructure and genotyping problems that relate to null alleles and allele imbalance.

1. Introduction

The Hardy–Weinberg law is a cornerstone principle of modern genetics, and marked the foundation of population genetics [1]. For an autosomal diploid variant, the principle establishes that genotype frequencies attain a stable composition in one generation of time; remaining, in the absence of disturbing forces, unaltered afterwards. For bi-allelic variants this implies the genotype frequencies will have relative frequencies $\left(AA=p^2,AB=2pq,BB=q^2\right)$, where $p$ and $q$ are the allele frequencies of $\mathrm{A}$ and $\mathrm{B}$ respectively with $p+q=1$. The Hardy–Weinberg principle becomes more complicated if one considers, for example, X chromosomal variants [2], systems with multiple alleles [3–6], systems with null alleles [7,8], copy number variation [9,10] or polyploid species [11,12]. The statistical methodology needed to address all these complications often lags behind, as exemplified by the fact that adequate statistical procedures for testing X chromosomal variants have only been recently developed [13,14]. In forensic genetics, Hardy–Weinberg proportions (HWP) are often assumed, in for instance matching probability calculations [15], and in the subdivided population model, the Balding-Nichols model [16]. The Hardy–Weinberg law is also crucial for the quality control of microsatellite data, statistical tests for HWP being routinely applied to autosomal microsatellites, also known as Short Tandem Repeats or STRs [17,18], indels [19], sequence-based STRs [20], Single Nucleotide Polymorphism (SNP) panels [21,22] and microhaplotypes (MHs; [23]). The analysis of STR data is often complicated by the existence of genotyping error and individuals that stem from different ethnicities or ancestries. Genotyping error, if substantial, can bias allele and genotype frequencies and so negatively affect all subsequent analysis of the data. Population substructure (in the form of ethnicities or genetic ancestries), when not accounted for, can provoke spurious findings in association studies, can lead to rejection of HWP when in fact subpopulations provide no evidence against it [24], and can suggest linkage disequilibrium (LD) between variants that are in fact independent in subgroups. The Hardy–Weinberg law is transitive in the sense that it carries over to reduced polymorphisms that can be generated from STRs by elimination or joining of alleles. For STRs, next generation sequencing has revealed additional sequence diversity [20,25,26], thereby increasing the number of STR alleles. Sequence-based (SB) STRs can always be reduced to length-based (LB) STRs, and this is important for backward compatibility with previous LB work. Under the usual assumption of absence of disturbing forces (no mutation, migration, genotyping error, selection, etc.) Hardy–Weinberg equilibrium is generally expected to hold, and in practice, indeed mostly not rejected in statistical tests when these assumptions are met. If the equilibrium assumption holds true, one therefore expects inferences made on HWP with SB and LB STRs to be consistent, meaning that a non-rejection of HWP for an SB STR typically also gives a non-rejection when the test is applied to the corresponding reduced LB STR. This is essentially the consequence of the transitive nature of the law. The main point of this article is that transitivity can be used to analyse STR data in more detail. In the following, we state the transitivity of the Hardy–Weinberg law, provide a straightforward theoretical proof, and exploit the principle in genetic data analysis with LB and SB STR data from the US National Institute of Standards and Technology (NIST).

2. Theory

The Hardy–Weinberg law states in essence that genotype frequencies are the product of allele frequencies. Let $\mathbf{p}={\left(p_1,p_2,\dots ,p_k\right)}^{\prime }$ be the column vector of allele frequencies for a genetic variant with $k$ alleles. Let $\mathbf{G}$ be a $k\times k$ matrix with genotype frequencies, rows representing male alleles and columns representing female alleles. Then the Hardy–Weinberg law can be concisely expressed as $\mathbf{G}={\mathbf{p}\mathbf{p}}^{\prime }$. In principle, this formulation distinguishes two subtypes of each heterozygote according to the provenance of the maternal and paternal alleles. In general, such distinction is not needed, and both $\mathbf{G}$ and $\mathbf{p}{\mathbf{p}}^{\prime }$ can always be folded around the diagonal towards a lower triangular matrix with entries $2p_i{p}_j$ below the diagonal and entries $p_i^2$ on the diagonal. We here maintain the distinction between the two heterozygote subtypes for mere mathematical convenience, such that $\mathbf{G}={\mathbf{p}\mathbf{p}}^{\prime }$ is a sufficient condition for HWP to hold. Assume a population to be in HWP. Intuitively, one might expect that if one allele and its corresponding genotypes are deleted from this population, the law will continue to hold for the reduced array of genotypes. This is indeed true, and a formal demonstration of the property is given below. We call the law transitive under elimination of alleles because the equilibrium property is “carried over” to the reduced population with $k-1$ alleles. Obviously, the process of deleting an allele and its genotypes can be repeated, and this implies that the genotypes of any subsystem of $i<k$ alleles of an equilibrium system will always be in HWP. This transitivity under allele deletion is the theoretical underpinning for the default recoding of multi-allelic variants as bi-allelic in the widely used PLINK software [27].

In genome-wide association studies, variants with multiple alleles are often recoded as bi-allelic variants, with the main goal of enabling the analyst to use available statistical methodology for the analysis of bi-allelic variants for all variants available in the database. The recoding can however, be carried out in various ways. If all genotypes that carry alleles beyond the two most common ones are recoded as missing values, then the foregoing implies that such variants, if in equilibrium, will retain this status. However, elimination of genotypes implies a loss of data, leading to smaller sample sizes and less power. The question arises to what will happen if alleles are grouped somehow. To create bi-allelic variants, a straightforward approach is to retain the major allele, and group all remaining alleles as non-major. It is shown below that the law is also transitive under joining of alleles.

Elimination of alleles

We first consider reduction by elimination of alleles. Let ${\mathbf{e}}_i$ be a set of $i=1,\dots ,m$ column vectors, where each ${\mathbf{e}}_i$ has one single 1, and all remaining elements equal to zero. We define the $m\times k$ selector matrix $\mathbf{S},m<k$, with a single 1 in each row and at most one 1 in each column, given by

$$\mathbf{S}=\left[\begin{array}{c}{\mathbf{e}}_1{}^{\prime }\\ {\mathbf{e}}_2{}^{\prime }\\ ⋮\\ {\mathbf{e}}_m{}^{\prime }\end{array}\right],$$

It holds that ${\mathbf{S}\mathbf{S}}^{\prime }={\mathbf{I}}_m$, and the operation $\mathbf{S}\mathbf{p}$ removes $k-m$ alleles. The vector of reduced and normalized allele frequencies ${\mathbf{p}}_r$ is given by

$${\mathbf{p}}_r=\mathbf{S}\mathbf{p}/{\mathbf{1}}^{\prime }\mathbf{S}\mathbf{p}.$$

Let ${\mathbf{G}}_r$ represent the reduced matrix of genotype frequencies, where all genotype frequencies that are carriers of the removed allele have been eliminated, and the remaining entries have been renormalized to sum to one. That is

$${\mathbf{G}}_r={\mathbf{S}\mathbf{G}\mathbf{S}}^{\prime }/{\mathbf{1}}^{\prime }\mathbf{S}\mathbf{G}\mathbf{S}{\mathbf{S}}^{\prime }\mathbf{1}={\mathbf{S}\mathbf{G}\mathbf{S}}^{\prime }/{\left({\mathit{1}}^{\prime }\mathbf{S}\mathbf{p}\right)}^2,$$

since ${\mathbf{1}}^{\prime }\mathbf{S}\mathbf{G}{\mathbf{S}}^{\prime }\mathbf{1}={\mathbf{1}}^{\prime }\mathbf{S}\mathbf{p}\mathbf{p}{\mathbf{S}}^{\prime }{\mathbf{S}}^{\prime }\mathbf{1}={\left({\mathbf{1}}^{\prime }\mathbf{S}\mathbf{p}\right)}^2$. As an example, the reduction of a tri-allelic ($\mathrm{A},\mathrm{B},\mathrm{C}$) to a bi-allelic ($\mathrm{A},\mathrm{C}$) is described by

$$\left[\begin{array}{lll}1& 0& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}{p}_A\\ p_B\\ p_C\end{array}\right]=\left[\begin{array}{l}{p}_A\\ p_C\end{array}\right]$$

and

$$\left[\begin{array}{lll}1& 0& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{p}_A^2& p_A{p}_B& p_A{p}_C\\ p_B{p}_A& p_B^2& p_B{p}_C\\ p_C{p}_A& p_C{p}_B& p_C^2\end{array}\right]\left[\begin{array}{ll}1& 0\\ 0& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}{p}_A^2& p_A{p}_C\\ p_A{p}_C& p_C^2\end{array}\right]$$

Demonstrating transitivity amounts to showing that the reduced genotype frequencies still satisfy

$${\mathbf{G}}_r={\mathbf{p}}_r{\mathbf{p}}_r{}^{\prime }.$$

We have

$${\mathbf{p}}_r{\mathbf{p}}_r{}^{\prime }={\mathbf{S}\mathbf{p}\mathbf{p}}^{\prime }{\mathbf{S}}^{\prime }/{\left({\mathbf{1}}^{\prime }\mathbf{S}\mathbf{p}\right)}^2={\mathbf{S}\mathbf{G}\mathbf{S}}^{\prime }/{\left({\mathbf{1}}^{\prime }\mathbf{S}\mathbf{p}\right)}^2={\mathbf{G}}_r,$$

and transitivity is thus established.

Joining of alleles

We also consider the reduction of the polymorphism by joining alleles, summing the corresponding allele and genotype frequencies. Joining alleles into a single, more frequent allele can be done by a selecting and summing operation on matrix $\mathbf{G}$. E.g. if alleles $\mathrm{A}$ and $\mathrm{B}$ are joined this can be seen as a relabelling of all $\mathrm{B}$ alleles as $\mathrm{A}$ alleles, such that $\mathrm{B}\mathrm{B}$ homozygotes and $\mathrm{A}\mathrm{B}$ heterozygotes become $\mathrm{A}\mathrm{A}$ homozygotes, and all $\mathrm{B}\mathrm{C}$ heterozygotes become $\mathrm{A}\mathrm{C}$ heterozygotes. We define $\mathbf{S}$ as the $m\times k$ selector-summing matrix with $m\le k$, given by

$$\mathbf{S}=\left[\begin{array}{c}{\mathbf{e}}_1{}^{\prime }\\ {\mathbf{e}}_2{}^{\prime }\\ ⋮\\ {\mathbf{e}}_m{}^{\prime }\end{array}\right],$$

The elements of each vector ${\mathbf{e}}_i$ are either 0 or 1; the matrix has a single 1 in each column and at least a 1 in each row. The vector of reduced and normalized allele frequencies is given by

$${\mathbf{p}}_r=\mathbf{S}\mathbf{p},$$

and the $m\times m$ matrix of reduced and normalized genotype frequencies is given by

$${\mathbf{G}}_r={\mathbf{S}\mathbf{G}\mathbf{S}}^{\prime }$$

As an example, the reduction of a tri-allelic to a bi-allelic by joining the $\mathrm{B}$ and the $\mathrm{C}$ alleles is described by:

$$\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 1\end{array}\right]\left[\begin{array}{c}{p}_A\\ p_B\\ p_C\end{array}\right]=\left[\begin{array}{c}{p}_A\\ p_B+p_C\end{array}\right]$$

and

$$\begin{array}{rr}& \left[\begin{array}{lll}1& 0& 0\\ 0& 1& 1\end{array}\right]\left[\begin{array}{ccc}{p}_A^2& p_A{p}_B& p_A{p}_C\\ p_B{p}_A& p_B^2& p_B{p}_C\\ p_C{p}_A& p_C{p}_B& p_C^2\end{array}\right]\left[\begin{array}{ll}1& 0\\ 0& 1\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cc}{p}_A^2& p_A\left(p_B+p_C\right)\\ p_A\left(p_B+p_C\right)& {\left(p_B+p_C\right)}^2\end{array}\right]\end{array}$$

By the same token as before, we have

$${\mathbf{p}}_r{\mathbf{p}}_r{}^{\prime }={\mathbf{S}\mathbf{p}\mathbf{p}}^{\prime }{\mathbf{S}}^{\prime }={\mathbf{S}\mathbf{G}\mathbf{S}}^{\prime }={\mathbf{G}}_r,$$

and transitivity is again established. When alleles are joined, the renormalization to unit-sum allele and genotype frequencies is not required.

3. NIST microsatellites

We illustrate the application of the formulated transitivity principle in genetic data analysis with microsatellites. We use a microsatellite database of the NIST website consisting of 1036 individuals of four different self-identified ethnicities genotyped for 29 autosomal LB STRs (https://strbase.nist.gov/). This data set has been described by Hill et al. [18], and posterior corrections are detailed by Steffen et al. [28]. A SB version of 27 STRs for the same individuals has been described by Gettings et al. [26]; the LB and SB data sets have 23 STRs in common. The sample sizes of the four ethnicities are: African American: 342, Asian: 97, Caucasian: 361 and Hispanic: 236. The NIST data set underwent extensive concordance evaluations and is probably one of most reliable STR databases publicly available. Hill et al. [18] report on HWP test results, and argue that after using a Bonferroni correction for multiple testing, only two significant deviations remain (D13S317 and F13B when tested overall). Gettings et al. [26] report no significant deviations from HWP in the SB data after correction for multiple testing.

Here, we present a HWP analysis of the LB and SB STR data exploiting the transitivity principle in various ways. In all cases we test for HWP by using the mid p-value, as this has been shown to have a rejection rate that is most close to the nominal level [29]. For bi-allelic variants, we calculate the exact mid p-value. For multi-allelic variants, we estimate the mid p-value with a permutation test using 17,000 random shuffles of the alleles. This estimates the exact mid p-value with a precision of 1% with 99% confidence [4,30]. To illustrate transitivity, we first use CSF1PO in the sample of Caucasian ethnicity only. For this STR, seven alleles are observed, and HWP is not rejected (p-value = 0.866) in a permutation test that uses the exact probability of the data table according to Levene’s distribution [31] as a test statistic. Table 1 shows mid p-values of seven permutation tests for HWP where just one allele is eliminated, each in turn. In all cases, HWP is not rejected for the reduced six-allelic polymorphisms as expected by transitivity. Table 1 also shows the mid p-values obtained after a bi-allelic recoding of all alleles (e.g. “8” versus “not-8”), using a standard bi-allelic exact test for HWP [32]. This also produces no significant results, as is again expected by transitivity. The results in Table 1 are representative for most STRs of the NIST database, when stratifying for ethnicity (results not shown). When the SB STRs are used, the same results are obtained because the Caucasian sample has no additional sequence variability for this STR.

Table 1.

Permutation test and bi-allelic test results for HWP of STR CSF1PO of the Caucasian sample (n = 361). SB-allele: identifier and sequence motif; LB-allele: repeat number; n: sample size (number of individuals) after elimination of the allele; p: allele frequency; p_mid : permutation test mid p-value obtained when deleting the allele; AA, AB, BB: genotype counts of the bi-allelified polymorphism (A = minor, retained allele, B = all other alleles); p_mid : mid p-value of bi-allelic exact test for HWP.

SB-allele		LB-allele	n	p	pmid	AA	AB	BB	pmid
-	-	-	361	-	0.8661	-	-	-	-
238	[ATCT]8	8	357	0.005	0.7570	0	4	357	0.5042
239	[ATCT]9	9	351	0.014	0.8463	0	10	351	0.5306
240	[ATCT]10	10	219	0.220	0.5810	17	125	219	0.9392
242	[ATCT]11	11	173	0.309	0.6892	35	153	173	0.8537
245	[ATCT]12	12	145	0.360	0.8520	44	172	145	0.5310
247	[ATCT]13	13	302	0.082	0.9198	0	59	302	0.1131
248	[ATCT]14	14	354	0.010	0.8336	0	7	354	0.5145

More interesting is the removal (or amalgamation) of alleles for a variant for which HWP is rejected. A large change in p-value, from clearly significant to clearly non-significant after removal can signal which allele(s) provoked the initial rejection of the null.

Table 2 shows such test results for the full database with all ethnicities for TH01. For this STR, HWP are rejected in the full database for both the LB and SB data (first row of Table 2). TH01 has one fractional allele, 9.3, which consists of 9 repeats of the core sequence (AATG) plus a partial repeat (ATG) involving only 3 of the four nucleotides (see sequence ID 386 in Table 2). This table shows that the elimination of fractional allele 9.3 renders the test non-significant, suggesting 9.3 is a disequilibrium-related allele. Fig. 1 shows a barplot of the allele frequencies of this STR for the four ethnicities. This reveals the 9.3 allele fluctuates strongly over the ethnicities, ranging from 4% in Asians to 34% in Caucasians. Interestingly, if the 9 and 9.3 alleles are joined, then there is no significant difference in allele frequencies between Asians, Caucasians and Hispanics. An alternative way to identify disequilibrium-related alleles is to calculate the contribution each allele makes to the chi-square statistic of the original data table; in this case the homozygote 9.3 makes the largest contribution. It is well-known that population substructure can drive disequilibrium when there are differences in allele frequencies across the groups. For all LB and SB STRs in the NIST database, a Fisher exact test for equality of allele frequencies across the four ethnicities is highly significant at a Bonferroni corrected significance level (0.05/29 = 0.0017 for LB; 0.05/27 = 0.0019 for SB; results not shown). It is thus imperative to account for ethnicity when testing for HWP.

Table 2.

Test results of a permutation test for HWP of TH01, after removal of a single allele. Allele: removed allele; p: allele frequency; n: sample size (number of individuals) after elimination of the allele; p_mid: mid p-value obtained in a permutation test.

Sequence-based (SB)					Length-based (LB)
ID	Allele	p	n	pmid	Allele	p	n	pmid
-	-	-	1036	0.0001	-	-	1036	0.0003
379	[AATG]5	0.0019	1032	0.0001	5	0.0019	1032	0.0001
380	[AATG]6	0.1959	669	0.0001	6	0.1959	669	0.0000
381	[AATG]7	0.2939	524	0.0036	7	0.2949	524	0.0035
382	[AATG]7-rs1051822965	0.0010	1034	0.0004
383	[AATG]8	0.1255	791	0.0001	8	0.1255	791	0.0001
384	[AATG]9	0.1684	729	0.0047	9	0.1689	728	0.0030
385	AGTG [AATG]8	0.0005	1035	0.0001
386	[AATG]6 ATG [AATG]3	0.2056	677	0.2338	9.3	0.2056	677	0.1958
387	[AATG]10	0.0068	1022	0.0001	10	0.0068	1022	0.0004
388	[AATG]11	0.0005	1035	0.0002	11	0.0005	1035	0.0002

Fig. 1.

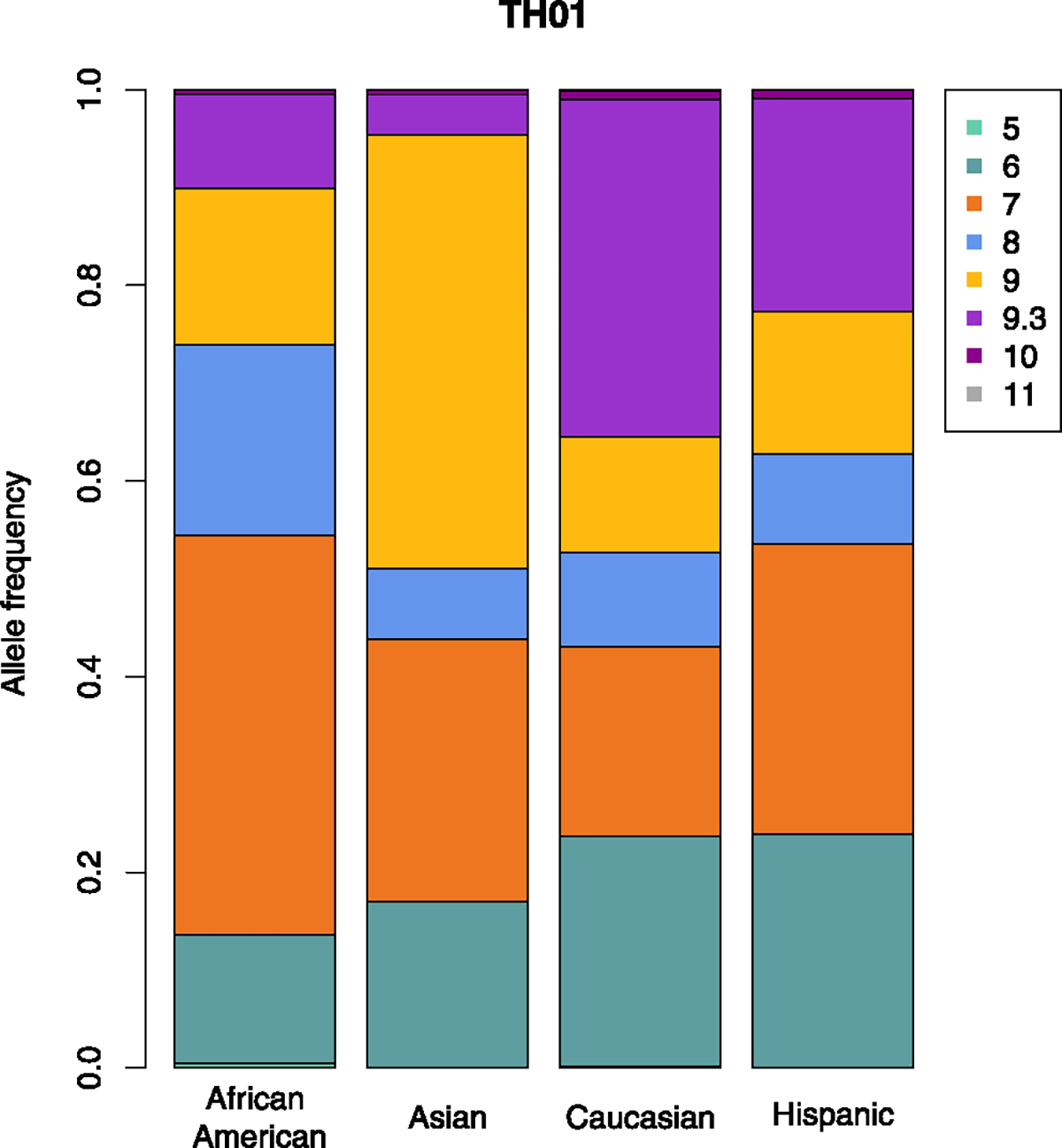
Allele frequencies of TH01 for four ethnicities.

The results obtained for LB and SB alleles in Table 2 are entirely consistent. In both cases the 9.3 allele is identified as disequilibrium-related. The two new alleles generated by using sequences are rare variations on repeats 7 and 9, and their separate elimination does not qualitatively alter the test result.

The testing of all STRs separately for each ethnicity provokes a multiple testing problem. Hill et al. [18] use a Bonferroni correction taking into account that 29 × 4 = 116 tests are being performed, using $\alpha =0.05/116=0.0004$. However, the Bonferroni correction is very conservative, and consequently, informative disequilibrium may easily go undetected. The extent of the multiple testing problem can be diminished by using restricted permutation test procedures [33] that account for the four-group structure of the data. We applied restricted permutation tests (permuting alleles only within ethnicities) and this allows us to test each STR for HWP just once, applying a less restrictive Bonferroni threshold of 0.05/29 = 0.0017 for the LB data, or 0.05/27 = 0.0019 for the SB data. At this level we found none of the tests to be significant, though the test of SE33 is close to the threshold. The test results for all LB and SB STRs are reported in Table 3. Qualitatively, test results obtained for LB and SB STRs are similar, and among the 23 common ones for which both LB and SB data are available, the two most significant tests are for the same loci, D22S1045 and FGA. When all STRs are considered, loci SE33 and D22S1045 give the most significant HWP tests.

Table 3.

Number of alleles (n_t) and mid p-values of both LB and SB NIST STRs using a restricted permutation test for HWP.

Nr.	Length-based (LB)			Sequence-based (SB)
	STR	nt	pmid	nt	pmid
1	SE33	53	0.0083	-	-
2	D22S1045	11	0.0294	16	0.0287
3	FGA	27	0.0703	40	0.0669
4	F13B	7	0.0804	-	-
5	vWA	11	0.0871	37	0.1512
6	F13A01	16	0.1648	-	-
7	D2S1338	13	0.1794	67	0.5908
8	LPL	9	0.2045	-	-
9	D13S317	8	0.2147	35	0.0934
10	D19S433	16	0.3359	24	0.4078
11	D7S820	11	0.3465	25	0.1633
12	FESFPS	12	0.3580	-	-
13	PentaC	12	0.3772	-	-
14	D6S1043	27	0.4301	38	0.4354
15	D2S441	15	0.4421	26	0.1901
16	D3S1358	11	0.4908	31	0.3500
17	D5S818	9	0.4961	19	0.8404
18	PentaD	17	0.5561	26	0.6183
19	D8S1179	11	0.5655	33	0.7313
20	CSF1PO	9	0.5817	14	0.5558
21	D16S539	9	0.5818	19	0.7445
22	D1S1656	15	0.5996	33	0.6155
23	D10S1248	12	0.6343	13	0.6404
24	TH01	8	0.7915	10	0.8006
25	PentaE	23	0.7931	29	0.7933
26	D21S11	27	0.8540	98	0.7425
27	D12S391	24	0.8554	96	0.7755
28	D18S51	22	0.9427	30	0.9445
29	TPOX	10	0.9757	11	0.9747
30	D4S2408	-	-	9	0.7350
31	D9S1122	-	-	21	0.2216
32	D17S1301	-	-	10	0.1494
33	D20S482	-	-	19	0.0671

If we finally test, albeit aggravating the multiple testing problem, each STR for HWP within each ethnicity, as is often done, then the test of SE33 of the Asian samples singles out as the most significant test, with permutation mid p-value 0.008. Table 4 shows the most significant tests of SB and LB STRs that have a p-value below 0.05 and their heterozygosities. D22S1045 and FGA are shared in the SB and LB list. However, the tests of SE33 and D4S2408 are the most significant ones.

Table 4.

Results of the most significant permutation tests (α = 0.05) for HWP within populations for both LB and SB STRs. STR: microsatellite identifier; n: sample size (number of individuals); p_mid: mid p-value obtained by permutation; H₀ observed heterozygosity; H_e : expected heterozygosity.

Length-based (LB)						Sequence-based (SB)
STR	Population	n	pmid	H0	He	STR	Population	n	pmid	H0	He
SE33	Asian	97	0.0078	0.9278	0.9392	D4S2408	Hispanic	236	0.0021	0.6864	0.7625
D6S1043	Caucasian	361	0.0217	0.7978	0.8232	D5S818	Hispanic	236	0.0121	0.7797	0.7874
Penta_C	Caucasian	361	0.0229	0.7701	0.7523	D22S1045	Asian	97	0.0272	0.7331	0.6865
D22S1045	Asian	97	0.0301	0.7010	0.7628	D12S391_1	Hispanic	236	0.0280	0.9576	0.9358
D2S441	Hispanic	236	0.0415	0.7542	0.7488	D22S1045	Hispanic	236	0.0416	0.7010	0.7628
FGA	Caucasian	361	0.0481	0.8670	0.8594	FGA	Caucasian	361	0.0429	0.8670	0.8596

If we take the results of Tables 3 and 4 together, then the main leads are SE33 and D22S1045; SE33 in the Asian sample, and D22S1045 in both the Asian and Hispanic sample. D221045 has a relatively larger difference between observed and expected heterozygosity; this is also observed for D4S2408 in Hispanics. We follow up these most important leads in an attempt to understand the nature of disequilibrium.

Microsatellite SE33 has many rare fractional alleles. Several rare fractional alleles (18.5, 20.2, 23.2, 28.2) occur in homozygote form, which is very unlikely under the HWP assumption. In non-Asian samples there is overall no evidence against HWP, but if SE33 is bi-allelified for its alleles, then 22 and 23.2 have the smallest p-values in Hispanics and African Americans again due to the existence of rare allele homozygotes. We tentatively suggest that some of the rare allele homozygotes may in fact be heterozygotes, and that checking for allele imbalance is called for (in particular in the light of the results described for D22S1045 below). We note that [34, Fig. 4] report a relatively lower allele coverage ratio $(\approx 0.60)$ for this STR, and that Just et al. [35] also reported problems with this locus.

The second most significant test is the one for D22S1045; there is evidence against HWP for this STR in the Asian sample $(p=0.0285)$, and by deletion of alleles and bi-allelification, repeat 17, a frequent allele, is identified as disequilibrium-related (see supplementary Table S1; the corresponding table for the SB STR is identical, because no additional sequence variation exists for the Asian sample). The reduced bi-allelic polymorphisms “17” versus “not-17” has a lack of heterozygotes. Investigating the same polymorphism in the other samples shows some evidence against HWP for this STR when it is bi-allelified for allele 16 or 17 (see supplementary Tables S2). Most notably, Peng et al. [36] reported allele imbalance for this STR in a sample from Tibet, with miscalling of heterozygotes as homozygotes, and Novroski et al. [37] reported heterozygote imbalance for D22S1045 and problems with allele 17 in a US sample, where allele 17 is more frequent in Asians.

For D4S2408 we find significant deviations only for the Hispanics; by deleting alleles and bi-allelification, sequence 170 (repeat 9) is identified as disequilibrium-related in Hispanics (results not shown); this pattern is however, not observed in other samples.

4. Discussion

We have given a formal proof of the transitivity of the Hardy–Weinberg law, and illustrated its use in genetic data analysis. Only the most simple reductions obtained by elimination of one allele and by bi-allelification have been used. Many additional reductions are possible, such as the reduction to all tri-allelic variants, all four-allelic variants, and so on. In principle, if equilibrium holds true, one expects HWP not to be rejected in most cases, except for chance effects. Reduction to tri-allelics and other multi-allelic forms has not been carried out in order not to further aggravate the multiple testing problem. The reduction of a multi-allelic polymorphism will inevitably change its allele frequencies, and this can alter the power of a test for HWP. Inconsistency of test results obtained with the full and the reduced polymorphism can thus arise due to changed power, in particular if it involves a large change in sample size or in the allele frequency distribution. This should be taken into account when interpreting the test results.

Bi-allelification or joining of alleles makes STR data less informative, but can nevertheless be beneficial for several reasons. First of all, it can make multi-allelic data suitable for methods that can deal only with bi-allelic data. Second, if there is any reason to suspect that some alleles or genotypes cannot be faithfully distinguished, grouping them can safeguard against the introduction of genotyping error.

For STRs, primer binding site mutations are known to provoke null alleles, also known as silent alleles [38]. A detailed explanation of how null alleles can be identified and circumvented is given by [39]. Results from many concordance studies that use alternative primers to detect the null alleles are given on the NIST website (https://strbase.nist.gov//NullAlleles.htm). Individuals that are heterozygous for the null allele are easily misinterpreted as homozygous for the non-null allele. If the null allele is common, a lack of heterozygosity may result, potentially ultimately leading to the rejection of HWP. If the primer binding site mutation is population specific, then this can explain why rejection of HWP may occur in a particular population, but not in others. Moreover, any rare allele most likely occurs in heterozygote form, jointly with a common allele. If a null allele is common, it can thus lead to rare alleles that are present as apparent homozygotes. This can easily trigger rejection of HWP, because rare homozygotes are unlikely under the equilibrium assumption. E.g., for a tri-allelic variant with a rare $\mathrm{C}$ allele, for the genotype counts $(\mathrm{A}\mathrm{A}=25,\mathrm{A}\mathrm{B}=50,\mathrm{A}\mathrm{C}=2,\mathrm{B}\mathrm{B}=25,\mathrm{B}\mathrm{C}=1,\mathrm{C}\mathrm{C}=0)$ equilibrium will not be rejected (exact p-value = 1.0). If two $\mathrm{A}$ alleles in $\mathrm{A}\mathrm{B}$ individuals are null due to a primer binding site mutation, equilibrium for the resulting counts $(\mathrm{A}\mathrm{A}=25,\mathrm{A}\mathrm{B}=48,\mathrm{A}\mathrm{C}=2,\mathrm{B}\mathrm{B}=27,\mathrm{B}\mathrm{C}=1,\mathrm{C}\mathrm{C}=0)$ will neither be rejected (exact p-value = 0.77), but if the two A null alleles occur in $\mathrm{A}\mathrm{C}$ individuals, giving counts $(\mathrm{A}\mathrm{A}=25,\mathrm{A}\mathrm{B}=50,\mathrm{A}\mathrm{C}=0,\mathrm{B}\mathrm{B}=25,\mathrm{B}\mathrm{C}=1,\mathrm{C}\mathrm{C}=2)$ equilibrium will be rejected (exact p-value 0.0008). STRs with a common null allele are therefore likely to contain false rare homozygotes that create disequilibrium. Alternatively, if an STR has rare homozygotes, one may suspect the presence of a null allele.

We note that STRs with a single (or a few) significant bi-allelified test for a particular STR allele (e.g. like D22S1045 in Table S2) may also arise from LD between a primer site binding mutation and specific STR alleles. Such LD can provoke that heterozygotes for the particular STR allele often carry the binding site mutation, and end up as homozygotes for in fact carrying a null allele. This can provoke an increase of homozygosity with respect to all other STR alleles. Under bi-allelification all other-allele homozygotes (including all false ones) are summed, such that evidence against HWP might accumulate, ultimately possibly leading to rejection of HWP for the bi-allelified polymorphism. Whether such rejection finally occurs or not, will depend on the allele frequency of the specific STR allele, the allele frequency of the primer binding site mutation, and their degree of LD. At any rate, LD between the binding site mutation and an STR allele will generally perturb the genotype frequencies.

Our proof of transitivity is written in plain matrix algebra. However, the operations we performed on genotype and allele frequencies can be rephrased in terms of basic operations known in compositional data analysis [40,41]. Genotype and allele frequencies can be considered as compositional data, as both are subject to a unit-sum constraint. The elimination of alleles then corresponds to the creation of a subcomposition, the corresponding (re)normalization of allele and genotype frequencies is known as closure, and the joining of alleles is known as the amalgamation of parts.

For the NIST data, testing each STR within each population using a Bonferroni correction seems too conservative and, as argued above, may leave important disequilibrium undetected. Alternatively, one might use the false discovery rate [42] which is less conservative than the Bonferroni correction. We suggest, at any rate, a flexible approach, where even tests of STRs that are strictly speaking not significant but close to the Bonferroni threshold are followed up for inspection of possible causes for disequilibrium. We suggest, as Ye et al. [43], the source of deviations from HWP to be investigated. Most importantly, we have shown that HWP tests can identify allele imbalance and pinpoint the problematic alleles. The combined inspection of HWP test results and allele coverage ratios seems particularly useful to identify problems. By using a restricted permutation test that permutes alleles only within ethnicities, each STR can be tested for HWP just once, accounting for the fact that allele frequencies can differ over ethnicities. This reduces the multiple testing burden.

Over the last few years, more SB STR data sets have become available for use in forensic genetics, and the statistical analysis of the data needs to be adjusted accordingly, as is for instance the case for the study of population substructure [44]. SB STRs have more alleles, and will likely provide additional insights for different topics in population genetics, such as STR mutation and genetic diversity.

Under the assumption of HWP, rare alleles most likely occur in heterozygote form. Significant deviations from HWP easily result if rare alleles occur in homozygote form. We have shown that the grouping of disequilibrium-related alleles can be used to reduce disequilibrium, as this may actually reduce genotyping error if the corresponding alleles that are joined can indeed not be faithfully distinguished. This preserves the assumption of allelic independence at the small cost of increasing allele frequency and decreasing the numerical strength of matching STR profiles. If there is indication that two alleles cannot be distinguished then it is prudent to combine them. This will preserve the sample size, and strengthen that the HWP requirement, omnipresent in forensic genetics, is met.