Benchmarking Aspects of Ab Initio Fragment Models for Accurate Excimer Potential Energy Surfaces

Abstract

While Coupled-Cluster methods have been proven to provide an accurate description of excited electronic states, the scaling of the computational costs with the system size limits the degree for which these methods can be applied. In this work different aspects of fragment-based approaches are studied on noncovalently bound molecular complexes with interacting chromophores of the fragments, such as π-stacked nucleobases. The interaction of the fragments is considered at two distinct steps. First, the states localized on the fragments are described in the presence of the other fragment(s); for this we test two approaches. One method is founded on QM/MM principles, only including the electrostatic interaction between the fragments in the electronic structure calculation with Pauli repulsion and dispersion effects added separately. The other model, a Projection-based Embedding (PbE) using the Huzinaga equation, includes both electrostatic and Pauli repulsion and only needs to be augmented by dispersion interactions. In both schemes the extended Effective Fragment Potential (EFP2) method of Gordon et al. was found to provide an adequate correction for the missing terms. In the second step, the interaction of the localized chromophores is modeled for a proper description of the excitonic coupling. Here the inclusion of purely electrostatic contributions appears to be sufficient: it is found that the Coulomb part of the coupling provides accurate splitting of the energies of interacting chromophores that are separated by more than 4 Å.

1. Introduction

Recent decades witnessed significant development of quantum chemical methodology; larger and larger molecules can be treated with increasing accuracy and, at the same time, the need for calculations to support experimental observations is becoming more relevant. For the electronic ground state, well established methods are available, and quantum chemistry, often by density functional theory (DFT), is able to study structures and even reactions of molecules as large as polypeptides. However, many important problems cannot be treated with ground state methods. These involve, for example, electron transfer between distant regions in biomolecules or situations associated with electronic excitations affecting multiple local domains. Since established methods cannot describe such processes, the demand for new tools to treat excited states in large systems is increasing.

There are two possible routes toward this goal. One option is to develop new approximate methods, but maintaining the accuracy and reliability is not a trivial task.¹⁻⁵ Alternatively, one can aim at defining (multiscale) approaches where only the important part of the system is treated at the high level, while the rest is approximated at a lower level. Different types of embedding methods, like quantum mechanics/molecular mechanics (QM/MM),⁶ “our own N-layered integrated molecular orbital and molecular mechanics” (ONIOM),⁷ projector-based embedding (PbE),⁸ frozen density embedding (FDE),^9,10 and local correlation methods,¹¹⁻¹⁷ are available for describing many processes in large systems. However, nonlocal phenomena are poorly suited for these approaches since they often require too large active partitions in these calculations.

Such collective events can indeed be very important. For example, we have found¹⁸ that excitations can be delocalized to at least four nucleobases in oligonucleotides. Indeed, this study left open the question of whether even more units play a role in excited states of RNA and DNA chains. For such situations fragment methods¹⁹ could be the preferred approach, where several “active” centers can be handled at a high level of theory and the properties of the entire system are calculated from those of the individual fragments, considering proper coupling terms between them. Fragment methods are well suited for calculations of noncovalently bound systems, since the choice of fragmentation is obvious. From the point of view of excited states, DNA is also one of such systems since the excitations do not delocalize anywhere but the nucleobases that interact in a noncovalent manner.²⁰

Regarding the route toward developing such a fragment-based method, our previous work²¹ investigated the possibilities of obtaining accurate ground state potential curves of noncovalent dimers using high-level Coupled Cluster (CC) methods applied to the electronic structure of the fragments. In the present work, we take another step forward by extending this methodology to (singly) excited states, thereby considering multichromophore systems.

The general Hamiltonian of two interacting fragments is expressed as

1

with being the Hamiltonian of the noninteracting fragments and 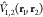that of their interaction. This Hamiltonian suggests a perturbative treatment with the product of the fragments’ wave functions as zeroth order. When considering the ground state and one excited state on each fragment, the product wave functions take the form

2

where the indices 1 and 2 refer to the two fragments. Φ_i,k is the kth eigenfunction of the Hamiltonian of fragment i:

3

The quality of such a perturbative approach depends on the strength of the interaction. A fraction of its effect can be captured by repartitioning the Hamiltonian of Eqn. 1:

4

where 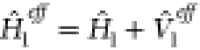and . 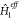is essentially an embedded Hamiltonian which can be used to describe the ground state and also local excited states in the presence of the other fragment. The accuracy of this approach will primarily depend on the choice of 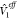and ΔV₁(r₁, r₂); several variants have been tested in our previous study on the ground state.²¹ This formalism can also be applied to the excited state of the complex, provided the excitation is localized on one fragment (see e.g. ref (22)).

This scheme can be extended to interacting chromophores by applying the excitonic model, as first suggested by Frenkel²³ and later by Davydov²⁴ and used in many applications (see e.g. refs (25−31) and references therein); after obtaining the fragment energies and wave functions of the effective Hamiltonians 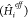, the resulting excited states are obtained by diagonalizing the Hamiltonian matrix defined in the space of the two locally excited product functions from Eqn. 2.

Thus, a fragment method describing a multichromophore system has two main ingredients. First, a proper definition of the effective Hamiltonian 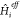is needed, which includes the intermolecular interactions compatible with the electronic structure method that is used. Eventually, a corresponding ΔV_i is necessary to include the missing interaction terms. Second, an appropriate approximation for the excitonic coupling between the excited states also needs to be established.

In this paper, on the way of defining a proper fragment method for investigating the excited states of e.g. DNA, we systematically test the possible components of such fragment methods. As of the interaction of the fragments, in our previous paper²¹ several schemes have been tested and we have found that both QM/MM and PbE methods (with a proper account for dispersion and Pauli (exchange) repulsion terms from the extended Effective Fragment Potential (EFP2)³²⁻³⁴ model) are capable of reproducing full dimer calculations of the same level of theory with high fidelity. It is worthwhile to generalize these schemes to excited states. With regards to the interaction of the different chromophores, we benchmark the accuracy of couplings calculated from transition dipole or transition densities. Similar methods have been suggested, among others, by Morrison et al.,²⁵ Sisto et al.,²⁶ Amadei et al.,²⁷ Head-Gordon et al.,³⁵ Höfener and Visscher,²⁹ Neugebauer,^36,37 as well as Caricato et al.²⁸ The novelty of the schemes tested here is the use of high-level CC theory for the electronic structure of the fragments and the careful selection of all components of the noncovalent interaction energy.

Obtaining proper reference data for validation of the models turns out to be a nontrivial task. Problems arise from converging the calculations to the appropriate states (in particular when diffuse basis functions are used), from the presence of charge transfer (CT) type electronic states in the low-energy spectrum at small intermolecular distances, as well as from the choice of counterpoise (CP) correction in excited states. The present study will also address these issues.

The paper is organized as follows. Section 2 gives a short summary of the available methodologies, with emphasis on the differences in theoretical formulations and the possibility of incorporating them into ab initio calculations. Section 3 presents the molecular systems used in the tests. Section 4 describes the computational details, while the results and discussion are presented in Section 5.

2. Methodologies for Modeling Intermolecular Interactions in Excited States

Let us introduce the proposed methodology on the simplest example of a supersystem consisting of two fragments, with just one excited state considered on both. To describe the excitonic coupling of the two excitations localized on the fragments, we select product functions describing the two locally excited states:

5

where r₁ and r₂ represent the coordinates of fragments 1 and 2, respectively. The first function describes the excited state localized on the first fragment, while the second function describes the one localized on the second fragment, and they belong to two different partitionings of the Hamiltonian:

6

where 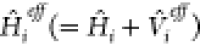includes the effect of the environment through an “embedding potential” . The fragment wave functions with a tilde are eigenfunctions of the corresponding effective Hamiltonians

7

and thus include the effect of the other fragment’s ground state through 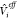, while the corresponding unadorned (Φ_1,0(r₁), Φ_2,0(r₂)) are eigenfunctions of the unperturbed subsystems (see Eqn. 3). The inclusion of the approximate “remaining potential” is necessary to correct for interactions which are not (or cannot be) accounted for when the eigenproblem of 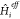is solved (see later).

is a good approximation for locally excited states with energy

8

but does not include any polarization between the two fragments. This expression is often used in QM/MM and other embedding schemes; we also have tested it in ref (22). The quality of this approximation depends on the electronic structure method used, as well as upon the choice of 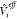and ΔV_i ; this will be discussed in detail in Section 2.1. Note that the above formalism does not consider the antisymmetrization of the wave functions; therefore, the corresponding “Pauli repulsion” contribution should be appropriately included in ΔV_i.

To consider Frenkel²³ (or excitonic) coupling of the two chromophores on the fragments, the matrix of the Hamiltonian in the basis of the functions in Eqn. 5 should be diagonalized, i.e.,

9

with

10

To evaluate this coupling, appropriate approximations need to be introduced as discussed in Section 2.3.

First, however, the multilevel approaches that can be applied for solving the eigenproblem of 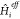, along with the appropriate choice for the “remaining potential”, are reviewed in Sections 2.1 and 2.2

2.1. Definition of the Effective Hamiltonian

In this study, as in ref (21), two approaches to define an effective Hamiltonian that can be used with CC methods are tested.

2.1.1. QM/MM

The multilevel scheme termed QM/MM⁶ revolves around the representation of the environment with point charges that usually reside on atomic sites, allowing the treatment of large complexes in a very economical manner. Within this scheme the effective Hamiltonian (H^₁eff) of Eqn. 6) is given by

11

where 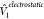represents the Coulomb interaction of fragments 1 and 2, the latter represented via the partial charges. The main advantage of this scheme is its straightforward incorporation into any quantum chemical method (and code), so that it is widely applied.

There are various ways to define the point charges; several sets are available, e.g., in traditional molecular force fields like AMBER^38,39 or CHARMM.⁴⁰ A more flexible parametrization can be achieved using atomic multipoles^41,42 as, e.g., within the Effective Fragment Potential (EFP) framework.⁴³⁻⁴⁵ In our previous paper on the ground state of noncovalently bound complexes²¹ the CHELPG (CHarges from ELectrostatic Potentials using a Grid-based) algorithm⁴⁶ was found to work well with CC methods. In the context of CHELPG, the partial charges at the atomic sites are fitted to reproduce the electrostatic potential and some low-order electrostatic moments of the molecule calculated at any level of theory; hence the one used for the active fragment (e.g., CCSD) can also be applied. Unlike in methodologies used in most conventional force field methods, this way an accurate set of charges can be obtained from fundamental considerations, consistent with the ab initio spirit of the present scheme.

One should realize, however, that the effective Hamiltonian in Eqn. 11 does not include important interaction terms, such as dispersion and Pauli exchange between the fragments. Thus, for accurate interaction energies also at short distances, the latter need to be added a posteriori via ΔV₁(r₁, r₂) (see Section 2.2).

2.1.2. Huzinaga Embedding Scheme

A more sophisticated consideration of the environment and its interactions can be achieved with multilevel quantum chemical embedding methods. Bottom-up frozen density embedding^9,10 and top-down projector-based embedding (PbE)⁸ strategies are both available. The former is computationally less demanding as subsystems are treated separately, while the latter avoids the issues arising from the lack of orthogonality between subsystems. PbE was first introduced by Manby and Miller⁸ who included an arbitrary level shift parameter in the Fock operator of the embedded subsystem, raising the energy of environment orbitals to near infinity. Orthogonality between subsystems can also be achieved by adapting the Huzinaga-equation⁴⁷ to the embedding problem⁴⁸ or via the projection scheme of Hoffmann and Khait.⁴⁹ PbE has been applied to the calculation of excited states with various goals in mind. Bennie et al.⁵⁰ improved the original PbE method for hydrogen-bonded complexes by including the most important occupied orbitals of the environment in the excited state calculation. Parravicini and Jagau⁵¹ studied ionization, electron attachment, and electronic resonances, also applying the concentric virtual orbital localization scheme.⁵² A benchmark study by Hégely et al.⁵³ compared various multilevel approaches including PbE for the calculation of excitation energies.

In the present study the embedding scheme of Hégely and co-workers,⁴⁸ based on the Huzinaga-equation, is chosen as the second approach for the description of the active fragment. Embedding a fragment treated at the CC level of theory into the environment of the other fragment described using density funcional theory (DFT) requires the a priori definition of the active subsystem and the environment. Following a DFT calculation on the entire system, the occupied molecular orbitals (MOs) of the fragments are localized, resulting in the splitting of the density matrix (D₁₂) into two parts D₁ and D₂. The localization can be extended to the virtual orbital space, reducing the computational cost of the CC calculations, as well as allowing a cleaner treatment of localized excited states by avoiding charge transfer contributions (see later). The SPADE (Subsystem Projected AO DEcomposition)⁵⁴ method offers a black-box way of localizing and partitioning the orbital space based on the difference of singular values in a singular value decomposition scheme, and can be applied to both occupied and virtual orbitals.

The Fockian of the active subsystem is

12

where h and 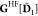are the core Hamiltonian and the two-electron part of the Fockian of subsystem 1, respectively, while the remaining terms in Eqn. 12 give the embedding potential. 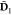is the one-electron density matrix of the embedded active subsystem reoptimized in a second Hartree–Fock calculation during which the orthogonality of the subsystems is ensured by solving the Huzinaga-equation with the orbitals of the environment kept frozen:

13

where S is the overlap matrix of the atomic orbitals, P₂ is the projector onto the environment orbitals, and 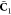is the MO coefficient matrix of the embedded orbitals whose orbital energies are in the diagonal matrix 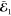. The orbitals obtained this way can be used in correlated wave function (WF) calculations for both ground and excited states.²²

The energy ansatz of this method for WF-in-DFT embedding is

14

where E^DFT_1,2 is the DFT energy of the entire supersystem, E^DFT₁ is that of the active fragment calculated using the localized supersystem orbitals, and E^WFT₁ is the WF energy of the embedded fragment. This energy ansatz is general, meaning that the ground and excited state energies differ only in the WF term that is calculated using the same embedding potential in both cases. This is the result of the frozen environment orbitals as they remain unrelaxed to changes in the active orbital space. Note that the Fockian here is constructed from similar principles as the effective Hamiltonian introduced in Eqn. 6; i.e., it includes the electronic embedding by the environment’s density. It is also apparent from the energy expression (Eqn. 14) that intersubsystem interactions are retained from the original ground state supersystem calculation at DFT level of theory. This means that not only the electrostatic interaction, but also the ground state Pauli repulsion is included in the final energy. Common DFT functionals are known to fail in giving a proper description of dispersion interactions, thus the latter is missing from this ansatz and has to be included separately.

The first term on the right side of Eqn. 14 can be formally divided into monomer energies calculated using the localized supersystem MOs and the interaction energy term:

15

Therefore, the original energy ansatz (Eqn. 14) above contains the fragment energies at two different levels of approximation: that of the active fragment from the wave function calculation 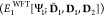, while the fragment playing the role of environment is treated at the DFT level (E^DFT₂[D₂]). This results in an incorrect asymptotic behavior of relative energy curves for non-homodimer systems. Therefore, we suggest the use of a modified energy expression:

16

2.2. Choice of the Remaining Potential ΔV_i

The schemes above lack some important intermolecular interactions: QM/MM does not include any van der Waals-type interactions, while dispersion is missing from the PbE approach. Based on our findings for the ground state in ref (21), correcting for dispersion and Pauli repulsion via the ΔV₁(r₁, r₂) term in the Hamiltonian is an appropriate approximation and the extended Effective Fragment Potential (EFP2) developed by Gordon and co-workers^{32−34,55−57} is an excellent choice. (See ref (21) for other possibilities.)

The essence of the EFP2³² is that an adequate parameter set for the potential is derived from first principle considerations. The algorithm is able to predict every important contribution to the intermolecular interactions, but here we shortly discuss only the Pauli repulsion and dispersion terms, which are used in the calculations. For a more detailed description of the EFP2 formalism, the reader is referred to refs (33, 34, and 57).

To obtain the dispersion contribution in EFP2,⁵⁸ a set of points are defined in the first step, located at the nuclear positions and the midpoints of covalent bonds. These serve as the centers of localized molecular orbitals (LMO) obtained from a HF or DFT calculation of the subsystem. Then the dynamic dipole polarizabilities around the centroids of these LMOs are determined by applying the time-dependent extension of the chosen method, which are then used to calculate the dispersion energies between the fragments. Additional damping parameters derived from the overlap of these orbitals are also used to correct the behavior at short intermolecular separations.

For the Pauli repulsion in the EFP2 scheme,³⁴ the necessary antisymmetrization is achieved by restricting the permutations to just two electrons and approximating the energetic effect with a power series with respect to the orbital overlaps (S). The terms beyond 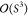are neglected, while additional simplifications are applied to the lower-order terms.

According to the literature,^59,60 EFP2 is a good model for interactions of molecules in the ground state. However, to our knowledge, only one attempt has been made to treat excited states with EFP2: Viquez Rojas and Slipchenko⁶¹ calculated the solvent effect on the excitation energies of nine chromophores. In this study, the Pauli repulsion term was included in the effective Hamiltonian (so-called QM/EFP2 scheme).^62,63 Important efforts have also been made by Hapka, Przybytek, and Pernal^64,65 to include the dispersion between the ground and excited states within SAPT (Symmetry-Adapted Perturbation Theory).^66,67 These methods are not yet available for routine applications.

Therefore, since the experience with the ground state clearly reveals that dispersion and Pauli repulsion are necessary to achieve the accuracy we aim at,²¹ we decided to check whether the ground state corrections are also applicable to the excited states. Note that this is a common practice in TD-DFT studies on excited states of noncovalent complexes.⁶⁸

The hope is that the error made this way is significantly smaller than the one introduced by the complete neglect of these terms. This idea is supported by the fact that, in excited states dominated by a single substitution, only a small fraction of the electrons are affected by the excitation and the dominant part of the electron density is similar in the ground and excited states. Although the results below show that this approximation works reasonably well, we hope that the success of the whole scheme presented in this paper will inspire research that will enable us to remove this restriction in the future.

To summarize, two conceptually different schemes will be tested in the present study. One is a QM/MM approach based on CHELPG point charges, augmented with (ground state) dispersion and Pauli repulsion from EFP2 (termed as QM/MM + EFP2 hereafter), while the other one is a Huzinaga projection based embedding model (PbE) augmented with an EFP2 (ground state) dispersion contribution (termed as PbE + EFP2).

2.3. Coupling Schemes

The off-diagonal elements of the Hamiltonian matrix (Eqn. 9) represent the coupling between excitations of the different chromophore groups. To consider possible approximations for Ṽ(1, 2), let us use the original partitioning of the Hamiltonian (Eqn. 1) which treats both fragments equivalently. With this Hamiltonian, it is more reasonable to use the unbiased basis (Eqn. 2) for the evaluation of the matrix elements. This approximation is not so severe since, presumably, the noncovalent interactions considered do not substantially change the fragment wave functions. This means that

17

i.e., the coupling is just the matrix element of the interaction potential .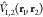

A simple way to calculate this term is to approximate the potential by the dipole approximation, first suggested by Förster⁶⁹

18

where R_1,2 is the vector connecting the center-of-mass (COM) of the two chromophores, R₁₂ is the distance between them, and 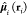is the dipole operator of fragment i.

With this approximation, the coupling can be calculated from the transition dipoles of the fragments

19

with

This approach (called the Transition Dipole Approximation (TrDA) hereafter) is a simple and economical way to estimate the coupling. Note that the second term in eq 19 is needed only if the two transition dipole moments are not parallel; i.e., it gives no contribution in the stacked systems we investigate here.

The dipole approximation can be extended by considering transition monopoles, e.g., at atomic centers⁷⁰ or by higher multipoles like in an extension of the PMM (Perturbed Matrix Method) approach (PMM-QQ).⁷¹ However, ref (71) reveals that the extension in this form does not necessarily improve the accuracy of the coupling.

A more accurate approximation of 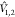is to consider the exact Coulomb interaction between the electrons of the two fragments

20

where the indices (i(1) and j(2)) run over the electrons of fragments 1 and 2, respectively. (The contribution of the nuclei to 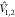vanishes in the commonly adopted Born–Oppenheimer and Condon approximations.⁷²) With this, the coupling becomes

21

i.e., it can be calculated from the transition densities 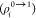of the two fragments.^72,73 Indeed, there are several successful attempts in the literature to calculate the Coulomb coupling from transition densities: Herbert and co-workers²⁵ with CIS, Martinez and co-workers,⁷⁴ Curutchet and Mennucci,⁷⁵ as well as Head-Gordon and co-workers⁷⁶ with TDDFT, Neugebauer with subsystem TDDFT,³⁷ and Fückel et al.⁷² as well as Höfner and Visscher²⁹ with CC2 and related methods. There is even a report by Caricato et al.²⁸ on a CCSD implementation. Note that efficient calculation of the coupling according to Eqn. 21 requires an integral-direct code.

Despite the elegant and general formulation, not many publicly available implementations exist, and to our knowledge, in particular, none exists for CC methods. Therefore, for the pragmatical reason we adapted the Transition Density Cube (TDC) algorithm of Krueger and co-workers^73,77 and implemented the grid representation of transition densities in the CFOUR^78,79 program system. This enables the calculation (within the numerical accuracy) of the electronic Coulomb interaction between the fragments at any theoretical level for which the transition density is available.

The proper consideration of the antisymmetry of the wave function introduces an additional term in the coupling which is often called the exchange or Dexter coupling.⁸⁰ Exchange coupling is easily obtained within DFT theory by calculating also the contribution of the exchange potential, similarly to Eqn. 21. As pointed out by Fückel et al.,⁷² by contracting the transition densities with the exchange integrals, it is also possible to obtain this quantity regardless of the method with which the transition density was evaulated. Unfortunately, no publicly available implementation is available and the TDC scheme is also not appropriate for this purpose. Since the Dexter coupling is known to be relevant only at short intermolecular distances⁷² we will not consider this term in this study; however, from the results presented, the distance where this term becomes important can be deduced.

Note that the same coupling also appears in Electron Energy Transfer (EET) processes,⁸¹ and many approximate schemes have been suggested to include it. An overview of these techniques is beyond the scope of this paper; more detail can be found e.g. in refs (82 and 83).

3. Molecular Systems

To find the approximation most suitable for excited states of noncovalently interacting dimers of nucleobases, we investigate, as in our previous paper on the ground state,²¹ bimolecular complexes of nitrogen-containing heterocycles: stacked homodimers of pyrrole (denoted by (Pyr)₂ hereafter), cytosine ((Cyt)₂), uracil ((Ura)₂), as well as the heterodimer cytosine–uracil complex (Cyt-Ura). In addition, homodimer of formaldehyde ((CH₂O)₂) was also included in this study. The test systems are shown in Figure 1. In the discussion below, the “distance” of monomers refers to that between the centers of masses. All the complexes were investigated in a stacked (sandwich) structure, with oppositely oriented dipoles, except for the (Pyr)₂ where the symmetry was lowered by a 10° in-plane rotation away from the C_2h structure. The equilibrium structures of the monomers (optimized at the MP2/6-31G* level) were taken from ref (84) and are documented in Tables S1–S4 of the Supporting Information along with the geometries of dimers at a representative distance in Tables S5–S9.

Figure 1.

Orientation of the molecules in the test systems used in this study. The measure of the distance is represented by the blue dotted line connecting the centers of mass of the fragments.

The performance of methods describing excitonic states, as it has also been pointed out recently by Hancock and Goerigk,⁶⁸ should not just be evaluated in single point calculations. Therefore, the tests presented here include potential curves along the intermolecular separation with the monomer structures kept frozen. Although the proposed methodology can be generalized to practically any number of states, in this first application we limit consideration to the interaction of just two states. These simplistic tests should provide a better understanding on how the different approximations work in the suggested scheme.

In order to investigate the interaction of just a pair of states, these need to be energetically well separated from other electronic states. It turned out that selecting such pairs is not an easy task, in particular in calculations with diffuse basis functions; Rydberg states appearing among the excited states of molecules with π electronic structure result in a high density of states with strong interactions between them. In addition, at short distances charge transfer (CT) states complicate the spectrum. This is demonstrated on Figure S5 in the Supporting Information in the case of (CH₂O)₂ which clearly shows that the rapidly descending CT curve intersects with all low-lying states at short distances. Therefore, to find appropriate states for the tests, certain compromises were necessary, which will be discussed later. The monomer electronic states considered in this study are summarized in Table 1.

Table 1. Summary of the Monomer Electronic States Investigated in This Study.

	Basis set	State	ΔE,a eV	fb
CH2O	cc-pVDZ	11A1 (ground)	0.00
		11B1 (σ–π*)	9.36	0.002
		21A1 (π–π*)	9.95	0.011
CH2O	aug-cc-pVDZ	11A1 (ground)	0.00
		21A1 (n–R)	8.07	0.058
		11B1 (σ–π*)	9.24	0.001
		31A1 (π–π*)	9.59	0.166
CH2O	aug-cc-pVTZ	11A1 (ground)	0.00
		21A1 (n–R)	8.22	0.054
		11B1 (σ–π*)	9.14	0.001
		31A1 (π–π*)	9.51	0.149
Pyrrole	cc-pVDZ	11A1 (ground)	0.00
		11B2 (π–π*)	7.03	0.146
Pyrrole	aug-cc-pVDZ	11A1 (ground)	0.00
		11B1 (n–R)	5.14	0.000
		11A2 (n–R)	5.87	0.021
Cytosine	cc-pVDZ	11A′ (ground)	0.00
		31A′ (π–π*)	6.07	0.157
Uracil	cc-pVDZ	11A′ (ground)	0.00
		21A′ (π–π*)	5.78	0.199

^aEOM-CCSD vertical excitation energies, in electron volts.

^bOscillator strength evaluated at the EOM-CCSD level.

4. Computational Details

The primary goal of developing fragment methods is to replace high level (Coupled Cluster (CC) type) electronic structure calculations on the complex with appropriately chosen calculations on the fragments. The family of CC-type methods allows systematic improvement of the accuracy, but approximate versions (like CC2⁸⁵ and ADC(2)⁸⁶ in particular with spin scaling^87,88) enable an increase of the size of the fragments, as well. Still, to avoid any ambiguity caused by the approximate methods, the first tests will be done with the Equation of Motion Coupled Cluster with Singles and Doubles (EOM-CCSD) method,^89,90 which can be performed not only for middle sized fragments considered in this work, but also for their complexes.

Double-ζ quality basis sets with diffuse functions have been selected for the calculations, giving a reasonable description of excited states and also of intermolecular interactions⁹¹ while making the corresponding EOM-CCSD calculations also feasible on the complexes. However, to be able to investigate valence π–π* excitations, the primary source for excimer states, some calculations had to be done without diffuse functions, even if the interaction energies obtained this way are clearly underestimated. One should proceed with great care when performing comparisons without diffuse functions, details are given below. In order to test basis set effects, augmented triple-ζ calculation have also been performed for the smallest system ((CH₂O)₂).

To summarize, all reference, QM/MM, and high-level steps of the PbE calculations were done with CCSD⁹² and EOM-CCSD^89,90 level of theory in the frozen core approximation. Three basis sets were used in these calculations: cc-pVDZ,⁹³ aug-cc-pVDZ, and aug-cc-pVTZ.⁹⁴ Only calculations using the same method and basis have been compared, allowing the evaluation of the fragment methods. Specific details of the calculations are discussed below.

4.1. Reference ab Initio Calculations

To assess the accuracy of a new scheme, appropriate comparison is necessary, which turned out to be a significant bottleneck of this study.

First, it was a major challenge to identify and converge valence excited states when diffuse functions were included in the basis due to the presence of interacting Rydberg states. This was not the case when the basis without diffuse functions was used. Clearly, this way just a limited portion of the interaction energy is captured, but with a careful selection of the parameters of the fragment calculations (see below) meaningful comparisons can be made.

Second, the calculations on the complex need to be corrected for basis set superposition error (BSSE) since the fragment calculations are free from this artificial lowering of the interaction energy. In our previous paper,²¹ we used counterpoise (CP) correction⁹⁵ to correct the ground state energies of the complex. Although it is often claimed that CP corrections overestimate BSSE, particularly in correlated calculations,⁹⁶ it is still the state of the art in studies of noncovalent interactions.⁹⁷ Note that the SNOOP method by Jørgensen et al.⁹⁸ is a noteworthy attempt to calculate a CP correction for correlated ground states, but requires special code which at present is only available in the LSDalton program suite.⁹⁹

The definition of BSSE corrections for excited states is not obvious. Rocha-Rinza et al.¹⁰⁰ suggested the use of the CP correction formula analogous to the ground state one. This has been used in some applications (see e.g. refs (101 and 102)) but diffuse basis functions were not usually included in these calculations. Serrano-Andrés and Serrano-Pérez, in their review on excited states,¹⁰³ suggested the use of the ground state CP correction also for the excited state due to the uncertainties of the above definition, particularly for delocalized situations. We have performed some test calculations applying the formula of Rocha-Rinza et al.;¹⁰⁰ the results are shown in Figure 2 for (CH₂O)₂ in the aug-cc-pVDZ basis. While for some low-lying states the CP correction is similar to the ground state value at any distance, some states show unreasonably large CP corrections at close interfragment distances. A quick look into this problem revealed that the CP correction removes the charge transfer component of the solution, which is an artifact; many excited states of interacting fragments indeed have charge flow. Considering that CP correction is a basis set effect and mostly influences the orbitals,⁹⁶ the CP correction obtained at the HF level was used for both the ground and the excited states. Note that this way the CP correction does not change the excitation energy, but does indeed influence the shape of the excited state energy surfaces. It is certainly worth investigating the problem in more detail, and such study is underway. Nevertheless, the present results indicate that this approximation is reasonable.

Figure 2.

Counterpoise (CP) corrections calculated for several states of (CH₂O)₂.

All reference calculations have been performed using the CFOUR program package.^78,79

4.2. Fragment Calculations

The QM/MM calculations were performed at the same levels of theory as the reference calculations using CFOUR,⁷⁹ with the CHELPG point charges incorporated into the one-electron Hamiltonian.

The CHELPG point charges were obtained at the CCSD level using GAMESS¹⁰⁴ with the aug-cc-pVDZ and aug-cc-pVTZ basis sets. The latter were used in the QM/MM/aug-cc-pVTZ calculations, the former in all other cases. Further details of the CHELPG calculations, as well as the determined atomic charges, can be found in the Supporting Information.

The PbE calculations were performed using the MRCC program suite¹⁰⁵ with the resolution of the identity (RI) approximation applied for both the SCF and correlation components of the calculations. The active subsystem was treated at the same level as the reference and the PBE functional¹⁰⁶ was used for the low level method. The localization and partitioning of the occupied and virtual orbital spaces was done by SPADE.⁵⁴ The energy expression of Eqn. 16 was used as the diagonal term in Eqn. 9. For all systems the PbE calculations used localized virtual orbitals; otherwise the excited state spectrum was spoiled by artifactual CT states. However, the (CH₂O)₂ dimer was also investigated using the full virtual space (in ground state calculation), as well as an extended SPADE-localized virtual space containing two additional orbitals to test the incorrect behavior of the method with diffuse basis functions (see Section 5.2).

The EFP2 dispersion and Pauli repulsion potentials were determined from the restricted Hartree–Fock wave function using the built-in routine of GAMESS¹⁰⁴ with the default settings as described in the manual of the program package.¹⁰⁷ The basis sets for these calculations were adjusted to the electronic structure calculations. For the augmented basis sets, these interaction terms were calculated with the 6-311++G(3df,2p) basis set as suggested by Slipchenko and Gordon.¹⁰⁸ On the other hand, to compare with the reference results obtained with the cc-pVDZ basis, which clearly includes only a smaller portion of the interaction energy, the EFP2 parameters were also obtained with this nonaugmented basis set. It will be checked below whether the EFP2 scheme gives reasonable interaction energies in this case.

4.3. Calculation of Interstate Couplings

The transition moments and transition densities of the investigated excited states were determined from monomer calculations on the same level as the reference calculations using CFOUR.⁷⁹ In the TDC scheme the transition densities were represented on a COM-centered grid of stepsize 0.25 Å with maximum dimension of 16 × 20 × 24 Å for formaldehyde and 20 × 20 × 20 Å for all other monomers corresponding to the Cartesian coordinates given in Tables S1–S4 in the Supporting Information. The numerical accuracy of the TDC procedure was evaluated by integrating the transition density for the entire space, as well as by comparing the transition moment obtained on the grid with that from the EOM-CC calculation.

Due to the biorthogonality of the CC framework, the above schemes need further adjustment. There are (slightly) different left and right transition properties which would result in slightly different interaction energies. Following the procedure that the physically relevant oscillator strength is calculated from the product of left and right transition dipoles, we use the geometric mean of the left and right transition properties to evaluate the coupling.

5. Results and discussion

In this section the different approximations constituting a fragment scheme are tested. The validity of approximations of the interaction energy is investigated in Section 5.1, and the performance of different coupling schemes is presented in Section 5.3, while the final results, i.e., the total PESs of both states in question, are evaluated in Section 5.4. In addition, in Ssection 5.2 the problem related to the virtual space localization of the PbE scheme is discussed.

5.1. Interaction Energy

For homodimers it is possible to separately investigate the quality of interaction potentials without the effect of the coupling, by comparing the EFP2-corrected QM/MM and PbE curves to the average of the two reference ones. It is important to keep in mind that this comparison is valid only in the two-state model: if in the dimer calculation substantial mixing with other states takes place at a certain distance, these are no longer a suitable reference for testing the fragment method. As we will see, in particular the appearance of charge transfer states (CT) at short distances can result in such mixing. Another factor to consider in the comparisons is the above-mentioned uncertainty of the CP correction for excited state reference calculations, which is often larger than the commonly accepted accuracy of the interaction energy. Since both these phenomena become more relevant at short intermolecular separations, reliable conclusions are more likely to be drawn from the long-distance regions of the PES.

In Figure 3 the distance dependence of various interaction potentials between two formaldehyde molecules, one in a valence excited state and the other in ground state, are plotted. The calculations were done at the CCSD level using aug-cc-pVDZ and aug-cc-pVTZ basis sets. The first observation is that there is a good agreement between the QM/MM + EFP2 and reference curves at large separations for both σ → π* and π → π* states, but at short distances the QM/MM + EFP2 curves show a minimum, while the reference curves do not. A closer analysis reveals an (avoided) crossing of the studied valence excited state with Charge Transfer (CT) states in this region which results in a mixed character of both wave functions and the fast descent of the reference curves (see Figure S3 in Supporting Information). Therefore, the reference points cannot be reliably used to test the fragment methods at short distances. Observe that the π → π* state is affected already at a longer distance than the σ → π* state, because it is higher in energy and therefore the crossing takes place earlier. One can thus conclude that comparison of the reference and present fragment calculations is only reasonable above 6 Å for the π → π* and above 4 Å for the σ → π* state. For these ranges the QM/MM + EFP2 model correctly describes the interaction, and the ground state Pauli exchange and dispersion interactions are well suited for these excited states.

Figure 3.

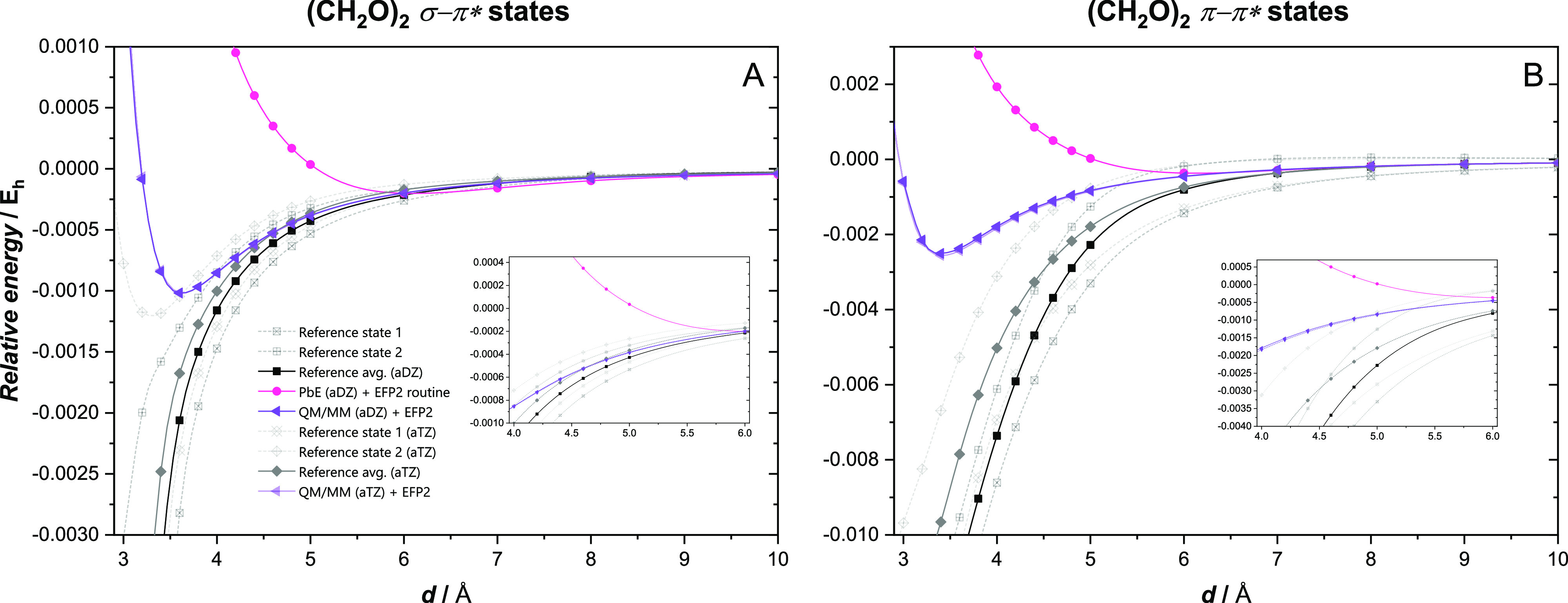
Distance dependence of various interaction potentials (not including interstate couplings) in the σ–π* (Panel A) and π–π* (Panel B) local valence excitations of the (CH₂O)₂ dimer, calculated with different models using the CCSD method with the aug-cc-pVDZ (aDZ) or the aug-cc-pVTZ (aTZ) basis sets as their wave function component.

The QM/MM + EFP2 curves obtained with the aug-cc-pVDZ and aug-cc-pVTZ basis sets are almost indistinguishable; this somewhat surprising result can be explained by the insensitivity of the CHELPG charges to the basis set (see Table S4 in Supporting Information) and the use of the same EFP2 parameters in both cases. The reference curves do differ, but the difference is small and it falls into the range of the uncertainty associated with the CP correction: using the correlated ground state CP correction instead of the HF one would lift the aug-cc-pVDZ curve (by 0.2 millihartrees at 3.6 Å), resulting in an almost perfect agreement of the two curves.

In contrast, the PbE + EFP2 scheme produces far too repulsive curves for both states; the reason for this failure is discussed below in more detail.

In Figure 4 the same comparisons are shown for valence excitations of the homodimers, obtained with the cc-pVDZ basis. The QM/MM + EFP2 curves overestimate the interaction energy in all cases: while for the larger systems the QM/MM + EFP2 curves stay below the reference at all distances and show quite accurate equilibrium positions but with much too large binding energy. In case of (CH₂O)₂ at very short distances the reference curves again show a rapid decay, presumably due to interaction with a CT state. The PbE + EFP2 results are remarkably close to the QM/MM + EFP2 ones above 4 Å but show minima at longer distances and with considerably lower binding energy.

Figure 4.

Distance dependence of various interaction potentials (not including interstate coupling) in valence excited states of the (CH₂O)₂ (Panels A and B), (Pyr)₂ (Panel C), (Ura)₂ (Panel D), and (Cyt)₂ (Panel E) homodimers calculated with different models using the CCSD/cc-pVDZ method as their wave function component.

The trends we see with the cc-pVDZ basis are quite different from those observed with the aug-cc-pVDZ basis for (CH₂O)₂. Although in the former case we have calculated the EFP2 vdW parameters also with the cc-pVDZ basis to ensure consistency with the reference calculation, obviously there is no evidence that EFP2 could reproduce the interaction energy in this rather artificial situation. For this reason we have performed an additional test calculation replacing the EFP2 term with the “exact” vdW correction of the ground state in the cc-pVDZ basis set, which was obtained as the energy difference of the reference ground state average energy and that of the uncorrected QM/MM and PbE energies. The corresponding curves are shown in Figure 5 for the (Ura)₂ and (Cyt)₂ systems. One finds a better agreement of the averaged reference curves and the models in both cases, but the curves from our models are now found above the reference ones, i.e., the interaction is underestimated. The error in the total binding energy is comparable in absolute terms to the cases where the ground state EFP2 vdW correction was used, but with a different sign. Two conclusions can be drawn from these comparisons. First, the EFP2 vdW interaction obtained at the cc-pVDZ level is much stronger than the one included in dimer calculation using the same basis. This finding is, nevertheless, of moderate importance since in real applications the fragment methods should and will be used with an appropriate basis set. More interesting is the second conclusion which tells us that the vdW interaction is stronger in the excited state than in the ground state; thus, to increase the accuracy of the fragment calculation, evaluation of this quantity from the excited state densities is warranted.

Figure 5.

Distance dependence of various interaction potentials in the π–π* excited states of the (Ura)₂ (Panel A) and (Cyt)₂ (Panel B) homodimers, with the vdW correction calculated from the ground state reference potential, at the CCSD/cc-pVDZ level of theory.

Continuing the investigation with the inspection of Rydberg states, in Figure 6 the distance dependence of various potentials for the Rydberg states of (CH₂O)₂ and (Pyr)₂ are shown, obtained with the augmented basis sets. A striking feature one observes here is the clearly inappropriate, strongly repulsive curve produced by the by PbE + EFP2 model (see Section 5.2 below). For QM/MM + EFP2 the situation is much better: the curves are qualitatively correct, although the interaction energy is underestimated. The discrepancy grows with decreasing intermolecular separation, resulting in longer equilibrium distances and lower binding energies. Note, however, that the CP correction employed here is very uncertain for the Rydberg states, making the reference curve unreliable anywhere below 4 Å.

Figure 6.

Distance dependence of various interaction potentials in Rydberg excited states of the (CH₂O)₂ (Panel A) and (Pyr)₂ (Panels B and C) homodimers, calculated with different models using the CCSD method with the aug-cc-pVDZ (aDZ) or the aug-cc-pVTZ (aTZ) basis sets as their wave function component.

The aug-cc-pVTZ results are also shown in Figure 6 for the (CH₂O)₂ dimer. The comparison to the corresponding aug-cc-pVDZ curves leads to different conclusions than for the valence states above. First, the two QM/MM + EFP2 curves differ significantly, resulting in stronger bonding in case of the larger basis set. Second, the reference curve obtained with the aug-cc-pVTZ basis set runs below the aug-cc-pVDZ one. Note that now the use of the correlated instead of the HF ground state CP correction would increase the difference between these two curves. Thus, despite the uncertainty about the reference curve, both the fragment and reference calculations confirm that for Rydberg states the use of a triple-ζ quality basis set is advised.

5.2. Failure of the Huzinaga Embedding Scheme with Diffuse Basis Sets

In the above discussions we have observed that the PbE + EFP2 scheme worked well for valence excited states if used with the cc-pVDZ basis, but repulsive potential curves were obtained with the diffuse aug-cc-pVDZ basis set. The possibility that the failure is caused by the EFP2 dispersion term can be excluded, since the same dispersion is used in QM/MM + EFP2, which works well.

On the other hand, an important feature of the present PbE scheme is the restriction of the virtual space to orbitals localized on the active fragment. As discussed earlier in Section 2.1.2, this step is necessary to avoid the appearance of artifactually too many charge transfer type CC excited states and to keep the cost of the correlated calculation to that of a single fragment. Unfortunately, this operation can result in a serious distortion of the virtual space, in particular if diffuse functions (Rydberg orbitals) are present whose localization to the individual fragments is less obvious.

To illustrate that it is this restriction causing the problem, we have performed additional calculations on (CH₂O)₂ including (a) all virtual orbitals of the complex (denoted as PbE + EFP2 with full virtual space) and (b) two additional, normally excluded virtual orbitals that have the largest contribution on the active fragment (PbE + EFP2 with extended virtual space). The results for the ground and valence excited states, as well as for Rydberg state, are included in Figure 7.

Figure 7.

Distance dependence of various interaction potentials of (CH₂O)₂   calculated with different PbE versions using the CCSD/aug-cc-pVDZ method as their wave function component. Panel A: ground state, Panel B: σ–π* state, Panel C: π–π* state, and Panel D: n–Rydberg state.

For the ground state (Panel A), even with just two additional orbitals in the extended virtual space, the potential becomes more attractive, in fact too attractive, especially if all virtual orbitals are included. Neither choice seems to be appropriate: with all orbitals included in the virtual space we see a special kind of BSSE since by decreasing the distance between the fragments, more and more virtual orbitals become available in the spatial region of the active fragment, an effect which is expected to be strong in particular with diffuse basis functions. On the other hand, restricting the virtual space to that of the active fragment causes a “reverse BSSE”: by decreasing the distance, the diffuse functions of the active fragment will spatially overlap with those of the environment, causing the localization procedure to assign them to the latter. Although this effect is only visible with diffuse basis sets, it should eventually appear also with basis sets lacking diffuse functions at very small distances.

For the valence excited states (Panels B and C) the PbE + EFP2 curve is repulsive, but now already with the extended virtual orbital space a minimum is observed. For both states much better agreement is found between PbE and QM/MM based models at long distances, but the discrepancy is still substantial below 5 Å. Note that the identification of proper states with the full virtual space was not possible due to the proliferation of artificial CT states.

The concept of “reverse BSSE” is strongly supported by the fact that for Rydberg excited states the PbE + EFP2 scheme always produces strongly repulsive potential curves (Panel D): here the effect is more severe since diffuse orbitals are needed to describe the dominant excitation but only orbitals spatially restricted to the active fragment are available. This effect is demonstrated on Figure S4 in the Supporting Information. Note that not even the above-described extension of the virtual space solves the problem here, the curve produced by embedding with extended virtual space being still repulsive.

In summary, the present PbE scheme does not work with diffuse basis sets, and a new version is needed with proper definition of the virtual space that includes all the virtual orbitals on the active fragment, but none on the other.

5.3. Quality of the Coupling Schemes

The other factor that plays a key role in reproducing the energy levels of interacting states is the accuracy of the coupling between local excitations, as defined in the schemes presented in Section 2.3. The models containing coupling terms predict a certain splitting (in the case of homodimers) or a shift (for nonsymmetric complexes) of the energy levels due to the interstate interaction. To evaluate the quality of the couplings, these energy changes should be compared to those of the respective reference calculations, i.e., high-level calculations on the entire complex. Figures 8–10 show the energy splittings in the symmetric complexes as functions of the intermolecular separation.

Figure 8.

Distance dependence of the splitting (in atomic units) of the π–π* energy levels of the (Pyr)₂ (panel A), (Cyt)₂ (panel B), and (Ura)₂ (panel C) dimers, as predicted by various coupling schemes at the CCSD/cc-pVDZ level of theory.

Figure 10.

Distance dependence of the splitting (in atomic units) of the first (Panel A) and second (Panel B) pairs of Rydberg energy levels in the (Pyr)₂ complex, as well as in the first n–Rydberg states of (CH₂O)₂ (Panel C), as predicted by various coupling schemes at the CCSD/aug-cc-pVDZ level of theory.

In Figure 8 the coupling curves in the π–π* valence states of the (Pyr)₂, (Cyt)₂, and (Ura)₂ dimers are depicted, as calculated in the cc-pVDZ basis set. The Coulomb coupling curves closely follow the reference in the cases of (Ura)₂ and (Cyt)₂ until, below 4 Å, a turning point on the reference curve is seen. This turnover is presumably caused by the Dexter coupling, which is missing from the Coulombic model. A similar feature is also seen in the (Pyr)₂ case; however, the deviation of the reference and the model curves is already observable at longer distances. Comparing the shape of the curves, we have observed that the 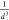theoretical dependence is fulfilled for the entire model curve, while for the reference one this is true only above 5 Å, suggesting that the effect caused by the change of the fragment wave functions becomes significant at shorter intermolecular separations. Again, the possible reason for this observation is the mixing with nearby or crossing states (see below), not handled by the two-state model.

The transition dipole approximation predicts larger couplings than the full Coulomb coupling in all cases, significantly overestimating also the reference values for (Ura)₂ and (Cyt)₂.

For the valence states of the (CH₂O)₂ system with aug-cc-pVDZ basis (Figure 9), a strong dependence of the results on the electronic state is apparent. In the σ–π* state the transition dipole approximation fails completely, predicting a practically zero splitting of the states. The full Coulomb coupling, on the other hand, gives accurate results above 4 Å separation, indicating that in this state the interaction is appropriately described by the electrostatic model if the charge distribution is considered at high resolution. At shorter distances, however, the two curves deviate. The above-mentioned neglect of the Dexter coupling cannot be responsible for this deviation since this term should further reduce the splitting, while the one predicted by the Coulomb coupling is already too small. An explanation can again be given by the failure of the two-state model, i.e., the reference states picking up CT character below 4 Å, as discussed earlier. For the π–π* state the Coulomb coupling is appropriate down to 6 Å and the increasing deviation at shorter distances again coincides with the appearance of the CT character in the reference states (see above). However, here the role of Dexter coupling cannot be excluded since now the reference curve shows a smaller splitting than the model calculations. Nevertheless, the shape of the curve suggests that the Dexter coupling does not become significant until around 3.5 Å.

Figure 9.

Distance dependence of the splitting (in atomic units) of the energy levels in the σ–π* (Panel A) and π–π* (Panel B) states of the (CH₂O)₂ dimer, as predicted by different coupling schemes at the CCSD/aug-cc-pVDZ level of theory.

We note that the results also have an obvious dependence on the electronic structure method through the accuracy of the transition density matrix predicted for the state in question. In this regard, both a close similarity as well as a significant discrepancy between the CC2 and CCSD levels could be observed, depending on the electronic state. Details are shown in Figure S2 of the Supporting Information.

The predicted splittings for the first and second pairs of Rydberg states in the (Pyr)₂ dimer and for the n-Rydberg states of (CH₂O)₂ are depicted on Figure 10, and a very different picture is seen than that for the valence states earlier. (Note that, obviously, the diffuse basis aug-cc-pVDZ was used here.) The transition dipole approximation shows a variable behavior for the three states: it predicts a zero coupling between the first pair of dark Rydberg states of (Pyr)₂ but also underestimates the coupling for the second one. For (CH₂O)₂ the magnitude is reasonable but crosses the reference curve showing that the distance dependence is quite different. The full Coulombic coupling provides a reasonable result for the first pair of (Pyr)₂ Rydberg states until 6 Å and until 4.5 Å for the (CH₂O)₂n–R states, but anywhere below these points the splitting is severely underestimated. This insinuates the conclusion that both models investigated here are inappropriate for modeling couplings between Rydberg type excited states.

The energy splitting of the investigated cytosine and uracil states in the asymmetric Cyt-Ura complex is shown on Figure 11. Since in this case the energy gap is nonzero even at infinite separation, the coupling introduces a shift in the energy levels, defined here as

22

and should be evaluated for both fragment methods, QM/MM and embedding, separately.

Figure 11.

Dependence of the difference (in atomic units) of the π–π* energy levels in the Cyt-Ura complex on the intermolecular distance, as predicted by various coupling schemes. The reference curve is defined relative to the energy gap at infinite separation. The results are from CCSD/cc-pVDZ level calculations.

The widening of the gaps with the distance is much smaller in this complex than in either the (Cyt)₂ or the (Ura)₂ systems. TrDA shows a behavior similar to the above cases, severely overestimating the growth of the energy gap with the fragments approaching each other. In contrast, the full Coulomb model shows a good agreement with the reference, with only a moderate underestimation of the widening below 5 Å. The characteristic turnback of the reference curve, associated with the appearance of the Dexter coupling, is also visible here around 3.3 Å.

In summary, we see that for valence states reliable splitting can be obtained above 4 Å of intermolecular separations by considering solely the Coulomb coupling. However, below this point other states can spoil the two-state model; thus reliable reference calculations are no longer available.

5.4. Potential Energy Curves

The different interaction energy and interstate coupling models result in a variety of final predictions for excited state potential energy curves. Since the evaluation of the coupling terms in Section 5.3 demonstrated the clear superiority of the full Coulomb coupling over the one obtained solely from transition dipoles, surfaces resulting from the combination of Coulomb couplings (calculated at the CCSD level of theory) and various interaction energy potentials will be discussed in this chapter to assess the final results. Due to the above-discussed factors that compromise the reliability of the reference at short distances, the 4–10 Å range of intermolecular separation is investigated here. The comparisons in this range are still relevant to Franck–Condon processes, since the ground state equilibrium distance normally falls in there.

5.4.1. Valence Excited States

The potential energy surfaces, relative to the sum of the respective monomer electronic energies, are shown for the valence type electronic states in Figures 12 and 13. For (CH₂O)₂, results obtained with the aug-cc-pVDZ basis set are shown (Figure 12), while for the larger complexes (Figure 13) the cc-pVDZ basis set was used.

Figure 12.

Potential energy curves (relative to the values at infinite separation, in atomic units) of the investigated σ–π* (Panel A) and π–π* (Panel B) valence excited states of the (CH₂O)₂ complex, calculated with different models using the CCSD/aug-cc-pVDZ method as their wave function component.

Figure 13.

Potential energy curves (relative to the mean total energies at infinite separation, in atomic units) of the investigated π–π* excited states in the (Pyr)₂ (Panel A), (Cyt)₂ (Panel B), (Ura)₂ (Panel C), and Cyt-Ura (Panel D) complexes, calculated with different models using the CCSD/cc-pVDZ method as their wave function component.

In the σ–π* state of (CH₂O)₂ the QM/MM + EFP2 model is generally well suited to describe the PES of both states in the whole investigated range, with the same accuracy. Severe discrepancies are seen for the PbE + EFP2 scheme, however: both states turn strongly repulsive at as early as 6 Å separation. This behavior stems from the incorrect virtual orbital selection as described earlier in Section 5.2.

The π–π* state of the formaldehyde dimer is, as discussed in Section 5.1, strongly influenced by an avoided crossing with a CT state below 6 Å if diffuse functions are present in the basis set. Since the models do not include charge transfer effects, neither method can be expected to produce a satisfactory result at short separations. This is, as seen on Figure 12, indeed the case, the surfaces obtained from the QM/MM + EFP2 model underestimating the attraction in both states, as seen already on the coupling-free surfaces of Figure 3. The PbE + EFP2 curves are so overly repulsive that only the lower one features a shallow intermolecular minimum around 5 Å, while the upper one exhibits a strong, obviously incorrect repulsive character. On the other hand, anywhere above 6 Å, both models agree well with the reference. From the two the QM/MM + EFP2 results are to some degree more accurate, but the difference is insignificant. This suggests that, without the interacting CT states complicating the wave functions, both approaches could produce meaningful potential energy surfaces even at shorter distances.

The effect of other states is mostly eliminated if no diffuse functions are present in the basis set, as seen on Figure 13. In the investigated π–π* state pair of (Pyr)₂ (Panel A) both the PbE + EFP2 and the QM/MM + EFP2 models produce a nearly perfect agreement with the reference until 6 Å. Below this point, the PbE + EFP2 potential energies start to become somewhat too low and show an unphysical minimum between 4 and 6 Å. This turn-back is likely caused by the truncation of the virtual orbital space in the PbE excitation energy calculations, artificially eliminating certain excitations of the dimer wave function. The QM/MM + EFP2 results are, in principle, correct until 5 Å, where both curves start to run under the reference. While the error still remains moderate for the rapidly decreasing lower state, the upper one is significantly overstabilized and fails to reproduce the repulsive nature of the reference surface.

The approximate models are generally well suited for the (Ura)₂ and (Cyt)₂ π–π* dimer states (Panels B and C of Figure 13). The shapes of the potential energy curves follow those of the reference, with a modest underestimation by both methods. The QM/MM + EFP2 approach turns out slightly more accurate until 4.5 Å, but the difference from the embedding results is negligible anywhere over 5 Å. The deviation from the reference is more significant in the (Cyt)₂ case, both in relative and nominal terms. Based on the findings discussed in Section 5.3 it is clear that the discrepancy is mostly caused by the error of the interaction energy modeling, as the interstate couplings are almost perfectly reproduced in the investigated region.

The potential energies of the same electronic states of the Cyt-Ura complex are shown in Panel D of Figure 13. (Note that the zero point of the energy scale is defined as the mean of the dimer excited state energies at infinite separation.) Here the PbE + EFP2 potentials are in good agreement with the reference in the entire region. The QM/MM + EFP2 result is also correct, almost indistinguishable from the PbE + EFP2 one above 4.5 Å, while a somewhat stronger underestimation of the reference energies is produced below this point. Generally, the relative agreement with the reference is better in this non-symmetric complex than expected from the results on the homodimers (Cyt)₂ and (Ura)₂. This accentuates the complexity of the excited state interactions in stacked π-complexes.

5.4.2. Rydberg States

Rydberg type electronic states, as seen above in Sections 5.1 and 5.3, represent a big challenge for the interaction modeling. The potential energy curves, shown on Figure 14 for (Pyr)₂ and (CH₂O)₂, reflect many features already seen on the interaction energies above. The PbE + EFP2 model produces nonphysical, repulsive surfaces for both interacting states in all cases. This makes it clear that this approach in its present form is not suited for Rydberg type excited states. The QM/MM + EFP2 energies, on the other hand, follow the reference with good parallelism in the whole range. However, due to the improper prediction of the coupling for Rydberg states (see Section 5.3), the splitting of the states is severely underestimated. The resulting surfaces are thus also incorrect from the very point where the interaction becomes significant—as early as 6 Å separation in these cases. This clearly indicates that for a qualitatively correct recovery of the Rydberg surfaces in the QM/MM + EFP2 framework, the appropriate modeling of the coupling is also indispensable.

Figure 14.

Potential energy curves (relative to the values at infinite separation, in atomic units) of the investigated Rydberg excited states in the (CH₂O)₂ (Panel A) and (Pyr)₂ (Panels B and D) dimers, evaluated with different models using the CCSD/aug-cc-pVDZ method as their wave function component.

6. Conclusions

On the route of developing a proper theoretical model for the excited states of noncovalently bound multi-chromophore systems, in this work fragment-based methods have been tested on symmetric and non-symmetric stacked complexes of formaldehyde, pyrrole, uracil, and cytosine. Special attention has been paid to the different components of the interaction energy, i.e., the electrostatic component described by QM/MM and PbE type electronic structure calculations, additional van der Waals contributions described by EFP2 potentials, as well as the exitonic coupling. Carefully selected reference results on the dimers were used in these benchmark comparisons.

Regarding the electronic structure calculations on the fragments, both the QM/MM model (with CHELPG point charges representing the environment) and the projector-based embedding approach (PbE) were found to be good choices, as long as no diffuse functions are present in the basis set. With diffuse basis functions included, QM/MM performs similarly, but a PbE model fails due to the use of a localized and truncated virtual space that results in incorrectly repulsive potential energy curves.

Achieving satisfactory accuracy for the potential energy curves requires that the van der Waals-type interactions (dispersion and Pauli repulsion) are also properly included. The examples presented in this work confirm that the respective EFP2 terms obtained for the ground state provide a convenient and suitable approximation for these interactions between a ground state and an excited state fragment.

An appropriate consideration of the exitonic splitting is also necessary to model interacting states; it was found that the relatively simple transition dipole approximation is not accurate enough and calculation of the full Coulomb coupling is necessary. Neglect of the Dexter part of the coupling was noticeable only at small intermolecular separations (below 4 Å in the complexes investigated here).

The proposed methodology produces reasonable agreement with the reference data for the potential energy curves above separations of 4 Å. Below this distance no reliable information could be obtained about accuracy, mostly because of uncertainties of the reference data, i.e., failure of the two-state model due to the interaction with, e.g., charge transfer states. The comparisons above 4 Å are nevertheless relevant since this range usually covers the ground state equilibrium and therefore, Franck–Condon processes.

Despite the encouraging results presented here, the desired accuracy has not been achieved yet and we see several points where the suggested methodologies could be improved. First, the PbE scheme needs to be made suitable for calculations with diffuse basis sets. To this end, a new localization scheme for the virtual orbitals is apparently needed. Second, the development of state-specific dispersion and Pauli repulsion terms could improve the reliability of the interaction energy. Note that similar developments are needed for TD-DFT methods to include state-specific dispersion interaction.⁶⁸ Third, to also reliably predict equilibrium structures of these complexes and the potential curves below 4 Å, the inclusion of the Dexter coupling is necessary. At present, the highest-level wave function method available for this purpose is CC2,⁷² but our results (discussed in the Supporting Information of this paper) show that the transition properties predicted by this method can be very different from those obtained with CCSD (see also ref (109)). Finally, the interaction between valence and charge transfer states needs to be included in this scheme, which could be done by means of the adaptation of the TD-DFT procedure suggested by Li et al.⁷⁴

Significant effort has also been put into producing CCSD-level benchmark data for a reliable test of the fragment methods. The associated difficulties (e.g., correction for BSSE of excited states) have also been discussed. These data can later be used in benchmarking cheaper supermolecular methods, similarly to a recent study by Hancock and Goerigk⁶⁸ on different TD-DFT methods. The data are provided in Tables S10–12 of the Supporting Information.

Data Availability Statement

The data supporting the findings of this study are available in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00104.

• Structures of the monomers and complexes evaluated in this study, ground state potential curves, the impact of “exact” ground state van der Waals terms on the homodimer excited state surfaces, comparison of the CCSD and CC2 excited state splittings in the (CH₂O)₂ system, excited state total energy curves of (CH₂O)₂ as well as the reference CCSD data for all studied states are presented here, the failure of the localization of virtual orbitals demonstrated by showing a Rydberg orbital obtained in the PbE procedure at different intermolecular distances, and details of the calculation of the CHelpG charges and their values used in this study (PDF)

The authors declare no competing financial interest.