Influence of the π–π interaction on the hydrogen bonding capacity of stacked DNA/RNA bases

Abstract

The interplay between aromatic stacking and hydrogen bonding in nucleobases has been investigated via high-level quantum chemical calculations. The experimentally observed stacking arrangement between consecutive bases in DNA and RNA/DNA double helices is shown to enhance their hydrogen bonding ability as opposed to gas phase optimized complexes. This phenomenon results from more repulsive electrostatic interactions as is demonstrated in a model system of cytosine stacked offset-parallel with substituted benzenes. Therefore, the H-bonding capacity of the N3 and O2 atoms of cytosine increases linearly with the electrostatic repulsion between the stacked rings. The local hardness, a density functional theory-based reactivity descriptor, appears to be a key index associated with the molecular electrostatic potential (MEP) minima around H-bond accepting atoms, and is inversely proportional to the electrostatic interaction between stacked molecules. Finally, the MEP minima on surfaces around the bases in experimental structures of DNA and RNA–DNA double helices show that their hydrogen bonding capacity increases when taking more neighboring (intra-strand) stacking partners into account.

INTRODUCTION

The structure and dynamics of nucleic acids are affected by two types of non-covalent interactions: H-bonding and parallel aromatic stacking (1–4). H-bonding, mostly governed by electrostatics (5), and aromatic stacking, mostly governed by London dispersion forces, have been intensively studied via theoretical methods (6–30). The π–π interaction, repeatedly stressed in many fields of chemistry and biochemistry (31–41) is also frequently accompanied by H-bonding in biomolecules; however, little is known about their functional interplay.

The influence of parallel π-stacking on the hydrogen bonding ability of pyridine has been recently investigated, showing that the basicity of pyridine depends on the chemical hardness of the stacking compound (42). In an analogous study on pyrimidine and imidazole stacked with a series of substituted benzenes, the role of the orientation between stacked compounds was investigated (43). There, it was found that parallel stacking rather than T-shaped stacking improves the hydrogen bond accepting capacity of the bases, and that this effect is larger for electron donating benzene substituents. Also, an inverse linear relationship was found between the electrostatic interaction of the cycles and the molecular electrostatic potential (MEP) around the basic nitrogen atom. In π-stacked quadruply H-bonded dimers of ureidopyrimidone, π-stacking was observed to strengthen the hydrogen bonds by increasing charge-transfer between H-bonded partners (44). Electrostatics based studies on hydrated DNA base pairs show that the stacked base pairs hydrate better than the corresponding H-bonded base pairs (45). Apart from the fact that more binding sites for water molecules are present in the stacked conformation, the most negative values of the MEP show up in the stacked conformations in contrast to the H-bonded ones.

Besides the significance of dispersion forces in π–π interactions, the role played by electrostatics is still a subject of debate. A series of experimental studies revealed that the interaction between phenyl rings increases monotonically when passing from an electron-donating to an electron-withdrawing substituent (46,47). In line with these results, Hunter and co-workers (33,48) proposed a set of rules stating that the aromatic ring can be described as ‘a positively charged σ-framework between two regions of negatively charged π-electron density’. According to this electrostatics based model, an electron-donating substituent on one of the interacting molecules should increase the negative charge of the π cloud and thus the repulsion between the two stacked aromatic cycles, whereas electron-withdrawing substituents should show the inverse behavior. However, in contrast to Hunter–Sanders rules and experimental results, several recent high-level computational studies of substituent effects on π–π interactions showed that in the parallel stacked benzene dimers, substituted benzenes with electron-withdrawing or electron-donating substituents bind stronger to benzene than unsubstituted benzene (49,50). It was stated that electrostatics, dispersion, induction and exchange-repulsion are all significant to the overall binding energies. In our latest studies, substituted benzenes were found to bind stronger to aromatic nitrogen bases than unsubstituted benzene (42,43).

In the first part of the present work, we will extend the approach of our previous studies to cytosine/benzene stacked complexes. Here, the influence of the stacking interaction on the hydrogen bonding capacity as well as the role of electrostatics will be briefly discussed in conjunction with the DFT-based reactivity descriptors. Cytosine, being a pyrimidine base, is chosen because of its small size and because it possesses both a nitrogen atom and an oxygen atom as hydrogen bond acceptors. Electrostatic and dispersion interaction energies computed from MP2 (51) wave functions for seven complexes are compared with the MEP computed around the N3 and O2 atoms of cytosine (as a measure of its hydrogen bonding capacity) and with intrinsic properties of the substituted benzenes, such as the global and local hardnesses and benzene ring polarizability. This work is in line with our ongoing interest in the development/use of DFT-based reactivity descriptors (conceptual DFT) (52–56) and their application to systems of biological interest (57–65).

In the second part of the study, we investigate the role of aromatic stacking between nucleobases on their hydrogen bonding potential. Primarily, the role of the particular orientation between the stacked bases is investigated by comparing experimental X-ray and gas phase optimized structures. We focus on the interaction energy contributions (dispersion, electrostatic), and the depth of the MEP around hydrogen bond accepting atoms. In addition to the MEP computed at defined points, we calculate the minima on electrostatic potential maps around stacked nucleobase pairs and compare the values for experimental and optimized structures. Finally, this approach was also followed for stacked trimers of adenine, cytosine, thymine and guanine to incorporate the effect of neighboring stacking partners in DNA–DNA and RNA–DNA hybrid helices.

THEORY AND COMPUTATIONAL DETAILS

Geometries

Complexes between cytosine and a series of seven substituted benzenes Ph-X (where X = H, CH₃, OH, NH₂, F, CHO, NO₂) were fully optimized at the MP2/6-31G* level of theory starting from a parallel displaced arrangement. In each optimized complex, the benzene substituent is located as far as possible from the hydrogen bond acceptor atoms of cytosine: N3 and O2, avoiding direct interactions between the substituent and these atoms (Figure 1).

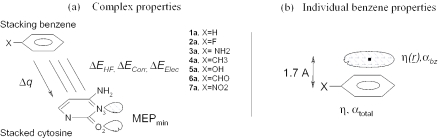
Figure 1.

Computed properties of cytosine and substituted benzenes arranged in the offset parallel conformation. (a) Complex properties: HF, correlation and electrostatic interaction energy components (ΔE_HF, ΔE_Corr assumed to represent mostly the dispersion interaction energy, ΔE_elec), MEP minimum around the nitrogen, charge transfer Δq. (b) Properties of the individual benzenes: substituent α_subst, and total substituted benzene polarizabilities α_total; global hardness η and local hardness η(r) (1.7 Å above the center of the ring).

To model the possible stacked dimers encountered in RNA/DNA chains, the 10 combinations with adenine, cytosine, guanine and uracil are considered. Each partner is first optimized at the MP2/6-31G* level of theory and then is kept fixed in all considered complexes (e.g. a strictly identical geometry for each monomer base is used in optimized or experimental structures). The optimized structures were taken from a study by Sponer et al. (66). For these, the vertical separation between the bases is 3.3 or 3.4 Å, the twist angle as well as the parallel displacement between the rigid bases were then optimized at the MP2/6-31G* level of theory. Experimental X-ray structures were taken from the Protein Data Bank (PDB) with a resolution ranging from 0.83 to 1.90 Å. The following complexes were considered: A7–A8 (1G4Q), A7–C8 (1DPL), G13–A14 (485D), A14–U15 (485D), C11–C12 (100D), C9–G8 (485D), C7–U6 (485D), G15–G16 (165D), G11–U12 (485D) and U7–U8 (157D). Each pre-optimized partner was then superimposed on the corresponding molecule in the crystal structure using the program Pymol (67).

In addition, RNA–DNA hybrid and DNA structures of dimers and trimers of adenine, cytosine and guanine were taken from the PDB. The following complexes were considered, DNA: A16–A17–A18 (403D), C17–C18–C19 (440D) and G2–G3–G4 (440D); RNA–DNA hybrid: A2–A3–A4 (1G4Q), C15–C16–C17 (1FIX) and G402–G403–G404 (1BL0). For these complexes, each pre-optimized partner was also superimposed on the corresponding molecule in the crystal structure.

Interaction energies

Post Hartree–Fock methods as Møller Plesset perturbation theory (MP) (51) and Coupled Cluster theory (68,69) have been tested in the past for their ability to describe the interaction energy between two benzene rings, RNA/DNA base pairs and aromatic amino acids (26,27,70,71). The use of the 6-31G*(0.25) basis set at the MP2 level containing one set of diffuse polarization functions with an exponent of 0.25 on second row elements, has been shown by Hobza and Sponer (72) to be a good compromise between computational cost and quality. Contrary to more extended basis sets, the 6-31G*(0.25) basis set does not overestimate too much the stacking energy compared with the coupled cluster methods. Therefore, single point calculations at MP2/6-31G*(0.25) were carried out on the geometries to get the interaction energy components. Basis set superposition errors were corrected by the counterpoise method (73). The total interaction energy ΔE _MP2 can be expressed as the sum of the HF interaction energy ΔE_HF and the correlation contribution ΔE_Corr to the interaction energy (Figure 1a). The HF interaction energy is roughly the sum of the electrostatic, induction and exchange-repulsion terms; the correlation interaction energy corresponds to the dispersion energy that is assumed to be the cause of the stabilization of parallel stacked systems (74).

The electrostatic interaction between the substituted benzenes and pyridine was calculated from a distributed multipoles analysis, a ‘technique for describing a molecular charge distribution by using local multipoles at a number of sites within the molecule’ (75). The distributed multipoles were calculated from the MP2/6-31G*(0.25) wave function at the nuclear positions up to rank 4 (hexadecapole) with GDMA version 1.3 (76). The electrostatic interaction energy between the molecules was then calculated with the ORIENT program version 3.2 (77).

Hydrogen bonding capacity

Only hetero-atoms of each base involved in the Watson–Crick base pairs as hydrogen bond acceptor are considered for their ability to accept a hydrogen bond. The hydrogen bonding capacity was computed as the minimum of the MEP V(r) for benzene/cytosine complexes and at 1.25 Å of the nitrogen or oxygen atoms for DNA/RNA base pairs. V(r) is given as

$$V\left(\underset{¯}{r}\right)={\displaystyle \sum _A}\frac{Z_A}{\left|\underset{¯}{r}-\underset{¯}{R_A}\right|}-\int \frac{\rho \left(\underset{¯}{r^{\prime }}\right)}{\left|\underset{¯}{r}-\underset{¯}{r^{\prime }}\right|}\text{d}\underset{¯}{r^{\prime }},$$ 1

where the summation runs over all the nuclei A of the system. The MEP represents the interaction energy of the system with a unit positive charge, and thus reflects mainly the hard–hard interactions between the molecules. The MEP has been known for a long time (78) to be a reliable descriptor of the hydrogen bond strength: the deeper the electrostatic potential, the stronger the electrostatic interaction with water molecules and with hydrogen bond donors in general (79–82).

In addition to the MEP calculated at a defined point, we computed the MEP maps from HF/6-31G* wave functions onto surfaces of molecular electron isodensity (0.002 electron/ų) using SPARTAN program (83). The minima on these surfaces were obtained for experimental and gas phase optimized structures of stacked bases.

Charge transfer to the stacked base was calculated as the sum of atomic CHelpG charges (84) on this base (Figure 1a).

Relationship between the interaction energy components and the local descriptors

In order to relate the dispersion energy to an intrinsic property of the stacked partners, a simple model was used, based on the London dispersion energy expression:

$$\Delta E_{\text{disp}}=-\frac{C·{\alpha }_1·{\alpha }_2}{r^6}$$ 2

with α₁ and α₂ being the polarizabilities, r the distance between the interacting partners and C a constant. For the series of complexes between cytosine and substituted benzenes, where one of the α-values is a constant (say α₁), the dispersion interaction energy can be expected to be proportional to α₂ · r⁻⁶. Regarding the optimized geometries of the cytosine substituted benzene complexes, the benzene substituent is located as far as possible from the N3 and O2 atoms of cytosine avoiding direct interactions with the π-electrons of cytosine (see Figure 1a). Hence, α₂ was computed as the polarizability of the benzene ring itself in the substituted benzene, α_bz [i.e. excluding the polarizability of the substituents (85–87)], as was performed in our previous works (42,43). Equation 2 thus becomes:

$$\Delta E_{\text{disp}}=-\frac{C^{\prime }·{\alpha }_{\text{bz}}}{r^6}.$$ 3

DFT-based reactivity descriptors

In order to trace back the substituent effect of the stacking substituted benzenes or to compare intrinsic properties of each RNA/DNA base, we used the global hardness η. The hardness η is a global property that has been sharply defined by Parr and Pearson (88) as the second partial energy derivative with respect to the number of electrons. Considering the variation in energy when one electron is added or removed from the system and using a finite difference approximation, one gets:

$$\eta =\frac{(I-A)}{2},$$ 4

where I is the vertical ionization energy, and A the vertical electron affinity. For the substituted benzenes considered in this study and for the RNA/DNA bases, the calculated electron affinity values were found to be negative; hence, the hardness was taken as half the ionization energy.

In the context of DFT-based reactivity descriptors, the local hardness η(r) has already been successfully used as a negative charge accumulation index at a defined point both in the study of electrophilic attacks (89) and in the prediction of the electrostatic interaction between stacked aromatic cycles (42). Although a debate in the literature on the exact formulation of the local hardness is still going on, the following proposal (89–94) clearly received by far the most attention and will be used here:

$$\eta \left(\underset{¯}{r}\right)=-\frac{V_{\text{el}}\left(\underset{¯}{r}\right)}{2N},$$ 5

where N is the number of electrons of the system, and V_el(r) the electronic part of the electrostatic potential (Equation 1). V_el(r) was evaluated at a distance of 1.7 Å above the isolated benzene rings (Figure 1b). This is about half the distance between the rings in the optimized complexes.

All calculations were carried out using the Gaussian 03 package (95).

RESULTS AND DISCUSSION

Cytosine-substituted benzene complexes

The largest distance and dihedral angle between the rings is found for the fluorine substituent; the smallest interaction energy is found for toluene and unsubstituted benzene (Table 1). The interaction energies computed here are less stabilizing than for the experimental structure of the stacked cytosine dimer computed at the same level, i.e. ΔE = −8.3 kcal/mol (66). Also, recent calculations at the same level on stacked substituted benzenes/pyrimidine complexes give lower interaction energies, i.e. ΔE = −4.2 kcal/mol (43). These results could be expected since the dispersion interaction increases with the number of π-electrons of the molecules.

Table 1.

Properties for the optimized complexes of cytosine and substituted benzenes

Substituent	Complex properties									Properties of the isolated substituted benzenes
	ΔEMP2	ΔEHF	ΔECorr	ΔEelec	Δq	MEP N3	MEP O2	Φ	r	α	αsubst	αbz	η	η(r)
NO2	−6.51	2.40	−8.91	−5.22	0.0087	−0.0828	−0.1311	18.9	3.56	76.84	18.08	58.76	0.392	0.0887
CHO	−6.37	3.31	−9.68	−4.84	−0.0088	−0.0881	−0.1355	10.2	3.47	64.91	9.64	55.26	0.359	0.0970
F	−5.33	1.81	−7.15	−4.35	−0.0057	−0.0883	−0.1361	25.7	3.70	59.45	2.41	57.04	0.346	0.1033
H	−5.32	4.30	−9.62	−3.18	−0.0232	−0.0941	−0.1421	13.5	3.46	58.38	0.26	58.13	0.343	0.1062
CH3	−5.05	3.51	−8.56	−3.72	−0.0180	−0.0911	−0.1421	17.7	3.59	70.71	12.12	58.59	0.331	0.1057
OH	−5.41	1.92	−7.33	−3.84	−0.0143	−0.0919	−0.1398	21.6	3.66	63.94	5.58	58.36	0.326	0.1050
NH2	−5.33	3.92	−9.25	−2.71	−0.0350	−0.0986	−0.1461	12.7	3.49	66.88	9.11	57.78	0.339	0.1130

Interaction energy components: ΔE_i (kcal/mol), charge transfer to the pyrimidine, Δq (a.u.), MEP minimum around the nitrogen and oxygen atoms (see Figure 1) (a.u.), dihedral angle between the ring planes, dihedral angle between the stacked rings, Φ (degree), distance between the rings and r (Å). Properties of the isolated substituted benzenes: substituent α_subst and total substituted benzene polarizabilities α_total (α_bz is calculated according to Equation 3); global hardness η and local hardness η(r) (1.7 Å above the center of the ring).

Compared with our previous studies cytosine exhibits the same behavior as the aromatic nitrogen bases (42,43). The correlation part of the interaction energy constitutes the major source of stabilization of the complexes, while the electrostatic term exhibit negative values (attractive). The influence of the stacking substituted benzenes on the hydrogen bonding ability of N3 and O2 of the stacked cytosine is quite obvious. The harder the stacking benzene, the lower the charge transfer. This is reminiscent of the hard and soft acids and bases principle (96) where the charge transfer between an acid A interacting with a base B is inversely proportional to the sum of the hardnesses of the interacting partners (56,97). For the series of substituted benzenes, one would expect that the smaller the hardness of the substituted benzene, the larger the charge transfer to cytosine (since the hardness of the latter is constant). Furthermore, the hydrogen bonding ability of the nitrogen hetero-atom and the exocyclic oxygen increases with the electron transfer to cytosine; the larger the electron flow the deeper the MEP. Thus, the less hard the stacking substituted benzene, the larger the hydrogen bonding ability of cytosine.

Comparing MEP minima computed for isolated cytosine (−0.1020 and −0.1090 a.u. for the N3 and O2 atoms, respectively) and the MEP values in Table 1 for the N3 and O2 atoms of stacked cytosine, one can see that the hydrogen bonding ability is increased only for the O2 atom upon stacking. In pyrimidine/benzene stacked complexes, the hydrogen bonding ability, related to the charge transfer, did not systematically increase whether a sandwich–parallel, parallel–displaced or T-shaped conformation was considered (43). Here, O2 is expected to attract the largest part of electrons upon charge transfer of cytosine, compared with N3, since the electronegativity of oxygen is larger than that of nitrogen.

Confirming previous theoretical studies (42,50), substituted benzenes show larger interaction energies than unsubstituted benzene, except toluene for which the difference with benzene is negligible. This seems, however, to contradict Hunter–Sanders rules (33,48), stating that substituent effects are determined by electrostatic interactions, and that the interaction energy sequence depends on the electron-donating or electron-withdrawing character of the substituent.

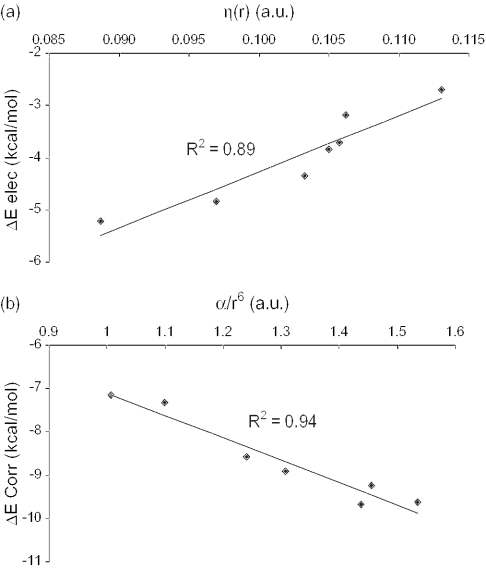
The discrepancy between the theoretical results and the Hunter−Sander rules (and experimental findings) can be attributed to the fact that the electron-withdrawing or electron-donating character of the substituent is not reflected in the π-electron density above the substituted benzene ring (42,43). Indeed, the electrostatic potentials of the π clouds are very similar for benzene, toluene and phenol (98). Concurrently, the local hardness η(r) (a measure of the accumulation of negative charge above the benzene ring) increases monotonically with decreasing electron-withdrawing character of the substituent up to the unsubstituted benzene, then slightly decreases for toluene and phenol and reaches a maximum value for amino-benzene (Table 1), whereas a progressive increase in η(r) values was expected. Hence, in agreement to Hunter–Sanders rules on π–π interactions, the larger the local hardness, the larger the repulsion between the stacked rings, or the less negative the electrostatic interaction should be. This is entirely reproduced in the ΔE_elec values, which correlate rather well with η(r) (R² = 0.89, see Figure 2a). Hence in the context of hard–hard interactions [for a recent critical account of the local hard and soft acids and bases principle, see Chattaraj (99)], the local hardness, η(r), can be safely used for the estimation of the electrostatic interaction between stacked aromatic rings such as benzenes.

Figure 2.

(a) Electrostatic interaction energy (ΔE_elec) between cytosine and the substituted benzenes Ph-X (kcal/mol) versus the local hardness η(r). (b) Correlation part of the interaction energy (ΔE_Corr) between cytosine and the substituted benzenes Ph-X (kcal/mol) versus the benzene ring polarizability divided by R⁶ (see Equation 3) (a.u.).

Similarly, the benzene ring polarizability α_bz (combined with an r⁻⁶ distance factor according to Equation 3), correlates very well with the correlation part of the interaction (Figure 2b). These results demonstrate that soft interactions, such as dispersion, are predominant in stacking can be estimated from the polarizability.

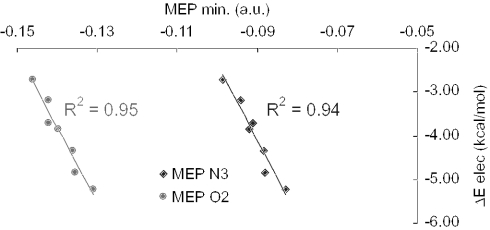
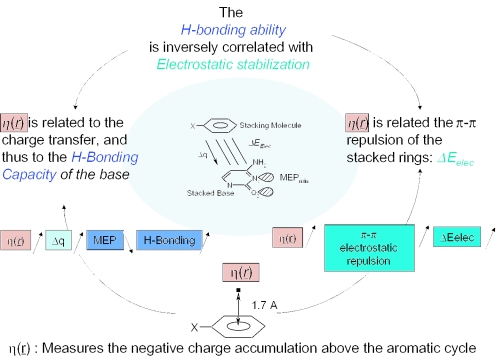
To sum up, the electrostatic interaction between cytosine and the substituted benzenes is inversely correlated with the hydrogen bonding capacity of cytosine (Figure 3). Electrostatics that leads to a smaller stabilization than dispersion (Table 1), is also related to the local and global hardnesses, the charge transfer and so to the hydrogen bonding ability of cytosine. η(r) appears to be a key index connecting the electrostatic component of the interaction energy with the hydrogen bonding capacity of cytosine (Figure 4).

Figure 3.

Electrostatic component of the interaction energy between cytosine and substituted benzene (ΔE_elec in kcal/mol) versus molecular electrostatic potential minimum (MEP_min) around the N3 and O2 atoms of cytosine (a.u.).

Figure 4.

η(r) can be used for the estimation of the electrostatic interaction and the hydrogen bonding ability.

Stacked DNA base pair complexes

In the gas phase optimized complexes, the parallel displacement between the rings, as well as the twist angle (defined as the rotation angle between one nucleobase and its nearest neighbor) were varied until a maximal stabilization of the complex was reached (66). However, in biologically relevant complexes, these parameters are imposed by the double helix structure of two interacting polynucleotide chains. For example, in the experimental structures considered in the present study (hybrid RNA–DNA helix), the twist angles range from 25° to 42° (see Table 2), in contrast to gas phase optimized structures for which we observe quite large rotations. The inter-ring distances in experimental structures show larger values, this can be explained by the fact that the planes of the nucleobases are not strictly parallel (tilt angle different from zero) in comparison with gas phase optimized structures and because the parallel displacement between stacked bases leads to larger distances in the case of pyrimidine dimers than for purine dimers.

Table 2.

Interaction energy components computed at the MP2/6-31G*(0.25) for the 10 considered stacked nucleic base dimers (kcal/mol)

		Optimized geometries							Experimental structures
		ΔEMP2	ΔEHF	ΔECorr	ΔEElec	R	r	Twist	ΔEMP2	ΔEHF	ΔECorr	ΔEElec	r	Twist	Φ
A	A	−8.82	4.00	−12.82	−3.21	3.3	3.31	−110	−5.91	4.19	−10.09	−1.47	3.47	30	5.26
A	C	−9.50	0.85	−10.36	−3.38	3.3	3.39	−100	−3.12	4.67	−7.79	1.43	3.62	25	5.56
A	G	−11.17	1.30	−12.48	−4.68	3.3	3.36	−240	−7.42	3.25	−10.67	−0.86	3.49	32	5.93
A	U	−9.09	1.25	−10.34	−2.79	3.3	3.48	140	−4.97	2.88	−7.86	−1.20	3.59	34	8.88
C	C	−8.26	−2.09	−6.17	−5.47	3.4	3.40	180	−1.96	3.20	−5.16	0.88	4.31	31	2.26
C	G	−9.32	−1.44	−7.88	−4.91	3.4	3.48	0	−8.75	−0.73	−8.02	−4.12	3.59	39	5.17
C	U	−8.52	−1.51	−7.02	−5.17	3.3	3.40	240	−3.80	2.20	−6.00	−0.71	4.25	31	11.74
G	G	−11.32	−0.84	−10.48	−4.25	3.4	3.42	−110	−3.39	8.47	−11.86	1.75	3.40	39	3.03
G	U	−10.63	−1.17	−9.46	−6.46	3.3	3.35	−270	−5.67	4.87	−10.54	−0.38	3.40	42	3.43
U	U	−6.53	0.46	−6.98	−4.46	3.3	3.54	180	−1.72	3.39	−5.11	1.22	4.36	33	11.78

Abbreviations: R, is the inter-planar distance between the bases for optimized structures only (Å); r is the distance between the center of the closest rings of each considered base pair (Å); Φ is the dihedral angle between the planes of the bases (degree); and the twist angle (degree).

As can be expected, the largest contribution to complex stabilization arises from dispersion, rather than from electrostatics (Table 2). For each base pair, gas phase optimized complexes appear to be more stable than experimental ones, owing to more stabilizing dispersion contributions and most probably due to higher repulsive (or less attractive) electrostatic contributions in the latter (see ΔE_elec and ΔE_HF values in Table 2). This is surprising since the distance between the rings are larger for experimental structures (these distances correspond to the distance between the centers of the closest rings of each base, r in Table 2). A previous study on the role of electrostatics in stacked DNA bases pairs showed that the electrostatic component of the stacking interaction closely mimics the total interaction energy (100). Indeed, Leszczynski and co-workers (100) found a good correlation between the total interaction energy and the electrostatic multipole term. Although a smaller correlation coefficient is observed for the experimental structures studied in the present work (R² = 0.74), the role of electrostatics on the total interaction energy is not negligible, as could be expected from Hunter–Sanders rules.

Also here, the global hardness of the stacking base is connected with the charge transfer of the stacked base and the MEP of the latter. The less hard the stacking base, the larger the charge transfer to the stacked base and the deeper the MEP computed around the oxygen and/or nitrogen atom of the stacked base. A real lack of correlation is observed for uridine as the stacked base in experimental structures, the other correlation coefficients ranging from R² = 0.80 to R² = 0.99.

MEP values for the isolated nucleobases (Table 3) can be compared with the stacked ones (Table 4). Remarkably, the MEP becomes less negative upon stacking in gas phase optimized structures, whereas the opposite is true for experimental structures. It appears that, apart from the hardness of the stacking base, the orientation between the bases (gas phase versus experimental structures) plays a dominant role in the modulation of the hydrogen bonding ability of the stacked base. Concomitantly, as mentioned above, the electrostatic component of the interaction energy is determined by the orientation of the stacked bases. Again, the hydrogen bonding ability seems to be associated with the electrostatic interaction between the stacked compounds; the more repulsive the electrostatic interaction, the larger the hydrogen bonding ability.

Table 3.

Properties of isolated bases

	η	α	Atom	MEP
A	0.3085	84.07	N1	−0.0942
C	0.3352	68.56	N3	−0.1020
C			O2	−0.1100
G	0.3087	90.62	O6	−0.0699
U	0.3588	62.13	O2	−0.0631

Global hardness η (a.u.); polarizability α (a.u.); and MEP values computed at 1.25 Å from hetero-atoms involved in Watson–Crick base pairs as hydrogen bond acceptors (a.u.).

Table 4.

Charge transfer between bases (Δq in a.u.) and MEP values computed at 1.25 Å from hetero-atoms involved in Watson–Crick base pairs as hydrogen bond acceptors (a.u.)

Stacked base	Stacking base	Optimized geometries			Experimental structures
		Δ(q)	MEP N1		Δ(q)	MEP N1
A	A	−0.0062	−0.0913		0.0086	−0.0986
A	C	0.0096	−0.0835		0.0099	−0.0989
A	G	0.0053	−0.0866		0.0056	−0.1097
A	U	0.0205	−0.0800		0.0151	−0.0932
		Δ(q)	MEP N3	MEP O2	Δ(q)	MEP N3	MEP O2
C	A	−0.0096	−0.0951	−0.1075	−0.0099	−0.1079	−0.1158
C	C	0.0000	−0.0923	−0.1064	0.0191	−0.1009	−0.1083
C	G	−0.0021	−0.0928	−0.1051	−0.0064	−0.1067	−0.1108
C	U	0.0118	−0.0915	−0.1017	0.0039	−0.1037	−0.1125
		Δ(q)	MEP O1		Δ(q)	MEP O1
G	A	−0.0053	−0.0698		−0.0056	−0.0780
G	C	0.0021	−0.0689		0.0064	−0.0751
G	G	−0.0048	−0.0754		−0.0090	−0.0774
G	U	0.0146	−0.0665		0.0177	−0.0701
		Δ(q)	MEP O1		Δ(q)	MEP O1
U	A	−0.0205	−0.0637		−0.0151	−0.0664
U	C	−0.0118	−0.0630		−0.0039	−0.0587
U	G	−0.0146	−0.0634		−0.0177	−0.0783
U	U	0.0000	−0.0541		0.0008	−0.0689

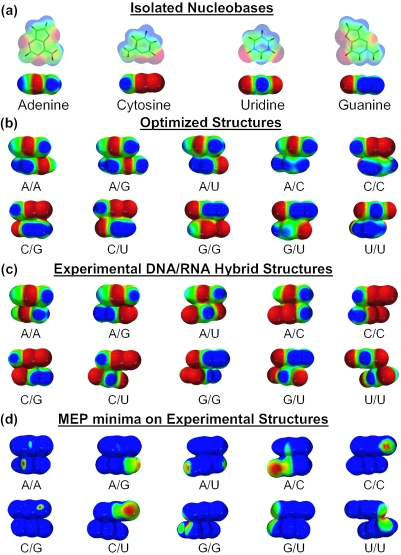
Figure 5b and c displays the electrostatic potential surfaces of the stacked complexes in the optimized and RNA–DNA hybrid experimental structures, for which the minima are given in Table 5. These MEP values obtained from Hartree–Fock wave functions are not identical with the values obtained at the MP2 level but comparisons between trends in different structures are valid (for the cytosine/substituted stacked complexes, the MEP values computed at the HF/6-31G* (0.25) show the same relative changes than MP2 calculations for the seven substituents used; they also give good correlation with the electrostatic interaction energies: R² = 0.94 for N3 atom and R² = 0.96 for O2 atom of cytosine). Again, the experimental structures clearly display more negative MEP values than the gas phase optimized structures. For some complexes, large differences in the MEP values between the structural arrangements are observed (Table 5), which can be rationalized from the electrostatic potential surfaces displayed in Figure 5. Systematically scrutinizing these surfaces, it is clear that the nucleophilic regions (shown in red) of the interacting partners overlap more in experimental structures than in gas phase optimized structures. This observation explains the more repulsive electrostatic interactions found in the former accompanied by a concomitant increase in the hydrogen bonding ability of the stacked bases. No major differences can be seen between isolated molecules and dimers. Only for adenine, the electrophilic region (in blue) around the C2 atom becomes less electrophilic upon stacking (or less ‘polarized’). On the other hand, the reader can see that nucleophilic regions (in red) are slightly more extended for experimental than for optimized structures and isolated nucleobases, while electrophilic regions show the inverse behavior [for example, the electrophilic regions (in blue) around the amino groups of cytosine (N4 atom) and guanine (N2 atom) in the experimental C/G dimer]. Figure 5d displays the region where the MEP has become deeper upon stacking. This region is not always shared by the two partners, but it is located on the Watson–Crick side of the stacked base pair.

Figure 5.

Electrostatic potential maps of (a) isolated nucleobases, (b) gas phase optimized structures and (c) experimental structures (code: nucleophilic regions are in red and electrophilic regions are in blue; intermediate potentials are assigned colors according to the color spectrum: red < orange < yellow < green < blue; scale: −30 to 30 kcal/mol). The Watson–Crick side of the top base faces the reader. (d) The region where the hydrogen bonding ability is increased (or where the MEP is deeper) upon stacking (i.e. from the isolated base to the stacked complex, experimental structures). The range used is: minimum of the MEP found for the isolated base to minimum of the MEP found for the complex.

Table 5.

Minima of the MEP surfaces of the optimized and experimental structures (kcal/mol)

		Optimized	Experimental
A	A	−45.17	−47.37
A	C	−63.72	−70.20
A	G	−60.02	−63.33
A	U	−43.95	−46.63
C	C	−62.52	−74.88
C	G	−62.02	−65.10
C	U	−59.26	−70.05
G	G	−61.26	−79.95
G	U	−56.19	−70.33
U	U	−40.90	−64.51

The surfaces were generated by mapping HF/6-31G* electrostatic potential values onto the 0.002 electron/ų isodensity surface, using the program SPARTAN.

The computation of the minimum of the MEP is very convenient to investigate the intrinsic effect of stacking upon the hydrogen bonding ability. However, it is not an easy task to quantify the effect of stacking via interaction energy calculations in three body systems (i.e. including the H-bonded partner). In a system comprising guanine H-bonded to cytosine and stacked by another guanine we found an increase of 2.3 kcal/mol in the hydrogen bond strength upon stacking (S. Loverix, P. Mignon and P. Geerlings, unpublished data). Apart from stacking other factors, such as ion binding, can affect the hydrogen bond strength of nucleobases. Analogous calculations on the effect of metal cations binding show an increase up to 6 kcal/mol on the hydrogen bond strength between guanine and cytosine for monovalent cations, and up to 22 kcal/mol for bivalent cations (101,102). However, one must take care before comparing these results, because the computed increase depends on the three body term ΔE₃ found to be negligible for our bases triplet (0.2 kcal/mol), which is not the case for cation metal bound to Watson–Crick base pairs (6 kcal/mol for monovalent cations and 15 kcal/mol for divalent cations). Similarly, the effect of bound water molecules may also be taken into account. Although most water molecules in X-ray structures of polynucleotides are situated in the vicinity of the phosphate group, a significant number of close contacts with nucleobases do occur (103–105). These interactions are not discussed in the present work but may be investigated in a future study.

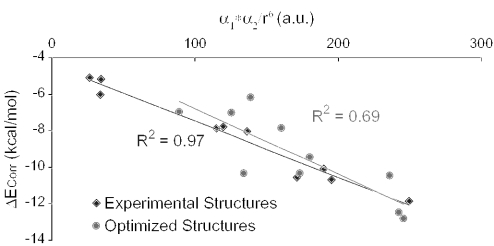
Another remarkable feature is that the experimentally observed arrangements seem to obey London's equation for the dispersion energy (Equation 2) better than the gas phase optimized complexes (Figure 6). Although the electrostatic interaction mimics rather well the total interaction energy, geometries depend on both the electrostatic and the dispersion forces.

Figure 6.

Correlation part of the interaction energy (ΔE_Corr) computed for the 10 stacked DNA/RNA base dimers (kcal/mol) versus the product of the polarizabilities of each base over R⁶ (see Equation 2) (a.u.).

Because the overlap between stacked bases may slightly differ for the various classifications, such as A-DNA and B-DNA, the experimental structures of DNA and hybrid RNA–DNA double helices were chosen to represent both forms, as well as an intermediate one. Moreover, the presence of other neighboring stacking partners may add to the observed effects in the stacked dimers. To address this point, we also computed electrostatic potential surfaces of various oligomeric complexes obtained from experimental structures (Table 6). The observed differences between hybrid RNA–DNA and DNA structures are small and it is found that in both cases the natural arrangement between stacked bases favors an increase in their hydrogen bonding capacity. Although the latter increases from dimers to trimers, the effect is less obvious than that found when comparing dimers with monomers. A similar tendency is seen in a cytosine tetramer suggesting that the MEP values may reach a plateau when adding stacking bases. It has to be noted that the minima of the MEP on the computed surfaces of trimers are located on the central base, except for the cytosine trimer in DNA for which the minimum is located on one of the outer bases, and for the adenine trimer in hybrid RNA–DNA for which two very similar minima are located on the central and outer bases.

Table 6.

Minima of the MEP surfaces for RNA–DNA hybrid and DNA structures (kcal/mol)

	RNA–DNA hybrid	DNA
A2	−45.8	−45.8
A1–A2	−48.6	−52.3
A1–A2–A3	−50.2	−55.4
C2	−67.9	−67.9
C1–C2	−75.0	−73.7
C1–C2–C3	−78.3	−75.7
C1–C2–C3–C4	—	−77.4
G2	−63.4	−63.4
G1–G2	−81.9	−77.6
G1–G2–G3	−86.9	−87.3
T2	−45.5	−45.5
T1–T2	−57.9	−54.8
T1–T2–T3	−59.0	−57.1

The surfaces were generated by mapping HF/6-31G* electrostatic potential values onto 0.002 electron/ų isodensity surface, using SPARTAN program.

CONCLUSIONS

In this study, we have shown that the hydrogen bonding ability of a stacked nucleobase depends on the hardness and the orientation of the stacking molecule. The less hard the stacking molecule, the larger the charge transfer to the stacked one and the larger its ability for hydrogen bonding. In model complexes of cytosine stacked with substituted benzenes, the hydrogen bonding ability is found to be directly related to the electrostatic part of the interaction between the rings. The local hardness appears to be a key index connecting the electrostatic interaction between the stacked aromatic rings and the hydrogen bonding ability of cytosine: the larger the local hardness, the larger the repulsion and the deeper the MEP around N3 and O2 atoms of the stacked cytosine. Moreover for stacked DNA base pairs, we observed an increase in the hydrogen bonding ability upon stacking only for experimental structures while the inverse is found for gas phase optimized structures. This effect originates from a more repulsive electrostatic interaction between the stacking bases. The enhancement of the hydrogen bonding potential of stacked nucleobases increases when more neighboring stacking partners in the same strand are taken into account, and seems to level off.