Abstract
Purpose:
Lymphopenia is a common side effect in patients treated with radiotherapy, potentially caused by direct cell killing of circulating lymphocytes in the blood. To investigate this hypothesis, a method to assess dose to circulating lymphocytes is needed.
Methods:
A stochastic model to simulate systemic blood flow in the human body was developed based on a previously designed compartment model. Blood dose was obtained by superimposing the spatiotemporal distribution of blood particles with a time-varying dose rate field, and used as a surrogate for dose to circulating lymphocytes. We discuss relevant theory on compartmental modeling and how to combine it with models of explicit organ vasculature.
Results:
A general workflow was established which can be used for any anatomical site. Stochastic compartments can be replaced by explicit models of organ vasculatures for improved spatial resolution, and tumor compartments can be dynamically assigned. Generating a patient-specific blood flow distribution takes about one minute, fast enough to investigate the effect of varying treatment parameters such as the dose rate. Furthermore, the anatomical structures contributing most to the overall blood dose can be identified, which could potentially be used for lymphocyte-sparing treatment planning.
Conclusion:
The ability to report the blood dose distribution during radiotherapy is imperative to test and act upon the current paradigm that radiation-induced lymphopenia is caused by direct cell killing of lymphocytes in the blood. We have built a general model that can do so for various treatment sites. The presented framework is publicly available at https://github.com/mghro/hedos.
Introduction
The immunologic status of cancer patients treated with radiotherapy is a prognostic factor for treatment outcome, and may be especially important for multi-modality treatments involving immunotherapy1. Specifically, radiation-induced lymphopenia (RIL), the depletion of the absolute number of circulating lymphocytes in the peripheral blood, has often been correlated with poor overall survival2,3. While the precise mechanism causing this depletion remains elusive, it is often assumed that direct cell kill of circulating lymphocytes in the blood is a main contributor4,5. This has led to the notion of blood as a dynamic organ at risk (OAR) in the context of RIL6. The OAR concept is familiar to radiation treatment planners and could be used to mitigate the immunosuppressive effects of radiotherapy, for instance by optimizing the treatment plan with respect to the blood dose.
Several efforts have been made to approximate the dose received by the blood during radiotherapy. Molloy has studied blood dose heterogeneity in the context of total body irradiation by describing blood flow as a sinusoidal motion in the craniocaudal direction7. Basler et al. calculated the dose to circulating lymphocytes for liver SBRT by assuming a homogeneous flow velocity in each liver lobe combined with a probabilistic reentry of lymphocytes8. Yovino et al. described a simplified version of the dose given to the blood during cranial treatment9. Even so, they were able to show that the volume of blood irradiated above some threshold depends on the dose rate and on the planning target volume size. Subsequent efforts have simplified the blood dose calculation further for thoracic irradiation, where the ‘mean blood dose’ is obtained by a formula relating it to lung, heart and integral dose, termed EDIC10. While simple in use, EDIC is limited in its applicability and ignores dose rate information, which influences the blood dose distribution rather than its mean, and presumably plays an important role due to the intrinsic time component of the problem.
To address these shortcomings, Shin et al. proposed a whole-body compartmental model of blood flow (HEDOS), in which blood particles jump stochastically from one compartment to the next based on transition probabilities11. A large number of blood particles are distributed over the compartments proportional to their relative blood volume. By simulating the stochastic blood flow process for a certain time period, a spatiotemporal distribution of blood particles throughout the human body is achieved. Subsequently, a blood dose distribution is obtained by accumulating dose increments over time, based on the organ dose-volume histograms and beam-on-time parameters. Recently, Xing et al. described the application of HEDOS for liver radiotherapy and augmented it with an explicit tracking of blood particles through the liver vasculature12. They show that both the treatment modality as well as treatment parameters, such as beam-on-time, impact blood dosimetry. In the present work, we improve on HEDOS and generalize the incorporation of explicit vascular modules in place of stochastic compartments. Specifically, we:
Revisit the mathematical framework of transition probabilities, thereby correcting an inaccuracy in the expression for the probability of a particle leaving a given organ (eq. 2 in Shin et al.).
Dynamically include a tumor compartment branching off from the compartment of the tumor-bearing organ.
Seamlessly integrate explicit models of organ vasculature in the stochastic model.
Increase the time resolution of the simulation from 1 second to 50 milliseconds.
Speed up blood dose calculations from hours to minutes allowing patient-specific blood flow calculations.
Assess the implications for dose accumulation in the blood.
This work is developed in the context of blood dose accumulation during radiotherapy. However, much of the discussion that follows applies to compartmental modeling in general and could be of interest to, for example, kinetic studies of (radio)pharmaceuticals as well.
Material and methods
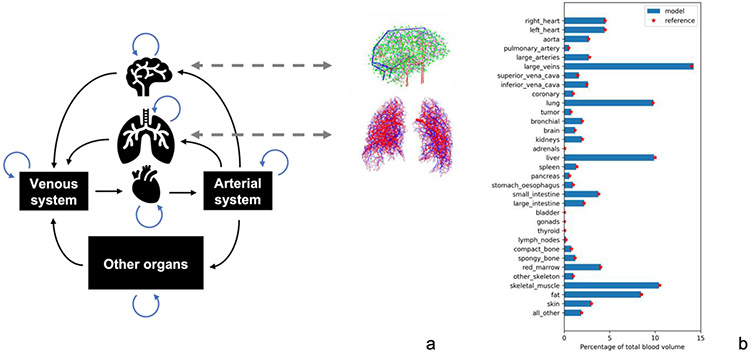
Previous research from our group introduced a blood flow compartmental model called HEDOS11, based on ICRP 89 reference data on blood flows and volumes in different organs in the human body13. In the model, the human body is represented by distinct compartments, representing different organs. Each of these organs has a blood volume assigned to it, and are linked in a way that reflects the anatomical connectivity of blood flow (Figure 1a). Blood flow is simulated by a stochastic process in which blood particles stochastically jump between compartments.
Figure 1.
a) Simplified depiction of the compartmental model. Stochastic compartments can be replaced by models of explicit vasculature as indicated. In b), the full list of included structures and their relative blood volume as maintained throughout the simulation. Reference values from ICRP 89 are also indicated.
The collective behavior of a large number of particles should be such that the reference flow between organs is maintained. Note however that different models for intra-compartmental blood flow could fulfill this requirement. In particular, we can replace stochastic models of intra-compartmental blood flow with explicit models while maintaining the continuity of the systemic blood flow as shown in Figure 1.
From transit time distributions to transition probabilities
The time it takes for a blood particle to traverse a given organ vasculature clearly depends on the path it took, and the flow velocity along the way, resulting in a distribution of transit times. When the system is in equilibrium, the mean of this transit time distribution (MTT) equals the turnover time of the compartment. That is,
| (1) |
where is the total flow out of compartment to its successors and is its blood volume. Similarly, the volumetric fraction of blood that leaves a given compartment in a small timestep is given by
| (2) |
In the model, blood flow is simulated by the constituent behavior of a large number of blood particles. Equation (2) indicates that we should take small enough to realistically model the continuous blood flow by a jumping process. At each timestep in the simulation, the probability that a particle jumps to a subsequent compartment is given by the conditional probability that the particle has not left the compartment until now but will do so during the current timestep. This leaving probability is related to the distribution (probability density function) of transit times , according to (see Supplementary Materials)
| (3) |
where the approximation becomes equality in the . Here, is the probability the particle leaves in the time window , which is conditioned on the requirement that the particle has ‘survived’ (stayed in the compartment) until time as given by the so-called survival function , where is the cumulative density function of transit times. The ratio over is known as the hazard function and describes the probabilistic rate at which particles leave. Hence, in general the transition probability depends on the aging of the particles (dwell time) inside the compartment, denoted by the time variable , which should be distinguished from , the global time variable of the simulation. Furthermore, when the system is in equilibrium, the age distribution in a compartment is given by the normalized survival function, . Therefore, the expected fraction of particles that leaves the compartment in timestep is given by
| (4) |
as before. The integration limits run from zero to infinity, and we have used that .
Note that our equations (2) and (3) should be compared to equations (1) and (2) in Shin et al11, respectively. In equation (2) we inserted the missing timestep, while equation (3) looks quite different altogether and is now based on survival analysis14. The impact of this correction is explored in the supplementary materials (Figure S1).
In practice, we choose a suitable transit time distribution for every compartment whose mean coincides with the mean transit time (MTT) determined from (1). The total number of blood particles is then distributed over the compartments according to volume fraction and their age initialized using the normalized survival function. The dwell time of the blood particles is incremented with each timestep and their probability to leave the compartment is determined from equation (3). When they do, they are stochastically assigned to successive compartments with a probability equal to the relative flow to each, and their dwell time set to zero. As an aside: transiting blood particles stochastically according to equation (3) is equivalent to sampling transit times from for each particle upon entry and transiting them when their dwell times exceed the assigned transit times.
So far, no assumption was made about the shape of the transit time distribution, other than that transit times are strictly positive. We will discuss the Weibull distribution, but other analytical distributions could be used as well. Moreover, experimentally determined transit time distributions could be used directly. These could be obtained from indicator dilution methods in which the concentration of a substance is repeatedly measured downstream of the organ after injection of a known amount upstream15 (Figure S2).
The transit time distribution
Many pharmacokinetic studies that use compartmental models typically assume first order dynamics, implying exponential transit time distributions and transition probabilities that are independent of compartmental dwell time. However, the validity of this implication is often questionable and certainly does not hold for blood flow, which requires some minimal amount of time to transit an organ. Hence blood particles with a very small transit time should be very unlikely. Furthermore, we expect the leaving probability to increase monotonically with time spent in the compartment. Both requirements are fulfilled by the Weibull distribution.
The Weibull distribution generalizes the exponential distribution by introducing an additional shape parameter :
| (5) |
In contrast to the exponential distribution (corresponding to ), result in monotonically increasing leaving probabilities, as desired, with more localized distributions for higher -values. For a chosen , the scale parameter is determined by requiring that the MTT coincides with the distribution mean:
| (6) |
where is the gamma function. In our simulations we typically use a shape parameter . The validity of this choice as well as alternative transit time distributions are discussed in the Supplementary Materials. Note that the gamma function scales between the mean transit time and the scale parameter . This was not included in the original HEDOS study which resulted in shifts of the equilibrium blood volumes in the compartments which had to be corrected for by retroactively adjusting the initial distribution11; this is no longer necessary with the new implementation as the system remains in equilibrium throughout the simulation.
Including tumor compartments
In cancer patients, part of the blood flows through a compromised tumor vasculature. Depending on the type, the tumor may be more or less perfused compared to surrounding tissue16. Previously, this spatial heterogeneity could not be taken into account in HEDOS, and the combined DVH for organ and tumor was used to calculate the blood dose. To improve on this, we dynamically branch off the tumor blood flow from the tumor-bearing compartment and account for the blood dose contributions of tumor and healthy tissue separately.
In our model, the tumor compartment branches off from the original in a parallel fashion and we assume that the total blood flow through the tissue-tumor complex remains unaffected; that is, the tumor ‘steals’ blood destined for the organ as shown in Figure 2. This approximation is valid if the ratio of tissue versus tumor volume is large. The relative perfusion and blood density of the tumor compared to normal tissue are kept as free parameters and may be determined from measurements or literature17. Together with the relative size of the tumor versus normal tissue, these values are used to determine how much blood is taken by the tumor and adjust the compartment parameters accordingly.
Figure 2.
Splitting off the tumor compartment from the original organ compartment.
Replacing compartments by explicit vascular models
External beam radiotherapy has become a very conformal treatment as a result of advances in treatment planning18, image guidance19, and the introduction of particle therapy20. Consequently, only a small fraction of a given compartment (organ) is typically irradiated to high dose. Treating different organs as vascular compartments does not capture the spatial dose heterogeneity within the organ. To improve on this, explicit models of organ vasculature were developed21,22, and incorporated in the compartmental model in place of their corresponding compartments. While our team has developed female and male organ vasculature for liver, lung, brain, and kidney so far, detailed vasculature models will be developed for all major organs, based on the ICRP reference mesh phantoms23.
The organ vasculature contain a large number of vessels through which flow rates are calculated; see Correa-Alfonso et al. (2022, 2023) for details21-22. For the purpose of calculating the dose to the blood, centerlines are extracted from the three-dimensional vessel structures and mathematically represented by a directed graph containing vertices linked by edges . The vertices (or nodes) hold the physical positions of the endpoints of the edges, which represent the centerlines of the blood vessels themselves and have assigned to them physical attributes such their flow, radius, length and type of vessel (arterial or venous). While the vasculature models are quite detailed, they do not go down to microvascular or capillary levels. Consequently, not all organ blood is captured in the vascular model, artificially shortening the organ MTT. To correct for this, a small surrogate vessel was introduced to represent the microvascular and capillary transition, where arterial turns into venous blood. The mean transit time of this transition was determined such that the vasculature MTT (and hence the organ blood volume) agreed with the compartmental model. While it is important that all blood is accounted for, the size of this missing microvascular step is smaller than the dimensions over which dose gradients vary appreciably in external beam radiotherapy. Hence, for blood dose calculations, this surrogate vessel approach was deemed appropriate.
Deforming the phantom vascular model to patient anatomy
The phantom vasculature needs to be registered with the patient anatomy in order to do dose accumulation of the circulating blood particles. To avoid some of the conceptual challenges that come with dose warping24, the phantom vasculature model was registered to the patient anatomy, and not the other way around.
To this end, we use the phantom organ mesh as a guiding structure. By registering it to the patient’s organ mesh, a dense registration field is obtained which is then used to warp the vertices of the vasculature graph. First a center of mass alignment is performed after which an iterative closest point algorithm finds the best rigid registration between the phantom and patient mesh. The rigidly matched meshes are then converted to distance maps which serve as input for the subsequent deformable registration. Distance maps are a richer representation of the segmentations which makes the ill-posed problem of finding an ‘optimal’ registration between them better defined.
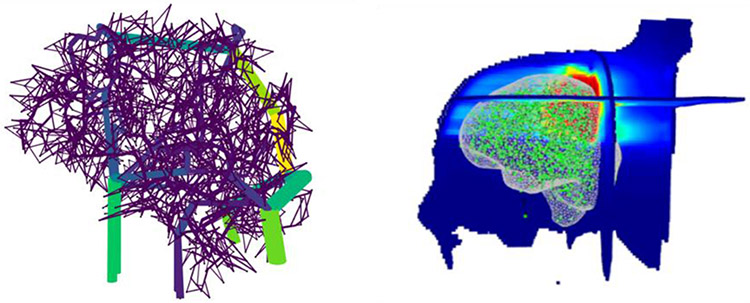
The deformation of the vasculature model should avoid large local disturbances of its architecture, but rather deform it as globally as possible. For this reason, we used a diffeomorphic registration algorithm which guarantees preservation of the topology of the warped shape25. To further encourage an as-global-as-possible registration, we used a multiscale implementation in which the registration is progressively refined. The registration module was implemented using SimpleITK26. An example of the brain vasculature registered to a patient is shown in Figure 3.
Figure 3.
Left: Phantom vasculature of the brain color coded for blood flow. Right: Centerlines are extracted, and its vertices (green) registered to a patient which is represented by orthogonal slices of the dose distribution. A mesh rendering of the patient brain is also shown for clarity (grey).
Particle tracking
The vasculature contains one or more source nodes where blood particles enter from previous compartments, and one or more terminal nodes from where they move on to subsequent compartments. There is a finite number of possible paths between each of these source and terminal nodes. Upon entry, blood particles are probabilistically assigned a path with a probability equal to the relative flow through each path. Let us now consider one such path, given by a collection of successive nodes , connected by edges. Let with be the trajectory of a particle traversing this path with traversal time . We approximate this trajectory using a spline function , so that
| (7) |
Here, is a normalized variable that parametrizes the path, running from at the source node to at the terminal node. Along this path, the flow velocity changes with position. Hence, the trajectory of a blood particle traveling along this path satisfies a simple ordinary differential equation (ODE):
| (8) |
which can be solved very efficiently using available packages (we used Scipy27). This process is repeated for every path separately since the traversal times and the functions and are clearly path-specific. Using the solution to (8) for every path, a look-up table can be constructed for a given time resolution, where the rows represent the different paths and the columns subsequent time points. Now the problem of finding the current path position for a large number of particles is reduced to sampling from this table, given the path and time since entry of each blood particle.
By warping the phantom vasculature to the patient anatomy, patient-specific instances of the vasculature model are created. It is in this ‘patient-space’ where the tracking of blood particles takes place. However, the path parametrizations are independent of their orientation in space. Therefore, the look-up table is constructed once, and reused for every patient. Patient-specific spline functions then map all path parametrizations to warped instances of the vasculature model. Hence, by finding a solution to the ODE in (8) up front only once for every path, an efficient implementation was achieved to model blood flow through the vasculature for individual patients that scales well with the number of particles used for simulation.
In contrast to the stochastic nature of transit times and spatial locations of the compartments, the vasculature model is deterministic once a particle has been assigned a path. However, similar to its compartmental counterpart, the vasculature module maps dwell times to physical locations in space. Because these modules are essentially doing the same thing, they can be seamlessly integrated into a hybrid model. Note that we first split off the tumor compartment when we do the explicit tracking through vasculature and administer the tumor contribution to the blood dose separately. Since the tumor will generally receive a very homogeneous dose, explicit tracking is not necessary.
Dose accumulation
In order to accumulate dose in the blood particles, we need to know their physical positions over time. However, in contrast to explicit vasculature models, stochastic compartments do not directly yield spatial information. Only when the organs of interest are segmented on medical scans, we can assign points in space to the corresponding compartments. Yet, the motion a blood particle describes as it traverses each of these segmentations is unknown. Hence, for stochastic compartments, two different methods of modeling the particles’ trajectories were compared in terms of the resulting dose distribution: 1. Uncorrelated motion, as a sequence of random locations inside the corresponding organ segmentation; 2. Correlated motion, as a random walk through the segmentation. Note that option 1 corresponds to taking random draws from the ‘dose rate histogram’ obtained for every organ volume separately.
With the spatiotemporal distribution generated for the blood particles, it can be overlayed with a, potentially varying, dose rate for dose accumulation. During each time step, the dose associated to a blood particle is incremented by . Finally, a dose histogram is obtained by binning the particles’ accumulated dose.
Results
Dose accumulation
Figure 4 shows calculated blood dose distributions for a lung cancer patient where we explicitly tracked blood particles through the lung vasculature whereas other organs are simulated using the compartment model. For comparison, the mean blood dose as calculated by the EDIC method10 has also been indicated. Uncorrelated motion of blood particles results in a distribution centered about the mean transit dose (top row). In contrast, the random walk implementation better resembles vasculature motion, in which a blood particle may travel through a high dose region or a low dose region, leading to a large variation in particle doses (middle row). The dose calculation can be further refined by splitting off the tumor compartment and including main thoracic vessels that are in the field of view (bottom row). These structures contribute substantially, due to the high administered dose (tumor) and high blood flow (vessels).
Figure 4.
Fractional blood dose distributions (left) and the dose contributions of different structures (right). Top row: only lung and heart are considered and with particles describing uncorrelated motion. Middle row: explicit vasculature tracking in the lung and a random walk in the heart. Bottom row: explicit vasculature tracking in the lung and a random walk in all other indicated structures. Vertical axis: number of particles out of 100,000.
It should be noted that changing the dose rate only changes the shape of the blood dose distribution, but not its mean. To calculate the contribution of each organ to the mean blood dose, it is sufficient to know mean organ dose and the fraction of the total blood volume that is in the given organ . The mean blood dose is then simply given by
| (9) |
By changing the dose rate, we can decide whether to increase dose to a small sub-volume of the blood to spare the rest (high dose rate), or to irradiate a larger volume but to lower dose (low dose rate). The definition of what is “high” and “low” should be considered with respect to the blood circulation time; doubling the dose rate has the same effect on the blood dose distribution as reducing the cardiac output by half.
As the model is explicitly designed to take the temporal component of blood dose calculation into account, we studied the effect of breathing motion in lung radiotherapy on the blood dose using the patient’s 4D CT. The exhale phase was warped to each of the other phases of the 4D CT and used to guide the motion of the vasculature, similar to the deformable registration described above. The particle’s motion is thus a superposition of the breathing motion of the patient’s vasculature with its motion through that vasculature. However, the effect of breathing motion on the blood dose was negligible (Figure S3), due to its limited range and its tendency to average out since respiratory cycles are typically shorter than beam-on times. In addition, free breathing represents the worst case scenario, and motion mitigation strategies are often employed in clinic.
Potentially, one may be interested in blood dose summed over multiple fractions. In Figure 5 fractional blood dose and blood dose summed over multiple equivalent fractions are shown side by side. We assumed total mixing of the blood by the time subsequent fractions occurred. Consequently, the summed dose becomes normally distributed by the central limit theorem.
Figure 5.
Fractional (right) and summed (right) blood dose distributions.
Timings and model parameters
Table 1 shows computation times for the simulation of 10 minutes of blood flow and subsequent dose accumulation for different number of simulated particles and different timestep sizes (run on a M1 iMac with 16 GB of memory). Typically, we performed simulations with 100,000 blood particles and a timestep of 0.05 seconds to ensure a fine enough time resolution to model a continuous flow by a discrete-time process. Including vasculature modules in the compartment model requires extra computational time. Still, the model is fast enough to include patient-specific parameters such as tumor perfusion, or organ blood volume or flow. Note that the time it takes for dose accumulation depends on the number of organs contributing to the dose (in the example used here, lungs, heart, aorta, pulmonary artery and superior vena cava), and should be taken as a rough estimate. For very large , we ran into memory issues, which could be circumvented by processing smaller chunks separately as blood particles operate independently of each other. However, we found that for 100,000 particles dose histogram variations due to stochastic fluctuations are negligible (see Figure S4), indicating that using 100,000 particles suffices for blood dose calculations.
Table 1.
Computation times (in seconds) of blood flow calculations and subsequent dose accumulations. Compartmental only is compared to the model with integrated vasculature (of the lungs).
| Compartmental only | With vasculature | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.05 | 0.025 | 0.1 | 0.05 | 0.025 | |
| Blood flow modeling | ||||||
| 1000 | 2.6 | 4.7 | 8.5 | 3.1 | 5.6 | 10.3 |
| 10,000 | 5.3 | 10.4 | 19.3 | 6.0 | 11.4 | 21.8 |
| 100,000 | 27.1 | 60.3 | 129.6 | 30.1 | 64.3 | 153.6 |
| Dose accumulation | ||||||
| 1000 | 2.2 | 2.2 | 2.3 | 4.1 | 5.1 | 7.1 |
| 10,000 | 2.6 | 3.1 | 3.3 | 6.3 | 9.6 | 16.0 |
| 100,000 | 6.6 | 10.1 | 17.9 | 31.6 | 60.7 | 198.7 |
Table 2 lists all model parameters used for the blood flow simulation. All parameters are user controlled. They fall into two categories: simulation parameters and biological parameters. The shape parameter of the Weibull distribution – or even the type of distribution itself – sits somewhere in between, providing the link between biology and simulation.
Table 2.
Model parameters for blood flow simulation.
| Parameter: | Obtainable from: | Value used: |
|---|---|---|
| Biological parameters | ||
| Organ blood volume | ICRP 89/measurements | Organ specific |
| Organ blood inflow | ICRP 89/measurements | Organ specific |
| * Relative tumor blood density | Literature/measurements | 1.0 |
| *Relative tumor perfusion | Literature/measurements | 1.0 |
| *Relative tumor size | Diagnostic scan | Tumor specific |
| Shape of transit time distribution | Assumption/measurements | 2.0 |
| Simulation parameters | ||
| Number of simulated blood particles | 100,000 | |
| Number of timesteps | 12,000 | |
| Timestep size | 0.05 s | |
compared to the tumor-bearing organ.
Discussion
We have presented a comprehensive framework to accurately calculate blood dose in patients receiving radiation treatment for various treatment sites, and we have given examples for brain and lung patients. We have provided a more formal treatment of the underlying mathematics of compartmental modeling of flow. Other novelties included the seamless incorporation of vasculature models as well as the ability to dynamically branch off tumor compartments where needed. For our application, we overlayed the spatiotemporal tracking of blood particles with the dose rate in order to accumulate dose during fractionated radiotherapy. While the model was developed in the context of external beam radiotherapy, it may also be useful for radiation protection studies, similar to how the ICRP phantom mesh is used for static organs at risk28
Blood dose calculations are fast and patient-specific and can be further personalized by including patient-specific parameters such as total blood volume, cardiac output and tumor perfusion parameters. Blood volume scales linearly with body weight, which can be readily included as an additional parameter. Other patient-specific characteristics, such as cardiac output and tumor perfusion, could potentially be non-invasively obtained from Doppler ultrasound or functional MRI measurements, but this is not standard practice. Hence, while the derived dose distribution comes with some uncertainty, this is not a limitation of the model itself and knowledge can be incorporated as it becomes available. Hence, the model represents our best estimate of the patient’s blood dose. Moreover, in comparative settings, these uncertainties become less relevant. Additionally, the presented tool returns the contribution of each of the considered structures to the total fractional dose. This can be useful for lymphocyte-sparing treatment planning, e.g. by tightening the dose constraints on the structures contributing most. Furthermore, we have shown that without access to explicit vasculature models, a good surrogate can be obtained by letting blood particles perform a random walk inside the corresponding volume.
It is unclear to what extent blood accumulates dose over multiple treatment fractions. We typically consider only fractional blood dose since we assume that sublethal damage is fully repaired in between fractions29. Alternatively, we could incorporate an explicit cell kill and repair model and accumulate dose over multiple fractions.
We should pause here to note that the assumption that blood dose is a good surrogate for lymphocyte dose, and therefore indicative of lymphocyte cell kill, is not necessarily correct. Multiple mechanisms are at play why this may not be so. First, lymphocyte cells must deform in order to squeeze through the narrow capillary network30,31. This process takes time, resulting in a higher concentration of lymphocytes in the capillaries32. Potentially we could model this by adjusting the mean transit time parameters accordingly. Second, lymphocytes are shown to recirculate multiple times a day between the blood, bone marrow, secondary lymphatic organs and certain non-lymphatic organs such as the lungs, the liver and the gut33,34. In fact, it is believed that only a small fraction (2-5%) resides in the blood at any given time35. In light of this, it is perhaps surprising that, while irradiation of lymphatic-rich tissue such as the spleen and lymph nodes contributes36-38, it is not required for lymphopenia to occur, as has been observed in patients undergoing cranial irradiation39, which contains only minimal lymphatics40. To truly capture lymphocyte circulation dynamics, additional lymphatic compartments should be included in the model, as was done by Jin et al.41. However, without extensive benchmarking against experimental data, the validity of such complications remains unknown. In conclusion, a better understanding of lymphocyte recirculation and its interaction with radiotherapy is needed to fully understand the extent to which dose to circulating lymphocytes contributes to radiation-induced lymphopenia.
Because of this lymphocyte recirculation, the situation of local administration of radiotherapy is more complex than total body irradiation in which all lymphocytes get the same dose, irrespective of their location in the body. Therefore, although blood dose is expected to correlate to some extent with lymphopenia, we have restrained here from developing a mechanistic connection between blood dosimetry and lymphocyte cell death due to the uncertainties in lymphocyte trafficking patterns. Consequently, it is challenging to directly validate our model by using lymphocytes as radiobiological dosimeters, based on -H2AX foci42, chromosomal aberrations (CA)43, or micronuclei (MN)44. A further complication is that all these measurements are time dependent. This is especially true for DNA double strand breaks, which are rapidly repaired so that the yield of -H2AX foci declines shortly after induction. CA and MN are more persistent and therefore perhaps more reliable biomarkers of radiation dose. Yet, while many cytogenetic studies have shown that radiotherapy induces increased levels of CA and MN in peripheral blood samples, it is not clear whether these aberrations are also induced in the blood or rather elsewhere in the body.
Finally, it is worthwhile to point out that the presented model of blood flow might also be useful in pharmacokinetic studies which typically make use of ODEs to model first order exchange between compartments, which corresponds to a constant transition probability in the limit of infinite particles in our model. The intrinsic stochasticity, the ability to track individual particles and to choose dwell time dependent transition probabilities could be interesting for these studies as well, with the caveat that our stochastic model is computationally more demanding and therefore harder to fit to measured datapoints.
Conclusion
We have presented a comprehensive framework to model human blood flow based on a stochastic compartment model in which explicit vasculature models can be seamlessly integrated. The model was developed in the context of calculating blood dose during radiotherapy, which is of relevance when studying the causes of radiation-induced lymphopenia and potential strategies for its mitigation.
Supplementary Material
References
- 1.Grassberger C, Ellsworth SG, Wilks MQ, Keane FK, Loeffler JS. Assessing the interactions between radiotherapy and antitumour immunity. Nat Rev Clin Oncol. 2019;16(12):729–745. doi: 10.1038/s41571-019-0238-9 [DOI] [PubMed] [Google Scholar]
- 2.Venkatesulu BP, Mallick S, Lin SH, Krishnan S. A systematic review of the influence of radiation-induced lymphopenia on survival outcomes in solid tumors. Crit Rev Oncol Hematol. 2018;123(January):42–51. doi: 10.1016/j.critrevonc.2018.01.003 [DOI] [PubMed] [Google Scholar]
- 3.Damen PJJ, Kroese TE, van Hillegersberg R, et al. The Influence of Severe Radiation-Induced Lymphopenia on Overall Survival in Solid Tumors: A Systematic Review and Meta-Analysis. Int J Radiat Oncol Biol Phys. 2021;111(4):936–948. doi: 10.1016/j.ijrobp.2021.07.1695 [DOI] [PubMed] [Google Scholar]
- 4.McCullum L, Shin J, Xing S, et al. Predicting Severity of Radiation Induced Lymphopenia in Individual Proton Therapy Patients for Varying Dose Rate and Fractionation Using Dynamic 4-Dimensional Blood Flow Simulations. Int J Radiat Oncol. 2023;Epub ahead. doi: 10.1016/j.ijrobp.2023.01.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ellsworth SG, Yalamanchali A, Lautenschlaeger T, et al. Lymphocyte Depletion Rate as a Biomarker of Radiation Dose to Circulating Lymphocytes During Fractionated Partial-Body Radiation Therapy. Adv Radiat Oncol. 2022;7(5). doi: 10.1016/j.adro.2022.100959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ladbury CJ, Rusthoven CG, Camidge DR, Kavanagh BD, Nath SK. Impact of Radiation Dose to the Host Immune System on Tumor Control and Survival for Stage III Non-Small Cell Lung Cancer Treated with Definitive Radiation Therapy. Int J Radiat Oncol Biol Phys. 2019;105(2):346–355. doi: 10.1016/j.ijrobp.2019.05.064 [DOI] [PubMed] [Google Scholar]
- 7.Molloy JA. Statistical analysis of dose heterogeneity in circulating blood: Implications for sequential methods of total body irradiation. Med Phys. 2010;37(11):5568–5578. doi: 10.1118/1.3495816 [DOI] [PubMed] [Google Scholar]
- 8.Basler L, Andratschke N, Ehrbar S, Guckenberger M, Tanadini-Lang S. Modelling the immunosuppressive effect of liver SBRT by simulating the dose to circulating lymphocytes: An in-silico planning study. Radiat Oncol. 2018;13(1):4–11. doi: 10.1186/s13014-018-0952-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yovino S, Kleinberg L, Grossman SA, Narayanan M, Ford E. The etiology of treatment-related lymphopenia in patients with malignant gliomas: Modeling radiation dose to circulating lymphocytes explains clinical observations and suggests methods of modifying the impact of radiation on immune cells. Cancer Invest. 2013;31(2):140–144. doi: 10.3109/07357907.2012.762780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xu C, Jin J-Y, Zhang M, et al. The impact of the effective dose to immune cells on lymphopenia and survival of esophageal cancer after chemoradiotherapy. Radiother Oncol. 2020;146(1):180–186. doi: 10.1016/j.radonc.2020.02.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Shin J, Xing S, McCullum L, et al. HEDOS-a computational tool to assess radiation dose to circulating blood cells during external beam radiotherapy based on whole-body blood flow simulations. Phys Med Biol. 2021;66(16). doi: 10.1088/1361-6560/ac16ea [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xing S, Shin J, Pursley J, et al. A dynamic blood flow model to compute absorbed dose to circulating blood and lymphocytes in liver external beam radiotherapy. Phys Med Biol. 2022;67(4). doi: 10.1088/1361-6560/ac4da4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.ICRP Publication 89: basic anatomical and physiological data for use in radiological protection—reference values. Ann ICRP 89. 2002;32 (3-4). [PubMed] [Google Scholar]
- 14.Miller RG. Survival Analysis. John Wiley & Sons, Inc.; 1998. [Google Scholar]
- 15.Stephenson JL. Theory of the measurement of blood flow by the dilution of an indicator. Bull Math Biophys. 1948;10(2):117–121. [DOI] [PubMed] [Google Scholar]
- 16.Vaupel P, Kallinowski F, Okunieff P. Blood Flow, Oxygen and Nutrient Supply, and Metabolic Microenvironment of Human Tumors: A Review. Cancer Res. 1989;49(23):6449–6465. [PubMed] [Google Scholar]
- 17.Jain R Perfusion CT imaging of brain tumors: An overview. Am J Neuroradiol. 2011;32(9): 1570–1577. doi: 10.3174/ajnr.A2263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Webb S The physical basis of IMRT and inverse planning. Br J Radiol. 2003;76(910):678–689. doi: 10.1259/bjr/65676879 [DOI] [PubMed] [Google Scholar]
- 19.Sonke JJ, Aznar M, Rasch C. Adaptive Radiotherapy for Anatomical Changes. Semin Radiat Oncol. 2019;29(3):245–257. doi: 10.1016/j.semradonc.2019.02.007 [DOI] [PubMed] [Google Scholar]
- 20.Paganetti H. Proton Beam Therapy. IOP Publishing; 2017. doi: 10.1088/978-0-7503-1370-4 [DOI] [Google Scholar]
- 21.Correa-Alfonso CM, Withrow JD, Domal SJ, et al. A mesh-based model of liver vasculature: implications for improved radiation dosimetry to liver parenchyma for radiopharmaceuticals. EJNMMI Phys. 2022;9(1). doi: 10.1186/s40658-022-00456-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Correa-Alfonso CM, Withrow J, Domal SJ, et al. Intra-brain vascular models within the ICRP mesh-type adult reference phantoms for applications to internal dosimetry. Phys Med Biol. 2023;Epub ahead. [DOI] [PubMed] [Google Scholar]
- 23.Kim CH, Yeom YS, Petoussi-Henss N, et al. ICRP Publication 145: Adult Mesh-Type Reference Computational Phantoms. Ann ICRP. 2020;49(3):13–201. doi: 10.1177/0146645319893605 [DOI] [PubMed] [Google Scholar]
- 24.Chetty IJ, Rosu-Bubulac M. Deformable Registration for Dose Accumulation. Semin Radiat Oncol. 2019;29(3):198–208. doi: 10.1016/j.semradonc.2019.02.002 [DOI] [PubMed] [Google Scholar]
- 25.Ashburner J A fast diffeomorphic image registration algorithm. Neuroimage. 2007;38(1):95–113. doi: 10.1016/j.neuroimage.2007.07.007 [DOI] [PubMed] [Google Scholar]
- 26.Lowekamp BC, Chen DT, Ibáñez L, Blezek D. The design of simpleITK. Front Neuroinform. 2013;7(DEC):1–14. doi: 10.3389/fninf.2013.00045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Virtanen P, Gommers R, Oliphant TE, et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods. 2020;17:261–272. doi: 10.1038/s41592-019-0686-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kim CH, Yeom YS, Nguyen TT, et al. New mesh-type phantoms and their dosimetric applications, including emergencies. Ann ICRP. 2018;47(3-4):45–62. doi: 10.1177/0146645318756231 [DOI] [PubMed] [Google Scholar]
- 29.Dale RG. Radiation repair models for clinical application. Br J Radiol. 2019;92(1093):1–7. doi: 10.1259/bjr.20180070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Downey GP, Doherty DE, Schwab B, Elson EL, Henson PM, Worthen GS. Retention of leukocytes in capillaries: Role of cell size and deformability. J Appl Physiol. 1990;69(5):1767–1778. doi: 10.1152/jappl.1990.69.5.1767 [DOI] [PubMed] [Google Scholar]
- 31.Hogg JC, Doerschuk CM. Leukocyte traffic in the lung. Annu Rev Physiol. 1995;57:97–114. doi: 10.1146/annurev.ph.57.030195.000525 [DOI] [PubMed] [Google Scholar]
- 32.Kuebler WM, Goetz. The Marginated Pool Wolfgang. Eur Surg Res. 2002;34(92):92–100. www.karger.comwww.karger.com/journals/esr [DOI] [PubMed] [Google Scholar]
- 33.Smith ME, Ford WL. The recirculating lymphocyte pool of the rat: a systematic description of the migratory behaviour of recirculating lymphocytes. Immunology. 1983;49(l):83–94. http://www.ncbi.nlm.nih.gov/pubmed/6840811%0Ahttp://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC1454101 [PMC free article] [PubMed] [Google Scholar]
- 34.Blum KS, Pabst R. Lymphocyte numbers and subsets in the human blood. Do they mirror the situation in all organs? Immunol Lett. 2007;108(1):45–51. doi: 10.1016/j.imlet.2006.10.009 [DOI] [PubMed] [Google Scholar]
- 35.Trepel F Number and distribution of lymphocytes in man. A critical analysis. Klin Wochenschr. 1974;52(11):511–515. doi: 10.1007/BF01468720 [DOI] [PubMed] [Google Scholar]
- 36.Liu J, Zhao Q, Deng W, et al. Radiation-related lymphopenia is associated with spleen irradiation dose during radiotherapy in patients with hepatocellular carcinoma. Radiat Oncol. 2017;12(1):1–7. doi: 10.1186/s13014-017-0824-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chadha AS, Liu G, Chen HC, et al. Does Unintentional Splenic Radiation Predict Outcomes After Pancreatic Cancer Radiation Therapy? Int J Radiat Oncol Biol Phys. 2017;97(2):323–332. doi: 10.1016/j.ijrobp.2016.10.046 [DOI] [PubMed] [Google Scholar]
- 38.Schad MD, Dutta SW, Muller DM, Wijesooriya K, Showalter TN. Radiation-related Lymphopenia after Pelvic Nodal Irradiation for Prostate Cancer. Adv Radiat Oncol. 2019;4(2):323–330. doi: 10.1016/j.adro.2019.01.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Harisiadis L, Kopelson G, Chang CH. Lymphopenia caused by cranial irradiation in children receiving craniospinal radiotherapy. Cancer. 1977;40(3):1102–1108. doi: [DOI] [PubMed] [Google Scholar]
- 40.Louveau A, Smirnov I, Keyes TJ, et al. Structural and functional features of central nervous system lymphatics. Nature. 2015;523(7560):337–341. doi: 10.1038/nature14432.Structural [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jin JY, Mereniuk T, Yalamanchali A, et al. A framework for modeling radiation induced lymphopenia in radiotherapy. Radiother Oncol. 2020;144:105–113. doi: 10.1016/j.radonc.2019.11.014 [DOI] [PubMed] [Google Scholar]
- 42.Rothkamm K, Horn S. -H2AX as protein biomarker for radiation exposure. Ann Ist Super Sanita. 2009;45(3):265–271. [PubMed] [Google Scholar]
- 43.Kelly S, Brown CD. Chromosome Aberrations as a Biological Dosimeter. Am J Public Heal Nations Heal. 1965;55(9):1419–1429. doi: 10.2105/AJPH.55.9.1419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tichy A, Kabacik S, O’Brien G, et al. The first in vivo multiparametric comparison of different radiation exposure biomarkers in human blood. PLoS One. 2018;13(2):1–21. doi: 10.1371/journal.pone.0193412 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.