Abstract
Precision medicine seeks to tailor therapy to the individual patient, based on statistical correlates from patients who are similar to the one under consideration. These correlates can and should go beyond genetics, and in general, beyond tabular or array data that can be easily represented computationally and compared. For example, in many types of cancer, cancer treatment and toxicity depend in large measure on the spatial disease spread—e.g., metastasizes to regional lymph nodes in head and neck cancer. However, there is currently a lack of methodology for integrating spatial information when considering patient similarity. We present a novel modeling methodology for the comparison of cancer patients within a cohort, based on the spatial spread of lymph node involvement in each patient. The method uses a topological map, bigrams, and hierarchical clustering to group patients based on their similarity. We compare this approach against a categorical similarity approach where patients are binned by their nodal involvement. We present similarity results on a 582 head and neck cancer patient cohort, along with two visual abstractions for analysis of the results, and we present clinician feedback. Our novel methodology partitions a patient cohort into clinically meaningful groups more susceptible to treatment side-effects. Such spatially-aware similarity approaches can help maximize the effectiveness of each patient’s treatment.
Keywords: Precision medicine, Spatial Similarity, Topology, Visual Interface, Oncology
1. Introduction
The United States National Cancer Institute estimates that more than 51,000 people in the United States were diagnosed in 2018 with head and neck squamous cell carcinoma (HNSCC) [1]. Of these HNSCC cases, more than 90% result as oropharyngeal carcinomas (OPC), which include cancers of the larynx (voice box), pharynx (throat), lips, tongue, and nose [2, 3]. At the same time, the large number of HNSCC cases makes possible the creation of big data repositories consisting of the demographic and clinical characteristics, treatments, and outcomes of patients undergoing therapy. These repositories present opportunities towards informing and further personalizing treatment on a per-patient level, rather than relying on clinician experience or institutional memory alone [4, 5]. Under a healthcare model termed ”precision medicine”, clinicians aim to use these patient repositories to tailor therapy decision to the individual patient, based on data from patients who are similar to the one under consideration. Currently, these correlates typically include age, performance status, clinical staging information, and sometimes genetics—attributes that can be statistically aggregated, matched and analyzed.
Yet, similar to most other cancer types, HNSCC treatment and side effects depend in large measure on the spatial location and spread of the cancer. In particular, for more than 50% of OPC patients, the treatment and side-effects are heavily influenced by the spread of disease to lymph nodes (LN) and their corresponding areas (levels), at risk for metastases. OPC generally metastasizes to regional LNs following the lymphatic drainage of the head and neck [6], often resulting in chains of affected LNs along the drainage pathway. These chains correspond to the spread of involvement to specific locations of the head and neck and are thus defined by their spatial attributes. Therefore, for those patients receiving intensity-modulated radiation therapy (IMRT), these chains represent additional targets that must receive radiation treatment. Further complicating matters, the soft tissue structures of the head and neck (organs, muscles, etc.) are highly susceptible to both direct and indirect radiation exposure [1], and the increased toxicity to specific regions has been shown to correlate with post-therapy quality of life. For example, aspiration and dysphagia side-effects affect as many as 30%−50% of patients treated with IMRT [7]. Therefore, clinicians believe that grouping patients by their patterns of nodal involvement spread can help improve treatment strategies regarding both efficacy and toxicity.
The state of the art in lymph pattern similarity uses either categorical matching of node labels, or relies on clinician memory. The first approach does not capture the spatial patterns of disease spread, and the second approach clearly does not scale well. Because within a patient cohort there are many rare or unique combinations of spatial involvement chains, analyzing and interpreting the results of any lymph similarity measure is further challenging. Precision medicine stands to benefit from scalable, rigorous computing methodology that takes into account both the information about metastasized nodes and about the pathways that connect them, and facilitates the analysis and interpretation of the resulting similarity measures.
At the same time, spatial similarity has been facilitated in many domains such as mechanical engineering [8], bioinformatics [9], and oncology [10, 11] by encoding spatial relationships through either topology-based or shape-based techniques. These techniques have the ability to ”exhibit common classes of descriptive spatial (topological) features that are quantified by definition of computable measures” [12]. Both topology and shape-based techniques aim to extract spatial attributes, then establish a relationship between corresponding attributes in different patients. However, shape-similarity based methods tend to focus on classifying models of very different shapes, and fall short of distinguishing anatomical objects within the same class unless the objects have easily identifiable structures, such as the mandible and outer body contour [10, 13, 14]. In the case of lymph nodes, structures are in the same class and do not have easily identifiable features. However, OPC patient analysis presents an opportunity for topology-based techniques.
In this paper, we present a novel topology-based modeling methodology for the comparison of patients within a cohort, based on the spatial pattern of lymph nodes affected by disease. As part of this methodology, we construct a topological map, we define computational representations, and we introduce a novel graph-based measure to derive patient LN involvement similarity. We further construct a novel visual interface to interpret the spatial similarity results, followed by a novel dendrogram visual encoding to communicate the results to clinicians. We evaluate this methodology on a clinical cohort of 582 post-therapy OPC patients. We perform hierarchical clustering on the output of the similarity ranking to test for correlations with post-therapy toxicity. We contrast these spatial measure results against the results obtained using a categorical labeling of the nodes. Specifically, we hypothesize that the underlying spatial information contained within the chains of affected LN levels would significantly correlate with post-therapy side-effects known to arise due to radiation toxicity. This computing methodology should further allow for binning of patients in cohorts deemed by clinicians as significantly more informative than categorical binning.
2. Materials and Methods
2.1. Method Overview
Our methodology is constructed as follows (Figure 1): the LN levels for eligible patients are manually segmented from contrast-enhanced computed tomography imaging data. We then construct a LN topological map, based on the level location and its surrounding local neighborhood, and using the medical literature [15] and clinician input; because of left-right symmetry in the human head and neck, this is a 2D map with cells for each node region. To facilitate patient comparison using the spatial information, we next define and construct a dual-graph representation over the topological map; this representation captures the neighbor relationships among the lymph nodes. We use the graph representation to compute the pair-wise similarity between each patient using a spatial measure. Next, we perform hierarchical agglomerative clustering and visual analysis on the similarity output and compare the resulting patient groupings. The results are then presented to the clinicians for interpretation of the rankings and clusters of patients. Finally, we perform a statistical analysis to determine if our spatial measure is significantly correlated with post-treatment toxicity outcomes. We describe below in detail each component of this method.
Figure 1:

Pipeline detailing the steps and data flow of our presented methodology. After receiving the contrast-enhanced computed tomography (CECT) images from the clinicians, we construct a topological mapping of each patient’s involved nodes and the connections between them. The result matrices are used to compute similarity using a Tanimoto coefficient; hierarchical clustering is performed on the ranked patient scores to determine patient groups; statistical and visual analysis is performed on the groups to determine groups with higher toxicity outcome rates and validate the results.
2.2. Patient Cohort
Oropharyngeal cancer (OPC) patients who were treated at the MD Anderson Cancer Center between 2005 and 2013 were retrospectively reviewed under an approved IRB protocol. Out of the 644 eligible patients who had a pathologically proven OPC, either with a positive biopsy or a surgical excision and received treatment (i.e., radiotherapy +/− chemotherapy) with a curative intent, 582 patients had affected lymph nodes and were included in this study. Affected lymph node (LN) levels were collected from contrast enhanced computed tomography (CECT) diagnostic scans which took place at patients’ initial visit for staging and disease assessment. LN levels (retropharyngeal (RP), submental (Ia), submandibular (Ib), upper, medial and lower jugular (II, III, IV respectively) and level V a, b) were defined based on anatomical landmarks and were coded in relation to tumor position. Patients’ relevant demographic, clinical, and toxicity data (toxicity of interest were feeding tube and aspiration at six months) were retrieved from electronic medical records.
Table 1 shows the post-therapy side-effect counts and patient characteristics across the cohort. Of the 582 patients who underwent intensity-modulated radiotherapy, 163 patients suffered from either post-therapy dysphagia side-effects, with 95 (16.32%) patients reporting aspiration (breathing a foreign material to the airways, such as saliva) and 99 (17.01%) requiring a feeding tube six months after the end of radiotherapy treatment (Feeding Tube at 6 months).
Table 1:
Patient Characteristics and Post-therapy Side Effects
| Characteristics | N (%) |
|---|---|
| Post-therapy Side Effect | |
| Feeding tube at 6 mo. | 99 (17.01%) |
| Aspiration | 95 (16.32%) |
| No side effect | 388 (66.67%) |
| Gender | |
| Male | 512 (87.97%) |
| Female | 70 (12.03%) |
| T-category (T) | |
| Tx | 1 (0.17%) |
| Tis | 1 (0.17%) |
| T1 | 129 (22.16%) |
| T2 | 245 (42.10%) |
| T3 | 121 (20.79%) |
| T4 | 85 (14.61%) |
| N-category (N) | |
| N1 | 72 (12.37%) |
| N2 | 492 (84.54%) |
| N3 | 18 (3.09%) |
2.3. Topological Map
To this end, we first defined and constructed a novel 2D topological map over the LN levels, based on the consensus guidelines for the delineation of the head and neck [15], and using the left-right symmetry of the human head and neck and input from our clinician collaborators. Each cell in this topology (shown in gray in Figure 2 (right)) corresponds to an LN level in the human head and neck, based on the spatial location and local neighborhood of each level. Over this topology, we then defined a dual graph representation (shown in red in Figure 2 (right)), where each cell was represented as a node in an undirected graph, and edges were created between each pair of adjacent faces. Using this abstraction, a chain of involvement would follow the links between the adjacent faces; for example, the path connecting LN levels 2B-2A-3 corresponds to a lymph chain of involvement. We decided to place the Retropharyngeal (RP) LN, a LN group near the base of the skull, as a disconnected node in the graph (upper left) because metastasis to this group bears a poor prognosis to OPC patients and requires specialized treatment.
Figure 2:
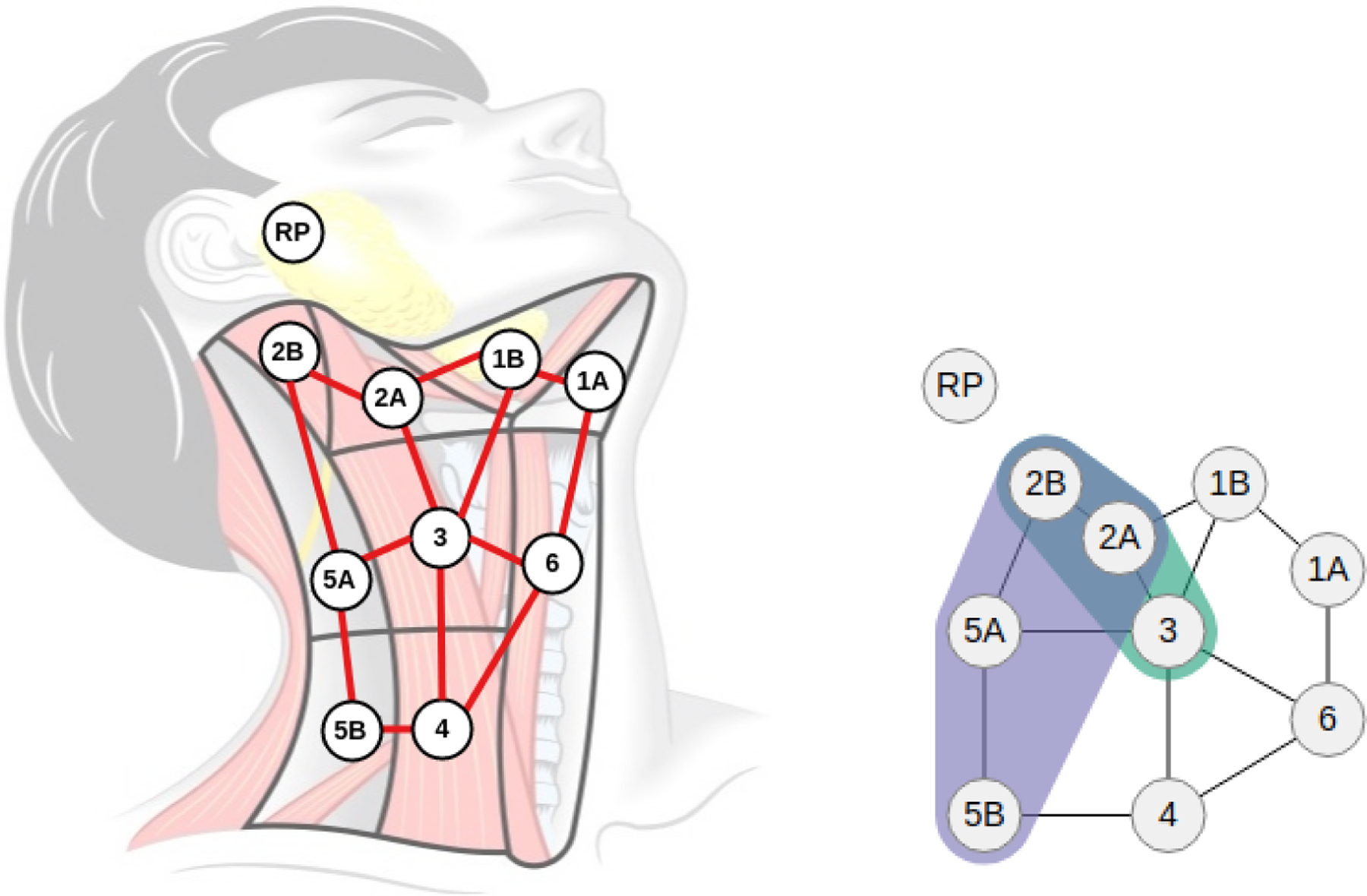
Topological map and graph representation. (Left) A novel topological map was constructed over the lymph node regions (shown in gray), overlaid with a dual graph representation (red) of the map showing the connectivity between the lymph node levels. The Retropharyngeal (RP) lymph nodes are a group of nodes near the base of the skull and are disconnected from the dual graph because their involvement requires specialized treatment. (Right) A compact visual representation was derived from the red graph representation to visually illustrate metastasis over both sides of the head and neck, using symmetry and color to distinguish between left (green), right (purple), and bilateral (blue) involvement.
Finally, to account for both sides of the head and neck, the graph was encoded as an adjacency matrix where the upper and lower triangles correspond to the left and right side, respectively; Figure 2 (left) illustrates metastasis over both sides of the head and neck. We initialized the matrix so that each row and column corresponded to one of the LN levels in the graph and assigned the LN levels (involved, not-involved) to each element along the diagonal, as follows:
| (1) |
where is the graph node corresponding to LN level , and is an edge between graph nodes and . Furthermore, edges between two involved LNs nodes were assigned a value of 1 in the matrix, according to the dual graph in Figure 2 (right). Since the RP LN level appears as a disconnected node on the graph, we handle it as a special case and encoded its status via two boolean flags related to the left and right involvement. Therefore, the resulting matrix has dimensions of 9×9, for the nine groups of lymph nodes that are connected in the graph representation.
For later analysis, we furthermore encode the laterality of nodal involvement for each patient using the position of their primary tumor: for patients with right-sided primary tumors, right-sided LNs are encoded as ipsilateral’ structures with tumor on the right; for patients with left-sided primary tumors, left-sided LNs are encoded as contralateral’ structures with tumor on the left.
2.4. Similarity Computation
We designed two similarity measures to investigate whether incorporating spatial information about the lymph node chains (i.e., the spatial location and neighborhood of the nodes involved) partitioned patients more meaningfully than only considering the level itself (i.e., non-spatial labels). Each measure was designed around the non-binary Tanimoto coefficient [16] using either: a) each patient’s LN level involvement status only (i.e., only the affected nodes in the graph representation) to measure the non-spatial similarity or b) a combination of status and pathways (affected nodes and edges in the graph representation) to measure the spatial similarity. We chose the Tanimoto coefficient based on its ability to produce the most ”meaningful” rankings for smaller, diverse graphs [17] when compared against subgraph [18] and substructure [19] measures.
2.4.1. Spatial and Non-Spatial Similarity measures
After constructing the adjacency matrices M (see Section 2.3), a vector was instantiated for each patient using the involvement status of their LN levels, as follows:
| (2) |
where is the vector element that corresponds to the involvement status of the left and right LN levels for patient . These values were extracted from the main diagonal of each patients’ matrix M. Then, to incorporate the spatial information into the measure, additional elements were appended to the resulting vector to encode the edges to and from the involved LNs as defined by the topological map. We enumerated every pair of involved LN levels connected by an edge as a bigram [20] label and added them to the involvement vector (Eq. 3). We choose not to enumerate further than the two-node combinations because of the small number of nodes in the graph – if all n-grams were enumerated, the similarity distance between patients would increase, and the similarity score for partial pattern matches would decrease. Furthermore, permutations of each bigram are considered once (e.g., bigram permutations between LN levels 2A and 2B, 2A-2B and 2B-2A, are considered as being the same).
Once enumerated, the bigrams on the left- and right-side were encoded into the vector:
| (3) |
where is the vector element that corresponds to the combined left- (L) and right-side (R) bigrams B of involved LNs and for patient . Overall, 13 bigrams weights were added to the vector to represent the 26 bigrams on both sides of head and neck.
Next, the cohort was ranked in pairwise-fashion by computing the Tanimoto coefficient between each of the newly constructed vectors:
| (4) |
where the function returns the Tanimoto coefficient between the vectors of patients and .
In order to examine the merits of the spatial measure, we likewise constructed a vector using only the involvement status of the LN level labels (Eq. 2) for the non-spatial (categorical) measure and again ranked the cohort in pairwise-fashion by computing a Tanimoto coefficient (Eq. 4).
To illustrate, in contrast, how these measures work, let us consider patients #14 and #245 from Figure 3 (top left). Patient #14 possesses a bilateral involvement between LN levels 2A, 2B, 3, 4, and 5B, and a unilateral involvement on one RP LN level, while Patient #245 possess a bilateral involvement between LN levels 2A, 2B, 3, and 4. Figure 4 illustrates the corresponding vectors that are constructed for the spatial (Fig. 4a) and non-spatial (Fig. 4b) measures using Eq. 2 and Eq. 3. Computing the Tanimoto coefficient (Eq. 4) between both sets of patient vectors results in a similarity score of 0.87 for the spatial measure and 0.76 for the non-spatial measure.
Figure 3:
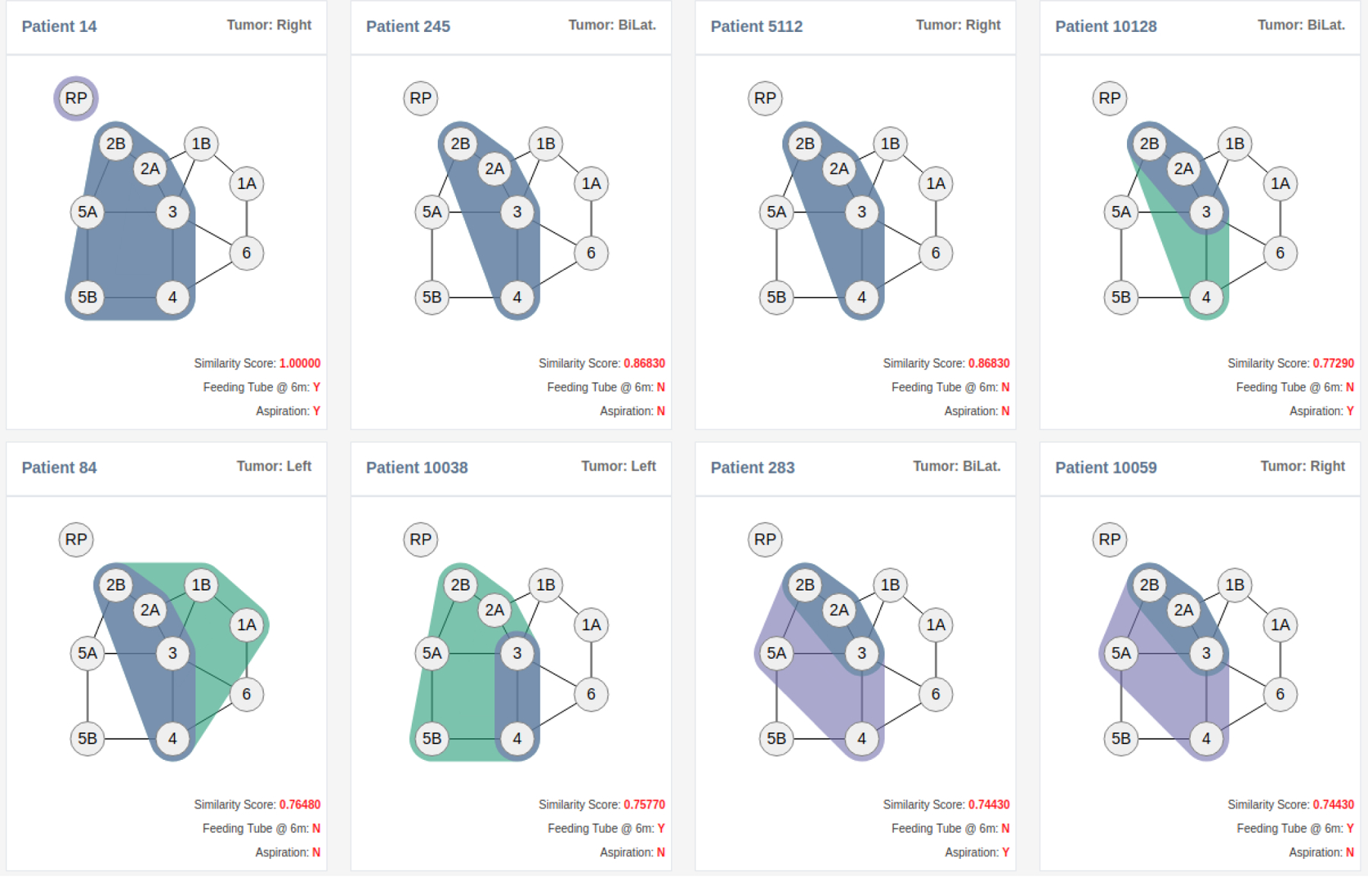
Example similarity ranking. Patient #14 (shown top left) is unique within the cohort, in that no other patient in the 582 patient cohort exhibits the same ten bilateral LN levels and RP involvement. Following Patient #14 are the seven closest-ranked patients (shown in left-right and top-down order) based on our spatial similarity measure. The two most similar patients share eight bilaterally involved LN levels; the next two have similar bilateral chains but either share fewer involved LN levels (Patient #10128) or possess two additional involved LN levels (Patient #84); while the last three similar patients have similar involvements but with significantly fewer LNs levels.
Figure 4:
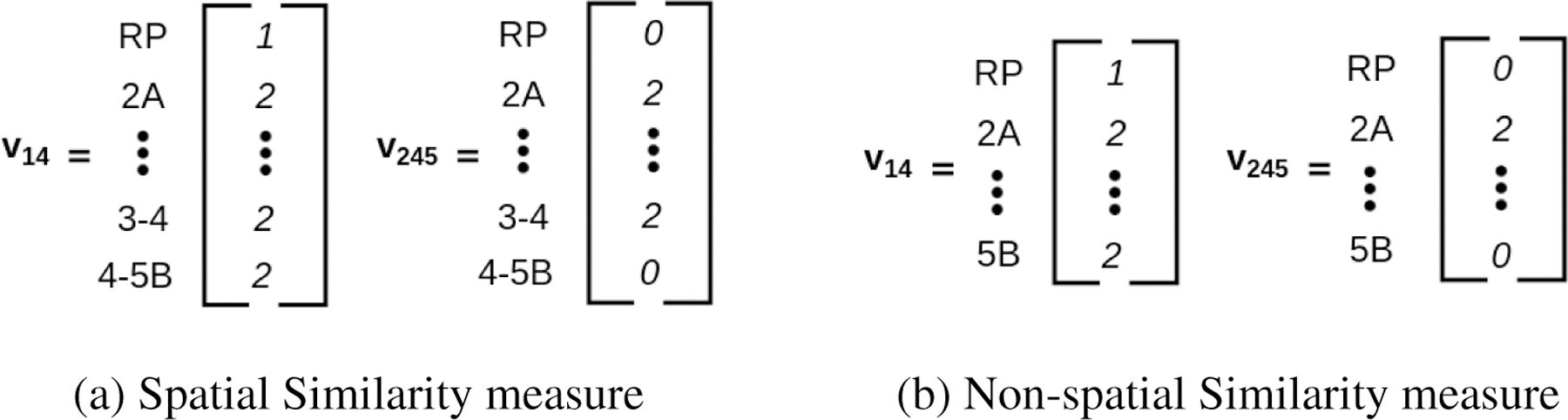
An illustration of the involvement vectors v constructed for Patient #14 and Patient #245. (a) The vectors v constructed for the spatial similarity measure (Eq. 2 and 3). (b) The vectors v constructed for the non-spatial measure (Eq. 2). Note that the spatial vectors (a) include bigrams while the non-spatial vectors (b) do not.
After ranking each patient, we construct two similarity matrices for the spatial () and non-spatial () measures, using the similarity scores between each patient pair in the cohort. The result of this step is a similarity matrix for each measure, with the number of rows/columns in each matrix equal to the number of patients in the repository. These matrices are then used in the hierarchical clustering analysis. The patient similarity was implemented using Python 2.7.
2.4.2. Hierarchical Clustering
Once a spatial measure is obtained, stepwise clustering techniques, such as hierarchical agglomerative clustering (HAC), are a quick yet practical approach to group similar subjects without a priori knowledge of the underlying data distribution [21, 22]. For example, recent studies [23, 24] have used hierarchical clustering to define anatomical subgroups of patients and test for clinical significance. Furthermore, Bruse et al. [24] investigated which distance/linkage combinations would provide the most ”clinical meaningfulness” when applied to a cohort of healthy and pathological aortic arches post-surgical repair patients. Their results show that hierarchical clustering using a Matthews correlation coefficient [25] combined with a weighted-linkage [26] function can yield significant patient subgroups based on spatial features. While we define our own similarity measure in this paper, we adopt the weighted-linkage function for determining the distance between the groups when performing our hierarchical clustering.
Following a bottom-up approach where each patient was first represented as a singleton cluster, we used a hierarchical agglomerative clustering (HAC) algorithm to iteratively combine clusters in a pairwise fashion, based on the computed similarity scores and linkage distance function. Based on the results from Bruse et al.’s study [24], we chose to use the weighted-linkage function [26] when determining the distance between clusters. At each iteration, the weighted-linkage function calculates the distance between every pair of clusters, and , by computing the arithmetic mean of distances (i.e., similarity scores) between all points in and . The algorithm then combines the ”nearest” (smallest distance) two clusters and continues iterating until only a single cluster remains.
The resulting clustering output for the spatial measure was further summarized in a dendrogram, a tree-like abstraction which illustrates how similar clusters were grouped (x-axis) and at what level/distance (y-axis) they merged. Finally, partitions of highly similar patients were formed by cutting the dendrogram at a specified level. This level was empirically determined based on the calculated expected values of toxicological outcomes, as described in the next section. Clustering was performed using the Matlab r2018a machine learning toolbox [27].
2.4.3. Statistical Analysis
Results from hierarchical clustering are commonly summarized using a dendrogram, a tree-like structure that displays how the elements are partitioned into groups based on the computed similarity and linkage functions [28, 29]. We construct such a dendrogram as described below.
The patient groupings were compared using the Rand Index [30] to determine the measure of similarity between the two measures’ clustering output. This measure quantifies the number of pairing agreements between two clusters into a frequency between 0.0 and 1.0, where a value of 0.0 indicates that the clusterings disagree on every pairing of samples and a value of 1.0 indicates that both clusterings are the same. Additionally, the Fisher’s exact test [31] was performed on both clusterings using two toxicity binary variables (Y/N) provided with the cohort: the post-treatment aspiration symptoms and feeding-tube necessity at six-months. We chose the more computationally-expensive Fisher’s exact test over the Chi-squared test because the high variation of nodal involvement patterns within the cohort yields small numbers of expected values within each group (e.g., for a clustering with clusters). While when using Chi-squared the number of expected values for each group should be at least 5, to guarantee the significance of the p-value (otherwise a small p-value could be in fact not significant), Fisher’s exact test works well on small numbers of samples. Using Fisher’s test, the most significant grouping was for as the number of clusters, and so both clusterings were cut at the level. Statistical tests were performed using the Matlab 2018a statistical toolbox [27].
2.4.4. Visual Analysis
To facilitate the assessment of our approach by clinicians, we have constructed an application to help interpret the abstracted nodal involvement of each patient in the cohort in the context of the computed similarity between patients. The visual interface (Figure 3) consists of small multiple representations of the abstract topological map (Section 2B) and control menus which allow a specific patient to be selected and viewed. To keep the representations compact, only one side of the head and neck was abstracted; color was used to distinguish between left (green), right (purple), and bilateral (blue) involvement. The visual interface wasimplemented using the web technologies JavaScript, HTML, CSS, and the D3 [32] Javascript library.
Additionally, we created an informational dendrogram (Figure 6 to convey the patient clustering and statistical analysis results to the collaborating radiation oncologists (co-authors CDF, HE, BE). Side-effect statistics are displayed atop each of the groups formed by the horizontal cut. The most frequently occurring involvement pattern for each cluster was determined based on the consensus nodal spread of each cluster along the x-axis (at ) and is shown in miniature at the bottom of each cluster along the bottom x-axis. The consensus was determined based on a two-thirds majority involvement status (i.e., a LN level is included in the graph if 67% of the patients share that involvement). The miniature consensus graphs are a variation of the previously described graph representations: solid and outlined nodes are consensus nodes, affected in more than 67% of the patients in that cluster, while square marks indicate nodes affected in less than 67% of the patients in that cluster. Unilateral involvement is shown by a single consensus graph, while bilateral involvement is shown by two stacked miniature graphs, one for each side of the head and neck. We note that the miniature consensus graphs do not provide a complete descriptor of cluster membership.
Figure 6:
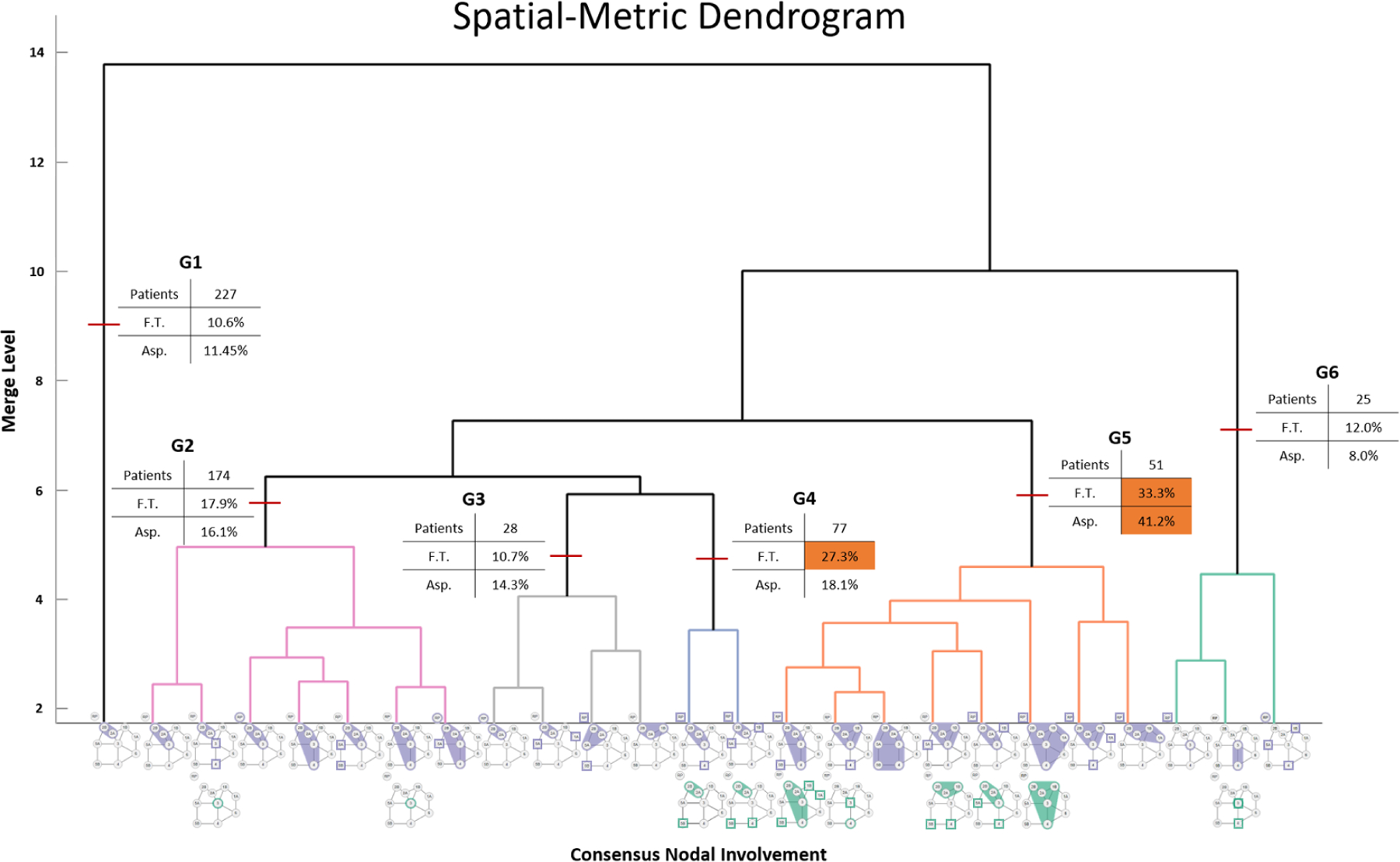
Dendrogram showing patient spatial groups (indicated by arrows) and toxicity correlates. A clear distinction between bilateral and unilateral nodal spread can be seen between groups G3 and G4, as well a divide between patients with and without LN level 3 involvement (G4 and G5). The consensus involvement (67%) of each group is shown along the x-axis.
3. Results
3.1. Spatial vs Categorical Node Patient Categorization
Our approach was able to successfully discriminate patients based on spatial involvement in cases where the categorical approach failed. For example, the spatial measure was able to discriminate between patients with bilateral spread and patients with unilateral node involvement by placing them into separate cohorts. The spatial measure also discriminated between RP node involvement versus no involvement, regardless of pattern spread complexity. Consequently, this approach allowed for binning of patients in cohorts that were deemed by clinicians and end-users (co-authors CDF, HE, BE) significantly more informative than categorical binning.
Figure 5 shows a representative example of the value of spatial-measure. Shown are two patients that have drastically geometrically different LN level involvements. Using clusters, these patients are erroneously binned together under the categorical measure (Fig. 5, bottom right), while our spatial approach successfully discriminates between them (Fig. 5, bottom left). In particular, Patient A possesses a bilateral lymphatic nodal spread as well as a LN level 3 involvement. Involvement of level 3 implies potential radiation dose to laryngeal structures and is thus a potentially meaningful correlate of radiation-associated sequelae [33]. Likewise, RP node positivity discriminates dose to superior pharyngeal constrictor which is atypical and has the potential for specific toxicity discrimination [34]. In the clinicians’ assessment, these are important distinctions, given prior data that shows differential swallowing toxicity as a function of superior pharyngeal constrictor (SPC) versus cricopharyngeus muscles [35, 36].
Figure 5:
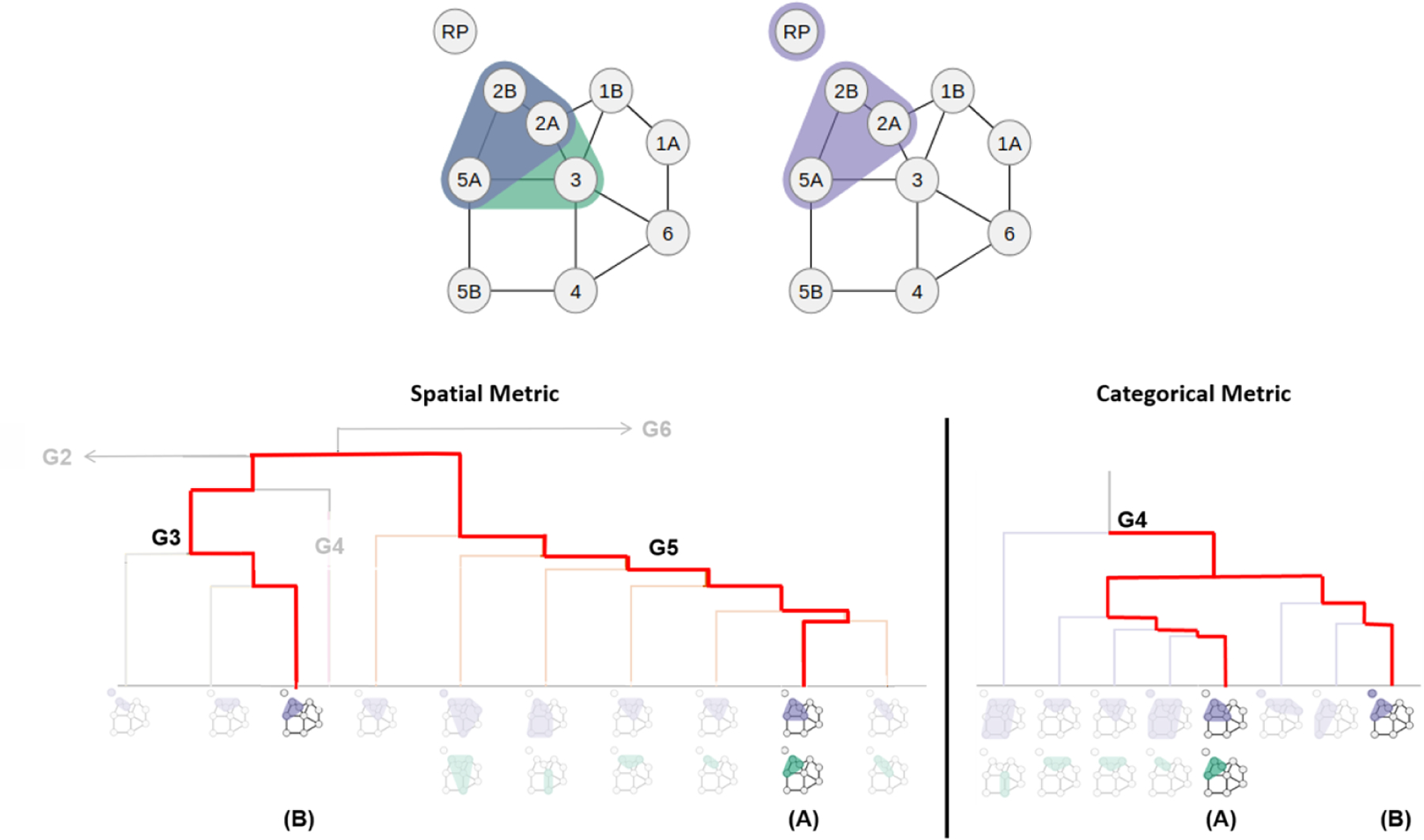
Two subjects with different groupings based on the similarity measure. Patient A (top left) possesses a bilateral nodal spread with LN level 3 involvement while Patient B (top right) only possesses a unilateral nodal spread with LN level 3 involvement. Because the spatial measure uses the geometrically different nodal involvement, it separates Patient A and B into the two main clusters, G3 and G5 (bottom left). In contrast, the categorical measure combines the two patients under the same main cluster, G4 (bottom right).
In the spatial measure, Patient A was also clustered together with other patients that have node 3 involvement, while Patient B was clustered together with no other patients that have node 3 involvement. Conversely, Patient B was primarily clustered together with patients with RP involvement (67% with RP involvement), while Patient A was not (16% with RP involvement). However, the RP partitioning may have been more related to the bilaterality of nodal involvement.
3.2. Domain Expert Feedback
Qualitative feedback from repeated evaluation with our collaborating clinicians emphasized the usefulness of this approach. When presented with the informational dendrogram (Fig. 6, one clinician stated that he felt confident he could take the visualization back to his clinic that day and use it when describing the potential outcome risks alongside proposed treatment plans to his patients. In addition to comparing patients of the cohort, the clinicians also identified several patients whose LN levels had been previously mislabeled in the dataset due to segmentation or data processing pipeline errors.
During the evaluation process, the clinicians noted that it is common practice to delineate patient groups based on bilateral involvements and the nodal spread between LN levels 2 and 3. Of the two approaches to group patients based on their lymphatic nodal spread, the clinicians felt that the spatial similarity measure, which inherently separated patients between uni- and bilateral involvements as well as the LN level 2 and 3 nodal spread, most closely represented what is expected in a clinical setting.
3.3. Hierarchical Clustering Analysis
Figure 6 displays the informational dendrogram resulting from patient binning using the spatial measure. In the dendrogram, clusters of highly similar patients are represented along the x-axis using the visual representation defined in Section 2 D5 to capture the consensus nodal involvement of the cluster.
In the dendrogram (Fig. 6), we identified two distinct groups by focusing on the nodal involvement across the x-axis of each group. First, the cut that separated groups G2-G4 from G5, near merge level 7, also partitioned the cohort according to the involvement laterality: groups G1-G3 consisted of patients with unilateral involvement, groups G4 and G5 of patients with bilateral involvement, and group G6 of patients with unique (singular to the cohort) nodal involvement. Next, the cut that separated groups G3 and G4, near merge level 5, also discriminated based on LN level 3 involvement, creating another clear distinction between groups with (G2, G4, G5) and without (G1, G3) the involved lymph node.
In contrast, the involvement status of LN level 3 occurred throughout each of the six groups generated through the non-spatial/categorical approach. Furthermore, four of the six groups generated through the categorical approach contained patients with bilateral involvement. Therefore, the categorical approach fails to capture a meaningful demarcation between LN level 2 and level 3 involvement, as well as patterns of bilateral involvement.
Measure Agreement:
In terms of agreement between the spatial and categorical approaches, we identified two identical groups between the spatial- and categorical-approach clusterings (G1 and G6). While these two groups represent 43% (252 patients) of the cohort, the consensus nodal involvements in each are also the simplest patterns in the cohort. For example, all 227 patients in both G1 groups possess a unilateral LN level 2 involvement. G6 groups together all the 25 unique LN level involvement patients in the cohort. Outside of these two groups, the categorical-approach did not have the discriminatory value of the spatial approach advocated in this paper.
After removing the two groups G1 and G6 from each of the clusterings, the computed Rand index between the spatial and the categorical results was a similarity measure of 0.55. This value indicates that outside of the two groups G1 and G6 of simple patterns, the two approaches are significantly dissimilar in terms of how they group the patients within the cohort.
3.4. Statistical Analysis Results
Statistical significance is reported assuming a level of , based on the occurrence of the toxicity symptoms within the groups. Table 2 shows the toxicity outcomes distributions of the four spatial-measure groups with the highest incidence rates. In terms of the toxicological outcomes, there was a significant difference in the rate of feeding tube (FT) placement among the spatial-measure groups (). The measure was able to identify two cohorts (G4, G5) that had almost double the outcome incidence compared to the other four (G1-G3, G6). G4 and G5 had FT placement rates of 27.3% and 33.3%, respectively, while G3-G6 had rates less than or equal to 17.9%. Additionally, the spatial measure identified one group (G5) with more than double the aspiration rate (41.2%) compared to the other five groups.
Table 2:
Toxicity Outcome Distributions of the Spatial-Metric Groups
| Feeding Tube Placement | Aspiration | ||||
|---|---|---|---|---|---|
| Group | Patients | W/ outcome | % w/ outcome | W/ outcome | % w/ outcome |
| G2 | 174 | 31 | 17.9% | 28 | 16.1% |
| G3 | 28 | 3 | 10.7% | 4 | 14.3% |
| G4 | 77 | 21 | 27.3% | 14 | 18.1% |
| G5 | 51 | 17 | 33.3% | 21 | 41.2% |
3.5. Performance
We performed all computation on a 4.0 GHz Quad Core i7 machine with 32G of RAM. The average runtime to compute the similarity on the cohort of 582 patients was approximately 90 seconds per similarity measure. The hierarchical clustering and statistical analysis averaged 45 seconds to partition the patients into groups, compute the Chi-squared and Fisher’s exact test, and output the statistics and dendrogram per measure.
4. Discussion
Our analysis of results and the domain expert feedback support our claim that spatial correlates can provide insight into therapy strategies where treatment depends on the spatial patterns of disease, such as intensity-modulated radiation therapy for HNSCC. The spatial method we introduce captures and ranks patients correctly and more clinically accurately compared to the categorical approach. Furthermore, we have shown that when combined with hierarchical clustering, our novel graph-based similarity measure partitions an OPC patient cohort into clinically meaningful groups. In particular, we have shown that our spatial approach can capture groups of patients more susceptible to dysphagia toxicity (aspiration and feeding tube) based on the pattern of nodal involvement.
In terms of limitations, our similarity measure captures but a few of the many features that can be used in therapy response-driven decisions and predictive outcome models. While toxicity is heavily predicated on the relationship between the spatial location of involvement and the administered radiation dose, many therapy outcomes and side-effects result from other non-spatial features. A direction of future research, while beyond the scope of this work, would be to combine our spatial similarity scores with other relevant non-spatial features, such as T-Category and patient age [37], to create a more semantically meaningful view of the patient regarding treatment response and survival. Likewise, our approach notes but does not explicitly incorporate into the similarity measure, the tumor location with respect to the lymph-structures (which is typically upstream in the head and neck). Other clinical applications may feature higher variability in the tumor location, and in those cases, the location of the tumor may need to be explicitly incorporated into the similarity measure.
Next, we note that our evaluation was limited to one moderately sized cohort of patients. Many of these patients were referrals whose data was collected outside of the treatment facility. As a result, a significant amount of time spent working with this cohort was spent cleansing the data of malformed classifications. Furthermore, our expert feedback was limited to radiation oncology clinicians who were all members of the same clinical lab. Last but not least, our approach is constructed around a 2D graph representation that takes advantage of the symmetry about one of the principal axes of the structural model. While this approach is ideal for domains where symmetry is inherently built into the model (e.g., symmetry about the head and neck), it may also be easily extended to non-symmetric situations. In contrast, extending this approach to situations where 3D location is important would require modifications to the underlying graph representations and similarity measure.
5. Conclusion
In conclusion, we have introduced and evaluated a novel methodology to compare head and neck cancer patients based on their spatial patterns of LN involvement. Our approach demonstrates how the spatial location and neighborhood of the head and neck LN levels can be abstracted to a 2D topological representation, which can then be used to quantify similarity within a cohort of patients based on their extracted spatial attributes. This work also contributes two novel visual representations that provide clinicians with response-based correlates within the ranked cohort. Statistical analysis and expert feedback indicate that our spatial methodology can be useful in clinical settings. Furthermore, we show that our spatial methodology provides superior patient similarity and groupings in terms of clinical relevance when compared to the categorical approach. The presented methodology may find application beyond the 2D head and neck lymph node analysis in other domains that feature topological structures.
Few, if any, studies have attempted to use spatial-similarity techniques to compare post-diagnosis patients and ”close the gap between mere data and useful knowledge, as desired in current Precision Medicine” [24]. Moving forward, we aim to integrate our proposed measure into a risk-prediction model. We believe that when applied to spatially-driven diseases such as OPC, approaches such as ours can play a vital role in fulfilling precision medicine’s goal of maximizing the effectiveness of each patient’s treatment through customized care [38].
Acknowledgments
This work is supported by the US National Institutes of Health, through awards NIH NCI-R01CA214825, NIH NCI-R01CA2251, and NIH NLM-R01LM012527.
References
- [1].N. C. Institute, Oral complications of chemotherapy and head/neck radiation (2018). URL http://www.cancer.gov/about-cancer/treatment/
- [2].Brandizzi D, Gandolfo M, Lucia Velazco M, Luis Cabrini R, Lanfranchi H, Clinical features and evolution of oral cancer: A study of 274 cases in buenos aires, argentina, Medicina oral, patologa oral y ciruga bucal (2008) E544–E548. [PubMed]
- [3].Stewart BW, Greim H, Shuker D, Kauppinen T, Defence of iarc monographs, Lancet (2003) 1300–. [DOI] [PubMed]
- [4].Zhang L, S Garden A, Lo J, Kian Ang K, et al. Multiple regions-of-interest analysis of setup uncertainties for head-and-neck cancer radiotherapy, Int. J. Rad. Onc., Bio., & Phys (2006) 1559–1569. [DOI] [PubMed]
- [5].Nakata A, Tateoka K, Fujimoto K, Saito Y, et al. The reproducibility of patient setup for head and neck cancers treated with image-guided and intensity-modulated radiation therapies using thermoplastic immobilization device, Int. J. Med, Phys., Clin. Eng. & Rad. Onc (2013) 117–124.
- [6].Timar J, Csuka O, Remenr E, Rpssy G, Ksler M, Progression of head and neck squamous cell cancer., Cancer Metastasis Rev (2005) 107–127. [DOI] [PubMed]
- [7].Cartmill B, Cornwell P, Ward E, Davidson W, Nund R, et al. Emerging understanding of dosimetric factors impacting on dysphagia and nutrition following radiotherapy for oropharyngeal cancer, Head & Neck (2013) 1211–1219. [DOI] [PubMed]
- [8].Widanagamaachchi W, Klacansky P, Kolla H, Bhagatwala A, Chen J, Pascucci V, Bremer PT, Tracking features in embedded surfaces: Understanding extinction in turbulent combustion, in: Proc. IEEE 5th Symp. on Large Data Anal. Vis. (LDAV), 2015, pp. 9–16.
- [9].Wenskovitch J, Harris L, Tapia J, Faeder J, Marai G, Mosbie: A tool for comparison and analysis of rule-based biochemical models, BMC Bioinform. J (2014) 1–22. [DOI] [PMC free article] [PubMed]
- [10].Teng C-C, Shapiro L, Kalet IJ, Rutter C, Nurani R, Head and neck cancer patient similarity based on anatomical structural geometry, Proc. IEEE Int. Symp. Biomed. Imag (2007) 1140–1143.
- [11].Yener B, Gunduz C, Gultekin SH, The cell graphs of cancer, Bioinform (2004) i145–i151. [DOI] [PubMed]
- [12].Gurcan MN, Boucheron LE, Can A, Madabhushi A, Rajpoot NM, Yener B, Histopathological image analysis: A review, IEEE Reviews Biomed. Eng (2009) 147–171. [DOI] [PMC free article] [PubMed]
- [13].Petrakis EGM, Faloutsos C, Similarity searching in medical image databases, IEEE Trans. Knowl. Data Eng. (TKDE) (1997) 435–447.
- [14].Kumar A, Kim J, Cai W, Fulham M, Feng D, Content-based medical image retrieval: A survey of applications to multidimensional and multimodality data, J. of Digital Imaging (2013) 1025–1039. [DOI] [PMC free article] [PubMed]
- [15].Gregoire V, Ang K, Budach W, Grau C, et al. Delineation of the neck node levels for head and neck tumors: A 2013 update. dahanca, eortc, hknpcsg, ncic ctg, ncri, rtog, trog consensus guidelines, Radiotherapy & Oncology (2014) 172–181. [DOI] [PubMed]
- [16].Tanimoto TT, An elementary mathematical theory of classification and prediction, Tin. Business Machines Corp, 1958.
- [17].Bajusz D, Rácz A, Héberger K, Why is tanimoto index an appropriate choice for fingerprint-based similarity calculations?, J. Cheminformatics (2015) 20–. [DOI] [PMC free article] [PubMed]
- [18].Klinger S, Austin J, Weighted superstructures for chemical similarity searching, in: Proc. 9th Joint Conf. Info. Sci, 2006, pp. 1–19.
- [19].Yan X, Yu PS, Han J, Substructure similarity search in graph databases, in: Proc. ACM SIGMOD Int. Conf. Mana. Data, 2005, pp. 766–777.
- [20].Tomovi A, Janii P, Keelj V, n-gram-based classification and unsupervised hierarchical clustering of genome sequences, Comp. Methods & Programs Biomed (2006) 137–153. [DOI] [PubMed]
- [21].King B, Step-wise clustering procedures, J. Amer. Stat. Assoc (1967) 86–101.
- [22].Murtagh F, A survey of recent advances in hierarchical clustering algorithms, Comp. J (1983) 354–359.
- [23].Dong A, Honnorat N, Gaonkar B, Davatzikos C, Chimera: Clustering of heterogeneous disease effects via distribution matching of imaging patterns, IEEE Trans. on Med. Im. (TMI) (2016) 612–621. [DOI] [PMC free article] [PubMed]
- [24].Bruse J, Zuluaga M, Khushnood A, Mcleod K, et al. Image data: Metrics analysis for hierarchical clustering applied to healthy and pathological aortic arches, IEEE Trans. Biomed. Eng. (TBME) (2017) 2373–2383. [DOI] [PubMed]
- [25].Baldi P, Brunak S, Chauvin Y, Andersen C, Nielsen H, Assessing the accuracy of prediction algorithms for classification: An overview, Oxford Bioinform (2000) 412–24. [DOI] [PubMed]
- [26].Sokal RR, Michener CD, A statistical method for evaluating systematic relationships, Univ. Kansas Sci. Bulletin (1958) 1409–1438.
- [27].M. Inc., Matlab and statistics toolbox release 2018a (2018).
- [28].Maimon OZ, Rokach L, Data mining and knowledge discovery handbook, Springer, 2010. [Google Scholar]
- [29].Manning CD, Raghavan P, Schtze H, Introduction to Information Retrieval, Cambridge Univ. Press, 2018. [Google Scholar]
- [30].Rand W, Objective criteria for the evaluation of clustering methods, J. Amer. Stat. Assoc (1971) 846–850.
- [31].Fisher RA, Statistical methods for research workers, Kalpaz, 2017.
- [32].Bostock M, Ogievetsky V, Heer J, D3 data-driven documents, IEEE Trans. Vis. Comp. Graph. (TVCG) (2011) 2301–2309. [DOI] [PubMed]
- [33].Rancati T, Schwarz M, Allen A, Feng F, Popovtzer A, et al. Radiation dose-volume effects in the larynx and pharynx, Int. J. Rad. Onc., Bio, & Phys (2010) S64–S69. [DOI] [PMC free article] [PubMed]
- [34].Spencer CR, Gay HA, Haughey BH, et al. Eliminating radiotherapy to the contralateral retropharyngeal and high level ii lymph nodes in head and neck squamous cell carcinoma is safe and improves quality of life, Cancer (2014) 3994–4002. [DOI] [PMC free article] [PubMed]
- [35].Dale T, Hutcheson K, Mohamed A, Lewin JS, et al. Beyond mean pharyngeal constrictor dose for beam path toxicity in non-target swallowing muscles: Dosevolume correlates of chronic radiation-associated dysphagia (rad) after oropharyngeal intensity modulated radiotherapy, Radiotherapy & Oncology (2016) 304–314. [DOI] [PMC free article] [PubMed]
- [36].Kamal M, Mohamed AS, Volpe S, et al. Radiotherapy dosevolume parameters predict videofluoroscopy-detected dysphagia per digest after imrt for oropharyngeal cancer: Results of a prospective registry, Radiotherapy & Oncology (2018) 442–451. [DOI] [PMC free article] [PubMed]
- [37].Mohamed ASR, Hobbs BP, Hutcheson K. A. e. a., Dose-volume correlates of mandibular osteoradionecrosis in oropharynx cancer patients receiving intensity-modulated radiotherapy: Results from a case-matched comparison, Radiotherapy & Oncology (2017) 232–239. [DOI] [PMC free article] [PubMed]
- [38].Fernald GH, Capriotti E, Karczewski KJ, Daneshjou R, Altman RB, Bioinformatics challenges for personalized medicine, Bioinform (2011) 1741–1748. [DOI] [PMC free article] [PubMed]


