Neural population geometry: An approach for understanding biological and artificial neural networks

Abstract

Advances in experimental neuroscience have transformed our ability to explore the structure and function of neural circuits. At the same time, advances in machine learning have unleashed the remarkable computational power of artificial neural networks (ANNs). While these two fields have different tools and applications, they present a similar challenge: namely, understanding how information is embedded and processed through high-dimensional representations to solve complex tasks. One approach to addressing this challenge is to utilize mathematical and computational tools to analyze the geometry of these high-dimensional representations, i.e., neural population geometry. We review examples of geometrical approaches providing insight into the function of biological and artificial neural networks: representation untangling in perception, a geometric theory of classification capacity, disentanglement, and abstraction in cognitive systems, topological representations underlying cognitive maps, dynamic untangling in motor systems, and a dynamical approach to cognition. Together, these findings illustrate an exciting trend at the intersection of machine learning, neuroscience, and geometry, in which neural population geometry provides a useful population-level mechanistic descriptor underlying task implementation. Importantly, geometric descriptions are applicable across sensory modalities, brain regions, network architectures, and timescales. Thus, neural population geometry has the potential to unify our understanding of structure and function in biological and artificial neural networks, bridging the gap between single neurons, population activities, and behavior.

Introduction

Neural circuits and artificial neural networks (ANNs) process information by constructing and manipulating highly distributed representations [1–4]. Patterns of activity in these systems, across either neurons or units, correspond to manifold-like representations (Box 1) — lines [5], surfaces [6,7], trajectories [8–10], subspaces [11], and clouds of points [12,13] — in a high dimensional ‘neural state space’, where coordinates represent the activities of individual neurons or units. Approaches focused on studying geometric properties of these manifolds are becoming more widely used as advances in experimental neuroscience expand our ability to probe large neural populations [14], and advances in ANNs [15,16] introduce new challenges of interpretation.

Box 1. Clarifications on the use of the term ‘manifold’ in neuroscience.

‘Manifold’ means a topological space that locally resembles a Euclidean space in mathematics. The term ‘neural manifold’ has been used to refer to a broad set of geometric structures in neural populati’on activity underlying various cognitive tasks, although these population structures in real neural data are often no longer technically ‘manifolds’ in a mathematical sense, mainly due to the presence of neural noise and but also often due to the sparse input sampling.

Object manifolds [6,7,13] or perceptual manifolds [5,12] refer to sensory neurons’ population structures that arise as a result of identitypreserving variabilities in the input stimulus space. The term neural manifold has been used more broadly to refer to low-dimensional subspaces underlying population activities embedded in high-dimensional neural state space, not only in (aforementioned) sensory brain regions but also in motor and cognitive brain regions [11,26,27].

Point-cloud manifolds: a point-cloud with an underlying manifold structure, where the typical source of the underlying manifold variability is stimulus variability (e.g., orientation or position) or neuronal variability (e.g., the shape of a neuron’s tuning curve). Despite the implied underlying manifold structure, the data often manifest themselves as point clouds due to the sparse sampling of data from the available range of the stimulus/neuronal variabilities and/or due to noise (input noise or stochastic neuronal noise).

Neural population geometry refers to the configurations of these neural manifolds embedded in ambient neural state space.

In neuroscience, driven by advances in recording techniques, mainstream analysis tools have subsequently transitioned from single-neuron approaches [17,18] to population-level frameworks [1–3,19,20] that quantify and decode information represented across many neurons. Challenges arise when we consider large neural populations involved in complex tasks, as neurons often show mixed selectivity, i.e., selectivity to multiple coding variables [21], and real-world tasks often require robustness to nontrivial variability [6], precluding simplistic tuning-based analyses. The geometric analysis provides an approach suitable for addressing these challenges.

Since a number of large-scale task-optimized ANNs have outperformed traditional neuronal models in accounting for neural activity [22,23], ANNs have become a promising model system for studying neural circuits. One often-heard objection to the use of ANNs in modeling neural circuits is that ANNs merely replace one complicated system with an equally complicated system [24]. Indeed, the challenges in interpreting high-dimensional ANNs, containing millions of parameters and neural populations are shared [25]. This highlights the need for powerful population-level tools that reveal mechanisms underlying neural network function. From this perspective, ANNs can serve as a testbed for developing population-level analysis techniques, such as geometric approaches, even if they are ultimately aimed at neuroscience applications.

In this review, we highlight important examples of how geometrical techniques and the insights they provide have aided the understanding of biological and artificial neural networks. We begin with an overview of recent theoretical developments linking neural population geometry to categorization capacity. We then discuss theoretical work on characterizing representational geometries across tasks and modalities, such as recognition and prediction in the sensory domain (perceptual untangling) and abstraction in the cognitive domain (disentanglement). We also discuss sensory or behavioral state transitions in the head direction system and hippocampus (topology discovery). Finally, we provide examples for which dynamical analysis of neural population geometry sheds light on representations in motor control (dynamic untangling) and complex cognitive tasks such as Bayesian inference.

The geometry of perception and decision making

Perceptual untangling

It has been hypothesized that the role of ventral visual stream processing is to transform the representations of visual objects so that they become ‘untangled’, meaning that they are transformed into a form that is linearly separable [6,7] (Figure 1a). The concept of linear separability goes back to the early days of ANNs [28,29], and it still plays a central role in the analysis of neural population geometry. A task in which a subject must divide a large set of stimuli into two categories requires the separation of the neural activity patterns evoked by these stimuli into two sets corresponding to the two categories. We know from machine learning that this discriminability can be achieved easily if a hyperplane can separate the two sets of activities. Such a representation is called linearly separable. If, instead, the separating surface must be curved, dividing the two sets of neural population activities is more difficult. This insight is central to a number of the approaches we discuss.

Figure 1.

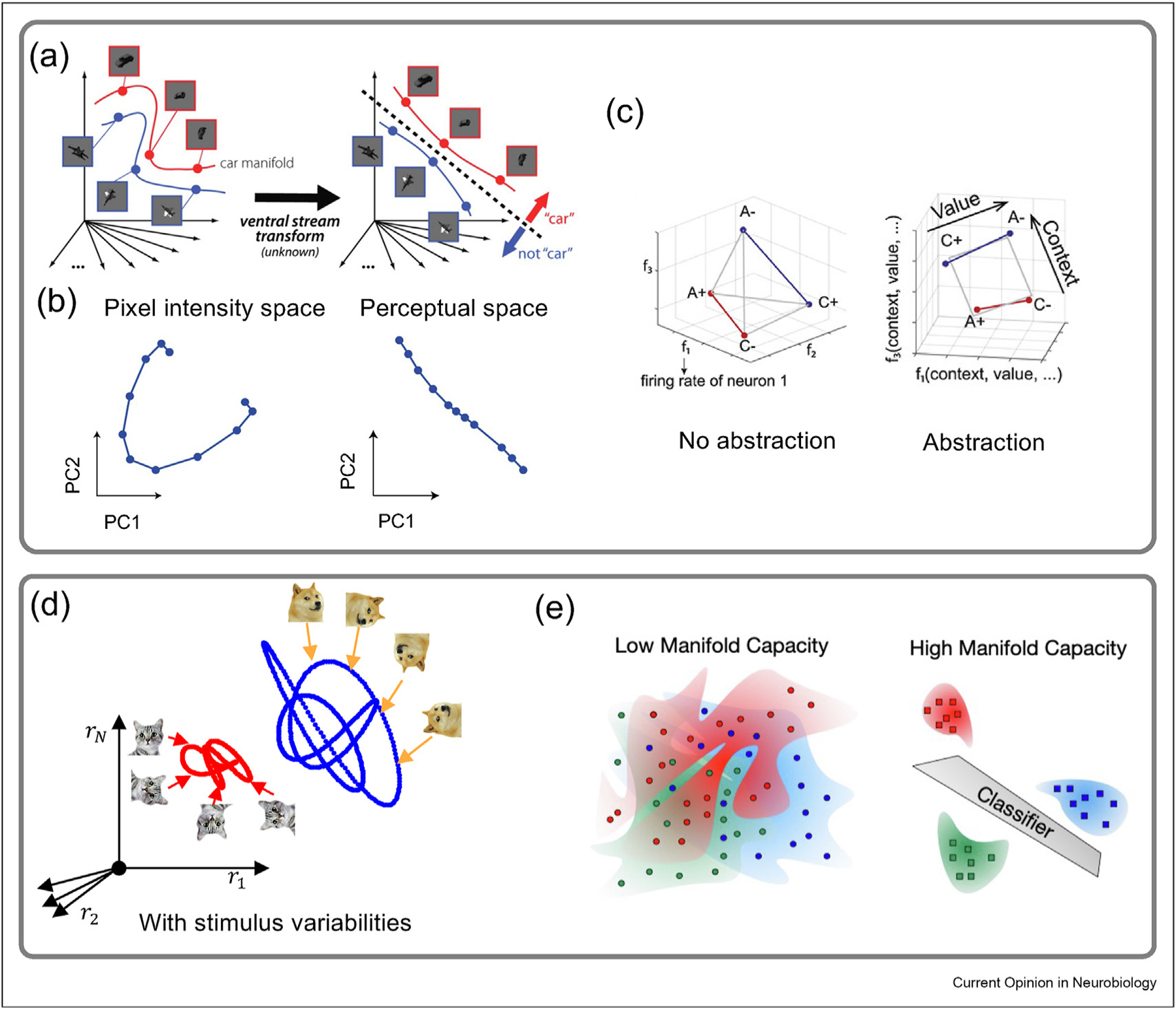
(a) Representation straightening for invariant object recognition (b) Temporal straightening for temporal natural video sequences. (c) Geometry of Abstraction. Representations encoding abstraction (i.e., cross-conditional generalization) show geometry where coding directions can be rotated or translated between conditions, known as parallelism (Right). (d) Neural manifolds arise as a result of stimulus variability. Population responses to two object classes (dog vs. cat) in the presence of the stimulus variability (orientation) give rise to two object manifolds. Invariant object recognition becomes the problem of classifying between two object manifolds. Axes represent the firing rates of neurons. (e) Manifold capacity is high if object manifolds are well separated and low when object manifolds are entangled in neural state space. Part (a) adapted from Ref. [7]. Part (b) adapted from Ref. [30]. Part (c) adapted from Ref. [31]. Part (e) adapted from Ref. [32].

The idea of untangling has been extended into the time domain [7,30]. In this case, neural population activity corresponds to a trajectory through neural state space. These studies posit that, at a given point in time, it is easier to predict future neural activity if this trajectory is straight than if it is convoluted. This led to the hypothesis that visual processing also serves to straighten temporal response trajectories [7]. This ‘temporal straightening hypothesis’ has been tested by measuring the curvature of the neural trajectory of responses to natural videos in neural network models and human perceptual space [30] (Figure 1b). Straightening of response trajectories occurs when natural video sequences, but not artificial video sequences, are presented.

The geometry of abstraction

The principle of linear separability can also provide insight into more complex tasks beyond categorization. Consider a task in which two sets of stimulus-response pairings, set A and set B, must be learned. The task involves uncued ‘context’ switches between the use of set A and set B. An efficient solution is to represent the stimulus-response pairings in such a way that a transition between contexts can be accomplished by the rotation and/or translation of a dividing surface in the neural state space (Figure 1c). Recordings from the prefrontal cortex, hippocampus, and results from task-trained neural networks [31] all indicate the use of ‘disentangled’ representation, quantified by a geometric measure called the parallelism score. These studies provide direct neural evidence on how two different contexts are involved in such a task, and thus, probe the level of abstraction and type of strategy being used by the animals and machines. An important idea here, which will reappear in another context in the next section, is that while abstraction is achieved, the representation does not simply discard information about other variables [31].

Extensions from points to manifolds

In the research covered thus far, neural population activity during a task has been considered to be a point (in the case of static stimuli) or a one-dimensional trajectory (in the case of time-dependent stimuli) in the neural state space. However, the same stimulus shown repeatedly will not result in the same point in state space being occupied; instead, neuronal variability will cause the points from different trials to jitter. The result is that each stimulus corresponds not to a point but to a point cloud whose size and shape depend on the amplitude and form of the neuronal variability. Furthermore, the presence of other sources of variability introduces the need to cluster responses into point-cloud manifolds (Box 1). For example, if we want to distinguish dogs from cats, we may want to group the responses to images for different viewing angles, sizes, and animal breeds into one dog manifold and one cat manifold (Figure 1d). In this perspective, the problem of invariant object discrimination becomes that of separating neural manifolds [12].

Determining the mechanism behind invariant object discrimination requires us to decipher how the structure across different instances of the same object is processed by the layers of the sensory hierarchy. This raises the question of how the structure of neural object manifolds is related to the separability of object categories. Theoretical work based on concepts from statistical physics has shown that linear separability of object manifolds, as defined by the object manifold capacity [12], a generalization of perceptron capacity, can be formally connected to the geometric properties of object manifolds such as their dimension, radius and correlation structure [12,13,33].

One result of this work is that the same level of linear separability can be achieved across different combinations of geometrical properties. For example, combinations of large/small dimensionality and small/large size of object manifolds can lead to similar capacities because there is a tradeoff between the dimensionality and the radius of these manifolds. The untangling hypothesis can be extended to the idea that visual processing aims to provide well-separated manifolds that provide information about object identity while maintaining other image-related variables such as pose, position, and scale (Figure 1a,d).

In this framework, the notion of manifold capacity has several interpretations. While the manifold capacity measures the linear separability of object classes, it also measures the storage capacity of object classes in a given representation (i.e., the maximum number of object classes that can be read out linearly). Small manifold dimensions and radii predict high manifold capacity and vice versa (Figure 1e). This theory has been used to show how categorical information emerges across layer hierarchy as a result of geometrical changes in ANNs implementing visual object recognition [13], speech recognition [32], and language prediction tasks [34]. These ANN models are known to have a high neural predictivity with corresponding brain regions in the macaque visual cortex [22,35], human auditory cortex [36], and language processing regions [37]. In addition, promising preliminary results in mouse and macaque visual cortex [38,39] show that this theory can also be used directly to characterize neural data. These examples demonstrate how the untangling hypothesis has motivated advancements in new theoretical frameworks, such as manifold capacity theory, allowing for a more refined geometric analysis of representations in biological and artificial neural networks.

The intrinsic geometry of representation

Another approach to understanding high-dimensional neural activity focuses on the observation that the neural activity lies on lower-dimensional subspaces, i.e., neural manifolds (Box 1). For understanding the structure of these neural manifolds, many recent studies have employed various dimensionality reduction techniques to the analysis of neural data. Dimensional reduction refers to manipulations used to identify the shape, location, and orientation of neural data within the neural state space. Widely used linear methods such as principal components analysis (PCA) provide a Cartesian coordinate basis describing subspaces in which the data lie. It is also useful to determine the geometric properties that characterize the intrinsic space defined by the data, which, in general, requires nonlinear dimensionality reduction methods. To be concrete, consider the responses of a population of neurons to a set of stimuli described by two variables (disregarding neural noise for simplicity). We might assume that these data can be described as a function of these two stimulus variables. If this is indeed the case, the responses lie on a two-dimensional surface, but that surface is not necessarily a flat plane. In fact, the surface might be convoluted and lie in a considerably higher dimension. PCA will find this higher dimensional embedding space, whereas nonlinear methods can find the curved surface itself.

A large number of nonlinear dimensionality reduction methods are available, including Isomap [40], LLE [41], tSNE [42], MDS [43], PHATE [44] and UMAP [45]. Although powerful, these nonlinear methods assume that underlying manifolds are topologically simple and can fail to capture the neural manifold structure if the underlying topology is complex. Computational advances have been made in an effort to understand how brain regions encode directional or spatial information, such as the head direction system and the hippocampus. Chaudhuri et al. [46] utilized a technique known as Spline Parameterization for Unsupervised Decoding (SPUD) (Figure 2a) to discover the ring structure underlying the mammalian head direction system. This technique uses an approach called persistent homology [47,48], in which persistent features determine the intrinsic dimension used to discover underlying nontrivial topological structure in the data.

Figure 2.

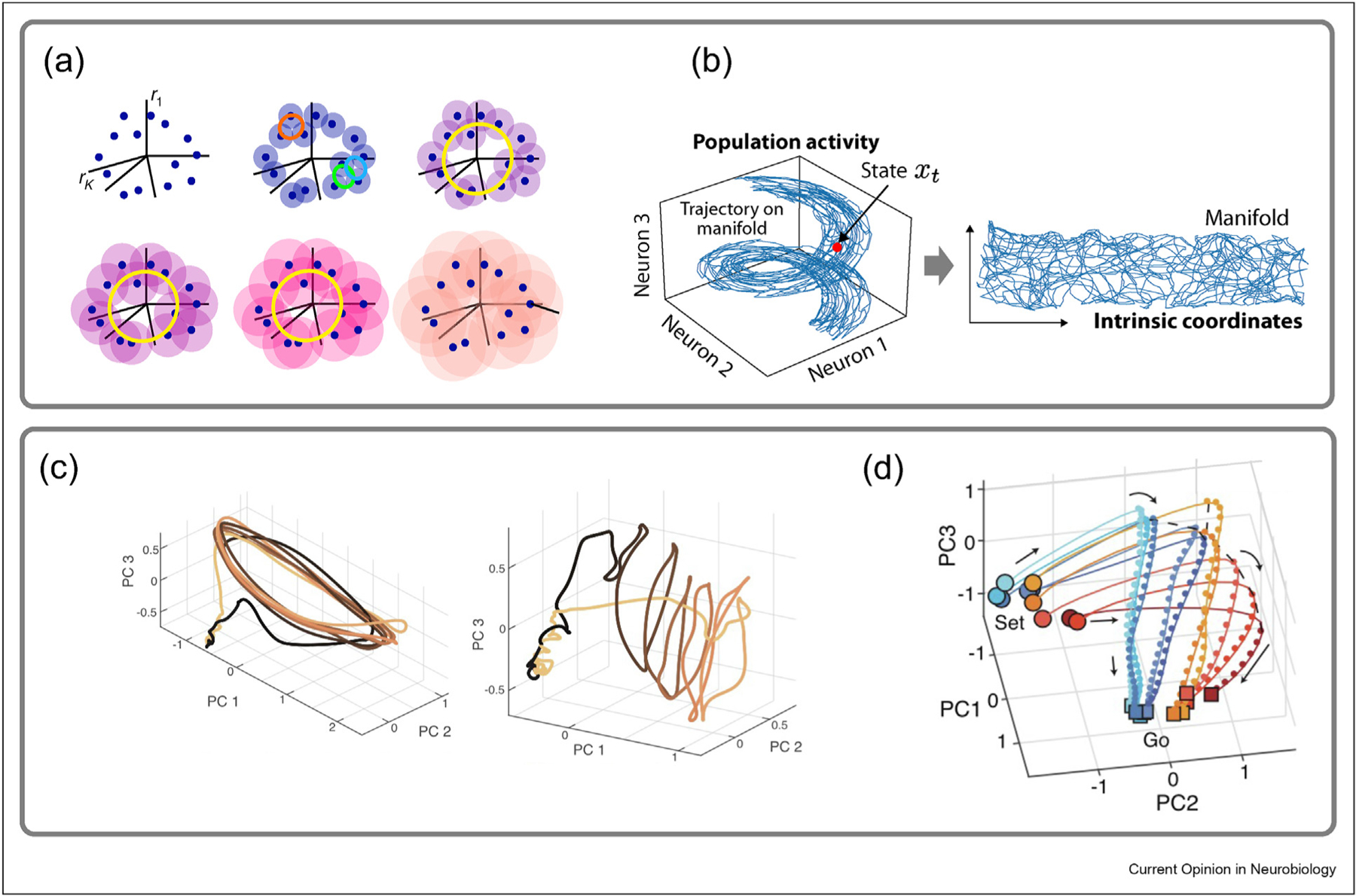
(a–b) Manifold discovery methods. (a) Spine Parameterization for Unsupervised Decoding (SPUD). (b) Manifold Inference for Neural Dynamics (MIND) (c–d) Population dynamics as cognition. (c) (Left) Temporal trajectories during macaque cycling task in M1 and (Right) SMA. (d) Dorsomedial Frontal Cortex (DMFC) response profiles during Bayesian computation. Part (a) adapted from Ref. [46]. Part (b) adapted from Ref. [10]. Part (c) adapted from Ref. [51]. Part (d) adapted from Ref. [8].

Meanwhile, recent work in the hippocampus introduced a topologically motivated method called Manifold Inference from Neural Dynamics (MIND) [49,50] (Figure 2b) to characterize neural activity in the CA1 region of the hippocampus during a foraging and sound manipulation task. In MIND, distances between nearby states are defined by transition probabilities, which gives rise to the notion of intrinsic dimensions relevant for topological maps underlying task implementation.

The geometry of movement and cognition

Dynamic untangling of internally generated activities

The concept of untangling has also been applied to the neural trajectories recorded from the motor cortex during movement. In studies of motor regions, we are interested not only in how body movements are represented but, importantly, in how they are generated. How can we determine whether a given region of the brain is playing a significant role in movement generation as opposed to merely reflecting the effects of activity generated elsewhere? In a closed dynamical system, the rate of change of any dynamic variable is a function of all the other dynamic variables. Thus, it is impossible for a single point in the state-space to be associated with two different rates of change. This is equivalent to the statement that state-space trajectories in such a system cannot cross over themselves. A’tangling index’ has been introduced to identify cases when the trajectories of recorded populations of neurons actually or come close to crossing [9]. By using this measure, it was shown that tangling is much lower in the primary motor cortex during a cycling task than in areas such as the primary sensory cortex or in muscle activities during the same task. This supports the idea that the motor cortex acts as a generator, whereas activity in the somatosensory system and muscles is a response to the motor drive.

Interestingly, a follow-up study of neural activity trajectories during the cycling task in the supplementary motor area (SMA) provided geometric evidence of the well-known role of this area in motor sequencing [51]. Activity in the motor cortex repeated across cycles of the cycling task, but SMA activity followed a helical trajectory, providing s neural representation of the sequence of cycles made during the task (Figure 2c). A similar result was obtained in model recurrent neural networks; a helical representation arose when the network was required to keep track of the number of cycles it had generated [51]. These examples illustrate the extension of the use of geometric analyses, which we first discussed in relation to perception to motor systems.

Population dynamics as cognition

There is a long history of relating dynamic motifs in recurrent networks to cognitive functions: fixed points and memory [52,53], line attractors and integration [54], and limit cycles with various neuronal oscillation patterns [55]. These ideas have more recently been extended to a general program linking dynamics to cognition [56,57].

For example, work in the macaque frontal cortex during a time reproduction task, which requires subjects to reproduce the duration of a time interval, demonstrated that experience warps neural population representations [8]. This mechanism allows for the incorporation of prior statistics in the map from sensory representation to motor output [8]. A geometric analysis of the activity in recurrent neural networks trained to perform this task revealed how curvature supports an underlying Bayesian computation (Figure 2d).

Conclusion

The neural population geometry approach suggests many open problems and future opportunities at the intersection between neuroscience and artificial intelligence. Below we enumerate opportunities and challenges for future study.

First, the neural population geometry can serve as a more accurate population-level descriptor compared to simple task-level probes, as representations with the same level of task capacity can have different geometric configurations [12,33]. Notably, dimensionality [58] is an important population-level metric capturing task information and representational redundancy. This can be further extended with other complementary measures necessary for a full understanding of computation. For example, invariant object classification capacity [12,13] is determined not only by an object manifold’s dimension but also, crucially, by its radius.

Second, as the list of tasks and brain regions showing interesting population geometric structure is growing at a rapid pace [26,59–63], future theoretical developments may need to address the formal connection between representational geometric properties and the encoded task information for a larger array of tasks.

Third, future directions should include uncovering the relationship between population geometry and specific biophysical properties of neurons. In the neural geometry underlying Bayesian computation [8], the curvatures of trajectories are linked to the distributions of priors encoded by each neuron. In deep networks performing visual object recognition, a single layer of homogenous units exhibits a trade-off between various geometric transformations, while common network motifs involve beneficial geometrical changes to multiple geometric properties, suggesting the benefit of heterogeneity in neural populations [13]. More broadly, different brain regions relevant for distinct tasks may implement optimal neural geometry engendered by specific neuronal constraints. Given the vast heterogeneity of cell types, synaptic connectivity patterns, neuronal activation profiles, and sparsity levels, which biological properties constrain and shape the critical task-encoding geometry?

As geometric descriptions are general across task modalities, brain regions, and characteristic timescales, the neural population geometry approach may hold a key for unifying the descriptions of structure and function in biological and artificial neural networks across brain regions and computational levels.