Abstract
A novel semi-organic crystal has been grown using slow evaporation technique by doping organic compound L-asparagine monohydrate (C4H8N2O3·H2O) with inorganic material Magnesium sulphate heptahydrate (MgSO4·7H2O). The crystallographic parameters like strain, dislocation density and crystallite size were calculated by powder X-ray diffraction method. Functional groups were identified and bond length, force constants were calculated from FT-IR spectroscopy. Energy dispersive X-ray (EDX) analysis was used to identify the constituent elements of the crystal. Kinetic and thermodynamic parameters, such as, activation energy Ea, change in Gibb's free energy (ΔG) and change in enthalpy (ΔH) have been determined by thermogravimetric analysis (TGA) analysis. Ea, ΔH and ΔG show positive values and change in entropy (ΔS) shows negative ones. The thermal degradation behavior of the crystals has been analyzed by differential scanning calorimetry (DSC) analysis. Various optical constants such as optical band gap, lattice dielectric constant, absorbance, extinction coefficient, the ratio of free charge carrier concentration to the effective mass, Urbach energy, optical and electrical conductivities were estimated from UV–vis transmittance data. High optical conductivity (1010 s−1) justifies the good photo response nature of the semi-organic crystal.
Keywords: L-asparagine, MgSO4·7H2O, Structural properties, Thermal characterization, UV–Vis spectroscopy, Optical band gap energy
1. Introduction
Frequency mixing, photonics, second harmonic generation and optoelectronics are the rapidly developing fields of modern era where the use of organic non-centrosymmetric compounds has played a pivotal role [1]. It is the π-bonds in the organic materials that cause high nonlinear susceptibility (χ) due to molecular hyperpolarizability (β). However, these organic crystals have some unfavorable features, such as volatility, low thermal stability and poor mechanical strength [2]. In comparison, inorganic materials have low nonlinear efficiency but excellent thermal and mechanical stability. Therefore, the growth of a new type of material known as semi-organic crystal has become a recent trend, where the strong physical and chemical features of inorganic crystals are combined with the excellent nonlinear optical characteristics of organic materials [3]. Over the past few decades, organic materials based on amino acid and their compounds have attained increasing significance for application in NLO devices. L-asparagine monohydrate is a well-known NLO substance in the amino acid group. Numerous studies have been conducted on L-asparagine doped compounds, notably l-asparagine l-tartaric acid, L-asparaginium picrate, and L-asparaginium L-tartrate [[4], [5], [6]]. Magnesium sulphate heptahydrate (MgSO4·7H2O) single crystal has become a significant compound of study for both academic and industrial purposes [7]. Accordingly, in the current study, single crystals of magnesium sulphate heptahydrate (MSHH) have been grown in pure form and semi-organic crystals have been grown by doping l-asparagine monohydrate (LAM) with MSHH using the slow evaporation method. The grown crystals have been characterized for thermal, structural, and optical properties.
2. Growth of the crystals
The crystal was grown in pure form and by adding AR grade LAM with MSHH in double-distilled water. Later the solution was stirred constantly for 4 h with a magnetic stirrer, and finally, Whatmann filter paper was used to filter the solution. Recrystallization was carried out to improve the crystal's quality. Thereafter, the solution was poured into a beaker and covered by a transparent plastic sheet with small pores. Finally, it was placed in a dust-free chamber. After 40 days, transparent and well-shaped crystals were obtained as shown in Fig. 1.
Fig. 1.
Image of the grown crystals: (a) MSHH + 0 mol% LAM, (b) MSHH + 0.2 mol% LAM, (c) MSHH + 0.4 mol% LAM, (d) MSHH + 0.6 mol% LAM, (e) MSHH + 0.8 mol% LAM, (f) MSHH + 1.0 mol% LAM.
3. Characterization method
The finely powdered crystals were subjected to powder X-ray diffraction test by Philips X'Pert PW 3040 Powder X-ray Diffractometer over the 2θ range of 10–80°, with angle step size of 0.02° with CuKα1 radiation (λ = 0.154 nm). The UV–Vis spectrophotometer (Shimadzu, UV-3100, Japan) was used to measure the optical transmittance spectrum of the crystals in the range of 190–1100 nm. For measuring the transmittance spectra, the crystal was gently polished until a thickness of 2 mm is reached. Simultaneous Thermal Analyzer STA 449 F3 Jupiter was used to perform the TG/DSC at a heating rate of 10 K/min in nitrogen atmosphere. The FTIR spectra of the powdered samples were recorded in the range of 4000–350 cm−1 using the KBr pellet technique by STA 449 F3 Jupiter.
4. Results and discussion
4.1. Identification of the crystal system of grown crystals
The narrow, strong and sharp peak of the X-ray diffraction is the evidence of growth of single crystal. The study identifies that the crystal belongs to orthorhombic nature with non-centro symmetric space group P212121 (Fig. 2). The lattice parameters of the unit cell were estimated from the d-spacing values provided by the instrument and the corresponding ESDs are also listed in Table 1. The unit cell volume is observed to increase from 948.890 (Å)3 to 969.893 (Å)3 indicating LAM incorporation into MSHH crystal structure. It is also seen that the calculated and the reported values match quite well.
Fig. 2.
XRD pattern of pure and LAM doped MSHH crystal.
Table 1.
Lattice parameters and calculated ESDs of pure and LAM doped MSHH crystals.
| Powder sample | a (Å) | ESD in a (Å) | b (Å) | ESD in b (Å) | c (Å) | ESD in c (Å) | Volume (Å)3 |
|---|---|---|---|---|---|---|---|
| MSHH (JCPDS no. 96-900-7484) | 6.857 | 11.868 | 11.996 | 976.221 | |||
| MSHH +0 mol% LAM | 6.773 | 0.063 | 11.911 | 0.030 | 11.761 | 0.074 | 948.890 |
| MSHH +0.2 mol% LAM | 6.525 | 0.028 | 12.309 | 0.031 | 11.827 | 0.003 | 949.980 |
| MSHH +0.4 mol% LAM | 6.544 | 0.039 | 12.331 | 0.044 | 11.877 | 0.045 | 958.368 |
| MSHH +0.6 mol% LAM | 6.537 | 0.029 | 12.337 | 0.042 | 11.930 | 0.029 | 962.076 |
| MSHH +0.8 mol% LAM | 6.769 | 0.029 | 11.934 | 0.047 | 11.929 | 0.028 | 963.683 |
| MSHH +1.0 mol% LAM | 6.796 | 0.079 | 12.136 | 0.034 | 11.759 | 0.017 | 969.893 |
4.1.1. Determination of crystallite size, strain, and dislocation density
The crystallite size (d) has been obtained using Scherrer's Eq. (1).
| (1) |
where the value of constant k is 0.9 (only for spherically shaped particle [8]), the wavelength of X-rays (λ) is 0.154 nm, and full width at half maximum (FWHM) of the peak is represented by β. The strain (ε) was determined from the slope of the curve, plotted between βcosθ and 4sinθ representing Williamson Hall Eq. (2).
| (2) |
The dislocation density has been determined using Eq. (3) as follows:
| (3) |
Crystallite size, strain, dislocation density are given in Table 2. The crystallite size is observed to increase from 99.039 nm to 154.060 nm and strain from 0.3 to 1.4, which reveals incorporation of LAM into MSHH crystal matrix. The dislocation density is seen to decrease from 0.1020 × 10−3 nm−2 to 0.0421 × 10−3 nm−2 due to the addition of LAM, which is a clear indication of good crystallinity.
Table 2.
Crystallite size, strain, dislocation density of pure and LAM doped MSHH crystals.
| Powder sample | Crystallite size D (nm) | Strain ε ( × 10−3) | Dislocation density δ ( × 10−3) (nm−2) |
|---|---|---|---|
| MSHH + 0 mol% LAM | 99.039 | 0.3 | 0.1020 |
| MSHH + 0.2 mol% LAM | 106.657 | 0.4 | 0.0879 |
| MSHH + 0.4 mol% LAM | 115.545 | 0.1 | 0.0749 |
| MSHH + 0.6 mol% LAM | 126.049 | 0.6 | 0.0629 |
| MSHH + 0.8 mol% LAM | 138.654 | 0.7 | 0.0520 |
| MSHH + 1 mol% LAM | 154.060 | 1.4 | 0.0421 |
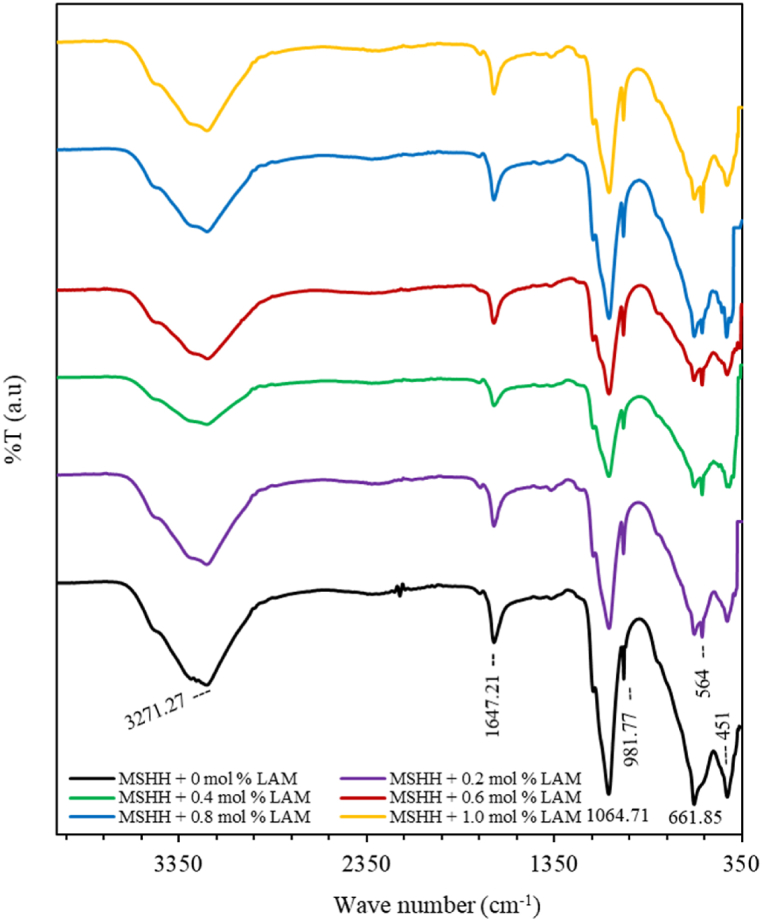
4.2. FTIR spectroscopy analysis
The FTIR spectra of a pure and LAM-doped MSHH crystal are shown in Fig. 3. The broad band at 3271.27 cm−1 with the characteristic OH stretching is caused by water molecules. At 1647.21 cm−1, the HOH bending vibrational band is observed. The peak for SO4−2 bending vibration can be seen at 981.77 cm−1, while the peak at 1064.71 cm−1 is the absorption band caused by SO4−2 stretching vibration. MgO group is reported to cause the peak at 661.85 cm−1 [9]. At 451 cm−1, the Td symmetry of the SO−2 ion can be seen [10]. The additional peak in spectra of LAM doped MSHH crystals at 564 cm−1 is caused by torsional oscillation of NH3+, which confirms the presence of LAM content in the doped sample.
Fig. 3.
FTIR spectra of pure and LAM doped MSHH crystal.
Eq. (4) is used to calculate the bond length of the functional groups. The unit of the force constant k is measured in dynes per centimeter.
| (4) |
Hook's law is applied in eq. (5) to determine the force constant (k) which is an indicator of the stiffness of the bond [11]. Bonds having shorter lengths are thought to be stronger and have a greater force constant (k).
| (5) |
where μ is the reduced mass (g) of the atoms being bonded and derived using Eq. (6) [12]:
| (6) |
where the atomic masses of the atoms are m1 and m2. Table 3 lists bond lengths, force constants of pure and LAM doped MSHH crystals.
Table 3.
Bonds and their lengths, force constants of pure and LAM doped MSHH crystals.
| Sl. No. | Bond | FTIR peaks (cm−1) | Force constant k (Mega dyne/cm) | Bond length r (Å) |
|---|---|---|---|---|
| 1 | OH | 3271.27 | 0.5938 | 3.0591 |
| 2 | HOH | 1647.21 | 0.1506 | 4.8333 |
| 3 | SO4−2 | 1064.71 | 0.7129 | 2.8783 |
| 4 | SO4−2 | 981.77 | 0.6062 | 3.0382 |
| 5 | MgO | 661.85 | 0.2479 | 4.0930 |
| 6 | SO4−2 | 451 | 0.1279 | 5.1032 |
| 7 | NH3+ | 564 | 0.0175 | 9.9031 |
4.3. Energy dispersive spectral analysis
Energy dispersive X-ray spectra shown in Fig. 4 provide evidence that LAM molecule has been absorbed into MSHH crystal structure. Additionally, the stoichiometries distribution of the chemical composition in the pure and LAM doped MSHH crystal is validated by the use of EDX spectra. The carbon content of LAM is observed to increase with doping concentration (Fig. 4).
Fig. 4.
EDX spectra of pure and LAM doped MSHH crystal, (a) pure MSHH, (b) MSHH + 0.2 mol % LAM, (c) MSHH + 0.4 mol % LAM, (d) MSHH + 0.6 mol % LAM, (e) MSHH + 0.8 mol % LAM, (f) MSHH + 1.0 mol % LAM.
4.4. Thermal analysis
Thermal analysis of the grown crystals has been conducted using thermogravimetric (TG) and differential scanning calorimetric (DSC) techniques. While DSC calculates heat (enthalpy) changes with temperature or time and TG analysis shows the mass change with the same [13]. Numerous kinetic and thermodynamic parameters are computed from TG curves. The TG profile in Fig. 5 shows that the mass loss happens in five stages and a respective shift in DSC curve is also evident. The first stage occurs in 60–80 °C temperature range where 1.5 % mass loss is observed, which indicates the release of one water molecule. According to Fig. 6, an endothermic reaction occurs in the initial dehydration stage, which is confirmed by the negative DSC peak [14].
Fig. 5.
TGA curve of pure and LAM doped MSHH.
Fig. 6.
DSC curve of pure and LAM doped MSHH.
The weight loss of 30 % appears as a steep fall in the second stage with a notable peak between 82 °C and 145 °C. A loss of roughly four water molecules of MSHH crystal and five water molecules for LAM doped MSHH samples may be responsible for the rapid decrease in mass [14,15]. The third stage, which occurred between 145 and 203 °C, represents 12 % of mass loss showing a steady decrease in weight loss. In total, six water molecules are lost in the second and third phases representing a mass loss of about 42 % [14]. An endothermic transition is evident by the negative DSC peak in the second and third dehydration steps. The fourth stage occurs between 204 and 221 °C. Between 291 and 365 °C, fifth stage is observed displaying a rate of 5 % mass loss which is slower than the previous stages. These phases feature the decomposition of MSHH molecules.
This indicates that MgSO4·6H2O is changed to anhydrous MgSO4 during these fourth dehydration steps [14]. It is believed that successive decompositions are driven by the removal of SO4−2 ions, which changes into SO2 and O2 and finally leave MgO as residue [10].
| MgSO4·7H2O → MgSO4 + 7H2O |
| MgSO4 → MgO + SO2↑ + O2↑ |
In Fig. 6, all DSC curves are observed to have endothermic peaks below 230 °C, confirming the dehydration step where energy is needed to eliminate moisture. The degradation of the crystal is indicated by succeeding exothermic peaks. Phase change is attributed to the small peak at about 340 °C.
4.4.1. Calculating the rate constant and half-life of the reaction by the TGA graph
Eq. (7) is a first-order reaction rate equation that has been applied to derive the activation energy along with other thermodynamic parameters [16].
| (7) |
Where, , wt is the sample's weight at a specific time t, wi and wf are starting and final weights. From Eq. (7), we can write
| (8) |
If a graph is plotted using Eq. (8), then it can be seen that each phase traces a straight line, indicating that the changes are reactions of the first order. The slope of every line was used to calculate the rate constant (k) for a specific phase, and Eq. (9) was applied to calculate the half-life (t1/2). Table 4 provides the k and t1/2 values.
| (9) |
Table 4.
Kinetic and thermodynamic parameters of all phases during thermogravimetric analysis.
| Parameter | Stages | MSHH +0 mol% LAM | MSHH +0.2 mol% LAM | MSHH +0.4 mol% LAM | MSHH +0.6 mol% LAM | MSHH +0.8 mol% LAM | MSHH +1.0 mol% LAM |
|---|---|---|---|---|---|---|---|
| Rate constant k (min−1) | Dehydrartion (1st stage) | 0.1906 | 0.1851 | 0.0662 | 0.1637 | 0.1919 | 0.1111 |
| Dehydrartion (2nd stage) | 0.041 | 0.0255 | 0.0041 | 0.0551 | 0.0604 | 0.2314 | |
| Dehydrartion (3rd stage) | 0.2234 | 0.1826 | 0.0213 | 0.1358 | 0.1091 | 0.3245 | |
| Dehydrartion (4th stage) | 0.0051 | 0.0023 | 0.0003 | 0.0053 | 0.0043 | 0.3672 | |
| Decomposition (5th stage) | 0.032 | 0.045 | 0.056 | 0.041 | 0.024 | 0.101 | |
| Half life T1/2 (min) | Dehydrartion (1st stage) | 3.636 | 3.744 | 10.468 | 4.233 | 3.611 | 6.238 |
| Dehydrartion (2nd stage) | 16.902 | 27.176 | 169.024 | 12.577 | 11.474 | 2.995 | |
| Dehydrartion (3rd stage) | 3.102 | 3.795 | 32.535 | 5.103 | 6.352 | 2.136 | |
| Dehydrartion (4th stage) | 135.882 | 301.304 | 2310.000 | 130.755 | 161.163 | 1.887 | |
| Decomposition (5th stage) | 21.656 | 15.400 | 12.375 | 16.902 | 28.875 | 6.861 | |
| ΔH (Jmol−1) ( × 103) | Dehydrartion (1st stage) | 118.10 | 84.42 | 76.65 | 67.34 | 66.89 | 7.67 |
| Dehydrartion (2nd stage) | 74.90 | 76.29 | 60.94 | 65.43 | 67.79 | 7.57 | |
| Dehydrartion (3rd stage) | 15.38 | 16.81 | 10.20 | 17.07 | 18.02 | 15.1 | |
| Dehydrartion (4th stage) | 30.62 | 30.41 | 9.12 | 10.65 | 9.73 | 113.73 | |
| Decomposition (5th stage) | 3.62 | 6.29 | 10.14 | 10.46 | 112.55 | 76.64 | |
| ΔG (Jmol−1) ( × 104) | Dehydrartion (1st stage) | 24.22 | 23.22 | 26.36 | 25.49 | 31.26 | 13.53 |
| Dehydrartion (2nd stage) | 22.72 | 24.53 | 25.71 | 32.13 | 17.19 | 15.95 | |
| Dehydrartion (3rd stage) | 25.64 | 26.19 | 36.17 | 15.89 | 15.88 | 14.36 | |
| Dehydrartion (4th stage) | 25.93 | 37.61 | 17.86 | 17.68 | 16.53 | 944.70 | |
| Decomposition (5th stage) | 36.14 | 15.62 | 16.41 | 14.23 | 941.24 | 680.68 |
The modified Coats and Redfern model is represented by equation (10). The kinetic parameters have been determined from this equation [[17], [18], [19], [20], [21], [22], [23]]:
| (10) |
where Ea stands for activation energy, T indicates temperature in Kelvin, R is the gas constant (8.3143 J mol-1 K−1), A is the pre-exponential factor, and the heating rate β is 20 °C/min. The basic thermodynamic equations [24] were applied to calculate the remaining parameters. The activation energy for each phase is measured using graphs that are plotted with ln [ln (1 - x)] as y-axis and 1000/T as x-axis (Fig. 7). According to the values in Table 4, every phase indicates non-spontaneous endothermic process.
Fig. 7.
Plot of ln [-ln (1 - x)] vs 1000/T of pure and doped MSHH crystals. (a) Pure MSHH, (b) MSHH + 0.2 mol % LAM, (c) MSHH + 0.4 mol % LAM, (d) MSHH + 0.6 mol % LAM, (e) MSHH + 0.8 mol % LAM, (f) MSHH + 1.0 mol % LAM.
4.4.2. Estimation of thermodynamic parameters
Eqs. (11), (12), (13) were used to calculate different thermodynamic parameters for each phase, including change in enthalpy (ΔH), change in Gibbs free energy (ΔG), and change in entropy (ΔS).
| (11) |
| (12) |
| (13) |
where A is the Arrhenius constant and kb is the Boltzmann constant [24]. Table 4 lists the estimated values for the thermodynamic parameters k, t1/2, ΔH, ΔG, and Ea, ΔS are displayed in Fig. 8. The change in enthalpy (ΔH) in a chemical reaction symbolizes the energy change between reactants and products. It has been found that there is a very low energy barrier (∼3 kJ/mol) between activation energy and change in enthalpy, indicating that the chemical reaction may begin easily [25].
Fig. 8.
Plot of (a) activation energy and (b) change in entropy of various stages with doping concentration.
4.5. Linear optical studies and relevant constants
Since the optical quality of a crystal is closely related to its electrical properties, atomic structure, and electronic band structure, it is very essential to know the optical characteristics of the crystal. In order to understand the optical behavior of a crystal, it is required to measure its optical transparency, absorption coefficient, extinction coefficient, band gap, and refractive index.
4.5.1. Optical band gap
Fig. 9 displays the optical transmittance of the grown crystals. Around at 257 nm, the cut-off wavelength is detected. The amine group having low scattering and low absorption nature is believed to eliminate defect centers making the doped crystals to have higher optical transmittance [26,27]. The absorption coefficient (α) was calculated by applying the equation:
| (14) |
where t and T represent the sample's thickness and transmittance (%). The relation between photon energy (hυ) and absorption coefficient (α) is given by
| (15) |
where A is a constant and Eg is the optical band gap [[28], [29], [30]], n is 1/2 and 2 for direct band gap and indirect band gap respectively. Table 5 lists the direct optical band gaps Egd which are calculated from Tauc's plot (Fig. 10). An important attribute for photonics and optoelectronic devices is good dielectric nature, which is clearly indicated by an increase in band gap values of the doped crystals. Likewise, the doped crystal can be employed in solar panels as an antireflection coating that requires low reflectance, good band gap, low absorption, and high transmission. In a different way, the material's optical band gap Eth was also assessed by applying Plank's equation given below.
| (16) |
where λ is cut-off wavelength. The values of Eth matched reasonably with that Egd as shown in Table 5. The high transmittance in the visible range is confirmed by the crystal's large band gap, and this crystal may be ideal for optoelectronic devices such as laser diodes [31].
Fig. 9.
UV–Vis spectra of pure and doped MSHH crystals.
Table 5.
Optical parameters of pure and LAM doped MSHH crystals.
| Optical Parameters | MSHH +0 mol% LAM | MSHH +0.2 mol% LAM | MSHH +0.4 mol% LAM | MSHH +0.6 mol% LAM | MSHH +0.8 mol% LAM | MSHH +1.0 mol% LAM |
|---|---|---|---|---|---|---|
| Egd (eV) | 5.2 | 5.23 | 5.26 | 5.3 | 5.34 | 5.37 |
| Eth (eV) | 5.27 | 5.31 | 5.34 | 5.36 | 5.36 | 5.38 |
| εL | 5.0867 | 3.817 | 3.2726 | 2.723 | 2.4481 | 2.0618 |
| N/m* (kg−1m−3) | 4.41 × 1055 | 2.33 × 1055 | 1.65 × 1055 | 1.11 × 1055 | 8.75 × 1054 | 6.05 × 1054 |
| Eu (eV) | 0.24 | 0.23 | 0.22 | 0.21 | 0.2 | 0.19 |
Fig. 10.
(αhν)2 as a function of photon energy for pure and LAM doped LSHH crystals.
4.5.2. Extinction coefficient
The extinction coefficient estimates the amplitude decay of the incident magnetic and electric fields which is represented by the following equation [32].
| (17) |
where the wavelength of the incident beam is λ. Fig. 11 depicts how the extinction coefficient changes with wavelength. It is observed that the extinction coefficient (k) increases with wavelength until the cut-off wavelength is met. The lower value of k is thought to be caused by a weak interaction between the electrons and photons in the material.
Fig. 11.
(a) Extinction coefficient of pure and doped MSHH crystals. (b) Relations of Electrical conductivity (σe) and Optical conductivity (σo) with photon energy for pure and LAM doped MSHH crystals.
4.5.3. Optical and electrical conductivity
The frequency response of the crystal to incident light, also known as optical conductivity (σop) was determined by applying the equation shown in Ref. [33].
| (18) |
where c is the speed of light, n is the refractive index, and α is the absorption coefficient. Fig. 11 shows how optical conductivity changes with photon energy of the incident light. The optical conductivity is observed to reduce with the increase in molar concentration. The high photo-responsive behavior of the crystal is confirmed by a higher optical conductivity value (1010 s−1), which validates as an appropriate material for use in computing and information processing [34]. The transit of a large quantity of charge carriers from the valence to the conduction band is indicated by exponential growth at high energy values. A sudden increase in optical conductivity is observed at 5.2 eV confirming the exactness of energy band gap estimations. The electrical conductivity (σe) can be written in terms of the optical conductivity and absorption coefficient as [35].
| (19) |
Variations of electrical conductivity with photon energy are presented in Fig. 11. The lower range of electrical conductivity values reveals the dielectric nature of the crystal.
4.5.4. Complex dielectric constant
Complex dielectric constant (εc) can be determined by the following equation [36].
| (20) |
where the real and imaginary parts of the dielectric constant are εr and εi respectively and their relation with the refractive index n and extinction coefficient k are as follows [37].
| (21) |
The parameters εr and εi are depicted as a function of photon energy in Fig. 12. The low value of the imaginary part of the dielectric constant is a crucial condition for optoelectronic device applications because it shows an impediment in the transmission of electromagnetic (EM) energy.
Fig. 12.
(a) Real and (b) imaginary part of dielectric constant with photon energy for pure and LAM doped MSHH crystal.
4.5.5. Lattice dielectric constant and carrier concentration
The following equation can be used to determine the lattice dielectric constant from the refractive index (n) [38].
| (22) |
where e is the electronic charge, c is the speed of light, and (N/m*) is the ratio of the carrier concentration to the effective mass. The plot of n2 versus λ2, is shown in Fig. 13 (a). From the slope of the linear part and from the intercept of the straight line to the n2-axis, the lattice dielectric constant εL and ratio N/m × are calculated respectively and shown in Table 5. Table 5 also lists Urbach energy Eu, which is determined from the plot of lnα versus photon energy as shown in Fig. 13 (b). The Urbach energy is found to decrease due to LAM doping, and this fall of Urbach energy is a clear indication of the decrease of defects in the doped crystals [39,40].
Fig. 13.
Plot of (a) n2 versus λ2, (b) ln α vs photon energy for pure and LAM doped MSHH crystals.
5. Conclusions
LAM doped MSHH semi-organic crystals with excellent optical quality have been grown by slow evaporation process from aqueous solutions and compared its properties with pure MSHH crystal. The XRD data showed that the grown crystals were orthorhombic. Additionally, the strong, sharp peaks and decrease of dislocation density show that LAM doped MSHH crystals have excellent crystalline structure. Increase of the unit cell volume, crystallite size and strain indicate the incorporation of LAM into MSHH crystal structure. Thermal investigation using TG and DSC showed that the doped crystals had improved thermal stability. All thermodynamic parameters, including a, ΔH, and ΔG values, are clearly positive while ΔS values are clearly negative, specifying a non-spontaneous chemical process. The fluctuation in activation energy is indicative that multi-reaction mechanisms exist during the process. It is evident from the DSC study that both endothermic and exothermic chemical processes are involved in the degradation process. The entrance of LAM molecule into the MSHH crystal lattice is confirmed by the energy dispersive X-ray and Fourier transform infrared spectroscopy. Furthermore, EDX analysis indicates the stoichiometric distribution of the C, Mg, S, and O components in the semi-organic crystal. LAM-doped MSHH semi-organic crystals have excellent transparency throughout the visible spectrum and can be applied to photonic and electro-optic devices. The band gap was determined based on UV–visible spectroscopy data and was found to increase with increasing doping concentration, making it suitable for applications in laser diodes. The estimated extinction coefficient confirmed its suitability for use in optical devices. For applications in optoelectronic devices, the low value of the imaginary part of the dielectric constant is a crucial requirement. The decrease in the Urbach energy and the increase in the optical band gap indicate that the defect bands have been partially eliminated due to doping. The large optical conductivity value indicates that the crystal has good photo responsive behavior, making it suitable for information processing and computer technology.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data statement
The data used for this article is derived from the experiments. These are not available online.
Author's contributions
.
Additional information
No additional information is available for this paper.
CRediT authorship contribution statement
Md Anisur Rahman: Data curation, Formal analysis, Investigation, Software, Validation, Writing – original draft. Jiban Podder: Conceptualization, Data curation, Project administration, Resources, Supervision, Validation, Writing – review & editing. Harinarayan Das: Formal analysis, Investigation, Resources, Validation.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This complete research work is carried out in the crystal growth lab of the Department of Physics, Bangladesh University of Engineering and Technology (BUET), Dhaka, Bangladesh. The authors are thankful to the Atomic Energy Centre, Dhaka, Bangladesh Atomic energy Commission for using the facilities of EDX, XRD, FTIR, UV–visible spectrometer for characterization of the as grown crystals.
References
- 1.Vijajalakshmi V., Dhanasekaran P. Growth and Characterization of γ-glycine single crystals for photonics and optoelectronic device applications. J. Cryst. Growth. 2019;506:117–121. doi: 10.1016/j.jcrysgro.2018.09.048. [DOI] [Google Scholar]
- 2.Jiang M., Fang Q. Organic and semiorganic nonlinear optical materials. Adv. Mater. 1999;11:1147–1151. doi: 10.1002/(SICI)1521-4095(199909)11:13%3C1147::AID-ADMA1147%3E3.0.CO;2-H. [DOI] [Google Scholar]
- 3.Ramabadran U.B., Zelmon D.E., Kennedy G.C. Electro-optic, piezoelectric, and dielectric properties of zinc tris thiourea sulfate. Appl. Phys. Lett. 1992;60:2589–2591. doi: 10.1063/1.106918. [DOI] [Google Scholar]
- 4.Srinivasan P., Kanagasekaran T., Gopalakrishnan R., Bhagavannarayana G., Ramasamy P. Studies on the growth and characterization of L-Asparaginium picrate (LASP)-A novel nonlinear optical crystal. Cryst. Growth Des. 2006;6:1663–1670. doi: 10.1021/cg060094+. [DOI] [Google Scholar]
- 5.Moovendran K., Srinivasan B.R., Sundar J.K., Martin Britto Dhas S.A. Structural, Vibrational and thermal studies of a new nonlinear optical material: L-Asparagine-L-tartaric acid. Spectrochim. Acta, Part A. 2012;92:383–391. doi: 10.1016/j.saa.2012.02.089. [DOI] [PubMed] [Google Scholar]
- 6.Vivek P., Murugakoothan P. Linear and nonlinear optical properties of a new organic NLO L-asparaginium L-tartarate (AST) single crystal. Optik Int. J. Light Electron. Opt. 2013;124:3510–3513. doi: 10.1016/j.ijleo.2012.12.004. [DOI] [Google Scholar]
- 7.Ferdous S., Podder J. Growth and characterization of epsomite single crystals doped with KCl from low temperature aqueous solutions. J. Bangladesh Acad. Sci. 2009;33:47–54. doi: 10.3329/jbas.v33i1.2949. [DOI] [Google Scholar]
- 8.Devaraja P.B., Avadhani D.N., Nagabhushana H., Prashantha S.C., Sharma S.C., Nagabhushana B.M., Nagaswarupa H.P., Parasad B.D. Luminescence properties of MgO: Fe3+ nanopowders for WLEDs under NUV excitation prepared via propellant combustion route. J. Radiat. Res. Appl. Sci. 2015;8:362–373. doi: 10.1016/j.jrras.2015.02.001. [DOI] [Google Scholar]
- 9.Tuama A.R., Al-Saadi T.M. Study the structural and optical properties of magnesium sulphate heptahydrate single crystal grown by solution growth method. Energy Proc. 2019;157:709–718. doi: 10.1016/j.egypro.2018.11.237. [DOI] [Google Scholar]
- 10.Ramalingom S., Podder J., Narayana Kalkura S. Crystallization and characterization of orthorhombic b-MgSO4·7H2O. Cryst. Res. Technol. 2001;36:1357–1364. doi: 10.1002/1521-4079(200112)36:123.0.CO;2-7. [DOI] [Google Scholar]
- 11.Kaya S., Chamorro E., Petrov D., Kaya C. New insights from the relation between lattice energy and bond stretching force constant in simple ionic compounds. Polyhedron. 2017;123:411–418. doi: 10.1016/j.poly.2016.12.028. [DOI] [Google Scholar]
- 12.Kaupp M., Danovih V., Shaik S. Chemistry is about energy and its changes: a critique of bond-length/bond-strength correlations. Coord. Chem. Rev. 2017;3:355–362. doi: 10.1016/j.ccr.2017.03.002. [DOI] [Google Scholar]
- 13.Das H.N., Podder J. Investigations on growth, thermal, electrical, and etching studies of KCl-doped triglycine sulfate single crystals. J. Therm. Anal. Calorim. 2012;110:1107–1112. doi: 10.1007/s10973-011-2115-3. [DOI] [Google Scholar]
- 14.Van Essen V.M., Zondag H.A., Cot Gores J., Bleijendaal L.P.J., Bakker M., Schuitema R., Van Helden W.G.J., He Z., Rindt C.C.M. Characterization of MgSO4 hydrate for thermochemical seasonal heat storage. J. Sol. Energy Eng. 2009;131 doi: 10.1115/1.4000275. [DOI] [Google Scholar]
- 15.Kathiravan P., Balakrishnan T. Synthesis, growth and characterization of pure and Cesium doped L – asparagine monohydrate single crystals. Struct. Chem. Crystallogr. Commun. 2015;1(1) doi: 10.21767/2470-9905.100009. [DOI] [Google Scholar]
- 16.Perveen S., Farrukh M.A. Influence of lanthanum precursors on the heterogeneous La/SnO2–TiO2 nanocatalyst with enhanced catalytic activity under visible light. J. Mater. Sci. Mater. Electron. 2017;28:10806–10818. doi: 10.1007/s10854-017-6858-x. [DOI] [Google Scholar]
- 17.Ramukutty S., Ramachandran E. Reaction rate models for the thermal decomposition of ibuprofen crystals. J. Cryst. Process Technol. 2014;4:71–78. doi: 10.4236/jcpt.2014.42010. [DOI] [Google Scholar]
- 18.Trache D. Comments on effect of hydrolysed cellulose nanowhiskers on properties of montmorillonite/polylactic acid nanocomposites. Int. J. Biol. Macromol. 2016;88:497–498. doi: 10.1016/j.ijbiomac.2016.03.073. [DOI] [PubMed] [Google Scholar]
- 19.Trache D. Comments on thermal degradation behavior of hypochlorite-oxidized starch nanocrystals under different oxidized levels. Carbohydr. Polym. 2016;151:535–537. doi: 10.1016/j.carbpol.2016.05.106. [DOI] [PubMed] [Google Scholar]
- 20.Atkins P., Paula J.D. W. H. Freeman and Company; New York: 2006. Atkins' Physical Chemistry. [Google Scholar]
- 21.Joshi V.S., Joshi M.J. FTIR spectroscopic and thermal studies of calcium tartrate trihydrate crystals grown by gel assistance. Indian J. Phys. 2001;75A(2):159–163. [Google Scholar]
- 22.Dabhi R.M., Joshi M.J. Thermal studies of gel grown zinc tartrate spherulites. Indian J. Phys. 2002;76A(2):211–213. [Google Scholar]
- 23.Joseph S., Joshi M.J. Kinetic study of dehydration in gel grown iron tartrate dehydrate crystals. Indian J. Phys. 1997;71A(2):183–189. [Google Scholar]
- 24.Farrukh M.A., Butt K.M., Chong K.K., Chang W.S. Photoluminescence emission behavior on the reduced band gap of Fe doping in CeO2-SiO2 nanocomposite and photophysical properties. J. Saudi Chem. Soc. 2019;23:561–575. doi: 10.1016/j.jscs.2018.10.002. [DOI] [Google Scholar]
- 25.Olszak-Humienik M., Mozejko J. Thermodynamic functions of activated complexes created in thermal decomposition processes of sulphates. Thermochim. Acta. 2000;344(1–2):73–79. doi: 10.1016/S0040-6031(99)00329-9. [DOI] [Google Scholar]
- 26.Khan I., Anis M., Bhati U. Influence of L-lysine on optical and dielectric traits of cadmium thiourea acetate complex crystal. Optik Int. J. Light Electron. Opt. 2018;170:43–47. doi: 10.1016/j.ijleo.2018.05.076. [DOI] [Google Scholar]
- 27.Al Faify S., Shkir M., Ganesh V., Anis M., Yahia I.S. A Comprehensive investigation on core optoelectranic and laser properties of ZTS single crystal: an effect of Mg2+ doping. Appl. Phys. B. 2018;124:196–207. doi: 10.1007/s00340-018-7066-y. [DOI] [Google Scholar]
- 28.Tauc J. Plenum Press; New York, NY: 1974. Amorphous and Liquid Semiconductors. [Google Scholar]
- 29.Kumar K., Ramamoorthy K., Koinkar P.M., Chandramohan R., Sankaranarayanan K. A novel in situ synthesis and growth of ZnAl2O4 thin films. J. Cryst. Growth. 2006;289:405–407. doi: 10.1016/j.jcrysgro.2005.11.007. [DOI] [Google Scholar]
- 30.Joshi J.H., Kalainathan S., Joshi M.J., Parikh K.D. Crystal growth, spectroscopic, second and third order nonlinear optical spectroscopic studies of L-phenylalanine doped ammonium dihydrogen phosphate single crystals. Arab. J. Chem. 2020;13:5018–5026. [Google Scholar]
- 31.Krishnan S., Justin Raj C., Dhinakaran S., Jerome Das S. Investigation of optical band gap in potassium acid phthalate single crystal. Cryst. Res. Technol. 2008;43(6):670–673. doi: 10.1002/crat.200711073. [DOI] [Google Scholar]
- 32.Jain J., Christuraj P., Anitha K., Balasubramanian T. Band gap enhancement on metal chelation: growth and characterization of cobalt chelated glycine single crystals for optoelectronic applications. Mater. Chem. Phys. 2009;118(2–3):284–287. doi: 10.1016/j.matchemphys.2009.07.061. [DOI] [Google Scholar]
- 33.Pal T., Kar T. Studies of microhardness anisotropy and Young's modulus of nonlinear optical crystal l-arginine hydrochlorobromo monohy-drate. Mater. Lett. 2005;59(11):1400–1404. doi: 10.1016/j.matlet.2004.03.056. [DOI] [Google Scholar]
- 34.Sabari Girisun T.C., Dhanuskodi S. Linear and nonlinear optical properties of tris thiourea zinc sulphate single crystals. Cryst. Res. Technol. 2009;44:1297–1302. doi: 10.1002/crat.200900351. [DOI] [Google Scholar]
- 35.Gupta V., Mansingh A. Influence of post deposition annealing on the structural and optical properties of sputtered zinc oxide film. J. Appl. Phys. 1996;80(2):1063–1073. doi: 10.1063/1.362842. [DOI] [Google Scholar]
- 36.Yakuphanoglu F., Erten H. The refractive index dispersion and analysis of the optical constants of an ionomer thin film. Opt. Appl. 2005;35(4):969–976. [Google Scholar]
- 37.Gaffar M.A., Abu El-Fadl A., Bin Anooz S. Influence of strontium doping on the indirect band gap and optical constants of ammonium zinc chloride crystals. Physica B (Amsterdam, Neth.) 2003;327:43–54. doi: 10.1016/S0921-4526(02)01700-3. [DOI] [Google Scholar]
- 38.Abeles F., editor. Optical Properties of Solids. North- Holland Publishing Company; Amsterdam, London: 1972. [Google Scholar]
- 39.Hafdallah A., Yanineb F., Aida M.S., et al. In doped ZnO thin films. J. Alloys Compd. 2011;509(18):7267. doi: 10.1016/j.jallcom.2011.04.058. [DOI] [Google Scholar]
- 40.Joshi J.H., Kalainathan S., Kanchan D.K., Chaudhari K., Joshi M.J., Parikh K.D. Crystal growth, structural, optical, photoluminescence, electrical and third-order nonlinear optical studies of pure and methylene blue dye-doped ammonium dihydrogen phosphate crystals. J. Mater. Sci. Mater. Electron. 2023;34:21. doi: 10.1007/s10854-022-09447-4. [DOI] [Google Scholar]