Complex Neck Loading and Injury Tolerance in Lateral Bending With Head Rotation From Human Cadaver Tests

Abstract

Advancements in automated vehicles may position the occupant in postures different from the current standard posture. It may affect human tolerance responses. The objective of this study was to determine the lateral bending tolerance of the head-cervical spine with initial head rotation posture using loads at the occipital condyles and lower neck and describe injuries. Using a custom loading device, head-cervical spine complexes from human cadavers were prepared with load cells at the ends. Lateral bending loads were applied to prerotated specimens at 1.5 m/s. At the occipital condyles, peak axial and antero-posterior and medial-lateral shear forces were: 316–954 N, 176–254 N, and 327–508 N, and coronal, sagittal, and axial moments were: 27–38 N·m, 21–38 N·m, and 9.7–19.8 N·m, respectively. At the lower neck, peak axial and shear forces were: 677–1004 N, 115–227 N, and 178–350 N, and coronal, sagittal, and axial moments were: 30–39 N·m, 7.6–21.3 N·m, and 5.7–13.4 N·m, respectively. Ipsilateral atlas lateral mass fractures occurred in four out of five specimens with varying joint diastasis and capsular ligament involvements. Acknowledging that the study used a small sample size, initial tolerances at the occipital condyles and lower neck were estimated using survival analysis. Injury patterns with posture variations are discussed.

Introduction

Injuries to the human head and spine may occur in different environments. In athletic related events, contact loading to the head can induce complex loading to the neck depending on the head-neck posture and location of the impact vector on the head [1]. In occupational environments, vibrations can induce pain and render instability via injuries to spinal components such as the intervertebral disk [2,3]. In military scenarios, the use of head supported mass such as helmet and head-mounted devices (night vision goggles) changes the head-neck mass and “neutral axis” of the cervical column, alters internal load paths, and coupled with g loads, spinal disorders such as accelerated onset of spondylosis, disk herniation, and neck and back pain may ensue [4,5]. Automotive impacts can result in spinal injuries such as fractures and dislocations to different regions of the neck and dorsal spine, and injury mechanisms may depend on head-neck posture [6,7]. While environments differ, in all these situations, external mechanical loads are transferred to the subaxial cervical spinal column (atlas and axis represent the two upper cervical vertebrae in the human spine, and the column inferior to the axis is commonly referred to as the subaxial cervical spinal column) via the occipital condyles of the head.

Postmortem human surrogate or human cadaver is the most relevant experimental model used in literature to determine the human tolerance to injury. This is primarily due to the anatomical and structural similarity and ability to reproduce injuries seen in the field. For the head-cervical spine, as applications to the automotive and military environments, studies have focused with the head-neck structure aligned in the midsagittal plane, i.e., simulating the forward facing seated occupant in the vehicle with the Frankfurt plane of the head maintained horizontal/parallel to the ground [1]. External loads to the head-neck complex have been applied using systems such as electrohydraulic testing devices and drop towers in which the inverted head-spine specimen is dropped on to a rigid force plate [8]. Using these approaches, studies have replicated injuries and developed tolerance data using the peak axial force and peak flexion–extension bending moment in the sagittal plane. In other words, off-axis loads are not included in the definition of human tolerance. For example, the neck injury criteria currently used in the U.S. Federal Motor Vehicle Safety Standards are based on these assumptions and use sagittal plane-measured biomechanical metrics, axial force, and sagittal bending moment at the occipital condyles [9].

Increasing levels of automation in modern automotive and military environments tend to relax the standard head Frankfurt plane horizontal posture and sagittal loading constraints assumed and used in previous tolerance studies. Different types of seat designs, anchors, seating arrangements with oblique seats or seats with reclined backs are used in the cabin space to increase comfort, and changes in the internal vehicle components to accommodate these features, create an out-of-position type of scenario and induce multiplanar loading [10]. The expected initial head rotated posture is a consequence of automation, and this type of posture alters the internal load path within the head-neck structures. Left or right initial rotation of the head induces asymmetric loads within the head-neck complex. Asymmetry in posture leads to multiplanar loading. Studies delineating injury responses and tolerances of the head-neck complex to such changed initial postures are not available in published literature. The objective of this study was to determine the biomechanical lateral bending tolerance of the head-cervical spine with an initial head rotation posture using loads at the occipital condyles and lower neck and describe the resulting injuries.

Materials and Methods

Loading Device.

Loading to the specimen was applied using a custom angular displacement device. The device converted the linear motion of a vertically oriented electrohydraulic piston to a torque about the occipital condyle joint and about the medial-lateral axis of the specimen. Figure 1 shows a schematic of the test setup. The device acted as a modified slider-crank/rank-pinion ((b) and (c) in Fig. 1) mechanism with the vertical piston ((a) in Fig. 1) rotating a transmission shaft ((d) in Fig. 1), joined to a rigid aluminum disk ((e) in Fig. 1). The disk was connected to the top of a six-axis load cell by an adjustable load transfer plate ((j) in Fig. 1) that centered the torque at the occipital condyles of the specimen.

Fig. 1.

Schematics of the loading device and the specimen attached to the device. The T1 vertebra is inside the PMMA fixation, and hence, not shown. The C1 vertebra is the first cervical vertebra below the base of the skull. x, y, and z refer to the antero-posterior, lateral, and axial directions, and forces along the x, y, and z (F_x, F_y, and F_z) axes correspond to the antero-posterior shear, lateral shear, and compressive forces, respectively, and xy, yz, and xz planes correspond to the axial, coronal, and sagittal bending moments, respectively, and these are labeled as M_z, M_x, and M_y moments, respectively.

Specimen Preparation and Positioning on the Loading Device.

The human cadaver study was approved by the Institutional Review Board and sponsor. Isolated head-neck complexes were excised from unembalmed human cadavers that were prescreened for blood-borne pathogens. Muscles were not stripped to maintain the integrity of the osteoligamentous column. Pretest X-rays and computed tomography images were obtained. The inferior end of the specimen was fixed in polymethyl-methacrylate such that the cervico-thoracic disk was unconstrained, and the top of the fixation was parallel to the transverse plane at the T1 vertebral level. The distal cranium was sectioned above and parallel to the Frankfurt plane. An aluminum interface plate was fixed to the top of the skull, and it was centered rostral to the foramen magnum. The soft tissues on the anterior region of the osteo-ligamentous cervical column were excised and sets of three noncollinear retroreflective targets were fixed to the second, fourth, and sixth vertebral bodies, on the zygomatic bone, and the distal fixation. Pretest X-rays of the preparation were obtained. The specimens were positioned such that the coronal plane of the spinal column was parallel to the rotating disk of the custom loading device.

The head was axially rotated to the left 20 deg such that the axis of rotation was through the center of the occipital condyles at an oblique angulation to the antero-posterior axis of the basilar skull and perpendicular to the coronal plane of the first thoracic vertebra. Left lateral bending loading was applied at a rate of 1.5 m/s.

Instrumentation and Data.

A six-axis load cell was attached to the superior surface of the interface plate (shown as upper load cell, (i) in Fig. 1) of the loading device. A second six-axis load cell was fixed to the inferior end of the specimen (shown as lower load cell, (f) in Fig. 1). Two load cells were used to obtain the upper and lower neck loads, paralleling the two load cells used in anthropomorphic test devices. Three linear accelerometers and angular velocity transducers were attached to the interface plate anterior to the cranium. The kinematics were measured using a six-camera motion capture system at 1 kHz and sensor data were recorded at 20 kHz. X-rays and computed tomography images were obtained after the test, and gross dissection was done. The resulting injuries were identified and stability of the head-neck complex was determined. Forces along the three anatomical axes and bending moments about the three planes at the occipital condyle and T1 were used to describe the biomechanical loads on the two ends of the head-neck complex.

Results

Specimen Demographics and Injuries.

The mean age, stature, weight, and body mass index of the five female specimens were 63 ± 10 years, 1.7 ± 0.01 m, 78.0 ± 12 kg, 28 ± 4 kg/m², respectively. Table 1 shows the data for each specimen used in the study. Four out of the five specimens sustained injuries to the upper cervical spine, all occurred at the C1 vertebral level. The other specimen remained intact. Joint diastasis along with the capsular ligament injury was identified in two out of the four specimens. All injuries were stable from a clinical perspective. Details of the injuries sustained by each specimen are provided in Table 2. Figure 2 shows the coronal and axial computed tomography images of injuries sustained by a specimen.

Table 1.

Demographics of the specimens

ID	Age (years)	Height (m)	Weight (kg)	Body mass index (kg/m2)
1	61	1.73	63.5	21.3
2	48	1.53	68.2	29.3
3	74	1.70	90.7	31.3
4	69	1.73	85.9	28.8
5	63	1.65	81.7	30.0

Table 2.

Injuries for each specimen

ID	Injury description
1	Left anterior inferior C1 lateral mass fracture without medial involvement, some diastasis, while transverse atlantal appears intact, suspicion of capsular ligament injury
2	None
3	Left anterior inferior C1 lateral mass fracture through and through without medial involvement, transverse atlantal appears intact
4	Left anterior inferior C1 lateral mass fracture without medial involvement, some diastasis, while transverse atlantal appears intact, suspicion of capsular ligament injury
5	Lateral mass fracture on the left side, involving the inferior aspect/articular surface

Fig. 2.

Computed tomography images showing the inferior anterolateral mass fracture. Left image shows the coronal view and right image shows the axial view.

Upper Cervical (Occipital Condyle) Loads.

The peak forces along the three anatomical axes and bending moments about the three anatomical planes at the occipital condyles are tabulated in Table 3. The peak axial and shear forces along the antero-posterior and medial-lateral axis ranged from 316 N to 954 N, 176 N to 254 N, and 327 N to 508 N, respectively. The peak coronal, sagittal, and axial bending moments ranged from 27.1 N·m to 37.8 N·m, 20.9 N·m to 38.4 N·m, and 9.7 N·m to 19.8 N·m, respectively.

Table 3.

Occipital condyle loads for each specimen

	Force, F (N)			Moment, M (N·m)
ID	Fx	Fy	Fz	Mx	My	Mz
1	145.8	200.1	559.1	30.0	13.0	13.4
2	115.0	250.2	677.0	39.5	21.3	5.7
3	166.8	351.9	1004.4	36.9	7.6	7.2
4	131.6	190.2	644.4	39.5	13.8	9.7
5	226.9	178.9	883.6	38.0	18.4	11.3

F_z represents the axial force, F_x represents the antero-posterior shear force, and F_y represents the lateral shear force, and M_x, M_y, and M_z represent the coronal, sagittal, and axial moments, respectively.

Lower Cervical (T1) Loads.

The peak forces and bending moments at the lower neck (T1 spinal level) are tabulated in Table 4. The peak axial and shear forces along the antero-posterior and medial-lateral axis ranged from 677 N to 1004 N, 115 N to 227 N, and 178 N to 350 N, respectively. The peak coronal, sagittal, and axial bending moments ranged from 30 N·m to 39.5 N·m, 7.6 N·m to 21.3 N·m, and 5.7 N·m to 13.4 N·m, respectively.

Table 4.

Lower neck (T1) loads for each specimen

	Force, F (N)			Moment, M (N·m)
ID	Fx	Fy	Fz	Mx	My	Mz
1	176.6	326.8	409.4	27.1	28.8	15.4
2	191.0	508.4	315.8	36.9	20.9	11.7
3	200.2	468.0	953.8	30.6	30.4	16.0
4	254.4	401.8	344.5	34.7	22.8	9.7
5	185.7	487.7	676.7	37.8	38.4	19.8

F_z represents the axial force, F_x represents the antero-posterior shear force, and F_y represents the lateral shear force, and M_x, M_y, and M_z represent the coronal, sagittal, and axial moments, respectively.

Discussion

As stated in the introduction section, the objective of this study was to determine the biomechanical lateral bending tolerance of the head-cervical spine with initial head rotation posture and describe injuries to the cervical spine. This was accomplished with a human cadaver model, typically used in tolerance studies in crashworthiness studies. The application of lateral bending to a head-neck complex specimen with initial head rotation poses challenges from loading and positioning perspectives. Consequently, a custom loading device was developed in the study. Specifically, to apply the lateral bending load, the vertical travel of the piston was converted to a torque about the occipital condyle axis. This mechanism induced a lateral bending moment to the prepared, initially rotated head-neck complex. The skull base was used instead of the intact head to enable easier coupling to the loading device/mechanism. The sectioning of the specimen above the Frankfurt plane maintained the integrity of the upper head-neck junction, i.e., occipital condyle attachments to the upper cervical vertebrae. Thus, while the superior region of the full cranium anatomy was not present in the simplified experimental model, all the intervertebral and bilateral facet joint connections of the osteoligamentous cervical spinal column to the base of the skull where the spine attaches to the head were fully maintained. From an anatomical perspective, the results of the model are realistic.

Injuries in the form of lateral mass fractures occurred to the atlas in four out of the five specimens, demonstrating that the initially head-rotated spine is susceptible to injury at the upper cervical region. Injuries to the lateral mass on the ipsilateral side is attributed to the axial force on the left side while the right lateral mass is in a relatively distractive mode, i.e., a consequence of asymmetric loading. Although not the purpose of this study, based on measurements from quantitated computed tomography images, the bone mineral density of the left lateral mass was lower (p < 0.05) than the density in the other regions of the atlas, measured at the bilateral arches and anterior and posterior tubercles. This regional density difference may have predisposed to the injury under this mode and have clinical significance. The lack of right capsular joint injuries and or fracture of the right lateral mass adds to the rationale of asymmetric distribution of the external load under this loading mode. This type of injury is not commonly produced in previous biomechanical studies. As stated earlier, previous studies were conducted with pure sagittal alignment, with or without the presence of the natural cervical lordosis [1,7,11–13]. Because of the pure sagittal alignment condition, the segmental and internal load paths were uniformly distributed between the two lateral mass regions in the upper and facet joints in the lower cervical spines. This was true regardless of the degree of lordosis, full or natural curvature to straightened column. The resulting injuries concentrated at the mid to lower cervical spines in specimens with lordosis removal [12]. Upper cervical injuries such as dens and odontoid fractures of the axis vertebra and C1 fractures were more prevalent in specimens with the maintenance of the lordosis [11]. In contrast to these two mechanisms of injury, this study produced injuries to the atlas emphasizing the role of the precondition, i.e., prehead rotation on the injury location. Taken together, these studies, albeit conducted with different postures, reinforce the role of posture in the mechanism and location of cervical spine injuries.

An interesting observation is that the specimen 2 was not injured, while all others sustained injuries. This specimen was the youngest in the ensemble (48 years versus a minimum age of 61 years for other specimens). Age may have played a role in the intactness of this specimen. It is well known that the human vertebral bone strength decreases with advancing age; however, published studies are lacking on the relationship between age and bone mineral density of C1. This study underscores the need to develop such a relationship. This is considered as a future research topic.

Clinical literatures have attributed injuries to the atlas due to the presence of the axial loading to the head, and the classic Jefferson fracture is a fracture of the bilateral arches in the anterior and posterior regions of C1 [14]. Variations of this injury have been reported [15,16]. The human cervical spine is devoid of the disks at the occiput-atlantal-axial complex (atlanto-occipital joint), and unique upper ligaments attach to the two vertebrae and base of the skull. The unique bony morphologies and interconnective ligaments allow the occipital condyle-atlas complex to primarily serve the flexion–extension function while the atlas-axis complex to serve the axial rotation function. From a neural perspective, vital structures are housed in this diskless region. The diastasis of the C1–C2 facet joint in two out of the four specimens may have clinical implications. Any injury to the capsular ligament with the distraction of the atlantal-axial joint may be a source of pain while the fracture is less likely to be unstable. In addition, any changes in the integrity of the transverse atlantal ligament with medial bone involvement may result in delayed instability. The magnitude of clinical stability cannot be quantified from cadaver studies, and medical images and clinical evaluations are needed. The loading variables and initial prehead rotation were not altered between specimens in this study with limited sample size. Additional samples should be tested to delineate the role of these variables in a future study.

The initial lateral head rotation of 30 deg is within the physiological limits [17,18]. The combination of rotation and lateral bending induced multiplanar loading to the specimen. Figures 3 and 4 show the mean forces and moments in all the anatomical axes and planes, and as can be seen, magnitudes between the axes/planes for these metrics are comparable. In other words, unlike the pure sagittal loading condition wherein sagittal moment and axial force are the major biomechanical tolerance metrics, for the prerotated condition, both force and moments metrics in multiple planes may be needed to define the human tolerance. For example, at the occipital condyles, the peak sagittal bending moment was approximately 40% of the coronal bending moment, and the off-axis axial bending moment was approximately 70% of the sagittal and 30% of the coronal moments. At the lower spine, the peak sagittal bending moment was approximately 80% of the coronal bending moment, and the off-axis axial bending moment (M_z) was approximately 50% of the sagittal (M_y) and 40% of the coronal bending (M_x) moments. The current neck injury criterion, N_ij, is applicable to the occipital condyle measurements [9]. It uses only the sagittal bending moment, while ignoring the axial and coronal bending moments. N_ij refers to the interaction metric in which force and moment are included in the injury criterion. For sagittal bending, the following formula is used to calculate the N_ij metric [19]. N_ij = (F_z/F_int) + (M_y/M_int), where F_Z and M_Y represent the axial force and sagittal bending moment, and F_int and M_int represent the critical intercepts for the force and moment, respectively.

Fig. 3.

Comparison of peak forces along the three anatomical axes at the occipital condyles and lower neck. Error bars denote standard deviations.

Fig. 4.

Comparison of peak bending moments about the three anatomical planes at the occipital condyles and lower neck. Error bars denote standard deviations.

For head-rotated postures, findings from this study suggest the need to include multiplanar moments for new injury criteria for automated vehicle postures. Although a similar criterion is not currently in the standards for the lower spine, a similar line of reasoning applies to the T1 bending moments. To develop injury risk curves, the present protocol can be used in a future study. The presence of multiplanar loading induces complex internal load-paths via changes in regional stress–strain responses and injuries. Because of the presence of multiplanar loads, injury risk curves derived for monoplanar loading may not be conservative or fully applicable.

The expected outcomes from tolerance studies often include investigation into the injuries, mechanisms, and injury criteria that may be in the form of a risk function. Using limited samples, this study produced relatively consistent injuries in four out of five cases, all focused on the atlas. Injury metrics were determined based on forces and moments in three dimensions. Analysis of peak metrics showed that the load distribution at the occipital condyles and at the lower neck are multiplanar. Development of a comprehensive set of injury probability curves is beyond the scope of the study, primarily due to sample size issues; however, with this acknowledgment, a preliminary set of risk curves can be developed as a first step using the exact censored assumption for the injured and right censored assumption for the intact outcomes.

To demonstrate the feasibility of obtaining an injury risk curve, using the survival analysis model and Akaike information criterion as the determinant statistic for selecting the distribution function, the Weibull distribution was found to be the optimum among the lognormal, Weibull, and loglogistic functions for the coronal moment at both ends of the spine [20,21]. The risk curve and its quality, expressed as the ratio of the width of the confidence interval at a given risk level to the mean value of the coronal moment at that risk level, are shown in Figs. 5 and 6, respectively [21]. Coronal moments of 37.6 N·m and 34.4 N·m were associated with 50% probability of failure at the upper and lower spines, respectively.

Fig. 5.

Comparison of injury risk curves for the axial force at the upper (OC) and lower (T1) spines

Fig. 6.

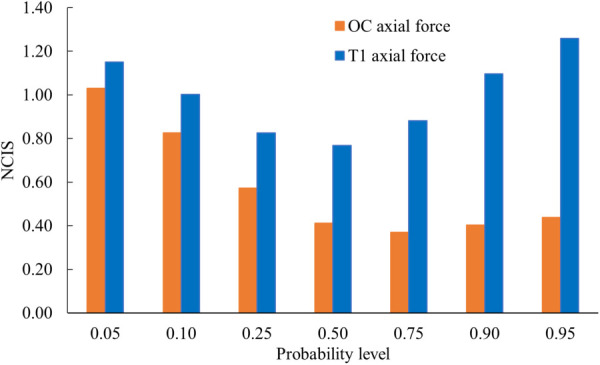
Comparison of the quality of the injury risk curves (NCIS—normalized confidence interval size, NCIS value of <0.5 considered good quality, 0.5–1.0 considered as fair quality, and 1.0–1.5 considered as marginal quality) for the axial force at the upper (OC) and lower (T1) spines

For the axial force, while the Weibull distribution was optimal at the upper spine, at the lower spine, the lognormal distribution was optimal among the three distributions. Figures 7 and 8 show that axial forces of 804 N and 558 N are associated with the same risk level at the upper and lower spines, respectively. These two-candidate force and moment metrics were chosen because they were considered primary variables under this loading mode. These injury risk curves should be considered as preliminary and because of the multiplanar loading, interaction-based criterion and risk curves should be developed in the future with additional sample size.

Fig. 7.

Comparison of injury risk curves for the coronal moment at the upper (OC) and lower (T1) spines

Fig. 8.

Comparison of the quality of the injury risk curves (NCIS—normalized confidence interval size, NCIS value of <0.5 considered good quality, 0.5–1.0 considered as fair quality) for the coronal moment at the upper (OC) and lower (T1) spines

A comparison of the present injuries with literature is not possible because similar cadaver studies with prehead rotation are not published, as discussed earlier. Clinical case reports have alluded to the mechanism for these types of cervical injuries: lateral bending and failure in tension or head in a laterally tilted posture [22,23]. The alignment of the specimen, lateral bending loading, and fracture outcomes from this study appear to confirm this postulate. It is reasonable to expect these patterns with automated postures that involve head pre-angulation.

Initial head rotation affects spinal joints in a dissimilar manner because of features such as the unique anatomy of the upper two cervical vertebrae that include facet joints, uncovertebral joints, and saddle shaped vertebral bodies from C3 to C7 [24]. The C1–C2 joint accounts for the maximum share of rotation in the entire cervical column; however, axial rotation is coupled with lateral bending in the lower spine [25–27]. This response contrasts with the flexion–extension mode in which the coupling action is minimal. The presence of prehead rotation influences the pattern of injury and often results in unilateral injuries that affect the facets, lamina or, pedicles on one side. For example, left-sided head rotation stretches the facet joints of the upper cervical spine on the contralateral side while the joint opposition is compromised on the ipsilateral side. This exposes the ipsilateral bony regions to injury. Unilateral fractures with prehead rotation have been documented in literature [22,28]. Sagittal injuries such as compression fractures have been documented in clinical and biomechanical studies without initial head rotation, and they are not unilateral [1,17,29]. The issue of severity of injuries depends on the magnitude of initial angulation and level of applied force transmitted to the head, which could result in unilateral fracture subluxation and more unstable type of cervical spine fractures.

While the sample size was small to analyze data based on demographic factors such as age and sex, biomechanical studies without initial head rotation have suggested that these factors also play a role. Injury risk curves have been developed with covariates of age and sex in one study [30]. Other studies have examined the role of curvature on injury mechanisms: lack of lordosis with straightened posture (loss of lordosis is more common with increasing age) leading to compression-related injuries while spines with curvature resulting in ligamentous trauma [6,7,13,31]. Additional factors such as osteoporosis, more common in older patients, may affect the risk of bony injury. Based on these studies, extending this study with additional samples may reveal the threshold of age and age-related osteoligamentous changes for specific injury risk levels.

While this study used only female specimens, as injury biomechanics are different between men and women spines, it is necessary to conduct similar experiments with male specimens and develop risk curves for this group. A loading rate of 1.5 m/s was chosen in this study, as studies without prerotation used a velocity of 3 m/s, and the tolerance is expected to be lower with the addition of the prerotation variable [15]. Additional tests with different rates are needed to investigate the effect of loading rate as human cervical spine tolerance is known to be dependent on factors such as age, sex, and loading rate. While this study was conducted with human cadaver specimens and developed injury risk curves, to compare these data to the dummy outputs, it would be necessary to conduct dummy tests using the same protocol, develop dummy-based risk curves, and obtain dummy-based injury assessment risk values to compare the responses between biological and physical human surrogates. The developed preliminary injury risk curves are based on a small sample size, and additional tests are needed. As cervical spine tolerances in the nonprehead rotation cases are known to depend on factors such as sex, age, and loading rate, it is important to consider these as covariates when additional samples are tested in the parametric survival analysis. These will be future research topics. It is well known that bone grows under stress (Wolff's law). The primarily axial direction of trabeculae orientation in certain regions of the bone predisposes to added stresses from the in vivo head mass and normal movements of the head-neck, and this results in increased density in those regions. In contrast, oblique trabecular orientations associated with hypodensity regions contribute to lower bone mineral densities in those regions.

Conclusions

Using a human cadaver model, this study determined the lateral bending tolerance of the head-cervical spine with initial head rotation posture using force and moment variables at the occipital condyles and lower neck. The response of the head-spine was found to be multiplanar. Injuries concentrated at the upper cervical level with involvement of the atlas lateral mass on the ipsilateral side and its joints. These injuries were different from those wherein the initial head rotation was not considered. These preliminary data may be applicable to future vehicle environments.

Funding Data

• Office of the Assistant Secretary of Defense for Health Affairs, through the Broad Agency Announcement (Award No. W81XWH-16-1-0010; Funder ID: 10.13039/100000182).

• National Institutes of Health (Award No. UL1TR001436; Funder ID: 10.13039/100000002).

• Department of Veterans Affairs Medical Research.