Micapipe: A pipeline for multimodal neuroimaging and connectome analysis

Abstract

Multimodal magnetic resonance imaging (MRI) has accelerated human neuroscience by fostering the analysis of brain microstructure, geometry, function, and connectivity across multiple scales and in living brains. The richness and complexity of multimodal neuroimaging, however, demands processing methods to integrate information across modalities and to consolidate findings across different spatial scales. Here, we present micapipe an open processing pipeline for multimodal MRI datasets. Based on BIDS-conform input data, micapipe can generate i) structural connectomes derived from diffusion tractography, ii) functional connectomes derived from resting-state signal correlations, iii) geodesic distance matrices that quantify cortico-cortical proximity, and iv) microstructural profile covariance matrices that assess inter-regional similarity in cortical myelin proxies. The above matrices can be automatically generated across established 18 cortical parcellations (100–1000 parcels), in addition to subcortical and cerebellar parcellations, allowing researchers to replicate findings easily across different spatial scales. Results are represented on three different surface spaces (native, conte69, fsaverage5), and outputs are BIDS-conform. Processed outputs can be quality controlled at the individual and group level. micapipe was tested on several datasets and is available at https://github.com/MICA-MNI/micapipe, documented at https://micapipe.readthedocs.io/, and containerized as a BIDS App http://bids-apps.neuroimaging.io/apps/. We hope that micapipe will foster robust and integrative studies of human brain microstructure, morphology, function, cand connectivity.

1. Introduction

The human brain is a complex network organized across multiple spatial and temporal scales (Betzel and Bassett, 2017). Neuroimaging, and in particular magnetic resonance imaging (MRI), provides versatile contrasts sensitive to the brain’s microstructure, connectivity, and function, offering a window into its organization in living humans (Turner, 2019; Larivière et al., 2019; van den Heuvel et al., 2019; Van Essen et al., 2013).

Recent years have witnessed the rise of multiple neuroimaging data acquisition efforts (Gordon et al., 2017; Royer et al., 2021; Van Essen et al., 2012) as well as initiatives for open data sharing to promote transparency and reproducibility (Milham et al., 2018). These initiatives offer researchers the ability to interrogate brain structure and function in thousands of individuals across multiple sites from around the world. In addition, a variety of tools and processing pipelines has previously been developed. These include tools for the automated analysis of cortical/subcortical morphology based on T1-weighted MRI (Fischl, 2012; Kim et al., 2005; Patenaude et al., 2011), approaches for the analysis of myelin-sensitive MRI contrasts to assess brain microstructure (Paquola et al., 2019b; Glasser and Van Essen, 2011; Waehnert et al., 2016), measurements of cortical geometry and proximity relationships (Ecker et al., 2013; Hong et al., 2018; Paquola et al., 2020), the study of intrinsic brain function and functional connectivity via resting-state functional MRI, rs-fMRI (Biswal et al., 2010; Craddock et al., 2013; Esteban et al., 2019), and analysis of structural connectivity inferred via diffusion MRI tractography (Cieslak et al., 2021; Daducci et al., 2012; Tournier et al., 2019; Cai et al., 2021; Theaud et al., 2020; Rheault et al., 2021). Individually, ongoing advances in MRI modelling approaches result in increasing biological validity (Craddock et al., 2015; Jbabdi et al., 2007; Mars et al., 2021), promising to extend findings and theory from classical neuroanatomy in non-human animals to humans. Yet, most tools developed to date generally focus on the processing of individual modalities, or the combination of only few different modalities (e.g., T1-weighted MRI and rs-fMRI).

System neuroscience has increasingly benefitted from paradigms that combine different imaging modalities (Paquola et al., 2020; Van den Heuvel et al., 2019; Van den Heuvel and Yeo, 2017). For example, multiple studies have begun to study brain function and functional connectivity in surface-based anatomical reference frames (Huntenburg et al., 2021; Tierney et al., 2013; Vos de Wael et al., 2018), and combined these assessments with diffusion MRI approaches (Liu et al., 2016; Hong et al., 2019). Further work integrating structural and functional neuroimaging modalities has propelled interest in examining structure-function relationships in the human brain (Huntenburg et al., 2018; Suárez et al., 2020; Benkarim et al., 2022; Paquola et al., 2019b; Vázquez-Rodríguez et al., 2019). Furthermore, there has been significant development towards the identification of multimodal parcellations (Fan et al., 2016; Eickhoff et al., 2018; Genon et al., 2021, 2018; Glasser et al., 2016) and large-scale gradients of brain organization (Vos de Wael et al., 2020, 2021; Margulies et al., 2016; Paquola et al., 2020, 2019a, 2019b; Valk et al., 2020; Müller et al., 2020; Tian et al., 2020). However, researchers interested in synergies across multiple modalities are often forced to develop custom-built image co-registration and data-integration procedures.

To build upon existing MRI processing pipelines that are primarily geared towards single modalities, we developed micapipe. The pipeline integrates processing streams for structural MRI, rs-fMRI, diffusion-weighted MRI, and myelin-sensitive MRI to automatically generate models of cortical geometry and microstructure, as well as structural and functional connectivity. Micapipe generates inter-regional matrices across different spatial scales, incorporating multiple cortical as well as subcortical/cerebellar parcellations (Desikan et al., 2006; Destrieux et al., 2010; Scholtens et al., 2018; von Economo, 2009; Fischl, 2012; Vos de Wael et al., 2020; Schäfer et al., 2018; Glasser et al., 2016; Patenaude et al., 2011; Diedrichsen et al., 2009). In a nutshell, micapipe transforms BIDS-conform MRI data (Gorgolewski et al., 2017) to process macroscale models of brain organization in an easy-to-analyze format, with it being the only pipeline providing models of structural connectivity, functional connectivity, geodesic distance, and microstructural similarity within a unified tool. Easy-to-verify outputs and visualizations can be produced for quality control (QC). In addition to its code-base being openly available on GitHub (http://github.com/MICA-MNI/micapipe), micapipe is also available as a Docker container, included as a BIDS App, and is accompanied by detailed tutorials and an expandable documentation (http://micapipe.readthedocs.io).

2. Results

Micapipe has a modular workflow that can incorporate multiple MRI data modalities (T1-weighted MRI, myelin-sensitive MRI, diffusion-weighted MRI, and resting-state functional MRI), converting BIDS-conform input into BIDS-conform surface, volume, and matrix data (Fig. 1A). The following sections describe key pipeline features, main outputs, and automated quality control (QC) visualizations. We also perform several validation experiments across a diverse range of datasets.

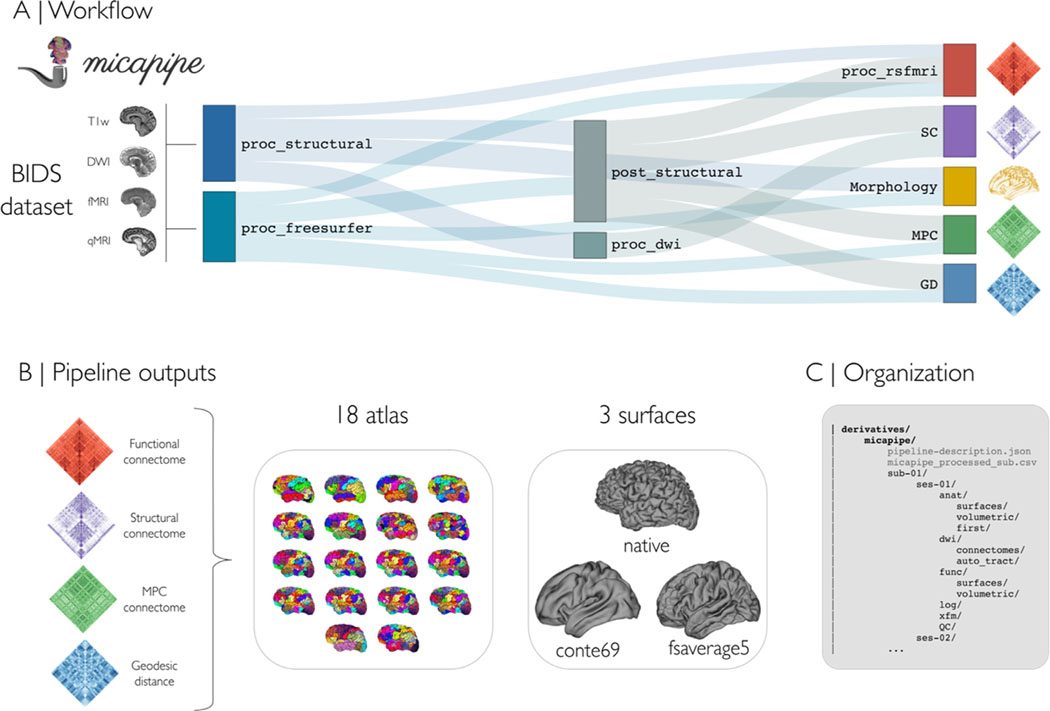
Fig. 1.

(A) Pipeline workflow. B) Outputs can be generated across 18 different cortical parcellations (100–1000 parcels), in addition to subcortical and cerebellar parcellations. Most results are mapped to three different surface spaces: native, conte69 and fsaverage5. C) Outputs are hierarchically ordered with BIDS-conform naming.

2.1. Pipeline workflow

Processing modules of micapipe can be run individually or bundled using specific flags via a command-line interface. Multimodal integration relies strongly on the characterization of anatomy via T1-weighted MRI processing. Using volume- and surface-based processing streams, the pipeline generates subcortical, cortical and cerebellar segmentations in subject- and modality-specific spaces. Using structural imaging data, in addition to other input modalities, inter-regional brain matrices can be generated across 18 combinations of cortical, subcortical, and cerebellar parcellations. Inter-regional matrices are: (i) structural connectomes (SC) derived from diffusion tractography (Smith et al., 2015a), (ii) functional connectomes (FC) derived from resting-state signal correlations (Biswal et al., 2010), (iii) geodesic distance (GD) matrices that quantify cortico-cortical proximity using cortical surface models (Ecker et al., 2013; Hong et al., 2018), and (iv) microstructural profile covariance (MPC) matrices that assess inter-regional similarity in intracortical intensity profiles from microstructurally-sensitive imaging (Paquola et al., 2019b). Surface-mapped features are made available across three surfaces (Fig. 1B): native, conte69 (Van Essen et al., 2012), and fsaverage5 (Fischl et al., 1999). Intermediary files and processed derivatives and matrices conform to BIDS naming conventions (Fig. 1C), facilitating future use and harmonization across datasets and software.

2.2. Quality control (QC)

The QC module visualizes outputs at the individual and group levels (Fig. 2A). Reports detail completed processing steps, including image registrations, surface parcellations, and inter-regional feature matrices. They are organized by modality and parcellation. These reports help users to identify missing data, poor image quality, and faulty registrations (Fig. 2A). Complementing subject-specific reports, group level QC automatically generates a report outlining completed and missing modules for each subject facilitating use for large datasets (Fig. 2B).

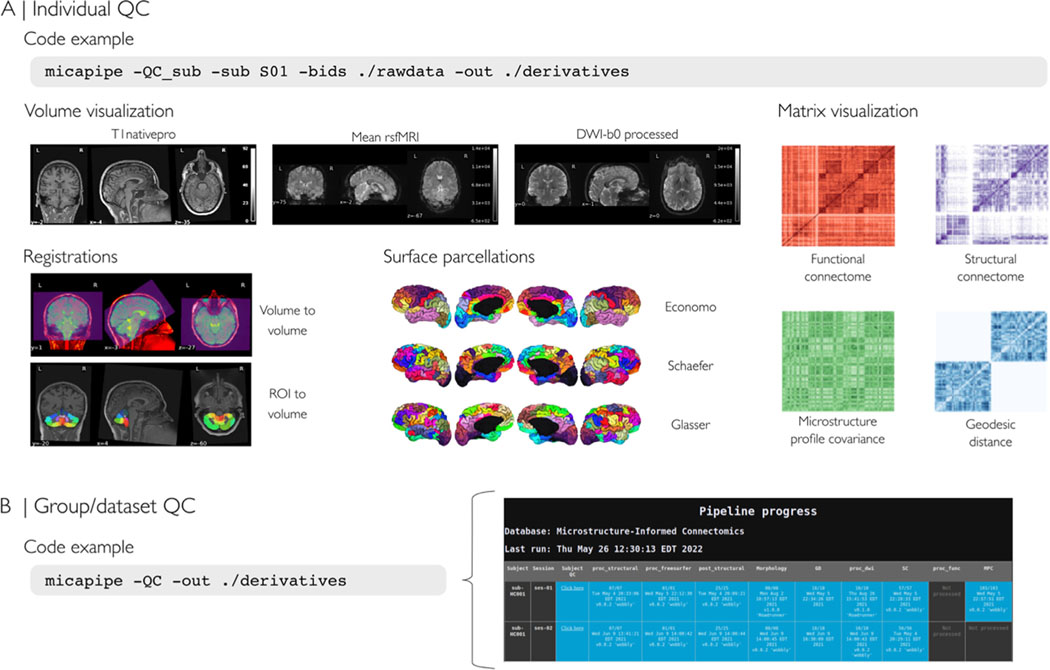
Fig. 2.

(A) Individual level quality control (QC), which can be run at any point during the processing. The QC procedure will generate a html report file for each subject containing visualizations of intermediate files for volume visualization, cross-modal co-registrations, and surface parcellations. Moreover, it allows inspection of inter-regional matrices such as the structural connectome (from diffusion MRI tractography), the functional connectome (from resting-state fMRI signal correlation), the microstructural profile covariance matrix (from correlations of intracortical microstructural profiles), and geodesic distance matrices. (B) QC can also be run at a group/dataset-level. The report consists of a color-coded table with rows as subjects and columns as the pipeline modules (blue: completed, orange: incomplete/error, dark gray: not processed).

2.3. Assessing output consistency within and between datasets

We evaluated whether micapipe yields consistent results across 50 individuals of an openly available multimodal MRI dataset [MICA-MICs; (Royer et al., 2021), and also compared processed outputs to those from six additional datasets (Table S1)].

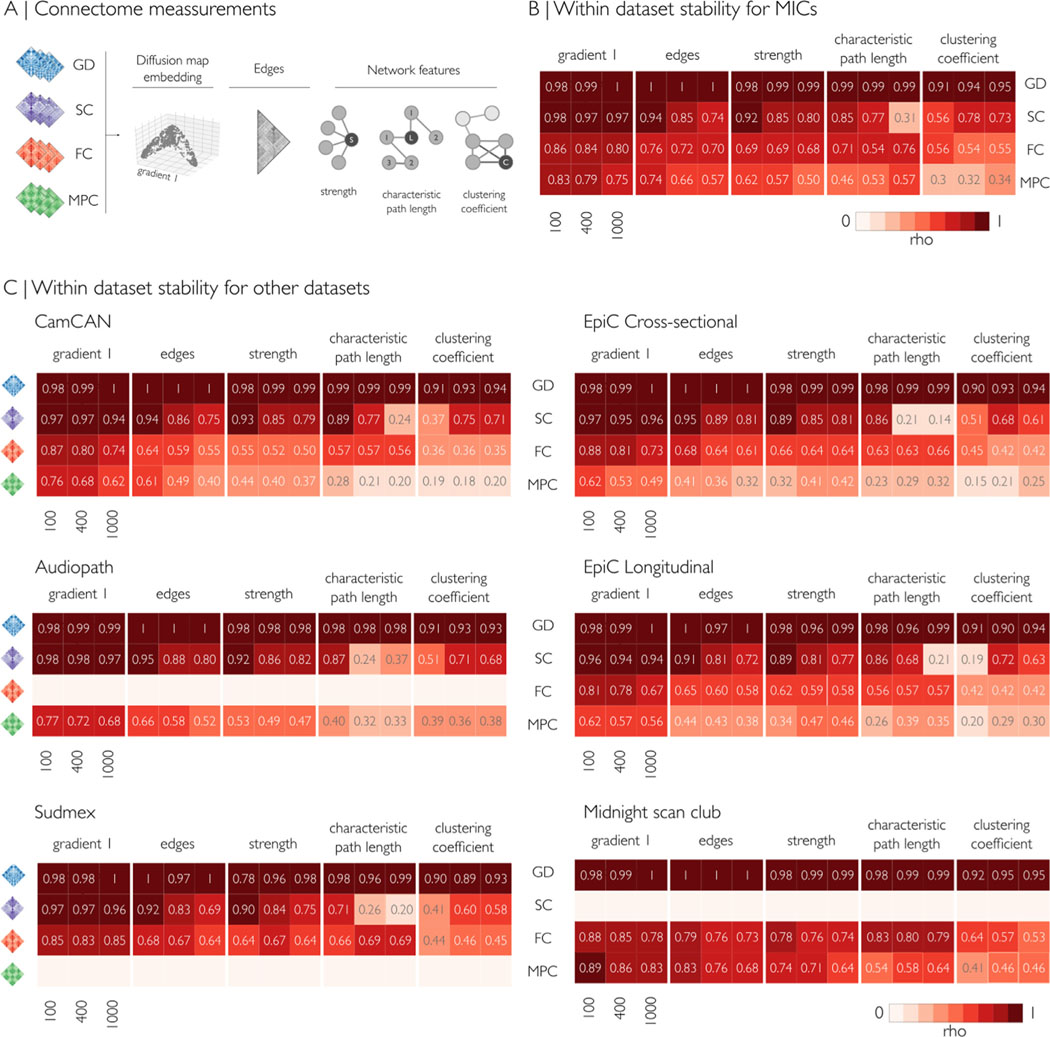
We first assessed within-dataset consistency for each modality (GD, SC, FC, MPC) at three different granularities (Schäfer 100, 400 and 1000 parcels) using five different metrics. We generated modality- and dataset-specific mean group matrices and computed consistency across the following features: the first eigenvector/gradient explaining the most data variance (calculated via diffusion map embedding (Coifman et al., 2006)), the matrix edges, as well as node strength, characteristic path length, and clustering coefficient as three representative graph features [(Rubinov and Sporns, 2010), Fig. 3A]. We correlated subject-level and group-level metrics to quantify within-dataset consistency (Spearman’s rho, see Supplementary Fig. 5). Correlations were highest for GD and SC, followed by FC and MPC. Gradient 1 was the most consistent measure across parcellations and modalities, followed by edges and node strength. Overall, characteristic path length was similar at lower granularity (100 parcels) but increasingly dissimilar at higher granularity (1000 parcels). Clustering coefficient had variable patterns depending on the modality and granularity (Fig. 3 B,C). Particularly, GD showed the highest within-dataset similarity over all datasets and measurements (rho range = 0.89–0.99), followed closely by SC in gradient 1, edges, and strength (rho range = 0.75–0.98). SC-derived characteristic path length was increasingly dissimilar at high granularity, whereas clustering coefficient had a peak of similarity at 400 parcels in all datasets (rho range = 0.6–0.78), and low similarity at 100 and 1000 parcels. FC gradient 1 similarity was consistent for all granularities and datasets (rho = 81.3 ± 5.7, mean ± sd), with a slight decrease at higher granularity. Edges and strength from FC had a good level of similarity (rho range = 0.68–0.79), with highest values observed in the Midnight scan club dataset, which notably had the highest resolution of rest-fMRI. MPC derived measurement showed lower similarity at higher granularities. Characteristic path length and clustering coefficient derived from MPC had a poor-to-fair within group similarity (rho range = 0.15–0.64), likely due to the topology of these matrices. Findings were consistent across datasets, and higher intra-group similarity probably reflected higher resolution of the MRI acquisitions (e.g., MICs and MSC).

Fig. 3.

Within dataset mean consistency, indicating the correlation between subject- and group-level measurements (Spearman’s rho), for Schaefer-100, Schaefer-400, and Schaefer-1000 parcellations. (A) For each modality, five measurements were evaluated: principal gradient, edges, node strength, path length, and clustering coefficient. Empty rows indicate modalities that were not analyzed due to missing acquisitions. (B,C) Across datasets, correlations were highest for GD and SC, followed by FC and MPC. Gradient 1 was the most consistent measure across parcellations and modalities, followed by edges and node strength. Overall, characteristic path length was similar at lower granularity (100 parcels) but increasingly dissimilar at higher granularity (1000 parcels). Clustering coefficient had variable patterns depending on the modality and granularity. MPC: microstructural profile covariance, FC: functional connectivity, SC structural connectivity, GD geodesic distance.

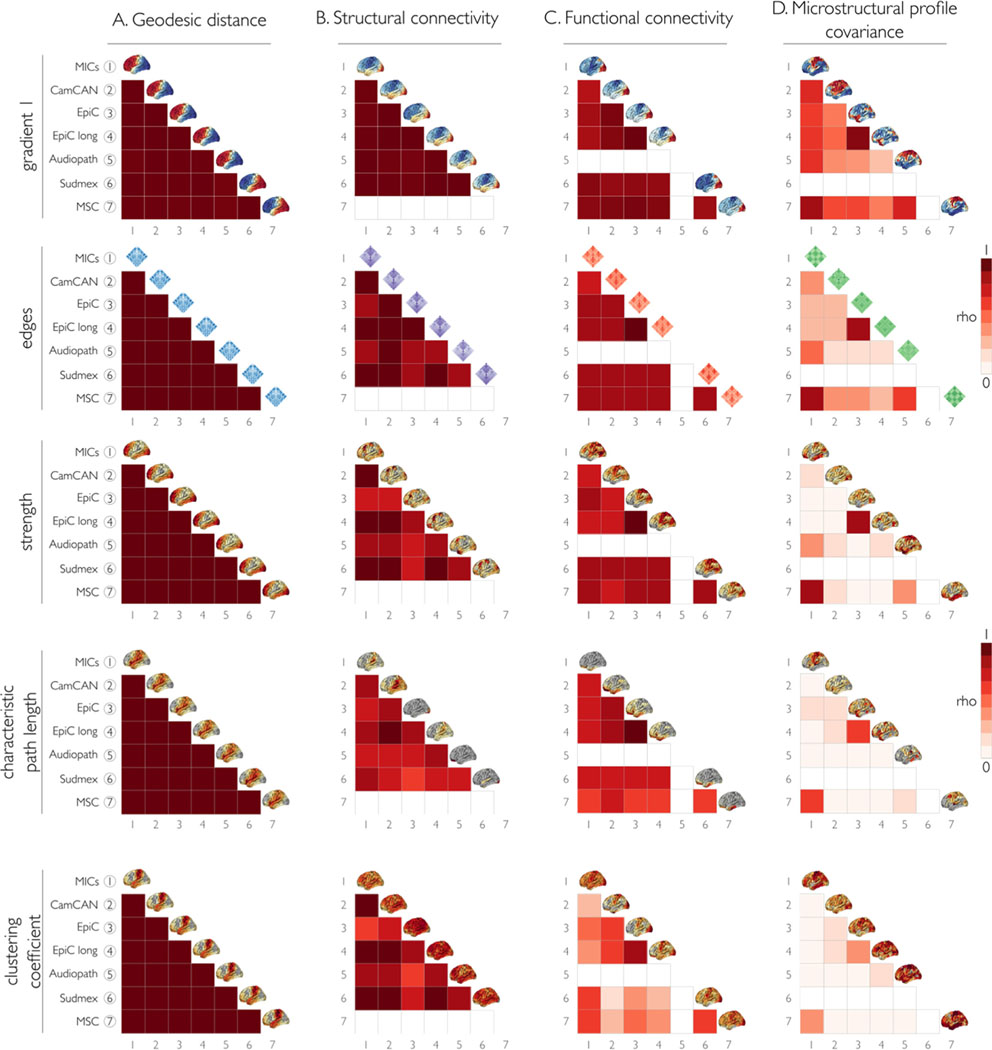
We also compared the consistency of each measurement between datasets (Fig. 4). As for the within-dataset analysis, we found the highest similarities for GD and SC, followed by FC and MPC. GD, SC and FC showed high similarity between datasets for the edges, first eigenvector/gradient, and node strength. MPC had the lowest between dataset consistency for all measurements, except for the comparison between EpiC and EpiC longitudinal, and MICs and MSC, whose values were mostly high except in the MPC clustering coefficient. Particularly, we observed high similarity between GD-derived metrics across all datasets. SC consistency between datasets was also high for most measurements, gradient 1 being the most similar, followed by the edges. The graph features derived from SC had good consistency but more variability between datasets. FC had decreased consistency between datasets for characteristic path length and clustering coefficient, compared to the good consistency for gradient 1 and edges. It should be noted that the highest consistency for FC across all measurements was between EpiC and EpiC longitudinal, likely because both datasets had similar acquisition parameters and included an overlapping subject sample.

Fig. 4.

We assessed consistency of matrix parameters across datasets using Spearman’s rho correlation coefficient for the same features as in Fig. 3A. Each column represents the different modality matrices: (A) geodesic distance, (B) structural connectome, (C) functional connectome, and (D) microstructural profile covariance. The diagonal shows the mean value plotted on the surface of each dataset by measurement. As for the within-dataset analysis, we found the highest similarities between datasets for GD and SC, followed by FC and MPC. GD, SC, and FC showed high similarity between datasets for the edges, first eigenvector/gradient, and node strength. FC had decreased consistency between datasets for characteristic path length and clustering coefficient. MPC had the lowest between dataset consistency for all measurements. Empty matrix entries (coloured in white) indicate missing data for a given dataset.

2.4. Assessing test-retest similarity

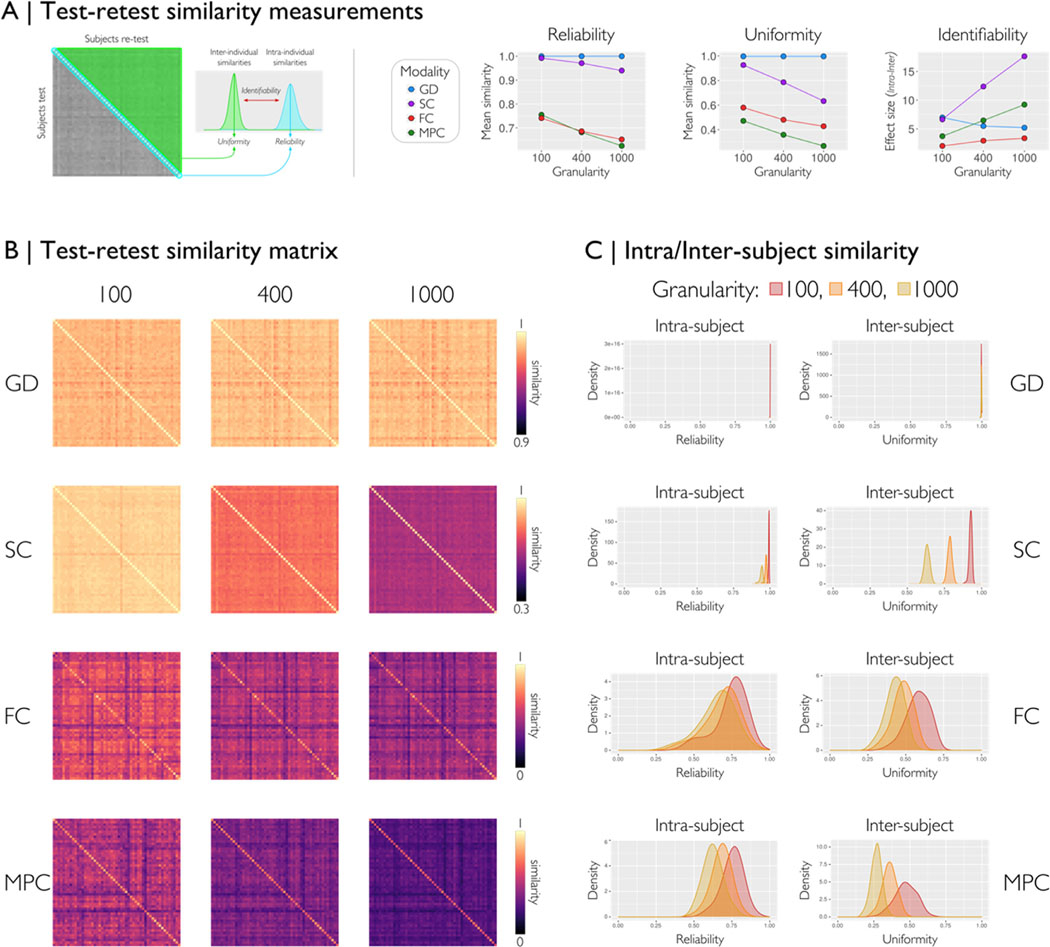
We assessed the test-retest reproducibility, using 53 subjects two acquisitions each from the Human Connectome Project, adopting a previously published framework (Seguin et al., 2022). Here, we generated similarity matrices between all pairs of subjects (subject-test by subject-retest) for each modality. From each similarity matrix, we computed three metrics: reliability, uniformity, and identifiability (Fig. 5A). The diagonal of the similarity represents the intra-individual similarity i.e., reliability when processing two acquisitions of the same subject. The uniformity or inter-individual similarity (triangular matrix) quantifies the mean similarity of matrices belonging to different individuals within a given dataset. Identifiability measures the extent to which matrices of the same individuals are differentiable from the rest of the group. Ideally, the processed matrices should be reliable (i.e., high reliability) and preserve inter-individual differences (i.e., low uniformity). For all feature matrices of each modality and three different parcellations (Fig. 5 B), we found reliability exceeding uniformity, leading to high identifiability. GD and SC had excellent reliability (Similarity >0.9), followed by FC and MPC, which decreased at higher granularity. Uniformity also decreased at high granularity for all modalities except GD. On the other hand, identifiability increased at higher granularities except for GD (Fig. 5A-left).

Fig. 5.

We assessed the capability of micapipe to generate reproducible outcomes in a test-retest scenario, adoping a prior framework (Seguin et al., 2022). For all modalities and three parcellations, we evaluated the similarity between matrices of two different acquisitions (53 subjects from HCP, run-1 and run-2 scans). (A) From each similarity matrix of subject-test by subject-retest, we computed three measures of similarity: reliability (intra-subject), uniformity (inter-subject), and identifiability (effect size between intra- and inter-). Reliability quantifies the mean processing consistency for an individual; uniformity quantifies the mean conformity of matrices belonging to different individuals, and identifiability quantifies how an individual can be recognized from a group based on the matrix features. The scatter plots with lines show the mean values of each similarity measure for each modality over three granularities (Schaefer-100, 400 and 1000). (B) Similarity matrices for each modality and granularity. (C) Density plots of the reliability and uniformity by modality and granularity of all subject pairs. For all feature matrices, we found higher reliability than uniformity, with excellent performance for GD and SC, and good results for FC and MPC. Overall, less granular parcellation data had higher similarity than more granular parcellation data across all modalities. GD=geodesic distance, SC=structural connectome, FC=functional connectome, and MPC=microstructural profile covariance.

2.5. Performance

We tested micapipe on seven different databases acquired using different MRI sequence/parameter combinations (Table S1). Processing times varied depending on the image resolution, the need to additionally process data using FreeSurfer, the number of streamlines selected for the structural connectome generation, and the type of acquisitions per dataset (Table S2). Processing was performed on the Brain Imaging Center (BIC) cluster of the Montreal Neurological Institute and Hospital on Ubuntu 18.04.5 LTS version workstations. A maximum virtual memory of 6GB, with 6–10 CPU cores, and 20 GB of RAM were required. Output size depended on image resolution and the length of the rs-fMRI acquisitions (Table S3).

2.6. Data and code availability statement

An expandable documentation at https://micapipe.readthedocs.io describes installation, usage, pipeline steps, updates, extra features, and provides a series of ready-to-use tutorials. All code can be found at https://github.com/MICA-MNI/micapipe, and is published under the General Public License 3.0. Micapipe is delivered as a docker container via BIDS-App [ http://bids-apps.neuroimaging.io/apps/ (Gorgolewski et al., 2017)], and available on ReproNim [ https://github.com/ReproNim/containers (Halchenko et al., 2021)]. Detailed steps to use the Docker container and to build a corresponding singularity container are available under the readthedocs documentation. Code for figures and tables can be found in the micapipe-supplementary GitHub repository (https://github.com/MICA-MNI/micapipe-supplementary).

3. Discussion

We present micapipe, an open software package to integrate and process raw multimodal MRI data into multiple measures of structural and functional human brain network organization. As a standalone BIDS App, micapipe inputs and outputs BIDS-conform MRI data. Its outputs consist of derivative features across multiple parcellations, available in both surface- and volume-based reference spaces. Notably, micapipe outputs include regional measures of e.g., brain morphology, microstructure, and function together with inter-regional matrices encoding (i) cortico-cortical spatial proximity (based on geodesic distance analysis along cortical surfaces derived from T1-weighted MRI), (ii) microstructural similarity (derived from intracortical profile covariance analysis of myelin-sensitive MRI), (iii) intrinsic functional connectivity (obtained from rs-fMRI signal correlations), and iv) structural connectivity (estimated from diffusion MRI tractography). Derivative features are available across in surface-, volume-, and parcellation-based reference spaces, incorporating up to 18 different cortical as well as sub cortical/cerebellar parcellations. micapipe furthermore offers advanced functionalities for individual and group-level quality control and visualization of intermediary as well as final outputs. The pipeline has been validated across multiple datasets. As a unified tool to fuse and analyze multimodal neuroimaging data, micapipe offers neuroscientists a workflow to robustly probe human brain organization across multiple scales.

A range of pipelines have previously been developed to process MRI images from specific modalities, including tools for the generation of cortical and subcortical segmentations based on T1-weighted MRI data (Das et al., 2009; Fischl, 2012; Kim et al., 2005), pipelines to process functional MRI data (Craddock et al., 2013; Esteban et al., 2019), as well as tools for diffusion MRI data handling (Cieslak et al., 2021; Jenkinson et al., 2012; Tournier et al., 2019). Several workflows have furthermore been developed for connectome mapping (Daducci et al., 2012; Whitfield-Gabrieli and Nieto-Castanon, 2012), which allow users to examine structural and functional network architecture in a systematic manner. Building upon these developments, micapipe offers a unified framework for multimodal fusion and data processing. As such, it is similar in scope to the Connectome Mapper tool (Daducci et al., 2012), although with notable differences. In particular, micapipe incorporates a stream for the surface-based mapping of intracortical myelin proxies and for the generation of microstructural profile covariance (Paquola et al., 2019b). A growing body of literature emphasizes the utility of myelin-sensitive MRI analysis for cortical parcellation (Carey et al., 2018; Glasser and Van Essen, 2011; Granberg et al., 2017), to assess brain and cognitive development (Deoni et al., 2012; Whitaker et al., 2016; Lebel and Deoni, 2018; Paquola et al., 2019a), and to interrogate microstructural imbalances in common brain disorders (Cooper et al., 2019; Du et al., 2019; Bernhardt et al., 2018; Larivière et al., 2019). Recent work has shown that the analysis of covariance patterns of intra-cortical microstructural profiles can generate new descriptions of large-scale network organization (Paquola et al., 2020; Royer et al., 2020). These networks appear primarily governed by systematic shifts in laminar differentiation and neuronal density, showing a principal organizational axes similar to those at the level of cytoarchitecture and intrinsic functional connectivity (Margulies et al., 2016; Paquola et al., 2021, 2019b). A further feature is the automated generation of cortico-cortical geodesic distance matrices, which indexes proximity between different regions on the folded cortical surface. Cortico-cortical geodesic distance has been suggested to relate to intrinsic, horizontal connectivity within the cortical ribbon as well as to cortical wiring cost (Ecker et al., 2013; Hong et al., 2018; Paquola et al., 2020). Moreover, several investigations into principles of macroscale brain organization have emphasized that the brain is a physically embedded network, and that thus inter-regional distance relationships may help in the understanding of the topographic layout of functional systems and the connections formed between them (Betzel et al., 2016; Betzel and Bassett, 2018; Margulies et al., 2016; Valk et al., 2020; Wang et al., 2022; Smallwood et al., 2021). As such, distance measures can be assessed as a feature of interest but also as an intrinsic variable one wants to control connectome analyses for in some situations.

A series of evaluations assessed consistency of micapipe outputs, studying data from 455 individuals across seven datasets. Our evaluations focused on the consistency of inter-regional matrix edges, the first eigenvector (gradient), and three widely used graph theoretical measurements (node strength, characteristic path length, clustering coefficient) for up to four matrix modalities (i.e., geodesic distance, functional connectivity, structural connectivity, microstructural covariance). Altogether, our results indicate a generally high consistency of the first gradient across datasets, with some variations across modalities. For example, geodesic distance and structural connectivity gradients were markedly consistent (r > 0.95), followed by functional connectivity and microstructural profile covariance. It is likely that functional connectivity measures and associated gradients may, in part, be influenced by state-to-state variations compared to the more static measures of structural connectivity and geodesic distance, likely in addition to data acquisition related effects. Edges and graph derived measurements followed an analogous pattern of consistency. With respect to the relatively low stability of microstructural profile covariance, one needs to highlight that the included datasets varied in terms of microstructurally sensitive MRI contrasts, featuring T1-weighted/T2w intensity ratio (Glasser and Van Essen, 2011), quantitative T1 relaxometry (Royer et al., 2021), as well as magnetization transfer imaging (Shafto et al., 2014). While these sequences are all thought to be sensitive to intracortical myelin content, their individual biophysical specificity remains to be established in future work.

Through the successful integration of several processing tools, micapipe provides multiple ready to use inter-regional feature matrices, i.e., structural connectomes, functional connectomes, microstructural covariance, and geodesic distance, together with QC procedures. Our pipeline is supported by a growing ecosystem of open tools for data and code sharing, notably Github, readthedocs, Docker, BIDS Apps (Gorgolewski et al., 2017), and repronim/datalad (Robert et al., 2016). By making micapipe openly accessible as well, we hope that it will be beneficial for future studies on human brain organization.

4. Materials and methods

Micapipe runs modular processing streams on BIDS-conform raw T1-weighted, microstructure-sensitive, diffusion-weighted, and resting-state functional MRI data to generate fully processed surface/volume features as well as inter-regional feature matrices. A documentation with detailed descriptions on the installation, implementation, as well as usage examples and output files are available at https://micapipe.readthedocs.io/.

4.1. Workflow and main processing modules

Micapipe requires the input dataset to be formatted in BIDS (Gorgolewski et al., 2016).

4.1.1. Structural processing

Structural processing operates on T1-weighted images. The structural processing workflow can perform volumetric (with command-line option: -proc_structural) and surface-based (-proc_freesurfer, - post_structural, -GD, -Morphology) processing. The workflow registers subject data to volumetric and surface-templates providing several useful structural metrics for further analyses. These include geodesic distance matrices (-GD) mapped to multiple parcellation schemes as well as vertex-wise cortical thickness and curvature data (-Morphology). The structural workflow includes tools from AFNI (Cox, 1996), FSL (Jenkinson et al., 2012), ANTs (Avants et al., 2011), Mrtrix3 (Tournier et al., 2019) and FreeSurfer (Fischl, 2012). Further information about the usage and outputs is found in the structural processing section in the online documentation.

Proc_structural.

Initial structural pre-processing (i.e., -proc_structural) keeps all data in volumetric format and generates a T1-weighted image in native processing space (nativepro, Fig. S1A). Each T1-weighted run is reoriented to LPI orientation (i.e., left-right, posterior-anterior, inferior-superior), de-obliqued, and oriented to standard space (MNI152). If multiple T1-weighted scans are found in the raw data, they are linearly aligned to the first run and averaged. Next, the average image is corrected for intensity nonuniformity (N4, Tustison et al., 2010) and intensity is normalized between 0 and 100. The resulting image is named T1nativepro, which stands for T1-weighted in native processing space. T1nativepro is skull-stripped, subcortical structures are segmented using FSL FIRST (Patenaude et al., 2011), and tissue types are classified (gray matter, white matter, CSF) using FSL FAST (Zhang et al., 2001). A non-linear registration to MNI152 (0.8mm and 2mm resolutions) is calculated (Tustison and Avants, 2013) and a five-tissue-type (5TT) image segmentation is generated for anatomically constrained tractography.

Proc_freesurfer.

Cortical surface segmentations are generated from native T1-weighted scans using FreeSurfer 6.0 (Fischl, 2012) and ordered under the FreeSurfer directory, following BIDS naming conventions. We provide an option for datasets that have already been quality controlled to easily integrate the results within the pipeline’s directory structure and an option to process with voxel sizes less than 1mm ³ at native resolution (-hires). We recommend that users carefully inspect and, if needed, manually correct FreeSurfer-generated cortical surface segmentations. As micapipe relies heavily on surface-based processing, poor segmentation quality may compromise downstream results.

Post_structural.

The first step of the post structural processing is to calculate an affine registration from native FreeSurfer space to T1nativepro space. It then registers a probabilistic cerebellar atlas (Diedrichsen et al., 2009) from MNI152 to the subject’s T1nativepro space using affine and non-linear transformations previously computed in the -proc_structural module. Next, a surface-based registration of fsaverage5 annotation labels to native surface is performed, and the surface-based parcellation in native FreeSurfer space is transformed into a volume. Finally, the transformation matrices are applied to bring each volumetric parcellation from native FreeSurfer space to T1nativepro space. In the last step of this module, the pipeline builds a conte69–32k sphere and resamples white, pial and midthickness native surfaces to the conte69–32k template.

The -post_structural module registers native FreeSurfer-space cortical surfaces to two different standard templates (fsaverage5 and conte69), in addition to mapping all cortical parcellation schemes to the subject’s native surface space and volumetric T1nativepro space (Fig. S1B). Micapipe provides a total of 18 cortical, subcortical and cerebellar parcellations at different resolutions according to anatomical, cytoarchitectural, intrinsic functional, and multimodal schemes, at different resolutions. Anatomical atlases available in micapipe include Desikan-Killiany (aparc, Desikan et al., 2006) and Destrieux (aparc.a2009s, Destrieux et al., 2010) parcellations provided by FreeSurfer, as well as an in vivo approximation of the cytoarchitectonic parcellation studies of Von Economo and Koskinas (Scholtens et al., 2018). Additionally, we include similarly sized sub-parcellations, constrained within the boundaries of the Desikan-Killiany atlas, providing matrices with 100, 200, 300, and 400 cortical parcels following major sulco-gyral landmarks (Fischl, 2012; Vos de Wael et al., 2020). Parcellations based on intrinsic functional activity are also included across several granularities (100, 200, 300, 400, 500, 600, 700, 800, 900, and 1000 nodes, (Schäfer et al., 2018). Lastly, we also provide a multimodal atlas with 360 nodes derived from the Human Connectome Project dataset (Glasser et al., 2016). All atlases are provided on Conte69 and fsaverage5 surface templates, and on each participant’s native surface to generate modality-specific matrices in subsequent modules.

Morphology.

This module registers cortical thickness and curvature measurements to two distinct templates. Both surface-based morphological features are registered to fsaverage5 and conte69 and smoothed with a gaussian filter with full width half maximum of 10mm.

GD: geodesic distance.

Individual GD matrices are computed along each participant’s native cortical midsurface using workbench tools (Marcus et al., 2011). First, a centroid vertex is defined for each cortical parcel by identifying the vertex with the shortest summed Euclidean distance from all other vertices within its assigned parcel. Then, the geodesic distance is calculated from the centroid vertex to all other vertices on the midthickness mesh using Dijkstra’s algorithm (Dijkstra, 1959). Notably, this implementation computes distances not only across vertices sharing a direct connection, but also across pairs of triangles which share an edge in order, thus mitigating the impact of mesh configuration on calculated distances. Vertex-wise GD values were averaged within parcels to improve computation performance.

4.1.2. Diffusion -weighted imaging processing

This section describes all DWI-related processing steps implemented in micapipe, which heavily rely on tools from MRtrix3 (Tournier et al., 2019). This includes image processing preparation for the construction of tractography-based structural connectivity matrices, as well as associated edge length matrices, all in native DWI space (Fig. S1C). Micapipe DWI processing has been optimized for multi-shell DWI but can also handle single-shell data. Geometric and inhomogeneity corrections are performed in datasets that contain one or more reverse phase encoding DWI. It is a mandatory requirement that all DWIs have associated bvec, bval and json files, with encoded phase direction and total readout time.

Proc_dwi.

This module processes DWI scans, and derives several potentially useful metrics (e.g., fractional anisotropy, mean diffusivity, Fig. S1C). First, if there is more than one set of DWI scans in the BIDS directory, they can optionally be aligned to each other using a rigid-body registration, and concatenated. All DWI images are then converted to Mrtrix Imaging format (mif), which encodes the bvec, bval, phase encoding direction and total readout time (also adjusting bvec information for potential transformations that were applied to the shells). Concatenated DWI images undergo denoising by estimating data redundancy in the PCA domain via a Marchenko-Pasteur approach [MP-PCA, (Veraart et al., 2016; Cordero-Grande et al., 2019)]. Then, Gibbs ringing artifact correction is applied (Kellner et al., 2016), and residuals are calculated from denoised images for QC purposes. Provided a reverse phase encoding, susceptibility distortion, head motion, and eddy currents are corrected (Andersson et al., 2003; Smith et al., 2004; Andersson and Sotiropoulos, 2016). If none is provided, only motion correction is performed. Additionally, outlier detection and replacement are applied (Andersson et al., 2016). After this step, the quality of the motion and inhomogeneity corrected diffusion images is assessed using eddy_quad (Bastiani et al., 2019), and a non-uniformity bias field correction (Tustison et al., 2010) is applied to finalize DWI preprocessing. Next, the b0 image is extracted from the corrected DWI and linearly registered to the main structural image (i.e., T1nativepro). A DWI brain mask is generated by registering the MNI152 brain mask to DWI space using previously generated transformations. A diffusion tensor model (Basser et al., 1994) is then fitted to the corrected DWI and the fractional anisotropy and mean diffusivity images are computed (Veraart et al., 2013). An estimation of the response function is calculated over different tissues: cerebrospinal fluid, white matter, and gray matter (Dhollander, et al., 2016). These are later used to estimate the fiber orientation distribution (FOD) by spherical deconvolution (Jeurissen et al., 2014; Tournier et al., 2004). Next, intensity normalization is applied to each tissue FOD (Raffelt, et al., 2017). A second registration, in this case non-linear, is calculated between the normalized white matter FOD and the T1-weighted image previously registered linearly to DWI space. The resulting warp field allows for an improved registration between the T1-weighted and the native DWI space in most datasets. Finally, the 5TT segmentation image is registered to native DWI space and a gray matter white matter interface mask is calculated. For QC purposes, a track density image (Calamante et al., 2010) is computed with 1 million streamlines using the iFOD1 algorithm (Tournier et al., 2012) and anatomically constrained tractography (Smith et al., 2012). Additionally, if the user has an already processed DWI image, we provide the possibility of skipping the processing module, and only running the corresponding steps of tensor fitting, FOD calculation and DWI registration to the T1nativepro (flag -dwi_processed). Furthermore, if the user has several DWI shells and desires to process them individually could run the pipeline specifying the shell to process with -dwi_main and the name of the acquisition with -dwi_acq (eg. The optional arguments to process the DWI would be: -proc_dwi -dwi_main sub-01/dwi/sub-01_desc-1000b_dwi.nii.gz -dwi_acq 1000b).

SC: structural connectome generation.

Structural connectomes are generated with Mrtrix3 from pre-processed DWI data from the previous module and subcortical and cerebellar parcellations are non-linearly registered to native DWI space. First, a tractography with 40 million streamlines (default but modifiable, maximum tract length = 400, minimum length = 10, cutoff = 0.06, step = 0.5) is generated using the iFOD2 algorithm and 3-tissue anatomically constrained tractography (Smith et al., 2012; Tournier et al., 2010). A second tract density image (TDI) of the resulting tractography is computed for QC. By default, the full brain tractography is erased at the end of this module but can be kept using the option “-keep_tck ”. Next, spherical deconvolution informed filtering of tractograms [SIFT2 (Smith et al., 2015a)] is applied to reconstruct whole brain streamlines weighted by cross-sectional multipliers. The reconstructed cross-section weighted streamlines are then mapped to each parcellation scheme, with (i) cortical, (ii) cortical and subcortical, and (iii) cortical, subcortical, and cerebellar regions (Smith et al., 2015b. These are also warped to DWI native space. The connection weights between nodes are defined as the weighted streamline count, and edge length matrices are also generated.

4.1.3. Resting -state fMRI processing

This module processes the rs-fMRI scans, in preparation for the construction of functional connectomes. This pipeline is optimized for spinecho images with reverse phase encoding used for distortion correction. The pipeline is mainly based on tools from FSL and AFNI for volumetric processing, as well as FreeSurfer and Workbench for surface-based mapping (Fig. S1D).

Initial fMRI processing steps involve the removal of the first five volumes to ensure magnetic field saturation, image re-orientation (LPI), as well as motion and distortion correction. Motion correction is performed by registering all time-point volumes to the mean volume, while distortion correction leverages main phase and reverse phase field maps acquired alongside rs-fMRI scans. Nuisance variable signal is removed either using an ICA-FIX classifier with a default training set or custom training set input by the user (Griffanti et al., 2014; Salimi-Khorshidi et al., 2014) or by selecting white matter, CSF, and global signal regression [for Discussion, see (Murphy et al, 2009, Murphy and Fox 2017, Vos de Wael et al. 2017)]. Additionally, a regression of time points with motion spikes is performed using motion outlier outputs provided by FSL. Volumetric timeseries are averaged for registration to native FreeSurfer space using boundary-based registration (Greve and Fischl, 2009), and mapped to individual surface models using trilinear interpolation. Native-surface and template-mapped cortical time series undergo spatial smoothing (Gaussian kernel, FWHM = 10 mm), and are subsequently averaged within nodes defined by several parcellation schemes. Parcellated subcortical and cerebellar time series are also provided and are appended before cortical time series.

FC: functional connectome generation.

Individual rs-fMRI time series are mapped to individual surface models. Native surface-mapped time series are registered to standard surface templates (fsaverage5, conte69). Native surface and conte69-mapped time series are averaged within cortical parcels. The subcortical and cerebellar parcellations are warped to each subject’s native rs-fMRI volume space and used to extract the time series within each node. Individual functional connectomes are generated by cross correlating all nodal time series.

4.1.4. Microstructural processing and microstructural profile covariance (MPC) matrix generation

This module samples intracortical intensities from a quantitative MRI contrast, generating a depth-dependent intracortical intensity profile at each vertex of the native surface mesh. By parcellating and cross-correlating nodal intensities, this module generates MPC matrices. This approach has been previously applied over the whole cortex (Paquola et al., 2019b), as well as in targeted structures such as the insula (Royer et al., 2020). The first processing step is a boundary-based registration from the quantitative imaging volume (default) or input microstructurally sensitive image contrast to FreeSurfer native space. Then, 16 equivolumetric surfaces (Waehnert et al., 2014) are generated between the pial, and white matter boundary previously defined from FreeSurfer. Intracortical equivolumetric surfaces are generated using https://github.com/kwagstyl/surface_tools. Surfaces closest to pial and white matter boundaries are discarded to minimize partial volume effects, resulting in 14 surfaces. A surface-based registration is performed to fsaverage5 and conte69–32k templates, and the vertex-wise intensity profiles are averaged within parcels for each parcellation. Nodal profiles are cross-correlated across the cortical mantle using partial correlations controlling for the average cortex-wide intensity profile. Several regions are excluded when averaging cortex-wide intensity profiles, including left/right medial walls, as well as non-cortical areas such as the corpus callosum and pericallosal regions.

4.2. Quality control

Micapipe includes an integrated QC module, which can be run at any point during processing. This step generates group-level and individual-specific QC reports allowing the user to identify missing files, verify registration performance, and check outputs requiring further inspection. Individual QC generates an html report with detailed information of each processing step (Fig. 2A). The report contains different tabs, one per module: main inputs and outputs of each module, main parameters of the processing steps (obtained from the metadata json sidecar files generated by micapipe), volume visualization of the main outputs, visualization of the main registrations, different surfaces generated by the pipeline, parcellations plotted on native surface, structural connectome matrices, functional connectome matrices, geodesic distance matrices, microstructural intensity profiles and connectomes and microstructural profiles (image intensities at each cortical depth) plotted on the native surface. Group level QC generates a color-coded table (with rows for subjects and columns for modules (Fig. 2B)).

4.3. Additional features

4.3.1. Automatic bundle segmentation

The micapipe repository also includes an optional automatic virtual dissection of major fiber tracts (Fig. S2A). This tool is an adaptation of XTRACT (Warrington et al., 2020) implemented using Mrtrix3 and ANTs, and its main purpose is to split a tractography (tck file) into the main white matter tracts. The automatic bundle segmentation uses already established automatic dissection protocols manually tuned for optimal performance. Derived from a full brain tractography, 35 bundles are virtually dissected using the LANIREM protocols. The quality of the full brain tractography will determine the quality of bundle separation. It is highly recommended to provide a tractography with more than one million streamlines, and QC for any errors. Strategies such as anatomically constrained tractography (ACT) and spherical deconvolution informed filtering of tractographies (SIFT), which are available in Mrtrix3, should aid in obtaining such high-quality tractographies. For processing a Non-linear (SyN) registration of the native FA map to the FA atlas (FMRIB58_FA_1mm) is calculated. Resulting transformations are then applied to each bundle protocol to register them to the native FA space (DWI). Finally, each white matter bundle is filtered according to the dissection protocols.

4.3.2. Anonymize function

A function to anonymize the anatomical images from the BIDS directory for data sharing is provided within the micapipe repository as an extra feature. Native structural images are anonymized and de-identified with one of three different methods: de-facing, linear refacing or refacing with a non-linear warp field (Fig. S2B). This tool uses a custom template and a set of ROIs specifically developed to identify the face and skull. The full head template was created using the T1-weighted images (resolution of 0.8 × 0.8 × 0.8 mm) of 60 randomly selected healthy individuals from the MICA-MICs dataset (Royer et al., 2021). An inter-subject non-linear registration was performed without any mask, then the template was built using the mean of the normalized images. Three masks were generated: an ROI that covers the face, a brain mask, and a brain and neck mask. Unlike other algorithms, micapipe_anonymize supports different anatomical modalities (e.g., quantitative T1 maps).

4.4. Feature matrices

Besides surfaces and parcellations, micapipe outputs up to four inter-regional matrices across several parcellation: structural connectome (SC), functional connectome (FC), geodesic distance (GD) and microstructural profile covariance (MPC). Rows and columns of GD and MPC matrices follow the order defined by annotation labels associated with their parcellation (see parcellations in the micapipe repository), including unique entries for the left and right medial walls. For example, row and column entries of the Schäfer-100 matrices are ordered according to: Left hemisphere cortical parcels (1 medial wall followed by 50 cortical regions), and right hemisphere cortical parcels (1 medial wall followed by 50 cortical regions). FC and SC matrices follow the same ordering, although entries for subcortical and cerebellar structures are appended before cortical parcels. As such, row and column entries of the Schäfer-100 FC and SC matrices are ordered according to: Subcortical structures and hippocampus (7 left, 7 right), cerebellar nodes (34 regions), left hemisphere cortical parcels (1 medial wall followed by 50 cortical regions), and right hemisphere cortical parcels (1 medial wall followed by 50 cortical regions). The ordering of all parcels and their corresponding label in each volumetric parcellation are documented in lookup tables provided in the micapipe repository (parcellations/lut). Further information about the organization and visualization of the output connectomes can be found in the respective section of the documentation.

4.5. Validation experiments

The pipeline was tested in 455 human participants from seven datasets (Tables S1 and S4): MICA-MICs, (Royer et al., 2021), EpiC-UNAM (Rodríguez-Cruces et al., 2020), Cam-CAN (Shafto et al., 2014), SUDMEX (Angeles-Valdez et al., 2022), MSC (Gordon et al., 2017), and 7T-Audiopath (Sitek et al., 2019). EpiC-UNAM consists of two separate acquisitions: one cross-sectional and one longitudinal. Acquisition and processing details for each dataset can be found in the section “Processing databases” of the online documentation.

4.5.1. Inter-subject consistency

We assessed inter-subject consistency at the level of the first eigenvector/gradient of each matrix, matrix edges, and three widely graph theoretical measures (node strength, characteristic path length, clustering coefficient). Evaluations were carried out across three selected parcellations (Schäfer-100, 400 and 1000). Inter-subject consistency was quantified as the Spearman correlation between each participant measure and the group average measure for each available modality. This procedure was applied for the gradient 1, edges, and the three graph features (Fig. 3).

To generate gradients, we used BrainSpace (http://brainspace.readthedocs.io, Vos de Wael et al., 2020), with the following options: normalized angle kernel, diffusion embedding with alpha = 0.5 and automatic estimation of the diffusion time (See micapipe-supplementary for details). Group-level gradients were constructed from the average of subject-level cortical matrices. For MPC, FC, and GD, matrices were thresholded row-wise to retain the top 20% edges (see ‘Building gradients’ in the documentation, Fig. S3 for an example at the MICs dataset). SC matrices were log-transformed to reduce connectivity strength variance, but not thresholded. Moreover, left and right hemispheres were analyzed separately for SC, given limitations of diffusion tractography in mapping inter-hemispheric fibers. Hemispheres were also analyzed separately for GD gradients, as the surface-based measure of geodesic distance used here is computed on distinct hemisphere surface spheres. The For each subject, we aligned the first gradient using Procrustes rotations to the group-level gradient for each modality, and computed correlations as a measure of inter-subject consistency.

Graph features:

Graph measurements were computed using the igraph R package (igraph.org/r). We focused on three widely used graph-theoretical parameters, node strength, characteristic path length, and clustering coefficient (Rubinov and Sporns, 2010). We computed the clustering-coefficient as a measure of segregation, which provides information about the level of local connections in a network. The characteristic path length quantified network integration with short path lengths indicating globally efficient networks. Dijkstra’s algorithm was used to calculate the inverse distance matrix (Dijkstra, 1959) and infinite path lengths were replaced with the maximum finite length (Van den Heuvel et al., 2008). Finally, we calculated strength to characterize the relevance of the individual nodes. FC strength was calculated only with positive values. Using the same thresholding as for the diffusion map embedding, GD, MPC and FC matrices were thresholded to retain the top 20% of the edges, and SC was analyzed using the un-thresholded, weighted networks.

4.5.2. Inter-datasets similarity

To assess stability across datasets, we computed Spearman’s correlation coefficients between the group-level measures of each pair of datasets for each MRI modality (Fig. 4).

4.5.3. Test-retest similarity

To assess the capabilities of micapipe to generate reproducible results in a test-retest scenario (Seguin et al., 2022), we used 53 subjects with full acquisitions from the Human Connectome Project. We processed run-1 as test and run-2 as retest for functional and structural modalities. For diffusion MRI we processed DWI_dir95 as test and DWI_dir96 as retest. MPC was calculated using the T1w/T2w images with run-1 and run-2 of each. We computed the similarity between each subject’s matrices using Pearson’s correlation for all rows, each indicating the similarity of a single node, then by averaging all node’s correlation to produce a single value of similarity between matrices (Mansour et al., 2022). This procedure was performed between all pairs of subjects to generate a subject-test by subject-retest similarity matrix for each modality (GD, SC, FC, and MPC) and three selected parcellations (Schaefer-100, 400, and 1000; Fig. 5A,B). We quantified both intra- and inter-individual matrix similarity of each modality by parcellation. Intra-individual similarities were averaged to index reliability, indicating the extent of processing consistency for an individual by modality (matrix diagonal). The inter-individual similarities were averaged to produce a measure of population uniformity of the processed matrices (triangular matrix). Ideally, the processed matrices should be reliable (i.e., high reliability) and preserve inter-individual differences (i.e., low uniformity). Hence, high reliability and low population uniformity is desirable. Additionally, we use a measure of Identifiability which quantifies how an individual can be recognized from a group based on the matrix features (Amico and Goñi, 2018, Mansour et al., 2021). Identifiability was calculated by the effect size of the difference in the means of intra-individual and inter-individual similarities divided by the pooled standard deviation of the two distributions.

4.6. Version control and containers

micapipe is executable via a Docker container, and we provide information on how to convert it to a singularity image either via directly pulling from dockerhub or converting a local image (Kurtzer et al., 2017). Each new version of micapipe is uploaded and tagged, and changes are documented. The current release version is v.0.1.2. Our goal is to maintain continuous integration. Additionally, our pipeline has adopted the standards of BIDS-Apps (Gorgolewski et al., 2017) and of the center for reproducible neuroimaging computation (Robert et al., 2016).

Data availability

Data will be made available on request.