Abstract
Phenotypic adaptation is a universal feature of biological systems navigating highly variable environments. Recent empirical data support the role of memory-driven decision making in cellular systems navigating uncertain future nutrient landscapes, wherein a distinct growth phenotype emerges in fluctuating conditions. We develop a simple stochastic mathematical model to describe memory-driven cellular adaptation required for systems to optimally navigate such uncertainty. In this framework, adaptive populations traverse dynamic environments by inferring future variation from a memory of prior states, and memory capacity imposes a fundamental trade-off between the speed and accuracy of adaptation to new fluctuating environments. Our results suggest that the observed growth reductions that occur in fluctuating environments are a direct consequence of optimal decision making and result from bet hedging and occasional phenotypic-environmental mismatch. We anticipate that this modeling framework will be useful for studying the role of memory in phenotypic adaptation, including in the design of temporally varying therapies against adaptive systems.
Significance
A memory-driven stochastic decision-making framework is developed to describe optimal cell phenotypic transitions for systems navigating fluctuating environments. Stochastic dynamic programming is applied for an arbitrary environmental landscape to identify the optimal strategy that achieves the maximal attainable sum of expected growth. When applied to study bacterial growth in oscillating nutrient environments, our model agrees with recent empirical observations of growth reductions in fluctuating environments relative to constant ones. Growth reduction is a universal feature in this model and arises as a consequence of phenotypic bet hedging, which suggests a methodology to identify and exploit environmental states giving rise to maximal growth penalties. This foundational framework is applicable for studying the dynamics of cellular systems optimally navigating uncertain environments.
Introduction
Biological systems commonly encounter and respond to exogenous environmental fluctuations, and their consequent adaptation generates a diversity of phenotypic responses at the population level (1,2,3,4). In bacterial populations, dramatic phenotypic changes that lead to persistence and long-term infection can occur as the result of relatively few molecular changes in simple biological circuits (5,6,7). Similar phenomena occur in mammalian systems and often complicate medical intervention with resistance to drug and targeted therapies (8,9,10).
Prior work has studied phenotypic switching in response to fluctuating environments in several biological contexts. Deterministic modeling characterized the trade-off between stress resistance and growth lag (11), where the mean behavior in response to stochastic fluctuations was considered by invoking the law of large numbers over sufficiently many cycles. In another study, combined modeling and experimental analysis explored the rate of variable phenotypic switching relative to that of environmental fluctuation (12). These results predicted that cells matching their rate of phenotypic switching to the characteristic rate of environmental fluctuation exhibited enhanced growth (1,2). A similar phenomenon was explained theoretically in the context of viral lytic and lysogenic decision making, wherein viruses that match their lysogenic rate to the environmental frequency of lytic collapse were found to maximize long-term population growth (13).
Cellular memory is a key defining feature of adaptive cells in changing environments, and recent empirical evidence has revealed a number of mechanisms by which this can occur at the single-cell level. Durable chromatin modifications can persist across cell division (14). Prior growth-factor signaling induces short-term memory that tunes subsequent receptor sensitivity (15). Even oligomeric protein condensates arising in response to previous environmental encounters enable cells to change their future behavior (16). Recent work has begun to highlight the importance of memory-driven decision making in navigating future environments, not just present ones (17,18,19).
The role of history dependence in cellular adaptation has also been considered in several previous studies. Historical effects of cell phenotypic switching in matched or mismatched fluctuating environments has provided more complete descriptions of phenotypic selection in a diverse ecology (20). Notably, (2) considered the difference in responsive (or “informed”) switching relative to stochastic switching among a variety of phenotypes and environments. This analysis considered two extremes where switching was based either on perfect information of the current state via sensing or no information at all in the stochastic case. Moreover, the existence and benefit of memory in cells navigating fluctuating environments has also been demonstrated using systems of ordinary differential equations in the context of hysteresis and gene expression delays that result from prior environmental cues in cell signaling networks (21).
Although all of these features are of direct importance for a mechanistic understanding of cellular adaptation, the role of a dynamic memory in stochastic optimal decision making and its corresponding impact on cell fitness are at present unknown. And, despite these approaches, the effects of prior memory capacity on the decision making of cells in fluctuating environments has not been quantitatively evaluated, particularly when future environmental transitions must be inferred from past environments. A corresponding theory of stochastic optimal adaptation is also currently lacking. To address this, and to further understand recent empirical findings of reduced-growth phenotypes in fluctuating environments (22), we developed a foundational mathematical framework to model memory-driven phenotypic switching in stochastic environments. In our model, adaptive populations leverage a memory of historical environmental exposures to forecast the optimal phenotypic strategy for unknown future landscapes. This simple model is amenable to explicit analytic characterization of the optimal strategy as a function of environmental history and memory capacity.
In the setting of navigating metabolic environments, our model quantifies the dynamical differences between fixed cellular phenotypes and those that may select a phenotypic strategy based on a memory of past experience to optimize their growth potential. In studying the role of memory capacity, we identify a fundamental trade-off between the accuracy of a cell’s estimation of the current environmental state and the speed at which it may adapt to new environments. We quantify the efficiency of systems employing a variable-memory scheme to balance constraints on adaptation speed and accuracy when compared to their fixed-memory counterparts. When applied to understand cellular growth rates in oscillating nutrient environments, our model predicts that memory capacities in excess of the period of environmental oscillation are most consistent with empirically observed dynamics. We show that memory-driven cellular decision making can explain the observation of slower growth in fluctuating nutrient environments when compared to constant ones. Our model predicts that this feature is universal across all fluctuating environments and a direct consequence of bet hedging in optimal memory-driven decision making.
Materials and methods
Environmental and phenotypic dynamics
Our model consists of single cells navigating type- and type- environments. Without loss of generality, the type- environment represents a beneficial or nutrient-high environment, whereas the type- environment represents a weakly beneficial or detrimental one. Cells exist in one of two phenotypic states, correspondingly denoted by and based on their fitness preference for environment or , respectively. The state may be viewed as a fast-growing, or sensitive, phenotype (23). Similarly, the phenotype devotes additional resources to mitigate the undesirable effects of a nutrient-poor or overtly detrimental environment (24). We will also distinguish adaptive cells—capable of phenotypic switching—from static ones, which cannot adapt. We represent a fluctuating environmental landscape by a (possibly random) sequence indicating the presence of the environment. In general, terms in this sequence may be correlated in time, and their relative frequencies may also change over time. For foundational understanding, we focus on environments identified by independent and identically distributed sequences . In this case, a stochastic environment may be represented by a single parameter denoting the likelihood of the environment:
| (1) |
We also allow for possible diversity in the intensity, , of each environment, which we assume to be Poisson distributed and environment specific:
| (2) |
In general, and are the intensity rates for each environment (applications to empirical data will assume constant and equal intensity values ). Of primary interest is the rate of benefit accrual per normalized unit time for each phenotype, given by
| (3) |
For the phenotype, type- environments generate a per-unit benefit , whereas type- environments incur a per-unit cost . The phenotype avoids this cost at the expense of less efficient navigation of type- environments, parameterized by .
An equivalent formulation can be applied in the case of strictly beneficial environments with low and high, and reversed interpretation of phenotypes . In this case, replacement of by characterizes the relative efficiency of the fluctuation-tolerant, slow-growth phenotype over in weakly beneficial environments. Lastly, Eq. 3 can also be written to explicitly account for empirically observed growth rates for direct comparisons with experimental data (see supporting material, Section S7.3).
Although the above model can represent a variety of cellular features that a system may actively optimize, including cellular signaling and phenotypic sustainment of microenvironmental features, we henceforth interpret benefit and cost with respect to a cell’s growth potential, or the rate at which cells acquire resources that are available for growth and division, which can be mapped to observable growth rates via a convex growth curve. A depiction of our phenotypic switching model is given in Fig. 1.
Figure 1.
Illustration of memory-driven phenotypic switching. (A) The model consists of cells capable of stochastic transition between two states, and , where state has an advantage in the -type environment. (B) The general model is applied to study cases where the environment may become hostile or may represent low nutrient availability. (C) Cellular decision making uses a memory of prior environments to optimally respond to future ones by selecting the phenotype that maximizes expected future growth.
Cellular memory
To navigate the -fluctuating environment, the cell creates a dynamically updated estimate, , of after each environmental encounter. We represent iterative updating through a Bayesian inference scheme, where at time the current estimate of environment may be represented by a prior distribution . Although this framework can, in general, handle arbitrary distributions that may describe the system’s prior belief of the environmental state, we shall consider
| (4) |
where represents the observed number of type- environments out of a total recalled memory of previous environments. Here, memory refers to the extent of previous environmental exposures the system has access to in making decisions about future phenotypes, which is expressed as the number of prior time steps in this discrete-time model. The cell is thus tasked with identifying the most likely environment—in the form of a posterior distribution for the estimated environment —given the most recent observation . This distribution can be written as
| (5) |
Moreover, for a uniform prior representing no bias in , the maximum likelihood estimate of , given by , agrees with the maximum a posteriori probability, so it suffices to track the number of observed environments, , at each time having memory capacity . To account for the additional possibility that cells may dynamically change their memory capacity (25,26), we consider cells possessing either a fixed memory capacity or an adaptive memory capacity as they navigate fluctuating environments.
Dynamic programming and optimal adaptation
The intriguing empirical observation of cellular decision making capable of navigating future events based on present decisions (13,17,18) is particularly well suited for the application of stochastic optimal decision making. Toward this end, we apply dynamic programming to characterize the optimal phenotypic strategy for cells that optimize their maximal attainable expected growth potential. The optimal phenotypic policy satisfies the time-homogeneous Bellman equation (27), which relates the time- value—or present maximal attainable growth potential—to the value in the future (at time ). An estimate of can be obtained by averaging the history of environments: . The optimal program can, in general, be written for systems with adaptive memory (see supporting material, Section S5) using the value function . For the fixed-memory case with memory size and denoting the sum of the most recent environments at time , the optimal program is given by:
| (6) |
where is an exponential discount factor assigning greater utility to earlier gains in growth potential, and is the expected growth assuming the optimal action is taken. Our analytical results are evaluated against large-scale stochastic numerical simulations.
Results
The following section presents the main findings of our analysis (full mathematical details are provided in the supporting material).
Environmental parameters determine preferred phenotype
The expected growth potential for each phenotype is given by
| (7) |
This implies that the phenotype is preferred over whenever the mean benefit-to-cost ratio exceeds the odds of the environmental frequency normalized by the inefficiency of the -phenotype:
| (8) |
Eq. 8 can equivalently be solved to identify a unique indifference probability :
| (9) |
describes the environmental landscape for which neither phenotype is preferred on average. Its value is determined by the relative fitness values of phenotypes matched or mismatched in each environment. The (resp. ) phenotype is preferred in stochastic environments having (resp. ). In addition to the mean dynamics, we also find that there is always a variance premium incurred for the phenotype, and, in this case, the cost and Poisson intensity terms decouple (see supporting material, Section S2.3).
Optimal strategy and maximal total growth
The solution to the two-state problem in Eq. 6 along with its infinite memory analog can be analytically solved. The optimal decision at each time is given by selecting a phenotype based on the historical abundance of previous environments through , and the growth potential is given by
| (10) |
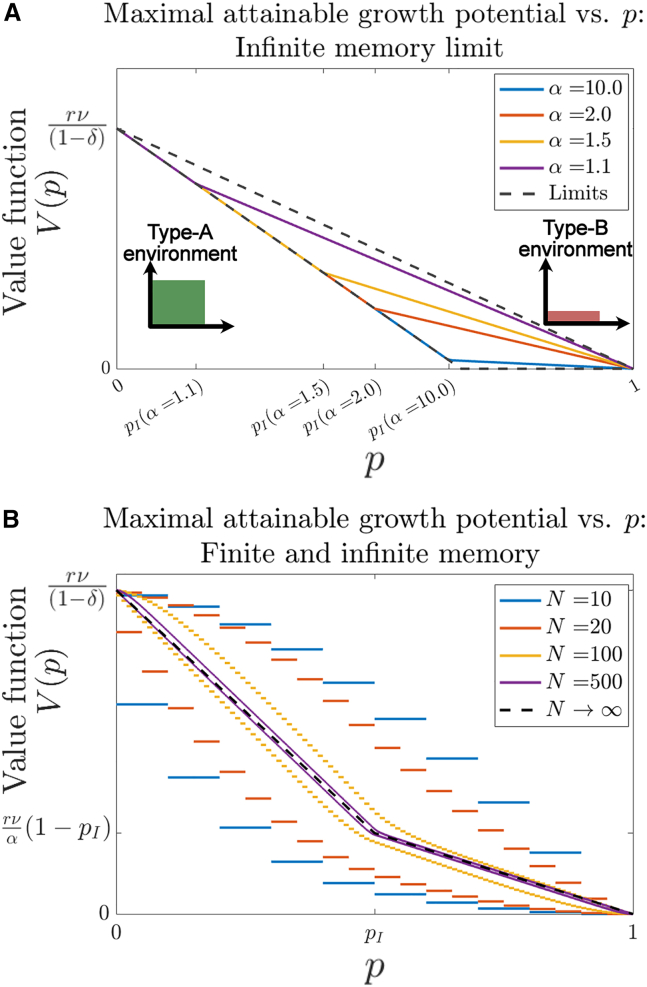
The corresponding value function, representing the maximal sum of future expected growth potential, can be identified for both finite- and infinite-memory cases (see supporting material, Section S5). In the infinite-memory case, its value matches Eq. 10 normalized by . The value function is plotted for a variety of intermediate and limiting (, ) values in Fig. 2 A. A similar calculation can be made for systems with finite memory (see supporting material, Section S5.1). In that case, the value function is discretized over available values of , with resolution proportional to memory capacity. The finite-memory case converges to the infinite-memory one as becomes large (Fig. 2 B). Using this updating scheme, the current value perceived by the adaptive system in the present decreases linearly as a function of , the observed environmental frequency, thereby quantifying the detriment to value resulting from an increasingly hostile environment. The inflection point emergent for larger memories illustrates the relative difference in marginal value between each environment around their point of indifference .
Figure 2.
Maximal attainable growth potential in fluctuating environments. The value function for cells optimally selecting their phenotypic state based on a history of fluctuating environmental states is given as a function of the underlying environmental parameter for (A) systems with infinite-memory and variable together with limiting behavior ( and ). (B) For systems with finite memory capacity, the value functions are plotted for over increasing memory size, along with the infinite-memory limit (in all cases, , , ).
Optimized phenotypic decision making hedges against future environmental uncertainty
One immediate consequence of memory-driven phenotypic adaptation is that populations faced with uncertain future environments capably adapt based on their estimates of the prior state. When the fluctuating environment is maintained at some , a corresponding fixed-phenotype state (either or ) is always preferred over phenotypic switching. Dynamic cells in unknown environments therefore experience reduced growth potential relative to their fixed-strategy, environmentally matched counterparts, but, in doing so, achieve enhanced growth potential across all environments, which contrasts with static phenotypes (Fig. 3 A). This is especially relevant for navigating detrimental environments, wherein dynamic cells are able to maintain positive growth despite environmental uncertainty. Thus, the benefit of phenotypic decision making is a hedge against environmental uncertainty that enables systems to survive changing environmental landscapes. This hedge results in reductions to the expected growth potential compared to what would otherwise be achieved in the best fixed-phenotypic state (Fig. 3 B), and the corresponding growth dynamics converge to the analytically predicted long-term expected behavior (see supporting material, Section S7.2). Lastly, the stochastic growth potential for static and dynamic strategies all collapse to a common process whenever .
Figure 3.
Growth in fluctuating environments. Representative stochastic trajectories of (A) cumulative growth potential and (B) averaged cumulative growth potential are depicted for cells navigating -predominant (left), neutral (middle), and -predominant (right) environments. Adaptive systems (blue) capable of phenotypic switching have lower growth potential than static phenotypes (red, yellow) matched to the proper environment, but outperform those phenotypes whenever the environment is mismatched. Growth dynamics for all strategies collapse to a common process in the neutral environment (in all cases, , , , , ).
Motivated by recent empirical evidence supporting distinct growth phenotypes in fluctuating environments (22), we next consider optimal decision making in nutrient-rich vs. nutrient-depleted environments. For the remainder of the results, we focus on studying strictly beneficial high (type-, ) and low (type-, ) nutrient environments with corresponding and matched phenotypes and (see supporting material, Section S7). In constant environments, memory size has no influence over the preference of fixed or adaptive phenotypes since the environmental parameter and estimate always coincide ( for ).
In fluctuating environments, larger memories mitigate estimation error by enhancing the resolvability of the environment relative to its indifference point, (see supporting material, Section S4.3). When switching from a constant to a fluctuating environment, cells with larger memory capacities trade longer adjustment periods—resulting in slower phenotypic transitions—for higher environmental estimation accuracy, which ultimately yields enhancements in long-term growth. This accuracy depends on both memory and on the proximity of the environmental state to indifference (Figs. 4 A, B, and S4). Memory capacity thus strikes a trade-off between the rate of adaptation and long-term growth efficiency.
Figure 4.
Dynamics of fixed and adaptive-memory systems navigating constant-to-fluctuating nutrient environments. (A) Fixed-memory cells experiencing low-constant to high-fluctuating nutrient environments undergo phenotypic switching. The maximal growth potential and switching times both vary directly with memory capacity. (B) Illustration of the probability distribution for the estimate of for varying memory sizes as in (A). Successful estimation occurs whenever (green arrow; right of dashed line). The probability of environmental mis-estimation occurs whenever (red arrow; left of dashed line). Cumulative averaged growth potential and memory sizes are plotted in time for adaptive cells undergoing (C) constant-high to fluctuating-low and (D) constant-low to fluctuating-high nutrient environments (in all cases, , giving . giving . All initial memory capacities tend toward a unique long-term limit (dashed horizontal lines). For (B) and (C) , , high-fluctuating environments were given by , low-fluctuating by , and memory was updated based on detected distance to environmental indifference . A total of stochastic simulations were averaged to generate growth and memory curves. Two stochastic realizations are depicted for initial memory sizes selected in via linear interpolation between and of the initial distance between and the high- (resp. low-) constant environments, modeled by (resp. 0).
Adaptive memory balances long-term growth enhancement with short-term reduction
In our model, phenotypic dynamism enables cells to execute optimal decisions, and their accuracy is proportional to total memory capacity . Given memory’s role in cellular decision making (14,15), we next asked how cellular systems with dynamic memory capacities compare to their fixed-memory counterparts when encountering fluctuating environments.
Here, memory capacity may be viewed as the control variable through which a cell tunes its ability to switch phenotypes. We considered several governing principles for adaptive decision making (see supporting material, Section S6), the one presented here is based on proximity to as follows: since estimation of the optimal phenotype becomes difficult for small , one plausible response for dynamical systems detecting a smaller distance is an increased memory capacity to more reliably estimate , whereas larger values benefit from smaller memories in their ability to quickly adapt to future changes. Although many functional forms can achieve this, we for simplicity considered linear interpolation between an upper and lower memory limit based on proximity of to
| (11) |
with incremental transitions so that . These dynamics describe a simple update scheme that allocates additional memory capacity when higher resolution is needed for resolving the environmental state. We also considered alternative schemes based on the system’s estimate of environmental variance (see supporting material, Section S6.1).
We applied this framework to compare growth trajectories for systems adopting fixed versus adaptive memory strategies. Our analysis was performed for cells transitioning from a constant environment to a -predominant fluctuating one (Fig. 4 C), from a constant environment to an -predominant fluctuating one (Fig. 4 D), and the analogous fluctuating-to-constant landscapes (Fig. S3). We plot the cumulative averaged growth potential to highlight both transient changes in growth during environmental switching and long-term equilibrium rates. In each case, we find that larger memory capacity improves long-term growth potential.
In constant-to-fluctuating environmental transitions, adaptive memories with lower initial memory correct more quickly than adaptive systems with large memory, demonstrating that fixed large memory capacities are not always the optimal choice (Fig. 4 D). On the other hand, fixed low-memory systems adjust more quickly but are ultimately eclipsed by their adaptive counterparts in the long run (Fig. 4 A). Moreover, adaptive systems with variable initial memory have growth dynamics that converge to a single predicted equilibrium state and a unique mean-reverting long-term memory capacity (see supporting material, Section S6.2). Collectively, our results predict additional adaptation enhancement in systems with adaptive memory when navigating changing environments relative to systems with a fixed memory size.
Memory-driven adaptation in oscillating environments
Our analysis thus far has focused on random environments with phenotypic switching determined by the environmental parameter , yet many experimental observations, including the dynamics observed in (22), occur in periodic (deterministic) environments, which are a specific restriction of environmental landscapes that comprise realizations of our general model. In prior empirical work, researchers tracked Escherichia coli cells grown for 3.5 h in a low-nutrient environment and then frequently measured their growth rates while subjecting cells to 60-min oscillating high- and low-nutrient environments. Their results demonstrate a distinct “adaptation-enhanced” phenotype capable of increasing its growth rate over six periods.
In applying our model to this setting, the intensities can be assumed to be fixed quantities that are equal ( from Eq. 2). We evaluate our framework in this experimentally constrained setting by utilizing a fixed-memory description of phenotypic transitions. We use a variation of our model capable of direct incorporation of measured growth rates (see supporting material, Section S7.3). We then directly estimate observed growth rates (Fig. 5 of (22)), which are then applied to study the distributional response of cell growth rates under variable memory size and intrinsic noise. These values give an estimate of the indifference probability , which is close to the environmental parameter in symmetric environments.
We find that memory sizes in excess of the environmental oscillation frequencies are most consistent with the dynamics and timescales of adaptation observed in the aforementioned experiments (Fig. 5 A). This observation is consistent with the earlier finding that large memory sizes are preferred whenever is small, as is the case here. Moreover, these distributional trajectories are in qualitative agreement with the experimentally observed timescales of growth rate stabilization across successive periods (Fig. 5 B). We also observe that average growth rates of cell populations with larger phenotypic memory can also be enhanced by intrinsic noise (Fig. S5).
Figure 5.
Phenotypic adaptation in oscillating environments. Adaptation dynamics are studied by considering the fluctuation experiment in (22) and imputing estimates of the corresponding growth rates for each phenotype-environment pair. (A) The average growth rate distribution of 100 adaptive cells in an oscillating-nutrient environment with period minutes is depicted as a function of time assuming intrinsic noise in each cell’s ability to identify the past environmental encounters. Model application for a variety of memory sizes recapitulates empirically observed timescales of adaptation memory sizes that are in excess of environmental oscillations. (B) Focusing on growth trajectories with memory size , the average growth rates over the nutrient-high , nutrient-low , and total time intervals are plotted (error bars depict standard deviation) and recover the dynamics observed in (22) ( as in see supporting material, Section S7.3).
Reduced growth in fluctuating environments results from inherent nutrient variability and memory-dependent environmental mis-estimation
Figs. 3 and 4 highlight the hedging strategy of a dynamic cellular phenotype. Namely, dynamic cells opt for lower expected growth potential relative to corresponding static phenotypes appropriately matched to a (fixed) environmental state in exchange for the ability to adapt and thus avoid large penalties in any environment of interest. On the other hand, the extent of relative growth reduction observed across all allowable environmental parameters remains unknown. To address this, we next consider how growth under rapid fluctuation compares to the corresponding weighted-average behavior between high and low states comprehensively for all random environments. In the empirical paper analyzed above, researchers identified growth reductions for cells in fluctuating environments relative to those in constant ones. Intriguingly, these reductions persisted even after accounting for those expected to result from the convexity of the growth-vs.-nutrient curve from Jensen’s inequality.
Since our model tracks the (linear) underlying growth potential as a function of phenotype and environment, Jensen’s inequality holds at equality, allowing us to directly compare the growth potential of dynamic cells in fluctuating environments with the corresponding weighted-average potential in constant environments (Fig. 6 A). Of course, our representation of available nutrients for growth can be mapped via one-to-one correspondence to growth rate via a convex transformation, but our goal here is to quantify the inherent deficit in the fluctuating growth phenotype that is independent of the convexity of the growth-vs.-nutrient curve. Our calculations, performed for all allowable fluctuating environments and corresponding (weighted-average) constant ones, recover the experimentally observed deficits (Figs. 6 A and S6). Moreover, our results suggest that this deficit is universal across all feasible parameter choices (Figs. 6 B, C and S6) and greatest for near-indifferent environments (Fig. 6 D).
Figure 6.
Growth deficits due to phenotypic switching in stochastic environments. describes the average environment given by the convex combination against which the rapidly fluctuating environment can be compared. (A) The dynamics of cumulative averaged growth potential for fixed- and adaptive-memory cells navigating fluctuating and comparable constant environments (, , ). Across all environmental parameters, , and allowable growth coefficients, , simulated long-run growth potential for (B) -random and (C) -averaged constant environments reveal a universal growth deficit (D) of the -fluctuating case relative to , which is particularly pronounced in the environment. (E and F) The total expected growth deficit of fluctuating environments consists of an intrinsic contribution maximized at and an extrinsic contribution (illustrated for adaptive cells with limited memory capacity) owing to the risk of environmental phenotypic mismatch. In all cases, , , , and stochastic simulations were evaluated for each simulation in (A) over time and at each parameter value in (B)–(F).
The total deficit can be decomposed into a sum of deterministic and random terms:
| (12) |
The intrinsic deficit , given by
| (13) |
occurs when an adapting cell under rapid environmental fluctuation correctly selects the best phenotype. The fluctuation, however, results in mismatch on occasion, and at a frequency that increases as the environment approaches the state of indifference . therefore represents a best-case minimal deficit provided that the cell selected the correct phenotype. In the event that the phenotype is mismatched to the environment , there is an additional extrinsic deficit:
| (14) |
The expected value of therefore depends on the product of its magnitude with the miss probability, . The effective cost of a mismatched phenotype increases linearly away from , whereas the miss probability (see supporting material, Section S7.4) varies inversely with larger memory, is maximized at , and decreases for larger deviations. This analytic description of deficit is in quantitative agreement with large-scale stochastic simulations of the process across all parameter values (Fig. 6 E and F).
Collectively, our results provide a statistical justification for observed growth deficits of fluctuating environments: adaptive cells encountering sufficiently rapid environmental fluctuations select their phenotypes based on the most recent past encounters. In the best case, the system correctly identifies the most likely environment relative to and selects the correct phenotype accordingly. In fluctuating landscapes, both environmental states occur, and so growth reductions inevitably result when the anomalous environment appears despite appropriate phenotypic selection. Should the system mis-estimate the environment—a risk mitigated by increasing memory capacity—it suffers a higher frequency of stochastic mismatch, thus further reducing growth.
Discussion
The dynamics underlying phenotypic cellular decision making is central to a variety of clinically significant phenomena, including drug resistance and disease progression. Analytical modeling approaches offer direct mathematical frameworks for studying the nature and extent of cellular adaptation, which can be applied to generate relevant and directly testable predictions for follow-up validation. Recent empirical findings implicate the role of phenotypic memory in adaptable systems, along with intelligent decision making that can anticipate future events. Given this, the precise impact of prior environmental memory on phenotypic dynamics, through observable signals such as growth, are of central importance.
Our predictions suggest that transient reductions in growth capacity followed by long-term optimization is an emergent and defining feature of systems with dynamical memory capacity that is absent in fixed-memory systems. This difference presents a means by which memory-driven adaptation could be distinguished experimentally. In our model, memory capacity is represented by the extent to which past environments are recalled, which, along with dynamic differences in memory size, depends on the underlying molecular mechanisms giving rise to cellular memory (28,14,15,16). Their mechanistic link to phenotypic decision making is a central question that will benefit from further experimental studies.
Here, we considered a generalized stochastic model of adaptation driven by cells choosing their optimal phenotype based on memory-driven estimation of fluctuating environments. By comparing the growth potential for cells in random environments to the corresponding weighted-average values in constant environments, we demonstrated that adaptation serves as a bet-hedging strategy that manifests as a growth reduction for cells navigating uncertain landscapes. Our model provides a statistical explanation for this growth deficit: the theoretically predicted extent of this deficit occurs due to the system’s existence in a stochastic environment, which inevitably experiences instances of phenotype-environment mismatch. Moreover, our model predicts that this effect can be mitigated, but never outright eliminated, by larger memory sizes.
Our results suggest the existence of fluctuating environments for which adapting cells perform most poorly, which has significant therapeutic implications for targeting adaptive threats such as infectious diseases and cancer. For example, careful environmental selection based on the timescale of cellular memory could lead to growth reductions. This intriguing possibility will benefit from subsequent mechanistic experimental and theoretical follow-up to determine conditions under which memory-driven stochastic versus deterministic growth strategies occur. The timescales and magnitudes of changes determining whether cellular systems perceive their environment as fluctuating or deterministic are poorly defined. Further empirical follow-up and model refinement will improve our understanding of the rules precisely governing such transitions, which we do not address here.
In addition to recapitulating empirical findings, our results offer testable strategies for further elucidating the dynamics of memory-driven phenotypic decision making. For example, identification of fluctuating environments giving rise to equal abundances of distinct cellular phenotypes having no significant difference in growth is one way of experimentally identifying the predicted critical indifference environment . Our results predict that cells in a neighborhood around this environment experience large growth deficits relative to cells in comparable constant environments. Moreover, rapid cycling or randomization between high and low nutrient states in a small neighborhood around could be performed to identify the environment at which the maximal deficit occurs, . Lastly, our theory suggests that deviation of from decreases for increasing memory sizes and larger efficiency .
When directly applied to study empirical data on growth rates in rapidly oscillating nutrient environments, our model predicted that the observed memory size, and hence the baseline phenotypic transition period, are greater than that of the periodic oscillations driving the fluctuating environment. Our findings deviate from prior predictions of optimal adaptation occurring with matched environmental and phenotypic switching (1,2). Intriguingly, such unmatched rates have more recently been predicted in the setting of growth rate asymmetries between each phenotype (29), which we predict to also hold in this experimental context. Our results support this more recent finding and, in the case of large asymmetries in phenotypic growth rates, offer a probabilistic explanation for low transitions rates relative to the oscillation period in optimal adaptation. Lastly, system-intrinsic noise increased the population’s average rate of adaptation during transitions from constant to oscillating environments. Our results demonstrate that memory-driven adaptation using statistical inference in stochastic environments may in fact be enhanced by intrinsic noise, which is reminiscent of stochastic resonance-stabilized sensing established previously in physical systems (30,31).
Since the convexity of the growth-versus-nutrient curve complicates quantification of phenotypic efficiency in biological systems (22), we focused our general analysis on growth potential, which is a linear function of the environmental parameter. In doing so, we were able to avoid the technicalities of invoking Jensen’s inequality when calculating phenotypic efficiency. To compare these cases, we assumed that nutrient availability for growth in constant environments interpolates linearly between low- and high-nutrient conditions and represents a distinct phenotypic program from cells in fluctuating environments, driven in our model by experiencing rapid stochastic fluctuations.
This model is not without limitations. Implicit in our modeling framework is an assumed constant energetic cost across all available memory capacities and zero cost for transitioning. We studied memory capacities assuming instant updates between successive time points. In reality, lags and energetic costs in environmental estimation and phenotypic switching may affect the optimal cellular strategy. This model considers how environmental changes affect cellular adaptation, but not the converse; in reality, phenotypic variability can play an equally important role in modulating the surrounding microenvironment. A more complete description of mutual phenotypic and environmental feedback is relevant to understanding a number of biological systems and is a topic of future research efforts. Applications of our model to describing empirical growth rate dynamics all considered environments that result in cell growth for both phenotypic states. Future efforts to further develop and apply this model to bacterial and cancer treatments will require an analysis of both cell division and death.
Historical inference in our model was assumed to be either perfect or uniformly imperfect based on intrinsic noise representing a decay in memory fidelity, which we assumed was fixed with respect to the age of individual memories. This assumption, along with possible diversity in the functional forms for memory-driven inference, can be expanded in describing particular biological mechanisms of memory-driven inference. Inference in our model occurred on arbitrary environments, where larger memories lead to more accurate environmental estimates. We applied our model to oscillating environments, which were comparable through by matching the relative abundances of environments over one period. We remark that periodic (deterministic) environments possess additional structure, and it is plausible that cellular adaptation mechanisms capably infer such global structure in a more complex scheme. Here, however, we describe optimal dynamics assuming that the environmental frequencies are what is being estimated.
The optimization objective we focused on was maximizing mean growth. It is possible that many biological settings are better represented by an alternative objective, such as variance minimization for settings requiring strictly uniform growth. Although our current results are capable of quantifying the variance profiles of dynamic decision making, additional model development would be required to identify the optimality conditions and solve for a corresponding optimal phenotypic strategy. This and other extensions, including an account of multiple independent environmental signals, are the topic of subsequent investigations.
In this work, we present a two-state, two-environment model. Although useful for characterizing memory-driven phenotypic transitions in some contexts (28), in others, multiple nutrient and signaling cues likely influence cellular decision making, with the possibility of several allowable phenotypic states (32,33,34). In these more complicated cases, the number of stable phenotypic states, along with their corresponding fitness in fluctuating landscapes, are important to evaluate. These scenarios will benefit both from extending the above modeling framework to characterize optimal decision making (35) along with data-driven analysis to define the phenotypic response to more complex environmental signatures. At present, our model does not account for durable alteration mechanisms, such as genetic mutations, that may also contribute to improved adaptation over time. Such mechanisms and their associated impact on phenotypic response are important for many evolutionary processes such as cancer; their incorporation is a priority for future model development. Nonetheless, we anticipate that this model can be used to establish microscopic environmental fluctuations as a generator of phenotypic diversity for single-cell populations and multicellular systems.
Author contributions
J.T.G. conceived of and designed the research, contributed new analytic equations, performed the analysis, and wrote the paper.
Acknowledgments
J.T.G. would like to thank Kerry E. Back and Thomas J. George for their helpful discussions on stochastic dynamic programming. J.T.G. was supported by the Cancer Prevention Research Institute of Texas (RR210080). J.T.G. is a CPRIT Scholar in Cancer Research.
Declaration of interests
The author declares no competing interests.
Editor: Jianhua Xing.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2023.10.019.
Appendix
Supporting material with full mathematical details are provided in the attached document.
Supporting material
References
- 1.Thattai M., Van Oudenaarden A. Stochastic gene expression in fluctuating environments. Genetics. 2004;167:523–530. doi: 10.1534/genetics.167.1.523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Edo K., Leibler S. Phenotypic diversity, population growth, and information in fluctuating environments. Science. 2005;309:2075–2078. doi: 10.1126/science.1114383. [DOI] [PubMed] [Google Scholar]
- 3.Ackermann M. A functional perspective on phenotypic heterogeneity in microorganisms. Nat. Rev. Microbiol. 2015;13:497–508. doi: 10.1038/nrmicro3491. [DOI] [PubMed] [Google Scholar]
- 4.van Boxtel C., van Heerden J.H., et al. Bruggeman F.J. Taking chances and making mistakes: non-genetic phenotypic heterogeneity and its consequences for surviving in dynamic environments. J. R. Soc. Interface. 2017;14 doi: 10.1098/rsif.2017.0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Balaban N.Q., Merrin J., et al. Leibler S. Bacterial persistence as a phenotypic switch. Science. 2004;305:1622–1625. doi: 10.1126/science.1099390. [DOI] [PubMed] [Google Scholar]
- 6.Choi P.J., Cai L., et al. Xie X.S. A stochastic single-molecule event triggers phenotype switching of a bacterial cell. Science. 2008;322:442–446. doi: 10.1126/science.1161427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tuchscherr L., Medina E., et al. Löffler B. Staphylococcus aureus phenotype switching: an effective bacterial strategy to escape host immune response and establish a chronic infection. EMBO Mol. Med. 2011;3:129–141. doi: 10.1002/emmm.201000115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hata A.N., Niederst M.J., et al. Engelman J.A. Tumor cells can follow distinct evolutionary paths to become resistant to epidermal growth factor receptor inhibition. Nat. Med. 2016;22:262–269. doi: 10.1038/nm.4040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Farquhar K.S., Charlebois D.A., et al. Balázsi G. Role of network-mediated stochasticity in mammalian drug resistance. Nat. Commun. 2019;10:2766–2814. doi: 10.1038/s41467-019-10330-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vitale I., Shema E., et al. Galluzzi L. Intratumoral heterogeneity in cancer progression and response to immunotherapy. Nat. Med. 2021;27:212–224. doi: 10.1038/s41591-021-01233-9. [DOI] [PubMed] [Google Scholar]
- 11.Geisel N., Vilar J.M.G., Rubi J.M. Optimal resting-growth strategies of microbial populations in fluctuating environments. PLoS One. 2011;6 doi: 10.1371/journal.pone.0018622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Acar M., Mettetal J.T., van Oudenaarden A. Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 2008;40:471–475. doi: 10.1038/ng.110. [DOI] [PubMed] [Google Scholar]
- 13.Maslov S., Sneppen K. Well-temperate phage: optimal bet-hedging against local environmental collapses. Sci. Rep. 2015;5 doi: 10.1038/srep10523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stewart-Morgan K.R., Petryk N., Groth A. Chromatin replication and epigenetic cell memory. Nat. Cell Biol. 2020;22:361–371. doi: 10.1038/s41556-020-0487-y. [DOI] [PubMed] [Google Scholar]
- 15.Spinosa P.C., Humphries B.A., et al. Luker K.E. Short-term cellular memory tunes the signaling responses of the chemokine receptor cxcr4. Sci. Signal. 2019;12 doi: 10.1126/scisignal.aaw4204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Reichert P., Caudron F. Mnemons and the memorization of past signaling events. Curr. Opin. Cell Biol. 2021;69:127–135. doi: 10.1016/j.ceb.2021.01.005. [DOI] [PubMed] [Google Scholar]
- 17.Itakura A.K., Chakravarty A.K., et al. Jarosz D.F. Widespread prion-based control of growth and differentiation strategies in saccharomyces cerevisiae. Mol. Cell. 2020;77:266–278.e6. doi: 10.1016/j.molcel.2019.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jiang Y., AkhavanAghdam Z., et al. Hao N. A protein kinase a–regulated network encodes short-and long-lived cellular memories. Sci. Signal. 2020;13 doi: 10.1126/scisignal.aay3585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Saigusa T., Tero A., et al. Kuramoto Y. Amoebae anticipate periodic events. Phys. Rev. Lett. 2008;100 doi: 10.1103/PhysRevLett.100.018101. [DOI] [PubMed] [Google Scholar]
- 20.Leibler S., Kussell E. Individual histories and selection in heterogeneous populations. Proc. Natl. Acad. Sci. USA. 2010;107:13183–13188. doi: 10.1073/pnas.0912538107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lambert G., Kussell E. Memory and fitness optimization of bacteria under fluctuating environments. PLoS Genet. 2014;10 doi: 10.1371/journal.pgen.1004556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nguyen J., Fernandez V., et al. Stocker R. A distinct growth physiology enhances bacterial growth under rapid nutrient fluctuations. Nat. Commun. 2021;12:3662–3712. doi: 10.1038/s41467-021-23439-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cesar S., Sun J., Huang K.C. Cellular memory of rapid growth is sensitive to nutrient depletion during starvation. Front. Microbiol. 2022;13:1016371. doi: 10.3389/fmicb.2022.1016371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wood T.K., Knabel S.J., Kwan B.W. Bacterial persister cell formation and dormancy. Appl. Environ. Microbiol. 2013;79:7116–7121. doi: 10.1128/AEM.02636-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ringrose L., Paro R. Epigenetic regulation of cellular memory by the polycomb and trithorax group proteins. Annu. Rev. Genet. 2004;38:413–443. doi: 10.1146/annurev.genet.38.072902.091907. [DOI] [PubMed] [Google Scholar]
- 26.Acar M., Becskei A., van Oudenaarden A. Enhancement of cellular memory by reducing stochastic transitions. Nature. 2005;435:228–232. doi: 10.1038/nature03524. [DOI] [PubMed] [Google Scholar]
- 27.Bellman R. The theory of dynamic programming. Bull. Am. Math. Soc. 1954;60:503–515. [Google Scholar]
- 28.Burrill D.R., Silver P.A. Making cellular memories. Cell. 2010;140:13–18. doi: 10.1016/j.cell.2009.12.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Belete M.K., Balázsi G. Optimality and adaptation of phenotypically switching cells in fluctuating environments. Phys. Rev. 2015;92 doi: 10.1103/PhysRevE.92.062716. [DOI] [PubMed] [Google Scholar]
- 30.Gammaitoni L., Hänggi P., et al. Marchesoni F. Stochastic resonance. Rev. Mod. Phys. 1998;70:223–287. [Google Scholar]
- 31.Gammaitoni L., Hänggi P., et al. Marchesoni F. Stochastic resonance: a remarkable idea that changed our perception of noise. Eur. Phys. J. B. 2009;69:1–3. [Google Scholar]
- 32.George J.T., Jolly M.K., Levine H., et al. Survival outcomes in cancer patients predicted by a partial emt gene expression scoring metric. Cancer Res. 2017;77:6415–6428. doi: 10.1158/0008-5472.CAN-16-3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Colman-Lerner A., Gordon A., et al. Brent R. Regulated cell-to-cell variation in a cell-fate decision system. Nature. 2005;437:699–706. doi: 10.1038/nature03998. [DOI] [PubMed] [Google Scholar]
- 34.Wang P., Song C., et al. Xing J. Epigenetic state network approach for describing cell phenotypic transitions. Interface focus. 2014;4 doi: 10.1098/rsfs.2013.0068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.George J.T., Levine H. Optimal cancer evasion in a dynamic immune microenvironment generates diverse post-escape tumor antigenicity profiles. Elife. 2023;12 doi: 10.7554/eLife.82786. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.