Control or overcontrol for covariates?

Abstract

Covariate adjustment can adjust for baseline differences in randomised controlled trials (RCTs) that may have arisen by chance. Furthermore, even if the groups do not differ significantly on any factors, using baseline variables that may be related to the outcome as covariates can reduce the within-group variance, thus increasing the accuracy of the estimates of treatment effects and the power of the statistical test. However, improper use of covariate adjustment can either magnify or diminish the difference between the groups. In RCTs, covariates must be chosen carefully and should not include variables that may have been affected by the treatment itself. The use of covariate adjustment in cohort studies is even more fraught and may result in paradoxical situations, in which there can be opposite interpretations of the results.

It is well known that using covariates in an analysis has a number of beneficial effects. It can adjust for baseline differences in randomised controlled trials (RCTs) that may have arisen by chance. Furthermore, even if the groups do not differ significantly on any factors, using baseline variables that may be related to the outcome as covariates can reduce the within-group variance, thus increasing the accuracy of the estimates of treatment effects and the power of the statistical test.¹ (It should be noted that although covariance adjustment is also frequently used in cohort studies, its use there is more controversial, at least among statisticians.^{1 2} There, it can lead to situations such as Lord's Paradox³ and Simpson's Paradox,⁴ as we'll discuss later). However, just because we can include covariates in our analyses does not mean we should include them. Unless they are carefully chosen, covariate adjustment can do more harm than good.

Ideally, there should be a small number of covariates, all of which are correlated with the dependent variable (DV), and none correlated highly with each other. Each covariate results in the loss of at least one degree of freedom (df), so that the reduced power resulting from this must be offset by the gain in power due to the reduction in the error sum of squares. Using covariates that are not related to the DV or that are highly correlated with each other merely reduces the dfs without the compensating shrinkage of the error.

A second, and perhaps more important, consideration is that the covariates must be independent of the intervention. If the covariates are related to it, then removing their effect also removes part of the effect of the intervention from the DV, a situation called ‘over-control’ or ‘over-adjustment.’ This can have two consequences. First, it moves the adjusted group means closer together than the unadjusted means would be, possibly resulting in a type 2 error; and second, it makes the results difficult to interpret.¹ The ideal covariates are those that are related to intrinsic properties of the participants, such as age or sex, or are measured before the randomisation, such as attitudes toward treatment or self-efficacy.

This is easy to state in theory, but more problematic in real life. There are many examples of variables that are measured after the trial has begun for which it seems, at least on an intuitive level, that we should adjust for. For instance, a recent RCT compared dialectical behaviour therapy versus general psychiatric management for patients with borderline personality disorder.⁵ Although the length of treatment was limited in both conditions, extra sessions were permitted in specific situations. Similarly, because this was a pragmatic trial (ie, it attempted to reflect how therapy is delivered in the real world, rather than imposing strict control over what could or could not be done⁶), no restrictions were imposed regarding the use of psychotropic medications not prescribed by the study's psychiatrists or seeking additional therapies from other agencies. Furthermore, the therapeutic alliance may have influenced the effectiveness of the treatment. The issue is whether these factors should be used as covariates in the final analyses.

At first glance, it may seem to make sense to do so. Having additional treatment sessions, or using medications that were not part of the treatment protocol, or receiving therapies over and above those delivered as part of the trial would affect the primary and secondary outcomes (frequency and severity of suicidal self-injurious behaviour episodes, psychiatric symptoms, anger, depression, treatment retention and so forth). Not accounting for these factors could have an effect on the results, either increasing or decreasing the differences between the groups, depending on how they were distributed.

However, using these factors as covariates would be a mistake, resulting not in control, but in overcontrol. The reason is that they are likely affected by the treatment itself. That is, patients who need extra sessions or who seek additional treatments are not a random subset of the population, equally distributed between the groups, but rather would be those who feel that the treatment they are receiving is insufficient or not working. Furthermore, it is quite probable that this would be a function of the treatments themselves. If treatment A is less effective than treatment B, then it would be expected that there would be more patients in the former group receiving additional help than in the latter. In this situation, covariance adjustment would result in increasing the difference between the groups, perhaps beyond what the true difference actually is.

On the other hand, the effectiveness of treatment may be affected by the therapeutic alliance between the patient and the therapist, and the alliance itself may be enhanced by allowing the patients to have additional treatment sessions (as well as other factors). Consequently, covarying out alliance in this situation would result in a decreased difference between the groups.

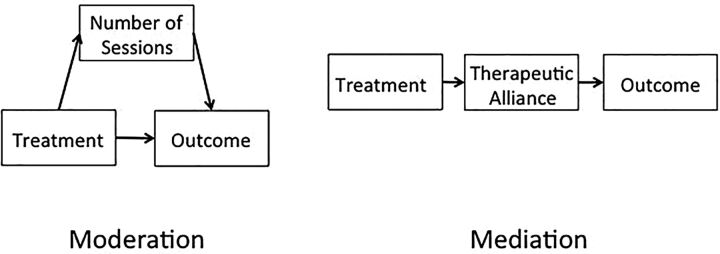
The first situation (additional sessions) is an example of the covariate as a moderator variable; that is, one that affects the relationship between the treatment and the outcome through an additional pathway, as seen in the left side of figure 1. In the second example, illustrated on the right side of the figure, therapeutic alliance is a mediating variable, in that it is on the direct pathway between treatment and outcome; that is, the treatment affects the alliance which in turn influences the outcome (for a thorough discussion of the difference between moderators and mediators⁷). Although in this example, adjusting for the moderating variables would increase the difference between the groups and adjusting for the mediating one would decrease it, this is not a universal truth. The direction of the bias varies from one situation to another, depending on the choice of covariates and their relationship to the independent and DVs. A more extended, mathematical discussion of the effects of overadjustment is presented by Schisterman et al.⁸

Figure 1.

The difference between a moderator variable (on the left) and a mediating variable (on the right).

To reiterate, variables that are unaffected by the treatment, such as gender, or those that are measured before the treatment begins, such as self-efficacy, can moderate the effects of the treatment and are fair game for covariate adjustment. On the other hand, variables measured after therapy has begun, such as the number of sessions or self-esteem, can be either moderators or mediators; the distinction often depends more on one's theory of the mechanism of action of the intervention than on statistics, and should rarely be used as covariates.

So far, we have discussed covariate adjustment within the context of an RCT and alluded only in passing to the difficulties it poses in cohort studies. Now let's consider the issue in more depth, and in particular, to Lord's Paradox. Although its existence causes many to cry out to the heavens in despair, it is actually named after Lord,^{9 10} who first wrote about it, not the one looking down on our statistical sins from on high. Since then, it has been shown to be similar to Yule's Paradox and Simpson's Paradox.⁴

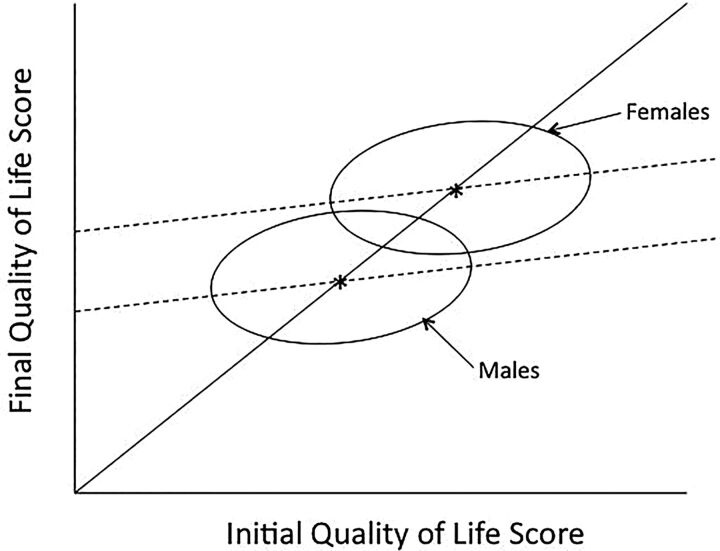
To illustrate it, let's make up a hypothetical example of comparing the quality of life (QoL) of males and females following treatment with an antidepressant. The results of this study are shown in figure 2. Statistician A looks at these data and states that the drug is ineffective. To support his conclusion he cites the fact that the centres of both ellipses (shown by the asterisks) fall on the 45° line, indicating no mean effect for either men or women. Statistician B analyses the same data with an analysis of covariance. Because the two regression lines through the ellipses (shown by the broken lines) are parallel, this approach is legitimate. She concludes that the females showed significantly greater improvement in QoL than males when allowance is made for the initial difference in scores, reflected by the fact that the regression lines for each group have different intercepts. That is, if you select a subgroup of men and women who have identical distributions of QoL at baseline, the regression lines show that the females will improve more than the males. In other terms, statistician A was trying to estimate the total effect (of gender on QoL), while statistician B was estimating the direct effect of gender on QoL, unmediated by, and therefore adjusting for, initial QoL.¹¹

Figure 2.

Results of a fictitious study showing the effects of treatment on quality of life for males and females.

So, which statistician was right—was there or was not there a difference due to the intervention? According to Lord, “there is simply no logical or statistical procedure that can be counted on to make proper allowances for uncontrolled preexisting differences between groups. The researcher wants to know how the groups would have compared if there had been no preexisting uncontrolled differences. The usual research study of this type is attempting to answer a question that simply cannot be answered in any rigorous way on the basis of the available data.” (ref. ⁷, p. 305).

Lord was correct when he wrote that, but that was 40 years ago. Since that time, though, techniques have been developed to analyse these situations using causal mediation methods. However, these require the researchers to specify a priori whether they are interested in direct or total effects.^{12 13} More importantly, they assume that there are no hidden confounders (sometimes called ‘collider variables’),¹⁴ as the result will yet again be overcontrol and a reduction or an increase in the between-group difference—it is impossible to predict beforehand which will be the case. Because we can rarely be confident that we know and have modelled all of the potential confounders, covariance adjustment in cohort studies remains problematic.

In summary, covariate adjustment can be a powerful tool in regression and analyses of variance for balancing groups with regard to baseline variables and for reducing within-group variance. However, the covariates must be carefully chosen, being wary to avoid variables that can be affected by the treatment or group assignment itself. Otherwise, it can either magnify or diminish group differences, depending on the relationships of the covariates with the independent and DVs.