Trend analysis of rainfall from 1981-2022 over Zambia

Abstract

There is insufficient paucity of information on trends in long-term monthly and decadal rainfall in Zambia. This study assessed the monthly and decadal trends in rainfall over the agro-ecological regions (AERs) and Zambia from 1981 to 2022. The Mann-Kendall test statistic was used at 5 % significant level to compute trends in rainfall at monthly and decadal time step on CHIRPS v2 at 0.05° resolution. R/RStudio Sen's slope estimator was used to give the magnitude of the observed trends. The monthly rainfall time series trend over Zambia ranges from −0.04 to 0.03. The decadal trend analysis of rainfall at annual and monthly time step exhibits a decreasing/increasing trend with Sen's slope between −49.27 and 71.26 mm. Decadal trend at annual time step in AERIII, AERIIa, AERIIa and AERI exhibits a Sen's slope of −44.11 to 62.48 mm, −15.29 to 41.58 mm, −6.08 and 71.26 mm, and 2.20–64.86 mm, respectively. The decadal trend at monthly time step in AERIII, AERIIa, AERIIa and AERI exhibits a Sen's slope of −132.08 to −3.15 mm, −123.39 to −8.57 mm, −73.08 to −15.17 mm, and −80.02 to −5.21 mm, respectively. Decrease in rainfall is expected to affect agriculture, energy, water resources, sanitation and socio-economic aspects. Rainfall pattern shows spatio-temporal variability over Zambia. The results provide valuable input into the National Adaptation Plan and also useful for strategic planning purposes in water resources management under a changing climate. It is evident that spatio-temporal time steps utilized in this study provides new insights of rainfall trends at seasonal, monthly, and annual and decadal time steps.

Highlights

• •Historical rainfall datasets whether in-situ or satellite estimate are generally utilized in planning and designing for water resources projects.
• •CHIRPS v2 dataset can be used to create a new dataset for rainfall to be used in risk and climate change analysis.
• •CHIRPS v2 daily dataset can be used to fill gaps in the observational datasets; and.
• •CHIRPS v2 rainfall dataset can be used in informing policy and National Adaptation Plans (NAPs).

Contribution to the field statement

The information generated at monthly and decadal trend can be used to inform both policy and the National Adaptation Plans (NAPs), National Development Plan (NDP). The CHIRPS v2 data can be used as proxy for gauge station at daily, monthly and annual spatio-temporal timesteps.

1. Introduction

Rainfall is an important component in water resources and hydrology, hydro-power generation, agriculture, fisheries, aquaculture and climate systems [1,2]. Further, rainfall has been severely affected by the changing climate globally [2]. The variability in rainfall are evident at regional and global scale and the impacts on the environment and human system are evident [3]. Spatio-temporal trends in rainfall is assessed using historical rainfall datasets [2,4]. These datasets are recorded using in-site observational rain gauge stations. Capturing rainfall data from observational networks is expensive especially over regions without rain gauge stations [2,5,6]. Moreover, rainfall datasets collected from observational station are inadequate in many parts of the world including Zambia due to sparse gauge station networks. However, satellite rainfall estimates have been used as an alternative and proxy to gauge station rainfall dataset for the purpose of filling gaps in gauge station datasets [7]. The historical rainfall datasets whether in-situ or satellite estimate are generally utilized in planning and designing water resources projects [8].

There are several Satellite Rainfall Products (SRPs) available that are produced by combining ground observations and satellite-based sensors. The SRPs are gridded datasets that cover both spatial and temporal resolution. The strengths of SRP include the fact that they can provide good spatial coverage and near real-time monitoring of rainfall, especially in areas where rain gauges are sparse or nonexistent. They can capture the spatial and temporal variability of rainfall, and provide high-resolution data for hydrological and meteorological applications. They can be produced from different types of satellite sensors, such as microwave and infrared, to estimate rainfall based on different physical principles and algorithms.

On the other hand, SRP can have errors and uncertainties due to factors such as cloud contamination, surface emissivity, atmospheric attenuation, and algorithm assumptions. They can have biases and inconsistencies due to differences in satellite orbits, sensors, calibration, and validation methods. The SRPs can have difficulties in estimating extreme rainfall events and complex terrain effects.

There are several SRPs available namely; Africa Rainfall Climatology version 2 (ARC2) [9], AgMERRA [[10], [11], [12], [13]], Climate Hazards Group InfraRed Precipitation with Station (CHIRPS) [14], Climate Prediction Center Morphing Algorithm (CMORPH) [15], Climate Research Unit Time series [16,17], Global Precipitation Climatology Project (GPCP) [18], IMERG-GPM [10,19], Integrated Merged Multi-satellite Retrievals (IMERG) [20], Multi-Source Weighted-Ensemble Precipitation (MSWEP) [21], NASA MERRA-2 [10,22,23], Climate Prediction Center (CPC) Morphing technique (CMORPH) [15], Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks (PERSIANN) [24], Rainfall Estimate (REF2) [18,25], Tropical Application of Meteorology Using SATellite (TAMSAT) [26], Global Precipitation Measurement (GPM) [27], Tropical Rainfall Measuring Mission (TRMM) [28], Water and Global Change (WATCH) project [29]. The SRPs highlighted above are popular due to their easy accessibility at high spatial (up to grid size of 1° × 1°) and temporal (daily, monthly, annual) resolution [30]. CHIRPS dataset have been applied in East Africa, Zambia and other regions [6,7,[31], [32], [33], [34]].

The detection of monthly, seasonal and decadal changes and trends in long-term time series of climate datasets is important for understanding of the climate and in developing mitigation and adaptation strategies at regional and local scale [31]. In Zambia, researchers have examined rainfall trends based on observational station data [32,[35], [36], [37], [38], [39], [40]]. Moreover, trend analysis studies utilizing SRPs are relatively limited [32]. SRPs datasets extend more than 30 years and provide rainfall datasets at diverse spatio-temporal resolution [41]. Methodologies have been developed to identify spatial trends in satellite-based netCDF and GeoTif datasets [2]. Three trend tests namely; Spearman rank order correlation (SROC) test, Kendall rank correlation (KRC) test and the Mann-Kendall (MK) test have been evaluated by scientists [2,6,42,43]. Comparatively, their evaluation revealed fair agreement at annual and monthly timescale. Studies reviewed indicated that the non-parametric Mann-Kendall test has been applied for detecting trends in rainfall datasets [2,4,[44], [45], [46]].

The Mann-Kendall test is a widely applied non-parametric test in identifying existence of pattern in a time series [[47], [48], [49]]. Further, the Mann-Kendall test is recommended for trend analysis as it allows for minimal assumptions to be made about the time series data. It is robust to outliers and missing values, and can handle data with seasonality or cyclic patterns [50]. It can detect both linear and nonlinear trends, and can identify the timing and magnitude of abrupt changes [44,51,52]. The test is suitable for analyzing non-normally distributed datasets and it requires serially uncorrelated time series [44]. The Mann-Kendall test has been used in agro-meteorological, climate change and hydrological studies [36,49,[53], [54], [55], [56]]. The studies have reveal the quality of the test in bringing out patterns in hydrological studies. The Mann-Kendall test has been applied in detecting trends at daily, monthly, seasonal, and annual rainfall and in trend-free pre-whitening approach [47,57]. Furthermore, recent studies have shown that pre-whitening of climate datasets does not improve trend identification when using Mann-Kendall test [2].

Other researchers have applied the modified Mann-Kendall test to rainfall and stream flow datasets [49]. The limitation of applying the Mann-Kendall test are associated with its null hypothesis (H_o), which assumes that the data are independently and identically distributed [56]. Moreover, it has low power to detect weak trends, especially when the sample size is small or the variance is large. It is sensitive to positive autocorrelation, and can inflate errors. Furthermore, the test cannot distinguish between different causes of trends, such as climate variability or human activities.

Zambia's economically important sectors (Agriculture, Energy, Forest, Health, Infrastructure, Mining, Transport, Tourism, Water and Wildlife) have continuously been ravaged with risk and vulnerabilities because of climate change impacts [58]. Climate hazards like droughts and floods are affecting these sectors. It is anticipated that in future, droughts and floods will intensify in Zambia and affect water and food security at the household and national levels [59,60]. Knowing how climate change will affect future water resources and food availability can benefit from understanding the variability and impacts of climate change to date [61].

Trend analysis of rainfall is important for many reasons. It can help understand the effects of climate change and variability on water resources, ecosystems, floods, and droughts. It can provide information on the spatial and temporal variability of precipitation, as well as its trends and anomalies. It can support hydrological modelling and forecasting, climate monitoring and analysis, agricultural and water resource management, and disaster risk reduction and humanitarian response.

Trend analysis of rainfall, Interactive effects of rainfall, temperature and water level and Climate change and crop choice in Zambia has been undertaken by researchers [46,62,63]. However, the studies focused on rural areas (Eastern, Northern) [62], Zambezi river basin headwater [46] and effects of rainfall, temperature and water level on fish yield in Lake Bangweulu [63]. Additionally, a study by Chisanga et al. [37] on trend analysis focused only at a research station in agro-ecological IIB. Mubanga and Umar [38] reported statistically insignificant 1.10 mm decrease of rainfall at annual timescale in southern Zambia from 1910 to 2009. Furthermore, rainfall in Zambia shows a spatial-temporal and interannual variation within each season and agro-ecological regions [64]. There is insufficient paucity of information on rainfall trend [65] analysis over Zambia at seasonal, monthly and decadal time steps. The strength of this study compared to past studies in Zambia is that it focuses on the whole country and evaluates spatio-temporal rainfall time series trend at seasonal, monthly and annual timescale. This study is important as it helps test a theory that rainfall in Zambia has been undergoing a northward shift in spatial distribution which was first proposed by Sichingabula [66] and adopted by subsequent authors such as Mubanga and Umar [38]. Therefore, the objective of this study was to assess the seasonal, monthly, and annual and decadal trends in rainfall over the agro-ecological regions (AERs) and Zambia from 1981 to 2022. This was for purposes of analyzing seasonal variability of rainfall and assessing whether there are significant changes in rainfall patterns during different seasons, as well as identifying any emerging trends. The alternative hypothesis tested in this study stated that there were statistically significant changes in rainfall trends over Zambia between 1981 and 2022.

2. Materials and methods

2.1. Study site

Zambia is a land-linked country located in southern Africa between the grid extent of Longitude: 21.400 | 33.400 and Latitude: −18.650 | −8.650. It lies between Angola in the west, Namibia, Botswana, and Zimbabwe in the south, Mozambique, Malawi, and Tanzania in the east, and the Democratic Republic of Congo in the north with an estimated 752,614 square kilometres in size as shown in Fig. 1. Its tropical continental climate has clearly defined four seasons divided on the basis of rainfall and temperature patterns [40,67,68]. These seasons are the; (i) Hot Season (September to October); (ii) Rainy Season (November to March); (iii) Post Rainy Season (April and May); and (iv) Cool and Dry Season (June to August) [67]. Zambia's rainfall is strongly influenced by the movement of the Inter-Tropical Convergence Zone (ITCZ) as well as the El Niño/Southern Oscillation (ENSO) phenomenon and varies from a seasonal average of 600 mm in the lower south up to 1300 mm in the upper north of the country.

Fig. 1.

Map showing the agro-ecological Regions (AERs; AERIII, AERIIA, AERIIB and AERI) of Zambia.

Zambia is divided into three Agro-ecological Regions (AERs) namely Agro -ecological Region 1 (AERI), Agro – ecological region IIa (AERIIa), Agro - ecological region IIb (AERIIb), and Agro-ecological region III (AERIII) based on amounts of rainfall and incorporates soils and other climatic characteristics. AERI is a low rainfall (<800 mm/year) area which covers the country's major valleys whilst AERIIa (800–1000 mm) and AERIIb, which only differ in soil characteristics, receives medium rainfall (800–1000 mm/year) and covers Sandveld plateau of Central, Eastern, Lusaka and Southern provinces. Further AERIII receives the highest rainfall in the country from 1000 to 1500 mm year⁻¹. The division between AERIIa and AERIIb is based on differences in soil type and rainfall, with sandy soils and less rainfall in Region IIb. Region IIa is located in the central and eastern plateaus of Zambia, comprising 28 % of the land area. The rainfall in this region ranges from 800 to 1000 mm, and summer temperatures range from 20 to 33 °C

2.2. Data sources

2.2.1. Description of Climate Hazards Group InfraRed Precipitation with station data (CHIRPS)

The Climate Hazards Group InfraRed Precipitation with Station data [14] is a 30+ year quasi-global rainfall dataset developed by the US Geological Survey (USGS), and the Climate Hazards Group at the University of California. The CHIRPS datasets are blended products that combine global climatologies, satellite observations and in-situ rainfall observations from Global Telecommunications System (GTS) [18]. The CHIRPS datasets ranges from 1981 to date and incorporates in-house climatology, CHPclim at 0.05° resolution satellite imagery, and in-situ station data to create gridded rainfall time series that can be applied for trend analysis and seasonal drought monitoring. It was selected on the basis of having relatively high spatial resolution (0.05° × 0.05°), long time series and it is freely available [14,18,32,69,70]. It is intended for drought and environmental monitoring, especially in areas where surface data is sparse or nonexistent. It can also provide information on the spatial and temporal variability of precipitation, as well as its trends and anomalies. The CHIRPS v2 climate data for the period 1981–2022 used in this study was downloaded from the following URL: https://data.chc.ucsb.edu/products/CHIRPS-2.0/global_monthly/netcdf/chirps-v2.0.monthly.nc. More information is provided by Refs. [18,69].

2.2.2. ESRI shape files

The shapefile data for Zambia were extracted from the GADM database (www.gadm.org), version 3.4, April 2018. The shapefile contained the following: gadm36_ZMB_0, gadm36_ZMB_1 and gadm36_ZMB_2 (cpg, dbf, prj, shp, shx).

2.2.3. Data analysis and evaluation

CHIRPS v2 climate dataset [7,34] was evaluated using the meteorological surface observations. The CHIRPS v2 climate data was compared to the observations using temporal (monthly, seasonal) and spatial (point) scales over the period 1981–2022. The statistical metrics used in comparing CHIRPS v2 climate data against ground observations were; coefficient of determination (R²), the Pearson's coefficient (r) and root mean square (RMSE) [18,[71], [72], [73], [74]] using Equation 1, Equation 2 and Equation 3. The correlation are considered very weak, weak, moderate, strong and very strong from 0.00 to 0.19, 0.20–0.39, 0.40–0.59, 0.60–0.79, and 0.80–1.0, respectively [75,76]. The lower the RMSE, the closer the CHIRPS are to ground observations [18].

Methods	Equation	Interpretation	Ideal value
Coefficient of determination (R2)	$R^2=1-\frac{\sum _{i=1}^n{\left(S_i-V_i\right)}^2}{\sum _{i=1}^n{\left(S_i-\bar{S}\right)}^2}$		1	Equation 1
Pearson's coefficient (r)	$\mathrm{R}=\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left({\mathrm{S}}_{\mathrm{i}}-\bar{\mathrm{S}}\right)\left({\mathrm{V}}_{\mathrm{i}}-\bar{\mathrm{V}}\right)}{\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{S}}_{\mathrm{i}}-\bar{\mathrm{S}}\right)}^2}\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{V}}_{\mathrm{i}}-\bar{\mathrm{V}}\right)}^2}}$	−1, 1	1	Equation 2
Root mean square error (RMSE)	$\text{RMSE}=\sqrt{\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{S}}_{\mathrm{i}}-{\mathrm{V}}_{\mathrm{i}}\right)}^2}{\mathrm{n}}}$		0	Equation 3

Where i is the location index, $V_i$ is the precipitation value from observations, $S_i$ is the precipitation value from CHIRPS v2 data, n is the total number of data inputs, and $\bar{V}$ is the average value of $V_i$.

2.2.4. Trend analysis

The trend analysis and p-value were computed at 5 % significant level using the methods proposed by Abdi et al. [77]. The trends in CHIRPS v2 dataset was analyzed using the tidyverse, lubridate, trend, raster, pals, metR and Kendall R packages. The metR package has been created by Elio Campitelli [78]. This package has useful functions for data grid climate data visualization and analysis. The Mann-Kendall trend test and p-value at 95 % Confidence Interval (CI) on CHIRPS v2 netCDF file format for monthly time series from 1981 to 2022 was performed using the scripts created by Abdi et al. [77]. The trends were computed at monthly, annual and December, January and February (DJF) time series using RStudio and R Programming software. The Mann-Kendall test is a frequently utilized nonparametric test for monthly and annual time series data to determine the trend [36,[79], [80], [81]].

The annual trend and its statistical significance was calculated using the trend R package [81,82]. The sens. slope function in trend R package was used to calculate the slope of the trend (increase/decrease per year) while the MK test function (Mann-Kendall test) was used to verify if the trend is statistically significant or if it is the result of the variability within the climate system [83]. More information on trend analysis is provided by Akinbile et al. [80], Butler [79] and Mcleod [84].

Equation (4), Equation (5), Equation (6), Equation (7), Equation (8) and Equation (9) were used to compute the Mann-Kendall [47,82,83,85,86]. However, Equation (10) and Equation (11) were used to calculate the Sen's slope method. Further, the null hypothesis is that the data come from a population with independent realizations and are identically distributed. For the two sided test, the alternative hypothesis is that the data follow a monotonic trend. The Mann-Kendall test statistic is calculated according to the following Equations 1-9:

$$S=\sum _{k=1}^{n-1}\sum _{j=k+1}^{n}sgn\left(x_j-x_k\right)$$ Equation 4

with sgn the signum function.

The mean of S is μ = 0. The variance including the correction term for ties is:

$${\sigma }^2=\left\{n\left(n-1\right)\left(2n+5\right)-\sum _{j=1}^p{t}_j\left(t_j-1\right)\left({2t}_j+5\right)\right\}/18$$ Equation 5

where p is the number of the tied groups in the data set and tj is the number of data points in the j-th tied group. The statistic S is approximately normally distributed, with:

$$z=\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.$$ Equation 6

If continuity = TRUE then a continuity correction will be employed:

$$z=sgn\left(S\right)\left(\left|S\right|-1\right)/\sigma$$ Equation 7

The trend is determined for Z as decreasing (negative) or increasing (positive) and the computed Z-statistics is greater or lesser than the z-value corresponding to the 5 % level of significance. Moreover, Z-statistics of zero indicated no trend.

The statistic S is closely related to Kendall's $\tau$:

$$\tau =S/D$$ Equation 8

where

$$D={\left[\frac{1}{2}n\left(n-1\right)-\frac{1}{2}\sum _{j=1}^p{t}_j\left(t_j-1\right)\right]}^{1/2}{\left[\frac{1}{2}n\left(n-1\right)\right]}^{1/2}$$ Equation 9

Equation (10) below was used to compute the slope (i.e. linear rate of change) and confidence levels according to Sen's method [82,83,86,87]. First, a set of linear slopes is calculated as follows:

$$d_k=\frac{x_j-x_i}{j-i}$$ Equation 10

for (1 ≤ i < j ≤ n), where d is the slope, x denotes the variable, n is the number of data, and i, j are indices.

To identify if trend exists in a time series dataset, a slope estimator (m) is considered ij as median for all data sets for various combination. The '+ve’ and '-ve’ value of (m) indicates an upward or downward trend, respectively. Sen's slope is then calculated as the median from all slopes using Equation (11). sens. slope function in trend R package also calculates the upper and lower confidence limits.

$$b_{Sen}=median\left(d_k\right)$$ Equation 11

3. Results

3.1. Seasonal statistical metrics between CHIRPS and ground observations

The CHIRPS seasonal and monthly mean totals against the observations are shown in Fig. 2, Fig. 3. The October (r = [0.60, 0.98], RMSE = [19.79, 116.43 mm]), November (r = [0.76, 0.98], RMSE = [19.76, 112.98 mm]), December (r = [0.59, 0.99], RMSE = [16.42, 92.88 mm]), January (r = [0.72, 0.98], RMSE = [30.25, 34.22 mm]), February (r = [0.98, 0.99], RMSE = [21.89, 72.63 mm]), March (r = [0.81, 0.98], RMSE = [17.65, 73.53 mm]) statistics for CHIRPS are satisfactory with r values > 0.50 for ONDJFM. The statistical metrics for October, November, December, January February, and March between CHIRPS and observations were >0.50 for CHIRPS and this is considered satisfactory for r values > 0.5. The R² and Pearson coefficient between the CHIRPS and observations ranged from 0.65 to 0.90 and 0.81–0.95, respectively. Moreover, the statistical metrics shows good skills at seasonal scale (r > 0.81).

Fig. 2.

Bar graphs of seasonal sums (OND, DJF, JFM) (mm/season) for the observations against CHIRPS.

Fig. 3.

Observed against CHIRPS monthly rainfall means in mm/month.

3.1. Monthly trend analysis of rainfall over Zambia and the AERs

Fig. 4 and Table 1 shows monthly trends in mean monthly rainfall over Zambia. The monthly rainfall time series (1981–2022) trend over Zambia ranges from −13.21 to −0.32 using CHIRPS v2 data (p-value = 0.20–1.00) as shown in Fig. 4 and Table 1. The trend analysis shows that rainfall for the period of 1981–2022 was statistically insignificant at 95 % confidence interval (p < 0.05) over Zambia. However, rainfall exhibited variability during the same period (1981–2022). The trend in monthly time step of rainfall over AERs are shown in Fig. 4. The AERIII exhibits positive and negative trend at monthly time step from −0.04 to 0.03 (p-value = 0.20–1.00) for the period 1981–2022. AERIIa exhibits a positive and negative trend with sen's slope of −0.03 to 0.03 mm (p-values = 0.33–1.00) while AERIIb shows both decreasing and increasing trend with sen's slope between −0.03 and 0.02 mm (p-value = 0.41–1.00). However, AERI shows both decreasing and increasing trend from −0.03 and 0.02 mm (p-value = 0.40–1.00). All the sen's slope at monthly time step in all the AERs were statistically insignificant with both decreasing and increasing trends.

Fig. 4.

Trends and significant change in monthly rainfall over Zambia and AERs (AERI, AERIIa, AERIIb and AERIII) using CHIRPS v2 data from 1981 to 2022.

Table 1.

Monthly and decadal rainfall trends over Agro-ecological Regions (AERs) and Zambia.

Time step	Monthly trend (mm)	Decadal monthly trend (mm)	Decadal annual trend (mm)
		Zambia (All the months)
Sen's slope	−13.21 to −0.32	−132.08 to −3.15	−49.28 to 71.26
p-value	0.089 to 0.95	0.09 to 0.95	0.00 to 1.00
		AERI
Sen's slope	−0.03 to 0.02	−80.02 to −5.21	2.20 to 64.86
p-value	0.40 to 1.00	0.19 to 0.63	0.00 to 0.98
		AERIIa
Sen's slope	−0.03 to 0.03	−123.39 to −8.57	−15.29 to 41.58
p-value	0.33 to 1.00	0.09 to 0.63	0.04 to 1.00
		AERIIb
Sen's slope	−0.02 to 0.01	−73.08 to −15.17	−6.08 to 71.26
p-value	0.41 to 1.00	0.19 to 0.63	0.00 to 1.00
		AERIII
Sen's slope	−0.04 to 0.03	−132.08 to −3.15	−44.11 to 62.48
p-value	0.20 to 1.00	0.09 to 0.95	0.00 to 1.00

3.2. Decadal annual and monthly rainfall over Zambia and the AERs

3.2.1. Decadal annual and monthly rainfall over Zambia

The decadal total annual and monthly rainfall trends over Zambia are shown in Fig. 5a and b, respectively. Results show that at annual time scale rainfall distribution exhibits both decreasing and increasing trends with sen's slope from −49.27 to 71.26 mm during the period 1981–2022. Increasing trends are evident in Western, Southern and Northern provinces. However, significant decreasing trends are noted in Luapula province. The p-value ranges from 0.00 to 1.00. The monthly rainfall trends are insignificant with decreasing rainfall trends especially in Luapula, Northern, Eastern and Muchinga provinces (Fig. 5b).

Fig. 5.

Significant change in decadal rainfall over Zambia using CHIRPS v2 data from 1981 to 2022. (a) Shows decadal trend and changes in total rainfall at annual time scale in Zambia (1981–2022) and (b) Shows decadal trend and changes in total monthly rainfall at monthly time scale in Zambia (1981–2022).

3.2.2. Decadal trend of rainfall at annual and monthly time step in AERs

The decadal trend of rainfall at annual and monthly time scale for all the AERs are shown in Fig. 6 and Table 1. Fig. 6a, c, e and g shows rainfall changes at decadal annual trend (1981–2020) whilst Fig. 6b, d, f and h shows rainfall changes at decadal monthly trend (1981–2020). The trend analysis at annual time step shows that rainfall from 1981 to 2022 was statistically either significant or insignificance at 95 % confidence interval (p < 0.05) within AERIII (−44.11 to 62.48 mm). The p-values ranged between 0.00 and 1.00. This indicates that rainfall exhibits both positive, and negative trends and variability from 1981 to 2022. The decadal trend in annual rainfall over AERIIa for the period 1981–2022 shows a both decreasing and increasing trend from −15.29 to 41.58 mm (p-value = 0.04–1.00). AERIIb shows similar trend patterns from −6.08 and 71.26 mm (p-value = 0.00–1.00).

Fig. 6.

Decadal trends in total annual and mean monthly total rainfall over AERs using CHIRPS v2 data from 1981 to 2022 at confidence interval (p < 0.05). (a, c, e, g) shows decadal trend in total annual rainfall (mm) in AERs (1981–2020); and (b, d, f, h) shows decadal trend in mean monthly rainfall (mm) in AERs (1981–2020).

The decadal trend in monthly time step of rainfall over AERIII for the period 1981–2022 shows a decreasing trend of −132.08 to −3.15 mm (p-value = 0.09–0.95) (Fig. 6b, d, f and h). The decadal trend in monthly rainfall over AERIIa for the period 1981–2022 shows both decreasing and increasing trend from −123.39 to −8.57 mm (p-value = 0.09–0.63). The decadal trend in annual rainfall over AERIIb for the period 1981–2022 shows both decreasing and increasing trend from −0.03 to 0.01 mm with p-value from 0.41 to 1.00. Similarly annual monthly rainfall trends are depicted over AERI from −0.03 to 0.02 mm (p-value = 0.40 to 1.00).

3.3. Seasonal trend analysis for OND, DJF, JFM and ONDJFM rainfall over Zambia

The decadal seasonal trends of annual and monthly rainfall are shown in Table 2 for the period 1981 to 2022. The seasonal monthly trends shows an increase and decrease in rainfall (Table 2). Moreover, the decadal annual trends in rainfall during the seasons, DJF, OND, DJF and ONDJFM exhibits both an increasing and decreasing trend in rainfall (Table 2). The decadal total annual and monthly rainfall sen's slope for DJF were −26.95 to 47.30 mm (p-value = 0.00–1.00) and −608.65 to 476.89 mm (p-value = 0.30–1.00), respectively. Conversely, OND shows an increase in rainfall of between 402.23 and 1480.20 mm which is statistical insignificant from 1981 to 2022.

Table 2.

Seasonal annual and monthly rainfall trends over Zambia.

Time step	Monthly trend (mm)	Decadal monthly trend (mm)	Decadal annual trend (mm)
		Zambia (DJF)
Sen's slope	−9.01e-02 to 0.26	−608.65 to 476.89	−26.95 to 47.30
p-value	2.19e-5 to 1.00	0.30–1.00	0.00–1.00
		Zambia (OND)
Sen's slope	−0.07 to 0.06	402.23 to 1480.20	−33.08 to 22.03
p-value	0.23 to 1.00	0.30 to 1.00	0.03 to 1.00
		Zambia (JFM)
Sen's slope	−5.55e-02 to 0.28	−844.136 to 736.57	−26.70 to 57.72
p-value	4.17e-06 to 1.00	0.30 to 1.00	0.00 to 1.00
		Zambia (ONDJFM)
Sen's slope	−0.07 to 0.11	−533.67 to 132.96	−51.83 to 78.17
p-value	0.01 to 1.00	0.06 to 1.00	0.00 to 1.00

Decadal trends for DJF total annual and monthly rainfall over Zambia are shown in Fig. 7a–b, respectively. Decadal trends for OND total annual and monthly rainfall over Zambia are shown in Fig. 8a–b, respectively. Decadal trends for JFM total annual and monthly rainfall over Zambia are shown in Fig. 9a–b, respectively. Decadal trends for ONDJFM total annual and monthly rainfall over Zambia are shown in Fig. 10a–b, respectively. The decadal seasonal (DJF, OND, JFM, ONDJFM) monthly trends in rainfall was insignificant (p < 0.05) at monthly time scale. Further, the decadal trend for OND total annual rainfall was insignificant (Fig. 8b). This indicates that rainfall exhibited variability from 1981 to 2022.

Fig. 8.

Decadal trends in total annual and monthly OND rainfall over Zambia using CHIRPS v2 data from 1981 to 2022 at confidence interval (p < 0.05). (a) Shows significant rainfall changes annual decadal trend (1981–2020) and (b) Shows significant rainfall changes monthly decadal trend (1981–2020).

However, the decadal trend for DJF, JFM and ONDJFM total annual rainfall was significant in selected parts of Zambia (Fig. 7a, 9a and 10a). Historically, rainfall exhibits an increasing trends in southern, western and northern parts of Zambia. The JFM exhibits an increasing trend in Western, North-western, Copperbelt, Luapula, Muchinga and Northern provinces. Significant decreasing trends in decadal annual rainfall were observed in Luapula and Northern provinces from 1981 to 2022. During ONDJFM, the western, southern and northern parts of Zambia exhibited a significant increasing trends in decadal annual rainfall. On the other hand, Luapula province experienced significant decreasing trend in decadal annual rainfall.

Fig. 7.

Decadal trends in total annual and monthly DJF rainfall over Zambia using CHIRPS v2 data from 1981 to 2022 at confidence interval (p < 0.05). (a) Shows significant rainfall changes annual decadal trend (1981–2020) and (b) Shows significant rainfall changes monthly decadal trend (1981–2020).

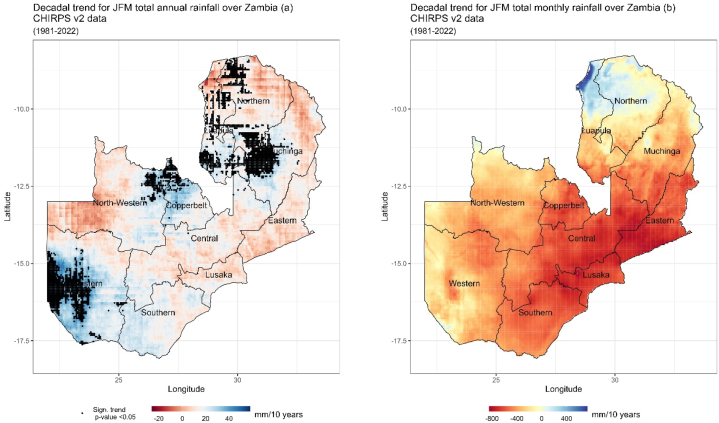
Fig. 9.

Decadal trends in total annual and monthly JFM rainfall over Zambia using CHIRPS v2 data from 1981 to 2022 at confidence interval (p < 0.05). (a) Shows significant rainfall changes annual decadal trend (1981–2020) and (b) Shows significant rainfall changes monthly decadal trend (1981–2020). Doted points show areas that are statistically significant changes.

Fig. 10.

Decadal trends in total annual and monthly ONDJFM rainfall over Zambia using CHIRPS v2 data from 1981 to 2022 at confidence interval (p < 0.05). (a) Shows significant rainfall changes annual decadal trend (1981–2020) and (b) Shows significant rainfall changes monthly decadal trend (1981–2022). Doted points show areas that are statistically significant changes.

4. Discussions

4.1. Seasonal statistical metrics between CHIRPS and ground observations

Literature reviewed indicated that different trend analysis methods are used to detect trend in rainfall time series at different seasonal, monthly and annual time steps [88]. Saragih et al. [89] suggested that CHIRPS rainfall products requires validation using observations. The statistical metrics for October, November, December, January February, and March between CHIRPS and observations were >0.50 for CHIRPS and this is considered satisfactory for r values > 0.5 [90]. The performance of CHIRPS is dependent on location of the ground observational station [32]. Further, the statistical metrics shows good skills at seasonal scale (r > 0.81). In other studies such as the one conducted in Indonesia, the performance of CHIRPS against observations was poor [89]. Others have reported low correlation values (<0.40) at daily time step such as in Iran and over the island of Cyprus [69,91]. The researchers stated an under-estimation of CHIRPS based on daily rainfall values [69,89,91]. However, the OND, DJF and JFM values were well reproduced by CHIRPS over Zambia [32]. CHIRPS datasets can be applied at spatio-temporal scale in ungauged regions and provides an alternative to observations at monthly time-step. Moreover, understanding the spatio-temporal variability of rainfall is vital for its application in climate and crop modelling, crop yield forecasting, hydrological modelling, risk assessment and drought monitoring [7,9,41,74,92]. CHIRPS have been assessed against gauge station datasets in Ghana, South Africa and Zambia [6,32,93]. Accurate observations of rainfall from satellites are important for monitoring rainfall variability and to properly understand the hydrologic cycle and regional climate [32].

CHIRPS rainfall data has been used as a proxy to observations for characterizing drought using a trend analysis in countries such as Iran, Jamaica and South Africa [6,91,94]. Researchers reported that statistical metrics shows that CHIRPS rainfall data performed better at annual and monthly time step with correlation greater than 0.60 in Iran, China, South Africa and Zimbabwe [6,42,45,91]. CHIRPS data was able to capture the spatial distribution of rainfall in Yunnan Province in China [42].

4.2. Monthly trend analysis of rainfall over Zambia and the AERs

Negative downward rainfall trends have been observed over Zambia [40,95]. Rainfall pattern shows spatio-temporal variability over Zambia [36,40]. The spatio-temporal variability is attributed to complex topography and existence of inland water bodies which modulate the climate system [40,96]. A study by Chisanga et al. (2022) detected statistically negative decreasing trend in total annual rainfall within the Zambezi River Basin.

Similar results have been report by Kampata et al. [46]. Kampata et al. [46] observed that analysis of rainfall data from five stations in the headstream regions of the Zambezi river basin exhibited downward trend which was insignificant. The climatic datasets like CHIRPS can be used as input into hydrological and crop models to estimate stream flow regime and crop yield [97]. moreover, low adaptive capacities and inter-seasonal rainfall variability limits rainfed agricultural production in Zambia [98,99]. A study utilizing 26 rainfall agromet stations showed a statistically insignificant trends in rainfall across Zambia [40].

Investigating the spatiotemporal changes in rainfall in the face of climate change especially in regions where agriculture is rainfed and contributes to economic development is essential [100]. Furthermore, researchers have applied trend analysis to quantify changes in rainfall at regional and national scale. Conversely, the impact of climate change on water resources was detected using a trend analysis in Trarza region, Mauritania [8]. On the other hand, a trend analysis by researchers in Saudi Arabia revealed a statistically significant decreasing trend on the selected gauge stations at all temporal scale [100]. Further, results showed that 10 stations along the north-west to south-west boundary did not exhibit significant trend. In Zimbabwe Gwatida et al. [45]reported a statistically insignificant trends in four rainfall characteristics.

4.3. Decadal annual and monthly rainfall over Zambia

Other researchers have reported decrease in annual rainfall of 2.3 % per decade since 1960 [67,101]. The decadal monthly rainfall time series shows decreasing trend and a p-value of −132.08 to −3.15 mm and 0.09 to 0.95, respectively. The Third National Communication (TNC) to the United Nations Framework on Convention Climate Change (UNFCCC) noted that observed trends of rainfall over districts of Sesheke (5.36 mm), Mumbwa (5.46 mm) and Mpika (2.82 mm) had statistically negative rainfall trends [40]. During 1960–1990, total annual rainfall has declined across Zambia by 2.3% decade⁻¹ [40,67,68]. Decadal and monthly rainfall over Zambia exhibits variability and uncertainty [102]. The detection of trend in climate data is a requirement for proper understanding and in developing of adaptation actions at regional or local scale [31].

Researchers have analyzed the spatio-temporal dynamics rainfall in Ethiopia [103]. Furthermore, it was noted that annual rainfall showed a decreasing trend. Asfaw et al. [103] recommended that strategies being designed within the agricultural sector should take into consideration decreasing rainfall [103]. Consequently, the changing pattern in rainfall makes the agricultural farming season shorter and affects the agricultural productivity [103,104].

4.4. Decadal trend of rainfall at monthly time step in AERs

The trend pattern ranges from −6.08 and 71.26 mm (p-value = 0.00–1.00) in AERIIb. Similar results have been reported by Chisanga et al. [37]. The researchers observed that extreme rainfall (PRCPTOT) exhibited statistically insignificant trend from 1963 to 2012 at Mount Makulu located in AERII [37]. AERI shows an increasing trend between 2.20 and 64.86 mm (p-value of 0.00–0.98). Analyzing climate datasets like CHIRPS and generating information on long-term patterns of rainfall trend is important for impacts assessment, development of National Adaptation Plans (NAPs) and mitigation strategies [105]. Further, Bartolomeu et al. [105] suggested that there is a growing need for more detailed information on rainfall variability due to climate change to inform policy.

4.5. Seasonal trend analysis for OND, DJF, JFM and ONDJFM rainfall over Zambia

Phiri and Chisanga [32] has shown that the CHIRPS v2 datasets are capable of reproducing seasonal rainfall amounts for OND, DJF and JFM. It is imperative to understand historical rainfall variability for agro-meteorological applications like crop modelling, crop yield forecasting, hydrological modelling and drought monitoring [7,9,41,74,92]. The CHIRPS v2 data has been utilized as an alternative to ground observations in Ghana and Zambia [32,93]. Other researchers reported that the annual rainfall in Zambia has decreased by 1.9 mm per month (2.3 % per decade) since 1960 mainly in DJF [67,101].

Rainfall has a high spatio-temporal variability and which can be analyzed using trend analysis [106]. An analysis of rainfall time series from 27 gauge stations in southern India revealed increasing or decreasing trend [106]. Analyzing spatio-temporal changes in rainfall at regional and national scale is vital for mitigating water related disasters [107]. A study undertaken in Portugal focused based on monthly, seasonal and annual rainfall series from 1913 to 2019 using 532 rain gauges concluded that rainfall exhibited decreasing trends [108]. Abebe et al. [109] reported insignificant annual rainfall trend from 1960 to 2019 in Tekeze-Atbara river basin, northwestern Ethiopia. Conversely, insignificant trends in seasonal and annual rainfall have been observed in Tanzania [110].

Trend in rainfall can be used to detect climate change using a long time series dataset. The time periods (1981–2022) used in this study is applicable in detecting climate change. Several studies have reported the effects of climate change and variability as revealed by the decreasing/or increasing rainfall anomalies [111]. Historical climate change can be assessed using past climate data based on either spatial or gauge station.

4.6. Impacts of trend in rainfall for agricultural sector in Zambia

Small scale farmers are experiencing impacts of climate change due to low adaptive capacity and their reliance on rainfed agriculture. The spatio-temporal variability of rainfall patterns in Zambia have rendered the crop sub-sector vulnerable to impacts of climate change [38]. It is important in examining agricultural production and productivity and food security at household and national level in rainfed regions [104]. Moreover, shorting agricultural season and seasonal rainfall characteristics indicates a need for the implementation of water harvesting technologies [109]. A proper understanding of the climatic conditions and agricultural management practices are vital in managing climate risk in the agricultural sector [110]. The reduction in rainfall and the start of the rainy season is likely to vary between provinces and AERs [64,112]. Additionally, this may result in inadequate rainfall to support effective establishment of crops and pasture during the months of October and November, which is traditionally associated with the start of the growing season. This in turn will result in variation to the timing of various agricultural activities such as field preparation, planting of seed, and weeding etc. The majority of the rainfed agricultural growing season is characterized by monthly rainfall deficits and is likely to result in fundamental changes to choice of crop choices and agricultural practices [64,99,113,114].

Researchers have recommended investments in research and development to identify locally-adapted and drought resilient cultivars to be promoted as alternative crops to vulnerable staples such as maize [64,115]. Moreover, investment is required in post-harvest processing facilities and marketing. Cassava has been recommended as an option for climate-resilient farming systems, particularly in comparison with annual cereal and legume crops which are poorly adapted to erratic rainfall. Additionally, promoting adoption of alternative, climate-resilient crops such as sorghum, beans, cowpeas, groundnuts and pigeon peas is inevitable. Millet and sorghum will not be impacted as negatively as maize and may be an appropriate option for further promotion and development as a climate-resilient alternative in combination with other staple cereal and legume crops [64].

4.7. Links to policy and national adaptation plans

Analyzing climate datasets like CHIRPS and generating information on long-term patterns of rainfall trend is important for impacts assessment, development of National Adaptation Plans (NAPs) and mitigation strategies [105]. Comprehensive analysis of rainfall variability and trends using historical time series are crucial in designing and implementing National Adaptation Plans (NAPs) to enhance climate resilient [110]. The findings provide valuable insights and information that can directly contribute to the national adaptation plans for Zambia. The trends generated in this study can be crucial in climate risk identification, informing climate change projections, assessing impacts on key sectors identified in the NAP such as water and agriculture. The results of this study also provide scientific evidence and data-driven insights to support decision-making and enhance resilient planning. Further, by understanding the historical trends and patterns, policymakers can develop policies that strengthen early warning systems, improve disaster preparedness, and enhance the ability to respond effectively to extreme rainfall events.

5. Conclusions

Zambia's economically important sectors have continuously been ravaged with risk and vulnerabilities because of climate change impacts. The study has demonstrated the need for analyzing climate trends based on spatio-temporal data with high spatial resolution for use in National Adaptation Plans (NAPs) and National Development Plans (NDPs) at local and regional scale. Long-term monthly and decadal trend analysis shows insignificant (except for small areas), decreasing and increasing spatial trend in rainfall over AERs and Zambia. The variability in rainfall is evident within Zambia and its impacts on the environment and human system are becoming obvious. High-resolution gridded historical CHIRPS dataset enables analysis of recent changes in rainfall at seasonal, monthly and annual time scale is most relevant for informing policy, research and decision-making. The findings of this study provides insights for targeting AERs and integrated adaptation actions in all the sectors within Zambia. This is important mainly due to the dependence of small scale farmers on rainfed agriculture. Furthermore, the findings can be used in implementing Zambia's National Adaptation Plan in terms of ensuring sustained availability of water and food security. In addition, further studies should focus on factors influencing trends by using sub-daily and daily satellite rainfall products. In conclusion, the alternative hypothesis is rejected and we accept the null hypothesis or the hypothesis of no difference. This implied that the general trends in rainfall over the country have not significantly changed over the period 1981 to 2022. The results dispel the widely held view that rainfall-based agro-ecological regions in Zambia have been undergoing a northward shift first proposed by Sichingabula [66].

Funding

This research received no external funding.

Data availability statement

The CHIRPS v2 data is available from CHIRPS database located at URL: https://data.chc.ucsb.edu/products/CHIRPS-2.0/. The R scripts used in the analysis and graphing can be provided by the corresponding author on request.

Declarations

Informed consent was not required for this study because it did not involve human or animal subjects.

CRediT authorship contribution statement

Charles B. Chisanga: Writing – review & editing, Writing – original draft, Software, Methodology, Formal analysis, Data curation, Conceptualization. Edson Nkonde: Software, Methodology, Data curation, Conceptualization. Elijah Phiri: Writing – review & editing, Validation. H. Mubanga Kabwe: Writing – review & editing, Data curation, Conceptualization. Catherine Lwando: Writing – review & editing.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:Charles B. Chisanga reports was provided by The Copperbelt University. Charles B. Chisanga reports a relationship with The Copperbelt University that includes: employment. Charles B. Chisanga has patent pending to NA. NA If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.