Abstract
In order to meet the needs of intelligent development of coal mines in China for transparency of geological conditions, identifying small faults with a drop of about 3 m has become one of the important geological tasks in structural interpretation. However, the accuracy of conventional 3D seismic exploration data interpretation methods for detecting small faults is still low. On the basis of introducing the basic principles of S-transform time-frequency analysis, principal component analysis, and RGB fusion, this paper proposes a method for identifying small faults in coal fields using multi-scale seismic curvature attribute fusion. The method uses S-transform to perform time frequency analysis to obtain seismic data volumes with multiple frequencies and seismic data volumes at different frequencies correspond to different scales of underground geological information portrayal. Perform spectral analysis on seismic data, determine parameters such as the dominant frequency and frequency bandwidth of seismic signals, and extract the maximum positive curvature attributes of seismic data volumes at different frequencies. Then the principal component analysis (PCA) method is used to analyze the seismic attributes of different frequency seismic data, the GRB fusion method is used to fuse the first three principal components. The application results of actual seismic data show that the results of multi-scale seismic curvature attribute fusion have obvious advantages in identifying small faults, and can improve the accuracy and interpretation accuracy of small faults in seismic data.
Keywords: Multi-scale seismic attribute, Maximum positive curvature attributes, Fusion, Small fault, RGB
1. Introduction
Identifying small faults in coal seams is very important for preventing accidents such as water inrush, gas outburst, roof caving, and ensuring safe production in mines [1]. With the continuous improvement of seismic exploration technology, the requirements for the accuracy of seismic data interpretation have become increasingly high. The interpretation of large faults has achieved good results, while the production capacity and benefits of fully mechanized mining faces largely depend on the degree of identification of small faults [2]. In order to meet the need for transparency in geological conditions due to the intelligent development of coal mines in China, identifying small faults with a drop of about 3 m has become one of the important geological tasks in structural interpretation [3]. However, the accuracy of conventional 3D seismic exploration data interpretation methods for detecting small faults is still low. Therefore, using new methods to interpret small faults in coal seams has become increasingly important.
In recent years, relevant scholars have conducted a lot of research on the technology and methods of small fault identification, mainly using methods such as instantaneous seismic attributes, time-frequency attributes, seismic coherence attributes, curvature attributes, and texture attributes [[4], [5], [6], [7], [8], [9]]. The commonly used techniques for predicting post stack fractures include coherence and curvature attributes. Coherent technology can highlight the overall spatial development characteristics of faults, micro-fractures, lithology or tectonics through coherent changes. Marfurt et al. [10] proposed a second generation (C2) coherence algorithm based on the similarity of multiple seismic channels. The third generation (C3) algorithm proposed by Gersztenkorn et al. [11] has good lateral resolution, but which is not sensitive to large inclination angles. Randen et al. [12] proposed an algorithm for calculating coherent attributes using gradient structural tensors based on the characteristics of seismic data. Cohen et al. [13] proposed a local structural entropy coherence algorithm, which can avoid the calculation of a large number of eigenvalues in the C3 algorithm. Lu et al. [14] proposed a coherent method based on higher order statistics, which has fast calculation speed, strong noise suppression effect, and high resolution.
In the research of using seismic curvature attributes to study fractures, Lisle [15] discussed the relationship between open fractures measured on a geological outcrop and Gaussian curvature. Ericsson et al. [16] demonstrated the relationship between oil and gas production and curvature. Roberts [17] elaborated on the basic theory of curvature attributes and proposed the first generation of curvature analysis methods. Hart [18] pointed out that the strike curvature of the strata in northwest New Mexico is closely related to open fractures. Bergbauer et al. [19] used filtering to calculate the curvature of different wavelengths. Sigismondi [20] calculated curvature attributes at different scales by adjusting the size of the analysis time window, thereby obtaining much smaller subsurface features than on the original time-structure profile. Al Dossar et al. [21] obtained the second generation curvature analysis method curvature attribute by using the spatial orientation information contained in the seismic data volume. Yang et al. [22] introduced the concept of curvature in differential geometry on the basis of frequency division imaging in wavelet domain. Yin et al. [23] proposed four eccentric window scanning methods to improve the accuracy and efficiency of curvature attribute prediction of cracks. Ye [24] studied fracture prediction and characterization techniques based on coherence, volume curvature, and frequency division ant body of stacked data volumes, using fracture body fusion as a means. Li [25] conducted research on the application of hybrid intelligent optimization algorithms in seam gas reservoir fracture detection. Li et al. [26] combined the whale optimization algorithm and neural network to detect fractures in coalbed methane reservoirs. Chen et al. [27] described the fault opening based on the results of 3D seismic Kalman filtering using curvature attributes. Ao et al. [28] proposed a volume curvature extraction method based on deep learning. Cao et al. [29] conducted research on coal structure using seismic curvature attributes.
Since Balch [30] successfully displayed seismic data in color, using the visual effects of color images to directly identify abnormal regions has become an effective means of seismic data interpretation. Onstott [31], Liu et al. [32], Guo et al. [33] have respectively used RGB algorithms to carry out applications in seismic attribute fusion, and have achieved good application results. Li et al. [34] provide reference for research on seismic attribute fusion technology by focusing on RGB attribute fusion, clustering analysis attribute fusion, and multiple linear regression attribute fusion.
In order to fully utilize the rich geological information contained in seismic attributes, this paper proposes a method for identifying small faults in coal fields using multi-scale seismic attribute fusion. The core idea is to use the S-transform time frequency method to perform frequency division processing on seismic data, extract the maximum positive curvature attribute that is sensitive to faults based on seismic data of different frequencies, and then use principal component analysis (PCA) method to perform PCA on them, RGB fusion algorithm is used to fuse the first three principal components in order to improve the accuracy of small fault interpretation of coal field seismic data.
2. Method principle
2.1. S-transform algorithm
In 1996, Stockwell et al. [35] proposed a time-windowed Fourier transform method, which can be expressed as “phase correction” of continuous wavelet transform. This transformation has a window function that changes with frequency, so the resolution of signal S-transform (ST) is related to frequency, and its results are lossless and reversible, which has been favored by scholars in recent years. However, the basic wavelet function in ST is fixed and cannot change the resolution of ST for different resolution purposes, so it is limited in practical applications. Many scholars have proposed improvement schemes: Gao et al. [36] proposed a generalized ST method to properly select or construct basic wavelet functions according to “actual needs”; Pinnegar [37] gave a generalized ST method that can adjust both the window standard deviation and asymmetry. Because the basic Gaussian window function in ST has a fixed shape, its application is limited. Therefore, based on the ST, Mansinha et al. [38] proposed a generalized ST method. The ST of seismic signal h (t) is defined as:
| (1) |
where t is time, τ represents the center point of the window function, which controls the position of the window function on the timeline; F is the frequency; (t) is a Gaussian window function, that is:
| (2) |
The basic wavelet is defined as:
| (3) |
It can be seen that the time window width of the ST varies inversely with frequency, i.e., the time window is wider in the low frequency band, resulting in higher frequency resolution. The narrow time window in the high-frequency band allows for higher temporal resolution. ST overcomes the disadvantage of fixed short-time Fourier transform (STFT) window and introduces multi-resolution analysis of wavelet, combining the advantages of both and overcoming their shortcomings. The ST is directly related to the Fourier spectrum, and the phase can be corrected. The inverse transform can be achieved by solving the inverse Fourier transform:
| (4) |
However, the basic Gaussian window function in the ST is fixed and cannot be adjusted according to the actual application. It lacks flexibility, which restricts its application. Because the time-frequency domain distribution characteristics of a signal are related not only to the signal itself but also to the selected basic transformation function, it is important to appropriately select or construct the basic transformation function for the purpose of analyzing the signal in the time-frequency domain.
2.2. Curvature attribute
Curvature is a measure used to describe the degree of curvature of an object. It is mathematically defined as the second derivative of a curve. In seismic interpretation, the curvature attribute is used to describe the geometric change of seismic reflection surface. The sensitivity of curvature to geometric changes in geological bodies is conducive to the precise characterization of small faults [21]. Common curvature attributes of faults and fractures include dip curvature, maximum curvature, minimum curvature, gaussian curvature, mean curvature, strike curvature, maximum positive curvature and minimum negative curvature. The maximum positive curvature in the normal curvature is called the maximum positive curvature. The minimum negative curvature in the normal curvature is called the minimum negative curvature, and the maximum positive curvature can amplify the fault information and some small geological structures on the surface. The function of the minimum negative curvature is similar to that of the maximum positive curvature. The main purpose of this paper is to describe small faults in coalfield, and the attribute of maximum positive curvature has better application effect on tectonics such as faults, anticlines and synclines [21]. Therefore, this paper mainly studies the prediction method of small faults based on the maximum positive curvature attribute.
The calculation of curvature cannot be separated from the derivation, so the derivation method determines the calculation method of curvature. Common curvature attribute calculation methods include curvature analysis method based on surface fitting, conventional Fourier transform method, Fourier analysis method of partial wavenumber and maximum principal curvature method. Currently, there are many methods for calculating curvature at the grid level, among which the most widely used method is curvature calculation based on surface fitting. In order to obtain different curvature attribute values, 3 3 difference meshes are used for calculation.
This method mainly calculates the derivative through the difference method. After gridding seismic horizon data, use the values of surrounding grid points to fit the local quadratic surface using the least square method, and the resulting structural surface can be represented by a quadratic equation:
| (5) |
Using a 3 3 grid element to approximate the derivative, the calculation of the coefficients in formula (5) can be simplified into a series of simple arithmetic expressions as follows:
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where is the value of grid points 1–9 on the layer, and x is the distance between grid nodes. Different curvature attributes can be obtained from the above coefficients.
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
where km is mean curvature, kg is gaussian curvature, kmax is maximum curvature, kmin is minimum curvature, kpos is maximum positive curvature and kneg is minimum negative curvature.
Amplitude curvature is the application of changes in amplitude values in seismic data to calculate the corresponding curvature, involving the amplitude changes of seismic data in the calculation process. Whether it is a fault or sedimentary body, it is not only an anomaly in geological structure morphology, but also a significant change in amplitude values. Therefore, this paper uses amplitude curvature to identify small faults in coal seams.
2.3. Seismic attribute fusion method
Currently, there are various types of seismic attributes, and people need to select data with practical application value from various seismic attributes and characterize the geological body under study. In this paper, PCA-RGB multi-attribute fusion technology is used. Firstly, PCA is used to reduce the dimensions of multiple similar seismic attributes to obtain corresponding principal components. Then, RGB color fusion technology is used to fuse the principal components of different types of seismic attributes for identifying small faults.
-
(1)
PCA method
PCA is a multi-variate statistical method that uses the idea of mathematical processing to reduce dimensions and attempts to recombine multiple indicators in practical problems into a new set of a few comprehensive indicators to replace the original indicators. Seismic attribute parameters are interrelated, so there must be a primary and secondary relationship between these interrelated parameters. The PCA technique is to select the most sensitive and fewer comprehensive variables from these parameters that are most sensitive to reservoir reflection, and express the original attribute parameters with these comprehensive variables.
With n samples and p variables to convert the original data body into a main component, which is a linear combination of original variables with orthogonal characteristics. That is, set the synthesized m (m < p) indicators as the eigenvector corresponding to the first eigenvalue of the variable correlation matrix, and can be represented by as sum:
| (18) |
the corresponding characteristic value is , and . Expressed by the following formula:
| (19) |
in the formula, the greater the contribution of a component to the overall information, the greater the contribution of the component.
-
(2)
RGB fusion
The basic idea of RGB color fusion technology is to endow three seismic data volumes with red, green, and blue colors in the color space. This display method has a good effect on highlighting the energy approximation feature areas in each attribute, highlighting commonalities, and weakening differences [32,33]. By defining a single R, G, B form:
| (20) |
The frequency spectrum of each parameter point of an seismic data can be divided into three frequency bands: R, G, and B:
| (21) |
In formula (21), , and are respectively the proportion of the spectral energy of the three frequency bands to the total energy. The above formula is discretization in frequency and written in matrix form:
| (22) |
The resulting vector is:
| (23) |
The RGB color fusion result can be obtained by converting the obtained , , a range between 0 and 255 and using a three primary color display method.
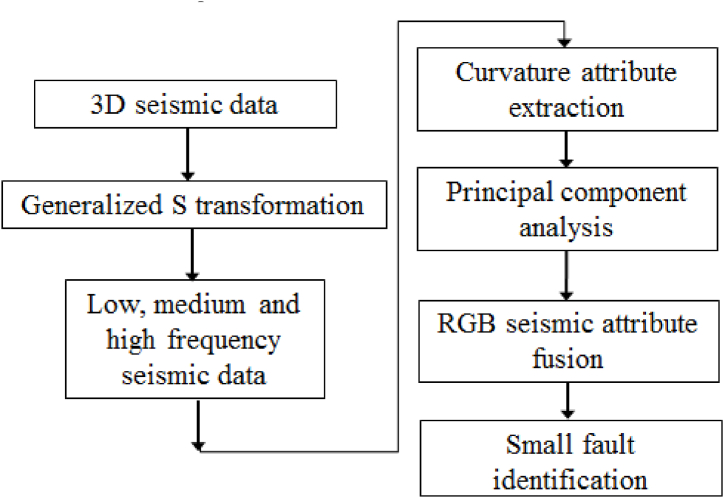
This paper proposes a flowchart of a method for identifying small faults in coal fields using multi-scale seismic curvature attribute fusion as shown in Fig. 1. Firstly, ST is used to conduct time-frequency analysis on seismic data to obtain seismic data volumes with multiple frequencies, and seismic data volumes at different frequencies correspond to different scales of underground geological information portrayal. Seismic data contains a large amount of underground geological information. To analyze this information to obtain accurate underground geological conditions, time-frequency analysis is a good technical means. Perform spectral analysis on seismic data, determine parameters such as the dominant frequency and frequency bandwidth of seismic signals, and extract the maximum positive curvature attributes of seismic data volumes at different frequencies; Using PCA method to analyze different seismic attributes; Finally, RGB fusion method is used to fuse the first three principal components after PCA decomposition, and the fusion results can be used for fine prediction of small faults in coal fields.
Fig. 1.
Flow chart of small fault identification in coalfield based on multi-scale seismic curvature attribute fusion.
3. Application of actual data
3.1. Overview of work area
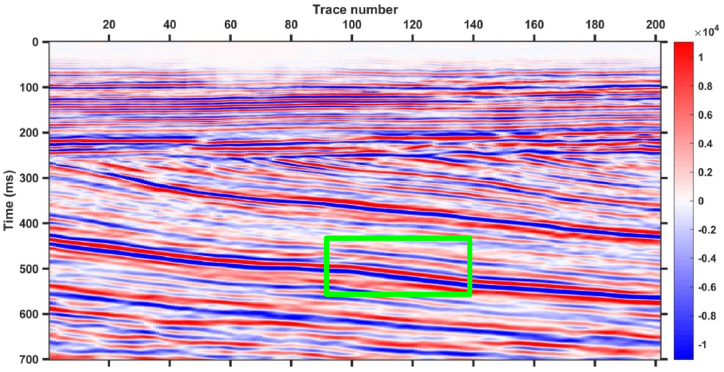
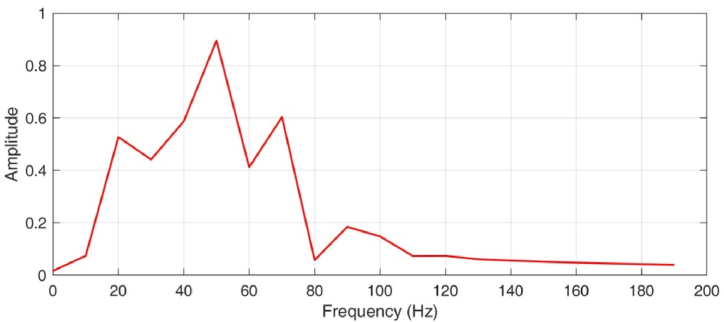
Due to the typical loess plateau landform in the study area, with vertical and horizontal surface gullies and covered by extremely thick loess layers, surface factors greatly restrict the quality of seismic data acquisition. On the basis of full band seismic data, there is strong uncertainty when using traditional single seismic attributes such as amplitude, coherence, dip angle, and azimuth to characterize small faults. At the same time, using the maximum positive curvature attribute in the full frequency range, the distribution of abnormal bands is consistent with the trend of surface elevation, which is prone to create the illusion of similar small faults. Therefore, this paper uses the method of multi-scale seismic curvature attribute fusion to characterize small faults. Fig. 2 is the original seismic profile of Inline140 and Fig. 3 is the spectrum analysis results of seismic data. The main frequency of this seismic data is around 50 Hz, and the effective frequency is mainly distributed in the range of 10–70 Hz. Therefore, a frequency of 10 Hz–70 Hz is selected for multi-scale curvature attribute analysis. The curvature attributes of 10 Hz and 30 Hz seismic data mainly reflect the characteristics of large-scale geological structures and can be used to characterize large-scale faults in coal seams. The curvature attributes of 50 Hz and 70 Hz seismic data reflect the small-scale faults in coal seams.
Fig. 2.
Original seismic profile of Inline140.
Fig. 3.
Spectrum analysis results of seismic data.
The instantaneous amplitude attribute and maximum positive curvature attribute extracted along the 5 # coal seam in the study area are shown in Fig. 4, Fig. 5. Faults may be developed in areas with small instantaneous amplitude attribute values and large maximum positive curvature values in this area. One obvious large fault is developed in the middle area, while the southern area is relatively developed, but the ability to describe small faults is relatively effective. Therefore, research on multi-scale seismic curvature attribute fusion methods has been carried out in order to provide more detailed characterization of small faults.
Fig. 4.
Instantaneous amplitude attribute along the 5 # coal seam.
Fig. 5.
Maximum Positive Curvature attribute alongthe 5 # coal seam.
3.2. Curvature seismic attributes
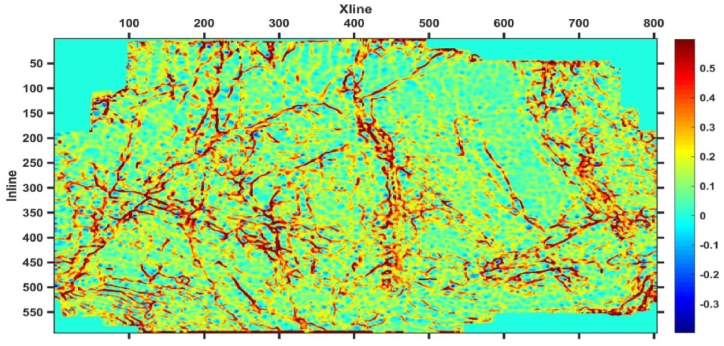
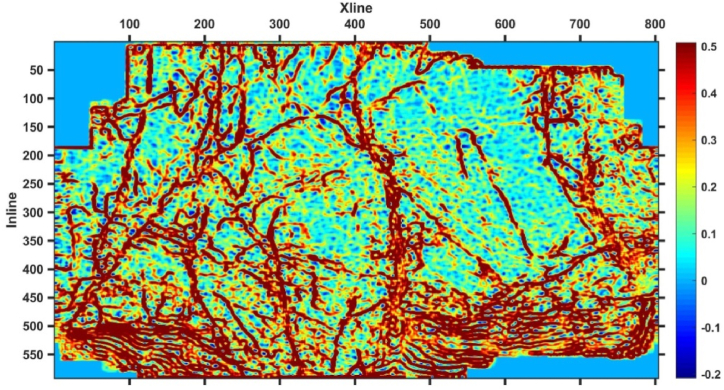
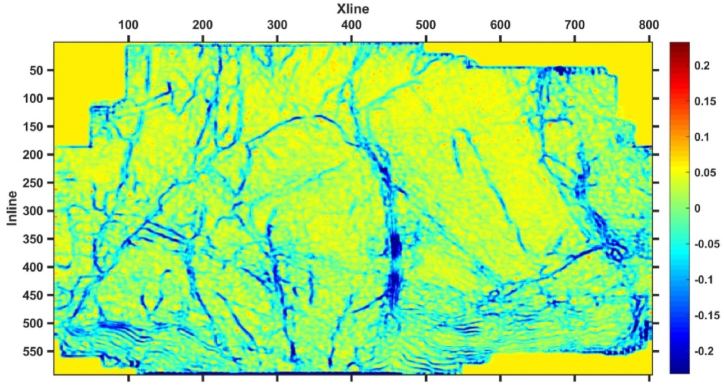
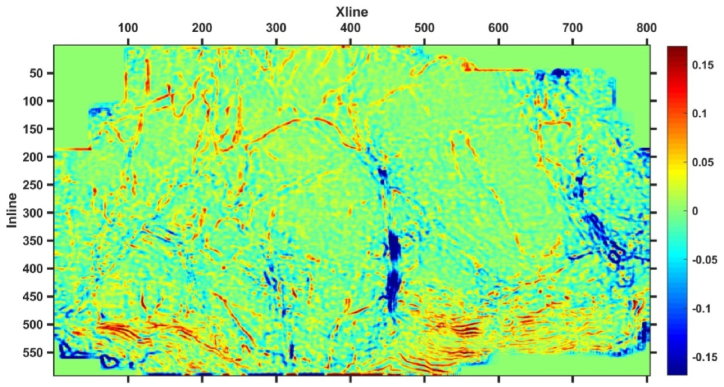
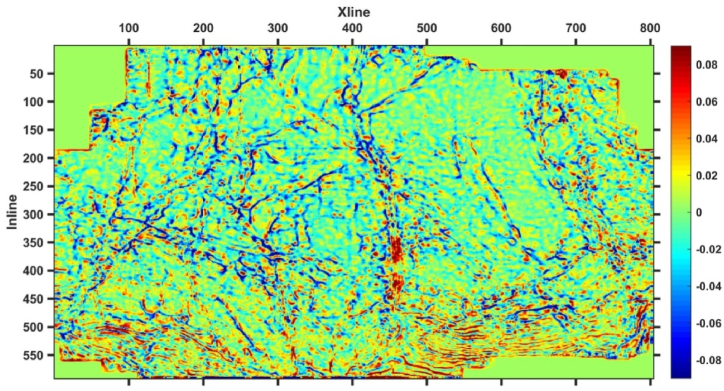
Extract the maximum positive curvature attribute from seismic data obtained using the ST time-frequency transformation method, and refer to the seismic dominant frequency and bandwidth information to extract the maximum positive curvature attribute of 10 Hz, 30 Hz, 50 Hz, and 70 Hz seismic data, as shown in Fig. 6, Fig. 7, Fig. 8, Fig. 9, there is a region with a large maximum positive curvature attribute value at Xline450 and Inline200-Inline400, while the maximum positive curvature value of Inline300-Inline500 is generally larger than that of Inline1-Inline300. The red area in the figure may be the location of fault development, and the darker the color, the greater the likelihood of fault development. The multi-scale maximum positive curvature attributes of different frequencies reflect the effective geological information of the 5 # coal seam in the study area at different scales, and there is a high correspondence between the effective geological information reflected by them, the large faults have obvious responses. As the frequency of seismic data increases, the geological information depicted becomes more and more detailed. Fig. 6, Fig. 7 clearly reflect the macroscopic characteristics of the faults in the study area, especially the fault characterization in the central region. Fig. 7, Fig. 8 better reflect the exact location and detailed characteristics of faults, while the depiction of large faults is not clear enough. Therefore, in order to fully utilize the effective information of the maximum positive curvature attributes at different scales, comprehensive utilization of the curvature attributes in Fig. 6, Fig. 7, Fig. 8, Fig. 9 can represent rich multi-scale feature information.
Fig. 6.
Maximum positive curvature attribute at 10 Hz
Fig. 7.
Maximum positive curvature attribute at 30 Hz
Fig. 8.
Maximum positive curvature attribute at 50 Hz
Fig. 9.
Maximum positive curvature attribute at 70 Hz
3.3. Principal component analysis
This article mainly conducts PCA fusion for seismic attributes sensitive to small faults through maximum positive curvature attributes of 10 Hz, 30 Hz, 50 Hz, and 70 Hz seismic data. As shown in Fig. 10, Fig. 11, Fig. 12, the contribution rates of the first, second, and third principal components are 54.5 %, 28.2 %, and 14.8 %, respectively, with the cumulative contribution rates of the first three principal components reaching 97.5 %. The first principal component (Fig. 10) contains most of the information of each seismic attribute fused. On the slice along the seam of 5 # Coal Seam, the development direction and boundary range of the main faults that exist have been clearly depicted, and some small faults that exist at the edges have also been clearly depicted. The overall effect is more prominent than the description of fault characteristics reflected by each single attribute.
Fig. 10.
Results of the first principal component analysis.
Fig. 11.
Results of the second principal component analysis.
Fig. 12.
Results of the third principal component analysis.
The second principal component (Fig. 11) contains some faults information, which clearly depicts the development direction and boundary range of the existing main faults, but it contains less seismic attribute information, and the description of some small faults is not clear enough to distinguish it from some formations with good continuity.
Due to the irrelevance of information between the new comprehensive attributes (principal components) obtained by principal component analysis (PCA), the third principal component (Fig. 12) only contains partial seismic attribute information, and the description of major faults is not as clear as PCA1 and PCA2, with a clearer description of the local development and boundary range of faults.
3.4. RGB attribute fusion
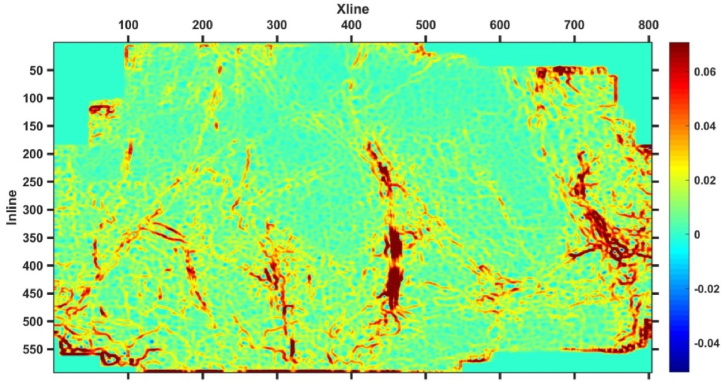
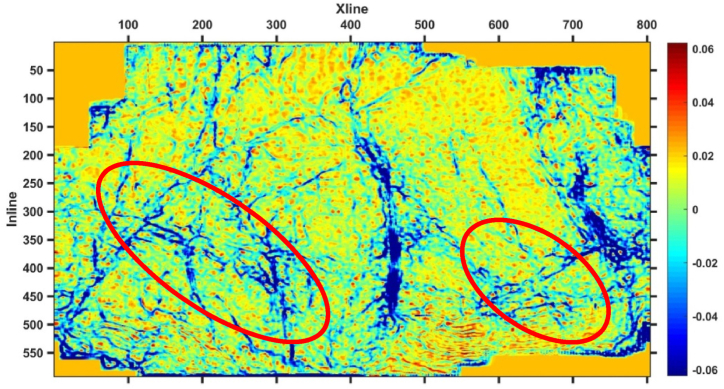
In order to fully utilize and enhance the effective information of the maximum positive curvature attributes of different scale bodies, the RGB algorithm is used to fuse the first three principal components of multi-seismic attribute PCA analysis, and the results are shown in Fig. 13. In the fusion results of the maximum positive curvature attribute, there are obvious anomalies at Xline450, Inline200 to Inline400, and there are more significantly abnormal in Inline300 to Inline500 than in Inline1 to Inline300. This is similar to the depiction of faults in Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, but the depiction of fault boundaries in Fig. 12 is clearer, the fault and fracture development zone information depicted by the fusion results is clearer, more detailed, and richer than that in Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12. The small faults in the red oval region in Fig. 13 are more developed, the characterization of small faults is also clearer and the RGB attribute fusion results have significant advantages in identifying small faults, which can improve the accuracy and accuracy of seismic data interpretation.
Fig. 13.
RGB attribute fusion results.
4. Conclusion
-
1)
The interpretation of coal field small faults using a single seismic attribute has multiple solutions and limitations. Developing research on multi-scale seismic attribute fusion methods can improve the accuracy and accuracy of coal field small faults prediction.
-
2)
The first principal component clearly depicts the development direction and boundary range of main faults and small fractures. Although the second principal component has relatively clear descriptions of major faults and small fractures, there is less seismic attribute information, and the display on the entire seismic attribute slice is relatively chaotic. The third principal component contains relatively little seismic attribute information and can be used to analyze the development direction of small faults.
-
3)
This paper proposes a method for identifying small faults in coal fields using multi-scale seismic attribute fusion. The core idea is to use ST to perform frequency decomposition processing on seismic attributes, extract maximum positive curvature attributes that are sensitive to faults based on seismic data of different frequencies, then perform PCA on them, and use RGB fusion algorithm to fuse the first three principal components. The application results in actual seismic data show that the results of RGB attribute fusion have obvious advantages in identifying small faults, and can improve the accuracy and accuracy of seismic data interpretation.
Data availability statement
Data will be made available on request.
Additional information
No additional information is available for this paper.
Additional information
No additional information is available for this paper.
CRediT authorship contribution statement
Lifeng Li: Conceptualization, Data curation, Writing – original draft, Writing – review & editing. Yaping Huang: Conceptualization, Data curation, Formal analysis, Funding acquisition, Writing – original draft, Writing – review & editing. Xuemei Qi: Conceptualization, Data curation, Writing – original draft, Writing – review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 42274180), the National Key R&D Program of China (grant no. 2021YFC2902003), and A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
Contributor Information
Yaping Huang, Email: yphuang@cumt.edu.cn.
Xuemei Qi, Email: qixuemei@cumt.edu.cn.
References
- 1.Dong S.D., Huang Y.H., Jin X.L., et al. Development status and trend of high-density 3D seismic exploration technology for coal fields. Coal Geol. Explor. 2023;51(2):273–282. [Google Scholar]
- 2.Du W.F., Su S.P. Prediction of small faults in coal seams using seismic layer curvature. Journal of rock mechanics and Engineering. 2008;27(S1):2901–2906. [Google Scholar]
- 3.Du W.F., Su S.P., Li X.W. Prediction of coal seam fractures based on seismic layer curvature volume attributes. Journal of Coal Mining. 2006;31(S0):30–33. [Google Scholar]
- 4.Wang R., Li Q., Sun H.J., et al. Application of fusion methods based on principal component analysis in fault identification. Geophysical and Geochemical Exploration Computing Technology. 2021;43(6):715–723. [Google Scholar]
- 5.Partyka G., Gridley J., Lopez J. Interpretational applications of spectral decomposition in reservoir characterization. Lead. Edge. 1999;18(3):353–360. [Google Scholar]
- 6.Partyka G., Bottjer R., Peyton L. Interpretation of incised valleys using new 3-D seismic techniques : a case history using spectral decomposition and coherency. Lead. Edge. 1998;17(12):1294–1298. [Google Scholar]
- 7.Marfurt K.J., Zhao T., Li F.Y. Constraining self-organizing map facies analysis with stratigraphy: an approach to increase the credibility in automatic seismic facies classification. Interpretation. 2017;5(2):163–171. [Google Scholar]
- 8.Wei X.D., Zhang Y.Q., Zhang Y.Z., et al. SEG Technical Program Expanded Abstracts; 2009. The Gradient of the Amplitude Spectrum of Seismic Data and its Application in Reservoir Prediction; pp. 1102–1106. [Google Scholar]
- 9.Bahorich M., Farmer S. 3-D Seismic coherency for faults and stratigraphic features. Lead. Edge. 1995;14(10):1053–1058. [Google Scholar]
- 10.Marfurt K.J., Kirlin R.L., Farmer S.L., et al. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics. 1998;63(4):1150–1165. [Google Scholar]
- 11.Gersztenkorn A., Marfurt K.J. Eigen-structure based coherence computations as an aid to 3-D structural and stratigraphic mapping. Geophysics. 1999;64(5):1468–1479. [Google Scholar]
- 12.Randen T., Monsen E., Signer C., et al. SEG Technical Program Expanded Abstracts; 2020. Three-dimensional Texture Attributes for Seismic Data Analysis; pp. 668–671. [Google Scholar]
- 13.Cohen I., Coifman R.R. Local discontinuity measures for 3D seismic data. Geophysics. 2002;67(6):1933–1945. [Google Scholar]
- 14.Lu W.K., Li Y.D., Zhang S.W. Higher-order-statistics and supertrace based coherence estimation algorith. Geophysics. 2005;70(3):13–18. [Google Scholar]
- 15.Lisle R.J. Detection of zones of abnormal Strains in structures using Gaussian curvature analysis. AAPG (Am. Assoc. Pet. Geol.) Bull. 1994;78(12):1811–1819. [Google Scholar]
- 16.Ericsson J.B., McKean H.C., Hooper R.J. Facies and curvature controlled 3D fracture models in a Cretaceous carbonate reservoir. Arabian Gulf. Geological Society, London, Special Publications. 1998;147(1):299–312. [Google Scholar]
- 17.Roberts A. Curvature attributes and their application to 3D interpreted horizons. First Break. 2001;19(2):85–100. [Google Scholar]
- 18.Hart B.S., Pearson R.A., Rawling G.C. 3-D seismic horizon-based approaches to fracture-swarm sweet spot definition in tight-gas reservoirs. Lead. Edge. 2002;21(1):28–35. [Google Scholar]
- 19.Bergbauer MukerjiT., Hennings P. Improving curvature analyses of deformed horizons using scale dependent filtering techniques. AAPG (Am. Assoc. Pet. Geol.) Bull. 2003;87(13):1255–1272. [Google Scholar]
- 20.Sigismondi M.E., Soldo J.C. Curvature attributes and seismic interpretation: case studies from Argentina basins. Lead. Edge. 2003;22(11):1123–1126. [Google Scholar]
- 21.Al-Dossary S., Marfurt K.J. 3D volumetric multispectral estimates of reflector curvature rotation. Geophysics. 2006;71(5):41–51. [Google Scholar]
- 22.Yang W.Y., Deng Y., Xu Y.Z., et al. Wavelet transform based curvature attribute extraction and reconstruction method. Natural Gas Industry Journal. 2007;27(5):55–77. [Google Scholar]
- 23.Yin X.Y., Gao J.H., Zong Z.Y. Curvature attribute extraction based on centrifugal window inclination scanning. J. Geophys. 2014;57(10):3411–3421. [Google Scholar]
- 24.Ye Y. Chengdu University of Technology; 2019. Research and Application of High Precision Comprehensive Prediction of Reservoir Fractures and Gas Bearing Property Detection. [Google Scholar]
- 25.Li M.Q. Chengdu University of Technology; 2018. Research on the Application of Hybrid Intelligent Optimization Algorithm in Seam Gas Reservoir Fracture Detection. [Google Scholar]
- 26.Li Q., Wang M.Q.R. WOA-BP algorithm and application research on fracture detection of coalbed methane reservoir. J. Geophys. 2022;65(2):773–784. [Google Scholar]
- 27.Chen G., Qi H.Y., Song Y., et al. Curvature attributes with the 3D seismic Kalman filter for fault opening description-An application to a shale oil reservoir in the Jimsar sag. Junggar Basin, Xinjiang, Geophysics. 2022;88(2):B91–B99. [Google Scholar]
- 28.Ao Y.L., Lu W.K., Jiang B.W., et al. Seismic structural curvature volume extraction with convolutional neural networks. IEEE Trans. Geosci. Rem. Sens. 2020;59(9):7370–7384. [Google Scholar]
- 29.Cao L.T., Yao Y.B., Liu D.M. Application of seismic curvature attributes in the delineation of coal texture and deformation in Zhengzhuang field, southern Qinshui Basin. AAPG (Am. Assoc. Pet. Geol.) Bull. 2020:1143–1166. [Google Scholar]
- 30.Balch A.H. Color sonograms: a new dimension in seismic data interpretation. Geophysics. 1971;36(6):1074–1098. [Google Scholar]
- 31.Onstott G.E. University of Texas; Austin: 1984. Processing and Display of Offset Dependent Reflectivity in Reflection Seismograms; pp. 40–54. [Google Scholar]
- 32.Liu J., Marfurt K.J. Multicolor display of spectral attributes. Lead. Edge. 2007;26(3):268–271. [Google Scholar]
- 33.Guo H., Marfurt K.J., Liu J. SEG Technical Program Expanded Abstracts; 2006. Principal Components Analysis of Spectral Components; pp. 988–992. [Google Scholar]
- 34.Li T.T., Wang Z., Ma S.Z., et al. Overview of seismic attribute fusion methods. Progress in geophysics. 2015;30(1):378–385. [Google Scholar]
- 35.Stockwell R.G., Mansinha L., Lowe R.P., et al. Localization of the complex spectrum: the S transform. IEEE Trans. Signal Process. 1996;44(4) 998-l001. [Google Scholar]
- 36.Gao J.H., Chen W.C., Li Youming Y.M., et al. Generalized s-transform and thin interbed seismic response analysis. J. Geophys. 2003;46(4):526–532. [Google Scholar]
- 37.Pinnegar C.R., Mansinha L. Time-local Fourier analysis with a scalable, phase-modulated analyzing function: the S-transform with a complex window. Signal Process. 2004;84(1):1167–1176. [Google Scholar]
- 38.Mansinha L., Stockwell R.G., Lowe R.P. Pattern analysis with two dimensional spectral localization: application of two-dimensional S-transform. Physica. 1997;239(3):286–295. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.