The dominant and nondominant arms are specialized for stabilizing different features of task performance

Abstract

We have previously proposed a model of motor lateralization, in which the two arms are differentially specialized for complementary control processes. During aimed movements, the dominant arm shows advantages for coordinating intersegmental dynamics as required for specifying trajectory speed and direction, while the nondominant arm shows advantages in controlling limb impedance, as required for accurate final position control. We now directly test this model of lateralization by comparing performance of the two arms under two different tasks: one in which reaching movement is made from one fixed starting position to three different target positions; and the other in which reaching is made from three different starting positions to one fixed target position. For the dominant arm, performance was most accurate when reaching from one fixed starting position to multiple targets. In contrast, nondominant arm performance was most accurate when reaching toward a single target from multiple start locations. These findings contradict the idea that motor lateralization reflects a global advantage of one “dominant” hemisphere/limb system. Instead, each hemisphere/limb system appears specialized for stabilizing different aspects of task performance.

Introduction

The roles of left and right cerebral hemispheres in movement planning and control are thought to be asymmetric, such that the left hemisphere of right-handers, or the hemisphere contralateral to the dominant arm in general, plays a dominant role in the movement of both arms (Liepmann 1905; Geschwind 1975; Thut et al. 1996). Recent findings from our laboratory, however, suggest a different model of motor lateralization: the two-hemisphere/limb systems are functionally lateralized, such that each system is specialized for controlling different features of movement (Sainburg 2002; Sainburg and Wang 2002; Bagesteiro and Sainburg 2002, 2003; Wang and Sainburg 2004, 2006). We have shown dominant arm advantages in adapting to novel dynamic conditions (Duff and Sainburg 2006; Sainburg 2002), in specifying torque amplitude (Sainburg and Schaefer 2004), and in coordinating intersegmental dynamics during reaching (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg 2002). Interestingly, however, the nondominant arm often achieves more accurate final positions, regardless of errors in coordination during the movement. In fact, during adaptation to novel dynamic conditions, the nondominant arm improves final position accuracy without accompanying improvements in movement curvature and intersegmental coordination (Duff and Sainburg 2006). These findings have led to the idea that nondominant control may be specialized for control of steady state limb position, which emerges only during the final phase of reaching movements, a hypothesis supported by a recent perturbation study (Bagesteiro and Sainburg 2003).

Interestingly, our model of lateralization has also been supported by studies of adaptation to novel task conditions that examine patterns of learning transfer from one arm to the other. Following adaptation to viusomotor rotations, different aspects of performance show asymmetric patterns of transfer: adaptation to visuomotor rotations with the left arm in right-handers improves the initial direction of subsequent right arm performance, while right arm adaptation improves only the final position accuracy of subsequent left arm performance (Sainburg and Wang 2002; Wang and Sainburg 2004). Our findings in left-handers showed the mirror imaged pattern of interlimb transfer, such that direction accuracy transferred to the left arm, while final position accuracy transferred to the right arm (Wang and Sainburg 2006). Collectively, these findings support a model of motor lateralization, in which the ‘nondominant’ system is not viewed as a poorly developed analog of the dominant system, but rather as having unique advantages that include the specification and control of steady state positions, plausibly due to advantages in control of limb impedance (Bagesteiro and Sainburg 2002).

Based on this hypothesis, we predict that when planning a simple reaching movement, the two arm controllers might stabilize different aspects of performance. Specifically, we expect that the dominant system is concerned with reducing the cost of dynamic aspects of control (Wolpert et al. 1995; Kawato 1999; Sainburg et al. 1999), while the nondominant system is concerned with achieving and maintaining steady state features of performance, such as final position. We, therefore, predict that the dominant controller should show more stable performance under task conditions in which initial limb configuration remains constant, such that initial torque can be most accurately specified. In contrast, we expect more stable performance of the nondominant arm under task conditions in which final position remains constant. In the present study, we test these predictions by comparing the adaptation pattern of simple reaching movement made with the two arms under two different task conditions: one in which reaching movement is made from one fixed starting position to three different target positions, and the other in which reaching is made from three different starting positions to one fixed target position.

Materials and methods

Subjects

Subjects were 24 neurologically intact right-handed adults, aged from 18 to 36 years old. Subjects were recruited from the university community, and were paid for their participation. Informed consent was solicited prior to participation. Right-handedness was assessed using the 10-item version of the Edinburgh inventory (Oldfield 1971).

Apparatus

Subjects sat facing a table with the right or left arm supported over a horizontal surface, positioned just below shoulder height, by a friction-less air jet system (Fig. 1a). A start circle (1.5 cm in diameter), target (2 cm in diameter), and cursor representing the index hand position were projected on a horizontal back-projection screen positioned above the arm (Fig. 1b). A mirror, positioned parallel and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the hand. Calibration of the display ensured that this projection was veridical. Position and orientation of each limb segment was sampled at 103 Hz using the Flock of Birds^® (Ascension-Technology, Burlington, VT) magnetic 6-DOF movement recording system. The position of the following three bony landmarks was digitized: (1) index fingertip, (2) the lateral epicondyle of the humerus, and (3) the acromion, directly posterior to the acromio-clavicular joint. As sensor data was received from the Flock of Birds^®, the position of these landmarks was computed by our custom software.

Fig. 1.

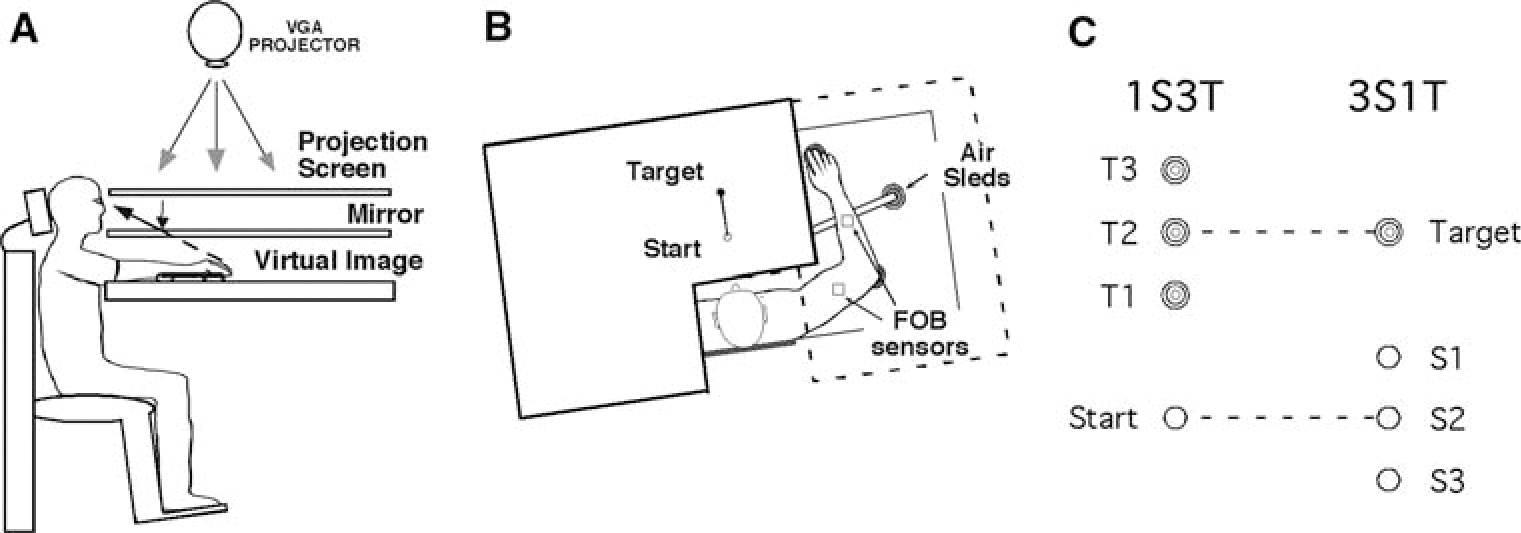
a Side view: subjects were seated in a chair with the arm supported by an air jet system that removed the effects of friction on arm movement. Targets and the cursor representing hand position were projected on a screen placed above the arm. b Top view: the positions of the start and target circles, and the Flock of Birds sensors are shown. c Locations of the start and target circles. The distance between every two targets under each condition is 5 cm. The distance between the start circle and the closest target is 15 cm. All these start and target circles are linearly aligned on the midline relative to the subject’s body

Experimental design

Subjects were randomly divided into two groups depending on the arm used: one group performed with the left arm, and the other with the right arm. Half of the subjects in each arm group made reaching movements that started from a single starting location to one of three target locations (1S3T condition), while the other half made reaching movements that started from one of three starting locations to a single target location (3S1T condition). As illustrated in Fig. 1c, starting and target locations were placed in such a way that the index of difficulty was identical between the two task conditions (i.e., the movement amplitudes were 15, 20 or 25 cm in both conditions). The only difference between the two conditions was that one condition had a fixed starting location, whereas the other condition had a fixed target location. Both starting and target locations were placed on the midline relative to the subject’s body. The experiment consisted of 150 trials, which were divided into 50 cycles, with each cycle containing all three starting or target locations consecutively. For each trial, one of three starting or target locations, presented in a pseudorandom sequence, was displayed prior to movement. Subjects were instructed to move straight from the starting circle to the target using a single, rapid motion in response to an auditory ‘go’ signal. A screen cursor representing the location of index finger tip was available prior to the onset of the first trial, so that subjects could use visual feedback to place their index finger to the starting circle. Visual feedback of this index finger location was turned off immediately after they moved their hand out of the starting circle. Following the completion of each trial, the screen cursor appeared again, so that they could place themselves back to the starting circle. At the end of each trial, knowledge of results (KR) was provided in the form of a hand-path between the starting circle and the target.

Data analysis

In this study, we calculated two performance measures to assess final position accuracy and variability: constant error and variable error. Constant error was calculated as the 2D distance between the index finger tip position at the movement termination of each trial and the center of the target. Variable error was calculated as the 2D distance between the index finger tip position at the movement termination of each trial and the center of all index finger tip positions obtained during the experiment. A two-way ANOVA was conducted to examine the effects of condition (1S3T vs. 3S1T) and arm (left vs. right) for each performance measure separately. Bonferroni corrections were made to adjust the alpha level for multiple comparisons (α = 0.05/2 = 0.025). Following the ANOVA, Tukey posthoc tests were used to assess the differences between the two conditions for each hand separately (α = 0.05).

Results

Figure 2a shows the changes in performance of the four subject groups across blocks (means of two consecutive cycles, or six consecutive trials). It appears that the right arm performance under the 1S3T condition reaches its final adaptation level within the first 3 blocks and remains stable, whereas under the 3S1T condition it takes much longer (at least until block 8) to reach the final adaptation level. In addition, performance of this arm appears much more variable under the latter condition. With regard to the left arm performances, they do not appear to be substantially different between the two conditions in terms of the adaptation rate. In terms of the final adaptation extent, however, the performance appears to be substantially better under the 3S1T condition as compared to that under the 1S3T condition. Because of the substantial change in performance from the initial phase of adaptation to the later phase, we divided the experimental session into two phases: practice phase (blocks 1–8) and test phase (blocks 9–25). Performance measures obtained during the test phase only were subjected to statistical analyses because the performance under every condition became relatively stable during this phase.

Fig. 2.

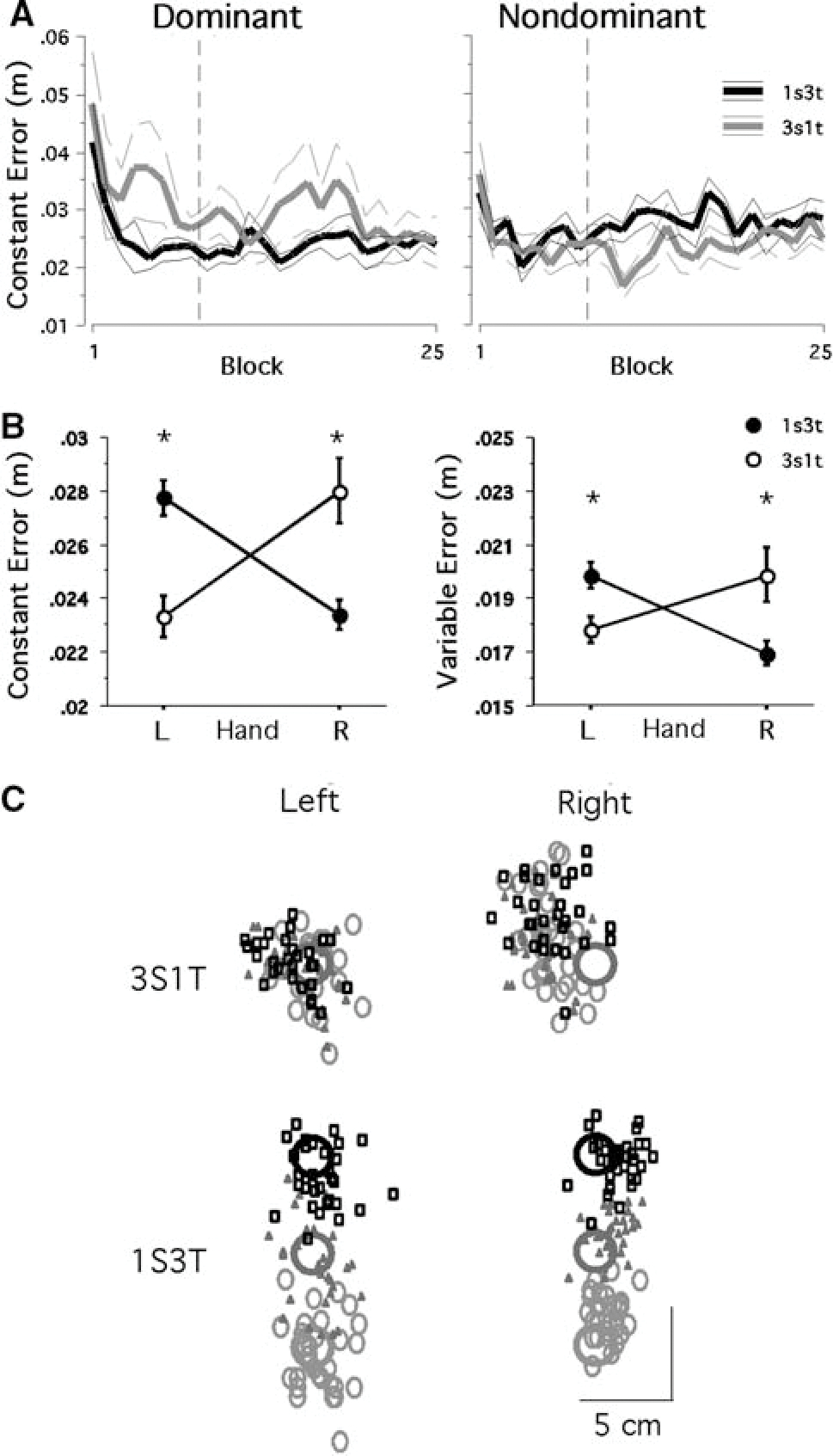
a Changes in final accuracy performance across blocks. Thick lines represent mean data averaged across subects; thin lines represent SE. b Mean performance measures of constant error (mean ± SE). *A significant difference at P < 0.05. c Scatter plots representing the distribution of data for each condition. Small circles, triangles and squares represent data from the movements made to the near, middle and far targets, respectively

A two-way ANOVA was conducted to examine the condition and arm effects, which revealed a significant interaction effect between the two variables for constant errors (P < 0.001), as illustrated in Fig. 2b. Post hoc analyses showed that the right arm performance was significantly better under the 1S3T condition than under the other condition (P < 0.05), whereas the left arm performance was significantly better under the 3S1T condition (P < 0.05). We measured tangential peak velocity of the reaching arm to make sure that performance accuracy was not influenced by movement speed. Results showed that the peak velocity was not significantly different between the two conditions for either arm (approx. 90 cm/s for both arms; P > 0.4), thus confirming that the performance difference between the conditions was not due to a difference in movement speed.

With respect to final position variability, our two-way ANOVA showed a significant interaction between the condition and arm effects for variable errors as well (P < 0.001). Post hoc analyses indicated that the left arm performance was significantly less variable under the 3S1T condition (P < 0.05), whereas the right arm performance was significantly less variable under the 1S3T condition (P < 0.05). The distributions of final positions obtained from four representative subjects (one subject per condition) during the test phase are illustrated in Fig. 2c. This figure shows that the final positions of reaching movement made with the left arm are clustered more tightly under the 3S1T condition, whereas those made with the right arm are clustered more tightly under the 1S3T condition. It is also notable in this figure that the right arm performance is substantially less variable than the left arm performance under the 1S3T condition, whereas the left arm performance is substantially less variable than the right arm performance under the 3S1T condition.

Discussion

We have previously suggested that the dominant arm controller might be specialized for coordinating intersegmental dynamics (Sainburg 2002; Bagesteiro and Sainburg 2002; Wang and Sainburg 2005), which appears to rely largely on a feedforward process that requires information about initial limb configuration (Sainburg et al. 1999, 2003). We have also suggested that the nondominant controller might be specialized for control of steady state posture during the final phase of reaching movements (Sainburg and Wang 2002; Bagesteiro and Sainburg 2003; Wang and Sainburg 2006). Thus, rather than viewing the dominant arm as generally “superior” to the nondominant arm, we suggest that control has become distributed across the two systems, such that each controller has become adapted for different, but complimentary cost-functions.

Based on these ideas, we hypothesized that the two arm controllers might employ different strategies for adapting to a simple reaching task. The dominant controller might stabilize dynamic features of the desired movement, such as segment torques (Wolpert et al. 1995; Kawato 1999; Sainburg et al. 1999), while the nondominant controller might stabilize end-point impedance for achieving steady state posture. We, thus, predicted more stable dominant arm performance under task conditions in which the initial limb configuration remained constant. This is because intersegmental dynamics vary substantially with changes in initial configuration. In contrast, we predicted more stable nondominant arm performance when final position remained constant. Our results indicated an unambiguous distinction between the two arms under these conditions. The dominant arm showed greater accuracy and more stable performance when reaching was made from one fixed starting position to three targets, as compared to reaching from three start positions to one target. In contrast, the nondominant arm performed more accurately and more stable when reaching to a single target from multiple start locations, rather than from one start location to multiple targets. These findings suggest that the two arm controllers might employ different cost-functions, in controlling such movements: the dominant system may be concerned with stabilizing task and limb dynamic strategies, as required for efficient coordination (Bagesteiro and Sainburg 2002). In contrast, the nondominant system may be more concerned with stabilizing steady state variables, such as final position. This distribution of function corresponds well to the natural distribution of labor observed during bilateral activities. For example, the dominant arm tends to perform the dynamic tasks of cutting and hammering, while the nondominant arm tends to stabilize position by impeding the forces imposed by the dominant system.

Because both of our movement conditions required exactly the same movement distances and accuracy requirements in the same workspace range, the advantages of each arm for different tasks can only be attributed to differences in the stability of starting/target locations, not to differences in task difficulty. It should be stressed that comparisons between the arms within each task condition showed that the nondominant arm performance was more accurate and less variable for the constant final position task whereas the dominant arm performance was better for the constant initial position task, a double dissociation that further supports our hypothesis of lateralization.

Our findings for dominant arm movements are consistent with the idea that this system might employ dynamic criterion in achieving stable performance, such as reduced amplitude of muscle forces and segment torques, which suggest neural representation of variables that correspond to these measures (Shadmehr and Mussa-Ivaldi 1994; Wolpert et al. 1995; Bhushan and Shadmehr 1999; Kawato 1999). Substantial evidence that the nervous system models the effects of environmental and musculoskeletal dynamics has come from studies in which subjects adapt to novel dynamic environments, such as robot-induced force fields, inertial conditions and artificial gravity environments (Shadmehr and Mussa-Ivaldi 1994; Lackner and Dizio 1998; Sainburg et al. 1999; Scheidt et al. 2000). The idea that such variables might be represented by the CNS is also supported by studies that emphasize the role of initial condition information in movement accuracy (Gordon et al. 1994; Vindras et al. 1998; Messier and Kalaska 1999; Wang and Sainburg 2005). This is because accurate prediction of limb and task dynamics requires reliable and high fidelity estimates of initial conditions (Wolpert and Kawato 1998; Kawato 1999; Sainburg et al. 1999). Our current findings clearly indicate that the dominant arm controller performs better when the initial limb configuration, as opposed to final limb position, is invariant. We suggest that this task condition allows more accurate predictions of task dynamics, which may be employed by the dominant system in stabilizing performance over sequential trials.

The nondominant control system may be primarily concerned with stabilizing steady state position, which could be achieved by specifying equilibrium postures (Polit and Bizzi 1978; Bizzi et al. 1982). According to the final position versions of equilibrium control models, limb trajectories can vary with changes in initial conditions and other transient mechanical events. However, given the same motor commands across conditions, the final equilibrium position should be unaffected by such variations, a phenomenon termed “equifinality”. Thus, accurate final positions can be achieved, even following transient mechanical perturbations (Polit and Bizzi 1978; Kelso and Holt 1980) and variations in initial conditions (Latash 1992; Jaric et al. 1994). It is thus, plausible that control variables that correspond to final position accuracy could be stabilized, independently from variables that correspond to control of the dynamic phase of the trajectory. Our current findings suggest that such variables might be preferentially stabilized by the nondominant controller.

We conclude from these findings that the two-hemisphere/limb systems have become specialized for stabilizing different features of task performance. We suggest that dominant arm control might be concerned with variables that correspond to dynamic features of performance such as segment torques, while nondominant control appears to be adapted for achieving and maintaining steady state position, and might employ cost functions that include variables that correspond to limb impedance and equilibrium postures. However, we do not suggest that the dominant and nondominant arms are controlled by either mechanism, exclusively. Rather, we propose that unilateral reaching movements always recruit dynamic predictions to specify features of the initial trajectory, while final position control mechanisms are recruited to decelerate the limb at the final position by modulation of limb impedance. We suggest that through evolutionary (Sainburg and Eckhardt 2005; Vallatorgia and Rogers 2005), as well as ontogenetic, development, each system has become better adapted for stabilizing different aspects of performance. In the adult, each hemisphere might be recruited to control the aspect of movement for which it has become specialized, resulting in bilateral activation for unilateral arm movements. In fact, this idea might explain the substantial activation of ipsilateral motor cortex that has been demonstrated during unilateral arm and finger movements (e.g., Kutas and Donchin 1974; Kim et al. 1993; Cisek et al. 2003). In addition, the fact that neuronal activities in motor and premotor cortices are correlated with a variety of movement parameters, including hand position (Kettner et al. 1988), movement direction and/or extent (Georgopoulos et al. 1983; Fu et al. 1993; Kurata 1993; Messier and Kalaska 2000), muscle activity (Kakei et al. 1999, 2001), and force (Evarts 1968; Fetz et al. 1976), supports the idea that both dynamic variables and endpoint kinematics may be parameterized during unimanual reaching movements.

The notion that a single controller can be concerned with minimizing dynamic costs associated with segment torques, as well as with minimizing positional costs by manipulating limb impedance has previously been elaborated (Hirayama et al. 1993; Gottlieb 1996). Hirayama et al. (1993), presented a two-phase neural network model, in which the specification of initial movement parameters occurs through a forward dynamic controller, while final position is achieved by specifying joint “viscosity” and stiffness about a final posture. A similar hybrid model was proposed by Gottlieb (1996). Our current findings agree with, and extend, these hybrid control models by suggesting that the two-hemisphere/limb systems might be differentially specialized for stabilizing different features of performance.