SOC Estimation of Vanadium Redox Flow Batteries Based on the ISCSO-ELM Algorithm

Abstract

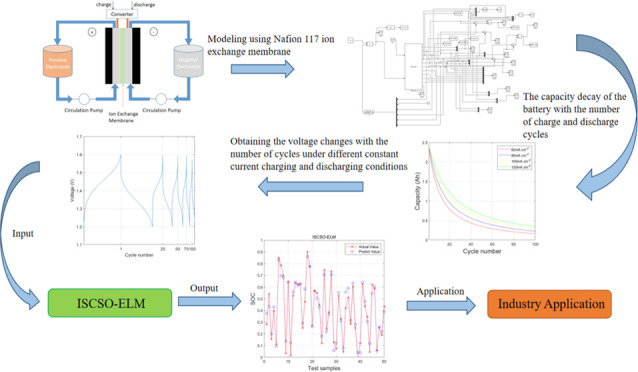
This study focuses on the stage of charge (SOC) estimation for vanadium redox flow batteries (VFBs), establishing an electrochemical model that provides parameters, including ion concentration. Second, considering the capacity decay of VFBs, an extreme learning machine (ELM) combined with an improved sand cat swarm optimization algorithm, named ISCSO-ELM, is integrated with SOC estimation to predict the battery’s SOC more effectively.

1. Introduction

To ensure robust global economic growth and address the challenges of energy consumption and environmental pollution, the international community is gradually shifting toward clean and renewable energy. This transition involves not only carbon capture, utilization, and storage (CCUS) technologies but also diversified approaches such as clean energy generation, energy saving, emission reduction, and hydrogen energy.^1,2

In the strategic context of global sustainable energy development, vanadium redox flow batteries (VFB) are emerging as an important asset. As an advanced clean energy storage technology, VFBs effectively support the stable supply and flexible application of renewable energy, especially in fields such as solar and wind power, where their application might yield unexpected results.^3,4 To guarantee the secure and consistent functioning of the VFB, precise acquisition of both the parameters of its equivalent model and the battery’s SOC is essential.

As a potential clean energy storage device, the VFB has shown great significance in the global pursuit of sustainable energy solutions. For accurate understanding and controlling of VFB performance, various modeling approaches have been utilized by scholars, and these can be broadly classified into two groups: the electrochemical model⁵⁻⁸ and the equivalent circuit model.

Electrochemical models for VFBs offer insights into internal chemical reactions and mass transfer processes, which are crucial for performance optimization and control strategies. In response to this, some scholars have proposed the corresponding electrochemical models of VFBs.⁹

The operation of the VFB is contingent upon the redox reactions of vanadium ions in assorted states of valence within the positive and negative half-cells, facilitating the interchange between electrical and chemical energies. The SOC serves as a crucial index for gauging the capacity of the battery. The SOC measurement methods for the VFB mainly include discharge experimentation, ampere-hour integration, and open-circuit voltage method, among others.^10,11 The discharge experiment method usually involves fully charging the battery and then discharging it. This process is very time-consuming. The ampere-hour integration method has an accumulation of current measurement errors, which can cause the SOC estimate to gradually deviate from the true value.¹² The open-circuit voltage method needs to wait for the battery to reach a stable state before making measurements, so there is a time delay.¹³ In conclusion, it is difficult to perform a real-time SOC estimation by traditional methods. Additionally, neural networks can be utilized for the VFB’s SOC measurement, known for their nonlinear characteristics and ability to quickly respond to external inputs. Through the utilization of machine learning algorithms for training, the SOC can be estimated with higher precision than traditional methods, as neural networks create a model that represents a functional-like relationship between inputs and outputs.

The extreme learning machine (ELM), initiated by Huang,¹⁴ constitutes a single hidden layer feedforward neural network (SLFN). Its impressive efficacy in handling both classification and regression challenges, coupled with a robust generalization capacity, has led numerous researchers to not only employ but also enhance the ELM methodology.¹⁵⁻¹⁷ Many researchers have combined ELM with battery SOC estimation and achieved good results. Ren et al.¹⁸ introduced a method for estimating the SOC in lithium-ion batteries by combining the ELM and an extended Kalman filter, which shows better accuracy than traditional methods. Lipu et al.¹⁹ presents a SOC estimation model for lithium-ion batteries, employing an ELM enhanced by a gravitational search algorithm that of approach, achieving higher accuracy than that of conventional neural network methods. Ren et al.²⁰ present an adaptive Kalman estimator that combines a genetic algorithm-optimized ELM (GA-ELM) with the Ah integration method for lithium-ion batteries’ SOC estimation, achieving an accuracy error of less than 1.2%.

Within this study, the VFB electrochemical model is formulated based on the underlying principles of the VFB, in conjunction with the mass conservation equation, and the capacity loss process of the Nafion117 membrane during charging and discharging is demonstrated. When estimating the SOC of the VFB through the ELM method, since the ELM’s weights and biases are allocated at random, unreasonable distributions will be generated, resulting in feature loss and a decrease in the accuracy of the model. To address this issue, the study innovatively combines the improved sand cat swarm optimization algorithm with the ELM and proposes a method named ISCSO-ELM. In the SOC estimation of the VFB, it has a higher performance.

2. Theory and Methods

2.1. Establishment of the Vanadium Redox Flow Battery Model

As shown in Figure 1, the VFB is principally made up of positive and negative liquid energy storage tanks, stacks, circulation pumps, electrolyte transmission pipelines, and battery management systems. The VFB carries out the battery’s charging and discharging process by transmitting the electrolyte to the stack for the reaction.

Figure 1.

Basic structure of the VFB.

The present membranes employed in VFBs are unable to completely impede the dispersion of vanadium ions. As such, the diffusion of these ions can trigger a series of self-discharge reactions, resulting in a decrease in the capacity of VFBs’ capacity.

2.2. Mass Conservation Equation of Vanadium Ions

When establishing the VFB model, we make the following assumptions:

• (1)The tank is completely occupied by the electrolyte, which is thoroughly blended.
• (2)The influence of side reactions can be disregarded.
• (3)The temperature remains stable at ambient conditions.
• (4)The volumes of the dual electrolytes are maintained constant.
• (5)The self-discharge reaction via the membrane occurs instantaneously.

Grounded on the aforementioned presumptions, the mass balance equation is constructed by employing Fick’s law

For V²⁺:

1

2

For V³⁺:

3

4

For VO²⁺:

5

6

For VO⁺₂:

7

8

As dictated by the Nernst equation of electrochemistry, the battery’s voltage E(t) can be determined as:

9

where c^t₂, c^t₃, c^t₄, c^t₅, c^s₂, c^s₃, c^s₄, and c^s₅ represent the density of V²⁺, V³⁺, VO²⁺, and VO⁺₂ in the fluid storage container and the battery stack and k₂, k₃, k₄, and k₅ represent diffusion coefficients of Nafion117 for V²⁺, V³⁺, VO²⁺, and VO⁺₂ across the membrane, respectively. The other parameters used in the simulation on Matlab and Simulink are shown in Table 1.⁹

Table 1. Simulation Parameters for the VFB.

parameters	value
concentration of vanadium, c	2 mol L–1
area of the exchange membrane, S	0.49 dm2
area of the electrode surface, A	50 cm2
cell formal potential, E0	1.4 V
Faraday’s constant, F	96 485 C mol–1
quantity of electrons exchanged in the reaction, z	1
temperature, T	298.15 K
tank volume, Vt	50 cm3
half-cell volume, Vs	15 cm3
gas constant, R	8.314 J mol–1 K–1
flow rate, Q	0.005 L s–1

2.3. Impact of Diffusion on the Reduction of Capacity

Due to its strong chemical stability and ion conductivity, Nafion117 is extensively utilized in the VFB field. In this paper, we choose Nafion117 as the ion exchange membrane of the VFB. Table 2 displays the parameters of Nafion117.^9,21

Table 2. Parameters of the Nafion117 Membrane.

parameters	value
k2	2.621 × 10–7 dm s–1
k3	4.377 × 10–7 dm s–1
k4	1 × 10–6 dm s–1
k5	1.395 × 10–6 dm s–1
resistance of Nafion117, r	0.94 Ω cm2

We selected the current densities of 60, 80, 100, and 120 mA cm^–2 to study the VFBs’ capacity loss using the Nafion117 membrane across various current density levels. The capacity decay of Nafion117 is shown in Figure 2. In 100 charge–discharge cycles with varying current densities, the high diffusion coefficient of Nafion117 enhances the dispersion of vanadium ions. We can see that with the increase of the number of cycles, Nafion117 will show obvious capacity attenuation. As the density of current grows, the capacity attenuation of the VFB has been alleviated to a certain extent.

Figure 2.

Reduction in the capacity for Nafion117 membranes in 100 cycles at varying current densities.

Across various levels of current density, the voltage distribution of the VFB at different cycles is shown in Figure 3(a–d).

Figure 3.

Voltage distribution of the VFB with the Nafion117 Membrane.

In the real world, we can estimate the SOC by the ion concentration and open-circuit voltage in the battery, and the open-circuit voltage and ion concentration are real time-measurable. At different densities of current, the open-circuit voltage of the battery is related to the SOC of the battery, and as the number of cycles increases, capacity decay occurs. Therefore, the data can be obtained through the established mechanism model to estimate the SOC of the battery. Considering the capacity decay caused by the charge–discharge cycle, we choose the voltage, current, and number of cycles as the input. In terms of data, we used the Simulink model to perform 10 constant current charge and discharge cycles at different current densities and obtained the data of the battery during the charge and discharge process. Each experiment randomly took out the voltage, current, cycle times, and SOC values at 205 nodes to ensure that the model had sufficient generalization ability.

2.4. Extreme Learning Machine

The ELM is a widely used SLFN. In contrast to other SLFNs, the ELM does not need to adjust parameters by iteration and does not have the characteristics of slow training speed. While the weights and biases are allocated at random, the least-square method is used to determine the weights for the output layer β.

Let the hidden layer of the ELM have n nodes. The ELM can select any nonlinear, piecewise continuous excitation function g(x). The weight matrix W and bias B are usually given randomly. The output of the hidden layer and the output matrix T can be expressed as:

10

11

The loss function E is expressed as:

12

Then, β is calculated as:

13

where H⁺ is the MP-generalized inverse matrix of H. The least-squares solution with the minimum norm is obtained by the MP-generalized inverse matrix, which makes the ELM have good robustness and generalization performance. Figure 4(a) depicts the structure of the ELM, while Figure 4(b) demonstrates its workflow.

Figure 4.

Structure and workflow of the ELM.

2.5. Sand Cat Swarm Optimization Algorithm

The sand cat swarm optimization algorithm (SCSO) is a smart optimization technique. The SCSO algorithm is mainly composed of the following three stages:²²

(1) Initialization

First, the parameters in the algorithm are initialized, the number of sand cats is set to 30, and an initialization matrix was created:

14

where X_i represents the ith sand cat. Each sand cat has its own fitness.

(2) Exploring stage

The exploration behavior and attack behavior are determined by the parameter 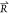. When |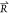| > 1, the exploration is carried out, and when || ≤ 1, the attack is carried out. During the iteration, the parameter 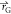is linearly reduced from 2 to 0 to approach the target position. The sound features of the sand cat were simulated by S_M and set to 2. 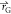and 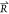are expressed as follows:

15

16

The scope of sensitivity among individual sand cats can be expressed as:

17

Each unit alters its location using the best candidate spot, its current location, and scope of sensitivity:

18

where 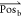is the best candidate location and 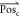is the current location.

(3) Exploitation stage

In the exploitation stage, consider the scope of sensitivity of each sand cat as a circle, and the direction of motion of the sand cat is specified by randomly setting the angle θ:

19

20

where represents the position, chosen at random, and guarantees that the relevant cat can be close to the prey.

2.6. Improved Sand Cat Swarm Optimization Extreme Learning Machine

In this paper, the improved SCSO algorithm is used to optimize the weight and bias of the ELM hidden layer. First, a triangular walk strategy is incorporated in the exploring phase. In the exploring stage, sand cats move around when approaching the prey, and the inclusion of the triangular walk strategy allows individual sand cats to explore the solution space in a more comprehensive way. The distance L₁ between the present location and the optimal candidate position is determined. According to L₁, the scope of step length L₂ is obtained:

21

22

The angle δ is randomly obtained, P, which is the length of the third side of the triangle with 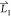, 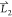is calculated as neighbors and the angle of δ, and then, the location is acquired according to the position obtained by the swimming and the prey:

23

24

Adding Levy flight strategy in the exploitation stage can provide a walking mode that conforms to the Levy distribution. The strategy can not only ensure detailed local search but also have the ability to move beyond the local optimum. The Levy flight strategy is as follows:

where C is the scaling factor, which is set to 0.3 in the exploitation stage, thus reducing the step size. The step size factor s that obeys the Levy distribution is shown below

25

where

In the ELM part, according to the rank of H, different methods are selected to construct the output weight matrix β.

Let H be a m × n matrix. If H in the ELM satisfies rank (H) = m, then

26

If H in the ELM satisfies rank(H) = n, then

27

If H in the ELM satisfies rank (H) < min(m, n), then, its MP-generalized inverse matrix is

28

The hyperparameters of the ISCSO-ELM used in this paper are configured as follows: the activation functions used are all sigmoid functions, the hidden layer nodes are set to 8, the initialization weights obey a uniform distribution from −1 to 1, and the bias obeys a uniform distribution from 0 to 1.

The schematic diagram of the ISCSO-ELM is illustrated in Figure 5.

Figure 5.

Workflow of the ISCSO-ELM.

3. Results and Discussion

All experiments in this paper are carried out on the Windows 10 system. MATLAB R2018a is used for all experiments and result visualization.

In this study, modeling was performed on a VFB, and data collection was conducted on the established VFB model. Current, voltage, and the number of charge–discharge cycles were selected as inputs, with current densities being 60, 80, 100, and 120 mA cm^–2. Considering the real-world interference in the charge–discharge process of the VFB, Gaussian noise was added to the simulated SOC data. The collected 205 battery datasets were divided into 155 training and 50 test sets. Figure 6 compares the prediction results of ISCSO-ELM with the actual results, indicating that the extreme learning machine optimized by the improved sand catalytic algorithm can accurately predict the SOC of the battery.

Figure 6.

Prediction results of the SOC using ISCSO-ELM algorithms.

To demonstrate the superiority of the ELM method, we chose other algorithms, back propagation (BP) and radial basis function algorithm (RBF), for comparison. To validate the proposed method, we compared it to the ELM, GA-ELM, and SCSO-ELM methods. The evaluation indicators MAE, MAPE, RMSE, and R² were employed, and the predictive performance of the model is presented in Table 3. The bold data represent the optimal performance.

Table 3. Comparison of Model Performances.

model	MAE	MAPE	RMSE	R2
BP	0.129	0.0087	0.1656	0.847
RBF	0.0806	0.0056	0.1062	0.863
ELM	0.067	0.0052	0.0866	0.894
GA-ELM	0.061	0.0050	0.0829	0.907
SCSO-ELM	0.057	0.0048	0.0708	0.922
ISCSO-ELM	0.051	0.0031	0.0591	0.943

The results show that the algorithm has a better search capability due to the incorporation of the triangular walk strategy and the Lévy flight strategy, which makes it easier to jump out of the local optimal solution to achieve a better search for weights and biases, and the ISCSO-ELM method shows the highest values in all the selected metrics compared to the SCSO-ELM, which shows an improvement in the accuracy of the prediction. This illustrates the effectiveness of the method proposed in this study. In industrial applications, the method proposed in this paper is implemented on MATLAB R2018a, which does not require additional high-performance computing resources and only needs to be combined with the VRFB system to receive data to estimate the SOC value of the battery in real time, in order to guide the battery to be charged and discharged more efficiently and to improve the battery life and performance. The proposed method also has some limitations. There are also other parameters in the electrochemical model that can be added to the input of the model to improve the model performance, such as temperature, ion concentration, etc. In long-time charging and discharging situations, the side reactions that continue to occur in the battery will also have a certain impact on the battery performance, and subsequent research can also address this point by adding an online learning mechanism to solve this problem.

4. Conclusions

This paper introduces a machine learning-based SOC prediction method for specific VFB conditions. Initially, an electrochemical model of the VFB is constructed based on the operating characteristics and conservation of mass equations. To address the problem of reduced accuracy due to randomly assigned weights and biases in the ELM, an integrated approach combining the ISCSO algorithm with the ELM, denoted as ISCSO-ELM, is proposed. This algorithm exhibits a high level of accuracy, outperforming all comparative methods used within this paper, effectively enabling SOC estimation for the VFB. Furthermore, due to the excellent generalization performance of the ELM, the scope of this method’s applicability can be extended to other types of batteries.

The authors declare no competing financial interest.