Abstract
The hazards and consequences of slope collapse can be reduced by obtaining a reliable and accurate prediction of slope safety, hence, developing effective tools for foreseeing their occurrence is crucial. This research aims to develop a state-of-the-art hybrid machine learning approach to estimate the factor of safety (FOS) of earth slopes as precisely as possible. The current research’s contribution to the body of knowledge is multifold. In the first step, a powerful optimization approach based on the artificial electric field algorithm (AEFA), namely the global-best artificial electric field algorithm (GBAEF), is developed and verified using a number of benchmark functions. The aim of the following step is to utilize the machine learning technique of support vector regression (SVR) to develop a predictive model to estimate the slope’s safety factor (FOS). Finally, the proposed GBAEF is employed to enhance the performance of the SVR model by appropriately adjusting the hyper-parameters of the SVR model. The model implements 153 data sets, including six input parameters and one output parameter (FOS) collected from the literature. The outcomes show that implementing efficient optimization algorithms to adjust the hyper-parameters of the SVR model can greatly enhance prediction accuracy. A case study of earth slope from Chamoli District, Uttarakhand is used to compare the proposed hybrid model to traditional slope stability techniques. According to experimental findings, the new hybrid AI model has improved FOS prediction accuracy by about 7% when compared to other forecasting models. The outcomes also show that the SVR optimized with GBAEF performs wonderfully in the disciplines of training and testing, with a maximum R2 of 0.9633 and 0.9242, respectively, which depicts the significant connection between observed and anticipated FOS.
Keywords: Machine learning, Support vector regression, Artificial electric field, Slope stability
1. Introduction
One of the most significant challenges in geotechnical and geological engineering research is predicting slope stability. Slope collapses are a widespread form of geological disaster and a natural occurrence that pose a significant natural hazard in many nations. Every year, they cause hundreds of millions of dollars' worth of damage to both public and private property and always generate significant social and economic losses. It became critical for engineers and experts to examine the slope’s stability and find ways to stop or lessen the damage it caused. However, it’s an extremely difficult procedure that involves a variety of input parameters. These influencing parameters, such as the soil’s water content, shear strength of geomaterials, and geometric shape, exhibit a high degree of uncertainty [1]. For generalizing the entire slope stability study procedure, which reflects the overall strength and vulnerability of the slope, the Factor of Safety (FOS) is used in the majority of analytical methodologies [1,2]. A very complex computation that takes a lot of time and effort is required to accurately determine slope stability. To calculate the FOS of a given slope, there are several analytical and numerical approaches available [3]. One of the classical and often employed approaches is the limit equilibrium method (LEM) [4]. However, it involves assuming a predetermined critical failure surface where collapse will happen, and a resistive force is calculated using mathematical model [5]. In addition to LEM, the finite difference method (FDM) and the finite element method (FEM) have emerged as superior numerical analysis (NA) techniques that can tackle challenging slope stability issues with high level of accuracy [5]. There are certain drawbacks despite all of its benefits, such as the lengthy time needed for the numerical simulation [6]. Also, for greater accuracy, these approaches need exact boundary conditions that can mimic the actual field situation, which can sometimes be challenging to determine [7]. These weaknesses and complexity of conventional methods, prompted the need for alternative methodology or procedure that can produce results quickly and with a higher degree of precision [8]. It should also be simple to implement and provide an easy-to-understand interpretation.
In recent years, robust machine learning (ML) and artificial intelligence (AI) methods have been introduced and have boosted researcher interest in solving highly complex, non-linear, multivariate problems. These techniques have excellent feature extraction and learning capabilities. Because of the obvious benefits of these approaches, several studies presented a critical review of the application of a special ML model for a specific application. Deep learning-based forecasting techniques for renewable energy were thoroughly and in-depth reviewed by Wang et al. [9] to examine their efficacy, efficiency, and potential for use. In relation to remote sensing picture classification, Sheykhmousa et al. [10] extensively reviewed the Random Forest (RF) and Support Vector Machines (SVM) ideas. Weerakody et al. [11] presented an in-depth review of recently published research that have effectively applied recurrent neural networks to forecast activities in a variety of disciplines using irregular time series data. Lindemann et al. [12] conducted a survey on cutting-edge anomaly detection employing long short-term memory networks. In an extensive survey of studies on the subject of sensitivity analysis, Antoniadis et al. [13] highlighted some interesting relationships between random forests and global sensitivity analysis. Nanehkaran et al. [14] have carried out an in-depth comparison of machine learning techniques for slope stability.
The support vector regression (SVR) approach has demonstrated the ability to handle a variety of technical challenges with only a small quantity of data [15,16]. SVR’s computational cost remains unaffected by the input space’s dimensions, which is one of its key advantages. Compared to other regression algorithms, it requires less computational effort. It also offers strong prediction accuracy, outstanding generalization capacity, and robustness to outliers. Although this strategy is effective at simulating a variety of phenomena, it has significant drawbacks that restrict its usage. Every SVR model contains a number of user-defined parameters that must be carefully selected by the user. The user’s incorrect entry of the aforementioned parameters can produce inaccurate, even erroneous results. Therefore, it is essential to use a powerful optimization technique when looking for the right value for these parameters. To this end, Dong et al. [17] employed chaotic cuckoo search, Zhang and Hong developed dragonfly algorithm [18] and chaotic grey wolf [19], Wei et al. [20] considered whale optimization and Harris hawks and Zhang et al. [21] applied improved cuckoo search to adjust the SVR parameters.
In the area of intelligent optimization, there are many different kinds of optimization algorithms, however, none of them can address every optimization issue [22]. As a result, numerous optimization strategies are frequently suggested or enhanced by the researchers [[23], [24], [25]]. The salp swarm algorithm as a recently developed metaheuristic was developed by Mirjalili et al. [26] and its modified versions were presented by Hegazy et al. [27], Khajehzadeh et al. [28], Li and Wu [29], Qais et al. [30], and Zhao et al. [31]. Another effective metaheuristic suggested by Heidari et al. [32] is the Harris hawks optimization (HHO). Some researchers presented enhanced versions of the HHO such as Elgamal et al. [33], Jiao et al. [34], Li et al. [35], Fan et al. [36], and Dhawale et al. [37]. Kaur et al., in 2020 [38] introduced a novel metaheuristic, namely the tunicate swarm algorithm (TSA). Later, the enhanced versions of the TSA have been suggested by Houssein et al. [39], Arabali et al. [40], Fetouh and Elsayed [41], Li et al. [42], and Rizk-Allah et al. [43]. Alsattar et al. [44] presented the bald eagle search algorithm (BES) in 2020. The improved forms of this algorithm have been proposed by Ramadan et al. [45], Alsaidan et al. [46], Ferahtia et al. [47], Elsisi and Essa [48], and Chaoxi et al. [49].
The artificial electric field algorithm (AEFA) is a recently created algorithm that models the process of charged particles moving in relation to one another while being subjected to the Coulomb force in an electrostatic field [50]. The AEFA benefits from a straightforward structure with simple equations, minimal adaptable parameters, an easy-to-understand algorithmic, and convenient implementation. This method can surpass several state-of-the-art approaches [50]. However, like with every metaheuristic approach, this one has certain limitations, such as local minima stagnation and limited exploration potential [51]. Furthermore, as stated by the No Free Lunch (NFL) theorem [22], the effectiveness of an optimization strategy in addressing a certain set of optimization issues does not ensure its efficacy in optimizing other types of problems. It is therefore difficult to claim that a certain technique is the most effective optimizer for every optimization issue. The NFL theorem has stimulated scholars to develop novel optimizers for addressing optimization challenges across several domains.
This paper’s originality and inventiveness are in developing an enhanced version of the AEFA algorithm, namely the global-best artificial electric field algorithm (GBAEF). In addition, the new GBAEF algorithm is applied to the fine-tuning of the SVR hyper-parameters. The prediction accuracy of the proposed models for forecasting the FOS is next examined.
According to the aforementioned explanations the study’s primary contributions can be summarized up as follows:
-
1.
A powerful optimization approach called the global-best artificial electric field algorithm (GBAEF) is introduced and verified using a number of benchmark functions.
-
2.
The proposed GBAEF is applied to fine-tune the support vector regression’s hyperparameters and the optimized SVR-GBAEF model is employed to forecast the soil slope’s minimum factor of safety.
-
3.
Conduct a comparative case study of earth slopes, comparing the proposed hybrid model (SVR-GBAEF) with traditional slope stability techniques.
2. Related research
Artificial intelligence (AI) approaches are thought to be the most advanced and accurate for assessing slope stability, and in recent years, these models have been frequently employed in slope stability prediction.
Suman et al. [52] created two AI models for FOS prediction, including genetic programming (GP) multivariate adaptive regression splines (MARS). As a consequence, the MARS model was determined to be the best strategy for predicting FOS in their investigation.
Gordan et al. [53] created an optimized artificial neural network using particle swarm optimization (PSO-ANN model) to predict the FOS of homogenous slopes using 699 datasets. Based on certain model performance metrics, such as root mean square error, it was discovered that the PSO-ANN approach outperforms ANN in terms of FOS prediction [53].
Hoang and Pham [54] developed an integrated hybrid AI model based on the Least Squares Support Vector Classification (LS-SVC) and Firefly Algorithm (FA) for slope safety prediction. A dataset of 168 real-world slope evaluation instances from different locations was utilized to develop and validate the hybrid technique. Experiment findings showed that the hybrid AI model improved classification accuracy when compared to other benchmark approaches [54].
Qi and Tang [55] suggested and analyzed six integrated AI techniques for slope safety forecasting, including decision tree, logistic regression, gradient boosting machine, random forest, multilayer perceptron neural network, and support vector machine. The firefly algorithm (FA) was employed to tune the AI models' hyper-parameters. The findings demonstrated that the combined AI techniques had a high potential for predicting slope stability, and FA was effective in hyper-parameter tuning.
Koopialipoor et al. [56] attempted to predict the FOS of homogeneous slopes under static and dynamic settings. To alter the weights and biases of the ANN model, they used a variety of optimization techniques such as the GA, artificial bee colony, imperialist competitive algorithm, and particle swarm optimization. In their investigation, they used 699 datasets with five model inputs. The archived finding demonstrated that, although all prediction models can approach slope FOS values, the PSO-ANN predictive model outperforms the others [56].
Gao et al. [57] applied the imperialist competition algorithm (ICA) to improve the ANN performance for the problem of slope stability design charts. The input parameters employed were slope angle, depth factor, and undrained shear strength ratio, with the output being a stability number. The findings demonstrated that the ICA-ANN model performs well in predicting the slope stability characteristics of cohesive soils [57].
Moayedi et al. [58] suggested a unique optimization technique, HHO (Harris Hawks' optimization), for improving the accuracy of the classic multilayer perceptron approach in forecasting the FOS in the presence of stiff footings. In this manner, four slope stability parameters were examined: rigid footing position, slope angle, soil strength, and applied surcharge. The study indicated that using the HHO increases the ANN’s prediction accuracy while studying slopes under unknown circumstances.
Wei et al. [20] suggested a novel hybrid intelligent model for slope analysis and FOS assessment. The Harris Hawk’s optimization (HHO) and whale optimization algorithm (WOA) were employed in their investigation to adjust the parameters of the support vector regression (SVR) model. Based on the ideal findings, the HHO demonstrated a more powerful process in adjusting the SVR parameters than the WOA methodology [20].
Ahangari et al. [59] tried to enhance slope stability by the utilization of diverse machine learning methodologies. Based on the findings, it was seen that the multilayer perceptron model had the best levels of accuracy, while the random forest model exhibited the lowest predictive performance.
Through an optimized least squares support vector machine (LSSVM), Zeng et al. [60] provided innovative and accurate models for predicting the FOS of slopes. Three alternative approaches, including the gravitational search algorithm (GSA), trial and error (TE), and whale optimization algorithm (WOA), were employed to examine the correct control parameters of the LSSVM [60]. Six effective parameters on the FOS were employed as input parameters in the developed LSSVM-TE, LSSVM-WOA, and LSSVM-GSA, techniques. The error criteria findings showed that both WOA and GSA can enhance the performance prediction of the LSSVM approach in predicting FOS.
In another study, Yang et al. [61] employed five machine learning algorithms, including the random forest, support vector machine, decision tree, closest neighbor, and gradient boosting. The genetic algorithm was utilized to solve the hyperparameter tuning of the ML models [61]. The findings revealed that, when the area under the curve value, accuracy, and other parameters were taken into account, the random forest method was chosen to be the best model.
A study of the published research reveals that soft computing approaches have been effectively used to estimate slope stability. However, referring to the ‘no free lunch’ theorem in Machine Learning [22], no specific method performs well across all potential cases. Furthermore, new information in soft computing approaches is constantly the objective of researchers to increase the accuracy and reliability of prediction algorithms in forecasting slope stability. In conclusion, in this research, a novel artificial intelligence model, SVR-GBAEF, was created and presented for slope safety prediction.
3. AFEA: artificial electric field algorithm
A recently developed population-based metaheuristic technique called the Artificial Electric Field Algorithm (AEFA) imitates the electrostatic force and motion of Coulomb’s law of attraction [50]. The potential candidates for the given problem’s solution in AEFA are shown as a group of charged particles. Each proposed solution’s performance is influenced by the charge attached to each charged particle. Each particle is drawn to one another by electrostatic force, causing a global movement in the direction of particles with heavier charges. The location and fitness function of charged particles, which establishes their charge and unit mass, relate to a potential solution to the issue. The AEFA’s procedures are as follows [50]:
-
Step 1
. Creation of the population.
The following formula represents how a population of k charged candidates is initialized:
| (1) |
where, xi,min and xi,max are, the ith variable’s lower and upper bounds. n shows the total number of charged candidates in the population.
-
Step 2
. Fitness assessment.
A fitness function is characterized as a function that accepts a potential solution as input and generates an output that demonstrates how well the potential solution fits with regard to the problem under consideration. Each charged particle’s performance in AEFA is affected by its fitness value for that particular iteration. The best and worst fitness are determined based on Eqs. (2), (3), respectively.
| (2) |
| (3) |
where, best (t) and worst (t) are the best and worst fitness of all charged candidates at iteration t.
-
Step 3
. Coulomb’s constant computation.
The Coulomb’s constant at time t, C(t), is calculated using Eq. (4).
| (4) |
In this case, C0 denotes the Coulomb’s constant’s initial value, which is set at 100 [50]. Current iteration ae well as the total number of iterations are represented, respectively, by t and Itermax.
-
Step 4
. Evaluate the charge of charged candidates.
Fi(t) represents the charge of the ith charged candidate at time t and can be evaluated by Eqs. (5), (6):
| (5) |
| (6) |
where, fitnessxi is the fitness of the ith charged candidate.
-
Step 5
. Calculate the charged particle’s acceleration and electrostatic force.
-
a.
Equation (7) is implemented to calculate the electrostatic force exerted on the ith charged candidate at time t:
| (7) |
where, is the impact force on the charged candidate i from charged candidate j and it is computed based on Eq. (8).
| (8) |
where ɛ is a small positive constant, and the distance between two charged candidates, i and j, is known as Rij(t). PjD (t) and xjD (t) are the global best and current position of the charged candidate at time t.
-
b.
Using the Newton rule of motion, Eqs. (9), (10) are used to calculate the acceleration of the ith charged candidate at time t in Dth dimension:
| (9) |
| (10) |
where EiD and MiD are the electric field and unit mass of ith charged candidate respectively.
-
Step 6
. Update the charged particle’s velocity and location.
The ith charged particle’s velocity and position will be updated according to Eqs (11), (12), respectively.
| (11) |
| (12) |
where veliD is the velocity of the ith charged candidate and rand is a uniform random number in the interval [0, 1].
The pseudocode of the standard AEFA is presented.
| Algorithm 1. AEFA pseudocode |
|---|
| Initialize n random positions of the candidate using Eq. (1) Set the velocity to 0 initially Evaluate fitness values of the initial population Set t = 1 whilet < Itermax Determine the best and the worst population using Eqs. (2), (3) fori = 1 to n Determine the values of fitness Using Eq. (7), calculate the total force in each direction Using Eq. (9) determine the ith agent acceleration. Utilizing Eq. (11) update the agent’s velocity. Utilizing Eq. (12) update the agent’s position. end t = t +1 end while Output the best solution |
4. GBAEF: global-best artificial electric field algorithm
Apart from the advantages of the AEFA, the standard algorithm is constrained to a local best solution and suffers from delayed convergence [51]. These drawbacks result from updating some solutions in favor of the local best option, even though there may be superior solutions available outside of the present solution space. The proposed GBAEF considers a new phase to increase the effectiveness of the conventional method in order to avoid those drawbacks. Moreover, in the proposed GBAEF, no further parameters are necessary to be set. Actually, with the suggested algorithm, AEFA will be enhanced in two steps.
In the first step, a new random population (Xnew) based on the conventional algorithm’s global best solution (xBest) is constructed using Eqs. (13), (14):
| (13) |
| (14) |
Then, by using the fitness function, the newly generated population will be evaluated. The GBAEF replaces the existing charged candidate with the new one based on Eq. (15), if the new population might enhance the value of the objective function.
| (15) |
In the second stage of the suggested GBAEF, the worst-charged candidate with the greatest objective function value will be swapped out at each iteration with a randomly created candidate.
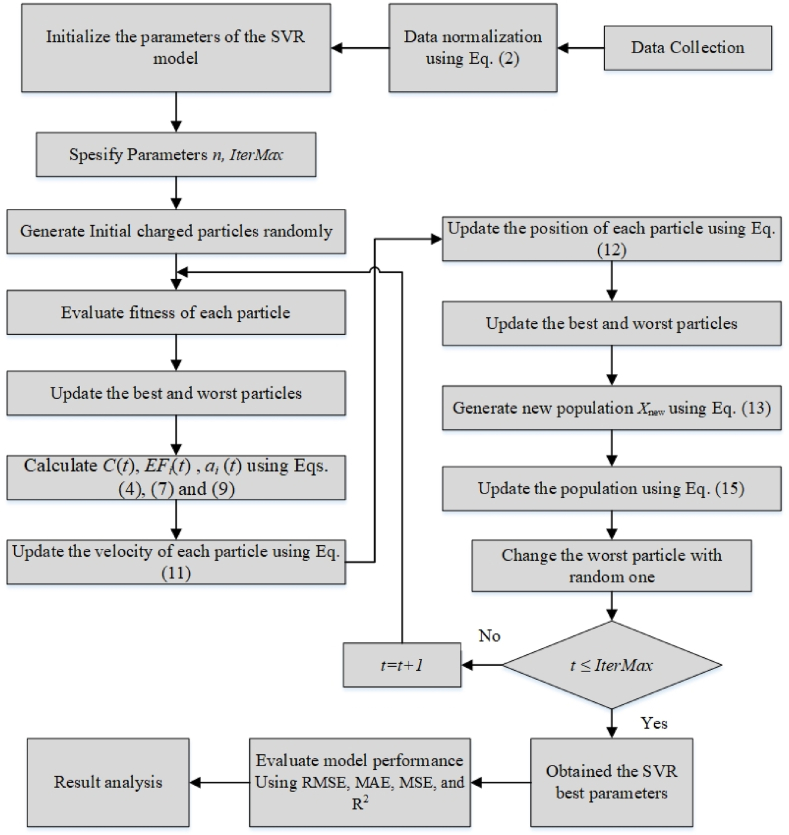
In comparison to the conventional AEFA algorithm, the suggested procedure enables the GBAEF to explore the search space more thoroughly and effectively, and improves the accuracy of the best answer. Fig. 1 depicts the flowchart of the proposed GBAEF approach for greater clarity and simplicity of implementation.
Fig. 1.
GBAEF workflow.
5. Support vector regression
The concept of support vector machines (SVMs) was first presented by Vapnik [62]. SVMs fall into two broad categories: Support Vector Classification (SVC) as well as Support Vector Regression (SVR). However, the most popular SVM application form is SVR. Due to its outstanding nonlinear prediction capacity, the SVR network is operated by academics to forecast a variety of complicated problems [15]. In cases when there is a lack of data or there are irregularities in the data, SVR can be a beneficial tool as an effective forecasting model.
Let’s use Eq. (16) to identify the training samples:
| (16) |
where n represents the quantity of training samples. The ultimate purpose of SVR is to develop a function f (x) that illustrates the dependence between the output yi and the input xi [63]. The function f (x) can be described by Eq. (17):
| (17) |
where, w stands for the parameters' vector (or weight). b is the bias and Ø is a kernel function. The determination of the aforementioned variables is achieved by the optimization of the empirical risk function utilizing the Support Vector Regression (SVR) theory, as outlined in Eq. (18) [18].
| (18) |
where, stands for the primary empirical risk, commonly known as the ɛ-insensitive loss function due to its theoretical description and is evaluated by Eq. (19).
| (19) |
C and ɛ are the parameters that must be estimated and play crucial roles in the SVR modeling process [18]. The SVR function’s gradient is in the second term (). The gradient and empirical risk are balanced using the constant C.
With the help of two slack variables, ξ and ξ*, it is possible to determine the distance among the boundary values and the real values of the ɛ-tube in order to solve Eq. (18). Then, using Eq. (20), equation (18) is transformed into a normal programming form with constraints [18] as presented below:
| (20) |
By utilizing the Lagrange multipliers approach as described in Eq. (21) the weight, w, is determined.
| (21) |
where, are positive Lagrange multipliers and .
When doing nonlinear regression, the kernel function is used to translate input data onto a higher-dimensional feature space to create a hyperplane for linear regression. Eq. (22) provides the SVR function as a final result.
| (22) |
where, is the kernel function that results from the inner product of the feature mapping functions .
There are various kinds of kernel functions, but we utilized one of the most popular and potent ones, the Radial Basis Kernel Function (RBF), which is described by Eq. (23).
| (23) |
where, σ is the RBF kernel parameter.
6. Optimizing SVR network by the GBAEF
The RBF kernel parameter (σ), the regularization parameter (C), and the error margin (ɛ), among other learning parameters, are critically important for SVR’s capacity to generalize [64]. These three (C, σ and ɛ) factors are the primary SVR parameters that should be optimized throughout the training phase. However, due to the very non-linear nature of the model with respect to these factors, it might be challenging to determine the ideal combination of hyper-parameters. In the current study, GBAEF, an efficient intelligent algorithm, is implemented to determine the SVR model’s optimal parameter values.
The process of optimizing the SVR model primarily consists of four steps:
6.1. Data preparation
At this step, the collected data sets are split into training and testing groups. The predictive models are trained using training data sets. Forecasting techniques can find patterns or correlations between inputs and outputs with the aid of training data sets. Test data are used to assess how well the models predict the future. In the study, 20% of the data was utilized for testing, while the remaining 80% of the dataset was employed for training the network.
6.2. Model establishment
The predictive model is applied to the data sets, and the model’s hyper-parameters' initial values are taken into account. For every prediction model, a separate set of hyper-parameters is used. The error margin, the RBF kernel parameter, and the regularization parameter are the three most crucial hyper-parameters for the SVR model. The starting population of size n for three parameters of an SVR model, as indicated in Eq. (1), should be randomized in the GBAEF framework.
6.3. Fitness evaluation
In this stage, the fitness values, which are utilized as indicators of forecasting accuracy, are assessed based on the initialized locations of three parameters. The hyper-parameters of the model are now tuned repeatedly until the model performs at its best. Some statistical assessment indices are used to assess the forecasting models' performance, including the mean absolute error (MAE), root mean square error (RMSE), mean square error (MSE), and coefficient of determination (R2). The following equations (Eqs. (24), (25), (26), (27))) are provided to calculate these indices:
| (24) |
| (25) |
| (26) |
| (27) |
where n is the number of samples in the training dataset. y and are the proposed model’s predicted and actual values, respectively.
6.4. Results analysis
In this stage, the predictive power of the optimized model is assessed by contrasting predicted and actual results.
The procedure of developing the optimized SVR model using GBAEF (GBAEF-SVR) is depicted in Fig. 2.
Fig. 2.
The whole workflow of the hybrid GBAEF-SVR model.
7. Slope stability evaluation
The majority of analytical methodologies employ the Factor of Safety (FOS) for the evaluation of slope stability. To determine the FOS of a given slope, a variety of analytical and numerical methods are available. Limit equilibrium methods, which are still relatively common, are used to determine the FOS of finite slopes. The slope safety factor has been calculated in numerous studies in recent decades, and some significant approaches have been suggested, such as the Bishop’s simplified technique [65], Janbu’s simplified technique [66], Spencer’s technique [67], and Morgenstern-Price’s technique [68]. These techniques involve slicing the slope into thin slices so that the base can be compared to a straight line, followed by the writing of the forces or moments equilibrium equations. They produce findings that are typically rather close. Fredlund [69] demonstrated the relation between limit equilibrium approaches, and Duncan and Wright [70] evaluated the precision of limit equilibrium methods. According to Duncan [71], there are often less than 6% variations between the safety factor values derived using the various approaches. The Mohr–Coulomb formula is used in all limit equilibrium techniques to calculate the shear strength () along the sliding surface. The Mohr-Coulomb theory states that cohesion, internal friction angle, and applied normal stress all influence the soil’s shear strength. According to this theory, Eq. (28) provides the shear strength of clayey soil.
| (28) |
where, is the shear strength, is the effective cohesion, is the normal stress and is the effective internal friction angle. According to Das [72], the FOS is often defined as the ratio of the driving and resisting forces and is provided by Eqs. (29), (30) with respect to slope strength.
| (29) |
| (30) |
where, is the average shear stress, is the effective cohesion, and is the angle of friction on the possible failure surface.
The mobilized shear stress is a function of the external forces acting on the soil masses, whereas the available shear strength is a function of the type of soil and the effective normal stress.
Various established publications in the literature, such as Nash [73] and Duncan [71], provide details on the available limit equilibrium approaches. Additionally, evaluations of slope stability can be carried out utilizing several geotechnical computer programs.
8. Verification of the proposed GBAEF
An extensive collection of benchmark functions from the literature is employed in this experiment to analyze the performance of the suggested GBAEF. Both unimodal functions (UFs) and multimodal functions (MFs) are included in this set of functions. The UFs (F1–F6) with a single global optimum can be used to show optimization algorithm exploration, whereas the MFs (F7–F12) with numerous local extrema can demonstrate optimization algorithm exploitation. Table 1 contains information about these benchmarking functions.
Table 1.
UFs and MFs benchmark functions.
| Function | Range | n (Dim) |
|---|---|---|
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
| 30 | ||
|
|
30 |
For comparisons with the GBAEF optimizer, some well-known optimizers are employed, including PSO [74], FA [75], MVO [76], SSA [26], TSA [38], and AEFA [50]. The criteria used in this comparison are the average and standard deviation (Std) of the best results so far provided by each optimizer under consideration. To have a fair comparison, for each optimizer, a population size and a maximum allowed number of function evaluations (FEs) are set at 50 and 50,000, respectively. The results are based on the average performance of the 30 runs performed individually by each optimizer for each function. The parameters of other comparative algorithms are based on literature-based suggestions [26,38,74,75].
The statistical findings for each method that was compared are shown in Table 2. The best values, denoted in bold.
Table 2.
Results comparison of UFs and MFs.
| F | Index | GBAEF | AEFA | PSO | FA | MVO | SSA | TSA |
|---|---|---|---|---|---|---|---|---|
| F1 | Average | 0 | 3.73 × 10−27 | 5.86 × 10−8 | 6.99 × 10−3 | 0.38 | 2.31 × 10−7 | 8.29 × 10−58 |
| Std. | 0 | 6.23 × 10−26 | 2.39 × 10−7 | 2.19 × 10−3 | 0.21 | 5.89 × 10−7 | 1.05 × 10−59 | |
| F2 | Average | 0 | 1.26 × 10−11 | 8.30 × 10−3 | 0.329 | 0.40 | 1.8911 | 9.28 × 10−34 |
| Std. | 0 | 1.65 × 10−10 | 2.79 × 10−3 | 0.167 | 0.14 | 1.5942 | 8.78 × 10−36 | |
| F3 | Average | 0 | 4.94 × 10+03 | 21 | 1.71 × 103 | 43.1 | 1.48 × 103 | 1.51 × 10−13 |
| Std. | 0 | 149 | 7.13 | 669 | 8.97 | 707.05 | 6.55 × 10−13 | |
| F4 | Average | 0 | 9.67 × 10−13 | 0.511 | 0.10 | 0.97 | 2.37 × 10−6 | 1.86 × 10−5 |
| Std. | 0 | 6.78 × 10−12 | 0.269 | 0.036 | 0.24 | 1.92 × 10−6 | 4.52 × 10−4 | |
| F5 | Average | 0 | 0 | 0.069 | 6.94 × 10−3 | 0.020 | 5.72 × 10−7 | 3.67 |
| Std. | 0 | 0 | 0.028 | 3.61 × 10−3 | 7.43 × 10−3 | 2.44 × 10−7 | 0.3353 | |
| F6 | Average | 1.91 × 10−6 | 0.025 | 0.089 | 0.066 | 0.052 | 8.82 × 10−5 | 0.0018 |
| Std. | 3.36 × 10−6 | 0.023 | 0.0206 | 0.042 | 0.013 | 6.94 × 10−5 | 4.62 × 10−4 | |
| F7 | Average | −1.22 × 104 | −3.01 × 103 | −6.01 × 103 | −5.85 × 103 | −6.92 × 103 | −7.46 × 103 | −7.89 × 103 |
| Std. | 5.21 × 102 | 1.70 × 103 | 1.30 × 103 | 1.61 × 103 | 919 | 634.67 | 599.26 | |
| F8 | Average | 0 | 0 | 47.2 | 1.51 × 10 | 101 | 55.45 | 151.45 |
| Std. | 0 | 0 | 10.3 | 1.16 × 10 | 19.00 | 19.27 | 36.32 | |
| F9 | Average | 4.44 × 10−16 | 7.07 × 10−13 | 0.042 | 0.046 | 1.23 | 2.93 | 2.500 |
| Std. | 0 | 6.12 × 10−12 | 0.21 | 0.012 | 0.7.7 | 0.65 | 1.392 | |
| F10 | Average | 0 | 0 | 4.50 × 10−3 | 4.13 × 10−3 | 0.563 | 0.234 | 0.0081 |
| Std. | 0 | 0 | 7.40 × 10−3 | 1.35 × 10−3 | 0.152 | 0.131 | 0.0060 | |
| F11 | Average | 4.91 × 10−28 | 7.54 × 10−27 | 0.011 | 4.24 × 10−4 | 2.38 | 7.28 | 7.401 |
| Std. | 2.48 × 10−28 | 8.51 × 10−25 | 0.021 | 2.67 × 10−4 | 2.42 | 2.80 | 4.512 | |
| F12 | Average | 8.66 × 10−28 | 2.21 × 10−25 | 0.40 | 2.08 × 10−3 | 0.066 | 21.31 | 2.897 |
| Std. | 1.92 × 10−28 | 3.51 × 10−24 | 0.54 | 9.62 × 10−4 | 0.043 | 16.99 | 0.643 |
Given that UFs have a distinct global optimum, the precision of their solutions is crucial. The comparisons made for the UFs by the studied optimizers are shown in Table 2. The best outcomes for all UFs can be found via GBAEF from Table 2. Overall, GBAEF offers the best final solutions for all UFs in terms of accuracy. These results from the competition show how effectively the UFs are exploited by GBAEF.
In addition, GBAEF appears to perform better than any of its rivals for functions F7–F12. This is due to the ability of the global search built into GBAEF that significantly increase the level of exploration. In contrast to its competitors, GBAEF is very competitive in exploring the solution space.
For the purpose of the statistical significance of two or more algorithms, it is necessary to do a non-parametric pairwise statistical analysis. To evaluate the relevant comparison between the suggested and alternative approaches, we followed the recommendation of Derrac et al. [37] and conducted a nonparametric Wilcoxon’s rank sum test on the collected outcomes. In this context, a pair-wise comparison is undertaken using the best outcomes achieved from the 30 runs of each approach. This statistical test provides three key outputs: the p-value, the sum of positive rankings (R+), and the total of negative ranks (R−). The results of the Wilcoxon’s rank sum test comparing GBAEF with other methods are presented in Table 3. The p-value represents the threshold of significance required to detect differences. In this investigation, the level of significance is set at p = 0.05. If the supplied algorithm’s p-value is greater than 0.05, then there is no discernible difference between the two methods being compared. The presence of “N.A” in the winner rows of Table 3 signifies this outcome. However, if the p-value is smaller than the predetermined significance level (α), it indicates with certainty that the superior outcome achieved by the top algorithm in each pairwise comparison is statistically significant and not a consequence of random chance. The acquired findings support the great advantage of GBAEF in the majority of cases, indicating that GBAEF consistently surpasses other comparison algorithms.
Table 3.
Results of Wilcoxon’s rank sum test.
| Benchmark | Wilcoxon test Parameters |
GBAEF vs AEFA | GBAEF vs PSO | GBAEF vs FA | GBAEF vs MVO | GBAEF vs SSA | GBAEF vs TSA |
|---|---|---|---|---|---|---|---|
| F1 |
p-value R+ R-Winner |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F2 |
p-value R+ R-Winner |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F3 |
p-value R+ R-Winner |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F4 |
p-value R+ R-Winner |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F5 |
p-value R+ R-Winner |
NAN 915 0 N.A |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F6 |
p-value R+ R-Winner |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
| F7 |
p-value R+ R-Winner |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
| F8 |
p-value R+ R-Winner |
NAN 915 0 N.A |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F9 |
p-value R+ R-Winner |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F10 |
p-value R+ R-Winner |
NAN 915 0 N.A |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
1.212 × 10−12 465 0 GBAEF |
| F11 |
p-value R+ R-Winner |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
| F12 |
p-value R+ R-Winner |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
3.019 × 10−11 465 0 GBAEF |
| Total | Superior/Inferior/N.A | 9/0/3 | 12/0/0 | 12/0/0 | 12/0/0 | 12/0/0 | 12/0/0 |
9. Datasets and pre-processing
In this work, a single historical data set for the slope is used to investigate the use of GBAEF-SVR model in the evaluation of slope stability and compare the outcome with other approaches. The data set includes 153 historical cases that were gathered from prior studies [[77], [78], [79], [80]]. Considering a prior investigation, the most important FOS-influencing parameters including slope angle (α), slope height (H), friction angle (φ), cohesion (c), unit weight (γ), and pore pressure ratio (ru), have been considered for this study. The value of FOS is the output parameter. The minimal and maximal values of the chosen input parameters are displayed in Table 4.
Table 4.
Statistical features of the parameters.
| Data | Parameter | Unit | Minimum | Maximum | Average | Standard deviation |
|---|---|---|---|---|---|---|
| Input | Unit Weight (γ) | kN/m3 | 12 | 31.3 | 21.54 | 4.35 |
| Cohesion (c) | kN/m2 | 0 | 300 | 34.66 | 48.29 | |
| Friction Angle (φ) | Degree | 0 | 45 | 28.92 | 10.56 | |
| Slope Angle (α) | Degree | 16 | 59 | 36.35 | 10.29 | |
| Slope Height (H) | m | 3.6 | 511 | 94.7 | 122.15 | |
| Pore pressure ratio (ru) | – | 0.0 | 0.5 | 0.216 | 0.158 | |
| Output | Factor of safety (FOS) | – | 0.625 | 2.31 | 1.3 | 0.374 |
Dimensions and units might regularly vary as a result of various input data. Normalization assists in accelerating model convergence while minimizing errors during training data. All data in this study are normalized in the range of zero to one using the Min-Max normalization procedure (Eq. (31)):
| (31) |
where X stands for the actual value, XR for the parameter’s normalized value, and Xmin and Xmax for the parameters' minimum and maximum values.
10. Models performance evaluation
In the experiment, 80% of the data is chosen at random to train the SVR model. In the meantime, 20% of the data is set aside for testing. The prediction model doesn’t know the slope condition of the testing data points. The testing data sets were employed to validate and assess the hybrid models when the model training was finished. As a result, testing data points serve as additional slope assessment tasks that must be evaluated and may be utilized to confirm the performance of the trained model.
10.1. SVR model evaluation
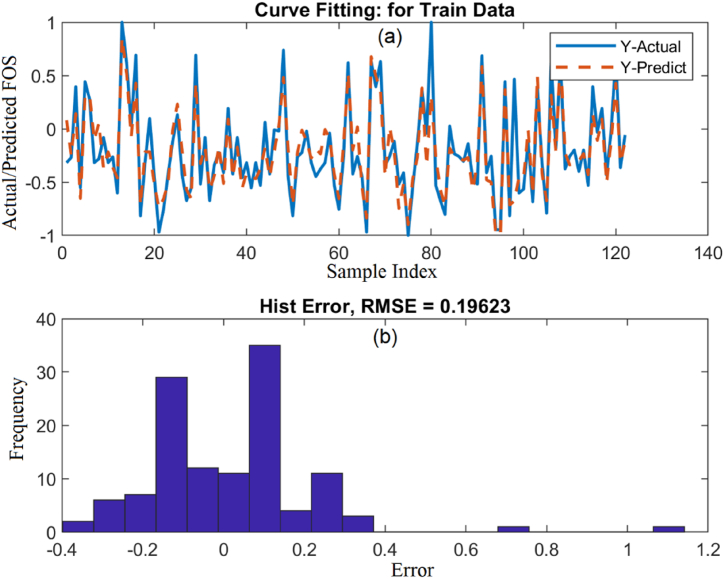
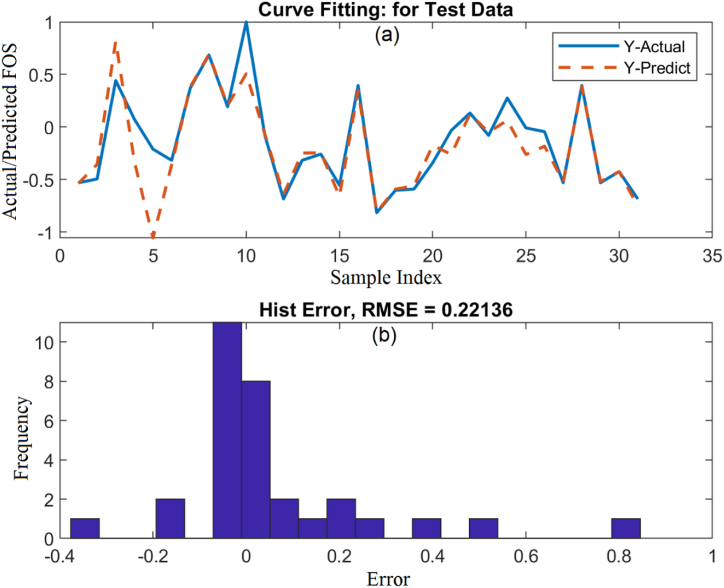
Without taking into account any method to optimize its hyper-parameters, the SVR model was run in the first stage. Fig. 3, Fig. 4 compares the estimated FOS values from the SVR model with the actual values for the training and testing data sets.
Fig. 3.
Predicted vs. measured FOS using SVR for training data; (a) Curve fitting, (b) Error histogram.
Fig. 4.
Predicted vs. measured FOS using SVR for testing data; (a) Curve fitting, (b) Error histogram.
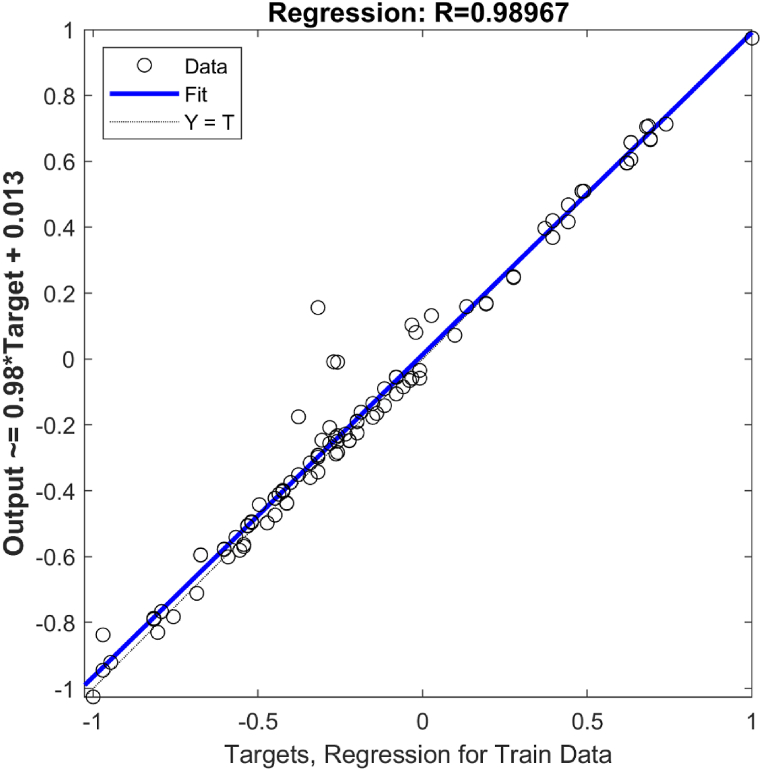
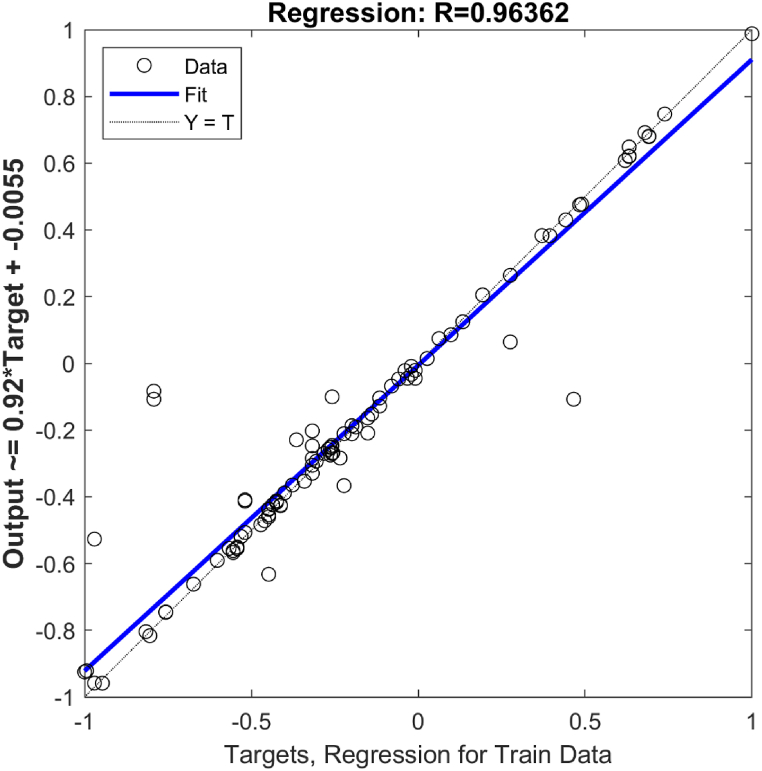
Fig. 3, Fig. 4 illustrates how well the forecast outcomes are for particular points and how well they match the measured ones. However, there are many situations where the variations between the observed values and predicted FOSs are considerable and not negligible. A comparison of FOSs estimated from the SVR with those achieved from the numerical simulation for training and testing data are depicted in Fig. 5, Fig. 6.
Fig. 5.
Coefficient of determination graph for observed and the predicted FOS during training of SVR model.
Fig. 6.
Coefficient of determination graph for observed and the predicted FOS during testing of SVR model.
10.2. Optimized-SVR models evaluation
The outcomes show that the SVR model’s FOS predictions are reasonable. However, we still require more precise predictions in order to confidently suggest it as a model for forecasting the FOS operation from new data. To achieve this, the SVR model’s hyper-parameters should be adjusted through employing effective optimization techniques. The proposed GBAEF and the usual AEFA optimization techniques are employed to this task in the next step. The SVR model is subsequently trained using these optimal values. The regularization parameter C, the RBF kernel parameter σ, and the error margin ɛ are the three most crucial hyper-parameters for the SVR model, as was previously indicated. The adapted parameters' values (C, σ, and ɛ) that produced the greatest accuracy were regarded as the best suitable parameter values. In this step, both AEFA and GBAEF are applied for evaluating the optimum value of these factors. Table 5 displays the best values of these parameters evaluated by each optimization approach.
Table 5.
SVR optimum parameter setting determined via AEFA and GBAEF.
| Optimum parameters | GBAEF | AEFA |
|---|---|---|
| regularization parameter C | 288.39 | 47.1828 |
| RBF kernel parameter σ | 1.835 | 1.7505 |
| error margin ɛ | 0.022 | 0.0121 |
| RMSE | 0.1024 | 0.1711 |
Fig. 7 shows the convergence procedure diagram of the AEFA and GBAEF performance. As it is appeared from this figure, the GBAEF could achieve a better convergence in a lower iteration. This figure also confirms the superior performance of the GBAEF.
Fig. 7.
Performance of the AEFA and GBAEF in training the SVR model.
For all data set throughout the training and testing phases, the values of the FOS estimated by the optimized SVR models by AEFA and GBAEF for training and testing data are compared with the actual values in Fig. 8, Fig. 9, Fig. 10, Fig. 11.
Fig. 8.
Predicted vs. measured FOS using GBAEF-SVR for training data; (a) Curve fitting, (b) Error histogram.
Fig. 9.
Predicted vs. measured FOS using GBAEF-SVR for testing data; (a) Curve fitting, (b) Error histogram.
Fig. 10.
Predicted vs. measured FOS using AEFA-SVR for training data; (a) Curve fitting, (b) Error histogram.
Fig. 11.
Predicted vs. measured FOS using AEFA-SVR for testing data; (a) Curve fitting, (b) Error histogram.
In addition, comparing the FOSs estimated from the both GBAEF-SVR and AEFA-SVR models with those consequents from the numerical analysis is represented in Fig. 12, Fig. 13, Fig. 14, Fig. 15. The outcomes show that the efficiency and effectiveness of the two models are comparable. However, it is apparent that the SVR combined with GBAEF could score higher than AEFA-SVR model, which is the proposed system in the factor of safety forecasting model.
Fig. 12.
Coefficient of determination graph for observed and the predicted FOS during training of GBAEF-SVR model.
Fig. 13.
Coefficient of determination graph for observed and the predicted FOS during testing of GBAEF-SVR model.
Fig. 14.
Coefficient of determination graph for observed and the predicted FOS during training and testing of AEFA-SVR model.
Fig. 15.
Coefficient of determination graph for observed and the predicted FOS during training and testing of AEFA-SVR model.
10.3. Prediction performance comparison with other ML approaches
To validate the efficacy and predicting performance of the suggested optimized model, the evaluation indices produced by the GBAEF-SVR model are compared with those obtained by the SVR and AEFA-SVR models, as well as those computed by the previously created models from the literature as discussed in the following.
Zeng et al [60] used three distinct optimization techniques, namely the trial and error (TE), whale optimization algorithm (WOA), and gravitational search algorithm (GSA), to adjust the control parameters of the LSSVM (least squares support vector machine) and applied the developed models for the FOS forecasting. Using particle swarm optimization, Rukhaiyar et al. [81] created an improved ANN for estimating the safety factor of earth slopes. Zhihao and Zhiwei [82] investigated the usage of BPNN (backpropagation neural network) and MARS (multivariate adaptive regression splines) for evaluating slope safety. It is worth noting that the networks in the above references were trained using the same data set.
Table 6 displays the outcomes of the statistical indices used to evaluate the developed models' predictions as well as those reported in the literature. The outcomes of Table 6 collectively show that, in terms of statistical assessment metrics as models’ effectiveness indices, it is obvious that the SVR optimized with GBAEF performs wonderfully in the disciplines of training and testing, with a maximum R2 of 0.9633 and 0.9242, respectively, which depicts the significant connection between observed and anticipated FOS.
Table 6.
Statistical evaluation metrics of different models.
| SVR Model | Data samples | RMSE | R2 | MSE | MAE |
|---|---|---|---|---|---|
| LSSVM-TE [60] | Training | 0.1206 | 0.9028 | - | - |
| Testing | 0.1345 | 0.9179 | - | - | |
| LSSVM-GSA [60] | Training | 0.0952 | 0.9364 | - | - |
| Testing | 0.1703 | 0.9028 | - | - | |
| LSSVM-WOA [60] | Training | 0.0608 | 0.9757 | - | - |
| Testing | 0.1412 | 0.9364 | - | - | |
| PSO-ANN [81] | Training | 0.11 | 0.96 | - | - |
| Testing | 0.21 | 0.87 | - | - | |
| MARS [82] | Overall data | – | 0.8629 | - | - |
| BPNN [82] | Overall data | – | 0.8931 | - | - |
| SVR | Training | 0.1962 | 0.8121 | 0.0385 | 0.1446 |
| Testing | 0.2678 | 0.6935 | 0.0717 | 0.1673 | |
| SVR-AEFA | Training | 0.1186 | 0.9276 | 0.0141 | 0.0424 |
| Testing | 0.2214 | 0.8581 | 0.049 | 0.1231 | |
| SVR-GBAEF | Training | 0.077 | 0.9633 | 0.0094 | 0.0272 |
| Testing | 0.164 | 0.9242 | 0.0233 | 0.0861 |
Furthermore, the findings produced by the GBAEF-SVR model are in excellent agreement with the results of the LSSVM-WOA model developed by Zeng et al. [60] and are significantly better than the findings generated by the other models in the literature.
Between the two developed models in the current study, the GBAEF-SVR model is more suitable than the AEFA-SVR by enhancing the R2 value from 0.9276 to 0.9633 for the train component and from 0.8581 to 0.9242 for the test section, with a 3.85% and 7.7% increase, respectively. By taking into account additional error indices such as MEA and RMSE (the lower value, the greater accuracy), it is reasonable to conclude that the SVR optimized through GBAEF outperforms the AEFA-SVR model.
For instance, for the RMSE index, GBAEF-SVR could gain 0.077 and 0.164 for the train and test sections, which are properly smaller than the AEFA-SVR model’s 0.1186 and 0.2214, respectively. By evaluating another index like MSE, the above descriptions also verified that good performance belonged to the GBAEF-SVR system. In contrast to the AEFA-SVR model, the GBAEF-SVR results are more precise, and it can be proposed as a reliable system for estimating the factor of safety.
10.4. Limitations
The SVR-GBAEF technique utilized in slope stability analysis exhibits certain shortcomings that necessitate more investigation in future research. In this study, the influence of external or triggering variables, such as earthquakes, rainfalls, and human actions, on slope stability is not considered because to the challenges associated with acquiring relevant data. Furthermore, a notable constraint of the SVR-GBAEF model is the very small size of the datasets used for modeling, with only 153 examples being included. To enhance the precision and dependability of the model, it is recommended to evaluate a more extensive dataset. In addition, as a metaheuristic, GBAEF has one major drawback: it is always possible that new optimization techniques will be created in the future that handle optimization applications more effectively.
11. Slope stability using the developed GBAEF-SVR model
This section tests the developed GBAEF-SVR model on a slope that has already been examined in the literature. The result is compared and displays the FOS value achieved using the suggested model as well as those noted in the literature. The slope utilized for the analysis was located in the Chamoli District of the Indian state of Uttrakhand and was taken from a study by Rukhaiyar et al. [81]. The geological profile of the slope is shown in Fig. 16. The slope has an average slope angle of 38° and is 170 m high. The unit weight of the slope material is 18 kN/m3. The slope material’s shear strength characteristics were determined to be cohesiveness at 100 kPa and internal friction at 32°. It has been considered that the in-situ pore water pressure coefficient is 0.15.
Fig. 16.
Slope geometry.
For this particular case, three distinct slope stability evaluations were used by Rukhaiyar et al. [81]. SLIDE V 6.0 [83], a commercial software offered by Rocscience Inc. Canada, was used to conduct the limit equilibrium study. The software has been used to determine the safety factors using the Bishops, Janbu, Spencer, and Morgenstern price methods. In addition, using the commercially available PHASE2V 8.004 [84] software from Rocscience Inc., Canada, a finite element analysis was carried out [81]. The FOS is defined in terms of the strength reduction factor (SRF) in finite element analysis. SRF is defined as the ratio of the slope’s initial shear strength parameters to the slope’s decreased strength parameter, which is the point at which the slope will fail. Finally, Rukhaiyar et al. [81] utilized the PSO-ANN, (ANN improved by PSO), for the analysis. The suggested GBAEF-SVR model has been used to analyze this problem. Table 7 displays the FOS of the slope computed using various techniques.
Table 7.
Factor of safety comparison for the case study.
| Analysis Method | Analysis Model | FOS | Refences |
|---|---|---|---|
| Limit Equilibrium Analysis | Bishops simplified | 1.29 | Rukhaiyar et al. [81] |
| Janbu Simplified | 1.23 | Rukhaiyar et al. [81] | |
| Spencer | 1.294 | Rukhaiyar et al. [81] | |
| Morgenstern price | 1.295 | Rukhaiyar et al. [81] | |
| Numerical Analysis | Finite Element Analysis | 1.17 | Rukhaiyar et al. [81] |
| Artificial Intelligence | PSO-ANN hybrid model | 1.421 | Rukhaiyar et al. [81] |
| GBAEF-SVR model | 1.316 | Present Study |
In Table 7, the value of FOS obtained by each method is presented. According to the results of this table, the minimum FOS can be evaluated by finite element analysis. However, the estimated FOS by the PSO-ANN is 1.421, which is greater as compared to investigations using limit equilibrium and numerical methods. As the findings demonstrate, when compared to the prior study, the predicted FOS using the proposed GBAEF-SVR is 1.316, which is almost 7% lower than that estimated by PSO-ANN and is much closer to the values of FOSs calculated with limit equilibrium techniques.
12. Conclusions
First, a new version of the artificial electric field algorithm (AEFA), known as the global-best artificial electric field algorithm (GBAEF), was suggested by this work. In addition, the proposed GBAEF algorithm was intended to precisely adjust the hyper-parameters of the SVR model (C, σ and ɛ). In the proposed GBAEF method, a new population will be generated randomly based on the global best particle found so far by the algorithm. The prior candidate solution will be dropped if the new candidate can enhance the objective function. The suggested method was initially applied to various benchmark problems, and the outcomes were compared with those of existing methods in order to demonstrate the efficacy of the proposed technique. When compared to the original AEFA, ABC, and ASO algorithms, the statistical outcomes of the test functions indicate that GBAEF demonstrated superior performance. In the following step, the factor of safety (FOS) of soil slopes is predicted using an optimized machine learning model called GBAEF-SVR. The model used a collection of 153 datasets with six input parameters and one target (FOS). According to the findings, the hyper-parameters of the SVR model can be tuned using a proposed optimization algorithm, which can significantly enhance the model’s prediction accuracy. Results from the hybrid model and the SVR-based manually optimized model were contrasted to show how the optimization strategies' effects on the SVR’s capacity for FOS prediction. Last but not least, application of the proposed model to a real-world case study of slope stability demonstrated that the GBAEF optimization technique can significantly improve SVR performance and the GBAEF-SVR model can be successfully applied to slope safety prediction.
CRediT authorship contribution statement
Mohammad Khajehzadeh: Writing - original draft, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Suraparb Keawsawasvong: Writing - review & editing, Writing - original draft, Visualization, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Conceptualization.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This study was supported by Thammasat Postdoctoral Fellowship.
References
- 1.Komadja G.C., Pradhan S.P., Roul A.R., Adebayo B., Habinshuti J.B., Glodji L.A., Onwualu A.P. Assessment of stability of a Himalayan road cut slope with varying degrees of weathering: a finite-element-model-based approach. Heliyon. 2020;6(11) doi: 10.1016/j.heliyon.2020.e05297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Renani H.R., Martin C.D. Factor of safety of strain-softening slopes. J. Rock Mech. Geotech. Eng. 2020;12(3):473–483. [Google Scholar]
- 3.Kang F., Xu B., Li J., Zhao S. Slope stability evaluation using Gaussian processes with various covariance functions. Appl. Soft Comput. 2017;60:387–396. [Google Scholar]
- 4.Azarafza M., Hajialilue Bonab M., Derakhshani R. A novel empirical classification method for weak rock slope stability analysis. Sci. Rep. 2022;12(1) doi: 10.1038/s41598-022-19246-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Griffiths D., Lane P. Slope stability analysis by finite elements. Geotechnique. 1999;49(3):387–403. [Google Scholar]
- 6.Abdalla J.A., Attom M.F., Hawileh R. Prediction of minimum factor of safety against slope failure in clayey soils using artificial neural network. Environ. Earth Sci. 2015;73:5463–5477. [Google Scholar]
- 7.Erzin Y., Cetin T. The prediction of the critical factor of safety of homogeneous finite slopes using neural networks and multiple regressions. Comput. Geosci. 2013;51:305–313. [Google Scholar]
- 8.Mao Y., Chen L., Nanehkaran Y.A., Azarafza M., Derakhshani R. Fuzzy-based intelligent model for rapid rock slope stability analysis using Qslope. Water. 2023;15(16):2949. [Google Scholar]
- 9.Wang H., Lei Z., Zhang X., Zhou B., Peng J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019;198 [Google Scholar]
- 10.Sheykhmousa M., Mahdianpari M., Ghanbari H., Mohammadimanesh F., Ghamisi P., Homayouni S. Support vector machine versus random forest for remote sensing image classification: a meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Obs. Rem. Sens. 2020;13:6308–6325. [Google Scholar]
- 11.Weerakody P.B., Wong K.W., Wang G., Ela W. A review of irregular time series data handling with gated recurrent neural networks. Neurocomputing. 2021;441:161–178. [Google Scholar]
- 12.Lindemann B., Maschler B., Sahlab N., Weyrich M. A survey on anomaly detection for technical systems using LSTM networks. Comput. Ind. 2021;131 [Google Scholar]
- 13.Antoniadis A., Lambert-Lacroix S., Poggi J.-M. Random forests for global sensitivity analysis: a selective review. Reliab. Eng. Syst. Saf. 2021;206 [Google Scholar]
- 14.Nanehkaran Y.A., Licai Z., Chengyong J., Chen J., Anwar S., Azarafza M., Derakhshani R. Comparative analysis for slope stability by using machine learning methods. Appl. Sci. 2023;13(3):1555. [Google Scholar]
- 15.Quan Q., Hao Z., Xifeng H., Jingchun L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2022:1–10. [Google Scholar]
- 16.Alade I.O., Abd Rahman M.A., Bagudu A., Abbas Z., Yaakob Y., Saleh T.A. Development of a predictive model for estimating the specific heat capacity of metallic oxides/ethylene glycol-based nanofluids using support vector regression. Heliyon. 2019;5(6) doi: 10.1016/j.heliyon.2019.e01882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dong Y., Zhang Z., Hong W.-C. A hybrid seasonal mechanism with a chaotic cuckoo search algorithm with a support vector regression model for electric load forecasting. Energies. 2018;11(4):1009. [Google Scholar]
- 18.Zhang Z., Hong W.-C. Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dynam. 2019;98:1107–1136. [Google Scholar]
- 19.Zhang Z., Hong W.-C. Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads. Knowl. Base Syst. 2021;228 [Google Scholar]
- 20.Wei W., Li X., Liu J., Zhou Y., Li L., Zhou J. Performance evaluation of hybrid WOA-SVR and HHO-SVR models with various kernels to predict factor of safety for circular failure slope. Appl. Sci. 2021;11(4):1922. [Google Scholar]
- 21.Zhang Z., Hong W.-C., Li J. Electric load forecasting by hybrid self-recurrent support vector regression model with variational mode decomposition and improved cuckoo search algorithm. IEEE Access. 2020;8:14642–14658. [Google Scholar]
- 22.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1(1):67–82. [Google Scholar]
- 23.Khajehzadeh M., Taha M.R., Eslami M. Multi-objective optimisation of retaining walls using hybrid adaptive gravitational search algorithm. Civ. Eng. Environ. Syst. 2014;31(3):229–242. [Google Scholar]
- 24.Eslami M., Shareef H., Mohamed A., Khajehzadeh M. IEEE; 2011. Optimal location of PSS using improved PSO with chaotic sequence; pp. 253–258. (International Conference on Electrical, Control and Computer Engineering 2011 (InECCE)). [Google Scholar]
- 25.Khajehzadeh M., Taha M.R., Eslami M. A new hybrid firefly algorithm for foundation optimization. Natl. Acad. Sci. Lett. 2013;36(3):279–288. [Google Scholar]
- 26.Mirjalili S., Gandomi A.H., Mirjalili S.Z., Saremi S., Faris H., Mirjalili S.M. Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems. Adv. Eng. Software. 2017;114:163–191. [Google Scholar]
- 27.Hegazy A.E., Makhlouf M., El-Tawel G.S. Improved salp swarm algorithm for feature selection. J. King Saud Univ.-Comput. Inf. Sci. 2020;32(3):335–344. [Google Scholar]
- 28.Khajehzadeh M., Iraji A., Majdi A., Keawsawasvong S., Nehdi M.L. Adaptive salp swarm algorithm for optimization of geotechnical structures. Appl. Sci. 2022;12(13):6749. [Google Scholar]
- 29.Li S., Wu L. An improved salp swarm algorithm for locating critical slip surface of slopes. Arabian J. Geosci. 2021;14(5):1–11. [Google Scholar]
- 30.Qais M.H., Hasanien H.M., Alghuwainem S. Enhanced salp swarm algorithm: application to variable speed wind generators. Eng. Appl. Artif. Intell. 2019;80:82–96. [Google Scholar]
- 31.Zhao X., Yang F., Han Y., Cui Y. An opposition-based chaotic salp swarm algorithm for global optimization. IEEE Access. 2020;8:36485–36501. [Google Scholar]
- 32.Heidari A.A., Mirjalili S., Faris H., Aljarah I., Mafarja M., Chen H. Harris hawks optimization: algorithm and applications. Future Generat. Comput. Syst. 2019;97:849–872. [Google Scholar]
- 33.Elgamal Z.M., Yasin N.B.M., Tubishat M., Alswaitti M., Mirjalili S. An improved harris hawks optimization algorithm with simulated annealing for feature selection in the medical field. IEEE Access. 2020;8:186638–186652. [Google Scholar]
- 34.Jiao S., Chong G., Huang C., Hu H., Wang M., Heidari A.A., Chen H., Zhao X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy. 2020;203 [Google Scholar]
- 35.Li C., Li J., Chen H., Jin M., Ren H. Enhanced Harris hawks optimization with multi-strategy for global optimization tasks. Expert Syst. Appl. 2021;185 [Google Scholar]
- 36.Fan Q., Chen Z., Xia Z. A novel quasi-reflected Harris hawks optimization algorithm for global optimization problems. Soft Comput. 2020;24:14825–14843. [Google Scholar]
- 37.Dhawale D., Kamboj V.K., Anand P. An improved Chaotic Harris Hawks Optimizer for solving numerical and engineering optimization problems. Eng. Comput. 2023;39(2):1183–1228. [Google Scholar]
- 38.Kaur S., Awasthi L.K., Sangal A., Dhiman G. Tunicate swarm algorithm: a new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020;90 [Google Scholar]
- 39.Houssein E.H., Helmy B.E.-D., Elngar A.A., Abdelminaam D.S., Shaban H. An improved tunicate swarm algorithm for global optimization and image segmentation. IEEE Access. 2021;9:56066–56092. [Google Scholar]
- 40.Arabali A., Khajehzadeh M., Keawsawasvong S., Mohammed A.H., Khan B. An adaptive tunicate swarm algorithm for optimization of Shallow foundation. IEEE Access. 2022;10:39204–39219. [Google Scholar]
- 41.Fetouh T., Elsayed A.M. Optimal control and operation of fully automated distribution networks using improved tunicate swarm intelligent algorithm. IEEE Access. 2020;8:129689–129708. [Google Scholar]
- 42.Li L.-L., Liu Z.-F., Tseng M.-L., Zheng S.-J., Lim M.K. Improved tunicate swarm algorithm: solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 2021;108 [Google Scholar]
- 43.Rizk-Allah R.M., Saleh O., Hagag E.A., Mousa A.A.A. Enhanced tunicate swarm algorithm for solving large-scale nonlinear optimization problems. Int. J. Comput. Intell. Syst. 2021;14(1):1–24. [Google Scholar]
- 44.Alsattar H.A., Zaidan A., Zaidan B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020;53:2237–2264. [Google Scholar]
- 45.Ramadan A., Kamel S., Hassan M.H., Khurshaid T., Rahmann C. An improved bald eagle search algorithm for parameter estimation of different photovoltaic models. Processes. 2021;9(7):1127. [Google Scholar]
- 46.Alsaidan I., Shaheen M.A., Hasanien H.M., Alaraj M., Alnafisah A.S. A PEMFC model optimization using the enhanced bald eagle algorithm. Ain Shams Eng. J. 2022;13(6) [Google Scholar]
- 47.Ferahtia S., Rezk H., Djerioui A., Houari A., Motahhir S., Zeghlache S. Modified bald eagle search algorithm for lithium-ion battery model parameters extraction. ISA Trans. 2023;134:357–379. doi: 10.1016/j.isatra.2022.08.025. [DOI] [PubMed] [Google Scholar]
- 48.Elsisi M., Essa M.E.-S.M. Improved bald eagle search algorithm with dimension learning-based hunting for autonomous vehicle including vision dynamics. Appl. Intell. 2023;53(10):11997–12014. [Google Scholar]
- 49.Chaoxi L., Lifang H., Songwei H., Bin H., Changzhou Y., Lingpan D. An improved bald eagle algorithm based on Tent map and Levy flight for color satellite image segmentation. Signal, Image Video Process. 2023;17(5):2005–2013. [Google Scholar]
- 50.Yadav A. AEFA: artificial electric field algorithm for global optimization. Swarm Evol. Comput. 2019;48:93–108. [Google Scholar]
- 51.Demirören A., Ekinci S., Hekimoğlu B., Izci D. Opposition-based artificial electric field algorithm and its application to FOPID controller design for unstable magnetic ball suspension system. Eng. Sci. Technol., Int. J. 2021;24(2):469–479. [Google Scholar]
- 52.Suman S., Khan S., Das S., Chand S. Slope stability analysis using artificial intelligence techniques. Nat. Hazards. 2016;84:727–748. [Google Scholar]
- 53.Gordan B., Jahed Armaghani D., Hajihassani M., Monjezi M. Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 2016;32(1):85–97. [Google Scholar]
- 54.Hoang N.-D., Pham A.-D. Hybrid artificial intelligence approach based on metaheuristic and machine learning for slope stability assessment: a multinational data analysis. Expert Syst. Appl. 2016;46:60–68. [Google Scholar]
- 55.Qi C., Tang X. Slope stability prediction using integrated metaheuristic and machine learning approaches: a comparative study. Comput. Ind. Eng. 2018;118:112–122. [Google Scholar]
- 56.Koopialipoor M., Jahed Armaghani D., Hedayat A., Marto A., Gordan B. Applying various hybrid intelligent systems to evaluate and predict slope stability under static and dynamic conditions. Soft Comput. 2019;23(14):5913–5929. [Google Scholar]
- 57.Gao W., Raftari M., Rashid A.S.A., Mu’azu M.A., Jusoh W.A.W. A predictive model based on an optimized ANN combined with ICA for predicting the stability of slopes. Eng. Comput. 2020;36(1):325–344. [Google Scholar]
- 58.Moayedi H., Osouli A., Nguyen H., Rashid A.S.A. A novel Harris hawks' optimization and k-fold cross-validation predicting slope stability. Eng. Comput. 2021;37(1):369–379. [Google Scholar]
- 59.Ahangari Nanehkaran Y., Pusatli T., Chengyong J., Chen J., Cemiloglu A., Azarafza M., Derakhshani R. Application of machine learning techniques for the estimation of the safety factor in slope stability analysis. Water. 2022;14(22):3743. [Google Scholar]
- 60.Zeng F., Nait Amar M., Mohammed A.S., Motahari M.R., Hasanipanah M. Improving the performance of LSSVM model in predicting the safety factor for circular failure slope through optimization algorithms. Eng. Comput. 2021:1–12. [Google Scholar]
- 61.Yang Y., Zhou W., Jiskani I.M., Lu X., Wang Z., Luan B. Slope stability prediction method based on intelligent optimization and machine learning algorithms. Sustainability. 2023;15(2):1169. [Google Scholar]
- 62.Vapnik V. Springer Science & Business Media; 1999. The Nature of Statistical Learning Theory. [Google Scholar]
- 63.Maity R., Bhagwat P.P., Bhatnagar A. Potential of support vector regression for prediction of monthly streamflow using endogenous property. Hydrol. Process.: Int. J. 2010;24(7):917–923. [Google Scholar]
- 64.Kang F., Li J., Dai J. Prediction of long-term temperature effect in structural health monitoring of concrete dams using support vector machines with Jaya optimizer and salp swarm algorithms. Adv. Eng. Software. 2019;131:60–76. [Google Scholar]
- 65.Bishop A.W. The use of the slip circle in the stability analysis of earth slopes. Geotechinque. 1955;5(1):7–17. [Google Scholar]
- 66.Janbu N. Publication of: Wiley (John) and Sons; Incorporated: 1973. Slope Stability Computations. [Google Scholar]
- 67.Spencer E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique. 1967;17(1):11–26. [Google Scholar]
- 68.Morgenstern N.R., Price V.E. The analysis of the stability of general slip surfaces. Geotechinque. 1965;15(1):79–93. [Google Scholar]
- 69.Fredlund D. vol. 3. 1981. The relationship between limit equilibrium slope stability methods; pp. 409–416. (10th. ICSMFE). [Google Scholar]
- 70.Duncan J.M., Wright S.G. The accuracy of equilibrium methods of slope stability analysis. Eng. Geol. 1980;16(1–2):5–17. [Google Scholar]
- 71.Duncan J.M. State of the art: limit equilibrium and finite-element analysis of slopes. J. Geotech. Eng. 1996;122(7):577–596. [Google Scholar]
- 72.Das B.M. Cengage learning; 2021. Principles of Geotechnical Engineering. [Google Scholar]
- 73.Nash D. A comparative review of limit equilibrium methods of stability analysis. Slope Stabil. 1981:11–76. [Google Scholar]
- 74.Kennedy J., Eberhart R. IEEE; Perth, WA, Australia: 1995. Particle swarm optimization; pp. 1942–1948. (Proceedings of ICNN'95-international Conference on Neural Networks). [Google Scholar]
- 75.Yang X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspired Comput. 2010;2(2):78–84. [Google Scholar]
- 76.Mirjalili S., Mirjalili S.M., Hatamlou A. Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016;27(2):495–513. [Google Scholar]
- 77.Sah N., Sheorey P., Upadhyaya L. Maximum likelihood estimation of slope stability. Int. J. Rock Mech. Min. Sci. Geomech. 1994:47–53. Elsevier. [Google Scholar]
- 78.Lu P., Rosenbaum M. Artificial neural networks and grey systems for the prediction of slope stability. Nat. Hazards. 2003;30:383–398. [Google Scholar]
- 79.Sakellariou M., Ferentinou M. A study of slope stability prediction using neural networks. Geotech. Geol. Eng. 2005;23(4):419–445. [Google Scholar]
- 80.Li J., Wang F. 2010. Study on the forecasting models of slope stability under data mining; pp. 765–776. (Earth and Space 2010: Engineering, Science, Construction, and Operations in Challenging Environments). [Google Scholar]
- 81.Rukhaiyar S., Alam M., Samadhiya N. A PSO-ANN hybrid model for predicting factor of safety of slope. Int. J. Geotech. Eng. 2018;12(6):556–566. [Google Scholar]
- 82.Liao Z., Liao Z. Slope stability evaluation using backpropagation neural networks and multivariate adaptive regression splines. Open Geosci. 2020;12(1):1263–1273. [Google Scholar]
- 83.SLIDE. v6.0 . Rocscience Inc.; Toronto, Canada: 2012. Program for Limit-Equilibrium Slope Stability Analysis. [Google Scholar]
- 84.Rocscience A. Geomechanics software and research, Rocscience INC; Toronto, Canada: 2012. 2D Finite Element Program for Calculating Stresses and Estimating Support Around the Underground Excavations. PHASE2 v8.004. [Google Scholar]