Interlimb transfer of visuomotor rotations: independence of direction and final position information

Abstract

Previous findings from our laboratory support the idea that the dominant arm is more proficient than the non-dominant arm in coordinating intersegmental dynamics for specifying trajectory direction and shape during multijoint reaching movements. We also showed that adaptation of right and left arms to novel visuomotor rotations was equivalent, suggesting that this process occurs upstream to processes that distinguish dominant and non-dominant arm performance. Because of this, we speculate that such visuomotor adaptations might transfer to subsequent performance during adaptation with the other arm. We now examine whether opposite arm training to novel visuomotor rotations transfers to affect adaptation using the right and left arms. Two subject groups, RL and LR, each comprising seven right-handed subjects, adapted to a 30° counterclockwise rotation in the visual display during a center-out reaching task performed in eight directions. Each group first adapted using either the right (RL) or left (LR) arm, followed by opposite arm adaptation. In order to assess transfer, we compared the same side arm movements (either right or left) following opposite arm adaptation to those performed prior to opposite arm adaptation. Our findings indicate unambiguous transfer of learning across the arms. Different features of movement transferred in different directions: Opposite arm training improved the initial direction of right arm movements under the rotated visual condition, whereas opposite arm training improved the final position accuracy, but not the direction of left arm movements. These findings confirm that transfer of training was not due to a general cognitive strategy, since such an effect should influence either hand equally. These findings support the hypothesis that each arm controller has access to information learned during opposite arm training. We suggest that each controller uses this information differently, depending on its proficiency for specifying particular features of movement. We discuss evidence that these two aspects of control are differentially mediated by the right and left cerebral hemispheres.

Introduction

The tendency for practice of a novel activity with one arm to affect subsequent performance with the other arm has previously been demonstrated for a number of tasks, such as finger tapping (Laszlo et al. 1970), keyboard pressing (Taylor and Heilman 1980), inverted and/or reversed writing (Parlow and Kinsbourne 1989, 1990; Latash 1999), figure drawing (Thut et al. 1996), ball catching (Morton et al. 2001), and reaching during Coriolis force perturbations (Dizio and Lackner 1995) or during visuomotor displacements (Elliott and Roy 1981; Imamizu and Shimojo 1995). However, the mechanisms underlying this transfer are not well understood. Intermanual transfer of motor adaptation is thought to reflect the sharing of specific learned information between left and right arm control systems, possibly through one of two alternative mechanisms: (1) the callosal access model: during initial training with one arm, a single memory, or engram, is stored in the dominant hemisphere regardless of the arm used. Thus, the dominant arm may benefit from the initial training with the non-dominant arm because the learned information is stored in the hemisphere that controls the dominant arm (Taylor and Heilman 1980). (2) The cross-activation model: during training with the dominant arm, a duplicate, but weaker, memory is stored in the non-dominant cerebral hemisphere. This information is then directly accessible to the non-dominant arm controller during subsequent movements (Parlow and Kinsbourne 1989).

Regardless of the mechanism underlying information transmission between left and right arm control systems, previous studies have indicated that the effect of opposite arm training on subsequent performance depends on whether the dominant or non-dominant arm is initially trained (Marzi et al. 1991). For example, Parlow and Kinsbourne (1989) showed that the non-dominant arm benefited more from opposite arm training than did the dominant arm for a reversed-inverted writing task. However, the opposite pattern has been shown to occur for a complex button press task (Taylor and Heilman 1980), whereas no asymmetry in the direction of bimanual transfer occurred for a visuomotor displacement task (Imamizu and Shimojo 1995). Still, other studies have indicated that individual elements of task performance can show opposite patterns of transfer across the arms. For example, Stoddard and Vaid (1996) showed that finger maze performance transferred better from the dominant to the non-dominant arm when the maze was either oriented the same for both arms, or was vertically reversed. In contrast, transfer was more effective from the non-dominant to the dominant arm when the orientation of the maze was horizontally reversed. Thut et al. (1996) showed, for a figure drawing task, that movement time transferred best from the dominant to the non-dominant arm, whereas spatial accuracy transferred best from the non-dominant to the dominant arm. These findings indicate that the pattern and direction of intermanual transfer depend on the specific elements of task performance employed during learning.

It is likely that specific control processes associated with a given task determine whether a performance variable will transfer across the limb control systems. This idea is strongly supported by the findings of Lackner and DiZio (Lackner and Dizio 1994, 1998; Dizio and Lackner 1995), who studied adaptation of reaching movements during Coriolis force perturbations applied by a rotating artificial gravity environment. Because this manipulation produces a velocity dependent force directed perpendicular to the moving hand, uncompensated perturbations produce curved hand-paths with a convexity directed away from the straight line to the target, as well as endpoint errors biased in the same direction as the convexity. Adaptation of movement endpoint and trajectory to such forces occurs independently, indicating separate control mechanisms for these two features of targeted reaching. Interestingly, following adaptation with the dominant arm, only endpoint information transferred to the non-dominant arm, which was reflected by straight movements to the wrong endpoints. Thus, specification and control of endpoint, but not the trajectory, transferred from the dominant to the non-dominant arm. Whereas this study did not directly assess transfer from non-dominant to dominant arms, the results indicate that selected elements of control transfer across the limb systems, while other elements do not.

Asymmetries in the direction of intermanual transfer of learning appear to be influenced by motor dominance, or handedness. Recent studies from our laboratory have suggested that the essential factor distinguishing dominant from non-dominant arm performance is the facility by which limb dynamics are controlled by the central nervous system (CNS). This dynamic dominance hypothesis emerged from studies demonstrating dominant arm advantages in controlling the effects of intersegmental dynamics during reaching movements (Sainburg and Kalakanis 2000; Sainburg 2002). Because specification of the trajectory of the hand is critically dependent on interjoint coordination and control of intersegmental dynamics (Sainburg et al. 1993, 1995, 1999), our findings suggested that the dominant arm controller is better adapted for trajectory control. We also showed that regardless of large deviations in the initial trajectory, the final positions of non-dominant arm movements were more accurate than those of the dominant arm. It is, thus, plausible that the non-dominant controller is better adapted for specification of final location. Indeed, a number of researchers have proposed independent mechanisms for controlling trajectory and final location (Hirayama et al. 1993; Dizio and Lackner 1995; Gottlieb 1996; Lackner and Dizio 1998; Sainburg et al. 1999). In light of these findings, it appears likely that the findings of DiZio and Lackner, indicating dominant to non-dominant transfer of final position information, result from specialization of the non-dominant arm controller for final position control. We now hypothesize that the pattern of intermanual transfer for a particular task variable is determined by the proficiency of the controller under question for specifying that variable. According to this hypothesis, we predict that trajectory, but not final position information, will transfer best from the non-dominant to the dominant arm. In contrast, we expect that final position information will transfer best from the dominant to the non-dominant arm.

The purpose of the current study is to examine the patterns of transfer of final position and trajectory information between the arms during a multidirectional reaching task, in which the visual display of the cursor has been rotated relative to the hand start position. We chose this task because this manipulation produces errors in both trajectory direction and final position, and because we have previously shown that adaptation to such a visuomotor rotation occurs with similar time course and extent for both left and right arms (Sainburg 2002). We, thus, expect that any observed asymmetries in transfer will be attributable to asymmetries in the connections mediating transfer, instead of asymmetries in the learning process itself.

Materials and methods

Subjects

Subjects were 14 neurologically intact right-handed adults (eight female, six male), aged from 18 to 36 years old. Only right-handers were recruited because left-handers do not represent a behaviorally (Oldfield 1971) or neurologically (Kim et al. 1993) homogeneous population, with regard to reaching coordination. Handedness was determined using the ten-item version of the Edinburgh inventory (Oldfield 1971). To ensure that subjects exhibited right-handedness, only subjects scoring a laterality quotient of 100 were selected. Subjects were recruited from the University community, and were paid for their participation. Informed consent was solicited prior to participation, which was approved by the Office of Regulatory Compliance of the Pennsylvania State University.

Experimental setup

Figure 1 illustrates the general experimental setup. Subjects sat facing a horizontally oriented projection screen, with either the right or left arm supported over a horizontal table top, positioned just below shoulder height (adjusted to subjects’ comfort), by a frictionless air jet system. A start circle, target, and cursor representing finger position were projected on a horizontal back-projection screen positioned above the arm. A mirror, positioned parallel and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the fingertip. Calibration of the display ensured that this projection was veridical. All joints distal to the elbow were immobilized using an adjustable brace. Position and orientation of each limb segment was sampled using the Flock of Birds (Ascension Technology) magnetic 6-df movement recording system. The maximum 3D position error that we measured during calibration of this system was 2.1 mm³. A single 6-df sensor was attached to each arm segment by a plastic splint. The digital data (103 Hz) from each sensor were transmitted to a Macintosh computer through separate serial ports, and were stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in Real Basic (Real Software Inc.), C, and Igor Pro (Wavemetric Inc.).

Fig. 1.

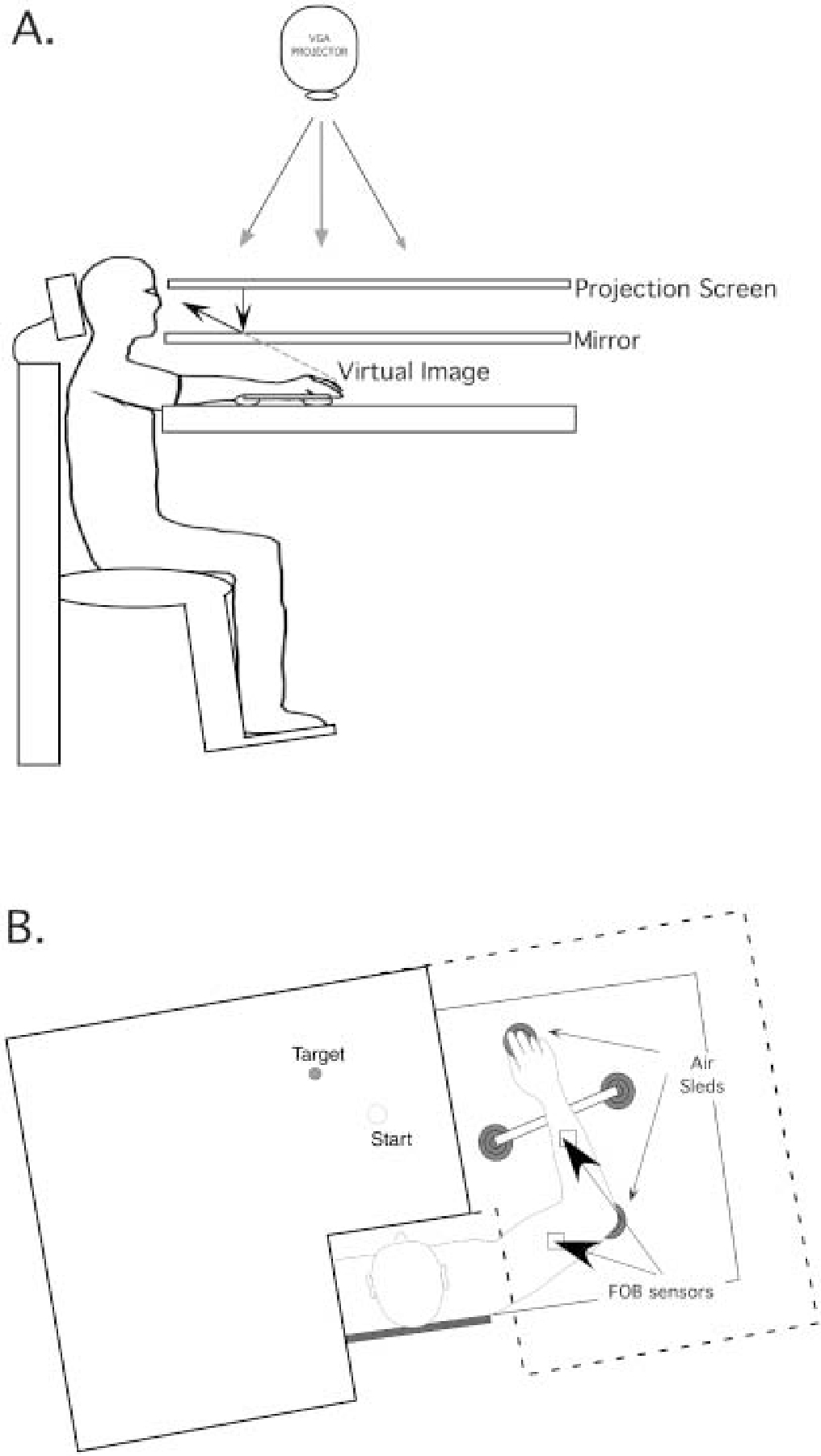
A Side view: subjects were seated in a dentist-type chair with the arm supported by an airjet system that removed the effects of friction on arm movement. Targets and the cursor representing finger position were backprojected on a screen placed above the arm. A mirror placed below this screen reflected the image, such that the projection was perceived in the plane of the arm. B Top view: the positions of the Flock of Birds sensors are shown

The position of the following three bony landmarks was digitized using a stylus that was rigidly attached to a Flock of Birds sensor: (1) index fingertip, (2) the lateral epicondyle of the humerus, and (3) the acromion, directly posterior to the acromioclavicular joint. A single 6-df sensor was attached to a rigid plastic forearm/hand splint, and to a rigid plastic upper arm cuff. The position of the bony landmarks, relative to the sensors attached to each arm segment, thus remained constant throughout the experimental session. As sensor data were received from the Flock of Birds, the position of these landmarks was computed by our custom software. The 2D position of the index fingertip was used to project a cursor onto the screen. This position was updated at 103 Hz, as data were received by the computer’s serial port. In order to examine the accuracy of this projection, the arm was viewed, along with the projected cursor, by illuminating the underside of the mirror (upon which the cursor was reflected). As predicted, the cursor remained centered on the index fingernail for all positions sampled on the workspace. Screen redrawing occurred fast enough to maintain the cursor centered on the fingertip during arm movements. During the experiment, the light was turned off, such that subjects were unable to view their arm.

Experimental task

Throughout the experiment, the index finger position was indicated by a screen cursor that was projected, in real time, as described above. Prior to movement, one of eight targets (15 cm long) arranged radially around the start position was displayed. Targets were presented in a pseudorandom sequence. Subjects were to bring the finger to a complete rest within the starting circle for 0.3 s. They were instructed to move the finger to the target using a single, uncorrected, rapid motion in response to an audiovisual “go” signal. At the end of each trial, knowledge of results was provided in the form of a display of the final location of index finger on the computer screen. Audiovisual feedback and points were awarded for accuracy for movements performed within a specified time window of 400–600 ms. Final position errors of less than 1 cm were awarded 10 points, while errors between 1 cm and 2 cm were awarded 3 points, and errors between 2 cm and 3 cm were awarded 1 point. Points were displayed following each trial.

Visual display modifications

In order to examine adaptation to novel visual-motor transformations, the position of the cursor, indicating index finger location, was rotated 30° counterclockwise relative to the start circle. This 30° rotation was chosen because we previously showed equivalent time course and extent of adaptation to this manipulation with dominant and non-dominant arms (Sainburg 2002).

Subject groups

The subjects were separated into two experimental groups (RL and LR) of seven subjects each. Each subject performed two experimental sessions, each session consisting of 2 blocks of 192 trials (24 trials to each of eight targets, presented in a pseudorandom sequence). Each 192-trial sequence comprised 24 cycles of movements. A single cycle was determined as a full series of movements to all eight of the targets. Each block of trials was separated by a 10-min break. Table 1 shows the sequence of the experimental blocks for each group. Both RL and LR groups performed the initial baseline session (B1 and B2) of trials with each hand without a visual rotation. This was done to ensure that subjects were adapted to the general features of the task with each hand, and to obtain baseline measures of performance. Following these two blocks of trials, subjects were exposed to the 30° counterclockwise rotation of the cursor position (R1 and R2). Subjects in the RL group first performed the exposure session with the right hand, followed by a session with the left hand. Subjects in the LR group first performed the exposure session with the left hand. Between-group comparisons were made between right-hand blocks performed by LR and RL groups. Similar between-group comparisons were made for left-hand blocks. Transfer of learning was assessed as the difference in performance between like-hand blocks performed by group LR and group RL.

Table 1.

Experimental design

Session	Baseline		Exposure
Block	B1	B2	R1	R2
Rotation	0°	0°	30°	30°
Group LR	Left	Right	Left	Right
Group RL	Right	Left	Right	Left

Kinematic data

The 3D positions of the index finger, elbow, and shoulder were calculated from sensor position and orientation data. Then, elbow and shoulder angles were calculated from these data. All kinematic data were low pass filtered at 12 Hz (3rd order, bidirectional, Butterworth) and differentiated to yield angular velocity and acceleration values.

Each trial usually started with the hand at zero velocity, but small oscillations of the hand sometimes occurred within the start circle. In this case, the onset of movement was defined by the last minimum (below 5% maximum tangential velocity) prior to the maximum in the index finger’s tangential velocity profile. Movement termination was defined as the first minimum (below 5% maximum tangential hand velocity) following the peak in tangential hand velocity.

Measures of task performance

Three measures of task performance were calculated from hand trajectory data: hand-path direction error at peak tangential hand acceleration (A_max), hand-path direction error at peak tangential hand velocity (V_max), and final position error. Hand-path direction error was calculated as the angular difference between the vector defined by the target and the vector defined by the hand-path position at movement start and the hand-path position at V_max or A_max. Final position error was calculated as the 2D distance between the index finger at movement termination and the location of the center of the target.

Data analysis and statistics

Each experimental session (a preexposure, or baseline, session and an exposure session) consisted of 2 blocks of 192 trials (24 cycles), 1 for each hand. In order to assess task adaptation under exposure session, each subject’s performance was quantified in the following way: First, for each hand, baseline performance was quantified as the mean direction error or final position error measure for the last eight cycles from the preexposure sequence. Second, to control for differences in baseline performance between arms, baseline measures were subtracted from all individual measures to yield “change from baseline” values. The last eight cycles of each exposure session were considered to represent final task adaptation. Thus, for each subject, a single final mean adaptation value for these eight cycles was calculated for each task performance measure.

A repeated-measures ANOVA was conducted with Group (RL, LR) as a between-group factor and Hand (R, L) and Target direction (eight directions) as within-group factors. In addition, because the purpose of this study was to compare performance between RL and LR groups, pairwise comparisons were conducted on all measures of task performance. Comparisons were made between left arm exposure trials from the RL group (Prior right arm exposure) and left arm performance from the LR groups (No prior exposure). Similarly, comparisons were made between right arm exposure trials from the LR group (Prior left arm exposure) and right arm performance from the RL group (No prior exposure). In order to assess transfer of learning, the first two cycles of each exposure session were averaged for each subject. Pairwise comparisons using Bonferroni/Dunn post hoc analyses were then conducted to test for significant differences between prior RL and LR group performance measures. In order to examine differences in the time course of adaptation between arms, measures from all the individual cycles of each exposure session were compared to the final mean adaptation values. The first cycle for which left and right arm performance was not significantly different from this final adaptation value was considered the “first adapted cycle.”

Results

According to the repeated-measures ANOVA, there was no significant interaction of Target with the other two factors for any parameter. Thus, the data were collapsed across eight targets and subjected to further analyses. Since the comparisons of main interest were between the same limbs of RL and LR groups, pairwise comparisons using Bonferroni/Dunn analyses are reported below.

Figure 2 shows typical hand-paths from two subjects, a subject from group RL, who first adapted to the visual rotation with the right arm, and a subject from group LR, who first adapted to the visual rotation with the left arm. Column 1 shows the last cycle of the preexposure block performed with either the right (top) or left (bottom) hand. Column 2 shows the baseline paths in gray, overlaid by hand paths from the first cycle of movement performed during initial exposure to the 30° visual rotation (dashed). As expected, these paths are initially directed roughly 30° counterclockwise to the target. Many trials show a late “hook” back toward the target at the end of motion, which likely reflects error corrections. The third column shows the effect of opposite arm adaptation on subsequent right (top) and left (bottom)-arm performance. The first cycle of right-arm trials (top: group LR, solid) following opposite arm adaptation are overlaid upon the trials from column 2 (top: group RL, dashed) for comparison. The effects of opposite arm adaptation are reflected by differences in accuracy between the solid and dashed paths in Fig. 2, column 3. As indicated by these examples, the right arm benefited substantially from opposite arm training, such that the initial direction at V_max of the first cycle of right arm movements was, on average, 5.5° less deviated following opposite arm training (P=0.004). The first cycle of left-hand trials (bottom: Group RL, solid) following opposite arm adaptation is shown in Fig. 2, column 3. Interestingly, opposite arm adaptation had no effect on left arm performance. This is indicated by the similarity of the solid hand paths (first cycle following opposite arm adaptation: RL group) and the dashed paths (first cycle of initial left-arm exposure: LR group). This indicates that the effects of opposite arm adaptation were not due to cognitive factors, because such factors would be expected to affect either hand equally. Interestingly, for the left hand, the “corrective” hooks at the end of movement become more accurate and consistent, following opposite arm training.

Fig. 2.

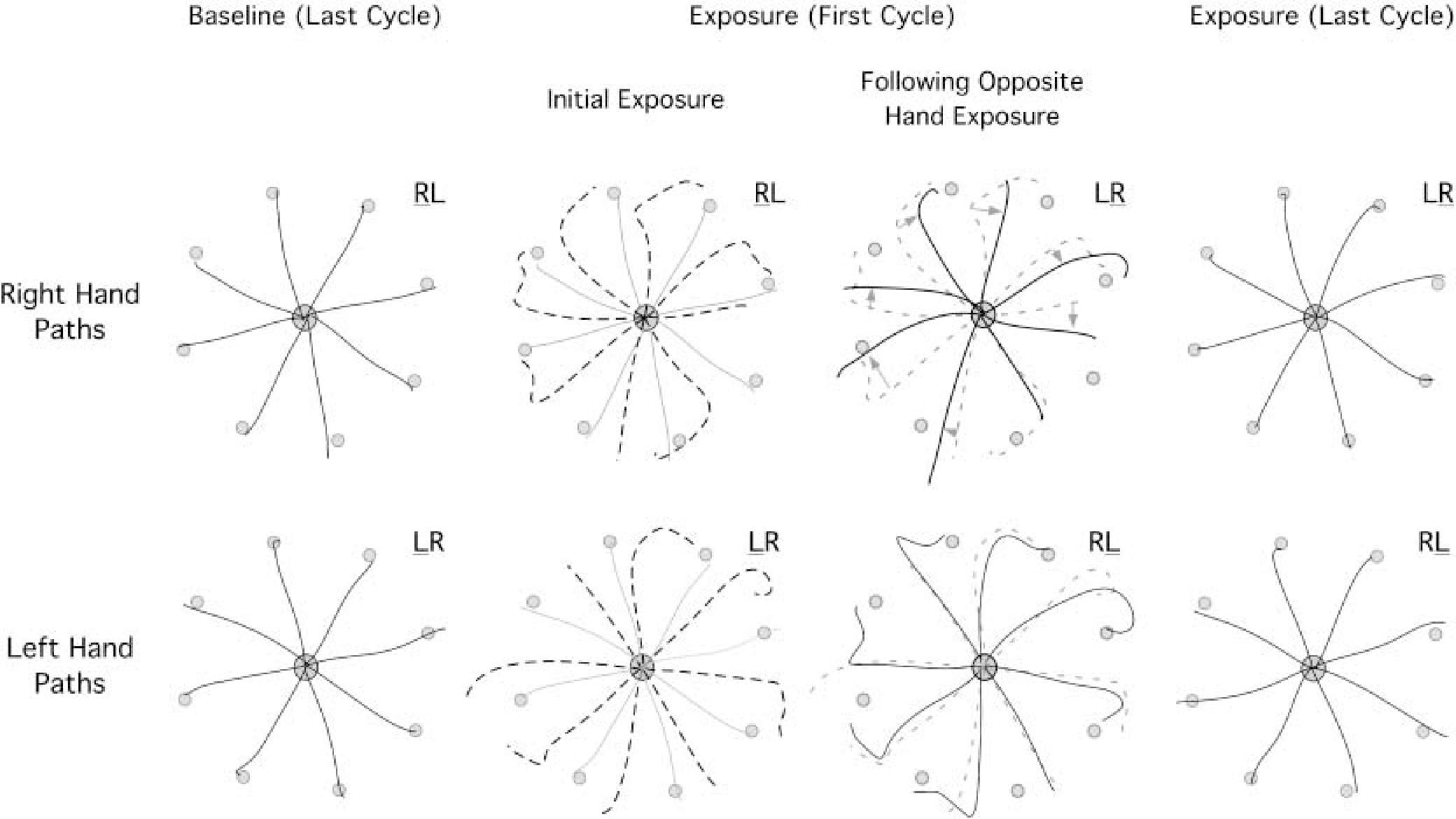
Representative hand-paths of a subject from the RL group are compared with those of a subject from the LR group to illustrate between group differences. Right-hand paths are shown along the top row, whereas left-hand paths are shown below. The first column shows the last cycle of movements performed during the preexposure session with the right arm (top) and the left arm (bottom). The second column shows the first cycle of movement performed under initial rotation exposure conditions with the right arm (top) and the left arm (bottom). These movements are shown as dashed lines, whereas the baseline movements from column 1 are shown as solid gray lines. The third column shows the first cycle of movements performed following opposite arm training for the right arm (top) and the left arm (bottom). These paths are shown as solid black lines, whereas the paths from column 2 are shown as dashed lines for comparison. The fourth column shows the last cycle of movements performed following opposite arm training for the right arm (top) and the left arm (bottom)

These effects of opposite arm adaptation on subsequent performance were reliable across all subjects. Figure 3 shows direction errors at peak tangential hand velocity (A) and at peak tangential hand acceleration (B), and final position errors (C) for left and right arm movements of the preexposure (left column) and exposure (right column) sessions. Data have been averaged across every 2 cycles of movement such that each point reflects 16 consecutive trials. The baseline value, taken as the average of the last eight cycles of movement from the preexposure session, were subtracted from each subject’s data to yield a change from baseline value (see “Materials and methods”). Each data point in Fig. 3 has been averaged across all seven subjects in each group. The arrows represent the first adapted cycle for left and right arm movements during the exposure session (see “Materials and methods”). Comparison of left-hand performance for RL and LR groups indicates that when initially exposed to the rotation, left arm movements are initially directed some 20° counterclockwise (RL: mean 14.8±1.4; LR mean 15.7±1.5 for direction error at V_max; RL: mean 20.3±2.4; LR mean 17.9±1.4 for direction error at A_max). Left arm improvement in performance following opposite arm training should be indicated by lower direction errors for RL data, as well as earlier adaptation, as reflected by the first adapted cycle (open arrow). Consistent with the examples shown in Fig. 2, opposite arm training did not influence the direction of the first cycles of left arm movements (A_max P=0.39; V_max P=0.66), nor did it improve the speed of adaptation, as reflected by the first adapted cycle. The fact that the path of the left hand was fairly straight until the end of motion is reflected by similar direction errors at V_max (bottom) and A_max (top).

Fig. 3.

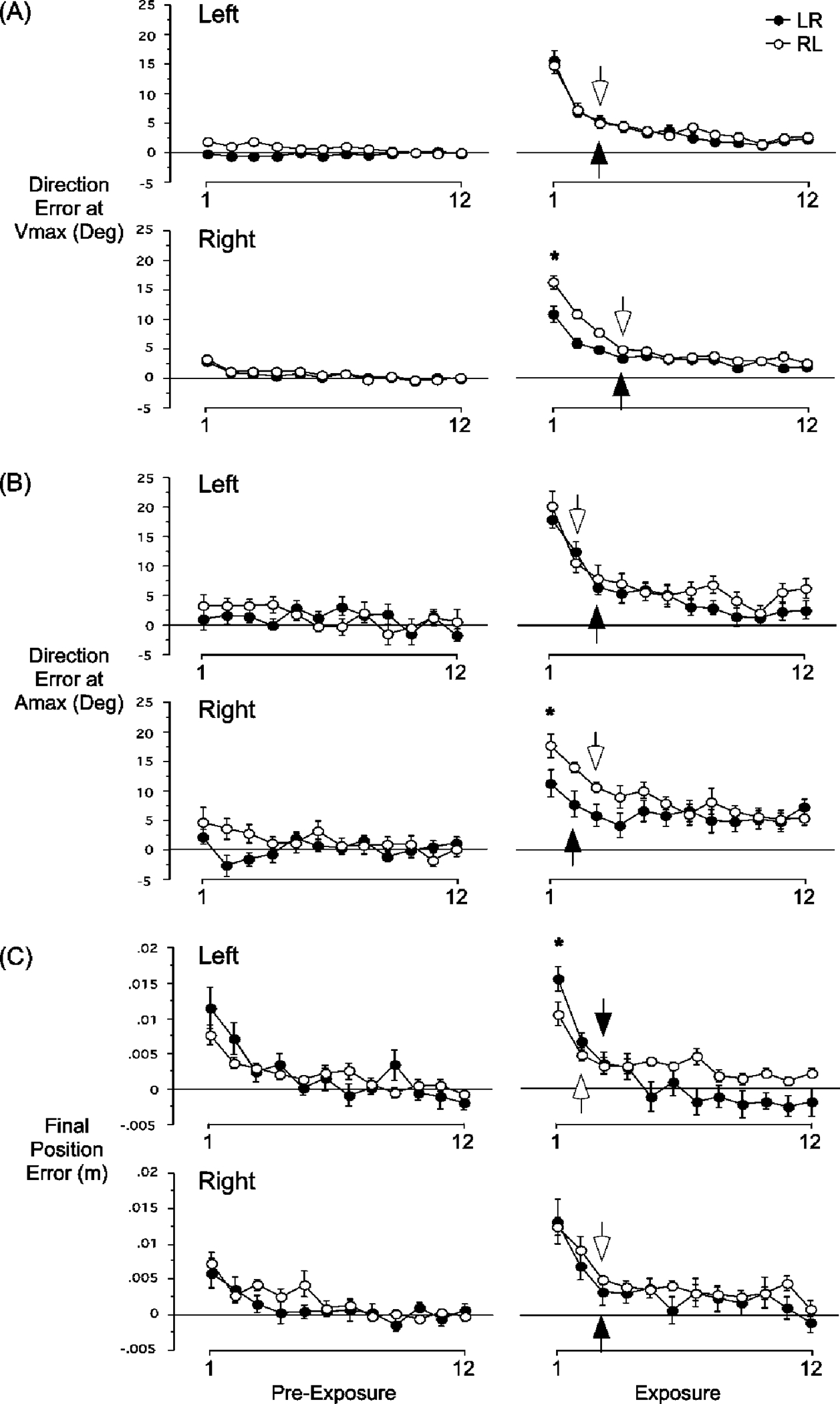
A–C Mean performance measures, direction error at V_max (top), direction error at A_max (middle) and final position error (bottom) are shown for left and right arms separately. Baseline performance, measured for each subject separately, has been subtracted from each value prior to computing the average across subjects. Thus, the performance measures shown represent a change from baseline performance. Every data point shown on the X-axis represents the average of two consecutive cycles across all subjects (mean ± SE). Performance measures for the LR group (filled circles) and RL group (open circles) are shown separately. Thus, differences in performance between groups represent the effects of opposite arm training. For example, the second row (right column) shows that following opposite arm training the direction error made with the right arm (LR group) is significantly smaller than that made with the right

Right arm improvement in performance following opposite arm training was substantial, as indicated by lower direction errors for LR data, as well as earlier adaptation, in terms of direction error at A_max, as reflected by the first adapted cycle (closed arrow). Consistent with the examples shown in Fig. 2, opposite arm training improved the initial direction of the first cycles of right arm movements (P=0.004 and 0.04 for direction error at V_max and A_max, respectively), such that these right arm movements (LR) were, on average, 5.5° and 6.5° (V_max and A_max, respectively) more accurate than movements made without opposite arm adaptation (RL). Therefore, the directional effects of opposite arm adaptation were substantial during the initial acceleration of right arm movements, and persisted throughout the movement, as reflected by substantial improvement in direction at V_max and A_max. The selective effects of opposite arm adaptation on the direction of right, but not left, arm movements suggests unidirectional communication between left and right arm controllers for this function.

Figure 3C shows the effects of opposite arm adaptation on final position errors for right and left arm movements. The effect of opposite arm adaptation on left arm movements is indicated by substantially lower final position errors for RL, as opposed to LR groups (P=0.04). This was exemplified by the more consistent and accurate “corrective” hooks at the end of motion displayed in Fig. 2, column 3. In addition, more rapid adaptation is indicated by an earlier first adapted cycle for RL groups (open arrow). In contrast, opposite arm adaptation had no effect on the final position accuracy of the initial cycles performed with the right arm (P=0.83). This is particularly interesting, since right arm movements, following opposite arm adaptation, were directed closer to the target from movement onset, as compared with right arm movements that did not follow opposite arm exposure. Therefore, the final position, but not the direction of left arm movements, was substantially improved by opposite arm training. In contrast, the direction, but not the final position, of right arm movements was substantially improved by opposite arm training.

Discussion

We tested whether opposite arm training to novel visuomotor rotations transfers to affect subsequent performance with the right and left arms. Two subject groups, each comprising seven right-handed subjects, adapted to a 30° rotation in the visual display. Group RL first adapted using the right arm, followed by left arm adaptation. Group LR first adapted using the left arm, followed by right arm adaptation. Comparisons were made between groups, such that the left arm movements of group RL (prior opposite arm adaptation) were compared with the left arm movements of group LR (No prior exposure), and vice versa. Our results indicate unambiguous transfer of learning across the arms. Interestingly, two aspects of task performance were differentially transferred. Following left arm adaptation, the direction of the very first movements made with the right arm were substantially more accurate than those movements made without the benefit of opposite arm adaptation. However, opposite arm training had no effect on the direction of left arm movements. This finding confirms that transfer of training was not due to a general cognitive strategy, since such an affect should influence either hand equally. In contrast to movement direction, final position accuracy transferred from right to left, but not from left to right arms. Thus, opposite arm adaptation substantially improved the final position accuracy of left arm movements, but had no effect on the final position accuracy of right arm movements. These findings support the hypothesis that each arm controller has access to information learned during opposite arm training. We suggest that each controller uses this information differently, depending on its unique proficiency for controlling specific features of movement.

Independent neural modules specify trajectory and final position

Previous findings from our laboratory support the idea that the dominant arm is more proficient in coordinating intersegmental dynamics for specifying the trajectory direction and shape, whereas the non-dominant arm is most effective at specifying final posture (Sainburg and Kalakanis 2000; Sainburg 2002). In those studies, dominant arm trajectory curvatures were made independent of the amplitude of the interaction torques that are transferred between the moving segments of the limb. In contrast, non-dominant hand path curvatures were enslaved to, and constrained by, these interactions. Dominant arm movements of comparable accuracy and speed were made with substantially lower muscle torque, indicating greater torque efficiency (Sainburg and Kalakanis 2000; Sainburg 2002). These results have since been supported by electromyographic evidence (Bagesteiro and Sainburg, in review), indicating that the dominant arm controller more effectively accounts for intersegmental dynamics in specifying neural commands to muscles. Based on these findings, we proposed the dynamic dominance hypothesis of handedness (Sainburg 2002), which states that the essential difference between dominant and non-dominant arm coordination is the facility governing control over limb dynamics. Furthermore, non-dominant arm proficiency in final position specification has repeatedly been demonstrated in our studies. Regardless of large deviations in initial hand path direction and curvature, all movements made by the left arm without visual feedback were either equally accurate to, or slightly more accurate than, those of the dominant arm (Sainburg and Kalakanis 2000; Sainburg 2002; Bagesteiro and Sainburg, in review).

Our current results support and extend previous reports indicating that two aspects of control, specification of initial movement direction and specification of final limb posture, are mediated by distinct neural modules (Hirayama et al. 1993; Gottlieb 1996). Hirayama demonstrated the plausibility of such control using a two-phase model to implement a simulation, in which movement was initiated through a forward dynamic controller (openlooped), while final position was achieved by increasing joint stiffness about an equilibrium posture (coactivation of antagonist muscles). Gottlieb (1996) elaborated a similar, three-element model, in which each component of control is differentially weighted depending on the current demands of the task. According to this model, initial trajectory features result from open-loop mechanisms (α), based on internal representations of task dynamics. The second element (λ) defines feedback-mediated control, largely affecting limb compliance. The third element (γ) describes active modulation of the feedback elements. If task dynamics are incompletely or incorrectly modeled by the controller, the effects of feedback can be amplified by way of the γ command, thereby increasing joint viscosity, as well as stiffness about a desired trajectory. This will reduce potential path deviations due to inaccurate predictions of impending mechanical interactions. In this particular case, control would mimic that described by the equilibrium point hypotheses, because joint torque will emerge largely as a function of the difference between the muscle lengths for the current and the desired limb positions (Bizzi et al. 1976, 1982; Polit and Bizzi 1979; Bizzi and Abend 1983; Feldman 1986; Bizzi 1987; Flash 1987). Under such conditions, the trajectory would be expected to deviate with task specific inertial dynamics, such as interaction torques. As the limb slows down and approaches the final position, the λ command becomes dominant, and feedback mediated increases in joint stiffness and viscosity substantially reduce potential path deviations and errors in final position. This type of mechanism is consistent with the behavior of the non-dominant arm in previous studies, which indicated that trajectory deviations, but not final position errors, varied with the magnitude of interaction torques (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg, in review).

Strong evidence for independent neural mechanisms governing specification of final position and trajectory features was provided by an elegant series of studies conducted by Lackner and DiZio (Lackner and Dizio 1994, 1998; Dizio and Lackner 1995). In these experiments, subjects reached toward targets while positioned at the center of a slowly rotating room. Subjects were not aware of the constant velocity rotation, as centripetal accelerations were minimized by positioning subjects at the room’s center of rotation. However, as they reached out from their bodies, substantial Coriolis forces acted perpendicular to the motion of the hand. When first encountered, these velocity dependent forces produced trajectory curvatures, with convexities directed away from the straight line to the target, and end position errors biased in the direction of these convexities. When subjects did not touch the table surface with their index finger at the end of motion, they adapted to the Coriolis forces by reducing trajectory curvatures, but did not adapt end point accuracies. When instructed to touch the surface with the index finger, they also adapted to final position. These findings support the idea that final position specification and trajectory specification are mediated by independent neural mechanisms. More importantly, these authors showed that following training with the dominant arm, transfer of learning was only apparent in the non-dominant arm final position accuracies, but not the trajectories. Their findings are consistent with the hypothesis that the non-dominant controller is specialized for control of final limb posture. Findings from our laboratory support this hypothesis and further indicate that the dominant arm controller is better adapted for control of trajectory direction (Sainburg and Kalakanis 2000; Sainburg 2002). Indeed, separate neural circuits may be required for each of these processes, due to the contradictory nature of each goal. For example, optimization of the final position of the hand during multijoint reaching would require subordination of hand trajectory features, such as direction, shape, and velocity.

Models of intermanual transfer of learning

Our findings indicate asymmetry in bimanual transfer of final position accuracy and initial movement direction. Opposite arm training substantially reduced final position errors during subsequent non-dominant arm movements, but had no effect on the trajectory direction of those movements. In contrast, opposite arm training reduced initial trajectory direction errors of dominant arm movements, but had no effect on final position accuracy. This is in agreement with our previous findings that the dominant arm is better adapted for trajectory control, whereas the non-dominant arm appears better adapted for final position control (Sainburg and Kalakanis 2000; Sainburg 2002). These findings are also consistent with a number of studies that have proposed independent mechanisms for controlling trajectory and final location (Hirayama et al. 1993; Dizio and Lackner 1995; Gottlieb 1996; Lackner and Dizio 1998; Sainburg et al. 1999). Our current findings provide further support for the hypothesis that the pattern of intermanual transfer for a particular task variable is determined by the proficiency of the controller employed, following initial learning, for specifying that aspect of performance.

It is plausible that this observed asymmetry in intermanual transfer occurred because, during initial training, the task was learned to a greater extent for one or the other arm (Taylor and Heilman 1980). As a result, more information is available to the contralateral controller for subsequent movements. If one controller learned the new transformation “better” or more “extensively” than the other arm, this should provide greater information during the course of intralimb adaptation, and thus lead to more rapid or more extensive adaptation for that arm. However, we previously showed that both arms adapt to visuomotor rotations with a similar time course and to similar extents (Sainburg 2002). Therefore, differences in the proficiency of initial learning are unlikely to have contributed to the observed asymmetries in transfer.

Instead, our findings modify and extend the “access model” of intermanual transfer proposed by Taylor and Heilman (1980), which states that during initial training a single memory, or engram, is stored in the dominant hemisphere regardless of the arm used. Thus, the information stored in the dominant hemisphere can subsequently be “accessed,” or read, by the non-dominant arm controller. According to this model, the dominant arm controller does not have access to the information stored during non-dominant arm learning. However, our findings on trajectory information transfer indicate that information stored during non-dominant arm training is subsequently accessed by the dominant arm controller. Thus, the current findings of transfer of final position information to the non-dominant arm and of trajectory information to the dominant arm lead to a “modified access model,” which proposes that information stored during learning with either arm controller can subsequently be accessed by its contralateral homologue. This modified access model further extends the previous model by proposing that the properties of the controller used following initial memory formation will determine the nature of the information transferred across the limb systems.

An alternative model of intermanual transfer has been proposed by Parlow and Kinsbourne (1989), which states that during initial learning with the dominant arm, a “copy” of the learned information is simultaneously stored in the non-dominant hemisphere. According to this “cross-activation model,” for certain tasks for which the dominant arm is more proficient, the information learned by the dominant arm is copied to the non-dominant hemisphere. This suggests that the elements of the tasks for which the dominant arm is most proficient will transfer. In other words, the information transferred depends on the proficiency of the controller used during initial learning. This idea predicts that initial training with the dominant arm should lead to improvements in trajectory control for subsequent non-dominant arm movements. Likewise, initial training with the nondominant arm should improve the final position accuracy of subsequent dominant arm movements. These predictions, however, are not supported by our current findings.

Hemispheric specialization for specification of trajectory versus final position

It is plausible that these two neural processes, control of final limb posture and specification of initial direction, are segregated to different hemispheres. Asymmetrical sensorimotor access of each arm to the underlying circuitry may, then, give rise to handedness. This idea suggests that both hemispheres are required for control of unilateral reaching movements with either arm. In fact, previous electrophysiological and neural imaging studies have revealed substantial activation of ipsilateral motor cortex during unimanual arm and finger movements (Kutas and Donchin 1974; Matsunami and Hamada 1981; Tanji et al. 1988; Macdonell et al. 1991; Kim et al. 1993; Kawashima et al. 1994, 1996, 1997, 1998; Salmelin et al. 1995; Gitelman et al. 1996; Urbano et al. 1996; Chen et al. 1997a, 1997b; Dassonville et al. 1997; Taniguchi et al. 1998; Viviani et al. 1998; Volkmann et al. 1998). Handedness has also been associated with morphological asymmetries in motor cortex, basal ganglia, and cerebellum (Kooistra and Heilman 1988; Snyder et al. 1995; Amunts et al. 1996). Thus, asymmetries in neural control are likely to be represented by both cortical and subcortical processes.

We now extend our dynamic dominance hypothesis to propose that dominant hemisphere mechanisms underlie specification of trajectory direction and shape, whereas non-dominant hemisphere mechanisms underlie specification of final limb position. The hypothesis that control of trajectory features and final posture are represented by different hemispheres is consistent with the recent findings of Boulinguez et al. (2001). These authors reported asymmetrical reaction time differences for dominant and non-dominant limb adaptations to changing the location of a target following movement initiation. The non-dominant arm was quicker to respond to changes in distance, whereas the dominant arm was quicker to respond to modifications in direction. In addition, Winstein and Pohl (1995) showed differential effects of right and left hemisphere lesions on the initial and final phases of reciprocal aimed movements. These authors assessed the contributions of right and left hemispheres to unilateral arm movement by studying the effects of unilateral brain damage on movement of the non-effected arm, ipsilateral to the brain lesion. Lesions in the hemisphere contralateral to the non-dominant arm caused prolongation of the deceleration phase of reciprocal movements made “as quick as possible.” By contrast, lesions of the hemisphere contralateral to the dominant arm caused prolongation of the acceleration phase of such movements. The authors proposed that sensory corrections (closed-loop mechanisms) are mediated by the right, or non-dominant, hemisphere, whereas programming the “ballistic” component of movements (open-loop mechanisms) is mediated by the left, or dominant hemisphere. This distinction is consistent with our findings, indicating a dominant arm advantage for trajectory specification and a non-dominant arm advantage for final position specification. We have previously shown that the former is based largely on feedforward (open-loop) mechanisms, whereas the latter is largely dependent on feedback mediated events (closed-loop) (Sainburg et al. 1999). Our current findings, therefore, both support and extend those of Winstein and Pohl, suggesting that the distinction between left and right hemisphere control is best described as trajectory specification, and final position control.