The symmetry of interlimb transfer depends on workspace locations

Abstract

We have previously shown that when both arms learn visuo-motor tasks within the shared midline workspace, transfer becomes asymmetrical: initial direction information only transfers from the nondominant to the dominant arm, whereas the final position information only transfers from the dominant to the nondominant arm. We now examine whether symmetry of interlimb transfer depends on the location of workspace provided for the two arms, by investigating the pattern of interlimb transfer when each arm adapts to a 30° rotation at its ipsilateral workspace. All subjects performed center-out reaching movements while adapting to a 30° rotation in the visual display. Half the subjects performed with the nondominant arm first and then the dominant arm, while the other half performed with the dominant arm first and then the nondominant arm. To assess transfer, naïve performance and the performance following opposite arm adaptation were compared for each arm separately. Our results indicate unambiguous transfer that is symmetrical: both arms benefited from opposite arm training in terms of initial direction control. In terms of final position information, neither arm benefited from opposite arm training. This clearly demonstrates that symmetry of interlimb transfer depends on the location of workspace provided for the two arms. Our findings suggest that when visuo-motor tasks are performed within a shared midline workspace, the nondominant controller is selectively inhibited from access to dominant controller information, due to a certain competition between the two limb/hemisphere systems that is introduced by the shared nature of the workspace.

Introduction

When an individual learns a novel motor task with one arm, this learning often generalizes to improve subsequent performance with the other arm. Numerous tasks have been employed to investigate interlimb transfer of motor learning, such as finger tapping, adaptation to prisms, keyboard pressing, inverted and/or reversed writing, figure drawing, ball catching, object grasping, and reaching during visuo-motor or dynamic perturbations. The majority of these studies have reported asymmetrical transfer (e.g., Laszlo et al. 1970; Hicks 1975; Taylor and Heilman 1980; Parlow and Kinsbourne 1989; Marzi et al. 1991; Halsband 1992; Dizio and Lackner 1995; Thut et al. 1996; Sainburg and Wang 2002; Criscimagna-Hemminger et al. 2003; Malfait and Ostry 2004; Wang and Sainburg 2004a, b), such that the transfer of information obtained during initial training is greater in one direction than in the other.

Previous studies indicate that asymmetry in interlimb transfer can depend on a variety of factors, such as the sequence of the arms in learning the task (nondominant arm first or dominant arm first), movement parameters being examined (e.g., direction error or final position error), and the nature of transformations underlying the process of learning (e.g., visuo-motor or dynamic transformations). For example, when a group of right handers used their nondominant arm first to adapt to a 30° rotation of visual display during center-out reaching movements, they benefited from this initial training to facilitate subsequent performance with the dominant arm only in terms of initial directional accuracy (Sainburg and Wang 2002; Wang and Sainburg 2004a). When the dominant arm was used first, however, opposite arm adaptation only improved the final position accuracy of subsequent performance with the nondominant arm. With regard to the nature of transformations underlying the process of adaptation, the direction of transfer changes depending on whether the adaptation involved visuo-motor or dynamic transformations. It has been repeatedly demonstrated that transfer in directional accuracy only occurs from the dominant to nondominant arm when subjects adapt to dynamic transformations dealing with Coriolis forces, velocity-dependent force fields, or acceleration-dependent force fields (Dizio and Lackner 1995; Cricimagna-Hemminger et al. 2003; Wang and Sainburg 2004b).

Although the patterns of transfer seem to be robust across studies, it is uncertain why transfer between the arms occurs asymmetrically. Asymmetrical transfer has been explained in the context of two hypotheses: (1) learning is asymmetrical because one arm/hemisphere system is superior to the other in learning certain tasks. (2) Once learning occurs, the access of each arm controller to the memory resources is asymmetrical. The first hypothesis is consistent with the proficiency model (Laszlo et al. 1970; also see Parlow and Kinsbourne 1989), which postulates that the dominant controller is superior to its counter-part in learning the tasks, thus resulting in better transfer from the dominant to nondominant arm. The second hypothesis is in accord with the callosal access model (Taylor and Heilman 1980), which suggests that the information obtained by either arm is always stored in the dominant brain hemisphere, thus the dominant arm controller has better access to the stored information than the nondominant controller. Unfortunately, these models are inadequate in explaining the findings in the literature that interlimb transfer of visuo-motor adaptations can occur asymmetrically even when both arms learn the task to the same extent and at the same rate (Sainburg 2002; Sainburg and Wang 2002). In addition, these models cannot explain the mixed findings in the literature, in terms of direction of transfer, because both models predict transfer in only one direction.

Alternatively, it is plausible that asymmetrical transfer occurs due to a competition between the two hemispheres for task performance. According to this idea, features of tasks for which one limb/hemisphere system is specialized should transfer only to that system when a competition exists. Thus, following opposite arm adaptation to visuo-motor rotations, for example, only the information regarding trajectory direction transfers to the dominant arm, while only that regarding final position accuracy transfers to the nondominant arm. This is consistent with our findings that the dominant system appears specialized for controlling trajectory dynamics, and the nondominant system for controlling final position (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg 2002; Sainburg 2002; Sainburg and Wang 2002; Wang and Sainburg 2003, 2004a, b). We propose that both limbs have symmetrical access to the learned information, but when a competition between the two hemispheres occurs, each system is selectively inhibited from utilizing the information for which the other system is specialized, resulting in asymmetrical transfer. This idea is in agreement with the findings of Gazzaniga and colleagues (Holtzman and Gazzaniga 1982; Franz et al. 1996) that cognitive and motor processes can compete against one another when two incompatible sets of information are concurrently processed.

Based on this idea, we now hypothesize that symmetry of interlimb transfer depends on the location of workspace provided for the two arms in visuo-motor adaptation. We investigated the pattern of interlimb transfer when each arm adapted to a 30° rotation at its ipsilateral workspace. We assumed that adapting to this visuo-motor task with both arms at a shared workspace would cause a competition between the two limb/hemisphere systems whereas doing so at a separate workspace for each arm would not. We, thus, predict that the pattern of interlimb transfer following visuo-motor adaptation, which is asymmetrical (i.e., transfer only occurs in one direction) when task space is shared in midline (Sainburg and Wang 2002), will become symmetric (i.e., transfer occurs in both directions) when each arm adapts to the task in a separate, and lateral, workspace. By symmetry, we do not mean that the amount of transfer will necessarily be identical, but rather mean that a substantial amount of transfer will occur in both directions.

Materials and methods

Subjects

Subjects were 12 neurologically intact right-handed adults (six female and six male), aged from 18 to 30 years old. Subjects were recruited from the university community, and were paid for their participation. Informed consent was solicited prior to participation. Right handedness was assessed using the ten-item version of the Edinburgh inventory (Oldfield 1971).

Apparatus

Subjects sat facing a table with either the right arm or the left arm supported over a horizontal surface, positioned just below shoulder height, by a friction-less air jet system (Fig. 1a). A start circle, target, and cursor representing the index finger position were projected on a horizontal back-projection screen positioned above the arm (Fig. 1b). A mirror, positioned parallel and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the fingertip. Calibration of the display ensured that this projection was veridical. Position and orientation of each limb segment was sampled at 103 Hz using the Flock of Birds^® (Ascension-Technology, Burlington, VT, USA) magnetic 6-DOF movement recording system. The position of the following three bony landmarks was digitized using a stylus rigidly attached to a FOB sensor: (1) index finger tip, (2) the lateral epicondyle of the humerus, and (3) the acromion, directly posterior to the acromio-clavicular joint. This sensor was then attached to a rigid upper arm cuff. Another FOB sensor was attached to a rigid forearm support. Thus, the position of the body landmarks relative to these sensors remained constant throughout the experiment, and these positions were computed by our custom software as sensor data was received from the Flock of Birds. For more detailed information, see Sainburg and Wang (2002).

Fig. 1.

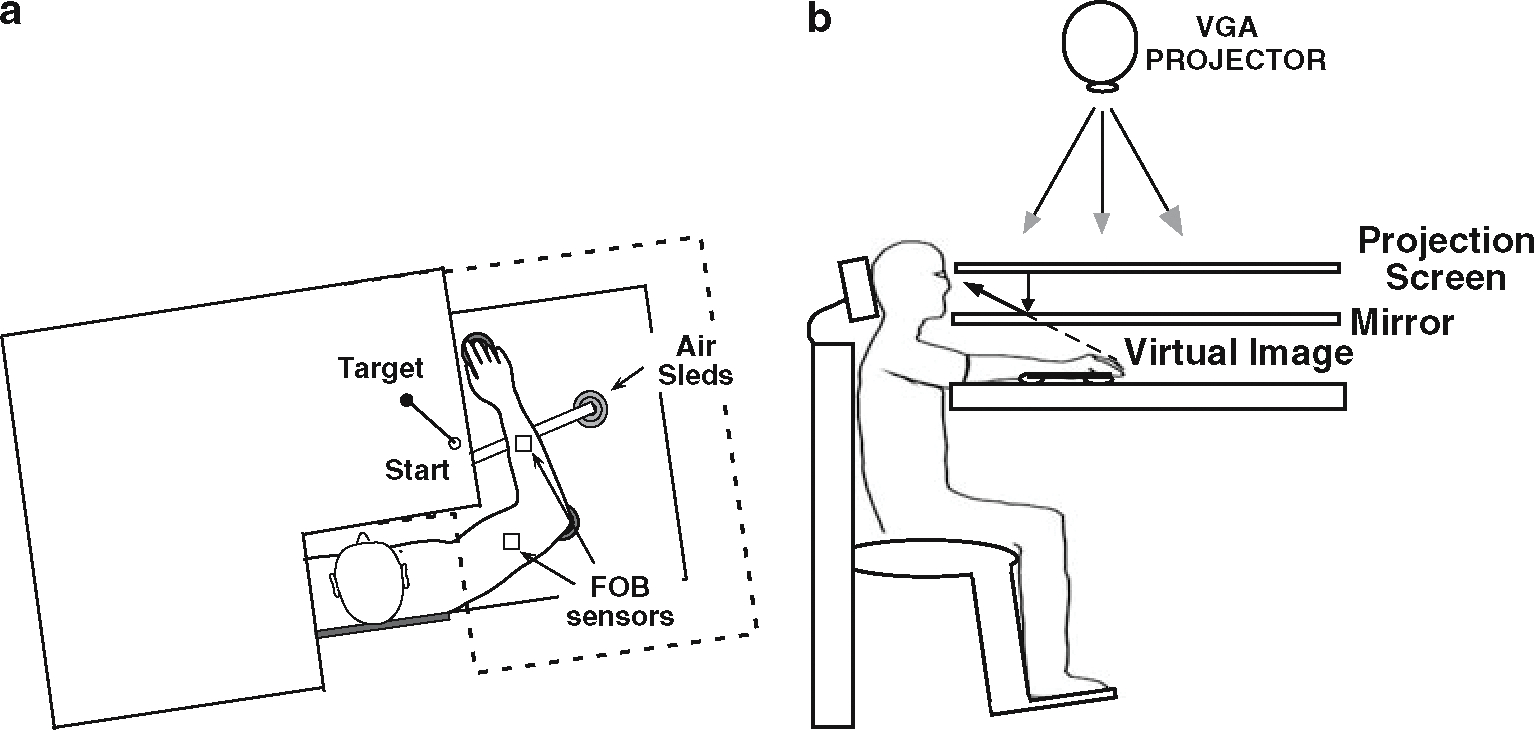
Experimental setup. a Top view: the positions of the Flock of Birds sensors are shown. b Side view: subjects were seated in a dentist-type chair with the arm supported by an air jet system that removed the effects of friction on arm movement. Targets and the cursor representing finger position were back-projected on a screen placed above the arm. A mirror placed below this screen reflected the image, such that the projection was perceived in the plane of the arm

Experimental design

In general, the experimental design of the current study is identical to that of our previous study (Sainburg and Wang 2002), except that the location of workspace for each arm is now separated in this study. As illustrated in Fig. 2, the starting circle and targets were presented in midline in our previous study, such that the two arms shared the task-space while adapting to visuo-motor rotations. In the current study, the starting circle and targets were presented 45 cm laterally from midline, such that each arm performed the task on its ipsilateral workspace from midline.

Fig. 2.

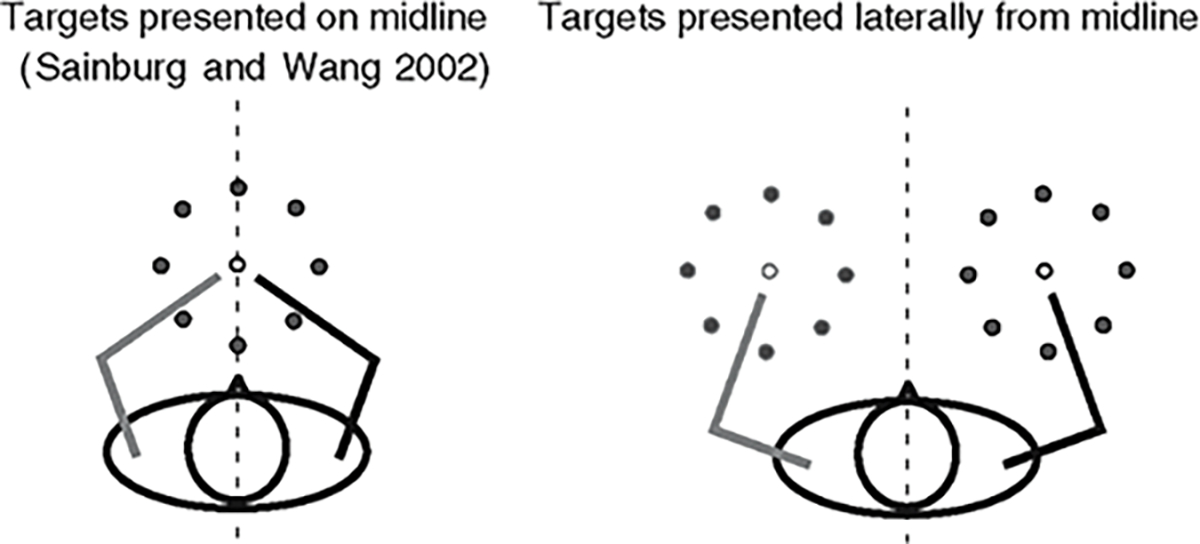
Target locations. Target was randomly displayed on one of the eight target locations in the midline workspace in our previous study (left), and laterally from the midline in the current study (right)

Prior to movement, one of eight targets (2 cm in diameter; 13 cm away from the starting position), presented in a pseudorandom sequence, was displayed on the horizontal tabletop. Subjects were asked to move the finger from the starting circle (1.5 cm in diameter) to the target using a single, rapid motion in response to an auditory ‘go’ signal. During the movement, visual feedback was provided by a screen cursor. At the end of each trial, knowledge of results was provided in the form of a circle indicating the final location of the index finger tip, and by points awarded for spatial accuracy (2D distance between the target and the final finger position): one point for accuracy <4 cm, three points for accuracy <2 cm, and ten points for accuracy <1 cm. No points were given for movements that took longer than 400 ms. In order to examine adaptation to visuo-motor rotations, the position of the cursor was rotated 30° counterclockwise (CCW) relative to the start circle. Table 1 shows the sequence of the experimental sessions and blocks for each subject group. The experiment consisted of two sessions: baseline (no visual rotation) and exposure (visual rotation) sessions. Subjects performed two blocks of trials in each session: one block with each arm. Half the subjects performed with the left arm first and then the right arm (group LR), while the other half performed with the right arm first and then the left arm (group RL). Each block comprised 192 trials, divided into 24 cycles, with each cycle containing all eight of the targets consecutively. Each block of trials was separated by a 10-minute break. Subjects were not informed about the CCW rotation provided during the exposure session.

Table 1.

Experimental design

Session		Baseline (no rotation)		Exposure (30° CCW rotation)
Block	LR (n=6)	L (NP)	R (OAA)	L (NP)	R (OAA)
	RL (n=6)	R (NP)	L (OAA)	R (NP)	L (OAA)
Trial/Cycle/Epoch		192/24/12	192/24/12	192/24/12	192/24/12

NP naїve performance, OAA performance following opposite arm adaptation

Data analysis

Three measures of performance were calculated: hand-path direction error at peak tangential arm velocity (V_max) and at peak tangential arm acceleration (A_max), and final position error. Direction errors were calculated as the angular difference between the vectors defined by the target and by the hand-path position at movement start and at V_max or A_max. Final position error was calculated as the 2D distance between the index finger at movement termination and the center of the target.

A repeated-measures ANOVA was conducted with group (LR and RL) as a between-subject factor, and cycle as a within-subject factor, for each arm separately. This was done for the two arms separately because the comparison between the arms was not of interest in this study. Because the purpose of this study was to examine the effect of initial training with one arm on subsequent performance with the other arm, we were more interested in post hoc pair-wise comparisons using Tukey tests, which were made between naïve performance and performance following opposite arm adaptation for the dominant arm blocks (right arm performances by LR and RL groups), as well as for the nondominant arm blocks (left arm performances by LR and RL groups). This effect of opposite arm adaptation was assessed for the first epoch (mean of cycles 1 and 2) and for the last epoch (mean of cycles 23 and 24) only, in order to examine initial information transfer and the extent of final adaptation, respectively. Between these two epochs, the pair-wise comparisons at the first epoch were of primary interest, because previous studies frequently showed substantial effects of initial training on the very first trials of the subsequent testing session (Krakauer et al. 1999; Sainburg and Wang 2002; Tong et al. 2002; Wigmore et al. 2002; Wang and Sainburg 2003, 2004a, b).

To compare the learning curves of the two arms, a line of approximation was constructed for each arm by finding a nonlinear logarithmic regression line. The slope and the intercept for this regression equation were obtained from each subject for each arm, and they were subjected to an independent t-test, as a post hoc test, to make a direct comparison between the dominant and nondominant arms (dominant naïve versus nondominant naïve performances, dominant versus nondominant performances following opposite arm adaptation). Alpha level was always 0.05 for both repeated measures ANOVA’s and post hoc tests.

Results

Figure 3 shows typical hand-paths of representative subjects during the final phase of the baseline session, and during the initial and final phases of the adaptation session. Naïve performance (gray lines) and performance following opposite arm adaptation (black lines) are illustrated for each arm separately, and differences in accuracy between these two sets of hand-paths represent the effect of opposite arm adaptation. On initial exposure to the visuo-motor rotation, hand-paths during naïve performance are initially directed approximately 20~30° CCW to the target, as expected (columns 2 and 3). During the performance following opposite arm adaptation, the initial direction of the hand-paths is less deviated than that observed during naïve performance. Surprisingly, this improvement in initial direction control following opposite arm adaptation is observed in the performance of both arms, which indicates that both dominant and nondominant arms benefited from opposite arm adaptation. Following adaptation to the visuo-motor rotation, hand-paths in both performance conditions are directed relatively straight to the target and become substantially more accurate (column 4).

Fig. 3.

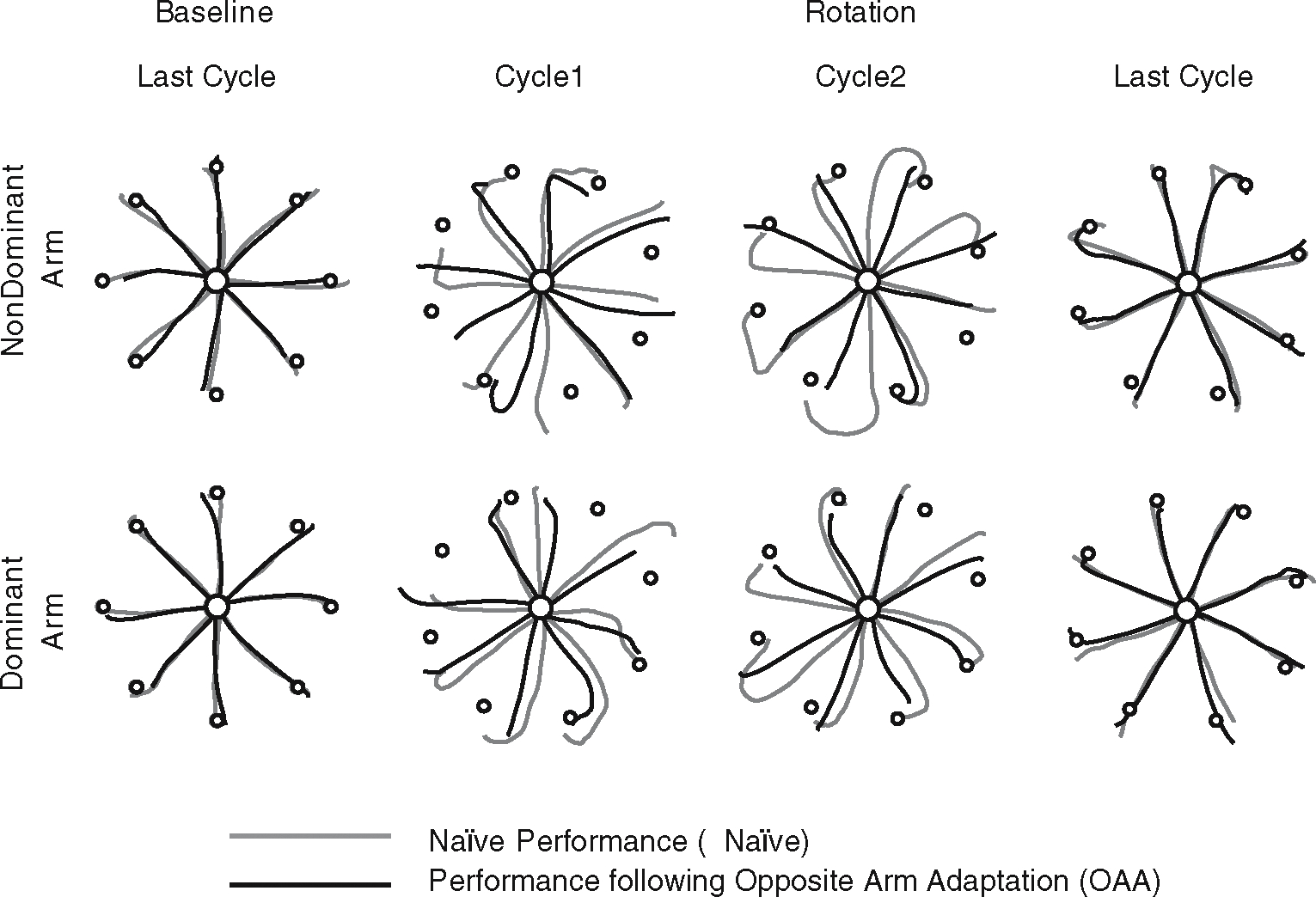
Hand-paths of representative subjects. Nondominant hand paths are shown along the top row, whereas dominant hand paths are shown below. Each column shows hand-paths of the eight consecutive trials of naïve performance (gray lines) and performance following opposite arm adaptation (black lines) for each target direction

This beneficial effect of opposite arm adaptation in controlling the initial direction of hand-paths was quantified by calculating the direction errors at V_max and A_max (Fig. 4). According to the repeated-measures ANOVA, there was a significant interaction between group and cycle for both arms (P<0.001) indicating that the two subject groups behaved differently across the cycles. We, thus, performed post hoc pair-wise comparisons using Tukey tests between naïve performance and performance following opposite arm adaptation at the first and the last epochs, for the two arms separately. The results demonstrated that at the first epoch (mean of cycles 1 and 2), the direction errors at both V_max and A_max were significantly lower in the performance following opposite arm adaptation than in naïve performance, not only for the dominant, but also for the nondominant arm (the amount of improvement for the dominant arm: 4.5° for V_max, 5.6° for A_max; for the nondominant arm: 5.3° for V_max, 5.2° for A_max; P<0.01 for all comparisons). At the last epoch (mean of cycles 23 and 24), there was no difference between the two performance conditions in either direction measures. We also calculated final position errors to assess the effect of opposite arm adaptation in controlling final position accuracy, although no significant difference was observed between the two performance conditions at either epoch (P>0.5). Collectively, these data clearly indicate that when the visuo-motor adaptation task is performed laterally from the midline, both the dominant and nondominant arms can benefit from the initial training with the opposite arm, with regard to the initial direction control of reaching movements.

Fig. 4.

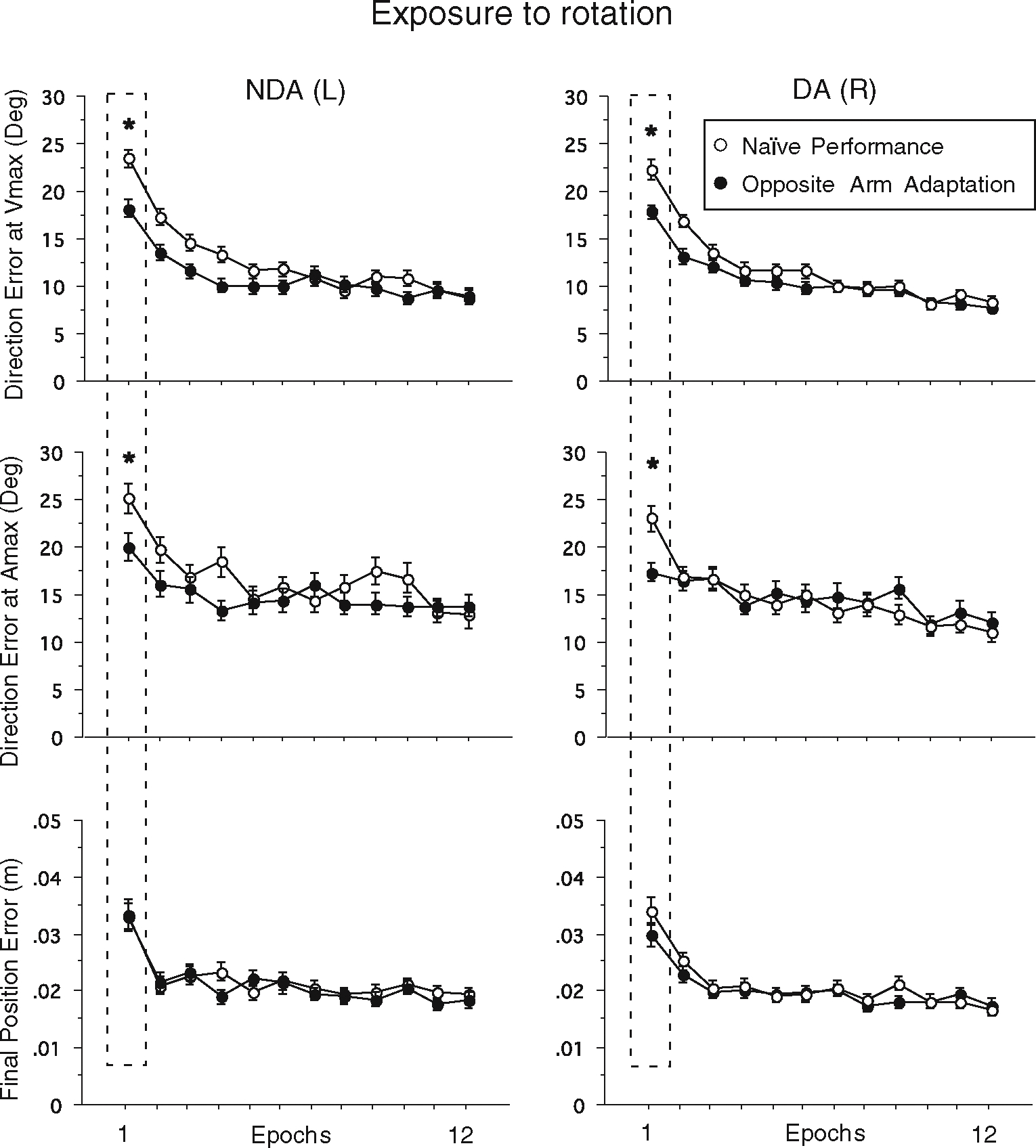
Mean performance measures of direction errors at V_max and A_max and final position error. Every data point shown on X-axis represents the average of 16 consecutive trials (epoch) across all subjects (mean ± SE). DA represents dominant arm, whereas NDA represents nondominant arm. Performance measures for naïve performance (open circles) and performance following opposite arm adaptation (filled circles) are shown separately. *represents a significant difference between naïve performance and performance following opposite arm adaptation (OAA) at P<0.01

To compare the learning curves of the two arms with respect to their initial direction control of movement, a line of approximation was constructed for direction errors at V_max and A_max by finding a nonlinear logarithmic regression line for each arm performance. The slope and the intercept of the regression equation obtained from each subject for each arm were subjected to independent t-tests to make a direct comparison between the dominant and nondominant arm performances following opposite arm adaptation (L of RL group versus R of LR group). As illustrated in Fig. 5, the nonlinear curves for the two arms were remarkably similar for both direction measures, and the slopes and the intercepts were not significantly different between the two arms (P>0.7 for both slopes and intercepts). The same comparison was also made between the dominant and nondominant naïve performances (R of RL group versus L of LR group), which also showed no significant differences between the learning curves of the two arms during naïve performance. These data indicate that the amount of transfer, or the amount of improvement following opposite arm adaptation, was symmetrical between the two arms.

Fig. 5.

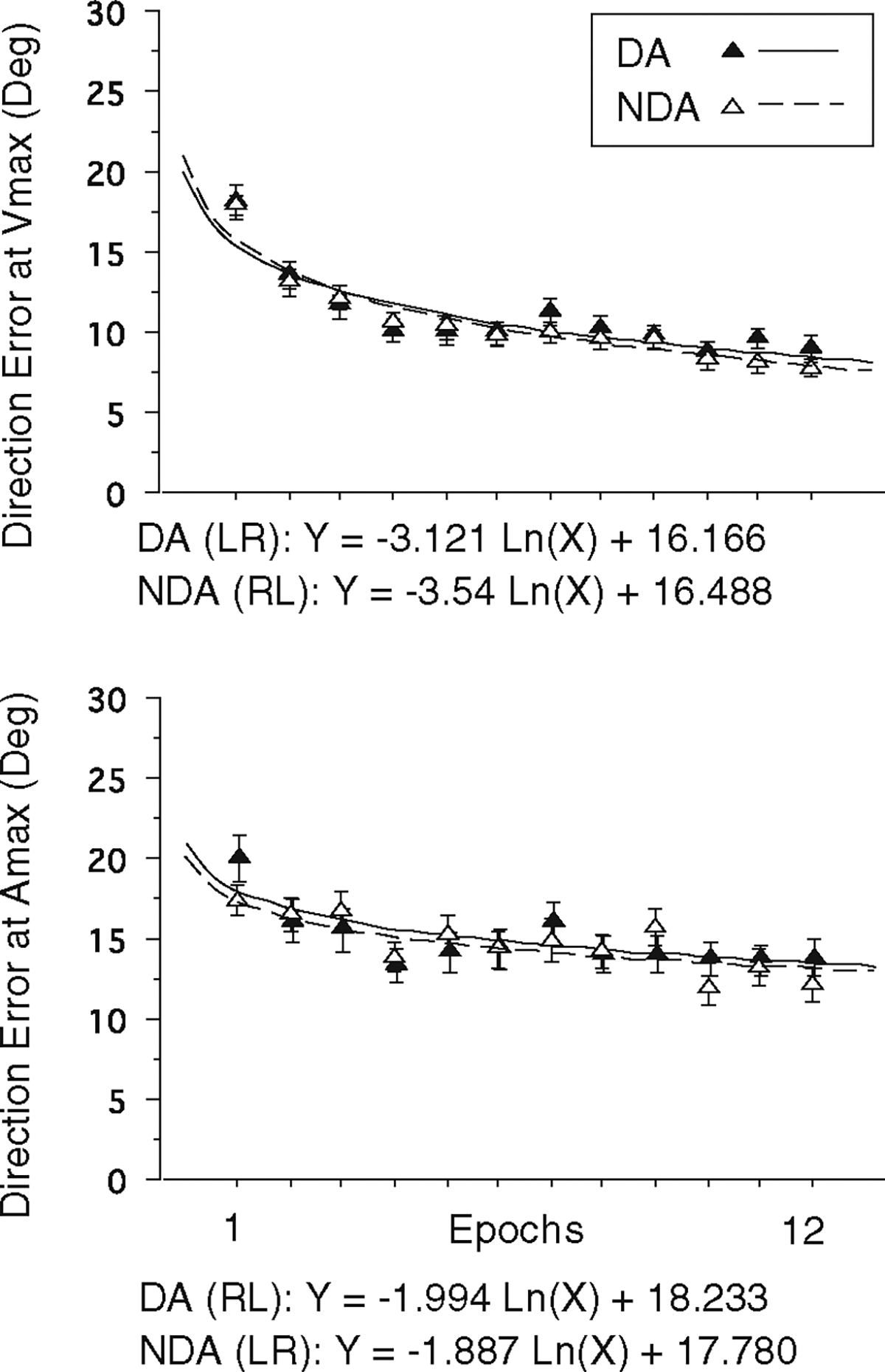
Learning curves of the dominant (DA) and nondominant arm (NDA) performance following opposite arm adaptation, for two direction measures. Solid lines represent nonlinear logarithmic curve fits for the dominant arm, while broke lines represent nonlinear logarithmic curve fits for the nondominant arm. Regression equations are shown for each arm for each measure

Discussion

Symmetry of interlimb transfer is dependent on the location of workspace provided for the two arms

We have consistently shown that when task-space is shared between the limbs, opposite arm training improves the direction of only dominant arm movements, and the final position of only nondominant arm movements (Sainburg and Wang 2002; Wang and Sainburg 2003, 2004b). We now examined whether separating task-space for the two arms would result in symmetrical interlimb transfer of visuo-motor transforms. Our results show that when task-space is separated between the two arms, both arms benefit from opposite arm adaptation in terms of initial direction control, and that this benefit is symmetric, thus providing support to the hypothesis that symmetry of interlimb transfer is dependent on the location of workspace provided for the two arms in adapting to a visuo-motor rotation.

We have previously demonstrated that substantial transfer in final position accuracy occurs from the dominant to nondominant arm when both arms adapt to the visuo-motor rotations within a shared midline task-space (Sainburg and Wang 2002; Wang and Sainburg 2003, 2004b). In the current study, however, no transfer of final position accuracy occurred between the limbs. It should be noted that in the previous studies, absolute target locations were identical for the two arms, whereas in the current study, absolute target locations were in separate regions of workspace. This provides additional support to our hypothesis regarding the effect of workspace location. Furthermore, this finding suggests that transfer of final position only occurs when target locations and associated learned hand positions are identical in absolute coordinates.

Why is interlimb transfer asymmetric when task-space is shared for both limbs?

When adapting to visuo-motor rotations presented in the midline, transfer of direction and final position information is asymmetric. We propose that this asymmetry results from competition between the two arm controllers for task performance at a shared workspace. In other words, when the two arms perform the task at separate workspaces, both arm controllers have symmetrical access to the information obtained during opposite arm adaptation. However, when the task is performed in the shared, midline workspace, the motor control system is presented with redundant solutions: both arms have symmetrical geometric access to the task-space. We envision that an executive decision-making process must be evoked in which task resources are allocated to the limb that has an advantage for control of the task under consideration. For example, in our reaching task, the dominant arm advantages in controlling limb dynamics appear to determine transfer of trajectory information to only the dominant arm (Sainburg and Wang 2002). Thus, the nondominant arm controller may be selectively inhibited from its access to learned information in order for the control system to remove ambiguity regarding which arm to use in this shared task-space. This hypothesis was inspired by the extensive findings reported by Gazzaniga and colleagues, indicating that cognitive and motor processes that take place in each brain hemisphere can interfere with each other, especially when these processes involve processing two incompatible sets of information (Holtzman and Gazzaniga 1982; Franz et al. 1996). For example, neurologically normal subjects are not able to draw incompatible spatial maps with the two hands simultaneously. However, split-brain patients show no deficit in performing this bimanual task (Franz et al. 1996). Gazzaniga and colleagues have also shown that when split-brain patients are presented with two series of geometrical shapes, one to the left and the other to the right half-brain, one half-brain is better at recalling the displayed stimuli under a condition in which the opposite hemisphere is working on processing a single repeated stimulus, as compared with a condition in which the opposite hemisphere is working on multiple stimuli (Holtzman and Gazzaniga 1982).

In the case of interlimb transfer, cognitive processes in each hemisphere do not take place concurrently because performance with one arm always follows that of the other arm. However, it is plausible that learning a task in a shared workspace with both arms can cause a cognitively demanding situation, such that the motor control system assigns features of control that are consistent with each limb only to that limb. Thus, trajectory features such as direction transfer only to the dominant limb, whereas final position features transfer only to the nondominant limb. This type of executive decision-making would ensure that tasks requiring positional and impedance control are performed by the nondominant system, whereas tasks that require trajectory specification are performed by the dominant system. This explanation accounts for the transfer of different task features in different directions, and is consistent with our previous findings of nondominant system specialization for control of limb impedance and position, and dominant specialization for control of trajectory (Sainburg 2005).

Is memory storage or access asymmetric?

With regard to the asymmetry in transfer of visuo-motor rotations that we observed previously, two reasonable hypotheses might explain our findings. First, the initial adaptation might have been asymmetrical, such that the nondominant arm learned the task more effectively. Thus, transfer of initial direction information occurred more effectively from the nondominant to dominant arm. Second, learning might have occurred symmetrically, but subsequent access of each arm controller to the stored memory might be asymmetrical. With respect to the first hypothesis, it has been suggested that the dominant arm is superior to the nondominant arm in learning motor tasks, thus resulting in better transfer from the dominant to nondominant arm (Laszlo et al. 1970; Parlow and Kinsbourne 1989). It is plausible that, for our task, the opposite proficiencies might occur, such that the nondominant arm more effectively learns the visuo-motor transform. This explanation, however, is unlikely because the rate and extent of adaptation to the 30° visuo-motor rotation studied here is equivalent between the arms. In addition, we also showed that, under separated task-space conditions, both learning and transfer become symmetric.

We next consider the hypothesis that access to the stored information is asymmetrical. However, previous findings from our laboratory have suggested that short-term memory resources for the two arm controllers are independent. This conclusion was based on the finding that when opposing visuo-motor rotations are provided, such that one arm learns a clockwise rotation and the other a CCW rotation, negative transfer does not occur (Wang and Sainburg 2003). Nevertheless, when the two rotations are in the same direction, substantial positive transfer does occur (Sainburg and Wang 2002). These findings indicate that interlimb transfer of visuo-motor transforms can be substantial, but is not obligatory. Therefore, each limb’s adaptation must be stored in independent memory resources that can be selectively accessed by the other controller. Our current findings extend this idea by indicating symmetric access of each arm controller to the memory stored by the opposite arm controller. Taken together, our previous and current findings contradict the callosal access model, as described by Taylor and Heilman (1980), which proposes that the information obtained during learning of a task by either arm is always stored in the dominant hemisphere. Our results, on the other hand, indicate that independent memory resources exist for the two arm controllers (Wang and Sainburg 2003) and that the arm controllers can have symmetrical access to these resources.

Interlimb transfer of visuo-motor rotations and task dynamics is different

It must be stressed that the current findings may not apply to all types of motor learning. In fact, Krakauer et al. (1999) have shown that adaptation to novel inertial dynamics and to visuo-motor rotations do not seem to share the same adaptive processes. Learning of one does not interfere with or facilitate subsequent adaptation to the other type of manipulation. Based on the findings of previous studies, we propose that asymmetry in transfer of novel dynamic loads results from asymmetry in the adaptation process itself. It has previously been shown that opposite arm adaptation to Coriolis forces, velocity-dependent forces, and inertial loads improves only nondominant arm performance (Dizio and Lackner 1995; Criscimagna-Hemminger et al. 2003; Wang and Sainburg 2004a). We have repeatedly demonstrated that the dominant arm is more proficient in coordinating intersegmental dynamics for specifying trajectory direction and shape as compared with the nondominant arm (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg 2002; Sainburg 2002). These findings suggest that learning with the dominant arm leads to the development of superior internal representations of the experimentally imposed dynamic conditions. This, in turn, should facilitate improvement in opposite arm performance (Wang and Sainburg 2004a). In contrast, the nondominant arm is less proficient at adapting to novel dynamic conditions, thus explaining the lack of transfer to the dominant arm.