Numerical simulation and experimental verification of fatigue crack propagation in high-strength bolts based on fracture mechanics

Abstract

To investigate the fatigue crack propagation behavior of high-strength bolts for high-speed train brake discs, the fatigue crack propagation of high-strength bolts with initial defects under various load ratios was numerically simulated and experimentally verified based on fracture mechanics in this paper. Firstly, the fracture mechanics model of a three-dimensional hexahedral mesh with initial root defects was established using ABAQUS-FRANC3D interactive technology. Then the stress intensity factor (SIF) of the crack front was calculated by the stress superposition of the crack surface to simulate the coupling effect of preload and axial cyclic load. Based on it, fatigue crack propagation was simulated. Finally, the corresponding fatigue experiments on prefabricated crack bolts were carried out. The results show that mode I cracks dominate in the process of crack propagation. The stable crack propagation zones of the fractured high-strength bolts all show a semi-elliptical cross-section. The SIF of the crack front decreases with the increase of the load ratio, thus making the crack propagation life increase with the increase of the load ratio. The experimental outcomes are in great agreement with the simulation results, which verify that the numerical simulation method can effectively and accurately evaluate the fatigue life of high-strength bolts with initial defects and provides an effective means for predicting the fatigue crack propagation life of the same type high-strength bolts in engineering applications.

Introduction

The most important components in modern high-speed trains are mechanical connections, especially high-strength bolt connections. The extensive use of high-strength bolts directly affects the effectiveness and safety of the structure. The effect of dynamic load on train operation can be counteracted by the effectiveness and safety of high-strength bolted connections.^1,2 However, more than 70% of engineering accidents are caused by fatigue failure of high-strength bolts during normal service. ³ This is due to the variabilities of the geometry and load transfer, ⁴ stress is concentrated at the thread bottom for the majority of bolts. ⁵ In the case of cyclic loading, the cracks will be initiated at the roots of the thread due to the plastic deformation caused by fatigue. In addition, the initial defects of high- strength bolts cannot be completely avoided due to factors such as manufacturing, material defects, or environmental corrosion, which lead to the initiation of micro-cracks. With the circulation of external loads, the crack will be expanded, and finally, the fracture of the bolt will be caused, resulting in the occurrence of serious accidents. Therefore, a thorough understanding of the fatigue behavior of bolts can provide valuable recommendations for optimizing the design of bolts to prolong service life and improve fatigue performance.

For most fatigue failures, the usual experimental assessments are cost-inefficient and time-consuming; therefore, numerical simulation techniques will probably be more suited to researching the fatigue crack propagation of high-strength bolts. At present, to simulate fatigue fracture, different numerical methods such as the finite-element method,^6–8 the boundary-element method, ⁹ the mesh-less method, ¹⁰ and the extended finite-element method ¹¹ have been utilized. However, the crack propagation of bolts can't be accurately simulated by traditional methods due to the influence of the complex three- dimensional geometry. Based on the M-integral, a more representative stress intensity factor (SIF) solution is provided by FRANC3D to assess crack propagation life, crack propagation path, fracture, and fatigue life, which has been proven very successful in many respects.^12–15

The fatigue fracture process of high-strength bolts is generally separated into three stages, namely, crack initiation at the bottom of the thread, crack stable propagation along the root of the thread, and rapid fracture stage. The first two stages can basically be considered as the entire bolt life cycle. At present, the research on the fatigue of bolts is focused on the whole life cycle, and the research on the fatigue crack initiation and fatigue crack propagation of high-strength bolts is rarely reported. By constant amplitude fatigue test, the effects of stress ratio (the ratio of the minimum stress to the maximum stress during the cyclic loading on the bolt), stress amplitude, pre-tightening force, and bolt grade on the fatigue properties of high- strength bolts have been studied by Xu Yazhou, ¹⁶ Shen Yu, ¹⁷ Yang, ¹⁸ Jiao, ¹⁹ MALJAARS. ²⁰ In their research, the macro-morphology of bolt fracture was analyzed, the S-N curve was fitted, and the fatigue life formula was given. Lei Honggang^21,22 did intensive research into high-strength bolt failure mechanisms under varied amplitude fatigue, and the calculation method of the bolt fatigue life was obtained. However, the crack propagation life of high-strength bolts is a crucial aspect of their entire life cycle. Therefore, it is of great significance to research the fatigue crack propagation of high-strength bolts.

Due to the complicated coupling effects of stress concentration and dynamic fatigue, a variety of factors can influence the formation of the fatigue crack propagation of high- strength bolts, ²³ the establishment of an accurate fatigue crack propagation model is thus a key tool for estimating the fatigue life of bolts. In this study, the fatigue crack propagation behavior of high-strength bolts under the coupling action of preload and axial cyclic loading was investigated by experimental and computational methods based on the theory of linear elastic fracture mechanics. Firstly, the digital accurate modeling was carried out by using MATLAB, and then combined with the interactive simulation of ABAQUS and FRANC3D, an accurate prediction of fatigue crack propagation could be achieved by acquiring high- quality meshes surrounding the crack tips with an adaptive mesh re-division technique.

The main research of this paper is as follows: firstly, the fatigue crack propagation characteristics, including the SIF of the crack front, the crack propagation path, the fracture surface, and the fatigue life, were analyzed by using the interactive simulation of finite-element software ABAQUS and FRANC3D. Subsequently, the fatigue crack propagation tests of high-strength bolts under different load ratios were carried out. The fracture mechanism of the high-strength bolts was investigated by microscopic morphology analysis of the fracture surfaces using optical microscopy and scanning electron microscopy techniques. The corresponding experimental results verify the accuracy of the prediction and provide an effective way for the fatigue crack propagation life evaluation of high-strength bolts.

Numerical simulation of crack propagation for high-strength bolts

In this paper, the finite-element software ABAQUS and the crack propagation program FRANC3D were used for interactive simulation. FRANC3D adopted the finite-element adaptive mesh technology, based on the principle of linear-elastic fracture mechanics, to accurately compute the SIFs at the crack front and to simulate the three-dimensional crack propagation and lifetime computation of engineering structures under arbitrary complex geometry, loading conditions, and crack patterns.

Related theory of fatigue crack propagation

The grid template for the crack front

For the accuracy of the SIF calculation, a template with elements of controlled size and shape is placed around all crack fronts. The template adopts the generalized cylindrical tube form of the unit, and the crack front is used as the axis of the cylinder. The wedge element is placed next to the crack front, and the outer layer is a two-ring hexahedral element ring, as shown in Figure 1.

Figure 1.

The grid template for the crack front.

The calculation of the SIF

Equivalent SIF

There are three possible modes for the stress field around a crack tip when the fracture crack develops in an isotropic homogeneous material: Mode I (opening), Mode II (sliding), and Mode III (tearing). The SIF is used to describe the stress field near the crack tip and to create fracture criteria to determine whether or not linear elastic materials experience rapid and unstable fatigue crack propagation. ²⁴ Specifically,

$$K_{equiv}={\displaystyle \frac{K_I}{2}+{\displaystyle \frac{1}{2}\sqrt{K_I^2+4{(1.155K_{II})}^2+4K_{III}^2}}}$$ (1)

where K_equiv is the equivalent SIF, K_I, K_II, and K_III are the SIFs for modes I, II, and III, respectively. According to the associated theories of fracture mechanics,^25,26 when K_equiv ≥K_c, where K_c is the plane strain fracture toughness of the bolt material, the crack propagation enters a rapidly unstable phase.

M-integral

The M-integral, or interaction integral, is applied to linear elastic fracture mechanics, a crack path-independent technique based on the J-integral to compute the global energy release rate, which may then be used to determine the SIF for the three fracture modes K_I, K_II, and K_III. The equivalent domain equations of M-integral are the most accurate method for calculating the SIF, and the effect of additional factors, such as temperature, residual stress, the friction factor of crack surface, etc., can be considered, ²⁷ namely,

$$\mathrm{M}=\underset{\mathrm{r}}{\oint }(W{x}_i{n}_i-T_j{u}_{j,i}{x}_i)ds$$ (2)

where г is an arbitrary integral path around the crack tip, W is the density of strain energy, defined as $W=\frac{1}{2}{\sigma }_{ij}{\epsilon }_{ij},{\sigma }_{ij}$ is the stress tensor, ε_ij is the strain tensor, n_i is the directional cosine of the exterior normal for the path г, T_j is the surface force vector outside the integral path, u_j,i is the displacement vector on the path г, x_i is the plane coordinate system, s is the integral arc microelement.

Sub-critical crack propagation

The sub-critical crack propagation includes the calculation of the local node kink angle Δθ_c and the local node propagation Δa_i along the crack front, then the crack front is fitted and extended.

Kink angle θ_c

During the growth of a crack, the growth direction is represented by the kink angle θ_c. As a way to help estimate the direction in which cracks will propagate, several criteria, including the maximum circumferential stress (MTS) criterion, the maximum shear stress criterion, the strain energy release rate criterion, etc., have been developed.

Among them, the MTS criterion is more intuitive, which has been verified by many experimental observations,^28–30 so it has been widely considered and applied. This method is also used to determine the crack propagation angle in this paper.

As shown in Figure 2(a), the principle of the MTS criterion is: SIF is calculated at each node of the crack front to determine the kink angle Δθ_c, and the crack will be kinked in the direction perpendicular to the MTS.

Figure 2.

Principles of crack propagation.

By using linear elastic fracture mechanics, ³¹ the circumferential stress in the polar coordinate is determined to be

$${\sigma }_{\theta \theta }={\displaystyle \frac{1}{\sqrt{2\pi r}}\cos {\displaystyle \frac{\theta }{2}\left[K_I\mathrm{co}{\mathrm{s}}^2{\displaystyle \frac{\theta }{2}-{\displaystyle \frac{3}{2}{K}_{II}\sin \theta }}\right]}}$$ (3)

where (r, θ) is the local polar coordinate system with the origin at the center of the crack tip.

When a crack propagates in the direction of the MTS, ³² the circumferential stress factor K_θθ is expressed as

$$K_{\theta \theta }=\underset{r\to 0}{\mathrm{Lim}}{\sigma }_{\theta \theta }\sqrt{2\pi r}=\cos {\displaystyle \frac{\theta }{2}\left[K_I\mathrm{co}{\mathrm{s}}^2{\displaystyle \frac{\theta }{2}-{\displaystyle \frac{3}{2}{K}_{II}\sin \theta }}\right]}$$ (4)

Thus, the σ_θθ of mode I crack can be rewritten as

$${\sigma }_{\theta \theta }={\displaystyle \frac{1}{\sqrt{2\pi r}}{K}_{\theta \theta }}$$ (5)

According to the MTS criterion, the direction of crack propagation θ_c at each crack tip is determined by the maximum value of K_θθ, namely

$${{\displaystyle \frac{\mathrm{\partial }{K}_{\theta \theta }}{\mathrm{\partial }\theta }}|}_{\theta ={\theta }_c}=0$$ (6)

substituting equation (4) into equation (6), then

$$K_I\sin {\theta }_c\pm K_{II}(3\cos {\theta }_c-1)=0$$ (7)

In this case, the crack propagation angle can be determined.

The extension Δa_i

Two extension types are provided for fatigue crack propagation in FRANC3D: median extension and cycle extension. In this paper, the median propagation method is adopted, in which, after calculating the equivalent SIF of each node at the crack front, FRANC3D automatically finds the middle value of K_equiv according to the specified built-in algorithm. To ensure the calculation accuracy, the propagation of the node representing the mean value of the SIF (median K) at the crack front is specified as 15% of the minimum characteristic size of the crack. As shown in Figure 2(b), if the extension of the node at the median K of the crack front is defined as Δa_m, the extension Δa_i at other nodes is expressed as:

$$\mathrm{\Delta }{a}_i=\mathrm{\Delta }{a}_m\times {\left({\displaystyle \frac{\mathrm{\Delta }{K}_i}{\mathrm{\Delta }{K}_{median}}}\right)}^n$$ (8)

where n is the rate parameter m of crack propagation in the Paris formula.

Fitting of the crack front

As shown in Figure 2(c), when fatigue crack propagation is simulated by using the mean value theorem, the nodes at the front of the original crack shift to new places after utilizing the fatigue growth model to calculate the results. These nodes can be connected at new locations to create a fresh crack front. Because it immediately connects many sites, the new crack front is often serrated frequently. Therefore, a third-order polynomial spline is needed for smoothing.

Crack propagation rate model

In regions with stable expansion, the crack propagation rate is frequently calculated using the Paris equation, but it does not apply to regions of initial crack expansion and final rapid expansion, since the crack expansion of both stages is nonlinear. ²⁴ To estimate the propagation rate throughout the entire crack propagation stage, the crack propagation rate model of NASGRO is decided to be adopted, which represents an upgrade to the FORMAN model I. In this model, the SIF is the key component for crack propagation, with the impacts of the propagation threshold, the stress ratio, and the fracture toughness all being taken into account. ³³

$${\displaystyle \frac{da}{dN}=C{\left[\left({\displaystyle \frac{1-f}{1-R}}\right)\mathrm{\Delta }K\right]}^n{\displaystyle \frac{{\left(1-{\displaystyle \frac{\mathrm{\Delta }{K}_{th}}{\mathrm{\Delta }K}}\right)}^p}{{\left(1-{\displaystyle \frac{K_{max}}{K_c}}\right)}^q}}}$$ (9)

where $\frac{da}{dN}$ stands for the rate of crack propagation, R is the load ratio, that is, the ratio of the maximum load to the minimum load during the cyclic loading on the bolt; f is a function of crack opening, ΔK is the amplitude of SIF, c, n, p, and q are material parameters, ΔK_th is the threshold of SIF amplitude, ΔK_max is the maximum SIF, and K_c is the material fracture toughness.

According to the material library provided by FRANC3D, the parameters of the tested material, A286, are shown in Table 1.

Table 1.

Material properties as used in the NASGRO version 3 equation (equation (9)) for A286.

Material	KC (MPa. $\surd \overline{\mathrm{mm}}$ )	C (mm/cycle)	n	p	q
A286	4865	4.4257×10−11	2.1	0.25	0.25

Modeling in ABAQUS

The research objective of this paper is the hexagonal head high-strength bolts (class 10.9) for high-speed train brake discs, which were produced by China Aviation Standard Parts Manufacturing Co., Ltd. The 2D structure is shown in Figure 3. Technical specifications include M16 × 1.5 × 110 mm, a tooth angle of 60°, and an effective length of screw thread of 38 mm.

Figure 3.

Schematic of the high-strength bolts.

To ensure the accuracy of calculation, according to the test sample characteristics mentioned in Figure 3, a 3D finite-element model of a bolt-nut fatigue experimental assembly considering the helix angle and no preset crack was accurately established using the interaction between MATLAB programming and the finite-element application ABAQUS, as shown in Figure 4. MATLAB programming was used to calculate the node coordinates and element numbers of the threaded part. Then, these data were imported into ABAQUS to generate a three-dimensional hexahedral mesh model of the thread teeth. The modeling of the screw part was completed directly in the ABAQUS software. Finally, the complete 3D finite-element models of the bolt and the nut were established by a Boolean operation. For the uncracked model, the C3D8R unit type was used by all components, with a total of 400,721 nodes and 366,904 elements, and the minimum element size is 0.13 mm.

Figure 4.

The 3D finite-element models of a bolt and nut: (a) the vertical view (b) the longitudinal profile.

In the finite-element model, there are three contact pairs were defined: the contact between the bolt head and the upper clamp (contact 1), the contact between the nut and the lower clamp (contact 2), and the contact between the bolt and the nut (contact 3). According to the actual load condition, the finite sliding was set to each contact pair, and the tangential and normal behaviors were simulated by the penalty function method with a friction coefficient of 0.15 and the hard contact, respectively.

The stress distribution of the bolt-nut connector under the preload is statically analyzed using ABAQUS.^34–36 Following the experimental conditions, the relevant material properties of A286 were set, fixtures 1 and 2 were completely fixed, and the rotation angle was applied to the nut to simulate the preload acting on the bolt for predicting the magnitude and location of the maximum stress. As can be seen from Figure 5, both the bolt and the nut have obvious stress concentration at the thread roots, and the degree of stress concentration gradually decreases from top to bottom, the maximum equivalent stress appears at the first thread root, which is consistent with previous tests and engineering practice.^37,38 Figure 6 shows the axial force distribution among each section of the nut according to the YAMAMOTO method ³⁹ and numerical simulation. Obviously, the finite-element results are in great accordance with the analytical solution, which effectively verifies the accuracy of the finite-element model.

Figure 5.

The stress distribution under the action of preload.

Figure 6.

The axial force results of the YAMAMOTO method and numerical simulation.

The stress concentration factors at the roots of the thread, which are the ratio of the local stress at the thread roots to the average stress of the bolt or nut, are shown in Figure 7. As can be observed, the stress concentration factor in the first three roots of the bolt-engaging threads is far greater than that in the remaining roots. Especially for the first root, the stress concentration coefficient is the highest, resulting in the highest level of plastic deformation. Therefore, under the action of alternating stress, the bolt is vulnerable to fatigue fracture in this location. With the increase in thread turns, the stress concentration factor decreases at a fast and then a slow rate. At the same time, the stress concentration factor at the bottom of the nut thread is relatively low, which is also one of the reasons why the bolt has fatigue fracture and the nut does not fail.

Figure 7.

The stress concentration factor under the action of preload.

Modeling in FRANC3D

Based on the interaction of FRANC3D and ABAQUS, the initial crack is presupposed at the maximum stress point of the bolt. To accurately simulate the propagation of fatigue cracks, the initial size and shape of the three-dimensional crack must be determined firstly. In general, the actual initial crack leading edge is an irregular curve, which is difficult to determine experimentally. Therefore, the length of the crack leading edge needs to be regularized. The finite-element simulation of the Dhamari^28,40 study shows that any initial crack shape will rapidly develop into a common profile, after which, the crack will propagate in a similar manner, as shown in Figure 8. Usually, an ordinary initial crack can be simplified to a surface crack with a length of 2c and a depth of a. A simple semicircular initial crack shape is postulated in this research, that is, a = c.

Figure 8.

Standardization of initial crack shape.

For engineering analysis, the initial flaw size of the objective studied in this article is generally considered to be 0.5 mm,^12,41 that is, a = c = 0.5 mm. After the initial micro-crack was introduced at the maximum stress position, the mesh around the crack was refined by the FRANC3D mesh algorithm, which can not only make the crack tip transition smoothly to the unmodified grid but also maintain good accuracy near the crack, as shown in Figure 9. The stress results under the action of preload were introduced into FRANC3D, and an axial alternating cyclic load was applied on clamp1 to realize the stress superposition on the crack surface, and the fatigue crack propagation simulation was realized by using the median crack propagation technique, to forecast the life of fatigue crack propagation.

Figure 9.

The stress cloud of the initial crack.

Experimental study on crack propagation of high-strength bolt

Fatigue specimens design of high-strength bolts

Since the high-strength bolts are generally cylindrical with a small diameter at the bottom of the thread teeth, and are affected by the interference of the thread teeth, the ideal semi-circular prefabricated cracks cannot be processed. Therefore, to promote the fatigue crack initiation of the bolts, a half-elliptical micro-crack with a depth of 0.5 mm was prefabricated by using wire-cut machining with a diameter of 0.08 mm at the root of the first engagement thread in the test bolt, as shown in Figure 10.

Figure 10.

The fatigue specimen.

The material of the bolts is A286, Fe-25Ni-15Cr, a Fe-based superalloy, which has good processing plasticity and thermal stability. Through a static tension test according to China Aviation Industry Standard Parts Manufacturing Co. LTD, the physical and mechanical properties of the sample material were achieved, as shown in Table 2.

Table 2.

Mechanical properties of A286.

Density (g cm−3)	Poisson's ratio	Modulus of elasticity (GPa)	Tensile strength yield (MPa)	Yield strength (MPa)
7.93	0.306	201	1379	1310

Experimental equipment and methods

Due to the influence of plane strain, the internal fatigue crack propagation rate of high-strength bolts is different from that of surface crack, and the bolts and nuts are always meshing during the test, it is difficult for the sensor to directly observe the propagation size of fatigue cracks. Therefore, in this paper, the constant amplitude fatigue loading scheme with different load ratios can only be used to characterize and analyze the fatigue crack propagation behavior by observing the morphology of the fracture surface after the specimens are broken.

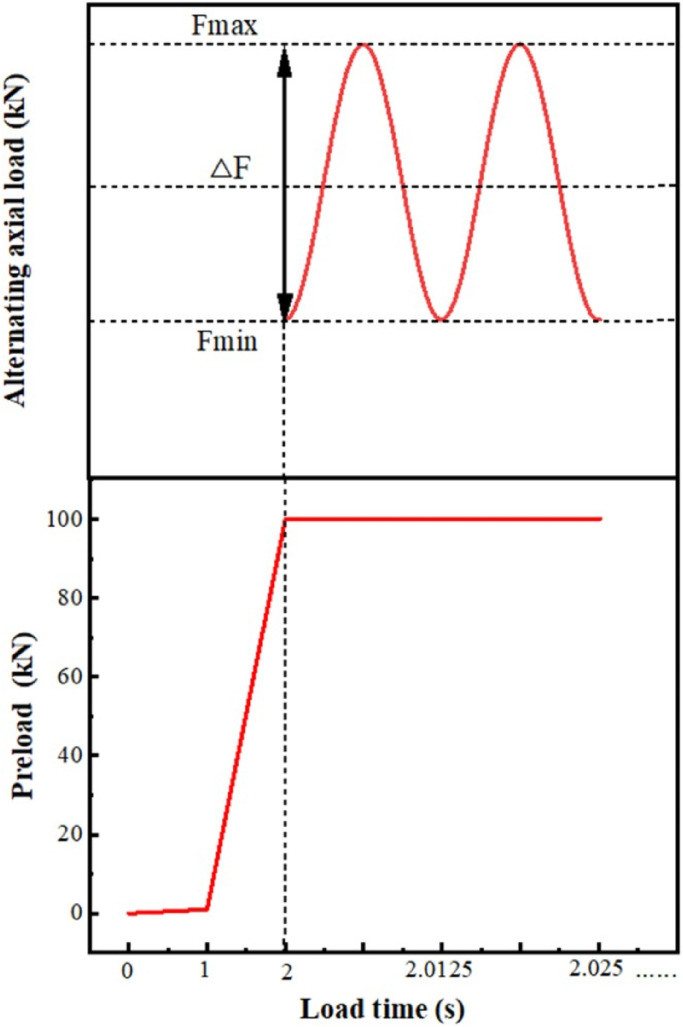
Before fatigue testing, the high-strength bolt was preloaded with the cooperation of a torque wrench and a pressure sensor, and the axial excitation load was imposed by a sine wave. By simulating the coupling action of preload and axial alternating load under the actual working state, the tension-tension constant amplitude fatigue life tests of the bolts were then carried out at room temperature on the QGB-500 electromagnetic resonance fatigue testing machine. As shown in Figure 11, the cyclic load was transferred to the experimental sample by the machine clamp: the clamp 2 is fixed and the clamp 1 moves slightly up and down.

Figure 11.

QGB-500 electromagnetic resonance fatigue testing machine.

According to the application of the research objective in this paper and the VDI2230-1 standard, it is recommended to apply the preload force F_p according to equation (10). Through calculation, the elastic limit of the high-strength bolt is 140 kN. In this paper, the preload is 70% of the limit, that is, F_p = 100 kN. The fatigue tests were carried out under constant amplitude excitation with a preload of 100 kN, a load frequency of 80 Hz, a maximum axial load of 100 kN, and load ratios of 0, 0.3, 0.4, 0.5, and 0.6, respectively. Among them, the frequency was automatically defined by the experimental equipment based on the specimen itself and loading parameters, and the maximum axial excitation load was obtained by multiplying the safety factor 2 by the actual load of the bolt in the brake disc of a high-speed rail. ⁴² The specimens were numbered P1–P12, and the detailed parameters of the test are given in Table 3.

$$F_P={\sigma }_s\cdot A_s$$ (10)

where σ_s is the yield stress of the high-strength bolt, A_s is the tensile stress area of the bolt threat.

Table 3.

Fatigue experimental parameters.

Specimens	Load ratio R	Frequency f（Hz）	Fmax (kN)	Fmin (kN)
P1 P2	0	80	100	0
P3 P4	0.3	80	100	30
P5 P6	0.4	80	100	40
P7 P8	0.5	80	100	50
P9 P10	0.6	80	100	60

During the fatigue test, the change in frequency of the experimental system was used to determine whether the crack propagated. It is worth noting that pre-crack loading was required to obtain sharp crack tips before stable fatigue crack propagation since pre-cracking can have some effect on fatigue crack propagation. ⁴³ The start-up stage of the fatigue testing machine used in this paper is actually the pre-cracking loading stage, in which the load amplitude and the average load gradually increase from 0 to the set value; therefore, crack prefabrication can be realized. Subsequently, the fatigue test was carried out at the specified load amplitude until the fatigue fracture of the sample occurred. The fatigue loading scheme is shown in Figure 12. After the fatigue tests, the corresponding crack depth and the circumferential crack length on the fracture surface of the specimen were measured by an optical microscope.

Figure 12.

Loading process.

Results and discussion

Simulation results

SIF

Usually, the three-dimensional crack fronts are irregular and variable in length. Therefore, it is necessary to normalize the size of the crack front. The normalized distance of the crack is taken as the percentage of arc length from a point on the crack front to the origin over the total arc length. A semi-circular crack with an initial size of 0.5 mm was introduced at the location of maximum stress, and the SIF (K_I, K_II, and K_III) of all nodes at the crack front were calculated based on M-integral. As shown in Figure 13, the horizontal coordinate is normalized crack length and the vertical coordinate is SIF.

Figure 13.

The SIFs K_I, K_II, and K_III of the initial crack.

Take R = 0.3 as an example.

From Figure 13, it is evident that the K_I of the crack front is between 1539 and 2657 MPa $\surd \overline{\mathrm{mm}}$ , while K_II and K_III are between −371 and 228 MPa $\surd \overline{\mathrm{mm}}$ , and −796 and 584 MPa $\surd \overline{\mathrm{mm}}$ , respectively. Since K_I is significantly larger than K_II and K_III, the fatigue crack is mainly propagated by model I in the current case, and the distribution rule is small in the middle and large at both ends. According to equation (1), the K_I equates to the K_equiv approximately, which is compared to the K_C to assess whether or not the stage of rapid instability is reached.

Figure 14 shows the distribution of the mode I SIF along the crack front and how it develops as it propagates from the original crack to the critical crack. From the diagram, it can be seen that the crack front node's maximum K_I is around 4870.4 MPa $\surd \overline{\mathrm{mm}}$ when the crack propagates to the 28th step, which exceeds the critical value K_C (4865 MPa $\surd \overline{\mathrm{mm}}$ ) of the A286, indicating that the crack propagation has reached an unstable stage. Figure 14 further illustrates that the crack propagation rate of different nodes is also different due to the different K_I values of the crack front.

Figure 14.

Mode I SIF(K_I) at step5, step13, step21, and step28.

Figure 15 shows the shape of a three-dimensional crack mapped on the X–Y plane, which is similar to a half-ellipse. It shows the beach strip propagation process of the whole stable propagation stage under the axial alternating load, and the crack front near the instantaneous fracture zone shows irregular characteristics. Compared with the actual crack fracture surface in Figure 16, it is clear that the predicted crack surface is very similar to the morphology observed in the actual fracture surface, and both of them have incomplete crack fronts in the physical fracture surface.

Figure 15.

Crack front evolution during the crack propagation.

Figure 16.

(a) The macro-morphology of bolt fractures; (b) The micro-morphology of crack propagation zone.

As the crack continues to propagate, the SIF of the crack front increases. Figure 17 shows how the maximum SIF varies with crack depth. As can be seen, when the crack length increases to a certain value, the tested bolt cannot satisfy the condition of continuous crack growth, and fatigue failure occurs.

Figure 17.

The variation of the maximum SIF along the crack depth.

Crack propagation

Take R = 0.3 as an example.

Figure 18 reveals the propagation of the root crack under the coupling of preload and axial cyclic load. The crack surface gradually evolves from the first half circle to the similar half ellipse. Figure 18(c) and (d) shows that as the crack propagates, the fracture cross-section area increases rapidly with fewer cycles, indicating that the crack has reached the rapid propagation stage. Comparing the stable crack propagation zone with the rapid crack propagation zone in Figure 18(d), it will be found that the area of the rapid crack propagation zone is approximately twice as large as the stable crack propagation zone.

Figure 18.

Circumferential and radial propagation paths of bolt root crack: (a) N = 2467; (b) N = 5907; (c) N = 8147; (d) N =  10,510.

The fatigue propagation of radial and circumferential cracks in the above four propagation steps was analyzed, as shown in Figure 19, the fatigue crack of the bolt propagates in a slow-to-fast manner. The radial and circumferential crack growth rates are different, and the circumferential crack growth rate is significantly higher than that of the radial crack. The reason is that the SIF value of the crack leading edge near the surface of the thread root is higher.

Figure 19.

Crack length versus load cycles for radial and circumferential cracks.

Experimental results

As shown in Figure 20, the fracture location of all tested bolts occurred at the first tooth engaged with the nut. After the fatigue test, the bolt fracture specimens of approximately 10 mm in length were obtained by ire-cut electrical discharge machining. These specimens were cleaned by an ultrasonic cleaning machine. To demonstrate the fatigue failure mechanism, the fractures’ macroscopic morphology was observed using an optical microscope. Using the 2D measuring program DS-300 in optical microscope, the crack propagation depth and crack propagation area can be precisely quantified.

Figure 20.

Fatigue fracture positions of the bolts.

Under constant-amplitude cyclic loading, the initial micro-cracks at the root of the thread propagate continuously along the direction of maximum stress at the crack tip and extend from the prefabricated defect to the opposite side. The fracture surface has obvious fatigue fracture characteristics, which can be divided into three different zones, namely, the crack initiation zone (CIZ), the crack propagation zone (CPZ), and the transient breaking zone (TBZ). For the same load ratio, the fatigue crack propagation depth and propagation life of bolts have slight differences due to initial crack manufacturing errors, experimental equipment errors, and material errors in the bolts themselves. However, for different load ratios, there is a significant difference between the macro-morphology of bolt fracture and the micro-morphology of the stable crack propagation zones, as shown in Figure 16.

As shown in Figure 16(a), before the fatigue test, the micro-crack was prefabricated by wire cutting at the maximum predicted stress at the root of the thread, and thus the prefabricated micro-crack area is regarded as the CIZ. The CPZ is a relatively smooth zone with a semi-elliptical leading edge that extends in all directions, perpendicular to the direction of crack propagation. The TBZ is a relatively rough zone. The central dimple zone and the marginal shear zone are typical shapes that exhibit typical plastic failure characteristics. This means that when the cross-sectional crack length reaches a certain threshold, the crack enters an unstable stage of rapid propagation, which eventually leads to the complete fracture of the bolt.

Due to the different axial fatigue load ratios of the bolts, there are also some differences in the CPZs. As shown in Figure 16(b), the stable crack propagation zones are mainly dominated by the fatigue striation propagation mechanisms, which are basically parallel wavy stripes. After each cyclic loading, a fatigue striation was left, and the fatigue band corresponded to the position of the crack tip. The number of cycles is equal to the number of fatigue bands, and the normal direction is roughly pointing in the direction of fatigue crack propagation. ⁴⁴ The smoothness and flatness of the stable crack propagation zone change with the load ratios: when the load ratio is small, the load amplitude is large, the crack propagation fatigue strip spacing is large, the microstructure of the propagation zone is rough, the crack propagation rate is large, the stable crack propagation zone is small, the instantaneous fracture zone is large, and the propagation life is short. With the increase in load ratio, the load amplitude decreases, the spacing of crack propagation fatigue strips decreases, the microstructure of the propagation zone is relatively smooth, the crack propagation rate decreases, the area of CPZ increases, the instantaneous fracture zone decreases, and the propagation life is long. It is concluded that the crack propagation life of bolts increases with the increase in load ratio, which matches the simulation results.

In order to fully comprehend the micro-fracture morphology and analyze the fatigue fracture mechanism of bolts, the bolt fracture morphology at different propagation stages was observed by scanning electron microscope. As shown in Figure 21, the fracture morphology of specimen 3 shows the change of the main fracture mechanism during crack propagation.

Figure 21.

Microscopic fracture morphology of specimen 3.

As shown in Figure 21(a), the particle residues in the area CIZ are mainly process residues and oxides produced by wire cutting during the prefabrication of micro-cracks. In Figure 21(b) and (c), the trans-granular fracture mechanism is observed to dominate, and the fracture surface undulation characterized by fatigue fringes is clearly formed. Among them, Figure 21(b) is the low-speed growth zone of the initial section, the crack propagation rate is relatively slow, and the fracture surface is smoother than the later stage of the crack propagation. As the number of fatigue cycles increases, the fatigue crack propagation rate increases, and the fracture surface becomes rough, as shown in Figure 21(c). The underlying cause is that the energy release rate of the crack front increases with the increase of the radial crack depth. This causes an exacerbation in the micro-mechanical activity of the crack tip and an increase in the fracture surface roughness. At the same time, in the high-speed propagation zone, we also observed some secondary cracks, which can release the strain energy of the crack front and reduce the propagation rate of the crack in the propagation plane to a certain extent. It is shown that the SIF at the crack tip is positively correlated with the crack propagation depth. As shown in Figure 21(d), there are a lot of loose pits in the typical fast fracture morphology. Due to the large preload, the friction and wear of the shear stress are restrained to some extent by the normal stress, the dimples in the instantaneous fracture zone are large, deep, and irregular, which are typical equiaxed dimples. It is concluded that the bolt crack propagation is carried out at a slow-fast rate. When the crack propagates to a critical value, an instantaneous fracture occurs, which also matches the simulation results.

Discussion

Simulation results

The relationship between fatigue crack propagation life and crack propagation length can be applied to evaluate qualitatively the effect of load ratio R on fatigue behavior.^29,30 Figure 22(a) shows that the fatigue crack of the bolt propagates in a slow and then fast manner. When the SIF of the crack front approaches the critical value, the crack enters a stage of rapid growth. And the load ratio also affects its growth rate. The smaller the load ratio is, the less obvious the stable propagation stage is, and the crack propagates rapidly to the final failure. This is due to the different SIFs caused by different load ratios. The smaller the load ratio is, the larger the stress amplitude is, the larger the SIF of the crack front is, the higher the propagation rate is, and the shorter the propagation life is. Figure 22(b) shows the fatigue life of bolts under different load ratios. The overall exponential rise observed from the figure is as follows:

$$N=0.06282{\mathrm{e}}^{\left(\frac{R}{0.15762}\right)}+0.84388$$ (11)

Figure 22.

(a) Crack propagation process for various axial cycle load ratio R; (b) Fatigue crack propagation lives versus the axial cycle load ratio R.

Validation of the crack propagation simulation method

Tables 4 and 5 are the simulations and experimental results of fatigue crack propagation life and crack propagation size of high-strength bolts under different load ratios. Note: The fatigue crack propagation life recorded in Table 4 refers to the crack propagation life after the average load and load amplitude reach the preset values, excluding the propagation life of the pre-crack loading stage.

Table 4.

Crack propagation life.

Load ratio R	Simulation	Experiment		Maximum error
0	9023	7998	8741	12.82%
0.3	12,739	12,073	11,596	9.86%
0.4	16,380	15,936	14,928	9.73%
0.5	23,372	22,351	21,323	9.61%
0.6	36,726	34,137	33,574	9.39%

Table 5.

Crack propagation size.

Load ratio R	Simulation	Experiment		Maximum error
0	2.770595	3.419	3.352	18.96%
0.3	2.89854	3.315	3.573	18.88%
0.4	2.846358	3.523	3.487	19.2%
0.5	3.412763	4.179	4.091	18.33%
0.6	3.413295	4.213	4.054	18.98%

As shown in Table 4, the crack propagation life under different load ratios obtained from the test is compared with the corresponding simulation results. It can be found that the two are very close, and the maximum life error is 10.49%. At the same time, we also found that the experimental life is shorter than the simulated life, because the experimental life of fatigue crack propagation refers to the total experimental life minus the life of initial vibration, and the simulated fatigue crack propagation life does not include the starting vibration life.

As shown in Table 5, comparing the crack propagation depth under different load ratios obtained from the tests with the critical failure size predicted by simulation, it can be found that the two are also very close, and the maximum depth error is 18.98%. At the same time, we also found that the crack propagation depth obtained by the experiment is larger than that obtained by the simulation, because the prefabricated crack begins to expand in the initial vibration stage of the experiment, and the simulated crack starts to expand at the specified expansion step, and there is no pre-crack propagation stage.

Of course, in addition to the above reasons, the errors in the numerical and experimental results are related to many parameters, such as the bolt material, the initial crack prefabrication error, ignoring the plasticity effects, experimental and measuring equipment accuracy, and so on.

Therefore, the research results of this paper effectively verify the accuracy of the interaction between ABAQUS and FRANC3D on the simulation analysis of crack propagation of high-strength bolts, which can provide effective theoretical guidance for the optimal design, effective prediction, and extension of the high-strength bolt fatigue life of the same type.

Conclusions

In this work, the fatigue crack propagation behavior of high-strength bolts with initial crack defects under various load ratios was studied by combining experimental and numerical simulation methods, including the shape of the crack propagation section, the propagation path, and the change rule of the SIF at the crack front. The experimental results are in good agreement with the simulation results, which verifies the effectiveness and accuracy of the numerical simulation method. The main points are as follows:

1. By establishing an accurate three-dimensional model for finite-element calculation, the stress state and the location of maximum stress concentration, that is, the fatigue crack sprouting point, were obtained for the high-strength bolts in the preloaded state. The finite-element results are in good agreement with the analytical solution, which effectively verifies the accuracy of the finite-element model.

2. The propagation process of fatigue cracks at the maximum stress concentration of bolts under the coupling of preload and axial excitation was effectively simulated by the ABAQUS-FRANC3D co-simulation. According to the simulation results of FRANC3D for SIFs in all directions, it is shown that the bolt mainly propagates with a mode I crack. Under a certain preload, the fatigue crack propagation life increases exponentially with the axial excitation load ratio. The SIFs at the crack front increase with crack propagation depth, and the crack propagates at a slow-to-fast rate.

3. The experimental results show that the fatigue fracture surface of the bolts can be obviously divided into three regions: CIZ, CPZ, and TBZ. The cracks in front of CPZ show a series of semi-elliptical shapes. It is also concluded that the crack propagation life of bolts increases with the increase in load ratio, and the crack propagation of the bolt is carried out at a slow-to-fast rate, which matches the simulation results.

4. The experimental outcomes agree very well with the simulation results, indicating that the numerical simulations based on linear elastic fracture mechanics can be effectively applied to predict the fatigue crack propagation life of high-strength bolts with initial defects, which is of great engineering significance.

5. Based on the research results of this paper, the average load, the load ratio, and the load amplitude can be optimized by numerical simulation to prolong the fatigue crack propagation life as much as possible and maximize the use value of high-strength bolts. In addition, the effects of temperature, corrosion, and surface treatment on the fatigue crack propagation behavior of high-strength bolts are also the focus of future work.

Author biographies

Ping Zhang is a doctoral student in Mechanical Engineering. Her area of research is the fatigue of mechanical structure, engineering mechanics, and fracture.

Jiachun Li is a professor in Mechanical Engineering. His area of research is mechanical optimization design and structural fatigue, focusing on crack initiation and crack propagation.

Yu Zhao is a master's graduate student. His area of research is thread rolling processing and fatigue analysis of standard parts.

Jiaxiao Li is an enterprise engineer. His area of research is the rolling processing of screw thread.