ConvexML: Scalable and accurate inference of single-cell chronograms from CRISPR/Cas9 lineage tracing data

Abstract

CRISPR/Cas9 gene editing technology has enabled lineage tracing for thousands of cells in vivo. However, most of the analysis of CRISPR/Cas9 lineage tracing data has so far been limited to the reconstruction of single-cell tree topologies, which depict lineage relationships between cells, but not the amount of time that has passed between ancestral cell states and the present. Time-resolved trees, known as chronograms, would allow one to study the evolutionary dynamics of cell populations at an unprecedented level of resolution. Indeed, time-resolved trees would reveal the timing of events on the tree, the relative fitness of subclones, and the dynamics underlying phenotypic changes in the cell population – among other important applications. In this work, we introduce the first scalable and accurate method to refine any given single-cell tree topology into a single-cell chronogram by estimating its branch lengths. To do this, we leverage a statistical model of CRISPR/Cas9 cutting with missing data, paired with a conservative version of maximum parsimony that reconstructs only the ancestral states that we are confident about. As part of our method, we propose a novel approach to represent and handle missing data – specifically, double-resection events – which greatly simplifies and speeds up branch length estimation without compromising quality. All this leads to a convex maximum likelihood estimation (MLE) problem that can be readily solved in seconds with off-the-shelf convex optimization solvers. To stabilize estimates in low-information regimes, we propose a simple penalized version of MLE using a minimum branch length and pseudocounts. We benchmark our method using simulations and show that it performs well on several tasks, outperforming more naive baselines. Our method, which we name ‘ConvexML’, is available through the <momospace>cassiopeia</momospace> open source Python package.

1. Introduction

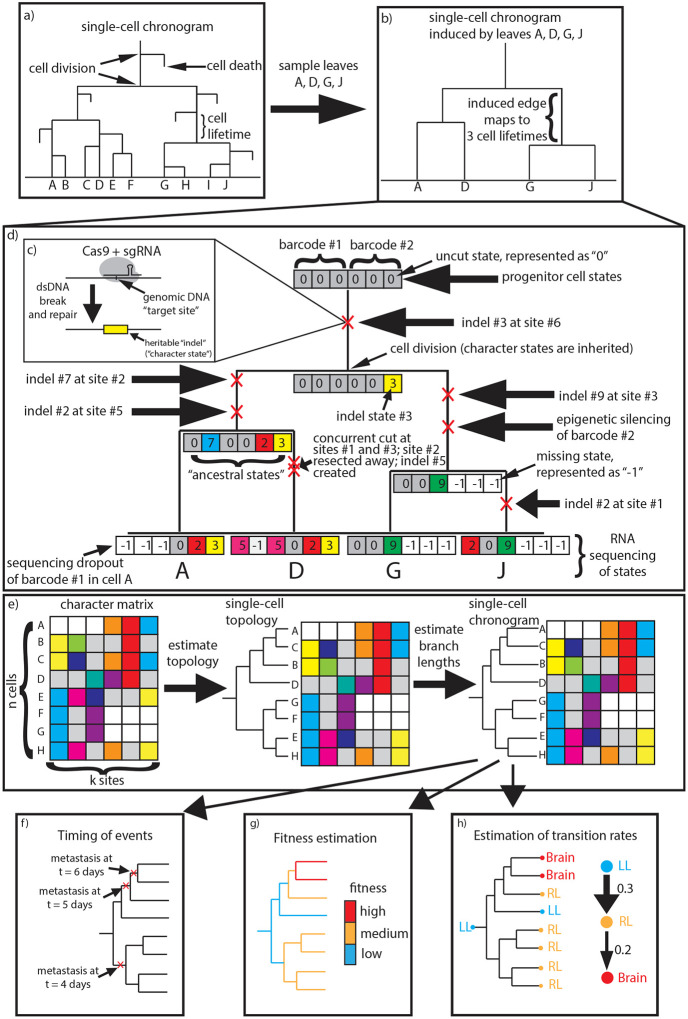
Many important biological processes such as development, cancer progression and adaptive immunity unfold through time, originating from a small progenitor cell population and progressing through repeated cell division. A realization of these processes can be described by a single-cell chronogram: a rooted tree that represents the history of a clone, where each edge represents the lifetime of a cell, and internal nodes represent cell division events, as depicted in Figure 1A. Single-cell chronograms thus capture the entire developmental history of the cell population, allowing us to understand when and how cells commit to their fates. Because of this, single-cell chronograms have been of interest for decades.

Figure 1:

(A) A single-cell chronogram over 10 cells A-J. (B) The single-cell chronogram induced by leaves A, D, G, J. (C) CRISPR/Cas9 binds and cuts a target site, introducing an indel at that site. (D) The CRISPR/Cas9 lineage tracing system recording the lineage history of a cell population. We represent the uncut state with ‘0’, distinct indels with positive integers, and missing data with ‘−1’. Note specifically our choice of representation of double-resection events. (E) Our approach to estimating single-cell chronograms from CRISPR/Cas9 lineage tracing data: A single-cell topology is first estimated using any of many available methods, such as those provided by the cassiopeia package [1] or otherwise [2]. Next, our novel branch length estimator is applied to estimate branch lengths for that topology. (F-H) Single-cell chronograms reveal the timing of events on the tree, single-cell fitness scores, and phenotypic transition rates, among other important applications.

Almost 40 years ago, the first single-cell chronogram for the development of C. elegans was determined through visual observation over the timespan from zygote to hatched larva [3, 4]. Since then, the advent of CRISPR/Cas9 genome editing and high-throughput single-cell sequencing technologies has enabled lineage tracing for thousands of cells in vivo [5, 6, 7, 8, 9, 10]. However, unlike microscopy-based techniques, these approaches record lineage history indirectly through irreversible heritable Cas9 mutations – called indels – at engineered DNA target sites, as depicted in Figure 1C. These target sites (or simply sites) are arranged into lineage tracing barcodes (or character arrays) that act as fake genes which mutate stochastically and are transcribed and measured through the transcriptome. Figure 1D depicts the evolution and inheritance of CRISPR/Cas9 lineage tracing barcodes on a single-cell chronogram. Inferring a lineage tree from this CRISPR/Cas9 lineage tracing data is challenging, and has led to the development of many computational methods [2].

Single-cell chronograms provide a detailed account of the cell population’s history, revealing the timing of events on the tree, the relative fitness of subclones, and the dynamics underlying phenotypic changes in the cell population – among others, as depicted in Figure 1F–H. This is in contrast to single-cell tree topologies, which are like single-cell chronograms except that they do not have branch lengths. Although single-cell tree topologies reveal the lineage relationships between cells, the lack of time resolution precludes them from tackling the aforementioned tasks.

Unfortunately, the task of estimating single-cell chronograms from CRISPR/Cas9 lineage tracing data is daunting, and methods developed so far have abandoned the hope of estimating single-cell chronograms to their full resolution. For one, only extant cells are sequenced, so it is not possible to pinpoint cell death events. Also, only a fraction of the cells in the population are sampled and sequenced, so one can only expect to estimate the single-cell chronogram induced by the sampled cells. Formally, the induced chronogram is defined as the subtree whose leaves are the sampled cells. For example, Figure 1B illustrates the induced chronogram obtained by sampling cells A, D, G, J in the chronogram from Figure 1A. Note that edges in the induced chronogram no longer map one-to-one to the lifetime of a cell; instead, they map one (edge)-to-many (cell lifetimes). Sampling cells greatly affects the distribution of branch lengths in the tree, as shown in Supplementary Figure S1. Most methods developed so far have not attempted to estimate branch lengths, opting instead to estimate just topologies [2], limiting their value.

The task of estimating single-cell chronograms is complicated by the fact that lineage tracing data are especially prone to go missing. There are three primary reasons for this. The first one is sequencing dropouts, whereby the limited capture efficiency of single-cell RNA-sequencing technologies leads to some barcodes not being sequenced. The second reason is heritable epigenetic silencing events. When this occurs, chromatin state is modified in such a way that a lineage tracing barcode is no longer transcribed and thus cannot be read out through the transcriptome. The third reason is double-resection events, wherein concurrent CRISPR/Cas9 cuts at proximal barcoding sites cause the flanked sites to get lost. Missing data from epigenetic silencing and double-resection events is inherited upon cell division. Double-resection events are particularly challenging to represent because they create an indel that spans multiple barcoding sites and introduce complex correlations between barcoding sites which complicate branch length estimation [11]. These three sources of missing data are illustrated in Figure 1D; note specifically our choice of representation of double-resection events, which will turn out to be crucial for branch length estimation.

The estimation of time-resolved trees from molecular data has a rich history outside of single-cell lineage tracing. The field of Statistical Phylogenetics has studied the problem extensively, with the goal of estimating gene trees and species trees from multiple sequence alignments of DNA and amino-acid sequences. Popular software for reconstructing phylogenetic trees includes FastTree [12], PhyML [13], IQ-Tree [14] RAxML [15], and BEAST2 [16]. Unfortunately, these methods are not suitable for CRISPR/Cas9 lineage tracing data because (1) they were designed for small, finite state spaces such as the 20 amino acid alphabet, (2) they require a known substitution model which is usually assumed to be reversible, or (3) they have an elevated computational cost characteristic of Monte-Carlo Bayesian methods, forbidding them from scaling beyond a few hundred sequences. CRISPR/Cas9 lineage tracing datasets contain hundreds of unique states, an unknown substitution model which is irreversible, and hundreds to thousands of cells.

Although attempts have been made to adapt Statistical Phylogenetics models to CRISPR/Cas9 lineage tracing data, they still suffer from elevated computational costs. The recent work TiDeTree [17] implemented withing the BEAST2 platform [16] takes several hours to infer a chronogram for a tree with just 700 leaves. This comes from the need to run MCMC chains for inference. Similarly, the GAPML method [18] which was designed specifically for the GESTALT technology takes up to 2 hours on a tree with just 200 leaves. This comes from modeling the correlations between sites caused by double-resection events, and the cost of marginalizing out the character states of the ancestral (unobserved) cells - which we shall call the ancestral states for short. This calls for new methods that can improve the trade-off between computational efficiency and statistical efficiency.

In this work, we introduce the first scalable and accurate method to estimate single-cell chronograms from CRISPR/Cas9 lineage tracing data. Our approach is modular: we propose first estimating a single-cell topology using any of many available methods [1, 2], and then refining it into a single-cell chronogram by estimating its branch lengths, as depicted in Figure 1E. To estimate branch lengths, we leverage a statistical model for the CRISPR/Cas9 mutation process with missing data, and use a conservative version of maximum parsimony to reconstruct most – but not all – of the ancestral states, while still producing essentially unbiased estimates. We pay particular attention to double-resection events, and propose a novel representation and treatment that is well-suited to our model. Taken together, all this leads to a convex maximum likelihood estimation (MLE) problem that can be readily solved with off-the-shelf convex optimization solvers. Because lineage tracing data can be of varying quality, we propose the use of a penalized version of MLE using a minimum branch length and pseudocounts. Our method typically takes only a few seconds to estimate branch lengths for a tree topology with 400 leaves using a single CPU core.

We develop a benchmarking suite with three tasks to asses the performance of single-cell chronogram estimation methods: (1) estimation of the times of the internal nodes in the tree, (2) estimation of the number of ancestral lineages halfway (time-wise) through the experiment, and (3) fitness estimation. We show that our method performs well on these tasks, outperforming more naive baselines. We also compare our method’s performance against that of an ‘oracle’ model that has access to the ground truth ancestral states and show that it has comparable performance. In contrast, naively employing maximum parsimony leads to biased branch length estimates. This validates the suitability of conservative maximum parsimony for CRISPR/Cas9 lineage tracing data, a key methodological innovation of our work which underlies our scalability. Similarly, we show the suitability of our novel representation of missing data, specifically that concerning double-resection events. To finish, we discuss some of the many extensions of our method that are made possible by its simplicity. We name our method ‘ConvexML’ and make it available through the cassiopeia open source Python package.

2. Methods

2.1. A Statistical Model for CRISPR/Cas9 Lineage Tracing Data

We start by describing how the CRISPR/Cas9 lineage tracing data are represented (or encoded). Let $n$ be the number of cells assayed and let $k$ be the number of lineage tracing sites or characters. The observed lineage tracing data – called the character matrix – is represented as a matrix $X$ of size $n\times k$ with integer entries. The $i$-th row of $X$ represents the observed character states of the $i$-th cell. The character states are grouped consecutively into barcodes of a known fixed size. Each non-missing entry of the character matrix represents an indel - an insertion or deletion of nucleotides at the given site. Indels are represented with distinct positive integers, and 0 is used to represent the uncut state. The integer −1 is used to represent missing data. Figure 1D illustrates the use of this notation. Of particular interest is our representation of double-resection events, which we shall discuss shortly. Our statistical model defines a probability distribution over $X$, and we shall subsequently use maximum likelihood estimation (MLE) to estimate branch lengths.

Data generation process:

To define our statistical model for the data $X$, we will define the data generating process in two steps. In the first step, lineage tracing data is generated without any missingness, which we call $Z$. In other words, we pretend that there are no sequencing dropouts, epigenetic silencing, nor double-resection events. In the second step, we retrospectively analyze the data $Z$ and determine what entries $R$ should have gone missing, thus obtaining $X$. We will formalize this two-step process below, but it is an important conceptual leap because by decoupling the missing data mechanism from the CRISPR/Cas9 mutation process, the distribution of $Z$ is easier to analyze since independence between sites holds, whereas this is not true for $X$. Indeed, sequencing dropouts, epigenetic silencing and double-resections all create correlations between different sites of $X$, since if there is a −1 in some site of a barcode, a −1 is more likely to also be present in an adjacent site of the barcode, as seen in Figure 1D.

To provide intuition for how this two-step process works, it is instructive to consider a simpler statistical model: one in which we roll $n$ dice, and each die roll has a probability $\varphi$ of being made to go missing. There are two equivalent ways to model this: in the first way, before rolling a die, we decide whether it will go missing. If so, we do not roll the die. In the second way, we first roll all the dice, obtaining die rolls $Z$, and afterward determine which die rolls to hide (by replacing their values with −1) to obtain the observed data $X$. Both models are equivalent in that they induce the same probability distribution for the observed data $X$. However, the second approach is richer because it provides us with extra random variables in $Z$ – essentially, counterfactuals for the values of the missing entries. This way of thinking is convenient for analyzing CRISPR/Cas9 lineage tracing data, as it simplifies the mathematical derivation of the MLE.

Statistical model:

Let us thus formally define the statistical model for CRISPR/Cas9 lineage tracing data $X$. We start by defining a model for $Z$ – the process without missing data. Let $𝒯$ be the given single-cell tree topology over the $n$ cells – that is to say, a leaf-labeled, rooted tree whose leaves correspond to the $n$ cells. The model is parameterized by branch lengths $l\in {\mathbb{R}}_{\ge 0}^m$ for $𝒯$; here $m$ is the number of edges of $𝒯$. Let ${𝒯}_l$ be the single-cell chronogram obtained by assigning the branch lengths $l$ to $𝒯$. The generative model for $Z$ is as follows:

1. The $k$ sites are independent and identically distributed.

2. Each site evolves down the tree ${𝒯}_l$ following a continuous-time Markov chain defined as follows:

   1. Each site starts uncut at the root (in state 0).

   2. CRISPR/Cas9 cuts each site with a rate of $c$, where $c$ is a nuisance parameter.

   3. When a site is cut, it takes on state $s\in \mathbb{N}=\{1,2,3,\dots \}$ with probability $q_s\ge 0$, where $q$ is nuisance probability distribution over $\mathbb{N}$.

   4. Once a state is cut, it can no longer be cut again.

We denote by $\theta =(l,c,q)$ the full set of model parameters including the nuisance parameters. By the end of the process we obtain $Z$, the states for all the leaves in the tree. More generally, the process described so far defines a statistical model $𝒫=\left\{p_{\theta }\right\}$ for lineage tracing data representing the character states for all the nodes in the tree $𝒯$; we denote these data by $\tilde{Z}$, which is a random matrix of size $\tilde{n}\times k$ where $\tilde{n}$ is the number of nodes in $𝒯$ (including internal nodes).

Missing data:

The final step is to model the missing data mechanism occurring over the tree, which explains how to obtain $X$ from $Z$. For this, following [19], let $\tilde{R}$ be the binary response/missingness mask matrix of size $\tilde{n}\times k$ indicating which entries of $\tilde{Z}$ ought to (not) go missing (with $\tilde{R}=0$ for missingness and $\tilde{R}=1$ for response). Given $\tilde{R}$ and $\tilde{Z}$, the actual data generated by the process at all nodes of the tree, which we denote as $\tilde{X}$, is:

$${\tilde{X}}_{i,j}=\left\{\begin{array}{ll}{\tilde{Z}}_{i,j},& \text{if}{\tilde{R}}_{i,j}=1,\\ -1,& \text{if}{\tilde{R}}_{i,j}=0.\end{array}\right.$$

The subset of $\tilde{X}$ corresponding to the leaf nodes is then $X$ – what we observe and were looking to model. We need to specify how $\tilde{R}$ is jointly distributed with $\tilde{Z}$. We will take a very general approach of Mealli and Rubin [20], and assume that missing data is missing always completely at random (MACAR), meaning the missing data mask $\tilde{R}$ is independent from the lineage tracing data $\tilde{Z}$. Formally, we assume a joint factorization $p_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{Z}=\tilde{z},\tilde{R}=\tilde{r})=p_{\theta }(\tilde{Z}=\tilde{z})g_{\varphi }(\tilde{R}=\tilde{r})$, where $\varphi$ are the parameters of the missing data mechanism (such as the sequencing dropout probability, epigenetic silencing rate, or temporal proximity of cuts required to induce a double-resection). However, we assume nothing else about the distribution $g_{\varphi }(\tilde{R}=\tilde{r})$, meaning that we take a non-parametric approach to missing data. In particular, the entries of the missing data mask $\tilde{R}$ may be correlated, as in sequencing dropouts, epigenetic silencing and double-resection events. Lastly, we will assume that $\varphi$ and $\theta$ are distinct, meaning that the value of $\theta$ puts no constrains on the value of $\varphi$ and vice versa; formally $(\theta ,\varphi )\in \mathrm{\Theta }\times \mathrm{\Phi }$ for some sets $\mathrm{\Theta }$ and $\mathrm{\Phi }$. The MACAR and distinctness assumptions are together called ignorability of the missing data mechanism, and are crucial for justifying maximum likelihood estimation with missing data [20], as we will do shortly.

Modeling double-resections:

An important use of ignorable missing data is to model double-resection events. Biologically, in a double-resection event, two sites $i$ and $j$ in the same barcode are cut close in time, resulting in the whole segment of sites between $i$ and $j$ to disappear, and a shared indel to be created spanning all sites $i$ through $j$. Double-resection events are quite common and can be identified from the sequencing reads. Just like epigenetic silencing events, double-resection events are heritable. Prior work has chosen to represent double-resection events using complex indel states called ‘indel tracts’ [18]. Unfortunately, this substantially complicates branch length estimation since complex correlations between barcoding sites need to be modeled. Instead, we propose a novel representation of double-resections which is computationally tractable and does not compromise the quality of branch length estimates. Mathematically, we choose to model double-resection events via an ignorable missing data mechanism, as follows: if concurrent cuts at sites $i$ and $j$ cause a double-resection, then sites $i+1$ through $j-1$ inclusive become ignorable missing data, as illustrated in Figure 1D. Note that sites $i+1$ through $j-1$ could have had mutations after the double-resection event in a reality with no missing data; these are precisely the counterfactuals modeled by $\tilde{Z}$. We choose not to model the fact that the indel created at sites $i$ and $j$ is shared; instead, we just retain the indels created by the model without missing data, i.e. two independent indels drawn from $q$ as if double-resections did not exist in the first place. As we will show later in a targeted experiment, this representation and treatment of double-resection events leads to accurate branch length estimates.

We have now defined a statistical model ${𝒫}^{(\text{mis})}=\{p_{\theta ,\varphi }^{\text{mis}}\}$ for the lineage tracing data $X$ with missingness. The full list of random variables defined is outlined in Table 1. We now proceed to discuss how this statistical model for $X$ aligns with the biology behind the CRISPR/Cas9 lineage tracing assay, and how it is misspecified.

Table 1:

Random variables used throughout. Upper case letters with tilde denote random matrices of size $\tilde{n}\times k$ with one row per node in the tree while capital letter without tilde denote the submatrix of size $n\times k$ corresponding to the leaf nodes.

Random Variables	Sizes	Meaning
$\tilde{Z},Z$	$\tilde{n}\times k,n\times k$	Lineage tracing states without missing data
$\tilde{R},R$	$\tilde{n}\times k,n\times k$	Binary response (1)/missingness (0) mask
$\tilde{X},X$	$\tilde{n}\times k,n\times k$	Lineage tracing states with missing data

Discussion of model assumptions:

First, let us discuss the assumption that the sites in $\tilde{Z}$ are independent. Since we choose to model sequencing dropouts, epigenetic silencing and double-resection events as missing data mechanisms, the missing data they introduce do not violate the independence of sites in $\tilde{Z}$ (instead, it is the sites in $\tilde{X}$ that are correlated). Secondly, CRISPR/Cas9 uses a different guide RNA sequence for each target site in a given barcode, so target sites within the same barcode evolve independently. Thirdly, barcodes are integrated randomly into the genome, so that they are far enough apart to interact with CRISPR/Cas9 independently. The only source of non-trivial model misspecification comes from our assumption that double-resections create two independent alleles at the two cut sites, when in fact the resulting indel should be shared and thus correlated, as seen in Figure 1D. This independent treatment of correlated indels may seem inappropriate, but it can be viewed as a form of composite-likelihood, which in general is known to retain consistency for parameter estimation under weak assumptions [21, 22]. As we show later, when paired with conservative maximum parsimony, our method can produce highly accurate estimates of branch length even with large double-resection events. Thus, overall, independence of sites in $\tilde{Z}$ turns out to be a reasonable assumption for branch length estimation.

Now let us discuss the assumption that sites in $\tilde{Z}$ are identically distributed. Due to the local state of chromatin, some lineage tracing barcodes might be more prone to CRISPR/Cas9 cutting than others, leading to different cut rates across sites. Site rate variation has received attention in the field of statistical phylogenetics, where it has led to the development of more sophisticated methods, such as [11, 23, 24]. However, models that assume equal rates across sites still perform well and have been used extensively, such as the seminal work of Whelan and Goldman [25]. Modeling site rate variation also leads to slower runtimes. Therefore, in this work we will assume that all sites are cut at the same (unknown) rate, leaving analysis of more sophisticated models for future work.

The Markov assumption governing site evolution is standard for analyzing molecular data, and is the workforce of Statistical Phylogenetics, enabling complex yet tractable statistical models. Hence, we adopt it in our work.

Regarding the ignorability of the missing data mechanism, we must consider the three different sources of missing data: sequencing dropouts, epigenetic silencing, and double-resections. Ignorability is true for sequencing dropouts, since all barcodes are equally likely to be dropped out during RNA-sequencing, regardless of their indel state, and the dropout probability is distinct from $\theta$. Ignorability can also hold for epigenetic silencing. For example, suppose that barcodes get silenced at each node $v$ of the tree $𝒯$ with some probability ${\varphi }_v$. In this case, the parameter of the missing data mechanism would be the vector of probabilities $\varphi$ of dimension $\tilde{n}$. It is distinct from $\theta$, and $\tilde{R}$ is independent of $\tilde{Z}$ for any $\theta ,$ $\varphi$, so that ignorability holds. On the other hand, suppose that the probability of epigenetic silencing at node $v$ of ${𝒯}_l$ depends on the branch lengths, for example ${\varphi }_v=1-\mathrm{e}\mathrm{x}\mathrm{p}(-t\eta )$ where $t$ is the distance from the parent of $v$ to $v$, and $\eta$ is a rate parameter. In this case, the epigenetic silencing mechanism is not ignorable because $\varphi$ is not distinct from $\theta$. For similar reasons, missing data created by double-resection events is generally not ignorable. However, because it hinders scalability and avoids imposing potentially-misspecified parametric assumptions on the epigenetic silencing mechanism and on double-resection events, we also assume they are ignorable. Any other missing data mechanisms, should they exist, are also treated as ignorable. As we show later, this ignorable model of missing data yields accurate branch lengths despite misspecification, showing its suitability.

2.2. Maximum Likelihood Estimation of Branch Lengths

Having defined a statistical model for lineage tracing data $X$ and discussed the suitability of the modeling assumptions made, we proceed to show how to perform maximum likelihood estimation of branch lengths under this model. Crucially, we show how to deal with unobserved ancestral states, missing data, and the nuisance parameters $c$ and $q$.

We first deal with unobserved ancestral states. Let $x$ be the observed value of $X$. The maximum likelihood estimator of branch lengths is given by:

$${\widehat{l}}_{\text{MLE}}\in \underset{l:{𝒯}_l\text{ultrametric}}{\arg \mathrm{m}\mathrm{a}\mathrm{x}}\underset{c,q,\varphi }{\mathrm{m}\mathrm{a}\mathrm{x}}\log p_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}\left(X=x\right).$$ (1)

Here, $\text{ultrametric}$ means that all leaves in the tree have the same distance from the root. This condition is imposed because all cells are sampled at the same time, but it is possible to relax this condition to account for temporal sampling of cells.

Unobserved ancestral states:

To deal with unobserved ancestral states, we reconstruct most – but not all – of the ancestral states with a conservative version of maximum parsimony. Concretely, we only reconstruct ancestral states that are unambiguous under all maximum parsimony reconstructions consistent with the evolutionary process, as described in detail in Appendix B. In other words, we only reconstruct ancestral states which we are confident about. Ambiguous states are not reconstructed – represented with the new symbol NONE (not to be confused with the missing data state −1) – and marginalized over by considering all possibilities, just like in an ignorable missing data mechanism. Intuitively, one can think about conservative maximum parsimony in terms of mutation mapping: we are trying to map each entry $s>0$ in the character matrix to exactly one edge in the tree (the edge on which said mutation was introduced); however, it is possible that an entry can be optimally mapped to more than one edge of the tree. In this case, the set of possible optimal edges will form a path. Since we do not know on which of those edges of the path the mutation happened, we do not reconstruct the state along the internal nodes of the whole path, using the symbol NONE instead. The state in nodes above the path is reconstructed as 0, and in nodes below the path as $s$. Concrete examples are shown in Figure S16 and Figure S17.

Essentially, what we have is a missing data mechanism (with missing data state NONE) on top of the original missing data mechanism (with missing data state −1). This is mathematically equivalent to a single ignorable missing data mechanism. Therefore, in what follows, we drop the NONE symbol and replace it with the missing data state −1, which thus now stands for sequencing dropouts, heritable missing data, double-resection missing data, and ambiguous ancestral states. All this missing data are treated as ignorable and hence marginalized out during MLE.

As we show in Theorem 5, conservative maximum parsimony has the key property that missing data states −1 can be marginalized out trivially. Importantly, the likelihood is essentially as easy to compute as if there were no missing data. Letting $\tilde{x}$ be the conservative maximum parsimony reconstruction of ancestral states (with NONE replaced by −1 as discussed, since it is mathematically equivalent), the MLE amounts to:

$${\widehat{l}}_{\text{MLE}}\in \underset{l:{𝒯}_l\text{ultrametric}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}\underset{c,q,\varphi }{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{l}\mathrm{o}\mathrm{g}{p}_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{X}=\tilde{x}).$$ (2)

We assume that the solution to the optimization problem Eq. (1) is close to that of Eq. (2). This is a good assumption if the ancestral states in $\tilde{x}$ are correctly reconstructed, but otherwise risks biasing the MLE. As we demonstrate later through simulation in Fig. 3, conservative maximum parsimony introduces essentially no bias, unlike naive maximum parsimony, and hence the reconstructions in $\tilde{x}$ are reliable.

Figure 3: Conservative maximum parsimony enables negligible bias.

By simulating a massive number of lineage tracing characters on a tree and performing MLE, we explored the bias of our conservative maximum parsimony approach as a function of the number of indel states. We can see that as the number of indel states increases, the bias quickly goes away, unlike for naive maximum parsimony. Because CRISPR/Cas9 lineage tracing systems are characterized by their large state space, this makes conservative maximum parsimony a powerful tool in this setting.

Missing data:

We next deal with missing data. The theory for dealing with ignorable missing data is well established [26, 20, 19], but we reproduce the necessary derivations here for a self-contained exposition; the key result is that under ignorability, we can treat the non-missing entries of $\tilde{X}$ as having been sampled from their marginal distribution.

We start by defining $\tilde{r}(\tilde{x})\in \{0,1{\}}^{\tilde{n}\times k}$ to be the missing data mask corresponding to $\tilde{x}$. We will use the following notation:

Definition 1.

Let $a$ and $b$ be matrices of the same dimensions, with $b$ being binary. We denote by $a\left[b\right]$ the vector obtained by concatenating the entries of $a$ for which the corresponding entries in $b$ equal 1. $A\left[b\right]$ is similarly defined for a random matrix $A$ of the same dimensions as $b$. We still index $a\left[b\right]$ and $A\left[b\right]$ as matrices for convenience, but it is important to note that they are just a subset of the matrix entries.

The following result establishes that we can ‘ignore’ missing data, as done in [26, 19]:

Proposition 1.

For all $\theta$, $\varphi$, $\tilde{x}$ it holds that:

$$p_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{X}=\tilde{x})=g_{\varphi }(\tilde{R}=\tilde{r}(\tilde{x}))p_{\theta }(\tilde{Z}[\tilde{r}(\tilde{x})]]=\tilde{x}[\tilde{r}(\tilde{x})]).$$

Importantly, since $\varphi$ is distinct from $\theta$, then $\varphi$ and $\theta$ can be optimized independently in Eq. (2). Therefore, the MLE reduces to:

$${\widehat{l}}_{\mathrm{M}\mathrm{L}\mathrm{E}}\in \underset{l:{𝒯}_l\text{ultrametric}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}\underset{c,q,}{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{l}\mathrm{o}\mathrm{g}{p}_{\theta }(\tilde{Z}[\tilde{r}(\tilde{x})]=\tilde{x}[\tilde{r}(\tilde{x})]).$$ (3)

Proof.

We have

$$p_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{X}=\tilde{x})$$

$$(\tilde{R}\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{f}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{f}\tilde{X})⟹=p_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{X}=\tilde{x},\tilde{R}=\tilde{r}(\tilde{x}))$$

$$(\text{definition}\text{of}\tilde{X})⟹=p_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{Z}[\tilde{r}(\tilde{x})]=\tilde{x}[\tilde{r}(\tilde{x})],\tilde{R}=\tilde{r}(\tilde{x}))$$

$$(\text{marginalize}\text{out}\text{missing}\text{data})⟹=\sum _y{p}_{\theta ,\varphi }^{\mathrm{m}\mathrm{i}\mathrm{s}}(\tilde{Z}[\tilde{r}(\tilde{x})]=\tilde{x}[\tilde{r}(\tilde{x})],\tilde{Z}[\mathbf{1}-\tilde{r}(\tilde{x})]=y,\tilde{R}=\tilde{r}(\tilde{x}))$$

$$(\text{MACAR}\text{factorization})⟹=g_{\varphi }(\tilde{R}=\tilde{r}(\tilde{x}))\sum _y{p}_{\theta }(\tilde{Z}[\tilde{r}(\tilde{x})]=\tilde{x}[\tilde{r}(\tilde{x})],\tilde{Z}[\mathbf{1}-\tilde{r}(\tilde{x})]=y)$$

$$(\text{marginalize}\text{out}\text{missing}\text{data})⟹=g_{\varphi }(\tilde{R}=\tilde{r}(\tilde{x}))p_{\theta }(\tilde{Z}[\tilde{r}(\tilde{x})]=\tilde{x}[\tilde{r}(\tilde{x})]),$$

where 1 in lines 4 and 5 denotes an all-ones matrix of the same dimensions as $\tilde{r}(\tilde{x})$. □

Nuisance parameters:

Finally, it remains to deal with the nuisance parameters $c$ and $q$. To do this, we first unclutter notation by using the standard notation ${\tilde{Z}}^{(1)}=\tilde{Z}[\tilde{r}(\tilde{x})]$, ${\tilde{x}}^{(1)}=\tilde{x}[\tilde{r}(\tilde{x})]$, and so on [20] (note that the dependence on $\tilde{x}$ is now implicit), using the superscript ‘ 1 ‘ to subset the non-missing entries of the object. Let $V$ be the vertex set of $𝒯$, and $E$ the edge set of $𝒯$. Since $𝒯$ is rooted, we give edges their natural orientation pointing away from the root. For a node $v$ and site $i$, we denote by ${\mathrm{g}\mathrm{p}\mathrm{a}}_i(v)$ the first ancestor of $v$ which has a non-missing state at site $i$ (read as ‘grandparent’). The log-probability in the MLE objective in Eq. (3) is then given by

$$\begin{array}{l}\text{log}{p}_{\theta }({\tilde{Z}}^{(1)}={\tilde{x}}^{(1)})=\sum _{i=1}^k\text{log}{p}_{\theta }({\tilde{Z}}_{:,i}^{(1)}={\tilde{x}}_{:,i}^{(1)})\\ =\sum _{i=1}^k\sum _{v\in V,u={\text{gpa}}_i(v):{\tilde{x}}_{v,i}\ne -1}\text{log}{p}_{\theta }({\tilde{Z}}_{v,i}={\tilde{x}}_{v,i}\mid {\tilde{Z}}_{u,i}={\tilde{x}}_{u,i}),\end{array}$$ (4)

where the first equality follows from the independence of sites. The second equality requires using combinatorial properties of the conservative maximum parsimony reconstruction, and is proved in Theorem 5 in Appendix B. Finally, letting $l_{uv}$ be the length of the path from $u$ to $v$ in the tree, we can compute the probability of an observed transition between nodes $u\to v$ where $u={\mathrm{g}\mathrm{p}\mathrm{a}}_i(v)$ as follows:

$$p_{\theta }\left({\tilde{Z}}_{v,i}={\tilde{x}}_{v,i}\mid {\tilde{Z}}_{u,i}={\tilde{x}}_{u,i}\right)=\left\{\begin{array}{ll}1,& \text{if}{\tilde{x}}_{v,i}={\tilde{x}}_{u,i}>0,\\ \mathrm{e}\mathrm{x}\mathrm{p}\left(-c{l}_{uv}\right),& \text{if}{\tilde{x}}_{v,i}={\tilde{x}}_{u,i}=0,\\ \left(1-\mathrm{e}\mathrm{x}\mathrm{p}\left(-c{l}_{uv}\right)\right)q_{{\tilde{x}}_{v,i}},& \text{if}{\tilde{x}}_{u,i}=0\text{and}{\tilde{x}}_{v,i}>0.\\ 0& \text{otherwise.}\end{array}\right.$$ (5)

Plugging this into Eq. (4), we arrive at

$$\text{log}{p}_{\theta }({\tilde{Z}}^{(1)}={\tilde{x}}^{(1)})=\sum _{i=1}^k\left[\sum _{v\in V,u={\text{gpa}}_i(v):{\tilde{x}}_{v,i}={\tilde{x}}_{u,i}=0}-c{l}_{uv}+\sum _{v\in V,u={\text{gpa}}_i(v):{\tilde{x}}_{u,i}=0\text{and}{\tilde{x}}_{v,i}>0}\text{log}(1-\text{exp}(-c{l}_{uv}))+\text{log}{q}_{{\tilde{x}}_{v,i}}\right].$$ (6)

Note that in Eq. (6), the term $\mathrm{l}\mathrm{o}\mathrm{g}{q}_{{\tilde{x}}_{v,i}}$ does not depend on $l$, so we can drop it from the objective function and hence, crucially, the MLE does not depend on $q$. To finish, let us denote by $\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{s}(u\to v)$ and $\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{s}(u\to v)$ the number of characters that go uncut and cut, respectively, on the path from $(u,v)$. In other words,

$$\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{s}(u\to v)=\#\left\{i\in \left\{1,\dots ,k\right\}:u={\mathrm{gpa}}_i\left(v\right),{\tilde{x}}_{v,i}={\tilde{x}}_{u,i}=0\right\},$$

$$\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{s}(u\to v)=\#\left\{i\in \{1,\dots ,k\}:u={\mathrm{g}\mathrm{p}\mathrm{a}}_i(v),{\tilde{x}}_{u,i}=0\text{and}{\tilde{x}}_{v,i}>0\right\}.$$

The MLE problem hence simplifies to

$${\widehat{l}}_{\text{MLE}}\in \underset{l:{𝒯}_l\text{ultrametric}}{\text{arg}\text{max}}\underset{c}{\text{max}}\sum _{u,v\in V}\left[-\text{uncuts}(u\to v)c{l}_{uv}+\text{cuts}(u\to v)\text{log}(1-\text{exp}(-c{l}_{uv}))\right].$$ (7)

Although the MLE no longer depends on $q$, it still depends on the nuisance parameter $c$. It is a well known fact that branch lengths $l$ and cut rate parameter $c$ are unidentifiable without further assumptions, since they can be scaled up and down by the same constant without changing the likelihood. To resolve this ambiguity, without loss of generality, we assume that the chronogram has depth exactly equal to 1, which is equivalent to assuming that without loss of generality the duration of the experiment is normalized to 1. In other words, we solve for:

$${\widehat{l}}_{\text{MLE}}\in \underset{\begin{array}{c}l:{𝒯}_l\text{ultrametric,}\\ {𝒯}_l\text{has}\text{depth}1\end{array}}{\text{arg}\text{max}}\underset{c}{\max }\sum _{u,v\in V}[-\text{uncuts}(u\to v)c{l}_{uv}+\text{cuts}(u\to v)\text{log}(1-\text{exp}(-c{l}_{uv}))].$$ (8)

This is equivalent to solving the MLE problem in Eq. (7) using a cut rate of $c=1$, and afterwards scaling the chronogram to unit depth. Since the MLE problem in Eq. (7) with $c=1$ is an exponential cone program in the variables $\left\{l_{uv}:(u,v)\in E\right\}$, it can be readily solved with off-the-shelf convex optimization solvers. When we implement the method, we exclude any terms in the objective where $\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{s}(u\to v)=0$ or $\mathrm{c}\mathrm{u}\mathrm{t}\mathrm{s}(u\to v)=0$ since they do not contribute, leading to a computation graph which has size essentially $O(n)$ rather than $O\left(n^2\right)$ and thus leads to significantly faster runtime. This concludes optimization under the proposed model. In our implementation, for trees with 400 leaves and as many as 150 characters, the optimizer takes just a few seconds. In contrast, a method like TiDeTree takes several hours on a tree with 700 leaves [17]. We leverage the cvxpy Python library [27, 28] and the ECOS [29] and SCS [30] solvers as the backend. We find that ECOS is faster but can sometimes fail, in which case we fallback to the slower but more robust SCS solver.

2.3. Regularizing the MLE

Due to limited lineage tracing capacity, it is not unusual for some cells in the population to have the exact same lineage tracing character states. When this happens, the single-cell tree topology will contain subtrees whose leaves all have the same character states. We call these homogeneous subtrees. As we show next, the MLE will estimate branch lengths of 0 for these subtrees. Moreover, the result is very general: it does not depend on whether ancestral states have been reconstructed with maximum parsimony or marginalized out, and it does not depend on the continuous-time Markov chain model. Concretely, we prove the following result:

Theorem 1 (Homogeneous Proper Subtree Collapse).

Consider any continuous-time Markov chain model (for example, the Jukes-Cantor model of DNA evolution, the WAG model of amino acid evolution [25], or the CRISPR/Cas9 lineage tracing model in this paper with fixed $c$, $q$). Let $p_l$ be the associated probability measure when running this Markov chain on ${𝒯}_l$. Let $𝒮$ be a proper subtree of $𝒯$ (meaning that it is distinct from $𝒯$). Let $z$ be states for the leaves of the tree such that all leaves of $𝒮$ have the same state, and let $\tilde{z}$ be a reconstruction of the ancestral states of $z$ where all nodes of $𝒮$ have the same state (as in a maximum parsimony reconstruction). Let $l$ be any ultrametric branch lengths for $𝒯$. Then there exist other ultrametric branch lengths $l^{\prime }$ for $𝒯$ that satisfy:

1. All the branch lengths of $𝒮$ are zero under $l^{\prime }$.

2. $p_l(\tilde{Z}=\tilde{z})\le p_{l^{\prime }}(\tilde{Z}=\tilde{z})$.

3. $p_l(Z=z)\le p_{l^{\prime }}(Z=z)$.

Proof.

See Appendix A for a proof. The proof relies on a simple probabilistic coupling argument. □

As a consequence, the MLE can always collapse homogeneous proper subtrees. We coin this phenomenon subtree collapse. More generally, we observed empirically that the MLE defined in Eq. (8) tends to estimate many branch lengths as 0, a phenomenon which we coin edge collapse.

Subtree collapse, and more generally edge collapse, are undesirable because it suggests that some cells have divided arbitrarily fast. To address this issue, and more generally to make the MLE robust in low-information regimes where there is little information to support branch lengths, we propose to combine two simple regularizers. The first is to impose a minimum branch length $ϵ$. This can be easily accomplished by adding the minimum branch length constraint to the MLE optimization problem of Eq. (8). The second is to add pseudocounts to the data, in the form of $\lambda$ cuts and $\lambda$ uncuts per branch. This is like pretending that we have observed $\lambda$ characters getting cut on each edge, as well as $\lambda$ characters remaining uncut on that edge. Intuitively, this regularizes the branch lengths towards trees that look more neutrally evolving. This also has the benefit of making the optimization problem strongly convex, ensuring there is a unique solution. With this, our method falls into the category of penalized likelihood methods [31] like GAPML [18], where the MLE is stabilized with a regularizer to aid in low-information regimes. Other alternatives include Bayesian methods such as TiDeTree [17], but suffer from higher computational costs.

Incorporating our two regularizers to the optimization problem, we obtain:

$${\widehat{l}}_{\text{MLE}}^{ϵ,\lambda }\in \underset{\begin{array}{c}l:{𝒯}_l\text{ultrametric,}\\ {𝒯}_l\text{has}\text{depth}\mathrm{1,}\\ l_{uv}\ge ϵ\forall (u,v)\in E\end{array}}{\text{arg}\text{max}}\underset{c}{\text{max}}\sum _{u,v\in V}[-(\text{uncuts}(u\to v)+\lambda )c{l}_{uv}+(\text{cuts}(u\to v)+\lambda )\text{log}(1-\text{exp}(-c{l}_{uv}))].$$ (9)

This is equivalent to solving the MLE problem Eq. (7) while adding $\lambda$ pseudocounts and imposing the constraints $c=1$ and $l_{uv}\ge ϵd\forall (u,v)\in E$ where $d$ is the depth of ${𝒯}_l$, and then finally normalizing the tree to have a depth of 1. This is still a convex optimization problem in the $\left\{l_{uv}:(u,v)\in E\right\}$ variables and can thus still be solved easily with off-the-shelf convex optimization solvers.

The value of $ϵ$ is interpretable and can thus be selected based on prior biological knowledge. Concretely, if the shortest amount of time that can pass between two consecutive cell division events is known to be approximately $t$, and if the length of the experiment is $T$, then $ϵ$ can be set to $t/T$. Imposing a minimum branch length avoids edge collapse completely.

Pseudocounts are a popular regularization technique with the advantage that the regularization strength $\lambda$ is interpretable in terms of a data perturbation. We explore using values of $\lambda$ equal to 0 (no said regularization), 0.1 (small regularization) and 0.5 (large regularization). Note that pseudocounts do not guarantee that a minimum branch length is satisfied, which is why we use both forms of regularization.

Other regularization strategies are possible, such as the one used by GAPML [18] where large differences in branch lengths are discouraged via an ${\ell }_2$ penalty in log-space. However, we use a minimum branch length and pseudocounts because their regularization strengths $ϵ$ and $\lambda$ are interpretable and thus easier to select without needing to perform an extensive grid search with cross-validation.

3. Results

3.1. Benchmarked Models

We benchmark several models, including ablations, oracles, and baselines. First, we benchmark our MLE using ground truth ancestral states, conservative maximum parsimony, or naive maximum parsimony, which we denote as ${\widehat{l}}_{\mathrm{G}\mathrm{T}+\mathrm{M}\mathrm{L}\mathrm{E}}^{ϵ,\lambda },{\widehat{l}}_{\mathrm{C}\mathrm{M}\mathrm{P}+\mathrm{M}\mathrm{L}\mathrm{E}}^{ϵ,\lambda },{\widehat{l}}_{\mathrm{M}\mathrm{P}+\mathrm{M}\mathrm{L}\mathrm{E}}^{ϵ,\lambda }$, respectively. We set $ϵ$ to a small value of $ϵ=0.01$ and vary $\lambda \in \{0,0.1,0.5\}$. The value of $ϵ=0.01$ was chosen to mimic biological knowledge of minimum cell division times (and may vary depending on the application); Supplementary Figure S2 shows that indeed $ϵ=0.01$ is a reasonable lower bound on cell division times in our simulated trees.

Second, we also benchmark a baseline model ${\widehat{l}}_{\text{Mutations}}$ which sets each branch length to the number of mutations on the branch. This baseline shows what happens if we ignore the mutation model. To avoid assigning a length of zero to edges without mutations, we set their edge length to 0.5 instead. To make the tree ultrametric, we extend all tips to match the depth of the deepest leaf. Finally, we scale the tree to have a depth of 1. Analogously to the MLE, we benchmark three versions of this model: ${\widehat{l}}_{\mathrm{G}\mathrm{T}+\text{Mutations}},{\widehat{l}}_{\mathrm{C}\mathrm{M}\mathrm{P}+\text{Mutations}}$ and ${\widehat{l}}_{\mathrm{M}\mathrm{P}+\text{Mutations}}$ respectively. When using conservative maximum parsimony, mutations that are mapped to $m$ edges are made to contribute $1/m$ mutations to each of those edges.

3.2. Simulated Data Benchmark

Simulation steps:

We evaluate the performance of the models on simulated data. Our simulations involve three steps: (1) simulating a ground truth single-cell chronogram, (2) simulating lineage tracing data on the chronogram, and (3) sampling leaves. Briefly, our ground truth single-cell chronograms are simulated under a birth-death process where the birth and death rates are allowed to change with certain probability at each cell division, allowing us to model changes in the fitness of subclones. The simulation ends when a specified population size is reached; if the whole population of cells dies, we retry. Our simulated lineage tracing assay controls the number of barcodes, the number of sites per barcode, the indel distribution, the CRISPR/Cas9 site-specific mutation rates, and the rates of epigenetic silencing and sequencing dropouts. Sampling leaves is done by specifying the number of sampled leaves.

Evaluation tasks:

Using our simulation framework, we set out to evaluate the performance of the different methods on several tasks, and across varying qualities of lineage tracing data. We considered the following three evaluation tasks and associated metrics:

1. “Internal node time” task: Mean absolute error at estimating the time of the internal nodes in the induced chronogram.

2. “Ancestral lineages” task: Relative error at estimating the number of ancestral lineages halfway (time-wise) through the induced chronogram.

3. “Fitness estimation” task: Spearman correlation at estimating the fitness of each sampled cell. The ground truth fitness of a cell is defined in our simulations as the difference between its birth and death rates. We use the Neher et al.’s LBI estimator [32] as implemented in the jungle package¹ to derive fitness estimates from our single-cell chronograms, as in the work of [33].

Using reconstructed tree topology:

Furthermore, since in real applications we do not have access to the ground truth single-cell tree topology, we also benchmark the performance of the branch length estimation methods when the tree topology must first be estimated. To do this, we first estimate the single-cell topology using the Maxcut solver based on Snir and Rao [34] from the cassiopeia package [1] – which is a supertree method based on triplets – and then apply the branch length estimator. We chose the Maxcut solver since it is a top performer at the triplets correct and Robinson-Foulds metric commonly used to evaluate topology reconstruction quality (Supplementary Figure S3) and runs much faster than the ILP algorithm. We resolve multifurcations into binary splits using a Huffman-tree algorithm wherein subtrees with the least size are merged first. Since the ground truth topology and the reconstructed topology differ, the internal node time task becomes harder to evaluate. To resolve this discrepancy, we create estimates for the time of each internal node $v$ in the ground truth tree by taking the mean time of the MRCA (most recent common ancestor) in the reconstructed tree of all pairs of leaves whose MRCA in the ground truth tree is $v$.

Questions of interest:

With our simulated data benchmark we seek to answer the following questions: (i) Does our method significantly outperform the naive baseline which estimates branch lengths as the number of mutations? (ii) How much does accuracy drop when the single-cell topology must be estimated first – as in real applications – as compared to when the ground truth topology is known? (iii) Does regularization stabilize branch length estimates, particularly in low-information regimes? (iv) Does conservative maximum parsimony provide accurate branch length estimates, as compared to naive maximum parsimony and to the oracle method which has access to ground truth ancestral states? (v) Similarly, does our treatment of double-resection event enable unbiased branch length estimates?

Simulating chronograms:

To answer the above questions, we perform the following simulations. We simulate 50 chronograms with 40,000 extant cells each, scaled to have a depth of exactly 1. We then sample exactly 400 leaves from each tree, thus achieving a sampling probability of 1%. The simulation is performed using a birth-death process with rate variation to emulate fitness changes, and is described in detail in Appendix C. The resulting trees display nuanced fitness variation, as can be seen in Supplementary Figure S4, which shows 9 of our 50 ground truth induced chronograms.

The default parameter regime:

For each chronogram, we simulate a lineage tracing experiment with 13 barcodes and 3 target sites per barcode, for a total of 39 target sites; we choose 3 target sites per barcode based on the technology used in [10, 35, 33]. The per-site CRISPR/Cas9 mutation rates are splined from real data to achieve an expected 50% of mutated entries in the character matrix, and are shown in Supplementary Figure S5. We consider 100 possible indel states with a non-uniform probability distribution $q$, as in real data, such that some states are much more common than others. Concretely, the $q_s$ are taken to be the quantiles of an exponential distribution with scale parameter 10⁻⁵. This non-uniform probability distribution is shown in Supplementary Figure S6. The indels are encoded as integers between 1 and 100 inclusive. We introduce sequencing dropouts and epigenetic silencing missing data mechanisms such that on average 20% of the character matrix is missing, with 10% arising from sequencing dropouts and 10% from epigenetic silencing. The missing data they introduce is represented with the integer −1. Epigenetic silencing occurs similarly to CRISPR/Cas9 mutations, happening with a fixed rate during the whole length of the experiment (which as discussed before, is in fact not an ignorable missing data mechanism). Double-resections are also simulated; they occur whenever two sites in the same barcode are cut before a cell divides, as illustrated in Figure 1D. When a double-resection event occurs at positions $i$ and $j$, we create an identical indel at positions $i$ and $j$ with integer encoding ${10}^8+2^i+2^j$ such that we can identify the endpoints of the double-resection as in real data; positions $i+1$ through $j-1$ go missing and are thus set to −1. If more than two sites in a barcode are cut before the cell divides, $i$ and $j$ are taken to be the leftmost and rightmost of these sites in the barcode. We call the collection of all these lineage tracing parameters the ‘default’ lineage tracing parameter regime. The branch length estimation methods are then evaluated on the three benchmarking tasks described above using the 50 simulated trees.

Varying parameters:

We then proceed to repeat the benchmark, this time varying each of the lineage tracing parameters in turn. This allows us to explore lineage tracing datasets with varying levels of quality, as in real life. We vary the number of barcodes in the set {3, 6, 13, 20, 30, 50}, the expected proportion of mutated character matrix entries in the set {10%, 30%, 50%, 70%, 90%}, the number of possible indels in the set {5, 10, 25, 50, 100, 500, 1000}, and the expected missing data fraction in the set {10%, 20%, 30%, 40%, 50%, 60%}, always keeping the expected sequencing missing data fraction at 10%, and adjusting the expected heritable epigenetic missing data fraction accordingly.

Assessing ancestral state reconstruction:

To specifically analyze the bias of conservative maximum parsimony, we perform a second targeted experiment where we simulate a very large number of lineage tracing characters – 100,002 characters consisting of 33,334 barcodes of size 3 – on one of the previously described trees and then apply the MLE using either (i) ground truth ancestral states, (ii) conservative maximum parsimony, or (iii) naive (standard) maximum parsimony. It is the scalability of our method that allows us to perform such a large-scale experiment to analyze its bias. Since the state space size is crucial for parsimony methods, we vary the number of indel states in the set $\{1,2,\dots ,9\}\cup \{10,20,\dots ,100\}$, so that in particular we explore a binary tracer with a unique indel state. Since missing data makes ancestral state reconstruction challenging, we use 60% expected missing data, with half coming from epigenetic silencing and the other half from sequencing dropouts. Since double-resection events indirectly increase the state space size (as they encode the indices of the outer sites), we initially exclude them from the experiment. Finally, unlike the default parameter regime, to ensure that the main source of model misspecification comes from the reconstruction of unobserved ancestral states, we use the same cut rate for all sites, thus excluding site rate variation from this specific experiment; the cut rate is chosen such that an observed entry of the character matrix has 50% change of being mutated.

Assessing the effect of double-resections:

To specifically explore the effect of double-resections, we repeat the previous experiment which has 100,002 characters but turning on double-resection events, which introduces more missing data but also indirectly increases the state space size. Moreover, to exacerbate the effect of double-resections, we perform a third version of the experiment where we not only simulate double-resections, but also increase the cassette size from 3 to 10 (while keeping the total number of characters controlled and equal to 100,000 by using 10,000 barcodes).

3.3. Performance Comparison

MLE outperforms the baseline estimator:

The performance of each model on the default parameter regime, with and without access to the ground truth topology, is shown in Figure 2. We can see that all variants of our MLE method outperform the baseline estimator. This pattern holds across all lineage tracing parameter regimes, shown in Supplementary Figures S7, S8, and S9.

Figure 2: Performance of branch length estimation methods under the default parameter regime.

For each branch length estimation method, we show the performance both with and without access to the ground truth topology (in black and blue respectively). When the topology is not provided, it is reconstructed with the Maxcut solver from the Cassiopeia package [1]. Branch length estimators are evaluated on three tasks: (A) Estimation of the times of the internal nodes in the tree, (B) Estimation of the number of ancestral lineages midway through the experiment, (C) Estimation of the relative fitness of the cells in the population.

The effects of using reconstructed tree topologies:

We find that using reconstructed single-cell tree topologies – as opposed to ground truth topologies – consistently degrades performance on the internal node time and fitness prediction tasks, as expected. On the ‘ancestral lineages’ task, however, this is not always the case. For example, on the default regime (Figure 2) using a value of $\lambda =0.5$ in our MLE leads to better performance with the reconstructed topology. We attribute this to the MLE being over-regularized and the bias introduced by regularization cancelling off with the bias of the topology reconstruction algorithm. The interaction between topology, branch length estimation procedure, and downstream metric is thus nuanced, and errors in the topology and branch length estimation steps can compound, or more interestingly, cancel each other.

The effects of regularization:

Using regularization improves performance most noticeably in low-information regimes such as when the amount of missing data increases, the expected proportion mutated decreases, or the number of lineage tracing barcodes decreases, as seen in Supplementary Figures S7, S8, and S9. This is expected since the purpose of regularization is precisely to stabilize branch length estimates in low-information regimes. Other than low-information regimes, the regularization strength $\lambda$ makes the most difference on the ancestral lineages task, where a small amount of regularization $\lambda =0.1$ provides the best results. Generally, using some level of regularization as opposed to none appears to be beneficial across the board.

Conservative maximum parsimony vs. naive maximum parsimony:

Conservative maximum parsimony tends to outperform naive maximum parsimony, the gap being most noticeable in high-information regimes such as when the number of lineage tracing barcodes is 50. This makes sense, as only at high sample sizes the risk of the estimator becomes dominated by the bias rather than by the variance. For the ‘internal node time’ task as we increase the number of barcodes, the performance of conservative maximum parsimony remains close to the performance of the oracle model with access to ground truth ancestral states. In contrast, the performance of naive maximum parsimony improves more slowly. For example, the performance of naive maximum parsimony with 50 barcodes is comparable to the performance of conservative maximum parsimony with just 30 barcodes.

In our second experiment, we dissected the bias of our conservative maximum parsimony approach by simulating a very large number of characters (100,002, as described in Section 3.2) on one of our trees and evaluating the performance of the MLE when using either (i) ground truth ancestral states, (ii) conservative maximum parsimony, or (iii) naive maximum parsimony. In the first version of the experiment, we excluded double-resection events since they indirectly increase the state space size. The results are shown in Figure 3. As the number of indel states increases, the bias of conservative maximum parsimony seems to converge to nearly 0 in a geometric fashion. The mean absolute error achieved is negligible when compared to the error for the default lineage tracing regime as seen in Figure 2, which is at least 0.05. Naive maximum parsimony, on the other hand, shows large bias with a MAE of 0.06, which is comparable to the MAEs seen in Figure 2. Since CRISPR/Cas9 lineage tracing systems are characterized by their large state space, this targeted experiment shows the suitability of conservative maximum parsimony for branch length estimation.

The effect of double-resections:

We finished by turning on double-resection events in our previous simulation with 100,002 characters. The results are shown in Supplementary Figure S10A. The indirectly increased state space size due to double-resections improves performance of our branch length estimator for a low number of states, while the misspecified treatment of double-resections minimally degrades performance for larger state space sizes. Increasing the barcode size from 3 to 10 while keeping the number of characters roughly the same magnifies these trends, as shown in Supplementary Figure S10B. Even with these barcodes of length 10, the error of conservative maximum parsimony remains close to 0 for large state space sizes. These results show that paired with conservative maximum parsimony, independent modelling of sites is accurate even in the presence of double-resection events – which is the key to the scalability of our method as compared to previous methods such as GAPML [18].

One may wonder what happens if one uses a different representation of double-resection events, e.g., if one encodes them by assigning the indel state to all sites $i$ through $j$, instead of only to sites $i$ and $j$; in Figure 1D, this would mean assigning state 5 to sites 1,2, and 3, instead of assigning state 5 to sites 1 and 3 and −1 to site 2. This is the current preprocessing behaviour of the Cassiopeia package [1]. The results are shown in Supplementary Figure S11. As we can see, performance deteriorates dramatically, even for the model with ground truth ancestral states. Intuitively, our novel representation of ancestral states is effective because it entails exactly two cutting events, which is the correct number.

Recommendation:

Based on these results, our recommendation to practitioners is to use conservative maximum parsimony with the regularized MLE ${\widehat{l}}_{\text{MLE-Reg}}^{ϵ,\lambda }$ setting $ϵ$ to the best known lower bound on the minimum time between cell division events, and explore values of $\lambda$ of 0.0, 0.1 and 0.5 as we did. For example, if cells are expected to take at least 1 day to divide and the experiment last 60 days, our recommendation would be to set the minimum branch length to $ϵ=1/60\approx 0.016$. Character-level cross-validation is a promising avenue to automate the choice of $\lambda$ (and even $ϵ$) and we leave it to future work. Double-resections should be encoded using our novel representation, with −1 (i.e., missing data) at the internal sites of the double-resection, and the indel state duplicated at the flanking sites, as seen in Figure 1D. To ensure that the indel state created by a double-resection event is distinct from any indel created by a standard single-site cut, we recommend using a modified encoding such as ${10}^{8}s+2^i+2^j$, where $s$ is the original encoding of the indel and $i$, $j$ are the sites of the double-resection. (In particular, note that in our simulations from Section 3.2, we are considering a worse-case scenario where only one indel state is possible during a double-resection.)

4. Discussion

In this work, we introduced the first scalable and accurate method to estimate branch lengths for single-cell tree topologies, refining them into single-cell chronograms. Specifically, we proposed using a regularized maximum likelihood estimator tailored to the CRISPR/Cas9 mutation process. Key to our approach is our treatment of missing data – particularly our representation of double-resection events – paired with our use of a conservative version of maximum parsimony to reconstruct only ancestral states which we are confident about. This simplifies the optimization problem considerably and without introducing the typical bias of maximum parsimony. Specifically, this leads to a convex optimization problem that can be solved in seconds with off-the-shelf convex optimization solvers. We proposed a simple regularization scheme based on a minimum branch length and pseudocounts to stabilize estimates in low-information regimes. We designed a synthetic benchmark with three task and showed that our method performs well on them, outperforming more naive baselines. We specifically showed the ability of our method to estimate branch lengths in an unbiased way even with large amounts of missing data and in the presence of large double-resection events. Finally, we commented on extensions of our method that are made easily available thanks to the convexity of our MLE. Our branch length estimator, which we title ‘ConvexML’, is implemented in the cassiopeia Python package which is publicly available, and the methods and simulation frameworks presented in this paper are also readily available.

The simplicity and scalability of our method enable numerous extensions, some of which we are currently pursuing. For instance, we are working on accounting for site rate variation (i.e., the fact that different target sites evolve at different rates) by allowing a different cut rate for each site; we expect that as lineage tracing technologies get better, site rate variation may become more and more relevant. The resulting optimization problem is essentially identical to the original one if the site-specific rates are known. If the site-specific rates are not known, they can be estimated using a simple coordinate ascent procedure wherein the branch lengths and site rates are optimized in turn. Another important extension is to estimate branch lengths for trees that are not ultrametric. This arises in applications where cells are sampled at different moments in time.

We also plan to explore the use of character-level cross-validation to automatically perform hyperparameter selection; although we aimed to make our hyperparameters as interpretable as possible, a cross-validation scheme would nonetheless decrease the burden on the user. Lastly, we look forward to leveraging our branch length estimator to infer the transcriptional dynamics of cell populations, a problem that is akin to learning amino acid substitution rate matrices and which has its own rich history in the field of statistical phylogenetics. By doing so, we seek to shed light into the transcriptional dynamics of cancer development; in this application, branch lengths are crucial to obtain good quantitative estimates.

Appendix

A. Proof of Subtree Collapse Theorem

We prove a slightly more general version of Theorem 1, which (essentially) implies that subtree collapse happens also when there is missing data and the missing data mechanism is ignorable. In phrasing this Theorem we use notation similar to Rubin’s missing data notation [26], but we make no reference to missing data mechanisms in order to make the result more self-contained. In what follows, let $L(𝒯)$ denote the leaf set of tree $𝒯$ and $V(𝒯)$ denote the node set of $𝒯$.

Theorem 2 (Homogeneous Proper Subtree Collapse, Generalized).

Consider any continuous-time Markov chain model with state space ${\mathbb{Z}}_{\ge 0}$ (for example, the Jukes-Cantor model of DNA evolution, the WAG model of amino acid evolution [25], or the CRISPR/Cas9 lineage tracing model in this paper with fixed $c$, $q$). Given a tree topology $𝒯$ and branch lengths $l$ for $𝒯$, let $\tilde{Z}:V(𝒯)\to {\mathbb{Z}}_{\ge 0}$ be the stochastic process obtained by running this CTMC down the tree ${𝒯}_l$, and let $p_l$ be the associated probability measure for $\tilde{Z}$. Let $Z:L(𝒯)\to Z_{\ge 0}$ be the restriction of $\tilde{Z}$ to the leaves of $𝒯$. Let $v\in V(𝒯)$ be different from the root, and let $𝒮$ be the subtree of $𝒯$ rooted at $v$. Let $L^{\prime }\subseteq L(𝒯)$ be a subset of the leaves of $𝒯$. Let $z^{(1)}:L^{\prime }\to {\mathbb{Z}}_{\ge 0}$ be a state assignment for this subset $L^{\prime }$ of the leaves of $𝒯$ such that all leaves of $𝒮$ in $L^{\prime }$ have the same state – meaning that $z^{(1)}\left(l_1\right)=z^{(1)}\left(l_2\right)$ for all $l_1,l_2\in L^{\prime }\cap L(𝒮)$ – and at least one leaf of $𝒮$ is assigned a state by $z^{(1)}$ - meaning that $L^{\prime }\cap L(𝒮)$ is non-empty. Let $V^{\prime }\subseteq V(𝒯)$ be such that $V^{\prime }\cap L(𝒯)\supseteq L^{\prime }$. Let ${\tilde{z}}^{(1)}:V^{\prime }\to {\mathbb{Z}}_{\ge 0}$ be an extension of $z^{(1)}$ – meaning that ${\tilde{z}}^{(1)}(l)=z^{(1)}(l)$ for all $l\in L^{\prime }–$ and such that all nodes in $𝒮$ are assigned the same state – meaning that ${\tilde{z}}^{(1)}\left(v_1\right)={\tilde{z}}^{(1)}\left(v_2\right)$ for all $v_1,v_2\in V^{\prime }\cap V(𝒮)$. Suppose that $l$ are ultrametric branch lengths for $𝒯$. Let ${\tilde{Z}}^{(1)}$ be the restriction of $\tilde{Z}$ to $V^{\prime }$ and let $Z^{(1)}$ be the restriction of $Z$ to $L^{\prime }$. Then there exist other ultrametric branch lengths $l^{\prime }$ for $𝒯$ that satisfy:

1. All the branch lengths of $𝒮$ are zero under $l^{\prime }$.

2. $p_l({\tilde{Z}}^{(1)}={\tilde{z}}^{(1)})\le p_{l^{\prime }}({\tilde{Z}}^{(1)}={\tilde{z}}^{(1)})$

3. $p_l(Z^{(1)}=z^{(1)})\le p_{l^{\prime }}(Z^{(1)}=z^{(1)})$

Note.

It turns out that it is important that ${\tilde{z}}^{(1)}$ assigns a state to at least one leaf of $𝒮$ (part (a) of the Theorem is false otherwise), but it actually does not matter whether $z^{(1)}$ assigns a state to some leaf of $𝒮$ (part (b) is trivially true in this case).

Proof of Theorem 2.

Let $w$ be the parent of $v$ (which exists since by hypothesis $v$ is not the root of $𝒯$). Let $u$ be a leaf of $𝒮$ assigned a state by $z^{(1)}$ (i.e. $u\in L^{\prime }\cap L(𝒮)$), which exists by hypothesis. Consider the following operation on ${𝒯}_l$, which we call the subtree collapse operation: we take the nodes in $𝒮$ and set their depths to the depth of the tree, thereby ‘collapsing’ $𝒮$ down onto the leaf $u$. We denote by $l^{\prime }$ the new branch lengths after this operation, and thus the new chronogram as ${𝒯}_{l^{\prime }}$. The operation is illustrated in Figure S12.

We claim that $l^{\prime }$ satisfies the sought properties. It is clear that $l^{\prime }$ are ultrametric branch lengths. To show that the likelihood of $z^{(1)}$ as well as of ${\tilde{z}}^{(1)}$ can only increase after the subtree collapse operation, we create a coupling between $p_l$ and $p_{l^{\prime }}$, as follows:

1. Let the Markov chain run as usual down ${𝒯}_l$.

2. For the part of ${𝒯}_l$ that was not perturbed by the subtree collapse operation – meaning any point on the tree $𝒯$ which does not descend from $v$, nor is on the edge $(w,v)$ – copy all of its Markov chain transitions onto ${𝒯}_{l^{\prime }}$, as in Figure S13.

3. Copy the transitions on the path from $w$ to $u$ in ${𝒯}_l$ onto the same path in ${𝒯}_{l^{\prime }}$, as in Figure S14.

The result of the two copy operations above results in transition operations getting created on all branches of ${𝒯}_{l^{\prime }}$, and is depicted in Figure S15.

The key (trivial) observation is that the process induced over ${𝒯}_{l^{\prime }}$ follows exactly $p_{l^{\prime }}$. As such, let $p$ be the coupling thus created over $p_l({\tilde{Z}}^{(1)})$ and $p_{l^{\prime }}({\tilde{Z}}^{(1)})$, and let ${\tilde{Z}}_l^{(1)}$, ${\tilde{Z}}_{l^{\prime }}^{(1)}$ be the random variables corresponding to ${\tilde{Z}}^{(1)}$ under $p_l$ and $p_{l^{\prime }}$ respectively. In other words, $p({\tilde{Z}}_l^{(1)},{\tilde{Z}}_{l^{\prime }}^{(1)})$ is a probability density which satisfies

$$p({\tilde{Z}}_l^{(1)})=p_l({\tilde{Z}}^{(1)})\text{and}p({\tilde{Z}}_{l^{\prime }}^{(1)})=p_{l^{\prime }}({\tilde{Z}}^{(1)})\text{.}$$

We now claim that

$$Z_l^{(1)}=z^{(1)}\Rightarrow Z_{l^{\prime }}^{(1)}=z^{(1)},$$

and, similarly,

$${\tilde{Z}}_l^{(1)}={\tilde{z}}^{(1)}\Rightarrow {\tilde{Z}}_{l^{\prime }}^{(1)}={\tilde{z}}^{(1)}.$$

Indeed, if $Z_l^{(1)}=z^{(1)}$ then this means that all the leaves of $𝒮$ which are assigned a state by $z^{(1)}$ have the same state as $u$, which is exactly the situation in $Z_{l^{\prime }}^{(1)}$ by construction, thus $Z_{l^{\prime }}^{(1)}=z^{(1)}$. Similarly, if ${\tilde{Z}}_l^{(1)}={\tilde{z}}^{(1)}$ then it means that all the nodes of $𝒮$ which are assigned a state by ${\tilde{z}}^{(1)}$ have the same state as $u$, which is exactly the situation in ${\tilde{Z}}_l^{(1)}$ by construction, hence ${\tilde{Z}}_{l^{\prime }}^{(1)}=\tilde{z}$; this is the step where it is important that at least one leaf of $𝒮$ be assigned a state by ${\tilde{z}}^{(1)}$. This completes the proof, for we obtain

$$p_l(Z^{(1)}=z^{(1)})=p(Z_l^{(1)}=z^{(1)})\le p(Z_{l^{\prime }}^{(1)}=z^{(1)})=p_{l^{\prime }}(Z^{(1)}=z^{(1)})$$ (10)

and analogously

$$p_l({\tilde{Z}}^{(1)}={\tilde{z}}^{(1)})=p({\tilde{Z}}_l^{(1)}={\tilde{z}}^{(1)})\le p({\tilde{Z}}_{l^{\prime }}^{(1)}={\tilde{z}}^{(1)})=p_{l^{\prime }}({\tilde{Z}}^{(1)}={\tilde{z}}^{(1)}),$$ (11)

as claimed. □

B. Conservative Maximum Parsimony

In what follows, we let $𝒯$ be a rooted tree topology with $n$ leaves and a total of $\tilde{n}$ nodes. We allow multifurcations (nodes with more than 2 children) and require that each internal node other than the root have at least 2 children (such that unifurcations are not allowed, except for the root node, as in a single-cell phylogeny). Let $V$ and $E$ be the vertex set and edge set of $𝒯$ respectively, and let $L$ be the set of leaves. We use $x:L\to \mathbb{Z}$ to denote the states of one specific character over the leaves of $𝒯$ – including the missing data state −1 – and we use $\tilde{x}:V\to \mathbb{Z}$ to denote the states of that specific character over all the nodes of $𝒯$. We call the root of $𝒯$ simply ‘root’ when indexing.

We first define what it means for a state assignment $\tilde{x}$ to be valid under the irreversible CRISPR/Cas9 mutation process:

Definition 2 (Valid $\tilde{\mathit{x}})$.

We say that a state assignment $\tilde{x}$ is valid if it satisfies the following three properties:

• The root is uncut: ${\tilde{x}}_{\text{root}}=0$.

• Heritability of missing data: $\forall (p,c)\in E,\left({\tilde{x}}_p=-1\Rightarrow {\tilde{x}}_c=-1\right)$.

• Irreversibility of the mutation process (not to be confused with the notion of irreversibility of a Markov Chain): $\forall (p,c)\in E,\left({\tilde{x}}_p>0\Rightarrow {\tilde{x}}_c\in \left\{{\tilde{x}}_p,-1\right\}\right)$.

An important quantity associated with a state assignment $\tilde{x}$ is its parsimony score:

Definition 3 (Parsimony score).

We define the parsimony score $\mathrm{P}\mathrm{a}\mathrm{r}(\tilde{x})$ of a state assignment $\tilde{x}$ as:

$$\text{Par}(\tilde{x})=\sum _{(p,c)\in E}\mathbb{1}\left\{{\tilde{x}}_p\ne {\tilde{x}}_c\right\},$$ (12)

where $\mathbb{1}\{\cdot \}$ denotes the indicator function.

Note:

With this definition, we are penalizing transitions involving the missing state −1. One could choose not to do this. With this alternative definition, the results that follow essentially remain unchanged. Importantly, to the best of our knowledge, algorithms 1 and 2 remain correct, with only very minor changes to the proofs. Therefore, we stick with this definition.

Unfortunately, we usually only know the state assignment $x$ for the leaves $L$ of the tree $𝒯$. Because of this, it is common to reconstruct the ancestral states $\tilde{x}$ from $x$ in some fashion. Since the mutation process is constrained, not every imputation of ancestral states is valid. We thus define what it means for $\tilde{x}$ to be a valid reconstruction of $x$:

Definition 4 (Reconstruction $\tilde{\mathit{x}}$ of $\mathit{x}$).

We say that $\tilde{x}$ is a reconstruction of $x$ if $\forall v\in L$, ${\tilde{x}}_v=x_v$.

Definition 5 (Valid reconstruction $\tilde{\mathit{x}}$ of $\mathit{x}$).

We say that $\tilde{x}$ is a valid reconstruction of $x$ if $\tilde{x}$ is valid, and if $\tilde{x}$ is a reconstruction of $x$.

Note that there always exists a valid reconstruction $\tilde{x}$ of $x$, by just setting all internal node states to 0. However, we usually seek for the ‘best’ valid reconstruction, in some suitable sense. This notion of ‘best’ is commonly chosen to be the most parsimonious solution, which is the one that minimizes the parsimony score $\mathrm{P}\mathrm{a}\mathrm{r}(\tilde{x})$:

Definition 6 (Valid maximum parsimony reconstruction).

We say that $\tilde{x}$ is a valid maximum parsimony reconstruction of $x$, abbreviated VMPR, if $\tilde{x}$ is a valid reconstruction of $x$ and $\tilde{x}$ achieves the lowest parsimony score (ties allowed) amongst all valid reconstructions of $x$; there may be multiple VMPRs for a given $x$.

We now give an algorithm to compute a VMPR from $x$. For this, we will need some definitions:

Definition 7 (Set of leaf descendants).

Given $v\in V$, we define $ℒ(v)\subseteq L$ as the set of leaves descending from $v$.

Definition 8 (Subset of leaf states).

Given a subset of leaves $L^{\prime }\subseteq L$, we define $x_{L^{\prime }}=\left\{x_u:u\in \right.\left.L^{\prime }\right\}$. In particular, $x_{ℒ(v)}$ is the set of states at the leaves descending from $v$.

We are ready to state our algorithm:

Algorithm 1.

A Valid Maximum Parsimony Reconstruction

1: procedure $\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}(𝒯,x)$

2: for $v$ in postorder traversal of $𝒯$ do

3: if $v$ is a leaf then

4: ${\tilde{x}}_v\leftarrow x_v$

5: else if $v$ is the root of $𝒯$ then

6: ${\tilde{x}}_v\leftarrow 0$

7: else

8: Let $u_1,\dots ,u_c$ be the children of $v$.

9: Let $S=\left\{{\tilde{x}}_{u_1},{\tilde{x}}_{u_2},\dots ,{\tilde{x}}_{u_c}\right\}$.

10: if $S=\left\{s\right\}$ for some $s\in \mathbb{Z}$ then

11: ${\tilde{x}}_v\leftarrow s$

12: else

13: if $-1\in S$ then

14: if $S\backslash \{-1\}=\left\{s\right\}$ for some $s\ge 0$ then

15: ${\tilde{x}}_v\leftarrow s$

16: else

17: ${\tilde{x}}_v\leftarrow 0$

18: else

19: ${\tilde{x}}_v\leftarrow 0$

20: return $\tilde{x}$

We now show that Algorithm 1 indeed computes a VMPR, which we call ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$:

Theorem 3.

Algorithm 1 computes a VMPR $\tilde{x}$ of $x$.

Proof.

Suppose otherwise. Consider the first step of the algorithm where the current state assignment (prior to executing the step) cannot be completed to any VMPR. We call this the ‘failing’ step. In the previous step, let $\tilde{x}$ be a VMPR compatible with the state assignment so far. We analyze several cases, depending on which line of the algorithm we fail on:

• We cannot fail in lines 4 nor 6 because $\tilde{x}$ is a valid reconstruction (Definition 5).

• If we failed on line 11 then changing ${\tilde{x}}_v$ to $s$ in $\tilde{x}$ would remain a valid reconstruction and improve the parsimony score by at least 1, contradiction.

• If we failed in line 15, then first note that ${\tilde{x}}_v\ne -1$ (or else by heritability of missing data $S=\{-1\}$, contradicting line 14). The only other option is ${\tilde{x}}_v=0$. But then if we change ${\tilde{x}}_v=s$ in $\tilde{x}$ we still have a valid reconstruction and the transition $0\to 0$ going into $v$ becomes $0\to s$, but at least one transition $0\to s$ leaving $v$ becomes $s\to s$, meaning that the new state assignment must be VMPR and is consistent with the algorithm the step it failed, contradiction.

• We cannot fail in line 17 or 19 because there are at least two different non-missing states $s_1,s_2\ge 0$. If one of these is a 0, then ${\tilde{x}}_v=0$ by validity. Otherwise, these two are distinct positive states, and again ${\tilde{x}}_v=0$ by validity.

This concludes the proof. □

We next give a direct, non-algorithmic characterization of the VMPR ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$ computed by Algorithm 1:

Proposition 2 (Structure of ${\tilde{\mathit{x}}}^{\mathbf{V}\mathbf{M}\mathbf{P}\mathbf{R}}$).

Let ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$ be the VMPR of $x$ computed by Algorithm 1. Then, for any internal node $v\in V$, the following properties hold:

1. If $v=\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}$, then ${\tilde{x}}_v^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

2. If $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(0\in x_{ℒ(v)}\right)$, then ${\tilde{x}}_v^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

3. If $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(0\notin x_{ℒ(v)}\right)\wedge \left(\exists s_1,s_2>0:s_1\ne s_2,\left\{s_1,s_2\right\}\subseteq x_{ℒ(v)}\right)$ then ${\tilde{x}}_v^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

4. If $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(x_{ℒ(v)}=\{-1\}\right)$, then ${\tilde{x}}_v^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=-1$.

5. If for some $s>0$ we have $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(\left\{s\right\}\subseteq x_{ℒ(v)}\subseteq \{-1,s\}\right)$, then ${\tilde{x}}_v^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=s$.

Moreover, the five cases above are disjoint and exhaustive, so they completely characterize ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$.

Proof.

We first observe that the five cases are disjoint and exhaustive: case (1) handles the root node; case (2) handles an internal node with some leaf state of 0; case (3) handles an internal node with no leaf state of 0 but two distinct non-zero leaf states; case (4) handles an internal node with all missing leaf states. If none of these four first cases hold, then it means that it is an internal node and there exists some $s>0$ such that $\left\{s\right\}\subseteq x_{ℒ(v)}\subseteq \{-1,s\}$, which is handled by case (5).

Now the proposition follows directly by induction on the nodes of $𝒯$ in postorder: The first three implications are true simply because ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$ is valid; the fourth implication is true because all the −1 in the subtree at $v$ will be propagated up the tree by the algorithm; and the fifth implication is true because positive states take precedence over missing states in the algorithm, specifically, in line 15, so as states −1 and $s$ are propagated up the subtree at $v$, the state $s$ will make it to the top. □

Unfortunately, maximum parsimony imputation tends to lead to biased branch lengths, as shown in Figure 3. A key contribution of our work is the idea of a conservative maximum parsimony reconstruction, which gets rid of the maximum parsimony bias, while being computationally just as tractable as a typical maximum parsimony reconstruction. The idea of conservative maximum parsimony is to just reconstruct ancestral states that all valid maximum parsimony reconstructions agree on, and leave the remaining ones without any state value, for which we shall use the new symbol NONE. Formally, we define:

Definition 9 (Conservative maximum parsimony reconstruction).

We say that $\tilde{x}:V\to \mathbb{Z}\cup$ {NONE} is the conservative maximum parsimony reconstruction of $x$, abbreviated CMPR, if for all nodes $v\in V$ it holds that:

• If there is some state $s$ such that ${\tilde{x}}_v^{\prime }=s$ for all VMPR ${\tilde{x}}^{\prime }$ of $x$, then ${\tilde{x}}_v=s$.

• If there is no state $s$ such that ${\tilde{x}}_v^{\prime }=s$ for all VMPR ${\tilde{x}}^{\prime }$ of $x$, then ${\tilde{x}}_v=\mathrm{N}\mathrm{O}\mathrm{N}\mathrm{E}$.

Unlike the VMPR, the CMPR is unique by definition. We shall denote ${\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$ the CMPR of $x$.

Figure S16 shows a minimal example of conservative maximum parsimony, while Figure S17 shows a larger example. Just as for the VMPR, we can give a non-algorithmic characterization of the CMPR which will be convenient for analyzing its properties. Unlike the VMPR, the structure of the CMPR is more involved, and determining the state of some nodes requires looking up though its list of ancestors, which we define as follows:

Definition 10 (Ancestor).

Given nodes $g$, $v$ in a $𝒯$, we say that $g$ is an ancestor of $v$ if there is a path from $g$ to $v$ in $𝒯$. A node is considered an ancestor of itself.

We can now prove:

Theorem 4 (Structure of the CMPR).

Let ${\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$ be the CMPR of $x$. Then, for any internal node $v\in V$, the following properties hold:

1. If $v=\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}$, then ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

2. If $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(0\in x_{ℒ(v)}\right)$, then ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

3. If $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(0\notin x_{ℒ(v)}\right)\wedge \left(\exists s_1,s_2>0:s_1\ne s_2,\left\{s_1,s_2\right\}\subseteq x_{ℒ(v)}\right)$ then ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

4. If $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(x_{ℒ(v)}=\{-1\}\right)$, then ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=-1$.

5. If for some $s>0$ we have $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(\left\{s\right\}\subseteq x_{ℒ(v)}\subseteq \{-1,s\}\right)\wedge (\exists g$ ancestor of $v$ different from the root such that $\left\{s\right\}\subseteq x_{ℒ(g)}\subseteq \{-1,s\}$ and $\exists u_1,u_2$ distinct children of $g$ such that $\left.\left\{s\right\}\subseteq x_{ℒ\left(u_1\right)},x_{ℒ\left(u_2\right)}\subseteq \{-1,s\}\right)$, then ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=s$

6. If for some $s>0$ we have $(v\ne \mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t})\wedge \left(\left\{s\right\}\subseteq x_{ℒ(v)}\subseteq \{-1,s\}\right)\wedge (\nexists g$ ancestor of $v$ different from the root such that $\left\{s\right\}\subseteq x_{ℒ(g)}\subseteq \{-1,s\}$ and $\exists u_1,u_2$ distinct children of $g$ such that $\left.\left\{s\right\}\subseteq x_{ℒ\left(u_1\right)},x_{ℒ\left(u_2\right)}\subseteq \{-1,s\}\right)$, then ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=\mathrm{N}\mathrm{O}\mathrm{N}\mathrm{E}$.

The first four properties above are analogous to that of Proposition 2 satisfied by ${\tilde{x}}_v^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$. Moreover, the six cases above are disjoint and exhaustive, so they completely characterize ${\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$.

Proof.

We first observe that the six cases are disjoint and exhaustive: these are the same cases as those of the VMPR structure Proposition 2, except that the last case was split into the two cases (5) and (6) by pivoting on the truth value of a somewhat involved condition depending on the non-root ancestors of $v$.

We now show each of the implications. The first 3 will be a simple consequence of VMPRs being valid, and the fourth will be a simple consequence of VMPRs being most parsimonious. The last two cases, however, require some work. The proof for each implication is as follows:

1. All VMPRs $\tilde{x}$ have ${\tilde{x}}_{\text{root}}=0$ since they are valid (Definition 2). Thus ${\tilde{x}}_{\text{root}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

2. By irreversibility of the mutation process and heritability of missing data, in a valid $\tilde{x}$ if a leaf has state 0, all its ancestors must have state 0, therefore ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

3. By irreversibility of the mutation process and heritability of missing data, in a valid $\tilde{x}$ the ancestors of a leaf with state $s>0$ can only have state $s$ or 0. Therefore, if $v$ has two descendent leaves with distinct positive states $s_1$, $s_2$, we must have ${\tilde{x}}_v=0$ for all valid reconstructions $\tilde{x}$ of $x$. Therefore ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=0$.

4. The parsimony score of the subtree rooted at $v$ when all states in the subtree are assigned states of −1 is zero, and any other assignment has parsimony score of at least 2 (take a state $s\ne -1$ in the subtree and go down two distinct daughter lineages - some change to −1 will occur on both lineages). Therefore, in any VMPR $\tilde{x}$ of $x$ if the subtree rooted at $v$ does not have all states equal to −1, we can change them all to −1 and this will still yield a valid reconstruction, while lowering the parsimony score by at least 1, contradiction. Thus all VMPRs $\tilde{x}$ of $x$ have ${\tilde{x}}_v=-1$ and so ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=-1$.

5. Consider the ancestor $g$ which satisfies the clause. We claim that for all VMPRs $\tilde{x}$ of $x$ we have ${\tilde{x}}_g=s$. If this is true, then ${\tilde{x}}_v$ cannot be −1 (since then by heritability of missing data $x_{ℒ(v)}=\{-1\}$), and ${\tilde{x}}_v$ cannot be 0 nor some other state $s^{\prime }\ne s$ (since the mutation process is irreversible). As a consequence, we would have that ${\tilde{x}}_v=s$ in all VMPRs $\tilde{x}$ of $x$, and so ${\tilde{x}}_v^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}=s$, as we want to show. Therefore, let us prove that for all VMPRs $\tilde{x}$ of $x$ we have ${\tilde{x}}_g=s$. Suppose otherwise to reach a contradiction. Let $\tilde{x}$ be a VMPR of $x$ with ${\tilde{x}}_g\ne s$. Then, the only option is that ${\tilde{x}}_g=0$ (because the ancestors of a state $s$ can only be 0 or $s$ by irreversibility of the mutation process and heritability of missing data). Now consider the subtree rooted at $g$, and consider the maximal connected component of 0 states at and below $g$. Change all these states to $s$, and let ${\tilde{x}}^{\prime }$ be the new states. We claim that ${\tilde{x}}^{\prime }$ is still a valid reconstruction of $x$. Firstly, ${\tilde{x}}^{\prime }$ is a reconstruction of $x$ since none of the leaf states have been perturbed, since $0\notin x_{ℒ(g)}$ by the assumption that $\left\{s\right\}\subseteq x_{ℒ(g)}\subseteq \{-1,s\}$. Next, to check validity of $\tilde{x}$, note that by assumption $g$ is not the root, so the state of the root is still all zeros. As for transitions, we only need to check the transitions that were affected by swapping 0 to $s$. Firstly, the edge going into $g$ was originally $0\to 0$ and now it is $0\to s$, which is still valid. Now, inspecting the transitions affected in the subtree rooted at $g$, we have that any $0\to 0$ transitions that became $s\to s$ are still valid. Transitions $0\to s$ become $s\to s$ which are valid, and similarly transitions $0\to -1$ become $s\to -1$ which are valid. This accounts for all affected transitions. Thus, ${\tilde{x}}^{\prime }$ is a valid reconstruction of $x$. Now let us analyze the parsimony score of ${\tilde{x}}^{\prime }$. The transition at the root was $0\to 0$ and now became $0\to s$, so the parsimony score got worse by 1. Among the remaining changes, only the transitions $0\to s$ which became $s\to s$ change the parsimony score, and they each improve it by exactly 1. We claim that there exist at least two such transitions. Indeed, by hypothesis, there are at least two leaves $l_1$, $l_2$ descending from $g$ on different daughter lineages through $u_1$ and $u_2$ which have a state of $s$. Consider the two distinct paths leading from $g$ to $l_1$ and $l_2$. In $\tilde{x}$, each of these paths must at some point transition from 0 to $s$ (note that transitioning from 0 to −1 is impossible because by heritability of missing data it would imply $x_{l_i}=-1$ for that leaf, a contradiction). Hence we obtain at least two new transitions $s\to s$ - one on each path - which jointly improve the parsimony score by at least 2. Hence $\mathrm{P}\mathrm{a}\mathrm{r}\left({\tilde{x}}^{\prime }\right)\le \mathrm{P}\mathrm{a}\mathrm{r}(\tilde{x})-1$. This contradicts the assumption that $\tilde{x}$ was VMPR, and so we are done.

6. It suffices to show that in this case there exist two different VMPRs $\tilde{x}$, ${\tilde{x}}^{\prime }$ of $x$ with ${\tilde{x}}_v=s$ and ${\tilde{x}}_v^{\prime }=0$. We construct these explicitly. For $\tilde{x}$ we choose ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$. By Proposition 2, we have that ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=s$. To construct a VMPR ${\tilde{x}}^{\prime }$ with ${\tilde{x}}_v^{\prime }=0$, start from ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$. Travel up the ancestors of $v$ until we find the last ancestor $g$ such that ${\tilde{x}}_g^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=s$. Let $v=a_1,a_2,\dots ,a_j=g$ be the sequence of ancestors visited. Note that $g$ cannot be the root node since ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$ is valid. If $p$ is the parent of $g$, then the only possibility is ${\tilde{x}}_p^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=0$ (by irreversibility of the mutation process and heritability of missing data). For every $a_i$, the fact that ${\tilde{x}}_g^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}=s$ means that the states that descend from $a_i$ are either −1 or $s$. However, by condition 6 only one of the daughter subtrees of $a_i$ can contain state $s$, so that the other one must consist fully of −1. The characterization of ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$ further implies that all these subtrees that have missing states at all leaves, have all internal nodes with state −1 too. This way, consider the following modification to ${\tilde{x}}^{\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}}$: change the state of all nodes $u=a_1,a_2,\dots ,a_j=g$ from $s$ to 0. This is still a valid reconstruction of $x$. The transition into $g$ from $p$ changes from $0\to s$ to $0\to 0$, so we win a parsimony score of 1. All the transitions $s\to -1$ from node $a_i$ into the subtrees with missing states at the leaves become $0\to -1$, so the parsimony remains unchanged by these transition changes. All that remains is the transition from $v$ into its unique subtree which contains a leaf with state $s$. This transition must originally have been $s\to s$ (since otherwise missing data is heritable), so that in ${\tilde{x}}^{\prime }$ the transition is now $0\to s$ and so we lose a parsimony score of 1. The net change in the parsimony score from $\tilde{x}$ to ${\tilde{x}}^{\prime }$ is thus zero, and so $\mathrm{P}\mathrm{a}\mathrm{r}\left({\tilde{x}}^{\prime }\right)=\mathrm{P}\mathrm{a}\mathrm{r}(\tilde{x})$, completing the proof. □

Figure S17 shows a larger example of CMPR, highlighting the subtlety of conditions 5 and 6 of the Theorem. As a remark, when there is no missing data, condition 6 of Theorem 4 can never hold, implying that the CMPR will reconstruct all ancestral states. In particular, this means that the VMPR is unique when there is no missing data. Thus, conservative maximum parsimony only makes a difference when there is missing data.

The characterization of the CMPR given by Theorem 4 allows us to implement it easily in time $𝒪(n)$ where $n$ is the number of nodes in the tree (i.e., the same time complexity as Fitch-Hartigan): we can just take the imputations given by Algorithm 1 and after the fact set to NONE all nodes that satisfy condition 6 of the CMPR Theorem 4. To determine which nodes satisfy this condition, we can use a bottom-up tree traversal to determine which nodes $v$ satisfy condition 5 with $g=v$, and then propagate this information down with a top-down tree traversal to determine which nodes $v$ satisfy condition 5 for any ancestor $g$. Any nodes that satisfy the original condition 5 of the VMPR Proposition 2 but not condition 5 of the CMPR Theorem 4 are exactly those with ambiguous states that need to be set to NONE. We provide the algorithm below in Algorithm 2:

Algorithm 2.

Conservative Maximum Parsimony Reconstruction

1: procedure $\mathrm{CMPR}\left(𝒯,x\right)$

2: $\tilde{x}\leftarrow \mathrm{VMPR}\left(𝒯,x\right)$

3: for $v$ in preorder traversal of internal nodes of $𝒯$ do

4: if $v$ is the root, or $0\in x_{ℒ(v)}$, or $x_{ℒ(v)}$ contains two distinct positive states, or $x_{ℒ(v)}=\{-1\}$ then

5: $\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]\leftarrow \mathrm{F}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}$

6: $\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]\leftarrow \mathrm{F}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}$

7: else

8: $\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]\leftarrow \mathrm{T}\mathrm{r}\mathrm{u}\mathrm{e}$

9: Let $s$ be the unique positive state in $x_{ℒ\left(v\right)}$

10: if $\mid \left\{u:u\right.\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\mathrm{o}\mathrm{f}\left.v,s\in x_{ℒ(u)}\right\}\mid \ge 2$ then

11: $\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]\leftarrow \mathrm{T}\mathrm{r}\mathrm{u}\mathrm{e}$

12: else

13: $p\leftarrow \mathrm{parent}\left(v\right)$

14: $\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]\leftarrow \mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[p]$

15: for $v$ in the internal nodes of $𝒯$ do

16: if $\mathrm{V}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]$ is True and $\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}\_\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\_5[v]$ is False then

17: ${\tilde{x}}_v\leftarrow \mathrm{N}\mathrm{O}\mathrm{N}\mathrm{E}$

18: return $\tilde{x}$

Armed with the characterization of the CMPR ${\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$ of $x$ provided by Theorem 4, we are ready to show that the likelihood $p_{\theta }({\tilde{Z}}^{(1)}={\tilde{x}}^{(1)})$ where $\tilde{x}={\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$ is tractable; in ${\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$, states that are not reconstructed and thus marked as NONE are without loss of generality replaced by −1 such that they are marginalized out as in an ignorable missing data mechanism:

Theorem 5 (${\tilde{\mathit{x}}}^{\mathbf{C}\mathbf{M}\mathbf{P}\mathbf{R}}$ has no unobserved confounders).

Let $\tilde{x}={\tilde{x}}^{\mathrm{C}\mathrm{M}\mathrm{P}\mathrm{R}}$ be the CMPR of the leaf states $x$ of one character, with NONE replaced by −1. For a node $v$, denote by gpa $(v)$ it closest reconstructed, non-missing ancestor in $\tilde{x}$ (not including $v$), that is to say its closest ancestor $u$ with ${\tilde{x}}_u\ne -1$. Then:

$$p_{\theta }({\tilde{Z}}^{(1)}={\tilde{x}}^{(1)})=\prod _{v\in V,u=\text{gpa}(v):{\tilde{x}}_v\ne -1}{p}_{\theta }({\tilde{Z}}_v={\tilde{x}}_v\mid {\tilde{Z}}_u={\tilde{x}}_u).$$ (13)

Proof.

It suffices to show that there are no unobserved confounders, that is to say, that if a node $v$ has ${\tilde{x}}_v=-1$, then all subtrees of $v$ except possibly one are fully missing. Indeed, in such case, we can repeatedly prune away all these missing subtrees and the missing node (replacing two edges by one) without changing the likelihood, leaving us with a tree where all nodes are observed. In this new tree, each remaining node $v$ is connected to $u=\mathrm{g}\mathrm{p}\mathrm{a}(v)$. We would thus obtain the factorization in Eq. 13. To prove that if a node $v$ has ${\tilde{x}}_v=-1$ then all subtrees of $v$ except possibly one are fully missing, we proceed by contradiction, supposing otherwise. Then $v$ (which is not the root) has at least two distinct subtrees with at least one observed leaf. Let $s_1$ and $s_2$ be the states of two such leaves. If we have $s_1\ne s_2$, then implication 3 of Theorem 4 implies that ${\tilde{x}}_v=0$, contradiction. Therefore, the only non-missing state in these subtrees is a single state $s$, and now implication 5 of Theorem 4 implies that ${\tilde{x}}_v=s$, again a contradiction, so we are done, since each observed state is conditionally independent from its observed non-descendants given its closest observed ancestor, giving the decomposition of Eq. (13). □

Finally, we should note that the Sankoff algorithm can be used to compute the CMPR in $𝒪\left(n{k}^2\right)$ time where $k$ is the number of states, and in fact in time $𝒪(nk)$ by leveraging irreversibility, and moreover in time $𝒪(n)$ by first precomputing the valid set of states based on states below (which can only be −1, 0, and one other state). We used this for testing our implementation, but note that the combinatorial characterization of the CMPR is not elucidated by such algorithm, and thus it does not explain why line 4 is true.

C. Tree Simulation details

Trees were simulated using a subsampled birth-death process. In this simulation, each cell has a birth rate and a death rate. The amount of time before a birth or a death event occurs follows an exponential distribution with the given birth and death rates. Additionally, a cell cannot divide before at least 0.01 units of time have passed, called the offset. Initial birth and death rates are set such that birth rate is ten times higher than death rate and such that under a birth-death process with these rates and offset, the expected population size after 1 unit of time is 40000. This yields a birth rate of 15.75 and a death rate of 1.575. Whenever a cell divides, its fitness changes with probability 6.4%. When such a change in fitness occurs, 90% of the time the birth rate becomes lower by multiplying it by 0.93. The remaining 10% of the time the birth rate becomes higher by multiplying it by 2.14. Once the cell population reaches 40000, we terminate the simulation and sample 400 leaves uniformly at random, to match a sampling probability of 1%. The chronogram induced by these 400 cells is then the ground truth chronogram used in the simulations. The fitness parameters described above were chosen to obtain trees that showcased interesting fitness variation, as displayed in Figure S4.