Handedness: Dominant Arm Advantages in Control of Limb Dynamics

Abstract

Recent findings from our laboratory suggest that a major factor distinguishing dominant from nondominant arm performance is the ability by which the effects of intersegmental dynamics are controlled by the CNS. These studies indicated that the dominant arm reliably used more torque-efficient patterns for movements made with similar speeds and accuracy than nondominant arm movements. Whereas, nondominant hand-path curvatures systematically varied with the amplitude of the interaction torques transferred between the segments of the moving limb, dominant hand-path curvatures did not. However, our previous studies did not distinguish whether dominant arm coordination advantages emerged from more effective control of dynamic factors or were simply a secondary effect of planning different kinematics. The purpose of this study was to further investigate interlimb differences in coordination through analysis of inverse dynamics and electromyography recorded during the performance of reaching movements. By controlling the amplitude of intersegmental dynamics in the current study, we were able to assess whether systematic differences in torque-efficiency exist, even when differences in hand-path shape were minimal. Subject’s arms were supported in the horizontal plane by a frictionless air-jet system and were constrained to movements about the shoulder and elbow joints. Two targets were designed, such that the interaction torques elicited at the elbow were either large or small. Our results showed that the former produced large differences in hand-path curvature, whereas the latter did not. Additionally, the movements with small differences in hand-path kinematics showed substantial differences in torque patterns and corresponding EMG profiles which implied a more torque-efficient strategy for the dominant arm. In view of these findings we propose that distinct neural control mechanisms are employed for dominant and nondominant arm movements.

INTRODUCTION

Handedness, the tendency to prefer the use of a consistent hand in performing selected tasks, is a prominent, yet poorly understood aspect of human motor performance. Whereas it is generally accepted that handedness results from differences in the neural control of each arm, the mechanisms responsible for these differences remain controversial. Previous studies examining handedness have quantified the reaction time, movement time, and final position accuracy of rapid aimed arm movements. Such performance measures were expected to differentiate “open-loop” mechanisms, which by definition are unaffected by sensory feedback, from “closed-loop” mechanisms, which by definition are mediated by sensory feedback. This division was inspired by the ideas of Woodworth (Woodworth 1899) and Fitts (Fitts 1966, 1992; Fitts and Radford 1966) and is supported by studies contrasting rapid aiming movements made under varying precision requirements (Keele and Posner 1968; Schmidt 1969; Schmidt and Russell 1972; Wallace and Newell 1983). However, such attempts to differentiate the effects of sensory feedback on dominant and nondominant arm performance have yielded equivocal results, leaving open the question of how else one might understand the neural basis of handedness (Carson et al. 1990, 1992; Elliott et al. 1994, 1995; Flowers 1975; Roy and Elliott 1986; Roy et al. 1994; Sainburg 2002; Todor and Cisneros 1985).

Recent findings from our laboratory demonstrate dominant arm advantages in controlling the effects of intersegmental dynamics during reaching movements (Sainburg 2002; Sainburg and Kalakanis 2000). These studies revealed that muscle torques were better coordinated across dominant arm shoulder and elbow joints, such that similar speed movements were produced with a fraction of the torque than that of nondominant arm movements. Moreover, dominant hand-path curvatures were independent of the interaction torques imposed on a limb segment by the motions of neighboring limb segments, whereas nondominant hand path curvatures appeared enslaved to such interactions (Sainburg and Kalakanis 2000). In a more recent investigation, we compared adaptation to novel inertial loads, and to novel visuomotor rotations, during reaching movements performed with the dominant and nondominant arms (Sainburg 2002). This study indicated that interlimb differences in control emerge downstream to visual motor planning, when the intended trajectory is transformed into the dynamic properties that reflect the forces required to produce motion.

The purpose of this study was twofold. First, we intended to examine whether both inverse dynamic analysis and electromyographic (EMG) recordings support our previous findings. Our inverse dynamic analysis approximates the limb as a planar, two-segment model, and does not account for separate flexor and extensor torques or for muscle activations. The dynamic effects of muscle co-activation are thus not accounted for in this model, nor are the forces that arise from noncontractile origins, such as soft tissue elasticity. Therefore we directly recorded muscle activities. Second, it is plausible that the coordination differences observed in our previous studies did not result from neural control mechanisms that favor a more torque-efficient strategy with the dominant arm. Instead it is possible that the nondominant arm pattern is preferred for some secondary reason that is related to the kinematic and not the dynamic elements of movement, such as planning different hand-path profiles. To test this hypothesis, we examined movements with different joint excursion requirements. Our first movement (target 1) required similar displacements (approximately 30°) at both shoulder and elbow joints. Because of the prominent intersegmental dynamics of this task, we expected substantial interlimb differences in hand-path direction and curvature. The second movement (target 2) also required approximately 30° extension at the elbow, but without required shoulder excursion. Because of the relatively smaller intersegmental forces associated with this task, we expected the handpath differences in this task to be minimal. We were thus able to ask whether interlimb differences in torque and EMG patterns persisted in the absence of substantial differences in kinematic performance.

METHODS

Subjects

Six neurologically intact right-handed adult (3 males and 3 females), aged from 20 to 28 years old were tested. Only right-handers were recruited; handedness was determined using a 12-item version of the Edinburgh inventory (Oldfield 1971), and only subjects with scores of 100% were accepted. The subjects gave informed consent prior to participation.

Experimental setup

Figure 1 illustrates the experiment setup. Subjects sat facing a table with either the right or left arm supported over the horizontal surface, positioned just below shoulder height (adjusted to subjects’ comfort), by an air-jet system, which reduces the effects of gravity and friction. A cursor representing finger position, a start circle, and a target were projected on a horizontal back-projection screen positioned above the arm. A mirror, positioned parallel and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the fingertip. Calibration of the display assured that this projection was veridical. All joints distal to the elbow were immobilized using an adjustable brace. Position and orientation of each segment was sampled using a flock of birds (Ascension Technology) magnetic 6-DOF movement recording system. A single 6-DOF sensor was attached to the upper-arm segment via an adjustable plastic cuff, while another sensor was fixed to the air sled where the forearm was fitted. The sensors were positioned approximately at the center of the limb.

FIG. 1.

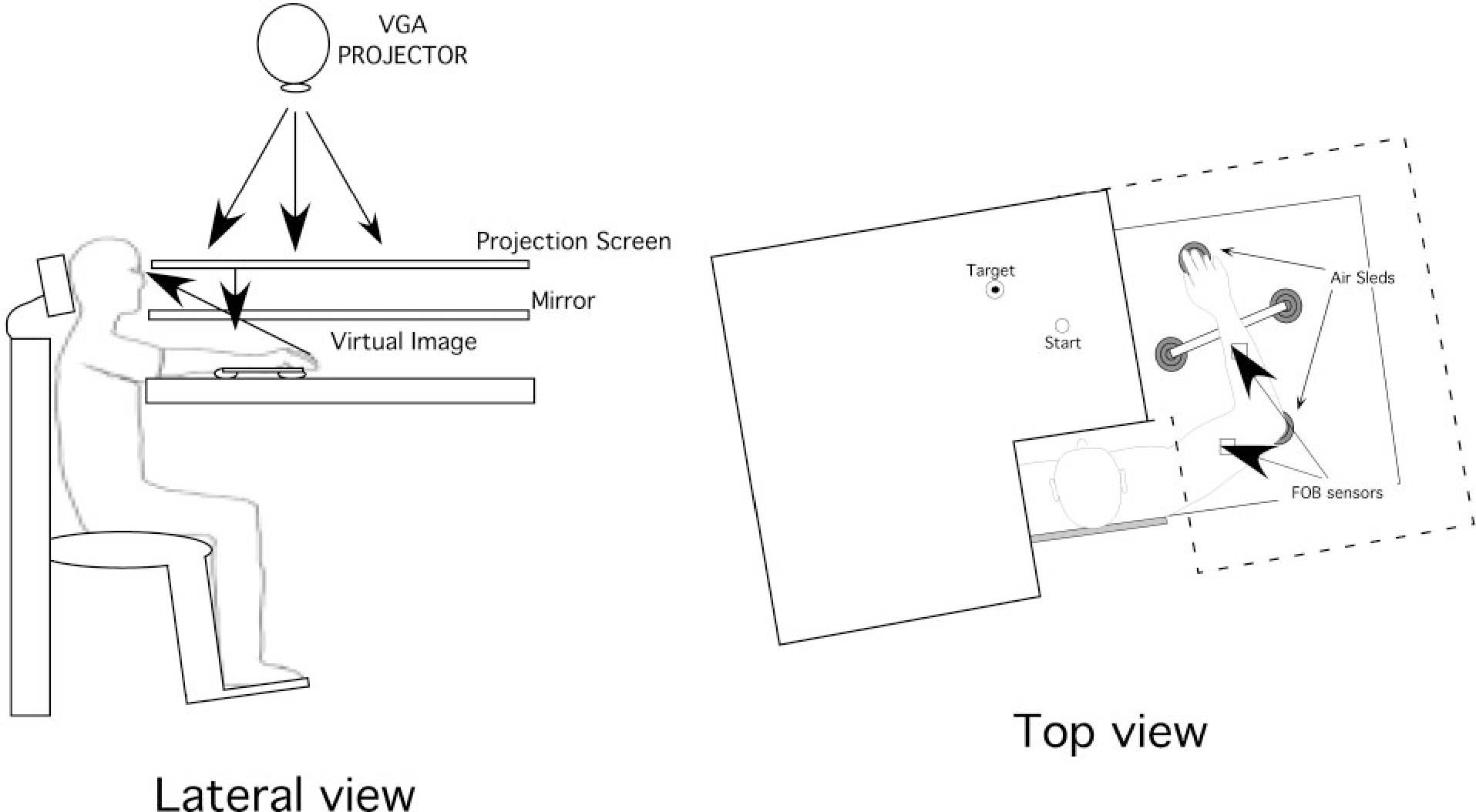
Experimental setup.

Digital data were collected at 103 Hz using a Macintosh computer, which controlled the sensors through separated serial ports and stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC (REAL Software), C, and IgorPro (Wavemetric). EMG was recorded with active, bipolar stainless steel surface electrodes (Liberty Mutual MY0111) with a band-pass of 45–550 Hz. The electrode contacts had a 3-mm diam and were spaced 13 mm apart. The EMG signals were digitized at 1000 Hz using a Macintosh computer equipped with an A/D board (National Instruments PCI-MIO-16xE-50). During recording, the EMG signals were displayed on an oscilloscope to verify digitized recordings. The EMG signals were full-wave rectified and bin integrated every 10 ms, thereby allowing direct comparison with the kinematic data.

Experiment task

Throughout the experiment, the index finger position was displayed in real-time as a screen cursor. We presented two targets that required 15-cm-long movements; target 1 oriented 135° relative to the horizontal axis and target 2 oriented at 45°. Prior to movement, one of the two targets was displayed. Subjects were to hold the cursor within the starting circle for 1.5 s to initiate each trial. They were instructed to move the finger to the target using a single, uncorrected, rapid motion in response to an audiovisual “go” signal. Feedback of the fingertip position (cursor display) was given to allow subjects to align the finger with the start location, and then was removed at the go-signal. At the final position subjects were given knowledge of results and points were awarded for accuracy only when movements were performed within a 400 ms time limit. Final position errors of <1 cm were awarded 10 points, while errors between 1 and 2 cm were awarded 3 points, and errors between 2 and 3 cm were awarded 1 point. Points were displayed following each trial. Each subject was given a practice session (16 trials) to familiarize with the task, followed by a 40-trial experimental session. Consecutive movements were alternated between the two targets.

Kinematic data

The three-dimensional position of the index finger, elbow, and shoulder were calculated from sensor position and orientation data. Elbow and shoulder angles were calculated from this data. All kinematic data were low-pass filtered at 8 Hz (3^rd order, dual pass Butterworth) and differentiated to yield angular velocity and acceleration values. Each trial usually started with the hand at zero velocity, but small oscillations of the hand sometimes occurred within the start circle. In this case, the onset of movement was defined by the last minimum (below 5% maximum tangential velocity) prior to the maximum in the index finger’s tangential velocity profile. Movement termination was defined as the first minimum (below 5% maximum tangential hand velocity) following the peak in tangential hand velocity.

Three measures of movement accuracy were calculated from the hand path: initial direction error, final position error, and hand-path deviation from linearity. The initial direction error was calculated as the angle between the target line and the line originating at the starting location of the hand and terminating at the point at which the peak tangential hand velocity occurred. Final position error was calculated as the distance between the index finger location at movement end and the target position. Deviation from linearity was assessed as the minor axis divided by the major axis of the hand path. The major axis was defined as the largest distance between any two points in the path, while the minor axis was defined as the largest distance, perpendicular to the major axis, between any two points in the path (Sainburg 2002; Sainburg et al. 1993).

Electromyographic data

EMG data was collected for representative muscles of the elbow and shoulder joints. Surface electrodes were positioned in biceps brachii (elbow flexor); triceps brachii-lateral head (elbow extensor); pectoralis major-superior lateral fibers (shoulder flexor); and posterior deltoid (shoulder extensor). The electrode position was determined according to a maximum EMG activity during isolated flexor or extensor movements of the respective joint. The integrated EMG data were normalized to percent of maximum EMG at each muscle within subjects and across conditions. The maximum EMG was measured at the end of each session. Subjects were asked to maintain maximal flexor and extensor forces at each joint, over a 5-s recording time. Each of these maximum force trials was scanned using a computer algorithm to find the highest integrated EMG magnitude for each muscle. The integrated value over the interval was defined as maximum EMG and provided a standard for comparison of agonist and antagonist EMG within a subject and session.

Kinetic data

Joint torques were calculated for shoulder and elbow using the equations detailed in the appendix. For the purpose of this study, we assumed that the upper extremity was two interconnected rigid links (upper arm and forearm) with frictionless joints at the shoulder and elbow. The shoulder was allowed to move freely, and the torques resulting from linear accelerations of the shoulder were included in the equations of motion for each joint (see appendix). To separately analyze the effects of intersegmental forces and muscle forces on the limb motion we partitioned the terms of the equations of motion at each joint into three main components, interaction torque, muscle torque, and net torque (Sainburg et al. 1995, 1999). At each joint, interaction torque represents the rotational effect of the forces due to the rotational and linear motion of the other segment. The muscle torque primarily represents the rotational effect of muscle forces acting on the segment. Finally, the net torque is directly proportional to joint acceleration, and equal to the combined muscle and interaction torques.

It is important to note that computed muscle joint torque cannot be considered a simple proxy for the neural activation of the muscles acting at the joint. Muscle joint torque does not distinguish muscle forces that counter one another during co-contraction and it also includes the passive effects of soft tissue deformation. In addition, the force generated by muscle to a given neural input signal is dependent on muscle length, velocity of muscle length change, and recent activation history (Abbot and Wilkie 1953; Wilkie 1956; Zajac 1989). Torques were computed and analyzed for the shoulder and elbow joints as detailed in the equations below. The inertia and mass of the forearm support are 0.0247 kg/m² and 0.58 kg, respectively. Limb segment inertia, center of mass, and mass were computed from regression equations using subjects’ body mass and measured limb segment lengths (Winter 1990).

Elbow joint torques

$$\begin{gathered} T_{{\mathrm{e}}_1=}=m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}})\ddot{x}-m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}})\ddot{y}-l_{\mathrm{s}}{m}_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}({\theta }_{\mathrm{e}}){\dot{\theta }}_{\mathrm{s}}^2 \\ -(I_{\mathrm{e}}+m_{\mathrm{e}}{r}_{\mathrm{e}}\left[r_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)\right]){\ddot{\theta }}_{\mathrm{s}} \end{gathered}$$

$$T_{{\mathrm{e}}_{\mathrm{N}}}=\left(I_{\mathrm{e}}+m_{\mathrm{e}}{r}_{\mathrm{e}}^2\right){\ddot{\theta }}_{\mathrm{e}}$$

$$T_{{\mathrm{e}}_{\mathrm{M}}}=T_{{\mathrm{e}}_{\mathrm{N}}}-T_{{\mathrm{e}}_1}$$

Shoulder joint torques

$$\begin{gathered} T_{{\mathrm{s}}_{\mathrm{l}}}=\left(m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}{l}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\right)\ddot{x}-\left(m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}{l}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)\right)\ddot{y} \\ -(m_{\mathrm{e}}{r}_{\mathrm{e}}(l_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right){\ddot{\theta }}_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}^2+2l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}{\dot{\theta }}_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}^2)) \end{gathered}$$

$$T_{{\mathrm{s}}_{\mathrm{N}}}=(I_{\mathrm{s}}+m_{\mathrm{s}}{r}_{\mathrm{s}}^2+m_{\mathrm{e}}{l}_{\mathrm{s}}^2+m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)){\ddot{\theta }}_{\mathrm{s}}$$

$$T_{{\mathrm{s}}_{\mathrm{M}}}=T_{{\mathrm{s}}_{\mathrm{N}}}-T_{{\mathrm{s}}_{\mathrm{l}}}+T_{{\mathrm{e}}_{\mathrm{M}}}$$

where $m$ is mass of segment, $r$ is center of mass of segment, $l$ is length of segment, $I$ is inertia of segment, ${\theta }_{\mathrm{s}}$ is shoulder angle, ${\theta }_{\mathrm{e}}$ is angle between center of mass of lower arm segment and upper arm, $x$ is shoulder position along $x$ direction, $y$ is shoulder position along $y$ direction, $T{e}_{\mathrm{I}}$ is elbow interaction torque, $T{e}_{\mathrm{M}}$ is elbow muscle torque, $T{e}_{\mathrm{N}}$ is elbow net torque, $T{s}_{\mathrm{I}}$ is shoulder interaction torque, $T{s}_{\mathrm{M}}$ is shoulder muscle torque, and $T{s}_N$ is shoulder net torque. The subscripts are defined as follows: $s$ is upper arm segment and e is lower arm segment (including support and air sled device).

Shoulder and elbow torque profiles were integrated from movement initiation to movement termination to obtain measures of shoulder and elbow torque impulses.

Statistical analysis

Bonferroni/Dunn post hoc analyses were used to test for significant differences between nondominant and dominant arm performance measures. Because the purpose of this study was to compare performance between nondominant and dominant arms, pair-wise statistical analyses were conducted on all measures of task performance, including hand-path linearity, final position error, and torque impulse.

RESULTS

Movements with large interaction torques: target 1

LIMB KINEMATICS.

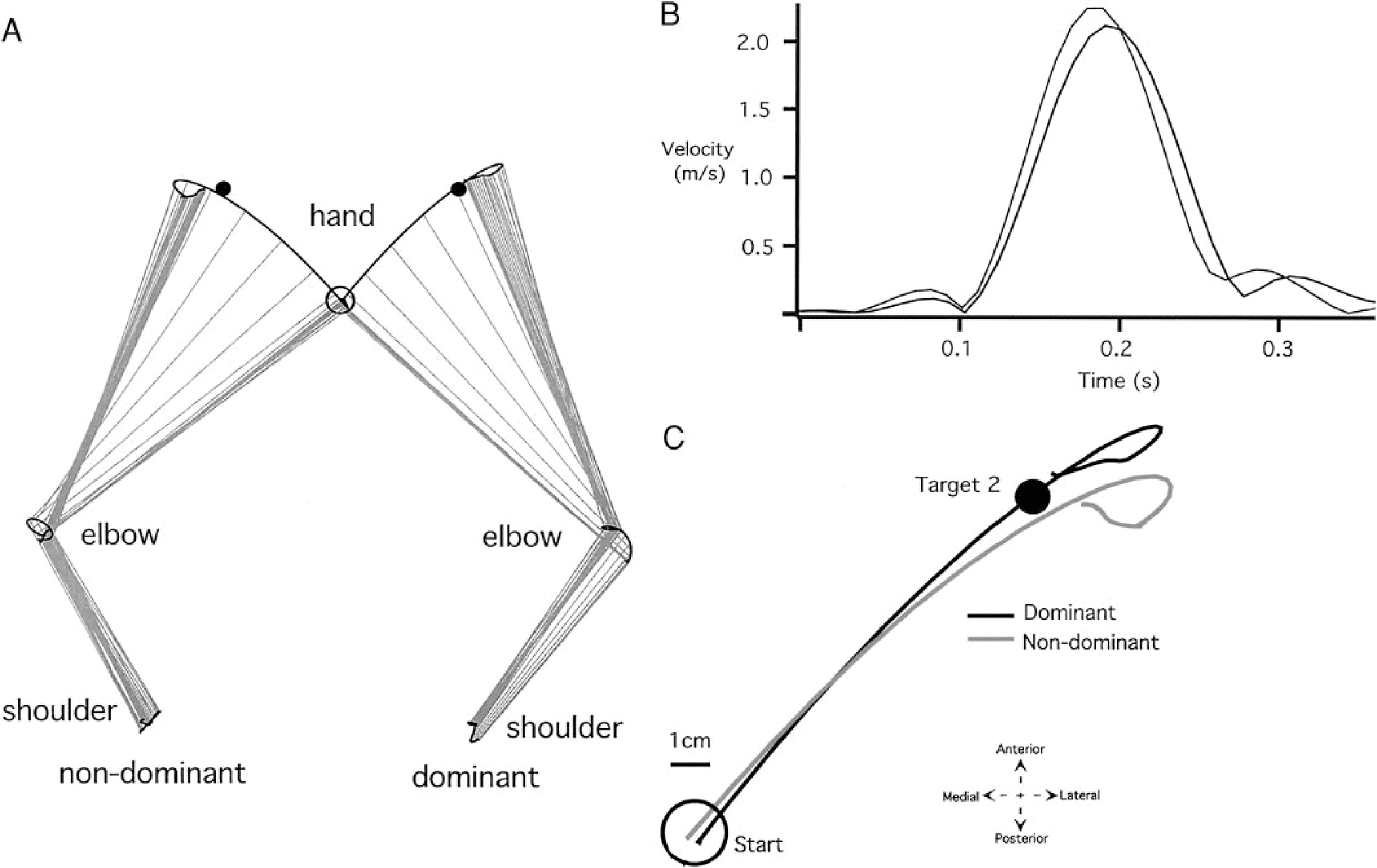
Typical nondominant and dominant arm shoulder, elbow, and hand trajectories for a movement performed to target 1 are illustrated in Fig. 2A. Successive upper arm and forearm/hand segment positions are drawn every 10 ms. Whereas starting position was in the midline for both movements, the positions were mirror reversed in Fig. 2B for clarity. This target was designed to require similar shoulder and elbow joint displacements for each arm. As illustrated in Fig. 2A, both arms displayed slight anterior-ward excursion of the scapula, substantial flexion of the shoulder joint, and substantial extension of the elbow joint.

FIG. 2.

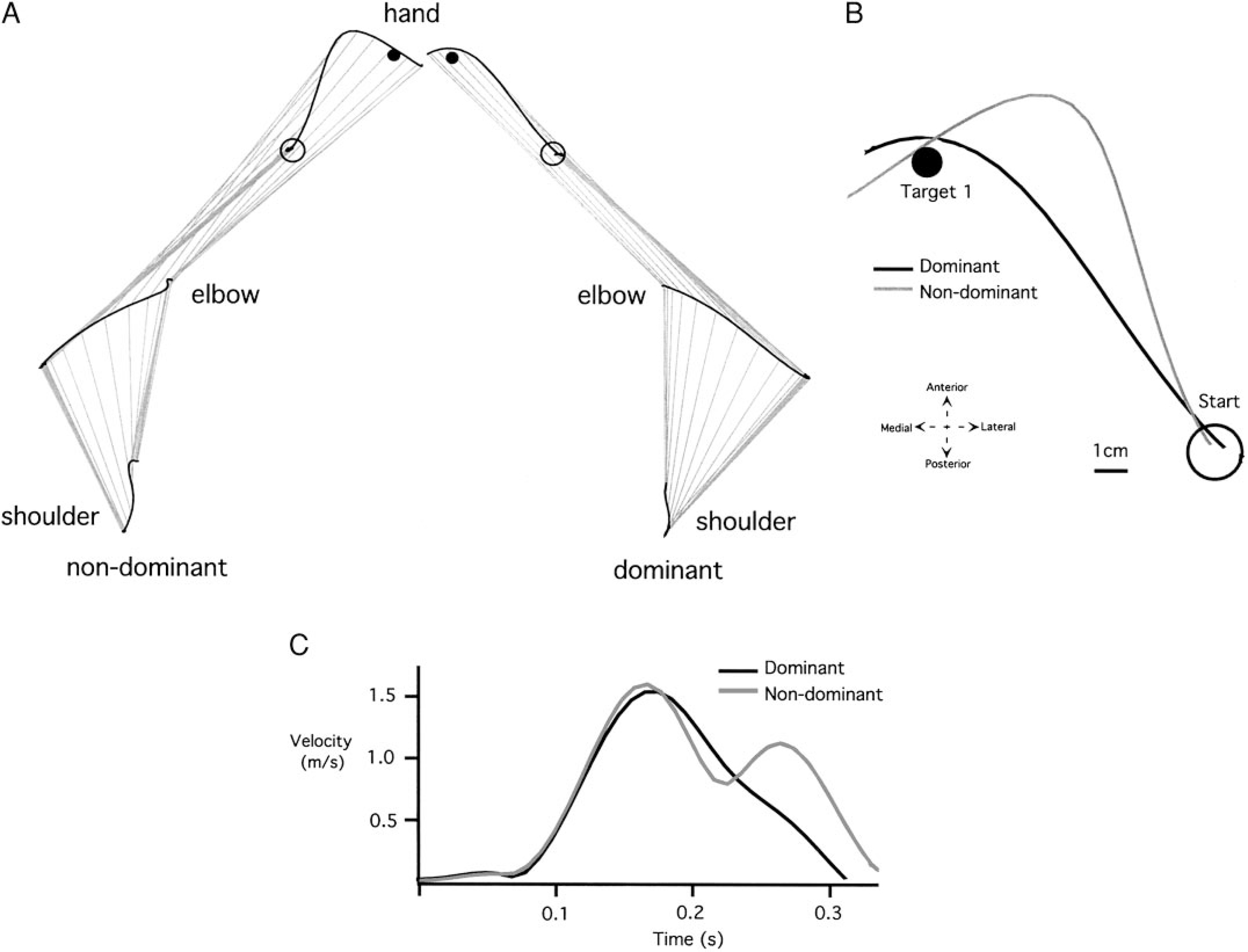
Representative trials made with the nondominant and dominant arms to target 1. A: individual arm graphs (shoulder, elbow, and hand trajectories. B: individual hand paths (starting circles displayed in the same midline position). C: individual velocity profiles.

The most obvious differences between the nondominant and dominant arm movements are noted in the hand trajectory profiles. Figure 2B illustrates these differences by displaying both dominant and nondominant hand-paths in a right-hand coordinate system, with the medial to lateral dimension directed along the positive x axis. The corresponding tangential hand velocity profiles are shown in Fig. 2C. While the dominant hand path is directed toward the target at movement initiation, the nondominant path is initially directed laterally, hooking back toward the target at the end of motion. Dominant and nondominant hand velocity profiles are similar until the peak $\left(V_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$. Afterward, the hook at the end of the nondominant hand profile is reflected by an additional peak in hand velocity. The reliability of these differences, across all subjects, is shown in Fig. 3, which compares measures of initial hand path direction deviation (Fig. 3A), tangential velocity maxima (Fig. 3B), hand-path deviation from linearity (Fig. 3C), and final position accuracies (Fig. 3D) for dominant and nondominant arm movements. Initial direction deviation, measured at peak tangential hand velocity $\left(V_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ is near zero (mean ± SE: −0.611° ± 2.892°) for the dominant arm. However, the nondominant hand paths were directed, on average, (mean ± SE: 15.001° ± 4.177°) lateral (clockwise) to the target. These differences were reliable across subjects (Bonferroni-Dunn: P = 0.0118). Regardless of these directional differences, both arms showed the same peak tangential hand velocities, as reflected in the bar plot in Fig. 3B, (Bonferroni-Dunn: P = 0.9984). The consistency of the “hook” toward the end of nondominant arm motion was reflected by our measure of linearity (Fig. 3C), indicating substantially more curved movements for the nondominant arm (Bonferroni-Dunn: P = 0.0138). The effectiveness of this correction is underscored by the fact that neither hand showed an advantage for final position accuracy (Bonferroni-Dunn: P = 0.5621; Fig. 3D).

FIG. 3.

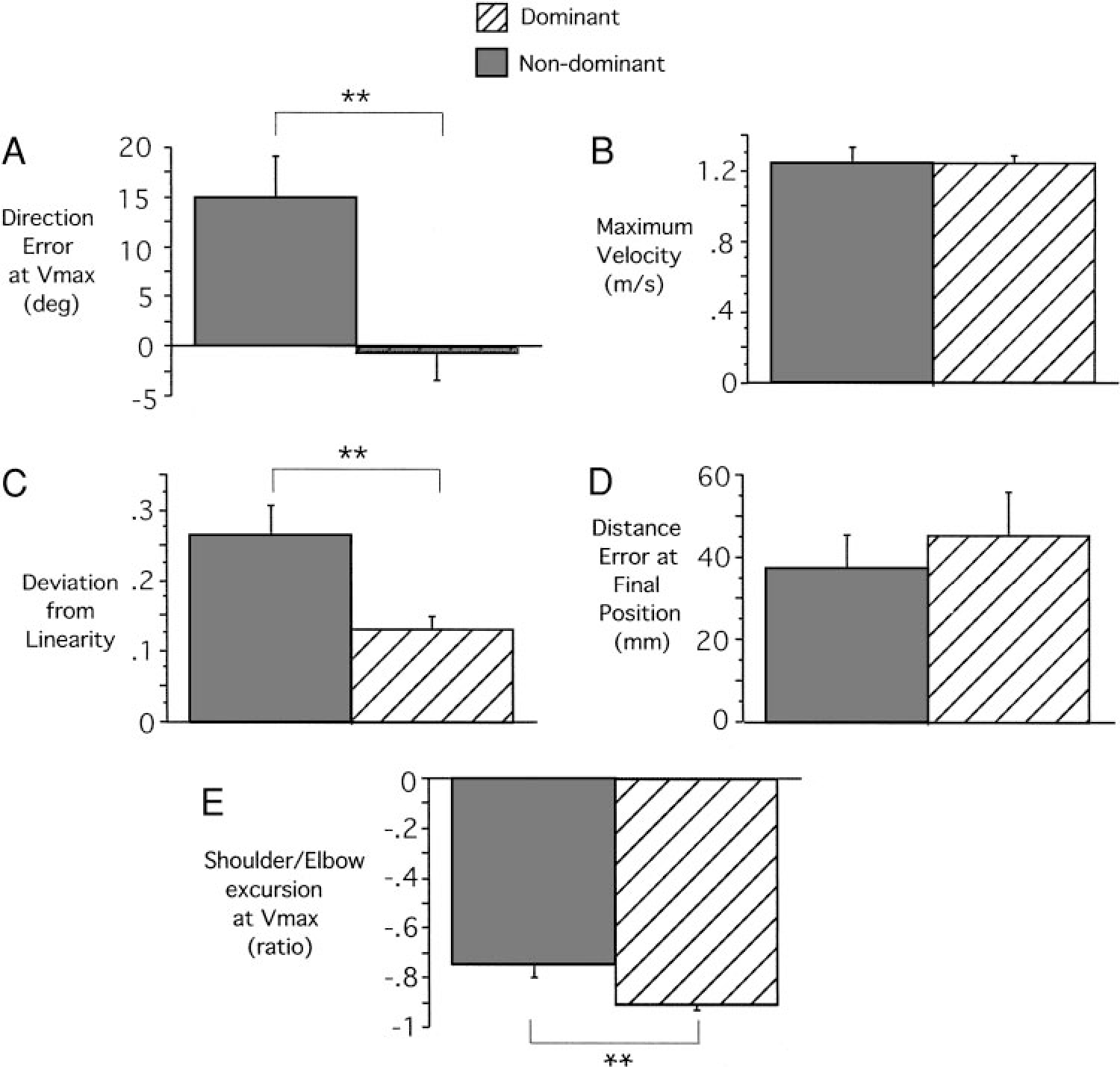
Kinematic comparisons for dominant and nondominant arm movements to target 1 across subjects. A: initial hand path direction deviation. B: tangential velocity maxima. C: hand-path deviation from linearity. D: final position accuracies. E: shoulder/elbow ratio at maximum tangential hand velocity location. Results from post hoc analysis (Bonferroni-Dunn) are significant (**).

The different directions and curvatures exhibited by dominant and nondominant hand-paths reflected consistent differences in elbow and shoulder joint coordination patterns. We quantified the joint contributions to the initial acceleration phase of motion as the ratio of shoulder excursion to elbow excursion, measured at peak tangential hand velocity. As indicated in Fig. 3E, the nondominant arm showed a smaller excursion ratio. Thus, compared to the dominant arm, nondominant arm movements were systematically initiated with greater elbow extension for a given amount of shoulder flexion (Bonferroni-Dunn: P = 0.0123). This resulted in the more laterally directed hand motion noted in Fig. 2B.

INVERSE DYNAMIC ANALYSIS.

The joint torque profiles that gave rise to these coordination differences are shown in Fig. 4A. Elbow and shoulder joint torque profiles are shown from 100 ms preceding movement initiation to 300 ms following movement initiation. At the elbow, interaction torque and muscle torque combine to produce net torque. For the dominant elbow, interaction torque, resulting from motion of the scapula and upper arm, accounts almost completely for net torque. Muscle torque, in contrast, remains near zero throughout the movement. Thus acceleration of the elbow results almost entirely from motion of the proximal segments, rather than from direct muscle actions on the forearm.

FIG. 4.

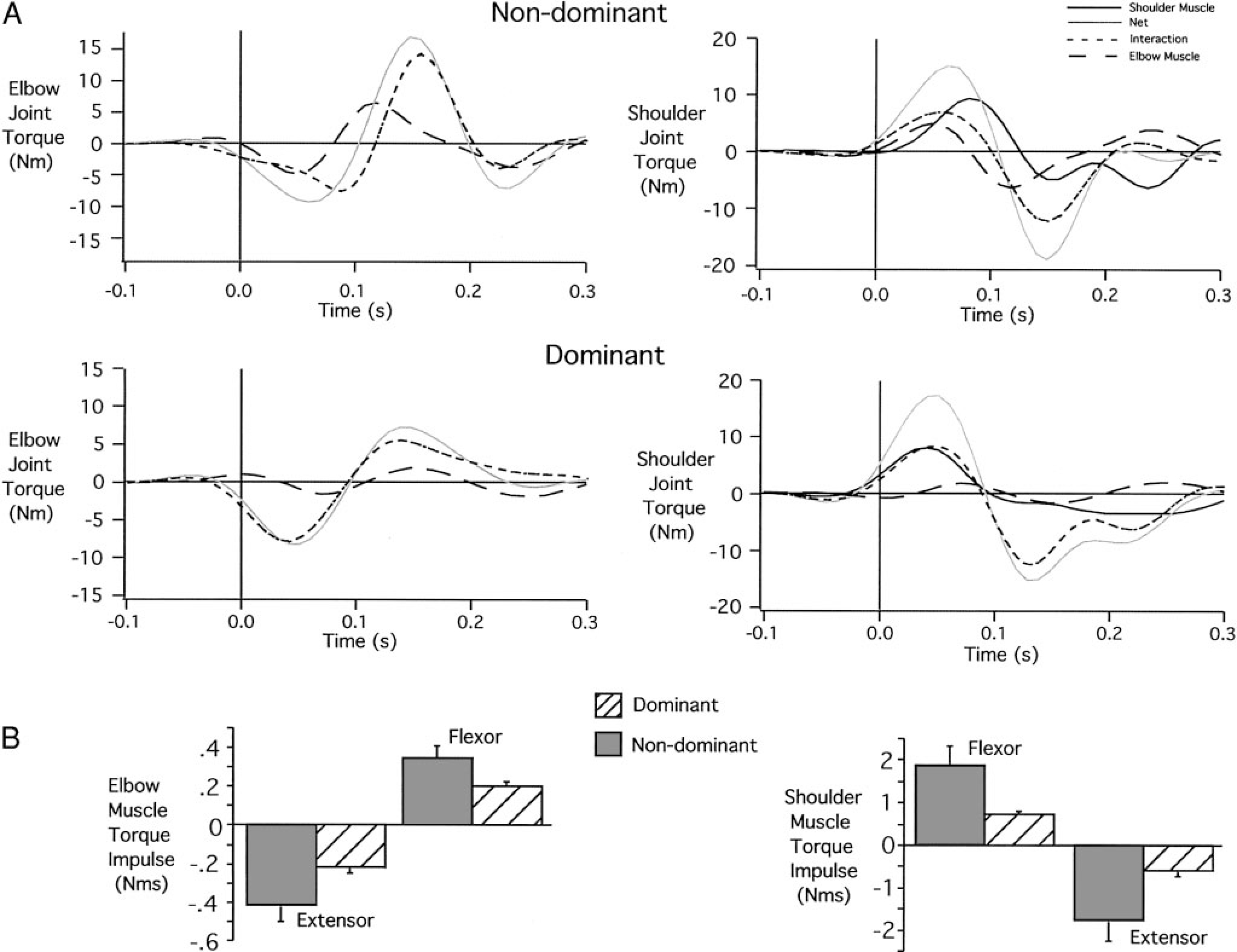
Nondominant and dominant joint torques for target 1 movements. A: individual elbow and shoulder torque profiles. B: elbow and shoulder muscle torque impulses (across subjects).

In contrast, nondominant elbow muscle torque contributes substantially to net torque. In the first phase of motion, extensor muscle torque combines with extensor interaction torque to produce large extensor net torque. This results in excessive elbow extension during movement initiation, which gives rise to the lateral deviation of the hand path. Figure 4B shows measures of flexor and extensor muscle torque impulse, calculated over the entire movement, for all subjects. Consistent with the data in Fig. 4A, dominant arm movements of all subjects used roughly one-half of the elbow flexor and extensor muscle torque impulse that was generated in the nondominant arm. This smaller torque output of dominant arm muscles was associated with equal speed and final position accuracy to that of the nondominant arm, suggesting a more torque-efficient strategy.

At the shoulder, four torque components are shown in Fig. 4A. Net torque at the shoulder results from interaction torque, shoulder muscle torque, and elbow muscle torque (elbow muscles acting on the distal end of the upper arm). For the dominant arm, elbow muscle torque is near zero, and initial flexor net torque results from equal contributions of shoulder muscle torque and interaction torque. All torque components cross zero simultaneously, and extensor net torque results primarily from interaction torque, with smaller contributions from elbow and shoulder muscles. At the nondominant shoulder, initial flexion net torque results from contributions of shoulder and elbow flexor muscle torque and flexor interaction torques. However, elbow muscle torque crosses zero about 60 ms prior to the zero crossing of net torque. As a result, nondominant shoulder muscle torque must counter the effects of elbow muscle torque to accelerate the upper arm. This requires greater shoulder muscle torque to generate a given net torque for the nondominant compared with the dominant arm.

The dominant arm control strategy appears to take better advantage of intersegmental dynamics by using less muscle torques at the shoulder and elbow joints. The nondominant arm strategy requires greater muscle torque and larger elbow excursions to produce similar speed movements with similar final position accuracies. The more torque-efficient control strategy used by the dominant arm was consistently demonstrated by all subjects as indicated by the plots of flexor and extensor torque impulse in Fig. 4B. Both flexor and extensor muscle torque impulses were substantially lower at dominant arm shoulder [Bonferroni-Dunn: P = 0.0283 (flexor); P = 0.0254 (extensor)] and elbow [Bonferroni/Dunn: P = 0.0459 (flexor); P = 0.0396 (extensor)] joints.

ELECTROMYOGRAPHIC ANALYSIS.

We next asked whether these systematic differences in torque were observable in electromyographic (EMG) recordings of elbow and shoulder muscles. We expected that both flexor and extensor EMG should show smaller amplitude activity for the dominant arm. Figure 5 shows recordings of elbow muscles (left: biceps brachii and triceps brachii) and shoulder muscles (right: pectoralis major and posterior deltoid) from the trials shown in Fig. 2. Recordings were digitized at 1 KHz, full-wave rectified, bin integrated every 10 ms, and then normalized to the largest bin recorded during maximal isometric contraction. Each bar indicates a 10-ms bin. At both the shoulder and the elbow, the most obvious differences were observable in flexor muscles. At the elbow, a distinct premovement burst was observable and was consistently smaller in amplitude for dominant arm movements. Following movement onset, flexor activity remained substantially lower for the dominant arm. We quantified the normalized EMG amplitude for individual subjects focusing on movement initiation, by integrating the EMG signal from 100 ms prior to movement to 100 ms following movement. Table 1 shows the results of Bonferroni-Dunn post hoc paired comparisons of the normalized elbow and shoulder EMG recorded for dominant and nondominant arms. Dominant arm biceps amplitude was significantly smaller for five of six subjects. This is consistent with the torque analysis described above. However, differences in triceps amplitude were not as consistent between the arms (see Table 1).

FIG. 5.

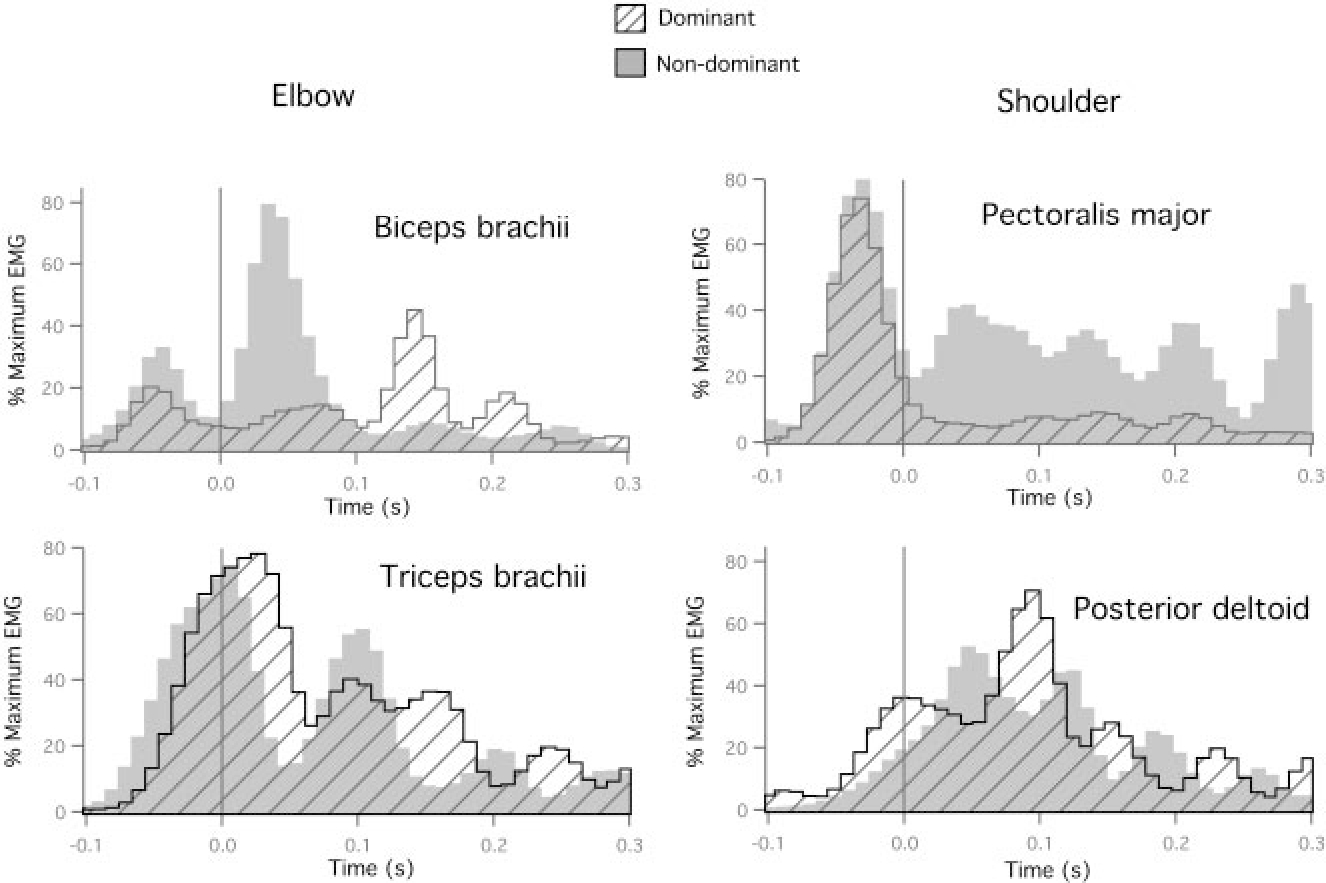
Dominant and nondominant electromyography (EMG) recordings for elbow muscles (left: biceps brachii and triceps brachii) and shoulder muscles (right: pectoralis major and posterior deltoid) for movements performed to target 1.

TABLE 1.

Statistical analysis (P value) of interlimb EMG impulses for target 1

Subject	Biceps Brachii	Triceps Brachii	Pectoralis Major	Posterior Deltoid
AR	<0.0001*	0.2219	<0.0001*	0.0002*
FL	<0.0001*	0.0007*	<0.0001*	0.6418
MM	0.0100	<0.0001*	0.0816	0.0008*
SV	<0.0001*	0.1183	0.0422*	0.7081
VK	<0.0001*	0.1576	0.4547	0.3766
YL	0.0065*	0.9845	0.0147*	0.2395

^*Statistically significant (Bonferoni-Dunn).

Similar results were observed for shoulder joint muscle activity. As shown in Fig. 5 (right column), pectoralis burst amplitude over time (flexor impulse) was significantly smaller for the dominant compared with the nondominant arm. This difference was significant in four of six subjects. Again, extensor muscle activity (posterior deltoid) was not reliably smaller across subjects (see Fig. 5 and Table 1).

In summary, interlimb differences in coordination corresponded to substantial differences in computed torque patterns: Dominant arm patterns reflected more efficient utilization of intersegmental dynamics. Electromyographic recordings of flexor muscles supported our inverse dynamic analysis, indicating reliably smaller amplitude activity for the dominant arm. However, recordings of extensor activity did not show consistent differences across subjects. It should be noted that substantial co-activation of muscles was observed in both arms, the dynamic effects of which is not reflected by inverse dynamic calculations.

Movements with smaller interaction torques: target 2

LIMB KINEMATICS.

We expected that movements requiring very little shoulder motion, but large elbow motions, should have fairly small interaction torques at the elbow. In addition, the forces transferred to the upper arm by motion of the forearm are small relative to the large inertial resistance of both segments resists such effects. As a result, interlimb differences in control of intersegmental dynamics should not lead to large differences in movement accuracy. Nevertheless, we expect that for such movements, interlimb differences in control of dynamics should remain observable through inverse dynamic analysis and EMG recordings. This is based on the idea that the differences in control between dominant and nondominant arms are fundamental to the control mechanisms employed. We, thus tested the hypothesis that even movements with small intersegmental effects should show significant differences in dynamic control strategies between dominant and nondominant arms.

Figure 6A shows representative dominant and nondominant arm trajectories, with associated tangential hand velocities (Fig. 6B) and individual hand paths (displayed at the same coordinate system—Fig. 6C), for movements to target 2. As evidenced by the display of upper arm and forearm position, these movements required substantial excursion of the elbow joint, but very little excursion of shoulder joint. As expected, dominant and nondominant hand trajectories were very similar.

FIG. 6.

Representative trials made with the nondominant and dominant arms to target 2. A: individual arm graphs (shoulder, elbow, and hand trajectories). B: individual velocity profiles. C: individual hand paths (starting circles displayed in the same midline position).

Figure 7 shows measures of peak tangential hand velocity (A), hand-path direction deviation at $\left(V_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ (B), hand-path deviation from linearity (C), and final position error (D) for dominant and nondominant arm movements. Consistent with the paths shown in Fig. 6, the initial direction deviation and the final position errors were not significantly different between dominant and nondominant arms. Nevertheless, small, but reliable differences between the trajectories were observed (Fig. 6, B and C). The nondominant hand trajectories were systematically more curved (higher deviation from linearity), resulting in reliable clockwise direction deviations of the nondominant arm, measured at final position. Whereas, for both arms, elbow excursion was substantially larger than shoulder excursion (see Fig. 7E), dominant shoulder excursion was consistently larger than that of the nondominant arm (Bonferroni-Dunn: P = 0.0416). As a result, the ratio of shoulder to elbow motion was significantly higher for the dominant arm (Fig. 7F; Bonferroni-Dunn: P = 0.0575). This increased shoulder flexion is observable in Fig. 6A and contributed to the straighter hand trajectories of the dominant arm.

FIG. 7.

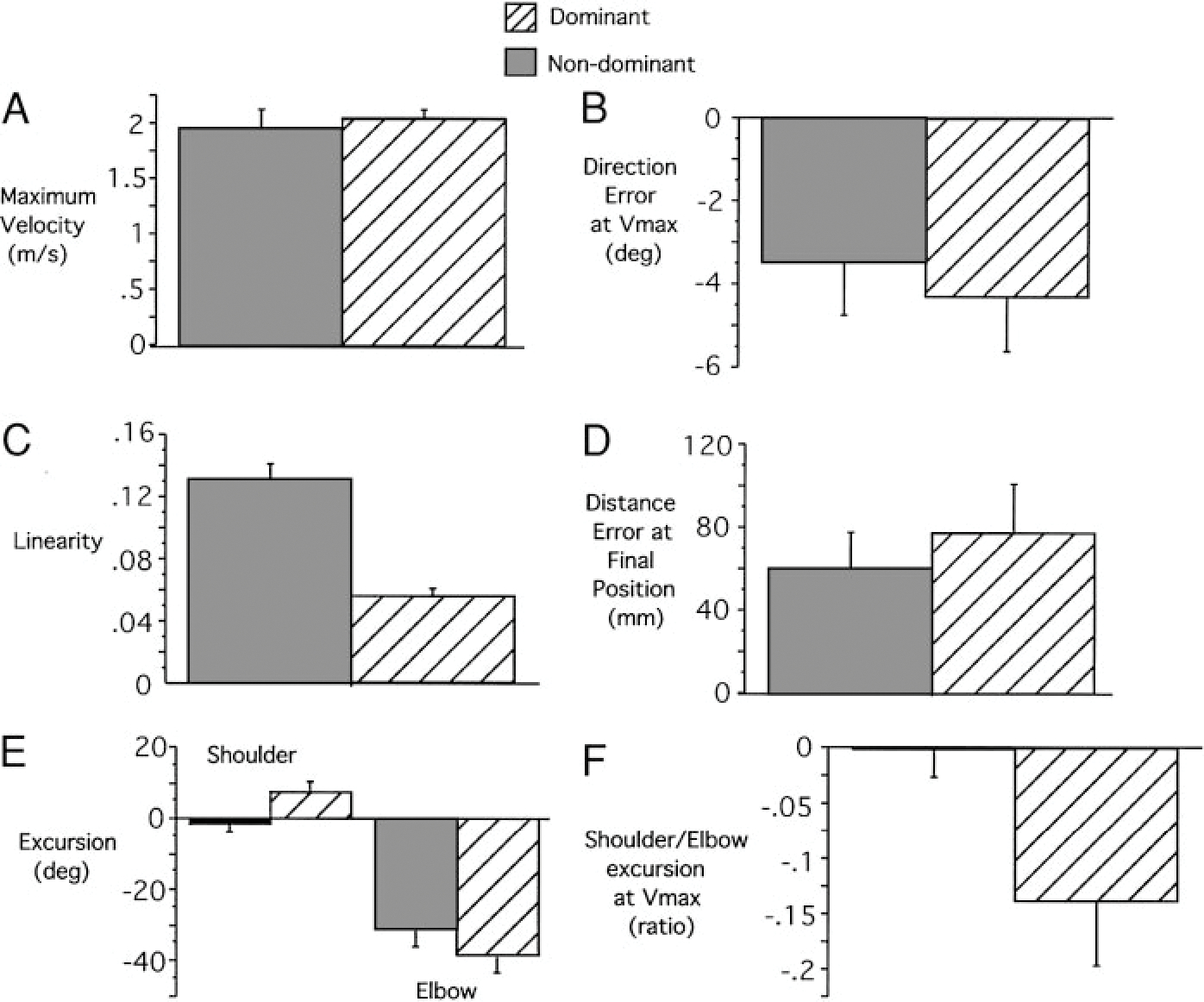
Kinematic comparisons for dominant and nondominant arm movements to target 2 across subjects. A: tangential hand velocity maxima. B: handpath direction deviation at $\left(V_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$. C: hand-path deviation from linearity. D: final position accuracies. E: shoulder and elbow movement excursions. F: shoulder/elbow ratio at maximum tangential hand velocity location.

INVERSE DYNAMIC ANALYSIS.

These slight differences in interjoint coordination were associated with substantial differences in joint torque profiles, as shown in Fig. 8A. At the shoulders, during the initial 100 ms following movement onset, flexor shoulder net torque is driven by elbow muscle actions on the upper arm (elbow muscle torque) and by interaction torque, which primarily results from motion of the forearm. Shoulder extensor muscle torque counters these effects, thereby stabilizing the shoulder. For the nondominant shoulder, extensor shoulder muscle torque is quite large, resulting in a small net torque and little shoulder displacement. However, for the dominant shoulder, extensor muscle torque is lower, resulting in higher net torque and larger shoulder displacement. As illustrated in Fig. 8B, dominant arm shoulder flexor (Bonferroni-Dunn: P = 0.0004) and extensor (Bonferroni-Dunn: P = 0.0006) muscle torque impulse was systematically lower across all subjects. Because the function of shoulder muscle torque is to counter shoulder motion for these movements, greater shoulder excursions are measured for dominant arm movements. Thus the dominant arm used less shoulder torque but allowed greater shoulder excursion.

FIG. 8.

Nondominant and dominant joint torques for target 2 movements. A: individual elbow and shoulder torque profiles. B: elbow and shoulder muscle torque impulses (across subjects).

At the elbow, net torque was almost completely driven by elbow muscle torque in both arms. However, reliable interlimb differences in the contributions of interaction torque occurred. For the nondominant arm, interaction torque counters net and muscle torque, resulting in higher peak muscle torques (flexor or extensor) than peak net torques. However, for the dominant arm, interaction torque contributed greater to net torque throughout the movement, resulting in higher peak net torques (flexor or extensor) than peak muscle torques. Consistent with this example, flexor (Bonferroni-Dunn: P = 0.2351) and extensor (Bonferroni-Dunn: P = 0.5335) elbow muscle torque impulse was higher for nondominant than dominant arm movements of all subjects (see Fig. 8B). Even though the dominant and nondominant arm movements were performed at similar speed and with similar final position accuracy, dominant arm movements were consistently performed with less muscle torque. Thus even for movements in which elbow joint interaction torques were small, the contribution of such interactions was more efficiently incorporated into control patterns for the dominant arm.

ELECTROMYOGRAPHIC ANALYSIS.

Electromyographic recordings are consistent with our inverse dynamic analysis, indicating reliably smaller amplitude muscle activities for the dominant arm. Figure 9 shows the EMG recordings from the movement trials shown in Fig. 6. Elbow flexor activity (biceps) was substantially smaller for the dominant arm, as was shoulder flexor (pectoralis) activity. However, elbow and shoulder extensor activities did not show reliable differences in amplitude. Table 2 shows the results of Bonferroni-Dunn post hoc pair-wise comparisons for all four muscles recorded, indicating reliable differences in elbow flexor activities (6/6 subjects) and shoulder flexor activities (6/6 subjects). Extensor muscle activities at the elbow (5/6 subjects) and shoulder (4/6 subjects) were generally smaller for the dominant arm, although the differences were less reliable across subjects.

FIG. 9.

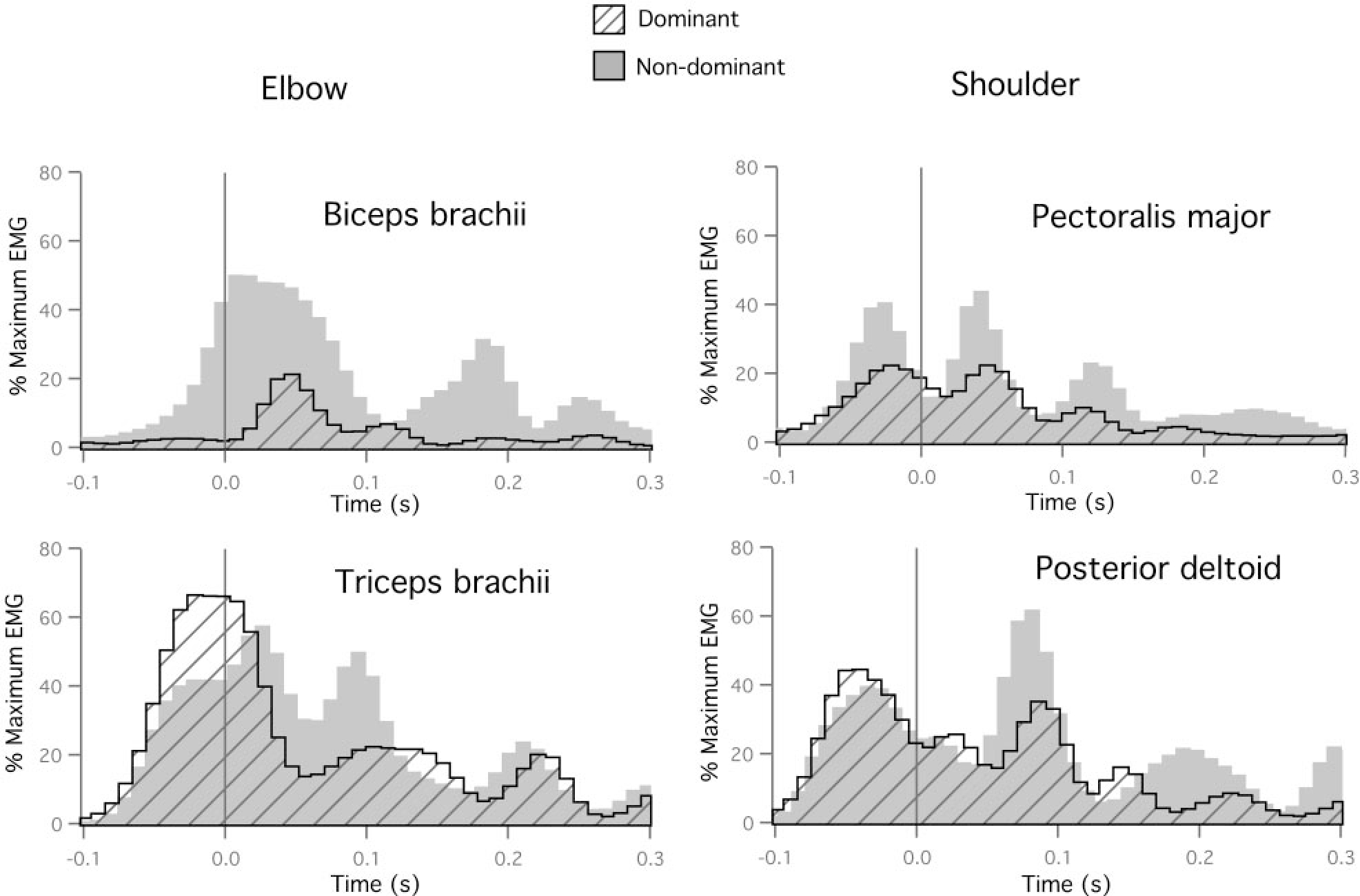
Dominant and nondominant EMG recordings for elbow muscles (left: biceps brachii and triceps brachii) and shoulder muscles (right: pectoralis major and posterior deltoid) for movements performed to target 2.

TABLE 2.

Statistical analysis (P value) of interlimb EMG impulse for target 2

Subject	Biceps Brachii	Triceps Brachii	Pectoralis Major	Posterior Deltoid
AR	0.0043*	0.5422	0.0004*	<0.0001*
FL	0.0003*	0.0005*	<0.0001*	0.5427
MM	0.0011*	<0.0001*	<0.0001*	0.0375*
SV	<0.0001*	0.0006*	0.0040*	0.6930
VK	0.0017*	<0.0001*	<0.0001*	0.0042*
YL	0.0148*	0.0193*	<0.0001*	0.0003*

^*Statistically significant (Bonferoni-Dunn).

DISCUSSION

This study examined interlimb differences in kinematics, dynamics, and electromyographic activity during horizontal plane reaching movements to two different targets. Whereas target 1 required approximately 30° shoulder extension and 30° elbow extension, target 2 required no shoulder excursion and 30° elbow extension to accurately reach the target. Movements to target 1 were thus expected to elicit substantial interaction torques transferred to the forearm from upper arm motion. In contrast, movements to target 2 were expected to elicit only small interaction torques at the elbow joint. We had previously shown that, for such planar reaching movements, dominant arm hand path curvatures did not depend on interaction torque amplitude. However, nondominant arm curvatures depended on the amplitude of interaction torques, such that movements with small interaction torques were straighter, while the ones with large elbow joint interaction torques were more curved (Sainburg and Kalakanis 2000). We expected that in this study, substantial interlimb differences in coordination would occur for target 1 movements, in which interaction torques were largest. We also expected that such differences would be minimal for target 2 movements, in which interaction torques were small. This design allowed us to ask whether interlimb differences in EMG and torque patterns were dependent on differences in kinematics or whether such differences in dynamic control occurred when kinematic features of movement appeared quite similar.

It should be noted that for one of the targets in our previous study (Sainburg and Kalakanis 2000), nondominant arm movements were systematically straighter than dominant arm movements. Inverse dynamic analysis revealed that the straighter movements of the nondominant arm required substantially greater muscle torques than the more curved movements of the dominant arm, even though movements of both arms were made with equivalent speeds and accuracies. Thus we do not expect that hand-path straightness reflects better or worse coordination patterns, but rather that inverse dynamic analysis can reveal the extent to which different coordination patterns account for the passive dynamics of the musculoskeletal system, as reflected by interaction torques. It is thus plausible that movements with similar hand-path curvatures could show substantial differences in the torque patterns responsible for the movements.

Target 1 movements

Our findings indicated that nondominant arm movements to target 1 were reliably deviated laterally at movement onset, whereas dominant arm movements were directed toward the target at movement onset. Nondominant arm movements consistently hooked toward the target in the late deceleration phase of motion. As a result, final position accuracies were not substantially different between hands. Both arms performed movements at similar speed. However, inverse dynamic analysis revealed that dominant arm movements were made with substantially lower muscle torque, measured as flexor and extensor torque impulse. Thus dominant arm movements appeared to be performed with greater torque efficiency than nondominant arm movements. EMG analysis supported our inverse dynamic findings by indicating reliably lower muscle activities for the dominant arm across subjects. Flexor muscle recordings were consistently smaller for the dominant arm than were extensor muscle recordings.

These findings support and extend our previous studies of dominant and nondominant arm reaching movements (Sainburg 2002; Sainburg and Kalakanis 2000). In those studies, movements of the dominant arm were made with a fraction of the muscle torque of nondominant arm movements performed with similar speed and accuracy. These findings provided the basis for the hypothesis that the essential difference between dominant and nondominant arm coordination is the facility governing control of limb dynamics. Consistent with this hypothesis, we showed that dominant hand path curvatures were independent of the amplitude of interaction torques, whereas nondominant hand path curvatures appeared enslaved to these interactions (Sainburg and Kalakanis 2000). A later study indicated that the dominant arm more effectively adapted to novel intersegmental dynamics, imposed by altering the position of an inertial load attached eccentric to the forearm’s long axis (Sainburg 2002). Our current findings provide support for our hypothesis by showing that recorded muscle activities, normalized to maximum voluntary isometric contraction, were substantially smaller for the dominant arm.

Target 2 movements

It should be emphasized that the causal relations between our dynamic and kinematic findings described above were indirectly derived. The lateral deviations of nondominant arm movements may have occurred secondary to a failure to take account of the large interaction torques driving the forearm lateral during the initial acceleration phase of nondominant arm movement. Conversely, the nondominant arm torque strategy may be adapted to make laterally directed movements that curve inward toward the target at the end of motion. In other words, the nondominant controller may have “planned” to produce such paths. Our results from the target 2 movements effectively ruled out this latter alternative. Both dominant and nondominant arm movements toward target 2 showed similar initial directions, speeds, and final accuracies. Dominant handpath curvatures were reliably smaller due to a slight, but significant, increase in upper arm motion. This upper arm motion produced larger interaction torques at the elbow joint, which were coordinated with muscle torques such that dominant arm movements were produced with less flexor and extensor elbow muscle torque impulse. In addition, the interaction torques transferred to the upper arm from forearm motion were also better coordinated with muscle actions on the upper arm, such that shoulder muscle torques were also reliably smaller for the dominant arm. Electromyographic recordings supported these findings, indicating smaller muscle activities for the dominant arm. Because movement kinematics were similar, these effects are not likely to be driven by different kinematic goals for the task. We therefore conclude that dominant arm movements reflect more efficient control of intersegmental dynamics.

Dominant arm specialization for control of limb dynamics

One might expect that the limitations in nondominant arm coordination resulted from a torque production deficit for that arm. However, the nondominant arm consistently used greater torque to produce movements of the same speed and accuracy of dominant arm movements. Therefore the nondominant arm limitation in dynamic control cannot be attributed to a torque production deficit. Instead, our inverse dynamic results suggest substantial qualitative differences in dynamic control, as implemented for dominant and nondominant arm movements. These findings are consistent with our previous findings indicating a dominant arm advantage in controlling limb segment inertial interactions (Sainburg and Kalakanis 2000) and in adapting to novel inertial loads (Sainburg 2002). Our results support the hypothesis that manual asymmetries result from interlimb differences in controlling the effects of limb dynamics (Sainburg and Kalakanis 2000).

It should be noted that dominant arm advantages do not apply to all tasks or all aspects of tasks. Healey et al. (1986) examined an extensive range of tasks through a questionnaire and found that four factors, or groups of tasks, accounted for 80% of the variance in hand preference among the 110 subjects tested. These authors found that some tasks were performed almost exclusively by the dominant arm, whereas others were most often performed by the nondominant arm. This study indicated that handedness could not simply be attributed to factors such as tool use, or proximal versus distal muscle involvement. Dominant arm tasks were almost exclusively associated with activities requiring precision in interjoint coordination and trajectory formation. For example, targeted ball throwing is dependent on the trajectory of the hand prior to ball release, and drawing performance is determined by the trajectory of the writing implement. Specification of the trajectory of the hand is critically dependent on interjoint coordination and control of intersegmental dynamics (Sainburg et al. 1993, 1995, 1999). In contrast, nondominant arm tasks involved spatially orienting a body segment posture. These tasks included posturing the hand to point toward a distant object, which is similar to other functional tasks such as holding a piece of paper that is being cut with scissors or orienting the hand in space for catching a baseball. These postural orientation tasks are less dependent on intersegmental dynamics, since the trajectory used to attain the posture is not critical for task success.

It should be mentioned that the differences in coordination between the limbs reflected in this study might reflect lifelong practice and experience that is often associated with dominant arm use. This idea is supported by previous studies indicating that accurate coordination of muscle forces with intersegmental and environmental forces is dependent on proprioceptive information (Ghez and Sainburg 1995; Sainburg et al. 1993, 1995) and learning (Lackner and Dizio 1994; Sainburg et al. 1999; Shadmehr and Mussa-Ivaldi 1994) and that such coordination develops over the first few years of life (Thelen et al. 1983, 1993; Zernicke and Schneider 1993). According to this point of view, the interlimb differences in dynamic control studied here may arise secondary to asymmetrical experience with each arm. This interpretation would require that a more primary factor is responsible for the initial asymmetry in use of the limbs. Alternatively, it has been proposed that the behavioral effects of handedness are determined by physiological asymmetries that are present before the opportunity for such experience develops (Annett 1992; Clark et al. 1996; Coryell 1985; Drea et al. 1995; McManus 1985; Melsbach et al. 1996; Tan 1990). According to this idea, handedness emerges from distinctive neural circuits in each hemisphere that are specialized for controlling different aspects of limb movements (Caplan and Kinsbourne 1976; Corryel 1985; Futagi et al. 1995; Hepper et al. 1991, 1998; Konishi et al. 1986, 1997; Ottaviano et al. 1989; Tan et al. 1992). It is plausible that the differences in such circuits are related to the facility for modeling and controlling the effects of limb dynamics. However, it is not possible from the current data to determine whether differences in neural circuitry give rise to asymmetries in dynamic control of the arms, or vise versa. Nevertheless, our current findings support the hypothesis that handedness in adults is associated with substantial interlimb differences in control of limb dynamics.

APPENDIX

The arm was modeled as a two-segment link with the shoulder joint free to move in the $xy$ horizontal plane (see Fig. A1). The length of each segment is denoted by $l$. Each segment is homogeneous, and the segment mass $m$ is assumed to be concentrated in the center of mass $CM$ (located at $r$ distance from the joints) with its respective moment of inertia $I$. The position for the center of mass of each segment in the base coordinate system is denoted by $p(x,y)$. Each joint generates a torque $T$, which tends to cause a rotational movement, and each segment is affected by forces $F$ and moments $M$.

fig. A1.

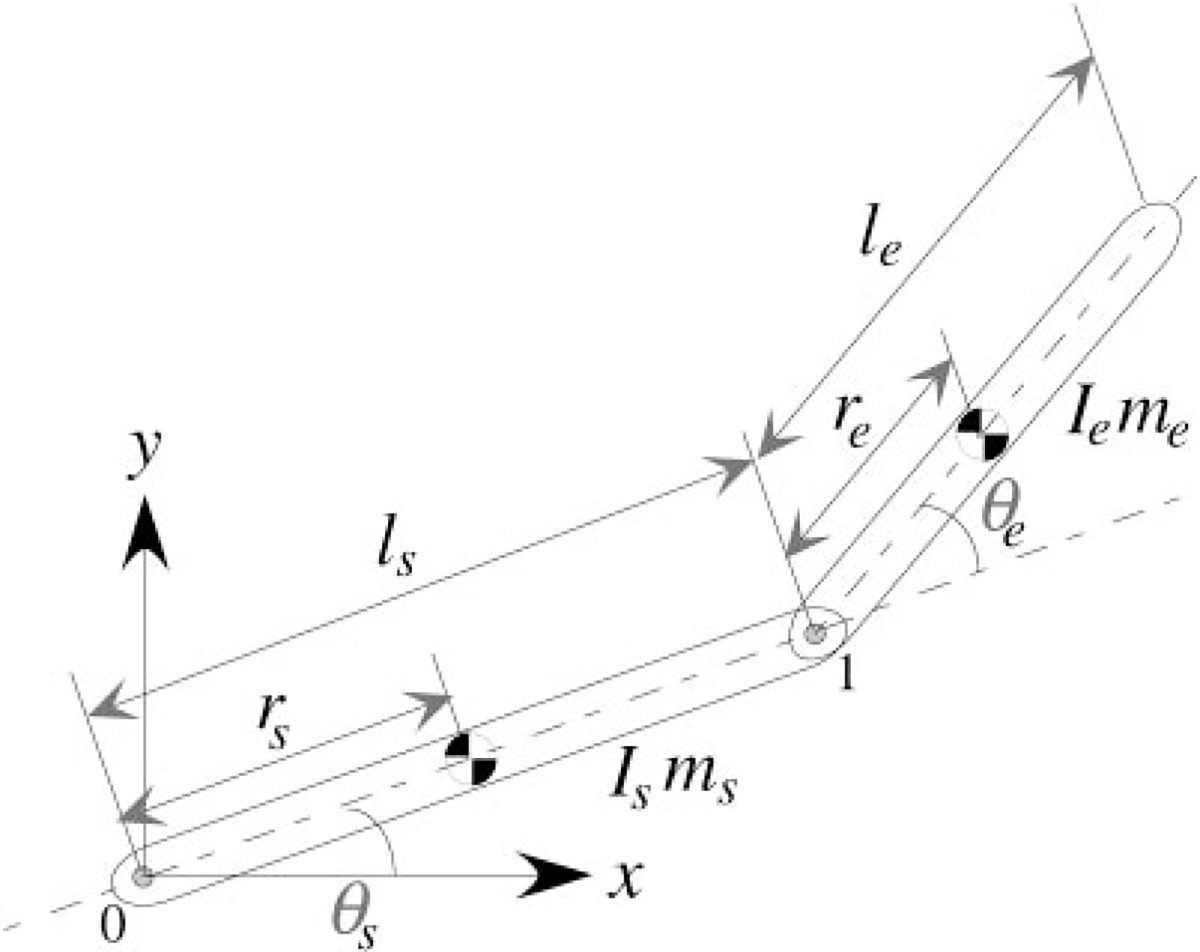
Two-segment link planar arm model.

The Newton-Euler equations for the shoulder (s) segment are given by

$$\begin{gathered} F_{\mathrm{s}}-F_{\mathrm{e}}+m_{\mathrm{s}}{\ddot{p}}_0-m_{\mathrm{s}}{\ddot{p}}_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}=0 \\ {M}_{\mathrm{s}}-M_{\mathrm{e}}+\left(p_1-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times F_{\mathrm{e}}-\left(p_0-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times F_{\mathrm{s}}-I_{\mathrm{s}}{\dot{\omega }}_{\mathrm{s}}=0 \end{gathered}$$ (A1)

and similarly to the elbow (e) joint

$$\begin{gathered} F_{\mathrm{e}}+m_{\mathrm{e}}{\ddot{p}}_0-m_{\mathrm{e}}{\ddot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}=0 \\ {M}_{\mathrm{e}}-\left(p_1-p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}\right)\times F_{\mathrm{e}}-I_{\mathrm{e}}{\dot{\omega }}_{\mathrm{e}}=0 \end{gathered}$$ (A2)

To obtain the dynamic equations, we first eliminate the joint forces and separate them from the joint torques, to explicitly involve the joint torques in the dynamic equations. For the planar two-segment link, the joint torques $T_{\mathrm{s}}$ and $T_{\mathrm{e}}$ are equal to the coupling moments $\left(M_{\mathrm{s}}\right.$ and $M_{\mathrm{e}}$), respectively. Eliminating $F_{\mathrm{e}}$ in Eq. A2, and subsequently eliminating $F_{\mathrm{s}}$ in Eq. A1, we obtain

$$T_{\mathrm{e}}-\left(p_1-p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{e}}{\ddot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}+\left(p_1-p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{e}}{\ddot{p}}_0-I_{\mathrm{e}}{\dot{\omega }}_{\mathrm{e}}=0$$ (A3)

$$\begin{gathered} T_{\mathrm{s}}-T_{\mathrm{e}}-\left(p_0-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{s}}{\ddot{p}}_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}-\left(p_0-p_1\right)\times m_{\mathrm{e}}{\ddot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}+\left(p_0-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{s}}{\ddot{p}}_0 \\ +\left(p_0-p_1\right)\times m_{\text{e}}{\ddot{p}}_0-I_{\text{s}}{\dot{\omega }}_{\text{s}}=0 \end{gathered}$$ (A4)

Rewriting the angular and linear velocities for shoulder and elbow joints, and the position vectors, using joint displacement angles $\left({\theta }_{\mathrm{e}}\right.$ and ${\theta }_{\mathrm{s}}$), which are independent variables, we have

$$\begin{array}{c}{\omega }_{\text{s}}={\dot{\theta }}_{\text{s}}\\ {\omega }_{\text{e}}={\dot{\theta }}_{\text{s}}+{\dot{\theta }}_{\text{e}}\\ p_{{\text{s}}_{\text{CM}}}=⌊\begin{array}{c}{r}_{\text{s}}\text{cos}\left({\theta }_{\text{s}}\right)\\ r_{\text{s}}\text{sin}\left({\theta }_{\text{s}}\right)\end{array}⌋p_{{\text{e}}_{\text{CM}}}=⌊\begin{array}{c}{l}_{\text{s}}\text{cos}\left({\theta }_{\text{s}}\right)+r_{\text{e}}\text{cos}\left({\theta }_{\text{s}}+{\theta }_{\text{e}}\right)\\ l_{\text{s}}\text{sin}\left({\theta }_{\text{s}}\right)+r_{\text{e}}\text{sin}\left({\theta }_{\text{s}}+{\theta }_{\text{e}}\right)\end{array}⌋\end{array}$$ (A.5)

$$\begin{gathered} {\dot{p}}_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}=\left[\begin{array}{c}-r_{\mathrm{s}}{\dot{\theta }}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\\ r_{\mathrm{s}}{\dot{\theta }}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)\end{array}\right] \\ {\dot{\mathrm{p}}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}=\left[\begin{array}{c}-\{l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\}{\dot{\theta }}_{\mathrm{s}}-r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}\\ \left\{l_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{s}}+r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right\}{\dot{\theta }}_{\mathrm{s}}+r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}\end{array}\right] \end{gathered}$$ (A6)

Substituting Eqs. A5 and A6 along with their time derivatives into Eqs. A3 and A4, we obtain the dynamic equations in terms of joint angles and shoulder position

$$\begin{gathered} T_{\mathrm{s}}=\alpha {\ddot{\theta }}_{\mathrm{s}}+\beta {\ddot{\theta }}_{\mathrm{e}}-\gamma {\dot{\theta }}_{\mathrm{e}}^2-2\gamma {\dot{\theta }}_{\mathrm{s}}{\dot{\theta }}_{\mathrm{e}}+\delta \\ {T}_{\mathrm{e}}=\epsilon {\ddot{\theta }}_{\mathrm{e}}+\beta {\ddot{\theta }}_{\mathrm{s}}+\gamma {\dot{\theta }}_{\mathrm{s}}^2+\phi \end{gathered}$$ (A7)

where

$$\alpha =m_{\mathrm{s}}{r}_{\mathrm{s}}^2+I_{\mathrm{s}}+m_{\mathrm{e}}\left[l_{\mathrm{s}}^2+r_{\mathrm{e}}^2+2l_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)\right]+I_{\mathrm{e}}$$

$$\beta =m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)+m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}$$

$$\gamma =m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right)$$

$$\begin{gathered} \delta =\left[m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}\left(r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)+l_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\right.\right. \\ \left.\left.\left({\theta }_{\mathrm{s}}\right)\right)\right]\ddot{y}-\left[m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}\left(r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)+\right.\right. \\ \left.\left.l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\right]\right]\ddot{x} \end{gathered}$$

$$\epsilon =m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}$$

$$\phi =\left[m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right]\ddot{y}-\left[m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right]\ddot{x}$$

$$m_{\text{s}}\text{and}{m}_{\text{e}}=\text{masses}\text{of}\text{upper}\text{arm}\text{and}\text{forearm}$$

$$r_{\text{s}}\text{and}{r}_{\text{e}}=\text{distances}\text{from}\text{the}\text{proximal}\text{joint}\text{to}\text{center}\text{of}\text{mass}\text{of}\text{upper}\text{arm}\text{and}\text{forearm}$$

$$l_{\text{s}}\text{and}{l}_{\text{e}}=\text{lengths}\text{of}\text{upper}\text{arm}\text{and}\text{forearm}$$

$$l_{\text{s}}\text{and}{l}_{\text{e}}=\text{lengths}\text{of}\text{upper}\text{arm}\text{and}\text{forearm}$$

$$I_{\text{s}}\text{and}{I}_{\text{e}}=\text{moments}\text{of}\text{inertia}\text{at}\text{center}\text{of}\text{mass}\text{of}\text{upper}\text{arm}\text{and}\text{forearm}$$

$${\theta }_{\text{s}}\text{and}{\theta }_{\text{e}}=\text{orientation}\text{angles}\text{at}\text{proximal}\text{end}\text{of}\text{segment}\text{for}\text{upper}\text{arm}\text{and}\text{forearm}.$$

Rigid body dynamic equations can be formulated in several ways, although the form of the equations that we used allowed us to quantify how muscles influenced limb motion as well as how the motion of one segment affected the other segment. At each of the two joints, we partitioned the torques into three categories (muscle torque, net torque, and interaction torque), which were defined as follows

Elbow joint torques

$$\begin{gathered} T_{{\mathrm{e}}_{\mathrm{M}}}=T_{{\mathrm{e}}_{\mathrm{N}}}-T_{{\mathrm{e}}_1} \\ {T}_{{\mathrm{e}}_{\mathrm{M}}}=\frac{\{\left(I_{\mathrm{e}}+m_{\mathrm{e}}{r}_{\mathrm{e}}^2\right){\ddot{\theta }}_{\mathrm{e}}\}}{{\mathrm{T}}_{{\mathrm{e}}_{\mathrm{N}}}}-\frac{\{m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\ddot{x}-m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\ddot{y} \\ -\left(l_{\mathrm{s}}{m}_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)+m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}\right){\ddot{\theta }}_{\mathrm{s}}-l_{\mathrm{s}}{m}_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}^2\}}{{\mathrm{T}}_{{\mathrm{e}}_{\mathrm{l}}}} \end{gathered}$$

Shoulder joint torques

$$T_{{\mathrm{s}}_{\mathrm{M}}}=T_{{\mathrm{s}}_{\mathrm{N}}}-T_{{\mathrm{s}}_{\mathrm{l}}}+T_{{\mathrm{e}}_{\mathrm{M}}}$$

$$\begin{gathered} T_{{\mathrm{s}}_{\mathrm{M}}}=\frac{\{\left(I_{\mathrm{s}}+m_{\mathrm{s}}{r}_{\mathrm{s}}^2+m_{\mathrm{e}}{l}_{\mathrm{s}}^2+m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)\right){\ddot{\theta }}_{\mathrm{s}}\}}{{\mathrm{T}}_{{\mathrm{s}}_{\mathrm{N}}}} \\ -\frac{\left(m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}{l}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\right)\mid \ddot{x}-(m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}{l}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right))\ddot{y} \\ -(m_{\mathrm{e}}{r}_{\mathrm{e}}(l_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right){\ddot{\theta }}_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}^2+2l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}{\dot{\theta }}_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}^2))\}}{T_{{\mathrm{s}}_1}} \\ +\frac{m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\ddot{\mathrm{y}}-m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\ddot{\mathrm{x}}\} \\ +\left(m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)+m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}\right){\ddot{\theta }}_{\mathrm{s}}+l_{\mathrm{s}}{m}_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}^2+\left(I_{\mathrm{e}}+m_{\mathrm{e}}{r}_{\mathrm{e}}^2\right){\ddot{\theta }}_{\mathrm{e}}}{T_{{\mathrm{e}}_{\mathrm{M}}}} \end{gathered}$$