Effects of Altering Initial Position on Movement Direction and Extent

Abstract

The purpose of this study was to examine the relative influence of initial hand location on the direction and extent of planar reaching movements. Subjects performed a horizontal-plane reaching task with the dominant arm supported above a table top by a frictionless air-jet system. A start circle and a target were reflected from a horizontal projection screen onto a horizontally positioned mirror, which blocked the subject’s view of the arm. A cursor, representing either actual or virtual finger location, was only displayed between each trial to allow subjects to position the cursor in the start circle. Prior to occasional “probe trials,” we changed the start location of the finger relative to the cursor. Subjects reported being unaware of the discrepancy between cursor and finger. Our results indicate that regardless of initial hand location, subjects did not alter the direction of movement. However, movement distance was systematically adjusted in accord with the baseline target position. Thus when the hand start position was perpendicularly displaced relative to the target direction, neither the direction nor the extent of movement varied relative to that of baseline. However, when the hand was displaced along the target direction, either anterior or posterior, movements were made in the same direction as baseline trials but were shortened or lengthened, respectively. This effect was asymmetrical such that movements from anterior displaced positions showed greater distance adjustment than those from posterior displaced positions. Inverse dynamic analysis revealed substantial changes in elbow and shoulder muscle torque strategies for both right/left and anterior/posterior pairs of displacements. In the case of right/left displacements, such changes in muscle torque compensated changes in limb configuration such that movements were made in the same direction and to the same extent as baseline trials. Our results support the hypothesis that movement direction is specified relative to an origin at the current location of the hand. Movement extent, on the other hand, appears to be affected by the workspace learned during baseline movement experience.

INTRODUCTION

The hypothesis that control of aimed movements requires a series of hierarchically organized sensorimotor transformations has evolved in part from considerations of robotic systems (Hollerbach 1990; Imamizu et al. 1998; Wolpert and Ghahramani 2000) and has gained support both from behavioral and physiological studies of biological motion and its control. An emerging view from this work is that at least three serially organized processes are associated with visually guided reaching (Ghez et al. 1991; Imamizu et al. 1998; Jordan and Rumelhart 1992; Kawato 1999; Kawato et al. 1988, 1990; Krakauer et al. 1999, 2000; Rosenbaum 1980; Rosenbaum and Chaiken 2001; Sainburg 2002): visuomotor transformations, where visual information about target position is translated into an internal reference frame, such as joint or segment angles; trajectory specification, where a time series of body positions is specified; and dynamic transformations, where the trajectory plan is transformed into dynamic properties reflecting the forces required to complete the motion. These processes can be associated with a variety of measurable variables, including direction, speed, extent, and final position of hand movements as well as joint excursions, muscle activations, and joint torques. Because of the interdependence between these factors, the CNS may represent and plan movements using almost any combination of such variables. In fact, neuron recording studies have revealed that neuronal activity in motor and premotor cortices shows correlations with hand position (Kettner et al. 1988), movement direction (Georgopoulos et al. 1983; Kalaska et al. 1983; Riehle and Requin 1989; Schwartz et al. 1988), movement extent (Kurata 1993), movement direction and extent (Fu et al. 1993, 1995; Messier and Kalaska 2000), muscle activity (Kakei et al. 1999, 2001), and force (Evarts 1968; Evarts and Tanji 1976; Fetz et al. 1976). Determining whether any combination of these factors best reflects the movement planning process can further distinguish the details and order of the sensorimotor transformations underlying movement control.

A large body of evidence has supported the idea that displacement vectors, reflecting movement direction and distance, are planned from an initial hand position (Bock and Eckmiller 1986; Georgopoulos et al. 1982, 1986; Ghilardi et al. 1995; Gordon and Ghez 1987a,b; Gordon et al. 1994b; Rosenbaum 1980). This requires that the CNS use information about initial hand position in planning targeted movements. Bock et al. (Bock and Arnold 1993; Bock and Eckmiller 1986; Bock et al. 1990) tested this hypothesis using a successive pointing task in which the final hand position of one trial represented the initial position for the next trial. Errors were shown to accumulate over successive trials, suggesting that initial position information is incorporated into the planning of subsequent movements. Further supporting the role of initial position information in movement planning, Ghez and colleagues (Favilla et al. 1989; Ghez et al. 1991; Gordon and Ghez 1987a,b; Gordon et al. 1994b; Hening et al. 1988) have shown, for both targeted force pulse tasks and planar reaching tasks, that movement direction and movement distance are planned, relative to hand start location, through separate but interacting processes (see also Rosenbaum 1980). Taken together, these findings provide evidence for neural coding of movement direction and distance relative to an initial position of the hand.

In contrast to this hypothesis, a separate line of research has supported the idea that limb configurations, corresponding to final hand position, best reflect the central representation of aimed movements (Bizzi et al. 1982; Feldman 1966; Feldman et al. 1998; Jaric et al. 1994; Latash and Gottlieb 1990; Latash and Gutman 1993; Polit and Bizzi 1978, 1979). The equilibrium point hypothesis, developed by Feldman (1966) and originally supported by an elegant series of experiments in deafferented monkeys (Polit and Bizzi 1978, 1979), proposes that the CNS controls movements by modifying the length-tension characteristics of muscles such that the equilibrium position for a set of agonist/antagonist muscles corresponds to a desired limb configuration. Jaric et al. (1992, 1994) have provided further evidence for such positional control mechanisms through a series of experiments in which different groups of subjects practiced single joint movements from several start locations to either a fixed position in space or a fixed distance from each of the start locations. Regardless of how the movements were initially practiced, both groups later performed the fixed position task best. The authors interpreted these studies to indicate planning of movements as intended final limb configurations. Consistent with these ideas, Rosenbaum et al. (1993, 1999) developed a model of control based on stored limb postures. A simulation based on this model was shown to predict salient hand kinematics during an experimental reach-and-grasp task (Meulenbroek et al. 2001).

We now examine the influence of initial position on the control of multijoint reaching movements. Subjects made repetitive reaching movements toward each of three movement directions with the dominant arm supported on a frictionless horizontal surface. Prior to each trial, subjects aligned a cursor, representing finger position, within a start circle. No cursor feedback was provided during movements. Prior to probe trials, the position of the hand was shifted to one of eight alternative locations by changing the relationship of cursor position to hand position. We thus probed the control strategies developed during baseline performance by examining the influence of changes of initial hand position (probe trials) on movement kinematics and dynamics.

METHODS

Subjects

Subjects were 15 neurologically intact right-handed adults (8 female, 7 male), 18–36 yr old. All subjects were right handed, as indicated by laterality scores of 100 on the 10-item version of the Edinburgh inventory (Oldfield 1971). Subjects were recruited from the University Community and were paid for their participation. Informed consent was solicited prior to participation, which was approved by the Office of Regulatory Compliance of the Pennsylvania State University.

Experimental setup

Figure 1 illustrates the general experimental setup. Subjects sat facing a table with the right arm supported over the horizontal surface and positioned just below shoulder height (adjusted to subjects’ comfort) by a friction-less air jet system. A start circle, target, and cursor representing finger position, were projected on a horizontal back-projection screen positioned above the arm. A mirror, positioned parallel and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the fingertip. Calibration of the display assured that this projection was veridical. All joints distal to the elbow were immobilized using an adjustable brace. In addition, movements of the trunk and scapula were restricted using a butterfly-shaped chest restraint. Position and orientation of each limb segment was sampled using the Flock of Birds (Ascension-Technology) magnetic 6-dof (3 Cartesian coordinates and 3 Euler angles) movement recording system. The maximum three-dimensional (3-D) position error that we measured during calibration of this system was 2.1 mm³. A single 6-dof sensor was attached to each arm segment by a plastic splint. The digital data (103 Hz) from each sensor was transmitted to a Macintosh computer through separate serial ports and was stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC (REAL Software), C, and Igor Pro (Wavemetric).

FIG. 1.

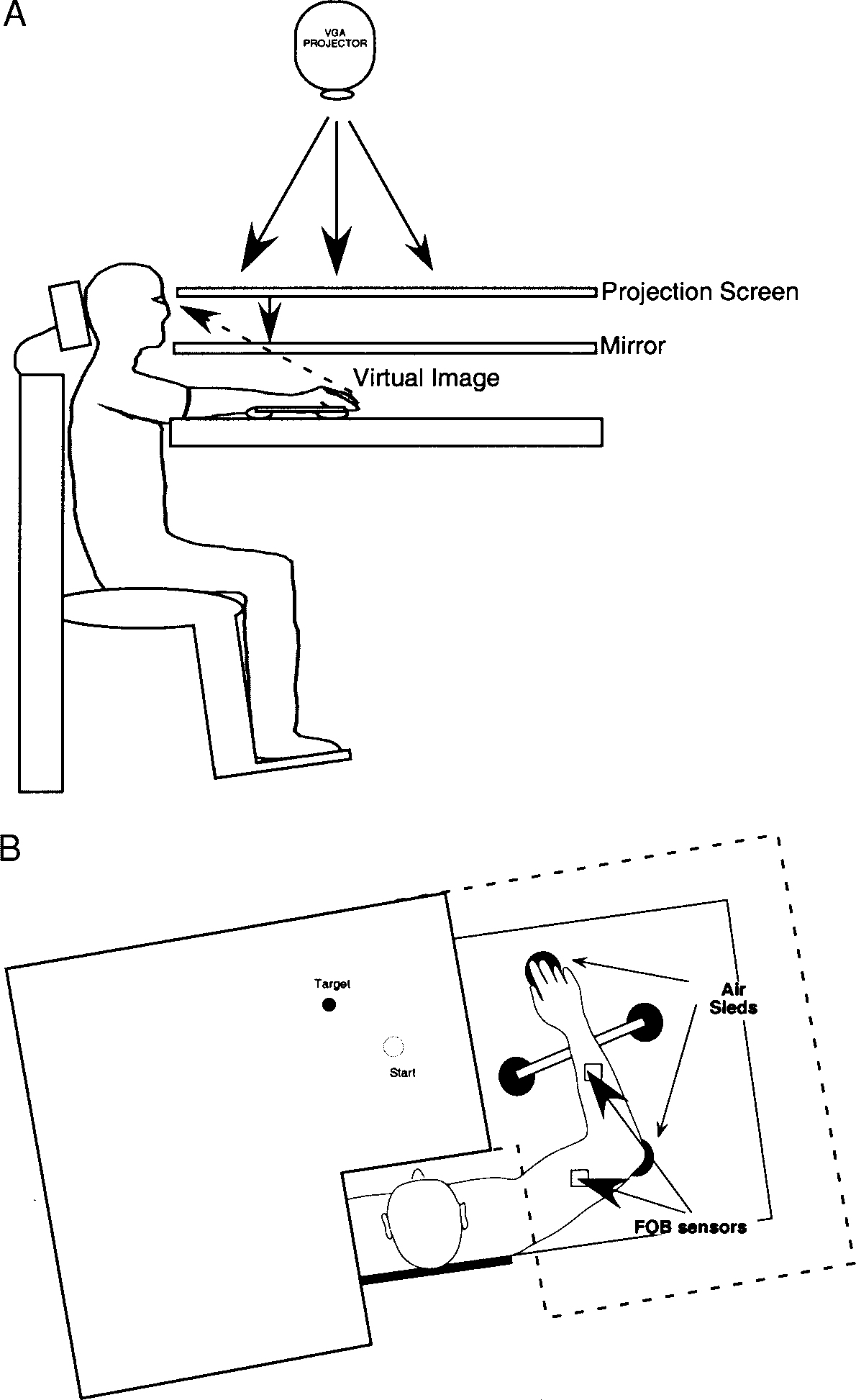
Experimental setup. The subject’s dominant arm was supported on a horizontal surface by a frictionless air-sled system. Two sensors (Flock of Birds) were attached to the upper arm and forearm. All joints distal to the elbow were splinted with a brace. Positioned above the subject was a VGA projector, which projected an image of a start circle, target, and a cursor representing finger position, onto a back projection screen and mirror, thus giving the illusion that the cursor was at finger level. The screen blocked vision of the subject’s arm and hand.

The following method was used to record limb segment positions relative to the Flock of Birds sensors. The position of the following three bony landmarks were digitized using a stylus that was rigidly attached to a sensor: index finger tip, the lateral epicondyle of the humerus, and the acromion, directly posterior to the acromio-clavicular joint. The position of the bony landmarks, relative to the sensors attached to each arm segment, thus remained constant throughout the experimental session. As sensor data were received from the Flock of Birds, the position of these landmarks was computed by our custom software. The two-dimensional (2-D) position of the index finger tip was used to project a cursor onto the screen. Screen redrawing occurred fast enough to maintain the cursor centered on the fingertip throughout the sampled arm movements. During the experiment, the light was turned off, such that subjects were unable to view their arm. View of the shoulder and upper arm was blocked by a bib running from the subjects’ neck to the edge of the mirror.

Experimental task

Three experimental blocks were provided per session, each block consisting of 250 movements to a single target, thus encouraging consistent performance toward each target. For the first 50 movements within a block, subjects made consecutive movements toward the single target. Prior to movement, a start circle and one of three target circles (15 cm radial distance) were displayed on the screen. A cursor, providing veridical feedback about the tip of the index finger, was to be positioned in the start circle (1 cm diam) for 300 ms. However, at the presentation of an audiovisual go signal, the cursor was blanked. Subjects were instructed to move the finger to the target using a single, uncorrected, rapid motion. Audiovisual feedback and points were awarded for accuracy for movements performed within a specified time window of 400–600 ms. Final position errors of less than 1 cm were awarded 10 points, whereas errors between 1 cm and 2 cm were awarded 3 points, and errors between 2 cm and 3 cm were awarded 1 point. Thus subjects were rewarded for trials with ≤20% final position error because we were more interested in encouraging consistent performance than requiring objective accuracy criteria. Points were displayed following each trial. Between trials, cursor feedback was only provided when the tip of the index finger was within a 3-cm radius of the center of the start circle. This was done to prevent adaptation to altered visual feedback during probe trials.

After 50 consecutive trials within each block, the relationship between the cursor and the index finger was altered prior to movement on occasional (every 6–8) probe trials. Maximum points were awarded for these trials, regardless of accuracy. To place the cursor in the start circle, the index finger was positioned from 3.5 to 5 cm outside the actual start circle (see Fig. 2). After the experiments, subjects reported being unaware of this manipulation.

FIG. 2.

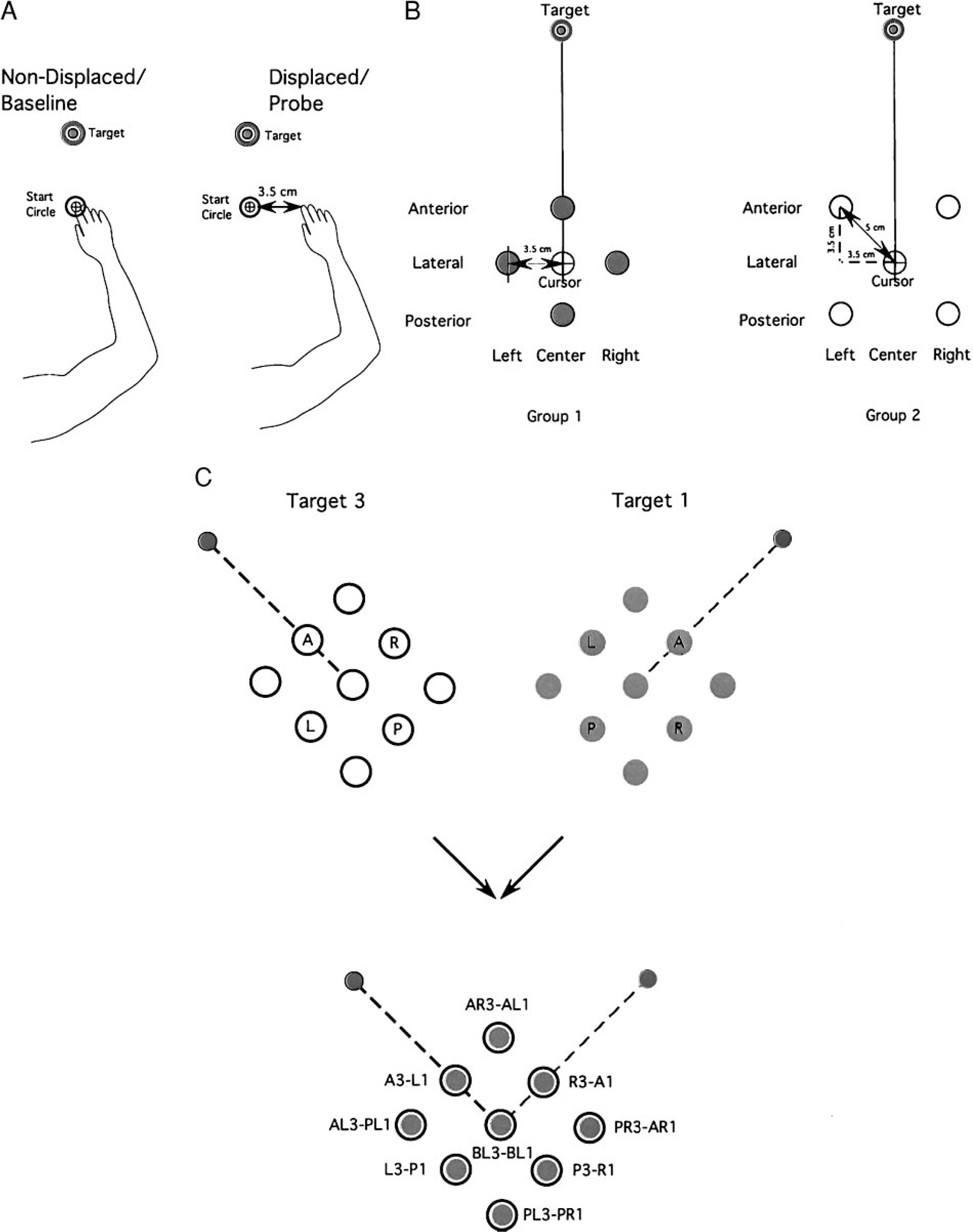
Experimental design. A, left: position of the hand for a non-displaced (baseline) trial. The location of the cursor position (shown within the start circle) corresponds to the actual position of the index finger. Right: position of the hand for a displaced (probe) trial. The location of the cursor position does not correspond to the position of the index finger. In this specific trial, the start location of the index finger is displaced 3.5 cm to the right of the cursor (within the start circle). B, left: schematic of the 4 index finger start positions used in the probe trials for a single target direction for group 1. The central location corresponds to the location of the cursor for all displaced finger start positions. Right: schematic of the 4 index finger start positions used in the probe trials for a single target direction for group 2. The central location corresponds to the location of the cursor for all displaced finger start positions. C: schematic of target locations and overlap. Top: the displaced start locations for targets 1 (gray) and 3 (black). Bottom: the overlay of target 1 start location on target 3 start locations. Targets 1 (45°) and 3 (135°) are perpendicular to each other. Notice that all displaced starting locations for target 1 have a corresponding displaced start location for target 3. For example, the anterior start position for target 1 corresponds to the right start position for target 3 (denoted A1-R3).

Start location changes

For each of the three target directions (45, 90, and 135°), four different start positions per experimental group for the finger were defined by the altered relationship between finger and cursor position. Baseline start position originated from the same place, regardless of target location. (see Fig. 2C) During the probe trials, visual appearance of the cursor was the same as that during baseline trials. Therefore proprioceptive information about hand location changed, but visual information about cursor location remained the same.

Shown in Fig. 2B (left) are the starting finger locations for subjects in group 1. The starting locations for group 1 were arranged either 3.5 cm anterior to the baseline start circle, along the axis of the target direction (anterior, A), 3.5 cm to the left or right of the baseline start circle, perpendicular to the axis of the target direction (left, L and right, R), or 3.5 cm posterior to the baseline start circle, along the axis of the target direction (posterior, P). Similarly shown in Fig. 2B (right) are the starting finger locations for subjects in group 2. Subjects in this group performed movements from start locations displaced both anterior and perpendicular to the baseline start circle (anterior left, AL and anterior right, AR) and posterior and perpendicular to the baseline start circle (posterior left, PL and posterior right, PR). Figure 2C illustrates that the nine starting positions for target 3 are the same as those employed for target 1. For each start location, with the exception of baseline, the relationship of the start position to the target is different. For example, the anterior start position for target 1 (A1) is in the same place as the right start position for target 3 (R3). Similarly, the anterior start position for target 3 (A3) is the same as the left start position for target 1 (L1). Thus any single pair of start positions to these two targets required exactly the same change in limb configuration, relative to the baseline start position. However, the relationship of each start position to each target was different. This allowed us to differentiate the mechanical or neuromuscular effects of altering the initial limb configuration from the effects associated with consistent changes in hand position relative to each target.

Experimental sessions

To reduce the number of probe trials per session, seven subjects performed sessions with probe trials for positions A, P, L, and R, and eight different subjects performed sessions with the AL, AR, PL, and PR start positions. Each subject performed three blocks, one toward each target. The order of the blocks was randomized between subjects. Within each session, 50 consecutive movements were performed before beginning probe trials. Starting with the 51st trial, the position of the cursor, relative to the hand was displaced prior to occasional probe trials, interspersed among sequential baseline trials performed without cursor displacement. The screen start position was always located in the same place relative to the target, so that to place the cursor in the start circle the subjects’ hand was displaced as described in the preceding text. These probe trials were pseudorandomly presented every six to eight trials. Subjects had no prior information about the change in hand position. On repositioning the cursor in the start circle, subjects only received cursor feedback when the hand was within 3 cm of the start circle.

Kinematic data

The 3-D position of the index finger, elbow, and shoulder were calculated from sensor position and orientation data. Then elbow and shoulder angles were calculated from this data. All kinematic data were low-pass filtered at 12 Hz (3rd order, Butterworth) and differentiated to yield angular velocity and acceleration values.

Each trial usually started with the hand at zero velocity, but small oscillations of the hand sometimes occurred within the start circle. In this case, the onset of movement was defined by the last minimum (below 8% maximum tangential velocity) prior to the maximum in the index finger’s tangential velocity profile. Movement termination was defined as the first minimum (below 8% maximum tangential hand velocity) following the peak in tangential hand velocity.

Measures of task performance

Three measures of task performance were calculated from hand trajectory data: initial direction difference from target vector, final direction difference from target vector, and radial distance. Radial distance was calculated as the 2-D distance between the start location of the fingertip and the final location of the fingertip. Final direction difference from target vector was calculated as the angular difference between the following displacement vectors: vector 1 was defined from the start location of the finger to the position of the finger at movement termination, whereas vector 2 was defined from the center of the start circle to the center of the target circle. Initial direction difference from target vector was similarly determined but with vector 1 ending at the position of the finger at the time of peak tangential finger velocity.

Hand-path averaging

For averaging of hand trajectories (see Fig. 3), the following methods were used: First, the X and Y hand-displacement profiles were time normalized, then decimated to 100 points. Each series of either x or y displacement profiles were point averaged to yield a mean and SE value for each consecutive point. As shown in Fig. 3, the mean X and Y values were plotted against one another to yield a mean 2-D hand-path profile. The SE for X displacement and Y displacement are displayed in Fig. 3 as horizontal, and vertical error bars, respectively.

FIG. 3.

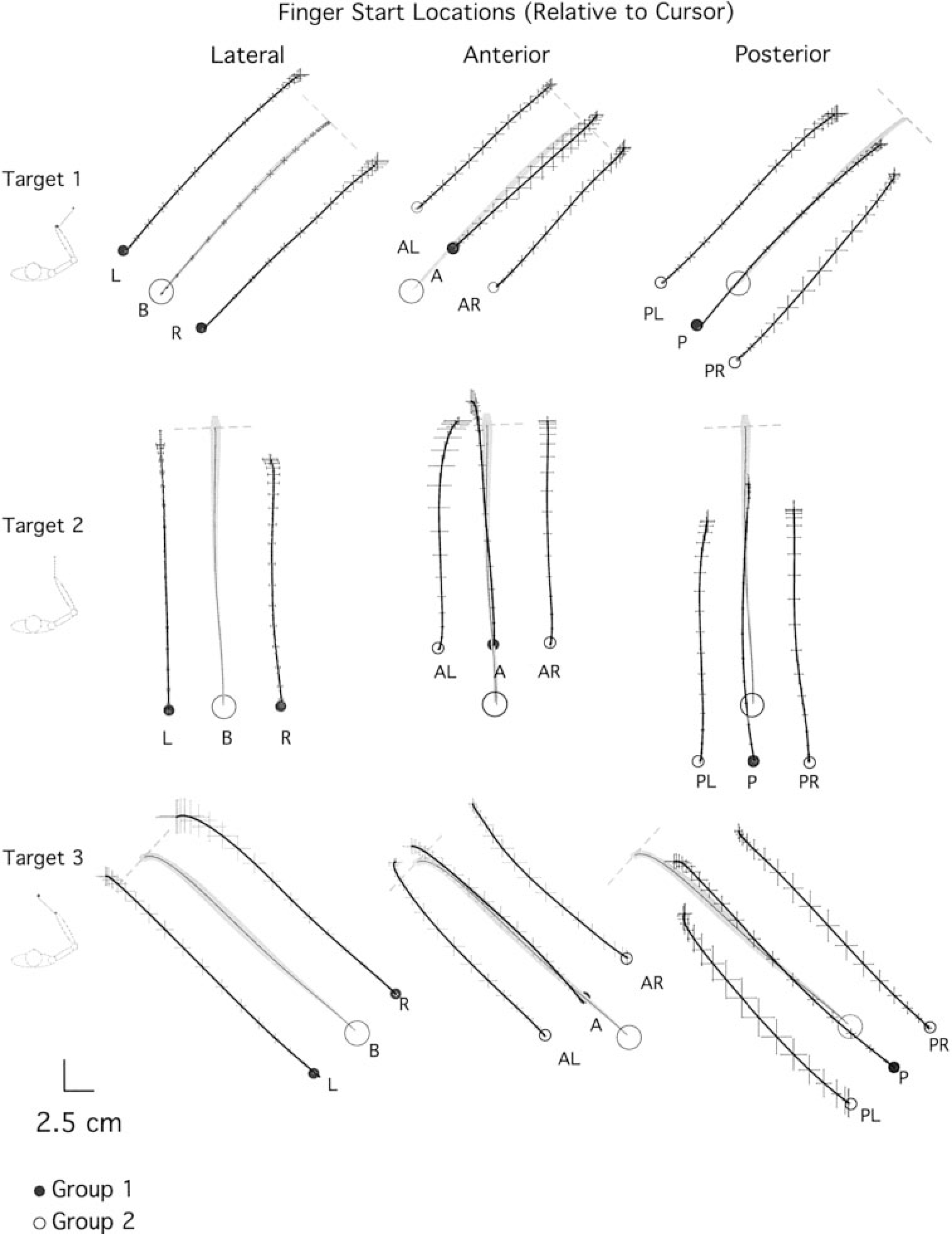
Averaged hand paths. Target direction is indicated to the far left of each row. Left: baseline (B) and laterally displaced start positions (L, R). Middle: baseline (B) and anteriorly displaced start positions (AL, A, AR). Right: baseline (B) and posteriorly displaced start positions (PL, P, PR). Movement time has been normalized. Notice the absence of endpoint conversion toward each target; movements are essentially parallel to those shown in baseline conditions. Grey shading outlines the SEs, computed along the X and Y dimensions.

Inverse dynamic analysis

The arm was modeled as a two-segment, inverted pendulum, with the proximal end (shoulder point) free to move in the horizontal plane. Thus an inverse dynamic analysis yields torque values for each joint (shoulder and elbow), as well as linear force components (X and Y) applied to the shoulder point (Sainburg et al. 1999). The resulting computed joint muscle torque primarily represents the rotational effect of muscle forces acting on the segment. However, it is important to note that this term cannot be considered a simple proxy for the neural activation of the muscles acting at that joint. Muscle joint torque does not distinguish muscle forces that counter one another during co-contraction, and it also includes the passive effects of soft tissue deformation. Additionally, the force generated by muscle to a given neural input signal is dependent on muscle length, velocity of muscle length change, and recent activation history (Abbott and Wilkie 1953; Wilkie 1956; Zajac 1989).

Torques were computed and analyzed for the shoulder and elbow joints as detailed in the APPENDIX. The inertia and mass of the forearm support were 0.0247 kg · m² and 0.58 kg, respectively. Limb segment inertia, center of mass, and mass were computed from regression equations using subjects’ body mass and measured limb segment lengths (Winter 1990). See APPENDIX for an explanation of the equations of motion used to calculate joint torques.

Muscle torque impulse

To quantify torque across multiple trials within each subject, torque impulse was calculated during the initial acceleration phase of motion, from movement initiation to the time of peak tangential hand velocity. All positive and negative integrals were summed to yield a single total muscle torque impulse for the initial phase of motion (Sainburg et al. 1999). Because this task was not designed to require specific joint configurations or displacements, a given hand displacement was associated with substantially different limb configurations, depending on the size and dimensions of subjects’ limbs. We, therefore could not expect torque values for similar hand movements to be similar across subjects. Therefore statistical analysis of torque impulse across different experimental conditions were conducted within subjects and reported separately for each subject.

Data analysis and statistics

ANOVA was conducted to test for effects of target direction and initial start location on experimental measures. Two different groups of subjects were used such that group 1 made movements from the baseline and A, P, L, and R start locations, whereas group 2 made movements from the baseline and AR, AL, PR, and PL start locations. This was done simply to increase the number of start locations examined, while keeping the number of trials performed per subject low. For each subject group, a three-target location by five-start location ANOVA was conducted on measures of initial direction error, final direction error, and movement distance. Significant interactions of target and start locations were decomposed by analyzing the simple main effects of start location for each target. Overall main effects and simple main effects of both target and location were tested using Bonferroni/Dunn corrected pairwise comparisons. For the torque analysis, however, planned comparisons (t-test) were used to test for differences between specific pairs of start locations (L vs. R and A vs. P).

The experiments in this paper were collected in partial fulfillment of J. Lateiner’s master thesis in the Department of Kinesiology, The Pennsylvania State University.

RESULTS

Movement direction does not vary with initial hand location

In this experiment, subjects first performed 50 trials to each target from the baseline start location. Following this, on occasional probe trials, the start location was altered by changing the relationship between the cursor and the finger when the subject positioned the cursor in the start circle. Figure 3 shows average hand-paths (mean ± SE, see METHODS for averaging technique) for a typical subject from each group, demonstrating the general results of the experiment for movements to target 1 (45°, top), target 2 (90°, middle), and target 3 (135°, bottom). On average, seven probe trials, per target, contributed to each average, and seven baseline trials were randomly selected for each average. The start positions (●) were performed by group 1 subjects, whereas, ○ reflect start positions for group 2 subjects. As can be seen from the paths, regardless of the start position of the hand, movements were generally straight and directed toward the target. For initial direction error, the ANOVA for each subject group showed no interaction between target direction and start location (group 1: P = 0.80; group 2: P = 0.61) and no main effect with start location (group 1: P = 0.31; group 2: P = 0.30). A significant main effect with target occurred for group 1 (group 1: P = 0.01; group 2: P = 0.12), reflecting direction-dependent direction errors, which have previously been well documented (Gordon et al. 1994a) and will not be addressed further in this study. Figure 4A shows the average (bars ± SE) initial direction error across all start locations. Regardless of the start location, all movements were directed parallel to baseline movements, reflecting less than 5° mean direction error.

FIG. 4.

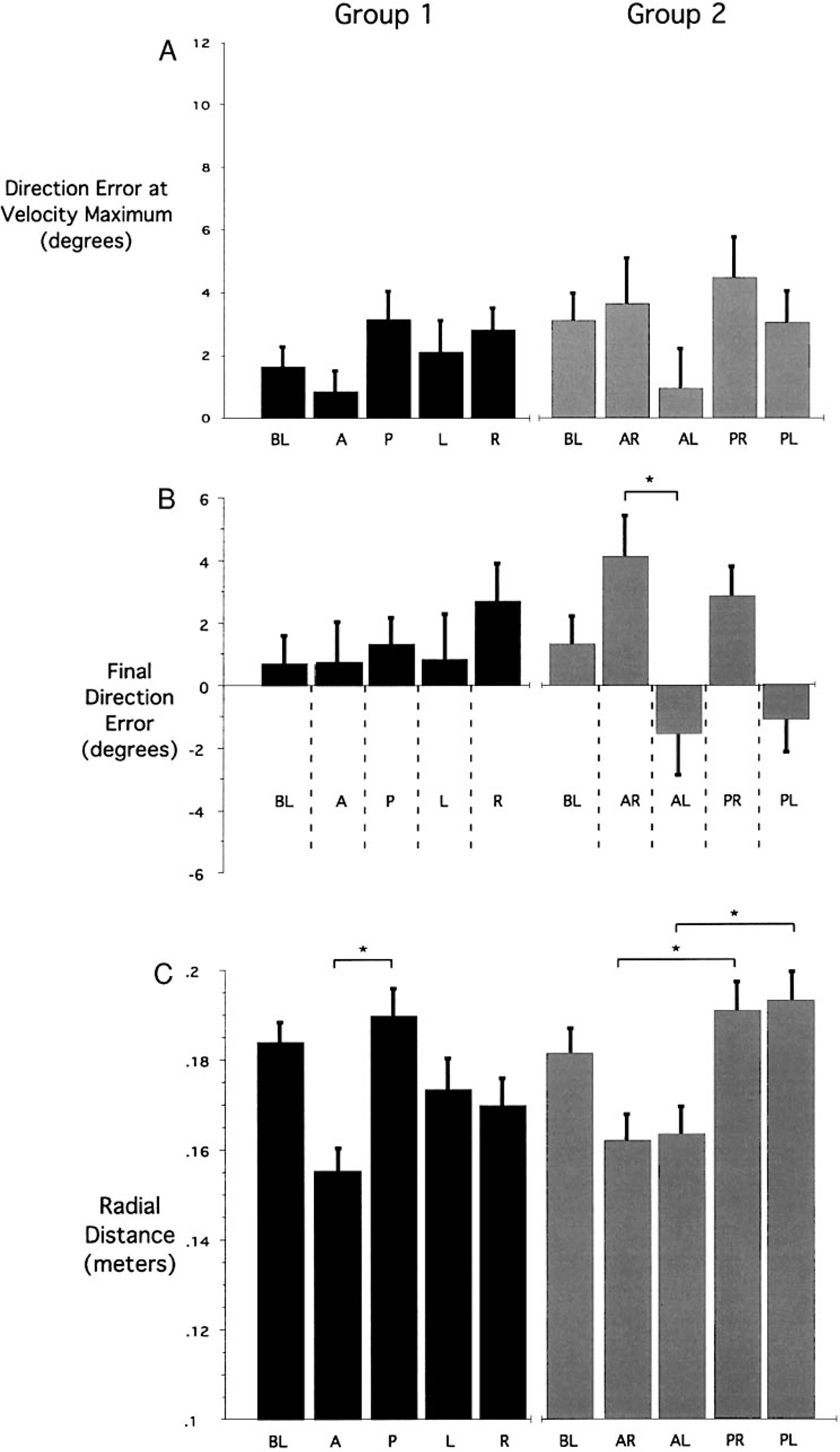
Averages in direction error for all trials and radial distance for all trials. All data has been averaged across the 3 targets (mean ± SE) A: differences in initial movement direction (from movement start to tangential velocity maximum) compared with target vector direction. B: differences in final movement direction (from movement start to movement end) compared with target vector direction. C: average radial distance traveled from movement start to end. *, significant differences between the identified measures (Bonferroni/Dunn post hoc).

As can be seen in Fig. 3, some of the movements appear to hook in toward the baseline final position at the end of movement. These hooks are very small and do not occur for all start positions. Our measure of final direction error revealed a main effect with start position only for movements performed by subject group 2 (ANOVA: P = 0.0002), but no interaction between target and start location (ANOVA: P = 0.271). Figure 4B shows the mean final direction error for all start locations. Whereas the deviations in direction error are very small, oppositely directed errors for left/right pairs of displacement only occurred between anterior-left and anterior-right displaced movements (P = 0.0003) but were not significant between posterior-left/posterior-right and right/left pairs. This weak trend to hook in toward the baseline trajectory at the end of movement may reflect a slight attraction toward the baseline paths during movement deceleration. However, the lack of significance in this trend for all left/right pairs of starting positions limits the support for this hypothesis.

Movement distance varies with initial hand location

All trials tended to overshoot the target, by close to 15%, such that the radial distance was, on average, 17.2 ± 3.12 (SE) cm. This was not surprising because points were awarded for up to 20% final position error (see METHODS). Whereas the initial movement direction did not depend on hand start location, movement distance showed a strong dependence on start location. As can be seen in Fig. 3, all movements initiated from the three anterior start positions were substantially shorter than the movements initiated from the three posterior start positions. For both subject groups, the ANOVA for movement distance showed a main effect of start location (group 1: P = 0.004; group 2: P = 0.001), no effect of target (group 1: P = 0.08; group 2: P = 0.32), and no interaction between start location and target (group 1: P = 0.99; group 2: P = 0.97). Figure 4C shows the mean (SE) movement distance for all start positions. There was a notable asymmetry in this trend, such that movement from all anterior start positions were significantly shorter than baseline movements (P < 0.01), whereas movements from all posterior start positions tended to be lengthened but were not significantly longer than baseline movements (P = 0.082). The systematic reduction in movement distance for anterior start locations varied with the orientation of the start position relative to the target, and not relative to the baseline start position. For example, movements toward target 3 from the anterior start position (Fig. 2C: A3-L1) were shortened relative to baseline. However, movements to target 1 from the same start location (perpendicular to target 1) were not shortened. This indicates that the systematic reduction in movement extent for movements from anterior displaced start locations did not result from biomechanical or neuromuscular changes associated with the starting limb configuration.

We next asked whether the reduction in amplitude of movements from the anterior positions was associated with approaching the limits of joint active or passive motion. The average elbow and shoulder angles at movement end for all targets were 118.6 ± 5.54 and 54.74 ± 4.70, respectively, near the center of each joint’s range of motion. It is, nevertheless, plausible that the “effective” range of the shoulder joint was limited by our trunk/scapulae constraint. This hypothesis is, however, contradicted by considering movements toward target 1. These movements elicited, on average, only 5.66 ± 1.74° shoulder excursion and ended at an angle of 40.53 ± 6.41°. Thus restrictions in shoulder range or scapular movement are extremely unlikely to have accounted for the observed shortening of target 1 movements. Indeed our ANOVA indicated no interaction between target and movement distance (group 1: P = 0.08, group 2: P = 0.32), further indicating that systematic changes in movement distance did not result from restrictions in scapulohumeral or elbow joint motion. The substantial reduction in amplitude of anterior displaced movements implies a workspace limitation that is not anatomical. Instead, we hypothesize that during the performance of baseline movements, subjects adapted to a working range of motion. This workspace range is apparently employed to plan subsequent movements from a variety of locations.

Peak acceleration and velocity scale with modifications in movement distance

Previous work has indicated that when subjects plan to make movements that cover a range of movement extents, peak tangential hand velocity and acceleration varies in amplitude with movement distance (Atkeson and Hollerbach 1985; Ghez et al. 1991, 1997; Gordon and Ghez 1987b; Gordon et al. 1994b). This suggests that scaling of velocity and acceleration profiles with movement amplitude reflects the movement planning process. We thus examined whether position-dependent changes in movement distance were reflected in the initial acceleration of movements made from the anterior and posterior displaced start positions. Figure 5A shows sample tangential finger velocity profiles for movements starting from anterior, posterior, and baseline positions from a single subject. As illustrated in Fig. 5A, the velocity profiles are fairly symmetrical and bell shaped. Peak amplitude of these profiles can be seen to vary with the required distance of the movements.

FIG. 5.

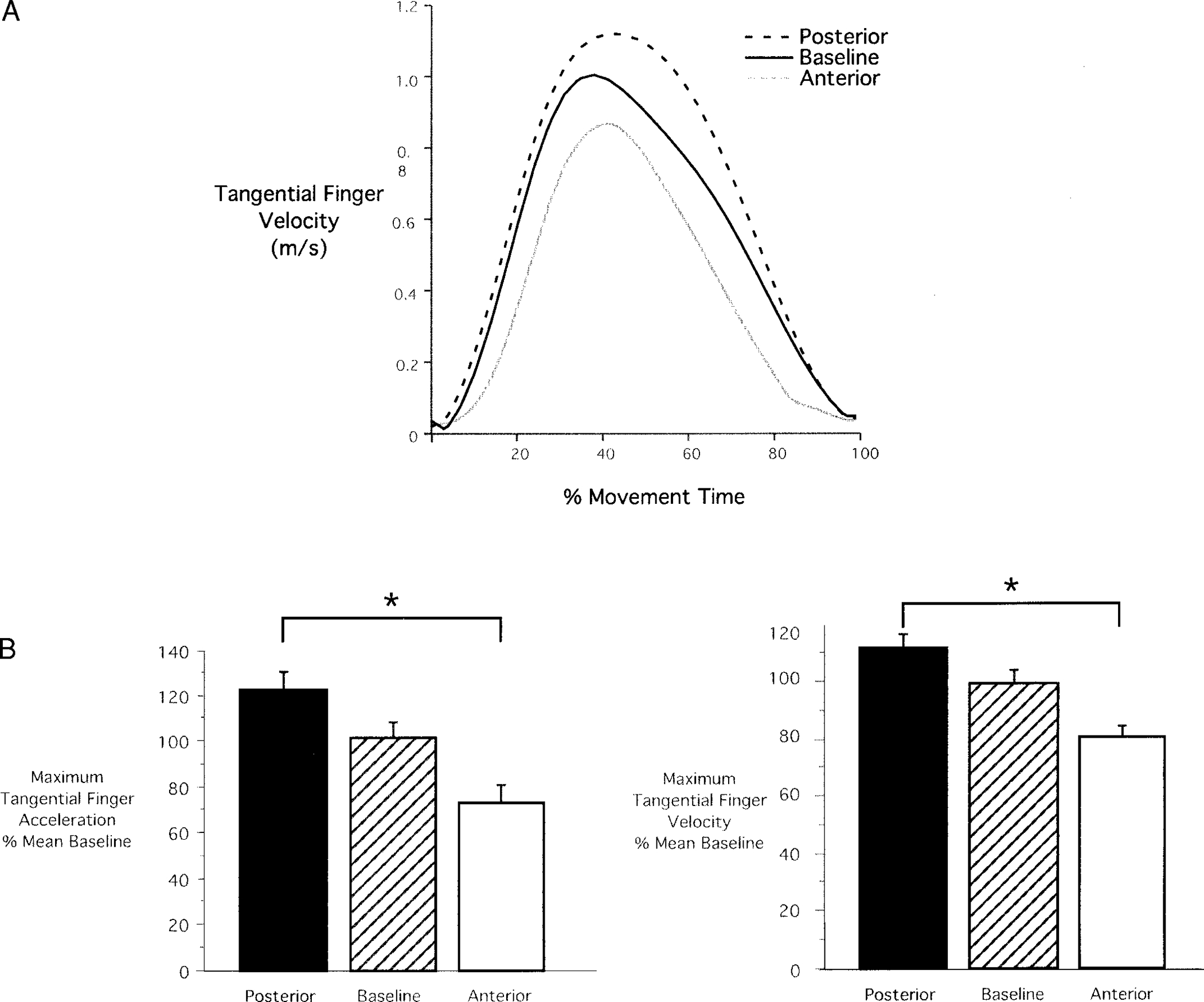
Tangential velocity and acceleration. A: sample velocity profiles for baseline (black), anterior (gray), and posterior (dashed) movements. Profiles are fairly symmetrical and bell shaped. Peak amplitude can be seen to vary with required movement distance. B, left: average (mean ± SE) tangential acceleration for anterior, baseline, and posterior start locations. Right: average tangential velocity for anterior, baseline, and posterior start locations. Values have been normalized to mean peak acceleration and velocity, respectively.

The bar plots in Fig. 5B show average peak tangential velocity (right) and peak tangential acceleration (left). Data from all trials performed from anterior, posterior, and baseline start locations are shown. These values have been normalized to mean peak velocity or acceleration of baseline movements to average values across different subjects with different baseline values. In all cases, peak velocity and acceleration can be seen to vary with the displacement of the finger, reflecting the distance requirements of the task. Movements from posterior starting positions had larger peak tangential finger velocities and peak tangential finger accelerations than those from the anterior starting positions. Thus the difference between anterior and posterior values for mean peak velocity and peak acceleration were 15 and 25%, respectively. Because tangential finger acceleration peaked within 121 ± 27 ms of movement onset, variation in peak acceleration with movement amplitude is likely to reflect preplanning of movement distance. We thus expect that modifications in movement distance with finger start location were, at least partially, planned prior to movement.

Inverse dynamic analysis reveals substantial changes in muscle torque with altered initial hand position

The fact that subjects show systematic reductions in the initial accelerations and velocities of anterior displaced trials suggests that the changes in initial position are compensated during movement planning. In addition, the lack of change in movement direction for laterally displaced trials also suggests that planning of movement direction is adjusted to the altered start positions. We further examined these hypotheses by comparing joint torque profiles of anterior/posterior and left/right pairs of displaced trials. We expected systematic adjustments in the computed torque profiles that might reflect compensations for the altered limb configurations.

Figure 6, left, shows limb trajectories, tangential hand velocity, and muscle torque profiles calculated from representative movements made by subject 3 toward target 2. Data (left) are from anterior (black) and posterior (gray) displaced positions. As expected, the anterior displaced movement was shorter, and its maximum velocity was substantially less than that of the posterior displaced movement. It is possible that this difference could result from the passive influence of the greater inertial resistance associated with the more extended limb configuration for the anterior displaced movements. However, as revealed in the muscle torque profiles, the anterior displaced movement is initiated with substantially lower muscle torque at both shoulder and elbow joints than the posterior displaced movement. Whereas, initial elbow extensor torque peaks near −2 Nm for the posterior movement, the analogous peak for the anterior movement is near −0.5 Nm. Similarly, for the posterior displaced movement, peak shoulder joint flexor torque is approximately twice that of the anterior displaced movement. It is highly unlikely that these large differences in initial muscle torque can be attributed to passive mechanical influences associated with the difference in limb configuration.

FIG. 6.

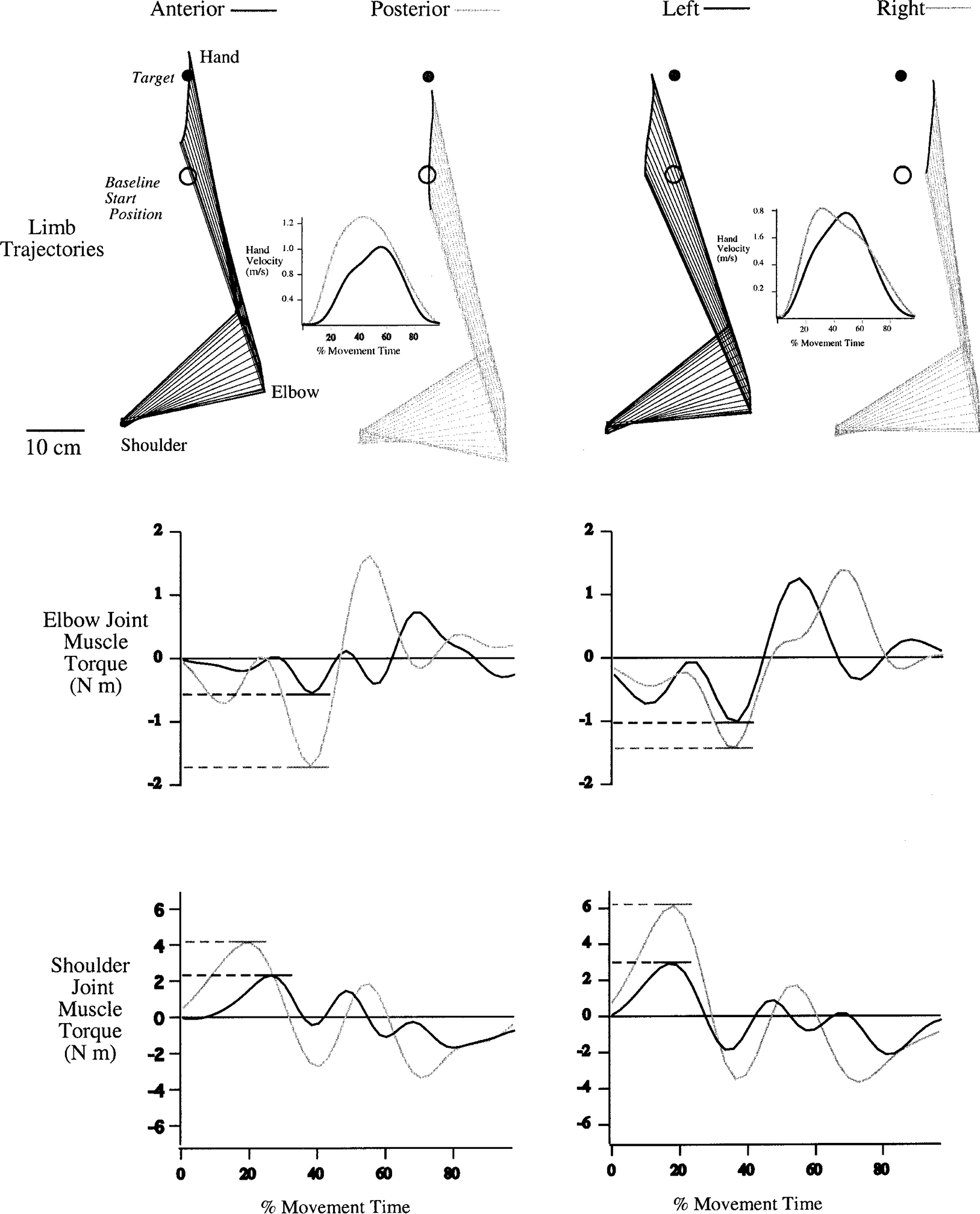
Limb trajectories and dynamic analyses. Top: limb trajectories and tangential hand velocity profiles calculated from representative movements made by subject 3 toward target 2. Left: kinematic profiles for anterior (black) and posterior (gray) displaced positions. Right: kinematic profiles for left (black) and right (gray) displaced trials. Bottom: muscle torque profiles at each joint. Left: elbow and shoulder joint muscle torques for anterior (black) and posterior (gray) movements. Right: elbow and shoulder joint muscle torques for left (black) and right (gray) movements. Torque profiles have been normalized to movement onset.

Figure 6, right, shows the similar kinematic profiles of left (black) and right (gray) displaced trials. The hand paths are parallel, similar in length, and the tangential velocity profiles are similar in amplitude. However, the elbow joint is more extended for the right than the left displaced trial. The muscle torque profiles at each joint are quite different, most notably at the shoulder. The initial peak in shoulder joint flexor muscle torque for the left displaced movement is near half that of the right displaced movement. This can be understood by considering the inertial effects of the two start positions. The left displaced movement starts at an elbow angle of 67°, whereas the right displaced movement starts with an elbow angle of 77°. The more extended configuration of the right displaced movement resulted in greater limb inertia, thus requiring larger shoulder torques to produce similar limb kinematics.

Consistent with the data shown in Fig. 6, for each group, a main effect of start position for elbow muscle torque occurred (ANOVA: P < 0.0001) but not for shoulder muscle torque (ANOVA: P = 0.091). As expected, elbow muscle torque impulse was also significantly influenced by target (ANOVA: P < 0.001), and there was a significant interaction between start position and target (ANOVA: P < 0.001). Simple main effects analysis revealed effects of start position for target 1 (P = 0.002) and target 2 (P < 0.001) but not for target 3 (P = 0.175). Planned comparisons revealed significant differences in elbow muscle torque impulse between anterior and posterior displaced pairs of trials (target 1: P = 0.001, target 2: P = 0.039) and significant differences between left and right displaced movements (target 1: P < 0.001, target 2: P < 0.001). It is not clear why significant differences between these displacements did not occur for movements to target 3 or for shoulder joint torque. However, variations in limb dimensions between subjects likely resulted in substantial variations in joint torque profiles. In fact, a separate ANOVA calculated for each subject indicated that two of the seven subjects showed main effects of start position on shoulder torque (BP: P = 0.001, SO: P = 0.001). Regardless of such variations, significant differences in elbow muscle torque impulse for both left/right and anterior/posterior pairs of displacements support our hypotheses that movement control strategies were specifically adapted to the altered start locations so as to ensure that all movements were made in the same direction. In addition, control strategies of movements made from anterior displaced start locations were adapted to produce shortened movements in accord with the recently experienced workspace range.

DISCUSSION

The purpose of this study was to examine the relative influence of initial limb position in specifying and controlling the direction and extent of planar reaching movements. By changing the finger position relative to the cursor, we systematically varied the start locations of the finger, while subjects were reportedly unaware of the discrepancy between cursor and finger. The location of the cursor remained the same for all trials, such that the target displacement vector defined by the start circle and target remained constant. Regardless of the fact that subjects reported that they were not aware of the manipulations, our results indicate that subjects specifically adjusted their control strategies to the altered initial positions such that movement direction remained parallel to that of the target. Thus when the hand start position was perpendicularly displaced, relative to the target direction, neither the direction nor the extent of movement varied relative to that of baseline. In addition, subjects systematically altered movement distance, such that the extent of movement appeared to be adjusted to the workspace experienced during baseline trials. The adjustment was most substantial for start positions that were displaced away from the body (anterior). This effect could not be attributed to anatomical workspace limits, such as nearing the edge of active or passive joint motion. Modifications in movement distance appeared to be planned prior to movement as indicated by scaling of peak hand acceleration and velocity to movement distance. Inverse dynamic analysis revealed substantial changes in elbow and shoulder muscle torque strategies for both right/left and anterior/posterior pairs of displacements. In the case of right/left displacements, such changes in muscle torque compensated changes in limb configuration such that movements were made in the same direction and to the same extent as baseline trials.

Our results indicate that somatosensory information about initial hand position is utilized in specifying movement direction and extent. However, control of movement extent seems to also be substantially influenced by the recently experienced workspace range. Adjustments in movement extent were at least partially planned prior to movement because joint torques showed substantial modifications in the initial acceleration phase of motion and because tangential hand accelerations and velocities were scaled with movement extent. These findings extend earlier reports that indicate specification of targeted movements in terms of a final posture (Jaric et al. 1992, 1994; Rosenbaum et al. 1993, 1999) as well as studies that indicate vectorial coding of movements, relative to hand start location (Bock and Eckmiller 1986; Bock et al. 1990). Our results indicate that planning of movement direction is adjusted to current hand location, such as represented by a unit vector with an origin at the hand. However, planning of movement distance is largely influenced by the recently experienced workspace range.

Specification of movement direction and extent

It has previously been suggested that planning of targeted movements occurs through the selection of an intended displacement vector with an origin at the starting location of the hand (Ghez et al. 1991). Such vectorial representations of movement have been supported by electrophysiological studies in primate cortex, which indicate that neuronal activity varies with the direction of intended hand motion (Georgopoulos 1994, 1995, 1996, 2000; Kakei et al. 1999; Kalaska 1988; Kalaska et al. 1983). However, it should be emphasized that this hypothesis remains controversial because other studies have reported correlations of motor and premotor unit activity with other variables including hand position (Kettner et al. 1988), movement extent (Kurata 1993), movement extent and direction (Fu et al. 1993, 1995; Messier and Kalaska 2000), muscle activity (Kakei et al. 1999, 2001; Todorov 2000), and force (Evarts 1968; Evarts and Tanji 1976). In addition, Scott et al. (2000) recently called into question the hypothesis that populations vectors constructed of neural activity in primary motor cortex of nonhuman primates could predict the direction of hand movement during reaching. In a study of horizontal plane reaching movements, these authors showed systematic biases between the population vectors computed from primary motor cortex cell activity and the direction of hand movement. Population vectors seemed to correspond to variables associated with limb dynamics, such as peak joint power. Thus neurophysiological evidence for vectorial coding of reaching movements remains inconclusive.

Previous psychophysical studies in humans have provided evidence for vectorial coding of reaching movements and for the idea that movement direction and extent are specified through independent neural processes. For example, in a pre-cued reaction time task, Rosenbaum (1980) showed that cues regarding movement direction and movement extent differentially affect reaction time. When subjects had prior information about movement direction, but not movement extent, reaction time was substantially shorter than when they had information about movement extent but not direction. Importantly, when they had both types of information, reaction time was reduced in an additive manner, suggesting serial processing of these parameters. Further support for independence in planning of movement extent and direction was provided by Favilla et al. (1989) using a forced reaction time paradigm during an isometric force pulse task. When subjects were required to move immediately following the presentation of target information [100 ms stimulus-response (S-R)interval], response direction was random and response amplitude was near the center of the target range. However, given more time to prepare their responses (S-R intervals up to 200 ms), subjects improved both the amplitude and direction of movement. Improvements in amplitude were made independently of improvements in direction such that wrong direction movements were often made with correct amplitudes. Gordon et al. (1994b) extended the implications of these findings to multijoint reaching movements by demonstrating that variable direction and extent errors, made during planar reaching movements, have independent distributions. For a given target direction, variable errors in direction were constant and independent of target distance, whereas variable errors in extent increased with target distance. Additionally, final position distributions were elliptical and oriented in the direction of movement, regardless of the hand’s position in the workspace. This latter finding supported the hypothesis that arm movements are planned as displacement vectors with the origin placed at the hand (Ghez et al. 1991). This idea was further supported by Bock et al. (1986) using a successive pointing task, in which errors in the final position of one movement contributed to errors in the next movement. Our current findings extend these studies, indicating that proprioceptive information about initial hand position is utilized to specify movement direction in accord with the visually displayed target. However, the extent of movement was not adjusted to the distance indicated by the visually displayed target, but instead, appeared to be primarily adjusted to the recently experienced workspace range. These findings appear consistent with the idea that planning of movement extent might represent an independent process from specification of movement direction.

Despite the human behavioral evidence for independent processing of movement direction and extent cited in the preceding text, neurophysiological evidence for independent coding of these variables remains controversial. Fu et al. (1993, 1995) examined single-unit activity in primary and premotor cortices of rhesus monkeys during horizontal plane reaching movements. Correlational analysis indicated that a substantial number of cells were modulated by different combinations of pairs of three parameters; movement distance, movement direction, and target location. Modulation of cell activity with each parameter was temporally sequenced, such that modulation by target direction occurred first, followed by modulation by target position, and movement distance. Most interestingly, cells that were modulated by two parameters showed temporal segregation of their partial correlations with those parameters, such that when the modulation by one parameter was strong, modulation by the other parameter was weak. The authors concluded that these parameters are processed fairly independently in premotor and primary motor cortex. However, Messier and Kalaska (2000) reported contrasting findings for recordings of dorsal premotor cells during an instructed delay task. These authors showed that the vast majority of recorded cells showed covariation in modulation by distance and direction, suggesting that these parameters are not processed independently in this area of cortex. It should be stressed that the human behavioral findings indicating segregation of the planning of movement direction and distance may reflect neural processes upstream to the premotor and motor cortices, such as posterior parietal cortex, or other association areas.

Specification of movement extent

Our results indicate that movement extent varied with initial start position in accord with the anterior/posterior relationship to the baseline position; this suggests a positional control mechanism that is not adapted to the target distance indicated by the visual display. This idea appears somewhat consistent with equilibrium point hypotheses, which suggest that central representation of aimed movements is best described as a series of programmed postures (Bizzi et al. 1982; Feldman 1966; Feldman et al. 1998; Jaric et al. 1994; Latash and Gottlieb 1990; Latash and Gutman 1993; Polit and Bizzi 1978, 1979). Jaric et al. (1992, 1994) provided evidence for such positional control through a learning study in which different groups of subjects practiced single joint movements from several start locations to either a fixed position in space or a fixed distance from start location. Regardless of their practice experience, subjects always performed the fixed position task best, suggesting that movements are represented as intended final positions for the limb. It should be noted that in single joint movements directed into either flexion or extension, only movement distance can specify endpoint accuracy.

Our current results indicating modulation of movement distance in accord with previously experienced workspace appear consistent with the findings of Jaric et al. (1992, 1994). However, the adjustments in movement distance made from different starting positions in the current study cannot be accounted for by assuming a constant equilibrium-point (EP) strategy. The EP hypothesis provides an explanation of control in which the spatial features of movement, corresponding to muscle equilibrium lengths, are specified by control signals (Feldman 1966, 1986; Latash and Gottlieb 1990; Latash and Gutman 1993). According to this idea, the observed similarities in movement directions could have resulted from planning the same equilibrium trajectories from all start positions. If one assumes that the movements were planned using the same equilibrium trajectories as the baseline movements, the EP hypothesis predicts movements over the same distance; however, this was not the case in our experiments.

Coordinate systems for planning movements

Specification of movement direction for reaching toward visual targets requires the integration of visual information about extrinsic spatial coordinates with somatosensory information about intrinsic body segment configuration. Our data provide evidence against direction planning in an absolute external system of coordinates or in a reference frame anchored at a point on the head, on the trunk, or on the shoulder (for review, see Soechting and Flanders 1992). This is because our subjects had undisturbed information about the location of the target in external space. Because motion of proximal body parts was restrained, this information was also undisturbed with respect to any other of the mentioned reference frames. The subjects, however, consistently made movements in the same direction from multiple displacements as though the target was represented and the movement planned in a reference frame anchored at the starting position of the hand. When the starting hand position shifted, movements were planned as a new displacement vector with its origin at the starting position of the hand.

In contrast to movement direction, movement extent was not adapted to the displaced starting positions for the hand. A plausible explanation for this finding is that movement extent is represented as the distance from an origin at or near the trunk. If this was the case, final location would be represented as percentage of a given workspace. Our findings suggest that this workspace is defined by recent movement experience, rather than anatomical, biomechanical, or neuromuscular limitations. Such a perceived range may explain why movements that originated more distant from the body were substantially shortened, whereas those that originated closer to the body were only minimally lengthened. It should be emphasized that because cursor feedback was not provided during movements, only somatosensory information about workspace range was available. Movement extent was thus not adapted to visual information about the target but appeared to be primarily influenced by somatosensory information about workspace range.

APPENDIX

The arm was modeled as a two-segment link with the shoulder joint free to move in the $xy$ horizontal plane. The length of each segment is denoted by $l$. Each segment is homogeneous, and the segment mass $m$ is assumed to be concentrated in the center of mass $CM$ (located at $r$ distance from the joints) with its respective moment of inertia $I$. The position for the center of mass of each segment in the base coordinate system is denoted by $p(x,y)$. Each joint generates a torque $T$, which tends to cause a rotational movement, and each segment is affected by forces $F$ and moments $M$.

The Newton-Euler equations for the shoulder ($\mathrm{s}$) segment are given by

$$F_{\mathrm{s}}-F_{\mathrm{e}}+m_{\mathrm{s}}{\ddot{p}}_0-m_{\mathrm{s}}{\ddot{p}}_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}=0$$

$$M_{\mathrm{s}}-M_{\mathrm{e}}+\left(p_1-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times F_{\mathrm{e}}-\left(p_0-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times F_{\mathrm{s}}-I_{\mathrm{s}}{\dot{\omega }}_{\mathrm{s}}=0$$ (A1)

And similarly to the elbow ($\mathrm{e}$) joint

$$F_{\mathrm{e}}+m_{\mathrm{e}}{\ddot{p}}_0-m_{\mathrm{e}}{\ddot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}=0$$

$$M_{\mathrm{e}}-\left(p_1-p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}\right)\times F_{\mathrm{e}}-I_{\mathrm{e}}{\dot{\omega }}_{\mathrm{e}}=0$$ (A2)

To obtain the dynamic equations, we first eliminate the joint forces and separate them from the joint torques so as to explicitly involve the joint torques in the dynamic equations. For the planar two-segment link, the joint torques $T_{\mathrm{s}}$ and $T_{\mathrm{e}}$ are equal to the coupling moments ($M_{\mathrm{s}}$ and $M_{\mathrm{e}}$), respectively. Eliminating $F_{\mathrm{e}}$ in (Eq. A2) and subsequently eliminating $F_{\mathrm{s}}$ in (Eq. A1), we obtain

$$T_{\mathrm{e}}-\left(p_1-p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{e}}{\ddot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}+\left(p_1-p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{e}}{\ddot{p}}_0-I_{\mathrm{e}}{\dot{\omega }}_{\mathrm{e}}=0$$ (A3)

$$\begin{gathered} T_{\mathrm{s}}-T_{\mathrm{e}}-\left(p_0-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right)\times m_{\mathrm{s}}{\ddot{p}}_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}-\left(p_0-p_1\right)\times m_{\mathrm{e}}{\ddot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}+\left(p_0-p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}\right) \\ \times m_{\mathrm{s}}{\ddot{p}}_0+\left(p_0-p_1\right)\times m_{\mathrm{e}}{\ddot{p}}_0-I_{\mathrm{s}}{\dot{\omega }}_{\mathrm{s}}=0 \end{gathered}$$ (A4)

Rewriting the angular and linear velocities for shoulder and elbow joints, and the position vectors, using joint displacement angles (${\theta }_{\mathrm{e}}$ and ${\theta }_{\mathrm{s}}$), which are independent variables. We have

$${\omega }_{\mathrm{s}}={\dot{\theta }}_{\mathrm{s}}$$

$${\omega }_{\mathrm{e}}={\dot{\theta }}_{\mathrm{s}}+{\dot{\theta }}_{\mathrm{e}}$$ (A5)

$$p_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}=\left[\begin{array}{c}{r}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)\\ r_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\end{array}\right]p_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}=\left[\begin{array}{c}{l}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)+r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\\ l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\end{array}\right]$$

$${\dot{p}}_{{\mathrm{s}}_{\mathrm{C}\mathrm{M}}}=\left[\begin{array}{c}-r_{\mathrm{s}}{\dot{\theta }}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\\ r_{\mathrm{s}}{\theta }_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)\end{array}\right]$$

$${\dot{p}}_{{\mathrm{e}}_{\mathrm{C}\mathrm{M}}}=\left[\begin{array}{c}-\left\{l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right\}{\dot{\theta }}_{\mathrm{s}}-r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}\\ \left\{l_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{s}}+r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right\}{\dot{\theta }}_{\mathrm{s}}+r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}\end{array}\right]$$ (6)

Substituting Eqs. A5 and A6 along with their time derivatives into Eqs. A3 and A4, we obtain the dynamic equations in terms of joint angles and shoulder position

$$T_{\mathrm{s}}=\alpha {\ddot{\theta }}_{\mathrm{s}}+\beta {\ddot{\theta }}_{\mathrm{e}}-\gamma {\dot{\theta }}_{\mathrm{e}}^2-2\gamma {\dot{\theta }}_{\mathrm{s}}{\dot{\theta }}_{\mathrm{e}}+\delta$$

$$T_{\mathrm{e}}=\epsilon {\ddot{\theta }}_{\mathrm{e}}+\beta {\ddot{\theta }}_{\mathrm{s}}+\gamma {\dot{\theta }}_{\mathrm{s}}^2+\phi$$ (A7)

Where

$$\alpha =m_{\mathrm{s}}{r}_{\mathrm{s}}^2+I_{\mathrm{s}}+m_{\mathrm{e}}\left[l_{\mathrm{s}}^2+r_{\mathrm{e}}^2+2l_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)\right]+I_{\mathrm{e}}$$

$$\beta =m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)+m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}$$

$$\gamma =m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right)$$

$$\begin{gathered} \delta =\left[m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}\left(r_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)+l_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)\right)\right]\ddot{y} \\ -\left[m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+m_{\mathrm{e}}\left(r_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\right]\ddot{x}\right. \end{gathered}$$

$$\epsilon =m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}$$

$$\phi =\left[m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right]\ddot{y}-\left[m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\right]\ddot{x}$$

$m_{\mathrm{s}}$ and $m_{\mathrm{e}}=$ masses of upper arm and forearm; $r_{\mathrm{s}}$ and $r_{\mathrm{e}}=$ distances from the proximal joint to center of mass of upper arm and forearm; $l_{\mathrm{s}}$ and $l_{\mathrm{e}}=$ lengths of upper arm and forearm; $I_{\mathrm{s}}$ and $I_{\mathrm{e}}=$ moments of inertia at center of mass of upper arm and forearm; ${\theta }_{\mathrm{s}}$ and ${\theta }_{\mathrm{e}}=$ orientation angles at proximal end of segment for upper arm and forearm.

Elbow joint torques

$$\begin{gathered} T_{{\text{e}}_{\text{M}}}=\left\{\left(I_{\text{e}}+m_{\text{e}}{r}_{\text{e}}^2\right){\ddot{\theta }}_{\text{e}}\right\}-\left\{m_{\text{e}}{r}_{\text{e}}\text{sin}\left({\theta }_{\text{s}}+{\theta }_{\text{e}}\right)\ddot{x}-m_{\text{e}}{r}_{\text{e}}\text{cos}\left({\theta }_{\text{s}}+{\theta }_{\text{e}}\right)\ddot{y}\right. \\ \left.-\left(l_{\text{s}}{m}_{\text{e}}{r}_{\text{e}}\text{cos}\left({\theta }_{\text{e}}\right)+m_{\text{e}}{r}_{\text{e}}^2+I_{\text{e}}\right){\ddot{\theta }}_{\text{s}}-l_{\text{s}}{m}_{\text{e}}{r}_{\text{e}}\text{sin}\left({\theta }_{\text{e}}\right){\dot{\theta }}_{\text{s}}^2\right\} \end{gathered}$$

Shoulder joint torques

$$\begin{gathered} T_{{\mathrm{s}}_{\mathrm{M}}=}=\left\{\left(I_{\mathrm{s}}+m_{\mathrm{s}}{r}_{\mathrm{s}}^2+m_{\mathrm{e}}{l}_{\mathrm{s}}^2+m_e{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)\right){\ddot{\theta }}_{\mathrm{s}}\right\}-\left\{\left(m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)+m_e{l}_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}\right)\right)\ddot{x}\right. \\ -\left(m_{\mathrm{s}}{r}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)+m_e{l}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}\right)\right)\ddot{y}-\left(m_{\mathrm{e}}{r}_{\mathrm{e}}\left(l_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right){\ddot{\theta }}_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{e}}^2\right.\right. \\ \left.\left.\left.+2l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}{\dot{\theta }}_{\mathrm{e}}+l_{\mathrm{s}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}^2\right)\right)\right\}+\left\{m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\ddot{y}\right. \\ -m_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{s}}+{\theta }_{\mathrm{e}}\right)\ddot{x}+\left(m_{\mathrm{e}}{l}_{\mathrm{s}}{r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{\mathrm{e}}\right)+m_{\mathrm{e}}{r}_{\mathrm{e}}^2+I_{\mathrm{e}}\right){\ddot{\theta }}_{\mathrm{s}} \\ \left.+l_{\mathrm{s}}{m}_{\mathrm{e}}{r}_{\mathrm{e}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{e}}\right){\dot{\theta }}_{\mathrm{s}}^2+\left(I_{\mathrm{e}}+m_{\mathrm{e}}{r}_{\mathrm{e}}^2\right){\ddot{\theta }}_{\mathrm{e}}\right\} \end{gathered}$$