Abstract
Previous research has shown that even when limb position drifts considerably during continuous blind performance, the topological and metrical properties of generated hand paths remain remarkably invariant. We tested two possible accounts of this intriguing effect. According to one hypothesis, position drift is due to degradation of limb-position information. This hypothesis predicted that drift of static hand positions at movement reversals should not depend on movement speed. According to the other hypothesis, position drift is due to degradation of movement information. This hypothesis predicted that drift of static hand positions at movement reversals should vary with movement speed. We tested these two hypotheses by varying the required movement speed when normal human adults performed back-and-forth manual positioning movements in the absence of visual feedback. Movement distance and direction were well preserved even though hand positions between movements drifted considerably. In accord with the movement error hypothesis, but not in accord with the position hypothesis, the rate at which hand positions drifted depended on movement speed. The data are consistent with the idea that hand position, which defines the origin of the trajectory control coordinate system, and movement trajectory are controlled by distinct neural mechanisms.
Keywords: Reaching, Proprioception, Drift, Position control, Motor control
Introduction
Vision, touch, and proprioception all contribute to our ability to locate our limbs with respect to the body and the external world (Graziano 1999; van Beers et al. 1998, 1999). One way these factors have been studied is through hand-position matching experiments, where participants indicate the location of an occluded (target) hand by matching its location with the other (reporting) hand. These experiments show that without vision, the accuracy with which finger location is reported appears to decay over time. Thus, perception of the target limb’s position appears to drift (Desmurget et al. 2000; Paillard and Brouchon 1968; Wann and Ibrahim 1993; Wolpert et al. 1998). Drift can be attenuated when passive or active movements are performed with the target limb between reports (Paillard and Brouchon 1968) or when brief isometric contractions are performed with the target limb between reports (Wann and Ibrahim 1993). These drift-attenuating effects suggest that drift arises because proprioceptive information about limb position is altered during prolonged periods without vision or without movement.
However, there are reasons to question the hypothesis that proprioceptive fading lies at the root of limb position drift. Desmurget et al. (2000), using the hand-position matching task outlined above, showed that drift did not grow over time when successive matching reports were separated by increasing intervals within a 20-s period. This result suggests that past observations of drift may not have measured the accuracy of position sense per se as much as they may have captured the growth of some bias resulting from repeated estimates made with the reporting arm.
The idea that the representation of static limb position simply weakens with time—what we call the proprioceptive fading hypothesis—is also challenged by experiments showing that when shapes are drawn continuously without vision, the positions of the shapes drift but their forms are preserved (Brown and Rosenbaum 2001; Verschueren et al. 1999; Zelaznik and Lantero 1996). The preservation of form accompanying change of position suggests that proprioception does not always provide accurate information about the arm’s current position, though it can nonetheless ensure preservation of appropriate, spatially defined movement trajectories. If proprioceptive information of any kind merely faded, one would not expect movement trajectories to maintain their spatial form when position information became less secure.
We now test two alternative hypotheses about the source of limb position drift during arm movements performed in the absence of visual feedback about limb position. We do so by evaluating the effects of movement speed on repetitive out-and-back hand movements made between two target positions on a horizontal surface. The proprioceptive fading hypothesis predicts, first, that movement trajectory performance, measured as the accuracy of movement distance and direction, should be affected by position drift. This is because previous studies have shown that initial position information is critical for movement accuracy (Bock and Arnold 1993; Bock and Eckmiller 1986; Bock et. al. 1990; Ghilardi et al 1995; Gordon and Ghez 1987a, 1987b; Rosenbaum 1980; but see Fel’dman 1986). Thus, progressive deterioration of limb position information should lead to degradation in movement trajectory performance. The proprioceptive fading hypothesis also predicts that limb drift should not depend on movement speed.
An alternative account—what we call the movement error hypothesis—suggests that position drift arises from movement error that accumulates as movements are repeated. Given the same movement trajectory requirements, this hypothesis predicts that movement error will increase as the required speed increases. Under such conditions, this hypothesis predicts that limb position should drift more rapidly, and possibly further, under fast speed conditions than under slow speed conditions.
Methods
Participants
Nine Pennsylvania State University students (six female, three male), aged 20–25 years, participated. All were right-handed according to the Edinburgh Handedness Questionnaire (Oldfield 1971), and had normal or corrected-to-normal vision. All participants gave informed consent prior to participation. The experiment was conducted in full compliance with the Institutional Review Board of Penn State University.
Apparatus
Each participant sat at a table, with his or her sternum up against the table’s horizontal surface. The participant’s fingers, hand, and wrist were immobilized with a splint, and the forearm was secured to a custom-made air sled that allowed the arm and hand to glide over the surface of the table with minimal friction. Arm and forearm movements were recorded with a magnetic motion recording system (Flock of Birds; Ascension-Technology, Burlington, VT, USA) controlled by a Macintosh computer. One 6-DOF sensor was mounted on a plastic cuff and was secured to the upper arm. A second sensor was mounted on the air sled. The two sensors transmitted position and orientation data at 103 Hz to the computer. Custom software written in REALbasic (REAL Software, Inc., Austin, TX, USA) controlled both the presentation of stimuli and collection of data.
A horizontal back-projection visual display system was suspended above the table surface as depicted in Fig. 1. A digital projector (Sanyo PLC/XP) projected a computer-generated display (120 Hz) onto a back-projection screen suspended 21 cm above a mirror that was in turn suspended 21 cm above the table surface. This arrangement provided the impression that the visual display was in the same horizontal plane as the table surface.
Fig. 1.
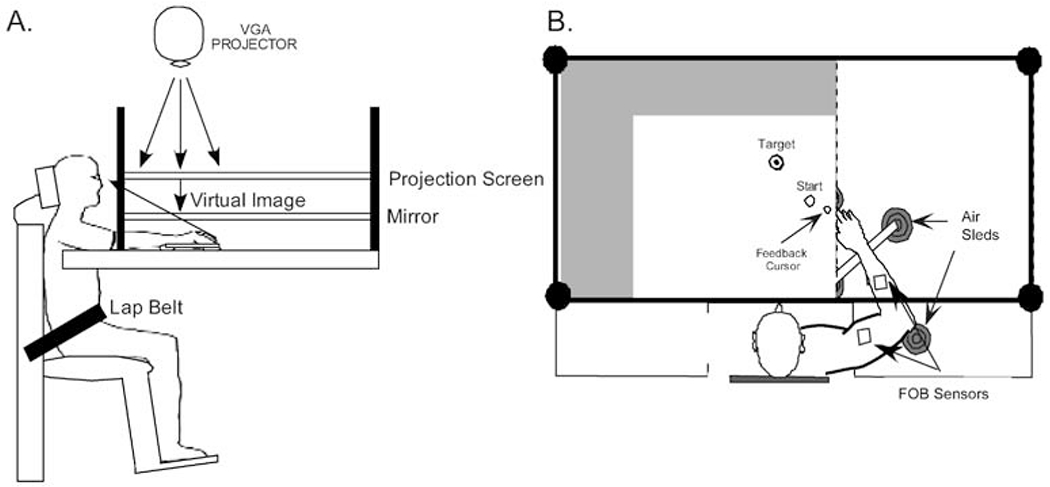
A, B The experimental setup. A A back-projection screen was suspended above a one-way mirror that was in turn suspended above a glass-covered table surface. This arrangement provided the impression that the display was in the same depth plane as the table surface. B The forearm was secured to a custom-made air-jet sled. Flock of Bird sensors (open squares) were fixed to the sled and the upper arm
The start location and targets were presented on a white rectangular display (90.7×67.0 cm), which was projected onto the framed, rectangular (87×153.5 cm) back-projection screen. The mirror through which the participant viewed the display (also 87×153.5 cm) was framed by dark green fiberglass. The room lights were extinguished. Light from the display was sufficient to keep the mirror’s frame illuminated. The frame reduced the likelihood that hand drift arose from visual drift (Adams 1912).
Experimental design and task
The experiment used a movement speed (slow, medium, fast) × movement direction (30°, 120°) × movement trial (1–75) within-participants design. A single start location, defined by initial shoulder and elbow angles of 50° and 90°, respectively, was customized for each individual. Joint angles were defined with respect to the extension of the parent (more proximal) limb. Target locations were defined such that movement direction was 30° or 120° counterclockwise with respect to the right-going 0° vector. The start and target circles were 2.3 cm and 4 cm in diameter, respectively, and were separated by 15 cm.
Each block of trials consisted of 75 back-and-forth movements between the start location and target. Movement speed to be achieved was conveyed with a metronome. Movements to the target and back were performed within 1.6, 1.3, or 1.0 s. When we decided to vary movement speed while controlling the number of movements performed in each block, we knew that this would cause block duration to vary with movement speed. We used this procedure because, as reviewed above in connection with the study of Desmurget et al. (2000), drift varies more with the number of matching movements than with the time between matching movements.
Each block was self-initiated, although participants were instructed to begin first back-and-forth movement, like all subsequent ones, in time with each metronome tone. During the first five movements, the participant viewed a 1-cm diameter cross-hair cursor that reflected the continuous location of the index fingertip. The participant initiated the block by placing the cursor within the start circle. At that time, a tone sounded for 50 ms. This tone recurred at regular intervals for the remainder of the block and did not depend on hand location. The participant was told that when she or he heard each tone, she/he should move quickly and accurately to the target and back to the start location before hearing the next tone. The participant was also told that she/he should return to the start location in enough time to treat the next tone as a signal to begin the next movement.
The participant was told that cursor feedback would be removed after the fifth movement and that she/he should continue to perform the task on-pace and as accurately as possible for the remainder of the block. To gain familiarity with the task, each participant performed two practice blocks of 25 movements at the fastest pace prior to performing the six blocks of 75 continuous movement trials that were required in the actual experiment. The six combinations of movement speed and movement direction were presented in a random order except for the constraints that each combination was tested only once per subject.
Kinematic analysis
The data were analyzed offline using custom-designed software developed with IgorPro (Wavemetrics, Inc., Lake Oswego, OR, USA) and Matlab (Mathworks, Inc.,Natick, MA, USA). Prior to data collection, the 3-D positions of the index fingertip, elbow, and shoulder with respect to the fixed arm and forearm sensors were measured with a calibration stylus. This allowed us to calculate the 3-D positions of the index finger, elbow, and shoulder from sampled sensor position and orientation data. Position data were filtered with a 3rd-order, dual-pass Butterworth filter (cutoff frequency 8 Hz) and differentiated with respect to time to obtain measures of linear velocity and acceleration at the fingertip, elbow, and shoulder. Movement initiation was defined as the last velocity minimum that fell below a 12% peak velocity cutoff threshold prior to peak velocity. Movement termination was defined as the first velocity minimum that both followed peak velocity and fell below a 12% peak velocity cutoff threshold. All velocity profiles were visually inspected to confirm selection of movement initiation and termination.
To characterize hand drift (i.e., hand start location changes over the block of movements), we calculated both cumulative and instantaneous hand drift for the first 70 movements in each block. We removed the final five movement trials from the analyses to eliminate artifacts associated with participants’ anticipating the end of the block. We defined cumulative drift as the Euclidean distance between the start location adopted during movement 1 and each successive start location (locationi – location1, i=1 through 70). We defined instantaneous as the Euclidean distance between each start location and the previously adopted start location (locationi – locationi-1, i=2 through 71). These distances are shown in Fig. 2A.
Fig. 2.
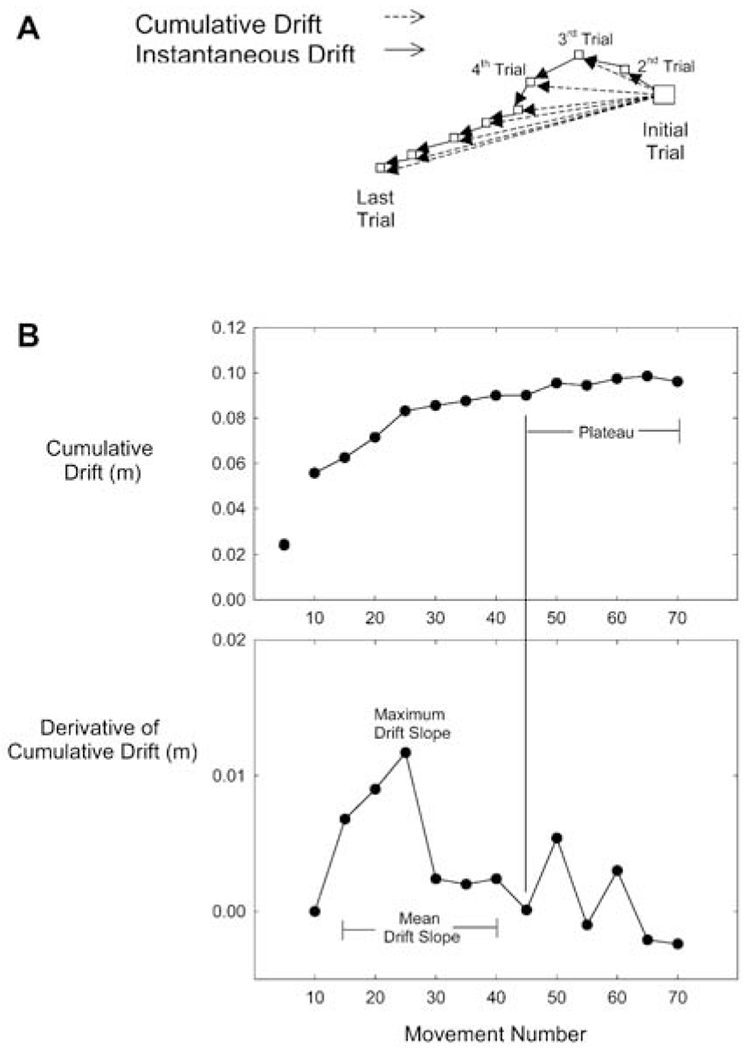
A, B Kinematic analysis. A Calculation of cumulative (dashed lines) and instantaneous drift (solid lines). Cumulative drift was defined as the Euclidean distance between the start location adopted on the initial trial and each successive start location. Instantaneous drift was defined as the Euclidean distance between each start location and the previously-adopted start location. B Calculation of mean drift slope and plateau level
Because our hypotheses made predictions about the effects of movement speed on both the rate of drift accumulation and the possible asymptotes of drift, we developed separate measures of these two features, as shown in Fig. 2B. For each participant, within each condition, the cumulative drift profile was averaged, in no-visual-feedback trials only, within bins of five movements to reduce noise. The binned profile was differentiated to produce a drift change profile. The first zero-crossing following the maximum slope was then identified. Mean drift slope (i.e., the rate of drift accumulation) was calculated as the mean of all the points on the differentiated curve between the first bin of no-visual-feedback trials and the first zero-crossing. For cases in which there was no zero-crossing, we identified the minimum change instead. We defined drift asymptote or “plateau” as the average level of cumulative drift between the first zero-crossing and the end of the profile.
We were interested in how drift was related to errors in movement distance and movement direction performance. To measure these effects, we calculated instantaneous and cumulative drift both parallel to and perpendicular to the main movement axis. We obtained these measures using the following two-step method. First, we rotated the movement vectors an amount equal and opposite to the target vector. Thus, movements performed in the 30° direction were rotated −30°, and movements performed in the 120° direction were rotated −120°, so the target vector lay parallel to the positive x-axis. On the basis of these transformations, we defined parallel instantaneous drift and parallel cumulative drift as occurring on the x-axis, and perpendicular instantaneous drift and perpendicular cumulative drift as occurring on the y-axis.
Statistical analysis
We submitted vision-absent trials to statistical analysis since these were the trials of interest in this study. We submitted measures of instantaneous drift and movement speed, time, distance, and direction to repeated-measures analysis of variance with required speed (slow, medium, fast) × required movement direction (30°, 120°) × movement number (6–70) as factors. Derived cumulative drift slope and plateau values were submitted to a required speed (slow, medium, fast) × required movement direction (30°, 120°) analysis of variance. When significant interactions were obtained, we investigated them further by decomposing them into their simple main effects. We further analyzed significant main effects using Bonferroni-corrected pairwise comparisons.
Results
Figure 3 shows a series of 70 movement paths produced by one participant performing at each speed and in each direction. The progression of the block of trials is represented by the grayness of the movement paths; the darker the gray, the earlier the observation. As seen in Fig. 3, hand position drifted substantially under all conditions, but there was no apparent change in either movement distance or direction. This impression was confirmed through statistical tests. Neither movement distance (F(64,512)=0.913, NS) nor movement direction (F(64,512)=0.922, NS) changed significantly over blocks of trials. Movement distance and movement direction were likewise uninfluenced by speed. This pattern of results is consistent with the movement error hypothesis, but not with the proprioceptive fading hypothesis.
Fig. 3.
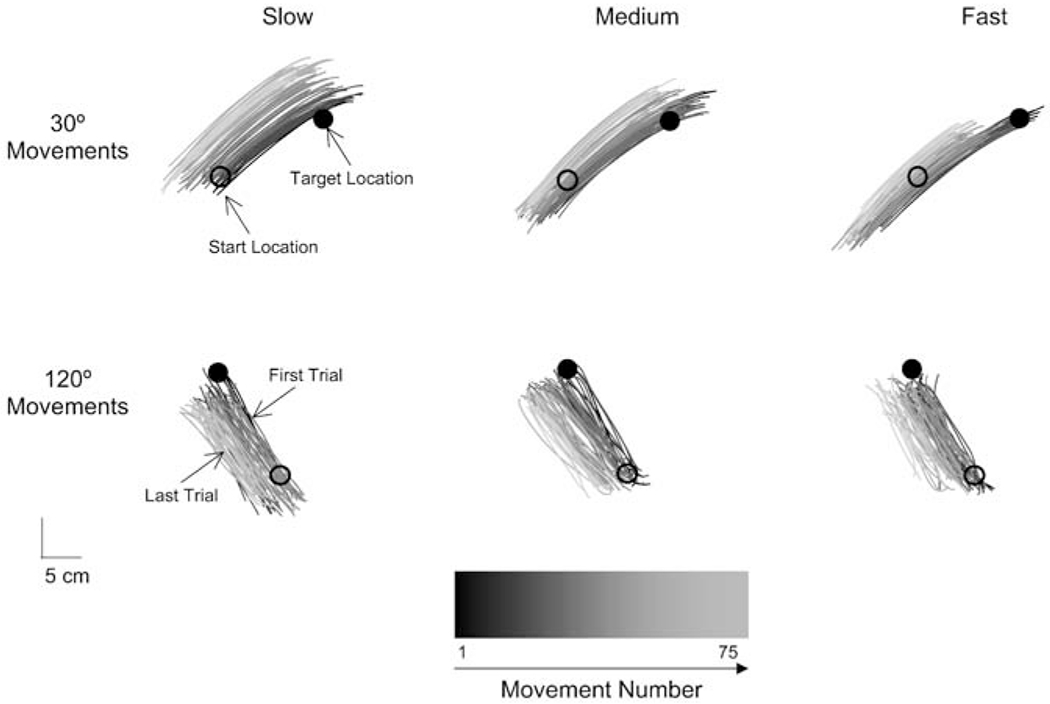
A series of 70 hand paths produced by one participant in each speed condition and movement direction. The start position and target are indicated by open and closed circles, respectively. Progression of trials over time is represented by the gray shade of the path, where early trials are darker than late trials. Trials with fingertip position feedback are drawn in black
Position-drift analysis
We next evaluated how speed influenced hand position drift. We first evaluated the effect of speed by assessing its effect on movement time, peak movement velocity, and mean movement velocity. The results for mean movement velocity appear in Fig. 4A. The corresponding statistics showed a significant main effect of speed for movement time (F(2,16)=17.61, P<0.001), peak velocity (F(2,16)=17.29, P<0.001), and mean velocity (F(2,16)=16.70, P<0.001), such that movement time decreased significantly, and peak and mean velocity increased significantly, as the required speed increased. We also found significant interactions of speed and direction for all three measures. Simple main effects showed that although there was a direction effect at the two highest speed levels, such that 30° movements were performed more quickly than 120° movements, this direction effect was not present at the lowest speed. Such direction-dependent speed variations have been described before and have been attributed to the inertial anisotropy of the human arm (Ghez et. al. 1991). Despite these effects, the foregoing analysis showed that the major variation in movement speed seen here was due to participants’ compliance with the pacing of the metronome.
Fig. 4.
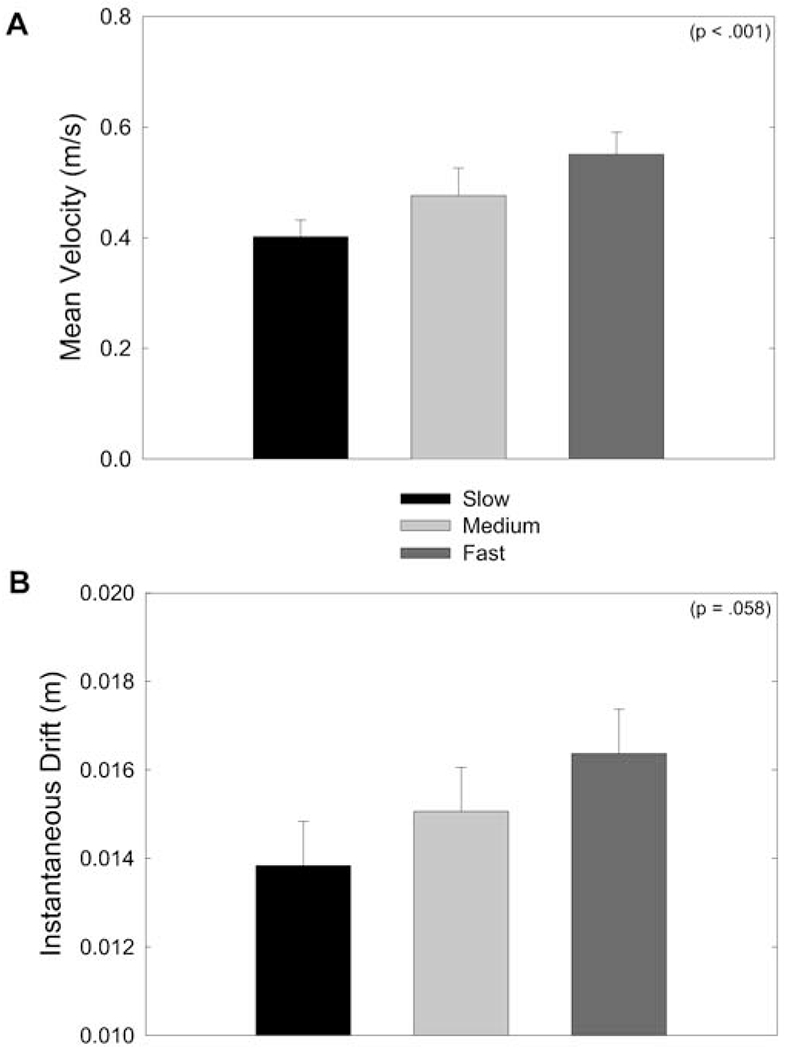
A, B Mean fingertip velocity and instantaneous hand position drift. A Mean velocity (m/s) as a function of speed condition (slow, medium, fast). B Mean instantaneous drift (m) as a function of speed condition. Instantaneous drift was greater for the high-speed condition than for the low-speed condition. Error bars represent the standard error of the mean
Instantaneous drift
Figure 4B shows mean instantaneous hand drift as a function of speed condition. Mean instantaneous drift is a measure of the change in hand start location between each successive outward movement. There was a marginal main effect for speed (F(2,16)=3.43, P=0.058), such that average instantaneous drift was greater under the high-speed condition (1.64±0.1 cm) than under the low-speed condition (1.38±0.1 cm). Hierarchical linear regression analysis with movement number, movement direction, and mean velocity as predictors showed that instantaneous drift varied significantly with mean movement velocity (P<0.001). Instantaneous drift did not change over the course of a block (F(64,512)=0.989), but did vary with movement direction (F(1,8)=37.08, P<0.001), such that it was consistently greater for movements to the 120° target (1.74±0.1 cm) than for movements to the 30° target (1.27±0.1 cm). There were no other significant main effects or interactions for these measures.
Cumulative drift
The proprioceptive fading hypothesis predicted that drift accumulation would not depend on speed, whereas the movement error hypothesis predicted that drift would accumulate less rapidly at low speeds than at high speeds. Data relevant to these competing predictions are shown in Fig. 5. Fig. 5A shows that both at high and low speeds, drift accumulation increased relatively quickly during the first portion of the block before leveling off during the latter portion. This pattern was confirmed by a main effect for movement number (F(64,512)=12.82, P<0.001). Hand position drift accumulated over the first 35 vision-absent trials (P=0.002), but did not accumulate appreciably beyond this point (P=0.106). On average, hand position drifted 5.84±0.41 cm from the initial start location.
Fig. 5.
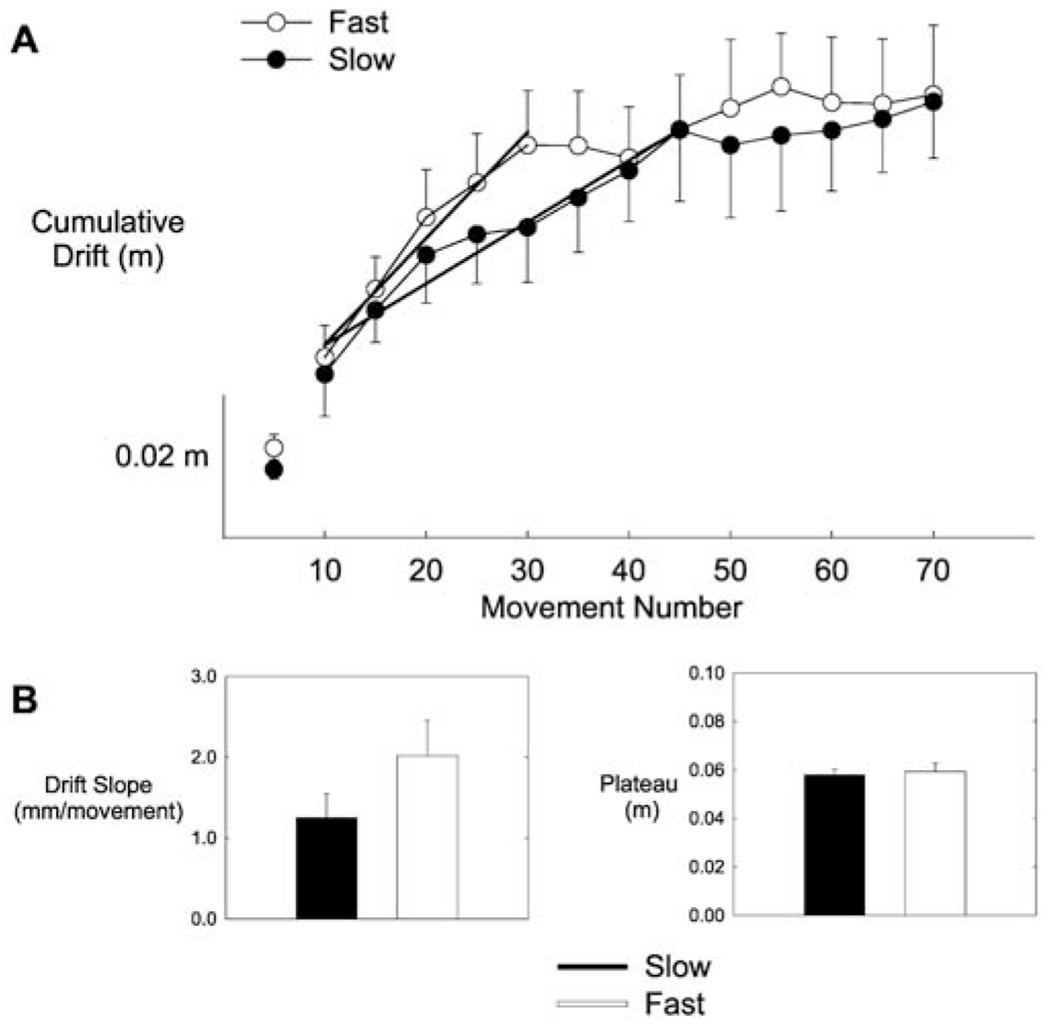
A, B Cumulative drift analysis. A Mean cumulative hand drift (m) as a function of speed (fast, slow) and movement number. This plot shows that drift accumulated more quickly in the fast condition than in the slow condition. B Left panel shows mean cumulative drift slope (mm/movement) as a function of speed condition. Slope was greater in the fast condition than in the slow condition. Right panel shows mean plateau (m) as a function of speed condition. There was no significant difference between speed conditions. Error bars represent the standard error of the mean
Of special interest for the two hypotheses, Fig. 5A also suggests that, during the first portion of the block, drift accumulated more quickly in the high-speed condition than in the low-speed condition. We checked this by calculating the mean rate of accumulation (mean drift slope) and the drift plateau level within each condition for each participant, as described in the Methods section. These measures were submitted to a repeated-measures analysis of variance with speed and direction as factors. The results are summarized in Fig. 5B, where it is seen that the mean slope was marginally greater for fast movements than for slow movements (F(2,16)=3.89, P=0.084), but did not vary with movement direction. Drift plateau, on the other hand, did not vary with movement speed (F(2,16)=0.246, NS).
Drift parallel to and perpendicular to the axis of movement
We next calculated movement-to-movement changes in hand position along the axis perpendicular to movement direction (perpendicular instantaneous drift) and movement-to-movement changes in hand position along the axis of movement (parallel instantaneous drift). Perpendicular instantaneous drift corresponds to direction error, whereas parallel instantaneous drift corresponds to distance error. As shown in Fig. 6, parallel instantaneous drift was larger and more variable than perpendicular instantaneous drift, replicating the well-known tendency for distance errors to be larger than direction errors (Gordon et al. 1994). Analyses of the effects of speed on these two measures indicated that perpendicular instantaneous drift was significantly greater for fast movements than for slow movements (F(2,16)=7.25, P=0.006; see Fig. 6, left), whereas parallel instantaneous drift was not significantly different for fast or slow movements (F(2,16)=1.41, P=0.273; see Fig. 6, right).
Fig. 6.
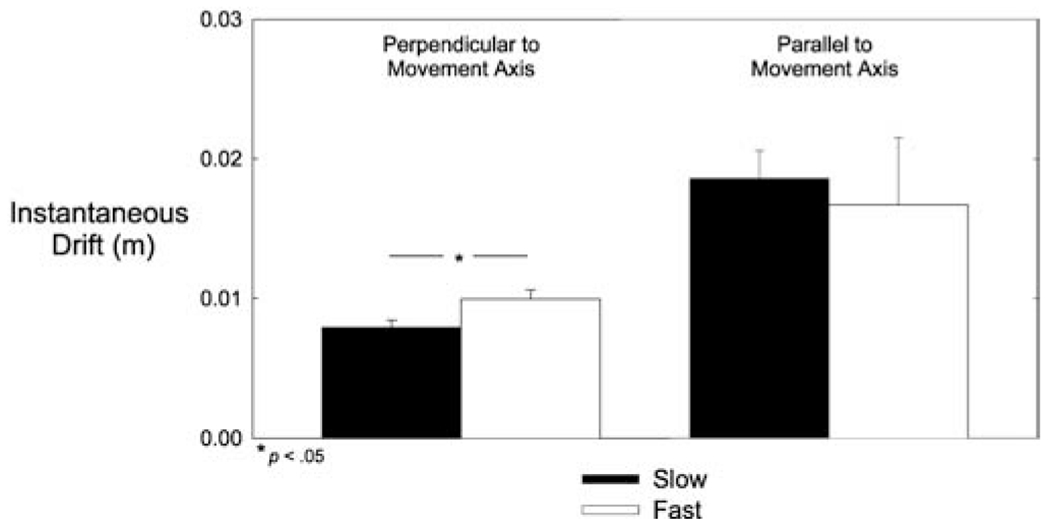
Instantaneous drift analysis. Mean instantaneous drift perpendicular and parallel to the axis of movement (m) as a function of speed condition (slow, fast). Error bars represent the standard error of the mean. Perpendicular drift was greater in the fast condition
Figure 7A shows that perpendicular drift accumulated more rapidly for fast movements than for slow movements, as just mentioned, but also that the same plateau was reached regardless of movement speed. The latter impression was confirmed by an analysis of mean drift slope and level of drift plateau, presented in the insets of Fig. 7A. Mean drift slope was significantly greater for fast movements than for slow movements (F(2,16)=3.80, P=0.045), but drift plateau did not vary with speed (F(2,16)=0.547, NS).
Fig. 7.
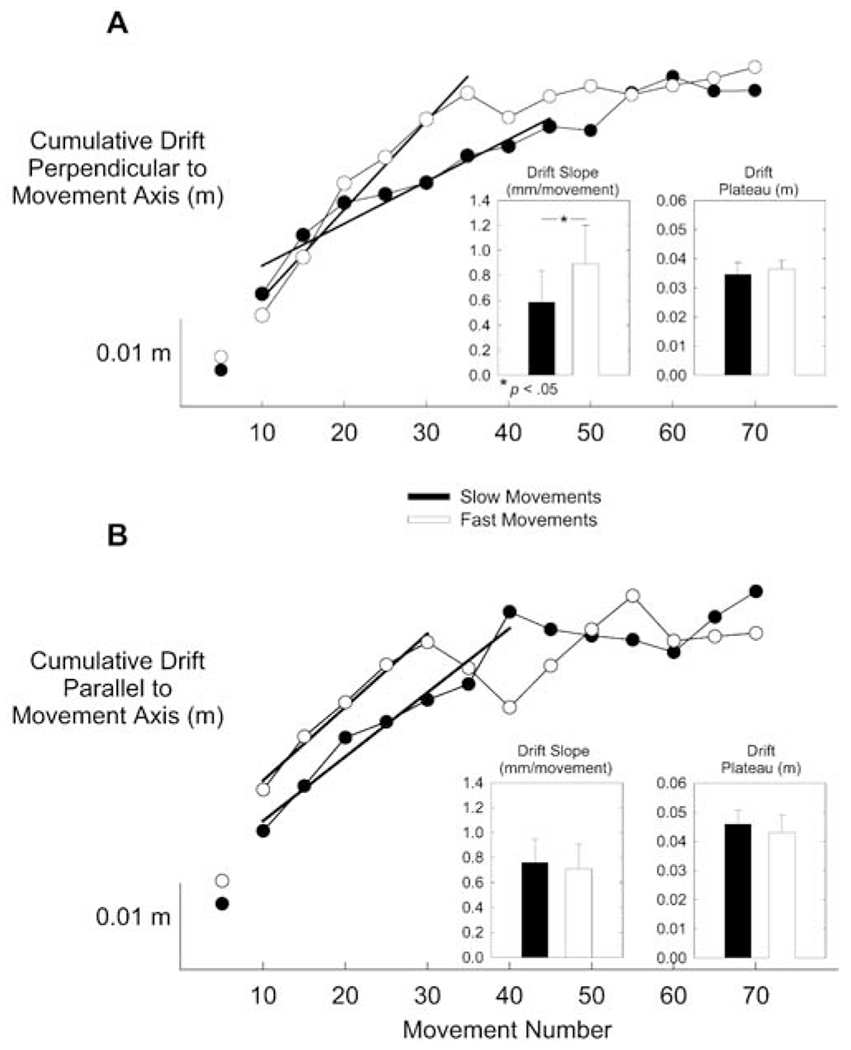
A, B Drift relative to the axes of movement. A Mean cumulative drift perpendicular to the axis of movement (m) as a function of speed condition (slow, fast) and movement number. Perpendicular drift accumulated more quickly under the fast movement condition than under the slow movement condition. Left inset: mean drift slope (mm/movement) is greater in the fast condition than in the slow condition. Right inset: drift plateau (m) does not vary with speed condition. B Mean cumulative drift parallel to the axis of movement (m) as a function of speed condition and movement number. Parallel drift accumulation did not vary with speed condition. Neither mean drift slope (left inset) nor drift plateau (right inset) varied with speed condition. Error bars represent the standard error of the mean
For the sake of completeness, we conducted analogous analyses for parallel instantaneous drift. As seen in Fig. 7B, parallel drift accumulated at the same rate for fast and slow movements and drift plateau did not vary with speed. This impression was confirmed by an analysis of parallel mean drift slope and drift plateau level, shown in the insets of Fig. 7B. Neither mean drift slope (F(2,16)=0.110, NS) nor mean drift plateau (F(2,16)=0.133, NS) varied with speed.
Discussion
The purpose of this experiment was to study limb position drift during blind back-and-forth movements carried out in different directions and at different speeds. We studied this task because previous research has left unclear what the determinants of limb position drift are.
To better characterize the causes of limb position drift, we contrasted two hypotheses—the proprioceptive fading hypothesis, and the movement error hypothesis. These hypotheses made different predictions about the dependence of movement trajectory performance on drift extent, and about the effect of movement speed on the rate of drift accumulation.
The results showed that hand position drifted an average of 6 cm from its original location, but hand movement distance and direction were preserved over repeated trials. The latter outcome replicates previous studies, which have shown that, even when limb position drifts considerably during continuous blind performance, the topological and metrical properties of generated hand paths remain remarkably invariant (Brown and Rosenbaum 2001; Brown et al. 2003; Miall et al. 1995; Verschueren et al 1999; Zelaznik and Lantero 1996). Our distance and direction data were discrepant with the proprioceptive fading hypothesis, which predicted that movement distance and direction would vary with drift magnitude. In agreement with our movement error hypothesis of limb drift, drift accumulated at a higher rate for faster movements than for slower movements. Interestingly, the asymptotic position to which the limb drifted was unaffected by movement speed. This suggests that the final extent of position drift is not dependent on the rate of drift accumulation.
Position versus movement controllers
Two of our current findings support the hypothesis that movement trajectory and limb position may be controlled independently. First, regardless of large changes in limb position, movement direction and distance remained constant. It has previously been documented that initial position information is crucial for accurate direction and distance control (Bock and Eckmiller 1986; Bock and Arnold 1993; Bock et. al. 1990; Ghilardi et al 1995; Gordon and Ghez 1987a, 1987b; Rosenbaum 1980). Indeed, with a multi-directional planar reaching study, Sainburg et al. (2003) showed that shifts in finger position of 5 cm or less required substantial changes in joint torque to preserve movement distance and direction. Thus, failure to account for these changes in finger position would be expected to produce systematic changes in movement direction and distance. This finding suggests a movement control mechanism that tracks limb position changes over time. Second, whereas the rate of position drift varied with movement speed, the final extent of drift was independent of our speed manipulation. This finding suggests a position control mechanism in which drift accumulation and final drift extent are regulated independently.
There are precedents for the claim that position and movement are controlled separately, and we see the present findings as adding support to this claim. We briefly review these precedents to put the present findings in context.
In one of the clearest demonstrations of the separation of position and movement control (Sittig et al. 1985), participants were asked to track a moving target with their finger while also being exposed to elbow flexor vibration. The participants reported that they were tracking accurately even though they lagged behind the target in a way that was consistent with the vibration illusion. Nonetheless, when they were asked to stop tracking and point to the target location, they did so accurately.
The claim that limb position and movement trajectory are controlled separately has also been supported adaptation studies. DiZio and Lackner (1995) reported that adaptation to Coriolis force perturbations selectively affected reach trajectory curvature and endpoint error. The adaptation they observed produced different aftereffect patterns in the trained and untrained arm, such that the trained arm showed curvature and endpoint aftereffects but the untrained arm showed only endpoint aftereffects. This outcome led DiZio and Lackner (1995, 2001; Lackner and DiZio 1994) to argue that learned end-positions and trajectories are represented separately. In a related study, Sainburg and Wang (2002) demonstrated that learned endpoint and trajectory information showed different patterns of interlimb transfer following adaptation to novel visuomotor rotations. Whereas post-adaptation movements made with the dominant arm revealed transfer of trajectory direction information, post-adaptation movements made with the non-dominant arm revealed transfer of information used to specify final position. These findings were consistent with earlier reports that the dominant arm controls intersegmental dynamics more efficiently than the non-dominant arm, whereas the non-dominant arm controls final position accuracy more efficiently than the dominant arm (Sainburg and Kalakanis 2000).
The notion that there are separate representations of position and movement is also supported by studies demonstrating that memory for position is better than memory for movement (Marteniuk and Roy 1972; Smyth 1984). The separation of position and movement is also supported by computational modeling. Rosenbaum et al. (2001) showed that computational simulation of motor planning works well when one assumes distinct representations for goal postures and movements. If one assumes that goal postures are represented at a different level from that of movements, many findings in the field of motor control are easily explained, and many basic competencies are also easily accounted for (e.g., the capacity for immediate compensation for changes in joint mobility). The data reported here lend support to the division between movements and goal positions assumed in the computational model of Rosenbaum and colleagues.
Direction versus distance controllers for movement
A striking result in the present study, as in previous studies of drift, is that even when there were large changes in limb configuration with drift the direction and distance of individual movement cycles remained nearly constant. This outcome is consistent with the idea that movements are planned relative to an origin at or near the hand, as previously hypothesized and supported by Ghez and colleagues (Ghez et al. 1991). Saying that movements are planned relative to a hand-centered origin suggests a vectorial basis for movement such that individual movements are coded in terms of their directions and distances.
This idea has been supported by electrophysiological studies of primate cortex, which indicate that neuronal activity varies with the direction but not the distance of intended hand motions (Georgopoulos 1995, 2000; Kakei et al. 1999; Kalaska 1988; Kalaska et al. 1983). Psychophysical studies also support the vectorial hypothesis of movement planning. For example, Rosenbaum (1980) showed that cues regarding movement direction and movement extent differentially affected reaction time, and that when subjects had both types of information reaction time was reduced in an additive manner, suggesting serial processing of these parameters.
The errors that actors make in planar reaching tasks also support the distance-direction dissociation for movement control. Gordon et al (1994) showed that variable error of movement direction and extent have independent distributions. For a given target direction, variable errors in direction were roughly constant and independent of target distance, whereas variable errors in extent increased with target distance. Additionally, final-position distributions were elliptical and oriented in the direction of movement, regardless of the hand’s position in the workspace. Additional studies of errors by Bock and his colleagues (Bock and Arnold 1993; Bock and Eckmiller 1986) have likewise supported the conclusion that movement direction and distance are controlled separately (but see van den Dobbelsteen et al. 2001).
Conclusion
Putting together all the results reviewed and obtained here, we are led to the view that there are at least three controllers for manual positioning. One is a controller for hand position per se. The other two are separate controllers for movement distance and for movement direction. This model provides a simple way of accounting for all the findings in this field of study known to us. Moreover, it finds support in the recent, striking findings of Graziano et al. (2002), who showed that sustained stimulation of the primary motor cortex and premotor cortex causes the unrestrained monkey to adopt characteristic postures depending on where the stimulation is applied. This finding helps provide the missing piece of neurophysiological evidence for the three-component model we favor. Previous neurophysiological studies have provided evidence for distinct controllers for movement distance and movement direction. The findings of Graziano and colleagues add evidence for distinct controllers for position.
Acknowledgements
This study was supported by grant #R01-HD39011 awarded to RLS by NIH-NICHHD (US National Institutes of Child Health and Human Development).
Contributor Information
Liana E. Brown, Department of Psychology, Pennsylvania State University, University Park, PA 16802, USA; Department of Kinesiology, Pennsylvania State University, University Park, PA 16802, USA
David A. Rosenbaum, Department of Psychology, Pennsylvania State University, University Park, PA 16802, USA
Robert L. Sainburg, Department of Kinesiology, Pennsylvania State University, University Park, PA 16802, USA
References
- Adams HF(1912) Autokinetic sensations. Psychol Monogr 14:1–45 [Google Scholar]
- Bock O, Arnold K (1993) Error accumulation and error correction in sequential pointing movements. Exp Brain Res 95:111–117 [DOI] [PubMed] [Google Scholar]
- Bock O, Eckmiller R (1986) Goal directed arm movements in absence of visual guidance: evidence for amplitude rather than position control. Exp Brain Res 62:451–458 [DOI] [PubMed] [Google Scholar]
- Bock O, Dose M, Ott D, Eckmiller R (1990) Control of arm movements in a 2-dimensional pointing task. Behav Brain Res 40:247–250 [DOI] [PubMed] [Google Scholar]
- Brown LE, Rosenbaum DA (2001) Coordinate systems for movement planning: evidence from positional drift. Psychon Soc Abstr 6:16 [Google Scholar]
- Brown LE, Rosenbaum DA, Sainburg RL (2003) Limb position drift: implications for control of posture and movement. J Neurophysiol (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmurget M, Vindras P, Grea H, Viviani P, Grafton ST (2000) Proprioception does not quickly drift during visual occlusion. Exp Brain Res 134:363–377 [DOI] [PubMed] [Google Scholar]
- DiZio P, Lackner JR (1995) Motor adaptation to Coriolis force perturbations of reaching movements: endpoint but not trajectory adaptation transfers to the nonexposed arm. J Neurophysiol 74:1787–1792 [DOI] [PubMed] [Google Scholar]
- DiZio P, Lackner JR (2001) Coriolis-force-induced trajectory and endpoint deviations in the reaching movements of labyrinthine-defective subjects. J Neurophysiol 85:784–789 [DOI] [PubMed] [Google Scholar]
- Fel’dman AG (1986) Once more on the EPH (λ model) for motor control. J Mot Behav 18:17–54 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP (1995) Current issues in directional motor control. Trends Neurosci 18:506–10 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP (2000) Neural aspects of cognitive motor control. Curr Opin Neurobiol 10:238–241 [DOI] [PubMed] [Google Scholar]
- Ghez C, Hening W, Gordon J (1991) Organization of voluntary movement. Curr Opin Neurobiol 1:664–671 [DOI] [PubMed] [Google Scholar]
- Ghilardi MF, Gordon J, Ghez C (1995) Learning a visuomotor transformation in a local area of work space produces directional biases in other areas. J Neurophysiol 73:2535–2539 [DOI] [PubMed] [Google Scholar]
- Gordon J, Ghez C (1987a) Trajectory control in targeted force impulses. II. Pulse height control. Exp Brain Res 67:241–52 [DOI] [PubMed] [Google Scholar]
- Gordon J, Ghez C (1987b) Trajectory control in targeted force impulses. III. Compensatory adjustments for initial errors. Exp Brain Res 67:253–69 [DOI] [PubMed] [Google Scholar]
- Gordon J, Ghilardi MF, Ghez C (1994) Accuracy of planar reaching movements. I. Independence of direction and extent variability. Exp Brain Res 99:97–111 [DOI] [PubMed] [Google Scholar]
- Graziano MSA (1999) Where is my arm? The relative role of vision and proprioception in the neuronal representation of limb position. Proc Natl Acad Sci USA 96:10418–10421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graziano MS, Taylor CSR, Moore T (2002) Complex movements evoked by microstimulation of precentral cortex. Neuron 34:841–851 [DOI] [PubMed] [Google Scholar]
- Kakei S, Hoffman DS, Strick PL (1999) Muscle and movement representations in the primary motor cortex. Science 285:2136–2139 [DOI] [PubMed] [Google Scholar]
- Kalaska JF (1988) The representation of arm movements in postcentral and parietal cortex. Can J Physiol Pharmacol 66:455–463 [DOI] [PubMed] [Google Scholar]
- Kalaska JF, Caminiti R, Georgopoulos AP (1983) Cortical mechanisms related to the direction of two-dimensional arm movements: relations in parietal area 5 and comparison with motor cortex. Exp Brain Res 51:247–260 [DOI] [PubMed] [Google Scholar]
- Lackner JR, DiZio P (1994) Rapid adaptation to Coriolis force perturbations of arm trajectory. J Neurophysiol 72:299–313 [DOI] [PubMed] [Google Scholar]
- Marteniuk RG, Roy EA (1972) The codability of kinesthetic location and distance information. Acta Psychol 36:471–479 [DOI] [PubMed] [Google Scholar]
- Miall RC, Haggard PN, Cole JD (1995) Evidence of a limited visuo-motor memory used in programming wrist movements. Exp Brain Res 107:267–280 [DOI] [PubMed] [Google Scholar]
- Oldfield RC (1971) The assessment and analysis of handedness: the Edinburgh Inventory. Neuropsychologia 9:97–113 [DOI] [PubMed] [Google Scholar]
- Paillard J, Brouchon M (1968) Active and passive movements in the calibration of position sense. In: Freedman SJ (ed) The neuropsychology of spatially oriented behavior. Dorsey Press, Homewood IL [Google Scholar]
- Rosenbaum DA (1980) Human movement initiation: specification of arm, direction, and extent. J Exp Psychol Gen 109:444–474 [DOI] [PubMed] [Google Scholar]
- Rosenbaum DA, Meulenbroek R, Vaughan J, Jansen C (2001) Posture-based motion planning. Psychol Rev 108:709–734 [DOI] [PubMed] [Google Scholar]
- Sainburg RL, Kalakanis D (2000) Differences in control of limb dynamics during dominant and nondominant arm reaching. J Neurophysiol 83:2661–2675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Wang J (2002) Interlimb transfer of visuomotor rotations: independence of direction and final position information. Exp Brain Res 145:437–447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Lateiner JE, Latash M, Bagesteiro LB (2003) Differential contributions of proprioception and vision to vectorial representations in reaching. J Neurophysiol 89:401–415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sittig AC, Denier Van Der Gon JJ, Gielen CCAM, Van Wijk AJM (1985) The attainment of target position during step-tracking movements despite a shift of initial position. Exp Brain Res 60:407–410 [DOI] [PubMed] [Google Scholar]
- Smyth MM (1984) Memory for movements. In: Smyth MM, Wing AM (eds) The psychology of human movement. Academic Press, London, pp. 83–117 [Google Scholar]
- van Beers RJ, Sittig AC, Denier von der Gon JJ (1998) The precision of proprioceptive position sense. Exp Brain Res 122:367–377 [DOI] [PubMed] [Google Scholar]
- van Beers RJ, Sittig AC, Denier von der Gon JJ (1999) Integration of proprioceptive and visual position information: an experimentally supported model. J Neurophysiol 81:1355–1364 [DOI] [PubMed] [Google Scholar]
- van den Dobbelsteen JJ, Brenner E, Smeets JBJ (2001) Endpoints of arm movements to visual targets. Exp Brain Res 138:279–287 [DOI] [PubMed] [Google Scholar]
- Verschueren SMP, Swinnen SP, Cordo PJ, Dounskaia NV (1999) Proprioceptive control of multijoint movement: unimanual circle drawing. Exp Brain Res 127:171–181 [DOI] [PubMed] [Google Scholar]
- Wann JP, Ibrahim SF (1993) Does limb proprioception drift? Exp Brain Res 91:162–166 [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Goodbody SJ, Husain M (1998) Maintaining internal representations: the role of the human superior parietal lobe. Nat Neurosci 1:529–533 [DOI] [PubMed] [Google Scholar]
- Zelaznick HN, Lantero D (1996) The role of vision in repetitive circle drawing. Acta Psychol 92:105–118 [DOI] [PubMed] [Google Scholar]


