Significance
Liquid–liquid phase separation (LLPS) at the microscale creates complex multiphase droplets relevant to medical science, pharmaceuticals, and cell biology. We show that fluid flow is key to the evolution and equilibria of such droplets. Cahn–Hilliard models that neglect fluid dynamics fail to attain minimum-energy equilibria observed in laboratory experiments. In contrast, models incorporating fluid dynamics reproduce experiments and illustrate how external forces drive internal flows that can accelerate droplet formation. These results suggest that fluid stresses play an important role in LLPS-driven generation of biomolecular condensates and point the way to methods for efficient and robust optimization of droplet-based microparticle manufacture.
Keywords: fluid dynamics, liquid–liquid phase separation, aqueous two-phase systems
Abstract
Liquid–liquid phase separation is key to understanding aqueous two-phase systems (ATPS) arising throughout cell biology, medical science, and the pharmaceutical industry. Controlling the detailed morphology of phase-separating compound droplets leads to new technologies for efficient single-cell analysis, targeted drug delivery, and effective cell scaffolds for wound healing. We present a computational model of liquid–liquid phase separation relevant to recent laboratory experiments with gelatin–polyethylene glycol mixtures. We include buoyancy and surface-tension-driven finite viscosity fluid dynamics with thermally induced phase separation. We show that the fluid dynamics greatly alters the evolution and equilibria of the phase separation problem. Notably, buoyancy plays a critical role in driving the ATPS to energy-minimizing crescent-shaped morphologies, and shear flows can generate a tenfold speedup in particle formation. Neglecting fluid dynamics produces incorrect minimum-energy droplet shapes. The model allows for optimization of current manufacturing procedures for structured microparticles and improves understanding of ATPS evolution in confined and flowing settings important in biology and biotechnology.
Liquid–liquid phase separation (LLPS) powers versatile techniques for creating complex microstructures useful throughout the medical, agricultural, and pharmaceutical industries (1, 2). LLPS also explains membraneless organelles (biocondensates) arising in cell biology (3–5) as well as several indicators and causes of cell dysfunction (6, 7). Recent work has sought to design morphologies of many-component phase-separating liquids by controlling surface energies and volume fractions of each phase (8–11). Here, we demonstrate the critical role of fluid dynamics in liquid–liquid phase separation. Specifically, we present a combined experimental, theoretical, and numerical investigation of an aqueous two-phase system (ATPS) consisting of a spherical drop of gelatin–polyethylene glycol (PEG) polymer solution suspended in a surrounding continuous phase that undergoes temperature-induced phase separation at 4 C (similar to ref. (12)). Morphology design for this system also has direct relevance to high-throughput manufacture of microparticles (13–15) used for scalable single-cell analysis (16–21), where LLPS obviates the need for complex flow-focusing microfluidics devices when constructing Janus microparticles (22–26).
In Section 1, we introduce a hierarchical suite of models of LLPS. We begin with surface-energy minimization (Section 1A), add spinodal decomposition with a ternary extension of Cahn–Hilliard/Model B (27), and finally incorporate surface tension– and buoyancy-driven incompressible viscous fluid dynamics with the Cahn–Hilliard–Stokes–Boussinesq model, an extension of Model H (27) (Section 1B). In Section 2, we illustrate the predictions of the surface-energy minimizing model (Section 2A), demonstrate the failure of Cahn–Hilliard to reproduce experiments (Section 2B) and then explore the effects of fluid dynamics on liquid–liquid phase separation in Section 2C. In particular, we show that
Cahn–Hilliard/Model B dynamics starting from mixed initial conditions evolves to a core–shell morphology, rather than energy minimizing crescents.
Cahn–Hilliard–Stokes–Boussinesq/Model H dynamics incorporating fluid forces evolves to the experimentally observed minimal-energy crescent shapes (Fig. 1).
Shear-induced recirculation, e.g., arising from pressure-driven channel flows, can drive a tenfold acceleration in crescent formation, speeding microparticle manufacture.
Fig. 1.
(A): The first row shows microscopic images of thermally induced phase separation in a gelatin–PEG mixture at 4 C with increasing time. Each droplet measures 50 microns in diameter. Experimental details are provided in Appendix A. The second row plots a volume rendering of a three-dimensional simulation of liquid–liquid phase separation using the Cahn–Hilliard–Stokes–Boussinesq model developed in Section 1B (corresponding to model CHSB in Fig. 8). Simulation parameters are detailed in Tables 1–3. The simulation time is nondimensional and must be rescaled to correspond to the physical time of the experimental snapshots, as we use an artificially large interfacial thickness parameter (detailed in SI Appendix). The patterns of phase separation evolving over time are in qualitative agreement. (B): Schematic of minimal-energy crescent-shaped particle at equilibrium for given surface tensions (red, green, blue) and contact angles (purple, orange, gray) of gelatin-rich (), PEG-rich (), and surrounding oil () phases.
We finally conclude with future directions for modeling fluid dynamics in liquid–liquid phase separation in Section 3. We expect our model to help optimize the speed of microparticle manufacture (13, 15) as well as the design of new classes of structured microparticles for drug delivery and tissue engineering. More broadly, our work bolsters the emerging importance of fluid dynamics (28, 29) in industrial (30–34), biological (5, 35), and mathematical (8–10) LLPS problems.
1. Theory
A. Surface Energy Minimization.
The simplest model of ternary fluids predicts each phase will arrange itself to minimize the total interfacial energy. This isoperimetric problem leads to interfaces that are either flat, or a portion of a sphere (36). At triple contact points, the angle spanned by each phase satisfies a force balance given by the Young condition
| [1] |
where is the surface tension across the interface. Triple contact points are unstable if any surface tension dominates the sum of the remaining two or equivalently if any wetting parameter is negative (with indices modulo ). SI Appendix solves this minimization problem to give explicit formulae for minimal energy shapes in ATPS droplets as a function of volume ratio and surface tensions.
B. Nonequilibrium Models: Cahn–Hilliard–Stokes–Boussinesq.
The surface energy minimization model only predicts equilibrium shapes. But droplet formation is inherently nonequilibrium, involving both thermally induced phase separation and fluid flow. To model dynamic phase separation from an initially mixed model, we begin with a ternary Cahn–Hilliard model from ref. (37), which generalizes several earlier advective Cahn–Hilliard models (38–42). After transforming to dimensionless quantities (SI Appendix), we neglect inertia and apply the Boussinesq approximation (ignoring density variation aside from the buoyancy term) at constant viscosity to derive the Cahn–Hilliard–Stokes–Boussinesq (CHSB) equations
| [2] |
| [3] |
| [4] |
for the concentrations (constrained by ), the fluid velocity and pressure . The chemical potentials , perturbation density , and mobility tensor are given by
| [5] |
| [6] |
The key dimensionless parameters are the interface thickness , the capillary number , Bond number , and Weber number , which compare viscosity, buoyancy, and inertia with surface tension forces, respectively:
| [7] |
where is the dimensional interface thickness between phases, a characteristic droplet length scale, the average density, the density variation scale, the average viscosity, the sum of dimensional surface tensions, the acceleration due to gravity, the gravitational unit vector, and the characteristic separation time scale. Droplet formation dynamics depends on the relative sizes of these dimensionless numbers. We note that the equilibrium of the Cahn–Hilliard model reduces to the surface-energy minimization model in the limit of vanishing interface thickness (43). Our goal is to investigate the role of buoyancy forces in the CHSB equations and to contrast this behavior with the ternary Cahn–Hilliard (CH) model, which simply sets the fluid velocity to zero .
2. Results and Discussion
A. Minimal Energy Configurations.
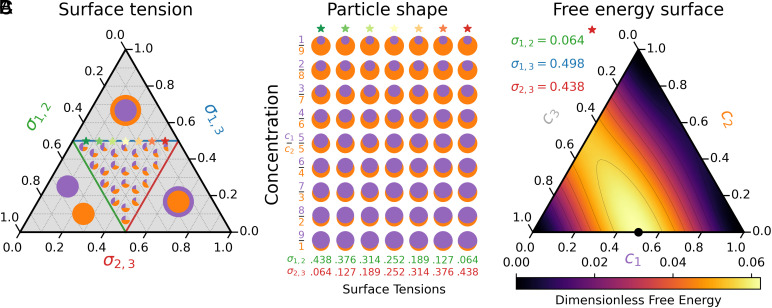
Four possible minimal energy regimes arise depending on the relative surface tensions. Scaling dimensionless surface tensions such that allows convenient representation on a ternary diagram. We summarize these regimes in Fig. 2 A and B. There are three separate wetting regimes, in which , or dominates the sum of the other two tensions. These correspond to separated drops, 1-in-2 shells, or 2-in-1 shells (the Left, Top, and Right regions of Fig. 2A, respectively). Between these regions, we can achieve stable triple points and non-trivial droplet shapes (Fig. 2B). These crescent shapes vary with two independent surface tension parameters as well as the relative concentration of to . Configurations close to the edges of the inner region give a single small angle (e.g., large gives small ). Explicit formulae for these shapes are provided in SI Appendix. We note that in the case of 1-in-2 or 2-in-1 shells, the energy minimizer is not unique. That is, the total energy does not depend on the location of the inner droplet (provided it does not intersect the outer shell). However, a near-crescent configuration is neither topologically or energetically equivalent to the actual crescents observed in experiments.
Fig. 2.
(A) Possible contact angles as a function of relative surface tensions . Wetting occurs if any surface tension dominates the other two (the Top, Left, and Right subtriangles of ternary diagram). (B) Example minimal energy configurations for varying surface tensions (horizontal axis) and relative concentrations (vertical axis). Surface tensions are chosen so that . The surface tensions of each column are indicated in the ternary plot with stars shifting from green () to red (). (C) The free energy used in simulations of experiments. The maximum is located at the black circle. The energy is more sensitive to than or .
We now focus on the experimental parameter regimes in Tables 1 and 2. Our laboratory experiments exhibit crescents with a contact angle of approximately (13). This constrains the possible surface tensions to lie close to the edge . We illustrate seven different possible contact angles in Fig. 2B, that vary from small (where ) to small (where ). Physically, we expect a lower surface tension between the aqueous polymer mixtures than between each mixture with the surrounding third phase. As such, we focus on the case with largest (corresponding to ) for which we plot the free energy surface in (Fig. 2C). The range of surface tensions leading to small contact angles is exceedingly narrow. Surface tensions must therefore be precisely tuned to achieve crescent particles that surround a significant volume. Finally, while this model is useful for understanding possible equilibrium shapes, and inferring necessary surface tensions for a desired shape, it does not capture the dynamics of LLPS.
Table 1.
Dimensional parameters for simulations
| Name | Symbol | Value |
|---|---|---|
| Time scale | ||
| Length scale | ||
| Surface tension scale | ||
| Mass density scale | ||
| Mass density variation scale | ||
| Kinematic viscosity | ||
| Gravity |
Table 2.
Nondimensional parameters for simulations
| Name | Symbol | Value |
|---|---|---|
| Interface thickness | ||
| Bond number | Bo | |
| Capillary number | Ca | |
| Weber number | We | |
| Surface tensions | ||
| Density perturbations | ||
| Initial concentrations |
B. The Failure of Ternary Cahn–Hilliard Dynamics.
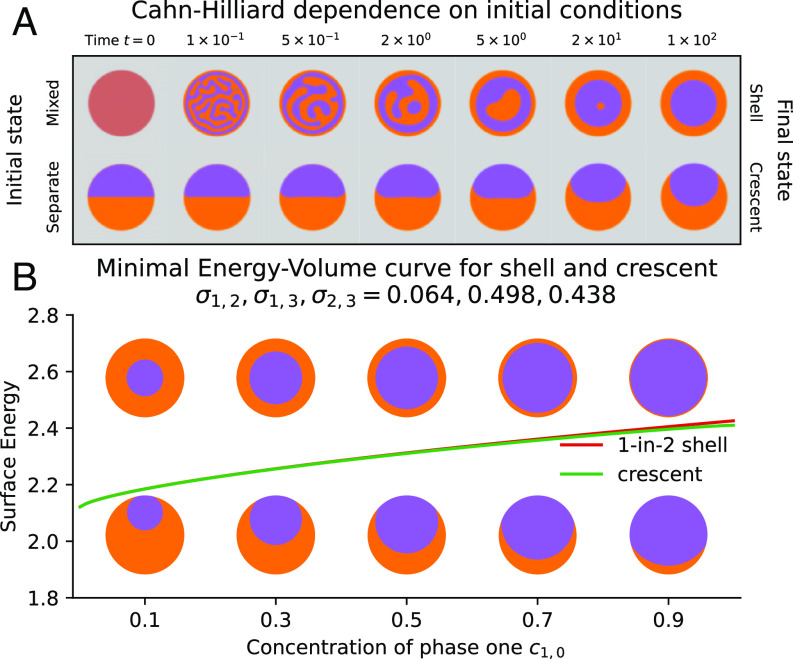
A sensible start for a model of dynamic LLPS is a three-phase extension of the canonical Cahn–Hilliard equation (27, 44). The Cahn–Hilliard model tends to a Mullins–Sekerka problem as the interface thickness tends to zero (43). Equilibria of the former should thus recover the same energy-minimizing equilibria of the latter—equivalent to the energy minimizing model of Section 1A. However, we show that this model does not always attain the global minimal surface energy configuration from Section 2A and that the final state instead depends on the choice of initial conditions. In Fig. 3A, we simulate the CH model for experimental parameters in Tables 1 and 2 and numerical parameters in Table 3 and compare the evolution of a compound droplet with equal concentrations starting from mixed (Top row) and separated (Bottom row) initial conditions. While the initially separated particle evolves to the minimal energy crescent, the initially mixed droplet (corresponding to the experiment in Fig. 1) evolves to a stable core–shell droplet shape after undergoing spinodal decomposition. Fig. 3B hints at why the CH model fails to attain the minimal-energy crescent shape when evolving from mixed initial conditions: The small value of means that the 1-in-2 shell is very close in energy to the crescent configuration. Similar patterns have been observed in earlier three-phase simulations of membrane manufacture in Cartesian geometries (31). These solutions do not evolve to an asymmetric crescent shape from well-mixed initial conditions, in contrast to our experiment. We must incorporate additional relevant physics. An obvious choice is fluid dynamics, either through buoyancy forces, viscous shear instabilities, or other destabilizing phenomena.
Fig. 3.
(A) Evolution of ternary Cahn–Hilliard model from different initial conditions (mixed vs separate). For equal concentration ratio , mixed initial conditions lead to shells, while initially separated drops form minimal-energy crescents. (B) Energy–volume curve for the shell (red) and crescent (green) configurations of figure (A) with surface tensions of Fig. 2C.
Table 3.
Numerical parameters for simulations
| Quantity | Value |
|---|---|
| Spatial modes | |
| Dealias factor | |
| Time step | |
| Time step scheme | SBDF2 |
C. Evolution Simulations.
Using the parameters inferred from experimental contact angles, we compare four different models:
(CH): the ternary Cahn–Hilliard model,
(CHS): the Cahn–Hilliard–Stokes model incorporating fluid dynamics but without buoyancy,
(CHSB ): the Cahn–Hilliard–Stokes–Boussinesq model including phase separation, fluid flow, and buoyancy forcing normal to a no-slip channel, and
(CHSB ): the Cahn–Hilliard–Stokes–Boussinesq model with buoyancy forcing parallel to a no-slip channel,
and six different initial concentrations (Fig. 4).
Fig. 4.
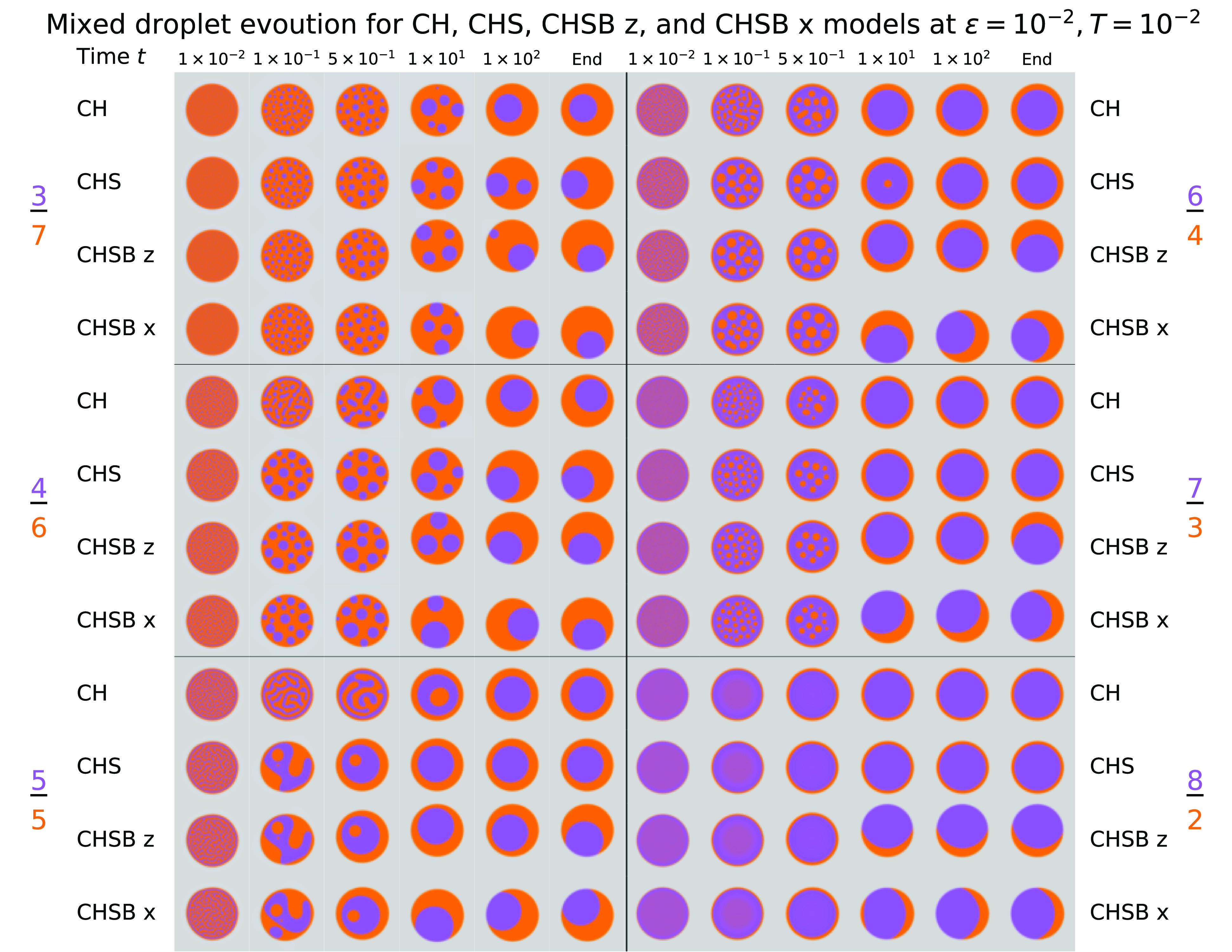
Comparison of CH, CHS, and CHSB () models in two dimensions for concentration ratios , for six time snapshots, under parameters given in Tables 1–3. Several regimes are apparent for different choices of initial concentration in each model. The final shape and time to equilibrium are strongly dependent on the presence and type of perturbations due to asymmetric fluid forces.
We estimate physical scales in Table 1, from which we derive the nondimensional parameters in Table 2. Precise dimensional parameters are difficult to measure. In particular, the interfacial length scale and the mobility (indirectly determined through the time scale ) are not directly measurable. They are instead constrained by computational resources. Here, we choose and to balance accuracy (smaller and larger ) with efficiency (larger and smaller ). SI Appendix has additional simulations at varying to validate our choice of model and parameters.
The numerical parameters for the simulations are provided in Table 3, with more details provided in SI Appendix. We examine higher-resolution simulations in both two-dimensional and three-dimensional simulations to fully capture the role of fluid dynamics.
C. 1. Concentration dependent coarsening.
The initial coarsening in Fig. 4 (also Movie S1) for reveals a strong dependence on initial concentration ratios, moderate influence of fluid dynamics, and weak influence of fluid perturbations due to buoyancy. At least five regimes can be discerned. 1) The first, at low initial concentrations (), leads to complete dissipation of throughout the domain (omitted from Fig. 4). No area forms a critical mass sufficient to nucleate a droplet, and the droplet concentration becomes homogeneous. 2) For intermediate -dominated concentrations , the initial separation dynamics generate coarsening droplets embedded in a connected phase. Some droplets form sufficiently close to the boundary to create a triple point. 3) For balanced initial conditions , the initial coarsening generates a mixture of two continuous phases, rather than one phase of small separated droplets. This leads to much faster coarsening; the CHS and CHSB systems settle to a 1-in-2 shell by , whereas multiple droplets remain at for lower initial concentrations. We also observe the most pronounced differences between the CH model and the models incorporating fluid dynamics. By , the CHS and CHSB systems have coarse and rounded features similar to experiments, while the CH model still demonstrates labyrinthine patterns of large aspect ratio. The evolution of the CH model is also much delayed compared to models incorporating fluid dynamics, as has been observed in other two-phase fluid studies (45, 46). 4) For intermediate -dominated concentrations , the initial evolution of the system leads to coarsening droplets within a continuous phase, which is itself enveloped by a thin shell (unlike the small case). The discrepancy between the CH and remaining models is also much reduced, almost disappearing for concentration ratio . 5) Finally, for sufficiently high concentrations of , complete dissipation of droplets occurs and a thin skin layer forms surrounding a homogeneous droplet.
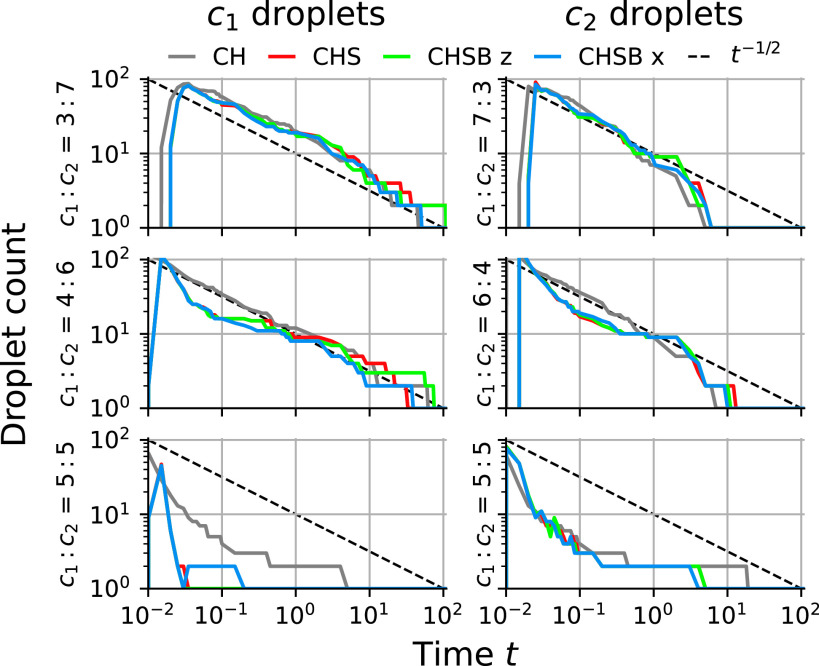
We quantify these coarsening observations in Fig. 5, where we plot the number of droplets over time for concentration ratios , and the number of droplets over time for , for each of the four models. Very little difference is apparent between the four models in droplet counts. For low or high concentrations, the particle counts are reasonably approximated by a coarsening law. This corresponds to an area per droplet scaling with and a droplet length scale proportional to . This agreement worsens near equal concentration ratios, where the system quickly evolves to two interpenetrating phases. The rate is slower than the standard diffusion-limited coarsening scaling exponent (5).
Fig. 5.
Plot of number of droplets (Left column) and droplets (Right column) over time, for different concentration ratios : , for CH (gray), CHS (red), CHSB (green), and CHSB models (blue). A line (dashed black) fits some coalescence regimes well. The CHS, CHSB z, and CHSB models show very little difference in particle counts. The CH model is similar for concentration ratios : of 3 : 7 and 7 : 3 but becomes increasingly distinct as the concentration ratio approaches 5 : 5. Droplet counts are omitted for other choices of droplet and concentration ratio because at most one drop ever forms.
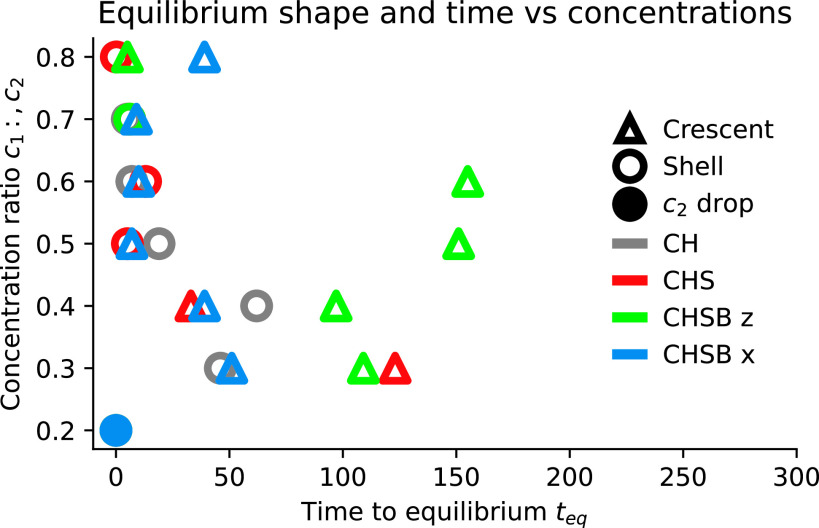
While coarsening does not immediately demonstrate the importance of fluid dynamics for LLPS, this changes when considering the long-time behavior of each system. Over longer time scales (), the system settles into a stable equilibrium given by either a shell or crescent configuration. The long-time behavior now differs between the CH, CHS, CHSB , and CHSB models. We quantify the final shape of each simulation and the time it took to reach this shape in Fig. 6. As observed in Section 2B, the CH model consistently selects a 1-in-2 core–shell morphology, despite the temporary formation of triple points for low initial concentration ratios (). The CHS model similarly fails to attain the minimal energy crescent for , though it does form crescents at . It is somewhat unintuitive that reducing the initial concentration has improved the robustness of the shell. A detailed perturbation analysis may resolve this finding, but is out of scope for this work.
Fig. 6.
Equilibrium shape (Crescent , shell , and droplet ) and dimensionless time to equilibrium for CH (gray), CHS (red), CHSB (green), and CHSB (blue) models. Asymmetric buoyancy forces destabilize shell configurations, causing crescent formation. Pressure-driven pipe flow causes stronger recirculation, accelerating crescent formation by up to two orders of magnitude. Low concentrations instead diffuse out of the drop, leading to -only drops.
In contrast, the CHSB models are sufficiently perturbed by buoyancy and shear flows to attain the minimal energy crescent. We observe a tenfold difference in time to equilibrium shape between the CHSB and CHSB models. The large fluid flows generated by pressure gradients in the CHSB model destabilize the 1-in-2 droplet configuration, leading to early formation of a crescent at . The CHSB model takes until at least to achieve the minimal energy crescent for intermediate concentration ratios .
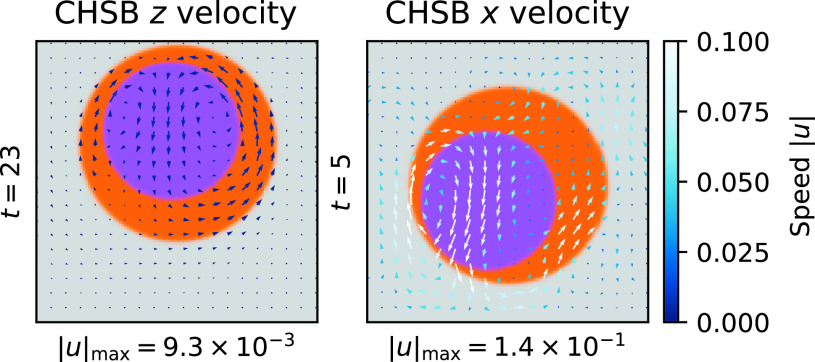
We provide an example snapshot of the velocity field in Fig. 7. We note that the CHSB figure actually plots the deviation of the velocity from the -averaged velocity profile. This is because an Poiseuille-type flow is set up by the pressure gradient, obscuring the smaller relative motion of the fluid within the droplet. The overall magnitude of the recirculation velocity within the CHSB droplet is an order of magnitude weaker than that in the CHSB droplet. Once the CHSB droplet has reached the top of the constraining box, only much weaker relative buoyancies between the and phase can drive the flow. This contrasts with the large shear-induced recirculation within the CHSB droplet. This difference of flows within the droplets is the origin of the reduced interval to droplet formation in the CHSB model. This suggests that crescent particle manufacture may be accelerated by pressure-driven shear flow through small confined channels.
Fig. 7.
Example snapshots of the velocity field for the 2D CHSB (Left) and CHSB (Right) models. Both simulations have an initial concentration ratio : = 0:5. The phases are illustrated in color (, , are purple/orange/gray) and the velocities indicated with arrows (colored by speed). The time of each snapshot is provided on the left of each axis, and the maximum speed indicated on the Bottom. The CHSB x model has been shifted into the droplet frame, and we have subtracted off the -averaged velocity profile to visualize the deviation from Poiseuille-type shear flow. The length scales of the velocities in each figure are different; however, both are colored according to the same velocity scale (Right).
In summary, the initial phase separation may dissipate , generate droplets of or , or form shells, depending on the initial concentration ratio . The long-time behavior will then either lead to a uniform droplet, a 1-in-2 shell, or a minimal energy crescent. The time to equilibrium depends on both the initial concentrations, as well as the strength of the fluid perturbations. If particles move due to pressure gradients, leading to shear flows, one observes recirculating flows within the droplet. This recirculating flow accelerates transport of the first phase to the droplet exterior, aiding crescent formation. If instead particles are constrained by a bounding box, the buoyancy-induced flows are weaker, causing much longer coalescence times. Without density variations between phase 1 and 2, the shell configuration remains stable, preventing crescent formation. We provide a side-by-side video of these simulations in SI Appendix.
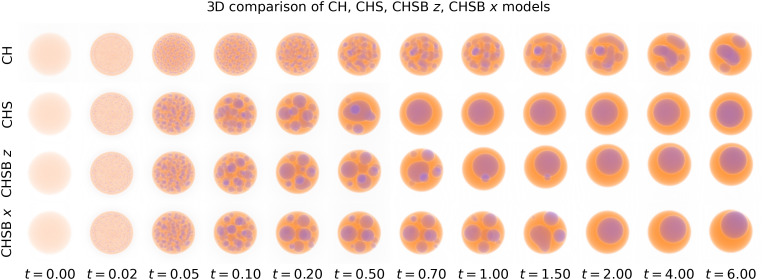
C. 2. Three-dimensional drop evolution.
We present three-dimensional simulations with initial droplet concentration ratio in Fig. 8 (and Movie S2). Our aim is to delineate agreement and disagreement between the three-dimensional (3D) simulations, the two-dimensional simulations, and experimental data. For the 3D models, we see agreement at early times . Differences in time to form a single bubble occur between to , where stronger fluid perturbations temporarily inhibit coarsening (the CHS model coarsens to a single droplet by time , in comparison to for the CHSB model and for the CHSB model). The CH and CHS models tend to a core-in-shell configuration, whereas the CHSB forms a crescent. CHSB should also reach an equilibrium crescent shape, though over a longer time period than our simulation. We provide a side-by-side video of the three-dimensional simulations in SI Appendix.
Fig. 8.
Evolution of CHS, CHSB , and CHSB simulations in three dimensions using parameters in Tables 1–3, for the initial concentration ratio : = 0:3 : 0:7. Overall coarsening times are accelerated compared to two-dimensional simulations. Only the CHSB model develops an energy minimizing crescent configuration.
The patterns of shell vs. crescent formation in two and three dimensions are in agreement—stronger recirculating flows in the CHSB model accelerate crescent formation compared to the CHSB model, and the CH and CHS models settle into a shell equilibrium. We also notice that the CH model forms elongated droplets compared to the spherical droplets of the CHS models and that the CH model evolves over a slower time scale, much as in the 2D case for concentration ratios near . However, the time to equilibrium for the 3D model is reduced when compared to the 2D model at the same concentration ratio (7 s for CHSB in 3D, vs. 47 s in 2D). This difference may partially be explained by simple geometry. In dimension , if the volume fraction of a droplet is given by , then the relative radius of the inner droplet to the whole is given by . That is to say, in three dimensions, an inner droplet is closer to the edge of the droplet than in two dimensions. We thus expect it to take less time to form a crescent in three dimensions. A fairer comparison between two and three dimensions may instead be that for which the radius ratio is equal, not the volume ratio. In this case, a 2D concentration ratio of is seen to take less time to form a crescent (between 6 s and 35 s for and respectively).
Fig. 1 demonstrates the qualitative correspondence between the 3D simulations and experiments of LLPS in a gelatin–PEG mixture. We also provide videos of the experiments in SI Appendix. The coarsening behavior, and final shapes of the particles, are in agreement. There is a discrepancy in time scales. The physical times suggested by the parameters in Table 1 suggest much faster evolution of the simulation than the experiment. A time rescaling reconciles this difference and is presented in SI Appendix.
3. Conclusions and Future Directions
We provide several mathematical models of liquid–liquid phase separation in aqueous two-phase systems. The simplest surface energy minimization model is able to concisely describe equilibrium droplet shapes using just three experimentally testable parameters, the surface tensions between each phase, and the relative concentration of the PEG and gelatin phases. However, this simple model does not account for the dynamics of the system during phase separation and coarsening. To understand these dynamics, we have developed a hierarchy of three models, a ternary Cahn–Hilliard model (CH), a Cahn–Hilliard–Stokes model (CHS) to incorporate surface tension–driven fluid flow, and a Cahn–Hilliard–Stokes–Boussinesq model (CHSB) to also consider buoyancy forcing. While all models agree with the minimal energy shape and contact angles predicted by the energy minimization model, we find that they give different predictions for the same initial conditions. For surface tension regimes corresponding to experiment ( and ), both the CH and CHS models equilibrate to radially symmetric shell configurations. This contrasts with experiment, where crescents can reliably be produced. Buoyancy forcing in the CHSB model resolves this disagreement. It breaks the symmetry of the shell configuration and encourages the heavier gelatin phase to sink to the Bottom of the shell. Different flow profiles for different containers can also further accelerate the phase separation process.
Several promising research directions follow. The first would be to investigate the behavior of the system for increasing separation time scales . This places more emphasis on the role of fluid dynamics but comes at steep computational cost, possibly requiring specialized time integrators (47, 48) to allow greater time steps than the current Implicit-Explicit scheme.
The consistent failure of the CH and CHS models to achieve energy minimization is also of mathematical and physical interest. How strongly must mixed initial conditions be perturbed to observe the emergence of minimal energy triple points? How does the size of the necessary perturbation depend on the relative surface tensions? Analysis inspired by ref. (49) could inform how precise the manufacturing process can be as well as connect to findings of skin layers in models of membrane manufacture (31, 33). We also observe that different fluid flows strongly affect the time to crescent formation; this process may be optimized for design manufacture.
It would be scientifically valuable to explore reduced asymptotic models of phase-separated low Reynolds number fluid dynamics. The reduced equations, derived using multiple-scales matched-asymptotics as (50–55), may provide a much more computationally efficient model of liquid–liquid phase separation, allowing comprehensive investigation of fluid dynamic effects on phase-separating polymer solutions.
Scientific advances could come from more general thermodynamic models. Non-constant mobilities (56, 57) and Flory-Huggins type free energies (58, 59) might extend the model to more widely varying temperature regimes, and further reduce free parameters of the model. Accounting for surfactants and Marangoni stresses would also be necessary for considering droplet interactions. Significant process on modeling cell-cell interactions has been made under a similar framework (60). However, quantitative accuracy would necessitate much more comprehensive experimental data (12, 61–63).
We emphasize the wide applicability of our key observations. Microparticle manufacture, colloid engineering, and condensates in biological systems all combine fluid dynamics and phase separation. We show that in such systems, fluid flows and forces can greatly alter the evolution and equilibria of liquid–liquid phase separation.
4. Materials and Methods
B. Experimental Determination of Densities.
To determine the densities of mixed homogeneous and individual phases post phase separation, we first prepared stock solutions of 4-arm PEG Acrylate (5 kDa, Advanced BioChemicals) at 20% w/v in phosphate-buffered saline (PBS) and cold water fish skin gelatin (sigma) at 10% w/v in deionized (DI) water. We mixed these in a PEG:gelatin ratio of 1.32:1 and added enough extra DI water until we observed a homogeneous solution. We weighed 50 L aliquots on a mass balance in triplicate of this single-phase solution. The solution was then incubated at 4 C for 15 min and centrifuged to obtain separate phases. Each individual phase was weighed in 50 L aliquots. Density was calculated by dividing the measured mass by volume of measurement and reported in g/ml units.
B. Experimental Temperature-Induced Phase Separation (13).
We prepared stock solutions of cold water fish skin gelatin (Sigma) at 10% (w/v) in DI water and 4-arm PEG Acrylate (5 kDa, Advanced BioChemicals) at 20% (w/v) in PBS. We then mixed these at the following PEG:gelatin ratios 3:2,1:1,1:2 and diluted each solution with DI water until we achieved a homogenous mixture. We then flowed this aqueous phase through a step emulsification microfluidic droplet generator at 5 L/min as the dispersed phase. Novec 7500 (3M) supplemented with 2% (v/v) PicoSurf (Sphere Fluidics) at 10 L/min was used as the continuous phase. This produced monodisperse droplets. We immersed these droplets in a reservoir placed in a cold water bath at 4 C. We imaged the droplets by acquiring a brightfield image every 30 s using a Photometrics Prime sCMOS camera at 10x magnification (Nikon) for 15 to 90 min to monitor phase separation until completion.
C. Numerical Methods.
We implement the Cahn–Hilliard–Stokes model in the Dedalus spectral code (64). Dedalus automatically parses text descriptions of partial differential equations into efficient numerical solvers. The framework is written in Python but uses compiled libraries for performance, enabling rapid prototyping and model comparisons, as well as efficient high-performance simulations. We simulate in two and three dimensions, using Fourier projections in the horizontal directions and Chebyshev polynomials in the vertical direction, to represent no-slip, non-wetting walls. Using basis recombination and the tau method (64) to enforce boundary conditions, the linear part of the system is discretized into sparse banded matrices that are parallelized over each Fourier mode using the MPI library. A second-order semi-implicit backward difference time stepping method iterates the linear part implicitly and the nonlinear part explicitly. In contrast to earlier methods involving iterative nonlinear implicit solves (65–68), constant coefficient preconditioning alleviates equation stiffness constraints with single matrix solves (similar to refs. (37, 69–73)). This affords an efficient solution routine with complexity approximately linear in the degrees of freedom. Further details are provided in SI Appendix, and the Mathematica derivation and simulation code are provided online (74).
Supplementary Material
Appendix 01 (PDF)
Side-by-side movie of 2D CH, CHS, CHSB z, and CHSB x models for varying initial concentration ratios.
Side-by-side movie of 3D CH, CHS, CHSB z, and CHSB x models.
Movie of temperature-induced phase-separation of a PEG-gelatin aqueous two phase system. Experimental details are listed in the methods section of the main paper.
Acknowledgments
This work is supported by Simons Foundation Math + X Investigator Award No. 510776. We acknowledge computing resources on Hoffman2 provided through the Institute for Digital Research and Education at UCLA.
Author contributions
E.W.H., S.C., D.D.C., and A.L.B. designed research; E.W.H., S.C., V.S., A.A., and B.P. performed research; E.W.H. analyzed data; S.C. development of mathematics and code, Critical revision of manuscript; D.D.C. and A.L.B. critical revision of manuscript; and E.W.H. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
Reviewers: M.P.B., Harvard University; and K.G., University of Arizona.
Data, Materials, and Software Availability
All code used for data generation and analysis is available at https://github.com/ericwhester/multiphase-fluids-code (74). The simulation data is too large to host online, but will be made available upon request.
Supporting Information
References
- 1.Xiao Z., Liu W., Zhu G., Zhou R., Niu Y., A review of the preparation and application of flavour and essential oils microcapsules based on complex coacervation technology. J. Sci. Food Agric. 94, 1482–1494 (2014). [DOI] [PubMed] [Google Scholar]
- 2.Ma Q., et al. , Cell-inspired all-aqueous microfluidics: From intracellular liquid-liquid phase separation toward advanced biomaterials. Adv. Sci. 7, 1903359 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hyman A. A., Weber C. A., Jülicher F., Liquid-liquid phase separation in biology. Annu. Rev. Cell Dev. Biol. 30, 39–58 (2014). [DOI] [PubMed] [Google Scholar]
- 4.Banani S. F., Lee H. O., Hyman A. A., Rosen M. K., Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 18, 285–298 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Berry J., Brangwynne C. P., Haataja M., Physical principles of intracellular organization via active and passive phase transitions. Rep. Prog. Phys. 81, 046601 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Shin Y., Brangwynne C. P., Liquid phase condensation in cell physiology and disease. Science 357, eaaf4382 (2017). [DOI] [PubMed] [Google Scholar]
- 7.Alberti S., Dormann D., Liquid-liquid phase separation in disease. Annu. Rev. Genet. 53, 171–194 (2019). [DOI] [PubMed] [Google Scholar]
- 8.Mao S., Kuldinow D., Haataja M. P., Košmrlj A., Phase behavior and morphology of multicomponent liquid mixtures. Soft. Matter. 15, 1297–1311 (2019). [DOI] [PubMed] [Google Scholar]
- 9.Mao S., Chakraverti-Wuerthwein M. S., Gaudio H., Košmrlj A., Designing the morphology of separated phases in multicomponent liquid mixtures. Phys. Rev. Lett. 125, 218003 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Shrinivas K., Brenner M. P., Phase separation in fluids with many interacting components. Proc. Natl. Acad. Sci. U.S.A. 118, e2108551118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang H., Wu Y., Wang F., Guo F., Nestler B., Phase-field modeling of multiple emulsions via spinodal decomposition. Langmuir 37, 5275–5281 (2021). [DOI] [PubMed] [Google Scholar]
- 12.Yanagisawa M., Yamashita Y., Mukai Sa., Annaka M., Tokita M., Phase separation in binary polymer solution: Gelatin/Poly(ethylene glycol) system. J. Mol. Liq. 200, 2–6 (2014). [Google Scholar]
- 13.Lee S., de Rutte J., Dimatteo R., Koo D., Di Carlo D., Scalable fabrication and use of 3D structured microparticles spatially functionalized with biomolecules. ACS Nano 16, 38–49 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang Y., et al. , Counting of enzymatically amplified affinity reactions in hydrogel particle-templated drops. Lab Chip 21, 3438–3448 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.de Rutte J., et al. , Suspendable hydrogel nanovials for massively parallel single-cell functional analysis and sorting. ACS Nano 16, 7242–7257 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Theberge A. B., et al. , Microdroplets in microfluidics: An evolving platform for discoveries in chemistry and biology. Angew. Chem. Int. Ed. 49, 5846–5868 (2010). [DOI] [PubMed] [Google Scholar]
- 17.Zarzar L. D., et al. , Dynamically reconfigurable complex emulsions via tunable interfacial tensions. Nature 518, 520–524 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li W., et al. , Microfluidic fabrication of microparticles for biomedical applications. Chem. Soc. Rev. 47, 5646–5683 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cai L., et al. , Anisotropic microparticles from microfluidics. Chem 7, 93–136 (2021). [Google Scholar]
- 20.Kim J. H., et al. , Droplet microfluidics for producing functional microparticles. Langmuir 30, 1473–1488 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Shang L., Cheng Y., Zhao Y., Emerging droplet microfluidics. Chem. Rev. 117, 7964–8040 (2017). [DOI] [PubMed] [Google Scholar]
- 22.Ma S., et al. , Fabrication of microgel particles with complex shape via selective polymerization of aqueous two-phase systems. Small 8, 2356–2360 (2012). [DOI] [PubMed] [Google Scholar]
- 23.Wang W., et al. , Hole-shell microparticles from controllably evolved double emulsions. Angew. Chem. 125, 8242–8245 (2013). [DOI] [PubMed] [Google Scholar]
- 24.Watanabe T., Motohiro I., Ono T., Microfluidic formation of hydrogel microcapsules with a single aqueous core by spontaneous cross-linking in aqueous two-phase system droplets. Langmuir 35, 2358–2367 (2019). [DOI] [PubMed] [Google Scholar]
- 25.Liu Q., et al. , Self-orienting hydrogel micro-buckets as novel cell carriers. Angew. Chem. Int. Ed. 58, 547–551 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chen Z., et al. , Microfluidic-generated biopolymer microparticles as cargo delivery systems. Adv. Mater. Technol. 2100733, 7 (2021). [Google Scholar]
- 27.Hohenberg P. C., Halperin B. I., Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435–479 (1977). [Google Scholar]
- 28.Paulsen J. D., Carmigniani R., Kannan A., Burton J. C., Nagel S. R., Coalescence of bubbles and drops in an outer fluid. Nat. Commun. 5, 3182 (2014). [DOI] [PubMed] [Google Scholar]
- 29.Shimizu R., Tanaka H., A novel coarsening mechanism of droplets in immiscible fluid mixtures. Nat. Commun. 6, 7407 (2015). [DOI] [PubMed] [Google Scholar]
- 30.Steinbacher J. L., McQuade D. T., Polymer chemistry in flow: New polymers, beads, capsules, and fibers. J. Polym. Sci., Part A: Polym. Chem. 44, 6505–6533 (2006). [Google Scholar]
- 31.Zhou B., Powell A. C., Phase field simulations of early stage structure formation during immersion precipitation of polymeric membranes in 2D and 3D. J. Membr. Sci. 268, 150–164 (2006). [Google Scholar]
- 32.Li Y. C., Shi R. P., Wang C. P., Liu X. J., Wang Y., Phase-field simulation of thermally induced spinodal decomposition in polymer blends. Modell. Simul. Mater. Sci. Eng. 20, 075002 (2012). [Google Scholar]
- 33.Tree D., et al. , Mass-transfer driven spinodal decomposition in a ternary polymer solution. Soft Matter 15, 4614–4628 (2019). [DOI] [PubMed] [Google Scholar]
- 34.Wang F., Ratke L., Zhang H., Altschuh P., Nestler B., A phase-field study on polymerization-induced phase separation occasioned by diffusion and capillary flow–a mechanism for the formation of porous microstructures in membranes. J. Sol-Gel. Sci. Technol. 94, 356–374 (2020). [Google Scholar]
- 35.Berry J., Weber S. C., Vaidya N., Haataja M., Brangwynne C. P., RNA transcription modulates phase transition-driven nuclear body assembly. Proc. Natl. Acad. Sci. U.S.A. 112, E5237–E5245 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bostwick J., Steen P., Stability of constrained capillary surfaces. Annu. Rev. Fluid Mech. 47, 539–568 (2015). [Google Scholar]
- 37.Dong S., Multiphase flows of N immiscible incompressible fluids: A reduction-consistent and thermodynamically-consistent formulation and associated algorithm. J. Comput. Phys. 361, 1–49 (2018). [Google Scholar]
- 38.Anderson D. M., McFadden G. B., Wheeler A. A., Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30, 139–165 (1998). [Google Scholar]
- 39.Jacqmin D., Calculation of two-phase Navier-Stokes flows using phase-field modeling. J. Comput. Phys. 155, 96–127 (1999). [Google Scholar]
- 40.Kim J., Lowengrub J., Phase field modeling and simulation of three-phase flows. Interfaces Free Boundaries 7, 435–466 (2005). [Google Scholar]
- 41.Boyer F., Lapuerta C., Study of a three component Cahn-Hilliard flow model. ESAIM: Math. Model. Numer. Anal. 40, 653–687 (2006). [Google Scholar]
- 42.Boyer F., Minjeaud S., Hierarchy of consistent n-component Cahn-Hilliard systems. Math. Models Methods Appl. Sci. 24, 2885–2928 (2014). [Google Scholar]
- 43.Alikakos N. D., Bates P. W., Chen X., Convergence of the Cahn-Hilliard equation to the Hele-Shaw model. Arch. Ration. Mech. Anal. 128, 165–205 (1994). [Google Scholar]
- 44.Cahn J. W., Hilliard J. E., Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28, 258–267 (1958). [Google Scholar]
- 45.Tjahjadi M., Stone H. A., Ottino J. M., Satellite and subsatellite formation in capillary breakup. J. Fluid Mech. 243, 297 (1992). [Google Scholar]
- 46.Stone H. A., Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid Mech. 26, 65–102 (1994). [Google Scholar]
- 47.Liu F., Shen J., Stabilized semi-implicit spectral deferred correction methods for Allen-Cahn and Cahn-Hilliard equations. Math. Methods Appl. Sci. 38, 4564–4575 (2015). [Google Scholar]
- 48.Glasner K., Orizaga S., Improving the accuracy of convexity splitting methods for gradient flow equations. J. Comput. Phys. 315, 52–64 (2016). [Google Scholar]
- 49.Bernoff A. J., Bertozzi A. L., Witelski T. P., Axisymmetric surface diffusion: Dynamics and stability of self-similar pinchoff. J. Stat. Phys. 93, 725–776 (1998). [Google Scholar]
- 50.Glasner K., A diffuse interface approach to Hele Shaw flow. Nonlinearity 16, 49–66 (2003). [Google Scholar]
- 51.Magaletti F., Picano F., Chinappi M., Marino L., Casciola C. M., The sharp-interface limit of the Cahn-Hilliard/Navier-Stokes model for binary fluids. J. Fluid Mech. 714, 95–126 (2013). [Google Scholar]
- 52.Lee A. A., Münch A., Süli E., Sharp-interface limits of the Cahn-Hilliard equation with degenerate mobility. SIAM J. Appl. Math. 76, 433–456 (2016). [Google Scholar]
- 53.Wang D., Wang X. P., Wang Y. G., The dynamics of three-phase triple junction and contact points. SIAM J. Appl. Math. 77, 1805–1826 (2017). [Google Scholar]
- 54.Hester E. W., Vasil G. M., Burns K. J., Improving accuracy of volume penalised fluid-solid interactions. J. Comput. Phys. 430, 110043 (2021). [Google Scholar]
- 55.Hester E. W., Couston L. A., Favier B., Burns K. J., Vasil G. M., Improved phase-field models of melting and dissolution in multi-component flows. Proc. R. Soc. A: Math. Phys. Eng. Sci. 476, 20200508 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Vrentas J. S., Vrentas C. M., A new equation relating self-diffusion and mutual diffusion coefficients in polymer-solvent systems. Macromolecules 26, 6129–6131 (1993). [Google Scholar]
- 57.Elliott C. M., Garcke H., On the Cahn-Hilliard equation with degenerate mobility. SIAM J. Math. Anal. 27, 404–423 (1996). [Google Scholar]
- 58.Huggins M. L., Solutions of long chain compounds. J. Chem. Phys. 9, 440–440 (1941). [Google Scholar]
- 59.Flory P. J., Thermodynamics of high polymer solutions. J. Chem. Phys. 10, 51–61 (1942). [Google Scholar]
- 60.Carrillo J. A., Murakawa H., Sato M., Togashi H., Trush O., A population dynamics model of cell-cell adhesion incorporating population pressure and density saturation. J. Theor. Biol. 474, 14–24 (2019). [DOI] [PubMed] [Google Scholar]
- 61.Zoller P., Standard Pressure-Volume-Temperature Data for Polymers (Technomic Pub. Co., Lancaster, PA, 1995). [Google Scholar]
- 62.R. Koningsveld, Polymer Phase Diagrams, R. Koningsveld, W. H. Stockmayer, E. Nies. Eds. (University Press, Oxford, 2001).
- 63.Yamashita Y., Yanagisawa M., Tokita M., Dynamics of spinodal decomposition in a ternary gelling system. Gels 4, 26 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Burns K. J., Vasil G. M., Oishi J. S., Lecoanet D., Brown B. P., Dedalus: A flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2, 023068 (2020). [Google Scholar]
- 65.Eyre D. J., Unconditionally Gradient Stable Time Marching the Cahn-Hilliard Equation. MRS Online Proceedings Library (OPL) 529, 39–46 (1998). [Google Scholar]
- 66.Lee H. G., Kim J., A second-order accurate non-linear difference scheme for the N -component Cahn-Hilliard system. Physica A 387, 4787–4799 (2008). [Google Scholar]
- 67.Chen W., Wang C., Wang X., Wise S. M., Positivity-preserving, energy stable numerical schemes for the Cahn-Hilliard equation with logarithmic potential. J. Comput. Phys. X 3, 100031 (2019). [Google Scholar]
- 68.Chen W., Wang C., Wang S., Wang X., Wise S. M., Energy stable numerical schemes for ternary Cahn-Hilliard system. J. Sci. Comput. 84, 27 (2020). [Google Scholar]
- 69.Badalassi V., Ceniceros H., Banerjee S., Computation of multiphase systems with phase field models. J. Comput. Phys. 190, 371–397 (2003). [Google Scholar]
- 70.Dong S., An efficient algorithm for incompressible N-phase flows. J. Comput. Phys. 276, 691–728 (2014). [Google Scholar]
- 71.Dong S., Physical formulation and numerical algorithm for simulating N immiscible incompressible fluids involving general order parameters. J. Comput. Phys. 283, 98–128 (2015). [Google Scholar]
- 72.Zhang J., Yang X., Decoupled, non-iterative, and unconditionally energy stable large time stepping method for the three-phase Cahn-Hilliard phase-field model. J. Comput. Phys. 404, 109115 (2020). [Google Scholar]
- 73.Yang X., A new efficient fully-decoupled and second-order time-accurate scheme for Cahn-Hilliard phase-field model of three-phase incompressible flow. Comput. Methods Appl. Mech. Eng. 376, 113589 (2021). [Google Scholar]
- 74.E. Hester, multiphase-fluids-code. Github. https://github.com/ericwhester/multiphase-fluids-code. Deposited 30 January 2023.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Side-by-side movie of 2D CH, CHS, CHSB z, and CHSB x models for varying initial concentration ratios.
Side-by-side movie of 3D CH, CHS, CHSB z, and CHSB x models.
Movie of temperature-induced phase-separation of a PEG-gelatin aqueous two phase system. Experimental details are listed in the methods section of the main paper.
Data Availability Statement
All code used for data generation and analysis is available at https://github.com/ericwhester/multiphase-fluids-code (74). The simulation data is too large to host online, but will be made available upon request.