Differential influence of vision and proprioception on control of movement distance

Abstract

The purpose of this study was to investigate the contribution of proprioceptive and visual information about initial limb position in controlling the distance of rapid, single-joint reaching movements. Using a virtual reality environment, we systematically changed the relationship between actual and visually displayed hand position as subjects’ positioned a cursor within a start circle. No visual feedback was given during the movement. Subjects reached two visual targets (115 and 125° elbow angle) from four start locations (90, 95, 100, and 105° elbow angle) under four mismatch conditions (0, 5, 10, or 15°). A 2×4×4 ANOVA enabled us to ask whether the subjects controlled the movement distance in accord with the virtual, or the actual hand location. Our results indicate that the movement distance was mainly controlled according to the virtual start location. Whereas distance modification was most extensive for the closer target, analysis of acceleration profiles revealed that, regardless of target position, visual information about start location determined the initial peak in tangential hand acceleration. Peak acceleration scaled with peak velocity and movement distance, a phenomenon termed “pulse-height” control. In contrast, proprioceptive information about actual hand location determined the duration of acceleration, which also scaled with peak velocity and movement distance, a phenomenon termed “pulse-width” control. Because pulse-height and pulse-width mechanisms reflect movement planning and sensory-based corrective processes, respectively, our current findings indicate that vision is used primarily for planning movement distance, while proprioception is used primarily for online corrections during rapid, unseen movements toward visual targets.

Introduction

It has been well established that perception of limb position with respect to both body and external world coordinates depends on information provided by vision, proprioception, and touch (Brown et al. 2003a, b; Graziano 1999; Lateiner and Sainburg 2003; Sainburg et al. 2003; Sober and Sabes 2003; van Beers et al. 1998, 1999). However, the rules used by the nervous system for combining these different sources of information remain controversial. Two main paradigms have employed visual/proprioceptive discrepancies in order to assess position perception, or movement production, respectively. First, the accuracy of targeted reaching has been assessed when visual information about initial hand position is distorted by the use of either optical prisms or virtual reality environments. Second, declarative information about static hand position is assessed under similar distortions in visual feedback. Under the latter conditions, subjects report their hand in a location that is between that specified by vision and the “actual” hand position, specified through proprioception (Pick et al. 1969; Warren and Cleaves 1971). A similar perception occurs when a distortion in proprioception is introduced through vibratory stimulation (Dizio et al. 1993; Lackner and Levine 1979). Most studies have indicated that, whether visual or proprioceptive information is perturbed, the perceived position of the hand is closer to that indicated by vision.

In contrast to the visual bias observed in perception studies, Rossetti et al. (1995) reported a proprioceptive bias when optical prisms were used to dissociate visual and proprioceptive information about starting hand location prior to reaching movements. These authors reported movement directions that were consistent with initial position estimates closer to the actual than the virtual, hand position. Rossetti et al. (1995), therefore, suggested that hand position is derived from a weighted fusion of visual and proprioceptive information, an idea supported by van Beers et al. (1996, 1999). Using modeling techniques in combination with empirical findings, Sober and Sabes (2003) quantified the contributions of each modality to two stages of movement planning, specifying a planned displacement vector, and transforming that vector into joint-based motor commands (inverse kinematics transformation). Their results indicated the greatest contributions of vision to direction planning, and predominance of proprioception for the inverse transformation. The latter idea is consistent with studies in deafferented patients, which indicate a strong role of proprioception in controlling intersegmental dynamics (Sainburg et al. 1995). However, Sober and Sabes did not address the control of movement distance. Because of substantial evidence that movement direction and distance are planned and controlled independently (Ghez et al. 1997; Gordon et al. 1994a; Rosenbaum 1980), it is likely that the contributions of sensory information may differ.

Recent findings from our laboratory have suggested differential contributions of vision and proprioception to specification of movement direction and movement distance (Lateiner and Sainburg 2003; Sainburg et al. 2003). In these studies, a discrepancy between virtual and actual finger start location was introduced prior to multijoint reaching movements. The results indicated that movement direction varied only with virtual start location, and that movement distance also varied with actual start location. Thus, in contrast to the role of vision in specifying movement direction, these studies suggest a substantial role of proprioception in addition to vision in controlling distance. Differential contributions of sensory information for specifying distance and direction are consistent with extensive evidence that these two features of movement are specified independently (Georgopoulos 1994, 1995, 1996, 2000; Kakei et al. 1999; Kalaska 1988; Kalaska et al. 1983).

The current study specifically addresses the relative contributions of vision and proprioception to specification of movement distance. By limiting our study to single-joint movements, we were able to eliminate demands for direction planning and control. In this study, we used a virtual reality display to dissociate visual and proprioceptive information about limb position prior to rapid, targeted elbow extension movements. Movements were made to two different visual targets, from four different start locations, and under four virtual/actual dissociation conditions. We were, thus, able to directly assess how subjects adjust movement distance, given a discrepancy between visual and proprioceptive information about start location. By analyzing tangential hand acceleration profiles, we could also infer the extent to which adjustments in distance could be predicted by early movement events, indicative of planning processes.

Materials and methods

Experimental setup

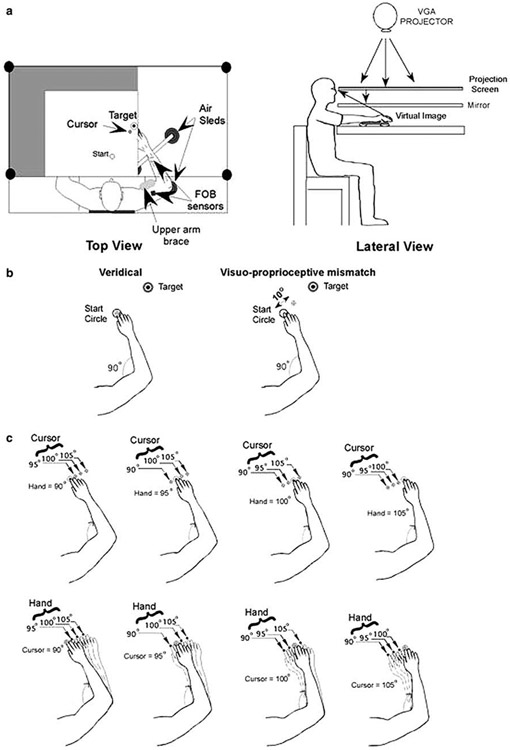
Figure 1a illustrates the general experimental setup used for this experiment. Subjects sat with the right arm supported over a horizontal surface, positioned just below the shoulder height (adjusted to subjects’ comfort), by a frictionless air-jet system. A start circle, target, and cursor representing the hand position were projected on a horizontal backprojection screen positioned above the arm. A mirror, positioned parallel and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the hand. Calibration of the display assured that this projection was veridical. This virtual reality environment assured that subjects had no visual feedback of their arm during the experimental session. All joints distal to the elbow were immobilized using an adjustable brace. In addition, the upper arm was immobilized by a brace, restricting arm movements to the elbow joint. Position and orientation of each limb segment was sampled using the Flock of Birds^® (FoB—Ascension-Technology) magnetic six-degree-of-freedom movement recording system. A single sensor was attached to the upper arm segment via an adjustable plastic cuff, while another sensor was fixed to the air sled where the forearm was fitted. The sensors were positioned approximately at the center of each arm segment. The position of the following three landmarks was digitized using a stylus that was rigidly attached to a FoB sensor: (1) hand point (38 cm away from elbow joint, i.e., landmark 2); (2) the lateral epicondyle of the humerus; (3) the acromion, directly posterior to the acromio-clavicular joint. Landmark 1 was chosen in order to assure the same set of targets/movements independent of subject’s forearm length. These positions relative to the sensors attached to each arm segment thus remained constant throughout the experimental session. As sensor data were received from the FoB, the position of these landmarks was computed by our custom software yielding the three-dimensional (3D) position of the hand point. Because the table surface defined our X–Y plane, perpendicular axis displacement was constant. We, thus, used the recorded X–Y coordinates of the hand point to project a cursor onto the screen. Screen redrawing occurred fast enough to maintain the cursor centered on the hand point throughout the sampled arm movements. Digital data were collected at 103 Hz using a Macintosh computer, which controlled the sensors through separate serial ports, and stored on a disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC^™ (REAL Software, Inc.), C and IGOR Pro^™ (WaveMetrics, Inc.).

Fig. 1.

a Experimental setup. b Experimental design: position of hand and cursor for the conditions tested: (1) veridical, (2) visuo–proprioceptive mismatch. c Possible hand start locations (90, 95, 100, and 105° elbow angle) and visual cursor start location conditions (difference between virtual and actual elbow angle: 0, 5, 10, and 15°)

Kinematic data

The 3D position of the hand, elbow, and shoulder were calculated from sensor position and orientation data. Then, elbow and shoulder angles were calculated from these data. All kinematic data were low pass filtered at 12 Hz (third order, no-lag, dual pass Butterworth), and differentiated to yield angular velocity and acceleration values. Each trial usually started with the hand at zero velocity, but small oscillations of the hand sometimes occurred within the start circle. In this case, the onset of movement was defined by the last minimum (below 8% maximum tangential velocity) prior to the maximum in the hand’s tangential velocity profile. Movement termination was defined as the first minimum (below 8% maximum tangential velocity) following the peak in tangential hand velocity. Visual inspection was performed on every single trial to ensure that movement onset, peak acceleration, peak velocity, and movement termination were correctly determined.

Subjects

Subjects were eight neurologically normal adults (four female, four male) from 21 to 34 years old. All subjects were right-handed, as indicated by laterality scores on a 12-item version of the Edinburgh Inventory (Oldfield 1971). Subjects were recruited from the university community, and were paid for their participation. Informed consent was solicited prior to participation, which was approved by the Institutional Review Board of the Pennsylvania State University.

Experimental task

The experimental session consisted of 320 repetitive elbow joint extension movements toward one of the two visual targets positioned at 115 or 125° of elbow angle from the start location (90, 95, 100, and 105° of elbow angle). Prior to movement, a start circle and a target circle were displayed (approximate target distances from start position: target 1 = 5, 8, 11, or 14 cm; target 2 = 11, 14, 17, 20 cm). A cursor, providing visual feedback about the hand point, was to be positioned in the start circle (1 cm diameter) for 300 ms. At the presentation of an audiovisual “go” signal, the cursor was blanked. Subjects were instructed to move the index fingertip to the target using a “single, uncorrected, rapid motion”. Despite movements being restricted to the elbow joint, subjects could easily perform the movement. Between trials, cursor feedback was only provided when the hand was within a 3 cm radius of the center of the start circle. Thus subjects returned their hands near the start circle under “blind” conditions. This was done to prevent adaptation to altered visual feedback. Within the 320 trials, 32 different conditions [i.e., (2 targets) × (4 initial hand locations) × (4 initial cursor locations)] were interspersed in a pseudo-random manner. The design of this study produced ten trials for each of the conditions tested. Subjects had no prior information about the mismatched positions.

Start location changes

During “veridical” trials, hand point and cursor position matched accurately; while during “displaced” trials cursor/hand positions were mismatched by 5, 10, or 15° real/virtual elbow angle (5° corresponded approximately to 3 cm in the present study). The schematic shown in Fig. 1b depicts examples of the relationship of the subjects’ hand to the cursor in veridical and mismatch conditions.

Measures of task performance

We analyzed hand trajectories of the movements calculating the following measures of task performance: total distance traveled, which was calculated as the 2D distance between the start and the final location of the hand. Additionally, we calculated peak velocity, peak acceleration, time-to-peak velocity (duration of the first acceleration pulse), time-to-peak acceleration, and movement duration. To examine the symmetry of the velocity profiles and the importance of the acceleration phase compared to the deceleration phase, the ratio of acceleration duration divided by movement duration was analyzed.

Statistical analysis

Dependant measures of movement acceleration, velocity, distance, and time were submitted to repeated-measures 2×4×4 analyses of variance with target distance (short and long), initial cursor position (start position: 90, 95, 100, and 105°), and initial hand position (start position: 90, 95, 100, and 105°) as factors. For all analysis, statistical significance was tested using an alpha value of 0.05 and Tukey’s method was used for post-hoc analysis.

In order to assess the relative contributions of vision and proprioception to movement distance specification, we calculated the slope of the relationship between movement distance and start position (of the cursor or the hand; see Figs. 2d, 3d). Within each subject, this slope was calculated for each starting position, separately (using the lineFit function in IGOR Pro’ WaveMetrics, Inc.), then averaged across starting positions. In addition, the slope of this relationship under veridical conditions was calculated within each subject. The ratio of displaced (cursor or hand) to veridical slope was then calculated to yield the percent contribution of each modality condition (vision or proprioception, respectively) to movement distance specification. Additionally, we calculated the slopes of the peak hand velocity curves as a function of start location, and determined the visual and proprioceptive contributions by comparing displaced and veridical conditions.

Fig. 2.

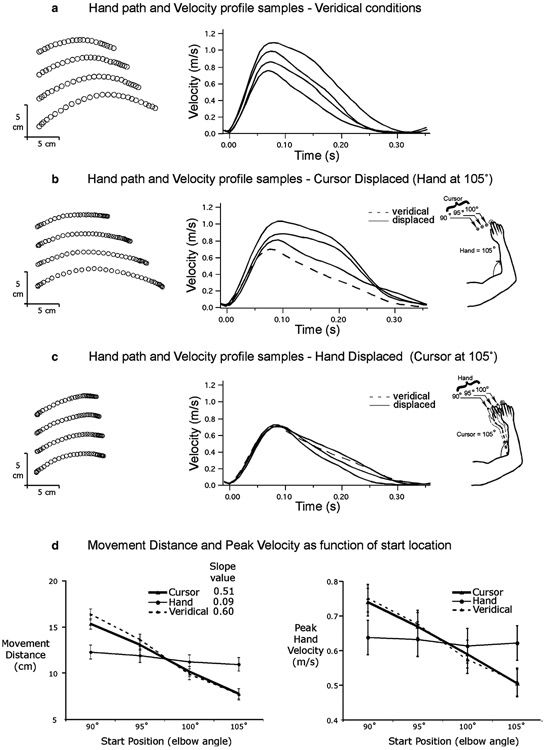
Target 1 (115° elbow position) movements: a representative samples of hand paths and velocity profiles under veridical condition; b representative samples of hand paths and velocity profiles for cursor displaced condition; c representative samples of hand paths and velocity profiles for hand displaced condition; d movement distance versus start position, and peak hand velocity versus start position plots

Fig. 3.

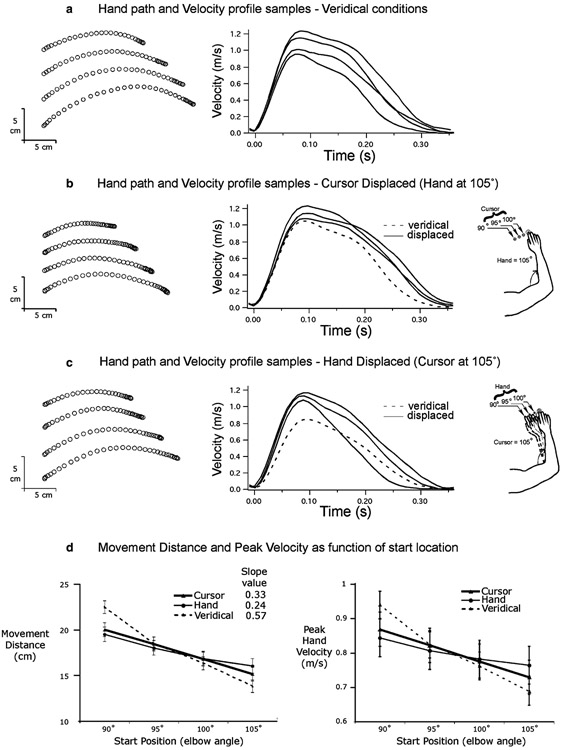
Target 2 (125° elbow position) movements: a representative samples of hand paths and velocity profiles under veridical condition; b representative samples of hand paths and velocity profiles for cursor displaced condition; c representative samples of hand paths and velocity profiles for hand displaced condition; d movement distance versus start position, and peak hand velocity versus start position plots

Results

In this experiment, we presented a discrepancy between proprioceptively derived (hand) and visually derived (cursor) initial position information. When asked, after completion of the experimental session, subjects reported that they were not aware of “anything odd” during the experiment. Some reported that the task seemed “difficult”, but did not express any specific concern. No one reported awareness of a discrepancy in the projected start position.

Figure 2 shows example of hand-path (left) and tangential velocity profiles (right) for movements toward the closer target (target 1, 115° elbow position). Figure 2a shows the results when the hand and cursor start locations were veridical. As expected, movement extent varied with start position, such that movements that began closer to the target were shorter. In addition, peak tangential hand velocity and acceleration scaled with movement extent, such that the shorter movements were slower and the longer movements were faster. These findings were consistent across subjects, as shown in Fig. 2d, which shows the mean (±SE) for movement distance (left) and maximum velocity (right) plotted across the four start positions. Veridical conditions, in which cursor and hand start positions corresponded, are shown as a dashed line. The scaling of movement distance and peak velocity with start position is shown by the steep slope of these lines. Also as expected, the 2×4×4 ANOVA showed a main effect of target distance on movement distance (F_1,217 = 1,628.8; P<0.001). Movements performed toward the further target (mean=17.6 cm) were significantly longer than those toward the closer target (mean=11.6 cm). Target distance also influenced peak velocity (F_{1, 217} = 525.9; P<0.001), as movements performed toward the further target reached a higher peak speed (mean=0.80 m/s) than those toward the closer target (mean=0.63 m/s).

Figure 2b shows the hand paths and velocity profiles for movements in which the cursor start position varied, but the hand start position remained in the 105° position. The results are very similar to veridical conditions: movement distance varied systematically according to the cursor start location. For example, when the cursor was seen further from the target compared to where the actual hand was, movement distance was increased. The ANOVA showed a main effect of initial cursor location on both movement distance (F_3,217 = 331.9; P<0.001) and peak velocity (F_3,217=121.4; P<0.001). The ANOVA also revealed an interaction between target distance and initial cursor location for movement distance (F_3,217 = 16.5; P<0.001) and peak velocity (F_3,217 = 7.1; P<0.001). The effect of initial cursor location was significantly greater for the closer target than for the further target (see Fig. 3). For the closer target, the similarity of the effect of varying the initial positions in veridical conditions and varying only the initial cursor position is shown in Fig. 2d, where movement distance (left) and peak tangential velocity (right) are plotted across the four cursor start locations (triangle markers).

When the hand start location varied but the cursor start location remained constant (Figs. 2c, 3c), movement distance varied, as indicated by the main effect of initial hand position (F_3,217=52.0; P<0.001). When the hand was further from the target, as compared to the cursor, subjects significantly increased movement distance. Peak velocity also varied according to initial hand position (F_3,217=9.6; P<0.001). However, Figs. 2d, 3d, and 4 show that the effect of actual starting hand position was smaller than that of cursor starting position. Moreover, the interaction between target distance and initial hand location for movement distance (F_3,217=16.5; P<0.001) and peak velocity (F_3,217=3.7; P<0.05) revealed that the effect of initial hand location was greater for the further target than for the closer target. This is reflected by the near flat relationship depicted of the “hand” data in Fig. 2d (closer target), which contrasts dramatically with the systematic variation in both distance and velocity for veridical conditions, and for the “cursor” data. In fact, post-hoc analysis revealed that there was no significant effect of actual initial hand position on peak velocity for the closer target (P>0.05). For the further target (Fig. 3d), the slope of the relationship depicted by the “hand” data was much steeper, highlighting the increased reliance on proprioceptive information of hand position in controlling movement speed and distance.

Fig. 4.

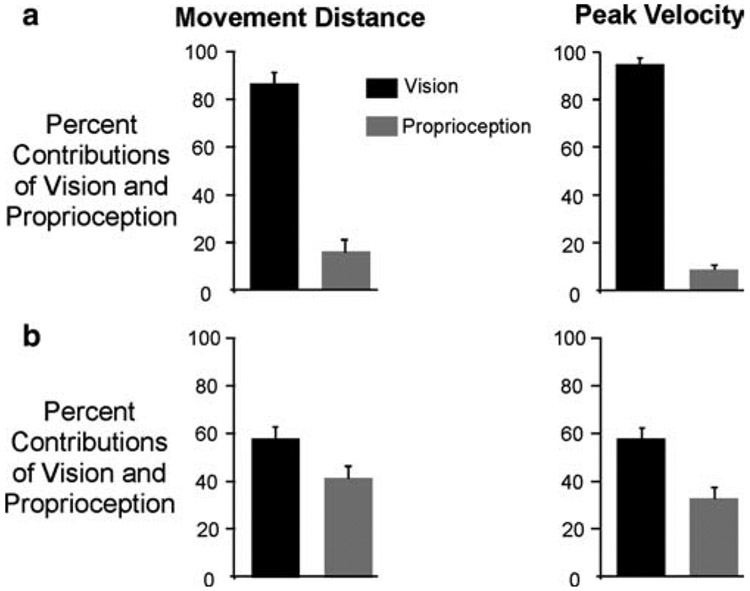
a Vision and proprioception relative contributions for target 1 movements; % average (mean ± SE) movement distance (left); % average (mean ± SE) tangential velocity (right). b Vision and proprioception relative contributions for the target 2 movements; % average (mean ± SE) movement distance (left); % average (mean ± SE) tangential velocity (right)

Because visual and proprioceptive contributions to the control of movement extent clearly varied as a function of target distance, these contributions were quantified separately for the two targets. We calculated the relative contributions of each type of information on movement extent and peak velocity specification. As detailed above, our results indicated that, for the closer target, distance and velocity were mainly determined by visually derived cursor information, compared to proprioceptive information, about hand location. As shown in the bar plots of Fig. 4a, the contribution of initial hand position to distance was only 15±3% (mean±SE), whereas that of initial cursor position was 86±4% (mean±SE). Similarly, the relative contributions of these factors to peak hand velocity were 94±2% for cursor position, and only 8±3% for hand position. Thus, visually derived cursor information contributed almost entirely to specification of movement distance toward the closer target. Considering now the further target, our measures of the contributions of visual and proprioceptive information to movement distance and velocity were similar to one another. This is depicted in the bar plots of Fig. 4b. The percent contribution of vision to movement distance was 58±3%, and to peak velocity was 58±2%. The percent contribution of proprioception to distance was 41±4%, and to velocity was 33±3%. Thus, for this more distant target, proprioceptive information about actual hand location played an increased role in determining both movement distance and speed.

As described above, the effects of initial position information on movement distance were well defined by the time of peak tangential velocity, which occurred at 28% of movement time of the rapid movements (mean peak velocity = 0.80 m/s and mean movement duration = 535 ms for the further target, mean peak velocity = 0.63 m/s and movement duration = 487 ms for the closer target). The scaling of velocity with intended movement distance for rapid, single-joint movements has previously been well characterized (Atkeson and Hollerbach 1985; Ghez et al. 1991, 1997; Gordon and Ghez 1987; Gordon et al. 1994a; Sainburg and Schaefer 2004). Previous research has indicated that peak velocity is determined through pulse-step mechanisms, in which both the height and duration of acceleration profiles scale with peak velocity. In such movements, peak acceleration typically occurs too early to be affected by a feedback. In the present experiment, time-to-peak acceleration was 57 ms on an average (there was no significant effect on this parameter; P>0.05). This short latency strongly suggests that pulse-height control is determined entirely through feedforward mechanisms, a hypothesis supported by previous perturbation studies (Bagesteiro and Sainburg 2003; Bennett et al. 1994; Bizzi et al. 1978; Bock 1993; Brown and Cooke 1981; Shapiro et al. 2002). On the other hand, pulse-width mechanisms are substantially modified by sensory feedback arising during the course of movement (Brown and Cooke 1981, 1984, 1986).

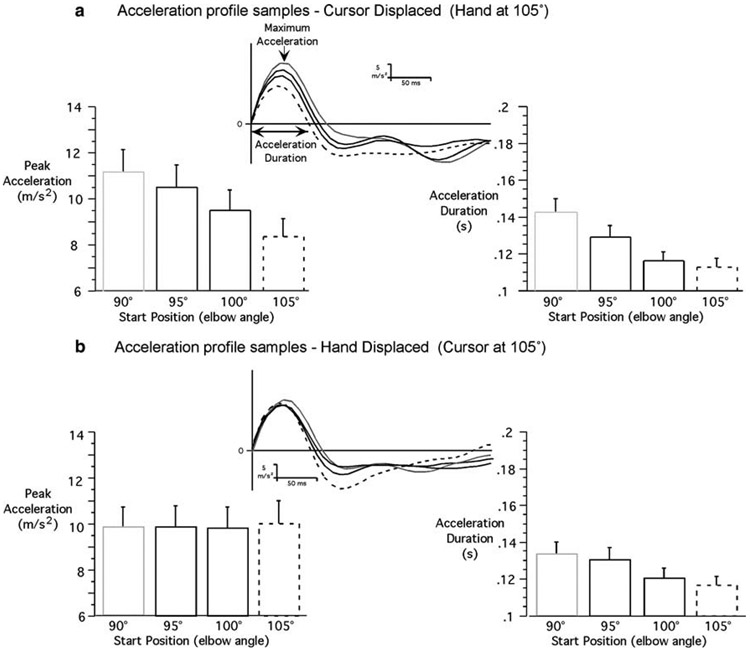
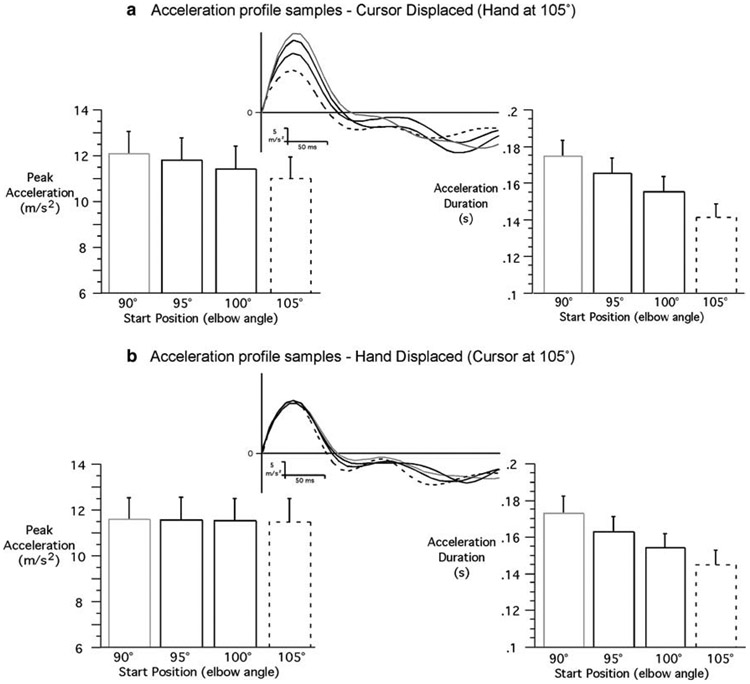
In order to better understand the differential contributions of vision and proprioception to control movement extent in the current study, we analyzed joint acceleration profiles, quantifying both acceleration peak (pulse-height) and the duration of the first acceleration pulse (pulse-width). The ANOVA revealed that there was neither main effect of starting hand location on peak acceleration (F_3,217=0.03; P = 0.99) nor interaction involving starting hand location. In contrast, there was a main effect of starting cursor location on pulse height (F_3,217=64.4; P<0.001). Figure 5 shows typical acceleration profiles that correspond to the displacement and velocity plots of Fig. 2, for the closer target. As reflected by the sample acceleration profiles when the cursor start location varied (top row), but the hand start location remained constant, both peak acceleration (pulse-height) and acceleration duration (pulse-width) varied with virtual start location (cursor position). However, when the hand location varied, but virtual start location remained constant, peak acceleration was constant. This indicates that pulse-height mechanisms varied with virtual, but not with actual start location. There was also an interaction between target distance and initial cursor location (F_3,217=11.5; P<0.001). The decomposition of the interaction revealed that the variation of peak acceleration according to initial cursor location was significantly greater for the closer target than for the further target (Figs. 5, 6). For the close targets, peak accelerations were all significantly different when the cursor was at 90, 95, 100, or 105° (respective means: 11.2, 10.5, 9.5, and 8.4 m/s²). On the other hand, for the further target, the only significant differences were: peak acceleration was greater when the cursor was at 90° (mean=12.0 m/s²) than when it was at 100 and 105° (respective means=11.3 and 10.9 m/s²); and peak acceleration was greater when the cursor was at 95° (mean=11.7 m/s²) than it was at 105°. This shows that the control of movement extent relies more on pulse-height control for short distances, and suggests that the role of pulse-width regulation increases with movement distance. Additionally, since there was no significant effect of proprioceptive information of hand position on peak acceleration, any significant effect of the actual initial hand position after peak acceleration would in fact suggest that proprioception influences movement control through feedback mechanisms.

Fig. 5.

Representative samples of acceleration profiles for short movements (target 1) and average (mean ± SE) peak tangential acceleration (left); average (mean ± SE) acceleration duration (right): a cursor displaced; b hand displaced

Fig. 6.

Representative samples of acceleration profiles for long movements (target 2) and average (mean ± SE) peak tangential acceleration (left); average (mean ± SE) acceleration duration (right): a cursor displaced; b hand displaced

In contrast to peak acceleration, acceleration duration varied with both actual (F_3,217=22.2; P<0.001) and virtual (F_3,217=43.1; P<0.001) start locations, indicating that pulse-width mechanisms vary with proprioceptive and visual hand location. There was also an interaction between initial cursor location and initial hand location (F_3,217=2.1; P<0.05). This indicated that the effect of initial cursor location on acceleration duration depended on actual hand position: the closer the hand was to the target, the less time-to-peak velocity varied with initial cursor position. The interaction also revealed that the closer the cursor was to the target, the less time-to-peak velocity varied with actual hand position. Because visual feedback was available only before movement onset, the variation of acceleration duration on the basis of visual information must have been preplanned. On the other hand, the fact that there was no significant effect of initial hand position (i.e., proprioception) on peak acceleration suggests that the variation of acceleration duration on the basis of proprioception occurred through feedback mechanisms. We also examined the ratio of acceleration duration/movement duration, which was significantly higher for the more distant target (30 vs. 26%; F_1,217=109.6; P<0.001). This indicates that less relative time was spent during the decelerative phase for the further target. This finding supports the idea that distance control relied more on the regulation of acceleration duration (pulse-width control) for the further target.

In summary, the findings described above show that similar control mechanisms were employed for the planning of the movements performed toward the closer and further targets. Only initial cursor location significantly influenced the peak acceleration (pulse-height), strongly suggesting that motor planning was based on initial visual information of hand position. Actual starting hand position did not significantly influence peak acceleration. However, actual hand position did influence time-to-peak velocity (pulse-width) and peak velocity (for the further target only). These results support the idea that proprioceptive information about actual hand position contributes only to pulse-width mechanisms through feedback mechanisms for rapid, unseen single-joint movements performed toward a visual target. The question then arises as to why this control contributes to peak velocity variations for the longer, but not the shorter movements. The answer appears to be in the differences in magnitude of both peak acceleration and acceleration duration for the longer movements. On average, peak acceleration of movements toward the further target (target 2) was 17% greater than that of target 1 movements, whereas, acceleration duration of movements toward target 2 was on average 27% greater than that of the movements toward target 1. Thus, larger accelerations were extended for longer periods, producing more substantial effects on peak velocity.

Discussion

We investigated the relative contributions of proprioception and vision to controlling the distance of rapid, single-joint reaching movements. Using a virtual reality environment, we provided a discrepancy between the actual and virtual start positions prior to reaching movements toward two visual targets. Visual feedback was used to position the hand at a start location, whereas no visual feedback was available during the movement. We asked whether subjects modified movement distance in accord with virtual or actual start locations. Movement distance was modified in accord with the virtual start location, and this modification was greatest for the closer target. Movement distance was also modified in accord with the actual start location, but to a lesser extent, and this modification was greatest for the further target. Analysis of acceleration profiles revealed that for movements to both targets, visual information about start location (cursor) determined the initial peak in tangential hand acceleration, which scaled with peak velocity and movement distance, a phenomenon termed “pulse-height” control. Instead of affecting pulse-height mechanisms, proprioceptive information determined the duration of initial acceleration, which also scaled with peak velocity and movement distance, a phenomenon termed “pulse-width” control. The effects of pulse-width variations on velocity and distance were larger for movements to the further target, because these movements entailed larger accelerations and longer durations than movements toward the closer target. As a result, proprioceptive information affected the peak velocity of only the movements toward the further target. In either case, visual information about virtual start location determined pulse-height mechanisms, while proprioceptive information influenced only pulse-width mechanisms. Previous research has suggested that these two mechanisms reflect movement planning and largely sensory-based corrective processes, respectively.

Contributions of visual and proprioceptive information to movement planning

A number of previous studies have reported differences in contributions of vision and proprioception to movement direction, but have not specifically addressed the effects of such sensory discrepancies on movement extent. Rossetti et al. (1995) used optical prisms to introduce a discrepancy between visual and proprioceptive information about hand start location, prior to movement. These authors reported movement directions that were consistent with initial position estimates closer to the actual, than the virtual, hand position. However, in this study, the discrepant condition was given as blocked repetitions toward a single target, which may have elicited adaptation to the discrepant visuo-motor conditions (Krakauer et al. 1999).

More recent studies that employed multiple targets under many sensory discrepancy conditions minimized the potential for adaptation by preventing sequentially repeated conditions. These studies revealed almost complete reliance on virtual start location (vision) to specify initial movement direction (Lateiner and Sainburg 2003; Sainburg et al. 2003; Sober and Sabes 2003). In addition, these studies analyzed the contributions of both modalities to different stages of the motor preparation process. Sober and Sabes (2003) employed a simulation of the control process, in order to quantify the contributions of actual and virtual finger positions to initial movement direction. Two stages of control were modeled: (1) specification of a movement vector, and (2) inverse kinematics transformation of that vector into a joint-based motor command. They assigned weighting constants, α_mov and α_inv at each stage of their model, respectively. These alpha values represented the contribution of vision to the start position, whereas, (1–α) was the weighting applied to proprioceptive information. The best fit with their empirical data yielded α_mov values that were greater than 0.5, and α_inv values that were less than 0.5. If one accepts their model, this suggests that visual information must have predominated for planning movement vectors, whereas, proprioception dominated the inverse kinematics stage of preparation. Most intriguing was the idea that the system could rely more heavily on one or the other modality, depending on the planning process to be performed. Regardless of the discrepancy in information, the CNS may not use a single “averaged” value, but rather appears to rely on each modality, differently, at each stage of planning. This suggests that at least two different representations of start position are independently maintained by the CNS.

The results of Sober and Sabes (2003) corroborated those that we obtained in a recent series of empirical studies (Lateiner and Sainburg 2003; Sainburg et al. 2003). In these studies, subjects performed multijoint horizontal-plane reaching, in the same virtual reality environment used here. Prior to movement onset, we changed the start location of the finger relative to the cursor (virtual position). Our results indicated that regardless of initial hand location, subjects did not alter the direction of movement. Thus, when the hand start position was displaced perpendicular to the target direction, neither the direction nor the extent of movement varied relative to that of baseline. Nevertheless, inverse dynamics analysis revealed substantial changes in elbow and shoulder muscle torque strategies that compensated changes in limb configuration (Sainburg et al. 2003). Even though subjects used the virtual start location to plan movement direction, they adjusted their dynamic strategy to the actual hand location. Therefore, our results, corroborated by those of Sober and Sabes (2003), indicate that visual information predominates in planning movement direction, whereas, proprioceptive information is used to place the planned movement vector at the actual location of the hand, and specify an appropriate joint-based strategy to accurately achieve the specified movement direction.

Differential contributions of vision and proprioception to distance specification

In contrast to the role of vision in specifying movement direction, our previous studies (Lateiner and Sainburg 2003; Sainburg et al. 2003) suggested a substantial role of proprioception in control of movement distance. Whereas, movement direction remained constant across changes in actual finger location, movement distance changed systematically with finger position. The current experiment was designed to further explore the relative contributions of vision and proprioception to control of movement distance. Previous research has indicated that two independent processes are employed for controlling the distance of rapid, single-joint movements: pulse-height and pulse-width modulation of joint torque (Brown and Cooke 1981, 1984, 1986; Ghez 1979; Ghez and Gordon 1987; Ghez and Vicario 1978; Gordon and Ghez 1984, 1987a, b; Sainburg and Schaefer 2004). These two mechanisms have been shown to reflect open- and closed-loop processes, respectively. The idea that pulse-height mechanisms reflect open-loop processes is supported by studies of load perturbations, which have indicated that appreciable changes in force do not occur at latencies less than 50 ms, roughly the time of peak acceleration in such studies (Bagesteiro and Sainburg 2003; Bennett et al. 1994; Bizzi et al. 1978; Bock 1993; Brown and Cooke 1981; Shapiro et al. 2002). In addition, a number of studies have revealed that pulse-height control mechanisms are resistant to manipulations of sensory information prior to or during rapid single-joint movements (Brown and Cooke 1981, 1984, 1986), whereas pulse-width mechanisms are directly modified by sensory information about unexpected perturbations. These studies were based on the findings that rapid single-joint movements are typically produced with triphasic EMG patterns (Day et al. 1983; Desmedt and Godaux 1979; Ghez 1979; Gordon and Ghez 1984), characterized by a first agonist burst (AG1) which corresponds to the amplitude and duration of initial acceleration. The onset time of the antagonist muscle burst (ANT) also corresponds with the duration, or cross-zero, of initial acceleration. Brown and Cooke (1981) showed that the duration of AG1 and the onset of ANT are modified by perturbations applied prior to or during movement onset. However, the amplitude of AG1 tends to be resistant to such peripheral influences (Brown and Cooke 1981). These studies supported the idea that pulse-height control reflects open-loop pre-programming processes, whereas, pulse-width control is substantially influenced by closed-loop, feedback-mediated processes.

In the current study, movement distance varied with changes in cursor start location for both targets. These changes were reflected in pulse-height scaling of peak acceleration profiles, reflecting the role of feedforward processes in distance control. Even more revealing was the fact that when initial hand location changed, but cursor location did not, no pulse-height modulation occurred. Therefore, we conclude that proprioceptive information about initial hand location had little influence on the planning of movement distance. The reliance on visual information about start location in pulse-height modulation of movement distance substantially extends our previous findings, as well as those of other authors.

In contrast to pulse-height mechanisms, changes in actual hand location produced substantial variations in pulse-width modulation of acceleration duration. As discussed above, this mechanism has been attributed to feedback-mediated control of movement distance. Such modulation of acceleration duration had little effect on velocity or distance of the movements to the closer target, but substantial effects on both speed and distance of the movements to the more distant target. This target-dependent effect was attributable to the higher accelerations and longer durations of the movements to the further target. Our findings indicate that proprioceptive information was employed to modulate movement distance through pulse-width mechanisms. In a recent study, Sarlegna et al. (2003) reported that when a visuo–proprioceptive mismatch was triggered near movement onset, visual feedback of hand position contributed very little to the online control of movement amplitude. Therefore, our current study supports the suggestion of Sarlegna et al. (2003) that movement distance is mainly controlled through feedforward and proprioceptive feedback control.

Our findings indicated that proprioceptive information had no affect on pulse-height mechanisms, but substantial effects on pulse-width modulation of acceleration duration. We now suggest that this control might be implemented through an online comparison of current with intended final limb position. Because the intended limb position must be determined during the planning process, this might explain why pulse-width mechanisms varied with visual, in addition to proprioceptive information. That is, the planning of movement extent, as reflected by pulse-height mechanisms, was completely dependent on visual information. This interpretation is consistent with a previous study from our laboratory, indicating differential reliance of pulse-height and pulse-width mechanisms for dominant arm and nondominant arm reaching (Sainburg and Schaefer 2004). That study was designed to test interlimb asymmetries in controlling movement extent. Subjects made unseen, rapid single-joint elbow extension movements, while the arm was supported on a horizontal, frictionless, air-jet system. Four targets of 10, 20, 35, and 45° excursions were randomly presented over the course of 200 trials. For both arms, peak tangential hand velocity scaled linearly with movement distance. There was no significant difference between either peak velocities or movement accuracies for the two arms. However, the mechanisms responsible for achieving these velocities and extents were quite distinct for each arm. For the dominant arm, peak tangential finger acceleration varied systematically with movement distance. In contrast, nondominant arm peak tangential acceleration varied little across targets, and as such, was a poor predictor of movement distance. Instead, the velocities of the nondominant arm were determined primarily by variation in the duration of the initial acceleration impulse, which corresponds to the time of peak velocity. These different strategies reflected pulse-height control and pulse-width control mechanisms. These findings indicated that the dominant arm system controls movement extent largely through planning mechanisms that specify pulse-height control, whereas the nondominant system does largely through feedback-mediated pulse-width control. Other studies from our laboratory have indicated nondominant arm specialization for controlling limb position (Bagesteiro and Sainburg 2005; Sainburg 2002; Sainburg and Wang 2002). Because of the specialization of the nondominant arm for pulse-width control, we now propose that pulse-width mechanisms reflect online modification of torque duration through proprioceptive feedback, in accord with the intended final limb position.