Evidence for a dynamic-dominance hypothesis of handedness

Abstract

Handedness is a prominent behavioral phenomenon that emerges from asymmetrical neural organization of human motor systems. However, the aspects of motor performance that correspond to handedness remain largely undetermined. A recent study examining interlimb differences in coordination of reaching demonstrated dominant arm advantages in controlling limb segment inertial dynamics (Sainburg and Kalakanis 2000). Based on these findings, I now propose the dynamic-dominance hypothesis, which states that the essential factor that distinguishes dominant from nondominant arm performance is the facility governing the control of limb dynamics. The purpose of this study is to test two predictions of this hypothesis: 1) adaptation to novel intersegmental dynamics, requiring the development of new dynamic transforms, should be more effective for the dominant arm; 2) there should be no difference in adapting to visuomotor rotations performed with the dominant as compared with the nondominant arm. The latter prediction is based on the idea that visual information about target position is translated into an internal reference frame prior to transformation of the movement plan into dynamic properties, which reflect the forces required to produce movement. To test these predictions, dominant arm adaptation is compared to nondominant arm adaptation during exposure to novel inertial loads and to novel visuomotor rotations. The results indicate substantial interlimb differences in adaptation to novel inertial dynamics, but equivalent adaptation to novel visuomotor rotations. Inverse dynamic analysis revealed better coordination of dominant arm muscle torques across both shoulder and elbow joints, as compared with nondominant arm muscle torques. As a result, dominant arm movements were produced with a fraction of the mean squared muscle torque computed for nondominant arm movements made at similar speeds. These results support the dynamic-dominance hypothesis, indicating that interlimb asymmetries in control arise downstream to visuomotor transformations, when dynamic variables that correspond to the forces required for motion are specified.

Introduction

Since Liepmann first proposed a left-hemisphere dominance for motor planning in right-handers (Liepmann 1905; Geschwind 1975; Taylor and Heilman 1980), a substantial body of evidence has supported the hypothesis that the cerebral hemisphere contralateral to the dominant arm (hereafter referred to as the “dominant hemisphere”) plays a special role in the movements of both arms. A number of studies have indicated that dominant hemisphere motor and/or premotor areas are more active than their nondominant counterparts during ipsilateral (Kim et al. 1993; Kawashima et al. 1997), contralateral (Kim et al. 1993; Dassonville et al. 1997; Taniguchi et al. 1998), and bilateral arm movements (Viviani et al. 1998). Such findings tend to be more consistent in right-handed subjects than in left-handed subjects (Kim et al. 1993; Viviani et al. 1998). In addition, studies of patients with unilateral brain damage have revealed movement deficits in the nondominant arm in response to dominant hemisphere lesions, but not in dominant arm movements in response to nondominant hemisphere lesions (Haaland et al. 1977; Haaland and Delaney 1981; Haaland and Harrington 1989b, 1994, 1996). These findings suggest that the dominant hemisphere contains essential circuitry for the control of both arms. Winstein and Pohl (1995) provided evidence that the nondominant hemisphere also plays a specialized role in the control of dominant arm movements. They found that in patients with unilateral brain damage, nondominant hemisphere lesions caused prolongation of the decelerative phase of reciprocal movements “made as quickly as possible” with the dominant arm. By contrast, dominant hemisphere lesions caused prolongation of the accelerative phase of such movements made with the nondominant arm. These results support the notion that each hemisphere supplies a unique contribution to the control of arm movements. However, the aspects of motor performance that correspond to these differences in neural organization, and thus account for handedness, are as yet poorly understood.

To determine the variables that constitute handedness, a number of investigators have focused on performance measures thought to differentiate “open-loop” mechanisms, which by definition are unaffected by sensory feedback, from “closed-loop” mechanisms, which by definition are mediated by sensory feedback. This division was inspired by the ideas of Woodworth (1899) and Fitts (Fitts 1966; Fitts and Radford 1966; Fitts 1992) and is supported by studies contrasting rapid aiming movements made under varying precision requirements (Keele and Posner 1968; Schmidt 1969; Schmidt and Russell 1972; Wallace and Newell 1983). However, attempts to differentiate the effects of sensory feedback on dominant and nondominant arm performance have yielded conflicting results. Whereas some reports have indicated a right arm advantage for visually based error correction (Flowers 1975; Todor and Cisneros 1985; Elliott et al. 1994, 1995; Roy et al. 1994), others have not supported such an effect (Roy and Elliott 1986; Carson et al. 1990, 1992). Attempts to differentiate dominant and nondominant control according to open-loop processes have also yielded conflicting results. Whereas a number of authors proposed a right arm/left hemisphere advantage for movement planning, initiation, or sequencing (Annett et al. 1979; Todor and Kyprie 1980; Todor and Smiley-Oyen 1987; Carson et al. 1995), other authors have suggested a left arm/right hemisphere advantage for movement preparation based on left hand advantages in reaction time tasks (Carson et al. 1990; Elliott et al. 1993). The equivocal nature of these findings suggests that the mechanisms underlying handedness are not well accounted for by open-loop/closed-loop distinctions (Carson 1993). This leaves open the question of how else one might understand the neural basis for handedness.

Hierarchical models of motor control describe serially organized processes that may be relevant in distinguishing interlimb differences in coordination. Such models evolved in part from considerations of robotic systems (Hollerbach 1990; Imamizu et al. 1998; Wolpert and Ghahramani 2000b) and have gained support both from behavioral and physiological studies of biological motion and its control. An emerging view from this work is that at least three serially organized processes are associated with visually guided reaching behavior (Rosenbaum 1980; Kawato et al. 1988; Ghez et al. 1989; Kawato et al. 1990; Ghez et al. 1991; Jordan and Rumelhart 1992; Imamizu et al. 1998; Kawato 1999; Krakauer et al. 1999; Krakauer et al. 2000; Rosenbaum and Chaiken 2001): (1) visuomotor transformations, where visual information about target position is translated into an internal reference frame, such as joint or segment angles; (2) trajectory specification, where a time series of body positions is specified; and (3) dynamic transformations, where the trajectory plan is transformed into dynamic properties reflecting the forces required to complete the motion.

Experimental evidence indicates that these processes are subserved by different neural substrates. Numerous studies have examined the mechanisms underlying trajectory specification (Rosenbaum 1980; Abend et al. 1982; Bizzi et al. 1982, 1984; Hasan 1986; Bizzi 1987; Massone and Bizzi 1989; Favilla et al. 1990; Kawato et al. 1990; Wolpert et al. 1995a; Gottlieb et al. 1996; Bhushan and Shadmehr 1999; Rosenbaum and Chaiken 2001), many of which implicate optimization (Flash and Hogan 1985; Uno et al. 1989; Viviani and Flash 1995; Nakano et al. 1999) or “satisficing” principles (Rosenbaum and Chaiken 2001) to account for trajectory selection. More recently, studies examining adaptation to novel task conditions have also indicated that distinct neural processes underlie visuomotor and dynamic transformations. Adaptation to either distortions in visual feedback, or to forces applied to the arm during movement is mediated through the development of neural representations of those experimental conditions. For example, when forces are first applied to the hand during reaching movements, subjects’ hand paths curve in the direction of those forces and gradually become straighter with practice. Following practice, removal of the forces leads to oppositely directed hand-path curvatures, termed “aftereffects,” that reflect neuromuscular compensations for the previously applied forces. (Shadmehr and Mussa-Ivaldi 1994; Sainburg et al. 1995; Gandolfo et al. 1996; Shadmehr and Brashers-Krug 1997; Sainburg et al. 1999; Scheidt et al. 2000; Shadmehr and Moussavi 2000) Aftereffects have also been demonstrated following adaptation to distortion visual feedback displays (Baily 1972; Ghilardi et al. 1995; Wolpert et al. 1995a; Goodbody and Wolpert 1998; Imamizu et al. 1998; Ghilardi et al. 2000). Shadmehr and colleagues (Shadmehr and Mussa-Ivaldi 1994; Brashers-Krug et al. 1996; Shadmehr and Brashers-Krug 1997; Shadmehr and Holcomb 1997) showed that adaptation to novel force fields occurs through a two-stage mechanism: motor memories are first stored in a short-term cache, then over the course of several hours are transferred to more stable storage that can be maintained indefinitely. When subjects are exposed to an equal and opposite force field during the first stage of the process, the memory of the original force field is lost, an effect termed retrograde interference. This finding indicates that initial adaptation to different force fields competes for the same working memory resources. Using a similar paradigm to study retrograde interference, Krakauer et al. (2000) showed that adaptation to inertial loads does not interfere with adaptation to visuomotor rotations. This result, which suggests independent neural mechanisms underlie adaptation to shifted force fields on the one hand and visuomotor mappings on the other, is consistent with neural imaging studies, which likewise indicate that visuomotor transformations (Ghilardi et al. 2000) and force-related transformations (Shadmehr and Holcomb 1997) are reflected in different brain regions. Taken together, the evidence summarized here supports three distinct stages in the control of visually directed reaching.

Recognizing that adaptation to new dynamic conditions may deploy mechanisms distinct from those associated with visuomotor mapping or trajectory specification may provide a new account of what distinguishes the dominant hand from its less dominant counterpart. According to this new hypothesis, the factor that differentiates the dominant arm from the nondominant arm is the facility with which the effects of limb segment dynamics are controlled. I now refer to this as the dynamic dominance hypothesis. Previous findings provide preliminary support for this hypothesis. Building on an earlier finding that control over the effects of limb segment inertial interactions (interaction torques) is dependent on the development of internal models of those torques (Sainburg et al. 1995; Sainburg et al. 1999), Sainburg and Kalakanis (2000) subsequently reported a dominant arm advantage in controlling limb segment inertial interactions. Using inverse dynamic analysis, we showed that the dominant arm torque strategy exploits interaction torques to a greater extent than does the nondominant arm torque strategy. A finding that figured heavily in this conclusion was that hand-path curvatures for the dominant arm did not vary with the magnitude of interaction torques, whereas the nondominant hand paths appeared to be enslaved to these interactions. Such interlimb differences in coordination suggest a dominant arm specialization for controlling the effects of limb dynamics.

The purpose of this study is to test two major predictions of the dynamic-dominance hypothesis. First, adaptation to novel intersegmental dynamics, which requires the development of new dynamic transforms, should be more effective for the dominant arm than for the nondominant arm. To test this prediction, interlimb differences in adaptation to a novel inertial load are examined by attaching a 1-kg mass eccentric to the forearm axis. Second, there should be no difference in the ease with which visuomotor transformations are learned in tasks performed with the dominant arm, as compared with the nondominant arm. This prediction follows from the idea that it is in the third stage of motor planning – the specification of dynamics – that handedness emerges. This prediction is tested by examining interlimb differences in adaptation to a 30° rotation in the visual display of finger position during reaching. The results indicate that adaptation to the visual rotation condition was equivalent for dominant and nondominant arm movements, and that adaptation to novel inertial dynamics was more complete for the dominant arm than for the nondominant arm.

Methods

Subjects

Subjects were six neurologically intact right-handed adults (3 female, 3 male), aged from 18 to 36 years old. Only right-handers were recruited because left-handers do not represent a behaviorally (Oldfield 1971) or neurologically (Kim et al. 1993) homogenous population with regard to reaching coordination. Handedness was determined using the ten-item version of the Edinburgh inventory (Oldfield 1971). To insure that subjects exhibited right-handedness, only subjects scoring a laterality quotient of 100 were selected. Subjects were recruited from the university community and were paid for their participation. Informed consent was solicited prior to participation, which was approved by the Pennsylvania State University’s Institutional Review Board.

Experimental setup

Figure 1 illustrates the general experimental setup. Subjects sat facing a computer screen with either the right or the left arm supported over a horizontal table top, positioned just below shoulder height (adjusted to subjects’ comfort) by a frictionless air jet system. A start circle, target, and cursor representing finger position were projected on a horizontal back-projection screen positioned above the arm. A mirror, positioned parallel to and below this screen, reflected the visual display, so as to give the illusion that the display was in the same horizontal plane as the finger tip. Calibration of the display assured that this projection was veridical. All joints distal to the elbow were immobilized using an adjustable brace. Position and orientation of each limb segment was sampled using the Flock of Birds (Ascension-Technology) magnetic six-degree-of-freedom (6-DOF) movement recording system. The maximum three-dimensional position error that we measured during calibration of this system was 2.1 mm³. A single 6-DOF sensor was attached to each arm segment by a plastic splint. The digital data (103 Hz) from each sensor was transmitted to a Macintosh computer through separate serial ports and was stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC (REAL Software), C, and Igor Pro (Wavemetric).

Fig. 1.

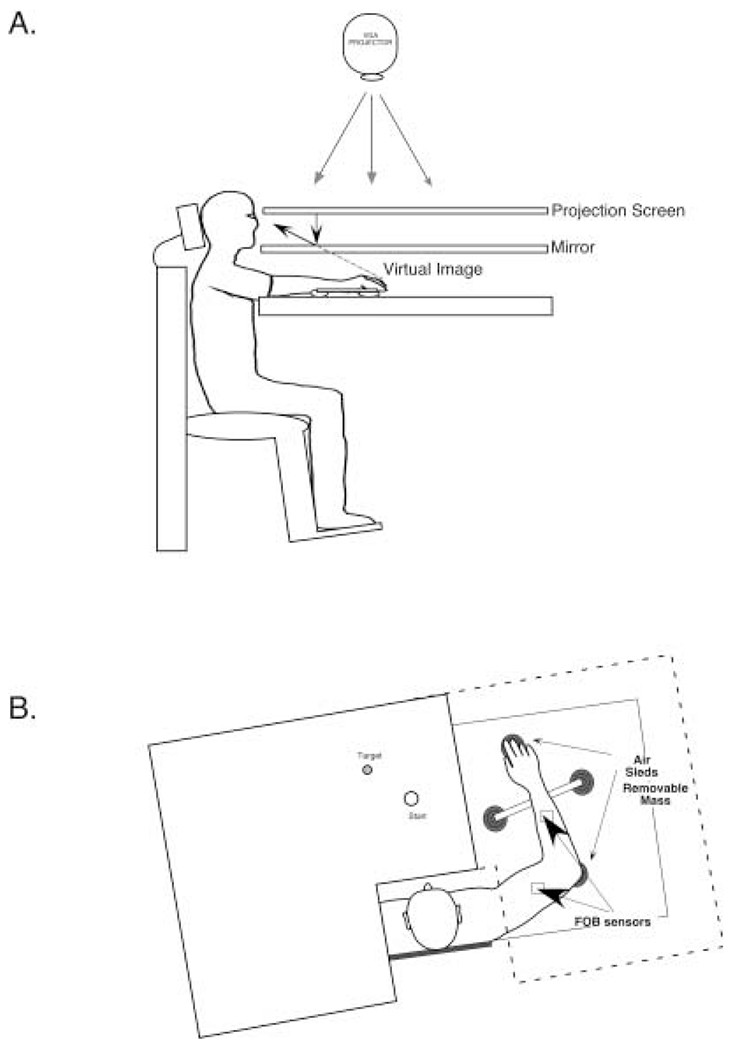
A Methods side view: subjects were seated in a dental-type chair with the arm supported by an airjet system that removed the effects of friction on arm movement. Targets and the cursor representing finger position were back-projected on a screen placed above the arm. A mirror placed below this screen reflected the image, such that the projection was perceived in the plane of the arm. B Top view of the system described above. The positions of the Flock of Birds sensors and the placement of the removable mass are shown

The position of the following three bony landmarks was digitized using a stylus that was rigidly attached to a Flock of Birds sensor: 1) index finger tip, 2) the lateral epicondyle of the humerus, 3) the acromion, directly posterior to the acromioߝclavicular joint. A single 6-DOF sensor was attached to a rigid plastic forearm/hand splint and to a rigid plastic upper arm cuff. The position of the boney landmarks relative to the sensors attached to each arm segment thus remained constant throughout the experimental session. As sensor data was received from the Flock of Birds, the position of these landmarks was computed by our custom software. The two-dimensional position of the index finger tip was used to project a cursor onto the screen. This position was updated at 103 Hz as data was received by the computer’s serial port. In order to examine the accuracy of this projection, the arm was viewed, along with the projected cursor, by illuminating the underside of the mirror (upon which the cursor was reflected). As predicted, the cursor remained centered on the index fingernail for all positions sampled on the workspace. Screen redrawing occurred fast enough to maintain the cursor centered on the fingertip during arm movements. During the experiment, the light was turned off, such that subjects were unable to view their arms.

Experimental task

Throughout the experiment, the index finger position was indicated by a screen cursor that was projected in real time, as described above. Prior to movement, one of eight targets (15-cm long) arranged radially around the start position was displayed. Targets were presented in a pseudorandom sequence. Subjects were to bring the finger to a complete rest within the starting circle for 0.3 s. They were instructed to move the finger to the target using a single, uncorrected rapid motion in response to an audiovisual “go” signal. At the end of each trial, knowledge of results was provided in the form of a display of the hand path on the computer screen. Audiovisual feedback and points were awarded for accuracy for movements performed within a specified time window of 400–600 msec. Final position errors of less than 1 cm were awarded 10 points, while errors between 1 cm and 2 cm were awarded 3 points, and errors between 2 cm and 3 cm were awarded 1 point. Points were displayed following each trial.

Each subject performed two experimental sessions separated by at least one week. In one session, subjects were exposed to a rotated visual display, and in the other a 1 kg mass, attached eccentric to the forearm axis. The order of these sessions was alternated between subjects. The inertial and visual manipulations are described below.

Inertial modifications

In order to study adaptations to novel inertial dynamics, a 1 kg mass was placed eccentric to the long axis of the forearm (Sainburg et al. 1999). This manipulation alters the center of mass of the forearm/load system, which substantially changes the inertia of the limb system, and thereby alters the mechanical interactions between the segments. In previous studies (Krakauer et al. 1999; Sainburg et al. 1999), subjects displayed specific adaptation to this manipulation, as reflected by aftereffects, following removal or a change in position of the load.

Visual display modifications

In order to examine adaptation to novel visual–motor transformations, the position of the cursor, indicating index finger location, was rotated 30° relative to the start circle. This manipulation has previously been performed for right arm movements (Krakauer et al. 1999). This 30° rotation was chosen because Krakauer and colleagues (1999) previously showed, for dominant arm movements, that adaptation to this manipulation is independent of adaptation to the inertial manipulation described above.

Experimental sessions

Within each session, each subject performed two blocks of trials, with the right arm and left arm, respectively. The order of these blocks was alternated between subjects. Within each block of trials, three sequences comprised of 192 movements were performed: 1) pre-exposure sequence to adapt to the task and establish baseline performance measures; 2) exposure sequence during exposure to either the visual display rotation or to the inertial load; 3) post-exposure sequence performed without the visual or inertial manipulation. The third sequence was done to assess aftereffects of learning. Each 192-trial sequence was comprised of 24 cycles of movements. A single cycle was determined as a full series of movements to all eight of the targets. Table 1 shows the sequence of sessions for a single subject.

Table 1.

Inertial adaptation session
Right arm or left arm
Pre-exposure	Inertial load exposure	Post-exposure
(24 cycles, 192 trials)	(24 cycles, 192 trials)	(24 cycles, 192 trials)
Rest: 45 min
Alternate arm
Pre-exposure	Inertial load exposure	Post-exposure
(24 cycles, 192 trials)	(24 cycles, 192 trials)	(24 cycles, 192 trials)
Visual rotation adaptation session
Right arm or left arm
Pre-exposure	Visual rotation exposure	Post-exposure
(24 cycles, 192 trials)	(24 cycles, 192 trials)	(24 cycles, 192 trials)
Rest: 45 min
Alternate arm
Pre-exposure	Visual rotation exposure	Post-exposure
(24 cycles, 192 trials)	(24 cycles, 192 trials)	(24 cycles, 192 trials)

Kinematic data

The three-dimensional position of the index finger, elbow, and shoulder were calculated from sensor position and orientation data. Elbow and shoulder angles were then calculated from these data. All kinematic data was low-pass filtered at 12 Hz (third-order no-lag Butterworth) and differentiated to yield angular velocity and acceleration values.

Each trial usually started with the hand at zero velocity, but small oscillations of the hand sometimes occurred within the start circle. In this case, the onset of movement was defined by the last minimum (below 5% maximum tangential velocity) prior to the maximum in the index finger’s tangential velocity profile. Movement termination was defined as the first minimum (below 5% maximum tangential hand velocity) following the peak in tangential hand velocity.

Measures of task performance

Two measures of task performance were calculated from hand trajectory data: hand-path deviation from linearity and final position error. Deviation from linearity was assessed as the minor axis divided by the major axis of the hand path. The major axis was defined as the largest distance between any two points in the path, while the minor axis was defined as the largest distance, perpendicular to the major axis, between any two points in the path (Sainburg et al. 1993). This measure reflects interjoint coordination, as differences in linearity necessarily result from differences in coordination between the segments during movement. Task accuracy was assessed as final position error, which was calculated as the two dimensional distance between the index finger at movement termination and the location of the center of the target. Assessment of task adaptation during the exposure sequences was determined by two measures: 1) the change from baseline of each performance measure, and 2) the first “adapted” cycle for each performance measure.

Inverse dynamic analysis

The arm was modeled as a two-segment inverted pendulum, with the proximal end (shoulder point) free to move in the horizontal plane. Thus, an inverse dynamic analysis yields net torque values for each joint (shoulder and elbow), as well as linear force components (x and y) applied to the shoulder point. In order to separately analyze the effects of intersegmental forces and muscle forces on limb motion, the terms of the equations of motion at each joint were partitioned into three main components: interaction torque, muscle torque, and net torque (Sainburg et al. 1995; Sainburg et al. 1999). At each joint, interaction torque represents the rotational effect of the forces due to the rotational and linear motion of the other segment. The muscle torque primarily represents the rotational effect of muscle forces acting on the segment. Finally, the net torque is directly proportional to joint acceleration, inversely proportional to limb inertia, and equal to the combined muscle and interaction torques.

It is important to note that the computed muscle joint torque cannot be considered a simple proxy for the neural activation of the muscles acting at that joint. Muscle joint torque does not distinguish muscle forces that counter one another during co-contraction, and it also includes the passive effects of soft tissue deformation. Additionally, the force generated by muscle to a given neural input signal is dependent on muscle length, velocity of muscle length change, and recent activation history (Abbott and Wilkie 1953; Wilkie 1956; Zajac 1989).

Torques were computed and analyzed for the shoulder and elbow joints as detailed in the equations below. The inertia and mass of the forearm support are 0.0247 kg m² and 0.58 kg, respectively. Limb segment inertia, center of mass, and mass are computed from regression equations using the subjects’ body mass and measured limb segment lengths (Winter 1990).

Contributions of muscle torque to net torque

The contributions of muscle torques to net torque at each joint were partitioned using the following method. Intervals during which the muscle torque acted in the same direction as the net torque were considered to contribute to a positive muscle torque impulse. Intervals during which the muscle torque acted in the opposite direction to net torque were considered to contribute to a negative muscle torque impulse. All positive and negative integrals were summed to yield a single total muscle torque impulse for the entire movement (see Sainburg and Kalakanis 2000).

Data analysis and statistics

Each experimental session consisted of three blocks of 192 trials (24 cycles), a pre-exposure sequence, an exposure sequence, and a post-exposure sequence. In order to assess task adaptation under each exposure sequence (rotation or mass), each subject’s performance was quantified in the following way: first, for each hand, baseline performance was quantified as the mean linearity or final position error measure for the last eight cycles from the pre-adaptation sequence. Second, to control for differences in baseline performance between arms, baseline measures were subtracted from all individual measures to yield “change from baseline” values. The last eight cycles of each adaptation sequence were considered to represent final task adaptation. Thus, for each subject, a single mean adaptation value was calculated for each task performance measure, deviation from linearity, and final position error.

Because the purpose of this study was to compare performance between left and right arms, pairwise statistical analyses were conducted on all measures of task performance, including hand-path linearity, final position error, and torque impulse. Bonferroni/Dunn post hoc analyses were used to test for significant differences between left and right arm performance measures. In order to examine differences in the time course of adaptation between arms, measures from all the individual cycles of the exposure sequence were compared to final adaptation measures. The first cycle for which the left and right arm performance was not significantly different from the measure of final adaptation was considered the “first adapted cycle.” In order to examine whether target direction affected inter-limb differences in task accuracy, we used a 2×8 ANOVA, using the hand and target as independent variables.

Results

Mass adaptation

When subjects were first exposed to the eccentric inertial load, they showed systematic errors in hand-path curvature and final position. Figure 2A shows two typical hand paths to each target for movements made during the mass adaptation session (subject 1). Paths shown were extracted from the three trial sequences: pre-exposure, mass-exposure, and post-exposure. The last two trials of the pre-exposure sequence, representing baseline performance, are shown in gray (dashed lines) underlying all other paths (see figure legend for details). The trials representing baseline performance are fairly straight and accurate for both hands. When first exposed to the eccentrically positioned mass (left column), both dominant and nondominant hand-paths showed similar direction-dependent increases in movement curvature. These hand-path deviations are predicted from the altered dynamics imposed by the mass and have previously been described in detail (Sainburg et al. 1999). After practice with the mass (middle column), paths became straighter and more accurate. However, the dominant hand paths became much more similar to the baseline than the nondominant paths. When the mass was removed (right column), the hand-paths for both arms showed curvatures that mirrored those displayed when the mass was first introduced. These curvatures reflect “aftereffects” of learning and represent neuromuscular adaptations to the inertial changes introduced by the mass (Sainburg et al. 1999). Similar aftereffects have been described following adaptation to a variety of forces (Lackner and Dizio 1994; Shadmehr and Mussa-Ivaldi 1994; Shadmehr and Brashers-Krug 1997; Krakauer et al. 1999; Sainburg et al. 1999).

Fig. 2.

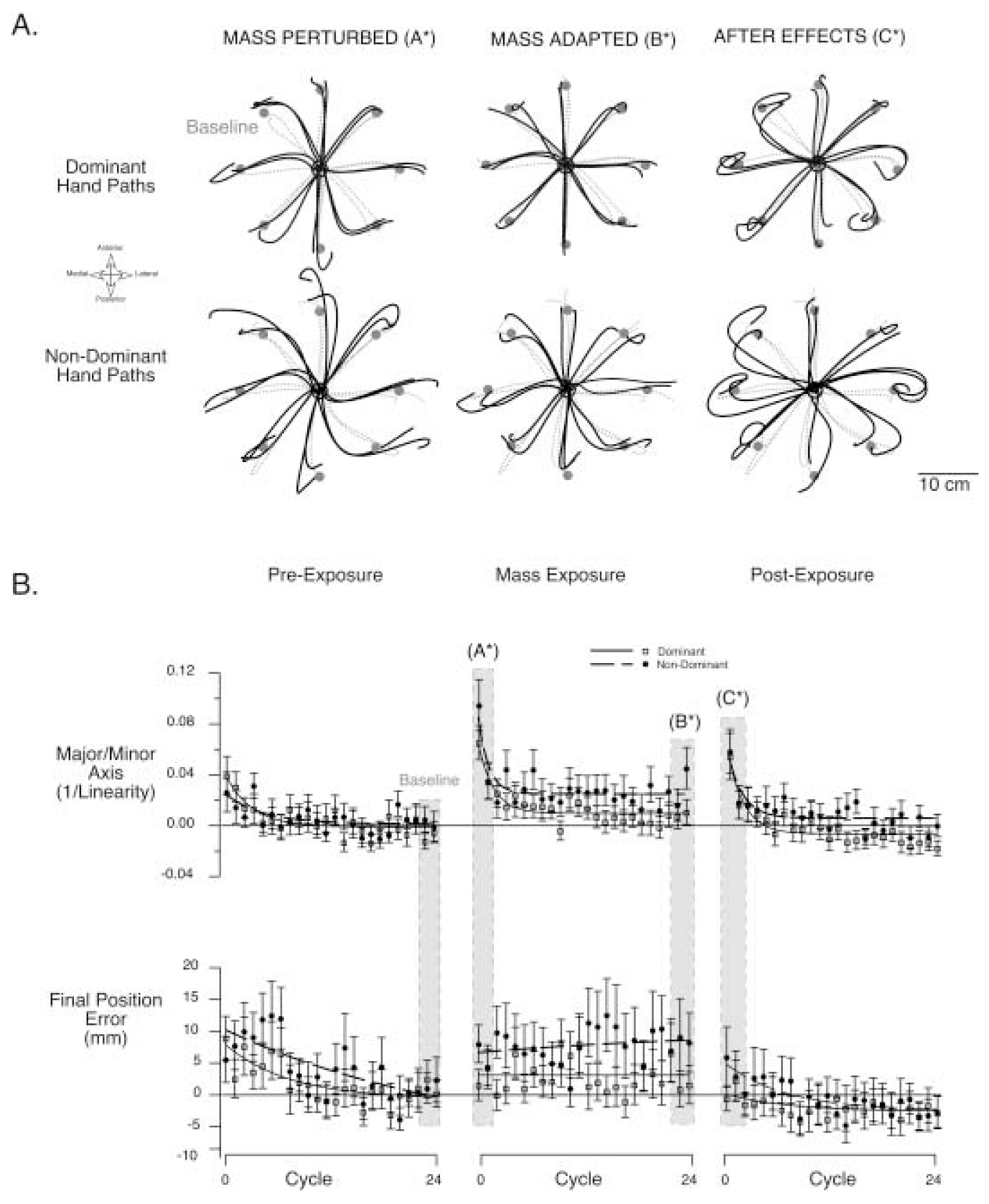
A Representative hand paths from subject 1 from all three experimental sequences are shown. The last two trials from the pre-exposure sequence are shown in gray (dashed lines), underlying all other trials. The first trials from the mass-exposure session (mass-perturbed, left column), the last two trials from the same session (mass-adapted, center column), and the first two trials from the post-exposure session (aftereffects, right column) are displayed. Dominant paths are shown above, whereas nondominant hand paths are shown below. B Mean performance measures, hand-path linearity and final position error, are averaged across all subjects and shown for individual cycles of movement. Baseline performance, measured for each subject as the average of the last eight cycles from the pre-exposure sequence, has been subtracted from each value prior to computing the average across subjects. Thus, the performance measures shown represent a change from baseline performance, and can be either positive or negative. Each cycle represents the average of a single movement to each of eight targets across all subjects (mean ± SE). The time course of each experimental sequence, pre-exposure, mass-exposure, and post-exposure, is shown. Vertically oriented gray bars mark the cycles for which the trials in Fig. 2A were extracted. Data have been fit to exponential functions, using the “CurveFit” function in Igor Pro (Wavemetrics)

Subjects showed a similar time course of adaptation to the altered mass condition with both dominant and nondominant arms. Figure 2B shows the time course of performance, measured as linearity (major/minor axis) and final position error, for the three sequences of trials: pre-exposure, mass-exposure, and post-exposure. For each point, the mean value across a cycle of movements (eight target directions) is averaged across all six subjects for dominant (black) and nondominant (blue) arms separately. Because baseline performance for dominant and nondominant arms is not equivalent (Sainburg and Kalakanis 2000), baseline performance (average of the last 8 cycles for pre-adaptation sequence) was subtracted from the values shown (see Methods). Thus, the ordinate of Fig. 2B represents “change from baseline” values. Adaptation is reflected as a return toward baseline in linearity and end error measures (0 value on ordinate axis). The change in performance measured over the course of 24 cycles (192 trials) is initially large and becomes asymptotic as performance approaches baseline. This is consistent with previous studies of such adaptation (Krakauer et al. 1999; Sainburg et al. 1999).

During the first pre-adaptation sequence of trials, progressive improvement in performance reflects adaptation to the task. During the first few cycles of the mass-exposure sequence, subjects showed large increases in curvature that were accompanied by slight increases in final position error. Over repetitive trials, both left and right hand paths became progressively more linear. The time course of this adaptation was measured by determining the first adapted cycle, the first cycle that was statistically indistinguishable from adapted performance (last eight cycles of exposure sequence, see Methods). The first adapted cycle for the left and right hands were the third (Bonferroni–Dunn: p=0.786) and fourth cycles (Bonferroni–Dunn: p=0.183), respectively. The slightly increased time for adaptation for the right arm is associated with substantially larger improvements in performance. Dominant arm performance became substantially more similar to baseline than did nondominant performance during the course of adaptation (interlimb comparison of mass adapted trials, Bonferroni–Dunn: p=0.003).

The final position error was increased for both arms at the initiation of the mass-exposure sequence, as compared with baseline (Bonferroni–Dunn: p<0.001). The change from baseline for the left arm is approximately double that of the right arm, and these differences are sustained throughout the adaptation sequence (comparison of mass-adapted trials, Bonferroni–Dunn: p=0.006). The lack of improvement in final position error with performance was attributable to the design of the task: because subjects received maximum points for errors under 1 cm, there was no incentive to improve performance beyond this range. The average error for each hand remained close to or within 1 cm throughout the adaptation session. Furthermore, the greater accuracy of right arm movements was not dependent on direction, as no interaction occurred between arm (left, right) and target for final position error (2×8 ANOVA: p=0.160). As indicated by the third column of Fig. 2B, when the mass was removed, both the dominant and nondominant arms showed decrements in performance that reflected after-effects from adaptation.

In summary, both arms showed progressive adaptation to the altered inertial condition over the 24 cycles of adaptation (192 trials). This adaptation was evidenced as a return of hand-path linearity close to baseline, and by predictable aftereffects when the mass was removed (Fig. 2A, right column). While the time course of adaptation was similar for both arms, the dominant arm showed more complete adaptation, as evidenced by adapted performance that was closer to baseline than that of the nondominant arm. Final position error remained close to criterion for the task, did not show progressive improvement, and was substantially closer to baseline for the dominant arm. The specificity of adaptation to the altered mass condition was demonstrated by aftereffects that mirrored the curvatures demonstrated during initial exposure to the mass. These types of aftereffects have been shown to result from specific adaptations to the changes in movement-dependent forces associated with the altered mass condition (Sainburg et al. 1999). The dominant arm showed substantial advantages for adaptation to an altered inertial load.

Visual–motor adaptation

Figure 3 shows representative handpaths and measures of linearity and final position error across all cycles of the three sequences of trials. Baseline performance reflects fairly straight and accurate paths for both hands (gray dashed lines). As indicated by the hand paths in Fig. 3A, when subjects were first introduced to the rotated visual display, they showed systematic errors in hand-path curvature and final position (left column). However, with practice, these errors are diminished and performance becomes very similar to baseline for both dominant and nondominant arm movements (center column). When rotation of the display was removed (right column), the hand paths for both arms showed curvatures that mirrored those displayed when the rotation was first introduced. These aftereffects represent visual–motor adaptations to the rotated condition and have been demonstrated in a number of previous reports (Ghilardi et al. 1995; Imamizu et al. 1995; Ghahramani et al. 1996; Ghahramani and Wolpert 1997; Goodbody and Wolpert 1998; Ghilardi et al. 2000; Krakauer et al. 2000; Rosenbaum and Chaiken 2001).

Fig. 3.

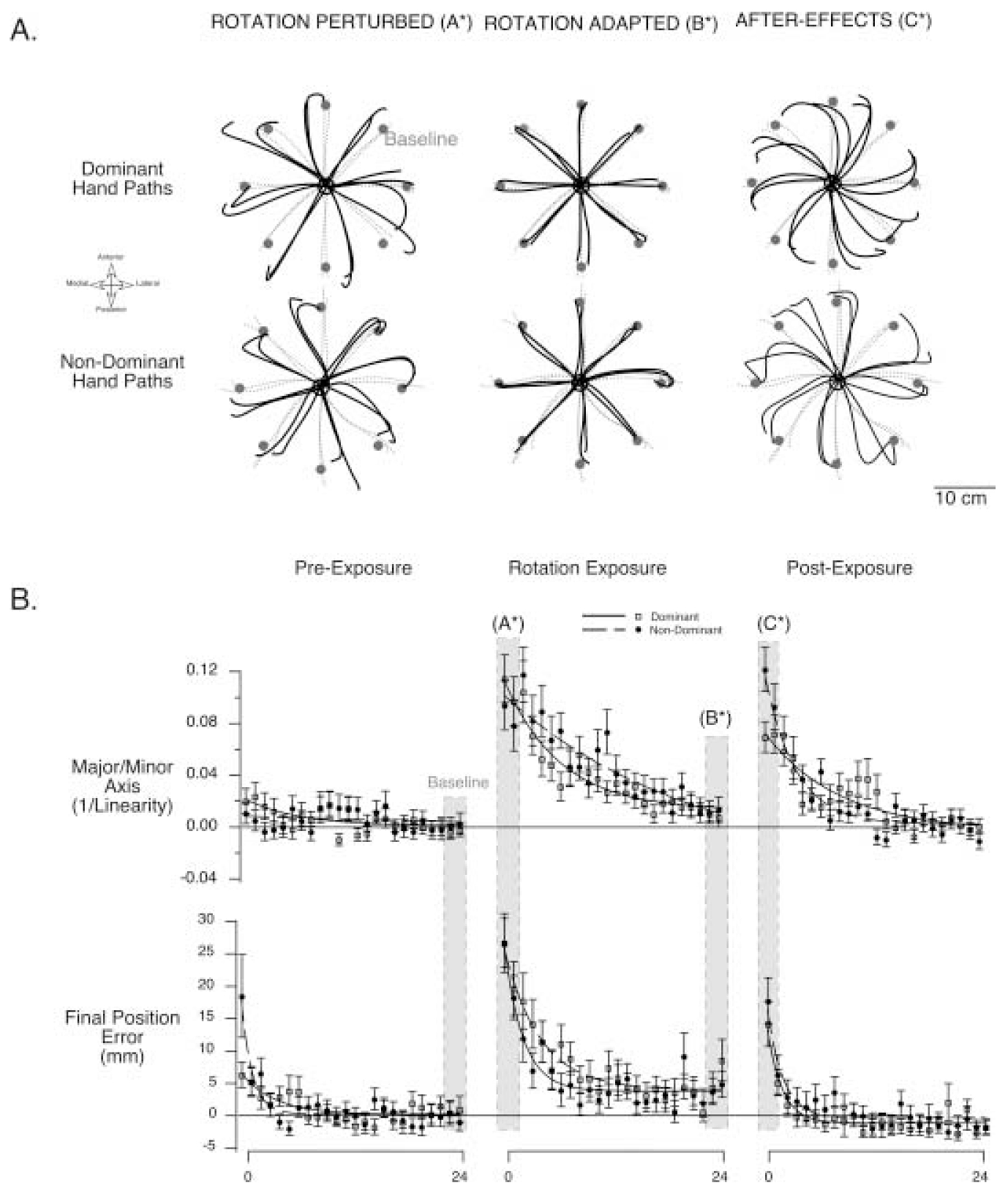
A Representative hand paths from subject 1 from all three experimental sequences are shown. The last two trials from the pre-exposure sequence are shown in gray (dashed lines), underlying all other trials. The first trials from the rotation exposure session (rotation-perturbed, left column), the last two trials from the same session (rotation-adapted, center column), and the first two trials from the post-exposure session (aftereffects, right column) are displayed. Dominant paths are shown above, whereas nondominant hand paths are shown below. B Mean performance measures, hand-path linearity and final position error, are averaged across all subjects and shown for individual cycles of movement. Baseline performance, measured for each subject as the average of the last eight cycles from the pre-exposure sequence, has been subtracted from each value prior to computing the average across subjects. Thus, the performance measures shown represent a change from baseline performance, and can be either positive or negative. Each cycle represents the average of a single movement to each of eight targets, across all subjects (mean±SE). The time course of each experimental sequence, pre-exposure, mass-exposure, and post-exposure, is shown. Data have been fit to exponential functions, using the “CurveFit” function in Igor Pro (Wavemetrics).Vertically oriented gray bars mark the cycles for which the trials in Fig. 2A were extracted

Subjects showed a similar time course of adaptation to the rotated visual display with both dominant and nondominant arms. In terms of linearity, the first adapted cycle for the left arm was cycle 6 (Bonferni–Dunn: p=0.162), while that for the right arm was cycle 5 (Bonferni–Dunn: p=0.128). However, the first adapted cycle, in terms of final position error, was cycle 3 for the left arm (Bonferni–Dunn: p=0.0861), and cycle 5 for the right arm (Bonferni–Dunn: p=0.106). Thus, taking both measures together, neither arm showed an advantage for the time course of adaptation. Comparing performance for the rotation-adapted trials (last eight cycles of exposure sequence), neither arm showed an advantage for final adaptation of linearity (Bonferni-Dunn: p=0.998). For these same trials, task accuracy, as measured by final position error, was not significantly different for right and left arm movements (Bonferni–Dunn: p=0.247). This similarity in accuracy for right and left arms was not dependent on direction, as no interaction occurred between arm (left, right) and target (2×8 ANOVA: p=0.853). Therefore, our results demonstrate a right arm advantage for adaptation to altered limb inertia, but equivalent adaptation to the rotated visual display.

Inverse dynamic analysis

Interlimb differences in dynamic control, reflected by nondominant arm limitations in adaptation to altered inertial dynamics, should be evident under baseline conditions. Figure 4 shows typical right and left arm trajectories for a movement to the 90° target (trial 176) from baseline trials of the pre-exposure sequence performed with each hand by subject 2. The 90° target was chosen because it is symmetric with regard to both arms, and thus is equivalent in terms of extrinsic spatial coordinates, as well as its relation to required limb segment excursions. As illustrated in Fig. 4, subjects made substantial movements at all four available degrees of freedom. Both left and right arms show a tendency to move the hand lateral to the target. The nondominant hand path hooks in toward the target at the end of motion, while the dominant hand path does not. The apparent correction at the end of left arm motion is associated with a small additional peak in the tangential hand velocity profile. Whereas the right arm shows a slightly higher maximum hand velocity for this movement, there was no significant difference in peak tangential velocity for left and right arms across all movements of all subjects (Bonferroni–Dunn: p=0.682).

Fig. 4.

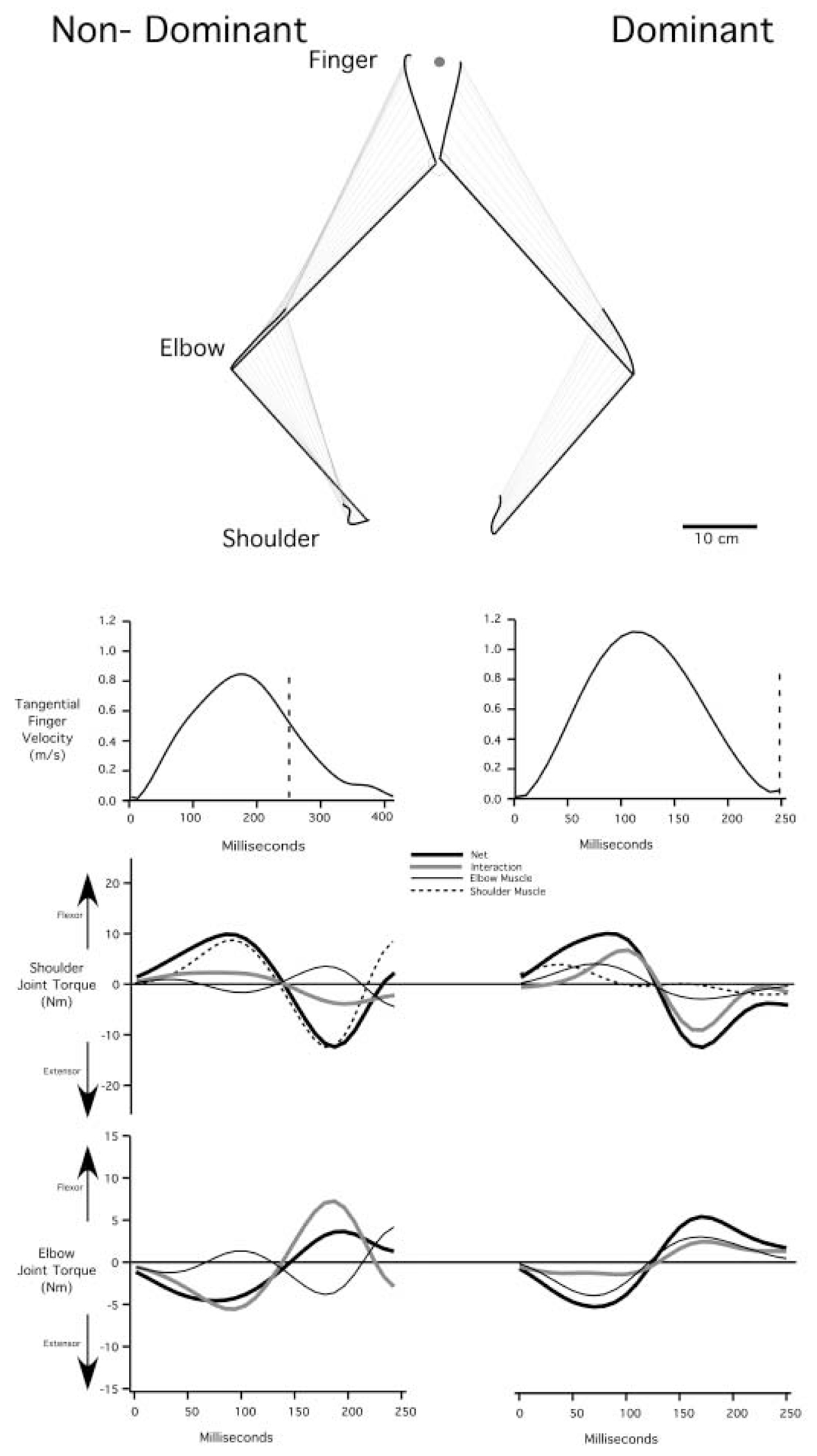
Representative baseline trials toward target 2: shoulder, elbow, and finger paths are shown for nondominant (left) and dominant (right) arms of subject 2 (top). Sequential upper arm and forearm positions are drawn every 10 msec. Time series graphs of tangential finger velocity, shoulder joint torque components, and elbow joint torque components are shown. For ease of comparisons, only the first 250 msec (Marked by vertical dashed line in tangential finger velocity graphs) of the movement is shown for the joint torque plots. Torque components include net torque (heavy black), interaction torque (heavy gray), elbow muscle torque (light black), and shoulder muscle torque (dashed). Note that the elbow muscle torque has equal amplitude, but opposite signs at both joints

While the right and left hand paths are similar, certain differences are notable. Planar motion of the scapula was not restricted and was included in the dynamic model used to compute joint torques (see Methods). For the nondominant arm, displacement of the scapula (shoulder point) primarily occurred in the medial to lateral direction, while the dominant arm scapula displaced posterior to anteriorly. The elbow path was more linear for the left arm, while the hand path was more linear for the right arm. Whereas these differences in kinematics are small, the associated differences in joint torques between these two movements were substantial.

Figure 4 displays the shoulder and elbow joint torque profiles for the movements shown above. In order to maintain equal time scales, the first 250 ms of each movement is displayed (vertical bar in tangential velocity profiles). This removes the additional inflexion in the left hand tangential velocity profile from analysis. At the shoulder, three torques contribute to net torque (see Methods): 1) interaction torque, resulting from motion of the scapula and the forearm segment; 2) elbow muscle torque, which originates from muscles spanning the upper arm and forearm; and 3) shoulder muscle torque, which originates from muscles spanning the scapula/trunk unit to the upper arm. At the elbow, two torques contribute to net torque: 1) interaction torque, resulting from motion of the upper arm; and 2) elbow muscle torque, originating from muscles spanning the upper arm and forearm segments.

The net torque profiles at the shoulder and elbow joints are similar for both arms, as expected from the similarity in kinematics. Due to the relatively large inertial load at the shoulder compared to the elbow, shoulder net torque is roughly twice the amplitude of elbow net torque.

Shoulder

Nondominant arm

For the nondominant arm, the shoulder net torque is determined almost entirely by shoulder muscle torque. This is evidenced by the similarity in phase and amplitude of the shoulder muscle and shoulder net torque profiles. Initial flexor net torque is accompanied by a similar flexor muscle torque profile. Both torques cross zero, nearly simultaneously. However, peak shoulder flexor net torque is countered by an extensor torque on the upper arm that is produced by the elbow muscles (elbow muscle torque). Similarly, peak extensor net torque is countered by a flexor torque that is produced by the elbow muscles acting on the distal upper arm. Thus, for the nondominant arm movement, elbow muscles counteract shoulder muscles in producing upper arm acceleration, and shoulder interaction torque contributes very little to motion of the shoulder.

Dominant arm

In contrast, dominant shoulder net torque results from substantial contributions of elbow muscle torque and shoulder interaction torque. In fact, the initial peak in flexor net torque results from a combination of flexor interaction torque and a flexor torque on the upper arm produced by elbow muscle torque. Shoulder muscle torque represents the smallest contribution to shoulder net torque, and is near zero throughout much of the movement.

Elbow

Nondominant arm

Nondominant elbow net torque is primarily driven by interaction torque, while muscle torque counters interaction torque for the majority of the motion. During initial elbow extensor acceleration, flexor muscle torque counters elbow net torque, and also counters shoulder flexor net torque by producing an extensor torque on the upper arm segment.

Dominant arm

For the dominant arm, both interaction and muscle torques combine to produce elbow joint acceleration throughout the movement. As compared to the nondominant arm, interaction torque contributes less to elbow net torque, requiring a larger contribution of elbow muscle torque. However, this increased torque at the elbow contributes positively to shoulder net torque, serving to accelerate both the upper arm and the forearm.

In summary, the dominant arm appears to more efficiently utilize the elbow muscles by contributing positively to net torque at both the shoulder and elbow. As a result, less shoulder muscle torque is required for the dominant arm movement. In contrast, while the nondominant arm “utilizes” interaction torques to drive the forearm, excess interaction torque requires elbow muscles to counter acceleration of the elbow. In countering elbow net torque, elbow muscle torque also counters shoulder acceleration. As a result, greater shoulder muscle torque is required to accelerate the nondominant shoulder. The dominant arm appears to more efficiently utilize the action of muscles across both segments.

Inverse dynamics analysis across subjects and conditions

Regardless of the similarity in movement velocity, substantial interlimb differences in muscle torque contributions, across subjects and trials, were consistant with the analysis described for the movements shown in Fig. 4. For baseline trials (left column), the contribution of elbow muscle torque to shoulder net torque was negative for the nondominant arm and positive for the dominant arm (mean, ±SE: nondominant 16.5%, 0.02%; dominant 2.1%, 1.7%). This difference was significant across all subjects and baseline trials (Bonferroni–Dunn: p<0.0001). As shown in the example of Fig. 4, this indicates that for nondominant arm movements, elbow muscle torque countered net torque at the shoulder, whereas for dominant arm movements, elbow muscle torque contributed positively to net torque at the shoulder. Similarly, the contributions of shoulder muscle torque to shoulder net torque were substantially different between the two arms (Bonferroni–Dunn: p<0.0001). For the nondominant arm, shoulder muscle torque accounted for 92.8% (mean, ±SE: 5%) of shoulder net torque. In contrast, for the dominant arm, shoulder muscle torque contributed only 33.8% (mean, ±SE: 4.4%) toward shoulder net torque. For the dominant arm, 2.1% of net torque was contributed by elbow muscle torque, and the remaining 64.1% of net torque was contributed by shoulder interaction torques due to motion of the forearm and the scapula. In summary, these interlimb differences in torque patterns indicate that the dominant arm more efficiently utilized the elbow muscles by contributing positively to net torque at both the shoulder and elbow, as compared with nondominant arm movements.

As demonstrated by the graphs in the center and right columns of Fig. 5, these same interlimb differences in torque occurred for mass-adapted and rotation-adapted trials. Whereas, with the mass attached to the nondominant forearm, elbow muscle torque no longer countered shoulder net torque, elbow muscle torque still contributed 30% more to shoulder net torque for the dominant than for the nondominant arm (mean, ±SE: nondominant 3.9%, 5.4%; dominant 33.8%, 3.6%; Bonferroni–Dunn: p=0.0017). Shoulder muscle torques contributed, on average, 100% (SE: 7.5%) to nondominant shoulder net torque. In contrast, dominant arm shoulder muscle torque contributed only 16.9% (mean, ±SE: 5.9%, Bonferroni–Dunn: p<0.0001) toward shoulder net torque. Thus, for the dominant arm, shoulder motion was driven by the synergistic contributions of elbow muscle actions, shoulder muscle actions, and interaction torques resulting from scapular and forearm motions. In contrast, nondominant shoulder motion was driven primarily by shoulder muscle actions.

Fig. 5.

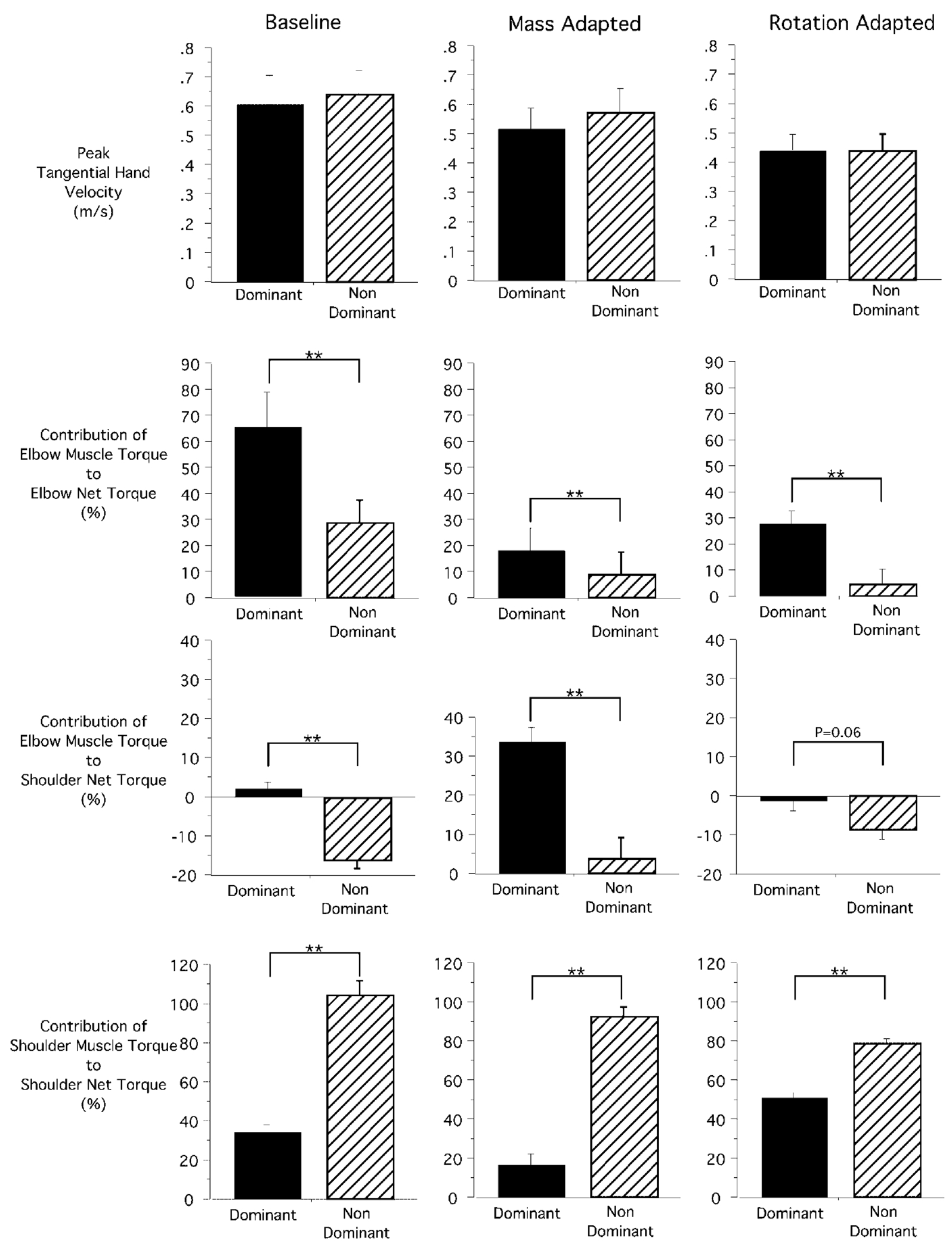
Measures of peak tangential finger velocity (top), and contributions of elbow muscle torque impulse (middle) and shoulder muscle torque impulse (bottom) to shoulder net torque impulse are shown for baseline trials (left), mass-adapted trials (center), and rotation-adapted trials (right). These measures have been quantified as a percentage of shoulder net torque. Means and standard errors across all subjects for the average measure computed across all trials for the last eight cycles of the preexposure sequence (left), the mass-exposure sequence (center), and the rotation-exposure sequence (right) are shown. The results of pairwise comparisons (Bonferroni–Dunn) are reported as significant (**), or the p-value is shown

The torque patterns for dominant and nondominant arms from rotation-adapted trials show the same trends as described for baseline and mass-adapted trials: dominant arm elbow muscle torque contributed 27% more to elbow net torque than that of the nondominant arm (Bonferroni–Dunn: p=0.0102). The nondominant elbow muscle torque countered shoulder net torque to a greater extent than that of the dominant arm. Although this difference was statistically marginal (Bonferroni–Dunn: p=0.06), the trend is the same as that of baseline and mass-adapted trials. In addition, the contribution of shoulder muscle torque to shoulder net torque was substantially lower for the dominant arm (Bonferroni–Dunn: p<0.0001), indicating a greater contribution of interaction torques to shoulder net torque. In summary, for all experimental conditions, dominant arm control remained well distributed across shoulder and elbow muscle torques: shoulder motion resulted from a combination of shoulder and elbow muscle torques (combined ~50%) and from interaction torques resulting from scapular and forearm motion. In contrast, nondominant arm shoulder acceleration resulted entirely from shoulder muscle torque, while interaction torques and elbow muscle torques countered one another.

These interlimb differences in torque patterns suggest that, for baseline and both adaptation conditions, the dominant arm utilized shoulder and elbow muscles more efficiently. This analysis would suggest that total mean-squared muscle torque, measured across both joints, would be smaller for the dominant than the nondominant arm. Indeed, the mean-squared torque for left arm movements was 22.19 N m² (SE 6.4 N m²), while that for the right arm was 4.84 N m² (SE 1.54 N m²). This fivefold increase in nondominant arm torque (Bonferroni–Dunn: 0.017) clearly indicates a less efficient strategy for coordinating movements, regardless of the similarity in peak tangential hand velocity. This suggests a fundamental limitation in nondominant arm coordination.

Discussion

Previous findings from this laboratory indicated dominant arm advantages in controlling the effects of inter-segmental dynamics during reaching movements, and lead to the hypothesis that the essential factors distinguishing dominant and nondominant arm performance correspond to asymmetries in controlling limb dynamics. This dynamic dominance hypothesis is based on a hierarchical model of motor control, which describes visual transformations, trajectory specification, and dynamic transformations as sequential processes. In this study, two major predictions of this hypothesis were assessed: 1) adaptation to novel intersegmental dynamics, requiring the development of new dynamic transforms, should be more effective for the dominant arm; 2) there should be no difference in visuomotor adaptation, as performed by the dominant and nondominant arms. This prediction is based on the idea that it is in the stage of motor planning, involving dynamic transformations, in which handedness emerges.

To test these predictions, adaptation to novel inertial loads and novel visuomotor rotations were assessed during reaching movements performed with the dominant and nondominant arms. The results support the predictions of the dynamic dominance hypothesis: substantial interlimb differences in adaptation to novel inertial dynamics, but equivalent adaptation to novel visuomotor rotations. Inverse dynamic analysis revealed interlimb differences in the torque strategies employed under baseline and both adapted conditions: for nondominant arm movements muscle torques were better coordinated across both shoulder and elbow joints, such that similar speed movements were produced with a fraction of the mean-squared torque than that of nondominant arm movements. This finding provides support to the hypothesis that manual asymmetries arise, downstream in the motor control sequence to visuomotor transformations, when the trajectory plan is transformed into dynamic properties that reflect the forces required to produce motion. The sections below will review our findings with respect to dynamic transformations, visuomotor transformations, and the implications for models of handedness.

Dynamic transformations

The current study indicates a dominant arm advantage for dynamic adaptation, as well as substantial qualitative differences in controlling the effects of inertial dynamics during dominant as compared with nondominant arm movements. For both baseline and mass-adapted conditions, the dominant arm was more efficient at utilizing elbow muscle torques to accelerate both segments. In contrast, the nondominant arm demonstrated less efficient torque patterns. Dominant shoulder muscle torque accounted for only 17% of shoulder net torque, while nondominant shoulder muscle torque accounted for nearly 100% of shoulder net torque. This indicates that elbow muscle torque and interaction torques, resulting from scapular and forearm motion, accounted for 83% of dominant shoulder net torque. In contrast, nondominant elbow muscle torque and shoulder interaction torque countered one another’s actions on the upper arm, such that the combined contribution to shoulder net torque was small. The exploitation of interaction torques and elbow muscle torques on upper arm motion would be expected to substantially increase the torque efficiency of movements because the inertial load of both segments resists shoulder acceleration. Indeed, the smaller contributions of muscle torques at the shoulder for the nondominant arm resulted in substantially reduced mean-squared muscle torque, as measured across both segments. These results are consistent with previous findings that indicated more efficient utilization of muscle torques by the dominant arm during rapid reaching movements (Sainburg and Kalakanis 2000).

One might expect that the limitations in nondominant arm adaptation to the novel inertial load resulted from a torque production deficit for that arm. However, the near frictionless horizontal plane movements studied here did not approach the limits of maximum torque production at each joint. Thus, limitations in maximum torque production would not be expected to influence performance on this sub-maximal task. More importantly, because the nondominant arm used greater mean-squared torque to produce similar speed movements, the nondominant arm limitation in dynamic adaptation cannot be attributed to a torque production deficit. Instead, our inverse dynamic results suggest substantial qualitative differences in dynamic control, as implemented for dominant and nondominant arm movements. These findings are consistent with our previous findings that indicate a dominant arm advantage in controlling limb segment inertial interactions (Sainburg and Kalakanis 2000).

The role of dynamic transformations in handedness is also supported by a previous report that investigated the factors contributing to observed advantages in reaching toward ipsilateral, as compared with contralateral targets (Carey et al. 1996). During fixed midline gaze, target information presented in the hemispace contralateral to the moving arm is projected to the cerebral hemisphere ipsilateral to that arm. Thus, reaching to contralteral targets, but not ipsilateral targets, requires interhemispheric transfer of target information for motor planning. By requiring subjects to reach to mirror imaged targets, the authors differentiated the requirements for interhemispheric processing from biomechanical features of the tasks. The results of that study indicated that advantages for reaching to ipsilateral targets were related to task mechanics rather than to the requirements for interhemispheric transfer of information. The dominant arm showed greater advantages for reaching to ipsilateral targets than the nondominant arm. Because such advantages resulted from task-related mechanical factors, these results are consistent with the dynamic dominance hypothesis, which states that manual asymmetries result from interlimb differences in controlling the effects of task dynamics (Sainburg and Kalakanis 2000).

It should be noted that dominant arm advantages do not apply to all tasks, or all aspects of tasks. Healey et al. (1986) examined an extensive range of tasks and found that four factors or groups of tasks accounted for 80% of the variance in hand preference among the 110 subjects tested. Tasks that were almost exclusively associated with dominant arm use included activities requiring precision in interjoint coordination and trajectory formation. For example, targeted ball throwing is dependent on the trajectory of the hand prior to ball release, and drawing performance is determined by the trajectory of the writing implement. Specification of the trajectory of the hand is critically dependent on interjoint coordination and control of intersegmental dynamics (Sainburg et al. 1993, 1995, 1999). In contrast, tasks that involved spatially orienting a body segment posture were more often performed with the nondominant arm. These tasks included posturing the hand to point toward a distant object, which is similar to other functional tasks such as holding a piece of paper that is being cut with scissors, or orienting the hand in space for catching a baseball. Such postural orientation tasks are less dependent on intersegmental dynamics, since the trajectory used to attain the posture is not critical for task success. The dynamic dominance hypothesis thus appears to account for the extent to which hand preferences for specific activities are lateralized.

Visual–motor transformations

The process of learning novel visuomotor transformations, such as the rotation studied here, is thought to depend on the acquisition of internal models that represent the mapping between visual coordinates that are extrinsic to the body and intrinsic coordinates, such as joint angles (Kawato et al. 1988; Jordan and Rumelhart 1992; Imamizu and Shimojo 1995; Imamizu et al. 1995; Wolpert et al. 1995b; Ghahramani et al. 1996; Ghahramani and Wolpert 1997; Imamizu et al. 1998; Kawato 1999; Krakauer et al. 1999; Krakauer et al. 2000; Wolpert and Ghahramani 2000a). Krakauer et al. (2000) showed that learning of novel visuomotor transformations and dynamic transformations occurs through independent neural mechanisms that represent distinct working memory processes. Recent neural imaging studies support this conclusion by indicating that visuomotor and dynamic transformations are associated with different neural activation profiles (Shadmehr and Holcomb 1997; Ghilardi et al. 2000). Thus, adaptation to novel visuomotor transforms occurs through neural mechanisms that are independent from those employed for adaptation to novel dynamic loads.

In an analogous task to that studied here, Ghilardi et al. (2000) recently demonstrated that adaptation to visual rotations was associated with ipsilateral posterior parietal activation for right arm movements of right-handers, assessed via PET scan. This finding is consistent with previous studies examining visually guided reaching (Goodale and Milner 1992; Clower et al. 1996; Klingberg et al. 1996) and also supports the idea that the right posterior parietal cortex is specialized for such visuomotor transformations. Based on these findings, one might predict that, in the current study, the left arm of right-handers would adapt better to visuomotor rotations due to more direct sensorimotor access to right hemisphere visuomotor processes. Indeed, a number of previous studies have indicated reaction time advantages when the target information is processed by the hemisphere contralateral to the performing hand (Berlucchi et al. 1971; Berlucchi 1978; Marzi et al. 1991). However, the current findings do not indicate nondominant arm advantages for adaptation to visuomotor rotations. The absence of such advantages may be due to the fact that direct sensorimotor access to visuomotor processes does not effect improvements in the adaptation studied here. Instead, it is plausible that adaptation to novel visuomotor rotations may rely heavily on assessment of knowledge of results following each trial. In this case, direct sensory motor access to right hemisphere visuomotor processes would be unlikely to afford performance advantages to the nondominant arm because learning occurs between trials when processing time is not limited. In support of this interpretation, Winstein has previously shown that knowledge of results information is critical for effective learning during visually directed reaching (Winstein et al. 1994).

Models of handedness

Hugo Leipmann first proposed the idea that handedness results from a left hemispheric specialization for motor programming in right-handers (Geschwind 1975; Taylor and Heilman 1980). This hypothesis has since been revised, such that a specific sensorimotor process is seen as mediated by neural circuits that are localized in one or the other hemisphere, but shared for control of both limbs (Haaland et al. 1977; Taylor and Heilman 1980; Haaland and Delaney 1981; Haaland et al. 1987; Haaland and Harrington 1989a, 1989b; Winstein and Pohl 1995; Desrosiers et al. 1996; Winstein et al. 1999; Sainburg and Kalakanis 2000). For example, Winstein and Pohl (1995) proposed that visual corrections are mediated by the right hemisphere, while programming the “ballistic” component of goal-directed movement is mediated by the left hemisphere. Manual asymmetries are thus hypothesized to arise due to preferential neural communication with the limb contralateral to the neural circuitry in question (Kuypers et al. 1962; Kuypers and Lawrence 1967; Lawrence and Kuypers 1968a, 1968b; Kuypers and Brinkman 1970; Kuypers and Maisky 1975; Holstege and Kuypers 1982a; Holstege and Kuypers 1982b; Kuypers 1982; Holstege and Kuypers 1987). This hypothesis of handedness has gained support by studies revealing activation of ipsilateral motor and premotor cortices during unimanual movements, many of which have indicated that the hemisphere contralateral to the dominant arm shows greater activation. (Kutas and Donchin 1974; Matsunami and Hamada 1981; Tanji et al. 1988; Macdonell et al. 1991; Kawashima et al. 1993; Kim et al. 1993; Kawashima et al. 1994; Salmelin et al. 1995; Gitelman et al. 1996; Kawashima et al. 1996; Urbano et al. 1996; Chen et al. 1997a, 1997b, 1997c; Dassonville et al. 1997; Kawashima et al. 1997; Kawashima et al. 1998; Taniguchi et al. 1998; Viviani et al. 1998; Volkmann et al. 1998; Ghilardi et al. 2000). Such asymmetries in the contributions of ipsilateral hemisphere to unilateral arm movements are consistent with the idea of asymmetrical access to shared circuits, and provide support to Leipmann’s hemispheric specialization hypothesis of handedness.

Our results indicate equivalent adaptation to novel visuomotor transforms, but asymmetry in adaptation to novel dynamic transforms. Consistent with previous reports (Carey et al. 1996; Sainburg and Kalakanis 2000), control of limb segment inertial dynamics was qualitatively different for the two limbs. Such qualitative differences in control of limb segment dynamics suggest that this aspect of control utilizes independent processes for the dominant and nondominant arms. In contrast, it is likely that visuomotor transformations are localized primarily to the right hemisphere, but are shared between the limbs. This idea is supported by neural imaging findings, which indicate that right arm (dominant) adaptation to the visuomotor rotation studied here is correlated with activity in the right posterior parietal cortex (Ghilardi et al. 1995). However, it is not possible from the data in the current study to distinguish whether the neural circuitry associated with dynamic or visuomotor transformations is shared between the limbs. These alternatives can be further assessed by examining whether learning of novel visuomotor and dynamic conditions with one arm transfers to affect the performance, and/or rate of adaptation when the other arm is exposed to the same experimental manipulation (Taylor and Heilman 1980; Elliott and Roy 1981; Bentin et al. 1984; Byrd et al. 1986; Parlow and Kinsbourne 1989, 1990; Marzi et al. 1991; Parlow and Dewey 1991; Charron et al. 1996).

Symbols:
M	Mass of segment
R	Center of mass of segment
L	Length of segment
I	Intertia of segment
Θ	Shoulder angle
ϕ	Angle between center of mass of lower arm segment and upper arm
X″	Linear acceleration of shoulder point along X-dimension
Y″	Linear acceleration of shoulder point along Y-dimension
Superscripts:	′ 1st derivative, ″ 2nd derivative
Subscripts:	1 Upper arm segment, 2 Lower arm segment, including support and attached mass
Shoulder:
Interaction torque
(M1R1SIN(Θ)+M2(L1*SIN(Θ)+R2SIN(Θ +ϕ)))X″
−L1M2R2SIN(ϕ)(Θ′2–(Θ′+ϕ′)2)–(I2+M2R2(R2+L1COS(ϕ)))ϕ″
(M1R1*COS(Θ)+M2(L1COS(Θ)+R2COS(Θ+ϕ)))Y″
+(I2+M2R2 2)ϕ″– M2R2SIN(Θ+ϕ)X″+M2R2COS(Θ+ϕ)Y″+L1M2R2SIN(ϕ)Θ′2
+(I2+M2R2(R2+L1COS(ϕ)))Θ″
Net torque
(I1+I2+M1R1 2+M2(L1 2+R2 2+2L1R2COS(ϕ)))Θ″
Muscle torque
Net – Interaction-muscle torque Elbow
Elbow:
Interaction torque
M2R2SIN(Θ+ϕ)X″–M2R2COS(Θ+ϕ)Y″–L1M2R2SIN(ϕ)Θ′2
−(I2+M2R2(R2+L1COS(ϕ)))Θ″
Net torque
(I2+M2R2 2)ϕ″
Muscle torque
Net – Interaction