Excited-State Dynamics during Primary C–I Homolysis in Acetyl Iodide Revealed by Ultrafast Core-Level Spectroscopy

Abstract

In typical carbonyl-containing molecules, bond dissociation events follow initial excitation to $n{\pi }_{\text{C}=\text{O}}^{*}$ states. However, in acetyl iodide, the iodine atom gives rise to electronic states with mixed $n{\pi }_{\text{C}=\text{O}}^{*}$ and $n{\sigma }_{\text{C}-\text{I}}^{*}$ character, leading to complex excited-state dynamics, ultimately resulting in dissociation. Using ultrafast extreme ultraviolet (XUV) transient absorption spectroscopy and quantum chemical calculations, we present an investigation of the primary photodissociation dynamics of acetyl iodide via time-resolved spectroscopy of core-to-valence transitions of the I atom after 266 nm excitation. The probed I 4d-to-valence transitions show features that evolve on sub-100-fs time scales, reporting on excited-state wavepacket evolution during dissociation. These features subsequently evolve to yield spectral signatures corresponding to free iodine atoms in their spin–orbit ground and excited states with a branching ratio of 1.1:1 following dissociation of the C–I bond. Calculations of the valence excitation spectrum via equation-of-motion coupled cluster with single and double substitutions (EOM-CCSD) show that initial excited states are of spin-mixed character. From the initially pumped spin-mixed state, we use a combination of time-dependent density functional theory (TDDFT)-driven nonadiabatic ab initio molecular dynamics and EOM-CCSD calculations of the N_4,5 edge to reveal a sharp inflection point in the transient XUV signal that corresponds to rapid C–I homolysis. By examining the molecular orbitals involved in the core-level excitations at and around this inflection point, we are able to piece together a detailed picture of C–I bond photolysis in which d → σ* transitions give way to d → p excitations as the bond dissociates. We also report theoretical predictions of short-lived, weak 4d → 5d transitions in acetyl iodide, validated by weak bleaching in the experimental transient XUV spectra. This joint experimental–theoretical effort has thus unraveled the detailed electronic structure and dynamics of a strongly spin–orbit coupled system.

Graphical Abstract

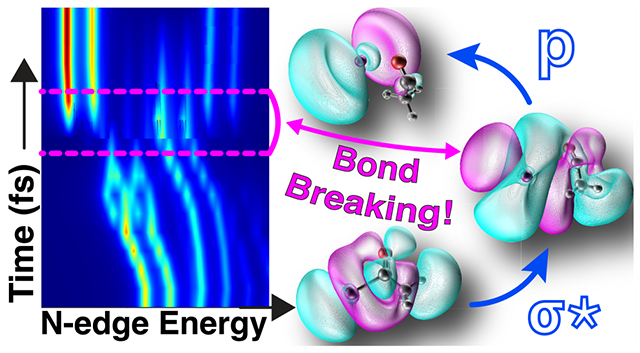
I. INTRODUCTION

Photodissociation of gas-phase organic molecules has been of keen interest to physical chemists for decades due to both its relevance to photochemical reactions in the atmosphere^1–5 and the opportunity it provides to understand electronic excited-state dynamics arising from the breakdown of the Born–Oppenheimer approximation.^6–9 A significant proportion of these studies have focused on the photodissociation dynamics of carbonyl-containing organic molecules^10–23 and alkyl halides,^24–27 which are both reported to play important roles in photochemical reactions in the atmosphere.^28–30 In carbonyl-containing molecules such as aliphatic aldehydes and ketones, it is well known that near-UV excitation of the $n\to {\pi }_{\text{CO}}^{*}$ transition leads to photodissociation via the Norrish type I process, where intersystem crossing (ISC) to the ³nπ* state results in cleavage of the α-C–C bond. Furthermore, depending on the excitation wavelength, small aldehydes and ketones can also dissociate into molecular products via a roaming mechanism.^31–35 In alkyl halides, on the other hand, near-UV excitation causes an $n\to n{\sigma }_{\text{C}-\text{X}}^{*}$ transition (X = halogen) within what is known as the Aband consisting of close-lying, strongly dissociative states. Excitation to these dissociative states ultimately leads to the ultrafast dissociation of the C–X bond, yielding an alkyl radical and a halogen atom. The halogen is typically formed in both its ground and spin–orbit excited states due to bifurcation of the excited-state wavepacket at conical intersections along the dissociation coordinate.³⁶

Acetyl halides (CH₃C(O)X, henceforth AcX), which contain both C=O and C–X chromophores, serve as a unique class of molecules in which competing photodissociation pathways arise due to the involvement of both $n{\pi }_{\text{C}=\text{O}}^{*}$ and $n{\sigma }_{\text{C}-\text{X}}^{*}$ states. The investigation of acetyl halide photodissociation has been the subject of several publications examining the energy content of the dissociation end-products.^37–41 Of the acetyl halides, AcCl is the most extensively studied system.^41–53 The UV absorption spectrum of AcCl shows a nπ* absorption band centered at 240 nm;⁵⁴ the nσ* band in AcCl is expected to be in the deep-UV region around 170–200 nm and thus is well separated in energy from the nπ* state.^55,56 Butler and co-workers showed that despite the similar bond energies of the α-C–C and α-C–Cl bonds in acetyl chloride, 248 nm excitation of this molecule to the nπ* state first results in the prompt dissociation of the C–Cl bond over a barrier formed from an avoided crossing with the $n{\sigma }_{\text{C}-\text{Cl}}^{*}$ state,⁴⁷ and the α-C–C bond is cleaved only via slower secondary dissociation of the acetyl radical. Thus, unlike the Norrish type I pathway in aliphatic aldehydes and ketones following ISC, the primary dissociation in AcCl is thought to occur on singlet states on ultrafast time scales. The time scale for the primary dissociation was estimated in photofragment translational spectroscopy and velocity map imaging experiments via the large observed anisotropy parameter, suggesting that the CH₃CO and Cl/Cl* fragments are formed on time scales faster than the ~70 ps rotational period of the parent molecule (based on rotational constants of AcCl from ref. 57). The isotropic angular distributions of the CH₃ and CO photofragments formed from secondary dissociation of the acetyl radical after excitation at 236 nm⁴³ suggested that secondary dissociation happens on time scales much longer than the rotational period. Ultrafast time-resolved studies of AcCl photodissociation by Suzuki et al. at 253 nm using multiphoton ionization and photofragment ion imaging found prompt fission into an acetyl radical and Cl within their instrument time resolution of 200 fs,⁵⁸ followed by secondary dissociation on a hundreds of picoseconds time scale, in agreement with previous estimates.⁵⁹

Fewer studies exist on the UV photodissociation of AcBr than AcCl,^40,60–62 and neither ultrafast time-resolved studies nor theoretical and experimental characterization of electronic excited states has been performed on this system. Unlike in AcCl where a UV photon at 220–300 nm unambiguously causes an n → π* transition, the character of the excited states in AcBr at these wavelengths is uncertain. In AcBr, 234 and 248 nm excitation has been shown to indeed result in primary C–Br dissociation followed by slow secondary dissociation of the acetyl radical, though it is unclear whether the C–Br dissociation occurs due to direct excitation to the $n{\sigma }_{\text{C}-\text{Br}}^{*}$ state⁴⁰ as in alkyl halides or whether UV excitation first populates the nπ* state followed by dissociation on the $n{\sigma }_{\text{C}-\text{Br}}^{*}$ state, as in AcCl.⁶⁰ This ambiguity arises as two absorption bands, centered at 210 and 240 nm, may cause excitation to states of varying character. The absorption band centered at 210 nm that Lee et al.⁴⁰ report to be of $n{\sigma }_{\text{C}-\text{Br}}^{*}$.character may also have nonvanishing absorption past 230 nm, opening the possibility of direct excitation to this state. Therefore, for excitation in the wavelength range of 234 to 248 nm, it is difficult to determine a priori which states might be populated.

As indicated above, the energy separation between the $n{\pi }_{\text{C}=\text{O}}^{*}$ and $n{\sigma }_{\text{C}-\text{X}}^{*}$ states decreases as a function of halogen substitution going down the period. Based on this trend, it is likely that the overlap of the nπ* and nσ* absorption features is even more pronounced in AcI, thus resulting in valence electronic states of mixed character and leading to complex excited-state dynamics. This hypothesis may be supported by the fact that AcI reportedly exhibits at least 10 times larger absorption coefficients in the near-UV compared to other acetyl halides,^39,63 perhaps due to the larger oscillator strength of the $n{\sigma }_{\text{C}-\text{I}}^{*}$ transition. However, to the authors’ knowledge, there have been no experimental or theoretical investigations of the valence electronic structure and ultrafast excited-state dynamics governing the photodissociation of AcI to rigorously test this hypothesis. The lone study on the photodissociation of AcI was performed by Kroger et al.³⁹ using photofragment translational spectroscopy following 266 nm excitation. Results from this work suggest anomalously fast secondary dissociation of the acetyl radical after the rapid loss of I from AcI. Based on the measured anisotropy and calculations of the rotational period of the parent molecule, this work estimated time scales of 100 fs for the primary C–I bond dissociation and 10 ps for the secondary C–C bond dissociation.³⁹

In this article, we present a joint experimental and theoretical effort geared toward characterizing the valence excited states accessed by 266 nm excitation and the subsequent ultrafast excited-state dynamics leading to the primary C–I bond dissociation in gas-phase acetyl iodide. Our experimental method of choice for this study is extreme ultraviolet time-resolved absorption spectroscopy (XUV-TRAS) due to its well-proven ability to combine site specificity with sensitivity to valence electronic structure. We use the equation-of-motion coupled-cluster (EOM-CCSD) theory for a robust characterization of the valence excited states of AcI accessed by 266 nm excitation. Our calculations confirm that the nature of valence states accessed at 266 nm is indeed a combination of n → σ* and n → π* character with strong spin–orbit coupling. Following 266 nm excitation, experimental transient core-level spectra capture the evolution of the excited-state wavepacket, revealing that primary C–I bond homolysis into acetyl radical and ground/spin–orbit excited iodine atoms occurs on a sub-100-fs time scale. A combination of time-dependent density functional theory (TDDFT)-driven nonadiabatic ab initio molecular dynamics and high-level EOM-CCSD calculations of the iodine N_4,5 edge allows a side-by-side comparison of theoretical and experimental XUV-TRAS spectra that corroborates sub-100-fs dissociation and reveals surprising contributions from weak, short-lived 4d → 5d transitions.

Furthermore, due to the paucity of high-level electronic structure calculations of acetyl halides in general, we present new EOM-CCSD calculations on AcBr and AcCl, which serve to further contextualize our results on AcI. In particular, we find that the nσ*/nπ* mixing becomes more pronounced as a function of halogen atom mass, resulting in an AcCl spectrum that exhibits only n → π* transitions, while the AcBr spectrum features low-energy nπ* states along with the possibility of direct 220 nm excitation into an nσ* state (in accordance with Lee et al.),⁴⁰ with AcI exhibiting strong mixing between nσ* and nπ* states throughout the entire spectrum. Overall, we find that the 266 nm accessible valence excited states of AcI, and therefore the photolysis dynamics, are fundamentally different from those of AcCl and AcBr due to strong spin–orbit coupling and the significant presence of low-energy n → σ* transitions. Our combined experimental and theoretical results offer the first characterization of the N_4,5-edge spectrum of AcI as the excited-state wavepacket evolves in time, allowing a full characterization of the dynamical core-level spectrum that reveals unique and unanticipated spectral features that may offer great utility in future studies of the C–I dissociation process in a variety of systems.

II. METHODS

II.A. Experimental Methods.

Pulses centered at 800 nm with a 35 fs full width at half-maximum (FWHM) pulse duration and 3 mJ pulse energy from a commercial Ti:sapphire amplified laser system pump our XUV-TRAS apparatus; schematics of the system are available in a previous report.⁶⁴ The output from this laser is split equally by a beamsplitter into a pump and a probe arm. To generate the extreme ultraviolet (XUV) probe, the transmission through the beamsplitter is focused by a f = 75 cm lens into a semi-infinite gas cell (SIGC) that is filled with neon gas and held at a pressure of 50 Torr to produce XUV via high harmonic generation. Between the lens and the SIGC, a type-1 BBO crystal (100 μm thick, cut for second-harmonic generation) generates a weak second-harmonic field (10% conversion efficiency). A dual wave plate rotates the polarization of the 800 nm to match the polarization of the 400 nm, and two calcite plates (thickness of 750 μm) temporally and spatially overlap the 800 and 400 nm beams in the SIGC by compensating for the temporal walk-off between the two colors introduced by the dual waveplate and a 2-mm-thick CaF₂ entrance window of the SIGC. The two-color field enables the generation of even and odd harmonics to achieve the necessary spectral coverage for transient absorption measurements. The output from the SIGC is then filtered by a 200-nm-thick Al filter to transmit XUV between 15 and 72.7 eV and block 800 and 400 nm. A toroidal mirror focuses the generated XUV on the interaction region, where a sample cell is placed. The XUV transmitted through the sample passes through a second, 600-nm-thick Al filter and is collected and frequency-resolved by a flat-field concave grating (Hitachi) and detected on an X-ray CCD camera (Andor Newton 840), resulting in an energy resolution of 15 meV at 44 eV and 40 meV at 72 eV.

The pump arm uses the reflected portion of the 50:50 beam splitter. The reflected 800 nm beam is first sent onto a retroreflector mounted on a motorized linear stage to provide a computer-controlled delay between the pump and probe pulses, allowing us to change the delay Δt stepwise in increments of 2.2 fs over a range of 660 ps. After the beam passes through a type-1 BBO crystal for second-harmonic generation (200 μm thickness), a calcite plate (900 μm thickness), a dual wave plate, and a type-1 BBO crystal for third harmonic generation (100 μm thickness), we use wavelength-separating dielectric mirrors that are coated to reflect 266 nm (reflectance >95%) and transmit 400 and 800 nm (transmittance >90%). We found that reflection off five wavelength-separating mirrors is sufficient to fully suppress any 400 and 800 nm. An f = 1 m CaF₂ lens focuses the 266 nm spectra into the sample cell. Inside the vacuum chamber and halfway between the lens and the sample gas cell, a 45° dielectric mirror reflects the 266 nm and sends it into the sample cell noncollinearly at an angle of ~0.8° with respect to the XUV. A beam block is inserted into the 266 nm beam after the sample cell to further reduce any 266 nm scatter from entering the XUV spectrometer. Pulse energies (266 nm) of up to 40 μJ can be generated.

In the interaction region, the sample gas flow cell is 10 mm long and contains 600-μm-diameter holes for the XUV and 266 nm beams to pass though. The internal volume of the cell is 68 mm³. Acetyl iodide (99% purity, Sigma-Aldrich) is flowed at room temperature with a static pressure of 5 Torr in the flow cell. Pump power studies (see Supporting Information Figure S7) for AcI reveal a one-photon dependence of signal intensity as a function of 266 nm pulse energy in the range of 1–12 μJ, with a clear saturation effect for pulse energies greater than 15 μJ per pulse; we used 10 μJ 266 nm pulse energy for all of the data reported herein. The spot size at the sample position of the two-color field driving HHG is 90 × 90 μm², and the spot size of the 266 nm at the sample position is 110 × 140 μm².

We characterized the temporal instrument response function (IRF), assuming a Gaussian distribution, to be 74 ± 3 fs FWHM (σ_IRF = 44 ± 2 fs) via the ponderomotive upshift of the atomic Xe resonance associated with the ²D_5/2 → ²P_3/2 core-excited Rydberg state at 65.1 eV.^65,66 The ponderomotive shift of this transition to 65.3 eV is limited to the duration of UV and XUV and can therefore be used as a measurement of the IRF. The experimentally measured pump–probe cross correlation is given in Figure S8 in the SI. We use this measurement also to determine the location of the pump–probe temporal overlap (t₀).

For the polarization-dependent measurements reported in the Supporting Information, we switched the polarization of the 266 nm light between s- and p-polarization while keeping the XUV at p-polarization. At each time delay, we collected 920 spectra for the parallel polarization configuration and 450 spectra for the perpendicular polarization configuration. Each spectrum was collected with an exposure of 80 laser shots, and the delay points were collected in a randomized fashion, resulting in a noise level of σ ≈ 1.4 mOD (mean in energy), measured as the standard error of the mean. The noise floor was suppressed during data analysis by applying adaptive iteratively reweighted principal component regression (airPCR),⁶⁷ which reduced the noise level to σ ≈ 0.8 mOD (mean in energy).

For the UV/vis measurement of AcI, we employed a Lambda 1050+ UV/vis spectrophotometer from PerkinElmer. A few drops of AcI were placed in a cuvette in a dry nitrogen environment to avoid reaction with moisture. The cuvette was then quickly placed inside the spectrophotometer, and the absorption spectrum of gas-phase AcI at its ambient vapor pressure of approximately 32 Torr (at 298 K) was measured.⁶⁸ Various path length cuvettes were used to determine the optical density. Due to moisture slowly leaking into the cuvette and possible liquid-phase AcI contamination on the walls of the cuvette, no absolute cross section was determined.

II.B. Computational Methods.

The geometries of AcCl, AcBr, and AcI were optimized at the ωB97M-V/Def2-ma-TZVPP level of theory.^69–71 With these structures, we computed valence spectra using EOM-CCSD. We use the Def2-ma-TZVP basis set for C and O atoms and Def2-TZVP for H, and for the halogen atoms, we use the all-electron x2c-TZVPall-2c basis set optimized for scalar one- and two-component relativistic calculations⁷² that we further augment with diffuse functions from the Def2-ma-TZVP basis set.^71,73

Next, we use a combination of ORCA v5.0.3⁷⁴ and SHARC v2.1^75–77 to run nonadiabatic ab initio molecular dynamics (aiMD) using Tully’s fewest switches surface-hopping (FSSH) approach to model the electronic populations.^78–80 The SHARC program allows us to include nonadiabatic and spin–orbit couplings between the five singlet and five triplet electronic states that we model throughout a 100 fs NVE simulation with 0.5 fs time steps. To model the nonadiabatic dynamics, we employ TDDFT with the ωB97X-D3 functional, which is one of the top performers for valence excited states.⁸¹ We use a fine DefGrid3⁸² quadrature to evaluate the exchange-correlation potential and account for scalar relativistic effects through the second-order Douglas–Kroll–Hess Hamiltonian,^83–85 along with a perturbative ab initio treatment of spin–orbit couplings via the Breit–Pauli Hamiltonian.⁸⁶ Prior to using TDDFT to model the dynamics of AcI, we ensured that the valence spectra using TDDFT are qualitatively similar to those obtained with EOM-CCSD, which was indeed the case as shown in Figure S1. Finally, the cc-pVDZ-DK basis set is used for C, H, and O atoms with the aug-cc-pVTZ-DK basis on I for all TDDFT-based aiMD calculations.^87–89

Interestingly, we found a large number of spurious high-intensity peaks in preliminary TDDFT calculations of the N_4,5-edge spectra (Figure S9), which may be due to a lack of orbital relaxation^90,91 but whose origins are unknown. Most concerning is the fact that many of these spurious transitions appear within the 40–50 eV energy range where we expect strong absorption from the free I atom, which could obfuscate the results. Therefore, all N_4,5-edge spectra are calculated using EOM-CCSD with spin-polarized orbitals in the all-electron x2c-SVPall-2c basis set that is again modified with diffuse functions, this time from the corresponding Def2-SVPD basis set.⁷³ Henceforth, we refer to the resultant basis set as x2c-SVPDall-2c. We decouple the core states from the valence excitations using the core–valence separation (CVS) scheme of Krylov and Coriani.⁹² This CVS-EOM-CCSD scheme differs from the original Coriani and Koch approach⁹³ in that the core electrons are frozen when the ground-state coupled-cluster amplitudes are calculated. Furthermore, we decouple transitions out of each d orbital from one another, as this stabilizes convergence and reduces the number of roots required to compute the spectra. All N_4,5-edge spectra feature 30 roots/d orbital, and all EOM-CCSD and CVS-EOM-CCSD calculations are carried out using a development version of the Q-Chem v6.0.2 software package.⁹⁴

We take both scalar and spin–orbit relativistic effects into consideration for all EOM-CCSD and CVS-EOM-CCSD calculations. In both cases, scalar relativistic effects are taken into account via a spin-free exact two-component (X2C) Hamiltonian.^95–101 For the valence EOM-CCSD calculations, we straightforwardly account for spin–orbit effects via the Breit-Pauli Hamiltonian,¹⁰² but because we use spin-polarized orbitals for the CVS-EOM-CCSD calculations, the predicted core excited states are somewhat spin-contaminated. Consequently, we apply simpler atomic spin-orbit corrections to account for spin–orbit coupling in CVS-EOM-CCSD. As we are already decoupling the d orbitals of the I atom from the rest of the system when we calculate the CVS-EOM-CCSD amplitudes, we expect this to be a reasonable approximation. For the excited states, we average the d-orbital transition energies for each transition and apply an empirical ω + 3J_d, ω – 2J_d doublet splitting where J_d is an empirical spin–orbit parameter that modulates the magnitude of the splitting. We set J_d = 0.34 eV in order to match the observed doublet splitting of 1.7 eV for the 4d orbitals of I.¹⁰³ The ground state of the I atom also exhibits substantial spin–orbit effects, with a doublet splitting of 0.9 eV between the ²P_1/2 and ²P_3/2 spin–orbit states. To resolve transitions out of both the true ²P_3/2 ground state and the ²P_1/2 state, we back-correct the ground-state reference energy, E₀, by accounting for the coupling between spin orbitals |p_z⟩ ⊗ |↑⟩ and |p_x,y⟩ ⊗ |↓⟩ (and vice versa). The corrected reference energy splits into E₀ + 2J_p and E₀ – J_p levels, therefore splitting the excitation energies into two spin–orbit channels,

$$\begin{gathered} {\omega }^{\text{SO}}\left({}^2{P}_{3/2}\right)={\omega }^{\text{NR}}+J_p \\ {\omega }^{\text{SO}}\left({}^2{P}_{1/2}\right)={\omega }^{\text{NR}}-2J_p \end{gathered}$$ (1)

where ω^NR is the nonrelativistic excitation energy and ω^SO(X) is the spin–orbit-corrected excitation energies for each excitation channel, X. We set a value of J_p = 0.3 eV for the ground state such that experimentally observed doublet splitting is achieved.^104,105 Finally, the intensities are scaled by the new excitation frequencies to satisfy the expected 2:3 (²D_3/2:²D_5/2) intensity ratio, and all forbidden ²P_1/2 → ²D_5/2 transitions are set to zero oscillator strength. This type of empirical treatment has been quite successful in the description of weak (J ≤ 0.5 eV) spin–orbit couplings; therefore, we expect it to perform similarly well here.^106,107

III. RESULTS AND DISCUSSION

III.A. Valence Electronic Structure and UV/Vis Absorption Spectra of Acetyl Halides.

Due to limited characterization of the valence electronic structure of acetyl halides, particularly AcBr and AcI, we first present theoretical assignments of the UV/visible absorption spectra of acetyl halides with the goal of unraveling the valence excited-state transitions that contribute to the observed spectra. The top panel of Figure 1 juxtaposes EOM-CCSD results with the experimental absorption spectrum of AcCl. The experiment shows one broad absorption feature centered at 5.1 eV with an absorption cross section of approximately 0.1 MBarn. Our calculations predict one bright transition at 5.3 eV due to the n → π* transition of singlet character, as expected from the existing literature. Repeating this exercise for AcBr in the middle panel of Figure 1, we see that the experimental spectrum consists of broad, overlapping features at 4.9 and 5.75 eV, resulting in a peak absorption cross section of approximately 0.3 MBarn. Our calculations reveal bands at 4.7, 5.0, and 5.8 eV. The 4.7 eV transition corresponds to direct excitation into the ³nπ* state, while the one at 5.0 eV arises due to the ¹nπ* state. Interestingly, we find that the high-energy band at 5.8 eV emerges from direct population of the ${}^{3}n{\sigma }_{\text{C}-\text{Br}}^{*}$ state. Hence, our calculations are in agreement with the hypothesis of Lee et al.,⁴⁰ who proposed the possibility of direct UV excitation into a state of $n{\sigma }_{\text{C}-\text{Br}}^{*}$ character at 210 nm (5.9 eV). This finding has significant implications for AcBr photolysis and prompts further investigation of the electronic states involved in AcBr photodissociation dynamics.

Figure 1.

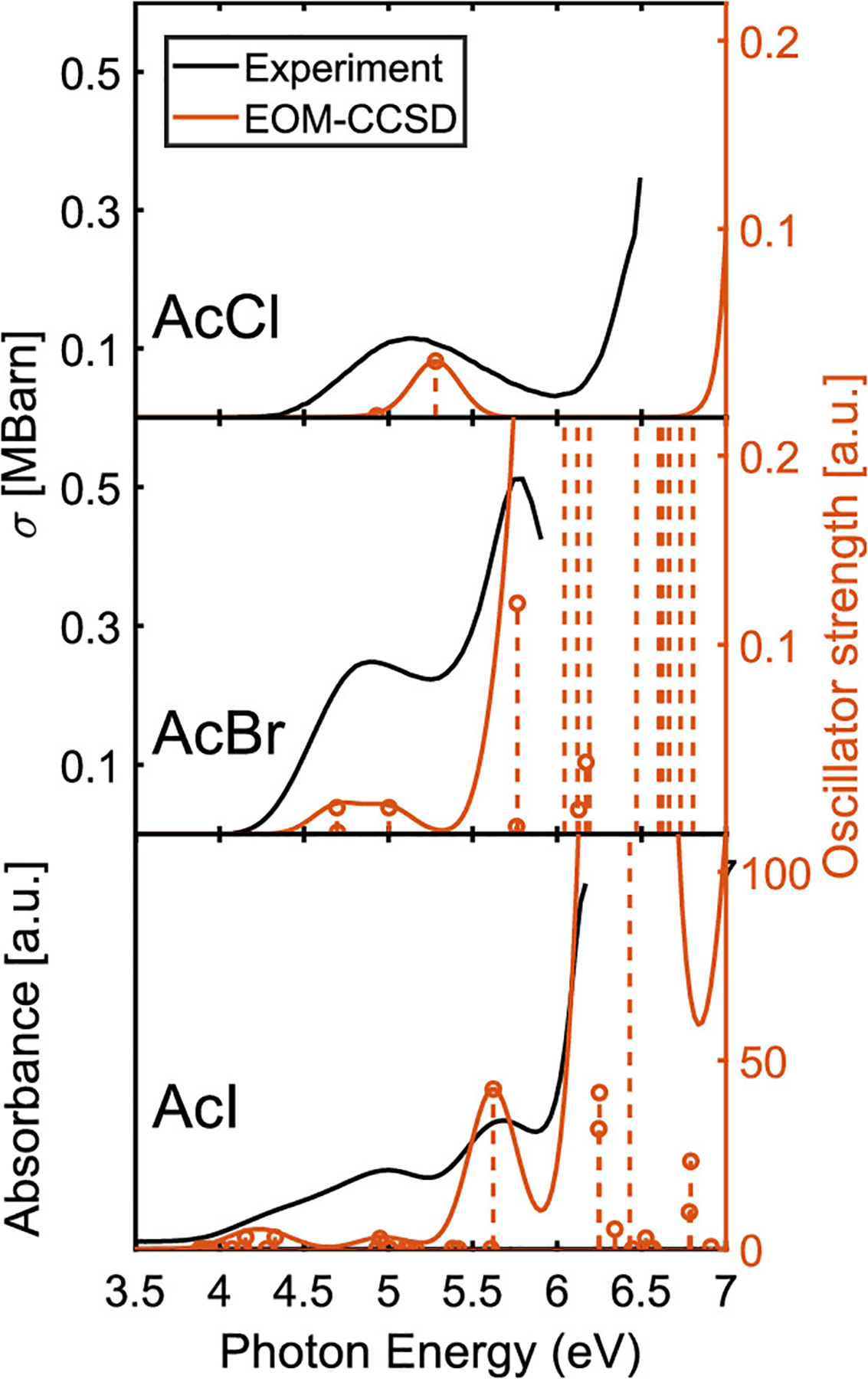
Experimental and calculated UV/visible absorption spectra of gas-phase acetyl halides. Absorption cross sections of gas-phase AcCl (top panel) and AcBr (middle panel) and the absorption spectrum of AcI at 32 Torr static pressure between 3.5 and 7 eV (bottom panel). Experimental data for AcCl and AcBr are reproduced with permission from ref 108, CC BY 3.0 2013, Earth System Science Data, and ref 62, copyright 2007, Royal Society of Chemistry, respectively.

Whereas published UV/vis absorption spectra exist for AcCl and AcBr over a range of wavelengths, the absorption cross section of AcI has been measured previously only by Etzler et al.⁶³ for a small set of wavelengths afforded by mercury emission lines. That work reports an increased absorption coefficient by a factor of approximately 10–20 in AcI compared to that in AcCl. Our experimental measurements extract an absorption cross section in excess of 2–6 MBarn; however, due to the reactivity of AcI with moisture and the lack of appropriate equipment for the rigorous measurement of cross sections, as mentioned in the Methods section, we refrain from reporting any definite numbers for its absorption cross section and limit our discussions to relative absorbance and peak locations. Our experimental UV/vis absorption spectrum of gas-phase AcI reveals absorption bands centered at 5.0 and 5.7 eV, along with a weak shoulder at 4.2 eV. The EOM-CCSD results in the bottom panel of Figure 1 show an offset of ~0.4 eV from the experimental results but remain in reasonable qualitative agreement with experiment, allowing us to make the most complete characterization of the spectrum as reported to date. The calculated spectrum (shifted by −0.425 eV) shows that the two overlapping features that make up the weak shoulder at 4.2 and 4.3 eV correspond to a combination of n → π* and n → σ* transitions of mixed singlet and triplet character. The 5.0 eV feature is also composed of mixed-spin nπ* and nσ* states, while the 5.6 eV feature can be attributed to a mixed-spin n → π* transition. Interestingly, while the UV/visible absorption features in AcCl are dominated by n → π* transitions, our results show that transitions of n → σ* character become more important at lower energies as a function of halogen size. The nσ* states are responsible for just the highest-energy feature in AcBr, while in AcI they are found to be interspersed throughout the entirety of the spectrum. As spin–orbit coupling imposes strong mixing of the accessible states in AcI, we expect to populate largely spin-mixed states on excitation at 266 nm (4.7 eV).

III.B. XUV Absorption Spectrum of Ground-State Acetyl Iodide.

We now lay the groundwork for subsequent discussions of 266 nm excitation-induced changes in the XUV absorption spectrum of AcI near the N_4,5 edge by characterizing the ground-state core-level absorption spectrum. The experimental XUV absorption spectrum of AcI in Figure 2 exhibits sharp absorption features at 50.6, 52.2, 54.3, and 56 eV due to core-to-valence transitions from the iodine 4d orbitals to unoccupied valence orbitals. These four transitions together comprise two doublets that show the expected ~1.7 eV spin–orbit splitting of the ²D_5/2 and ²D_3/2 states with an I(4d) core hole, suggesting that the atomic spin–orbit approximation outlined in the Computational Methods section is reasonable. The spin–orbit-corrected CVS-EOM-CCSD results align quite well with experiment, appearing only slightly shifted by ~0.6 eV relative to experimental features, which is well within the anticipated error margins of CVS-EOM-CCSD of roughly 1 to 2 eV¹⁰⁹ for core excitations. Our errors are likely somewhat smaller because of less-pronounced orbital relaxation effects in the N_4,5 edge relative to K-edge transitions.¹¹⁰ We also note that the calculations overestimate the strength of the absorption of the higher-energy doublet at 54.3 and 56 eV. In any case, the straightforward comparison with experiment allows us to ascribe d → σ* transitions to the features at 50.6 and 52.2 eV and transitions of mixed d → σ*/π* character to the higher-energy doublet features at 54.3 and 56 eV. As we will later discuss, the σ* nature of these excited states is key to understanding the dynamics of C–I bond cleavage, so it is quite promising to see that d → σ* transitions make up a significant contribution to both doublet features.

Figure 2.

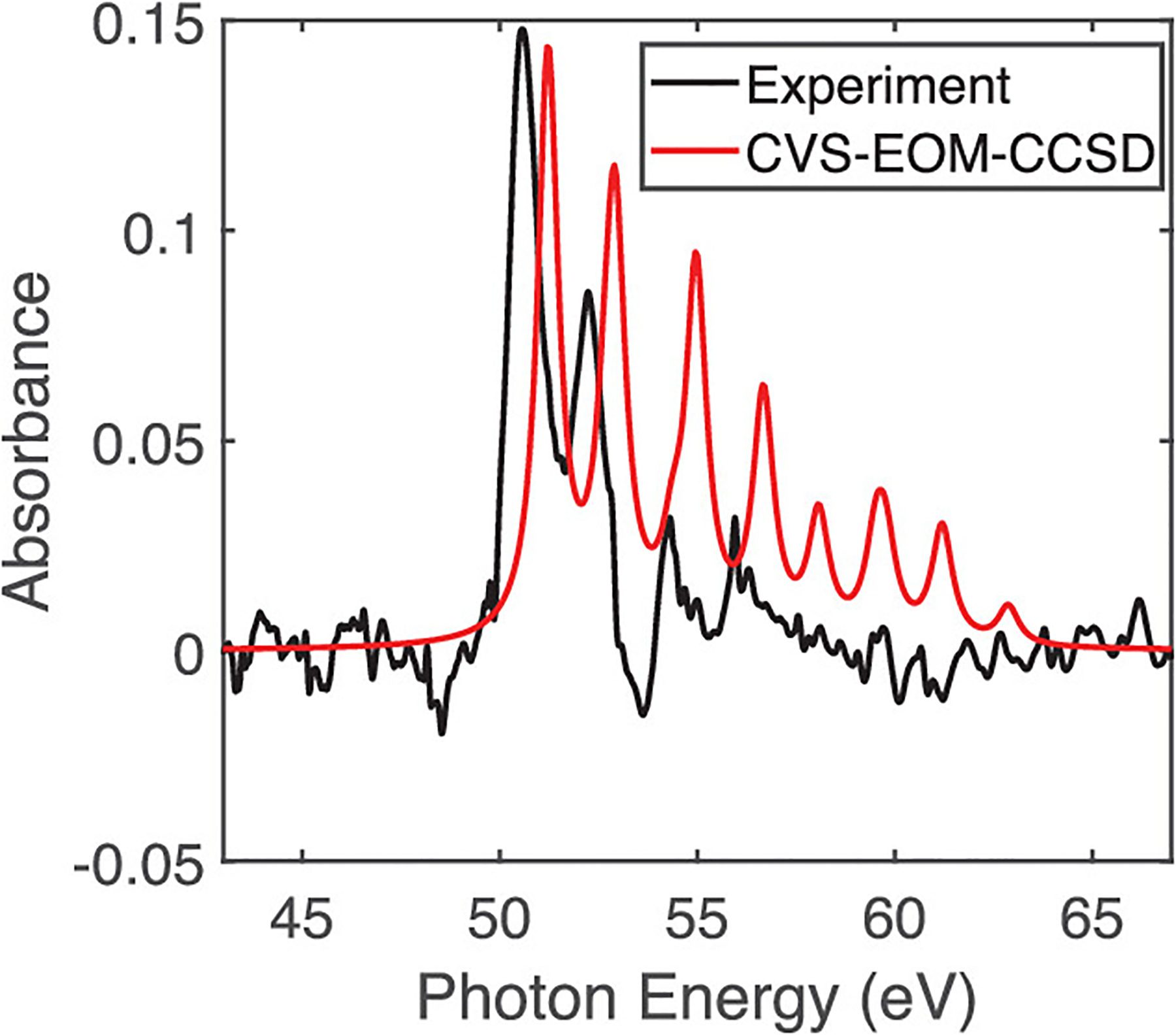
XUV absorption spectrum near the iodine N_4,5 edge of gas-phase AcI at 3 Torr static pressure. The y axis is the measured optical density, defined by OD = log₁₀(I/I₀), where I and I₀ are the intensities of XUV through the interaction region with and without AcI. A broad, unstructured absorption, in excess of 0.45–0.65 OD, due to valence ionization, was subtracted from the experiment. The raw experimental spectrum is shown in Figure S2.

Though not clearly observed in the static XUV absorption spectrum of AcI, the CVS-EOM-CCSD calculations also predict several low-intensity peaks at 58.1, 59.6, 61.2, and 62.9 eV that correspond to 4d→5d transitions. While these d→d transitions are formally symmetry-forbidden, their weak intensity can be attributed to hybridization with orbitals on the acetyl group that acts to break the symmetry of the 5d orbitals. Some example 5d orbitals are shown in Figure S10. In principle, these 4d → 5d transitions could be used to probe C–I bond breaking because as the I··· C₂H₃O distance increases, they lose their hybridization with the C₂H₃O orbitals, thus becoming pure atomic 5d orbitals that strictly satisfy spatial symmetry selection rules. This should cause the 4d→5d transitions to be truly dark in the case of pure iodine and to gradually trend toward zero intensity as the C–I bond is broken. Indeed, in the case of a free I atom (as shown in Figure S14) there are no high-energy 4d→5d transitions in the spectrum. While no sharp absorption lines are observed above 56 eV in our experimental spectrum shown in Figure 2, we observe a broad, negative differential absorbance on the order of <1 mOD surrounding the induced absorption features at 55.5 and 57.5 eV in Figure 3. Furthermore, Figure S3 clearly shows the persistent bleach signal that extends to 65 eV. It is potentially valuable to note that these high-energy features could provide a powerful spectroscopic handle for directly probing C–I dissociation in this and other related systems using attosecond XUV spectroscopy.

Figure 3.

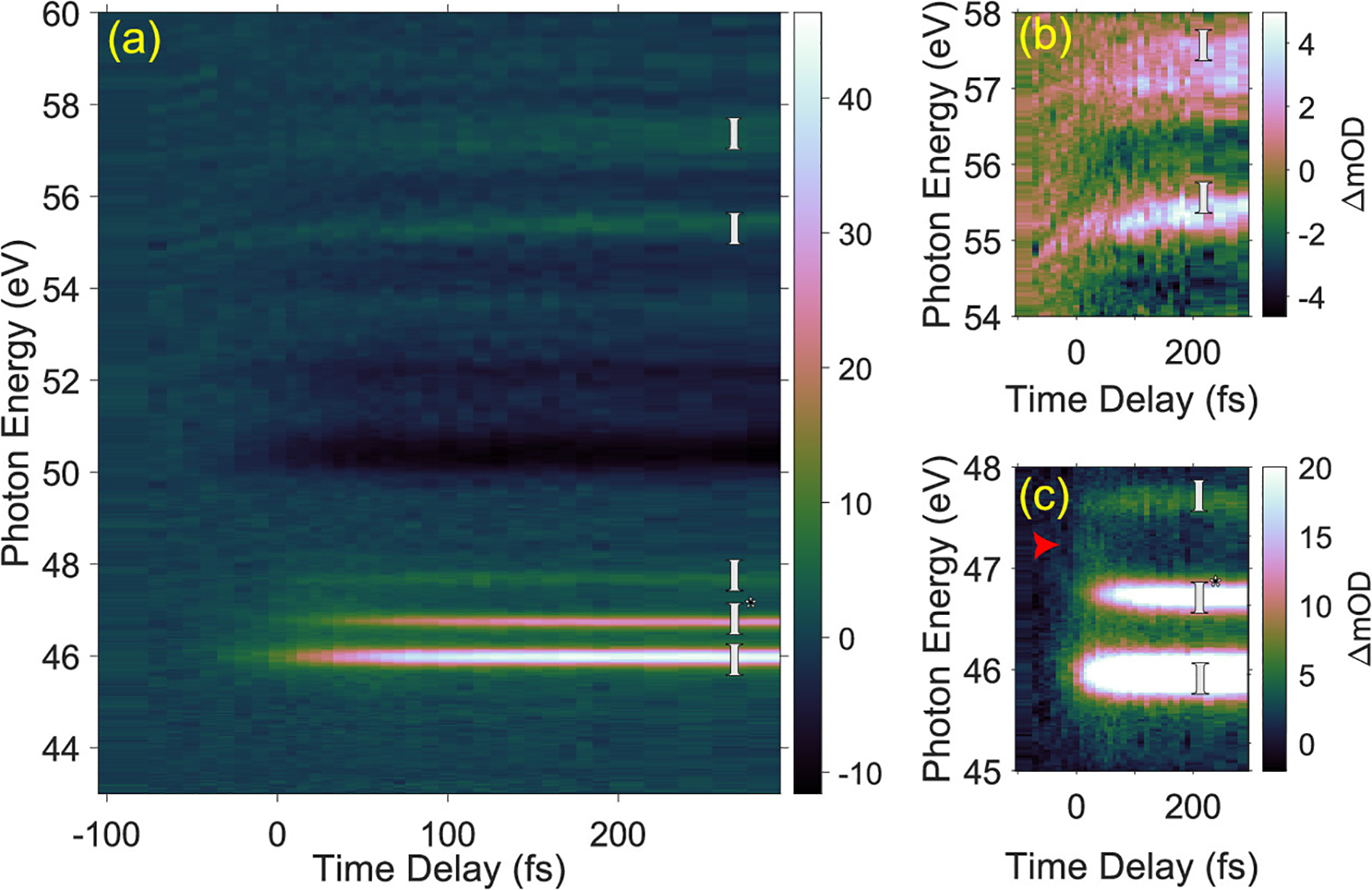
Experimental time-resolved XUV absorption spectra. (a) Time-dependent differential XUV absorption, energy resolved between 43 and 60 eV. Strong bleach features between 50 and 53 eV associated with ground-state acetyl iodide are observed, and sharp induced absorption features due to atomic resonances of free iodine are detected. Time-dependent signatures associated with regions of high interest from 45 to 48 eV and from 54 to 58 eV are shown in panels (b) and (c). (b) Induced absorption between 55.1 and 55.6 eV shifts its center photon energy from 55.3 to 55.5 eV in the first 150 fs after t₀. (c) A weak short-lived signal at 47.1 eV is marked with a red arrow. An alternative color figure is given in Figure S4 in the SI.

III.C. Transient XUV Absorption Spectra and Photodissociation Dynamics of Acetyl Iodide.

We performed XUV-TRAS in AcI in two orthogonal polarization configurations, and while these data show subtle differences in time-dependent behavior near t₀, we restrict our discussion to the data pertaining to parallel pump and probe polarization configurations where both the XUV and UV were p-polarized. (Perpendicular polarization data are reported in the Supporting Information.)

Figure 3a shows a two-dimensional false color map of the change in optical density after 266 nm excitation as a function of the time delay between pump and probe for XUV photon energies of 43 to 60 eV. The location of t₀, when pump and probe coincide in time, is defined by a time-zero measurement in xenon gas, as described in the Experimental Methods section. Measurements of the transient signal were performed in a time window from −300 to 1000 fs, with a 7 fs step size around t₀ to sufficiently sample the early dynamics. Positive delay values indicate the pump pulse preceding the probe pulse. After the first 250 fs, no changes in the differential absorbance are present, and as such, we show data only up to 300 fs in delay. (See Figure S4 for the false color map out to 1 ps.)

At long time delays (Δt > 100 fs), the differential absorption displayed in Figure 3 (and in Figure S3 as an outline) shows bleach features (defined as a negative absorption change) at 50.6, 52.2, 54.3, and 56 eV associated with the depletion of ground-state AcI and induced absorption features (defined as positive absorption changes) associated with atomic resonances of iodine previously assigned to transitions in ground-state I from ²P_3/2 → ²D_5/2 at 46.1 eV, ²P_3/2 → ²D_3/2 at 47.8 eV, and 4d → 6p/7p at 55.5 and 57.5 eV and spin–orbit excited I*(²P_1/2 →²D_3/2) at 46.8 eV.¹¹¹ The atomic iodine features show a spectral width of ~300 meV FWHM, and the experimentally measured branching ratio of I*(²P_1/2 →²D_3/2):I(²P_3/2 →²D_5/2) is 1:1.1, after taking into account the differences in the oscillator strengths between the core-level transitions of I and I*.^36,112 For comparison, in AcCl, the ratio Cl*:Cl is reported to be 3.3:1,⁴¹ and in AcBr, the ratio Br*:Br is 1:2.⁴⁰ Dissociation of the C–I bond in methyl iodide has been reported to yield a I*:I ratio of 3:1,²⁶ whereas in i-C₃H₇I (nearly the same molecular mass as acetyl iodide), an I*:I ratio of 1:2 was observed.³⁶ In alkyl iodides, trends in this ratio as a function of alkyl substitution have been attributed to differences in wavepacket bifurcation at a conical intersection between two electronic states along the dissociation coordinate.³⁶ In AcI, however, cuts through the potential energy surfaces, as shown in Figure S11, reveal the involvement of multiple electronic states in the dissociation dynamics. This is corroborated by the time-dependent state populations extracted from our aiMD simulations (Figure S12), which show that many electronic states participate in the nonadiabatic dynamics leading up to C–I bond dissociation. With so many states involved, a straightforward interpretation of this ratio is complicated.

At short time delays (Δt < 100 fs), additional features are visible near t₀. Figure 3b,c shows the most significant changes on a sub-100-fs time scale seen in the experiment. Aside from the bleach features associated with the loss of ground-state AcI and induced absorption features due to free I/I*, we observe a weak, short-lived feature at 47.1 eV (indicated by an arrow in panel (c)). We also observe a shift in the time-resolved differential absorbance at 55.3 eV, which undergoes a center-of-mass shift to 55.5 eV in less than 200 fs, as shown in Figure 3b.

In Figure 4, we present outlines and fits of selected features as a function of the pump–probe delay. At t₀, the bleach associated with AcI and induced absorption associated with free iodine rise promptly and reach an asymptotic plateau within the first 150 fs. We thus fit this steplike time evolution of these transient features to a Gaussian cumulative distribution function (CDF) convolved with our IRF (σ_IRF = 44 fs). The bleach features at 50.6 and 52.2 eV are measured with a temporal width (σ) of 41 ± 8 fs and no measurable offset with respect to t₀. The induced absorption features associated with free iodine at 46.1 and 46.8 eV both show identical temporal behavior, best described by a CDF with a σ of 47 ± 5 fs and an offset in time of 24 ± 7 fs with respect to t₀. The short-lived feature at 47.1 eV spectrally overlaps with the induced absorption at 46.8 eV, and hence we subtract a scaled CDF function that characterizes the step response of the neighboring induced absorption at 46.8 eV (as detailed in Figure S5 of the Supporting Information). After this subtraction, it is clear that the 47.1 eV feature is mostly confined around t₀. An exponential decay fit (convolved with the IRF) to the time profile of this feature yields an offset of 35 ± 15 fs from t₀ and a temporal width of σ = 30 ± 10 fs. For the 55.5 eV feature, a fit to the shift in energy results in a CDF with a σ of 60 ± 37 fs and an offset in time of −8 ± 27 fs, while a fit to its amplitude using a CDF extracts a σ of 48 ± 20 fs and an offset in time of 60 ± 15 fs. The induced absorption at 57.5 eV does not show a shift in energy but rises with a σ of 89 ± 12 fs and an offset of 84 ± 9 fs.

Figure 4.

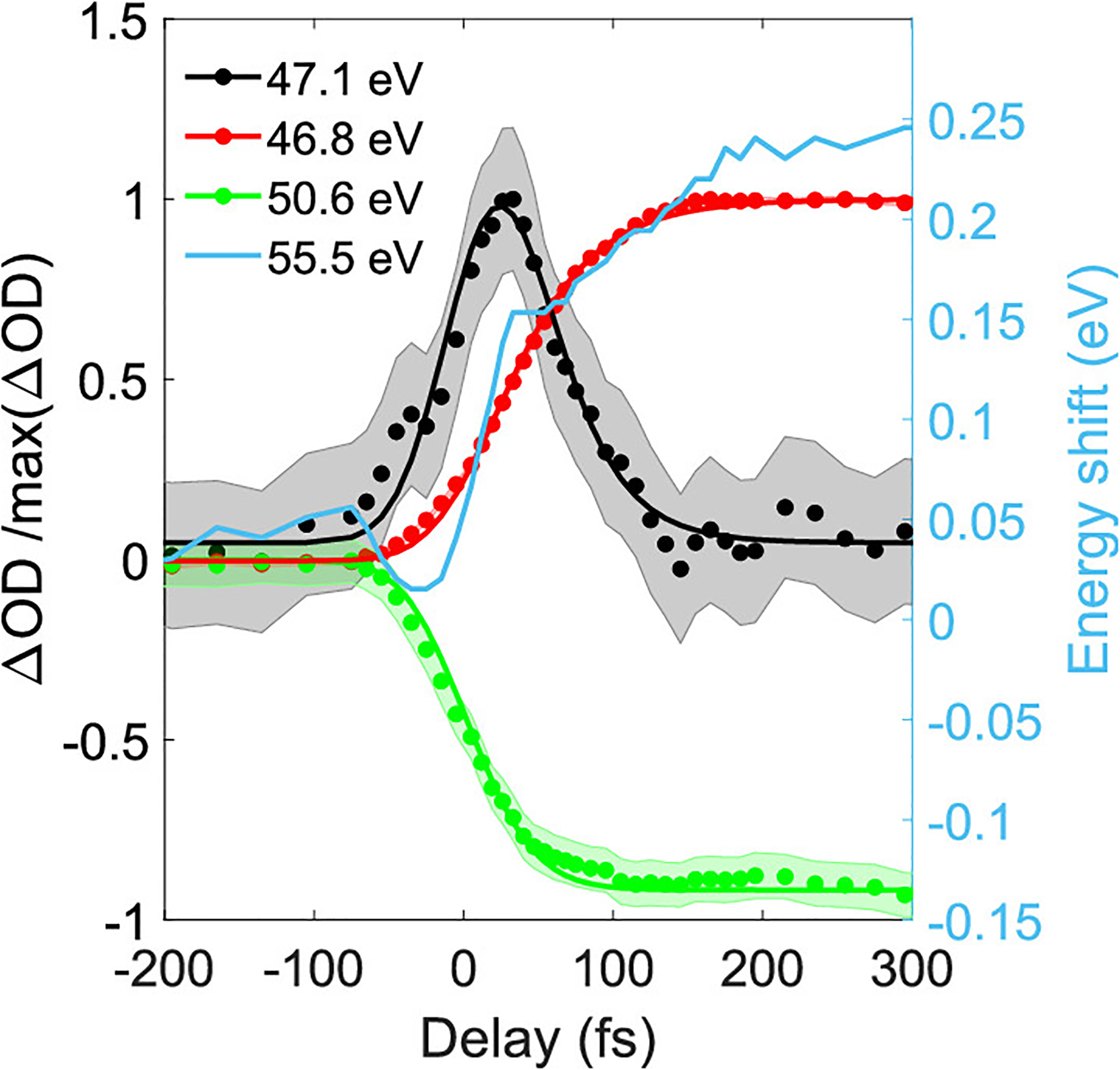
Integrated differential absorbance of individual absorption features, divided by their maximum or minimum, shown as filled circles. Furthermore, a step function has been subtracted from the 47.1 eV outline, as indicated in the text. The shaded region corresponds to the ±1σ error bar. Fits to these time traces are shown in color-matched solid lines. The energy shift of the 55.5 eV feature is shown in light blue.

To begin understanding the dynamics after 266 nm excitation, Figure S11 presents cuts through the potential energy surface for pure singlet and triplet states in AcI as a function of C–I displacement from its equilibrium bond length. This reveals that all spin-pure excited states are inherently dissociative, suggesting that we should expect prompt dissociation of the C–I bond on any optical transition that is accessible via the 266 nm pump. Indeed, our nonadiabatic and spin–orbit-inclusive aiMD simulations corroborate this notion. We begin the dynamics in the lowest-energy bright spin–orbit state (root 12, at 254 nm/4.9 eV) that is most likely to be excited by the 266 nm pump pulse, and we see immediate C–I bond dissociation. We track $\langle {\widehat{S}}^2\rangle$ of the excited state (Figure S13) as a simple metric for bond breaking, as we expect the formation of two doublet radicals homolytic bond cleavage) or $\langle {\widehat{S}}^2\rangle =2$ corresponding to a triplet final state. This supposition is verified by examining the lowest-energy excited state in Figure S11, which is a triplet that corresponds to a spin-flip excitation (p_I→n_Ac) out of the doubly occupied p orbital in a spin-restricted reference, leading to separated I and CH₃CO radicals with an overall triplet multiplicity. $\langle {\widehat{S}}^2\rangle$ tracks well with the C–I distance and reaches a pure triplet state by just 50 fs after initial excitation, corroborating the notion of prompt C–I photolysis. Notably, this metric also correlates very well with the collapse of state populations in Figure S12, wherein many states are involved during the suspected bond-breaking timeline between 30 and 50 fs followed by a collapse into two triplet states that oscillate back and forth after 50 fs due to quasi-degeneracy.

The CVS-EOM-CCSD spectrum of the I atom (Figure S14) helps to contextualize the spectra of AcI at various points throughout the dynamics. Iodine (²P_3/2) exhibits a low-energy doublet with peaks at 45.8 and 47.5 eV that are due to d→5p(β) transitions into the vacant β spin orbital along with a high-energy doublet at 56 and 57.7 eV due to d → 5p(α) transitions. Spin–orbit excited I(²P_1/2) leads to just two peaks at 46.6 and 56.8 eV rather than two doublets because the ²P_1/2 →²D_5/2 transitions are forbidden. Importantly, iodine lacks any of the high-energy 4d → 5d transitions that appear above 56 eV in AcI.

Turning our gaze toward the dynamical picture in Figure 5, we can see the rapid trend in the AcI N_4,5-edge spectrum toward that of pure iodine. By just 80 fs, the spectrum more strongly resembles free I and spin–orbit excited I* than that of t₀ acetyl iodide, again supporting sub-100-fs C–I dissociation.

Figure 5.

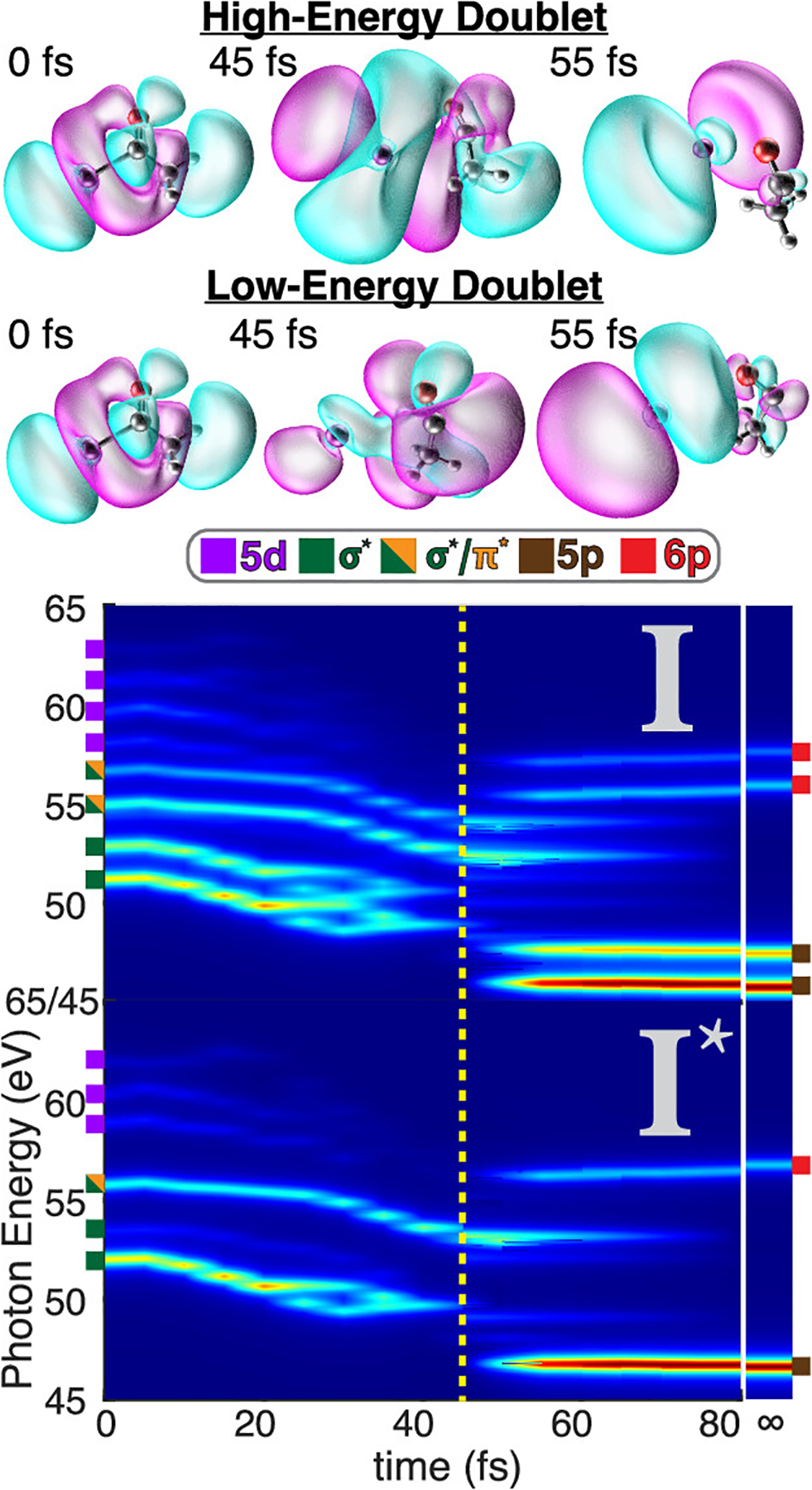
False color map of the CVS-EOM-CCSD N_4,5-edge spectrum along the nonadiabatic aiMD trajectory taken in 5 fs increments. The I (²P_3/2) and spin–orbit excited I* (²P_1/2) excitation channels are shown in the top and bottom spectra, respectively. Colored notches on the left and right sides indicate the transitions (4d→A, where A = 5d, σ*, σ*/π*, 5p, or 6p) that give rise to the features at t = 0 and 80 fs, respectively. The σ* orbitals that contribute to the four lowest-energy features in the AcI (²P_3/2) spectrum are shown above the false color map. The initial σ* orbital (left) becomes distorted as the C–I bond breaks, yielding σ*-like orbitals that still exhibit significant hybridization between I and C₂H₃O fragments at t = 45 fs (center) just prior to bond breaking. After bond breaking (right), the primary transitions take on the character of pure iodine p orbitals. The spectrum of the iodine atom is shown after the break in the x axis as an approximation for t = ∞ to allow comparison to the finite-time spectra.

To show the temporal evolution of the AcI N_4,5-edge spectrum toward I/I* and C₂H₃O, we computed CVS-EOM-CCSD spectra at 5 fs increments throughout the aiMD trajectory and constructed the heat map in Figure 5. From the outset at t = 0 fs until around 50 fs, there is a significant red shift of all peaks in AcI as the C–I bond distance increases, with the exception of one 4d → 5d transition at 63 eV that features a slight blue shift. Interestingly, at times >50 fs the higher-energy doublet hits an inflection point and begins to sharply blue shift. Due to the finite experimental time resolution, this blue shift, manifested clearly in the feature at 55.3 eV, is all that is observed in the experiment (Figure 3b). Interestingly, even at 80 fs, the calculated 4d → 6p transitions at 55.6 eV remain red-shifted from the 4d→6p transitions in free iodine by ~0.3 eV, implying residual (nonbonding) interactions between the acetyl radical and iodine fragments at times exceeding 80 fs. The residual interactions are more clearly seen in the 4d → 6p bands than those associated with 4d → 5p transitions, where the 4d → 5p bands converge to the free-iodine result by about 60 fs. This can be justified by considering that core-excitation energies are strongly influenced by charge donor–acceptor interactions,¹¹³ which are exponentially sensitive to orbital overlap. Because the 6p orbital is far more diffuse than the 5p orbital, it engages in donor/acceptor interaction with the acetyl fragment at longer I···CH₃CO distances and thus at longer times. We thus attribute the blue shift of the 55.3 eV feature seen in the experiment to shifting of the 4d → 6p transition as the iodine continues to depart from the acetyl fragment.

More intriguing is that the C–I homolytic bond cleavage occurs right around 50 fs according to our $\langle {\widehat{S}}^2\rangle$ metric, which is precisely where we predict the inflection point in the high-energy doublet dynamics. The inflection point is punctuated by the disappearance of the $d_{\text{I}}\to {\sigma }_{\text{AcI}}^{*}$ transitions from the spectrum, giving way to d_I → p_I transitions that exhibit far less hybridization, thus taking on more of the character of the d_I → p_I excitations of free iodine and shifting the excitation energies higher. We note that this inflection point occurs near the Coulson–Fischer point (yet another metric for bond breaking),¹¹⁴ which we observe in coincidence with spin-symmetry breaking of the Hartree–Fock reference at times of ≥60 fs.

By shifting the focus to the low-energy doublet in Figure 5, we can see that the very last moments of C–I dissociation are captured by the experimental XUV-TRAS measurements. Namely, the short-lived 47.1 eV feature in Figure 3 can be understood as d_I→p_I/n_Ac, where the primary transition is to a p orbital that is strongly mixed with the unoccupied n_Ac orbital on the acetyl fragment. This resolves by roughly 60 fs, where the C–I bond has been broken, leading to a primary transition of d_I → p_I character with very little orbital mixing. Therefore, we suspect that the 47.1 eV feature in the experiment is the footprint of a small fraction of AcI molecules on the cusp of full dissociation and that this signal rapidly merges with the brighter feature at 46.8 eV. Furthermore, the observed offset of 25 fs in the appearance of the experimental induced absorption corresponding to free iodine at 46.1 and 46.8 eV with respect to the instantaneous appearance of the bleach of AcI is due to a slightly delayed formation of free iodine following electronic excitation of AcI. This is consistent with our theory, which predicts that the growth of free iodine is delayed by 20 fs with respect to the loss of ground-state acetyl iodide signal.

We also note that the 4d→5d transitions predicted by CVS-EOM-CCSD that correspond to the doublets at energies >56 eV in AcI appear as weak features at early times but rapidly subside until they are no longer visible by roughly 40 fs. As we had predicted earlier, this is an indicator that the iodine 5d orbitals are no longer hybridizing with those of the acetyl fragment, taking on pure d-orbital symmetry. In the experiment, we detect a broad, unstructured bleach between 60 and 65 eV that appears promptly and can be associated with the loss of these transitions.

IV. CONCLUSIONS

Herein, we present the first study of the ultrafast excited-state dynamics of acetyl iodide following 266 nm excitation. Our calculations using equation-of-motion coupled-cluster theory with single and double substitutions (EOM-CCSD) reveal that the valence excited states accessed by a 266 nm photon are spin-mixed and spin-pure singlets with nπ* and nσ* character, which are dissociative along the C–I bond. Experimental time-resolved I 4d-to-valence absorption spectra unveil spectral features that evolve on <100 fs time scales, which, through a combination of ab initio molecular dynamics (aiMD) simulations and EOM-CCSD, we ascribe to C–I bond dissociation dynamics. Specifically, EOM-CCSD calculations of the N-edge spectra along the aiMD trajectory show that spectral features of electronically excited AcI prior to dissociation correspond to $d_{\text{I}}\to {\sigma }_{\text{AcI}}^{*}$ transitions at early times that pass through a d_I→p_I/n_Ac intermediate on the verge of C–I bond breaking, finally giving way to d_I → p_I transitions of free I upon C–I dissociation. Additionally, calculations reveal the presence of 4d → 5d transitions that are weakly allowed due to hybridization with the acetyl moiety in intact AcI, which proceed to disappear when the C–I bond breaks and these transitions become strictly forbidden. These predicted transitions turn out to be experimentally detectable as a broad unstructured bleach feature in the transient spectrum.

Whereas our calculations show that UV excitation of AcCl populates states of solely nπ* character, valence-excited states in this energy range in AcI and AcBr also include participation of states of nσ* character. In AcBr, valence states at 4.7 and 5.0 eV have nπ* character, while the state at 5.8 eV has ${}^{3}n{\sigma }_{\text{C}-\text{Br}}^{*}$ character. For AcI, we find that photodynamics are driven by the superposition of nπ* and nσ* states with strongly mixed singlet and triplet character. This interplay of spin-pure singlet and spin-mixed states of different spatial symmetry is also in stark contrast to alkyl halides, where excited states have been described as having singlet or triplet nσ* character. The sub-100-fs lifetimes of the low-energy doublet in the 46–48 eV region observed here show parallels to the dynamics reported for alkyl iodide dissociation.^26,36 In addition, our study reveals and interprets sub-100-fs dynamics in the high-energy doublet near 55 eV, which, to the best of our knowledge, has not been done in ultrafast XUV studies of alkyl iodides.

Our joint experiment–theory investigation has provided spectroscopic signatures of the excited-state dynamics during the primary C–I bond dissociation in acetyl iodide. In particular, we identify avenues for future exploration on attosecond time scales for probing the coupled electronic and nuclear dynamics in real time by closely monitoring the spectral region associated with 4d → 5d transitions. This article was restricted to the investigation of the primary dissociation of AcI; a follow-up time-resolved study of the secondary dissociation of the acetyl radical probed with soft X-ray spectroscopy of the carbon K-edge is forthcoming.