A trusted medical data sharing framework for edge computing leveraging blockchain and outsourced computation

Abstract

Traditional cloud-centric approaches to medical data sharing pose risks related to real-time performance, security, and stability. Medical and healthcare data encounter challenges like data silos, privacy breaches, and transmission latency. In response to these challenges, this paper introduces a blockchain-based framework for trustworthy medical data sharing in edge computing environments. Leveraging healthcare consortium edge blockchains, this framework enables fine-grained access control to medical data. Specifically, it addresses the real-time, multi-attribute authorization challenge in CP-ABE through a Distributed Attribute Authorization strategy (DAA) based on blockchain. Furthermore, it tackles the key security issues in CP-ABE through a Distributed Key Generation protocol (DKG) based on blockchain. To address computational resource constraints in CP-ABE, we enhance a Distributed Modular Exponentiation Outsourcing algorithm (DME) and elevate its verifiable probability to “1”. Theoretical analysis establishes the IND-CPA security of this framework in the Random Oracle Model. Experimental results demonstrate the effectiveness of our solution for resource-constrained end-user devices in edge computing environments.

1. Introduction

The rapid proliferation of digitization in the healthcare sector has generated a vast amount of patient-related medical and health data. Responsible and ethical use of this information is critical to protecting the personal privacy of patients. Scholars have conducted significant research in the effective collection [1] and statistical classification [2] of medical data. However, there are currently various issues associated with the sharing of medical information. Medical data is susceptible to tampering or loss during transmission, making it challenging to facilitate seamless sharing. The phenomenon of ‘data silos' in various healthcare organizations is notably prevalent. Furthermore, most medical data is controlled by healthcare providers, raising concerns about data being transmitted and utilized without the patient's knowledge, leading to security risks and potential conflicts between healthcare providers and patients [3].

Compared to traditional healthcare systems that store user health data and health records in physical paper format, cloud-based healthcare systems have significantly improved efficiency and reduced storage costs over a period of time. However, with the explosive growth of medical data, cloud-based healthcare systems face challenges such as network latency, bandwidth limitations, privacy breaches, and security attacks.

First, the network latency and limited bandwidth of cloud storage can result in slower medical data transmission speeds, thereby reducing the real-time capabilities of healthcare systems. This is particularly critical for applications such as emergency care and surgery that require quickly access to patient data. In addition, medical data frequently needs to be shared among different systems and applications to support healthcare decisions. However, if cloud-based systems encounter network congestion, it can lead to the issue of inconsistencies in medical data, potentially resulting in inaccurate or outdated information.

Second, although outsourcing the storage of patient health data and EHRs to cloud service providers is convenient, efficient, and cost-effective, it results in users relinquishing control over their health data and EHRs upon digitization and cloud storage. On one hand, in the event of a security breach at a cloud service provider, there is a risk of exposing patient health data and other private information. Conversely, cloud service providers and healthcare organizations may face temptations to disclose patient health data or electronic health records for financial gain [4].

Third, cloud storage systems are vulnerable to security attacks. Traditionally, medical data has been predominantly housed in centralized databases or cloud storage systems, which introduce a singular point of vulnerability, leaving them exposed to various threats such as phishing, man-in-the-middle attacks, impersonation, and identity theft [5]. Furthermore, there is the overarching issue of attackers, malevolent users, and hackers cloning or duplicating a range of medical documents.

Yang et al. [6] introduced a CPRE scheme centered around cloud computing facilities, with support for user revocation in cloud environments. This proposed approach demonstrates reduced computational and communication overhead, facilitating easy access to cloud data using resource-constrained devices. Nevertheless, this cloud-centric data sharing strategy is susceptible to single points of failure and communication latency issues.

Edge computing, a technology designed to process data at the network's edge, overcomes the limitations of traditional cloud computing in terms of real-time processing and efficient bandwidth usage. Blockchain technology, recognized as a state-of-the-art approach for ensuring the security and immutability of data, has a broad range of applications in ensuring trust and sharing of data, spanning areas such as VANET [7] and healthcare. As a result, this paper introduces a blockchain-based architecture for secure sharing of medical data in edge computing environments, with the aim of improving both the efficiency and security of data processing in healthcare systems based on the cloud.

CP-ABE functions as a form of public key encryption, facilitating one-time encryption and multi-user sharing. This method plays a crucial role in enabling precise control over data access, ensuring the security of data sharing [8,9]. It has been widely applied in trustworthy data sharing scenarios within edge computing environments [10,11]. For instance, Suyel Namasudra et al. [12] have proposed a secure taxi-sharing system utilizing attribute-based encryption algorithms and re-encryption schemes integrated with blockchain technology. This system provides decentralization, immunity against single point of failure, resilience against collusion attacks, and data leakage prevention. Additionally, the encryption algorithms presented demonstrate remarkable scalability and can be applied to various domains, including the Internet of Things, big data, healthcare, and more.

However, there are several challenges in achieving trustworthy and secure data sharing based on CP-ABE in current edge computing environments:

First, traditional CP-ABE does not meet the real-time requirements of attribute authorization services in edge computing environments. In such environments, where data processing takes place at the network edge, there is a significant demand for real-time services. However, traditional MA-ABE schemes cannot satisfy this real-time requirement.

Second, there is the issue of unreliable edge nodes and the security of CP-ABE keys. In edge computing environments, edge nodes may be vulnerable to physical attacks, malware intrusion, and additional threats that could compromise the security of CP-ABE keys.

Finally, the contradiction between the resource-constrained end devices and the computational complexity of CP-ABE. CP-ABE requires substantial computational resources with the computational effort increasing linearly with the complexity of the attribute set or access policy [13]. This poses a challenge for resource-constrained end devices, especially in edge computing environments, where these devices have limited computational power, storage space, and battery life, making them unable to handle the extreme computational complexity of CP-ABE.

Therefore, the main focus of this paper is to address the challenge of achieving real-time, secure, and computationally efficient medical data sharing in edge computing environments by building on the foundation of CP-ABE data sharing mechanisms and incorporating blockchain technology. The primary contributions of this paper are as follows:

• (1)Propose a Blockchain-based Trusted Data Sharing Scheme in the Edge Computing Environment (BTDS), addressing privacy leakage and data silos issues in medical data sharing.
• (2)To address the real-time requirements of attribute authorization services in edge computing environments, this paper introduces a Distributed Attribute Authorization strategy based on blockchain (DAA). The distributed deployment strategy eliminates the central attribute authority while deploying the Attribute Authorization Center (AC) closer to end-users. This approach achieves a completely decentralized attribute authorization service and ensures real-time requirements for attribute authorization services in the edge computing environment.
• (3)To address the issue of key security in CP-ABE within edge environments, this paper presents a Distributed Key Generation protocol based on blockchain (DKG). This protocol ensures ‘useable but invisible’ privacy protection for the CP-ABE system's master key and user private keys, effectively resolving the problem of key storage in untrusted edge computing environments.
• (4)To address the issue of resource-constrained terminal devices, this paper combines blockchain technology to enhance a distributed modular exponentiation outsourcing algorithm (DME). This algorithm is applied to the encryption and decryption operations of CP-ABE, and its verifiability probability is improved to ‘1'.
• (5)This paper conducts a formal correctness and security analysis of the proposed BTDS architecture, along with the design of simulation experiments. The results demonstrate the effectiveness of the BTDS architecture for resource constrained end devices in edge computing environments.

The paper is structured as follows: In Section 2, we discuss relevant previous research. Section 3 provides the necessary background to comprehend the proposed architecture. Section 4 presents the system model, along with formal definitions and security considerations for the BTDS architecture. Section 5 delves into the specific implementation details of BTDS. Section 6 is dedicated to correctness and security proofs. Section 7 showcases the experimental results and offers a performance analysis. Finally, in Section 8, we draw our conclusions and outline directions for future research.

2. Related work

2.1. Medical data sharing based on blockchain

In the field of blockchain-based medical data sharing, numerous researchers have conducted valuable demonstration studies. Li et al. [14] introduced and implemented a lightweight blockchain-based solution for medical data sharing. They employed proxy re-encryption techniques to ensure secure data sharing among healthcare professionals and patients, as well as between patients themselves. VIKAS JAIMAN and colleagues [15] introduced a data sharing framework that incorporates standardized ontology consent and data request models, drawing from the DUO and ADA-M models. They also devised a smart contract to automate a universal consent model, which underwent testing on the LUCE data sharing platform.

Pratima Sharma et al. [16] conducted an analysis of the substantial security and privacy challenges encountered by traditional healthcare systems. Subsequently, they developed a contemporary decentralized application tailored for healthcare departments, harnessing blockchain-based Internet of Things (IoT) systems. PRATIMA SHARMA et al. [17] introduced a distributed architecture for a healthcare system featuring privacy protection, employing blockchain technology. They developed a distributed application designed for the creation and access of healthcare certificates. Renpeng Zou et al. [18] addressed the challenge of inefficient data retrieval in blockchain-based electronic health systems. They introduced an electronic health system named SPChain, which is built on blockchain technology and is dedicated to medical data sharing and privacy protection. To expedite data retrieval, the solution incorporates special key blocks and mini-blocks for patients to store their electronic medical records. Additionally, they implemented a reputation system to incentivize the participation of medical institutions in SPChain.

Exploring the integration of blockchain technology for medical data sharing within an edge computing environment is a pivotal research direction. Alaa Awad Abdellatif et al. [19] have introduced an innovative collaborative healthcare system that utilizes both edge computing and blockchain technologies to facilitate efficient and large-scale medical data exchange. RAIFA AKKAOUI et al. [20] have introduced an authentication and authorization framework known as EdgeMediChain for the sharing of health data. This comprehensive framework encompasses EMRs and PHD generated by Medical Internet of Things (MIoT) devices, utilizing the synergy of edge computing for scalability and blockchain technology for enhanced security.

2.2. Data sharing in edge computing environments based on CP-ABE

Considerable research efforts have been dedicated to addressing the challenge of data sharing based on CP-ABE within edge computing environments. In the context of real-time attribute authorization services in edge computing environments [21,22], Alshehri et al. [23] introduced the concept of fog node alliances and proposed a distributed authorization scheme based on blockchain and fog node alliances to tackle issues related to time delays and communication overhead among fog nodes. Additionally, Fargana J et al. [24] introduced a Fog Computing layer positioned between the cloud and users, aimed at mitigating the heightened risk of data errors occurring during network transmission.

In the realm of CP-ABE key security research [[25], [26], [27], [28]], Li et al. [29] introduced an innovative online/offline multi-authority CP-ABE scheme. This scheme leverages password reverse firewalls to safeguard against backdoor attacks and enhances the efficiency of MA-CP-ABE through an online/offline approach, consequently reducing storage and computational burdens for users. Remamany et al. [30] put forward a CP-ABE scheme based on Bloom filters. Within this scheme, the access policy is individually examined during the key generation process to ensure the integrity of access policies, thereby fortifying key security. Cheng et al. [31] introduced a CP-ABE scheme rooted in cloud-fog computing. This approach incorporates white-box tracing, maximum user access counts, and reward-penalty mechanisms to establish robust defenses against key leakage. Employing artificial intelligence to mitigate network security risks [32] is also a viable strategy for enhancing CP-ABE key security. For instance, Mohammad Kazim Hooshmand et al. [33] devised a method for network anomaly detection utilizing deep learning techniques.

Addressing the issue of resource-constrained devices in the edge computing environment, researchers have started exploring solutions focusing on the outsourcing of CP-ABE [[34], [35], [36], [37], [38], [39]]. A common approach in these studies is to offload some computational tasks to more powerful devices or cloud servers to reduce the computational burden on resource constrained devices. Touati et al. [40] enabled resource-constrained sensor nodes to implement CP-ABE within an Internet of Things (IoT) environment by orchestrating collaborative efforts among diverse nodes. This process entailed the delegation of computationally intensive operations to a group of auxiliary nodes.

Kiraz et al. [41] proposed a novel algorithm for outsourcing modular exponentiation operations securely to a single trusted cloud server while ensuring the correctness of computations. This algorithm is known to be the most efficient solution that utilizes a single untrusted server and provides the best verifiability probability. Moffat et al. [42] conducted an extensive review of CP-ABE applications in mobile cloud computing and the Internet of Things (IoT). The article underscores that, given the heterogeneity and resource limitations of IoT devices, applying research findings from mobile devices to attribute-based encryption within the IoT domain represents a significant avenue of research.

Li et al. [43] applied secure outsourcing algorithms for exponentiation to CP-ABE schemes and achieved the concealment of both the base and exponent information while supporting verifiability of the computation results. However, the probability of correct verification in their approach is only 1/2. Yan et al. [44] improved the modular exponentiation outsourcing algorithm based on the work of Li et al. [43] and applied it to the encryption and decryption phases of ciphertext-policy attribute-based encryption, increasing the verifiability probability to 1.

In summary, researchers have made valuable contributions to address the challenges associated with CP-ABE attribute authorization service real-time requirements in edge computing environments, protecting CP-ABE System Key security, and achieving efficient CP-ABE computation on resource constrained devices. However, these approaches, while partially addressing the aforementioned issues, still have limitations. While the work in Ref. [23] addressed the time delay and communication overhead between fog nodes, ensuring real-time attribute authorization services in large-scale edge computing environments remains a challenge. Although online/offline key generation techniques and cryptographic reverse firewalls, as seen in Refs. [[29], [30], [31]], can enhance the security of CP-ABE keys, preventing key leakage in an unreliable edge computing environment is an issue that needs additional attention. Additionally, while offloading some computational tasks to more powerful devices or cloud servers, as explored in Refs. [[40], [41], [42], [43], [44]], can alleviate the computational burden on resource-constrained devices, achieving efficient CP-ABE computations in edge environment while ensuring computational correctness remains an urgent challenge.

3. Preliminary knowledge

The notation used in this paper is presented in Table 1.

Table 1.

Symbol description.

Symbol	Description	Symbol	Description
$\lambda$	Security parameter	$m$	Plaintext
$PK$	Public key	$T$	Access structure
$MSK$	Master private key	$CT$	Ciphertext
$A$	System attributes	$C{T}_m$	Intermediate ciphertext
$S$	User attributes	$C{T}^{\prime }$	Partially decrypted ciphertext
$TK$	Transformation key	${\psi }_i$	Public key fragment
$SK$	User private key	${\kappa }_i$	Private key fragment

3.1. Bilinear mappings

According to the standardized definition provided in Ref. [45], let $q$ be a large prime number, and ${\mathbb{G}}_1,{\mathbb{G}}_2$ be two groups of order $q$ with operations called addition and multiplication, respectively. The bilinear map $e:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_2$ from ${\mathbb{G}}_1$ to ${\mathbb{G}}_2$ satisfies the following property [46].

• (1)Bilinear: The mapping is said to be bilinear if, for any $P,Q,R\in {\mathbb{G}}_1$ and $a,b\in Z$, $e\left(aP,bQ\right)=e{\left(P,Q\right)}^{ab}$, or $e\left(P+Q,R\right)=e\left(P,R\right)·e\left(Q,R\right)$ and $e\left(P,Q+R\right)=e\left(P,Q\right)·e\left(P,R\right)$.
• (2)Non-degenerate: The map doesn't map all the elements in ${\mathbb{G}}_1\times {\mathbb{G}}_1$ (that is, the even elements) to the unit in ${\mathbb{G}}_2$. Since ${\mathbb{G}}_1,{\mathbb{G}}_2$ is an order prime group, this means that if $P$ is a generator of ${\mathbb{G}}_1$, then $e\left(P,P\right)$ is a generator of ${\mathbb{G}}_2$.
• (3)Computability: For any $P$ and $Q$ in ${\mathbb{G}}_1$, there exists an effective algorithm to compute $e\left(P,Q\right)$.

3.2. LSSS

A secret sharing scheme $\prod$ on a set of parties $P$ is referred to as a Linear Secret Sharing Scheme (LSSS) on $Z_p$ if it satisfies the following conditions:

• (1)The secret share distributed to each entity consists of a vector in $Z_p$.
• (2)For a secret sharing scheme $\prod$, there exists a matrix $M$ of $\mathcal{l}\times n$, and the mapping function $\rho$ maps each row of the matrix to an associated party. For $i=1,...,\mathcal{l}\text{,}\rho \left(i\right)$ represents the participant associated with the $ith$ row. Consider a column vector $\overrightarrow{v}={\left[s,y_2,y_3,...,y_n\right]}^T$, where $s$ is the shared secret in $Z_p$, and $y_i$ is a random value for $i=2,...,n$. According to the scheme $\prod$, the matrix $M\overrightarrow{v}$ represents the secret $s$ being shared into $\mathcal{l}$ secret shares, where ${\lambda }_i={\left(Mv\right)}_i$ represents the secret share held by participant $\rho \left(i\right)$.
• (3)In a linear secret sharing scheme with linear refactoring features, if $S$ is a set of access authorizations in $A$, there exists a constant ${\left\{w_i\in Z_p\right\}}_{i\in I}$ such that $\sum _{i\in I}{w}_i{\lambda }_i=s$, where ${\lambda }_i$ is an effective share of the secret $s$ held by participant $\rho \left(i\right)$, and $I=\left\{i:\rho \left(i\right)\in S\right\}$.

3.3. Blockchain

Blockchain technology embodies an innovative distributed infrastructure and computational paradigm that harnesses the data structure of blockchain for data verification and storage. It employs a distributed node consensus algorithm to facilitate data generation and updates, while ensuring secure data transmission and access through cryptographic methods. Additionally, it relies on smart contracts, which consist of automated script code, for data programming and manipulation [47].

Blockchain functions as a decentralized ledger within a peer-to-peer network, with each participating node maintaining a complete copy of the ledger [48,49]. This redundancy guarantees data accessibility, even in the event of a single node failure, effectively mitigating the risk of data loss. Blockchain technology possesses several noteworthy characteristics, including decentralization, immutability, traceability, high trust, and high availability [50].

3.4. DBDHE

Let $p$ be a large prime number, ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ be two cyclic groups of order $p$, and $g$ G be a generator of ${\mathbb{G}}_1$. We define $e:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_2$ as a bilinear mapping. Given a set of elements: $h,g,g^{{\sigma }^1},...,g^{{\sigma }^n},g^{{\sigma }^{n+2}},...,g^{{\sigma }^{2n}}$, the objective of the decisional bilinear Diffie-Hellman problem is to determine whether $Z=e\left(h,g^{{\sigma }^{n+1}}\right)$ or $Z=R_1$, where $R_1\in {\mathbb{G}}_2$. The advantage of the attacker $\mathcal{A}$ in solving the decisional bilinear Diffie-Hellman exponent (DBDHE) problem is defined as follows: $Ad{v}_{DBDHE}\left(\mathcal{A}\right)=\left|\mathrm{Pr}\left[Z=e\left(h,g^{{\sigma }^{n+1}}\right)\right]-\mathrm{Pr}\left[Z=R_1\stackrel{R}{\leftarrow }{\mathbb{G}}_2\right]\right|$. If $Ad{v}_{DBDHE}\left(\mathcal{A}\right)$ is less than a negligible value, then the DBDHE problem is considered difficult.

3.5. Edge computing Outsourcing Framework

Li et al. [51] proposed a secure and verifiable framework for outsourcing edge computing tasks, utilizing multiple non-collusive edge nodes. The framework involves two types of participants. Users with limited computing resources aim to outsource computationally intensive tasks, denoted as $F\left(\right)$, to edge nodes that possess substantial computational capabilities. However, due to concerns regarding trustworthiness, users cannot fully rely on the edge nodes. The edge nodes are assumed to be non-collusive, meaning they do not collaborate to compromise data privacy [52]. In order to safeguard the data privacy of the edge nodes, the user performs a transformation on the original input $x$, resulting in a modified input denoted as $x^{\prime }$. Following the transformation of the input $x^{\prime }$, the user divides it into individual components $\left(x_1^{\prime },x_2^{\prime },...,x_i^{\prime },...,x_n^{\prime }\right)$. These components are then transmitted separately to the edge nodes, along with the computational task $F\left(\right)$. Each edge node $i$ is responsible for executing the corresponding computation task $F\left(x_i^{\prime }\right)$ using the received input $x_i^{\prime }$. Upon completion, the edge node generates a response $y_i^{\prime }$. Users can collect the responses $\left\{y_1^{\prime },y_2^{\prime },...,y_i^{\prime },...,y_n^{\prime }\right\}$ and evaluate them to verify the correctness of the overall result $y^{\prime }$. If the result is validated, the user can recover the real result $y$ from the evaluated result $y^{\prime }$. Otherwise, if the validation fails, the user outputs “error” [53].

The proposed algorithm's overall framework consists of the following modules:

• (1)Precompute Module: This module precomputes static parameters to accelerate processing.
• (2)Problem Transformation Module: In this module, the user transforms the computational input $x$ into an encoded value $x^{\prime }$. Additionally, the user generates and stores a secret value ${\theta }_x$ for the verification and recovery process.
• (3)Problem Resolution Module: In this module, the encoded input $x^{\prime }$ is divided into separate components $\left(x_1^{\prime },x_2^{\prime },...,x_i^{\prime },...,x_n^{\prime }\right)$. The user then transmits each component along with the computation task $F\left(\right)$ to the respective edge node.
• (4)Calculation Module: In this module, the edge nodes perform the computation task $F\left(\right)$ based on the received encoded input $x_i^{\prime }$. Each edge node computes the result $y_i^{\prime }=F\left(x_i^{\prime }\right)$ corresponding to its assigned component.
• (5)Results Module: In this module, the user collects the encoded results $\left\{y_1^{\prime },y_2^{\prime },...,y_i^{\prime },...,y_n^{\prime }\right\}$ from the edge nodes. These results are then merged to obtain the overall encoded result $y^{\prime }$.
• (6)Validation Module: In this module, the validity of the encoded result $y^{\prime }$ is verified using the secret value ${\theta }_x$. If the encoded result is valid, the output is set to 1; otherwise, it is set to 0.
• (7)Recovery Module: In this module, the user can recover the true results $y$ based on the encoded result $y^{\prime }$ and the secret value ${\theta }_x$.

4. Methodology

This section begins by describing the system model of BTDS, including the overall architecture, entity composition, and workflow. Subsequently, the algorithms involved in the scheme are formally defined. Finally, we present a security model for BTDS.

4.1. System architecture

The Trusted Medical Data Sharing Architecture in Edge Computing Environment (BTDS) in an edge computing environment is illustrated in Fig. 1. This architecture can be divided into three layers: End-user layer, edge service layer, and cloud storage layer. The End-user layer consists of Data Owners (DO) and Data Users (DU). The edge service layer includes Attribute Authorities (AA) and the Outsourcing Service Provider (OSP). The cloud storage layer comprises the Medical Cloud Computing Center (Cloud). The specific functions of the six participants in the BTDS architecture are as follows:

• (1)Data Owner (DO): DO, as the patient, is the owner of medical data (e.g., electronic health records) and holds the data's ownership. DO encrypts the original data by specifying access policies from electronic health records.
• (2)Data User (DU): DU, as a healthcare professional, typically a doctor, is the user of medical data. DU can only use the user's private key assigned by the medical institution alliance blockchain when their user attribute set (system privileges) satisfies the access policy set by the patient. This allows DU to further decrypt the ciphertext to obtain plaintext electronic health records.
• (3)Attribute Authorization Center (AC): Each healthcare institution serves as an Attribute Authority (AA) node in the CP-ABE algorithm. AA nodes elect shard representatives to act as Attribute Authorization Centers (AC) within the shard. ACs are responsible for providing attribute authentication and key distribution services to users within the shard.
• (4)Edge Blockchain (EBC): EBC is the edge blockchain composed of AA nodes, also known as the medical alliance blockchain. EBC has two roles: first, it adds an additional security verification mechanism to traditional medical cloud storage by storing cryptographic digests of medical data. Second, it provides distributed and secure key generation for CP-ABE.
• (5)Outsourcing Service Provider (OSP): OSP is a computing outsourcing service provider composed of AA nodes, responsible for the distributed execution of modular exponentiation operations outsourced by DO and DU.
• (6)Medical Cloud Computing Center (Cloud): Medical ciphertext data files uploaded by patient DO are stored on the medical cloud server.

Fig. 1.

The BTDS architecture.

The specific steps for patient A, who generates an electronic medical record at hospital A with doctor A, to share this record with doctor B at hospital B are shown in Fig. 1 as follows.

• Step 1Patient A arrives at hospital A for medical treatment, where doctor A generates electronic medical record information for patient A.
• Step 2After medical treatment, patient A can choose to synchronize their electronic medical record with the medical institution consortium, enabling future cross-domain medical treatment. The process of uploading an electronic medical record consists of using an edge outsourcing service on a patient's mobile device to upload an electronic medical record with attribute-based encryption to a medical cloud server. In addition, a cryptographic digest of the electronic medical records is uploaded to the Medical Institutions Alliance blockchain for verification.
• Step 3When patient A visits hospital B for medical treatment for the second time, doctor B can easily access patient A's electronic medical records from the medical cloud server using their own identity privileges, which are verified via the Medical Institutions Alliance blockchain.

The execution of CP-ABE encryption in BTDS architecture consists of three phases. The details of the process are as follows:

• (1)System Initialization Phase.

The BTDS architecture network is initially set up using the DAA sub-algorithm. Subsequently, the EBC initiates the system initialization smart contract of the CP-ABE master algorithm, leading to the distributed generation of the system's public key, master private key, and public parameters.

• Step 1Initially, the system employs the K-Means algorithm to perform preliminary partitioning of DUs and AAs based on their geographic association. Subsequently, within each partition, the AAs elect the AA with the best performance as the AC for that partition, which is responsible for serving the terminal users within that partition.
• Step 2The EBC executes the smart contract for system initialization within the CP-ABE algorithm, resulting in the generation of the system's public parameters. Each AA independently generates fragments of the system's public key and master private key. These key fragments are embedded within transaction blocks on the blockchain, while the fragments of the master private key are securely retained.
• (2)Data Encryption Phase.

The DO employs the CP-ABE main algorithm for attribute-based encryption on the original data. Subsequently, the encrypted data is uploaded to the medical cloud storage center. Simultaneously, the DO uploads the digest's hash value to the EBC. In this process, the DO utilizes the DME sub-algorithm to outsource the complex modular exponentiation computations to the OSP.

• Step 1The DO specifies the access policy and carries out simple exponentiation and XOR operations on the data.
• Step 2The DO utilizes the DME sub-algorithm to outsource the complex modular exponentiation computations to the OSP.
• Step 3The OSP returns a portion of the ciphertext for the data. The DO verifies the results returned by the OSP. Upon successful verification, the DO combines them with its own computed results to form the complete data ciphertext.
• Step 4The DO uploads the ciphertext to the Cloud and transmits the hash value of the data, which is packaged and then sent to the EBC.
• (3)Data Decryption Phase.

• In the data decryption phase, the DU initially downloads the ciphertext from the medical cloud storage center and then sends a request for the decryption key to the AC associated with the corresponding shard. Subsequently, the DU executes the decryption algorithm provided by the CP-ABE scheme. Successful decryption is contingent on the attribute set of the DU aligning with the access structure defined for the ciphertext.

• Step 1The DU initiates a request for a private key from the AC node of their shard, providing their attribute set. The AC node subsequently returns the requested private key to the user.
• Step 2The DU proceeds to download the complete ciphertext from the Cloud and conducts a comparison between the hash of the downloaded ciphertext and the hash of the ciphertext stored on the EBC. If a match is found, the decryption process continues. However, in the event of a mismatch, the user's data access attempt fails, triggering a system alert.
• Step 3If the user's attribute set meets the access policy requirements defined in the ciphertext, the DU proceeds to outsource the exponentiation and bilinear pairing operations to the OSP. This is achieved using a transformation key to obtain partial plaintext results.
• Step 4The OSP returns the computation results, which are partial plaintext results. The DU utilizes the decryption key to compute the complete plaintext results.

4.2. Formal definition of main algorithm: CP-ABE

• (1)$Setup\left(1^{\lambda },{\left\{\mathrm{0,1}\right\}}^{*}\right)\to PP$. The system invokes the sub-algorithm DAA to create the EBC. The algorithm for uploading the EBC is established, and the public parameter smart contract is executed by the designated endorsement node. The algorithm takes as input the security parameter $\lambda$ and the system attribute set ${\left\{0，1\right\}}^{*}$, yielding the system public parameter $PP$ as the output.
• (2)$Encrypt\left(PP,m\in {\left\{\mathrm{0,1}\right\}}^{\lambda },T\right)\to CT$. The algorithm is executed collaboratively by DO and OSP. The input to the algorithm includes the system public parameters $PP$, the plaintext $m$, and the access structure $T$. Initially, the DO triggers the DKG sub-algorithm to calculate the system public key and conduct partial encryption operations. Subsequently, the OSP employs the DME sub-algorithm to produce the partial data ciphertext, denoted as $C{T}_m$. Ultimately, the complete data ciphertext, denoted as $CT$, is generated through the encryption operation carried out by the DO.
• (3)$KeyGen\left(PP,S\right)\to SK$. The key generation algorithm is executed by the AC fragment. It accepts the system public parameters $PP$ and the user attribute set $S$ as inputs. DU initiates a request to AC for the key with its user attribute set $S$. Subsequently, the AC initiates the DKG sub-algorithm to generate the user private key designated for DU.
• (4)$Transform\left(TK,CT\right)\to C{T}^{\prime }$. The algorithm is performed by OSP using the transformation key $TK$ and the ciphertext $CT$. OSP executes the decryption operation to generate the converted ciphertext $C{T}^{\prime }$.
• (5)$Descrypt\left(SK,C{T}^{\prime }\right)\to m$. The algorithm is performed by DU using the decryption key $SK$ and the converted ciphertext $C{T}^{\prime }$. DU executes the decryption operation to generate the complete data plaintext $m$.

4.3. Security model

• A.Goals of the Proposed Work.

The BTDS architecture outlines the following design objectives:

• 1)Access control: Privacy breaches are the number one challenge for medical data sharing systems. Traditional medical cloud storage systems, which are based on cryptographic methods, do not allow users to decide the key-sharing process. When users upload their data to a cloud storage center, they relinquish control over their personal data, making it susceptible to potential data breaches. Therefore, the BTDS architecture, which relies on CP-ABE encryption, necessitates fine-grained access control to safeguard the data owner. This ensures that while achieving privacy protection for medical data, patients also retain autonomous control over their personal medical data.
• 2)Security: Security during medical data sharing is one of the primary objectives of the BTDS architecture. The proposed CP-ABE scheme, which is based on blockchain and multiple attribute authorities, must ensure load balancing, verifiability, secrecy, and protection against collusion attacks.
• 3)Performance: For edge computing with high real-time requirements, achieving lightweight and efficient CP-ABE is crucial. An efficient system is necessary, so efforts are made to ensure that the computational and communication overhead of the proposed BTDS architecture remains within reasonable limits.
• B.Correctness Definition

Definition 1: Correctness of BTDS, that is, assuming that each algorithm in the scheme is executed exactly, correct results will always be obtained. For example, $neg\left(\lambda \right)$ is a negligible function of the security parameter $\lambda$.

$$\mathrm{Pr}\left[\begin{array}{c}Setup(1^{\lambda },{\left\{\mathrm{0,1}\right\}}^{*}\to PP\\ Encrypt\left(PP,m\in {\left\{\mathrm{0,1}\right\}}^{\lambda },\left(M,\rho \right)\right)\to CT\\ KeyGen\left(PP,S\right)\to SK\\ Transform\left(TK,CT\right)\to C{T}^{\prime }\\ Descrypt\left(SK,C{T}^{\prime }\right)\to m\end{array}\right]\ge 1-neg\left(\lambda \right)$$ (1)

• C.Security Definition
• 1)Zero-Knowledge Property of DKG and DME

In the context of distributed key generation and distributed outsourcing of modular exponentiation computation, we aim to ensure that any participant in the system cannot acquire sensitive information (such as private keys) from other participants and cannot obtain any information about the plaintext from the OSP, while still being able to verify the correctness of the obtained results. In the following, we define the zero-knowledge property of distributed keys and outsourced computation results in this model through security experiments. The attacker $\mathcal{A}$ is allowed to communicate with any participant in the system, including Attribute Authorization Centers (AC) and Outsourcing Service Providers (OSP). The task of $\mathcal{A}$ is to attempt to obtain the private information of other participants, including private keys and detailed results of outsourced computations, while deceiving the system to verify the correctness of the computation results. The design of the security experiment is as follows:

$$\begin{array}{l}Ex{p}_{\mathcal{A}}^{Zero-Knowledge}\left[PP,SK,C,\lambda \right]\text{:}\\ PP\leftarrow Setu{p}_{DME}\left(u,a,p\right)\text{;}\\ \left(SK,C\right)\leftarrow \mathcal{A}\left(PP\right)\text{;}\\ ifCheckZeroKnowledge\left(SK,C\right)=1\text{:}\\ output1\text{;}\\ else\text{:}\\ output0\text{;}\end{array}$$ (2)

In the above experiment, the attacker $\mathcal{A}$ can communicate with any participant in the system, including access to private information and outsourced computational results. The challenger then executes the $CheckZeroKnowledge$ function to verify if the attacker has successfully obtained the private information. If the verification is successful, indicating that the attacker cannot obtain private information, the output is 1, indicating that the system satisfies the zero-knowledge property. If the verification fails, indicating that the attacker has successfully obtained private information, the output is 0, indicating that the system does not satisfy the zero-knowledge property. The advantage of the attacker $\mathcal{A}$ is defined as follows:

$$Ad{v}_{\mathcal{A}}^{Zero-Knowledge}\left(PP,\lambda \right)=\mathrm{Pr}\left[EX{P}_{\mathcal{A}}^{Zero-Knowledge}=1\right]$$ (3)

Definition 2: If $Ad{v}_{\mathcal{A}}^{Zero-Knowledge}\left(PP,\lambda \right)$ is extremely tiny and approaches zero, then the system possesses a strong zero-knowledge property, indicating that the attacker cannot acquire private information.

• 2)Verifiability of DME

In the context of distributed modular exponentiation outsourcing, security definitions of verifiability focus on the confidentiality of the verification key and the correctness of the outsourced computation. The following security experiment is designed to define the verifiability of the outsourcing scheme.We define the attacker $\mathcal{A}(·)=\left({\mathcal{A}}_0,{\mathcal{A}}_1\right)$, where ${\mathcal{A}}_0,{\mathcal{A}}_1$ are two probabilistic polynomial-time simulators. The security experiment is structured as follows:

$$\begin{array}{l}Ex{p}_{\mathcal{A}}^{Verifiability}\left[DME,\lambda \right]\text{:}\\ pp\leftarrow Setup\left(1^{\lambda }\right)\text{;}\\ \left(VK,SK\right)\leftarrow KeyGen\left(pp\right)\text{;}\\ \epsilon VK\leftarrow {\mathcal{A}}_0\left(pp,VK\right)\text{;}\\ b\stackrel{R}{\leftarrow }\left\{\mathrm{0,1}\right\}\text{;}\\ Out\leftarrow Compute\left(pp,b\right)\text{;}\\ \hat{b}\leftarrow {\mathcal{A}}_1\left(\epsilon VK,Out\right)\text{;}\\ ifb=\hat{b}\text{:}\\ output1\text{;}\\ else\text{:}\\ output0\text{;}\end{array}$$ (4)

For any $\lambda \mathbb{\in }\mathbb{N}$, the advantage of attacker $\mathcal{A}$ in verifying the confidentiality of the verification key in DME is defined as follows:

$$Ad{v}_{\mathcal{A}}^{Verifiability}\left(DME,\lambda \right)=\left|\mathrm{Pr}\left[Ex{p}_{\mathcal{A}}^{Verifiability}\left(DME,\lambda \right)=1\right]-\frac{1}{2}\right|$$ (5)

Definition 3: If $Ad{v}_{\mathcal{A}}^{Verifiability}\left(DME,\lambda \right)\le negl\left(\lambda \right)$, where $negl\left(\lambda \right)$ is a negligible function, then the DME scheme achieves verifiability in the outsourcing computation scheme.

• 3)Confidentiality of BTDS

Definition 4: The privacy of encrypted data is defined using a security game that is not distinguishable under a chosen plaintext attack between the attacker $\mathcal{A}$ and the challenger $\mathcal{B}$. Specifically, the scheme is considered indistinguishable under chosen plaintext attack (IND-CPA) secure if the absolute value of the difference between the probability $\left|\mathrm{Pr}\left[Wi{n}_{\mathcal{A}}\left(b=b^{\prime }\right)-1/2\right]\right|$ is less than or equal to $\epsilon$, where $\epsilon$ represents a negligible probability.

$Init$: The attacker $\mathcal{A}$ initiates the interaction with the challenger $\mathcal{B}$ by sending a set of attributes ${\left\{\mathrm{0,1}\right\}}^{*}$.

$Setup$: The challenger $\mathcal{B}$ executes the $Setup$ algorithm and generates the public parameters $PP$. The challenger then sends the public parameters $PP$ to the attacker $\mathcal{A}$.

$Phases1\&2$: The attacker $\mathcal{A}$ queries the challenger $\mathcal{B}$ for a decryption key $SK$. The challenger performs the key generation algorithm $KeyGen$ to generate the key $SK=\left(z,TK\right)$, and sends it to the attacker $\mathcal{A}$.

$Challenge$: The attacker $\mathcal{A}$ sends two plaintext messages of equal length $m_0,m_1$ to the challenger $\mathcal{B}$. The challenger $\mathcal{B}$ randomly selects one of the plaintext messages $m_{b\in \left\{\mathrm{0,1}\right\}}$ and performs the encryption algorithm $Encrypt$ to generate the corresponding ciphertext.

$Guess$: The attacker $\mathcal{A}$ outputs a guessed value $b^{\prime }\in \left\{\mathrm{0,1}\right\}$ as their speculation for the value of $b$. If $b=b^{\prime }$, we consider the attacker to have won the game. The advantage of the attacker is defined as follows: $Ad{v}_{\mathcal{A}}=\left|\mathrm{Pr}\left[Wi{n}_{\mathcal{A}}\left(b=b^{\prime }\right)-1/2\right]\right|$.

5. Concrete scheme

This section is devoted to the specific details of the BTDS scheme, including the Medical Institution Alliance Edge blockchain, the Distributed Attribute Authorization Policy, the Distributed Key Generation Protocol, the Distributed Modular Exponential Outsourcing Algorithm, and the detailed construction of the CP-ABE master algorithm based on the blockchain and multiple authorization centers.

5.1. Medical Institution Alliance Edge Blockchain

The Medical Institution Alliance Edge Blockchain (EBC) is a consortium blockchain consisting of various healthcare institutions, deployed at the edge layer of the network, which is susceptible to network attacks. Each healthcare institution acts as an edge node, providing outsourced computing services to resource-constrained end users, including patients and doctors. Traditional healthcare institutions typically deploy internal networks to physically insulate themselves from cyber attacks. However, this network defense approach results in the inability of patient data to be shared among different healthcare institutions, leading to the phenomenon of “data silos” between them.

Some healthcare organizations have adopted cloud storage centers to alleviate this problem, but this approach simultaneously poses a risk of personal medical data leakage. Therefore, the BTDS architecture proposed in this paper leverages healthcare institutions as blockchain nodes, forming a Medical Institution Alliance Edge Blockchain (EBC). This approach maintains the existing cloud storage approach, while enhancing it with a blockchain verification mechanism. This ensures both data security and fine-grained access control for patients over their personal medical data.

As shown in Fig. 2, the EBC network architecture of the Medical Institutions Alliance Edge Blockchain utilizes the Hyperledger Fabric framework, a widely used open-source consortium blockchain framework known for its high configurability and scalability. It is highly suited for constructing medical consortium blockchains. The EBC network consists mainly of two types of nodes: super blockchain nodes and peer blockchain nodes.

• 1)Super Blockchain Nodes (Government Nodes): These nodes are deployed in government regulatory departments or trusted institutions' data centers. They are responsible for storing the entire ledger information and overseeing network operations. These nodes should have a high degree of physical and cyber security.
• 2)Peer Blockchain Nodes (Medical Institutions Nodes): These nodes are deployed in various medical institutions and serve as edge nodes. They provide outsourced computing services for patients and healthcare professionals while maintaining a portion of the ledger data. Each medical facility may have one or several nodes, depending on its size and requirements. In addition to storing ledger information, peer blockchain nodes may also undertake CP-ABE attribute authorization and key generation tasks. These nodes elect an Attribute Authorization Center (AC) within their respective shards based on their computational and storage capabilities. The AC is responsible for providing attribute authentication and key distribution services to users within the shard.

Fig. 2.

Example of EBC network deployment.

EBC (Medical Institutions Alliance Edge Blockchain) places a strong emphasis on security features such as data integrity, key security, and resistance to malicious intrusion attacks to ensure the privacy and trustworthiness of medical data. The following is a detailed description of the security properties of EBC:

• 1)Data Verification Mechanism:

EBC leverages blockchain technology to verify and ensure the integrity of data stored on the blockchain through mechanisms such as hash values and blockchain fingerprints (e.g., Merkle trees). These mechanisms effectively detect data tampering and provide reliable verification of data integrity. In addition, EBC serves as a complementary verification mechanism for medical consortium blockchains, further preventing attackers from tampering with patient's personal data in the cloud and enhancing data security.

• 2)Key Security:

EBC adopts the CP-ABE (Attribute-Based Encryption) system to achieve fine-grained data access control. Key security is crucial in edge computing environments. To mitigate the risk of key leakage, EBC introduces a distributed key generation protocol. This mechanism does not rely on a single Attribute Authorization Center (AC), ensuring that even if one AC experiences network failures or attacks, it will not lead to key leakage. EBC ensures that only legitimate users have access to the appropriate keys, thereby maintaining data confidentiality.

• 3)Resistance to Malicious Intrusion Attacks:

EBC employs a decentralized architecture where data is no longer centrally stored on a single server, but distributed across multiple nodes. This architecture makes it difficult for an attacker to pinpoint a single intrusion target as the data is scattered throughout the network. To maintain network consistency and data trustworthiness, EBC applies consensus algorithms such as Byzantine Fault Tolerance (BFT) algorithms. Even if some nodes are attacked or compromised, the network can continue to function normally, ensuring data security and integrity.

5.2. Sub-algorithm DAA: distributed attribute authorization strategy

The distributed attribute authorization strategy in the blockchain-based scheme is implemented through AA nodes deployed in the edge layer, forming an Edge Blockchain (EBC). The system attribute set is agreed upon by the AA nodes and stored in the EBC for consensus. Following the principles of the K-Means clustering algorithm [54], the end-users and AA nodes are initially divided into shards based on their distance. Within each shard, an attribute authorization center (AC) is dynamically elected from the AA nodes as a representative. The AC is responsible for providing attribute authentication and key distribution services to the users within the shard. This distributed deployment strategy ensures that the AC is located closer to the end users, aligning with the concept of edge computing and meeting the real-time requirements of attribute authorization services in the edge computing environment.

• (1)Shard initialization

In the shard initialization algorithm, the topology of the nodes is based on the actual distribution of edge nodes in the medical data sharing consortium scenario, assuming that the IoT nodes are randomly distributed. This means that the node locations are randomly distributed and are not constrained by a particular mesh rule. In this scenario, the shard initialization algorithm remains applicable since it utilizes the K-means clustering algorithm, which can adapt to various node distribution patterns, including random distributions.

Suppose the system consists of $N$ AA nodes and $H$ terminal users(U). Each AA node, $A{A}_i$, can be represented by a two-dimensional coordinate $\left(x_i,y_i\right)$. The distance between $A{A}_i$ and $A{A}_j$ is defined as follows: $D\left(A{A}_i,A{A}_j\right)=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}$. The K-Means clustering algorithm divides AA nodes into $K$ shards. Initially, $K$ AA nodes are randomly selected as the initial shard representatives, also known as the shard's authorization center (AC), which provides services to the end users within the shard. The following two steps are then iterated until convergence:

• ①Assign each AA node to the nearest shard representative.
• ②Set the shard representative (AC) to the average position of all AA nodes in a shard.

Assumptions: The position of the end user $U_u$ is represented by the two-dimensional coordinates $\left(x_u,y_u\right)$, and the position of the shard representative $A{C}_c$ is represented by the two-dimensional coordinates $\left(x_c,y_c\right)$. The distance between the end user $U_u$ and the shard representative $A{C}_c$ nodes is defined as follows: $D\left(U_u,A{C}_c\right)=\sqrt{{\left(x_u-x_c\right)}^2+{\left(y_u-y_c\right)}^2}$, where $u=\mathrm{1,2},...,H$ and $c=\mathrm{1,2},...,K$.

The K-Means clustering algorithm is used to divide users into shards according to the following steps:

• a.Randomly assign $H$ users to $K$ shards.
• b.Compute the distance $D\left(U_u,A{C}_c\right)$ between each user $U_u$ and its corresponding shard representative $A{C}_c$.
• c.Redistribute users: For each user $U_u$, find the nearest shard representative $A{C}_c$, and redistribute the user $U_u$ to the shard represented by $A{C}_c$.
• d.Iteration: Repeat steps b and c until no shard changes occur for any user or until a predetermined maximum number of iterations is reached.

The algorithm in question, as depicted in the pseudocode provided in Table 2, is described as follows:

• (2)Dynamic Selection of Shard AC

Table 2.

Shard initialization Algorithm.

In the shard, a performance measurement function is defined based on the CPU, memory, bandwidth, and other performance indicators of AA nodes:

$$P\left(A{A}_i\right)={\omega }_{1}CPU\left(A{A}_i\right)+{\omega }_{2}Memory\left(A{A}_i\right)+{\omega }_{3}Bandwidth\left(A{A}_i\right)$$ (6)

Among them, ${\omega }_1,{\omega }_2$ and ${\omega }_3$ are weight values that can be adjusted according to specific requirements. $CPU\left(A{A}_i\right),Memory\left(A{A}_i\right)$ and $Bandwidth\left(A{A}_i\right)$ represent the CPU performance, memory size, and bandwidth of node $A{A}_i$ respectively.

Next, the performance score of each AA node is calculated and sorted in descending order. The AA node with the highest performance score is then selected as the shard representative.

The algorithm in question, as depicted in the pseudocode provided in Table 3, is described as follows:

• (3)Distributed Load Balancing

Table 3.

Shard AC Dynamic Election Algorithm.

We employ a distributed load balancing strategy, which distributes the load balancing task to individual shards for processing. Load balancing operations are performed based on node load information and utilize a sorted list to enhance lookup efficiency, reducing time complexity to O(log N), making it more suitable for large-scale network environments.

• 1)For each shard:
• ①Calculate the load of each AA node as follows:

$$L_{A{A}_i}=\alpha \times CP{U}_{usag{e}_{A{A}_i}}+\beta \times Me{m}_{usag{e}_{A{A}_i}}+\gamma \times Ne{t}_{dela{y}_{A{A}_i}}$$ (7)

Where, $CP{U}_{usag{e}_{A{A}_i}}$ represents the CPU usage of the AA node, $Me{m}_{usag{e}_{A{A}_i}}$ represents the memory usage of the AA node, and $Ne{t}_{dela{y}_{A{A}_i}}$ represents the network latency of the AA node. The parameters $\alpha ,\beta ,\gamma$ are weight factors used to adjust the influence of CPU usage, memory usage, and network latency on the load.

• ②The average load for each shard $P_d$ is calculated as follows: $L_{P_t}=\left(1/n\right)·\sum _{i=1}^N{L}_{A{A}_i}$, where $n$ is the number of nodes in a shard and $d=\mathrm{1,2,3}...,K$.
• 2)Set the load threshold $T$ based on the system's actual requirements and capabilities. When $L_{P_t}>T$, triggering the load balancing operation:
• ①Define a list of loaded nodes, $NodeList$, to store the load information of all nodes in the current shard.
• ②For each AA node in the shard, the load information $L_{A{A}_i}$ of the node $A{A}_i$ is inserted into NodeList in sorted order.
• ③Define a function $FindLowLoadNodes\left(NodeList,T\right)$ to find the list of nodes in the shard with load below $T$.
• ④Define a function $FindHighLoadNodes\left(NodeList,T\right)$ to find the list of nodes within the shard with loads above $T$.
• ⑤Execute the migration of nodes from $LowLoadNodes$ to adjacent shards or perform other load balancing operations:

$$LowLoadNodes=FindLowLoadNodes\left(NodeList,T\right)$$ (8)

Alternatively, nodes can be migrated from HighLoadNodes to newly created shards, or additional load balancing operations can be performed:

$$HighLoadNodes=FindHighLoadNodes\left(NodeList,T\right)$$ (9)

The algorithm in question, as depicted in the pseudocode provided in Table 4, is described as follows:

• (4)Recovery of Shard AC Failure

Table 4.

Distributed Load Balancing Algorithm.

Assume that a shard can be in either a normal state (0) or a failed state (1) at any given time $t$. The state of a shard can be represented as a binary random variable $S\left(t\right),S\left(t\right)\in \left\{\mathrm{0,1}\right\}$. If $S\left(t\right)=0$, it indicates that the shard is in a normal state at time $t$. If $S\left(t\right)=1$, it indicates that the shard has failed at time $t$.

For a failed shard, the failure recovery mechanism should elect the AA node with the best performance in the shard as the new shard representative, i.e., the AC node, to provide services for the users in the shard. Assuming that at time $t$, the AC node of shard $P_d$ fails, the recovery process involves selecting the node with the highest performance score from the queue of AA nodes within the shard to serve as the new AC node.

Assuming that $AA\left(P_d,rank\right)$ represents the $rank-th$ AA node within shard $P_d$, we can define a failover function $R\left(P_d,rank,t\right)$. When the AC node fail $S\left(P_d,t\right)=1\text{,}R\left(P_d,rank,t\right)=AC\left(P_d,rank+1\right)$, indicating that at time $t$, the new AC node for shard $P_d$ is set to the $\left(rank+1\right)-th$ AA node within the shard.

The algorithm in question, as depicted in the pseudocode provided in Table 5, is described as follows:

Table 5.

Shard AC fault recovery Algorithm.

5.3. Sub-algorithm DKG: distributed key generation protocol based on blockchain

Based on the distributed key generation protocol based on Generalized VSS introduced in Zhang et al.'s scheme [55], this paper incorporates blockchain as a trusted third party and presents a distributed key generation protocol based on blockchain. This protocol decentralizes the key management of CP-ABE across multiple participants, and the system public key is generated through consensus in the EBC. The system master key is not explicitly stored in any node, and the user private key can only be calculated when multiple AA nodes collaborate.

The system consists of $n$ participants, denoted as $A{A}_1,A{A}_2,...,A{A}_n$, which form the group $AA=$ $\left\{A{A}_1,A{A}_2,...,A{A}_n\right\}$. The participants have a monotone access structure, meaning that certain subsets of $AA$ can collaborate to recover shared secrets. The base set ${\mathrm{\Gamma }}_0=\left\{A{C}_1,A{C}_2,...,A{C}_t\right\}$ represents the minimal set of elements under the inclusion relation in $\mathrm{\Gamma }$. In the system, each AA possesses a master private key denoted as $\kappa \in Z_q$, and the corresponding public key to the system is represented as $\psi =g^{\kappa }\left(\mathrm{mod}p\right)$.

• (1)Initialization phase
• ①Selection of large prime numbers $p$ and $q$ such that $q|\left(p-1\right)$.
• ②Selecting a finite cyclic group $G_q$ based on the discrete logarithm problem, where the order is $q$, and $g,h$ as generators of $G_q$.
• ③Choose a residue class ring modulo $q$ denoted by $Z_q$.
• (2)System master private key generation phase
• ①$A{A}_i$ generates a secret value ${\kappa }_i$ for their access to the shared structure $\mathrm{\Gamma }$, where $i=\mathrm{1,2},...,n$. The specific process is as follows:
• a.When $A{A}_i$ wants to share a secret ${\kappa }_i\in Z_q$, it makes the following commitment: $E_{i0}=E\left({\kappa }_i,e_i\right)=g^{{\kappa }_i}{h}^{e_i}$, where $e_i$ is a randomly chosen secret value from $Z_q$.
• b.$A{A}_i$ stochastically selects a polynomial $F_i\left(\kappa \right)={\kappa }_i+F_{i,1}\kappa +...+F_{i,n-1}{\kappa }^{n-1}$ of degree $n-1$ from the ring $Z_q\left[K\right]$, where ${\kappa }_i$ represents a secret value. Subsequently, ${\kappa }_{ik}=F_i\left(k\right),k=\mathrm{1,2},...,n$ is computed. Afterwards, $A{A}_i$ randomly selects $G_{i1},G_{i2},...,G_{i,n-1}\in Z_q$ and computes the commitment to $F_{ij}$ as $E_{ij}=E\left(F_{ij},G_{ij}\right)=g^{F_{ij}}{h}^{G_{ij}},i=\mathrm{1,2},...,n-1$, which is then broadcasted to the participants.
• c.Generate $G_i\left(\kappa \right)=e_i+G_{i1}x+...+G_{i,n-1}{x}^{n-1}$ where $e_{ik}=G_i\left(k\right),i=\mathrm{1,2},...n$. For each minimal qualified subset $A{C}_j=\left\{A{A}_{j1},A{A}_{j2},...,A{A}_{jk}\right\}$, $A{A}_i$ is represented by $k+1$ points: $\left(\left(j_1,G_i\left(j_1\right)\right),\left(j_2,G_i\left(j_2\right)\right),...,\left(j_k,G_i\left(j_k\right)\right),\left(0,e_j\right)\right)$. By applying Lagrange interpolation, another $k$-degree polynomial $G_{ij}\left(\kappa \right)$ is calculated. The values of $F_{ij}\left(n+1\right)$ and $G_{ij}\left(n+1\right)$ are computed and publicly disclosed to all participants, where $j=\mathrm{1,2},...,t$.
• d.$A{A}_i$ securely transmits the secret share $\left(x_{ik},e_{ik}\right)$ to $A{A}_k$ for holding the share of the secret ${\kappa }_i$, where $j=\mathrm{1,2},...,t$.
• e.Upon receiving its allocated share of the secret, $A{A}_k$ validates the integrity of the share by verifying whether $E_{ik}=E\left(x_{ik},e_{ik}\right)=\prod _{j=0}^{n-1}{E}_{ij}^{k^i}$. For each minimum qualified subset $A{C}_j=\left\{A{A}_{j1},A{A}_{j2},...,A{A}_{jk}\right\}$, all participants have the ability to verify the integrity of the public data $F_{ij}\left(n+1\right)$ and $G_{ij}\left(n+1\right)$ by confirming whether $E\left(F_{ij}\left(n+1\right),G_{ij}\left(n+1\right)\right)=\prod _{m=0}^k{E}_{i{j}_m^m}^b$. Here, $b_0=\prod _{i=1}^k\left(n+1-j_i\right)/\prod _{i=1}^k\left(-j_i\right)$ and $b_m=\left(n+1\right)\sum _{1\le i\le k,i\ne m}\left(n+1-j_i\right)/j_m\sum _{1\le i\le k,i\ne m}\left(j_m-j_i\right)$, where $m=\mathrm{1,2},...,k$.
• ②If the validation of $A{A}_k$ fails (i.e., $x_{ik},e_{ik}$ is invalid), $A{A}_k$ broadcasts the values $x_{ik},e_{ik}$ and files a complaint against $A{A}_i$.
• ③In the event of a complaint from $A{A}_k$ against $A{A}_i$, it is incumbent upon $A{A}_i$ to broadcast the valid share it had provided to $A{A}_i$.
• ④If $A{A}_i$ receives complaints from all members of a qualified subset or is complained by some members and the broadcasted share in step③remains invalid, each member's share is reset to 0, i.e., $x_{ik}=0=e_{ik}$. Simultaneously, $A{A}_i$ sets the selected secret value ${\kappa }_i$ to zero, and both $F_i\left(\kappa \right)$ and $G_i\left(\kappa \right)$ are treated as zero polynomials.
• ⑤Each member $A{A}_k$ performs calculations on their private key share $s_k=\sum _{i=1}^n{\kappa }_{ik}\left(\mathrm{mod}q\right)$ and the sum of their random values $u_k=\sum _{i=1}^n{e}_{ik}\left(\mathrm{mod}q\right)$. When a user needs to utilize the system's master private key, they can compute $\kappa =\sum _{i=1}^n{\kappa }_i\left(\mathrm{mod}q\right)$.
• (3)Extraction of the System Public Key Phase
• ①Each attribute authorization node $A{A}_i$ calculates its respective shard of the system public key as ${\psi }_i=g^{{\kappa }_i}$, where $i=\mathrm{1,2},...,n$.
• ②Each $A{A}_i$ broadcasts its public key shard ${\psi }_i$ to the EBC.
• ③After retrieving the public key shard ${\psi }_i$ from the EBC, when a user needs to use the private key, they compute $g^{\kappa }=\prod _{i=1}^n{\psi }_i=\prod _{i=1}^n{g}^{{\kappa }_i}$. Additionally, because $e{\left(g,g\right)}^{\kappa }=e\left(g^{\kappa },g\right)$, the CP-ABE public key system parameter $e{\left(g,g\right)}^{\kappa }$ can be obtained.
• (4)User private key generation phase
• ①The user (DU) sends the set of user attributes $S$ it possesses to the attribute authorization center (AC) of its shard. The AC then aggregates the set $S$ and uploads it to the Edge Blockchain (EBC).
• ②Each attribute authorization node $A{A}_i$ generates a partial user private key based on the master secret key ($MSK$) fragment and the attribute set $S$ it holds.
• a.For each attribute $x$ in the attribute set $S$, attribute authorization node $A{A}_i$ randomly selects a value $t_i\in Z_p$. Then, it calculates the user's private key parameter as $K_{x_i}^{\prime }=g^{F\left(x\right)·t_i}$.
• b.Attribute authorization node $A{A}_i$ utilizes its holdings of the $MSK$ fragment ${\kappa }_i$ to calculate the user's private key parameters. It calculates $K_i^{\prime }=g^{{\kappa }_i+a·t_i},L_i^{\prime }=g^{t_i}$.
• c.$A{A}_i$ packages the calculated $K_i^{\prime }$ and $K_{x_i}^{\prime }$ and uploads them to the EBC.
• ③Shard AC collects all the calculated $K_i^{\prime },L_i^{\prime }$ from each member, as well as the corresponding $K_i^{\prime },L_i^{\prime }$ for each attribute. Using Lagrange interpolation, it calculates $K^{\prime }=\prod _{i=1}^n{K}_i^{\prime {\lambda }_i}$, $K_x^{\prime }=\prod _{i=1}^n{K}_{x_i}^{\prime {\lambda }_i}$, and $L^{\prime }=\prod _{i=1}^n{L}_i^{\prime {\lambda }_i}$.
• ④Shard AC randomly selects a conversion factor $z\in Z_p$. It sets the converted keys as $TK={\{K={K^{\prime }}^{1/z},L={L^{\prime }}^{1/z},\{K_x={\left(K_x^{\prime }\right)}^{1/z}\}}_{x\in S}\}$.
• ⑤AC returns the user's private key $SK=\left(z,TK\right)$ to DU.

5.4. Sub-algorithm DME: distributed modular exponentiation outsourcing algorithm based on blockchain

Based on the scheme proposed in literature [51], the DME sub-algorithm enhances the secure outsourcing algorithm for distributed modular exponentiation based on blockchain. The algorithm can be described as follows:

• (1)$Setup\left(u,a,p\right)\to \left(EK,VK\right)$ This step is carried out by the User's User and the OSP. It involves performing a modular exponentiation operation on the base $u$ with the exponent $a$ modulo $p$. The resulting value $y=u^a\mathrm{mod}p$ is the evaluation key $EK$, and it is accompanied by the verification key $VK$. The following details explain the process in more depth:
• ①The User inputs the prime number $p$ and initiates the Rand subroutine to generate six blinds in the form of $\left(k_1,g^{k_1}\right),\left(k_2,g^{k_2}\right),\left(k_3,g^{k_3}\right),\left(k_4,g^{k_4}\right),\left(k_5,g^{k_5}\right),\left(k_6,g^{k_6}\right)$, where $g\in Z_p$ and $b\in Z_p$.
• ②The User selects a random number $r$ from the set $Z_p$ to perform a logical division of the base $u$:

$$\begin{array}{l}{u}^a={\left(u{g}^{k_1}\right)}^a{\left(g^{k_2}\right)}^{t_1}{g}^{k_3}={\left(v_1{w}_1{g}^{k_1}\right)}^a{\left(g^{k_2}\right)}^{t_1}{g}^{k_3}={\left(g^{k_5}{w}_1{g}^{k_1}\right)}^a{\left(g^{k_2}\right)}^{t_1}{g}^{k_3}\\ u^{ra}={\left(u{g}^{k_4}\right)}^{ra}{\left(g^{k_5}\right)}^{t_2}{g}^{k_6}={\left(v_2{w}_2{g}^{k_4}\right)}^{ra}{\left(g^{k_5}\right)}^{t_2}{g}^{k_6}={\left(g^{k_6}{w}_2{g}^{k_4}\right)}^{ra}{\left(g^{k_5}\right)}^{t_2}{g}^{k_6}\end{array}$$ (10)

Among them, the values of $w_1,w_2,t_1,t_2$ are calculated as follows: $w_1=u/v_1,w_2=u/v_2,t_1=\left(-k_3-k_{1}a\right)/k_2\mathrm{mod}q,t_2=\left(-k_6-k_{4}ra\right)/k_5\mathrm{mod}q$.

• ③The load balancing smart contract in the EBC, which consists of computing nodes, will initiate the selection of computing nodes for this round. The specific steps are as follows:

Initially, a segmented approach is employed to achieve load balancing among the edge nodes. The load segmentation method is defined as follows: $h_j=L/\left(1-{\lambda }^j\right)$, where $L$ represents the exponent size, $\lambda =\phi /\left(2+\phi \right),j\in \left[1,n\right]$， $\phi =MM/MS$ (where $MS$ and $MM$ correspond to the cost of a modular square operation and a modular multiplication operation, respectively). The value $h_j$ denotes the segmentation points, with $h_0=0$ being the initial point. The compute nodes are launched, and the number of nodes $n$ is determined as $n=\left[{\log }_{\lambda }1/\left(1+2L\left(1-\lambda \right)\right)+1/2\right]$.

• ④The User partitions the logical indices $a,ra,t_1,t_2$ into $n$ segments through binary decomposition:

$$\left(\begin{array}{c}a\\ t_1\\ ra\\ t_2\end{array}\right)=\left(\begin{array}{cccc}{e}_{11}& e_{12}& \cdots & e_{1n}\\ e_{21}& e_{22}& \cdots & e_{2n}\\ e_{31}& e_{32}& \cdots & e_{3n}\\ e_{41}& e_{42}& \cdots & e_{4n}\end{array}\right)\left(\begin{array}{c}{2}^0\\ 2^{h_1}\\ ⋮\\ 2^{h_{n-1}}\end{array}\right)\mathrm{mod}p=\left(\begin{array}{c}\left(e_{11}{2}^0+e_{12}{2}^{h_1}+...+e_{1n}{2}^{h_{n-1}}\right)\mathrm{mod}p\\ \left(e_{21}{2}^0+e_{22}{2}^{h_1}+...+e_{2n}{2}^{h_{n-1}}\right)\mathrm{mod}p\\ \left(e_{31}{2}^0+e_{32}{2}^{h_1}+...+e_{3n}{2}^{h_{n-1}}\right)\mathrm{mod}p\\ \left(e_{41}{2}^0+e_{42}{2}^{h_1}+...+e_{4n}{2}^{h_{n-1}}\right)\mathrm{mod}p\end{array}\right)$$ (11)

• ⑤Let the verification key be denoted as $VK=\left\{r\right\}$, and the evaluation key as $EK$, which can be represented as $\{\left(g^{k_5}{w}_1{g}^{k_1},e_{1j},h_{j-1}\right),\left(g^{k_2},e_{2j},h_{j-1}\right)$, $\left(g^{k_6}{w}_2{g}^{k_4},e_{3j},h_{h-1}\right),{\left(g^{k_5}{e}_{4j,}{h}_{j-1}\right)\}}_{jϵ\left[1,n\right]}$

• (2)$Compute\left(EK\right)\to \left\{{\sigma }_j,{\pi }_j\right\}$.

This step is carried out by the distributed computing nodes, which compute the results ${\sigma }_j$ and generate evidence ${\pi }_j$. Here are the detailed steps:

• ①The compute nodes, denoted as $j,j\in \left[1,n\right]$, perform the following steps sequentially:

$$\begin{array}{l}{d}_{1,j}={\left(g^{k_5}{w}_1{g}^{k_1}\right)}^a={\left(g^{k_5}{w}_1{g}^{k_1}\right)}^{e_{1j}{2}^{h_{j-1}}}\mathrm{mod}p\\ d_{2,j}={\left(g^{k_2}\right)}^{t_1}={\left(g^{k_2}\right)}^{e_{2j}{2}^{h_{j-1}}}\mathrm{mod}p\\ d_{3,j}={\left(g^{k_6}{w}_2{g}^{k_4}\right)}^{ra}={\left(g^{k_6}{w}_2{g}^{k_4}\right)}^{e_{3j}{2}^{h_{j-1}}}\mathrm{mod}p\\ d_{4,j}={\left(g^{k_5}\right)}^{t_2}={\left(g^{k_5}\right)}^{e_{4j}{2}^{h_{j-1}}}\mathrm{mod}p\end{array}$$ (12)

• ②The compute node returns the computed result and evidence as ${\sigma }_j=\left\{d_{1,j},d_{2,j}\right\}$ and ${\pi }_j=\left\{d_{3,j},d_{4,j}\right\}$, respectively.

• (3)$Verify\left(VK,{\sigma }_j,{\pi }_j\right)\to \left\{y,\perp \right\}$.

This step involves the User verifying the correctness of the result, which is done as follows: The User computes $y=\sum _{j=1}^n(d_{1,j}·d_{2,j})\text{,}{y}^{\prime }=\sum _{j=1}^n(d_{3,j}·d_{4,j})$. If $y^r=y^{\prime }$, then output the final result $y$; otherwise, output $\perp$.

5.5. Main algorithm: blockchain-based CP-ABE with multi-attribute authority center

The main algorithm of this paper's scheme is built upon the approach presented in Ref. [44]. Below, we provide a detailed description of the algorithm.

• (1)$Setup\left(1^{\lambda },{\left\{\mathrm{0,1}\right\}}^{*}\right)\to PP$.
• ①The algorithm takes as input the security parameters $\lambda$, the large prime number $q$, and the system properties from the collection ${\left\{\mathrm{0,1}\right\}}^{*}$.
• ②A prime order $p$ is selected, and $g$ is chosen as a generator element for the double linear group $G_1$. A bilinear mapping $e:G_1\times G_1\to G_2$ is then generated.
• ③A hash function $F:{\left\{\mathrm{0,1}\right\}}^{*}\to G_1$ is selected. Two collision-resistant hash functions $H:\left\{\mathrm{0,1}\right\}*\to Z_q^{*}$ and $H_1:{\left\{\mathrm{0,1}\right\}}^{*}\to G_1$ are chosen.
• ④Randomly selecting a parameter $a\in Z_p$, the system parameters $PP=\left(g,g^a,F,H,H_1\right)$ can be defined.
• (2)$Encrypt\left(PP,m\in {\left\{\mathrm{0,1}\right\}}^{\lambda },\left(M,\rho \right)\right)\to CT$.

The algorithm randomly selects $r\in G_2$, computes $s=H\left(r,m\right)$, and $R=H_1\left(r\right)$. Then it invokes the child algorithm DKG to compute the public key to the system as $PK={(g,e\left(g,g\right)}^{\alpha },g^a,F,H,H_1)$. Given a plaintext $m$, DO calculates $C=R·e{\left(g,g\right)}^{\alpha s},C^{\prime }=g^s,C^{″}=m\oplus R$.

In this algorithm, $M$ represents a matrix with dimensions $\mathcal{l}\times n$, and $\rho$ denotes an injective function that associates each row of matrix $M$ with its corresponding attribute. The encryption process can be outlined as follows:

• ①Randomly select a vector $\overrightarrow{v}={\left(s,x_2,...,x_n\right)}^T\in Z_p$ to be used for sharing the encrypted exponent $s$.
• ②For each row of the matrix $M$, denoted as $M_i$, calculate the inner product ${\lambda }_i=M_i·\overrightarrow{v}$, where $i$ ranges from 1 to $\mathcal{l}$ and $M_i$ represents the $i$-th row of matrix $M$.
• ③Randomly select $r_1,r_2,...,r_{\mathcal{l}}$ from $Z_p$, and invoke the sub-algorithm DME. The User and OSP work together to compute the intermediate ciphertext $C{T}_m=\left\{C_i=g^{a{\lambda }_i}{g}^{F\left(\rho \left(i\right)\right)\left(-r_i\right)},D_i=g^{r_i}\right\}$.

The detailed process of the first sub-algorithm DME with ${\left(g^a\right)}^{{\lambda }_i}$ is as follows:

• a.Execute the system initialization algorithm $Setup\left(g^a,{\lambda }_i,p\right)$ within the DME sub-algorithm. This process yields the verification key $VK$ as $\left\{r\right\}$, and the evaluation key $EK$ as $\{\left(g^{k_5}{w}_1{g}^{k_1},e_{1j},h_{j-1}\right),\left(g^{k_2},e_{2j},h_{j-1}\right)$, $\left(g^{k_6}{w}_2{g}^{k_4},e_{3j},h_{h-1}\right),{\left(g^{k_5}{e}_{4j,}{h}_{j-1}\right)\}}_{jϵ\left[1,n\right]}$.
• b.The distributed computing nodes on the OSP are deployed to execute the $Compute\left(EK\right)$ algorithm in a decentralized manner, resulting in the computed values ${\sigma }_j=\left\{d_{1,j},d_{2,j}\right\}$ and the corresponding evidence ${\pi }_j=\left\{d_{3,j},d_{4,j}\right\}$.
• c.Execute the $Verify\left(VK,{\sigma }_j,{\pi }_j\right)$ algorithm to validate the calculated results obtained from outsourcing, and output the verification outcome.

In a similar manner, calculate $g^{F\left(\rho \left(i\right)\right)\left(-r_i\right)}$ and $g^{r_i}$ using the DME algorithm.

• ⑤Upon successful execution of the computation by the OSP, the DO can generate the complete ciphertext $CT=\left\{C,C^{\prime },C^{″},C_i,D_i\right\}$, where $C,C^{\prime },C^{″}$ are computed by the DO, and $C_i,D_i$ are computed by the OSP and subsequently verified by the DO.
• (3)$KeyGen\left(PP,S\right)\to SK$.

DU initiates the process by submitting its attribute set $S$ to the respective shard AC node. The AC node then invokes the sub-algorithm DKG to generate the user's private key $SK=\left(z,TK\right)$.

• (4)$Transform\left(TK,CT\right)\to C{T}^{\prime }$.

After obtaining the successful grant of $SK$, DU downloads the ciphertext $CT$ from the Cloud and verifies its integrity by comparing the ciphertext hash stored in EBC. DU then combines the decryption key $TK$ with the ciphertext $CT$ and sends them to OSP for further processing. OSP invokes the child algorithm DME to unlock a portion of the ciphertext, resulting in the transformed ciphertext $C{T}^{\prime }=\left\{C,C^{″},C{T}_{transform}\right\}$.

• ①Let $I\subset \left\{\mathrm{1,2},...,\mathcal{l}\right\}$ be defined as $I=\left\{i:\rho \left(i\right)\in S\right\}$, where $I$ represents a subset of attributes from the system's complete attribute set.
• ②When the user attribute set $S$ satisfies the access policy $\left(M,\rho \right)$, and there exists a valid set of secret shares $\left\{{\lambda }_i\right\}$ for the secret $s$ with respect to the access matrix $M$, it is possible to compute a constant set ${\left\{w_i\in Z_p\right\}}_{i\in I}$ in polynomial time, such that the linear combination ${\sum }_{i\in I}{w}_i{\lambda }_i=s$ is achieved.
• ③The transformed ciphertext $C{T}_{transform}$ is computed according to the following procedure:

$$C{T}_{transform}=\frac{e\left(C^{\prime },K\right)}{{\prod }_{i\in I}\left[e\left(C_i^{w_i},L\right)·e\left({D_i}^{w_i},K_{\rho \left(i\right)}\right)\right]}=e{\left(g,g\right)}^{s\alpha /z}$$ (13)

• (5)$Descrypt\left(SK,C{T}^{\prime }\right)\to m$.
• ①After receiving the partially decrypted ciphertext $C{T}^{\prime }$, DU performs the following computations: $r=C/{\left(C{T}_{transform}\right)}^z,m=C\oplus H_1\left(r\right)$ and $s=H\left(r,m\right)$.
• ②If the calculated values of $C=r·e{\left(g,g\right)}^{\alpha s}$ and $C{T}_{transform}=e{\left(g,g\right)}^{s\alpha /z}$ validate the correctness of the OSP's computation, the decrypted plaintext $m$ is produced as the output.

6. Proof of correctness and security

6.1. Proof of correctness

This section will provide a proof of correctness for the proposed BTDS system. The fundamental CP-ABE algorithm used in BTDS is based on the classic paper by GREEN et al. [56], so there is no need to reprove its correctness. This section will mainly focus on demonstrating the correctness of BTDS architecture, particularly in the context of the improved distributed key generation and distributed modular exponentiation outsourcing as discussed in Ref. [56].

Theorem 1

Correctness of Algorithm DKG,if EBC performs this algorithm correctly, it can guarantee that the output key is always correct.

Proof: According to the description of the sub-algorithm DKG, the master private key parameter $\mathrm{\kappa }$ of the system is shared by all participants.

• a)$\mathrm{A}{\mathrm{A}}_{\mathrm{i}}$ commits to a key ${\mathrm{\kappa }}_{\mathrm{i}}$: During the initialization phase, each $\mathrm{A}{\mathrm{A}}_{\mathrm{i}}$ publicly reveals a commitment $\mathrm{E}\left({\mathrm{\kappa }}_{\mathrm{i}},{\mathrm{e}}_{\mathrm{i}}\right)={\mathrm{g}}^{{\mathrm{\kappa }}_{\mathrm{i}}}{\mathrm{h}}^{{\mathrm{e}}_{\mathrm{i}}}$, where ${\mathrm{\kappa }}_{\mathrm{i}}$ is their chosen secret value, and ${\mathrm{e}}_{\mathrm{i}}$ is a randomly chosen secret value. This commitment ensures the relationship between ${\mathrm{\kappa }}_{\mathrm{i}}$ and ${\mathrm{e}}_{\mathrm{i}}$.
• b)Polynomial Interpolation Calculation: In step (2)c, participants calculate a polynomial ${\mathrm{G}}_{\text{ij}}\left(\mathrm{\kappa }\right)$ concerning the secret value ${\mathrm{\kappa }}_{\mathrm{i}}$ through polynomial interpolation. This ensures that each participant has a portion of the polynomial ${\mathrm{G}}_{\text{ij}}\left(\mathrm{\kappa }\right)$, where $\mathrm{j}$ denotes different minimum qualified subsets. Thus, each participant shares information about the secret value ${\mathrm{\kappa }}_{\mathrm{i}}$.
• c)Secret Share Distribution and Verification: Participants send their secret shares $\left({\mathrm{x}}_{\text{ik}},{\mathrm{e}}_{\text{ik}}\right)$ to other participants. These shares include information about the secret value ${\mathrm{\kappa }}_{\mathrm{i}}$. Receivers verify the validity of these shares, ensuring that they satisfy the commitment relationship. This ensures that each participant holds valid secret shares.
• d)Computation of the System Master Private Key Parameter $\mathrm{\kappa }$:Each member $\mathrm{A}{\mathrm{A}}_{\mathrm{k}}$ calculates their share concerning the system's master private key parameter $\mathrm{\kappa }$, represented as ${\mathrm{s}}_{\mathrm{k}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{\kappa }}_{\text{ik}}\left(\mathrm{mod}\mathrm{q}\right)$. This is achieved by adding up the secret shares, which are part of the information about each participant's secret value ${\mathrm{\kappa }}_{\mathrm{i}}$. Finally, by summing all shares, the system's master private key parameter $\mathrm{\kappa }$ is correctly reconstructed.

Thus, based on the above proof, Algorithm DKG guarantees the correctness of the system's master private key parameter $\mathrm{\kappa }$. This also implies that, in theory, the correctness of the BTDS architecture is guaranteed only if the sub-algorithm DKG is executed exactly. It forms the basis for ensuring the correctness of the BTDS architecture.

Theorem 2

Correctness of Algorithm DME. Under the assumption of correct execution by OSP, Algorithm DME ensures the integrity and accuracy of the outsourced computation results.

Proof: For Algorithm DME, given the input ${\mathrm{u}}^{\mathrm{a}}\mathrm{mod}\mathrm{p}$, where $\mathrm{u}$ and $\mathrm{a}$ are variables, the correct computation can be performed by following these steps:

• ①Correctness of blind segmentation: The base exponent can be accurately reconstructed after blind segmentation.

$$\begin{array}{l}{\mathrm{u}}^{\mathrm{a}}={\left(\mathrm{u}{\mathrm{g}}^{{\mathrm{k}}_1}\right)}^{\mathrm{a}}{\left({\mathrm{g}}^{{\mathrm{k}}_2}\right)}^{{\mathrm{t}}_1}{\mathrm{g}}^{{\mathrm{k}}_3}={\left(\mathrm{u}{\mathrm{g}}^{{\mathrm{k}}_1}\right)}^{\mathrm{a}}{\left({\mathrm{g}}^{{\mathrm{k}}_2}\right)}^{\left(-{\mathrm{k}}_3-{\mathrm{k}}_1\mathrm{a}\right)/{\mathrm{k}}_2}{\mathrm{g}}^{{\mathrm{k}}_3}={\left(\mathrm{u}{\mathrm{g}}^{{\mathrm{k}}_1}\right)}^{\mathrm{a}}{\left({\mathrm{g}}^{{\mathrm{k}}_2}\right)}^{\left(-{\mathrm{k}}_3-{\mathrm{k}}_1\mathrm{a}\right)/{\mathrm{k}}_2}{\mathrm{g}}^{{\mathrm{k}}_3}={\mathrm{u}}^{\mathrm{a}}\\ {\mathrm{u}}^{\text{ra}}={\left(\mathrm{u}{\mathrm{g}}^{{\mathrm{k}}_4}\right)}^{\text{ra}}{\left({\mathrm{g}}^{{\mathrm{k}}_5}\right)}^{{\mathrm{t}}_2}{\mathrm{g}}^{{\mathrm{k}}_6}={\left(\mathrm{u}{\mathrm{g}}^{{\mathrm{k}}_4}\right)}^{\text{ra}}{\left({\mathrm{g}}^{{\mathrm{k}}_5}\right)}^{\left(-{\mathrm{k}}_6-{\mathrm{k}}_4\text{ra}\right)/{\mathrm{k}}_5}{\mathrm{g}}^{{\mathrm{k}}_6}={\mathrm{u}}^{\text{ra}}{\mathrm{g}}^{{\mathrm{k}}_4\text{ra}}{\mathrm{g}}^{-{\mathrm{k}}_6}{\mathrm{g}}^{-{\mathrm{k}}_4\text{ra}}{\mathrm{g}}^{{\mathrm{k}}_6}={\mathrm{u}}^{\text{ra}}\end{array}$$ (14)

• ②The accuracy of edge node computation: The sub-algorithm DME ensures the detection and resolution of potential errors in computation results provided by the edge nodes. This guarantee is established through a rigorous proof by contradiction. Suppose there is a scenario where a compute node deviates from the protocol during the execution of the sub-algorithm DME and produces incorrect computation results. In such a case, when DU performs the verification algorithm, a contradiction arises. Specifically, if ${\mathrm{y}}^{\mathrm{r}}=\sum _{\mathrm{j}=1}^{\mathrm{n}}({\mathrm{d}}_{1,\mathrm{j}}·{\mathrm{d}}_{2,\mathrm{j}})$ does not equal $\sum _{\mathrm{j}=1}^{\mathrm{n}}({\mathrm{d}}_{3,\mathrm{j}}·{\mathrm{d}}_{4,\mathrm{j}})={\mathrm{y}}^{\prime }$, the program outputs $\perp$ and triggers the monitoring mechanism. OSP takes appropriate measures to penalize the erroneous node and initiates a new round of computation with a different compute node. This process is repeated until DU's verification equation holds, ensuring the output of the correct computation result $\mathrm{y}$.

Inference 1: Based on Theorem 1 and Theorem 2, it can be inferred that the correctness of BTDS is guaranteed. If the CP-ABE main algorithm based on blockchain and multi-attribute authorization center, as described in this paper, is executed correctly, then it ensures that the BTDS architecture will consistently share data correctly.

6.2. Security proof

Theorem 3

If there exists a probabilistic polynomial-time attacker $\mathcal{A}$ such that $\text{Ad}{\mathrm{v}}_{\mathcal{B}}^{\text{Zero}-\text{Knowledge}}\left(\text{PP},\text{ZK},\mathrm{\lambda }\right)\ge \mathrm{\epsilon }\left(\mathrm{\lambda }\right)$, then $\mathcal{A}$ can devise an algorithm $\mathcal{F}$ to violate the zero-knowledge property of both DME and DKG.

Proof: To begin, it is necessary to construct an Challenger $\mathcal{B}$ to challenge the zero-knowledge properties of DME and DKG. The objective is to prove that $\text{Ad}{\mathrm{v}}_{\mathcal{B}}^{\text{Zero}-\text{Knowledge}}\left(\text{PP},\text{ZK},\mathrm{\lambda }\right)$ is negligible, meaning that Challenger $\mathcal{B}$ cannot break the zero-knowledge properties within an ignorable amount.

$\text{Init}$:Attacker $\mathcal{A}$ selects an attribute set ${\left\{\mathrm{0,1}\right\}}^{*}$ to challenge and sends it to the challenger $\mathcal{B}$.

$\text{Setup}$:Challenger $\mathcal{B}$ runs the $\text{Setup}$ algorithm and sends the generated public parameters $\text{PP}$ to attacker $\mathcal{A}$. During this phase, attacker $\mathcal{A}$ cannot interfere with or influence the generation of system parameters since this is part of the zero-knowledge property.

$\text{Phase}1\&2$:(1) Attacker $\mathcal{A}$ sends a decryption key $\text{SK}$ query to Challenger $\mathcal{B}$, and the challenger executes the key generation algorithm $\text{KeyGen}$ to generate the key $\left(\text{SK},\text{TK}\right)$, which is then sent to attacker $\mathcal{A}$.

• (2)In this phase, there may be communication and interaction between attacker $\mathcal{A}$ and challenger $\mathcal{B}$, but attacker $\mathcal{A}$ cannot obtain the key $\text{SK}$ or any other private information. If attacker $\mathcal{A}$ can successfully challenge the zero-knowledge property of DME, it means that attacker $\mathcal{A}$ c annot distinguish whether the key $\text{SK}$ generated by challenger $\mathcal{B}$ is real or not because attacker $\mathcal{A}$ cannot access the detailed information of $\text{SK}$.

$\text{Challenge}$:Attacker $\mathcal{A}$ sends two equally long plaintext messages $\left\{{\mathrm{m}}_0,{\mathrm{m}}_1\right\}$ to challenger $\mathcal{B}$,and $\mathcal{B}$ randomly selects one plaintext message ${\mathrm{m}}_{\mathrm{b}\in \left\{\mathrm{0,1}\right\}}$ and performs the encryption algorithm $\text{Encrypt}$ to generate a ciphertext.

$\text{Guess}$:Attacker $\mathcal{A}$ outputs a value ${\mathrm{b}}^{\prime }\in \mathrm{0,1}$ as the guess for $\mathrm{b}$, and if ${\mathrm{b}}^{\prime }=\mathrm{b}$,then attacker $\mathcal{A}$ wins the game.

If attacker $\mathcal{A}$ can successfully challenge the zero-knowledge property of DME, it means that attacker $\mathcal{A}$ cannot gain access to private information $\text{SK}$ or other sensitive information. Therefore, attacker $\mathcal{A}$ also cannot break the zero-knowledge properties of DME and DKG. Thus, DME and DKG satisfy zero-knowledge properties.

Theorem 4

If there exists a probabilistic polynomial-time attacker $\mathcal{A}$ such that the advantage $\text{Ad}{\mathrm{v}}_{\mathcal{B}}^{\text{Verifiability}}\left(\text{DME},\mathrm{\lambda }\right)\ge \mathrm{\epsilon }\left(\mathrm{\lambda }\right)$, then $\mathcal{A}$ is capable of constructing an algorithm $\mathcal{F}$ that undermines the $\mathrm{\alpha }$-Verifiability property of the outsourced results of DME.

Proof: To begin, it is necessary to construct a Challenger $\mathcal{B}$ to challenge the verifiability properties of DME. The objective is to prove that $\text{Ad}{\mathrm{v}}_{\mathcal{B}}^{\text{Verifiability}}\left(\text{DME},\mathrm{\lambda }\right)$ is negligible, meaning that Challenger $\mathcal{B}$ cannot break the verifiability properties within an ignorable amount.

$\text{Init}$: Attacker $\mathcal{A}$ selects a verification key secrecy experiment to challenge, denoted as DME,and sends it to the Challenger $\mathcal{B}$.

$\text{Setup}$: Challenger $\mathcal{B}$ randomly generates the public parameters $\text{PP}$ for DME and DKG and sends them to attacker $\mathcal{A}$.

$\text{Phase}1\&2$: Attacker $\mathcal{A}$ executes the simulator ${\mathcal{A}}_0$ to simulate the verification key secrecy experiment and generates a simulated verification key $\text{VK}$. Challenger $\mathcal{B}$ randomly selects a bit $\mathrm{b}\stackrel{\mathrm{R}}{\leftarrow }\left\{\mathrm{0,1}\right\}$.

$\text{Challenge}$: Challenger $\mathcal{B}$ performs the outsourced computation and generates a computation result $\text{Out}$.

$\text{Guess}$: Attacker $\mathcal{A}$ executes the simulator ${\mathcal{A}}_1$ to estimate whether the computation result generated by the challenger is correct, i.e., $\hat{\mathrm{b}}={\mathcal{A}}_1\left(\epsilon \text{VK},\text{Out}\right)$.

For any $\mathrm{\lambda }\in \mathbb{N}$, $\text{Ad}{\mathrm{v}}_{\mathcal{A}}^{\text{Verifiability}}\left(\text{DME},\mathrm{\lambda }\right)=\left|\mathrm{Pr}\left[\text{Ex}{\mathrm{p}}_{\mathcal{A}}^{\text{Verifiability}}\left(\text{DME},\mathrm{\lambda }\right)=1\right]-\frac{1}{2}\right|\le \text{negl}\left(\mathrm{\lambda }\right)$, demonstrating that the DME scheme achieves the verifiability properties of the outsourced computation.

Theorem 5

Given the decidable $\mathrm{q}-\text{BDHE}$ hypothesis in the groups $\mathrm{G}$ and ${\mathrm{G}}_{\mathrm{T}}$, it can be concluded that the proposed BTDS scheme achieves IND-CPA security within the random oracle model.

Proof: Suppose there exists a polynomial-time attacker $\mathcal{A}$ that breaks the BTDS scheme with a non-negligible advantage $\mathrm{\epsilon }$. In this case, we can construct a challenger algorithm $\mathcal{B}$ that can solve the $\mathrm{q}-\text{BDHE}$ hard problem with a non-negligible advantage.

In the specific interactive game, a group $\mathrm{G}$ is selected with a generator $\mathrm{g}$, and a bilinear mapping $\mathrm{e}:\mathrm{G}\times \mathrm{G}\to {\mathrm{G}}_{\mathrm{T}}$ is established. The challenger $\mathcal{B}$ is provided with a hardness input $\left(\mathrm{g},{\mathrm{g}}^{\mathrm{s}},{\mathrm{g}}^{{\mathrm{s}}^2},...,{\mathrm{g}}^{{\mathrm{s}}^{\mathrm{q}}},\mathrm{\zeta }\right)$, where $\mathrm{\alpha },\mathrm{s}\in {\mathrm{Z}}_{\mathrm{p}}$. Without possessing the knowledge of $\mathrm{s}$ and $\mathrm{\alpha }$, the challenger $\mathcal{B}$ engages in an interactive game with the attacker $\mathcal{A}$ and computes $\mathrm{\zeta }=\mathrm{e}{\left(\mathrm{g},\mathrm{g}\right)}^{\mathrm{\alpha }{\mathrm{s}}^{\mathrm{q}+1}}$.

$\text{Init}$: The attacker $\mathcal{A}$ selects an access strategy to challenge ${\mathrm{T}}^{*}=\left({\mathrm{M}}^{*},{\mathrm{\rho }}^{*}\right)$ and sends it to the challenger $\mathcal{B}$.

$\text{Setup}$: The challenger $\mathcal{B}$ randomly selects $\mathrm{a}\in {\mathrm{Z}}_{\mathrm{p}}$, and computes the public parameters $\text{PP}=<\mathrm{G}\text{,}{\mathrm{G}}_{\mathrm{T}},\mathrm{g}\text{,}{\mathrm{g}}^{\mathrm{a}},\mathrm{e}>$. These parameters are then sent to the attacker $\mathcal{A}$.

$\text{Phase}1\&2$: The challenger $\mathcal{B}$ initializes empty tables ${\mathrm{T}}_1,{\mathrm{T}}_2,{\mathrm{T}}_3$, an empty set $\mathrm{D}$, and an integer $\mathrm{j}=0$. The attacker $\mathcal{A}$ is allowed to perform multiple queries on attribute sets according to the following rules.

• (1)$\text{Random}\text{Oracle}\text{Hash}{\mathrm{H}}_1\left(\mathrm{R},\mathrm{m}\right)$: If the entry $\left(\mathrm{R},\mathrm{m},\mathrm{s}\right)$ exists in the table ${\mathrm{T}}_1$, it returns $\mathrm{s}$; Otherwise, it randomly selects a value $\mathrm{s}\in {\mathrm{Z}}_{\mathrm{p}}$, records the entry $\left(\mathrm{R},\mathrm{m},\mathrm{s}\right)$ in table ${\mathrm{T}}_1$, and returns $\mathrm{s}$.
• (2)$\text{Random}\text{Oracle}\text{Hash}{\mathrm{H}}_2\left(\mathrm{R}\right)$: If the entry $\left(\mathrm{R},\mathrm{t}\right)$ exists in the table ${\mathrm{T}}_2$, it returns $\mathrm{t}$; otherwise, it randomly selects a value $\mathrm{t}\in {\left\{\mathrm{0,1}\right\}}^{\mathrm{\lambda }}$, records the entry $\left(\mathrm{R},\mathrm{t}\right)$ in table ${\mathrm{T}}_2$, and returns $\mathrm{t}$.
• (3)$\text{Creat}\left(\mathrm{S}\right)$: The attacker $\mathcal{A}$ submits an attribute set $\mathrm{S}$ to the challenger $\mathcal{B}$ for private key inquiries. The challenger $\mathcal{B}$ increments $\mathrm{j}$ by 1. The challenger $\mathcal{B}$ randomly selects a value $\mathrm{z}\in {\mathrm{Z}}_{\mathrm{p}}$ and runs the $\text{KeyGen}$ algorithm. It sets the conversion key as $\text{TK}={\{\mathrm{K}={{\mathrm{K}}^{\prime }}^{1/\mathrm{z}},\mathrm{L}={{\mathrm{L}}^{\prime }}^{1/\mathrm{z}},\{{\mathrm{K}}_{\mathrm{x}}={\left({\mathrm{K}}_{\mathrm{x}}^{\prime }\right)}^{1/\mathrm{z}}\}}_{\mathrm{x}\in \mathrm{S}}\}$ and the private key as $\text{SK}=\left(\mathrm{z},\text{TK}\right)$. Finally, the entry $\left(\mathrm{j},\mathrm{S},\text{SK},\text{TK}\right)$ is stored in the table ${\mathrm{T}}_3$ and returned to the attacker $\mathcal{A}$.
• (4)$\text{Corrupt}\left(\mathrm{i}\right)$: The challenger $\mathcal{B}$ verifies whether there exists an entry $\left(\mathrm{i},\mathrm{S},\text{SK},\text{TK}\right)$ in the table ${\mathrm{T}}_3$ corresponding to the index $\mathrm{i}$. If such an entry is found, the challenger $\mathcal{B}$ returns the private key $\text{SK}$ to the attacker $\mathcal{A}$. Otherwise, the output is $\perp$. $\text{Challenge}$: The attacker $\mathcal{A}$ submits two plaintext messages of equal length, ${\mathrm{m}}_0$ and ${\mathrm{m}}_1$, to the challenger $\mathcal{B}$. The challenger $\mathcal{B}$ randomly selects one of the plaintext messages, denoted as ${\mathrm{m}}_{\mathrm{b}\in \left\{\mathrm{0,1}\right\}}$, and encrypts it using the encryption algorithm $\text{Encrypt}$. The resulting ciphertext $\text{CT}=\left\{\mathrm{C},{\mathrm{C}}^{\prime },{\mathrm{C}}^{″},{\mathrm{C}}_{\mathrm{i}},{\mathrm{D}}_{\mathrm{i}}\right\}$ is then transmitted to the attacker $\mathcal{A}$.

Guess: The attacker $\mathcal{A}$ provides a value ${\mathrm{b}}^{\prime }\in \mathrm{0,1}$ as their conjecture for $\mathrm{b}$. If ${\mathrm{b}}^{\prime }=\mathrm{b}$, the challenger $\mathcal{B}$ outputs 0, indicating that the conjecture for $\mathrm{\zeta }=\mathrm{e}{\left(\mathrm{g},\mathrm{g}\right)}^{\mathrm{\alpha }{\mathrm{s}}^{\mathrm{q}+1}}$ is correct. Otherwise, the challenger outputs 1, indicating that the conjecture for $\mathrm{\zeta }$ is a random element in the group ${\mathrm{G}}_{\mathrm{T}}$. When $\mathrm{\zeta }=\mathrm{e}{\left(\mathrm{g},\mathrm{g}\right)}^{\mathrm{\alpha }{\mathrm{s}}^{\mathrm{q}+1}}$, the challenger $\mathcal{B}$ can provide a valid simulation, which leads to the following expression: $\mathrm{Pr}\left[\mathcal{B}{(\mathrm{g},{\mathrm{g}}^{\mathrm{s}},{\mathrm{g}}^{{\mathrm{s}}^2},...,{\mathrm{g}}^{{\mathrm{s}}^{\mathrm{q}}},\mathrm{\zeta }=\mathrm{e}\left(\mathrm{g},\mathrm{g}\right)}^{\mathrm{\alpha }{\mathrm{s}}^{\mathrm{q}+1}})=0\right]=\text{Ad}{\mathrm{v}}_{\mathcal{A}}+1/2$. When $\mathrm{\zeta }$ is a random element, the value of ${\mathrm{m}}_{\mathrm{b}}$ is completely random to the attacker $\mathcal{A}$, thus we have: $\mathrm{Pr}\left[\mathcal{B}\left(\mathrm{g},{\mathrm{g}}^{\mathrm{s}},{\mathrm{g}}^{{\mathrm{s}}^2},...,{\mathrm{g}}^{{\mathrm{s}}^{\mathrm{q}}},\mathrm{\zeta }\right)=0\right]=1/2$.

In summary, the challenger $\mathcal{B}$ can successfully challenge and break the decidability of the $\mathrm{q}-\text{BDHE}$ hypothesis with a non-negligible advantage.

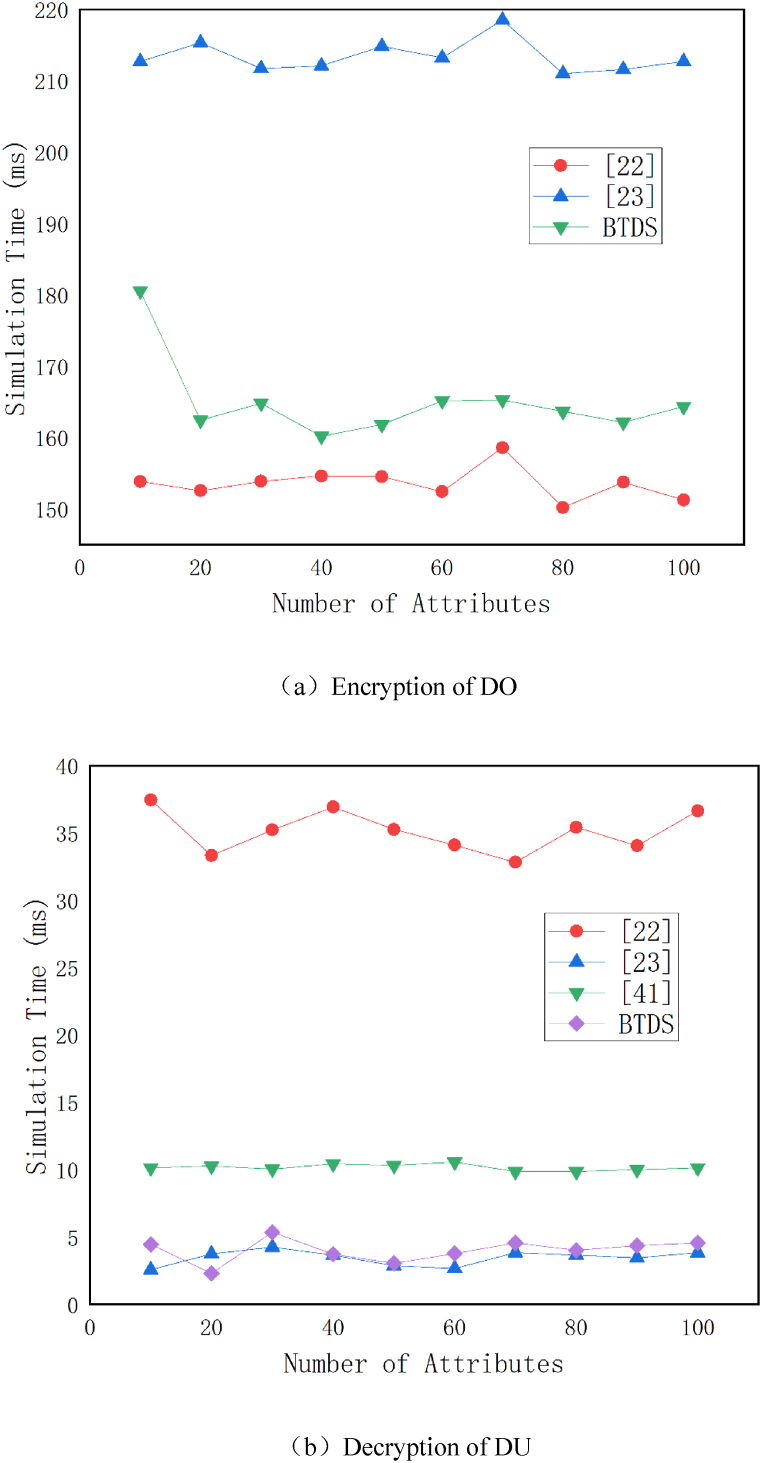
7. Simulation experiment and performance analysis

7.1. Comparison of schemes

Table 6 and 7 focus on the functional analysis and computational complexity analysis of the BTDS architecture. To facilitate quantitative comparison of the schemes, we denote by $E$ the exponentiation operation, $M$ the modular exponentiation operation, $P$ the bilinear pairing operation, $n$ the number of attributes used in the access strategy, and $\mathcal{l}$ the number of rows in the access structure matrix based on LSSS.

Table 6.

Functional analysis.

Scheme	Multi-authority	Encryption Outsourcing	Decryption Outsourcing	Key Generation Outsourcing	Verification Probability	Distributed Outsourcing	Blockchain
[56]	Single	×	✓	×	✓	×	×
[43]	Single	✓	✓	×	✓	×	×
[57]	Single	✓	✓	✓	✓	×	×
[58]	Multi	×	✓	×	✓	×	×
BTDS	Multi	✓	✓	✓	✓	✓	✓

Table 7.

Computational complexity analysis.

Scheme	DO		DU		OSP
	Data Owner Encryption	Data Owner Verification	Data User Verification	Data User Decryption	Encryption outsourcing	Decryption outsourcing
[56]	$\left(4+3n\right)E+1M$	–	$2E+1M$	$1M$	–	$2M+\left(2n+1\right)P$
[43]	$2E$	$2E+1M$	$5E+4M+1P$	$1M$	–	–
[57]	$3E+1M$	–	–	$3M$	$\left(2\mathcal{l}+1\right)M$	$sM+\left(2s+4\right)P$
[58]	$5E+1M$	–	–	$1E+1M$	–	$1E+2M+3nP$
BTDS	$2E+\left(2M\right)$	$3M$	$2E+1M$	$1E+1M$	$1E+2lM$	$2M+n\mathcal{l}P$

Green et al. [56] proposed the first ABE scheme with outsourced decryption. This scheme involves semi-trusted servers performing (2n + 1) bilinear pairing operations and 2n modular exponentiations to generate partially decrypted ciphertext. The user can then retrieve the original message with a single exponential operation. During the encryption process, the data owner requires (4 + 3n) exponentiation operations and one modular exponentiation.

Li et al. [43] outsourced both encryption and decryption operations to cloud servers, significantly reducing the computational load on user terminals. They not only support outsourced encryption and decryption operations, but also introduce two types of secure outsourced exponentiation algorithms for exponentiation operations in outsourced encryption. These algorithms use mathematical partitioning and blinding operations to hide the bases and exponents contained in the ciphertext components, thus ensuring data privacy. However, the correctness verification probabilities for multiple-base modular exponentiation secure outsourcing algorithms and single-base modular exponentiation secure outsourcing algorithms were only 2/5 and 1/2, respectively. In the [43] scheme, data owners were involved in only 2 exponentiation operations during the encryption computation phase, requiring 2 exponentiation operations and 1 modular multiplication operation in the encryption verification phase. Data users, on the other hand, require only one modular multiplication operation during the decryption computation, but five exponential operations and one bilinear pairing operation during the decryption verification phase. Bilinear pairing computations are significantly more expensive than modular multiplication computations.

Zhao et al. [57] proposed a fully outsourced ciphertext policy attribute-based encryption scheme that supports verifiable key generation, encryption, decryption computations, and the verification of outsourced computation results. During the encryption process, the data owner needs three exponentiation operations and one modular exponentiation operation. In the decryption phase, the data user needs only one exponentiation operation and one modular exponentiation operation.

The aforementioned works [43,56,57] are based on single-authority CP-ABE outsourcing schemes. Sana Belguith et al. [58] introduced a policy-hiding outsourced ABE scheme called PHOABE, based on multi-authority CP-ABE, which delegates the computationally expensive part of the decryption process to a semi-trusted cloud server. During the encryption phase, the data owner needs to perform five exponential operations and one modular exponential operation. Data users outsourced computationally expensive operations, including 3n bilinear pairing operations, 2 modular exponentiation operations, and 1 exponentiation operation, to semi-trusted cloud servers. As a result, the data user only needs to perform 1 exponentiation operation and 1 modular exponentiation operation during the decryption phase.

In this work, we replace the modular exponentiation outsourcing algorithm with a distributed modular exponentiation outsourcing algorithm more suitable for edge computing scenarios, based on the PHOABE scheme. In addition, we use a distributed key generation algorithm in conjunction with EBC to ensure key security while generating user private keys. Unlike the scheme in Ref. [43], our scheme requires data owners to perform 2 additional modular exponentiation operations when using the system public key for encryption operations for the first time. However, it only requires 3 modular exponentiation operations during the encryption verification phase. Data users require one additional modular exponentiation operation during decryption computations but perform fewer operations, including 3 exponentiation operations, 3 modular exponentiations, and 1 bilinear pairing operation, during the verification phase compared to the scheme in Ref. [43].

In addition, the communication overhead of outsourced computations in the BTDS architecture is another significant performance factor. A comprehensive analysis of the communication overhead of the DME algorithm reveals that the user needs to send $4n*Lenp+4n*Lenp=\left(24*1024+160*4\right)/8*1024\approx 3KB$ of data to n edge computing nodes and all edge computing nodes together need to send $4n*Lenp=4n*1024/8*1024=3KB$ of data to the user [51]. Thus, the communication cost can be considered negligible compared to the computational time cost within a reasonable healthcare scenario distance.

Finally, the implementation cost of EBC should not be neglected. The storage of ciphertext data copies in the blockchain has a negligible impact on the time cost of the system, since the BTDS architecture is an incremental improvement over the original healthcare cloud storage-based system. All operations take place in the background of the system and do not alter the user experience. Therefore, the primary consideration for the implementation cost of EBC lies in the key generation process when performing the CP-ABE algorithm. The DKG sub-algorithm is a distributed secure key generation protocol implemented on top of EBC, and it guarantees the ‘useable but invisible’ property of the entire CP-ABE algorithm execution. This means that no AA at risk of key leakage can have the system's master private key independently, yet they can still collaborate to generate the user's private key. During this process, the sharing of the system's public key and uploading to the blockchain consensus are performed offline during the system initialization phase, so the real-time cost of this part can be considered negligible. In the user private key generation process, each $A{A}_i$ generates user private key parameters $K_i^{\prime }{K}_{x_i}^{\prime },L_i^i$, which include the random selection of $t_i$, computation of exponentiations $\left(g^{F\left(x\right)t_i},g^{{\kappa }_i+\alpha t_i},g^{t_i}\right)$, and uploading of these parameters to EBC. The computational cost of each $A{A}_i$ depends on the required exponentiation and data transfer. However, since each AA node is responsible for generating a portion of the private key, the computational cost of a single AA is limited and this cost can also be considered negligible to some extent. The main cost in this section is concentrated in the Lagrangian interpolation computation of the AC ensemble and all partial private keys generated by the AAs. The time complexity of Lagrange interpolation in BTDS architecture mainly depends on the number of input points (AA nodes) and the distributed computing environment's setup. If the number of input points for Lagrange interpolation in BTDS is n, then theoretically, the time complexity of Lagrange interpolation is O(n). This is because the cost of computing each Lagrange basis function is O(1), and there are a total of n basis functions. However, BTDS operates in a distributed computing environment, where different nodes may be responsible for processing different input points. In such a scenario, each node can compute the basis functions it is responsible for in parallel, thus reducing the overall interpolation time cost. Taking everything into consideration, the cost of Lagrange interpolation in BTDS can be approximated as O(n), or even further improved through parallel computation.

Overall, when properly utilizing parallel computing to address the cost of Lagrange interpolation in distributed key generation, this paper's scheme, based on the foundation of literature [43], which incorporates distributed modular exponentiation outsourcing algorithms and distributed key generation protocols better suited for edge computing environments, performs better in terms of computational cost compared to the reference scheme. While it involves an additional computational cost for the public key to the system during the initial encryption operation, it guarantees a 100 % verification probability and significantly reduces the computational cost during the encryption verification phase, making the overall computational cost superior to the compared schemes.

7.2. Experimental analysis

Based on the theoretical analysis presented above, the proposed scheme is better suited for data trust sharing scenarios in edge computing environments in terms of functionality and computational cost. To further evaluate the practical performance of this scheme, this section conducts experiments to analyze the computational overhead on terminal devices, including the encryption time for data owners and the decryption time for data users, in comparison to the literature [43,44,57].

Experimental Environment: The experiments were conducted in a controlled environment using a Windows 10 operating system, an Intel(R) Core(TM) i5-8250U CPU @1.60 GHz 1.80 GHz processor, and 8 GB of memory. The code was developed and executed within the IntelliJ IDEA 2022 development environment, utilizing the JPBC-2.0.0 function library for implementation.

Experimental Setup: In the CP-ABE scheme, the encryption time and decryption time are influenced by the number of attributes. As this paper focuses on the application of CP-ABE in the edge computing environment, the encryption time and decryption time were specifically tested when the Data Owner (DO) and Data User (DU) were considered as terminal nodes. During the experiment, the number of attributes was gradually increased with an average increment of 10. The base value was set to 10, and the results were incremented by a factor of 10. The final experimental results were obtained by averaging the results of 10 iterations.

Fig. 3 consists of two sub-figures: sub-figure (a) shows the computational time comparison for DO during the encryption process, while sub-figure (b) presents the computational time comparison for DU during the decryption process. From Fig. 3, it can be observed that the time spent by DO during the encryption phase and DU during the decryption phase in both the literature [43,44,57] schemes and this paper's scheme does not increase with the number of attributes.

Fig. 3.

Comparison of simulation time.

In Fig. 3 (a), it is evident that the scheme presented in literature [57] outsources all CP-ABE key generation, encryption, and decryption operations to a cloud server, resulting in significantly lower encryption costs for data owners (DO) compared to the schemes in literature [43,44] and this paper's scheme. Literature [43,44] only outsources the computationally expensive modular exponentiation and bilinear pairing operations in the CP-ABE encryption and decryption phases to a cloud server. To better adapt to edge computing environments, this paper replaces the modular exponentiation outsourcing algorithm used in literature [43,44] with the distributed modular exponentiation outsourcing algorithm proposed in literature [51]. This approach outsources the modular exponentiation and bilinear pairing operations in the CP-ABE encryption and decryption phases to edge nodes for parallel computation. Compared to the DO encryption time in the literature [43] scheme, the literature [44] scheme requires more computational time due to the increased correctness probability. However, due to the reduction in DO verification time through the use of distributed modular exponentiation outsourcing, the encryption time is lower than that of the literature [44] scheme.

From Fig. 3 (b), it is evident that literature [43] requires significantly additional time for DU during the decryption and verification phase due to the need for one computationally expensive bilinear pairing operation. Consequently, the overall decryption time for literature [43] is much higher than that of literature [44,57], and this paper's scheme. The decryption time for this paper's scheme is almost identical to that of the literature [44] scheme and considerably lower than that of literature [57].

In summary, the computational time of DO and DU in the proposed scheme does not increase with the number of attributes or the complexity of the access strategy. In this paper, our scheme achieves critical security for CP-ABE at the edge and increases the verifiability probability of the distributed modular exponentiation outsourcing algorithm to 100 %. While maintaining security, the proposed scheme keeps the efficiency of the CP-ABE algorithm within a reasonable range. Therefore, based on these experiments, it is feasible to apply the proposed scheme for trusted sharing of medical data in an edge computing environment.

8. Conclusion

In this paper, we address the issue of trustworthy medical data sharing in edge computing environments and present a blockchain-based Trustworthy Medical Data Sharing (BTDS) solution. We begin by considering the real-time demands of attribute authorization services in edge computing environments and propose a Distributed Attribute Authorization (DAA) strategy based on blockchain. To mitigate the key security concerns of CP-ABE in edge environments, we introduce a Distributed Key Generation (DKG) protocol built on blockchain. To overcome resource limitations in end-user devices, we enhance a Distributed Modular Exponentiation (DME) outsourcing algorithm and apply it to the encryption and decryption outsourcing computations in CP-ABE.

Lastly, we prove the security of the BTDS architecture under the Random Oracle Model and conduct simulation experiments. The results indicate that the computational time for DO and DU in our solution does not increase with the growth in the number of attributes or the complexity of access policies. Instead, it remains within a reasonable and lower range. In summary, the proposed BTDS architecture aligns with the initial design intent of providing fine-grained data access control for resource-constrained end-user devices in edge computing environments.

However, there are some limitations to our study. For instance, the performance of our scheme in large-scale real-world edge computing environments and how to further optimize our scheme to accommodate more complex real-world edge computing scenarios are issues worth investigating. We hope that future research will contribute more in these areas.

Nevertheless, it is important to acknowledge the limitations of our study and identify potential avenues for future research. Specifically, the performance of our scheme in large-scale edge computing environments and the optimization of our scheme to cater to more intricate edge computing scenarios warrant further investigation. We encourage future researchers to delve deeper into these areas, aiming to make significant advancements and contribute valuable insights.

Data availability statement

Data related to this study has not been deposited in a publicly available repository, but will be available upon request.

Ethics declarations

This research study does not require review and/or approval from an ethics committee because it does not involve animal experiments, human subjects, behavioral research, clinical trials, or any form of medical research.

CRediT authorship contribution statement

Gaoyuan Quan: Writing – review & editing, Writing – original draft, Validation, Methodology, Formal analysis, Data curation, Conceptualization. Zhongyuan Yao: Writing – review & editing, Validation, Supervision, Methodology, Funding acquisition, Conceptualization. Longfei Chen: Visualization, Validation, Software, Funding acquisition, Data curation. Yonghao Fang: Visualization, Software, Data curation. Weihua Zhu: Supervision, Project administration, Funding acquisition. Xueming Si: Supervision, Resources, Project administration, Funding acquisition, Conceptualization. Min Li: Writing – review & editing, Investigation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.