Negative durotaxis: cell movement toward softer environments

Abstract

How cells sense tissue stiffness to guide cell migration is a fundamental question in development, fibrosis and cancer. Although durotaxis – traditionally defined as cell migration toward increasing substrate stiffness – is well established, it remains unknown whether individual cells can migrate toward softer environments. Using microfabricated stiffness gradients, we observed directed migration of U-251MG glioma cells toward lower stiffness. This ‘negative durotaxis’ did not coincide with changes in canonical mechanosensitive signaling or actomyosin contractility. Instead, motor-clutch-based modeling predicted migration toward cell-intrinsic ‘optimal stiffness’, where cells generate maximal traction. As predicted by the model, negative durotaxis was selectively disrupted and even reversed by partial inhibition of actomyosin contractility. Conversely, positive durotaxis was switched to negative experimentally by lowering the optimal stiffness via downregulation of a key clutch component, talin. Our results identify the molecular mechanism driving context-dependent positive or negative durotaxis, determined by a cell’s contractile and adhesive machinery.

The capacity of living cells to undergo controlled migration is critical for tissue homeostasis and development, and underlies pathological conditions like cancer metastasis^1,2. Cells migrate in response to chemical and physical cues including the elasticity, or stiffness, of the surrounding extracellular matrix (ECM). The well-known tendency for many cells to migrate toward stiffer substrates, known as durotaxis ^3–8, has implications for both developmental morphogenesis^9,10 and cancer cell invasion^8,11,12.

Despite progress in empirically identifying environmental conditions and molecular components that enable or promote durotaxis^4,5,13–15, our understanding of its fundamental mechanisms in different cell types is lacking. A long-standing mathematical model for cell migration is based on the motor-clutch mechanism^16–19, in which F-actin filaments polymerize against the plasma membrane to push the cell edge forward, while being simultaneously pulled away from the cell edge by ATP-dependent myosin II (‘molecular motors’) and pushed by force from the ATP-dependent polymerization itself. Retrograde F-actin flow can be mitigated by mechanical connections or ‘clutches’, typically integrin-mediated adhesions, between the F-actin and ECM to generate traction and bias cell movement toward more adhesive environments^20,21. These traction forces are critical for cell migration and as a result, they have also been linked to durotaxis. For example, fibroblasts on stiffness gradients exhibit asymmetric traction which has been postulated to contribute directly to their polarization and migration up the gradient^6,22. Recently, differences in intracellular contractility and adhesivity to the ECM have been proposed to explain why some cells are more prone to durotax than others¹². Interactions between actomyosin machinery and integrin-mediated adhesions have also been implicated in neuronal growth and mechanosensitive pathfinding^23–25. However, the unifying principles underlying these behaviors across cell types have not been established.

Recently, cellular traction forces were shown to be maximal on substrates of an ‘optimal stiffness’ that can be predicted by the motor-clutch model^{18,19,26–30}. However, the biological relevance of this on cell behavior remains to be fully elucidated. Due to the key role of traction in driving mesenchymal cell migration, we predicted that any cell whose adhesion dynamics are governed by the motor-clutch model could potentially migrate toward softer environments, if such environments were closer to the cell’s optimal stiffness for maximal traction generation. We call this behavior ‘negative durotaxis’.

To test our hypothesis, we seeded U-251MG human glioblastoma cells, previously shown to exhibit maximal traction at an optimal stiffness of 5–10 kPa (Fig. 1a)²⁹, on fibronectin-functionalized polyacrylamide hydrogels having a continuous stiffness gradient of approximately 0.5–22 kPa (Fig. S1a–b)³¹ – a range representative of healthy and malignant brain tissue³². We observed a strong tendency for these cells to undergo negative durotaxis, migrating from the stiffest areas to regions of intermediate stiffness over time (Fig. 1b–c). Fewer cells were observed in the softest regions, implying that cells below the optimal stiffness underwent conventional positive durotaxis. To exclude cell proliferation as a cause of these differences, we quantified the rate of EdU incorporation in cells cultured on homogeneous 0.5, 9.6 and 60 kPa substrates. Proliferation was equal on 9.6 kPa and 60 kPa hydrogels and only slightly lower on 0.5 kPa substrates (Fig. S2a–b), suggesting that the absence of cells in the stiffer regions of the gradient was indeed due to biased migration. This was further validated by live-cell tracking of individual cells on the stiffness gradients. The cells initially located in areas below the optimal stiffness (<10 kPa) exhibited movement toward increasingly stiff regions, whereas cells residing in areas above the stiffness optimum (>10 kPa) displayed a significant tendency to migrate toward the softer regions (Figs. 1d, S3a–b).

Figure 1. U-251MG glioblastoma cells undergo negative durotaxis.

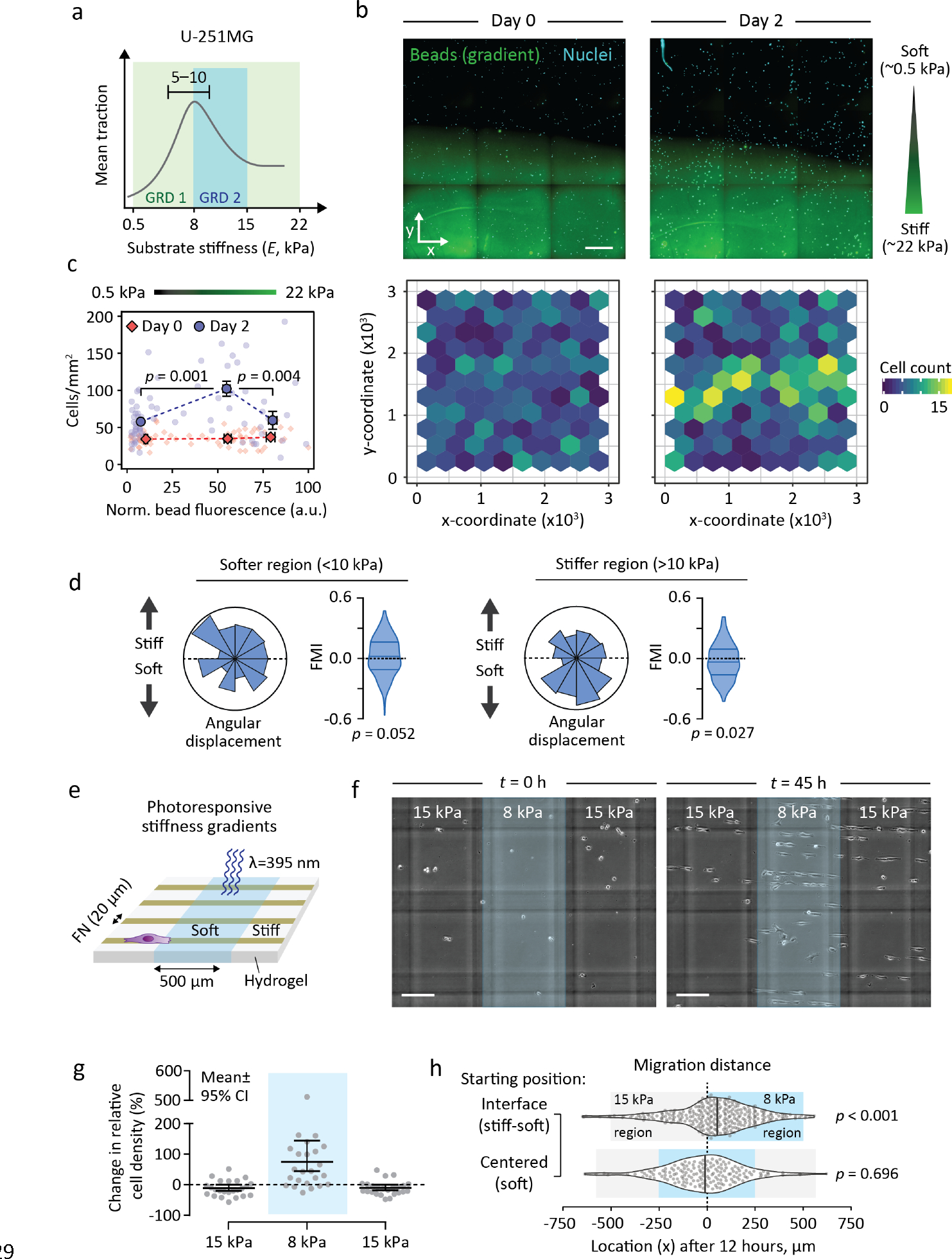
(a) Schematic representation of U-251MG traction, maximal on 5–10 kPa substrates²⁹, and how it relates to the two stiffness gradients employed here. (b) (Top) Representative region of a diffusion-based polyacrylamide stiffness gradient (Young’s modulus ~0.5–22 kPa), at the outset of the experiment and 48 hours later. U-251MG cells are indicated by nuclear staining. Scale bar, 500 μm. (Bottom) Quantification of cells across the gradient. (c) Cell density in different parts of the stiffness gradient. Bins denote pooled regions of interest in the bottom, middle and top third of the gradient, respectively. Mean ± SEM of n = 14–42 ROIs, analyzed by Kruskal-Wallis one-way ANOVA and Dunn’s post hoc test. (d) Angular displacements and forward migration indices of individual U-251MG cells migrating in the softer (<10 kPa, left) and stiffer (>10 kPa, right) regions of a 0.5–22 kPa gradient. n = 174–264 cells from three independent experiments. Analyzed by Wilcoxon signed rank test. (e) Schematic representation of photoresponsive hydrogels with steep repeating stiffness gradients. (f–h) U-251MG migration on photoresponsive gradient hydrogels. A representative example (f) and quantification (g) of the change in cell density across the gradients over time. Blue overlay denotes softer, UV-exposed regions. Vertical and horizontal gray lines in (f) are out-of-focus markings in the underlying glass, used as a reference. Scale bar, 200 μm. Mean ± 95% CI from n = 24 fields of view, from two independent experiments. (h) Violin plots of accumulated distance migrated by individual cells along the x-axis over 12 hours, starting from a gradient (top) or from the middle of a compliant region (bottom). Vertical lines denote medians, n = 164–296 cells from two independent experiments. Analyzed by sign test.

As an additional demonstration of negative durotaxis, we cultured U-251MG cells on photoresponsive hydrogels with alternating 8 and 15 kPa regions, connected by steep stiffness gradients (Figs. 1e, S4a–b, S5a–d; Supplementary Text 1). 20 μm wide fibronectin lines were printed across the gradients to facilitate cell motility. Live-cell imaging revealed that cells migrated along the fibronectin lines and clustered preferentially in the softer 8 kPa regions (Figs. 1f–g, S3c–d; Movie S1). Moreover, tracking of individual U-251MGs confirmed that any cells making contact with a stiffness gradient migrated preferentially to the softer 8 kPa side (Figs. 1h, S3e; Movie S2). Finally, we confirmed that the biased migration on either type of stiffness gradient was not due to differences in fibronectin density, i.e. haptotaxis, as ligand distribution appeared uniform in both experimental models (Figs. S1c, S5e–f). Taken together, these data demonstrate that U-251MGs are capable of negative durotaxis from stiff to soft environments, consistent with their stiffness optimum for maximal traction.

To gain insight into the molecular basis of negative durotaxis, we investigated key mediators of mechanotransduction, whereby biomechanical cues are translated into changes in cell signaling and behavior³³. We speculated that a biphasic response in any of these could, in part, modulate the negative durotaxis of U-251MGs. However, no changes were observed in myosin II light chain (MLC2), focal adhesion kinase (FAK) or extracellular signal-regulated kinase (ERK) phosphorylation in U-251MGs cultured on substrates with moduli of 0.5, 8 or 50 kPa (Fig. 2a–b). These results were surprising because, in most adherent cell types, increasing substrate stiffness supports integrin clustering and focal adhesion (FA) growth, promoting the activation of mechanosensitive downstream signaling pathways^19,34,35.^35,35,34

Figure 2. U-251MG cells display limited mechanosensitive signaling and adhesion maturation.

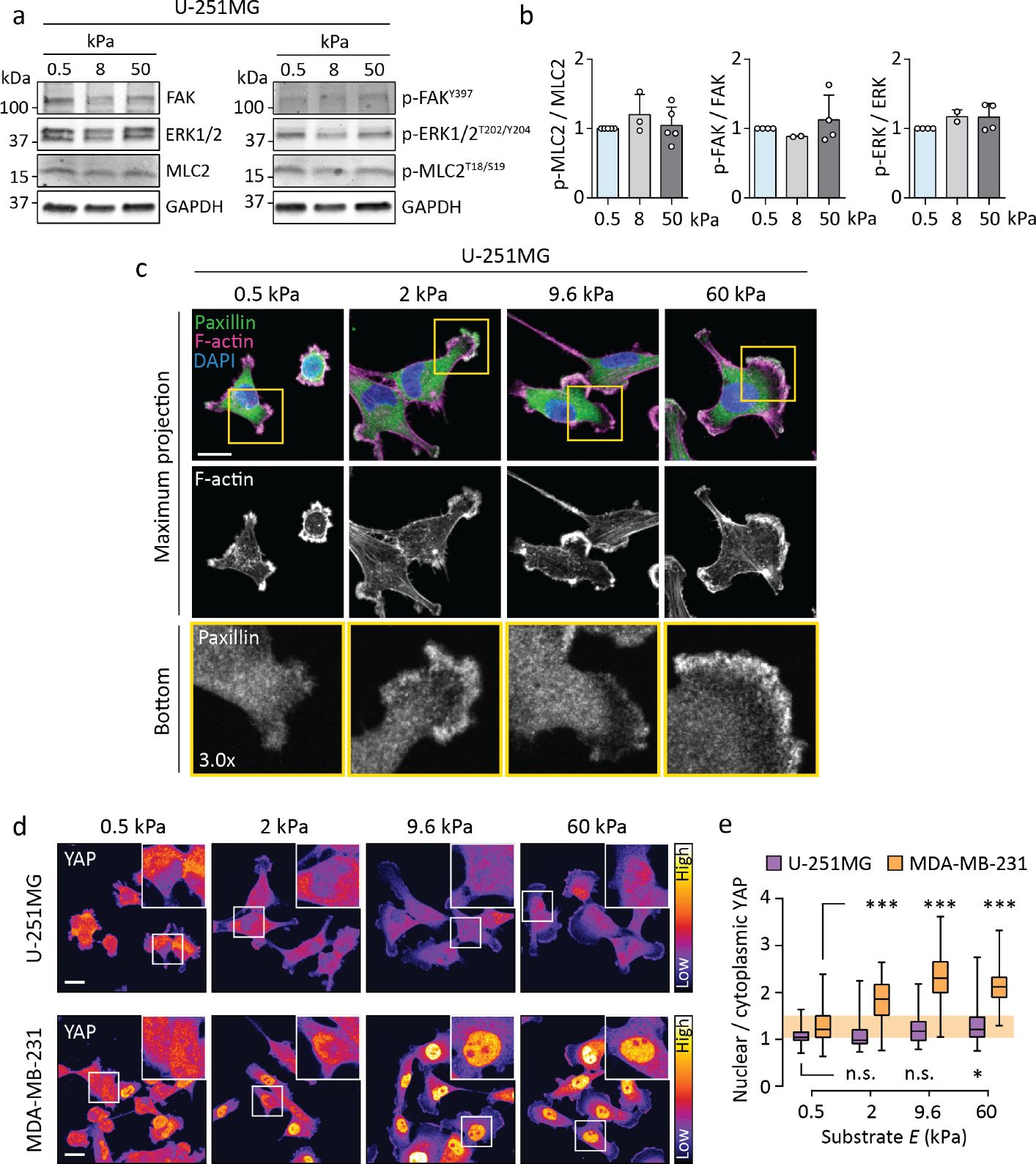
(a–b) Representative western blot (a) and quantification (b) depicting protein phosphorylation in U-251MGs on 0.5–50 kPa substrates. Mean ± SD of 2–5 independent experiments. (c) Immunofluorescence images of paxillin and F-actin in U-251MGs on 0.5–60 kPa substrates. The bottom panels show individual focal planes from confocal stacks, corresponding to the basal side of each cell. Scale bar, 20 μm. (d–e) Immunofluorescence images (d) and quantification (e) showing the intracellular localization of YAP as a function of substrate stiffness in U-251MG and MDA-MB-231 cells. Insets depict representative nuclei. Scale bar, 20 μm. Each box displays upper and lower quartiles and a median, the whiskers denote minimum and maximum values. n = 57–135 cells, ***p < 0.001, *p = 0.018, n.s. = not significant, analyzed by Kruskal-Wallis one-way ANOVA and Dunn’s post hoc test.

This prompted us to compare focal adhesions in U-251MGs, capable of negative durotaxis, and MDA-MB-231 breast adenocarcinoma cells, which reportedly undergo positive durotaxis⁸. As expected, MDA-MB-231s displayed stiffness-induced growth of paxillin-positive FAs (Fig. S6a) whereas U-251MGs displayed very few FAs even on 60 kPa substrates, as confirmed by immunostaining of paxillin (Fig. 2c) and additional FA markers, vinculin and phosphorylated FAK (Fig. S6b). This was not due to low expression of mechanosensitive adhesion proteins talin-1, talin-2 or vinculin, or due to low myosin II activity (p-MLC2), as these were expressed at comparable levels in U-251MG, MDA-MB-231, and human osteosarcoma U-2 OS, another FA-forming³⁶ cell line (Fig. S6c–d). Nevertheless, U-251MGs displayed high β1-integrin activity and their spreading on fibronectin was sensitive to β1-integrin inhibition with a function-blocking antibody (Mab13) (Fig. S6e–g), suggesting that they interact with their substrate primarily through integrins.

Hippo-family proteins yes-associated protein 1 (YAP) and transcriptional co-activator with PDZ-binding motif (TAZ) are transcriptional co-regulators that integrate cues from different mechanical and biochemical sources to direct cell behavior. Nuclear localization and activation of YAP/TAZ on stiff substrates are linked to increased F-actin assembly and FA formation; conversely, YAP/TAZ can promote adhesion turnover and cell migration³⁷ and baseline YAP activity may even be necessary for conventional durotaxis¹⁴. We stained endogenous YAP from MDA-MB-231s and observed robust stiffness-induced nuclear translocation (Fig. 2d–e). In contrast, U-251MGs displayed much lower nuclear YAP on both soft and stiff substrates, with a slight increase but no visible peak between 0.5 and 60 kPa (Fig. 2d–e). Thus, mechanosensitive signaling responses of U-251MGs are minimal and not specific to the 5–10 kPa range, and cannot explain negative durotaxis.

The optimal stiffness for U-251MG traction and the increasing overall motility of these cells (random motility coefficient, RMC) with stiffness up to 100 kPa can be explained by motor-clutch dynamics²⁹. Without talin unfolding and vinculin-mediated ‘clutch reinforcement’ and FA growth, the motor-clutch model naturally predicts a biphasic dependence of traction forces on substrate stiffness¹⁹. After confirming that U-251MGs migrated preferentially toward their known stiffness optimum in all of our experimental conditions (Fig. 1a–h), we investigated whether stochastic computational simulation of cell-level motor-clutch dynamics would be sufficient to reproduce negative durotaxis (Fig. 3a, Supplementary Text 2). We simulated the migration of individual U-251MGs on mechanically homogeneous substrates for one hour to allow the system to reach a dynamic steady state, then placed each cell on a continuous substrate consisting of alternating 60 μm wide regions of low and high stiffness, joined together by continuous 30 μm wide stiffness gradients (Fig. 3b).

Figure 3. Motor-clutch simulations recapitulate negative durotaxis.

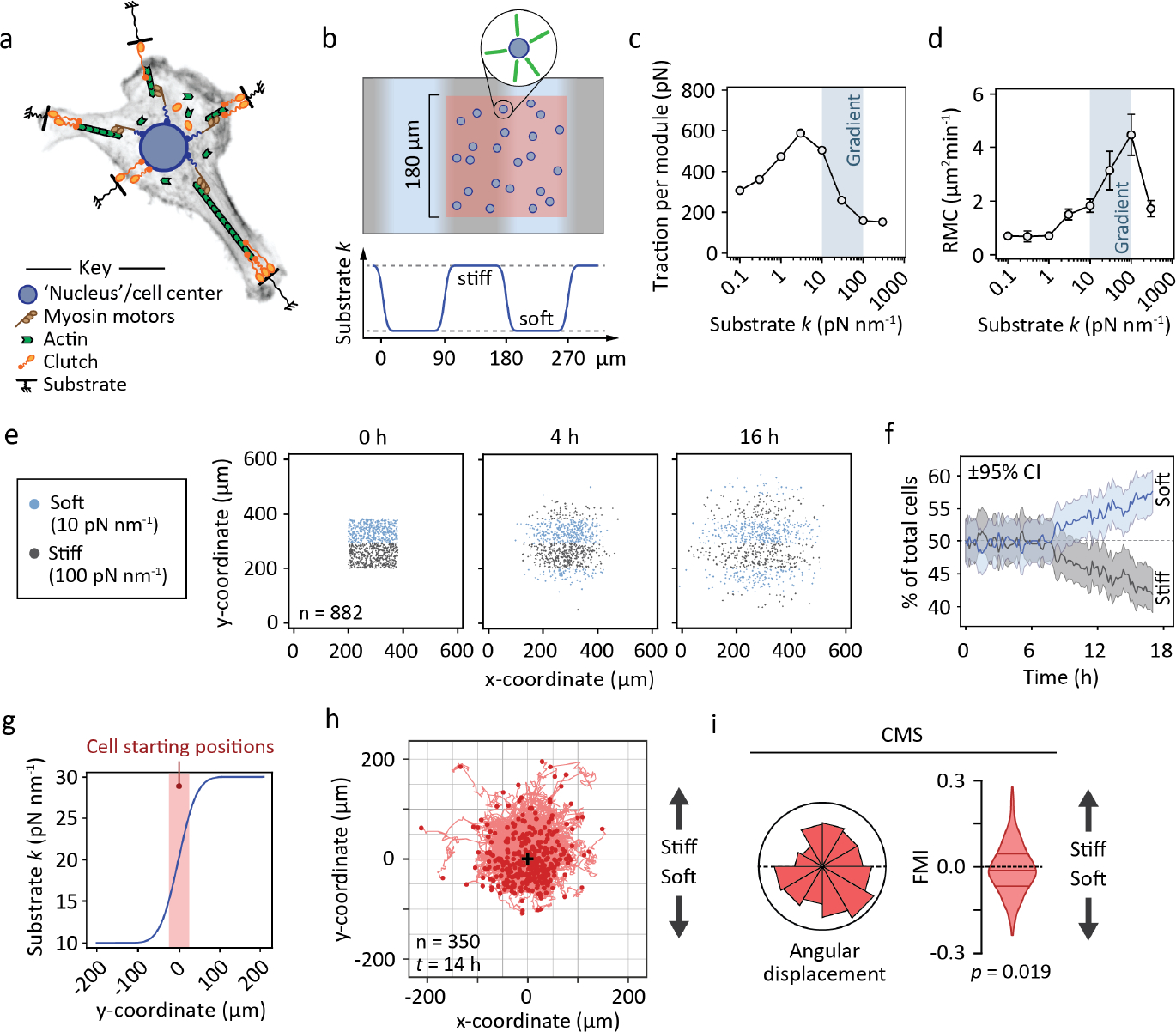
(a) Schematic representation of the cell migration simulator²⁹. Individual modules and a central cell body are attached to the elastic substrate by sets of clutch molecules (Supplementary Text 2). (b) Experimental setup used here and in Figs. S8 and S9. Simulated cells in a dynamic steady state were placed on a substrate with repeating stiff and soft regions and tracked over time. An equal number of cells were placed on both stiffnesses (red area). (c–d) Module-wise traction forces (c) and RMC (d) of the simulated cells as a function of substrate stiffness. Overlays highlight the range of the 10–100 pN nm⁻¹ gradient in (e–j). Mean ± SEM of n = 10 cells. (e–f) Evolution of cell density on mechanically heterogeneous substrates over time. (e) Coordinates of individual cells 0, 4 and 16 hours into the simulation. Stiff (≥55 pN nm⁻¹) and compliant (<55 pN nm⁻¹) regions are indicated by gray and blue, respectively. (f) Fraction of cells residing in the stiff and soft regions over the course of the simulation. ±95% CI, n = 882 cells. (g) Experimental setup used for investigating the migration tracks of individual simulated cells on a continuous stiffness gradient. Cells in a dynamic steady state were placed randomly on the linear part of a 10–30 pN nm⁻¹ gradient and tracked for 14 simulated hours. (h) Tracks from individual cells on the 10–30 pN nm⁻¹ gradient. The origo (0, 0) is highlighted by a black (+), n = 350 cells. (i) Angular displacements and forward migration indices of the cells depicted in (h). Analyzed by Wilcoxon signed rank test.

On 10–100 pN nm⁻¹ gradients, corresponding to ~10–100 kPa for typical adhesion sizes³⁸, and where the cells’ optimal stiffness for maximal traction overlaps with the softer regions (Fig. 3c–d), we found that the majority of cells translocated away from stiffer areas in the first 12 hours of the simulation (Fig. 3e–f). This occurred despite the cells being less motile (i.e. having lower RMC) on the softer substrate (Fig. 3d). On stiffness gradients, cellular protrusions (modules) displayed higher average traction on soft than on stiff regions (Fig. S8a–c), and cells also turned preferentially toward the softer areas (Fig. S8d). By altering the range of the gradient, such that the side associated with higher predicted traction was the stiffer one, durotaxis could be reversed and cells clustered primarily in the stiff regions (Fig. S9). Finally, we replaced the repeating graded substrates with a 200 μm continuous stiffness gradient of 10–30 pN nm⁻¹ to study the tracks of individual cells in quantitative detail. Each cell was placed randomly on the linear region of the gradient (Fig. 3g) and tracked for 14 simulated hours (Fig. 3h). We confirmed that the majority of simulated cells migrated toward the softer substrate, recapitulating the behavior observed in U-251MGs in vitro (Fig. 3i).

We verified the generality of these principles by applying them to model axonal pathfinding in neuronal development and regeneration (Figs. S10, S11; Supplementary Text 3). Indeed, the tendency for Xenopus retinal ganglion cells to grow toward softer tissue is closely analogous to negative durotaxis²⁴. Neurite elongation and pathfinding via the actin-rich neuronal growth cone (GC) at the distal end of the axon involves contractile filopodia of variable length and orientation (Fig. S10a). Applying our model to individual filopodia (Fig. S10b) and to GCs with multiple filopodia (Fig. S11a), we found that the protrusions elongated faster and generated more traction on soft substrates (0.01–0.1 pN nm⁻¹) (Fig. S10c–h). This was consistent both with earlier predictions of relatively low optimal stiffness for neurons^18,39,40, and with our hypothesis that positive and negative durotaxis are governed by motor-clutch dynamics in concert with optimal stiffness. The results also suggested that gradient strength may further increase propensity for negative durotaxis: GCs steered to more compliant regions on substrates with stronger gradients (reaching a maximum at ~10 pN nm⁻¹/20 μm), but did not change direction on mild gradients (~0.1 pN nm⁻¹/20 μm) or on substrates that were overall stiff compared to the optimum (>1 pN nm⁻¹) (Fig. S11c–e).

The motor-clutch model of cell migration states that a cell’s capacity to respond to substrate mechanics is intrinsically linked to its pool of available molecular motors, or actomyosin contractility, such that partial inhibition of intracellular contractility would be expected to shift the cell’s stiffness optimum up slightly²⁷. We confirmed this using our CMS model and observed a three-fold increase in the optimal substrate stiffness when motor numbers were gradually decreased, before the system stalled, stopping actin dynamics and cell migration on all but the stiffest substrates (Fig. 4a–b).

Figure 4. Decreasing actomyosin contractility selectively inhibits negative durotaxis in U-251MG cells.

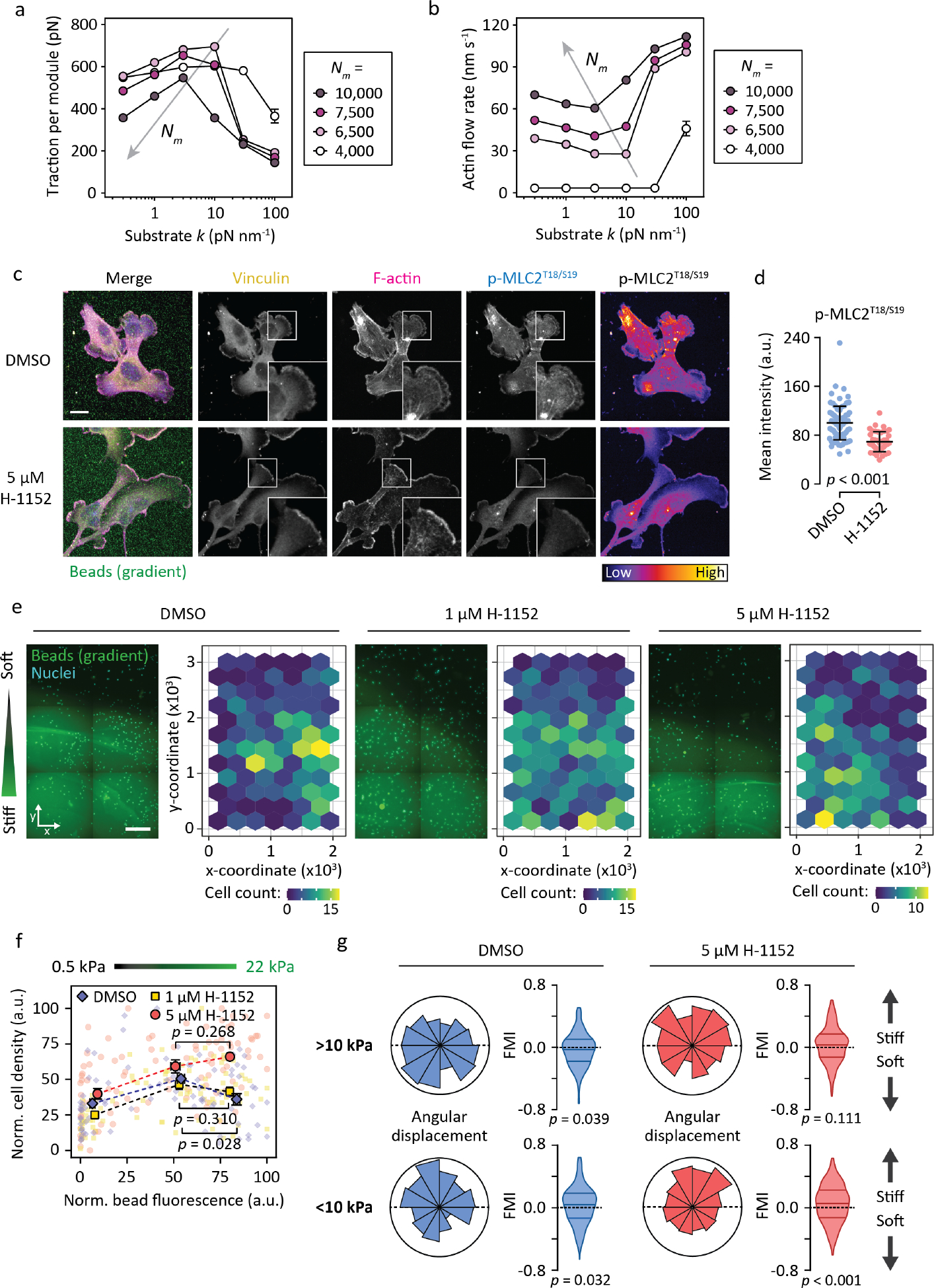
(a–b) Simulated (CMS) traction forces (a) and actin retrograde flow rates (b) as functions of substrate stiffness, for different pools of molecular motors. Gray arrows denote shifts in local minima/maxima upon increasing motor numbers. Mean ± SEM of n = 10 cells. (c–d) Immunofluorescence images (c) and quantification (d) depicting vinculin and levels of phosphorylated MLC2 in U-251MG cells after 48 h on 0.5–22 kPa gradients, with or without ROCK inhibitor H-1152. Scale bar, 20 μm. Mean ± SD of n = 42–83 cells, analyzed by Mann-Whitney test. Representative of two independent experiments. (e) Representative regions of three 0.5–22 kPa stiffness gradients, 48 hours after being seeded with U-251MG cells and supplemented with varying concentrations of H-1152. Scale bar, 500 μm. Interspaced with depictions of cell counts across the gradients. (f) Relative cell densities in different parts of the gradients, overlaid with binned data. Mean ± SEM of n = 16–41 ROIs per bin, from two gradient hydrogels per condition, representative of two independent experiments. Analyzed by Mann-Whitney test. (g) Angular displacements and forward migration indices of individual U-251MG cells migrating in the stiffer (>10 kPa, top) and softer (<10 kPa, bottom) regions of 0.5–22 kPa gradients. n = 177–327 cells from one (DMSO) to two (H-1152) independent experiments. Analyzed by Wilcoxon signed rank test.

We sought to validate these observations experimentally by treating U-251MG cells with intermediate (1 μM) and high (5 μM) concentrations of Rho-associated kinase (ROCK) 1/2 inhibitor H-1152. High concentrations of the inhibitor reduced intracellular contractility (MLC2 phosphorylation) significantly and increased the formation of actin-enriched ruffles at the cell periphery, whereas mature vinculin-positive adhesions remained undetectable similar to the control cells (Fig. 4c–d; S12a). Importantly, H-1152 suppressed the characteristic negative durotaxis of the U-251MGs and promoted localization to the stiffer regions of the 0.5–22 kPa gradients over time, in a dose-dependent manner (Fig. 4e–f). Live-cell imaging of control and H-1152-treated U-251MGs further confirmed a shift in the durotaxis: whereas control cells initially located in stiffer areas (>10 kPa) migrated significantly more toward softer substrate regions, the ROCK inhibitor-treated cells had lost their negative durotaxis and instead displayed a trend of positive durotaxis, with trajectories mainly toward stiffer substrate (Fig. 4g, S12c; Movie S3). A similar effect was detected when U-251MGs were treated with intermediate concentrations (5 μM) of myosin II inhibitor blebbistatin (Fig. S12b, d), while higher concentrations (25 μM) inhibited durotaxis (and possibly migration) altogether (Fig. S12d). These modeling and experimental data indicate actomyosin contractility as a key determinant in tuning cell durotactic behavior.

While U-251MGs and neurons exhibit biphasic traction forces in the physiological stiffness range, many adherent cell types do not^11,19,41,42. Rather, their traction increases as a function of substrate stiffness unless talin- and vinculin-mediated FA formation is disrupted, e.g. by depletion of both talin isoforms¹⁹ (Fig. 5a). Therefore, we hypothesized that targeting adhesion reinforcement can generate an intermediate stiffness optimum and enable negative durotaxis in cell types that normally undergo only positive durotaxis. To test this, we used siRNAs to reduce talin-1 and talin-2 expression in MDA-MB-231 cells that exert increasing traction with increasing substrate stiffness⁴² and undergo positive durotaxis in the 2–18 kPa range⁸. Talin knockdown (Figs. 5b, S13a) resulted in significantly fewer and smaller FAs (Figs. 5c–e, S13b–c) and reduced traction on ~20 kPa substrates, where adhesion reinforcement is expected to counteract clutch dissociation by rapidly accumulating forces (Figs. 5f–h, S14a). EdU incorporation increased from 0.5 to 9.6 kPa and plateaued thereafter, with and without talin silencing (Fig. S14b–c). While control MDA-MB-231s seeded on 0.5–22 kPa stiffness gradients migrated toward the stiffest regions available, talin-low MDA-MB-231s phenocopied the negative durotaxis seen in U-251MGs and clustered predominantly in regions of intermediate stiffness (Figs. 5i–j, S13d–e). Thus, the familiar positive durotactic behavior can be converted to negative durotaxis by manipulating the adhesive and contractile machinery of a cell to change its optimal stiffness.

Figure 5. Lowering stiffness optimum by blocking adhesion reinforcement shifts MDA-MB-231 cells from positive to negative durotaxis.

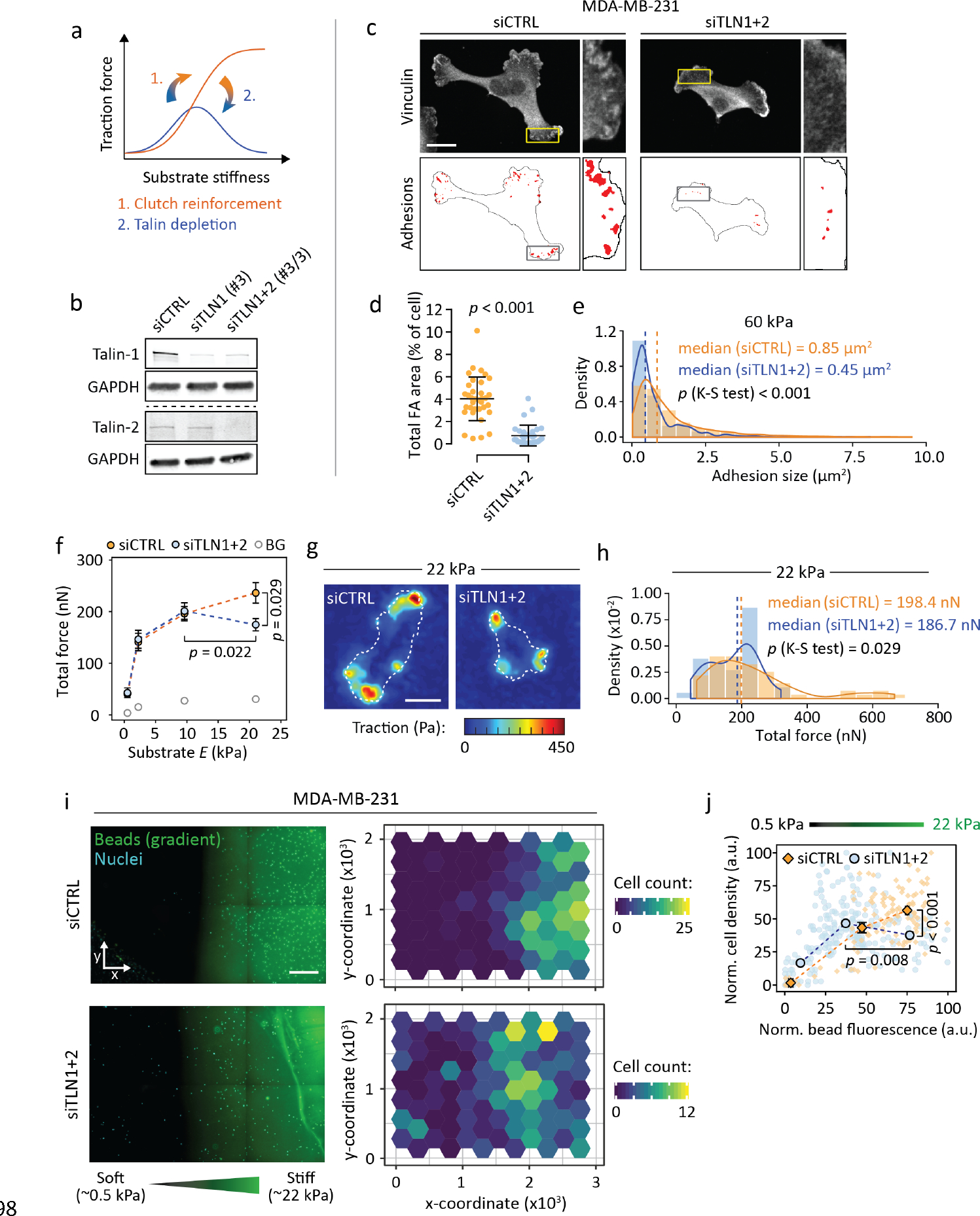
(a) Schematic representation of the relationship between traction forces, substrate stiffness and talin/vinculin-mediated ‘clutch reinforcement’. Depletion of these clutch components forces some cell types back into a biphasic traction regime¹⁹. (b) Representative western blot depicting talin-1 and talin-2 double knockdown in MDA-MB-231 cells. (c–d) Immunofluorescence images (c) and quantification (d) of focal adhesions in MDA-MB-231s on 60 kPa substrate, without and after talin knockdown. Scale bar, 20 μm. Mean ± SD of n = 32–35 cells, analyzed by Mann-Whitney test. (e) Distribution of focal adhesion sizes in control and talin-low cells. Histograms overlaid with probability density functions, dashed lines indicate medians. n = 524–1844 adhesions from 32–35 cells, analyzed by Kolmogorov-Smirnov test. Representative of two independent experiments. (f–h) Traction force analysis of control and talin-low MDA-MB-231s. (f) Total force exerted by the cells as a function of substrate stiffness. Background, BG. Mean ± SEM of n = 18–55 cells from three independent experiments. (g) Representative traction maps from cells on 22 kPa substrate. Cell outlines are indicated by white dashed lines. Scale bar, 20 μm. (h) Histograms of the 22 kPa data overlaid with probability density functions, with dashed lines indicating medians. n = 37–55 cells from three independent experiments, analyzed by Kolmogorov-Smirnov test. (i) (Left) Representative regions of two 0.5–22 kPa polyacrylamide stiffness gradients, 72 hours after being seeded with MDA-MB-231 cells (indicated by nuclear staining). Scale bar, 500 μm. (Right) Quantification of cells across the gradients. (j) Relative cell densities in different parts of the gradients, overlaid with binned data. Mean ± SEM of n = 13–141 ROIs per bin, from one (siCTRL) or two (siTLN1+2) gradient gels, representative of three independent experiments. Analyzed by Mann-Whitney test.

The concept of cells moving toward environments where they can exert more traction is intuitive, but has been previously understood in the context of denser, stiffer ECM providing cells with more stable anchorage⁷. Our results demonstrate the additional capacity of individual cells to migrate toward softer environments, i.e. negative durotaxis, which can be explained by a motor-clutch-based model. Cells that lack robust adhesion reinforcement, such as U-251MG glioma cells or talin-low MDA-MB-231 breast cancer cells, tend to exert maximal traction on substrates of intermediate stiffness, and migrate along gradients to reach this optimum by positive or negative durotaxis (Fig. S15). The same mechanism is likely to contribute to the recently described neurite growth toward soft matrix²⁴. Together with other mechanosensitive cellular responses, such as increased proliferation or overall motility on mechanically distinct substrates^29,43, durotaxis can contribute to a variety of biological processes, including central nervous system development and cancer metastasis.

Besides directly reinforcing connections to stiff matrix, mechanosensitive FA formation may promote positive durotaxis by additional mechanisms. Preferential trafficking of adhesion components toward existing FAs⁴⁴, local activation of mechanically gated ion channels⁴⁵ or other biochemical signaling pathways initiated at the FAs³⁵ may all contribute to further polarization of cell-matrix adhesion and, consequently, of cellular traction forces. How these factors influence stiffness optima on different substrates, and in different biological conditions, will be an interesting topic for future research. Taken together, our results point to a single, conserved mechanism for stiffness sensing and durotaxis across a broad range of cell types, with motor-clutch dynamics driving traction generation and choices between positive and negative durotaxis.

Materials and Methods

Cell culture, reagents and transfections

U-251MG human glioblastoma cells were obtained from Dr. G. Yancey Gillespie (U. Alabama-Birmingham), authenticated using a short tandem repeat assay (University of Arizona Genetics Core) and cultured in Dulbecco’s modified Eagle’s medium (DMEM)/F-12 (Gibco, 11320–074) supplemented with 8% fetal bovine serum (Sigma, F7524). MDA-MB-231 human breast adenocarcinoma cells were purchased from American Type Culture Collection and authenticated using a short tandem repeat assay (Leibniz Institute DSMZ – German Collection of Microorganisms and Cell Cultures, Braunschweig, Germany). U-2 OS human osteosarcoma cells were acquired from DSMZ. Both MDA-MB-231 and U-2 OS were cultured in high-glucose DMEM (Sigma, D5796–500ML) supplemented with 10% fetal bovine serum (Sigma, F7524), 2 mM L-glutamine (Sigma, G7513–100ML) and 1x non-essential amino acids (Sigma, M7145–100ML). The cells were tested for mycoplasma contamination and cultured at +37 °C, 5% CO₂ in a humidified incubator. ROCK1/2 inhibitor H-1152 was acquired from Calbiochem (Merck Millipore, 555550) and myosin II inhibitor (−)-blebbistatin was acquired from STEMCELL Technologies (72402).

For transient downregulation of target proteins, the cells were transfected with corresponding siRNAs at a 50 nM concentration per oligo. The transfections were conducted using Opti-MEM Reduced Serum Medium (Thermo Fisher Scientific, 31985–047) and Lipofectamine RNAiMAX reagent (Thermo Fisher Scientific, 56532) according to the manufacturer’s instructions. The siRNAs used were Hs_TLN1_3 FlexiTube siRNA (Qiagen, SI00086975), Hs_TLN1_2 FlexiTube siRNA (Qiagen, SI00086968), Hs_TLN2_3 FlexiTube siRNA (Qiagen, SI00109277), Dharmacon ON-TARGETplus Human TLN2 (83660) (Horizon Discovery, J-012909–05-0002) and AllStars Negative Control siRNA (Qiagen, 1027281). Silenced cells were grown for 24 (beginning of migration experiments) to 72 hours before they were used for experiments.

Antibodies

The following antibodies were used at the indicated dilutions: ms anti-paxillin (BD Biosciences, 612405, 1:200 for IF), rbt anti-paxillin (Santa Cruz Biotechnology, sc-5574, 1:200 for IF), ms anti-vinculin (Sigma, V9131, 1:200 for IF, 1:1000 for WB), ms anti-talin-1 (Novus, NBP2–50320, 1:1000 for WB), ms anti-talin-2 (Novus, NBP2–50322, 1:1000 for WB), ms anti-FAK (BD Biosciences, 610088, 1:1000 for WB), rbt anti-p-FAK (Y397) (Cell Signaling Technology, 8556, 1:100 for IF, 1:1000 for WB), rbt anti-MLC2 (Cell Signaling Technology, 3672, 1:1000 for WB), rbt anti-p-MLC2 (T18/S19) (Cell Signaling Technology, 3674, 1:1000 for WB), rbt anti-ERK1/2 (Cell Signaling Technology, 9102, 1:1000 for WB), rbt anti-p-ERK1/2 (T202/Y204) (Cell Signaling Technology, 4370, 1:1000 for WB), ms anti-YAP (Santa Cruz Biotechnology, sc-101199, 1:200 for IF), rbt anti-vimentin (Cell Signaling Technology, 5741, 1:1000 for WB), ms anti-GAPDH (HyTest, MAb 6C5, 1:5000 for WB), ms anti-active β1-integrin (clone 12G10, in-house production, 5 μg/ml for IF), rat anti-inactive β1-integrin (clone Mab13, in-house production, 10 μg/ml for cell culture), and normal rat IgG2a kappa isotype control (eBioscience, 14–4321-85, 10 μg/ml for cell culture).

Additionally, the following secondary antibodies were used for immunofluorescence and immunoblots at the indicated dilutions: Alexa Fluor 488/568-conjugated secondary antibodies raised against mouse (Invitrogen, A21202 and A10037, 1:400 for IF) and rabbit (Invitrogen, A21206 and A10042, 1:400 for IF), IRDye 800CW Donkey anti-Mouse IgG (LI-COR Biosciences, 926–32212, 1:5000 for WB), IRDye 800CW Donkey anti-Rabbit IgG (LI-COR Biosciences, 926–32213, 1:5000 for WB), and IRDye 680LT Donkey anti-Mouse IgG (LI-COR Biosciences, 926–68022, 1:5000 for WB).

EdU incorporation assay

To measure the rate of EdU (5-ethynyl-2ʹ-deoxyuridine) incorporation into DNA, cells were grown on hydrogels for 24 hours, after which they were prepared into fluorescence microscopy samples using an EdU Proliferation Assay Kit (Abcam, ab222421), according to the manufacturer’s instructions. Briefly, the cells were supplemented with 20 μM EdU for 2 hours, fixed, permeabilized, and the EdU was stained with iFluor 647 azide via a copper-catalyzed click reaction. Nuclei were counterstained before imaging (see below).

Blocking β1-integrin function with antibodies

U-251MG cells were grown on 0.5 kPa and 60 kPa hydrogels for 24 hours, after which they were treated with 10 μg/ml of anti-inactive β1-integrin (i.e. function-blocking) clone Mab13 or normal rat isotype control for 2 hours (see the list of antibodies for details). The cells were fixed and processed for immunofluorescence imaging.

Cell migration on stiffness gradient substrates

For analysis of cell migration on continuous 0.5–22 kPa stiffness gradients, 15,000 (MDA-MB-231)–20,000 (U-251MG) cells were seeded on a fibronectin-functionalized stiffness gradient hydrogel. Even distribution of cells in the beginning of the experiment was confirmed visually (via brightfield microscopy) and by recording the positions of individual nuclei along the gradient using SiR-DNA. The plate was returned to the incubator for 48 (U-251MG) or 72 hours (MDA-MB-231), after which the cells were fixed and nuclei were re-visualized with DAPI. Alternatively, 30,000 U-251MG cells were seeded on a stiffness gradient and left to adhere for one hour. For inhibitor experiments, the culture was then supplemented with 1–5 μM H-1152, 5–25 μM blebbistatin, or vehicle (DMSO). Imaging was started two to three hours after seeding and time-lapse movies were acquired overnight at 15 min intervals. After the experiment was finished the culture was fixed and prepared for immunofluorescence imaging (vinculin and phosphorylated MLC2) as described below. Migration tracks from individual cells were analyzed for angular displacements and forward migration indices (defined here as Δy/total accumulated distance, where positive values correlate with migration toward stiffer substrate).

For live-cell imaging of U-251MG migration on photoresponsive stiffness gradient hydrogels, 10,000 cells were seeded per dish and allowed to settle in the incubator for 30 min prior to imaging. Time-lapse movies were acquired at 20 or 30 min intervals for 45 to 60 hours. The number of cells in the soft and stiff regions of the gel, in the beginning and end of the experiment, was quantified. Additionally, the movies were analyzed for cells directly on top of a stiffness gradient. Such cells were tracked over time to investigate their bias for migrating toward either stiffness. Mitotic, dying or crowded cells were excluded from the analysis.

Western blotting

Cells on hydrogels were placed on ice, rinsed twice with ice-cold PBS and scraped into lysis buffer [50 mM Tris-HCl pH 7.5, 150 mM NaCl, 1% SDS, 0.5% Triton X-100, 5% glycerol, supplemented with protease (Roche, 05056489001) and phosphatase (Roche, 04906837001) inhibitors]. The lysates were vortexed, placed on a heat block (+90 °C) for 10 min and sonicated before separation by SDS-PAGE (4–20% Mini-PROTEAN TGX Gels, Bio-Rad, 456–1096). Next, the proteins were transferred to nitrocellulose membranes and visualized using 1% Ponceau S staining solution. The membranes were blocked with 5% skimmed milk in TBST and incubated with the indicated primary antibodies overnight at +4°C, followed by fluorophore-conjugated secondary antibodies for 1 to 2 hours at room temperature. All the antibodies were diluted in StartingBlock blocking buffer (Thermo Fisher Scientific, 37538). Finally, the membranes were scanned using an Odyssey infrared imaging system (LI-COR Biosciences).

Conventional polyacrylamide hydrogels

Glass-bottom dishes (Cellvis, D35–14-1-N) were treated for 20 min at room temperature with 100 μl of Bind-Silane solution – a mixture of 3-(trimethoxysilyl)propylmethacrylate (7.15% by volume, Sigma-Aldrich, M6514) and acetic acid (7.15% by volume) in absolute ethanol – to promote gel attachment to the glass surface. After the Bind-Silane was aspirated, the glass was washed twice with ethanol and left to dry completely. For homogeneous (constant Young’s modulus) hydrogels, pre-defined ratios of 40% (w/v) acrylamide (Sigma-Aldrich, A4058) and 2% (w/v) N,N-methyl-bis-acrylamide (Sigma-Aldrich, M1533) were mixed in PBS on ice and vortexed carefully. The final concentrations were adjusted to yield a desired Young’s modulus (Table S1). Gels that were indicated for traction force microscopy were supplemented with additional 0.2 μm yellow-green fluorescent (505/515) microspheres (~1.5 × 10¹⁰/ml final concentration, Invitrogen, F8811), which were sonicated for 3 min prior to use. Polymerization was initiated by addition of 10% ammonium persulfate (APS, final 0.1% by volume, Bio-Rad) and N,N,Nʹ,Nʹ-tetramethylethylenediamine (TEMED, final 0.2% by volume, Sigma-Aldrich, T-9281) to the solution. Immediately afterwards, 13 μl of the solution was pipetted onto the glass-bottom dish and a 13 mm circular coverslip was placed on top of the droplet. After polymerization for ~1 hour at room temperature, the gel was immersed in PBS for 5 min, the top coverslip was gently removed, and the gel was washed twice with PBS to remove any excess acrylamide. Hydrogels with continuous 2D stiffness gradients were fabricated as described previously³¹. Briefly, 0.5 kPa and 22 kPa acrylamide prepolymer solutions were prepared and 0.1 μm fluorescent (505/515) microspheres (~1.2 × 10¹¹/ml final concentration, Invitrogen, F8803) were added to the 22 kPa solution. After polymerization was initiated, the two solutions were allowed to diffuse together on a glass-bottom dish, under a glass coverslip, to yield a gradient wherein microsphere density correlates linearly with the Young’s modulus of the substrate.

Prior to use, the hydrogels were activated by a combination of 0.2 mg/ml Sulfo-SANPAH (Thermo Fisher Scientific, 22589) and 2 mg/ml N-(3-dimethylaminopropyl)-Nʹ-ethylcarbodiimidehydrochloride (EDC, Sigma-Aldrich, 03450) in 50 mM 4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid (HEPES). 500 μl of the solution was added on top of the hydrogel and incubated for 30 min at room temperature, protected from light and subjected to gentle agitation. The gel and solution were then UV-irradiated for 10 min (28–32 mW/cm²) to activate the Sulfo-SANPAH, and the plate was washed with PBS three times to remove any residual compounds. Finally, each hydrogel was functionalized by incubation in 10 μg/ml fibronectin solution overnight at +4°C.

Cells that were collected for protein lysates were cultured on commercial hydrogel-coated 6-well plates (Matrigen, SW6-EC-0.5/SW6-EC-8/SW6-EC-50). These gels were similarly coated with 10 μg/ml of fibronectin before use.

Synthesis of o-NBbA

2-nitro-4-ethyl aniline (S2)

p-Ethyl aniline (5 g, 41.3 mmol) was added dropwise to a cold solution of concentrated H₂SO₄ (30 ml) and stirred for 5 min. In a separate flask, 5.3 ml of 70% HNO₃ (82.6 mmol) was mixed with an equal volume of H₂SO₄, and added dropwise to the reaction vessel, followed by 15 min stirring at 0 °C. Thin layer chromatography (TLC) analysis (Hex:EtOAc, 2:1, v/v) indicated complete conversion to the product. The reaction was quenched by pouring the mixture into 200 ml ice water. The resulting precipitate was filtered and washed with H₂O to yield compound S2 (6.2 g, 90%).

¹H NMR (500 MHz, CDCl₃) τ ppm 1.099 (t, J = 7.5 Hz, 3H), 2.612 (q, J = 7.0 Hz, 2H), 5.558 (s, 2H), 6.804 (dd, J = 8.0, 2.5 Hz, 1H), 7.041 (d, J = 2.5 Hz, 1H), 7.095 (d, J = 8.5 Hz, 1 H)

¹³C NMR (100 MHz, DMSO-d6) 149.3411, 147.8646, 131.6051, 124.0586, 118.8417, 107.9194, 24.4890, 15.3093

HRMS (m/z): [M]⁺ calcd for [C₈H₁₀N₂O₂]⁺ 166.0737, found 166.0737.

4-ethyl-3-nitrophenol (S3)

Compound S2 (6.2 g, 37.3 mmol) was suspended in a mixture of H₂SO₄ and H₂O (1:3, v/v, 25–50 ml) by sonication (if sonification did not yield a homogenous suspension, a few ml of THF was used to dissolve the solid S2, which was then added to the mixture of aqueous H₂SO₄). NaNO₂ (3.86 g, 56.0 mmol) dissolved in H₂O (2.5 ml) was added slowly to the reaction flask and stirred at room temperature for 1.5 h. In a separate flask H₂SO₄:H₂O (4:3, v/v, 75 ml) was added and heated to reflux. To the refluxing mixture, the S2 solution was added dropwise and stirred for 30 min. The mixture was quenched with ice water and extracted with EtOAc (3 × 75 ml). After drying the organic layer with Mg₂SO₄, the solvent was removed in vacuo and the crude product was purified by silica gel flash chromatography (Hex:EtOAc, 2:1) to give S3 (3.11 g, 50%) as a yellow oil.

¹H NMR (500 MHz, CDCl₃) δ ppm 1.249 (t, J = 7.5 Hz, 3H), 2.842 (q, J = 8.5 Hz, 2H), 7.030 (dd, J = 8.5, 2.5 Hz, 1H), 7.230 (d, J = 8.5 Hz, 1H), 7.383 (d, J = 2.5 Hz, 1H)

¹³C NMR (100 MHz, CDCl₃) 154.2470, 149.5150, 132.3914, 131.3014, 120.7326, 111.4436, 25.6617, 15.1987

HRMS (m/z): [M - H]⁻ calcd for [C₈H₈NO₃]⁻ 166.0510, found 166.0524.

tert-butyl 2-(4-ethyl-3-nitrophenoxy)acetate (S4)

Compound S3 (3.11 g, 18.6 mmol) and tert-butyl 2-bromoacetate (4.35 g, 22.3 mmol) were dissolved in DMF (25 ml). Solid K₂CO₃ (5.14 g, 37.2 mmol) was added to the reaction flask and left to stir at +70 °C for 1.5 h until TLC analysis (2:1 Hex:EtOAc, v/v) indicated complete conversion to the product. The solvent was removed in vacuo and redissolved in 100 ml EtOAc. The organic layer was washed with saturated NH₄Cl (50 ml) and brine, then dried over Na₂SO₄. Solvent removal in vacuo afforded S4 (4.97 g, 95%) as a yellow oil.

¹H NMR (500 MHz, CDCl3) δ ppm 1.253 (t, J = 7.5 Hz, 3H), 1.5 (s, 9H), 2.857 (q, J = 7.5 Hz, 2H), 4.554 (s, 2H), 7.116 (dd, J = 8.5, 2.5 Hz, 1H), 7.277 (d, J = 8.5 Hz, 1H), 7.391 (d, J = 3 Hz, 1H)

¹³C NMR (100 MHz, CDCl3) 167.3932, 156.3652, 149.4567, 132.3149, 132.2128, 120.6270, 110.0036, 83.0951, 66.0518, 28.1809, 25.7638, 15.1222

HRMS (m/z): [M + Na]⁺ calcd for [C₁₄H₁₉NO₅Na]⁺ 304.1155, found 304.1160.

tert-butyl 2-(4-(1-bromoethyl)-3-nitrophenoxy)acetate (S5)

Compound S4 (4.97 g, 17.7 mmol), N-bromosuccinimide (3.8 g, 19.5 mmol) and benzoylperoxide (0.2 g, 1 mmol) were dissolved in CCl₄ (100 ml) and refluxed for 4 h. The reaction mixture was cooled to room temperature and washed with 0.1% NaHCO₃ (aq) and brine, then dried over Na₂SO₄. The solvent was removed in vacuo and the crude product was purified by silica gel flash column chromatography (3:1 Hex:EtOAc, v/v) to afford S4 (5.7 g, 90%) as a yellow oil.

¹H NMR (500 MHz, CDCl₃) δ ppm 1.498 (s, 9H), 2.054 (d, J = 7 Hz, 3H), 4.571 (s, 2H), 5.787 (q, J = 7 Hz, 1H), 7.184 (dd, J = 8.5, 3 Hz, 1H), 7.299 (d, J = 2.5 Hz, 1H), 7.784 (d, J = 9 Hz, 1H)

¹³C NMR (100 MHz, CDCl₃) 167.0028, 157.7588, 148.0010, 131.1486, 130.8123, 120.7031, 109.7326, 83.3722, 66.0153, 42.0634, 28.1845, 27.3715

HRMS (m/z): [M - Br]⁺ calcd for [C₁₄H₁₈NO₅]⁺ 280.1179, found 280.1163.

2-(4-(1-bromoethyl)-3-nitrophenoxy)ethan-1-ol (S6)

Compound S5 (5.7 g, 15.9 mmol) was dissolved in 100 ml THF and cooled down to −78 °C. DIBAL-H (39.8 mmol) was added to the reaction flask and stirred at −78 °C for 20 min, and then left to stir for an additional 2 h at 0 °C. TLC analysis (3:1 Hex:EtOAc, v/v) indicated essentially complete conversion to the product. The reaction was quenched by slowly adding 30 ml H₂O to the mixture, followed by the addition of 5% HCl (aq) solution until the aqueous solution became acidic (pH = ~4, as judged by pH paper). After vigorously mixing the biphasic mixture in a separatory funnel, the separated organic layer was washed with brine, then dried over Na₂SO₄. The solvent was removed in vacuo and the crude product was purified by silica gel flash column chromatography to yield S6 (3.23 g, 60%) as a yellow oil.

¹H NMR (500 MHz, CDCl₃) δ ppm 2.056 (d, J = 5 Hz, 3H), 4.006 (dd, J = 4.5, 4.5 Hz, 2H), 4.142 (dd, J = 4, 4 Hz, 2H), 5.785 (q, J = 7 Hz, 1H), 7.201 (dd, J = 8.5, 2.5 Hz, 1H), 7.356 (d, J = 2.5 Hz, 1H), 7.783 (d, J = 8.5 Hz, 1H)

¹³C NMR (100 MHz, CDCl₃) 158.5634, 148.1515, 131.0462, 130.2806, 120.5139, 109.6535, 70.1749, 61.2504, 42.1290, 27.3423

HRMS (m/z): [M - Br]⁺ calcd for [C₁₄H₁₈NO₅]⁺ 210.0761, found 210.0761.

1-(4-(2-hydroxyethoxy)-2-nitrophenyl)ethan-1-ol (S7)

S6 (3.23 g, 11.1 mmol) was dissolved in 250 ml H₂O and refluxed for 1 h. TLC analysis (1:1 Hex:EtOAc, v/v) indicated essentially complete conversion to the product. The product was extracted with EtOAc (3 × 50 ml). The organic layer was washed with brine and then dried over Na₂SO₄. The solvent was evaporated in vacuo and S7 (2.0 g, 80%) was used for the next step without further purification.

¹H NMR (500 MHz, CDCl₃) δ ppm 1.540 (d, J = 6.4 Hz, 3H), 3.997 (dd, J = 4.6, 4.6 Hz, 2H), 4.120 (dd, J = 7.1, 7.1 Hz, 2H), 5.341 (q, J = 6.2 Hz, 1H), 7.201 (dd, J = 8.8, 2.8 Hz, 1H), 7.410 (d, J = 2.7 Hz, 1H), 7.734 (d, J = 8.8 Hz, 1H)

1-(4-(2-(acryloyloxy)ethoxy)-2-nitrophenyl)ethyl acrylate (o-NBbA, S8)

To a solution of S7 (2.0 g, 8.88 mmol) and acryloyl chloride (26.6 mmol) in CH₂Cl₂ (75 ml), TEA (3.5 eq) was added and the mixture was stirred at room temperature for 24 h. The mixture was washed with H₂O and brine and then dried over Na₂SO₄. The solvent was evaporated in vacuo and the crude material was purified by silica gel flash column chromatography (2.5:1 Hex:EtOAc, v/v) to yield S8 (1.79 g, 60%) as a yellow oil.

¹H NMR (500 MHz, CDCl₃) δ ppm 1.653 (d, J = 6.5 Hz, 3H), 4.253–4.272 (m, 2H), 4.517–4.536 (m, 2H), 5.849 (dd, J = 16.5, 1.5 Hz, 1H), 5.87 (dd, J = 16.5, 1.5 Hz, 1H), 6.135 (dd, J = 33, 10.5 Hz, 1H), 6.135 (dd, J = 10.5, 1.5 Hz, 1H), 6.333 (dd, J = 6.5, 6.5 Hz, 1H), 6.425 (dd, J = 38.5, 1.5 Hz, 1H), 6.425 (dd, J = 4, 1 Hz, 1H), 7.181 (dd, J = 8.5, 2.5 Hz, 1H), 7.471 (d, J = 2.5 Hz, 1H), 7.547 (d, J = 8.5 Hz, 1H)

¹³C NMR (100 MHz, DMSO-d6) 165.3601, 164.6091, 157.8246, 148.5720, 132.2687, 132.0463, 128.7689, 128.2840, 127.9741, 127.9522, 120.6063, 109.4215, 67.2670, 66.6545, 62.5167, 21.2189

HRMS (m/z): [M + Na]⁺ calcd for [C₁₆H₁₇NO₇Na]⁺ 358.0897, found 358.0888.

Fabrication of photoresponsive polyacrylamide hydrogels

Photoresponsive polyacrylamide gel substrates were prepared based on a previously reported method⁴⁶. Briefly, Grid-500 high glass-bottom dishes (Fischer, 50–305-810) were activated for gel attachment by sequential treatment with 0.1 M NaOH, 97% (3-aminoproyl)trimethoxysilane (Sigma Aldrich, 281778) and 0.5% glutaraldehyde (Polysciences, 01909). A prepolymer mixture of 40% (w/v) acrylamide solution (25% by volume, Fisher, BP1402), 2% (w/v) bis-acrylamide solution (2.5% by volume, Fisher, BP1404), 50 mM o-nitrobenzyl bis-acrylate (in DMSO, 3.25% by volume), 1M HEPES (pH 7.0, 1% by volume, Sigma Aldrich, H6147) solution, 71.7 mM acrylic acid N-hydroxysuccinimide ester (in DMSO, 4% by volume, Sigma Aldrich, A8060), and H2O (63.25% by volume) was prepared. After degassing for 30 min, polymerization was initiated by adding 10% (w/v) APS (0.6% by volume, Bio-Rad, 161–0700) solution and TEMED (0.4% by volume, Fisher, BP150). Immediately after initiation, 200 μL of gel solution was pipetted onto the activated glass culture dish and covered with a fibronectin-patterned glass coverslip face down (fabricated as described below). After 30 min of polymerization, PBS was added on the dish and the coverslip was removed. Finally, the gel was washed with PBS.

Preparation of 1D fibronectin micropatterns

1D lines of fibronectin were created on the photoresponsive hydrogels following a microcontact printing method widely applied in the field of surface protein fabrication⁴⁷. Briefly, PDMS stamps fabricated by photolithography and containing topographical patterns (21 μm width, 40 μm spacing) were obtained from the M. Piel laboratory (Inst. Curie) and used as received⁴⁸. The patterned side of the stamp was inked with 100 μg/ml fibronectin (Sigma Aldrich, F1141) for 1 h. After drying the stamp using a stream of air, the fibronectin-coated stamp was stamped onto a 12 mm no. 1.5 circular coverslip (Fisher, 12–545-80), rinsed with ethanol and treated with plasma (Harrick Plasma) for 60 sec, and a 20 g weight was placed on top of the stamp. The fibronectin pattern was finally transferred to the gel surface by placing the coverslip face down on the prepolymer solution as described above, immediately upon the initiation of polymerization.

Fabrication of steep stiffness gradients by controlled UV exposure

Stiffness patterns were fabricated on photoresponsive hydrogels using a Nikon Eclipse Ti-E epifluorescence microscope and Plan Fluor 10x/0.30NA objective (Nikon), controlled by NIS-Elements software (Nikon). The fibronectin-patterned photoresponsive gel was placed on the stage and, using phase-contrast imaging, two regions were selected such that they were ‘A’ mm (A > 2) apart. A hypothetical line connecting the two regions ran across the fibronectin patterns perpendicularly (Fig. S3). The field diaphragm lever was then adjusted so that the diameter of the illuminated area on the substrate was 500 μm. Fluorescence imaging using a 395/25 nm LED (315 mW) and DAPI filter set with LED fluorescence illumination from a SpectraX light Engine (Lumencor) was initiated, and a time lapse movie of the two regions was captured at 0 s intervals for ‘15 × A’ min, leaving the active shutter open during stage movement. This led to a 500 μm × ‘A’ mm region being photoirradiated to the extent that all the photolabile crosslinkers in the exposed region were cleaved. The process was repeated in regions parallel to and 500 μm apart from the first irradiated area, resulting in a gel that had alternating, 500 μm wide stiff (~15 kPa) and soft (~8 kPa) regions.

Stiffness characterization by bead indentation

The irradiation time-dependent change in the Young’s modulus of the photoresponsive polyacrylamide gel was measured using a bead indentation method¹⁸ based on Hertzian indentation theory. A thick (>1 mm) hydrogel was created by pipetting 300 μl of prepolymer solution onto an activated glass culture dish and covering it with a 25 mm no. 1.5 circular coverslip (Fisher, 12–545-102). After polymerization, the coverslip was removed in PBS and the gel was washed with additional PBS. A silica bead (Polysciences, 1 mm diameter) was placed on the gel after 200 nm crimson fluorospheres were first gravity-settled on the gel surface to function as markers for measuring bead contact area with epifluorescence microscopy. At each irradiation time point, the bead indentation depth $\delta$ was calculated from the bead radius $R$ and the contact radius $\left(r\right)$ according to equation (1):

$$\delta =R-\sqrt{R^2-r^2}$$ (1)

From this indentation depth, the Young’s modulus $\left(E\right)$ was calculated using the Poisson ratio of the hydrogel $\left(v\right)$ and buoyancy corrected bead force $\left(f\right)$ according to the Hertz solution:

$$E=\frac{3(1-v^2)f}{4R^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\delta }^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$$ (2)

For polyacrylamide gels, $v=0.3-0.5$ (here, $v=0.3$ was used). The glass bead density was measured to be ~2600 kg/m³.

Immunofluorescence staining

Samples were fixed for 10 min with warm 4% PFA, followed by permeabilization and blocking for 20 min with 0.3% Triton X-100 in 10% horse serum (Gibco, 16050–122). Primary antibodies were diluted in 10% horse serum and samples were incubated with the antibody overnight at +4 °C. Secondary antibodies were diluted in PBS and samples were incubated with the antibody for one to two hours at room temperature. Where indicated, the nuclei were counterstained using 5 μg/ml DAPI (4’,6-diamidino-2-phenylindole) or 500 nM SiR-DNA (Spirochrome, SC007; for live cells) and filamentous actin using 200 nM SiR-actin (Spirochrome, SC001).

Fluorescence and brightfield microscopy

Most fluorescent specimens were imaged using a Marianas spinning disk confocal microscope with a Yokogawa CSU-W1 scanning unit, controlled by SlideBook 6 software (Intelligent Imaging Innovations). The objectives used were a 20x/0.8 Plan-Apochromat (Zeiss) and 40x/1.1 W LD C-Apochromat (Zeiss), and images were acquired using an Orca Flash4 sCMOS camera (Hamamatsu Photonics). The 2D stiffness gradient hydrogels with cells were imaged using a Nikon Eclipse Ti2-E widefield microscope, controlled by NIS-Elements AR 5.11 software (Nikon). The objective used was a 10x/0.3 CFI Plan-Fluor objective (Nikon), and images were acquired using an Orca Flash4 sCMOS camera (Hamamatsu Photonics) and 2×2 binning. For live-cell tracking on the same substrates, the samples were maintained in a stage top humidified incubator at +37 °C/5% CO₂.

Live phase contrast imaging of U-251MG cells on photoresponsive hydrogels was done using a Nikon Eclipse Ti-E microscope and an Andor Zyla 5.5 sCMOS camera (Andor Technology). The objective was a Plan Fluor 10x/0.30NA objective (Nikon) and samples were maintained in a Bold Line stage top humidified incubator (Okolab) at +37 °C/5% CO₂.

Traction force microscopy

To measure the tractions exerted by MDA-MB-231 cells on their substrate, polyacrylamide hydrogels of varying stiffness (fibronectin-functionalized and supplemented with fluorescent microbeads) were manufactured on glass-bottom dishes as described above. Cells were seeded on the gels (5,000 cells/plate) approximately 24 hours after transfection with the indicated siRNAs, and grown for another 48 hours before the experiment was conducted. For imaging the cells and beads, a Marianas spinning disk confocal microscope with a stage top incubator unit (+37 °C/5% CO₂) was used. Brightfield images of single cells and fluorescence z-stacks of the beads embedded in the hydrogel were captured before and after cell detachment by addition of 2% sodium dodecyl sulfate.

The resulting data were analyzed using a previously described implementation of Fourier transform traction cytometry⁴⁹. First, displacement fields were calculated using high-resolution subsampling and assuming no outward deformation of the substrate. Optimal L2-regularization was performed on sets of images acquired from soft and stiff gels to determine the final regularization parameter λ = 5 × 10⁻⁶, which was then used for calculating all the subsequent traction fields. The background, or noise, of the measurements was estimated by analyzing five empty (i.e. no cells) fields of view per substrate stiffness.

Finite element analysis

To estimate the effective spring constant around the interface of a stepwise stiffness gradient, a finite element model using COMSOL Multiphysics (COMSOL, Inc., Burlington, MA) multibody dynamics module was utilized. Two three-dimensional blocks (120 μm × 60 μm × 20 μm) were created and interfaced at (x = 0). Linear elastic material properties were prescribed to both blocks with Poisson’s ratio = 0.4, density = 1000 kg/m³ and Young’s modulus = 1 kPa and 10 kPa. A lateral 0.5 nN force was applied on a circular (1 μm radius) surface contact (Figure S5a). Fixed boundary conditions were applied to all surfaces except the top surface. The displacement field due to applied loads was computed on a model created using built-in automatic meshing routines (extra-fine mechanics-based mesh). These data were used to calculate effective spring constant at the contact zone (k_eff = applied force/average displacement under the circular contact area). The location of the circular contact and direction of the force were varied, and effective spring constants were calculated accordingly (Figure S5b).

Computational modeling of single-cell migration and growth cone steering on stiffness gradients

A previously described³⁸ C++ version of the stochastic cell migration simulator (CMS) was modified to account for spatial variations in substrate stiffness. The detailed algorithms and equations governing the base CMS have been described in full in²⁹. Briefly, the CMS uses the Gillespie Stochastic Simulation Algorithm⁵⁰ to simulate an entire cell by connecting several motor-clutch modules to a central cell body and then balancing forces at the center (Fig. 3a). Here, the cells were simulated for 60 min to allow them to reach a dynamic steady state, after which each cell was displaced randomly to a 180 μm × 180 μm region on a substrate with repeating soft and stiff areas and connecting stiffness gradients (Fig. 3b). Cell positions and traction forces were recorded every second and used to calculate RMC and mean traction force per module. Custom MATLAB code was used to quantify module forces on soft and stiff substrates, and to track the displacement of individual cells, from gradients or soft regions, over time. All the CMS simulations were conducted at the Minnesota Supercomputing Institute (MSI). For additional details on the cellular level model and its implementation, see Supplementary Text 2.

The CMS was further modified to investigate filopodial and GC dynamics on substrate stiffness gradients. The filopodia were represented by individual CMS modules that were arranged around an initially semicircular GC. Each filopodia was allocated a set number of molecular clutches – the corresponding substrate clutches were distributed randomly and their spring constants varied linearly with position along the gradient. The details of the GC model and corresponding simulations are presented in Supplementary Text 3.

Image analysis

Images were analyzed using ImageJ (National Institutes of Health) and CellProfiler v2.2.0 (Broad Institute) software. For analysis of YAP nuclear localization, a custom CellProfiler pipeline was used to segment the cells into nuclei (corresponding to the nuclear counterstain) and cytoplasm (a region of max. 4 μm around the nucleus, excluding parts outside the cell). The mean gray value in the nucleus was divided by the corresponding value in the cytoplasm. For analysis of vinculin-positive adhesions in MDA-MB-231s, a semi-automatic ImageJ script was used: an individual confocal plane from the basal side of the cell was subjected to background removal (rolling ball) and thresholding to exclude cytoplasmic signal and peripheral ruffles. The number and sizes of the remaining adhesions were recorded.

Statistical analysis

Statistical analyses and plotting were performed using GraphPad Prism v6.05 (GraphPad) and R v3.5.1 (R Core Team). Confidence intervals for means were calculated using bias-corrected and accelerated (BCa) bootstrap intervals from 10,000 resamples. Confidence intervals for binomial data were calculated using Wilson score interval. Whenever data were deemed to follow a non-normal distribution (according to Shapiro-Wilk normality test), analyses were conducted using non-parametric methods. The names and/or numbers of individual statistical tests, samples and data points are indicated in figure legends. Unless otherwise noted, all results are representative of three independent experiments and two-tailed p-values have been reported.

Data Availability

The data supporting the findings of this study are available within the article and from the authors on reasonable request.