Dual-Mode 1D Linear Ultrasound Array for Image-Guided Drug Delivery Enhancement Without Ultrasound Contrast Agents

Abstract

Pulsed high-intensity focused ultrasound (pHIFU) uses nonlinearly distorted millisecond-long ultrasound pulses of moderate intensity to induce inertial cavitation in tissue without administration of contrast agents. The resulting mechanical disruption permeabilizes the tissue and enhances the diffusion of systemically administered drugs. This is especially beneficial for tissues with poor perfusion such as pancreatic tumors. Here we characterize the performance of a dual-mode ultrasound array designed for image-guided pHIFU therapies in producing inertial cavitation and ultrasound imaging. The 64-element linear array (1.071 MHz, aperture of 14.8 mm x 51.2 mm, and pitch of 0.8 mm) with elevational focal length of 50 mm was driven by the Verasonics V-1 ultrasound system with extended burst option. The attainable focal pressures and electronic steering range in linear and nonlinear operating regimes (relevant to pHIFU treatments) were characterized through hydrophone measurements, acoustic holography, and numerical simulations. The steering range at ±10% from the nominal focal pressure was found to be ±6 mm axially and ±11 mm azimuthally. Focal waveforms with shock fronts of up to 45 MPa, and peak negative pressures up to 9 MPa were achieved at focusing distances of 38–75 mm from the array. Cavitation behaviors induced by isolated 1 ms pHIFU pulses in optically transparent agarose gel phantoms were observed by high-speed photography across a range of excitation amplitudes and focal distances. For all focusing configurations the appearance of sparse, stationary cavitation bubbles occurred at the same P₋ threshold of 2 MPa. As the output level increased, a qualitative change in cavitation behavior occurred, to pairs and sets of proliferating bubbles. The pressure P− at which this transition was observed corresponded to substantial nonlinear distortion and shock formation in the focal region and was thus dependent on the focal distance of the beam ranging within 3–4 MPa for azimuthal F-numbers of 0.74 to 1.5. The array was capable of B-mode imaging at 1.5 MHz of centimeter-sized targets in phantoms and in vivo pig tissues at depths of 3 cm to 7 cm, relevant to pHIFU applications in abdominal targets.

I. Introduction

ULTRASOUND contrast agents (UCAs), such as microbubbles and nanodroplets, have been successfully used in combination with acoustic cavitation for targeted drug delivery [1]. In one approach, UCAs are intravenously administered and travel through the circulatory system to the target location and can be monitored using ultrasound imaging. Upon reaching the target, the UCAs can then be activated by applying ultrasound of sufficient amplitude to rupture the UCAs, thereby either releasing their payload or affecting the vasculature and/or perivascular tissue permeability. All of the above effects enhance diffusion of coadminsitered or subsequently administered drug to the targeted tissue. While the approach has been studied and successfully used over the past decade, many types of tumors, such as pancreatic ductal adenocarcinoma (PDAC) and liver metastases thereof, present barriers to targeted anticancer drug delivery, such as dense stroma, high interstitial fluid pressures, and irregular vascularization [2]. As microbubbles are confined to blood vessels and perivascular space [3], this greatly reduces the efficacy of UCAs for targeted drug delivery in PDAC [4].

It has been demonstrated that pulsed high-intensity focused ultrasound (pHIFU) is capable of inducing de novo cavitation (i.e., without the need for contrast agents) throughout tissue, thereby permeabilizing the tissue and increasing the passive diffusion of drugs and other bioagents systemically administered concurrently [5]. Such tissue permeabilization was shown to improve chemotherapeutic drug uptake in a preclinical mouse model of pancreatic cancer [6].

In contrast to drug delivery with UCAs, where a single diagnostic US imaging probe is commonly used for both guidance and activation of the UCAs to generate cavitation, the studies reported in Refs. [5] and [6] combined a diagnostic imaging array with a spherically-focused HIFU transducers. Studies relating the characteristics of de novo cavitation to parameters of the HIFU array have shown that transducers with larger F-numbers (the ratio of focal length to transducer aperture) induce inertial cavitation at lower values of acoustic power and peak rarefactional pressure [7]. Additionally, it was observed that a qualitative change in cavitation behavior occurred at an acoustic power threshold corresponding to significant nonlinear distortion and the formation of shocks in the focal region [8], above which sparse, stationary cavitation bubbles begin to divide into multiple proliferating bubbles. This transition to proliferating behavior was seen to happen at lower peak rarefactional pressure values for transducers with larger F-numbers (i.e. less focused). The reason for this dependence is that focal pressure waveforms generated by less focused transducers become nonlinearly distorted and shocked at lower values of peak rarefactional pressure [9]. Strongly nonlinear waves appear to aid in rectified growth of initially stationary bubbles over multiple cycles, and then facilitate the gradual formation of daughter bubbles through scattering off those large bubbles [8]. Such proliferating clusters of bubbles are expected to result in greater tissue disruption than isolated stationary bubbles, and do so more reliably.

The spherically focused HIFU arrays used in the previous drug delivery studies have limitations. It was previously thought that the acoustic power levels required to induce de novo cavitation in tissues were high enough to require a transducer with a large spatial footprint. This requirement reduced the quality of coaxial ultrasound imaging due to the large water standoff used for coupling, and complicated finding the acoustic access to abdominal targets, which are frequently adjacent to or behind gas containing regions such as the stomach or bowel. Reflection of the HIFU beam from gaseous regions carries a high risk of collateral damage and should be avoided. Coaxial ultrasound imaging guidance can help alleviate this problem, but not completely avoid it, because the two-dimensional imaging plane is not fully conformal with the 3D conical HIFU beam, and thus the insonated region can not be visualized fully.

These previous studies suggest that an ultrasound array, with the overall dimensions similar to a conventional diagnostic probe, and operating at lower frequency (e.g. 1 MHz) would be beneficial for inducing de novo cavitation in tissue, while also providing an opportunity for simultaneous ultrasound imaging for targeting. To this end, we have developed a single probe for dual-mode therapeutic-targeting use. The linear array was designed to have an electronically adjustable focal length and steering in the azimuthal dimension. During the design process, the expected beam profiles, steering limits, and shock generation capabilities were determined using both linear and nonlinear numerical modelling [10]. These design-stage models assumed a uniform velocity magnitude distribution over each of the rectangular array elements, and that the elements were cylindrically curved to provide elevational focusing.

Prior to clinical treatment with the dual-mode array, it is expected that the target region can be first imaged with a clinical scanner to obtain higher resolution images of the treatment region and identify landmarks to use for guidance and targeting during treatment. The dual-mode array subsequently is not required to provide images of the same quality as a clinical scanner, but rather to provide images of sufficient quality for identifying cm-sized landmarks at depths of approximately 50 mm. During our envisioned treatment scheme, the pHIFU therapy pulses will be interleaved with B-mode scans for locating these landmarks, along with plane-wave Doppler ensembles so that the progression of the treatment can be monitored in real time.

A number dual-mode ultrasound arrays for combined therapy and imaging have been previously reported. Multi-frequency arrays have been fabricated and used for transcranial therapy using microbubbles along with simultaneous 3D passive cavitation mapping [11–13]. Piezoelectric elements with different fundamental frequencies ranging from 306 to 1224 kHz were combined in the array, allowing for different combinations of transmit and receive frequencies. Ballard et al. [14] explored the use of a spherically-curved linear dual-mode array for the treatment of abdominal targets which were partially obstructed by the ribcage, such as tumors of the liver. The 64 element array had an operating frequency of 1 MHz, a radius of curvature (ROC) of 100 mm, and F-number of 0.8, and was intended to be coupled through a therapeutic operating fluid. A linear array with a spherically curved surface and ROC of 40 mm was used in [15] to successfully ablate the carotid bodies in spontaneously hypertensive rats. Imaging and HIFU pulses, both at a frequency of 3.2 MHz, were interleaved to allow for monitoring and closed-loop control of induced tissue boiling. More recently, in [16] a dual-mode linear array was developed for image-guided therapy using microbubbles, capable of imaging at a frequency of 4 MHz and generating therapeutic pules at 500 kHz. Another dual-frequency linear array, combining a 20 MHz imaging array stacked on top of a 1 MHz HIFU array, was presented in [17] for use in image-guided immunotherapeutic treatment of skin cancer using microbubbles. In contrast with these efforts, the array presented in this work was designed specifically towards inducing de novo cavitation without the need for UCAs, at a nominal tissue depth of 50 mm. The dimensions of the probe have been chosen based on the typical acoustic window providing access to the pancreas. Rather than using a spherically or cylindrically curved surface for focusing, the present work uses a combination of a cylindrical lens and electronic focusing, resulting in a surface profile which can more easily coupled with the skin without the need for a liquid-filled bath or bolus. The scope of this work includes characterization of the fabricated array performance in attaining the destructive cavitation behaviors and in limited imaging mode for targeting purposes. The acoustic output of the array was characterized in both linear and nonlinear regimes, through a combination of hydrophone measurements, acoustic holography, and simulations. High speed imaging was used to characterize the capability of the array for generating inertial cavitation in gel phantoms, and B-mode imaging capabilities were demonstrated using off-the-shelf imaging phantoms and by imaging abdominal organs in the in vivo anesthetized swine.

II. Methods

A. HIFU transducer and drive electronics

A photograph of the dual-mode transducer is shown in Fig. 1 The linear ultrasound array was fabricated by Sonic Concepts, Inc., (Bothell, WA, USA) and comprises 64 piezocomposite elements, 14.8 mm tall and 0.7 mm wide with a pitch of 0.8 mm, resulting in an overall aperture of 51.2 mm by 14.8 mm. Electronic phasing of the individual elements provided focusing and steering along the azimuth, while a silicone rubber cylindrical lens provided elevational focusing with a nominal focal length of Z_F = 50 mm, corresponding to a typical depth for pancreatic tumors when imaged using ultrasound [10, 18]. A summary of relevant physical parameters for the array is given in Table I. The use of lower frequencies have been shown to reduce the cavitation threshold and generate larger bubbles in agarose phantoms [8], while imaging resolution increases with higher center frequency. The design center frequency of 1.05 MHz was chosen as a compromise between being able to generate sufficient cavitation activity at a nominal tissue depth of 5 cm and the ability to produce B-mode ultrasound images of acceptable quality for guidance during therapy when operating near the upper limit of the matched bandwidth. The array was connected to an inductive matching network, designed to present an input impedance to the drive electronics of 100 ohms per element at a frequency of 1.05 MHz.

Fig. 1.

Photograph of the fabricated array. A cylindrical silicone rubber lens provides focusing in the elevational direction, while element phasing provides azimuthal steering and focusing.

TABLE I.

Dual-Mode Array Parameters

Parameter	Value
Center frequency	1.05 MHz
Matched bandwidth (−3dB)	0.71 MHz
Aperture	51.2 mm x 14.8 mm
Element count	64
Element pitch	0.8 mm
Elevational focal distance, ZF	50 mm
F-number (F/#) azimuthal/elevational	0.98/3.4
Max. electrical power, average	320 W

For all measurements, the probe was driven with a four-board Verasonics V-1 ultrasound research system (Verasonics, LTD., Kirkland, WA, USA), configured with an extended burst option, a 1200 W external power supply (Aim-TTI QPX600DP, Huntingdon, U. K.), and custom capacitor bank for generation of high-amplitude short HIFU pulses [19]. To increase the current delivered to each transducer element, each element of the array was connected through the matching network to two transmitters of the V-1 system driving the element in parallel. The Verasonics system provides two methods for controlling the effective amplitude of the transducer stimulus voltage: directly adjusting the power supply voltage, or varying the duty cycle of the stimulus waveform. Because the period of the driving voltage waveform must be an integer number of system clock cycles, the actual drive frequency for pulsed HIFU generation was 1.071 MHz, slightly higher than the center frequency of the transducer. The center frequency used for imaging pulses was 1.5 MHz, near the upper limit of the matched bandwidth of the transducer.

To facilitate comparison of measurements for different beam configurations with nonlinear simulations, the transducer power output was measured as a function of the voltage supplied by the system to the matching network using the radiation force balance method [20], for focal lengths of 38 mm, 50 mm, and 75 mm. The angular spectrum approach was employed to calculate a correction factor for each beam configuration, using measured holograms according to the procedure outlined in Ref [21]. The total acoustic power was also used to compute an effective source pressure, 𝑃₀, calculated as

$$P_0=\sqrt{2\frac{{\rho }_0{c}_0{W}_0}{S_{eff}}},$$ (1)

where $W_0$ is the acoustic power, ${\rho }_0$ and $c_0$ are the density and speed of sound in water, respectively, and $S_{eff}$ is the effective surface area. Values were chosen to represent water at 20 °C: ${\rho }_0=997.9 kg/m^3$, $c_0= 1482.4\text{ m/s}$, and $S_{eff}=(51.2\hspace{0.17em}\text{mm}\times 14.8\hspace{0.17em}\text{mm})=758\times {10}^{-6}{\text{m}}^2$.

B. Hydrophone measurements

Hydrophone measurements were performed in a water tank with automated scanning system. The dual-mode ultrasound array was mounted to a fixed frame positioned above the tank with the face submerged in water to a depth of approximately 10 mm. The water was de-ionized using a custom filtration system and degassed to less than 20% dissolved O2 using a permeable gas-liquid separation membrane. The hydrophone was connected with a mounting fixture to a computer-controlled three-axis positioner comprising stepper motors and linear slides from Velmex (Velmex Inc., Bloomfield, NY, USA) with a positioning resolution below 10 µm per step.

Three different hydrophones were used to accommodate a range of measured pressures. Measurements in the linear regime with peak negative pressures below 100 kPa were made using an Onda HGL-0200 lipstick hydrophone coupled to an AH-2020 preamplifier (Onda Corporation, Sunnyvale, CA, USA). A needle probe hydrophone with a 75 µm active element (Precision Acoustics model NH0075 with preamp model HP, Dorchester, Dorset, UK) was used for measuring peak pressures between 100 kPa and 1 MPa. Nonlinear focal pressure measurements were made using a fiber optic probe hydrophone (model FOPH 2000, RP Acoustics, Leutenbach, Germany).

For the measurements of beam profiles and focal pressure waveforms in both linear and nonlinear regimes, the hydrophone voltage was captured by a digital oscilloscope (model MSOX3034T, Keysight Technologies, Santa Rosa, CA, USA), which was connected to a desktop computer running a custom Matlab (The MathWorks, Inc., Natick, MA, USA) program used for controlling the positioning system and data acquisition. During all hydrophone measurements, 64-cycle bursts were used, and peak pressures were reported as an average of at least 6 consecutive cycles within steady-state region of the pulse.

Nonlinear focal pressure waveforms were measured with FOPH as a function of transducer driving voltage within 1.6–58 V range for different focusing distances (38 mm, 50 mm, and 70 mm). The location of the focus was defined as the location of the largest peak positive pressure in shock-forming regime for a stimulus voltage of 40 volts (corresponding here to total peak acoustic power of 216 watts for the case of Z_F= 50 mm). For drive voltages below 28 V, 32 waveforms were acquired and time-averaged, while 8 averages were used for voltages above 28 V.

C. Acoustic holography

Holograms for the array operating in the CW regime were measured using the scanning tank setup described in Section 2.A, for three different beam configurations: (1) all array elements driven in phase so that only elevational focusing was provided by the lens, (2) with electronic azimuthal focusing along the axis of the probe at a focal length of Z_F = 50 mm, henceforth referred to as the nominal focus location, and (3) with the beam focused at Z_F = 50 mm and also steered to a lateral focal position of X_F=10 mm. For these measurements, the Onda HGL-0200 hydrophone with AH-2020 20 dB preamplifier was connected to a 14-bit digitizer (Gage Razor 14, DynamicSignals LLC, Lockport, IL, USA), and a custom program written in Labview (NI, Austin, TX, USA) was used to control the positioner and acquire data. The Whittaker-Nyquist-Kotelnikov-Shannon sampling theorem requires that the spacing between hydrophone scan points be less than one-half of an acoustic wavelength in order for the hologram to represent all components of the propagating field without spatial aliasing artifacts [22]. Holograms were measured at an array stimulus frequency of 1.071 MHz, with a sample spacing of 0.65 mm in both the X and Y directions such that the criteria for the sampling theorem were met.

Determining the magnitude and phase of the pressure at each hydrophone scan point was done by windowing the recorded pulse to a section of 5 cycles where CW conditions were well approximated, and applying the fast Fourier transform (FFT) algorithm in Matlab. Directivity of the hydrophone was accounted for by computing the angular spectrum of the hologram using a 2D FFT and scaling the amplitude of each component of the resulting angular spectrum by a directivity factor based on the incidence angle upon the hydrophone [23]. After computing the holograms, it was apparent that the acoustic axis of the transducer and the Z axis of the positioner had a small angular misalignment, which was corrected during postprocessing using a coordinate transform approach [24]. The holograms in the measurement plane were then backpropagated to reconstruct the source distribution at the face of the transducer using numerical evaluation of the Rayleigh integral as described in Appendix A of Ref. [22].

D. High-speed photography

A schematic illustration of the high-speed imaging setup used for direct observation of cavitation behavior in agarose gel phantoms is shown in Fig. 2. Agarose was used as the tissue-mimicking gel because of its ease of fabrication, optical transparency, low toxicity, and for comparison with results of previous studies [8]. The gel was prepared by adding agarose powder (UltraPure Agarose, Invitrogen, Waltham, MA, USA) to deionized water for an agarose/water concentration of 1.5% w/v. The solution was degassed by boiling in a microwave oven for 5 minutes, and then was immediately poured into a sample holder fabricated from acrylic plates and left to cool at room temperature for three hours. A corrugated absorber cast from silicone rubber was positioned in the bottom of the mold to reduce the effect of reverberations from the bottom of the sample holder. Once the agarose had polymerized, a layer of degassed water was added to the sample holder on top of the agarose to provide acoustic coupling between the dual-mode ultrasound probe and the agarose sample. The probe was suspended above the sample holder from a computer controlled 3-D positioner mounted above the workbench, while the sample holder with agarose was mounted on top of a manual linear positioning stage. This allowed the agarose to be moved relative to the HIFU focus so that a fresh region of the gel could be used for each exposure.

Fig. 2:

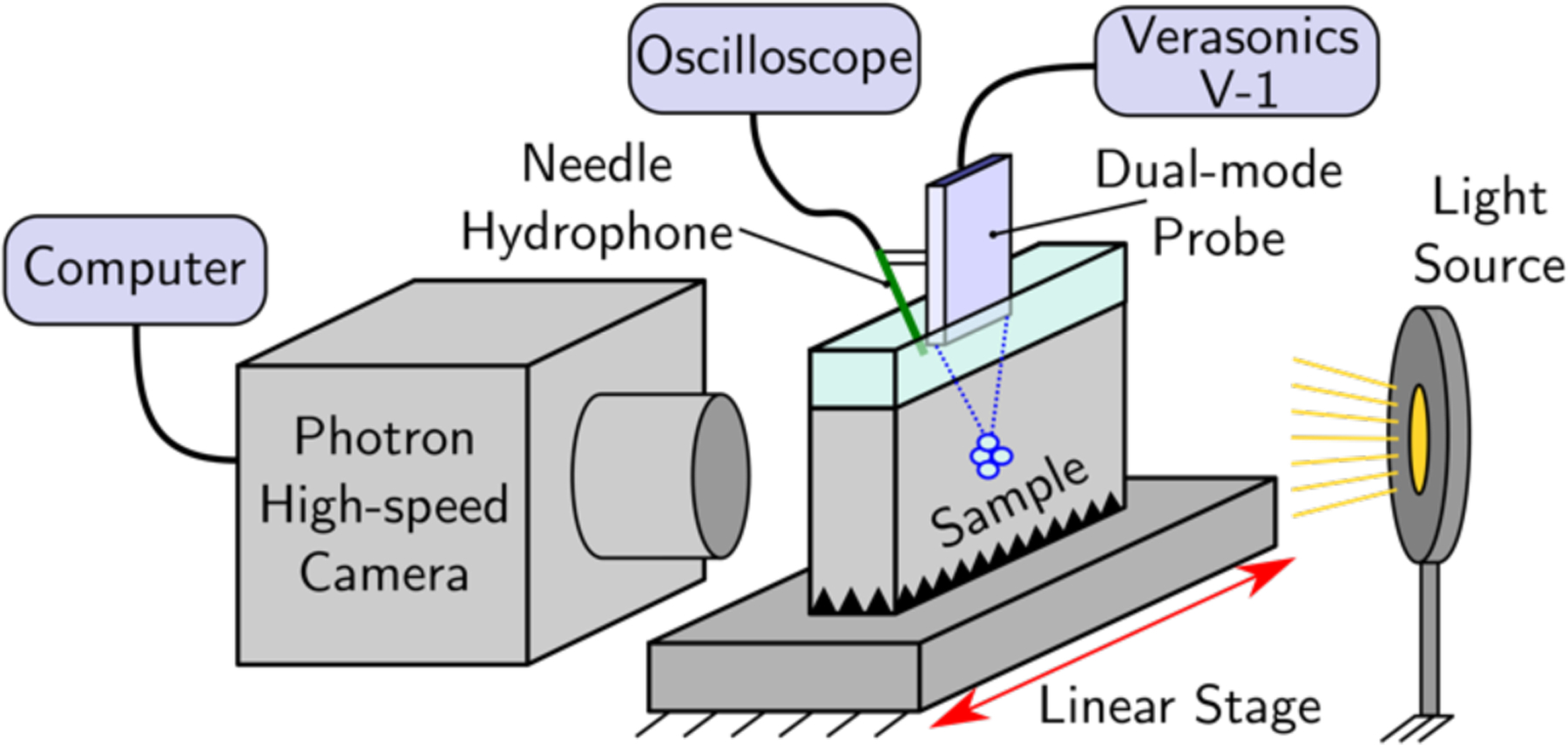
Schematic illustration of the hardware used for high-speed imaging of cavitation induced in agarose gel phantoms.

A Photron high-speed camera (model APS-RX, San Diego, CA) was used with a Carl Zeiss lens (model Makro-Planar 2/100 ZF, Thornwood, NY, USA) and bellows extension, located on one side of the sample holder. A 12-watt LED with collimating lens was positioned on the opposite side of the sample holder. To align the camera focus with the focus of the ultrasound beam, the agarose sample holder used for cavitation filming was replaced with a dummy sample holder with identical dimensions and with a 400 micron diameter wire positioned in the center. The probe was operated in the B-mode imaging regime to identify the location of the wire relative to the probe and to align to it. The lens focus and camera position were adjusted to provide an imaging resolution of 10 microns/pixel, based on the measured diameter of the wire target, for an overall field of view of 768 × 192 pixels (i.e., approximately 7.7 × 1.9 mm). For most of the acquired frames showing cavitation activity about the focus, the camera frame rate was 20 kfps with an exposure period of 4 μs. In addition to cavitation activity near the focus, a small number of images were captured with a larger field of view (1024 × 1024 pixels) and a frame rate of 3 kfps in order to determine the overall extent and distribution of the cavitation bubbles.

Each pHIFU exposure consisted of a single pulse at a stimulus frequency of 1.071 MHz, with a duration of 1 ms. Stimulus voltages were chosen to generate peak rarefactional pressures at the focus ranging from 1 MPa to 7 MPa, in 1 MPa increments, based on the saturation curves measured with the FOPH. For each value of stimulus pressure, three exposures were performed with corresponding camera frames. For each exposure, a trigger signal sent from the Verasonics to the camera initiated the acquisition of 25 image frames, with one image taken before the start of each pHIFU pulse for background subtraction. After each exposure, the agarose sample holder was moved 3 mm in the azimuthal direction using the linear stage, in order to position the pHIFU focus in a region of unexposed agarose in preparation for the next exposure.

E. Nonlinear fields simulated from reconstructed source

Nonlinear simulations were performed using realistic source boundary conditions reconstructed from the measured acoustic holograms in order to compute the full transmitted pressure field in three dimensions at amplitudes required for generating cavitation. Directly measuring such a field with the FOPH would not only take a prohibitive amount of time, but also could introduce errors at high shock amplitudes due to averaging over the effective fiber tip diameter, limited hydrophone bandwidth, and small positioning errors. Accurate nonlinear simulations are capable of providing a more realistic representation when shocks develop at the focus [25].

For each particular beam configuration simulated (i.e., beam focal length and steering angle) a boundary condition of specified acoustic pressure in the source plane z = 0 was found by backpropagating the measured hologram from the measurement plane to the source plane using a combination of the Rayleigh integral and angular spectrum method as described in Sec. II.C of [10]. The numerically propagated pressure field was used to identify the central acoustic axis of the beam, and any small angular misalignment between the projected beam axis and the z axis of the numerical reconstruction grid was corrected for prior to reconstruction in the source plane. This was done to ensure the acoustic axis of the transducer coincided with the z axis of the computational domain.

A one-way formulation of the Westervelt equation convenient for forward propagation of beams (i.e., no backscattering) was used for simulation of nonlinear acoustic fields transmitted by the dual-mode array over a range of output power levels. The equation accounts for the effects of diffraction, nonlinearity, and thermoviscous absorption, and has been described in detail in a number of prior works [26–28]. Briefly, modeling forward propagation of the transmitted field, the Westervelt equation in a retarded coordinate system was used:

$$\frac{{\partial }^{2}p}{\partial z\partial \tau }=\frac{c_0}{2}\text{Δ}p+\frac{\beta }{2{\rho }_0{c}_0^3}\frac{{\partial }^2{p}^2}{\partial {\tau }^2}+\frac{\partial }{2c_0^3}\frac{{\partial }^{3}p}{\partial {\tau }^3}$$ (2)

where $p$ is the acoustic pressure, $z$ is the spatial coordinate along the beam axis, $\tau =t-z/c_0$ is the retarded time, 𝑡 is the time, and ∆ is the full three-dimensional Laplace operator. Physical properties for the propagation medium 𝑐₀, 𝜌₀, 𝛽, and δ are the small-signal sound speed, density, coefficient of nonlinearity, and sound diffusivity, respectively. Eq. (2) was solved using the method of fractional steps, with an operator-splitting procedure of second-order accuracy [29]: when marching over a grid step along the coordinate z, the equation (2) is divided into multiple simpler equations, which separate the operators for diffraction, nonlinearity, and absorption. The computed pressure field was represented in either the time domain or the frequency domain using a finite Fourier series expansion. The diffraction operator and absorption were both calculated in the frequency domain for each harmonic component of the pressure, while the nonlinear operator was calculated using two different methods. A frequency-domain approach was used at smaller axial distances where shock fronts were not yet formed, and a shock-capturing time-domain approach was used as the waveform steepness increased and more harmonics were therefore required. Further details of the solution procedure are found in [10].

Various conventions for reporting the shock amplitude P_sh can be found in the literature and differ by application. For example, in boiling histotripsy applications, a definition of shock amplitude was used based on the slope of the pressure waveforms, which was found to correlate well with calculated heat generation rates [27]. For the purposes of this work, where reflection strongly nonlinear or shocked wavefronts from bubbles is more important than thermal effects, the reported shock amplitude effectively corresponds to the magnitude of the pressure jump at the shock front. When making comparisons between measured and simulated waveforms, the third derivative of the simulated pressure waveforms was calculated in order to find the point along the waveform where the change in curvature was the largest, and this was taken to be the start of the shock. Because of noise in the measured waveforms, correct identification of the shocks using this algorithm based on curvature was not possible. Instead, each of the experimentally measured focal pressure waveforms was inspected for abrupt jumps in pressure of similar amplitude to the numerically simulated values over a period corresponding to the 100 MHz bandwidth of the FOPH. If a measured waveform included a pressure jump of 8 MPa or greater (the minimum shock amplitude seen in the simulations) over a period of 10 ns, the amplitude of the pressure jump was recorded as the shock amplitude P_sh. This was done for three consecutive cycles of each waveform, and the values were averaged.

F. Ultrasound Image quality assessment

The imaging capabilities of the probe and the impact of different imaging parameters on overall image quality were investigated using both a commercial ultrasound quality assurance (QA) phantom (model 040GSE, CIRS Inc., Norfolk, VA, USA) and imaging liver and kidneys in vivo in an anesthetized pig. Beam generation and reconstruction of a B-mode image using the V-1 Verasonics system requires the specification of many acoustic and image reconstruction parameters. which influence the quality of the final image, including the center frequency of stimulus waveform, number of cycles in the pulse, number of transmitted beams used to reconstruct the image, the geometry of the transmitted beams (aperture, focal depth, beam angle, etc.), filter settings, and pulse timing. These imaging parameters were varied while viewing wire targets and hyperechoic inclusions in the CIRS QA phantom to optimize the image contrast and resolution at 30–70 mm depth range relevant to pancreatic tumor locations.

Once nominal imaging parameters had been determined, the resulting focal pressures for the transmitted beam were measured using the scanning tank setup of Section 2.B to determine the mechanical index (MI) in tissue as a function of source voltage. Finally, to demonstrate the suitability of the identified imaging parameters and capability for in vivo targeting of centimeter-sized objects, B-mode images of the liver and kidneys of anesthetized pigs (n=3) used in experiments by another group were collected.

III. Results

A. Beam profile measurements and steering limits

Measured beam profiles are shown below in Fig. 3, along with the expected profiles based on ideal simulations in the linear operating regime, normalized to the peak pressure at the nominal focus position (i.e., Z_F = 50 mm and X_F = 0). Fig. 3(a) shows the beam profiles measured along the central axis of the probe when no azimuthal steering is used, for focal distances Z_F of 44 mm, 50 mm, and 56 mm. During the design of the probe, simulations in the linear regime were used to determine the steering limits of the beam, defined as the range of steered focus positions where the maximum pressure remains within a ±10% deviation from that for the nominal focusing position. This definition was chosen order to maintain a similar field structure, focal pressure amplitudes, and nonlinear effects when steering, while still allowing the beam to cover our intended treatment targets. Other conventions for steering limits may be found in the literature, such as those for thermal HIFU based on limiting heat generation in sidelobes [30, 31], but are not relevant to the present work where thermal effects are not of concern. Based on the simulations, the expected axial steering limits were determined to be approximately ±6 mm from the nominal focus position, for a range in Z_F from 44 mm to 56 mm, and the azimuthal steering limits were determined to be X_F = ±22 mm [10]. The measured axial steering limits were found to agree well with those predicted by simulations, although the measured focal lobes were slightly longer along the acoustic axis of the beam.

Fig. 3.

Beam profiles, measured through the focus, when electronic phasing is used to focus the beam along the Z axis (a) and for azimuthal steering along the X axis (b). Lines indicate the beam profiles numerically simulated during probe design [10], while the measured beam profiles are indicated with the × markers. The pressure amplitudes have been normalized to the peak value at the nominal focus location, p_F. Good agreement is seen in the axial profiles, while the measurements deviate from the simulated profiles as the steering angle is increased.

For circularly symmetric focused sources, pronounced pressure nulls are expected prefocally and postfocally [32] due to destructive interference between on-axis arrivals of the direct and edge wave. For rectangular sources, the lack of a single edge wave results in less interference and higher pressures in these nulls. This behavior is also predicted by analytical models for focused rectangular sources [33]. Note that while the pressure amplitude gradually decreases when steering transversely from the focus and electronically focusing beyond the nominal focal length, it increases when moving the focus closer to the transducer array. The focusing gain of the transducer comprises two components: gain from focusing in the elevational plane provided by the fixed-length cylindrical lens, and gain from electronic focusing in the azimuthal plane. As the azimuthal focus is moved closer to the face of the transducer from the nominal focal length of 50 mm, the azimuthal gain increases. On the other hand, the two foci will no longer coincide. The increase in gain from reducing the azimuthal focal length is the dominating effect, owing to the smaller F-number for the azimuthal focusing, and the peak focal pressure increases as a result despite the difference in focal lengths.

Transverse beam profiles, when the beam was steered azimuthally with a nominal focal distance of Z_F = 50 mm, are shown in Fig. 3(b), along with beam profiles expected from the ideal simulations. It is seen that for small steering angles, measurements and simulations are in excellent agreement, while focal pressures are overestimated by the simulation as the steering angle is increased. The azimuthal steering limit was determined from the envelope of these profiles to be approximately X_F = ±11.5 mm, significantly less than the limit of ±22 mm predicted by the ideal model. While only profiles in the positive X direction are shown in Fig. 3(b), the steering limits were seen to be similar in the negative direction as well. Finally, it may be noted that it is possible to steer the beam more than 11.5 mm azimuthally if the restriction on the 10% allowed pressure deviation is relaxed, as indicated in Fig. 3(b) by the measured profile when the electronically steered focus is set to X_F= 20 mm (in red).

B. Acoustical holography

The source pressure magnitude and phase distributions, computed from the measured acoustic holograms, are shown in Fig. 4 for the following source configurations: all elements driven in phase (top row), elements phased for a focal length of Z_F = 50 mm along the axis of symmetry (middle row), and with the beam focused at Z_F = 50 mm and steered to X_F = 10 mm.

Fig. 4.

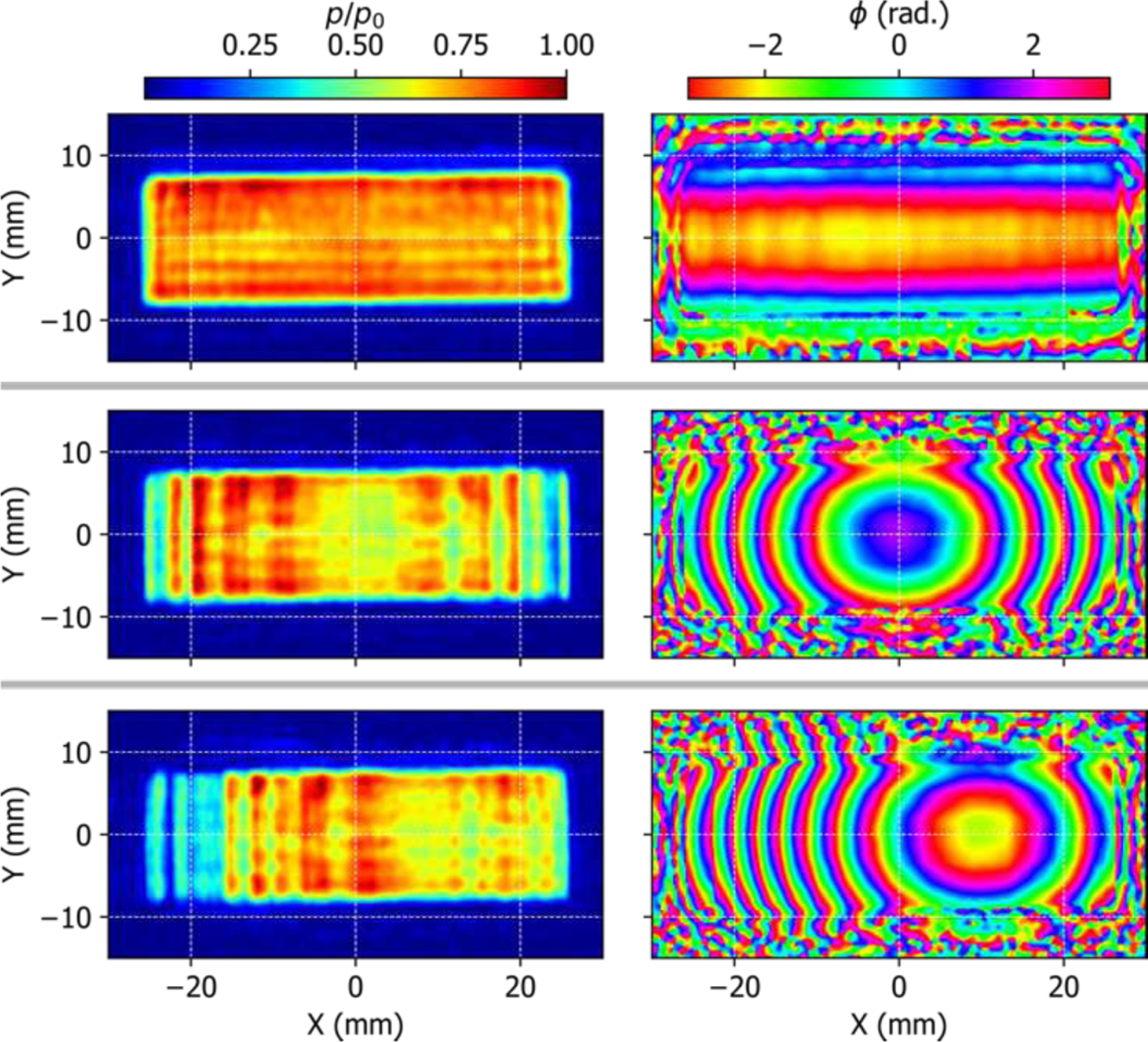
The source pressure magnitude and phase distributions, reconstructed from the measured holograms, when the array is configured for no electronic focusing (top row), on-axis focusing at 50 mm (middle), and focusing at 50 mm and steering towards 10 mm (bottom). The effect of the cylindrical lens is clearly visible in the phase distribution when electronic focusing is disabled.

Comparing the source magnitude and phase distributions for the three cases reveals several noteworthy features. For the case of uniform-phase excitation, the amplitude distribution is not perfectly uniform across the face of the array, but instead the distribution shows a region of higher magnitude near the upper left corner of the array. The variation of the phase distribution in the Y (elevational) direction is the effect of cylindrical focusing lens. However, some variation in phase along the X axis may be indicative of nonideal variations in lens thickness or bonding with the active elements, which may also be a cause of the areas with higher magnitude. Because the element size and pitch are smaller than the acoustic wavelength of λ = 1.39 mm, the individual elements are not spatially resolvable in the source reconstruction but instead appear blended together.

The effects of adding electronic focusing and steering are both seen in the phase distributions, as expected, but also have a significant impact on the magnitude distribution across the face of the array. This variation in magnitude resulting from electronic focusing was not expected based on linear field simulations performed during the design of the probe (see Fig. 2(c) of Ref. [10]). The source boundary condition used during the design-stage simulations assumed a uniform velocity magnitude distribution across the elements of the array, and assumed that the elements were cylindrically curved in the Y direction to provide elevational focusing. One possibility is that the observed variation in magnitude across the transducer face is an artifact of the absorptive rubber lens used to provide elevational focusing for the fabricated array, rather than the cylindrically-curved elements assumed in the simulations.

The accuracy of the source boundary conditions (BCs) reconstructed from the measured holograms was ascertained by computing the propagating field in the linear regime using the reconstructed BC as the source, and comparing the resulting field with direct hydrophone measurements of the beam profiles. The profiles were seen to be in good agreement, with differences in the peak pressure less than 3%, well within the typical uncertainty of the hydrophone measurements. A plot showing a comparison of the azimuthal beam profiles for the nominal focusing case and for steering to X_F =10 mm can be found in Fig. S1 of the supplementary material. As a consequence of this agreement in the linear propagation regime, nonlinear simulations using these reconstructed boundary conditions were expected to provide an accurate representation of the field in the nonlinear propagation regime as well.

C. Generation of nonlinear HIFU pulses

The measured and simulated nonlinear focal pressure waveforms are plotted in Fig. 5 at pulse-averaged acoustic power levels of 21 W, 110 W, and 411 W. The agreement is excellent up to 110 W, where the waveforms are nonlinearly distorted but without shocks. At the highest power of 411 W, however, peak positive pressure from simulation is higher than the measured value by more than 33%, whereas peak negative pressure is still in agreement within 7%. Large steep shock fronts are visible in both waveforms. Previous studies using diagnostic probes and therapeutic arrays have shown similar discrepancies between simulated and measured focal waveforms that contain shocks [25, 34]. The most likely reasons for this discrepancy are the spatial resolution of the FOPH, the accuracy with which the FOPH can be positioned in the center of the focus, and well as the bandwidth of FOPH limited by 100 MHz. At high power levels, the azimuthal beamwidth in terms of P₊ becomes comparable to the effective diameter of the fiber tip, so that the measured pressure is spatially averaged. As a result, the nonlinear simulations based on the reconstructed boundary conditions were expected to give a more accurate representation of the true nonlinear acoustic field near the focus.

Fig. 5.

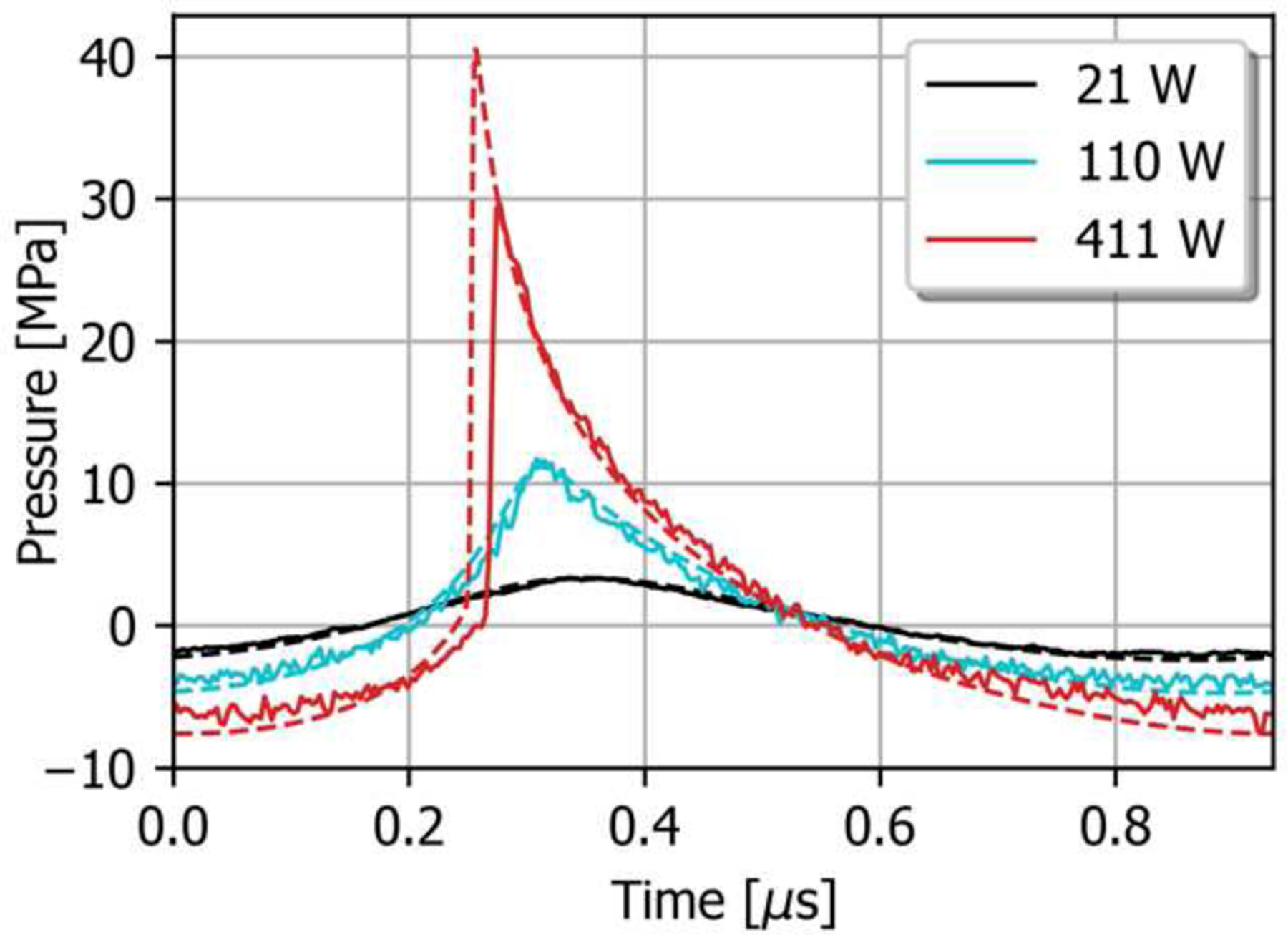
Comparison of measured focal pressure waveforms (solid lines) and nonlinear simulation results based on the reconstructed boundary condition (dashed lines) for the nominal focus position, at three different stimulus levels. The waveforms are in good agreement when shocks are not present, while the hydrophone tends to measure a lower peak pressure once shocks form at the focus.

As discussed in Section I, the degree of focusing of a HIFU transducer, represented its F-number, has a marked impact on the pressures required to generate nonlinearly distorted waveforms and shocks at the focus. Measured focal values of P₊ and P₋ are plotted in Fig. 6 as a function of effective source pressure, P₀, calculated using Eq. 1, for focal distances Z_F of 38 mm, 50 mm, and 75 mm without transverse beam steering. These focal distances correspond to azimuthal F-numbers of 0.74, 0.98, and 1.46, respectively. Also plotted is the shock amplitude, P_sh, for those voltages sufficient for generating shocks at the focus. It is seen that the simulations and measurements are in excellent agreement in the quasilinear regime and for P₀ values below the threshold where shocks form in the simulated waveforms. Above this threshold, peak positive pressures measured using the FOPH, as well as the resulting shock amplitudes, are significantly lower than the simulation results, as was shown in the individual waveforms of Fig. 5.

Fig. 6.

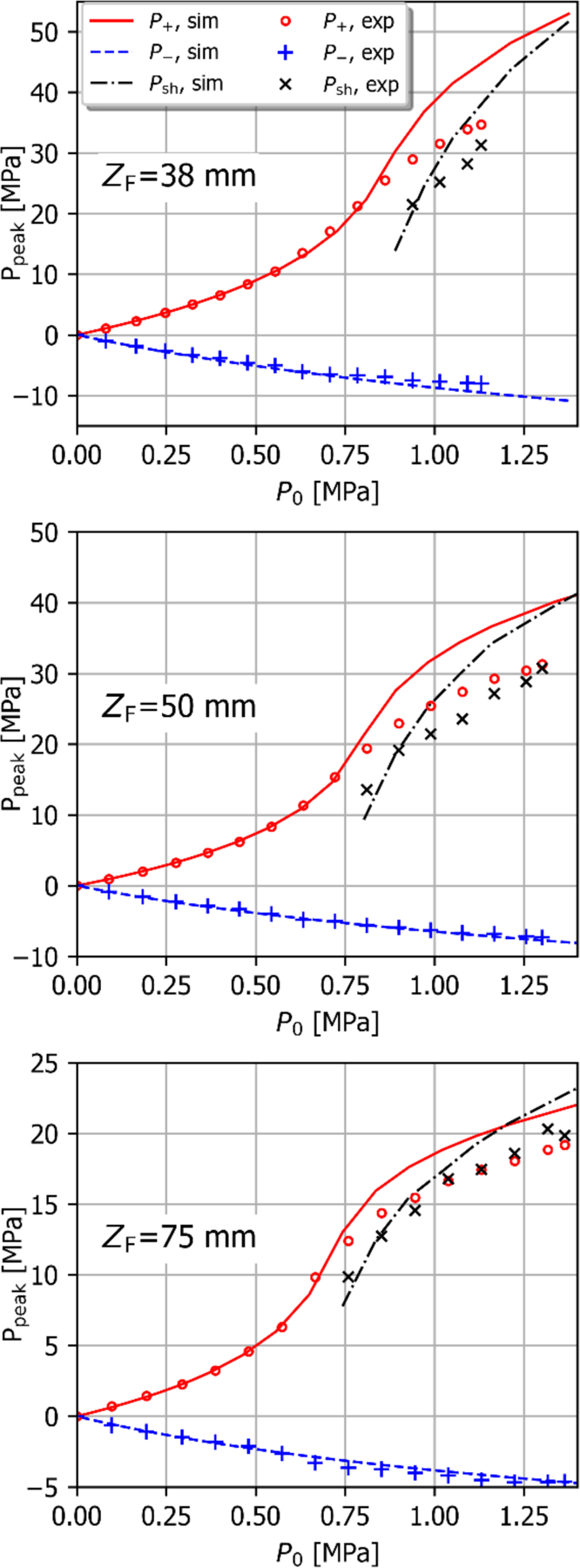
Measured nonlinear focal pressures and shock amplitudes as a function of stimulus voltage for focal distances of 38 mm, 50 mm, and 75 mm without transverse beam steering (markers) compared with results from nonlinear simulation based on the holographic boundary conditions (lines). At pressures above those required for shock development, the FOPH underestimates the peak positive pressure and corresponding shock amplitude.

The transmitted power, effective source pressure, and peak pressure values at the onset of shock formation are shown in Table II. Because the FOPH measurements of focal pressure underestimate the true pressure once shocks form at the focus, P₊ and P₋ values are taken from the nonlinear simulations with holographic source BCs.

TABLE II:

Acoustic parameters at the shock formation threshold as a function of focal length in water, taken from the nonlinear simulations

ZF [mm]	W0 [W]	P0 [kPa]	P− [MPa]	P+ [MPa]
38	203	890	8.0	30.2
50	165	803	5.6	21.3
75	141	743	3.1	13.0

Maintaining the nonlinear field characteristics needed for cavitation generation when the beam is steered off-axis is critical to the therapeutic applications. Fig. 7 illustrates the measured peak focal pressures for Z_F=50 mm, both with and without off-axis steering to X_F=10 mm. Steering the beam azimuthally by 10 mm decreases the focal pressure, as expected, (see Fig. 3), so that higher stimulus amplitudes are required to generate shocks at the focus as indicated in the black and red curves of Fig 8. However, when the voltage is scaled such that the same focal pressures are achieved with and without steering in the linear regime (a scale factor of about 1.08 for the voltage with steering), the peak pressure curves are in better agreement as seen in the blue “adjusted” curve. For this relatively small steering angle, the structure of the focal lobe in terms of its length and width is very similar to the nominal case. Therefore, when driven at voltages resulting in the same focal pressures in the linear regime, the nonlinear characteristics will be similar as well. This is in agreement with similar observations for large spherically focused HIFU arrays [19].

Fig. 7.

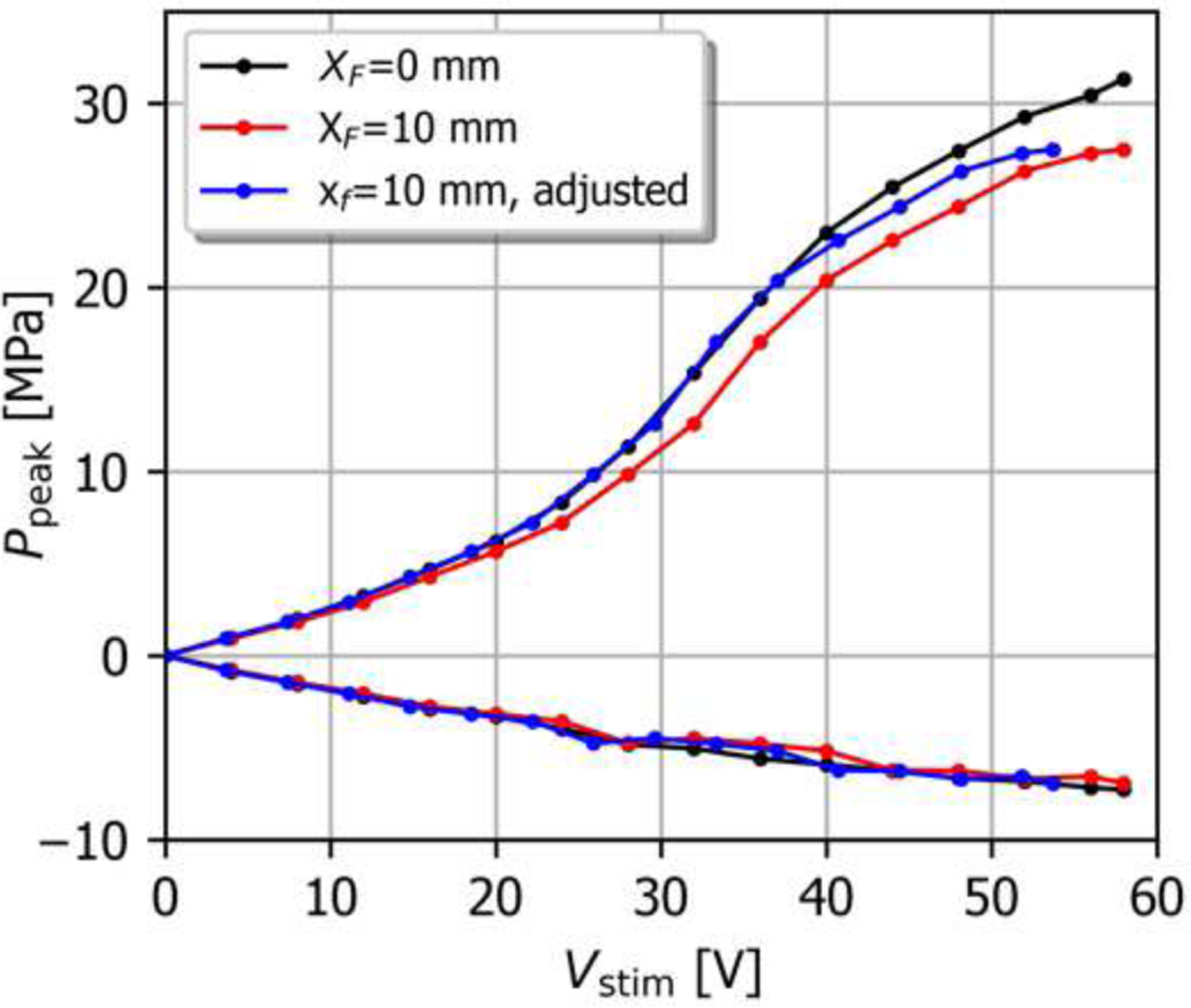
Peak pressures for the nominal steering configuration and for beam steering to X_F = 10 mm and Z_F = 50 mm, vs. applied stimulus voltage. For the “adjusted” curve, V_stim has been normalized by 1.08 in order to account for the difference in focal pressure in the linear regime when steering is employed (Fig. 3b).

Fig. 8.

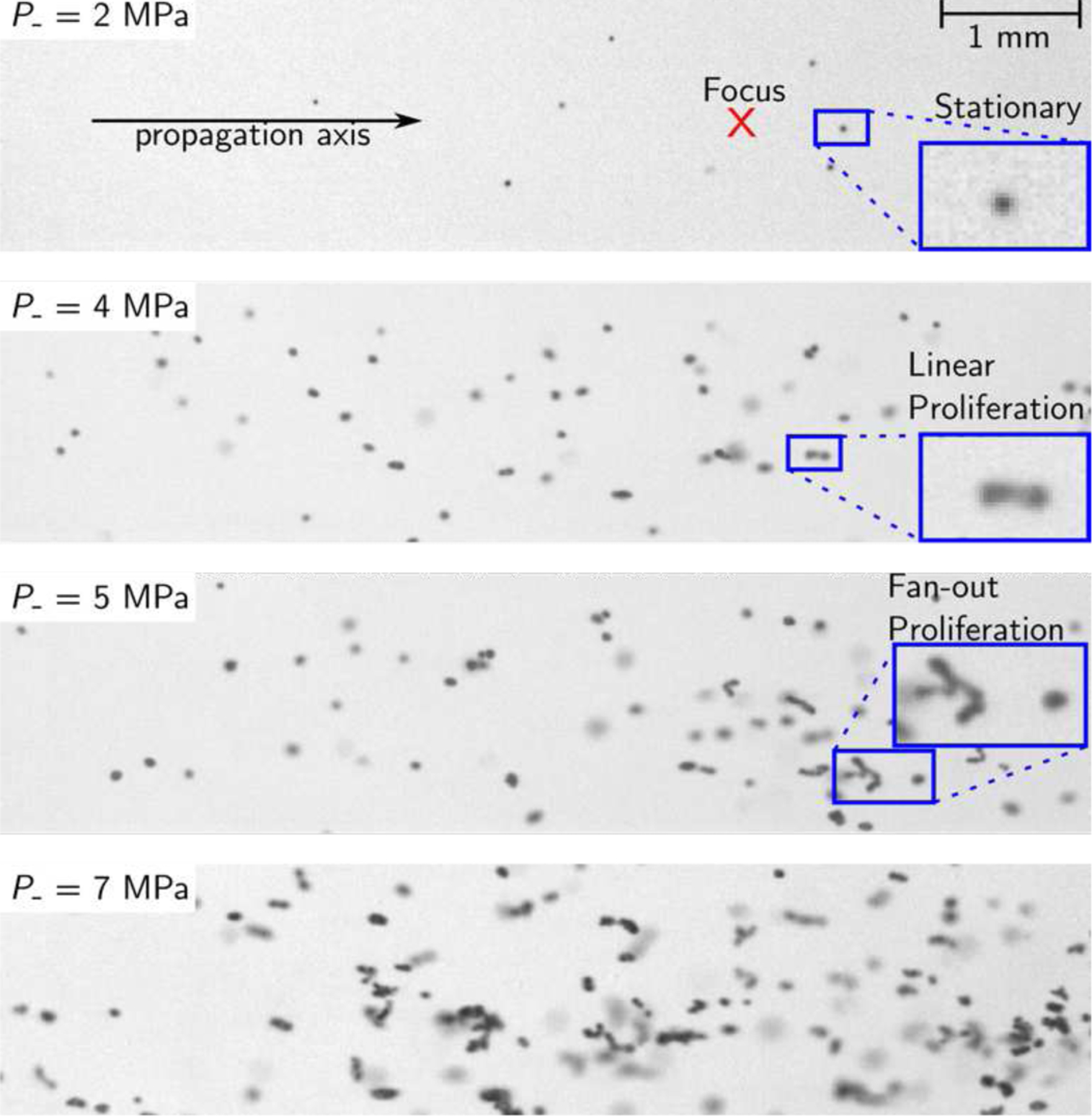
High-speed camera images showing the distribution of induced cavitation bubbles in the focal region, for on-axis beam focusing at Z_F=50 mm. At P₋=2 MPa, stationary cavitation bubbles are observed. The transition to proliferating behaviors occurred starting at a peak negative pressure of 4 MPa. Fan-out proliferation was seen for P₋ values at and above 5 MPa.

D. High-speed photography

A series of high-speed camera frames showing induced cavitation bubble distributions near the focus and at the end of the 1 millisecond HIFU pulse are shown in Fig. 8, for a range of focal P₋ values from 2 MPa to 7 MPa. No cavitation was observed in any camera exposures for a peak negative pressure of P₋ = 1 MPa. At P₋= 2 MPa, isolated cavitation bubbles were observed, and appeared stationary over the camera frames. When P₋ was increased to 4 MPa, a qualitative change in behavior was seen: with some of the cavitation bubbles initially isolated and stationary starting to split primarily along the direction of wave propagation into pairs and sets of bubbles, proliferating towards the transducer. This form of bubble proliferation behavior has been referred to as linear proliferation in previous studies [8]. As the peak rarefactional focal pressure was increased to 5 MPa, bubbles were seen to proliferate laterally as well as axially, greatly increasing the number and spatial density of cavitation bubbles, which is known as fan-out proliferation behavior. As the pressure was increased further, this effect became even more pronounced, as seen in the image for P₋ = 7 MPa. It should be noted that, in general, a combination of bubble behaviors was observed for pressures above the proliferation thresholds, where bubbles near the focus proliferated in a fan-out fashion, while those farther from the focus showed stationary cavitation behavior.

Proliferation behaviors were categorized for on-axis focal distances of 38 mm, 50 mm, and 75 mm, as a function of P₋ from 1 MPa to 7 MPa in increments of 1 MPa. For a given combination of Z_F and P₋, Fig. 9 indicates the categories of proliferation that were observed. A particular cavitation behavior is indicated if it was seen to occur in at least one camera frame in at least one exposure at a given pressure. Also indicated in the figure are the ranges where shocks form at the focus, based on the nonlinear field simulations. While all three focal lengths were shown to induce stationary cavitation at P₋ = 2 MPa, the transition to proliferating behaviors generally occurs at a smaller P₋ value as the focal distance increases, and for the cases of 50 mm and 75 mm the transition occurs at about the same pressure where focal shocks are seen to form.

Fig. 9.

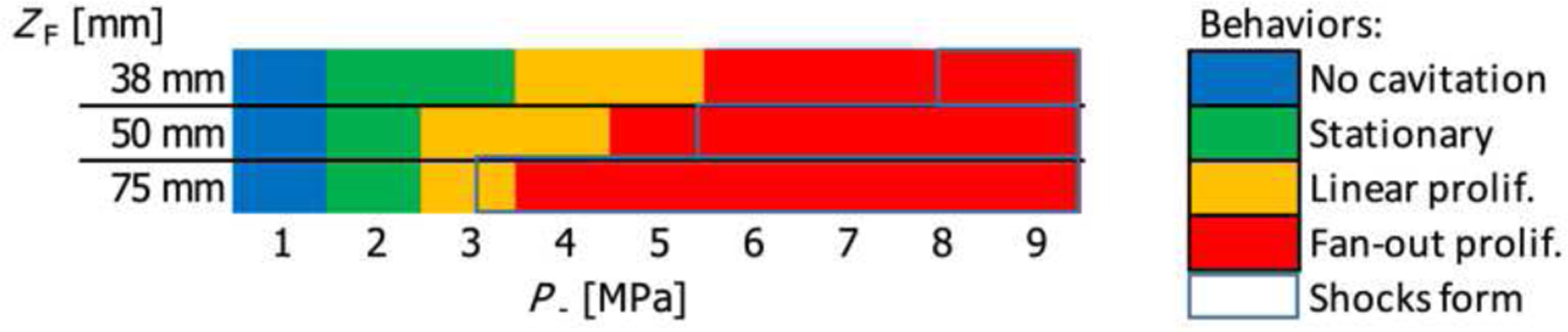
Categories of cavitation behavior observed in high-speed images for peak negative focal pressures between 1 MPa and 9 MPa, for on-axis focusing with focal lengths of 38 mm, 50 mm, and 75 mm.

A comparison of the observed bubble distributions with and without azimuthal beam steering to X_F=10 mm is shown in supplementary Fig. S2 when the focal pressure in the on-axis case is P₋= 6 MPa. In order to achieve the same peak negative focal pressure, the source amplitude was increased by 8% when beam steering was added. It was seen that the distribution of bubbles had the same general overall structure, and the transition from stationary to proliferating cavitation occurred near the same pressure threshold.

The distribution of bubbles observed in the focal region can be compared with the pressure distribution in the same region, computed from nonlinear simulations based on the measured holograms. The resulting distributions for both peak positive and peak negative pressures are shown in Fig. 10, for a peak negative focal pressure of P₋=6 MPa. The overall distribution of bubbles corresponds well with the region of the beam where P₋ exceeds the stationary cavitation threshold of about 2 MPa in the gel, as indicated by the blue contour in the top figure. As expected, the highest spatial density of bubbles was observed near the focus of the beam, where peak pressures are the greatest. It should be noted that while there were many bubbles outside of the nonlinear focal region in terms of P₊, most of the proliferating bubble behavior occurred near the region where the pressure waveforms exhibited significant nonlinear distortion. This reinforces the significant role nonlinearity to play in the transition from stationary to proliferating bubble behavior [8], and is critical for application to tissue permeabilization where proliferating bubbles are expected to result in more tissue disruption than stationary bubbles. Even though bubbles are generated outside of the region where waveform nonlinearity is high, the localization of proliferating bubbles will result in a more localized effective response than would be implied by the overall size of the induced bubble distribution.

Fig. 10.

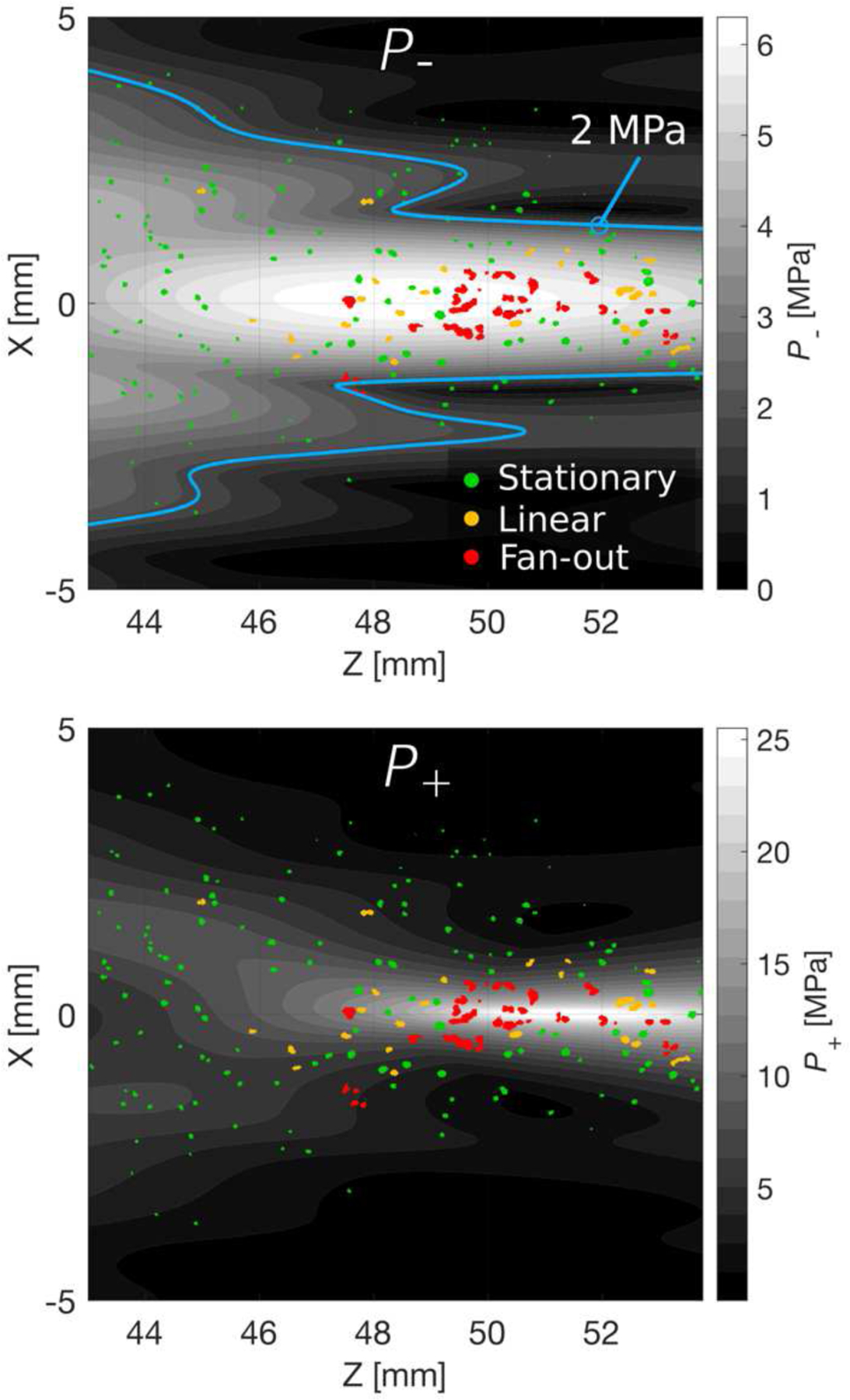
Contour plots showing the peak negative pressure distribution (top) and peak positive (bottom) near the beam focus in the azimuthal plane, computed by nonlinear simulation with the source boundary condition measured by holography. The distribution of bubbles observed from high-speed photography for P₋=6 MPa is overlaid on each distribution and roughly agrees with the pressure distribution near the focus of the beam. The blue contour on the upper plot indicates the region where the pressure exceeds the cavitation threshold of 2 MPa.

E. Quality of B-mode images

Acceptable images were formed using 128 transmit beams, swept over an angle of 65 degrees, with the geometric focus set to a depth of 75 mm and F-number of 6.25. The array was operated in a pseudo-curvilinear mode, rather than the linear scan mode, in order to enlarge the field of view. Each transmitted pulse was two cycles in duration with a center frequency of 1.5 MHz, which is near the upper limit of the bandwidth of the probe. Images collected of three different targets using the dual-mode probe connected to the V-1 system are compared with those acquired with a commercial 6C2s diagnostic imaging probe in Fig. 11. The 6C2s was connected to a BK3000 scanning system and was operated at a frequency of 2.5 MHz and an MI of approximately 1.4, while the MI for the dual-mode probe was approximately 0.40. The top and middle rows of Fig. 11 show images collected on a kidney and the liver, respectively, of two different anesthetized domestic farm pigs weighing between 45 kg and 50 kg. In both cases it was possible to clearly resolve centimeter-sized features, which could be used as anatomical landmarks for targeting during therapy. Images collected on the CIRS QA phantom are shown in the bottom row. The dual-mode probe was still capable or resolving most of the small, embedded wire targets as well as the larger grayscale inclusions, while the 6C2s probe provided better image quality, with a smaller point spread and improved definition of the embedded targets. The lower operating frequency for the dual-mode probe resulted in a wider point-spread function, clearly seen in the point targets, as well as a larger characteristic size of the background speckle. Reverberations of the imaging pulse within the mechanical structure of the dual-mode probe initially resulted in a bright region covering a region approximately 1 cm to 2 cm from the face of the probe, and targets within 2 cm of the front of the probe were not resolvable. The TGC was set to the minimum possible level to eliminate this bright region at the top of the images collected with the dual-mode probe.

Fig. 11.

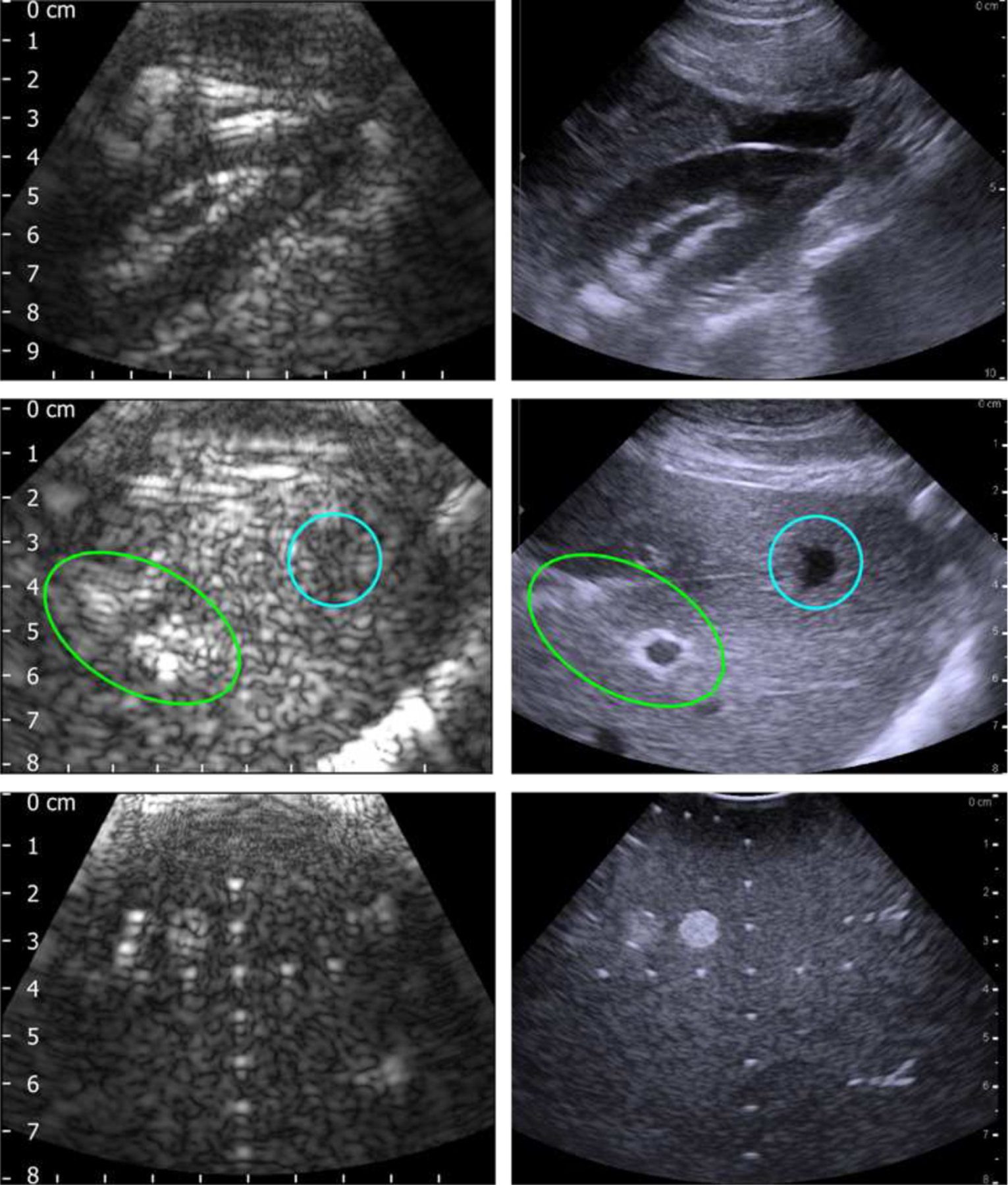
B-Mode images acquired with the dual-mode probe and Verasonics V-1 system at 1.5 MHz (left column), compared with those collected using a 6C2s probe and BK3000 scanner at 2.5 MHz (right column). Images were collected on a commercial QA phantom (top row), pig kidney (middle row), and pig liver (bottom row).

One measure of the resolution of an imaging system is the combined pulse-echo spatial impulse response of the system, also known as the point spread function [35]. The apparent diameter of a small wire target in the CIRS phantom was used to estimate the point spread function. The intensity from the B-mode image shown in the lower left corner of Fig. 11 was extracted along a vertical line near the center of the image, through one of the wire targets at a depth of approximately 4.7 cm, and is plotted in Fig. 12(b). The full width at half maximum (FWHM) diameter of the spot seen in the image is 2.5 mm, approximately 2.4 times the wavelength used for imaging. The focal pressure waveform for a single imaging pulse, measured using the 75 μm needle probe hydrophone is seen in Fig. 12(c), used for calculating the MI corresponding to the chosen imaging parameters. It is seen that even though the transducer was driven with a stimulus voltage pulse consisting of two cycles, many more cycles are seen in the pressure waveform due to the finite bandwidth of the transducer.

Fig. 12.

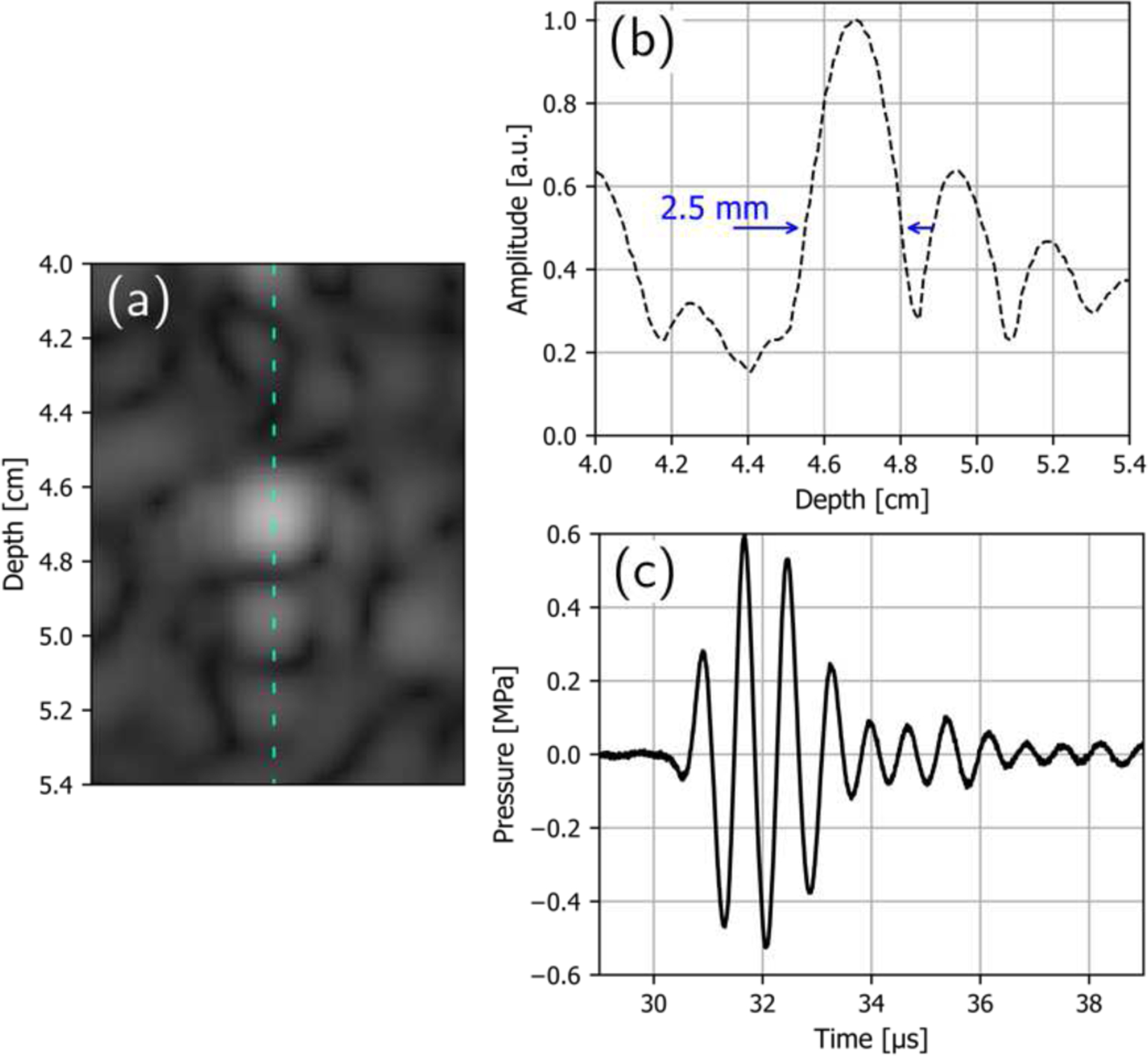
B-mode image of a single wire target in the CIRS phantom with a diameter of 100 µm and at an axial depth of approximately 4.7 cm (a), the intensity profile extracted through the center of the target image (b), and the pressure waveform measured at the focus of the imaging beam (c). The FWHM diameter of the resolved target is 2.5 mm.

IV. Discussion

This work presents the practical implementation and performance characterization of the dual-mode pHIFU array previously designed [10] for cavitation-based tissue permeabilization in the context of enhancing image-guided drug delivery in PDAC. Using a single probe for both targeting via B-mode imaging and generating cavitation has two major advantages over using a focused therapy array combined with a coaxial imaging array as was done for previous studies [6, 36]. First, using a single probe eliminates the need for axial alignment of the therapeutic beam and imaging beam. Second, the use of a spherically-focused HIFU transducer results in a beam which has high-intensity components propagating in three full dimensions while standard imaging probes only image in a two-dimensional plane. As a result, it is not possible with such a configuration to observe the entire three-dimensional region being insonated by the therapeutic beam. Using a dual-mode array for both targeting and application of pHIFU ensures that any anatomical feature insonated by the probe is also visible in the B-mode image, so that it is easier during clinical applications to avoid applying HIFU to sensitive or highly reflective structures such as bones or gaseous regions in the digestive tract.

In terms of acoustic output, the electronic steering range in the linear regime, defined here as the peak focal pressure being within 10% of that without steering, was measured and compared to the expectations from design-stage numerical modeling. The axial steering performance was in excellent agreement with the expectations, whereas the azimuthal steering limits almost a factor of two lower than expected (11.5 mm vs. 22 mm). The most likely reason for this discrepancy is that the design-stage model assumed perfect cylindrical focusing in the elevational direction and did not account for refraction and imperfections in acoustic coupling of the array elements into the rubber lens. Additionally, the design-based model assumed that each element could be represented by a uniform rectangular velocity source. Any deviation of the actual velocity distribution at the face of an array element could modify the directivity of the element, which would have a subsequent impact on the overall steering performance of the array.

For azimuthally steered beams it was seen that similar nonlinear saturation curves result when the stimulus waveform amplitude is adjusted to account for the decrease in focal pressure due to steering in the linear operating regime [19]. When the beam is steered azimuthally within the limits, the overall structure of the transmitted linear field remains similar to the nominal field. This justifies use of azimuthal steering limits based on the 10% pressure variation for therapeutic applications where the focus of the beam is swept through the target region using electronic steering.

Regarding nonlinear acoustic behavior when the focal length is electronically varied, the trends observed in Fig. 6 are in agreement with expectations from previous studies [7, 9, 19]. First, as the focal distance increases, the focal gain in the quasilinear operating regime is reduced due to the steering effect, as evidenced in the curves for both P₊ and P₋ at values of P₀ below approximately 0.5 MPa. Second, it was seen that less focused beams (i.e., beams with larger F-numbers) were able to generate shocks at the focus at lower power values and lower peak focal pressures, in agreement with previous studies [9]. This occurs because the focal lobe is longer for less focused fields, and thus nonlinear effects accumulate over longer distances prefocally. The ability to electronically increase the focal length and F-number for the dual-mode probe allows for generating highly nonlinear pulses at decreasing peak negative pressures. The degree of nonlinearity and subsequent tissue disruption therefore can be tailored to the requirements of a given therapeutic application. This capability makes the probe potentially useful for applications beyond drug transport enhancement, such as using pHIFU to generate an inflammatory response or immune response [37, 38] with simultaneous B-mode targeting.

High-speed photography in agarose gel phantoms demonstrated the ability of the dual-mode array to induce de novo cavitation with characteristics necessary for efficient tissue permeabilization. At the nominal focal length of Z_F = 50 mm, the threshold for inducing stationary cavitation at the focus corresponded to a peak negative pressure value of P₋ = 2 MPa, while a transition to fan-out proliferating bubble behavior was observed at P₋ = 5 MPa, when substantial nonlinear distortion and shock formation started. While for the case of Z_F = 38 mm the transition to fan-out bubble proliferation occurred at a pressure below that required for shocks to form at the focus, the focal pressure waveforms still showed significant asymmetry due to nonlinearity, with peak positive pressure at the focus greater than the peak negative pressure by a factor of about 2. In agreement with previous studies, changing the focal length of the beam had a notable impact on the acoustic power required to generate proliferating cavitation at the focus, as the reflection of highly nonlinear pressure pulses from bubbles plays a major role in the formation of proliferating bubble clouds [8] and nonlinear focal pressure waveforms occur at lower peak pressures for beams with larger F-numbers. The cavitation behaviors were categorized in this study based on the simple criteria of whether or not they were observed in any camera frame over three exposures at a particular power level and should thus be interpreted as minimum levels at which certain behaviors could be observed.

To illustrate the importance of both peak positive and peak negative pressure on the distribution of generated bubbles and transition to proliferating behavior, the bubble distribution directly captured using the high-speed camera for a maximum of P₋=6 MPa in agarose was overlaid on contour plots of pressure near the focus. Stationary cavitation bubbles were seen to form throughout the region where P₋ exceeded the cavitation threshold of 2 MPa in the gel, while proliferating behaviors were only observed near the focus where the waveforms show a high degree of asymmetry due to nonlinear distortion and shock formation.

Regarding the potential for off-target tissue damage by stationary cavitation bubbles outside of the focal region, multiple factors should be considered.

First, research on the use of cavitation to enhance uptake of doxorubicin in a mouse model of pancreatic cancer revealed that transport rates increased with the intensity of induced bubble activity, as quantified using PCD signals [6]. At lower cavitation intensities some subtle amount of tissue disruption was seen to result, but the damage was not histologically significant. Proliferating bubbles move more vigorously than do stationary bubbles and are therefore expected to cause more tissue disruption than stationary bubbles. As a result, the effective treatment region will be smaller than is implied by the overall extent of the bubble distribution.

Next, the cavitation threshold for pancreatic tumors is reported to be around 3 MPa to 4 MPa, which is higher than the cavitation threshold observed for our agarose gel phantoms. For the same peak focal pressure, a smaller region of the beam will exceed the cavitation threshold in tissue than for the agarose gel, and therefore the overall size of the bubble distribution in tissue will be reduced. We intend to target tumors with characteristic sizes of approximately 3 cm to 4 cm, as smaller tumors (less than about 2 cm) can be surgically resected, and the dimensions of our focal region are appropriate for these targets.

Finally, research on the use of extracorporeal pHIFU for cardiac pacing in rats has shown that de novo cavitation may be induced in tissues at peak pressures of up to 3 MPa without resulting in gross tissue damage [39]. Future work will examine the extent of tissue disruption resulting from different categories of proliferating cavitation in ex vivo and in vivo tissues induced using our dual-mode array, including the potential for off-target bioeffects.

While the B-mode images rendered using the dual-mode probe lack the resolution of the clinical diagnostic imaging system, they are of sufficient quality for identifying cm-sized targets and anatomical landmarks during pHIFU treatment. In the envisioned clinical scenario, a clinical ultrasound imaging system could be used to obtain high-quality images before treatment, and the dual-mode system could then be used to find anatomical landmarks for relative positioning of the pHFIU treatment area. The basic algorithm employed for B-mode imaging in this study, where a beam was swept across the imaging plane at a single focal depth, leaves room for additional image improvement using more advanced imaging techniques. For instance, multiple beams with different focal lengths and different center frequencies may be compounded in order to reduce speckle and improve image quality [35], which may be incorporated into the system in the future. In addition, nonlinear pulsing schemes such as pulse inversion and amplitude modulation harmonic imaging may be used to increase the imaging contrast by using the second harmonic of the transmitted pulse for image reconstruction [40]. The limited bandwidth of 0.71 MHz for the dual-mode array prevented the use of harmonic imaging in this study, as the amplitudes of the received second harmonic signals were effectively filtered out by the inductive impedance matching network. Future work will investigate methods for improving the bandwidth of the system on the receiving side as a potential means for enabling harmonic imaging. Image quality may also be improved through the addition of a high-frequency transducer stack within the probe [17].

V. Conclusions

A new 64-element linear ultrasound array has been developed and characterized by several methods. Measured performance of the array was found in many aspects to be in agreement with expectations from modeling performed in the design stage. The probe can induce proliferating de novo cavitation in tissue-mimicking agarose gel phantoms, at peak rarefactional pressures as low as 3 MPa for linear proliferation and 4 MPa for fan-out proliferation, which is expected to result in significant tissue disruption. B-mode imaging is capable of resolving centimeter-sized features in tissue at depths of 3 cm to 7 cm, sufficient for landmark identification in therapeutic pHIFU applications.

Future work will involve integrating active and passive cavitation detection [36, 41] for real-time monitoring of the induced cavitation, development of quantitative metrics relating recorded cavitation activity to resulting tissue disruption, and validating those metrics in the ex vivo and in vivo tissues. Combining B-mode imaging and cavitation detection along with the ability to induce proliferating cavitation, without the need for contrast agents, is a promising approach for image-guided drug delivery enhancement therapy.

Biographies

Randall P. Williams (Member, IEEE) received the B.S. degree from Texas A&M University in College Station, TX, in 2006, and the M.S. and Ph.D. degrees from The University of Texas at Austin in 2012 and 2020, respectively.

His research interests include electroacoustic transducer development, acoustical holography, acoustic microelectromechanical systems (MEMS), and therapeutic ultrasound. Before studying at The University of Texas, he spent six years as a systems engineer for Nuventix, Inc. in Austin, TX, where he developed electromagnetic transducers and acoustically-driven air jets used for electronics cooling known as synthetic jets. In 2014 he became a Licensed Professional Engineer registered to practice in the State of Texas. He is currently a postdoctoral fellow with the Applied Physics Laboratory at the University of Washington.

Maria M. Karzova received the M.S. degree in physics from Lomonosov Moscow State University (MSU), Moscow, Russia, in 2012, and the Ph.D. degree in acoustics from the École Centrale de Lyon (ECL), Écully, France, in 2016, according to the double Ph.D. Program of the French Government.

After her graduation from the Ph.D. Program, she was appointed by Lomonosov Moscow State University, where she is currently a Senior Researcher with the Department of General Physics and Condensed Matter Physics, Physics Faculty. She was with the Department of Fluid Mechanics, Acoustics, and Energetics, ECL, with a focus on irregular reflection of N-waves from smooth and rough surfaces. Her research interests are in nonlinear acoustics, therapeutic ultrasound, and optical methods for measuring acoustical pressure waveforms in air.

Petr V. Yuldashev received the M.S. degree in physics from Lomonosov Moscow State University (MSU), Moscow, Russia, in 2008, and the Ph.D. degree in acoustics from the École Centrale de Lyon (ECL), Écully, France, in 2011, according to the double Ph.D. Program of the French Government.

After his graduation from the Ph.D. Program, he was appointed by Lomonosov Moscow State University, where he is currently an Associate Professor with the Department of General Physics and Condensed Matter Physics, Physics Faculty. He was with the Department of Fluid Mechanics, Acoustics, and Energetics, ECL, with a focus on the propagation of shock waves in a turbulent atmosphere and the utilization of nonlinear acoustics effects to calibrate high-frequency broadband microphones. His research interests pertain to simulation of nonlinear wave propagation in inhomogeneous media, shock wave focusing, sonic booms, and shadowgraphy measurement methods for acoustic phenomena.

Azamat Z. Kaloev received the B.S. degree in physics in 2021 from Moscow State University (MSU), Moscow, Russia. He is currently pursuing the M.S. degree in quantum physics at Institut Polytechnique, Palaiseau, France. His research interests are high-intensity focused ultrasound (HIFU) in therapy and noninvasive surgery, acoustic holography, quantum cryptology and quantum communication.

Fedor A. Nartov received the B.S. degree in physics in 2022 from Lomonosov Moscow State University (MSU), Moscow, Russia. He is currently pursuing the M.S. degree at the Department of Acoustics, Physics Faculty, MSU.

His research interests are high-intensity focused ultrasound (HIFU) in therapy and noninvasive surgery and numerical modeling in acoustics.

Vera A. Khokhlova received the M.S. degree in physics and the Ph.D. and D.Sc. degrees in acoustics from Lomonosov Moscow State University (MSU), Moscow, Russia, in 1986, 1991, and 2012, respectively.

After her graduation from the Ph.D. Program, she was appointed by Lomonosov Moscow State University, where she is currently an Associate Professor with the Department of Acoustics, Physics Faculty. Since 1995, she has been with the Center for Industrial and Medical Ultrasound, Applied Physics Laboratory (APL), University of Washington, Seattle, WA, USA. Her research interests are in the field of nonlinear acoustics, therapeutic ultrasound including metrology and bioeffects of high intensity focused ultrasound fields, shock wave focusing, nonlinear wave propagation in inhomogeneous media, and nonlinear modeling.

Bryan W. Cunitz has been working in the field of Ultrasound for over 22 years. His academic background includes an undergraduate degree in both Physics and Electrical Engineering and a Master’s degree in Electrical Engineering specializing in signal processing and system integration. He has worked exclusively in ultrasound for the past 16 years both for the CIMU group at the Applied Physics Lab as well as a French Ultrasound company SuperSonic Imagine. During this time his experience has included: developing methods of characterizing acoustic outputs of diagnostic and therapeutic ultrasound transducers, developing a software based single channel vector-Doppler ultrasound system to analyze internal bleeding blood flow, developed an image guided HIFU system for acoustic hemostasis research, and developed many customized acoustic output characterization tools for unique therapy transducers. Since 2009, his work has primarily been focused on both imaging and therapeutic applications of ultrasound for kidney stones. This works includes the development and testing of the ultrasonic propulsion system, optimizations of ultrasound imaging for enhanced detection and sizing of kidney stones, development of amplifier hardware for BWL, and specialized imaging sequences for BWL for monitoring treatment efficacy and safety real-time. Most recently he has worked on projects involving high-frequency imaging systems as well as very high channel count (>1024 channels) real-time ultrasound systems.

Kyle P. Morrison (Member, IEEE) received the B.S. degree in manufacturing engineering from Western Washington University, Bellingham, WA, USA, in 2003, and the M.S. degree in medical engineering from the University of Washington, Seattle, WA, USA, in 2012.

He is currently the President of Sonic Concepts, Inc., Bothell, WA, USA, where he leads its multidisciplinary engineering teams that develop premium ultrasonic transducers and systems for preclinical and clinical applications.

Tatiana D. Khokhlova (Member, IEEE) received her Ph.D. degree in physics from Moscow State University (MSU), Moscow, Russia, in 2008.

After graduation from the Ph.D. program, she moved to the University of Washington (UW), Seattle, WA, USA, for postdoctoral training at the Applied Physics Laboratory. She is currently an Associate Professor of Research with the Department of Medicine, UW. Her research interests are in physical acoustics, cavitation-based therapeutic ultrasound applications and ultrasound imaging methods for therapy guidance.