Assessing diagnostic and screening tests

Diagnosis, the first step in clinical management, is a powerful determinant of the interventions and health care resources physicians use. Diagnosis involves interpreting the history, clinical observations, laboratory test results, or imaging studies—all of which are “tests” undertaken to help physicians refine their estimate of the probability that a patient has a particular condition.

Diagnosis is rarely definitive: clinicians often implicitly measure diagnostic uncertainty with the use of terms like certain, probably, possibly, and unlikely and thereby estimate the probability of the presence of a condition. The degree of certainty required for a particular diagnosis in a particular patient depends on the possible risks and benefits of therapy and the patient's preferences about testing and treatment. A physician might well be prepared to try a bronchodilator in a child in whom there was an 80% chance her symptoms were due to asthma, but the physician would want to be close to 100% certain of a diagnosis of leukemia before starting cytotoxic therapy.

Summary points

• Diagnosis does not imply certainty but carries an implicit probability

• All diagnostic test results may sometimes be wrong

• The value of a test for predicting a condition depends on pretest probability (underlying probability of that condition) and test performance (measured by the likelihood ratio or sensitivity and specificity)

WHEN IS A TEST WORTH DOING?

It is easier for a physician to determine whether more good than harm will come from therapy if the probabilities that disease is present, the therapy will be beneficial, and adverse effects will occur are made explicit. Testing is worthwhile only if it will change management or provide clinically important information about a patient's prognosis. Clinicians often intuitively decide when testing is worthwhile (see example 1).

Example 1 The ongoing measurement of oxygen saturation in a pink baby with no respiratory tract symptoms (probability of hypoxia nearly 0%) will add nothing to management because a low saturation value is more likely to be monitor error than real. Likewise, if the saturation monitor reads “100%” in an acutely cyanotic patient, measurement error should be assumed and the decision to cancel oxygen treatment obviated. For patients whose condition is unstable, or those in respiratory distress who are not obviously cyanotic, oxygen saturation monitoring can be useful.

In Example 1, clinicians have implicitly defined a group of patients at intermediate risk, for whom the result of the test is likely to change clinical management. Thresholds on either side of this group of patients have been defined: a test:treat threshold, above which a patient would be given treatment without testing and below which testing should be done, and a test:no-test threshold, above which the patient should be tested and below which the patient should not.¹ The action threshold is in the middle range, representing the point at which the harm caused by giving oxygen to patients who are not hypoxic is equivalent to the harm of not giving oxygen to those who are.

WHAT DETERMINES WHETHER A TEST WILL CHANGE A PHYSICIAN'S ACTION?

A test will be useful if the test results move the patient across the action threshold. The likelihood that a particular test finding will move a particular patient across the action threshold depends on 2 important factors:

• The estimated probability of disease in a patient before a test is done (pretest or “prior” probability) Pretest probability can be estimated by using clinical skills and the knowledge of disease frequency in similar populations (gained from studies of groups of similar patients).

• How well the results of the test separate those with disease from those without it (expressed as likelihood ratios or sensitivity and specificity)

Test performance is measured by an unbiased comparison of the test result against a gold standard (also called a reference or criterion standard) for the diagnosis. The sensitivity of a test is the proportion of diseased patients who have a positive test result—that is, it measures how well the test correctly labels people who actually have the condition. The specificity is the proportion of nondiseased patients who have a negative test result—that is, it measures how well the test is correctly labels people who do not have the condition. Calculations are shown in tables 1 and 2 using the numbers from example 2.

Table 1.

Calculating sensitivity and specificity and likelihood ratio (LR) of a diagnostic test in 81 patients^*

	Echocardiographic finding
Clinical examination finding	Heart defect, no.	No heart defect, no.	Total patients, no.
Murmur	18 (a)	3 (b)	21
No murmur	16 (c)	44 (d)	60
Total	34	47	81

^*Calculated as follows:

Sensitivity = a/(a + c) → 18/34 = 53%

Specificity = d/b + d) → 44/47 = 94%

LR = [a/(a + c)]/[b/(b + d)] → 53%/6% = 8.8

Table 2.

Calculating probability of heart defect in a hypothetical group of 10,000 normal babies, using known sensitivity and specificity of clinical examination as a test

	Reference standard: echocardiography
Test: clinical examination	Major defect, no.	No major defect, no.	Total patients, no.
Positive result	19	638	656
Negative result	16	9,327	9,344
Total	35	9,965	10,000

Example 2 About 3.5/1,000 apparently healthy full-term babies have major congenital heart disease,² and you want to know whether clinical examination of an apparently healthy newborn can detect this condition. The only study you find is done in a regionally representative group of newborns with Down syndrome.³ All infants had a clinical examination (the “test”) and all, whether or not they had a murmur, also had echocardiography (the “gold standard”). Of the 34 infants with major cardiac defects, 18 had a murmur on clinical examination (53% sensitivity), and of the 47 infants who did not have cardiac defects, 44 had no murmur (94% specificity). Assuming that clinical examination (the test) works the same way in infants without Down syndrome, you apply the pretest probability, sensitivity, and specificity of the test to a hypothetical group of 10,000 apparently healthy babies. Of the 35 babies in this hypothetical group with major cardiac defects, 19 will have a heart murmur, and of the 9,965 normal babies, 9,327 will not have a murmur. However, 638 will have a murmur but no heart disease. The result is that for every “true-positive” heart murmur, there are about 35 “false-positives.”

Likelihood ratios

Interpretation of the test result depends greatly on how likely it is that the disease was present in the first place. In fact, using a positive predictive value (the probability that a disease is present, given a positive test result) is risky; it actually applies only to a patient or group with the same pretest probability as the one that was studied. Sensitivity and specificity are generally similar across groups and are less dependent on prevalence. However, using sensitivity and specificity by calculating hypothetical 2 × 2 tables for every situation is more work than anyone needs. Instead, the probability that a particular test result will occur in patients with disease can be compared with the probability that the same test result will occur in patients without the disease. In the case cited in Example 2, 53% of patients with heart defects and 6% of patients without heart defects have a murmur, so the ratio is calculated as: 53%/6% = 8.8. This ratio (called the likelihood ratio [LR]) reflects the performance of the test. In fact, the pretest odds that the disease is present can actually be multiplied times the LR to get the post-test odds. Note that these are “odds,” not probability. The conversion is simple but not intuitively obvious: odds = probability/1 - probability, and probability = odds/1 + odds.

SIMPLE WAYS TO USE LR

For those who wish to avoid converting odds, Fagan developed a nomogram (figure).⁴ In this nomogram, a straight line drawn from a patient's pretest probability of disease (which is estimated from experience, local data, or published literature) through the LR for the test result that may be used will point to the post-test probability. The farther an LR is above or below 1.0, the better the test separates patients with from those without the disease. For tests with only 2 possible results (positive and negative), the LR can be quickly calculated from the sensitivity and specificity:

Likelihood ratio for a positive test = sensitivity/1 - specificity

Likelihood ratio for a negative test = 1 - sensitivity/specificity

Many clinical and laboratory tests do not have a single cutoff value, or a simple “positive” or “negative” result, but rather give a range of values. Clinical experience and common sense tell us that the more abnormal a test result, the more likely that it reflects actual disease than a test result that is mildly abnormal. Using the data in strata, rather than a series of cutoff values for positive versus negative, is more efficient use of the information that investigators have provided. The LR for each level of the test result is the ratio of the proportion of patients with the disease who had that particular test result to the proportion of those without the disease who had that same test result. The pretest probability (again, derived from clinical experience with similar patients, from local data about the group, or from the literature) can be converted to the post-test probability using the LR and the LR nomogram.

The sensitivities, specificities, and LRs found in the literature are estimated from patient samples, so they are not exact. For each one, a 95% confidence interval—representing the range of values within which the true value is likely to be found—can be calculated. If confidence intervals are not provided by the authors, they can be calculated. Physicians should be aware that the smaller the study, the wider the confidence intervals, and the less precise are the estimated values of sensitivity, specificity, and LRs.

Example 3 You are examining a patient with abdominal pain, who in your clinical judgment has about a 10% chance of having appendicitis. The white blood cell (WBC) count comes back 13.0 × 10⁹/L (13,000/dL), and your student asks you what the cutoff value is for WBC count in appendicitis. You wonder if using a single cutoff value makes sense. Logically, the higher the WBC count, the more likely it is that the patient has appendicitis (Andersson et al found this to be true in their investigation⁵). Using a WBC count of 12.0 × 10⁹/L (12,000/dL) as a cutoff value, the LR for appendicitis if the patient has a WBC count of 13.0 × 10⁹/L is 3.8 (table 3). Using the nomogram shows that with a 10% pretest probability of appendicitis being present, this test result would raise that probability to about 30%. However, when the same data are arranged in a strata of increasing WBC counts, the LR for this WBC count is much higher, at 7.0, so that the post-test probability is 45%. The same phenomenon exists for the negative end of the test: if the patient's WBC count is 7.5 × 10⁹/L (7,500/dL), and a single cutoff value of 12.0 × 10⁹/L is used for an abnormal test result, then the post-test probability is 5%; if the LRs from the stratified data are used, the post-test probability is down to 2% (table 4).

Table 3.

Calculating likelihood ratio (LR) for appendicitis with a cutoff value of white blood cell (WBC) counts of 12 × 10⁹/L (12,000/dL)^*

WBC count, × 109/L	Appendicitis present, no.†	Appendicitis not present, no.†	LR
>12	113	46	3.8
≤12	77	251	0.5
Total	190	297

^*From Andersson et al.⁵

^†Values are number of patients.

Table 4.

Calculating likelihood ratio (LR) for appendicitis with increasing white blood cell (WBC) counts^*

WBC count, × 109/L	Appendicitis present no.†	Appendicitis not present, no.†	LR
≤15	63	14	7.0
12-<15	50	32	2.4
10-<12	35	49	1.1
8-<10	26	49	0.8
<8	16	153	0.2
Total tested	190	297

^*From Andersson et al.⁵

^†Values are number of patients.

CHANGING THE CUTOFF VALUE FOR A POSITIVE TEST RESULT

Some situations will demand that a single cutoff value be chosen for a test. For example, for a screening test, any value above or below a certain cutoff level might trigger further investigation. Regardless of which cutoff value is chosen, there will be false-positive and false-negative results; as the sensitivity increases, specificity is lost, and vice versa. The choice of a particular cutoff value depends on how the test result will be used—to rule out disease, to rule in disease, or to screen the population. Some useful mnemonics have been developed to help with this.

Useful tips: “SpPIn, SnNOut”

Choosing among tests with different properties or choosing the cutoff value for a single test depends on the purpose of getting the test result and may seem counterintuitive. When the objective is to rule out a disease, the test with the fewest false-negative results should be chosen. Because sensitivity is the proportion of people with disease who have a positive test result, a test with high sensitivity has the fewest false-negatives. Because nearly all diseased patients have a positive test result, few diseased patients have a negative test result (few false-negatives). On the other hand, when the objective is to confirm a diagnosis, the physician should choose the test with the fewest false-positives; that is, a test with high specificity. A simple way of remembering the effect of different properties of tests is to use the mnemonics “SpPIn” and “SnNOut.” If a highly Specific test is used, a Positive result rules In the diagnosis; hence, the mnemonic SpPIn. On the other hand, if a highly Sensitive test is used, a Negative result rules Out the diagnosis: SnNOut.

SCREENING

Screening, as defined by the 1998 UK National Screening Committee,⁶ is “The systematic application of a test, or inquiry, to identify individuals at sufficient risk of a specific disorder to warrant further investigation or direct preventive action, amongst persons who have not sought medical attention on account of symptoms of that disorder.”

Although the dividing line between case finding in clinical practice and screening is arbitrary, the key difference is an ethical one. In clinical practice, patients approach professionals and ask for help, whereas in screening programs, professionals actively encourage people to undergo a procedure on the basis that they will benefit. Clinicians have a responsibility to do the best for their patients within the limits of knowledge. For screening programs, the benefits of the program (including effective treatment) need to clearly outweigh the potential harms.

A particular problem faced in screening is that it often involves uncommon disorders (ie, the pretest probability of disease is low). To avoid missing cases requires a highly sensitive test. However, when the cutoff value is set to maximize sensitivity, the trade-off is a loss of specificity. In this situation, diagnostic facilities are in danger of being swamped by patients labeled as having a positive result on a screening test who do not have the condition of interest. There is also evidence that some families suffer long-term problems when their children “fail” screening tests but are subsequently found not to have the condition.⁷ A careful approach is required in the way results of screening tests are given to parents and in subsequent confirmatory testing. The overall assessment of the possible costs and benefits of any screening program includes an assessment of the potential for harm.

The approach to the evaluation of tests or clinical observations outlined earlier is the same for screening tests. However, the performance of screening tests should not be considered in isolation from other aspects of the screening program, including the effectiveness of the interventions and the availability of facilities for diagnosis and treatment.

CONCLUSIONS

A test should be used only if it is likely to change what is done to patients. This depends on the action threshold—the probability that a disease is present for which an intervention would be offered because it would do more good than harm—patients' pretest probability of disease, and the test performance (measured by LRs or sensitivity and specificity). For all tests, there is an inverse relationship between sensitivity and specificity. The decision to introduce a screening program depends on the availability of appropriate screening and diagnostic tests and their cost, the prevalence and prognosis of the condition, the availability of effective treatment, and the potential for testing to cause harm.

Figure 1.

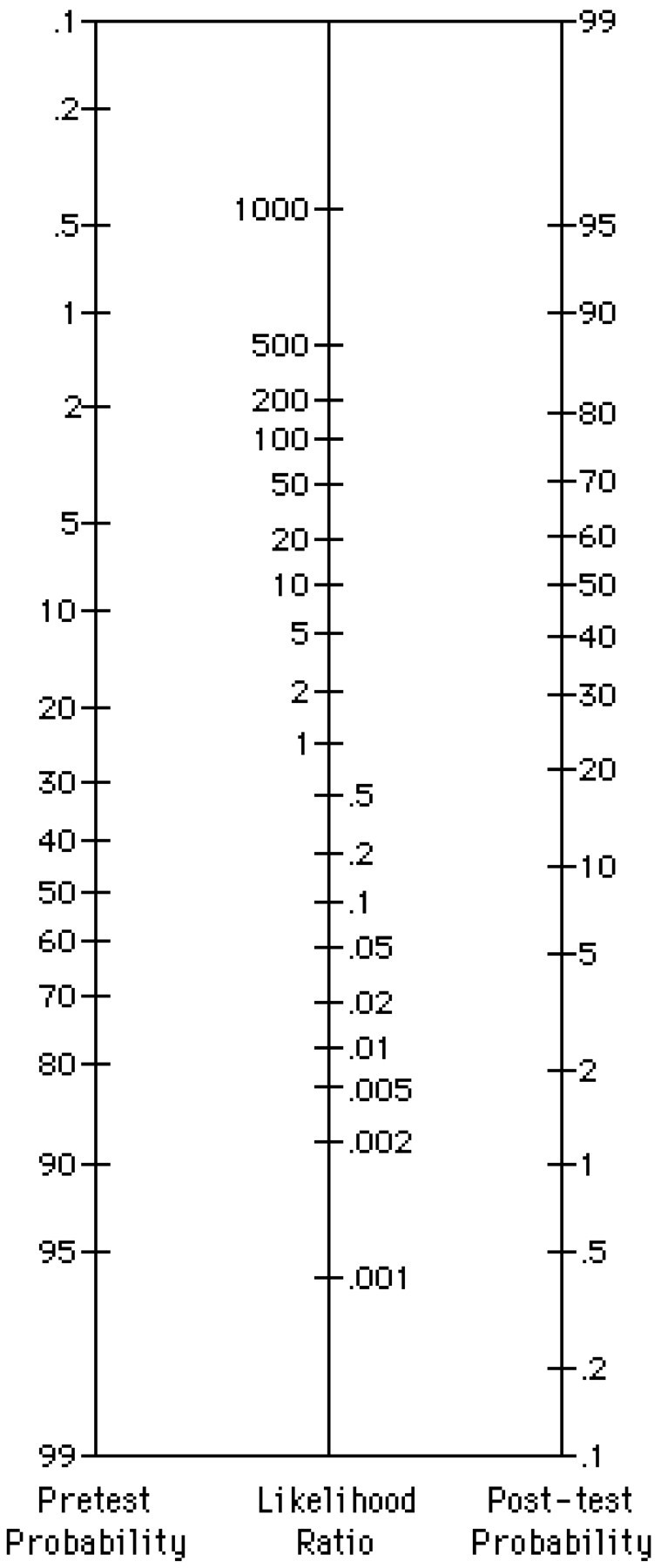
The likelihood ratio nomogram (adapted from Fagan⁴)

Figure 2.

The higher the white blood cell count, the more likely it is that a patient has appendicitis