Quantum Capacitance of Two-Dimensional-Material-Based Supercapacitor Electrodes

Abstract

Electrochemical energy storage technology has emerged as one of the most viable solutions to tackle the challenge of fossil-fuel-based technology and associated global pollution. Supercapacitors are widely used for high-power applications, and there is tremendous ongoing effort to make them useful for high-energy storage applications. While electrode materials of supercapacitors play a central role in charge storage performance, insights into the contribution from different charge storage mechanisms are crucial from both fundamental and applied aspects. In this context, apart from the electric double layer and fast redox reaction at/near the surface, another pronounced contribution from the electrode is quantum capacitance (C_Q). Here, the origin of C_Q, how it contributes to the total capacitance, the possible strategies to improve it, and the state-of-art C_Q of electrode materials, including carbon, two-dimensional materials, and their composites, are discussed. Although most of the studies on quantifying C_Q are theoretical, some case studies on experimental measurements using standard electrochemical techniques are summarized. With an overview and critical analysis of theoretical studies on quantum capacitance of electrode materials, this review critically examines the supercapacitor design strategies, including choosing the right materials and electrolytes. These insights are also relevant to other types of clean energy storage technologies, including metal-ion capacitors and batteries.

1. Introduction

A supercapacitor (SC, also commonly termed as an electrochemical capacitor) is one of the rapidly emerging electrochemical energy storage devices for diverse clean energy technologies. Indeed, it can store a charge around 10–100 times higher than the conventional dielectric capacitor and is well-known for its superiority in high-power applications over conventional batteries.¹ In terms of energy and power densities, a supercapacitor delivers a higher (lower) energy density than the conventional capacitor (battery) and has a higher power density and cycle life than the battery (Table 1).² The reason behind the effective usage of SC in power applications is the excellent power density and prolonged life cycle. This makes SC a popular candidate in applications, such as hybrid electric vehicles, grid stabilization systems, forklifts, load cranes, aerospace equipment, etc. The global challenge of SCs is to enhance the energy density to compete with established battery technologies.

Table 1. Comparison Table of Supercapacitors, Conventional Capacitors, Metal-Ion Batteries, Metal-Ion Capacitors, and Redox Flow Batteries³⁻⁶.

	supercapacitor	capacitor	Li-ion battery	Li-ion capacitor	redox flow batteries
storage mechanism	physical	physical	chemical	chemical and physical	chemical
operating voltage (V)	1.0–3.2	4–630	2.5–4.3	2.2–3.8	1.0–2.1
energy density (Wh/kg)	2.5–15	<0.1	75–250	10–100	<10–70
power density (W/kg)	500–10000	>1000000	150–315	300–5000	10–100
cycle life	>105	>106	103–104	104–106	>103
operating temperature (°C)	from −40 to 70	from −20 to 100	from −20 to 60	from −25 to 85	from 0 to 60
efficiency (%)	95	99	85–90	90	60–85
self-discharge	very high	very high	very low	low	low
safety	good	good	needs improvement	good	low
voltage monitoring	not required	not required	needed	needed

Like other electrochemical energy storage devices, SCs mainly consist of electrode materials and electrolytes. Thus, one can easily identify that the electrode materials are one of the keys to enhance the energy density of the device (E) via the relation E = 1/2CV², where C is the specific capacitance and V is the voltage of the device. There are two types of energy storage mechanisms in SCs: one is storing the charge via double-layer formation at the electrode/electrolyte interface, and the other mechanism is based on the rapid redox reactions at the surface or near-surface. The former mechanism is known as the electric double-layer capacitance (EDLC), whereas the latter mechanism is called the pseudocapacitance. Among them, the pseudocapacitor can store 10–100 times higher charge than the electric double-layer (EDL) capacitor, whereas the latter features excellent electrochemical stability, rate performances, and better charge-transfer kinetics.

In the case of the EDLC mechanism, the specific (or areal) capacitance (C_dl) is related to the surface area (A) of active materials as

1

where ε₀ = 8.85 × 10^–12 F/m, ε is the dielectric constant of the electrolyte, A is the surface area, and d is the radius of the counterions. It can be seen from Figure 1 that the gravimetric capacitance of porous carbon increases with the surface area, and unfortunately, the areal capacitance shows the opposite trend.⁷ Apart from the gravimetric capacitance, the high areal and volumetric capacitances make it highly desirable to use the SC for high-power applications over a small footprint area. Importantly, considering the surface area of 1500 m²/g, C_dl should be 30–70 μF/cm² depending upon the choice of electrolyte. However, the areal capacitance obtained with porous carbon was only 4–5 μF/cm².⁷ Furthermore, graphene, with a theoretical surface area of 2600 m²/g, showed the areal (gravimetric) capacitance of 13.5 μF/cm² (355 F/g),⁷ and activated microwave-expanded graphite oxide with a surface area of 3100 m²/g exhibited the areal (gravimetric) capacitance of 6 μF/cm² (200 F/g) in an aqueous electrolyte.⁸ Although predicted, the gravimetric capacitance of graphene of around 550 F/g has not been achieved thus far. These observations certainly ensured that increasing the surface area is not the only solution for enhancing the specific capacitance. Moreover, the higher surface area reduces the volumetric capacitance of the supercapacitor electrodes.

Figure 1.

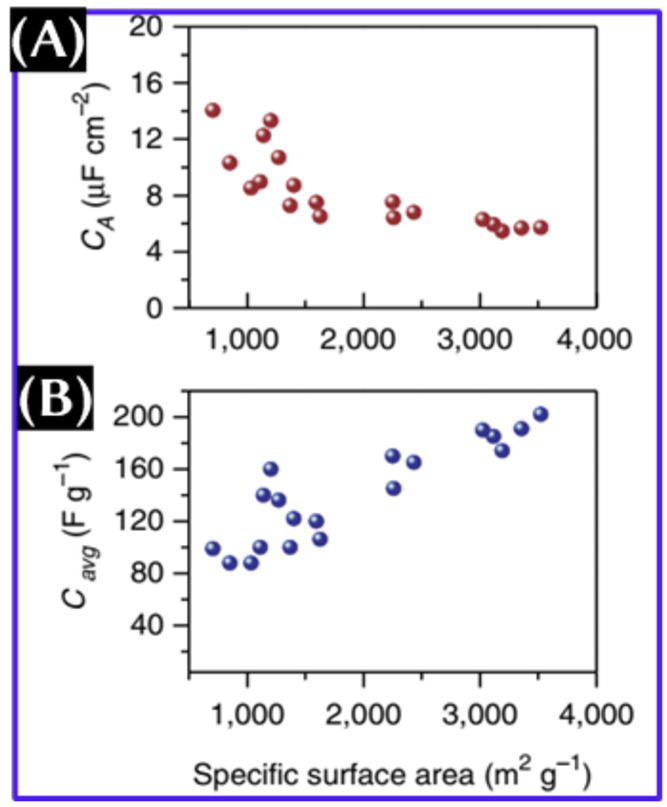
Areal capacitance (orange) and gravimetric capacitance (blue) of porous carbon with respect to the specific surface area. This figure was reproduced with permission from ref (7). Copyright 2014 Springer Nature, Limited.

The lower values of capacitance and energy density of carbon-based materials are due to the low packing density, chemical inertness, hydrophobicity in aqueous electrolyte, and low density of states (DOS).^9,10 To enhance the storage performance, the common strategies are doping or functionalizing,⁹ introducing defects,¹¹ and designing heterostructures with pseudocapacitive material (metal-based materials, conducting polymers, etc.).¹² In all cases, one can see that the major changes in the pristine structure are surface area modification and micro-, macro-, and mesopore optimization for the effective electrolyte ionic accessibility to the entire surface of an electrode, improvement in electrical conductivity and/or structure for better charge-transfer kinetics, changes in wettability to improve the electrode/electrolyte interaction, etc. To explore the phenomena at the surface in dynamic conditions (during charging/discharging), major attention is given to the in situ investigations by Raman spectroscopy, X-ray diffraction techniques, microscopic techniques, etc. These investigations provide a wealth of information to understand the charge storage mechanisms and help improve the electrode material structure, morphology, and property by means of standard synthesis and/or post-synthesis methods, to choose the appropriate electrolyte or the electrolyte modification, etc. Besides the changes in the structural, morphological, and other intrinsic properties of pristine materials by the above-mentioned methods, electronic DOS is also affected. While functional groups or dopants and heterostructures mostly contribute via pseudocapacitance, the changes in the DOS of electrode material are responsible to contribute to quantum capacitance (C_Q). While modifying the carbon structures with the above-mentioned methods, one can notice that the modified structure can provide a higher surface charge density and higher C_Q in either positive or negative bias. This fact is quite important to decide whether the electrode can be used for a symmetric supercapacitor or an asymmetric supercapacitor.

Besides carbon-based materials, such as MXene, and transition metal chalcogenides also provide quantum capacitance that can be increased further by modifying the structure. The physical properties of carbon and two-dimensional (2D) material electrode are summarized in Table 2. However, modification does not always enhance the quantum capacitance of the final structures, and one needs to pay attention to the structural stability as well. Some other factors, like doping and defect concentration, number of layers, and curvatures, also have a significant impact on the quantum capacitance. It has also been seen from the simulation results that quantum capacitance also depends upon the type of electrolyte ions and the temperature.¹³⁻¹⁷ Hence, a proper combination of pristine electrode materials, heteroatoms, defects, and types of electrolyte ions is necessary to obtain the best quantum capacitance value and, hence, the total capacitance, energy/power density, and other key parameters of SCs.

Table 2. Comparison of Physical Properties of Carbon and 2D Materials.

material	element and hybridization	surface area (m2/g)	electrical properties or electrical conductivity	normalized capacitance of the supercapacitor
porous carbon7	carbon with all hybridization	∼3500 (maximum)	10–2–103 S/cm	4–5 μF/cm2
graphene	sp2-bonded carbon	2600 (theoretical)	∼108 S/cm	13.5 μF/cm2 (355 F/g);7 300 F/cm3 18
graphyne	sp–sp2-bonded carbon	5510 (theoretical)19
carbyne	sp carbon	13000 for H2	tunable depending upon the bonding
transition metal dichalcogenides	MX2, a layer of transition metals (Mo, W, Ta, etc.) sandwiched between two layers of chalcogens (S, Se, and Te)	up to ∼200 depending upon morphology	semimetal or semiconducting	400–700 F/cm3 20
MXene	Mn+1XnTx; 2D metal carbide/nitride, where M is a metal, X is C and N, and T is a functional group (e.g., O, F, OH, and Cl)	up to around 200 depending upon morphology21	metallic or semiconducting	1500 F/cm3 or 380 F/g22

2. Scope and Structure

There is plenty of theoretical research based on density functional theory (DFT), first-principles calculations, etc. to understand the importance of C_Q and how it can be tailored. Indeed, there are some experimental attempts to evaluate C_Q using the standard electrochemical characterization approach. However, there is no exhaustive coverage on this specific topic of quantum capacitance of supercapacitor electrodes, except the partial discussion in ref (23). This review is intended to serve as a supplement to the many comprehensive theoretical results and discussions of the most recent results dealing with the quantum capacitance of the supercapacitor electrode (Figure 2). To provide insights and updates on this topic, the key considerations are summarized as follows:

• This review is based on the theoretical or simulation results published in the cited articles. Thus, we are encouraging authors to read the cited references for the detailed simulation methods. Indeed, we summarized the outcome of the theoretical results with critical analysis and discussed the experimental feasibility of the proposed results based on the simulations.

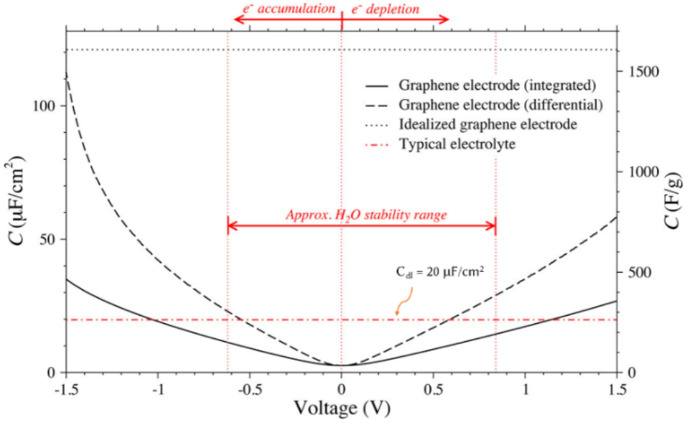
• On the basis of the literature review, the cited theoretical article reports either the integrated quantum capacitance or differential quantum capacitance based on the method used. For example, the integrated capacitance is derived for continuum capacitance modeling, and differential capacitance is for first-principal calculations.²⁴ Experimentally, integrated or differential capacitance can be obtained from cyclic voltammetry and galvanostatic measurements, whereas differential capacitance can be obtained from impedance spectroscopy. There is certainly a difference between the value obtained for the integrated and differential C_Q of the electrode, as shown in Figure 3.²⁴ For the sake of simplicity, we mentioned the maximum C_Q of electrode materials obtained using the theoretical simulations for all references cited.

• In all reports, DOS calculation has been carried in the range from −0.6 to +0.6 V for aqueous electrolytes and from (≤)–1.2 to (≥)1.2 V for ionic/organic electrolytes (Figure 3). This fact can be identified from the potential window (V) used in the C_Q–V plot.

Figure 2.

Scope and structure of this review.

Figure 3.

Integrated (solid black line) and differential (dashed black line) quantum capacitances and double-layer capacitance (red dashed line) for pristine graphene. The calculation is based on the fixed-band approximation. Aqueous electrolytes can be operated within the H₂O stability range, whereas a wider window is used for organic/ionic electrolytes. This figure was reproduced with permission from ref (24). Copyright 2013 American Chemical Society.

In the present review, section 3 provides a detailed conceptual background of quantum capacitance. Sections 4–7 discuss the quantum capacitance of various electrode materials based on carbon, 2D materials, and their heterostructures and the possible strategies to enhance it further. The 2D-material-based supercapacitor electrodes are under investigation as a result of their high surface area, rapid charge/discharge capabilities, excellent electrical conductivity, tailorable properties, and potential for flexible and environmentally sustainable energy storage solutions, driving innovation in energy storage technologies. In sections 8 and 9, one can see the dependency of C_Q upon the temperature and electrolyte used, respectively. While discussing the quantum capacitance of the supercapacitor electrode materials, we also shed light on the experimental viewpoints or the experimental feasibility of the theoretically predicted strategies to enhance C_Q. Section 10 deals with the experimental approach to measure C_Q of the electrode using standard electrochemical characterization. Finally, the challenges and outlook are discussed in section 11.

3. Quantum Capacitance (C_Q)

To explore the concept of quantum capacitance, let us consider the parallel-plate capacitor consisting of 2D metal (graphene, in this case) and normal metal electrodes separated by insulating materials, as shown in Figure 4A.²⁵ The difference in electrochemical potential (V) can be expressed as eV = eφ + μ, where φ is the potential drop between the electrodes and μ is the chemical potential. Upon differentiation of the above equation with respect to the carrier concentration

2

and

3

where C_EE is the capacitance as a result of the electrode/electrolyte interaction, n is the carrier concentration, and dn/dμ is the thermodynamic DOS (Figure 4B). The contribution of C_Q for metal electrodes is negligible, because they have infinite DOS near the Fermi energy level. However, the contribution is significant for the electrode materials only when the magnitudes of C_dl (for Figure 4B, C_EE = C_dl) and C_Q are in a similar order. Because the electrochemical energy storage device is a combination of electrodes and electrolytes (panels B and C of Figure 4), one can easily validate eq 1 that the total capacitance is the combination of capacitance as a result of the electrode/electrolyte interactions (double-layer capacitance and/or pseudocapacitance) and the intrinsic capacitance of the electrode (quantum capacitance). The double-layer capacitance is in series with quantum capacitance, as seen in Figure 4B.

Figure 4.

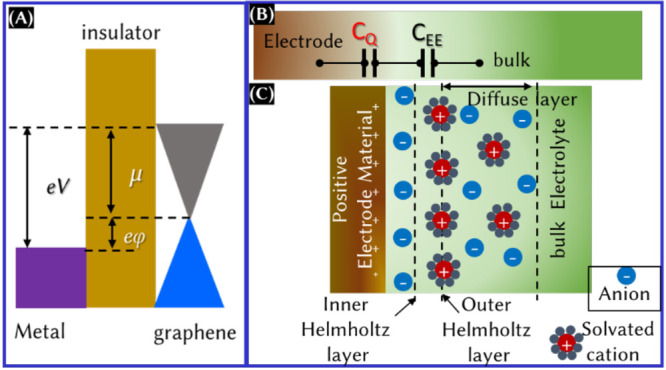
(A) Schematics of metal–insulator–graphene capacitors with a band diagram at a finite bias, (B) schematic of the equivalent circuit with the double-layer capacitance (C_EE) and C_Q, and (C) electric double-layer formation model.

C_Q is an intrinsic property of the materials, which arises from the kinetic, exchange–correlation, and electron–phonon interaction energies in the total energy functional.^26,27 For the graphene–vacuum–graphene capacitor, considering the kinetic term k_BT ≪ eV, C_Q can be expressed as²⁴

4

or because the total energy storage capacity is based on the integrated value over a complete charge–discharge cycle, integral C_Q can be expressed as

5

Thus, one can define the capacitance associated with the DOS as the quantum capacitance. Therefore, increasing the density of states and, hence, quantum capacitance is another solution to increase the total capacitance. It is important to note that C_Q cannot be zero at room temperature and has a minimum positive value at 0 V because there is always thermal broadening of the electron energy distribution.²⁸

4. Carbon-Based Materials

Among the SC electrode materials, the mostly studied and even commercially used materials (e.g., activated carbon) are carbon-based materials.²⁹⁻³¹ The reason behind this is, as the activated carbon stores the charge via a EDLC (a physical mechanism) and, hence, better power density, cycle life, and chemical stability can be obtained, surface morphology and porosity can be tailored. Carbon-based materials offer certain benefits, such as having different dimensionality [from zero-dimensional (0D) to three-dimensional (3D)], and their optical, electrical, mechanical, biocompatible, and other properties can be effectively controlled.^9,32 The main carbon nanostructures discussed in this section are graphene, carbon nanotubes (CNTs), graphyne, etc. Thanks to the unique properties and structure of graphene that are quantified by numerical modeling and simulations, graphene engineering becomes possible. Thus, graphene is adapted as a model structure. Moreover, by rolling, folding, cutting, etc., one can transform graphene into carbon nanotubes, fullerene, and graphene nanoribbons. If CNTs are taken as an example, strain, curvature, and chirality (armchair or zigzag, which define its conducting properties, like metallic or semiconductor) should be considered. Importantly, reduced graphene oxide (RGO) or graphene nanoplatelets (GNPs) cannot be defined as graphene; they are the members of the wider graphene family. Unfortunately, RGO or GNPs are termed as graphene in many works, while we are strict on the definition of graphene, where sp²-bonded carbon is arranged in a single-layer hexagonal honeycomb lattice and without attached functional groups. Because the C_Q value of pristine graphene is limited, it is possible to increase it by adjusting the number of graphene layers,⁷ doping or functionalizing,³³ surface rippling, and causing tensile strain,²⁴ as discussed below.

4.1. Effects of the Number of Graphene Layers and Local Strain

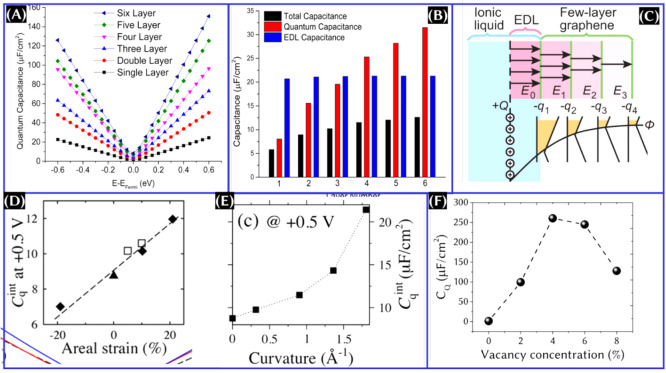
Dependent upon the number of layers, one can categorize them into graphene (one layer only), bilayer graphene, trilayer graphene, few-layer graphene, or multi-layered graphene (number of layers being ≥4). It is well-known that the intrinsic properties of graphene strongly depend upon the number of layers. It is quite interesting, as seen from Figure 5A, that the DOS and, hence, C_Q can be enhanced by increasing the number of layers, and one can reach the saturation value (mostly after four layers), beyond which the enhancement in C_Q is quite negligible. On the basis of the theoretical results, the effect of the graphene layer on C_Q can be realized (Figure 5B), and one needs to pay attention that the number of layers of graphene has an insignificant impact on C_dl.³⁴ While increasing the number of layers, one also needs to consider the screening effect (Figure 5C). As a result, there will be space charge capacitance in series with C_dl and C_Q. When another foreign atom is introduced in the parent matrix, the simulated maximum C_Q for N/P/Ti-doped multi-layered graphene is found to be 158.94 μF/cm² at 0.54 V, which is even higher than that of pristine multi-layered graphene (3.55 μF/cm² at 0 V). This result reflects that dopants or foreign atoms have a significant effect on the enhancement of C_Q. More details are given in sections 4.3 and 4.4. However, it has also been predicted theoretically that co-doped multilayered graphene has a lower C_Q compared to co-doped single-layer graphene (163.19 μF/cm² at positive bias), which is attributed to the interaction of dopants located in the adjacent layers.³⁵ This observation suggests that merely increasing the number of graphene layers of the doped graphene-based structures may not be the most effective way to boost DOS or C_Q.

Figure 5.

(A) Quantum capacitance of graphene with respect to the number of layers in a 1.0 M NaF aqueous electrolyte and (B) C_Q, C_dl, and total areal capacitance of graphene with respect to the number of layers. These panels were reproduced with permission from ref (34). Copyright 2015 American Chemical Society. (C) Schematic of the charge distribution of few-layer graphene in ionic liquid showing the screening effect. This panel was adapted with permission from ref (36). Copyright 2013 Nature Portfolio. Integrated C_Q of graphene at different applied (D) axial strains and (E) curvature. These panels were reproduced with permission from ref (24). Copyright 2013 American Chemical Society. (F) C_Q of graphene with respect to the vacancy defect concentration. Data for panel F are taken from the text of ref (13).

4.2. Strain, Curvature, and Defects in Graphene

Apart from the number of layers, the introduction of local strain (uniaxial or biaxial) and local curvature was also found to be influential in enhancing the quantum capacitance (panels D–E of Figure 5). Curvature, folding, or ripples are quite common in graphene when it is transferred to the desired substrate by standard transfer techniques, and they are common in graphene oxide when prepared, for example, by the Hummers method. Whatever the case, by increasing the number of layers or introducing strains or curvatures, the enhancement of C_Q may not be significant, as seen from panels A and B of Figure 5. Alternatively, the introduction of defects in the structure is promising and more feasible. Integrated C_Q for pristine graphene and graphene with a single vacancy (SV), double vacancy (DV), triple vacancy (TV), and quadruple vacancy (QV) was estimated, using DFT calculations, to be 10.72 μF/cm² at 0.6 V, 107.61 μF/cm² at −0.04 V, 39.16 μF/cm² at 0.6 V, 160.29 μF/cm² at 0.02 V, and 119.6 μF/cm² at −0.06 V, respectively.³⁷ This result reflects that a triple vacancy in graphene leads to the highest C_Q. The defect concentrations for graphene with SV, DV, TV, and QV were 3.12, 6.25, 9.37, and 12.5%, respectively. Eventually, the vacancy defect was found to be more influential (120.72 μF/cm²) compared to the other types of defects, like the Stone–Wales defect (44.38 μF/cm²), where theoretically estimated C_Q of pristine graphene was 21.37 μF/cm².³⁸ It is important to note that modified graphene does not lose its conductivity even after introducing vacancy and Stone–Wales defects.³⁸ The vacancy defect induces p-type behavior as a result of the electron deficiency and, hence, shifts the Fermi level into the valence band. However, there is a trade-off between C_Q and thermodynamic stability of defected graphene,³⁷ which has been tackled by introducing nitrogen in the graphene matrix. The highest integrated C_Q (260.68 μF/cm² at 0.04 V) with the least formation energy (0.25 eV/Å) was found from simulation results for single-vacancy trimerized nitrogen³⁷ to lower the formation energy feasible to synthesize the material experimentally. It can be enhanced further by increasing the defect concentration up to a certain limit (Figure 5F).¹³

If we consider graphene-based materials synthesized at lab- or mass-scale, like graphene foam or vertical graphene nanosheets, for example, this 3D graphene structure unavoidably contains plenty of folded edges, with a local strain developed during the growth, vacancy, and boundary-like defects, and they are the structure with few layers of graphene (specifically, one can find single layer, bilayer, and/or few layers from the graphene-based structure). Indeed, the theoretical study reveals that the presence of edges on the graphene surface is also beneficial to improve the DOS.³⁹ In particular, graphene nanoribbons with zigzag edges were found to have significant enhancement in C_Q, and it increases further with the decrease of the nanoribbon width.³⁹ Thus, one can say that a 3D structure consisting of few-layer graphene could be preferential over its single-layer counterpart, keeping the screening effect in mind. Furthermore, 3D graphene structures also provide plenty of electrochemically active surfaces compared to graphene, where only the top surface interacts with the electrolyte. Practically, both the higher areal and volumetric capacitances of vertical graphene nanosheets have been reported over the planar nanographitic structure.⁴⁰ In this scenario, it is important to understand how the number of layers of graphene with curvatures and strain can be combined with doping or adsorbing foreign atoms to enhance the performance further.

4.3. Functionalization of Graphene

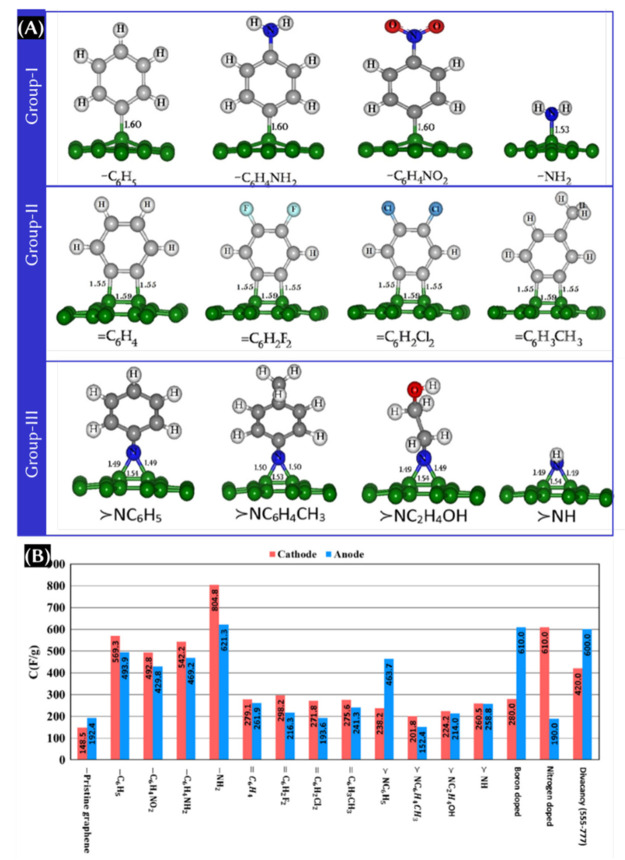
Graphene can be functionalized with various non-covalent aliphatic and aromatic molecules and radicals. The aliphatic group fragments include alkene, alkyne, ketones, amines, amides, nitriles, carboxylic acids, and sulfoxides. The aromatic molecules are benzene, aniline, phenol, anthracene, toluene, and naphthalene.⁴¹ The highest C_Q values obtained for the graphene functionalized with the acetone radical and phenol radical are 235 and 237 μF/cm², respectively.⁴¹ The substituted group is categorized into groups I, II, and III, which is shown in Figure 6A.⁴² On the basis of the result obtained from this study,⁴² group I functionalized material can be used as both positive and negative electrodes, whereas group II and III functionalization is recommended as a negative electrode. Whatever the case, a recent study⁴² reveals that −NH₂-functionalized graphene showed the highest theoretical integrated C_Q (Figure 6B).

Figure 6.

(A) Categories of substituted groups for functionalized grapheneL groups I, II, and III. (B) Theoretical integrated C_Q at the anode and cathode within the H₂O stability voltage range for different functionalized graphene. This figure was reproduced with permission from ref (42) Copyright 2015 Elsevier, Ltd.

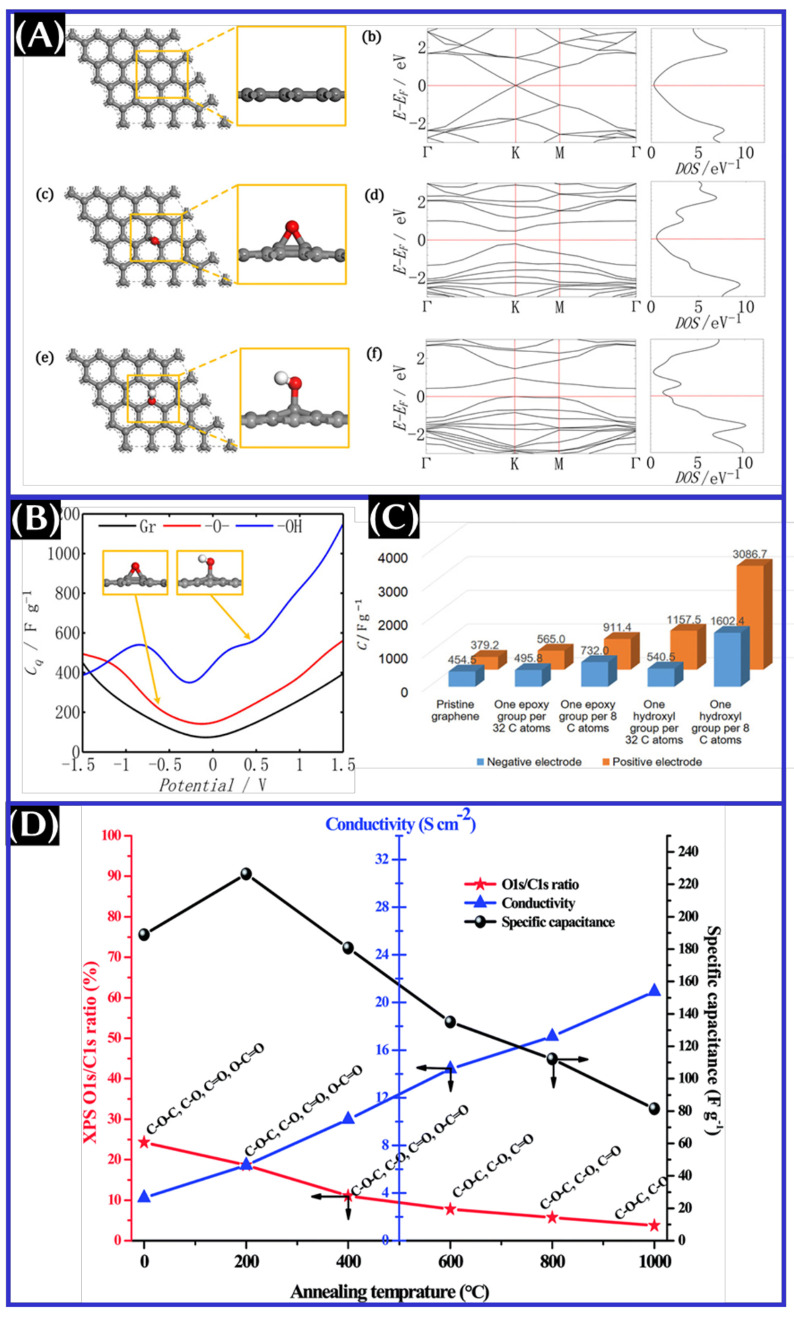
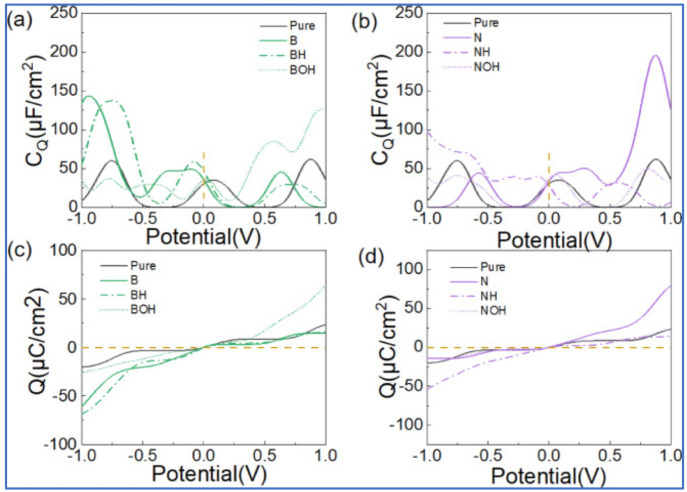
The carbon surface, including most of the nanocarbons, is basically functionalized with physisorbed oxygen-related functional groups. This can be easily identified from the typical X-ray photoelectron spectra.⁴³ However, the bare carbon surface is mostly hydrophobic in nature,¹⁰ except for highly porous amorphous carbon nanofoam prepared by pulsed laser deposition, for example, and this negligible amount of functional group may not have a significant impact on the charge storage contribution. Oxidizing the carbon surfaces enhances the number of electrons transferred to the sp² network and also makes the surface near-hydrophilic or hydrophilic depending upon how the surfaces are activated (chemical activation, plasma functionalization, etc.).^44,45 According to the DFT calculations, the electrochemically oxidized CNT yarn resulted in 0.016 electron transfer (0.001 for pristine CNT yarn) during the interaction with a single water molecule.⁴⁶ On the other hand, graphene oxide (GO), which can be treated as highly oxidized graphene, has received significant attention as a result of its mass production, easy synthesis, low cost, and unavoidably relatively higher amounts of oxygen functional groups.^47,48 The oxygen functional groups that are attached on the edge plane of GO in large quantities are epoxy and hydroxyl, whereas small amounts of carboxyl (−COOH) and carbonyl (C=O) are attached on the basal plane. Among them, the higher hydroxyl group (−C–OH) in the carbon matrix leads to a higher C_Q, as obtained from the simulation result, which is attributed to the enhanced electronic states near the Fermi level (Figure 7A).⁴⁹ Moreover, we emphasize that the −COOH groups on the graphene surface are found to be unstable experimentally with time, and an increase in the −COOH group resulted in lowered total geometric capacitance.⁴⁵ Despite higher gravimetric capacitance obtained experimentally, GO showed degraded performance at a higher discharge rate.⁵⁰ However, the transportation of electrons through the electrodes could be effectively enhanced by removing the functional groups from the surface. In other words, RGO provides better charge-transfer kinetics and conducting pathways for the electrons, but one needs to compromise the total gravimetric capacitance.⁵⁰ Because RGO has very limited epoxy and hydroxyl groups, C_Q is found to be lower than that of GO (panels B and C of Figure 7).⁴⁹ However, in comparison to the GO, graphene nanoribbons, anodic and cathodic electrochemically exfoliated graphene, and liquid-phase exfoliated graphene (95% capacitance retention after 15 000 cycles in most of these cases), it has been seen from the experimental investigation that RGO has poor cyclability (70%) and higher equivalent series resistance after several charge–discharge cycles.⁴⁷ To obtain an overall idea of the differences in properties and performance between GO and RGO, see Figure 7D.

Figure 7.

(A) DFT-optimized structures with corresponding band structures and DOS, (B) plot of quantum capacitance, and (C) capacitance at positive and negative biases of pristine graphene, graphene oxide with an epoxy group, and graphene oxide with a hydroxyl group. These panels were reproduced with permission from ref (49). Copyright 2018 Wiley-VCH Verlag GmbH & Co. KGaA. (D) Plot of physicochemical properties of graphene oxide versus the annealing temperature. This panel was reproduced with permission from ref (50) Copyright 2014 Royal Society of Chemistry.

4.4. Doped Carbon

For oxygen, two configurations can be considered: oxygen functionalization (covered in section 4.3) and in-plane oxygen incorporation in the graphene matrix. The latter case can only be considered as oxygen doping. Indeed, the dopants that received significant attention to tailor the fundamental and charge storage properties of carbons are boron (B), nitrogen (N), phosphorus (P), sulfur (S), halogens (Cl, Br, and F), silicon (Si), etc., with each of them having their advantages and limitations. Hence, we refer to ref (9) for more detailed information on each doped graphene electrode performance. The major advantageous feature of doping includes that it does not add any additional mass and enhances the double-layer capacitances while improving the charge-transfer kinetics.⁹ Because one can tailor the doping concentrations, the number of dopants (co-doping), and the defect level associated with doping, there are multiple options to enhance the quantum capacitance of the electrode in the structures,⁵¹⁻⁵³ which is discussed in the following sections.

How doping can enhance the C_Q value of the final structure can be followed from

6

where n_Q is the dopant-induced carrier density and v_F is the Fermi velocity. As mentioned above, dopants help to improve the stability of the structure while also changing DOS and, hence, C_Q.

4.4.1. Dopant Type

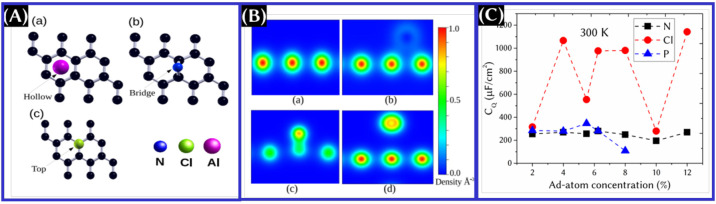
Obviously, each dopant has preferential adsorption sites on the graphene matrix (Figure 8A).¹³ One can also see the electron density associated with pristine and doped graphene in Figure 8B.¹³ Among the dopants, nitrogen is anticipated as the most promising and became more popular as a result of the (i) comparable size and ability to form strong valence bonds with carbon atoms, (ii) N doping being quite simple to manipulate the local electronic structures, and (iii) N–C bond distance being similar to the C–C bond length and, hence, the graphene symmetry being preserved even after N doping.⁵⁴ Eventually, on the basis of the binding energy calculations, N-doped graphene is more stable than defected graphene.⁵⁵ However, although the charge transfer/atom to N from the graphene sheet is 0.5e compared to that of P (0.3e),⁵⁴ DFT calculations showed that P-doped graphene delivered higher C_Q (143.42 μF/cm² at 0.57 V) than S-doped graphene (95.78 μF/cm² at 0.54 V) and N-doped graphene (135.50 μF/cm² at 0.23 V).³⁵ Moreover, P-doped graphene has new states around the Fermi level without any shift⁵⁶ and showed the capability to store the charge at an extended potential window in an aqueous electrolyte.⁵⁷ On the basis of theoretical studies, Cl doping allows for the highest C_Q values to be obtained in comparison to doping with other elements, as evidenced by the maximum charge redistribution on graphene, shown in Figure 8B. This result reveals that the charge redistribution of doped graphene is another key parameter to obtain higher C_Q. Importantly, one must pay attention to the atomic radius of the dopant. The dopant with a larger size than the carbon atom can produce severe stress in the structure, and hence, there will be failure of structural stability of the doped structure.

Figure 8.

(A) Preferred adsorption position of dopants in the graphene matrix. (B) Contour plots for the electron density of pristine and doped graphene. These panels were reproduced with permission from ref (13). Copyright 2019 IOP Publishing, Ltd. (C) C_Q of doped graphene at different doping concentrations. To plot this, data are taken from the text of ref (13).

4.4.2. Doping Concentration

Let us look at the effect of the doping concentration on C_Q of the final structure. At higher doping concentrations, C_Q is found theoretically to be higher for N-doped graphene (Figure 8C) and the structure is found to be more stable.⁵⁸ However, there should be an optimum level of doping concentrations, and it may not have a monotonic relationship (Figure 8C). Beyond this, the doped structure can be unstable, and C_Q was found to be reduced.^13,58 Moreover, at a higher Cl-doping concentration, a stronger interaction of Cl–Cl can take place, leading to the Cl₂ formation with a possibility of desorption from the surface. Noteworthy, the interactions between the layers could also lower C_Q compared to the doping on single-layer graphene, except the Al case among B, N, and P doping.⁵⁴

4.4.3. Doping Configuration

Many configurations exist for the dopants on the parent matrix. Considering nitrogen as a dopant for graphene, the possible configurations are pyridine (N-6), pyrrolic N/pyridone N (N-5), quaternary/graphitic nitrogen (N-Q), oxidized pyridine N (N-X), and nitrogen oxide (N-Ox). It has been predicted that C_Q increases with N-6 and N-Q concentrations and remains constant with the pyrrolic N concentration.⁵⁹ Pyrrolic N has a very small contribution to the total capacitance compared to pristine graphene. For the pyrrolic N case, there is an extra electron from the N atom in the p_z orbital because the N–H bond formation is balanced by the loss of one electron in the delocalized π bond as a result of the associated C vacancy. Among the possible configurations, N-6 shows higher C_Q than N-Q and pyrrolic N.⁵⁹ On the contrary, the maximum C_Q follows the descending order as pyrrolic (195.12 μF/cm² at −0.18 V) > graphitic (123.77 μF/cm² at −0.54 V) > Stone–Wales (110.85 μF/cm² at −0.41 V) > pyridinic (91.39 μF/cm² at 0.6 V) > pristine graphene (22.17 μF/cm² at −0.6 V).^51,60 Surprisingly, the maximum C_Q is found to be increased theoretically to 215.55 μF/cm² at −0.07 V when combined with Stone–Wales defects and 486.32 μF/cm² at 0.2 V at 6.38% concentration of pyrrolic N.⁶⁰ When the stability of the structure is considered, the graphitic structure stands out as a better candidate compared to the pyridinic and pyrrolic structures being the least stable structures.⁶⁰ Thus, the discrepancy between the above reports on the role of pyrrolic N needs further clarification.

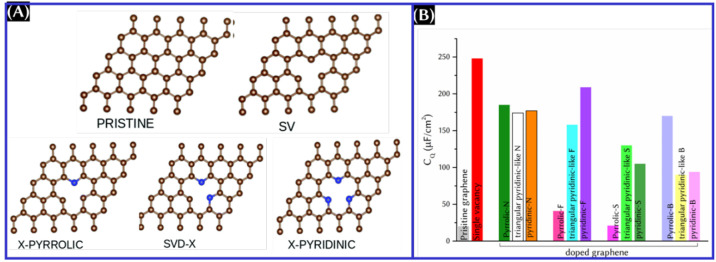
Figure 9 summarizes the simulation result of the dopant configuration-dependent C_Q of doped graphene. Three different configurations for dopants (X = N, F, S, and B) taken into consideration are pyrrolic X, triangular pyridinic-like X doped (SVD-X), and pyridinic X (Figure 9A).⁵¹ From the theoretical comparison, the C_Q value is the highest for a single-vacancy (SV)-defected graphene compared to doped graphene. Among the doping configurations, pyrrolic N and pyrrolic B exhibited the highest C_Q, whereas the highest maximum C_Q is obtained from pyridinic F and SVD-S (Figure 9B). However, more systematic investigations on the configuration dependent upon dopants, such as P, Cl, and Si, on the quantum capacitance is not investigated theoretically thus far to the best of our knowledge via the literature survey and could be a subject of future research.

Figure 9.

(A) Atomic presentation and (B) maximum C_Q of doped graphene with different doping configurations. Panel A was reproduced with permission from ref (51). Copyright 2020 Royal Society of Chemistry. For the plot of panel B, data are taken from the text of ref (51).

4.4.4. Co-doping

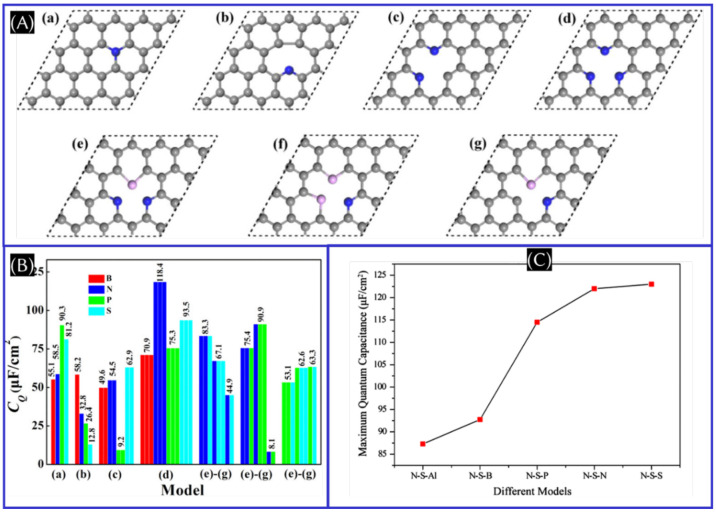
Co-doping is found to be an appealing approach because it provides more stability over single doping with vacancies⁵⁸ and also generated new electronic states near the Fermi level, and as a consequence, there is a significant enhancement in charge accumulation and C_Q.⁶¹ To be specific from the DOS calculations, the new localized states have been seen near Fermi level DOS for pyridine B-doping among single doping with model b [single-vacancy graphene with single pyridine N (B, P, and S) doping], for all doping with model c [single-vacancy graphene with the double N (B, P, and S) doping], except P doping, which has no localized states near the Fermi level, and all doping for the triple B, N, P, and S doping with model d (Figure 10A).⁵⁸ Among the chain model structures (N–N–N, N–N–S, N–S–N, N–S–S, S–N–S, and S–S–S), N–S–S is found theoretically to be the most stable structure and provides the highest C_Q, which ensures that the 1:2 ratio of N/S co-doping is the most optimum ratio (panels B and C of Figure 10).⁶² On the contrary, the DFT calculation suggests that a low S concentration is preferable to achieve the highest C_Q for N/S co-doped graphene.⁵⁵ It has also been reported that the triple N doping with a single vacancy [model d: single-vacancy graphene with the triple N (B, P, and S) doping] performed best at a positive potential and triple S doping with a single vacancy performed best at a negative potential.⁵⁸ One needs to note that the co-dopants occupying the sites near the vacancy are quite stable compared to the occupied sites away from the vacancy.⁵⁸ It has also been theoretically reported in the presence of pyrrolic N that the S dopant tends to dislocate from the graphene plane by approximately 1.32 Å to form the sp³ hybridization, whereas S-embedded pyridinic N-doped graphene retains the sp² hybridization and showed the highest quantum capacitance even at a low S concentration.⁵⁵

Figure 10.

(A) Proposed doping model of graphene: (a) quaternary N (B, P, and S)-doped graphene (model a), (b–d) single-vacancy graphene with the single pyridine N (B, P, and S) doping (model b), double N (B, P, and S) doping (model c), and triple N (B, P, and S) doping (model d), and (e–g) single-vacancy graphene with NNS(P) co-doping (model e), NSS(P) co-doping (model f), and NS(P) co-doping (model g). (B) corresponding C_Q of doped graphene. These panels were adapted with permission from ref (58). Copyright 2019 American Chemical Society. (C) Plot of the maximum quantum capacitance of co-doped graphene. This panel was reproduced with permission from ref (62). Copyright 2019 Springer Nature.

For the heterostructure of graphene/CNT, it has been shown that one can tune C_Q by choosing the structure to be defected. To be specific, the defected graphene–CNT hybrid exhibited a peak C_Q of 85.72 μF/cm² at 0.4 V, whereas the pristine graphene-defective CNT hybrid exhibited a peak C_Q of 69.04 μF/cm² at −0.4 V.⁶³

4.5. van der Waals Heterostructure or Composites

At the beginning of this section, let us clarify the concepts and terminology used here. When an atom with a higher atomic size substitutes a carbon atom from a graphene matrix, for example, it is obvious that the foreign atom is protruding out from the in plane of graphene. There are other issues, such as the stability of the structure, strain in the structure, etc. Moreover, large-atom (like Cs with an atomic radius of 260 pm and Ti with an atomic radius of 140 pm) substitution in the graphene matrix (atomic radius of carbon is 70 pm), for example, may not be feasible experimentally. In the experimental point of view, most of the fabrication methods produce nanoparticle-decorated nanocarbon.⁶⁴ For example, Zn-doped RGO is named in ref (65), where one can hardly see any experimental evidence of Zn doping (atomic radius of Zn is 135 pm) in the graphene matrix. Indeed, the existence of ZnO in the structure has been confirmed from the X-ray diffraction (XRD), energy-dispersive X-ray (EDX), and transmission electron microscopy (TEM) analyses.⁶⁵ In this case, we prefer the terminology of “nanoparticle decoration”, “foreign atom adsorption”,¹⁴ or sometimes “heterostructure”.⁶⁶

Figure 11A summarizes the theoretical results of the quantum capacitance of nanoparticle-decorated graphene and vacancy-defected graphene.^54,67,68 However, all the structures are not stable (Figure 11B).⁶⁷ In some cases, like Zn@graphene or Zn@vacancy-defected graphene, C_Q is found to be lower than that of pristine graphene.⁶⁷ However, when Zn is adsorbed on oxygenated graphene, it delivered 5.5 times higher C_Q than pristine graphene.⁶⁵ It should be noteworthy to mention that the attachment of the Co₃O₄ nanocube is found to be more favorable than the decoration of the nanocube on graphene or the graphene surface with substitutional graphitic oxygen (G*).⁶⁹ Moreover, the charge transfer for 3D GO/Co₃O₄ and 3D G*/Co₃O₄ is estimated to be 1.99e and 2.25e, respectively, which is higher than the other possible composites (1.15e for 2D G/Co₃O₄, 1.32e for 2D G*/Co₃O₄, 1.38e for 2D GO/Co₃O₄, 0.88e for 2D RGO/Co₃O₄, 1.73e for 3D G/Co₃O₄, and 1.13e for 3D RGO/Co₃O₄).⁶⁹ Consequently, the maximum C_Q values obtained theoretically from 3D G*/Co₃O₄ and 3D G/Co₃O₄ are 862.81 and 880.34 F/g, respectively.⁶⁹ This result again supports the necessity of a 3D film over the 2D film as an effective electrode material and suggests that forming a heterostructure on graphene with in-plane oxygen could be the better possible strategy to obtain a high charge storage property compared to the heterostructure on oxygen-functionalized graphene. However, we also emphasize that the structure, like Ni@G and Co@G, could be impressive to deliver higher theoretical C_Q. There are many misleading experimental reports on these materials, where one can clearly see a battery-like feature instead of pseudocapacitance from them.^64,70 Of course, one needs to choose a proper electrolyte and proper range of potential, where one can obtain pseudocapacitive behavior experimentally (panels C and D of Figure 11).⁷¹

Figure 11.

(A) Surface charge density and (B) structural stability of various metal-absorbed graphenes at positive and negative biases. These panels were reproduced with permission from ref (67). Copyright 2021 Elsevier, Ltd. Supercapacitive performance of the Ni nanoparticle-decorated CNT network (C) at a different potential window and (D) in different aqueous electrolytes. These panels were reproduced with permission from ref (71). Copyright 2017 Elsevier B.V.

4.6. 2D Carbon Materials beyond Graphene

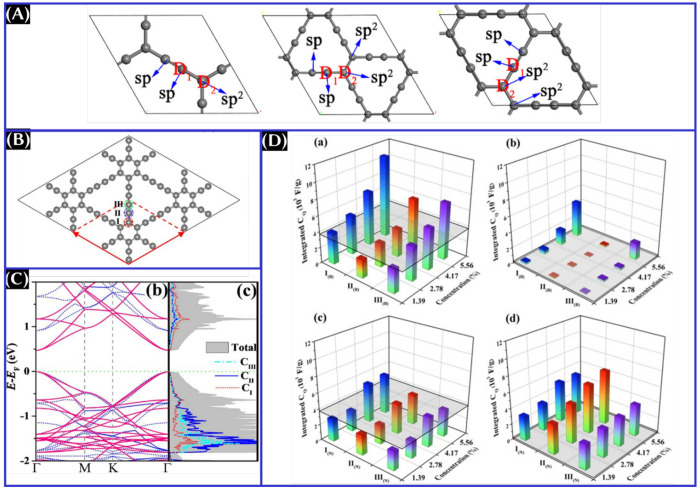
Besides graphene, there are emerging 2D carbon structures, such as graphynes and graphdiynes, that are formed by sp- and sp²-hybridized carbon atoms.⁷² In comparison to graphene, graphyne and graphdyne are anticipated as better charge storage electrodes theoretically. Eventually, the theoretical specific surface areas of α-, β-, and γ-graphynes are 5510, 4418, and 3457 m²/g, respectively, which are higher than that of graphene (2633 m²/g). It has been shown that not only is the specific capacitance of graphyne higher than that of graphene but also the quantum capacitance as well. The minimum C_Q values of α- and β- graphynes estimated using the DFT calculation are 78.7 and 541.3 F/g at 0 V, which are higher than that of graphene (42.6 F/g).¹⁹ The doping affects graphyne too, which depends upon the position of the dopants (Figure 12). Among the possible configurations, the maximum C_Q values obtained from B-doped α-graphyne, O-doped α-graphyne, and N-doped β-graphyne are 4531.6 F/g (0.26 V) at the D₁ position, 4120.7 F/g (0.27 V) at the D₁ position, and 1472.9 F/g (0.12 V) at the D₂ position.¹⁹ It should be noted that the graphene structures are distorted when B and N are doped.

Figure 12.

(A) Atomic arrangement of graphynes. This panel was reproduced with permission from ref (19). Copyright 2020 IOP Publishing, Ltd. (B) Atomic arrangement, (C) density of states, and (D) integrated C_Q of pristine and doped graphdiynes. These panels were reproduced with permission from ref (73). Copyright 2020 Elsevier B.V.

In the case of graphdiyne, simulated differential C_Q was 1805 F/g at −0.6 V, which is much higher than that of graphene (285 F/g). It has been simulated that differential C_Q of B-doped graphdiyne increases with the doping concentration and depends upon the position of the dopant. The B-doped graphdyine doped at site III with a doping concentration of 5.56% delivered the maximum theoretical differential C_Q of 4317 F/g.⁷³ However, the most stable site of boron in the graphdiyne matrix is site I. Likewise, N-doped graphdiyne doped at site II with a concentration of 5.56% exhibited differential C_Q of 6150 F/g at 0.6 V. The theoretical report also estimated integrated C_Q, because total storage capacity depends upon it, with the B-doped graphdiyne as the anode and N-doped graphdyine as the cathode being 10 557 and 6938 F/g at the doping concentration of 5.56%, respectively.⁷³ For further enhancement, Cu adsorption on B/N-doped graphdyne presented a compelling advantage over the doping alone case.¹⁴ These high C_Q values are appealing and, thus, need further investigations.

As seen from Figure 12A, there is the presence of sp-hybridized carbon atoms with sp²-hybridized carbon atoms. It could be possible that the outstanding theoretical C_Q of graphyne may be due to the presence of sp carbon. Moreover, the appealing properties of sp-hybridized carbons include a very high theoretical surface area for H₂ of 13 000 m²/g, Young’s modulus of 32 TPa, specific stiffness of 109 Nm/kg, thermal conductivity of 80 ± 26 kW m^–1 K^–1 at room temperature, and tunable electronic properties depending upon the bonding arrangement.⁷⁴⁻⁷⁷ Looking over it, the experimental investigation is carried out with a carbyne structure, and the areal capacitance of the supercapacitor device is found to be superior to many carbon nanostructures.⁷⁸ There are also reports on sp-carbon-rich or carbyne-rich nanostructures as supercapacitor electrodes in three-electrode configurations.^79,80 The maximum gravimetric (areal) capacitance obtained is 106.12 F/g (53.06 mF/cm²) for carbyne-enriched carbon anchored on nickel foam at a 5 mV/s scan rate in a 1 M Na₂SO₄ electrolyte,⁷⁹ and the maximum areal capacitance is 0.32 mF/cm² at 0.05 V/s for carbyne-rich nanostructured carbon in an ionic electrolyte.⁸⁰ It is important to note that there is a major issue with the structural stability of as-synthesized carbyne.

5. Transition Metal (Di)chalcogenides

Layered 2D transition metal dichalcogenides have received significant attention for energy storage applications as a result of their high surface area, hydrophilic nature, variable oxidation states, high volumetric capacitance, etc.^2,81,82 The general chemical formula of transition metal dichalcogenides is MX₂, where M is the transition metals (Mo, W, Ti, Ta, Nb, V, etc.) and X is chalcogens (S, Se, and Te).

Among the transition metal dichalcogenides, MoS₂ is actively researched both theoretically and experimentally as a promising SC electrode as a result of its high volumetric capacitance of 400–700 F/cm³ for the metallic 1T phase compared to graphene (300 F/cm³). Other phases that exist are the semiconducting 2H phase, 3R phase, and distorted 1T′ phase. Among them, 1T-MoS₂ is hydrophilic and much more electrically conducting (specifically 10⁷ times higher than the 2H phase). The hydrophilic surfaces are advantageous for a better electrode/electrolyte interaction, and good electrical conductivity is needed for excellent electronic transportation. The 2H phase shows a bandgap of 1.65 eV with zero DOS at the Fermi level, whereas both metallic 1T and 1T′ phases exhibit plenty of DOS around the Fermi level. Thus, C_Q is found to be higher for MoS₂ with the metallic 1T phase (321 μF/cm² at −0.6 V) and 1T′ phase (395 μF/cm² at 0.6 V) than 2H-MoS₂ (almost insignificant as a result of the absence of energy states near the Fermi level) (Figure 13).¹⁸ Distorted 1T′-MoS₂ can be achieved by introducing carbon nanostructures (CNT or graphene) underneath, which induces localized strain effects leading to the distortion and phase transformation.¹⁸ In comparison to 1T′-MoS₂/graphene (358 μF/cm² at potential −0.6 V), 1T′-MoS₂/CNT showed the enhanced DOS and, hence, theoretical C_Q of 500 μF/cm².¹⁸ Moreover, heterostructures are not always profitable to have a higher C_Q. For example, theoretical C_Q of MoS₂/graphene is 0.28 μF/cm² at 0 V, which was even lower than that of graphene (2.55 μF/cm²) and the MoS₂ monolayer (65.22 μF/cm²).⁸³ Of course, one can tailor the vacancy in MoS₂/graphene, such as Mo, S, and C vacancies. S-vacancy MoS₂/graphene showed a higher theoretical C_Q (273.98 μF/cm²) compared to its C vacancy (72.93 μF/cm²) and Mo vacancy (257.15 μF/cm²). The simulation result also shows that the maximum C_Q of Fe-doped Mo-vacancy defected MoS₂/G was 346.99 μF/cm² at a positive bias.⁸³ On the contrary, it has also been reported that the Mo vacancy can change the electronic structure drastically compared to the S vacancy, such that a large amount of DOS was introduced, which, in turn, enhances C_Q to 209.733 μF/cm².⁸⁴

Figure 13.

(A) Comparison of the theoretically estimated quantum capacitance value of MoS₂-based structures. This panel was reproduced with permission from ref (18). Copyright 2021 Elsevier, Ltd. (B) Theoretically estimated quantum capacitance and (C) cyclic voltammogram of bare VSe₂ and Co-doped VSe₂. These panels were reproduced with permission from ref (85). Copyright 2022 IOP Publishing, Ltd. (D) Comparative cyclic voltammogram of TiS₂, WS₂, MoS₂, and MoSe₂ coin cell devices. This panel was adapted with permission from ref (86). Copyright 2016 Elsevier, Ltd.

For the case of doping, the two common approaches include Mo substitution by transition metals or S atom replacement by group V (N, As, Sb, and Se) and group VII atoms (F and Cl). The maximum simulated C_Q is obtained for the N-substituted MoS₂ monolayer (203.047 μF/cm²). However, there are no observable changes in the electronic states for the Se doping. For the group VII functionalization, C_Q is 139 and 252 μF/cm² for F and Cl. In the case of Mo substitution, vanadium (V) could be the best choice because estimated C_Q is 263.721 μF/cm² among Co, Cu, and Ni.⁸⁴ It has been reported that substituting S by Al in single-vacancy MoS₂ could be the choice for symmetric SC application and substituting S by B in pristine MoS₂ could be the choice for asymmetric SC application among the Ti-, Au-, Ag-, Cu-, Al-, B-, N-, and P-doping pristine and single-vacancy MoS₂ monolayer.⁸⁷ Further enhancement of maximum C_Q and surface charge density can be achieved by increasing the doping concentration. It could be interesting to investigate the changes in electronic properties, DOS, and hence C_Q of the MoS₂-based heterostructure with Mo substitution, Mo vacancy, and S substitution, simultaneously.

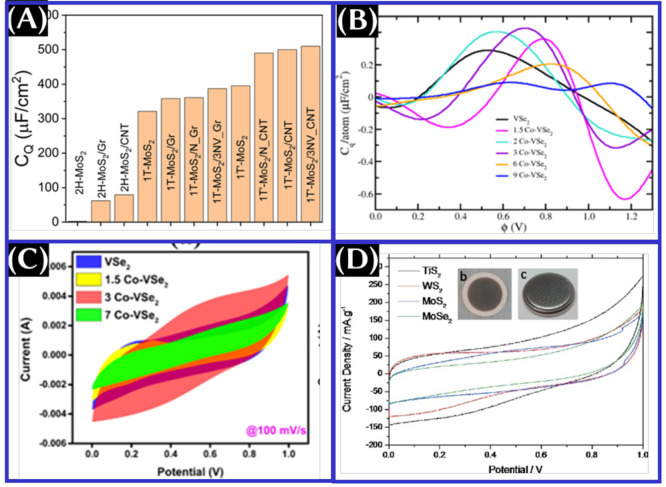
Another transition metal dichalcogenide, 1T-VS₂ monolayer, showed high DOS near the Fermi level, and the highest simulated C_Q obtained is 377 μF/cm² at +0.19 V. It can be enhanced further by introducing materials, like monolayer black phosphorus, underneath it via charge transfer from black phosphorus to VS₂. As a result, the improved highest C_Q obtained is 428 μF/cm² at +0.17 V.⁸⁸ It is important to note that monolayer black phosphorus does not have DOS near the Fermi level. Doping is another adoptable strategy for V-based dichalcogenides. However, beyond the 3% level, Co doping of 1T-VSe₂ shows adverse effects on the quantum capacitance and gravimetric capacitance (panels B and C of Figure 13). While the experimental results are compared for total gravimetric capacitance of different transition metal dichalcogenides (Figure 13D), the trends of capacitance value follow as TiS₂ (4.60 F/g) > WS₂ (3.50 F/g) > MoS₂ (3.40 F/g) > MoSe₂ (2.57 F/g) at a 10 mV/s scan rate in a 1 M Na₂SO₄ aqueous electrolyte. The MoS₂ cell exhibits the lowest phase constant of 60° at a low frequency compared to that of TiS₂ (75°). The higher capacitance value of TiS₂ is attributed to the low density and higher electrical conductivity.⁸⁶

FeS is another emerging material that can be considered as an energy storage electrode. C_Q of hexagonal FeS is estimated from first-principles calculations to be 408 F/g. When the vacancy is introduced in the structure, C_Q enhanced to 2280 F/g at a positive bias.⁸⁹

6. MXene

MXenes have recently emerged as promising 2D materials of transition metal carbide/nitride/carbonitride in the field of energy storage and other suitable applications as a result of the features of metallic conductivity, large interlayer spacing, easy functionalization, and redox-active surface oxide-induced pseudocapacitive behavior.^2,90 The general formula for MXenes is M_n+1X_nT_x, where M, X, and T_x stand for the transition metal, carbon and/or nitrogen, and surface terminations with n = 1–4, respectively. Some of the most researched and significantly attracted MXenes are Ti₃C₂T_x, Ti₂CT_x, V, and Nb. Importantly, the volumetric capacitance of Ti₃C₂T_x MXene hydrogel obtained is 1500 F/cm₃ with respect to Hg/HgSO₄ at 2 mV/s in H₂SO₄, which is much higher than that of MoS₂ or graphene.²²

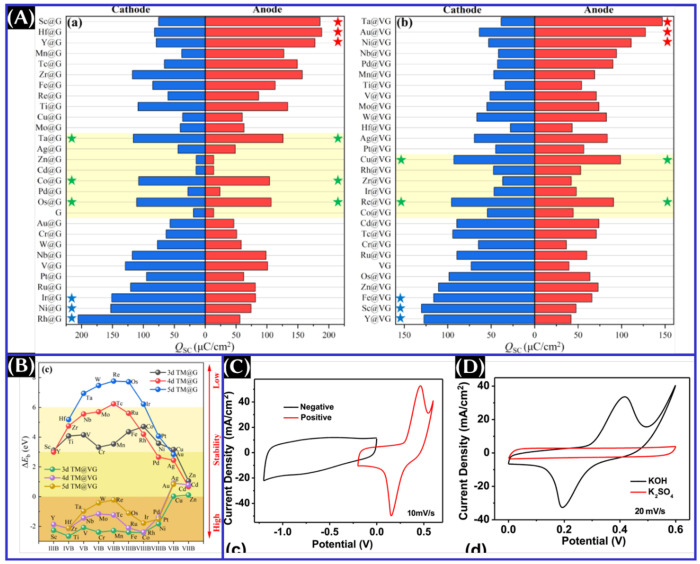
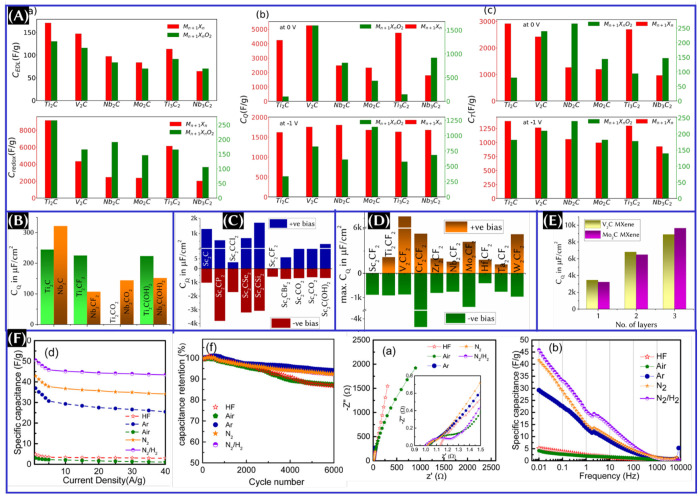
In contrast to the pristine carbon-based materials, MXenes generally show higher values of the DOS and C_Q. Figure 14A⁹¹ summarizes the contribution from EDLC, redox capacitance, C_Q, and total capacitance (C_T) of Ti-, V-, Nb-, and Mo-based MXenes. To calculate theoretically, a few assumptions made in ref (91) are MXene being negatively charged, H⁺ ion adsorption on the electrode surface, and C_Q and C_T measuring at 0 and −1 V because they have two extrema close to those two voltages. The total capacitance calculated theoretically is mostly in good agreement with the experimentally obtained result. MXenes commonly feature the functional/terminated groups (denoted as T_x) on the surface. On the basis of the synthesis techniques, T_x can be different. For example, T_x is O, OH, Cl, and F for chemical etching,⁹² O and OH for hydrothermal, and Cl or halides with O-functional groups for molten salt techniques. Oxygen functional groups are considered unavoidable because of the chemical process involved in all techniques, and they are responsible for aiding the pseudocapacitance. Eventually, the theoretical calculations on C_Q and surface charge density suggested V₂CT₂ MXene with mixed terminations as a suitable anode material of asymmetric supercapacitors in aqueous and ionic/organic systems.⁹³ The result obtained theoretically for pristine and functionalized MXenes (Figure 14) can be summarized as follows:⁹¹ (i) Ti₂C has the highest EDLC and C_T, even compared to Ti₃C₂, whereas V₂C has a higher C_Q at 0 and 1 V, and Nb₂C has the highest C_Q at 1 V among the studied pristine MXenes. (ii) O functionalization lowered the EDLC, C_Q, and C_T for all MXenes.⁹⁴ (iii) Among the functionalized MXenes, O-functionalized V₂C has a higher C_Q at 0 V and O-functionalized Mo₂C has the highest C_Q at 1 V. However, O-functionalized Nb₂C has the highest total capacitance at both 0 and 1 V.

Figure 14.

(A) Double layer, quantum capacitance, and total capacitance of bare and oxygen-functionalized MXenes. This panel was reproduced with permission from ref (91). Copyright 2021 IOP Publishing, Ltd. Theoretical quantum capacitance of (B) functionalized Ti₂C and Nb₂C MXenes,⁹⁴ (C) functionalized SC₂C MXene with different termination groups,⁹⁵ (D) MXene with a F-terminated group,⁹⁶ and (E) V₂C and Mo₂C MXenes with respect to the number of layers. Data for panels B–E are either taken from the text/table or extracted from the corresponding references using the WebPlotDigitizer software authored by Ankit Rohatgi. (E) Experimental charge storage performance of the modified Ti₃C₂T_x MXene/KOH electrolyte symmetric cell. This panel was reproduced with permission from ref (97). Copyright 2015 American Chemical Society.

Instead of the O-functional group, the charge storage capacity can be enhanced with the replacement of carbon in a titanium octahedron by oxygen in Ti₃C₂T_x MXene. It has been reported that O-doped MXene synthesis from the O-functionalized MAX phase is a more facile approach, called in situ oxygen doping.⁹⁸ From the O doping, the DOS near the Fermi level is improved, which is reflected in the enhanced interfacial capacitance of O-doped Ti₃C₂T_x compared to its bare counterpart.⁹⁸ In this way, one can decrease the valence state of the inner Ti atoms, which promotes electronic transport, and increase the valence state of outer Ti atoms, which is responsible for the enhanced pseudocapacitance.

The above result (Figure 14A) is based on only the O-functional or termination group. On the basis of the synthesis procedure, as mentioned above, there are other functional groups. Studies reveal that, like O-functional groups, the existence of other functional groups also has similar adverse effects on the Ti₂C and Nb₂C MXenes.⁹⁶ As seen from Figure 14B, along with −OH, −F also has the least impact on C_Q for Ti₂C MXene.⁹⁹ Despite the lower C_Q values of V₂C and Mo₂C caused by the introduction of functional groups, the functionalized MXenes still have a higher C_Q compared to the other electrode materials.⁹⁶ There is also an exception for Sc₂C MXene with other functional groups as well. The maximum differential C_Q of Sc₂CSi₂ with T of P, Cl, Se, and Si is higher than that of monolayer Sc₂C in both aqueous and organic electrolytes (Figure 14C).⁹⁵

In reality, after the synthesis, MXenes possess multiple termination groups, and these are unavoidable. Theoretical results suggest that removing the functional groups from the surface of electrode materials could be a better option to obtain a high energy storage performance. From the experimental side, on the basis of testing in a two- or three-electrode configuration, it is also observed that post-annealing as-synthesized MXene has better performances. The alkalinized (by KOH treatment) and annealed (under Ar at 673 K) Ti₃C₂T_x film exhibits higher gravimetric (volumetric) capacitance of 543 F/g (2063 F/cm³) at 1 A/g with 98% capacitance retention after 8000 cycles, which is higher than the untreated Ti₃C₂T_x film (281 F/g).¹⁰⁰ Among the post-annealing under different environments (air, Ar, N₂, and N₂–H₂), Ti₂CT_x MXene annealed at N₂–H₂ provides the best storage properties compared to as-synthesized MXene.⁹⁷ In both cases,⁹⁷¹⁰⁰ the improvement in performances is mainly attributed to the increased surface area, increased interplanar distance, increased crystalline order, highest carbon content, and removal of −F and −OH terminal groups. On the contrary to F removal, the C_Q value obtained theoretically from F-functionalized MXene is quite impressive.⁹³ Ca-adsorbed Ti₃C₂F₂ and Li-adsorbed Ti₃C₂F₂ showed the highest C_Q of 488.153 and 259.490 μF/cm², respectively, among the all of possible combinations.⁹⁹ We emphasize that the use of F is not recommended because it reduces the electrochemical reactivity and electrical conductivity of MXene, while it is also hazardous and causes some safety issues.

The harsh synthesis techniques of MXene from its parent structure leave an atomic vacancy in the MXene structure, which has a significant impact on the diffusion behavior of electrolyte ions (Li⁺, Na⁺, K⁺, etc.). The (opto)electronic properties of the final structure obviously depend upon the vacancy type.¹⁰¹ It has been predicted that C_Q of Ti₂CO₂ can be enhanced at a positive potential further by increasing the oxygen vacancy concentration because a larger charge transfer takes place for neighboring O and Ti atoms. It is also important to note from the theoretical study that one oxygen vacancy is more effective compared to two or three oxygen vacancies.¹⁰² Ti₂CO₂ with oxygen vacancy concentrations of 11.11 and 16.67% has a lower maximum C_Q of 3131.18 and 3573.14 μF/cm² at a positive potential, respectively. Apart from the O vacancy, the C or M vacancy also enhances the DOS at the Fermi level. As predicted, Zr₂CO₂ MXenes with Zr vacancy can be chosen as cathode materials, whereas Zr₂CO₂ MXenes with C and O vacancies can be a good choice for anode materials.¹⁰¹

Apart from the termination groups, doping is another approach for MXene as well to change the DOS and, hence, C_Q.^15,103 The dopants apparently determine the intrinsic properties of the final structure.¹⁵ To increase C_Q further, two cobalt (Co) atoms were doped, and the increased C_Q was attributed to the increased DOS contribution from 3d and 4s electrons of Co. N doping into carbide-based MXene could be another alternative approach to enhance C_Q.

We stress that, apart from the carbide-based MXene, there are also nitride-based MXenes. It could be interesting to evaluate the superiority between N-doped carbide and nitride MXenes. Eventually, in contrast to Nb₂C MXene, niobium nitride MXene emerges as promising electrode material. We highlight that simulated C_Q of NbN at negative and positive biases is found to be 834.5 and 1683.7 F/g compared to Nb₄N and Nb₅N₆.¹⁰⁴ The maximum C_Q has been observed for Nb₂N (1196.28 μF/cm² at −1 V and 844.8 μF/cm² at 0.5 V) and Nb₄N₃ (174.86 μF/cm²).¹⁰⁵ Remarkably, increasing the number of layers has profound effects on enhanced C_Q for both Nb₂N and Nb₄N₃.

7. Other 2D Materials

There are many 2D materials, apart from graphene, transition metal chalcogenides, and MXenes, in the pipeline, and they have remarkable features. They are sometimes even found to be superior to graphene based on the theoretical calculation. C_Q of silicene is predicted to be 2 times higher than that of graphene, even at a low bias.¹⁰⁶ To improve C_Q of these materials, the strategy is similar to graphene, namely, doping, introducing defects, etc. Among these, silicene with a six vacancy-defected structure performed better at the voltage of 0–0.5 V.^107,108 It is reported on the basis of the theoretical calculation that the co-doping with the transition metal and nitrogen to silicene delivered higher charge storage and C_Q compared to the single doping with the transition metal or N. The DOS contribution near the Fermi level only comes from the 3d state of the transition metal atom and the 3p state of the Si atom, whereas N helps to stabilize the system. The higher the N concentration, the more stable the structure.¹⁰⁹ Theoretical C_Q of germanene (3.51 μF/cm²) is also found to be higher than that of graphene at 0 V. Although doping can have a significant effect on DOS, this is not always the case. For example, N-doped germanene showed a theoretical C_Q of 45.32 μF/cm² at 0.01 V, and Ti-doped germanene exhibited the highest C_Q of 91.47 μF/cm² at 0.2 V compared to Cr, Co, and Mn doping,¹⁰⁸ whereas boron and aluminum doping does not show any significant enhancement. There are other 2D materials, like arsenene¹¹⁰ and δ-6 borophene,¹¹¹ and theoretical studies have been conducted focusing on tailoring the electronic properties, DOS, and hence C_Q by means of doping, defect, or heterostructure formations.

As seen from the above literature analysis, the major issues of these 2D materials as an energy storage electrode include (i) mass-scale production of these 2D materials and, in particular, synthesis of the freestanding film, which remains a challenge, (ii) material stability, and hence (iii) very limited studies on the applications because there is a lack of experimental confirmation of theoretical predictions.¹¹²

8. Temperature Dependency

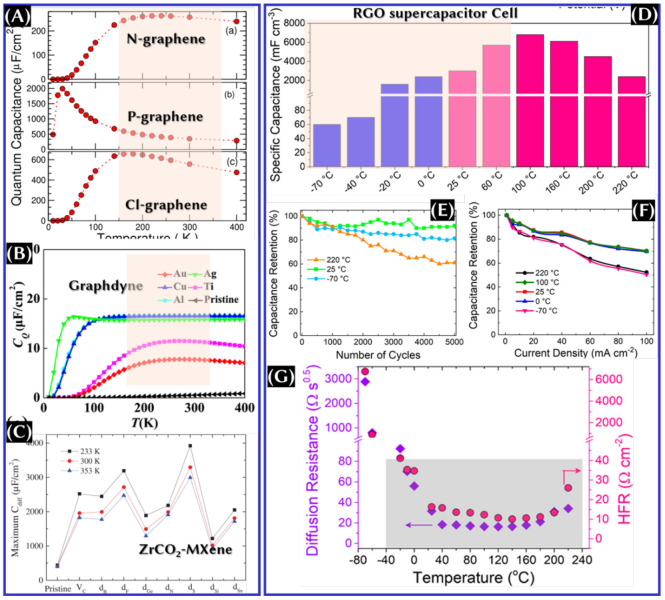
This section discusses the temperature dependence of the quantum capacitance. Most of the simulations and even experimental testing as supercapacitor electrodes are carried out at room temperature. However, supercapacitors should be capable of working in the range from −100 °C (173 K) to 60 °C (343 K), with extremely low failure rates. Because the quantum capacitance is an intrinsic property of electrode materials, it is interesting indeed to see what happens to C_Q of electrodes at various temperatures. Considering pristine graphene-based materials, structures are theoretically found to be quite stable at elevated temperatures theoretically. However, once functionalized or doped, structural properties change (Figure 7D). Eventually, drastic changes can also be seen in C_Q with respect to the temperature (Figure 15), which is attributed to the Kondo effect.¹³ This effect is confirmed by a spin-polarized DFT study that doped adatoms show magnetic behavior and there is localization of DOS near Fermi energy.¹³ In the case of graphdiyne, no significant changes in C_Q have been observed,¹⁴ whereas metal-adsorbed graphdiyne shows increasing trends of C_Q up to a certain temperature and then becomes saturated. We assign the temperature where it saturates as the cutoff temperature. The cutoff temperature is found to be different for the different metals adsorbed on the surface of graphdiyne (Figure 15B).¹⁴ In the case of ZrCO₂, C_Q of pristine MXene has almost no impact on the temperature. However, C_Q becomes lower and higher at lower and higher temperatures with respect to room-temperature C_Q, respectively, and this effect does not depend upon whether it is vacancy-defected or heteroatom-doped.¹⁵ Within the temperature region of interest (from −100 to 60 °C or from 173 to 343 K), as highlighted by the shadowed color in panels A, B, and D of Figure 15, C_Q of the electrode has an almost decreasing trend with the temperature. We also emphasize the changes in the electrode and/or device that happen in the performance from real test results (panels D–G of Figure 15).¹¹³ In terms of the total capacitance of the cell, it is obvious to observe that the higher electrolyte ion mobility (even if there is the possibility of evaporation and freezing of ionic movement at respective higher and lower temperatures), the improved electrical conductivity of the electrode at higher temperatures, which is, in turn, higher specific capacitance, better coulombic efficiency, and higher specific energy/power density of the electrode and the cell up to a certain temperature. There is also the possibility of the phase change of the SC electrodes made of metal-oxide-type materials with the temperature operation, and sometimes, it cannot be reversible.

Figure 15.

Theoretical quantum capacitance variation of (A) graphene,¹³ (B) graphdyne,¹⁴ and (C) ZrCO₂ MXene¹⁵ with respect to the temperature. These panels were reproduced with permission from refs (13−15). Copyrights 2019 IOP Publishing, Ltd., 2023 Royal Society of Chemistry, and 2021 Wiley Periodicals LLC, respectively. (D) Volumetric capacitance, (E) capacitance retention, (F) rate performance, and (G) changes in diffusion resistance and high-frequency resistance of the RGO symmetric cell. This panel was reproduced with permission from ref (113). Copyright 2020 American Chemical Society.

9. Electrolyte Dependency

This section explores the dependence of C_Q upon specific electrolytes. The expected answer is certainly not because C_Q is an inherent property of the electrode. First-principles calculations on the desolvation behavior of Li⁺, Na⁺, and K⁺ at the edge plane pores and basal plane pores of porous carbon materials confirmed that there are no significant changes in the total DOS near the Fermi level.¹¹⁴ On the other hand, a recent theoretical study revealed that the maximum C_Q was found for the B-doped CNT in the alkaline electrolyte at a positive bias, the B-doped CNT in the acidic electrolyte at a negative bias, and the N-doped CNT in the alkaline electrolyte at a negative bias (Figure 16).¹⁶ Likewise, C_Q of 1T-TaS₂ is found to be enhanced with K⁺ and Na⁺ ion intercalation and lowered with Li⁺ ion intercalation. Moreover, the highest theoretical C_Q is found for 2H-TaS₂ intercalated with Li⁺ ions and 3R-TaS₂ with K⁺ ion intercalation.¹⁷ Eventually, the alkali ion intercalation into 2H- and 3R-phase MoS₂ transformed them into the stable metallic 1T-MoS₂ phase.¹¹⁵ Moreover, despite higher C_Q values obtained from K⁺ and Na⁺ ions, the reversibility is maintained in the case of Li-ion intercalation. For the overall best performance from the electrode, the Li⁺/Na⁺ co-intercalation is proposed. These results reveal that the C_Q values of the electrode depend upon the electrolyte used, and it is recommended to choose the appropriate electrolyte for the specific electrode.

Figure 16.

Theoretical quantum capacitance of CNT and doped CNT in acidic (H) and alkaline (OH) electrolyte media. These panels were reproduced with permission from ref (16). Copyright 2022 Elsevier B.V.

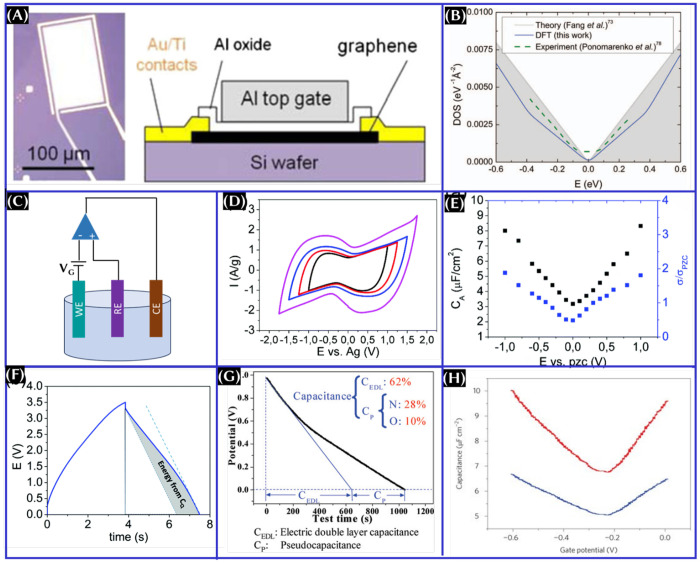
10. How To Measure C_Q Experimentally

The concept of quantum capacitance was first introduced by Luryi for 2D electron gas in a quantum well, by neglecting the screening effect that occurred for metals.¹¹⁶ From the experimental point of view, of course, one can obtain the quantum capacitance by measuring the applied gate voltage from Hall measurements (Figure 17A). The discrepancy between the theoretical and experimental results (Figure 17B) near 0 V is attributed to the oxide layer thickness, defects present in graphene, and graphene–oxide surface interaction.²⁸ Here, we highlight that the meaning of oxide is the SiO₂ layer/Si (most used substrate for the Hall effect measurements). In this review, our concern is the estimation of C_Q of the electrode when the electrochemical energy storage device testing is conducted under a defined electrolyte (Figure 17C).

Figure 17.

(A) Schematic of the graphene–Al₂O₃–Al capacitor. This panel was reproduced with permission from ref (117). Copyright 2010 American Physical Society. (B) Comparison of density of states of graphene from theory, experiment, and DFT. This panel was reproduced with permission from ref (28). Copyright 2012 IOP Publishing, Ltd. (C) Schematic of the quantum capacitance measurement setup for the graphene electrode.¹¹⁸ (D) CV at 50 mV/s at different voltage limits, (E) area-normalized capacitance and normalized conductivity versus potential at zero charge obtained from electrochemical impedance at 10 mHz and different bias voltages, and (F) charge–discharge profile of the symmetric device made with macroscopic fibers of CNTs as electrodes and 1-butyl-3-methylpyrrolidinium bis(trifluoromethylsulfonyl)imide (PYR14TFSI) as the ionic liquid electrolyte used. These panels were reproduced with permission from ref (119). Copyright 2016 Royal Society of Chemistry. (G) Capacitive contribution from nitrogen-enriched nanocarbons with a 3D continuous mesopore structure. This panel was reproduced with permission from ref (120). Copyright 2010 American Chemical Society. (H) Total capacitance (blue line) and quantum capacitance (red line) of graphene can be measured with the measurement setup presented in panel C. This panel was reproduced with permission from ref (118). Copyright 2009 Nature Publishing Group.

The voltage-dependent butterfly-shaped cyclic voltammetry (CV), a common behavior of the quasi-metallic nature of carbons, corresponds to the quantum capacitance (Figure 17D). The quasi-metallic behavior of the electrode can also be ascertained from the plot of the area-normalized capacitance and longitudinal conductivity versus the applied potential (Figure 17E). The data presented in Figure 17D are obtained from the impedance measurements in the three-electrode cell with respect to the potential at zero charge (pzc). The quantum capacitance contribution can be calculated from the charge–discharge profile by plotting a discharge line with the slope at pzc (Figure 17F).¹¹⁹ However, the extended line of the discharge profile is also used to estimate the pseudocapacitive contribution for the symmetric cell made with nitrogen-enriched nanocarbons with a 3D continuous mesopore structure (Figure 17G).¹²⁰ It could be interesting to estimate the EDLC, C_Q, and pseudocapacitive contributions from the discharge profile of doped carbon or any other structure by compiling the estimation procedure mentioned in refs (119 and 120). In another method, a gate voltage can be applied to the electrode/electrolyte system (Figure 17C) to obtain the total capacitance from a V-shaped capacitance–gate voltage curve in the electrolyte with respect to the reference electrode (blue line in Figure 17H). To measure the value of C_Q (red line in Figure 17H), one can subtract the total capacitance by C_dl. C_dl is basically measured from the three-electrode test using the cyclic voltammogram within the scanning range of the linear region, where only non-faradic activity occurs,¹²¹ or using the impedance spectroscopy.⁷ Alternatively, C_dl/A can be calculated using eq 1.¹¹⁸

11. Summary, Challenges, and Outlook

11.1. Summary

Supercapacitors or electrochemical capacitors are promising energy storage devices that provide more charge storage capacity than conventional capacitors and higher cycle life and higher power density than the battery. The electrode material of the energy storage device plays a key role, and the total charge storage capacitance contribution comes from the electrode/electrolyte interactions and quantum capacitance of the electrode (C_Q). C_Q is connected in series with C_EE (capacitance as a result of the electrode/electrolyte interaction). In summary, we have discussed the quantum capacitance of various electrode materials, namely, carbon, 2D materials, and their composites, and hence, it has a significant impact on the total capacitance. Table 3 summarizes the theoretical calculations of C_Q of carbon and 2D materials. Besides the knowledge of the surface engineering of the electrode, electrolyte modification, and electrode/electrolyte interaction improvements, the enhancement of C_Q became equally important to obtain high storage performance from the fabricated supercapacitor device. By tuning the density of states by introducing defects, dopants, or other heterostructures, one can enhance the quantum capacitance of the electrode materials and the potential window of the energy storage device. Dependent upon the performance of the electrode and its quantum capacitance behavior, one can choose the right material and the best approach for its potential applications, because all strategies may not be leading to the enhanced C_Q. The electrode material with a high C_Q value in the positive bias and a low C_Q value in the negative bias window is a suitable choice as an anode of an asymmetric supercapacitor. Meanwhile, the electrode materials with high and low C_Q values in the negative bias and negative bias window, respectively, can be a choice as cathode materials for asymmetric supercapacitors.⁶⁸ One can also measure the surface charge density at positive bias (Q_a) and negative bias (Q_c). The value of Q_a/Q_c can be an indication of the choice of the electrode.⁶⁷ In general

Moreover, C_Q of the electrode also has a dependency upon the temperature of operation as the surface charge density, and DOS depends upon the temperature. It has also been seen that C_Q of the electrode can be tailored by the intercalation of different electrolyte ions; this result can guide experimentalists to choose the right electrolyte for the desired electrode materials.

Table 3. Quantum Capacitance of Carbon and 2D-Material-Based Supercapacitor Electrodes Based on the Theoretical Calculations^a.

electrode material		dopant(s)/metal adsorbed/ion intercalated	quantum capacitance, CQ	method of determination/approach
graphene38		pristine	2.55 μF/cm2 at 0 V	ab initio density functional theory (DFT)
		vacancy defect	44.38 μF/cm2 at 0 V
		Stone–Wales defect	120.72 μF/cm2 at 0 V
		silicon (Si)	169.76 μF/cm2 at −0.29 V
			49.02 μF/cm2 at 0.11 V
		aluminum (Al)	113.73 μF/cm2 at −0.39 V
			79.89 μF/cm2 at 0.06 V
		phosphorus (P)	76.73 μF/cm2 at −0.3 V
			56.07 μF/cm2 at 0.45 V
		boron (B)	112.52 μF/cm2 at 0 V
		Al + Stone–Wales defect	102.61 μF/cm2 at −0.38 V
		B + Stone–Wales defect	76.18 μF/cm2 at −0.42 V
		P + Stone–Wales defect	59.36 μF/cm2 at 0.12 V
		sulfur (S) + Stone–Wales defect	88.31 μF/cm2 at −0.46 V
graphyne19		α-graphyne	78.7 F/g at 0 V (42.6 F/g for graphene)	ab initio DFT
		β-graphyne	541.3 F/g at 0 V
		B-doped α-graphyne	4531.9 F/g at 0.26 V
		B-doped β-graphyne	3626.2 F/g at 0.25 V
		B-doped γ-graphyne	3587.7 F/g at 0.16 V
		N-doped α-graphyne	1196.3 F/g at 0.48 V
		N-doped β-graphyne	1472.9 F/g at 0.12 V
		N-doped γ-graphyne	1221.1 F/g at −0.06 V
		O-doped α-graphyne	4120.7 F/g at 0.27 V
		O-doped β-graphyne	1417.7 F/g at −0.02 V
		O-doped γ-graphyne	1586.5 F/g at −0.60 V
graphdyne73		pristine	1805 F/g at −0.6 V (264 F/g for graphene)	DFT-based first-principles calculations
		5.56% B	4317 F/g at −0.3 V
		5.56% nitrogen (N)	6150 F/g at 0.6 V
single-walled carbon nanotube122		Sc	52.58 μF/cm2 at −0.6 eV	ab initio spin-polarized DFT
		Cr	43.21 μF/cm2 at −0.6 eV
		Fe	55.91 μF/cm2 at −0.35 eV
		Ni	59.74 μF/cm2 at 0.29 eV
		Co	31.40 μF/cm2 near 0 V
		Ti	41.36 μF/cm2 near 0 V
		vanadium	33.54 μF/cm2 near 0 V
		Mn	36.94 μF/cm2 near 0 V
		Cu	52.73 μF/cm2 at −0.47 eV
		Zn	50.87 μF/cm2 at −0.11 eV
transition metal dichalcogenides (TMD)	monolayer MoS284	S substitution by N	203.047 μF/cm2 at Fermi energy	ab initio DFT
		S substitution by F	139 μF/cm2 at Fermi energy
		S substitution by Cl	252 μF/cm2 at Fermi energy
		S substitution by As	189.672 μF/cm2 at Fermi energy
		S substitution by Sb	188.955 μF/cm2 at Fermi energy
		S substitution by Se	0.595 μF/cm2 at Fermi energy
		Mo substituted by Co	152.794 μF/cm2 at Fermi energy
		Mo substituted by Cu	191.658 μF/cm2 at Fermi energy
		Mo substituted by Ni	202.439 μF/cm2 at Fermi energy
		Mo substituted by vanadium	263.721 μF/cm2 at Fermi energy
		5.5% S vacancy	0.190 μF/cm2 at Fermi energy
		11% S vacancy	2.5 μF/cm2 at Fermi energy
		16.5% S vacancy	33.665 μF/cm2 at Fermi energy
		11.5% Mo vacancy	209.733 μF/cm2 at Fermi energy
	three-layered 1T-MoS2115	pristine*	2063.49 F/g at −0.2 V	ab initio DFT HASI, horizontally aligned similar ions; DASI, diagonally aligned similar ions; and VASI, vertically aligned similar ions
		H+ ion intercalated*	2419.04 F/g at 0.005 V
		Li+ ion intercalated*	2342.85 F/g at 0.005 V
		Na+ ion intercalated*	2787.30 F/g at −0.002 V
		K+ ion intercalated*	2736.5 F/g at −0.002 V
	three-layered 2H-MoS2115	pristine*	772.09 F/g at −0.5 V
		H+ ion intercalated*	474.42 F/g at −0.008 V
		K+ ion intercalated*	3302.32 F/g at 0.3 V
		Li+ ion intercalated*	3004.65 F/g at 0.3 V
		Na+ ion intercalated*	3246.51 F/g at 0.3 V
		LiNa intercalated (HASI)	3163 F/g at 0.3 V
		LiNa intercalated (DASI)	3111 F/g at 0.3 V
		LiNa intercalated (VASI)	3143 F/g at 0.3 V
2D heterostructure	MoS2/graphene83	pristine	16.36 μF/cm2 at −0.2 V	ab initio DFT
		carbon vacancy*	74.4 μF/cm2 at −0.32 V
		Mo vacancy*	258.13 μF/cm2 at 0.08 V
		S vacancy*	273.98 μF/cm2 at 0.11 V
		Sc	73.12 μF/cm2 at −0.2 V
		Sc@S vacancy	166.51 μF/cm2 at −0.06 V
		Ti	75.21 μF/cm2 at −0.2 V
		V	48.26 μF/cm2 at −0.2 V
		Cr	23.44 μF/cm2 at −0.2 V
		Mn	77.56 μF/cm2 at −0.2 V
		Fe	206.30 μF/cm2 at −0.2 V
		Fe@Mo vacancy	309.15 μF/cm2 at 0.11 V
		Fe@S vacancy	144.95 μF/cm2 at 0.16 V
		Co	45.97 μF/cm2 at −0.2 V
		Co@Mo vacancy	304.02 μF/cm2 at −0.47 V
		Co@S vacancy	207.94 μF/cm2 at −0.18 V
		Ni	16.19 μF/cm2 at −0.2 V
		Ni@S vacancy	283.11 μF/cm2 at 0.37 V
MXene	Nb2C94	pristine	324.1 μF/cm2 at 0.5 V	ab initio DFT
	Ti2C94	pristine	246.2 μF/cm2 at 0.5 V
	V2C96	pristine	3465.51 μF/cm2 at −0.5 V
	Mo2C96	pristine	3243.99 μF/cm2 at −0.5 V
	Ti3C299	pristine	398.19 μF/cm2 at −0.072 V	ab initio DFT
		H terminated	212.10 μF/cm2 at −0.072 V
		O terminated	158.87 μF/cm2 at −0.072 V
		F terminated	244.27 μF/cm2 at −0.072 V
		OH terminated	296.28 μF/cm2 at −0.072 V
		Li adsorbed	291.23 μF/cm2 at −0.072 V
		Na adsorbed	359.19 μF/cm2 at −0.072 V
		K adsorbed	289.45 μF/cm2 at −0.072 V
		Ca adsorbed	342.65 μF/cm2 at −0.072 V
		Mg adsorbed	364.69 μF/cm2 at −0.072 V
		Al adsorbed	398.193 μF/cm2 at −0.072 V
		Li adsorbed on F terminated	228.833 μF/cm2 at −0.408 V
		Na adsorbed on F terminated	227.076 μF/cm2 at −0.432 V
		K adsorbed on F terminated	222.581 μF/cm2 at 0.048 V
		Ca adsorbed on F terminated	242.453 μF/cm2 at −0.408 V
		Mg adsorbed on F terminated	224.492 μF/cm2 at −0.432 V
		Al adsorbed on F terminated	488.153 μF/cm2 at 0.12 V
	Ti2C99	pristine	272.37 μF/cm2 at 0.048 V
		H terminated	135.36 μF/cm2 at 0.048 V
		O terminated	48.22 μF/cm2 at 0.048 V
		F terminated	184.98 μF/cm2 at 0.048 V
		OH terminated	157.79 μF/cm2 at 0.048 V
		Li adsorbed	187.85 μF/cm2 at 0.048 V
		Na adsorbed	152.41 μF/cm2 at 0.048 V
		K adsorbed	219.72 μF/cm2 at 0.048 V
		Ca adsorbed	159.61 μF/cm2 at 0.048 V
		Mg adsorbed	132.96 μF/cm2 at 0.048 V
		Al adsorbed	444.192 μF/cm2 at 0.312 V
		Li adsorbed on F terminated	259.490 μF/cm2 at −0.24 V
		Na adsorbed on F terminated	247.689 μF/cm2 at 0.048 V
		K adsorbed on F terminated	231.497 μF/cm2 at 0.048 V
		Ca adsorbed on F terminated	220.885 μF/cm2 at 0.048 V
		Mg adsorbed on F terminated	226.881 μF/cm2 at 0.048 V
		Al adsorbed on F terminated	252.554 μF/cm2 at 0.072 V
δ-6 borophene111		1 layer in aqueous electrolyte	203.09 μF/cm2 at −0.6 V	DFT
		4 layers in aqueous electrolyte	600.36 μF/cm2 at −0.15 V
		1 layer in ionic liquid electrolyte	209.24 μF/cm2 at −1 V
		4 layers in ionic liquid electrolyte	663.27 μF/cm2 at −1 V
silicene107		pristine	363.66 F/g at −0.5 V	DFT
		monovacancy	711.20 F/g at −0.25 V
		trivacancy	673.41 F/g at −0.5 V
		six vacancy	2004.54 F/g at 0.50 V
germanene108		pristine	3.51 μF/cm2 at 0 V (minimum)	DFT
		N doped	45.32 μF/cm2 at 0.01 V
		Ti doped	91.47 μF/cm2 at 0.20 V
		Cr doped	40.96 μF/cm2 at −0.20 V
		Mn doped	39.36 μF/cm2 at −0.03 V
		Co doped	59.70 μF/cm2 at 0.32 V
		B/Co doped	146.99 μF/cm2 at −0.54 V
		Co doped + vacancy	123.33 μF/cm2 at −0.42 V
		B/Co doped + vacancy	116.46 μF/cm2 at −0.55 V

^aAn asterisk represents the data estimated either from the plot using WebPlotDigitizer software authored by Ankit Rohatgi or available data from the reference.

11.2. Challenges

On the basis of this discussion, the key challenges that we foresee in this emerging area are outlined as follows:

• The structural stability of doped and defected electrode material systems is quite challenging.⁵⁴ Basically, there is a trade-off relation between a stable system and the best charge storage performance, as evidenced by the theoretical calculation.¹⁰⁹ For instance, TMN₃–Si is the most stable system, but ScN₂–Si showed the highest C_Q of 224.88 μF/cm².

• For the doped/functionalized graphene, as an example, the total contribution comes from double-layer capacitance, dopant/functionalized-group-assisted pseudocapacitance, and quantum capacitance. It is unclear from the available reports on the theoretical calculation whether the pseudocapacitance part is considered or not. Moreover, space charge capacitance should be added in the calculation, while one is considering few-layer or multi-layer graphene.¹²³

• Adding pseudocapacitive materials into the EDLC materials can enhance the specific capacitance dramatically, and one needs to consider the mechanical properties of the composite because pseudocapacitive materials are mostly brittle.

• It is highly desirable to use dopants with a smaller atomic size and shorter bond lengths. Dopants with a larger atomic size may have other effects. For example, the larger bond length of C–P than C–C leads to the lattice expansion of the original graphene symmetry, and the structure may fail to retain its symmetry.⁵⁴ Larger dopants, e.g., Al³⁺ monovacancy on graphene, is clearly not favorable because it has the higher formation energy.⁵⁴

• Hybrid electrode materials have a synergy effect on the total charge storage performance. However, one needs to keep in mind that many components in the heterostructure have more complexity in theoretical computation because it consists of more constituent material along with the presence of the defect and curvature, and sometimes, it has been observed that a heterostructure with fewer components has superior performance over multicomponent heterostructures.

Therefore, an in-depth understanding and further insights into the quantum capacitance of electrode materials are increasingly necessary to advance clean energy storage technology, and this trend will continue in the future.

11.3. Outlook and Perspective

Certainly, discussing potential future perspectives in research methodologies, both experimental and modeling, in the context of quantum capacitance of 2D-material-based supercapacitor electrodes is essential for keeping pace with the evolving landscape of the field. The following are some key areas to consider:

• Advanced microscopy and microanalysis: The development of in situ and operando experimental techniques is beneficial to directly observe the quantum capacitance behavior of 2D materials with deeper insights into the underlying mechanisms. Similarly, nanoscale probing techniques, such as atomic force microscopy (AFM) and scanning tunneling microscopy (STM), can be further refined for better control and optimization to study the quantum capacitance properties at the nanoscale. Furthermore, these studies are also essential to probe the reaction environments and the changes within the electrodes.

• Exploration of novel 2D materials: We can explore and synthesize new 2D materials, such as MXene, borophenes, phosphorene, germanene, etc., with tailored electronic properties for superior quantum capacitance characteristics, leading to enhanced supercapacitor electrodes.

• Quantum mechanical modeling: Advancements in theoretical computational techniques, particularly quantum mechanical modeling (e.g., DFT, tight binding, etc.), can be harnessed to predict the quantum capacitance of 2D materials accurately. This can guide experimental efforts and reduce the need for extensive trial-and-error experiments. Moreover, machine learning and artificial intelligence can also play a leading role in modeling quantum capacitance, allowing for the rapid screening of materials and configurations.

• Multiscale modeling: Integrating multiscale modeling approaches that bridge quantum mechanical calculations with meso- and macroscopic simulations (e.g., electronic structure, interfacial charge transfer, defect density, and surface work function) can provide a comprehensive understanding of quantum capacitance effects in real supercapacitor devices.

• Materials engineering: Future research may focus on engineering the band structures of 2D materials through doping, strain engineering, defect engineering, or heterostructure design to tailor their quantum capacitance for specific applications.

• Device integration: Integration of 2D-material-based supercapacitor electrodes into practical devices from small flex devices for personal use to large-scale commercial energy storage, such as wearable electronics or energy storage systems used for hybrid electric vehicles, will be crucial. This involves addressing scalability, stability, and compatibility issues.

• Energy storage system optimization and measurement guidelines: Beyond materials, future research should focus on the holistic optimization of supercapacitor systems, including electrolytes and device architectures, to maximize the benefits of high-quantum capacitance materials. Moreover, one has to pay attention to the electrochemical measurements at current density, potential, and electrolyte concentrations. For example, reporting the specific capacitance of the device and/or electrode equal or above a 20 mV/s scan rate or a 2 A/g current density is more useful. The information on self-discharge, leakage current, and cell voltage considering the potential drop is other important parameters that can be taken into account.

• Standardization and benchmarking: Developing standards and benchmarking protocols for measuring the quantum capacitance values will be important for ensuring consistency and reliability in the field.

Incorporating these future perspectives into research methodologies, both experimental and modeling, will contribute to the continued advancement of 2D-material-based supercapacitor electrodes and their role in the evolving landscape of energy storage technology.

Biographies

Subrata Ghosh is a Marie Skłodowska-Curie Postdoctoral Fellow at Politecnico di Milano, Italy. Prior to his current position, he was awarded a Seal of Excellence Fellowship at Politecnico di Milano and a Brain Korea 21 Postdoctoral Fellowship at Chungbuk National University, Republic of Korea. He continued his research as a research associate at the University of Manchester, U.K., and at the Indira Gandhi Centre for Atomic Research, India. He received Ph.D. degree from Homi Bhabha National Institute, India, in 2016. His research involves designing smart nanostructures of carbon, 2D materials, metal oxide, and their composites, understanding the growth mechanism, and exploring them for next-generation energy storage applications (supercapacitors and batteries). He has published 40 peer-reviewed journal or conference articles and served as a reviewer for Science Citation Index (SCI)-indexed journals.

Sushant K. Behera is a Dr. D. S. Kothari Postdoctoral Fellow at the Indian Institute of Science (IISc), Bengaluru (Karnataka, India). He received his Ph.D. degree in physics from Tezpur University (Assam, India) in 2020. He was a postdoctoral fellow at the National Institute of Science Education and Research (NISER) in Bhubaneswar (Odisha, India). His main research interests are method development within the density functional theory and the application of electronic structure methods for investigations in nanoscience with a special focus on two-dimensional van der Waals quantum materials. He has published 26 peer-reviewed international journals or conference proceedings and 1 book chapter.

Ashutosh Mishra is an assistant professor at Motilal Nehru National Institute of Technology, Allahabad, India. He won a prestigious DGFS Fellowship to pursue his Ph.D. degree in mechanical engineering from Homi Bhabha National Institute, India, and he completed his doctorate in 2016. His area of research is thermomechanical studies, structural mechanics, mechanics of energy storage materials, thermal and mechanical abuse testing of batteries, and material modeling. He worked as an application engineer at Clyde Pumps India Pvt Ltd in 2011, been involved in several government turnkey power projects, and worked as a principal investigator of a funded project on the development of materials for space industries. He has authored 2 book chapters and published 16 journal papers and 2 patents.

Carlo S. Casari is a professor in physics of matter at Politecnico di Milano, Italy. Since 2004, he has been working in the Micro and Nanostructured Materials Laboratory (NanoLab) of the Department of Energy. He was born in Milan, Italy, in 1974, and he graduated in electronic engineering at Politecnico di Milano in 1999 before receiving a Ph.D. degree in materials engineering in 2004. He has experience in the field of nanostructure and nanostructured material, nanostructured metal oxide, and carbon-based nanomaterial deposition of thin films, scanning probe techniques (atomic force microscopy and scanning tunneling microscopy), and inelastic light scattering [Raman, surface-enhanced Raman spectroscopy (SERS), and Brillouin, even in situ]. He has published more than 140 papers [more than 120 in International Scientific Indexing (ISI) journals].

Kostya Ken Ostrikov is an expert in plasma applications for the production of advanced functional nanomaterials, electrified processes for clean energy and green chemistry technologies, catalysis, and nanotechnology. His achievements include multiple high-profile honors and awards, including the Humboldt Research Award, Foreign Member of the European Academy of Sciences and Academia Europaea, and Building Future Award. His experience in synthesis and modification of materials using diverse sources, material design, and fabrication techniques is translated into applications toward energy-efficient, green technologies for a sustainable future.

The authors declare no competing financial interest.