Characterization and Finite Element Validation of Transchondral Strain in the Human Hip during Static and Dynamic Loading

Abstract

Distribution of strain through the thickness of articular cartilage, or transchondral strain, is highly dependent on the geometry of the joint involved. Excessive transchondral strain can damage the solid matrix and ultimately lead to osteoarthritis. Currently, high-resolution transchondral strain distribution is unknown in the human hip. Thus, knowledge of transchondral strain patterns is of fundamental importance to interpreting the patterns of injury that occur in prearthritic hip joints. This study had three main objectives. We sought to 1) quantify high-resolution transchondral strain in the native human hip, 2) determine differences in transchondral strain between static and dynamic loading conditions to better understand recovery and repressurization of cartilage in the hip, and 3) create finite element (FE) models of the experimental testing to validate a modeling framework for future analysis. The transchondral strain patterns found in this study provide insight on the localization of strain within cartilage of the hip. Most notably, the chondrolabral junction experienced high tensile and shear strain across all samples, which explains clinical data reporting it as the most common region of damage in cartilage of the hip. Further, the representative FE framework was able to match the experimental static results and predict the dynamic results with very good agreement. This agreement provides confidence for both experimental and computational measurement methods and demonstrates that the specific anisotropic biphasic FE framework used in this study can both describe and predict the experimental results.

INTRODUCTION

Mechanical overload of articular cartilage can result in damage to the solid matrix and ultimately lead to osteoarthritis (OA) (Henak et al., 2017; Occhetta et al., 2019). Variations in strain through the thickness of the articular layers, referred to herein as transchondral strain, can result in distinct types of damage. In the superficial zone (at the articular surface), the most common damage pattern is fissuring due to tensile strain overload (Atkinson et al., 1998; Henak et al., 2017; Kelly and O’Connor, 1996; Thompson et al., 1991; Wilson et al., 2006). In contrast, shear overload within the middle or deep layers can lead to delamination (Askew and Mow, 1978; Ateshian et al., 1994; Beck et al., 2005; Broom et al., 1996; Flachsmann et al., 1995). Thus, knowledge of transchondral strain patterns is of fundamental importance to interpreting the patterns of injury that occur in prearthritic joints.

Despite the importance of transchondral strain variations to interpreting injury patterns, little is known regarding transchondral strains in the articular layers of the hip in situ. This is primarily due to the difficulty in obtaining experimental strain measurements from the congruent and confined geometry of the hip joint and the relatively thin dimensions of the articular layers. Although previous studies have measured one-dimensional compressive strain (changes in thickness of the articular layers) in the hip in vivo using MRI or CT (Greaves et al., 2009; Greaves et al., 2010; Kim et al., 2019), these methods do not provide sufficient spatial resolution to quantify transchondral gradients in tensile, compressive, and shear strain. If higher resolution measurements of transchondral strain components could be achieved, the resulting data would provide an improved understanding of loading of the articular layers in the normal hip joint and possible mechanisms of cartilage damage.

Our study had three main objectives. First, we sought to quantify transchondral strain in the human hip via an experimental setup that allowed direct visualization of the cross-sectional deformation of the articular layers. We hypothesized that transchondral strain patterns would show localization of strain and provide insight to corresponding mechanisms for tissue overload. Next, we determined differences in strain between static and dynamic loading conditions to better understand recovery and repressurization of cartilage in the hip. We hypothesized that static and dynamic loading would produce different magnitudes of compressive strain over time due to fluid repressurization during the unloading phase of dynamic loading. Finally, FE models of the experimental testing were analyzed to compare with experimental strain results to validate the modeling framework. Using this comparison, we hypothesized that a biphasic constitutive model with a physiological fibril distribution mapped via gradient through the thickness and strain-dependent, anisotropic permeability could describe and predict the experimentally measured mechanical response of articular cartilage in the human hip.

METHODS

Specimen preparation

Eight hip samples from four donors with no visible evidence of cartilage damage were tested (3 male and 1 female, BMI 23.12 – 29.4 kg m⁻², age 42–66 years ). We used stringent selection criteria for the donors to avoid factors known to degrade cartilage quality, specifically we required age < 65 years, BMI < 35, and no history of diabetes, smoking, arthritis, radiation therapy, osteoporosis, or bone metastasis. The hip capsule was left intact while all other tissue was removed. The frozen joint was mounted in a custom jig with adjustable brackets and sectioned with a vertical band saw (Hobart Corporation, Troy, OH) at a plane 30° anterior to the coronal plane (Figure 1A). This plane bisected a region of high loading and incidence of chondral injury in the hip. (Kapron et al., 2019)

Figure 1:

Sectioning and mounting of the hip joint. A) Mockup of the experimental sectioning of the hip joints, showing a YZ viewpoint of the XZ sectioning plane oriented in the saw. Sectioning of the joint was oriented 30° anterior to the coronal plane. B) After sectioning, the joint was aligned with the femoral neck parallel to the direction of loading (Z axis), and the acetabulum was aligned according to its position during sectioning, with the top edges of the labrum aligned perpendicular to the femoral neck (on the X axis). C) The hip joint was potted in custom fixtures and positioning was further refined with an XY translation stage. D) Verhoeff’s stain was applied to the joint using an airbrush for digital image correlation to compute high-resolution strain.

The sample preparation in this study follows the protocol of a previous study that determined transchondral strain in the patellofemoral joint. (Guterl et al., 2009) The femur and acetabulum were separated and potted in custom fixtures with polymethyl methacrylate (PMMA; Fricke Dental International, Inc., Streamwood, IL, USA). The joint was aligned so the loading vector would be applied in a reproducible and physiologically-relevant manner; with the femoral neck parallel to the direction of loading (Z axis) and the acetabulum aligned with the top edges of the labrum aligned perpendicular to the femoral neck (on the X axis) (Figure 1B). The applied loading vector was chosen for repeatability and did not directly correspond to a particular activity of daily living; however, the orientation is similar to a standing position since the custom jig orientation puts the hip in a neutral position with about 0° flexion. Verhoeff’s stain was applied to the cut plane via airbrush to create a speckle pattern for strain tracking through digital image correlation (DIC).

Testing protocol

The samples were mounted in a material testing machine (ElectroForce 3300 Series II, TA Instruments, Eden Prairie, MN). The sectioned plane was positioned against an acrylic plate so the cross-section of the articular cartilage could be visualized during testing (Figure 1B). X- and Y-axis translation stages, mounted below the acetabular fixture, were used to align the joint and to ensure that both cartilage layers sealed against the acrylic plate to prevent fluid flow out of the cartilage. The acetabular fixture was filled with 1xPBS at room temperature to retain normal hydration of the articular layers. The actuator was vertically displaced to a zero-load configuration, where the femoral cartilage was seated within the acetabular cartilage, but no force was applied through the femur. This was achieved by adjusting the x- and y- translation stages that were affixed below the acetabular fixture. The samples were allowed to equilibrate in the test bath for 10–20 minutes before testing. For all tests, a preload was applied with a sinusoidal waveform between 25–100% donor body weight (BW) at 0.5 Hz for 2 minutes. The tissue was allowed to recover for 1 hour. Next, static loading was applied at 100% BW for 10 minutes. The tissue recovered again for 1 hour. Finally, dynamic loading was applied in a sinusoidal wave pattern between 25–100% BW at 1 Hz for 10 minutes. The tests were recorded with a digital camera with a 100 mm 1:1 macro lens with a resolution of 1920 × 1200 pixels at 30 frames/sec. The average resolution was 35 μm per pixel. The cartilage thickness for the samples ranged between 1.5 and 2.5 mm, corresponding to between 43 and 71 pixels through the thickness of the cartilage.

Data analysis

Strain fields were computed from the image sequences using commercial DIC software (VIC-2D, Correlated Solutions, Irmo, SC). All analyses utilized search window sizes (subset sizes) of 27×27 pixels surrounding data analysis points, which were incrementally chosen at every second pixel horizontally and vertically throughout the region of interest (step size of 2). Each image was compared to the reference image for correlation with a confidence margin of 0.05 pixels.

First (E₁, most tensile) and second (E₂, most compressive) principal Lagrange strain and maximum shear strain (G_max) fields were determined over time. Maximum shear strain was calculated as G_max = |E₁-E₂|/2 under the assumption that the out-of-plane shear strain components were negligible. Transchondral strain values were compared quantitatively in the femoral cartilage at the location of maximum compressive strain at short-time (10 s after load applied to account for any early noise) of static loading. For comparison, the strain values through the thickness were normalized to the sample’s maximum strain value and plotted as a function of relative position between the osteochondral interface and articular surface. For the quantitative transchondral analysis, we focused on the femoral cartilage due to noise from the attachment site of the femoral ligament in the acetabular cartilage of some samples.

Finite element simulation of experiments

We created a finite element (FE) model representing the experimental setup in order to optimize biphasic material parameters to describe the static strain results and subsequently evaluate the model’s ability to predict the dynamic results. The FE model was created by fitting hemispheres to the cartilage surfaces of a representative specimen (Figure 2A). The cartilage layers were assigned a constant thickness of 2 mm based on reported values of thickness in hip cartilage (Anderson et al., 2008; Liu et al., 2016; Shepherd and Seedhom, 1999). The assumptions for the FE model were chosen to provide accurate prediction of the magnitude and trends of compressive strain over time. This was done so the general model could be optimized with the average data and confirm that general trends of cartilage under static and dynamic loading could each be predicted with our constitutive framework.

Figure 2:

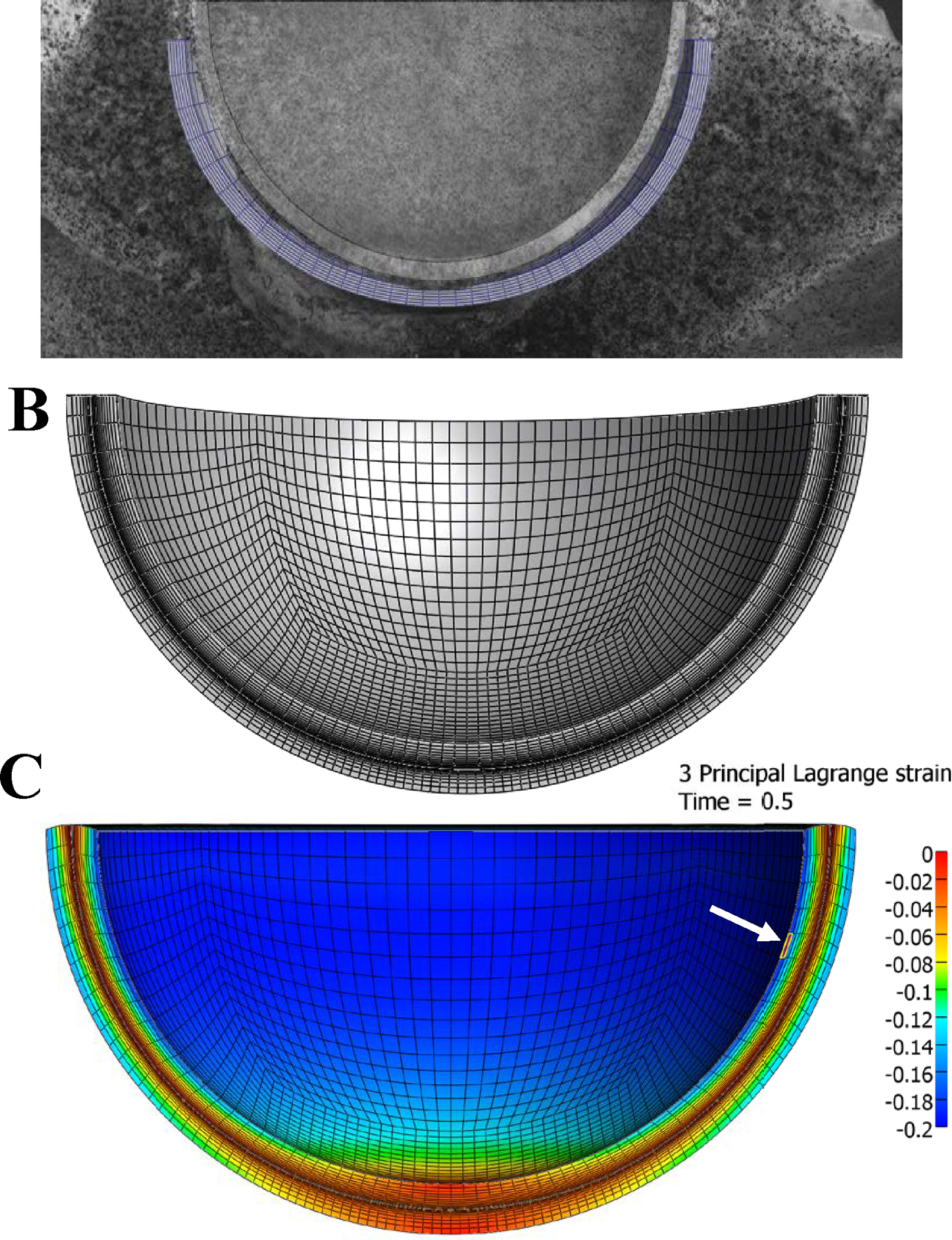
Construction of finite element mesh. A) Hemispheres were fit to the articular cartilage layers of a representative sample. B) the resulting hemispheres were discretized using linear hexahedral elements finite element representation of the transchondral strain experiment. The converged mesh consisted of 59,904 linear hexahedral elements, with 12 elements through the thickness of each articular layer, biased towards the articular surface. C) Representative finite element prediction of compressive strain (3rd principal strain) pattern at loading and element location of maximum compressive strain used for data collection (white arrow).

The constitutive model was set to represent the physiological characteristics of articular cartilage and matches a previous FE simulation of cartilage mechanics in the human hip (Todd et al., 2018). It consisted of a biphasic material with a neo-Hookean ground matrix reinforced with a continuous fibril distribution. The collagen fibril orientation was varied through the thickness of the articular cartilage to match physiological orientation of collagen fibrils. The permeability was strain-dependent and anisotropic, with the radial permeability selected to be ten times greater than the permeability in the circumferential direction (Reynaud and Quinn, 2006).

The subchondral bone was assumed to be rigid and the osteochondral interfaces were represented by prescribing zero displacements to the nodes on the relevant surfaces. Nodes on the cut plane were fixed in the direction normal to the plane to simulate the constraint of the acrylic plate in the experiment. Free-draining conditions were set between the cartilage layers while the bony interfaces on the cut plane were impermeable. Loading was applied through the femur identically to the experimental conditions and the body weight of the representative sample was used. All FE models were created and analyzed using the FEBio software suite (Maas et al., 2012).

A mesh convergence study was performed by increasing mesh refinement through the thickness of the cartilage and across the surface. The mesh was considered converged when doubling the elements in either direction resulted in less than 5% difference in maximum compressive strain. The final model consisted of 59,904 linear hexahedral elements, with 12 elements through the thickness biased towards the articular surface (Figure 2B). The location of maximum compressive strain sampled for the convergence study and for subsequent analysis is shown in Figure 2C.

Optimization of material coefficients

The initial material coefficients were selected to match those used in previous FE simulations of cartilage mechanics in the human hip (Todd et al., 2018). Neo-Hookean elastic modulus, initial fibril modulus, and permeability were determined to be key parameters, as these parameters had the greatest effect on strain magnitude. The FEBio optimization framework (using the Levenberg-Marquardt method) was used to determine the material coefficients which produced the best correlation to the experimental compressive strain data during static loading over time. The FEBio parameter optimization module minimizes an objective function $f\left(\mathit{a}\right)$ of the form:

$$f\left(\mathbf{a}\right)=\sum _{i=1}^n{\left[y_i-y\left(x_i;\mathbf{a}\right)\right]}^2,$$

where the vector $\mathit{a}$ contains the material coefficients (described on lines x-x) that minimize the function. In this application, the data pairs ${(x_i,y}_i)$ represent the average compressive strain response during static loading, where $y_i$ is the experimental compressive strain at time $x_i$ and $y\left(x;\mathbf{a}\right)$ is the function that extracts the corresponding data from the FE model.

The resulting optimized material coefficients were then used in a separate forward FE analysis of the model under dynamic loading conditions to assess their predictive capability.

Statistical analysis

Agreement between experimental and FE results was determined using average error and root-squared-mean-deviation (RSMD). Error was calculated as the absolute value of the difference between FE strain and experimental strain at each timepoint. For static data, FE model timepoints were set to the respective experimental timepoints for direct comparison. Dynamic comparisons were performed by first obtaining the moving average of experimental and FE data, then interpolating FE data to match timepoints of experimental data.

Changes in strain over time were compared for both static and dynamic sample data between loading and after 600 s by fitting a multilevel model with repeated measures from time (0 and 600 seconds) nested within hip (left hip/right hip) and hip nested within subject (α = 0.05) {Aarts, 2014 #42}. This mimicked a paired sample t-test accounting for lack of independence introduced by having two hips per subject. Additionally, changes in each strain component (tensile/compressive/shear) between transchondral regions (superficial/middle/deep) at loading were compared by fitting a multilevel model with repeated measures from transchondral location (deep, middle, superficial) nested within hip and hip nested within subject (α = 0.05). The normalized distance from the osteochondral interface was used to divide the cartilage layer evenly into three regions, and the data within these regions were each compared.

RESULTS

Transchondral strain patterns in the femoral cartilage showed that E₂ and G_max were highest in the deep zone, whereas E₁ was highest in the superficial zone of the cartilage (Figure 3A–C). Significant differences were found between transchondral regions for each strain component (tensile/compressive/shear, p < 0.05) except for G_max between deep and middle layers, where p = 0.075 (Figure 3D). Across all samples, strain component magnitudes, particularly tensile and shear strain, were elevated in the region near the chondrolabral junction. Transchondral strain patterns were similar between static and dynamic loading scenarios, though the magnitude of strain differed. Over time, there was a significant decrease in static compressive strain (−11.6% ± 5.06% to −17.5% ± 6.22% over 600 s, p = 0.025) (Figure 4). Dynamic compressive strain also significantly decreased over time (−10.5% ± 4.28% at loading and −14.44% ± 7.09% at 600 s, p = 0.013).

Figure 3:

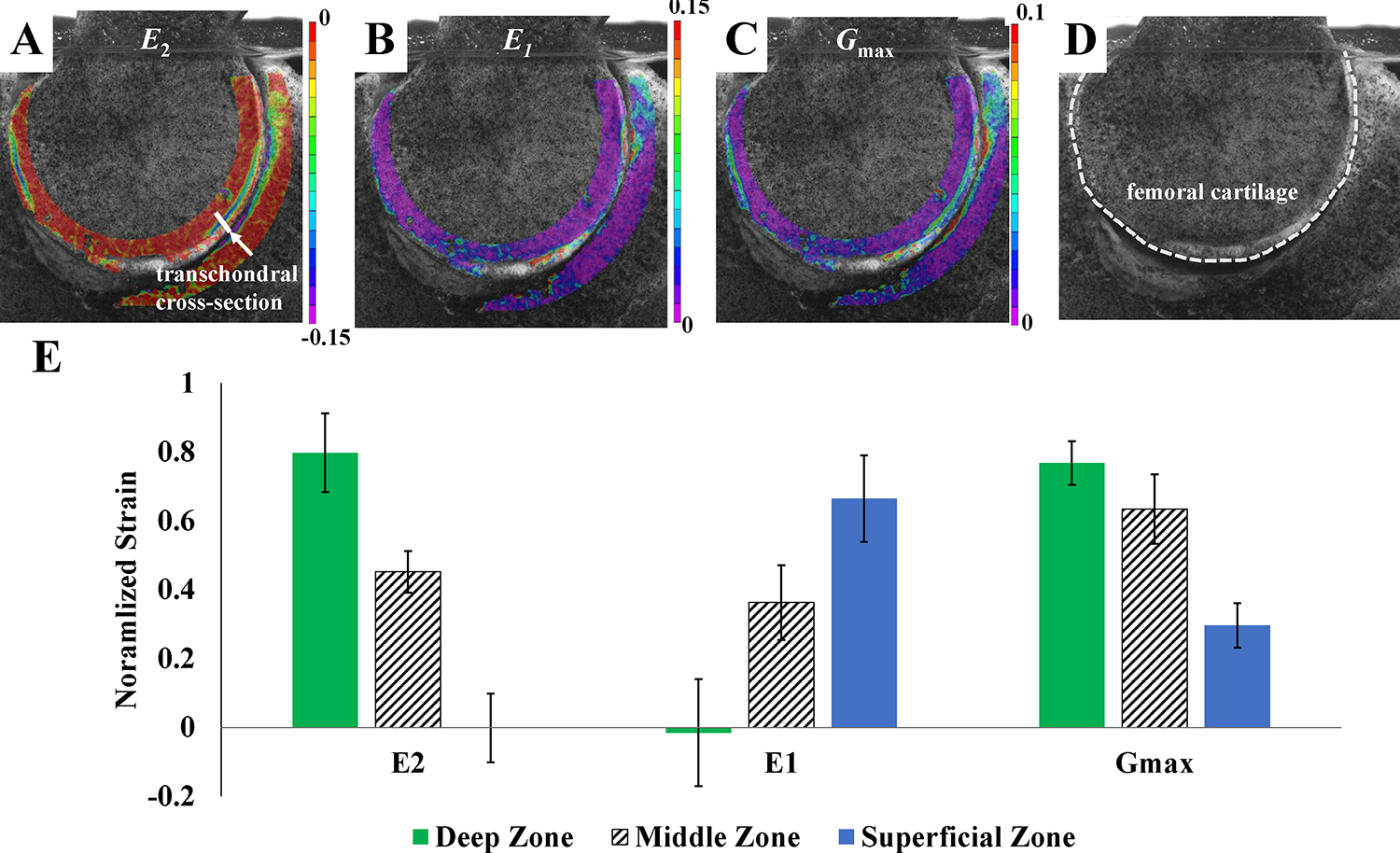
Experimental results for transchondral strain for A) compressive strain (E₂), B) tensile strain (E₁) and C) maximum shear strain (G_max). Strain components experienced concentrations in the region near the chondrolabral junction, particularly tensile (E₁) and shear strain (G_max). D) The femoral cartilage boundary is marked for clarity. E) Transchondral strain values were compared quantitatively in the femoral cartilage (across the transchondral cross-section marked in panel A) under static loading at short-time (10 s after load applied to account for any early noise). Transchondral strain values were normalized to the maximum strain in the sample and grouped into deep/middle/superficial zone. Across all samples, the compressive (E₂) and shear strain (G_max) components were highest in the deep zone, and tensile strain (E₁) was highest in the superficial zone. Results are mean ± standard deviation.

Figure 4:

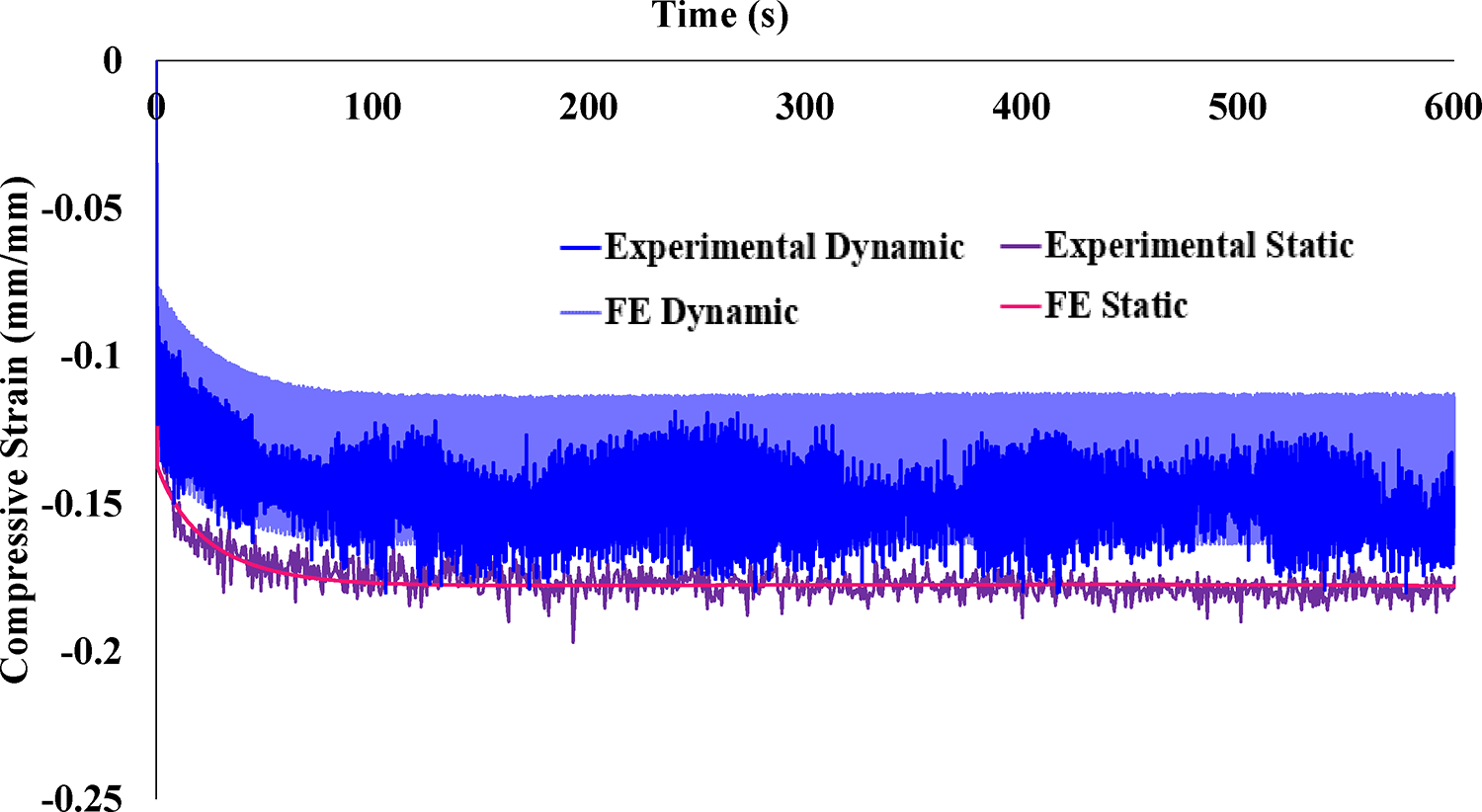
Average experimental compressive strain (E₂) and optimized FE results over time. Error bars on the experimental data have been omitted for clarity. Static loading produced a steady-state compressive strain of approximately 18%. Dynamic loading compressive strain was lower in magnitude, approximately 15% at equilibrium. The FE model coefficients were optimized using the static experimental data, and the FE results for the dynamic case were obtained using those best fit coefficients. The resulting FE model provided an excellent description of the static strain-time curve as well as excellent prediction of the dynamic strain-time curve.

FE simulations of the experiment with optimized material coefficients demonstrated very good agreement with the compressive strain over time for the average static experimental data (Figure 4). The average error between experimental and FE results during static loading was 0.346% strain and the RMSD was 1.944×10^-05. When the dynamic loading scenario was analyzed using material coefficients optimized from the static data, the model predictions of compressive strain also demonstrated very good agreement with the average dynamic experimental results. The average error during dynamic loading between experimental and FE results was 1.367% strain and the RMSD was 5.016×10^-03. Final optimized parameters are listed in Table 1. Qualitative comparison of the compressive strain results shown in Figure 2C and Fig 3A show good agreement between the transchondral trend of compressive strain, which is highest at the osteochondral interface. Individual samples were also optimized in the same manner and demonstrated good agreement with the static and dynamic experimental data, though geometric differences for each sample affected magnitude and localization, and our approach used the idealized the geometry to focus on validation of overall magnitude and trends to approximate the average hip response. Once the FE material coefficients were optimized, fluid pressure results were compared between static and dynamic scenarios. Fluid pressure was measured at the location of maximum compressive strain (location shown in Figure 2C) and experienced depressurization in the static case (−11.6% from 0.259 MPa at loading compared to 0.229 MPa after 600 s), whereas the peak fluid pressure during dynamic loading remained constant (approximately 0.259 MPa) (Figure 5).

Table 1:

(column width)

	Initial Coefficients (Todd 2018)	Optimized Coefficients	Literature Range, Human Articular Cartilage (Athanasiou 1994; Demarteau 2006)
Elastic modulus	1.2 MPa	0.101 MPa	Aggregate modulus: 0.679 – 1.816 MPa
Initial Fiber Modulus (ξ)	9.19 MPa	1.32 MPa
Permeability	0.00895 mm4/N-s (transchondral) 0.00475 mm4/N-s (radial)	0.1 mm4/N-s (transchondral) 0.01 mm4/N-s (radial)	0.00025 – 0.001133 mm4/N-s

Figure 5:

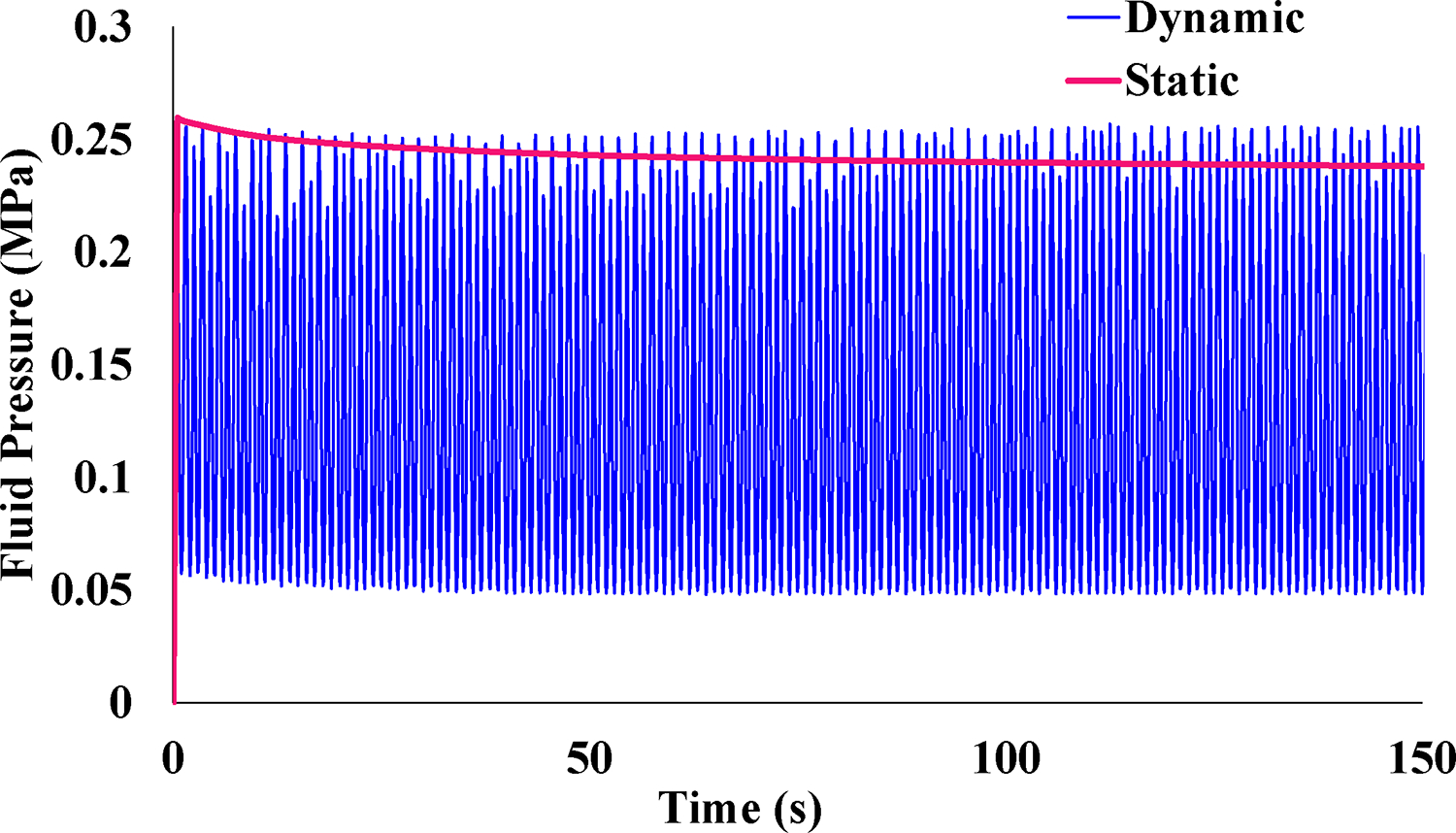
Once the FE material coefficients were optimized, fluid pressure results were compared between static and dynamic scenarios. Fluid pressure measured at the element of maximum compressive strain experienced significant depressurization in the static case (−11.6% from 0.259 MPa at loading compared to 0.229 MPa after 600 s), while the peak fluid pressure during dynamic loading remained constant (approximately 0.259 MPa). 150 s out of 600 s total is shown for better visualization.

DISCUSSION

The transchondral strain patterns found in this study provide insight into the localization of strain within cartilage of the hip. Clinically, the chondrolabral junction is the most common region of damage in cartilage of the hip (Kapron et al., 2019; Kaya et al., 2016). In the current study, this region experienced high tensile and shear strain across all samples. These strain components are largely responsible for cartilage fissuring and delamination, respectively and this result may indicate that the area is at risk for damage due to strain overload. Further, although it is widely reported that the labrum functions as a fluid seal for the hip, Todd et al suggested that it may be more important as a mechanical boundary to prevent deformation of the cartilage edge. (Todd et al., 2018) The high degree of strain near the labrum seen in the current study provides further justification for targeted labral repair strategies, which prioritize the labrum’s function to prevent excess deformation of the cartilage edge.

Comparison of static and dynamic loading shows dynamic loading may protect the solid matrix of articular cartilage from high compressive strain. The fluid pressure results from our finite element model may explain this result, since the dynamic loading scenario preserved the high fluid pressurization in areas of elevated compressive strain, whereas the cartilage depressurized over time under static loading. Similar results have been reported for the recovery of cartilage during sliding due to rehydration with migrating contact area (Caligaris and Ateshian, 2008; Graham et al., 2017).

Our representative FE model was able to match the static results and predict the dynamic results with very good agreement. This finding supports our confidence in both experimental and computational measurement methods and demonstrates that our specific FE model can both describe and predict the experimental measurements of strain. Thus, the framework can be applied to future modeling studies for further analysis of strain in varied conditions placed on the hip.

The FE material coefficients determined in this study provide insight into the relative properties of physiological constituents for articular cartilage within the current modeling framework. Previous studies have reported aggregate moduli of human articular cartilage tested in unconfined compression or biphasic creep indentation between 0.679 – 1.816 MPa (Athanasiou et al., 1994; Demarteau et al., 2006), compared to 0.101 MPa found in this study for the neo-Hookean elastic modulus of the ground matrix with fibril reinforcement with an initial modulus of 1.32 MPa. Although the permeability values found in the current study of 0.1 mm⁴/N-s (transchondral) and 0.01 mm⁴/N-s (radial) are higher than the hydraulic permeabilities of 0.00025 – 0.001133 mm⁴/N-s reported from human articular cartilage (Athanasiou et al., 1994; Demarteau et al., 2006), the strain-dependent permeability constitutive equation causes apparent permeability to decrease in areas of compression, which likely explains our higher initial permeability value.

Although there is a wide range of compressive strain values reported for cartilage of the hip joint, as well as other joints, the range of compressive strain in the present study is likely more accurate due to the high-resolution measurements allowed with DIC. MRI studies of static loading in the hip report maximum compressive strains of 31–45% for intact cartilage (Greaves et al., 2009; Greaves et al., 2010). Even greater ranges in compressive strain have been reported in other joints; for example, maximum compressive strains in the tibiofemoral joint are reported to range from 7–35% during dynamic activities (Lad et al., 2016; Liu et al., 2010). The larger variation in strain may be due to methodological differences, such as applied load magnitude and contact area achieved, or resolution of the strain measurement method. To this point, Henak et al. measured both bulk strain (calculated using manually measured sample depth and cartilage deformation metrics from intensity-based image registration) and local strain (computed through DIC) of cartilage samples and reported the peak local second principal strain (most compressive strain) was about 3.5 times larger than the peak bulk strain (also compressive) (Henak et al., 2017). Therefore, large discrepancies may occur between measurement methods. Since the donors used in the current study were relatively young with no known joint issues, and considering the magnitude of compressive strain reported to induce cellular changes is around 30% (Occhetta et al., 2019), our compressive strain magnitudes (which equilibrated around 18% and 15% for static and dynamic loading, respectively) are within a reasonable range and are likely representative of the expected nominal range during activities of daily living.

Although the transchondral strain patterns found in this study shed light on deformation in the context of the hip joint, the findings are in agreement with analytical and computational results for general cartilage models. Askew et al. analytically solved an anisotropic, inhomogeneous, layered, continuum model of a cartilage layer with an axisymmetric, parabolically distributed, normal traction applied over a circular area (Askew and Mow, 1978). For this model, the bone was modeled as elastic with a modulus 2 orders of magnitude higher than cartilage. Ateshian et al. also used an analytical model with two biphasic cartilage layers placed on two rigid, impermeable bones of equal radii (Ateshian et al., 1994). Both studies found high shear stresses at the cartilage-bone interface and concluded this result is caused by the stark change in stiffness between cartilage to bone. Further, Meng et al. performed a rigorous parametric study on the effects of fibril orientation in a biphasic finite element model representing a cartilage layer (Meng et al., 2017). When the fibril orientation for their models was derived from diffusion tensor magnetic resonance (DT-MR) data, the strain results agreed with the current study: maximum compressive and shear strain were found on the osteochondral interface and tensile strain concentrations were seen at the articular surface.

Interestingly, although transchondral results for the current FE model showed concentrations of compressive and shear strain at the osteochondral interface, the model did not predict maximum tensile strain values at the articular surface. A similar result was reported by Meng et al. when orthotropic fibril models with distinct zones of varied orientation were used (Meng et al., 2017). However, as stated above, the DT-MR results compared well with our experimental results, with concentrations of tensile strain at the articular surface. Meng et al. noted that differences in transchondral strain results between the DT-MR and zonal orthotropic fibril orientation models were likely due to the higher degree of disorder in the orientation of the collagen fibril bundles and concluded it may be necessary to incorporate a physiologically realistic orientation of the fibers to determine localization of stress/strain in the cartilage layer. Based on the discrepancy between strain results of the current FE model and DT-MR-based fibril orientation model by Meng et al., the current modeling approach may require further refinement of fibril orientation to predict better transchondral localization of tensile strain in articular cartilage.

A few limitations of the current study should be noted. First, sectioning of the joint could have disrupted the fibril reinforcement and caused softening of the cartilage. Second, the loading vector applied was chosen for repeatability and did not directly correspond to a particular activity of daily living; however, the orientation is similar to a standing position since the custom jig orientation puts the hip in a neutral position with about 0° flexion. Also, the labrum was not directly loaded with this loading vector, so its influence was not directly studied. However, previous studies have found that the labrum supports little load during walking for normal hips (Henak et al., 2014; Henak et al., 2011). Further, the FE model was created by fitting hemispheres of constant thickness to a representative specimen. Previous models have shown that idealized geometry and constant cartilage thickness influence the FE results (Anderson et al., 2010); however, the goal of the FE study was not to quantify specimen-specific results, but to provide material properties for a general population and validate the constitutive framework for strain predictions. A more general model could be optimized with the average data and confirm that trends of cartilage under static and dynamic loading could each be predicted with our constitutive framework. Additionally, the slight variation of peak values reported for the dynamic FE results is due to the viscoelasticity of the material, as well as our sampling method. The peak strain and especially the peak fluid pressure values were not exactly aligned with the peak loading due to the viscoelasticity of the material. The model used an average timestep of 0.100 s during the 600 s. This resulted in high temporal resolution but sometimes did not capture the absolute peak values.

There were several notable advances of the current study. To our knowledge, this is the first report of direct transchondral strain measurement in the human hip. We used young donors with healthy cartilage, which provides an accurate assessment of the natural state of the hip joint. Our FE validation process incorporated a highly complex and physiological constitutive model, consisting of a biphasic neo-Hookean ground matrix reinforced with a continuous fibril distribution mapped via gradient through the thickness, as well as strain-dependent, anisotropic permeability. The validation of this model demonstrates that our specific framework can both describe and predict the experimental results.