Temporal Variation in Introgressed Segments’ Length Statistics Computed from a Limited Number of Ancient Genomes Sheds Light on Past Admixture Pulses

Abstract

Hybridization is recognized as an important evolutionary force, but identifying and timing admixture events between divergent lineages remain a major aim of evolutionary biology. While this has traditionally been done using inferential tools on contemporary genomes, the latest advances in paleogenomics have provided a growing wealth of temporally distributed genomic data. Here, we used individual-based simulations to generate chromosome-level genomic data for a 2-population system and described temporal neutral introgression patterns under a single- and 2-pulse admixture model. We computed 6 summary statistics aiming to inform the timing and number of admixture pulses between interbreeding entities: lengths of introgressed sequences and their variance within genomes, as well as genome-wide introgression proportions and related measures. The first 2 statistics could confidently be used to infer interlineage hybridization history, peaking at the beginning and shortly after an admixture pulse. Temporal variation in introgression proportions and related statistics provided more limited insights, particularly when considering their application to ancient genomes still scant in number. Lastly, we computed these statistics on Homo sapiens paleogenomes and successfully inferred the hybridization pulse from Neanderthal that occurred approximately 40 to 60 kya. The scarce number of genomes dating from this period prevented more precise inferences, but the accumulation of paleogenomic data opens promising perspectives as our approach only requires a limited number of ancient genomes.

Introduction

Hybridization is defined as the interbreeding between divergent lineages and is widespread in nature (Mallet 2005; Schwenk et al. 2008; Payseur and Rieseberg 2016). Where crossing between populations or species produces viable and fertile hybrids capable of backcrossing with parental individuals, genetic material can be transferred between lineages resulting in introgression. Previously underappreciated, recognition of the commonness of introgressive hybridization has stimulated research for both its detection and characterization. This includes interest in studying the direction, the frequency, the magnitude, the timing, the duration, and the mode of introgression (i.e. admixture pulses or continuous exchange of genetic material between lineages). While pulses of admixture are intuitively understood as discrete periods of interbreeding between divergent entities, it remains ambiguously characterized and poorly understood. Note that we will use the word “lineages” to refer to evolutionary units at different taxonomic levels, whether genus, species, subspecies, or groups of individuals within species.

Over the last decades, multiple approaches have been designed to study introgression (Payseur and Rieseberg 2016; Corbett-Detig and Nielsen 2017; Medina et al. 2018; Shchur et al. 2020; Gower et al. 2021; Iasi et al. 2021; Hibbins and Hahn 2022). Among phylogenetic-based techniques, the D-statistic, or ABBA-BABA test (Green et al. 2010; Durand et al. 2011), has been the most widely used to infer gene flow between lineages (Eaton and Ree 2013; Streicher et al. 2014; Good et al. 2015; Maxwell et al. 2019). With the advent of next-generation sequencing technologies, large genomic data sets could be generated across many individuals, fostering the inclusion of coalescence modeling into the hybridization analytical toolbox. Combined with approximate Bayesian computation (Beaumont et al. 2002; Blum and François 2010), these methods have provided a powerful means to detecting among-lineage gene flow (Rougemont and Bernatchez 2018; Mondal et al. 2019; Di Santo et al. 2022). Importantly, these methods leverage present-time genetic information to infer historical gene flow, whereas patterns in introgression statistics evaluated temporally throughout ancient and modern samples may be able to provide a clearer picture of a lineage admixture history.

Following hybridization, genomic fragments from a donor lineage will enter a recipient lineage and only shorten with every backcrossing event due to recombination. Researchers have noticed the potential of this dynamic across generations to estimate the timing of admixture (Gravel 2012; Corbett-Detig and Nielsen 2017; Skov et al. 2018; Iasi et al. 2021), the strength of admixture (Pool and Nielsen 2009), and, more recently, the duration of admixture (Iasi et al. 2021), as well as the strength of selection (Shchur et al. 2020). However, recombination may also challenge the inference of the number of admixture events, as time would most likely erase signatures of hybridization pulses within the genome (but see Medina et al. 2018). If previous studies were based on the analysis of large samples of contemporary genomes (Gravel 2012; Ni et al. 2016; Fortes-Lima et al. 2021), analyzing the size distribution of introgressed fragments in time series genomic samples may present a promising avenue to accurately estimating the number and timing of multiple admixture events between lineages.

Genomic summary statistics including the average length of introgressed fragments and within-genome variation in introgressed fragments’ lengths could be useful to estimate the number and timing of admixture pulses between hybridizing lineages. On the one hand, they can readily be estimated on single genomes. This is particularly important as the availability of ancient genomes may often be limited. On the other hand, both statistics are expected to vary substantially following gene flow between lineages. Indeed, each pulse of admixture is anticipated to increase genome-wide average of the size of introgressed fragments before the action of recombination with passing generations ultimately erodes their size. Similarly, we predict the influx of longer fragments into a genomic background of shorter segments to increase within-genome variation in introgressed sequences’ (VIS) lengths before the action of recombination homogenizes the size of introgressed fragments over time. This statistic can be computed from ancient individuals in a temporal sequence, making it a very promising candidate for studying archaic admixture. Overall, both average length of introgressed segments and within-genome VIS’s lengths are expected to leave a perceptible and leverageable imprint, but they have yet to be described within a temporal context.

Recent advances in paleogenomics and the ensuing, ever-growing accessibility to ancient human genomes (Mathieson et al. 2018; Olalde et al. 2018; Narasimhan et al. 2019; Wang et al. 2021), together with the considerable attention given to the history of archaic introgression into the genome of Homo sapiens during the past decade (Gopalan et al. 2021; Liu et al. 2021), identify our species as a candidate system to test this analytical framework. All non-African present-day humans share approximately 2% of their genomes with Neanderthal (Homo neanderthalensis) (Green et al. 2010; Reich et al. 2010; Prüfer et al. 2017). This result was first interpreted as evidence for a single pulse (SP) of admixture between H. sapiens and Neanderthals in the Middle East following the Out-Of-Africa (OOA) expansion (Green et al. 2010). However, in contrast to these findings, it was later found that East Asian populations may be more introgressed (by approximately 8% to 20%) than European populations (Wall et al. 2013; Sankararaman et al. 2014; Vernot and Akey 2014; Chen et al. 2020). This led scientists to hypothesize that H. sapiens may have admixed with distinct Neanderthal populations through multiple pulse (MP) of hybridization during their shared evolutionary history (Mondal et al. 2019; Villanea and Schraiber 2019; Taskent et al. 2020). Moreover, a continuous model of hybridization through space and time is also compatible with the current Neanderthal introgression rate in humans (Currat and Excoffier 2011; Quilodrán, Tsoupas, and Currat 2020), although it is difficult to relate this model to a number of pulses. Ultimately, a decade of exploring the overlapping evolutionary history of modern and archaic hominins has shed light on the complexity of studying interspecies hybridization, particularly when one wishes to evaluate the timing, number, and origin of hybridization pulses.

With this study, we first used genomic simulations to explore temporal patterns of introgressed segments’ length and its variation within individuals, in addition to introgression proportions and related statistics, asking the question: can introgression summary statistics through time be leveraged to infer the number and timing of admixture pulses? Subsequently, we applied the knowledge gained from simulations to real empirical data, using the hybridization history between Neanderthals and H. sapiens as a case study, to determine whether hypothesized pulses of admixture between these hominins could be identified based on proposed genomic summary statistics. Our study expands upon previous and contemporary work exploring and characterizing introgressive admixture within and between species, focusing on temporal patterns of admixture tract lengths as well as previously underexplored introgression statistics, within-genome variation in introgressed segments’ lengths, to explicitly infer the number and timing of admixture pulses between divergent lineages. We apply our approach to studying archaic introgression in anatomically modern humans.

Results

Admixture Simulations

Temporal patterns of genomic summary statistics were generated by simulating the neutral genomic evolution through time of 2 populations connected by gene flow (a source—provider of migrants—and a sink—receiver of migrants—population) using individual-based modeling. Each population was populated by multiple individuals, whose genomic background was modeled as a single pair of homologous chromosomes experiencing recombination. Unadmixed individuals carry alleles typical of either the sink population or the source population. We considered 2 distinct models of admixture (Fig. 1), 1 simulating a SP of hybridization (referred to as the SP model, Fig. 1A) and 1 simulating 2 pulses of hybridization (referred to as the MP model, Fig. 1B). We also evaluated the effect of hybridization intensity on between-population exchange of genetic material by simulating both SP and MP with admixture rates of 0.03, 0.1, and 0.3 (hereafter referred to as scenarios). Following simulations, introgression within sink population was summarized using 6 population-scale genomic summary statistics, three of which are discussed and presented here in details: (i) the average length of introgressed sequences (LIS), (ii) the average intraindividual VIS’s lengths, and (iii) the average proportion of introgression (PI). The other remaining summary statistics, including skewness, kurtosis, and standard deviation of the distribution of introgression proportions across individuals, are discussed below and presented in the Supplementary material.

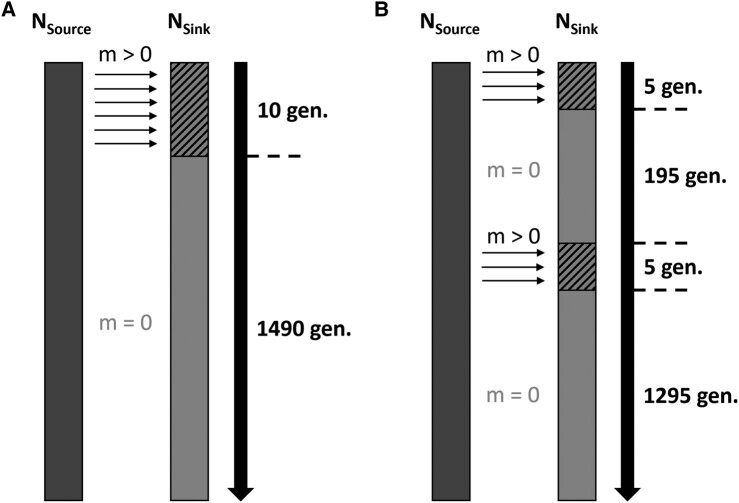
Fig. 1.

Schematics of admixture models, each simulated for a total of 1,500 generations. A) SP model. B) MP model. Rectangles represent source (dark gray) and sink (gray) populations, with solid rectangle depicting generations in isolation and hashed rectangles depicting generations of admixture, small unidirectional arrows symbolize gene flow between populations and indicate its direction, and solid large arrows represent time with the number of generations spent in isolation or admixing given on the side. N_Source/N_Sink, Source/Sink initial population size (100 individuals); m, migration/admixture rate (either 0.03, 0.1, or 0.3 depending on the scenario simulated).

Lengths of Introgressed Sequences

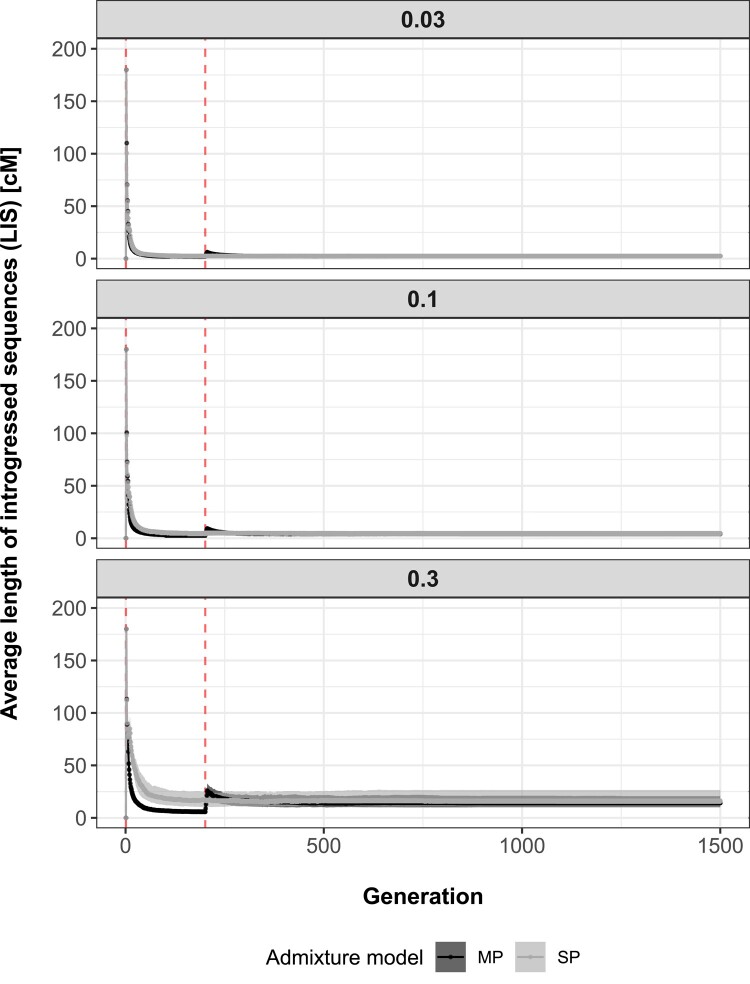
A general temporal pattern in LIS was observed across admixture models (Fig. 2). For the SP model, LIS was the longest at the beginning of the single admixture event, to shorten with advancing generations because of recombination. For the MP model, the same dynamics throughout generations applied, except it occurred twice, once after each admixture pulse. The peak in LIS associated with the second pulse of hybridization was considerably smaller than the one associated with the first admixture pulse for all admixture rate scenarios simulated. Average LIS associated with the second pulse of admixture shall always be smaller, as shorter fragments resulting from recombination occurring during the time interval separating admixture pulses will weigh down these averages. This is particularly evident for small admixture rates, where the input of longer sequences via gene flow is limited. Additionally, as time spent in isolation decreases between bouts of admixture, peaks will come closer and closer to each other until they can hardly or even no longer be teased apart (supplementary appendix S1, Supplementary Material online). This indicates that, to be successfully differentiated, admixture pulses need to be separated by a period of genomic isolation.

Fig. 2.

Average LIS (cM) (y axis) across generations (x axis), assuming a SP of admixture (gray) or MPs of admixture (black). Shaded areas represent interquartile ranges delimited by the 25% (lower limit) and 75% (upper limit) quantiles of the distribution of introgressed sequences’ length averages (based on 100 simulation replicates) at each recorded generation (1 to 1,500), while points and solid lines show median trends. Vertical dashed red lines indicate the generation at which each admixture pulse starts (total time spent admixing: SP—generations 1 to 10, MP—generations 1 to 5 and 201 to 205). Results are separated by simulated admixture rates between source and sink populations (0.03, 0.1, and 0.3).

Simulations also revealed that the speed at which introgressed fragments shorten differs among admixture scenarios as LIS declined faster for smaller admixture rate. In increasing order of admixture rates (0.03, 0.1, and 0.3), decay rates between generations 2 and 200 were estimated at 0.319, 0.197, and 0.059 for SP and 0.363, 0.311, and 0.180 for MP, respectively. This dynamic may reflect a higher probability of homologous introgressed sequences to recombine together with increasing admixture rate, thus slowing down LIS decay. This same dynamic also contributed to the greater difference in LIS between SP and MP during generations separating hybridization pulses, when admixture increases. After the first pulse, there are more introgressed segments within the sink population under the SP model due to a longer period of hybridization (5 vs. 10 generations of admixture for MP and SP, respectively), thus increasing the probability of 2 introgressed segments to recombine, ultimately lowering LIS decay.

Following the second pulse of admixture, average LIS stabilized for both SP and MP to subsequently plateau at similar values, values increasing with admixture rates simulated. Once again, the probability of 2 sequences originating from the source population to recombine within the sink population increases with higher admixture rates, resulting in higher LIS plateaus. Lastly, temporal patterns of LIS were robust to a decrease in the number of generations recorded and the number of individuals sampled within the sink population per generation, although peaks associated with the first event of admixture were often smaller when less individuals per generation were sampled (supplementary appendix S2, Supplementary Material online).

Intraindividual VIS’s Lengths

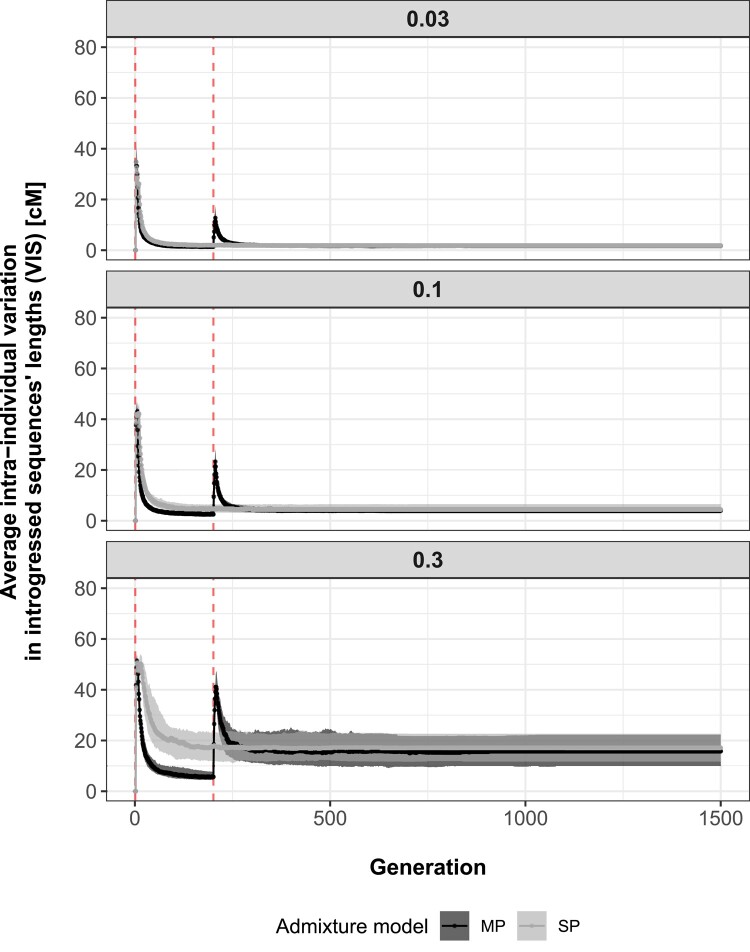
Patterns of average VIS resembled closely those obtained for average LIS (Figs. 2 and 3). For both models (SP and MP) across admixture scenarios, the summary statistic increased at the beginning of hybridization pulses to decrease the following generations due to recombination homogenizing fragments’ sizes within individuals. This process occurred faster as gene flow between populations was small, with VIS decay rates between generations 3 and 200 estimated at 0.082, 0.062, and 0.029 for SP and 0.125, 0.105, and 0.067 for MP under admixture rates of 0.03, 0.1, and 0.3, respectively. The lower probability of 2 introgressed fragments to recombine for small admixture rates likely explains the faster decline of VIS over time.

Fig. 3.

Average intra-individual VIS’s lengths (cM) (y axis) across generations (x axis), assuming a SP of admixture (gray) or MPs of admixture (black). Shaded areas represent interquartile ranges delimited by the 25% (lower limit) and 75% (upper limit) quantiles of the distribution of variation averages (based on 100 simulation replicates) at each recorded generation (1 to 1,500), while points and solid lines show median trends. Vertical dashed red lines indicate the generation at which each admixture pulse starts (total time spent admixing: SP—generations 1 to 10, MP—generations 1 to 5 and 201 to 205). Results are separated by simulated admixture rates between source and sink populations (0.03, 0.1, and 0.3).

As observed for LIS, peaks of VIS associated with the second pulse of admixture were smaller than those characterizing the first pulse. Peaks’ heights were positively correlated with gene flow simulated, becoming taller as the admixture rate increased. On the one hand, the input of longer introgressed sequences from immigration, increasing the range of possible fragments’ lengths within individuals, may explain peaks observed when the second hybridization pulse occurred. Scenario-specific peaks’ heights, on the other hand, are the consequence of a higher expected frequency of recombination between introgressed segments for elevated admixture rates. Indeed, while recombination between introgressed and local segments mainly produces short fragments for small admixture rates, increased probability of recombination between 2 introgressed segments for higher admixture rates may produce a wider range of possible fragments’ lengths (i.e. long, intermediate, and short), overall increasing intraindividual variation. Note that, like observations made with LIS, generations of genomic isolation were necessary to produce admixture pulse-specific VIS peaks (supplementary appendix S1, Supplementary Material online).

As the last admixture pulse ended and the sink population remained genetically isolated, VIS decreased to ultimately stabilize to values increasing with admixture rate. Importantly, as observed previously for LIS, a gap in VIS emerged between admixture models SP and MP during the time interval separating hybridization pulses as admixture rate increased. This phenomenon may result from the same combination of factors as those discussed above for LIS. Finally, while temporal patterns were qualitatively robust against a decrease in the number of generations recorded and the number of individuals sampled within sink population per generation, quantitative differences in peaks’ height could be observed, particularly when a reduced number of individuals were sampled at any given timepoints (supplementary appendix S2, Supplementary Material online).

PI and Related Summary Statistics

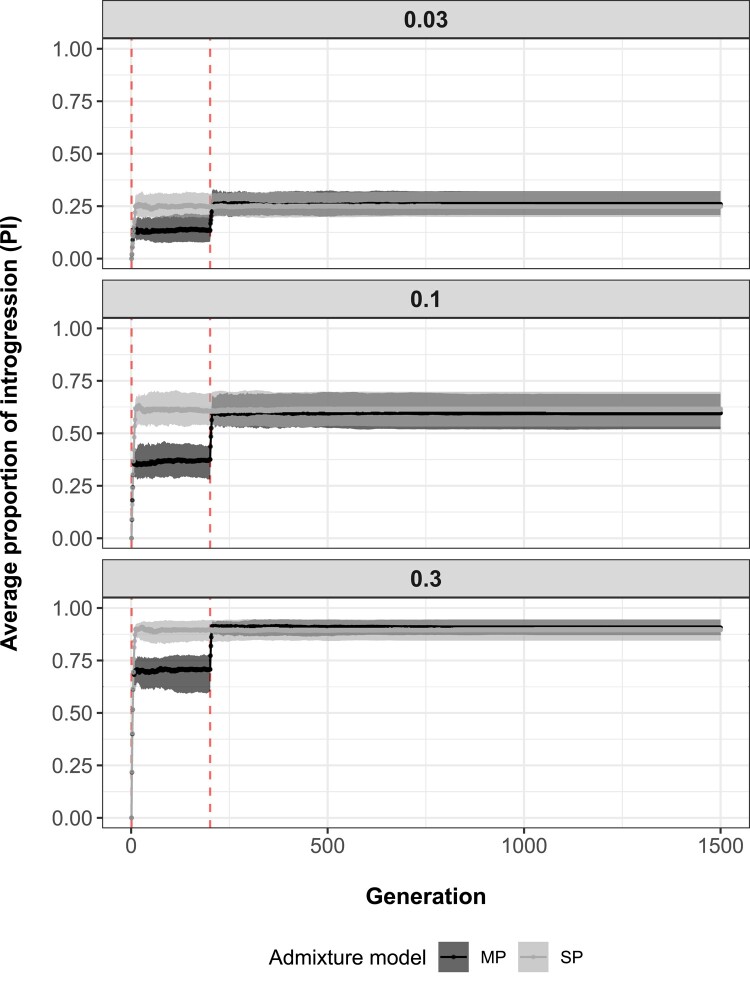
Throughout generations, regardless of the admixture model and scenario of admixture rate simulated, average PI primarily increased while hybridization between source and sink populations was permitted and plateaued shortly after population isolation (Fig. 4). Plateaus positively correlated with admixture scenarios, with the highest PI observed for the highest admixture rate. PI did not considerably vary between admixture models, except during the time period separating the first from the second pulse of admixture. This result suggests that, under equal intensity of admixture (1 pulse of 10 generations for SP and 2 pulses of 5 generations for MP), the number of admixture pulses could only be identified during generations separating them. Additional simulations demonstrated that these patterns were not only qualitatively but also quantitatively robust to scarcity in the availability of temporal samples, including both the number of individuals sampled per generation and the total number of generations recorded (supplementary appendix S2, Supplementary Material online).

Fig. 4.

Average PI (y axis) across generations (x axis), assuming a SP of admixture (gray) or MPs of admixture (black). Shaded areas represent interquartile ranges delimited by the 25% (lower limit) and 75% (upper limit) quantiles of the distribution of introgression proportion averages (based on 100 simulation replicates) at each recorded generation (1 to 1,500), while points and solid lines show median trends. Vertical dashed red lines indicate the generation at which each admixture pulse starts (total time spent admixing: SP—generations 1 to 10, MP—generations 1 to 5 and 201 to 205). Results are separated by simulated admixture rates between source and sink populations (0.03, 0.1, and 0.3).

Finally, temporal patterns of the standard deviation, kurtosis, and skewness of the distribution of introgression proportions mimicked those observed for LIS and VIS, each peaking during an admixture pulse to decrease the following generations (supplementary appendix S3, Supplementary Material online). Note, however, that this pattern for kurtosis and skewness could only be obtained after increasing sink population size from ca. 100 to 500 individuals due to the complete homogenization of introgression among individuals when simulating smaller populations. Furthermore, peaks in higher moment statistics were admixture rate dependent, decreasing in magnitude with increasing admixture permitted between populations. All 3 introgression proportion-related statistics were qualitatively robust to changes in the number of generations recorded, with interindividual variation in introgression proportions being, in addition, also quantitatively robust to scarce temporal sampling.

Neanderthal Introgression into H. sapiens

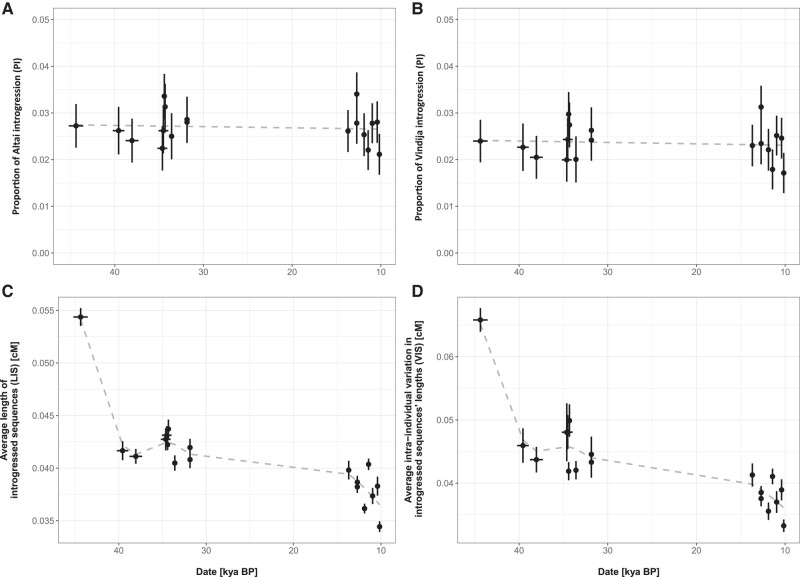
To apply insights gained from simulations to our understanding of archaic introgression into modern humans, we analyzed H. neanderthalensis and H. sapiens genomes older than 10,000 yr from the Allen Ancient DNA Resource (AADR) and summarized Neanderthal introgression using similar genomic statistics as those calculated on simulated data. While we detected significant Altai ($\hat{\mu }$ = 0.027, $t_{17}$ = 32.15, P < 0.001) and Vindija ($\hat{\mu }$ = 0.024, $t_{17}$ = 26.80, P < 0.001) Neanderthal introgression throughout ancient genomes over time, we observed no clear trends between PI and genomes’ age (Fig. 5A and B). Indeed, generalized additive model (GAM) regressions between Altai ($F_{1,16}$ = 0.134, $R_{\mathrm{adj}}^2$ = −0.054, P = 0.72) and Vindija ($F_{1,16}$ = 0.165, $R_{\mathrm{adj}}^2$ = −0.052, P = 0.69) introgression proportions and ancient genomes’ age were both nonsignificant.

Fig. 5.

Genomic summary statistics (y axis) estimated for 18 ancient H. sapiens genomes dating back from approximately 10 to 45 kya (x axis). A) Proportion of Altai introgression (PI). B) Proportion of Vindija introgression (PI). C) Average LIS (cM). D) Average intra-individual VIS’s lengths (cM). The temporal dynamics of each parameter evaluated using GAM regression is represented as a dashed gray line. Horizontal and vertical solid black lines around each point represent the error around genomes’ age (standard deviation) and evaluated genomic summary statistics (standard error), respectively.

In contrast to PI, both LIS ($F_{4.77,12.23}$ = 26.72, $R_{\mathrm{adj}}^2$ = 0.886, P < 0.001) and VIS ($F_{4.56,12.44}$ = 20.35, $R_{\mathrm{adj}}^2$ = 0.854, P < 0.001) delineated a distinguishable pattern (Fig. 5C and D) resembling theoretical expectations under MPs of admixture (Figs. 2 and 3). First, we observed a steep decrease in both summary statistics between approximately 40 and 45 kya, indicating the occurrence of a pulse of admixture between Neanderthal and H. sapiens prior to 45 kya. Then, we observed a second, smaller peak in LIS and VIS around 35 kya, overall suggesting that 2 pulses of admixture between archaic and modern humans may have occurred during their cohabitation time. Nonetheless, we stress here that the signal associated with the second peak is extremely weak and might only represent a statistical artifact resulting from the small sample size of available paleogenomes.

Our study describes general expectations in introgression-related summary statistics under what could be considered low, intermediate, and high admixture rates, without intending to replicate Neanderthal—H. sapiens admixture history in particular. Our simulation framework thus describes patterns of introgression in a sink population of small size and experiencing considerably higher admixture than what is currently estimated between the 2 hominin species. Nonetheless, we performed an additional set of simulations specifically designed to reproduce important aspects of Neanderthal—H. sapiens admixture history, and found no qualitative differences in temporal patterns of targeted introgression-related summary statistics (supplementary appendix S4, Supplementary Material online). Note, however, that distinguishing the SP from the MP model during the time period separating admixture pulses using PI was hindered by an important variation in introgression proportions across simulation replicates, most likely resulting from smaller admixture rates simulated.

Discussion

The growing field of paleogenomics offers the opportunity to explore novel empirical means to evaluate interlineage admixture and to improve our understanding of the complex evolutionary history of hybridizing species, including our own. Here, we used individual-based modeling to assess temporal patterns in 6 introgression summary statistics, including introgression proportions (PI), as well as standard deviation and higher moments (skewness and kurtosis) of the distribution of introgression proportions, lengths of introgressed fragments (LIS), and intraindividual variation in introgressed fragments’ lengths (VIS) to determine whether they could be used to infer admixture pulses. Subsequently, we leveraged insights gained from simulations to evaluate whether targeted genomic statistics retain empirical value, estimating and interpreting them within the context of H. sapiens and H. neanderthalensis admixture history.

Introgression Proportions and Related Summary Statistics Provide Limited Insights into Lineage Admixture History

Our results show that when one aims to infer the number of admixture pulses, the PI may have limited value, reinforcing previous observations (Verdu and Rosenberg 2011; Gravel 2012; Buzbas and Verdu 2018; Fortes-Lima et al. 2021). Regardless of the admixture rate permitted between populations, our simulations demonstrated that a given amount of introgressive hybridization, occurring in either 1 (SP) or 2 (MP) pulses of admixture, largely resulted in similar PI. For instance, Verdu and Rosenberg (2011) showed that various admixture scenarios, while different from ours, lead to the same final amount of PI. It is only during the interpulse period that SP and MP models could be differentiated from one another, suggesting that any temporal sampling failing to capture genomes from within this period would miss the signature of multiple admixture events. While PI is a widely used summary statistics in hybridization studies (e.g. Eaton and Ree 2013; Sankararaman et al. 2014; Hamlin et al. 2020; Quilodrán, Tsoupas, and Currat 2020; Quilodrán et al. 2023), this finding highlights the challenges associated with using PI to differentiate admixture pulses and supports the use of alternative statistics when trying to reconstruct interlineage hybridization history. Variation and higher moments of the distribution of introgression proportions have been shown, in accordance with theoretical expectations, to be informative about the history of admixture between hybridizing lineages (Verdu and Rosenberg 2011; Gravel 2012; Fortes-Lima et al. 2021). Our results supported these observations, demonstrating temporal patterns in the form of peaks at and around an admixture event for these statistics. Noteworthily, our results also indicate that higher moment statistics are the most informative when estimated on a large sample size of a relatively highly reproductively isolated population. Unfortunately, not only skewness and kurtosis but also variance in introgression proportions requires many individuals at each timepoint to be estimated, a type of empirical data not yet available. Nonetheless, as more paleogenomes are sequenced, these summary statistics may become increasingly valuable to study lineages’ admixture history.

LIS and Its Variance within Genomes Could Confidently Distinguish Admixture Pulses

We showed that LIS and its variation within individuals (VIS) peaked during a short period of time around admixture pulses before decreasing because of recombination, similar to what was previously shown for statistics related to PI (Verdu and Rosenberg 2011; Gravel 2012; Buzbas and Verdu 2018). These peaks, more pronounced for VIS, thus provide a means to approximate the timing and number of admixture events between 2 interbreeding lineages. Nonetheless, this also indicates that the time window (restricted here to the generation of admixture and the few dozen following it) to detecting a hybridization event is narrow. Importantly, simulations revealed that the admixture signal within introgressed fragments’ length statistics fades slower with weaker reproductive barriers between lineages (i.e. higher admixture rates). This observation is in accordance with the expectations of Pool and Nielsen (2009), as well as Gravel (2012) showing that LIS decreases faster under lower admixture rates. Consequently, the breadth of time windows allowing the detection of admixture pulses appears to be context dependent, and while priority should be given to samples spanning predicted times of admixture, the expected rate of reproductive isolation between interbreeding systems deserves consideration. In contrast to the findings of Liang and Nielsen (2014), our simulations do not suggest temporal LIS (or VIS) measurements could lead to the overestimation of the number of hybridization pulses. Indeed, our results demonstrate that the number of peaks in VIS or LIS may not be indicative of the number of admixture pulses if they occurred close to each other in time. The tendency would therefore be to underestimate the number of hybridization events rather than overestimate it. While the ancient genome database for H. sapiens may remain the largest to date (Orlando et al. 2021) and consequently be used to test the empirical value of introgressed segments’ length statistics, ancient genomes are progressively being sequenced for nonhuman animals, plants, and pathogens and microorganisms (Fellows Yates et al. 2021; Orlando et al. 2021). As more of these genomes become available, our analytical framework could be used to study hybridization and differentiate between admixture pulses across a wider taxonomical breadth.

The term “admixture pulse” is commonly used in the literature, oftentimes described as a discrete period of time during which gene flow between distinct lineages is occurring (Browning et al. 2018; Villanea and Schraiber 2019; Choin et al. 2021; Iasi et al. 2021). However, this definition of an admixture pulse may be considered relatively broad. With our simulations, we found that multiple bouts of admixture are translated into peaks in introgressed sequences’ length statistics, as long as a period of genomic isolation separates hybridization events. Based on these results, we would like to propose a revisited definition of an admixture pulse as follows: “a continuous series of generations during which genetic material is exchanged between lineages, followed by a consecutive number of generations spent in genetic isolation.” We believe this definition remains inclusive enough so it can be applied across a wide variety of hybridizing lineages, while being specifically associated with a quantifiable signal in readily computable introgression summary statistics.

A Clear Admixture Pulse Detected prior to 45 kya between Modern Human and Neanderthal

Temporal patterns of introgression statistics estimated for ancient H. sapiens genomes within the context of its admixture with Neanderthal supported the practicality of introgressed fragments’ length statistics in detecting the pulse of hybridization. Regression analyses identified a decrease in average LIS and VIS between approximately 40 to 45 kya, confirming our ancestors likely admixed with Neanderthal prior to 45 kya. Indeed, this estimate agrees with previous findings, placing the admixture time between 40 and 60 kya (Sankararaman et al. 2012; Fu et al. 2015; Moorjani et al. 2016; Skoglund and Mathieson 2018; Iasi et al. 2021). In addition, GAM regressions identified a second peak, and thus another admixture event, around 35 kya. However, a statistical artifact could not be excluded given the weak signal observed. The lack of temporal patterns found in both Altai and Vindija Neanderthal introgression proportions further supports this conclusion. Indeed, simulations demonstrated that under a MP scenario, a stairs-like pattern in PI would be expected over time, in which plateaus reached increase in a stepwise fashion after each admixture pulse, a feature absent from ancient H. sapiens genomes analyzed here. Additionally, with Neanderthal believed to have disappeared between 35 and 50 kya (Benazzi et al. 2011; Higham et al. 2011), such an introgression event would have to have occurred at the time Neanderthal was supposedly on the brink of extinction. This being said, smaller LIS and VIS peaks for a second admixture event follow theoretical expectations, and while no greater signal in VIS relative to LIS could be observed, a trend expected from MP simulation results, we showed weaker second-peak signals in VIS are plausible when scarcer temporal samples were available. Ultimately, addressing this uncertainty will necessitate additional paleogenomes spanning the time period from 15 to 40 kya to be sequenced.

Limitations

While our study provides insightful observations on the temporal dynamics of various introgression summary statistics when distinct lineages admix on 1 or 2 discrete instances, our simulation framework could be easily expanded to simulate more than 2 admixture pulses. For both LIS and VIS, we observed a noticeable decline in peak height associated with the second event of admixture. If this dynamic holds for subsequent hybridization pulses, there might be a limitation in the number of admixture events that could be detected using these statistics. Peaks would become shorter with any additional interbreeding events until no more increase can be observed. Alternatively, it might be possible that peaks would decrease until reaching an equilibrium, where any additional admixture pulse would leave a weak, yet perceptible, genomic hybridization signal. Future studies simulating additional hybridization events using a similar framework to the one presented here would help shed some light on temporal patterns in introgression statistics expected when lineages admix on multiple occasions.

Particularly interested in patterns expected under neutrality, we did not consider the impact of selective forces in our simulations. Nevertheless, natural selection can impact the length distribution of introgressed segments, and acknowledging this additional force may be important in some systems, including modern humans, where both negative selection and positive selection are hypothesized to have had a significant impact on the level of Neanderthal ancestry (Sankararaman et al. 2014; Vernot and Akey 2014; Harris and Nielsen 2016; Juric et al. 2016; Shchur et al. 2020; McArthur et al. 2021). Future work incorporating natural selection into the simulation framework may be performed to evaluate its impact on temporal patterns of length summary statistics. In addition, we did not incorporate gene flow with other populations into our simulations, which could impact the proportion of introgressed segments in the sink population (Vernot and Akey 2015; Quilodrán et al. 2023). While introgression and admixed segments’ lengths vary temporally, they also vary spatially (Currat et al. 2008; Duranton et al. 2019; Quilodrán, Tsoupas, and Currat 2020). To complement the temporal assessment conducted here, future research simulating introgression statistics using a spatiotemporal model would allow expected patterns to be described for more complex, realistic evolutionary scenarios. Within this context, it is important to notice that we considered ancient genomes from Eurasia and the Americas as belonging to a single sink population in our model. Nonetheless, the detection of a Neanderthal admixture pulse into H. sapiens whose dates correspond to estimations made using other methods demonstrate that our results are robust to this assumption on the scale considered. A more detailed exploration of models with several source and sink populations would however be necessary to analyze ancient human genomic data on a finer scale.

Conclusion

Our study demonstrates that, in addition to the well-established timing of hybridization (Gravel 2012; Corbett-Detig and Nielsen 2017; Medina et al. 2018; Skov et al. 2018; Iasi et al. 2021), LIS may be used to infer the number of admixture pulses between interbreeding entities when assessed temporally. We also showed that a derived statistic, within-genome standard deviation in introgressed fragments’ lengths (VIS), provides a valuable means to estimating the timing and number of hybridization pulses, particularly when admixture between lineages is limited. Furthermore, additional simulations revealed introgressed fragments’ lengths statistics are at least qualitatively robust to scarcer temporal sampling of both individuals within populations and generations. VIS may thus provide an advantageous substitute to interindividual variation in either PI (Verdu and Rosenberg 2011) or LIS (Gravel 2012), which cannot be estimated when only a single genome is available for a given timepoint, as it is often the case with ancient DNA. Overall, while simulation experiments featured signals of introgression bouts in the form of length and variation peaks, empirical estimation of these parameters on ancient H. sapiens genomes accurately retrieved a previously hypothesized hybridization event with Neanderthal. In conclusion, although this framework necessitates temporally distributed genomic data, it illustrates the practicality and limitations of a set of readily quantifiable introgression summary statistics to studying potentially intricate hybridization scenarios in an era where paleogenomics is popularizing.

Materials and Methods

Individual-Based Genomic Simulations

Overview of the Model

To evaluate genomics patterns emerging following temporal pulses of introgressive admixture between genetically differentiated lineages, we used the evolve() function implemented within the R package “glads” (Quilodrán, Ruegg, et al. 2020) to conduct individual-based, forward-in-time, genomic simulations. Note that we did not use the version of the package available on GitHub (https://github.com/eriqande/glads), but an updated version of the package was provided as Supplementary material (see Data Availability). The main simulation function, evolve(), was also edited to match the needs of the study (see below for details on edits made to the function). The purpose of the individual-based model (IBM) implemented within this package is to explore how a range of genetic and demographic processes can influence genomic patterns between divergent lineages.

The IBM approach at the starting generation comprises individuals characterized by their genomic background (modeled as a single pair of homologous chromosomes), sexual identity (male or female), and their assigned population identity. Newborns have the same defining characteristics and will form the next generation of individuals within a population following reproduction. The pair of homologous chromosomes forming the genetic background of individuals is modeled using a suite of fixed characteristics: the length of homologs (in Mbps), the number and location of genetic markers (e.g. single-nucleotide polymorphisms [SNPs]), the genotype (biallelic or multiallelic) at each genetic variant, the mutation rate per base pair, and the chromosome-wide average recombination rate per base pair. Values defined for each genomic parameter are shared among all individuals.

While various processes reflecting different evolutionary scenarios can be simulated using “glads,” we used the scenario simulating the neutral evolution of chromosomes, including stochastic changes in population size through time (type = “dynamic”). For this scenario, first-generation individuals are created within a user-defined number of populations using the set of genomic and demographic parameters described above. Sexes are assigned to individuals using a binomial distribution with the probability of being a male equal to a given sex ratio. Then, reproduction within populations occurs by randomly forming mating pairs (consisting of 1 male and 1 female), generating haploid parental gametes based on recombination and mutation rates provided, and segregating haplotypes within mating pairs to produce the genotypes of newborns. Sexes of newborns are assigned as described above for first-generation individuals. The number of newborns produced per breeding pair is determined by 2 additional parameters: the population-specific mean number of descendants per breeding pair and the density-dependent demographic effect (to prevent exponential growth of populations). Ultimately, the number of offspring each breeding pair can have for a given generation will be calculated as follows:

$$O(t)=Pois(\lambda )-N(t)\delta ,$$ (1)

where $O(t)$ is the number of offspring produced by a breeding pair at generation t, λ represents the population-specific mean number of descendants per breeding pair, $N(t)$ represents the population size at generation t, and δ represents the density-dependent demographic effect (for details, see Quilodrán, Ruegg, et al. 2020). Following reproduction, newborns replace parental individuals and, if migration rates are specified for this generation, movement of offspring among populations occurs with the probability of each newborn to migrate from population i to population j equal to the migration rate $m_{ij}$. Importantly, because migrants entering a new population are considered as potential mates during reproduction occurring in the next generation, this framework simulates interpopulation gene flow. Eventually, the size of any population i in the next generation will be calculated as follows:

$$N_i(t+1)={\displaystyle \sum _{n=1}^{p_i}}{O}_n(t)-m_{ij}{N}_i(t)+m_{ji}{N}_j(t),$$

where ${\sum }_{n=1}^{p_i}{O}_n(t)$ represents the overall reproductive output of all mating pairs within population i ($p_i$) at generation t (see Equation 1), $m_{ij}{N}_i(t)$ represents the number of individuals lost to emigration to population j at generation t, and $m_{ji}{N}_j(t)$ represents the number of individuals gained from immigration from population j at generation t. The simulation ends when populations evolved for a provided number of generations t and genotypes of individuals at all SNPs within each population are returned as an output.

To increase flexibility of the IBM framework, we modified the evolve() function by incorporating 4 new features into the function. First, the function now can output genotypes of individuals within each population for a set of user-defined generations, while it could previously only output the genetic background of populations in the last generation or every x generation, where x was the elapsed time between each generation output. In addition, the function now can keep track of immigrants each generation and allow the user to change fitness and phenotype-related parameters from a user-defined generation up until the last generation simulated where it previously could not. Finally, an argument can now be specified so that the size of all populations simulated is recorded each generation, a feature absent from the original function.

Initialization

We used a simulation framework considering the evolution of individuals distributed in 2 populations (a source—provider of migrants—and a sink—receiver of migrants—population). Both source and sink populations had an initial size of 100 individuals and evolved neutrally, this framework assuming equal sex ratio and equal fitness of genotypes. Note, however, that demographic stochasticity was introduced in populations according to Equation 1, so while fitness of genotypes was equal, the fitness of individuals within populations was not. Nonetheless, differences in among-individual fitness were stochastic and thus did not violate the neutrality assumption. The parameters λ = 4 and δ = 0.02 were identical between populations and were selected (i) based on fitness estimates for ancient hunter–gatherer populations (Page and French 2020) and (ii) their propensity to stabilize population sizes around the initial value of 100 individuals across generations, therefore avoiding the simulation of strong bottlenecks and population growths (see supplementary appendix S5, Supplementary Material online, and below for relevance). Populations were allowed to evolve for 1,500 generations, providing a biologically relevant timeframe for simulation. Indeed, this corresponds grossly to the timing of admixture between Neanderthal and H. sapiens during their OOA expansion (∼1,500 to 1,800 generations ago; Iasi et al. 2021).

Finally, to realistically mimic the genomic dynamics of a biological system in our simulations, we again leveraged the literature available for H. sapiens to choose appropriate genetic parameters. Following Kong et al. (2002), the genomic background of each individual was modeled as a single pair of homologous chromosomes with an average recombination rate of 1.2e⁻⁸/bp. Each chromosome had a length of 150 Mb with 201 evenly spaced genetic markers. The major objective of these simulations was to track the fate of introgressed sequences through time and not to reproduce faithful population genetic diversity, the mutation rate was set to 0, and source and sink populations at generation 1 were fixed for alternate alleles at all 201 loci (allele 1 for sink and 2 for source). This way, the introgressed allele could always be differentiated from the local allele, facilitating downstream analyses. One additional population-specific genetic marker was simulated at the end of each homolog, a marker that was used as diagnostic for immigrants so they could be removed when estimating introgression-related summary statistics. Note that in simulations, following a reproduction event, this marker was changed to the one specific to the population progenies were in, as they could not be considered immigrants anymore but introgressed individuals.

Simulations

To assess whether differences in temporal patterns of introgression exist between genomes experiencing single or MPs of introgressive hybridization, 2 contrasting admixture models were considered: one simulating a SP of admixture (SP model) and another considering 2 independent pulses of admixture (MP model). Both models shared general IBM parameters described previously but differed in how hybridization was simulated. For the SP model, admixture only happens once from generation 1 to generation 10, followed by 1,490 generations of genetic isolation and neutral evolution (Fig. 1A). Contrastingly, for the MP model, admixture happens twice, once from generation 1 to generation 5 and once from generation 201 to generation 205 (Fig. 1B). Admixing time was kept identical between models so that the effect of the number of pulses could be disentangled from the effect of admixture intensity on genomic summary statistics investigated. To represent the effect of admixture, migration was set as unidirectional in both SP and MP models, always from the source to the sink population, to keep the former population free of the latter population's allele. This way, we avoided dealing with uncertainties pertaining to shared ancestries between the source and sink populations in estimating introgression-related summary statistics.

In addition to the number of hybridization pulses, we also investigated the impact admixture rate may have had on the temporal dynamics of genomic summary statistics (note that here what we call admixture rate is in fact the migration rate [$m_{ij}$] between populations in “glads”). SP and MP models were each run 3 times using a different admixture rate (referred to as scenarios). Specifically, SP and MP models were simulated with an admixture rate from source to sink population of 0.03, 0.1, and 0.3. In summary, 3 scenarios were considered and implemented for each admixture model (SP and MP), scenarios differing only by the intensity of interpopulation admixture simulated. We mentioned earlier those parameters incorporating demographic stochasticity into simulations (λ and δ, respectively) were chosen as they allowed sizes of source and sink populations to stabilize around the initial population size provided of 100 individuals over time, allowing temporal patterns of introgression to reflect mainly the impact of gene flow levels, as opposed to the impact of population size variation. Finally, variability in genomic patterns of introgression stemming from the stochastic evolution of chromosome pairs within the sink population was accounted for by simulating each scenario per admixture model 100 times. Genotypes of all individuals within sink and source populations were recorded for all 1,500 generations simulated to estimate introgression summary statistics of interest and their evolution over time.

Estimation of Population-Level Genomic Summary Statistics

Using simulation outputs of recorded generations, we estimated 6 summary statistics for sink population replicates to describe genomic patterns of introgression. These include the average LIS, the average intraindividual variation in the lengths of introgressed sequences (VIS), the average PI, and the variance and higher moments of the distribution of introgression proportions, including skewness and kurtosis. To estimate the LIS, each homologous chromosome present within individuals assigned to the sink population was first scanned for continuous tracts of the source population's allele (allele 2). This was performed by evaluating, when at least one was present, the number of consecutive introgressed alleles along the sequence of a homolog and considering the suite of such alleles as an introgressed segment. Then, positions of the first and last genetic marker forming an introgressed segment were retrieved and lengths were calculated as the number of base pairs separating these 2 markers. Finally, values obtained were multiplied by 1.2e⁻⁶ to convert base pairs into centimorgans (cM). Ultimately, the population-level estimate for the statistic was estimated by averaging lengths in cM over all inferred introgressed segments across individuals. The second statistics, the average intraindividual VIS’s lengths, was estimated by calculating the standard deviation of the lengths of all introgressed segments inferred for each sink individual separately and then by averaging these values over all individuals within that population. Noteworthily, as the length in cM for introgressed segments long of only 1 genetic marker cannot be calculated, we discarded these segments before estimating population averages of the above genomic summary statistics. The third statistics, the PI, was calculated for each individual as the number of introgressed alleles across homologs, divided by the total number of haploid markers (402). Variation and higher moments of the distribution of introgression proportions across individuals were evaluated using the R functions sd(), as well as the functions skewness() and kurtosis(), both implemented within the R package “moments” (Komsta and Novomestky 2022; R Core Team 2023). Finally, the population-level estimate of the introgression proportion was obtained by averaging individual-specific proportions of introgression across all individuals forming the sink population. Note that for each recorded generation, genotypes of immigrants were discarded from the sink population using the diagnostic allele to avoid biasing estimates of genomic summary statistics. In addition to immigrants, the diagnostic allele was removed from the genetic background of all individuals prior to estimating introgression-related statistics. Functions required to conduct simulations, filter immigrant individuals from the sink population, remove the diagnostic allele from simulated chromosomes of individuals, and compute genomic summary statistics were compiled into a R package, dependent on “glads,” entitled “companions4glads2” provided as Supplementary material (see Data Availability).

Temporal changes in genomic summary statistics were eventually assessed by evaluating the distribution of population-level averages, variance, and higher moments estimated for all 100 simulation replicates across recorded generations. The estimation of the decay rate of LIS and VIS over time was performed for all admixture rates and models separately by regressing median values of population-level averages across generations using R nls() function and a negative exponential equation:

$$y(t)=y_f+(y_0-y_f)e^{-\alpha t}+\epsilon ,$$

where $y(t)$ is the value of the summary statistic at generation t, $y_0$ is the value from which the summary statistic starts to decay, $y_f$ is the value toward which the summary statistic decays, α is the rate of decay, and $\epsilon$ the residual error. All analyses were conducted in R versions 4.3.0 and 4.3.1 (R Core Team 2023).

Ancient Genome Analysis

Data Collection and Filtering

To determine whether patterns of introgression observed in simulations could be replicated with empirical data, analyses like those conducted on simulated data were performed using ancient genomes available from the AADR (https://reich.hms.harvard.edu/allen-ancient-dna-resource-aadr-downloadable-genotypes-present-day-and-ancient-dna-data). The whole database (version v50.0, released on 10/10/2021) was downloaded and subsequently filtered in R. Among all H. sapiens genomes, we kept only those with a base coverage greater than 4 and removed duplicated samples, retaining genomes with the highest coverage and number of SNP calls on autosomes. These filters were applied (i) to keep genomes optimizing the accuracy of inferences while minimizing genome loss for adequate temporal sampling and (ii) to ensure genome independence. Interested in temporal patterns of Neanderthal introgression within H. sapiens, we then only kept human genomes from Eurasia and the Americas that were 10,000 yr old or older. Neanderthals and H. sapiens likely temporally overlapped from when modern humans started to disperse outside Africa (∼75 kya; Karmin et al. 2015) and into Eurasia (∼47 to 55 kya; Poznik et al. 2016; Skoglund and Mathieson 2018) and Neanderthal extinction (∼35 to 50 kya; Benazzi et al. 2011; Higham et al. 2011). Consequently, we believe 10,000 yr old and older genomes should provide an appropriate time window to study the consequences of introgressive hybridization between the 2 hominin species. Finally, we selected 2 distinct Neanderthal genomes and 1 Denisovan genome with the highest coverage and number of SNP hits, namely the Altai_published.DG, Vindija_snapAD.DG, and Denisova_published.DG genomes, 1 outgroup genome (chimpanzee—Chimp.REF), and 1 presumably nonintrogressed African genome (S_Dinka-1.DG). These genomes were selected to be used as references for the computation of f4 ratios and for the inference of introgressed segments (see below). Overall, 23 genomes were retained for downstream analyses, including 18 ancient H. sapiens genomes (Eurasians and Americans), 1 contemporary H. sapiens genome (African), 2 Neanderthal genomes (Altai and Vindija), 1 Denisovan genome, and 1 outgroup (chimpanzee) genome.

Estimation of Genomic Summary Statistics

Genome-wide average of Altai and Vindija Neanderthal introgression proportions (PI) were estimated for all 18 ancient H. sapiens individuals separately using the R package “admixr” (Petr et al. 2019). These proportions were measured as f4 ratios (Patterson et al. 2012):

$$\mathrm{PI}={\displaystyle \frac{f4(A,O;X,C)}{f4(A,O;B,C)},}$$ (2)

a statistic capable of inferring ancestry fractions in admixed populations given genotypes from a presumed gene donor population (i.e. a Neanderthal genome; B in Equation 2), genotypes from a population closely related to the gene donor (i.e. Vindija_snapAD.DG when B is Altai_published.DG and vice versa; A in Equation 2), genotypes from putatively introgressed populations (i.e. an ancient H. sapiens genome; X in Equation 2), genotypes from a nonintrogressed reference population (i.e. S_Dinka-1.DG; C in Equation 2), and genotypes from an outgroup species (i.e. Chimp.REF; O in Equation 2).

The average length of introgressed Neanderthal segments was assessed for the same 18 ancient H. sapiens genomes using the software “admixfrog” (Peter 2020). This program is a hidden Markov model allowing to identify distinct ancestry fragments within genomes, given sources of ancestry are provided. We defined 3 sources of ancestry (--states): (i) Neanderthal, using the Altai_published.DG and Vindija_snapAD.DG genomes as references, (ii) Denisova, using the Denisova_published.DG genome as reference, and (iii) H. sapiens, using the S_Dinka-1.DG genome as reference. Although the program includes functionality to account for a source of contamination, we declared no contamination within the data (--c0 --dont-est-contamination). Lastly, to better mimic manipulations done to simulated data, we used physical instead of recombination distances for binning (--pos-mode) and multiplied lengths of inferred fragments in base pairs by 1.2e⁻⁶ to convert them to cM (see Estimation of Population-Level Genomic Summary Statistics above). All remaining parameters were kept to default.

Statistical Analyses

For each individual genome, “admixfrog” reported the length in base pairs of every inferred introgressed fragment per chromosome and their probable ancestry. Ancestries reported could either be confidently attributed to one of the sources provided (Neanderthal, Denisova, and H. sapiens) or be a combination of 2 sources (e.g. Neanderthal and Denisova). With tracts of Neanderthal ancestry being the only ones of interest to us, we filtered the data set to keep only fragments of Neanderthal origin, regardless of whether this ancestry tract was identified as being specific to Neanderthal or shared between Neanderthal and Denisova. In addition, to stay as close to simulated data as possible, we filtered the data set further by removing introgressed segments identified on sexual chromosomes. Finally, more interested in genome-wide rather than chromosome-specific patterns of admixture, we averaged the lengths of introgressed segments per chromosome, and then across chromosomes, generating a single mean value per individual (LIS). Intraindividual variance in introgressed sequences’ lengths (VIS) was similarly processed. Standard deviation of segments’ lengths was calculated for each chromosome independently and averaged across chromosomes, providing a single mean value per individual. No additional processing or filtering of “admixr” outputs was required, with all genome-specific proportions of Altai and Vindija introgression exhibiting a Z-score ≥ 3.

Temporal patterns of Neanderthal introgression into the genome of modern humans were evaluated with a GAM using the “mgcv” R package (Wood 2017). Each genomic summary statistic (response) was regressed and smoothed over the average age of each sample (predictor), estimated based on either calibrated radiocarbon dating or an archeological context, and recorded within the AADR. This method was selected as it is particularly powerful when trying to evaluate nonlinear relationships and may thus allow more complex trends hidden with simpler regression methods to be put forward. Note, however, that the shape of the relationship may largely be influenced by the basis dimension used to represent the smoothing term (also known as the k parameter). To find the k value fitting the data best, we used the function AIC() to identify, over all possible k values, the one producing the model with the lowest Akaike Information Criterion (AIC) value. When no k value was better than another (AIC values were identical up to the fifth significant digit), we chose the lowest k value (k = 3), as increasing the basis dimension did not improve the model. This selection process was repeated for every GAM regression involving a different genomic summary statistic.

Supplementary Material

Supplementary material is available at Molecular Biology and Evolution online.

Author Contributions

L.N.D.S. designed the study, performed the simulations, analyzed the ancient genomes, interpreted the results, and led the writing of the manuscript. C.S.Q. and M.C. designed the study, interpreted the results, and wrote the manuscript.

Data Availability

No novel data sets were generated as part of this study. Genomic summary statistics and other details on ancient genomes analyzed are presented in supplementary appendix S6, Supplementary Material online. The complete set of functions used to conduct simulations and estimate introgression summary statistics were compiled into a small R package entitled “companions4glads2” (version 2.1.5.9). This package and its updated complement, “glads” (version 0.1.5), are available as supplementary appendix S7, Supplementary Material online.