Open-loop dynamic and static characteristics of the carotid sinus baroreflex in rats with chronic heart failure after myocardial infarction

Abstract

We estimated open-loop dynamic characteristics of the carotid sinus baroreflex in normal control rats and chronic heart failure (CHF) rats after myocardial infarction. First, the neural arc transfer function from carotid sinus pressure to splanchnic sympathetic nerve activity (SNA) and its corresponding step response were examined. Although the steady-state response was attenuated in CHF, the negative peak response and the time to peak did not change significantly, suggesting preserved neural arc dynamic characteristics. Next, the peripheral arc transfer function from SNA to arterial pressure (AP) and its corresponding step response were examined. The steady-state response and the initial slope were reduced in CHF, suggesting impaired end-organ responses. In a simulation study based on the dynamic and static characteristics, the percent recovery of AP was reduced progressively as the size of disturbance increased in CHF, suggesting that a reserve for AP buffering is lost in CHF despite relatively maintained baseline AP.

Introduction

The arterial baroreflex is an important negative feedback system that stabilizes systemic arterial pressure (AP) against exogenous disturbances. The rapidness of AP regulation may be best described by the system dynamic characteristics. With respect to the sympathetic arterial baroreflex system, previous studies in rabbits [1] and rats [2] have indicated that the transfer function of the baroreflex neural arc from baroreceptor pressure input to efferent sympathetic nerve activity (SNA) exhibits “derivative” characteristics, which means that the dynamic gain of the SNA response to pressure perturbation becomes greater as the modulation frequency increases. On the other hand, the transfer function of the baroreflex peripheral arc from SNA to AP shows “low-pass” characteristics, which means that the dynamic gain of the AP response to SNA variation becomes smaller as the modulation frequency increases. In short, the neural arc provides an accelerating mechanism of the dynamic AP response in the arterial baroreflex system [1].

Although a number of studies have indicated that the baroreflex function is depressed in heart failure [3–6], dynamic characteristics of the arterial baroreflex in heart failure have not been fully described. The aim of the present study was to identify the open-loop dynamic characteristics of the carotid sinus baroreflex in a rat model of chronic heart failure (CHF) after myocardial infarction. To obtain a total picture of the AP regulation in CHF, we also estimated the open-loop static characteristics of the carotid sinus baroreflex.

Materials and methods

Animals were cared for in strict accordance with the Guiding Principles for the Care and Use of Animals in the Field of Physiological Sciences, which has been approved by the Physiological Society of Japan. All experimental protocols were reviewed and approved by the Animal Subjects Committee at the National Cerebral and Cardiovascular Center.

Myocardial infarction

Coronary artery ligation was performed under sterile conditions in 8-week-old male Sprague-Dawley rats according to a previously established procedure [7]. After inducing anesthesia by halothane inhalation, the rat was intubated and mechanically ventilated. The left chest was opened at the fourth intercostal space and the left coronary artery was ligated with a 5-0 polypropylene suture (PROLENE, Ethicon, GA, USA). An electrocardiogram was monitored for 1 h after the coronary ligation, and the heart was defibrillated as necessary by manual prodding. Thereafter air was evacuated from the thoracic cavity and the incision was closed. The rats were allowed to recover from anesthesia, and were fed ad libitum with a standard laboratory chow and given free access to water. Although we initially planned to wait until the rats showed an objective sign of advanced heart failure such as facial edema or labored breathing, the rats with such severe heart failure were too weak to survive the acute baroreflex study described in the following section. Accordingly, the rats that survived for 100–200 days (156 ± 18 days) after myocardial infarction were used without solid criteria for starting the acute baroreflex study. Instead, the rats were regarded as experiencing CHF when the central venous pressure was higher than 2.5 mmHg or the biventricular weight was greater than 2.5 g/kg body weight at the time of the acute baroreflex study.

Acute baroreflex study

Experiments were performed in normal control (n = 12) and CHF (n = 7) rats. Sham operation was not performed in the control rats. Among the control rats, eight rats were matched with the CHF rats based on body weight, but they were younger in age due to the retardation of growth in the CHF rats. The remaining four rats were age-matched with the CHF rats, but they were heavier in body weight. Because none of the parameters of the baroreflex dynamic and static characteristics differed statistically between the two subgroups of the control rats, we report pooled data obtained from the 12 control rats.

Each rat was anesthetized with an intraperitoneal injection (2 ml/kg) of a mixture of urethane (250 mg/ml) and α-chloralose (40 mg/ml), and mechanically ventilated with oxygen-enriched room air. A venous catheter was inserted into the right femoral vein, and 20-fold diluted anesthetic mixture was administered continuously (2–3 ml kg⁻¹ h⁻¹). An arterial catheter was inserted into the right femoral artery to measure AP. Heart rate (HR) was obtained from AP through a cardiotachometer. Another venous catheter was inserted into the left femoral vein and advanced into the inferior vena cava to measure central venous pressure and to supply Ringer solution (6 ml kg⁻¹ h⁻¹).

A postganglionic branch from the splanchnic sympathetic nerve was exposed through a left flank incision, and a pair of stainless steel wire electrodes (Bioflex wire AS633, Cooner Wire, CA, USA) was attached to record SNA. The nerve and electrodes were covered with silicone glue (Kwik-Sil, World Precision Instruments, FL, USA) for insulation and fixation. To quantify the nerve activity, the preamplified nerve signal was band-pass filtered at 150–1,000 Hz, and then full-wave rectified and low-pass filtered with a cut-off frequency of 30 Hz. Pancuronium bromide (0.4 mg kg⁻¹ h⁻¹) was administered to prevent muscular activity from contaminating the SNA recording. At the end of the experiment, we confirmed the disappearance of SNA in response to an intravenous bolus injection of a ganglionic blocker, hexamethonium bromide (60 mg kg⁻¹), and recorded the noise level.

Bilateral vagal and aortic depressor nerves were sectioned at the neck to avoid reflexes from the cardiopulmonary region and aortic arch. The carotid sinus regions were isolated from the systemic circulation bilaterally according to previously reported procedures [8, 9]. Briefly, a 7-0 polypropylene suture with a fine needle (PROLENE, Ethicon, GA, USA) was passed through the tissue between the external and internal carotid arteries, and the external carotid artery was ligated close to the carotid bifurcation. The internal carotid artery was embolized using two to three steel balls (0.8 mm in diameter, Tsubaki Nakashima, Nara, Japan) injected from the common carotid artery. Under these conditions, the brain stem area was perfused by patent bilateral vertebral arteries. The isolated carotid sinuses were filled with warmed Ringer solution through catheters inserted into the common carotid arteries. Carotid sinus pressure (CSP) was controlled using a servo-controlled piston pump. Heparin sodium (100 U kg⁻¹) was given intravenously to prevent blood coagulation. Body temperature was maintained at approximately 38°C with a heating pad.

Protocols

After the above surgical procedures were completed, reflex responses in SNA, AP, and HR to CSP input were monitored for more than 30 min. The rat was excluded from further study and analysis in the event that the reflex responses became smaller within this period. Possible causes for the deterioration in the reflex responses include surgical damage to the carotid sinus nerves and brain ischemia due to the bilateral carotid occlusion.

To estimate the dynamic input-output relationship of the carotid sinus baroreflex, CSP was perturbed for 20 min using a Gaussian white noise (GWN) signal with the mean of 120 mmHg and standard deviation of 20 mmHg. The selection of the mean pressure and amplitude of GWN does not significantly affect the estimation of the system dynamic characteristics except for a factor of proportionality (see Appendix 1 for details). The switching interval of GWN was set at 500 ms. The input power spectral density was relatively constant up to 1 Hz, which covered the upper frequency range of interest with respect to the sympathetic arterial baroreflex in rats [2].

To estimate the static input-output relationship of the carotid sinus baroreflex, CSP was decreased to 60 mmHg for 4–6 min, and then increased stepwise from 60 to 180 mmHg in increments of 20 mmHg every minute [10].

Data analysis

Data were sampled at 200 Hz using a 16-bit analog-to-digital converter and stored on a dedicated laboratory computer system. In each rat, the noise level of SNA recorded after the administration of hexamethonium bromide was treated as zero. Because the absolute voltage of SNA varied among animals depending on the recording conditions, SNA averaged during the last 10 s at CSP of 60 mmHg in the stepwise input protocol was defined as 100%. The same normalization factor was used for the analysis of the baroreflex dynamic characteristics.

Dynamic characteristics of the baroreflex neural arc, peripheral arc, total baroreflex, and HR control were estimated by an open-loop transfer function analysis as follows [11]. Data were analyzed from 90 s after the initiation of the GWN input. The input-output data pairs were resampled at 10 Hz and segmented into 50% overlapping bins of 1,024 points each. For each segment, a linear trend was removed, and a Hanning window was applied. Fast Fourier transform was performed to obtain the frequency spectra of the input and output signals. The ensemble averages of the input power spectral density [S _XX(f)], output power spectral density [S _YY(f)], and cross spectral density between the input and output signals [S _YX(f)] were calculated over 12 segments, where f denotes frequency. Finally, the transfer function [H(f)] from input to output was estimated as:

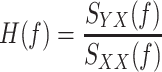1

The transfer function is a complex-valued function that can be expressed by the modulus and phase at each frequency. In the present study, we refer to the modulus of the transfer function as the dynamic gain. To quantify the linear dependence between the input and output signals, a magnitude squared coherence function [Coh(f)] was calculated as:

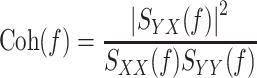2

The coherence function is a real-valued function ranging from zero to unity. When the output signal is perfectly explained by the linear dynamics with the input signal, the coherence value becomes unity. When the output signal is totally independent of the input signal, the coherence value becomes zero.

To facilitate understanding of the transfer function, the step response was also calculated as follows. The system impulse response was derived from the inverse Fourier transform of H(f). The step response was then obtained from the time integral of the impulse response.

To quantify the open-loop static characteristics of the carotid sinus baroreflex, mean SNA, AP, and HR were obtained during the last 10 s at each CSP level of the stepwise input protocol. In each rat, data from two consecutive step cycles were averaged. The static characteristics of the baroreflex neural arc (the CSP-SNA relationship), the total baroreflex (the CSP-AP relationship), and the HR control (the CSP-HR relationship) were described by fitting four-parameter logistic functions to the input-output data as follows [10, 12]:

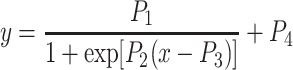3

where x and y denote the input (CSP) and output (SNA, AP, or HR), respectively; P ₁ is the response range of output; P ₂ is the slope coefficient; P ₃ is the midpoint pressure of input; and P ₄ is the minimum value of output. For convenience, the maximum slope or the maximum gain of the logistic function is reported by a positive value as P ₁ P ₂/4.

The static characteristics of the baroreflex peripheral arc (the SNA-AP relationship) were quantified by a linear regression analysis as follows [10, 13]:

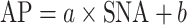4

where a and b represent the slope and intercept, respectively, of the regression line.

Statistical analysis

All data are presented in mean and SE values. Unpaired t tests were used to compare the parameters of the baroreflex dynamic and static characteristics between the control and CHF groups [13]. To compare the transfer functions between the two groups, we arbitrarily selected the dynamic gain values at 0.01, 0.1, and 1 Hz (G _0.01, G _0.1, and G ₁). For the step response relating to the neural arc transfer function, the negative peak response (S _peak), the time to the negative peak (T _peak), the value of the step response at 10 s (S ₁₀), the steady-state response at 50 s (S ₅₀), and the ratio of the peak response to the steady-state response (S _peak/S ₅₀) were calculated. For the step response relating to the peripheral arc, total baroreflex, or HR control, an initial slope of the response was calculated (see Appendix 2) in addition to S₅₀. Differences were considered significant when P < 0.05.

Simulation study

Once the open-loop dynamic and static characteristics of a system are both identified, closed-loop system responses can be simulated [14–16]. To compare closed-loop behavior of the carotid sinus baroreflex between control and CHF conditions, step inputs ranging from −10 to −60 mmHg were applied as exogenous disturbances, and resulting AP responses were simulated. Percent recovery was calculated as the magnitude of steady-state AP recovery relative to the size of step disturbance. The initial slope for the recovery response was also calculated (see Appendix 2).

Results

Postmortem examination confirmed that the left ventricular free wall was reduced to a membrane-like scar in the CHF group. Biventricular weights, both absolute and relative to body weight, were significantly greater in the CHF than in the control group (Table 1). The central venous pressure was significantly higher and the baseline AP and HR were significantly lower in the CHF group. Although the duration after myocardial infarction ranged from 100 to 200 days in the CHF group, there was no significant correlation between the duration and biventricular weight (y = 0.0012x + 2.53, r ² = 0.035, P = 0.72, x duration in days, y biventricular weight in grams per kilogram) or between the duration and central venous pressure (y = −0.013x + 7.5, r ² = 0.07, P = 0.58, x duration in days, y central venous pressure in millmeters of mercury).

Table 1.

Age, body weight, biventricular weight, central venous pressure, mean arterial pressure, and heart rate of the normal control and chronic heart failure (CHF) rats

	Control (n = 12)	CHF (n = 7)	P value
Age at experiment (weeks)	24 ± 3	30 ± 3	0.237
Body weight (g)	565 ± 28	538 ± 19	0.474
Biventricular weight (g)	1.16 ± 0.04	1.45 ± 0.08**	0.002
Biventricular weight (g kg body weight−1)	2.05 ± 0.06	2.71 ± 0.13**	<0.001
Central venous pressure (mmHg)	2.0 ± 0.2	5.4 ± 0.9**	<0.001
Mean arterial pressure (mmHg)	134 ± 4	121 ± 4*	0.037
Heart rate (beats min−1)	414 ± 11	350 ± 12**	0.001

Data are presented as mean ± SE

** P < 0.01 and *P < 0.05 by unpaired t test

Typical experimental recordings obtained from a control rat are shown in Fig. 1a. m-SNA indicates a 2-s moving averaged signal of SNA. In the dynamic input protocol, CSP was changed dynamically according to a GWN signal. m-SNA varied dynamically in response to the CSP perturbation. Although AP changed dynamically, the AP variation seemed more sluggish than the SNA variation. Changes in HR were less obvious from the time series data. In the static input protocol, a stepwise increase in CSP decreased m-SNA, AP, and HR. The noise level of SNA obtained after the intravenous administration of hexamethonium bromide was set at zero. Because of the normalization procedure, m-SNA during the last 10 s at CSP of 60 mmHg approximated 100%. Figure 1b represents CSP and SNA signals sampled at 200 Hz during the dynamic input protocol. High CSP inputs suppressed SNA to a noise level.

Fig. 1.

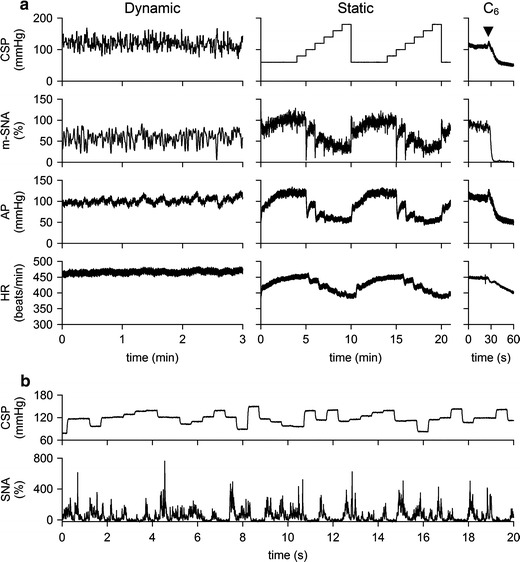
a Typical recordings (10-Hz decimated data) of carotid sinus pressure (CSP), 2-s moving averaged sympathetic nerve activity (m-SNA), arterial pressure (AP), and heart rate (HR) obtained from a control rat. In the dynamic protocol, CSP was changed according to a Gaussian white noise signal. In the static protocol, CSP was increased from 60 to 180 mmHg. Hexamethonium bromide (C₆) was administered intravenously at the end of the experiment (arrowheads). The noise level of the nerve activity recorded after C₆ administration was assigned 0%, while the m-SNA value averaged for the last 10 s at CSP of 60 mmHg was assigned 100%. b CSP and SNA sampled at 200 Hz during the dynamic input protocol

Typical experimental recordings obtained from a CHF rat are shown in Fig. 2a. In the dynamic input protocol, CSP was changed dynamically according to a GWN signal. Although m-SNA varied dynamically in response to the CSP perturbation, changes in AP and HR were not obvious from the time series data. In the static input protocol, a stepwise increase in CSP decreased m-SNA, AP, and HR. The magnitudes of the responses in m-SNA, AP, and HR seem smaller than those in the control rat. Figure 2b represents CSP and SNA signals sampled at 200 Hz during the dynamic input protocol. High CSP inputs suppressed SNA to a noise level.

Fig. 2.

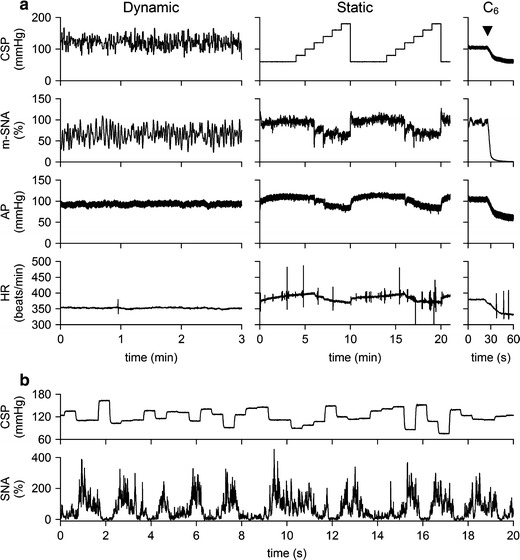
a Typical recordings (10-Hz decimated data) of CSP, m-SNA, AP, and HR obtained from a chronic heart failure rat. In the dynamic protocol, CSP was changed according to a Gaussian white noise signal. In the static protocol, CSP was increased from 60 to 180 mmHg. The noise level of the nerve activity recorded after C₆ administration was assigned 0%, while the m-SNA value averaged for the last 10 s at CSP of 60 mmHg was assigned 100%. b CSP and SNA sampled at 200 Hz during the dynamic input protocol

Dynamic characteristics of the carotid sinus baroreflex

Figure 3 summarizes the open-loop dynamic characteristics of the carotid sinus baroreflex averaged for the control and CHF rats. The neural arc transfer function from CSP to SNA showed derivative characteristics (Fig. 3a). G _0.01 tended to be lower in the CHF rats, whereas G _0.1 and G ₁ did not differ significantly between the two groups (Table 2). The phase plot showed an out-of-phase relationship in the frequency range from 0.01 to 1 Hz in both groups. The coherence plot with values less than unity suggests that SNA contained an unknown noise signal unrelated to the baroreflex and/or a nonlinear system response to the CSP input. The bottom panel of Fig. 3a represents the step responses of SNA for a unit increase in CSP. Although S ₁₀ and S ₅₀ were significantly attenuated in the CHF rats, S _peak, T _peak, and S _peak/S ₅₀ did not differ significantly between the two groups (Table 2).

Fig. 3.

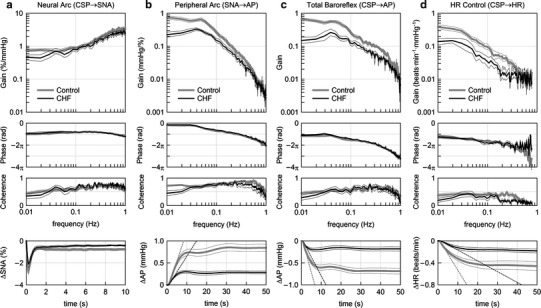
Dynamic characteristics of the carotid sinus baroreflex averaged for the control rats (n = 12) and chronic heart failure (CHF) rats (n = 7). a Transfer function of the baroreflex neural arc from CSP to SNA. Gain, phase, and coherence plots are shown. The bottom panel represents the step response of SNA calculated from the transfer function. There is no significant difference in the negative peak response or the time to peak between control and CHF rats. b Transfer function of the baroreflex peripheral arc from SNA to AP. The bottom panel represents the step response of AP induced by a unit increase in SNA. Both initial slope (dotted lines) and steady-state response are attenuated in CHF. c Transfer function of the total baroreflex from CSP to AP. The bottom panel represents the step response of AP induced by a unit increase in CSP. Both initial slope (dotted lines) and steady-state response are attenuated in CHF. d Transfer function from CSP to HR. The bottom panel represents the HR step response calculated from the transfer function. Both initial slope (dotted lines) and steady-state response are attenuated in CHF. In each plot, bold and thin lines indicate mean and mean ± SE, respectively

Table 2.

Parameters of the dynamic characteristics of the carotid sinus baroreflex

	Control (n = 12)	CHF (n = 7)	P value
Neural arc
G 0.01 (% mmHg−1)	0.80 ± 0.10	0.50 ± 0.08	0.051
G 0.1 (% mmHg−1)	0.99 ± 0.11	0.85 ± 0.14	0.432
G 1 (% mmHg−1)	3.49 ± 0.34	2.64 ± 0.30	0.093
S 50 (%)	0.75 ± 0.09	0.39 ± 0.06*	0.012
S 10 (%)	0.78 ± 0.09	0.42 ± 0.06*	0.010
S peak (%)	2.88 ± 0.25	2.13 ± 0.30	0.076
T peak (s)	0.29 ± 0.01	0.31 ± 0.01	0.327
S peak/S 50	5.30 ± 1.60	6.06 ± 1.06	0.743
Peripheral arc
G 0.01 (mmHg %−1)	0.81 ± 0.09	0.24 ± 0.05**	<0.001
G 0.1 (mmHg %−1)	0.29 ± 0.04	0.16 ± 0.02*	0.023
G 1 (mmHg %−1)	0.0032 ± 0.0005	0.0050 ± 0.0015	0.211
S 50 (mmHg)	0.84 ± 0.08	0.28 ± 0.03**	<0.001
Initial slope (mmHg s−1)	0.134 ± 0.014	0.071 ± 0.009**	0.007
Total baroreflex
G 0.01 (mmHg mmHg−1)	0.70 ± 0.06	0.17 ± 0.03**	<0.001
G 0.1 (mmHg mmHg−1)	0.28 ± 0.03	0.13 ± 0.02**	0.001
G 1 (mmHg mmHg−1)	0.013 ± 0.002	0.010 ± 0.002	0.324
S 50 (mmHg)	0.69 ± 0.07	0.18 ± 0.05**	<0.001
Initial slope (mmHg s−1)	0.166 ± 0.014	0.086 ± 0.009**	<0.001
Heart rate control
G 0.01 (beats min−1 mmHg−1)	0.43 ± 0.06	0.16 ± 0.03**	0.005
G 0.1 (beats min−1 mmHg−1)	0.11 ± 0.02	0.04 ± 0.01*	0.026
S 50 (beats min−1)	0.46 ± 0.08	0.18 ± 0.03*	0.021
Initial slope (beats min−1 s−1)	0.059 ± 0.009	0.020 ± 0.004**	0.006

Data are presented as mean ± SE

** P < 0.01 and *P < 0.05 by unpaired t test

The peripheral arc transfer function from SNA to AP showed low-pass characteristics (Fig. 3b). G _0.01 and G _0.1 were significantly smaller in the CHF rats, whereas G ₁ did not differ significantly between the two groups (Table 2). The phase was close to zero radians at the lowest frequency and delayed with an increase in frequency in both groups. The coherence plot with values less than unity indicates that a part of AP variation was not explained by the linear dynamics with the SNA variation. In the step response of AP for a unit increase in SNA (Fig. 3b, bottom), S ₅₀ was significantly smaller and the initial slope (the dotted line) was significantly gentler in the CHF than in the control rats (Table 2).

The total baroreflex transfer function from CSP to AP showed low-pass characteristics (Fig. 3c). G _0.01 and G _0.1 were significantly smaller in the CHF than in the control rats (Table 2), but G ₁ did not differ significantly. The phase was close to −π radians at the lowest frequency in both groups, reflecting the negative feedback operation attained by the total baroreflex. The phase delayed with an increase in frequency. The coherence values seem lower than those in the peripheral arc transfer function. In the step response of AP for a unit increase in CSP (Fig. 3c, bottom), both S₅₀ and the initial slope (the dotted line) were significantly attenuated in the CHF in comparison with the control rats (Table 2).

The transfer function from CSP to HR also displayed low-pass characteristics (Fig. 3d). G _0.01 and G _0.1 were significantly smaller in the CHF than in the control rats (Table 2). We did not compare G ₁ because the coherence values close to zero and the irregular change in the phase shift above 0.8 Hz suggested poor reliability of the estimated transfer function. In the step response of HR for a unit increase in CSP (Fig. 3d, bottom), both S ₅₀ and the initial slope (the dotted line) were significantly attenuated in the CHF in comparison with the control rats (Table 2).

Static characteristics of the carotid sinus baroreflex

Figure 4 summarizes the open-loop static characteristics of the carotid sinus baroreflex obtained from the control and CHF rats. The baroreflex neural arc showed a decreasing SNA response with an increase in CSP (Fig. 4a). The response range of SNA was significantly narrower in the CHF rats (Table 3). Consequently, the minimum SNA was significantly higher in the CHF rats. The midpoint pressure on the CSP axis was significantly lower in the CHF rats. Despite the significant attenuation in the response range of SNA, the maximum slope of the neural arc was not reduced in the CHF rats compared with the control rats.

Fig. 4.

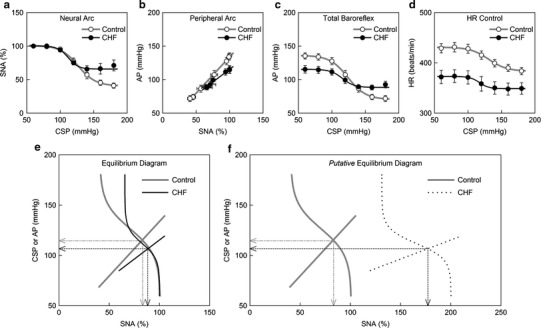
Static characteristics of the carotid sinus baroreflex averaged for the control (n = 12) and chronic heart failure (CHF; n = 7) rats. a Static characteristics of the baroreflex neural arc. An increase in CSP decreases SNA. The response range in SNA is significantly attenuated in CHF. b Static characteristics of the baroreflex peripheral arc. An increase in SNA increases AP in a linear manner. The slope of the regression line is significantly gentler in CHF. c Static characteristics of the total baroreflex. CSP and AP show an inverse sigmoidal relationship. The response range of AP and the maximum gain are significantly smaller in CHF. d Static characteristics between CSP and HR. CSP and HR show an inverse sigmoidal relationship. The response range of HR and the minimum HR are significantly smaller in CHF. e Baroreflex equilibrium diagram constructed from the fitted logistic function for the neural arc and the regression line for the peripheral arc. f Putative baroreflex equilibrium diagram in which the SNA axis is scaled so that the maximum absolute SNA in CHF becomes two times higher than that in control. In panels e and f, the dotted lines with arrowheads indicate the operating-point AP and SNA in CHF. The dash-dot lines with arrowheads indicate the operating-point AP and SNA in control

Table 3.

Parameters of the static characteristics of the carotid sinus baroreflex

	Control (n = 12)	CHF (n = 7)	P value
Neural arc
P1, response range (%)	62 ± 4	42 ± 6**	0.008
P2, slope coefficient (mmHg−1)	0.10 ± 0.01	0.16 ± 0.03*	0.048
P3, midpoint pressure (mmHg)	128 ± 4	115 ± 4*	0.043
P4, minimum SNA (%)	39 ± 4	60 ± 6**	0.008
Maximum slope (% mmHg−1)	1.62 ± 0.27	1.54 ± 0.27	0.839
Peripheral arc
a, slope (mmHg %−1)	1.10 ± 0.08	0.75 ± 0.10*	0.013
b, AP intercept (mmHg)	23.5 ± 7.7	40.7 ± 7.2	0.152
Total baroreflex
P1, response range (mmHg)	64 ± 4	31 ± 6**	<0.001
P2, slope coefficient (mmHg−1)	0.10 ± 0.01	0.13 ± 0.01	0.144
P3, midpoint pressure (mmHg)	122 ± 3	117 ± 4	0.326
P4, minimum AP (mmHg)	74 ± 4	85 ± 3	0.065
Maximum gain	1.62 ± 0.22	0.95 ± 0.17*	0.048
Heart rate control
P1, response range (beats min−1)	49 ± 5	30 ± 6*	0.033
P2, slope coefficient (mmHg−1)	0.10 ± 0.01	0.13 ± 0.01	0.099
P3, midpoint pressure (mmHg)	131 ± 4	117 ± 4*	0.046
P4, minimum HR (beats min−1)	383 ± 7	343 ± 13*	0.011
Maximum slope (beats min−1 mmHg−1)	1.28 ± 0.23	0.93 ± 0.20	0.313
Equilibrium diagram
Operating-point AP (mmHg)	116 ± 3	106 ± 3*	0.042
Operating-point SNA (%)	84 ± 3	90 ± 4	0.227
Operating-point total baroreflex gain	1.23 ± 0.28	0.96 ± 0.39	0.578

Data are presented as mean ± SE

** P < 0.01 and *P < 0.05 by unpaired t test

The peripheral arc from SNA to AP approximated a straight line in both the control and CHF rats (Fig. 4b). The slope of the regression line was significantly less steep in the CHF rats, whereas the AP intercept did not differ significantly between the two groups (Table 3).

The total baroreflex function from CSP to AP approximated an inverse sigmoidal curve (Fig. 4c). The response range of AP was significantly narrower in the CHF rats (Table 3). The slope coefficient, the midpoint pressure on the CSP axis, and the minimum AP did not differ significantly between the two groups. The maximum gain was significantly smaller in the CHF rats compared with the control rats.

The static CSP-HR relationship also approximated an inverse sigmoidal curve (Fig. 4d). The response range of HR was significantly narrower, and the minimum HR was significantly lower in the CHF rats (Table 3). The midpoint pressure on the CSP axis was significantly lower in the CHF rats. The slope coefficient and the maximum slope did not differ significantly between the two groups.

The baroreflex equilibrium diagram is obtained by plotting the neural and peripheral arcs on a pressure-SNA plane (Fig. 4e). The ordinate is either CSP (for the neural arc) or AP (for the peripheral arc). The intersection between the neural and peripheral arcs gives the closed-loop operating point [17, 18]. The operating-point AP (the horizontal arrow) was significantly lower in the CHF rats, whereas the operating-point SNA (the vertical arrow) did not differ significantly between the two groups (Table 3). The total baroreflex gain at the operating point, calculated from the product of the tangential slope of the neural arc (ΔSNA/ΔCSP) and the slope of the peripheral arc (ΔAP/ΔSNA), did not differ significantly between the two groups (Table 3): ΔCSP, ΔSNA, and ΔAP indicate small changes in CSP, SNA, and AP, respectively, at the intersection point. Figure 4f depicts a putative baroreflex equilibrium diagram where the SNA axis is scaled so that the maximum value of SNA in the CHF group becomes two times higher than that in the control group (see Discussion).

Simulation study

A block diagram of the simulation study is shown in Fig. 5a [14–16]. We used impulse responses derived from the group-averaged neural and peripheral arc transfer functions (H _N and H _P) to calculate dynamic responses of the carotid sinus baroreflex. The steady-state gains of H _N and H _P were normalized to unity in order that absolute values of the steady-state gains could be determined by their corresponding static characteristics. The static characteristics of the neural and peripheral arcs were modeled as a logistic function and a regression line, respectively, using group-averaged parameter values (Table 3). A sinusoidal wave with an amplitude of 15 mmHg (peak-to-peak pressure of 30 mmHg) and a frequency of 5 Hz (corresponding to 300 beats/min) was added to the output from the peripheral arc to mimic pulsatile pressure. The AP signal was fed back into the neural arc to achieve a closed-loop simulation. After the AP signal reached steady state, step disturbances ranging from −10 to −60 mmHg were imposed.

Fig. 5.

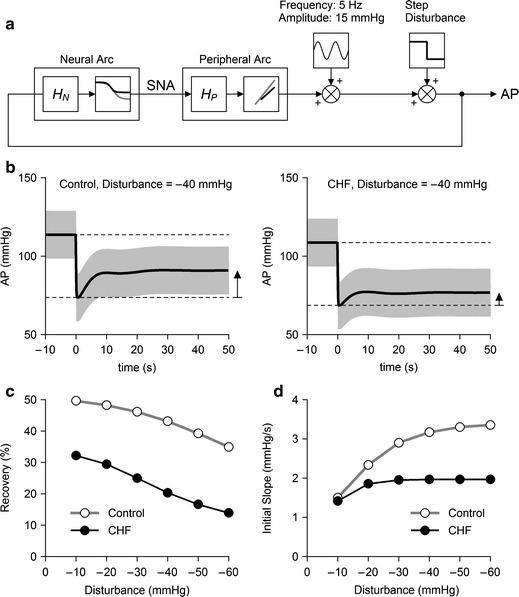
a Block diagram for the simulation of AP regulation. H_N and H_P represent dynamic characteristics of the neural and peripheral arcs, respectively. The static characteristics of the neural arc were modeled as a logistic function. The static characteristics of the peripheral arc were modeled as a straight line. Parameters for the logistic function and the regression line were derived from mean values shown in Table 3. A 5-Hz sine wave with an amplitude of 15 mmHg was added to mimic pulsatile pressure. Exogenous step disturbances ranging from −10 to −60 mmHg were applied, and the closed-loop AP responses were calculated for control and CHF conditions. b Typical simulation results during an exogenous pressure disturbance of −40 mmHg. The pulsatile pressure is shown in gray, and mean AP signal is shown as a bold line. The horizontal dotted lines indicate the mean AP values just before and after the onset of step disturbance. AP recovers less efficiently in the CHF simulation compared to the control simulation. c Percent recovery of AP as a function of the size of disturbance. d The initial slope of the recovery as a function of the size of disturbance

Typical examples of the transient AP response to a step disturbance of −40 mmHg under control and CHF conditions are shown in Fig. 5b. In each panel, the pulsatile pressure is shown in gray, and the mean AP signal is shown as a solid bold line. The horizontal dashed lines represent the mean AP values immediately before and after the onset of the step disturbance. The AP signal decreased abruptly by 40 mmHg at time zero and recovered gradually thereafter. The upward arrow indicates the magnitude of steady-state AP recovery. The recovery was greater in the control than in the CHF simulation.

Figure 5c depicts the percent recovery of AP relative to the size of the step disturbance. The steady-state AP recovery was approximately 50% in the control and approximately 32% in the CHF simulation for a step disturbance of −10 mmHg, indicating that the feedback AP regulation in the CHF simulation was approximately 64% as effective as that in the control simulation. On the other hand, the AP recovery was approximately 35% in the control and approximately 14% in the CHF simulation for a step disturbance of −60 mmHg, indicating that the efficiency of feedback AP regulation in the CHF simulation reduced to only 40% of that in the control simulation.

Figure 5d shows the initial slope of the AP recovery. The initial slope increased as the size of step disturbance increased in the control simulation. Although the initial slope of the AP recovery in the CHF simulation was comparable to that in the control simulation for a step disturbance of −10 mmHg, it did not increase significantly with an increase in the size of step disturbance.

Discussion

The major findings of the present study are (1) the dynamic characteristics of the baroreflex neural arc were preserved in CHF, whereas those of the baroreflex peripheral arc were significantly depressed (Fig. 3), and (2) the total baroreflex gain at the closed-loop operating point seemed preserved in CHF, whereas the range of baroreflex operation was significantly narrowed (Fig. 4). Because of these modulations in the baroreflex characteristics, the AP regulation was less robust against exogenous disturbances in CHF (Fig. 5), which may partly explain the incidence of acute decompensation in stable CHF patients caused by noncompliance with salt and water restriction [19].

Dynamic characteristics of the carotid sinus baroreflex in CHF rats

The derivative characteristics of the neural arc are preserved in the CHF rats (Fig. 3a), being consistent with a previous study in heart failure rabbits [20]. Moreover, the present results indicate that the dynamic AP response to SNA is significantly depressed in CHF (Fig. 3b), suggesting impaired end-organ responses to SNA. The total baroreflex function in terms of the AP regulation was more sluggish in the CHF rats (Fig. 3c, bottom) despite the preserved neural arc derivative characteristics.

In the transfer function from CSP to HR, dynamic gain values were significantly attenuated in the CHF rats (Fig. 3d). Because the dynamic gain of the neural arc transfer function did not reduce significantly (G _0.1), the attenuation of the dynamic gain of the HR control may be attributable to the reduced HR response to SNA such as that related to the downregulation of β-adrenergic receptors [21].

Static characteristics of the carotid sinus baroreflex in CHF rats

In both the control and CHF rats, the input-output relationship of the peripheral arc approximated a straight line (Fig. 4b), and the sigmoidal nonlinearity is primarily attributed to the neural arc (Fig. 4a). The impairment of the total baroreflex in the CHF rats, characterized by a significant attenuation of the response range of AP and a reduction of the maximum gain (Fig. 4c, Table 3), is in essence similar to that obtained previously in canine models of heart failure [3, 5, 6].

Wang et al. [4, 5] reported poor end-organ responses and normal central control of renal SNA in the heart failure dogs. The attenuated slope of the peripheral arc in the CHF rats (Fig. 4b) may be consistent with the poor end-organ responses. Although the response range of SNA in the neural arc was narrowed in the CHF rats (Fig. 4a), the maximum slope of the neural arc did not change significantly, which should contribute to the maintained total baroreflex gain within a small range around the operating point (Fig. 4e, Table 3).

The response range of HR was significantly reduced in the CHF rats (Fig. 4d) in agreement with the depressed dynamic HR response to CSP (Fig. 3d). Although 24-h averaged HR was higher in the CHF rats in a previous study [7], the minimum HR was significantly lower in the CHF than in the control rats. Anesthesia and vagotomy might have affected the results, and further studies are needed to reconcile some of the discrepancies between the present and previous results.

Equilibrium diagram and simulation study

A baroreflex equilibrium diagram provides information on the closed-loop operating point (Fig. 4e) [10, 17, 18, 22–26]. Because absolute SNA is considered to be higher in CHF [7], if we can use the absolute value for SNA, the SNA axis of the equilibrium diagram should be scaled in a manner that renders the peripheral arc much shallower in the CHF than in the control rats (Fig. 4f). The operating-point AP was decreased only by 10 mmHg in the CHF rats and the total baroreflex gain at the operating point did not differ between the control and CHF rats. The baroreflex function may therefore seem preserved in the CHF rats when it is assessed only within a small range around the closed-loop operating point.

We used splanchnic SNA to construct a baroreflex equilibrium diagram. The analysis based on SNA of only one limb of the sympathetic nervous system can be an oversimplification in light of the well-known regional differences in SNAs [27–29]. One rationale for using splanchnic SNA is that the splanchnic region has been regarded as a major site for the blood flow redistribution [17, 30]. Furthermore, we have continued to observe insignificant differences in the steady-state responses to CSP between left and right cardiac SNAs [31], between cardiac and renal SNAs [32], and among cardiac, renal, and muscle SNAs [33] in anesthetized rabbits. It seems that the carotid sinus baroreflex brings about common activity in addition to regional activity among sympathetic nerves innervating several districts (see Appendix 3). Whether the similarity among SNAs to different districts will hold in other experimental conditions awaits future investigations.

The simulation study is useful and necessary for the integrated understanding of the estimated dynamic and static characteristics of the carotid sinus baroreflex (Fig. 5a). The feedback AP regulation becomes much weaker in CHF as the size of step disturbance increases (Fig. 5c, d), suggesting that a reserve for AP buffering is lost in CHF. Because not only the baroreceptor input but also loading conditions to the heart are changed during orthostatic tilt, the results of the present simulation can not be directly extrapolated to the actual tilting conditions. However, it may be of notice that patients with severe congestive heart failure show a significant drop in systolic AP upon orthostatic tilt regardless of relatively maintained baseline AP [34]. The exogenous disturbance in the opposite direction may also be hazardous. Even though baseline AP appears normal in stable CHF patients, noncompliance with salt and water restriction may easily collapse the AP regulation and induce acute decompensation [19].

Study perspective

The progression of CHF is closely associated with the autonomic imbalance between sympathetic and vagal nerve activities. Although pharmacological treatments such as β-adrenergic blockers [35], angiotensin converting enzyme inhibitors [36], and angiotensin receptor blockers [37] have been developed, the therapeutic outcome is not always satisfactory and the mortality rate for CHF remains high. Novel therapeutic strategies for CHF beyond conventional treatments such as electrical vagal nerve stimulation are expected to be developed [7, 38].

Although the mechanisms for the autonomic imbalance in CHF are not completely understood, the loss of baroreflex control of the sympathetic and vagal systems has been considered an important factor [39, 40]. Zucker et al. [41] demonstrated that chronic baroreceptor activation improved the survival of dogs with pacing-induced heart failure. The study seems rudimentary, however, in that the stimulation intensity of the carotid sinus baroreceptors was adjusted intermittently to obtain a prescribed sympathoinhibitory response. The stimulation could be too strong or too weak during the intervals of adjustments. If the stimulation intensity is feedback-controlled continuously, the therapeutic effect and safety could be enhanced.

Quantification of the dynamic characteristics of a target system is the first step for developing a robust controller [42–44]. Next, the controller should be designed in such a way that the variation of the target system dynamics does not affect the controlling result much [45]. The simulation of the closed-loop AP response in CHF, such as that shown in Fig. 5, will be utilized in designing a robust controller system of the carotid sinus activation.

Limitations

First, we used normal rats without sham operation as the control group. Sham-operated rats may serve as a more appropriate control. Although the surgical operation of thoracotomy itself could have affected the baroreflex function in the CHF group, because over 100 days had elapsed after the surgical operation, the effect of surgical operation might have been limited. Actually, two rats that underwent coronary ligation but did not meet the criteria for CHF retained the maximum gain of the total baroreflex close to the control group (rat A: central venous pressure = 2.28 mmHg, biventricular weight = 1.94 g kg⁻¹, total baroreflex gain = 1.61; rat B: central venous pressure = 1.69 mmHg, biventricular weight = 2.33 g kg⁻¹, total baroreflex gain = 1.67).

Second, the data were obtained under anesthetic conditions. Because the anesthesia affects autonomic nervous activities, the results should be carefully interpreted. Vagotomy and lower perfusion of the brain due to carotid artery occlusion might have also affected the baroreflex function. Nevertheless, the present results would provide a unique clue to integrated understanding of the impaired baroreflex function in CHF.

Third, we did not measure cardiac output or peripheral vascular resistance. Subdividing the peripheral arc into the cardiac and vascular components will be necessary to identify the mechanisms for an approximately linear relationship between SNA and AP in both the control and CHF rats.

Conclusions

The dynamic and static characteristics of the neural arc, peripheral arc, and total baroreflex were analyzed comprehensively in rats with CHF after myocardial infarction. Although the derivative characteristics of the baroreflex neural arc are preserved in the CHF rats, the dynamic AP regulation is depressed in both the magnitude and response speed. The equilibrium diagram indicates that the baroreflex gain may seem preserved in CHF in a small range around the closed-loop operating point. However, the percent recovery of AP and the speed of recovery are reduced progressively as the size of exogenous disturbance increases in the CHF rats. The reserve for AP buffering may be lost in CHF despite the relatively maintained baseline AP.

Appendix 1: feature of a Gaussian white noise input

The neural arc of the arterial baroreflex may be roughly modeled by a cascade system, which consists of a dynamic linear subsystem followed by a static nonlinear subsystem [14]. In this type of system, the selection of the mean input pressure and the amplitude of input does not significantly affect the estimation of the system linear dynamics except for a factor of proportionality when the system is tested with a Gaussian white noise (GWN) signal [46]. In order to demonstrate the above notion, we performed a simulation study. In reference to Fig. 6a, the dynamic linear subsystem for the baroreflex neural arc was modeled by the following equation:

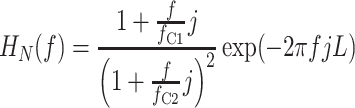5

where f _C1 and f _C2 are the corner frequencies determining the frequency-dependent changes in the dynamic gain, L denotes the pure dead time, f and j indicate frequency and an imaginary unit, respectively. We set f _C1 = 0.1 Hz, f _C2 = 0.9 Hz, and L = 0.1 s to mimic the neural arc transfer function. The static nonlinear subsystem of the neural arc was modeled by the logistic function (Eq. 3) with parameters of P ₁ = 60%, P ₂ = 0.1 mmHg⁻¹, P ₃ = 120 mmHg, and P ₄ = 40%. Using this model, the linear input-output relationship was estimated by a GWN input or a binary white noise (BIN) input. Mean input pressure was changed among 120, 90, and 150 mmHg (P ₃, P ₃ – 30, and P ₃ + 30 mmHg).

Fig. 6.

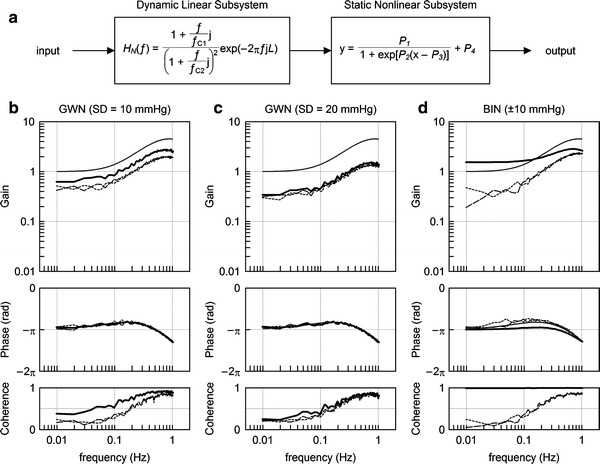
a A cascade model for the baroreflex neural arc, which consists of a dynamic linear subsystem and a static nonlinear subsystem. The dynamic linear subsystem represents the neural arc transfer function. The static nonlinear subsystem represents the sigmoidal nonlinearity for the neural arc. b Estimation results of the system dynamic characteristics using a Gaussian white noise (GWN) input with a standard deviation (SD) of 10 mmHg. c Estimation results of the system dynamic characteristics using a GWN input with an SD of 20 mmHg. d Estimation results of the system dynamic characteristics using a binary white noise (BIN) input with an amplitude of 10 mmHg. In panels b through d, the thin smooth curve indicates the transfer function of the given dynamic linear subsystem. The solid bold curve, dotted thin curve, and dashed thin curve represent the estimation results obtained by the input signals with mean input pressures of 120, 90, and 150 mmHg, respectively (see text for explanation)

Figure 6b through 6d shows the estimation results. In each panel, thin smooth curves in the gain and phase plots indicate the transfer function of the dynamic linear subsystem described by Eq. 5. The solid bold curves, dotted thin curves, and dashed thin curves represent the estimation results obtained by mean input pressures of 120, 90, and 150 mmHg, respectively. Figure 6b and c represents the estimation results obtained by GWNs with standard deviations of 10 and 20 mmHg, respectively. As can be seen, the estimated gain plots are nearly parallel to the gain plot of the given dynamic linear subsystem. The estimated phase plots are superimposable on the phase plot of the given dynamic linear subsystem.

Figure 6d shows the estimation results obtained by BINs with an amplitude of 10 mmHg (i.e., the peak-to-peak pressure of 20 mmHg). None of the estimated gain plots are parallel to the gain plot of the given dynamic linear subsystem. The estimated phase plots also deviated from the phase plot of the given dynamic linear subsystem. When the system was tested by the BIN input with the mean input pressure of 120 mmHg, the coherence value became close to unity, suggesting that the BIN input had caused on-off behavior in the system output.

The above simulation results confirm that the selection of the mean input pressure and the amplitude of GWN does not significantly affect the estimation of the dynamic characteristics of the system except for a factor of proportionality when the mean input pressure and the standard deviation of GWN are not far beyond the system operating range.

Appendix 2: estimation of the initial slope of the step response or recovery response

To characterize the speed of the response, the initial slope of the response was calculated as follows. First, a response threshold is determined as the 5% value of the steady-state step response. In the case of the recovery response, 5% of the maximum recovery is used as the threshold. Next, an initial time point at which the response exceeds the threshold value is determined. Starting from this initial time point, a linear regression analysis giving a slope and an intercept is performed repeatedly while increasing the number of analyzed data points. The steepest slope thus obtained is used as the initial slope of the response. By setting the 5% threshold, the linear regression can be performed excluding the initial data points constituting the dead time.

Appendix 3: comparison of splanchnic and renal SNAs under the present experimental conditions

We compared splanchnic and renal SNAs under the present experimental conditions in an additional three rats. A branch of the right renal sympathetic nerve was exposed through a right flank incision, and renal SNA was recorded simultaneously with splanchnic SNA. Figure 7a presents time series of 10-Hz decimated CSP, splanchnic SNA, and renal SNA obtained from one rat. White lines in splanchnic and renal SNAs indicate 2-s moving averaged signals. In each of the splanchnic and renal SNAs, a 10-s averaged value for the last 10 s at CSP of 60 mmHg was defined as 100%, and a 10-s averaged value after the administration of hexamethonium bromide was defined as 0%, in the same manner as the main study. Figure 7b shows the relationships of SNAs versus CSP. Although the renal SNA values were slightly greater than the splanchnic SNA values at CSPs of 160 and 180 mmHg in this rat, the general sigmoidal relationships were similar between the two SNAs. The regression line for renal SNA (y) versus splanchnic SNA (x) was y = 0.94x + 5.8 (r ² = 0.998) in this rat (Fig. 7c). The other two rats showed regression lines of y = 1.01x + 0.3 (r ² = 0.999) and y = 0.99x + 3.7 (r ² = 0.995), suggesting that both splanchnic and renal SNAs can represent common activity for the AP regulation during the stepwise input protocol under the present experimental conditions.

Fig. 7.

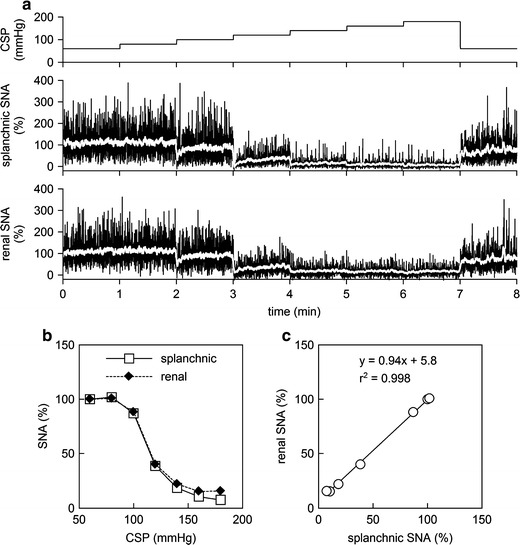
a Typical recordings of 10-Hz decimated CSP, splanchnic SNA, and renal SNA obtained from a normal rat in an additional study using the same experimental settings as the main study. The white lines in the SNA recordings represent 2-s moving averaged signals. An increase in CSP decreased splanchnic and renal SNAs. b Static characteristics of the baroreflex neural arc drawn based on splanchnic and renal SNAs. c Correlation between splanchnic and renal SNAs during the stepwise input protocol. In panels b and c, splanchnic and renal SNA data were obtained as the averaged values during the last 10 s at each CSP level