Automated assembly of centromeres from ultra-long error-prone reads

Abstract

Centromeric variation has been linked to cancer and infertility, but centromere sequences contain multiple tandem repeats and can only be assembled manually from long error-prone reads. Here, we describe the centroFlye algorithm for centromere assembly using long error-prone reads, and apply it to assemble human centromeres on chromosomes 6 and X. Our analyses reveal putative breakpoints in the manual reconstruction of the human X centromere, demonstrate that human X chromosome is partitioned into repeat subfamilies, and provides initial insights into centromere evolution. We anticipate that centroFlye could be applied to automatically close remaining multi-megabase gaps in the reference human genome. AU abstract edits ok? We accepted all edits in the paper that you proposed.

Introduction

Long-read technologies (such as Pacific Biosciences and Oxford Nanopore) have greatly increased the contiguity of genome assemblies as compared to short-read technologies. However, the existing long-read assemblers, such as Falcon¹, Miniasm², Flye³, HINGE⁴, Canu⁵, Marvel⁶, and wtdbg2⁷ typically fail to resolve long segmental duplications⁸ and long tandem repeats³. This paper focuses on the latter challenge of assembling long tandem repeats, and specifically on centromere assembly, a problem that was viewed as intractable until recently. As shown in Kolmogorov et al., 2019³, the existing long-read assemblers are inaccurate, even in the case of relatively short bridged tandem repeats that are spanned by long reads. Although Flye improved on other tools in assembling such repeats³, assembly of unbridged tandem repeats remains an open problem.

Centromeric satellite repeats are among the longest tandem repeats in the human genome and the biggest gaps in the reference human genome assembly (for brevity, below we refer to such regions simply as centromeres). As a result, studies of associations between sequence variations and genetic diseases currently ignore ≈3% of the human genome. This is unfortunate since centromeres play crucial roles in chromosome segregation and a large component of genetic disease result from aneuploidies arising during meiosis⁹. In addition, variations in centromeres are linked to cancer and infertility^10–18. Centromere sequencing is also important for addressing open problems about centromere evolution^19–23. These studies revealed fast evolution of centromeres, indeed, complex higher-order chromosome-specific centromeric repeats are unique to the hominid lineage and are not chromosome-specific even in closely related species such as gibbons²⁴. Recent discovery of large archaic blocks of Neanderthal DNA spanning human centromeres reveals the potential of centromeres for studies of human population history²⁵.

Human centromeres comprise long tandem repeats (also known as satellite DNA) that are often repeated thousands of times with extensive variations in copy numbers in the human population. Although long-read technologies facilitated analysis of centromere on Y chromosome²⁶, there is no software tool for centromere reconstruction and it remains unclear how accurate semi-manual centromere reconstructions are.

We report the centroFlye algorithm for centromere assembly and apply our algorithm to enable automatic reconstruction of the centromeres on chromosomes 6 and X (referred to as cen6 and cenX).

Results As suggested, we extended the description and emphasized the Method here

Centromere structure.

The alpha satellite repeat family forms ≈3% of the human genome²⁷. Each alpha satellite (monomer) is ≈171 nucleotides in length. Blocks of multiple consecutive monomers form higher-order repeat (HOR) units that can be repeated thousands of times. Individual monomers within a HOR show low (50–90%) sequence identity to each other while HORs within a single centromere show high (95%–100%) sequence identity. Organization and nucleotide sequence of HORs is specific for a particular chromosome. HORs typically occupy multi megabase-sized segments that may include rearrangements and transposon insertions²⁸. Since centromere assembly of a diploid genome is particularly challenging, studies of the centromeres on X and Y chromosomes in the male genome represent a simpler (albeit still very complex) problem^19,29–31. AU does this description of centromere structure feed into the description about the pipeline? We shortened this description to ensure that everything feeds into the description about the pipeline

Human centromeres differ widely with respect to their architecture. For example, centromere on chromosome X (cenX) is built from a single 12-monomer HOR with very few abnormal HORs. In contrast, centromere on chromosome 6 (cen6) has a highly irregular architecture formed by three HORs (consisting of 15, 16, and 18 monomers) and many abnormal HORs. These two examples (highly regular and highly irregular centromere architectures) exemplify two extremes and result in two different algorithmic challenges. centroFlye thus has two modes: the HOR mode (designed for centromeres with a single HOR like cenX) and the monomer mode (designed for centromeres with multiple HORs and irregular architecture like cen6).

CentroFlye pipeline.

centroFlye in the HOR mode (centroFlye_HOR) takes a read-set from the entire genome and a consensus HOR (characterizing a specific centromere) as an input. It further classifies a read as centromeric if it contains at least one HOR and assembles the centromeric reads. centroFlye_HOR modifies the approach to resolving unbridged repeats used in the Flye assembler³ for the case of tandem repeats. Flye finds divergent positions within an unbridged repeat (positions where repeat copies differ from each other) and uses them as stepping stones for resolving these repeats. However, since mapping of reads within cenX is unknown, it is unclear how to infer the divergent positions between various copies of a HOR. centroFlye_HOR instead defines a set of rare k-mers (k-mers that appear in a single or a few copies of a HOR) and uses them for reconstructing centromeres. Supplementary Fig. 1 reveals frequencies of rare k-mers in the assembly.

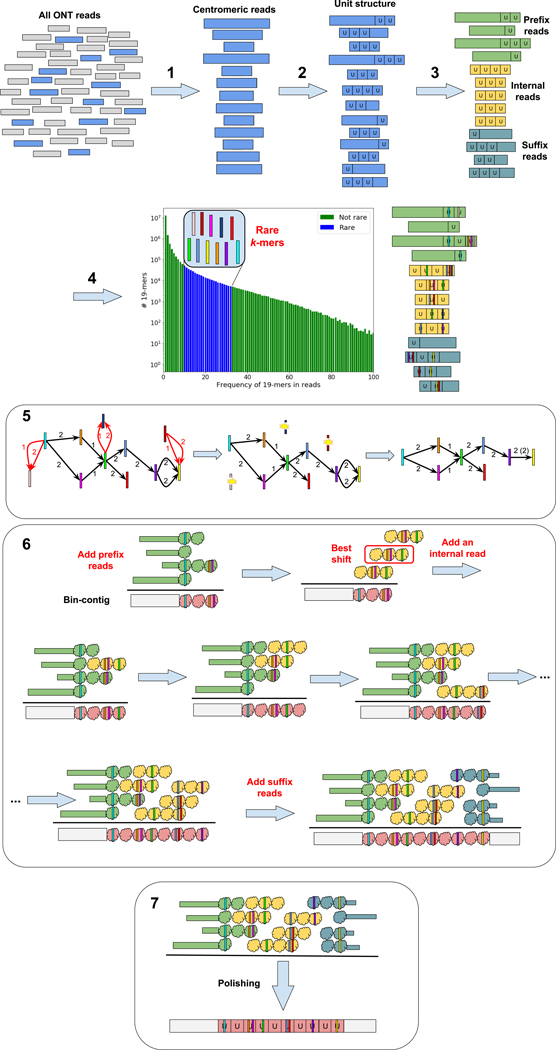
The centroFlye pipeline in the HOR mode consists of the following steps (Fig. 1): (i) recruiting centromeric reads, (ii) partitioning centromeric reads into units, where each unit represents a HOR copy, (iii) classifying centromeric reads into prefix reads (that start before the centromere and “enter” it), internal reads (located entirely within the centromere), and suffix reads (that start in the centromere and “leave” it), (iv) identifying rare centromeric k-mers, (v) constructing the distance graph to filter out false positives among rare centromeric k-mers, (vi) reconstructing the centromere, and (vii) polishing the reconstructed centromere sequence. Online Methods describe each of these steps and illustrate them using the cenX assembly.

Figure 1. centroFlye_HOR pipeline.

1: Recruitment of centromeric reads from the entire read-set. 2: Partitioning each read into units, where each unit represents a HOR copy. 3: Classifying centromeric reads into prefix, internal, and suffix reads. 4: The frequency histogram of all k-mers in centromeric reads reveals rare k-mers. Each colored vertical bar represents a rare k-mer. k-mers with lower frequencies than rare k-mers likely represent sequencing errors. 5: Construction of the distance graph. Rare k-mers represent vertices and each edge connects a pair of rare k-mers occurring in the same read. Edge labels represent distances (in units) between rare k-mers in a read. An edge is red if there are conflicting parallel edges connecting corresponding vertices, and black otherwise. (Left) The distance graph constructed on all rare k-mers. (Middle) The distance graph with conflicting parallel edges and isolated vertices removed. (Right) The final distance graph with collapsed multi-edges. 6: Reconstruction of a centromere. Each unit in each read is represented as a bin (see Methods) with colored bars representing unique k-mers. After all prefix reads are added to a bin-contig, the best alignment (shift) of each read against the bin-contig is selected and the read with the highest-scoring alignment is added to the growing bin-contig. This procedure is repeated until the suffix reads are added to the bin-contig. 7: Polishing the reconstructed centromere sequence.

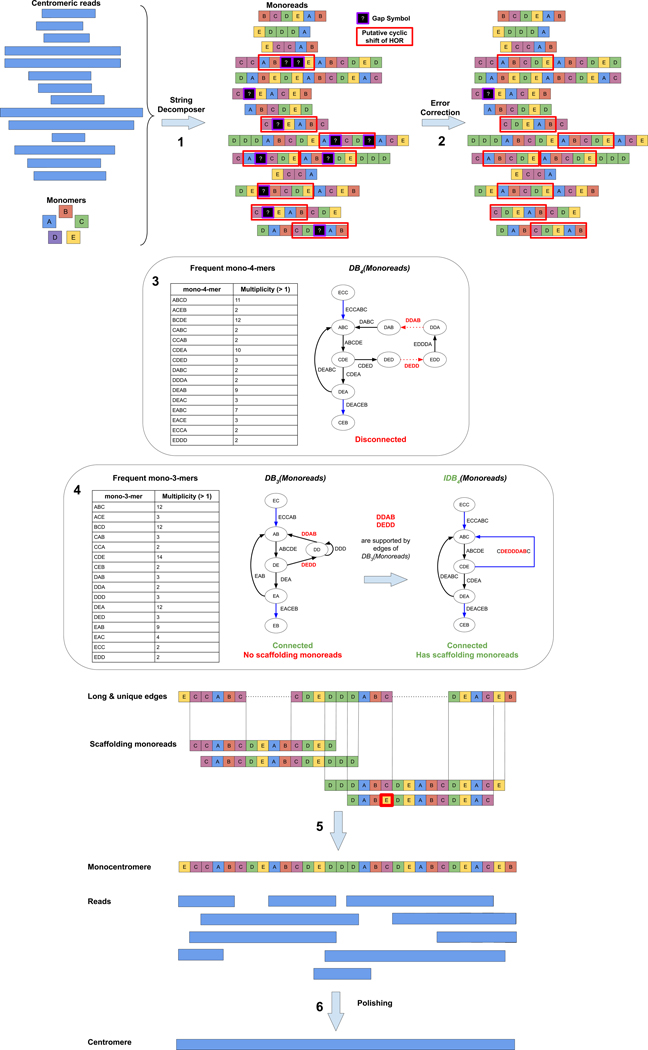
In difference from centroFlye in the HOR mode (that under-utilizes abnormal units in assembly), centroFlye in the monomer mode (referred to as centroFlye_mono) uses abnormal units as markers for assembly. centroFlye_mono takes a read-set from the entire genome and the set of monomers for a specific chromosome as an input (Fig. 2). It includes the following steps (Fig. 2): (i) recruiting centromeric reads, (ii) transforming reads into monoreads. i.e., translating each read from the nucleotide alphabet into the monomer alphabet, (iii) error correction of monoreads, (iv) constructing the iterative de Bruijn graph ^32,33 of monoreads, (v) assembling monocentromere by scaffolding in the iterative de Bruijn graph, and (vi) translating monocentromere back from the monomer to the nucleotide alphabet. Online Methods describe each of these steps and illustrate them using the cen6 assembly. Below we focus on cenX assembly.

Figure 2. centroFlye_mono pipeline.

For the sake of illustration, we assume only 5 monomers forming a HOR ABCDE. 1: Transforming centromeric reads into monoreads. 2: Error correction of monoreads. 3: The de Bruijn graph DB₄(Monoreads) (with k=3) is shown just to illustrate the limitations of standard de Bruijn graph for centromere assembly and to motivate our use of the iterative de Bruijn graphs instead. The graph DB₄(Monoreads) is constructed on frequent mono-4-mers (minMultiplicity = 2). Red dotted edges DEDD and DDAB are not present in this disconnected graph since they represent infrequent mono-4-mers. Long (MinLength = k+2) and unique edges are shown in blue. 4: Construction of the iterative de Bruijn graph IDB₄(Monoreads) starts from constructing the standard de Bruijn graph DB₃(Monoreads). Though DB₃(Monoreads) is connected, it does not enable unique centromere assembly since there are no scaffolding reads that span two long and unique edges. However, both mono-4-mers DEDD and DDAB (that are missing in DB₄(Monoreads)) represent edges in DB₃(Monoreads) that are inherited by IDB₄(Monoreads). As a result, unlike DB₄(Monoreads), IDB₄(Monoreads) is connected. It contains three long and unique edges. 5: Assembling monocentromere by scaffolding in IDB₄(Monoreads). A mismatch in a monoread is highlighted with a red border. 6: Translating monocentromere back from the monomer to the nucleotide alphabet. Only monoreads that have unambiguous mapping to the monocentromere are used for polishing.

cenX assembly.

We analyzed the dataset of Oxford Nanopore Technologies (ONT) reads generated by the Telomere-to-Telomere consortium³⁴ and released on March 2, 2019. The dataset contains 11,069,717 reads (155 Gb total length, 50x coverage, N50=70 kb) generated from the CHM13hTERT female haploid cell line. 999,562 ultralong reads (longer than 50 kb) have the biggest impact on the centromere assembly and result in ≈32x coverage.

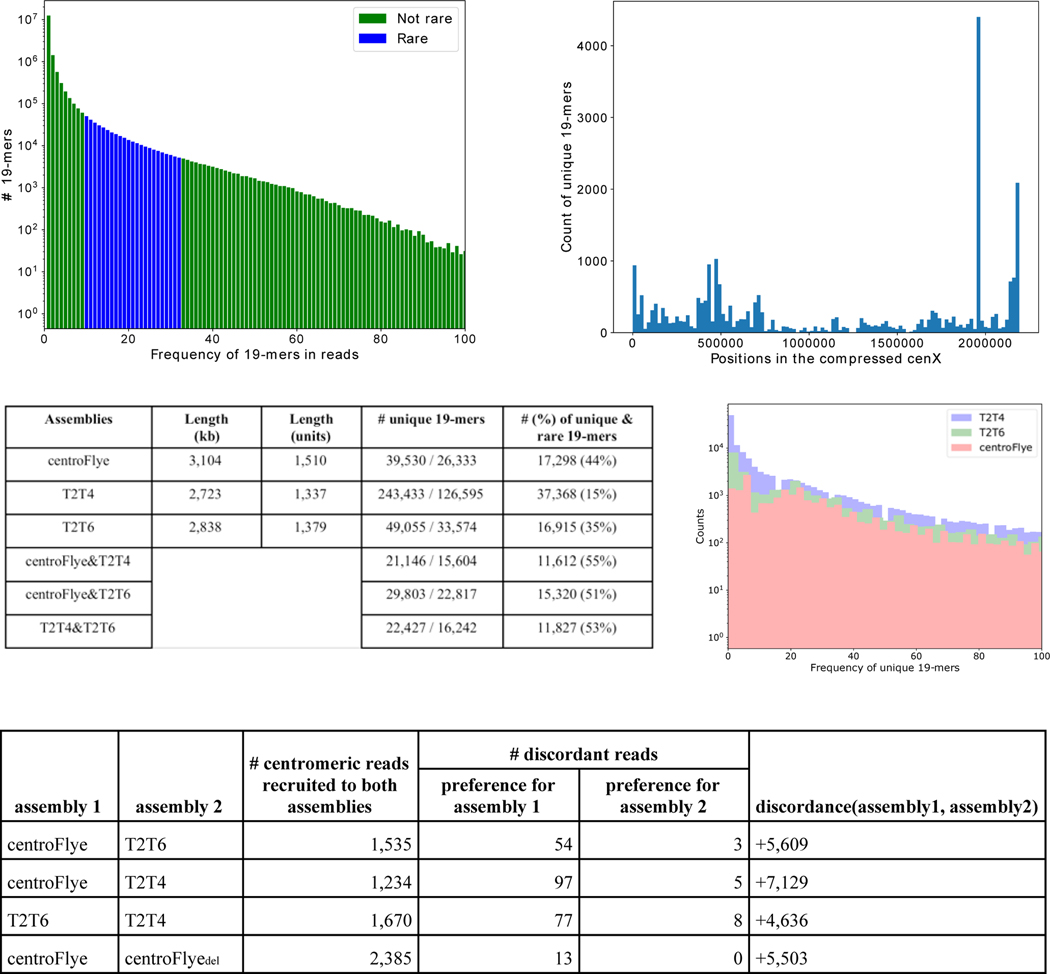
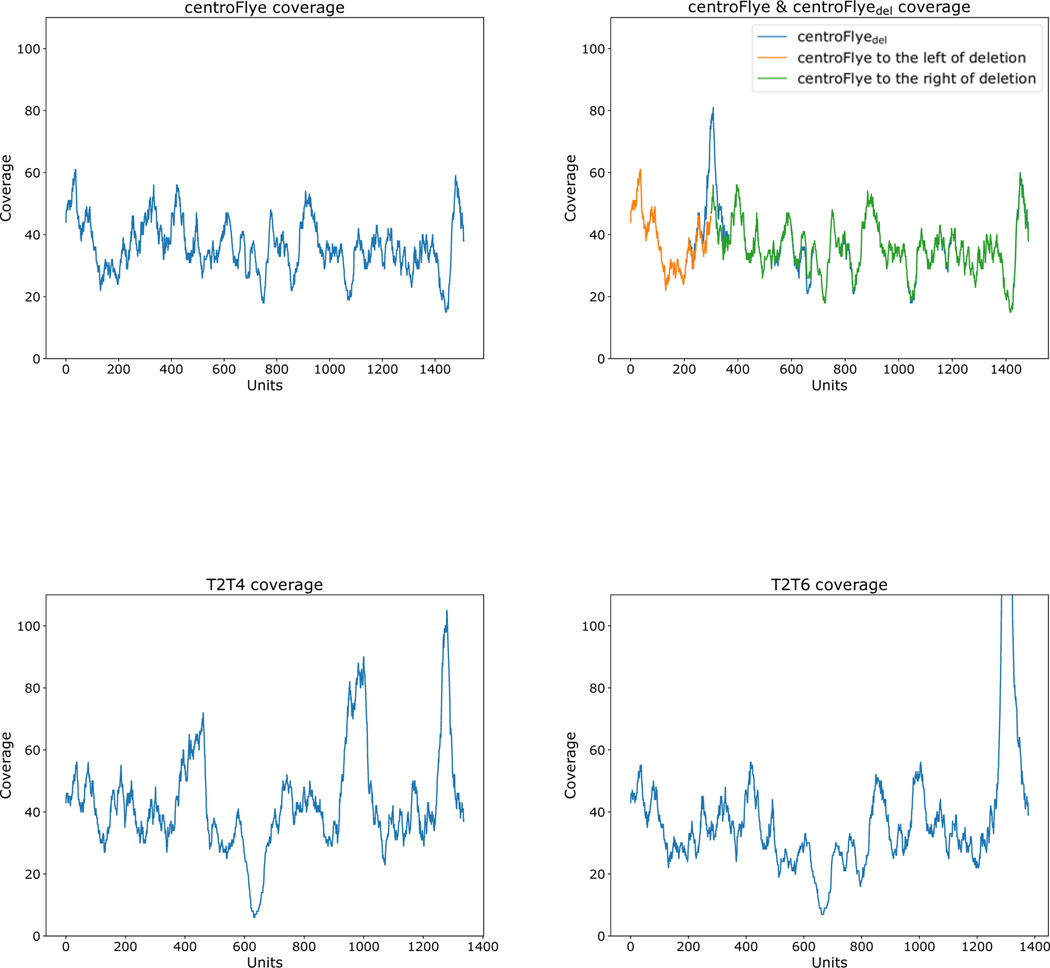
In addition to the centroFlye assembly, we analyzed the Telomere-to-Telomere consortium assemblies v0.4 (referred to as T2T4 assembly), and v0.6 (referred to as T2T6 assembly). Fig. 3 presents information about cenX assemblies. Since ONT assemblies often have inflated lengths of homonucleotide runs, we compressed each homonucleotide run into a single nucleotide (in the read-set and assemblies) and recomputed the number of unique 19-mers. Fig. 3 shows the distribution of frequencies of unique 19-mers in the compressed assemblies and illustrates that centroFlye and T2T6 assemblies have similar distributions of frequencies, while T2T4 assembly has many low-frequency unique 19-mers which are likely erroneous.

Figure 3. Information about cenX assemblies. (Top left) Frequency histogram of 19-mers in the centromeric reads.

Each bar represents the number of 19-mers in units of centromeric reads with given frequency (log-scale). The bars corresponding to the rare 19-mers are shown in blue. Only 19-mers with frequencies that do not exceed 100 are shown. 19-mers with lower frequencies than rare 19-mers likely represent sequencing errors. (Top right) Distribution of unique 19-mers along the compressed cenX sequence. Each bar represents the number of unique 19-mers in a segment of length ~20 kb (out of 26,724 unique 19-mers in the compressed cenX sequence). A large peak at positions 1,955,990 — 1,960,812 corresponds to a 4,822 nucleotide long (compressed) LINE insertion in cenX. (Middle left) Comparison of centroFlye, T2T4, and T2T6 assemblies. The column “number of unique 19-mers” shows the number of unique 19-mers before/after compression of homonucleotide runs. The column “number (percentage) of unique & rare 19-mers” refers to the number (percentage) of unique 19-mers in an assembly that are rare in reads. The T2T4 centromere has 57,811,689 — 60,534,892 coordinates and the T2T6 centromere has 57,827,622 — 60,665,308 coordinates on chromosome X. (Middle right) Distribution of frequencies (in logarithmic scale) of unique 19-mers in the compressed centroFlye, T2T4, and T2T6 cenX assemblies. (Bottom) Number of recruited reads, discordant reads and the discordance score for all pairs of assemblies.

Given a centromere assembly, one can map each centromeric read to this assembly using its unique k-mers. Below we describe how to use this mapping for comparison of various assemblies. To illustrate the effect of an indel on various quality metrics we constructed an artificial centroFlye_del assembly by introducing a deletion of length 50 kb (25 units) in the centroFlye assembly at position 600 kb (300 units).

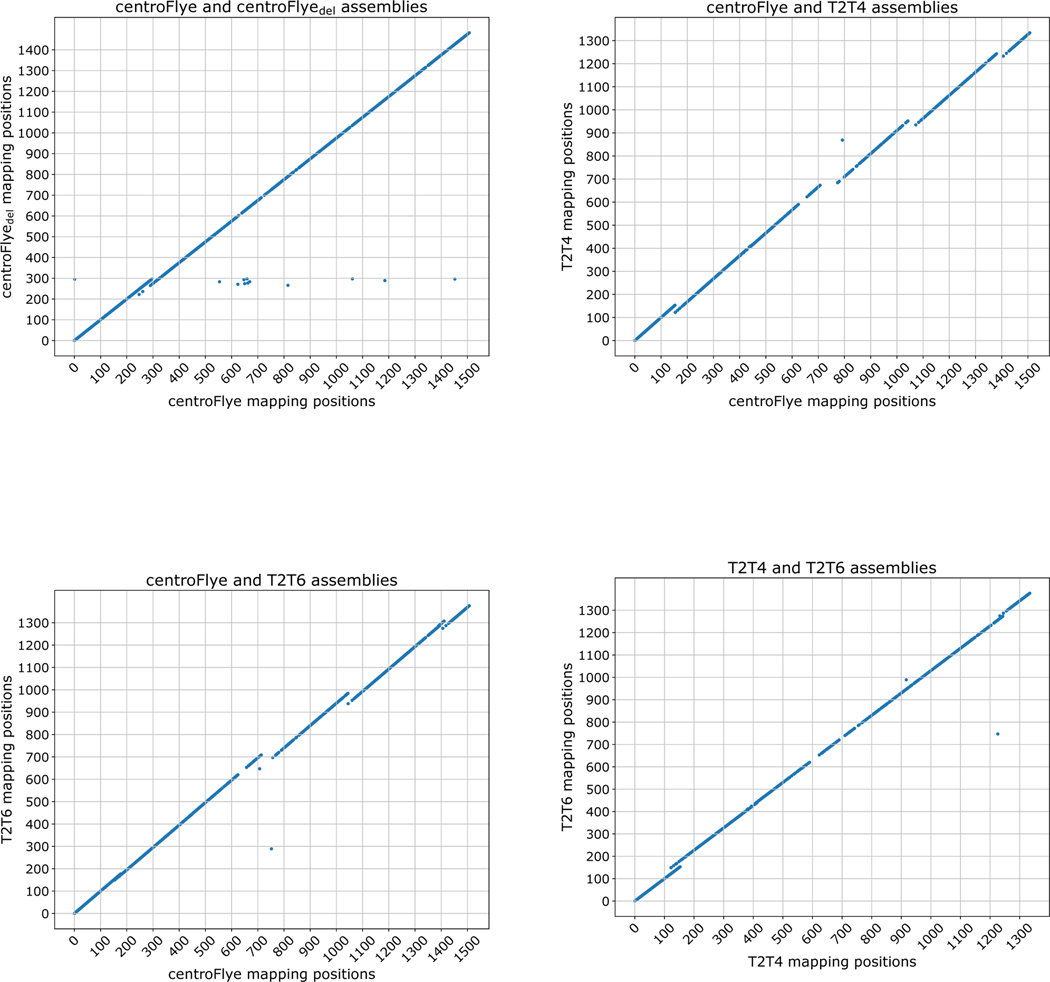
For each pair of assemblies, we used their shared unique 19-mers to align centromeric reads to them. Fig. 4 compares positions of read alignments to each pair of assemblies and reveals structural discrepancies between them. Comparison of centroFlye and centroFlye_del assemblies reveals an expected discrepancy around unit 300. Both T2T4 and T2T6 assemblies differ from the centroFlye assembly around units 150–180 in the centroFlye assembly although the centroFlye and T2T6 are more complaint in this area. The size of deletion in T2T4 is ≈32 units (around unit 135), and in T2T6 — only 5 units (around unit 175). Four other discrepancies are shared between both versions of T2T and the centroFlye assembly (Fig. 4). Below we argue that T2T assemblies have putative misassembles in the surrounding areas.

Figure 4. Comparison of read mappings between the centroFlye, centroFlye_del, T2T4, and T2T6 assemblies.

Each dot corresponds to a centromeric read. X- and Y-coordinate represent the starting unit position in the corresponding assemblies. (Top Left) Comparison of centroFlye and centroFlye_del assemblies reveals a discrepancy around unit 300 — 25 units deletion in the centroFlye_del assembly. (Top Right) Comparison of centroFlye and T2T4 assemblies reveals discrepancies around the following units in centroFlye (T2T4) assemblies: 150 (135) — 32 units deletion in T2T4, 450 (410) — 2 units deletion in T2T4, 750 (700) — 56 units deletion in T2T4, 1050 (950) — 47 units deletion in T2T4, and 1400 (1250) — 36 units deletion in the T2T4 in the centroFlye (T2T4) assembly. (Bottom Left) Comparison of centroFlye and T2T6 assemblies reveals discrepancies around the following units in centroFlye (T2T assemblies): 180 (175) — 5 units deletion in T2T6, 450 (445) — 1 units deletion in T2T6, 750 (720) — 56 units deletion in T2T6, 1050 (975) — 47 units deletion in T2T6, 1400 (1300) — 24 units deletion in T2T6. (Bottom Right) Comparison of T2T4 and T2T6 assemblies reveals discrepancies around the unit 150 and 1240 in both assemblies.

Quality assessment of the centromere assemblies.

Although Supplementary Note 1 demonstrates that centroFlye accurately reconstructs simulated centromeres using reads simulated by the NanoSim simulator³⁵, it is unclear how to evaluate assemblies of real centromeres. Benchmarking of various genome assemblers would not be possible without the quality assessment tools such as QUAST³⁶. However, since QUAST is not applicable for analyzing centromere assemblies, we developed some metrics for the reference-free quality assessment of centromere assemblies.

Errors in an assembly affect the coverage near the assembly breakpoints. Thus, in the case of a uniform coverage, regions with abnormal coverage may point to assembly errors. For example, a deletion inflates the coverage near the deletion breakpoint (doubles the coverage in the case of a long deletion) and an insertion reduces the coverage in the inserted segment. Fig. 5 shows the coverage plots for all assemblies and reveals that a deletion in centroFlye_del assembly inflates the coverage by ≈60% at the deletion breakpoint (from ~50x to ~80x).

Figure 5. Coverage plots for centroFlye, centroFlye_del, T2T4, and T2T6 assemblies.

centroFlye_del refers to the centroFlye assembly of cenX with artificially introduced a 50 kb (25 units) deletion at position 600 kb (unit 300). The peak around unit 1,300 in T2T6 gives coverage almost 1,000 and was cut. The reduction in the number of mappable reads caused by the deletion in centroFlye_del assembly affects the coverage near the deletion in this assembly: 1,696 and 1,676 reads were mapped to centroFlye and centroFlye_del assemblies respectively.

It turned out that analyzed ONT dataset is characterized by a non-uniform read distribution, making it difficult to infer assembly errors from irregularities in the read coverage (Supplementary Fig. 2). Even though T2T assemblies of cenX demonstrate higher coverage variations than the centroFlye assembly, these variations do not necessarily point to assembly errors, necessitating a need to introduce additional metrics for centromere assemblies. The T2T6 assembly coverage is more similar to the centroFlye assembly coverage (as compared to T2T4 assembly), but has a large spike at the end of the array, which is coordinated with a discrepancy in Fig. 4.

A k-mer is shared between an assembly and a read aligned to this assembly if it occurs in both the assembly and the read at the same position in their alignment. Given a set of k-mers Anchors, we define shared_Anchors(Read,Assembly) as the number of k-mers from Anchors that are shared between Read and Assembly. The larger is shared_Anchors(Read,Assembly), the better the assembly “explains” the read. Given a read-set Reads, we define shared_Anchors(Reads,Assembly) as the sum of shared_Anchors(Read,Assembly) over all reads in Reads.

To compare assemblies Assembly and Assembly’, we define Anchors as the set of shared unique k-mers between them (default k=19) and compute the discordance between these assemblies as discordance(Assembly,Assembly’)=shared_Anchors(Reads,Assembly)-shared_Anchors(Reads, Assembly’). For centroFlye and T2T6 assemblies, discordance(centroFlye,T2T6)= 5,609, suggesting that the centroFlye assembly is a better fit for the read-set than the T2T6 assembly (Fig. 3).

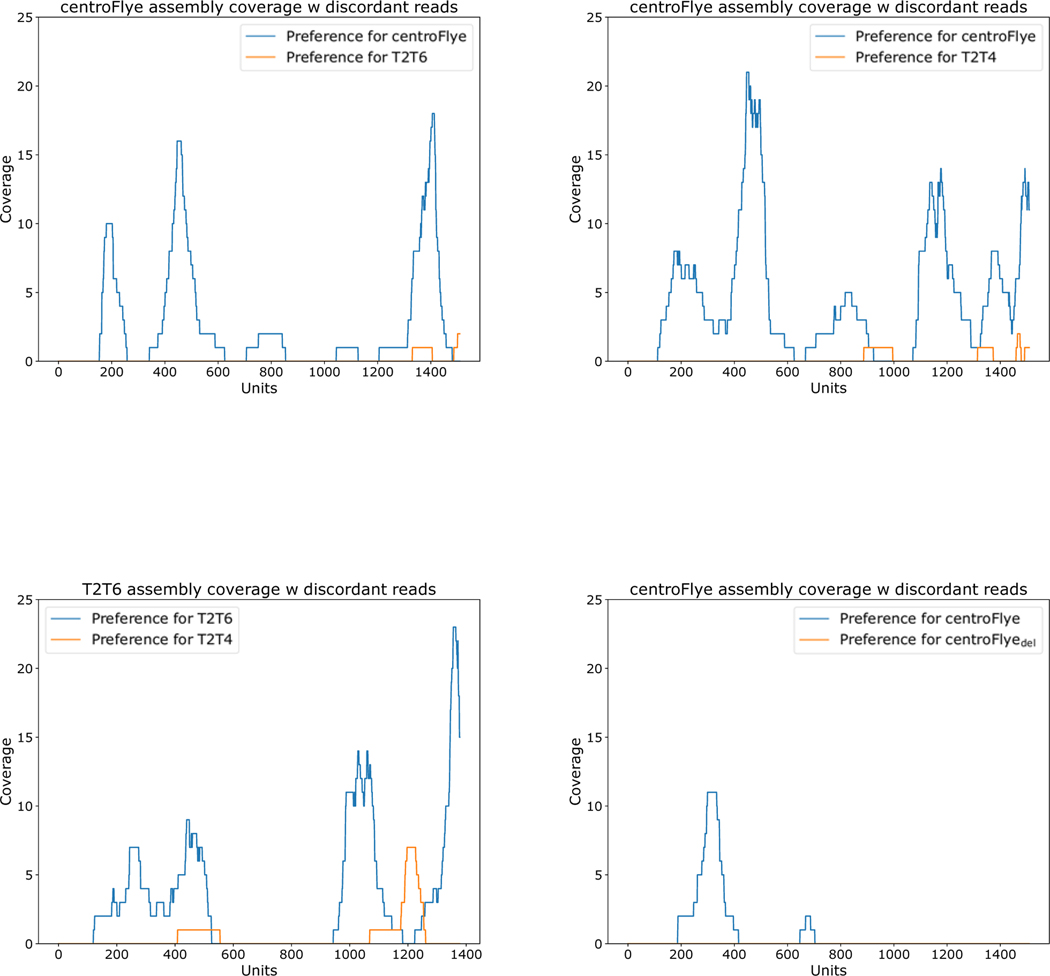
We classify a read Read as discordant with respect to assemblies Assembly and Assembly’ and a k-mer-set Anchors if there is a large difference (by at least k) between shared_Anchors(Read,Assembly) and shared_Anchors(Read,Assembly’), thus showing preference for one of the assemblies. A discordant read votes for Assembly (Assembly’) if this difference is positive (negative). There are 54 (3) discordant reads voting for centroFlye (T2T6) assemblies. Fig. 3 illustrates that the centroFlye assembly improves on other assemblies with respect to the discordance score.

A concentration of discordant reads at a certain region voting for Assembly over Assembly’ suggests that Assembly’ has a multi-unit deletion in this region. Fig. 6 reveals three clusters of discordant reads voting for centroFlye over T2T6 assembly at the regions ~200, ~400–600, ~1400 units in the centroFlye assembly (only two discordant reads vote for the T2T6 over the centroFlye assembly). These regions are coordinated with discrepancies shown in Fig. 4 and likely point to large deletions in the T2T6 assembly. Similar comparison between centroFlye and T2T4 assemblies reveals putative misassembles in T2T4 at units ~200, ~400, ~800, ~1150, and ~1400 in the centroFlye assembly. As expected, comparison of centroFlye and centroFlye_del detects a single deletion at unit 300.

Figure 6. Coverage of various cenX assemblies by discordant reads.

Supplementary Note 2 describes the hanging index test and the breakpoint test that provide additional support for the centroFlye assembly.

Variations in HORs provide insights into centromere evolution.

Various copies of a repeat are usually partitioned into subfamilies that reflect evolutionary history of this repeat. For example, Alu repeats in the human genome are split into over 200 subfamilies that provide insights into evolutionary history of Alu repeats³⁷. Some “active” Alu copies continue to produce variation by “jumping” to new genomic locations, thus posing the mutagenic threat to the human genome³⁸.

To reveal subfamilies of the cenX HOR, we align each canonical HOR in the homonucleotide-compressed centroFlye cenX assembly (1471 out of 1510 units) to the compressed DXZ1* and use the resulting multiple alignment to construct the profile logo for every position of DXZ1*. Although the vast majority of positions in units are highly conserved, some positions reveal significant variations (Supplementary Fig. 3). We select divergent positions such that the ratio of the secondary vote to the majority vote is greater than minRatio (default value minRatio = 0.3) and the secondary vote is not a deletion. This procedure reveals seven divergent positions. Each divergent position is characterized by its majority vote frequency and secondary vote frequency

We consider pairs of divergent positions that are at least minDistance (default value minDistance = 100) positions apart and select the “most correlated” pairs using the biprofile approach³⁹. Afterward, we apply the χ² test of independence and select the pair of divergent positions with the smallest p-value. The divergent positions 580 and 695 with majority votes 71% and 72% (for nucleotides ‘AA’) and secondary votes 30% and 28% (for nucleotides ‘GG’) were selected. For these positions, the biprofile frequency for ‘AA’ and ‘GG’ is 69% and 27%, respectively, resulting in p-value < 10⁻¹⁰. We split the set of all units into two clusters with respect to nucleotides at the selected pair of positions, resulting in a split of all canonical HOR into two clusters with 1010 and 389 units, respectively. We repeat this process iteratively for each of the new clusters until no more clusters of size greater than minSize (default value minSize = 100) are generated. This process stops after two iterations and results in four subfamilies of cenX HOR. Supplementary Figure 4 reveals that units in different subfamilies are alternating along cenX, providing an initial insight into how subfamilies “colonize” cenX during its evolution.

Since we derived HOR subfamilies without using positions of the units, clustering of each subfamily into close positions along cenX suggests that the algorithm originally described for identifying Alu subfamilies3⁷ also works for HOR subfamilies. However, our results also reveal a new phenomenon of HOR recombination and suggest that analysis of centromere evolution may be more complex that analysis of Alu evolution (Supplementary Figure 5).

Discussion

Although the role of centromeres (chromosome segregation) is conserved throughout evolution, centromere sequences vary among species. For example, the X chromosome is highly conserved across all mammals, but the mammalian X centromeres vary across mammalian species. Here, we enable detailed study of centromeres by devising and validating centroFyle, an automatic tool for centromere assembly.

We compared centroFlye assembly with the semi-manual T2T assemblies and identified several misassembled parts in the T2T assembly. Fig. 4 reveals five large discrepancies (deletions) between centroFlye and T2T6 assemblies, Fig. 5 shows highly inflated coverage around unit 1300 in T2T6 assembly, Fig. 6 describes discordant reads that reveal three problems in T2T6 assembly, Supplementary Note 2 describes high hanging index in five regions in T2T6 assembly and five potential breakpoints in the T2T6 assembly. The TandemTools software for analyzing centromere assemblies⁴⁰ confirmed our conclusions and demonstrated that the problems we detected in the T2T assemblies are not specific to the mapping method. The latest version of the T2T cenX assembly published on Oct 24, 2019 (T2T v0.7) incorporates some elements of centroFlye assembly, e.g., corrects the duplication errors in the previous assembly, and was further polished using a novel marker-assisted read mapping strategy using both nanopore and PacBio CLR reads.

Although centroFlye could be used to fill the largest remaining gaps in the human genome and study centromere evolution, further algorithmic developments are needed to assemble all human centromeres. For example, although centroFlye revealed 37 abnormal HORs in cenX assembly (Supplementary Note 3), these HORs were not used to guide the centroFlye_HOR assembly. We thus extended the functionality of the centroFlye algorithm by developing the centroFlye_mono mode for analyzing centromeres with highly irregular HORs such as cen6. Although this approach successfully assembled cen6 it remains unclear how to recruit reads to centromeres with shared monomers. For example, some chromosomes share the same monomers or HORs with other chromosomes, e.g., human chromosomes 1, 5, and 19 share the same HOR D1Z7/D5Z2/D19Z3⁴¹. We hope to extend centroFlye to address the read recruitment challenge as well as the challenges of reconstructing centromeres in diploid genomes and identifying functional centromere sequences by co-analyzing centromere assemblies and Chip-seq data⁴².

Online Methods

Recruiting centromeric reads (Fig. 1.1).

centroFlye_mono recruits centromeric reads for a specific chromosome by identifying all reads that align to HORs from this chromosome. It uses the fitting alignment of HORs to all reads and recruits reads with sequence identity exceeding a threshold. centroFlye_mono uses a sequence identity threshold (the default value is 83% because most human HORs differ from the HOR consensus by less than 5% and the error rate in reads is ≈12%). In the case of cenX, centroFlye_mono recruits 2,680 centromeric reads (total length ~133 Mb) that align to DXZ1 or its reverse complement.

Below we assume that all centromeric reads have DXZ1 in the forward orientation and complement a read if it is not the case (Supplementary Note 4). 150 centromeric reads have lengths varying from 2 to 5 kb, 1,382 reads are longer than 30kb and 897 of them are ultralong. The longest centromeric read is 527 kb.

Partitioning centromeric reads into units (Fig. 1.2).

DXZ1 was derived at the dawn of the sequencing era based on limited sequencing data⁴³. Supplementary Note 5 describes how to infer a more accurate consensus HOR DXZ1* for cenX.

We use the Noise-Cancelling Repeat Finder (NCRF)⁴⁴ to partition each centromeric read into units. Given a read and a consensus HOR, NCRF partitions a read into units, each unit representing a single copy of a HOR. Although NCRF was not designed to characterize the possible gaps between units (e.g., transposon insertions or small rearrangements), this limitation of NCRF does not significantly affect the centroFlye results. If NCRF reports several alignments for a given read, the longest one is kept. Incomplete units appearing at prefix or suffix of a read are discarded.

centroFlye discards all centromeric reads with (the longest) alignment shorter than three units. 295 centromeric reads (including 42 ultralong reads) of total length 7 Mb were discarded. NCRF identified 56,138 units in the remaining 2,385 centromeric reads, including 39,363 units in the remaining 855 ultralong reads.

Classifying centromeric reads (Fig. 1.3).

A centromeric read is classified as a prefix (suffix) read if it has a prefix (suffix) of length at least prefixThreshold that does not match the HOR consensus (default threshold prefixThreshold=50 kb). Otherwise, a read is classified as internal. NCRF revealed 15 prefix, 2,357 internal, and 13 suffix reads. This classification is important for “moving inside the centromere” using an approach similar to the approach for reconstructing unbridged repeats in Flye³.

Identifying rare centromeric k-mers (Fig. 1.4).

We define the frequency of a k-mer as the number of occurrences of this k-mer in units of reads from a centromeric read-set. centroFlye identifies rare centromeric k-mers by analyzing k-mers with frequencies that fall into a predefined interval (centroFlye uses the default value k=19). Since a HOR may be repeated in a centromere thousands of times (with small variations), we expect most k-mer from a HOR to have high frequencies. Our goal is to identify rare k-mers that appear just once (unique k-mers) or a few times in a centromere and use them for centromere assembly. Note that a k-mer from a genome “survives” without errors in a read with the survival rate that can be approximated as survivalRate(k)=(1-p)^k, where p is the probability of an error at a given position of a read. A more accurate estimate from the real data suggests that the survival rate of 19-mers in the ONT reads is 0.34. Thus, since the recruited set of ultralong cenX reads has ≈32x coverage, we expect that a unique k-mer from a given position in the genome survives in ≈11 ultralong centromeric reads.

We define the interval [bottom, top] and classify a k-mer as rare if its frequency is larger than bottom*survivalRate*coverage and smaller than top*survivalRate*coverage (the default values bottom=1 and top=3). Although 391,361 k-mers from centromeric reads were classified as rare (Fig. 3, top left), many of them represent erroneous versions of k-mers from a HOR copy rather than truly rare k-mers in cenX. Indeed, the number of reads containing a given k-mer b is affected by the number of genomic positions with k-mers similar to b since error-prone reads covering these similar k-mers may contain b. Since many HOR copies may contain k-mers similar to a unique k-mer, this observation explains the complications in inferring the set of unique/rare k-mers. For example, a single nucleotide insertion in a k-mer from a genome occurs in an ONT read with probability 0.03⁴⁵. Thus, each such insertion in a k-mer from DXZ1* has a high chance to be classified as a rare k-mer. Below we describe how to filter out such spurious rare k-mers using the distance graph.

Constructing the distance graph (Fig. 1.5).

The key observation to separate false positives from unique k-mers is that the distances between unique k-mers in reads are likely to be conserved but distances between false positive k-mers are not necessarily conserved. The distance graph reveals pairs of unique k-mers that are separated by roughly the same distance in multiple reads.

Given a set of rare centromeric k-mers V, we define the weighted directed distance graph with the vertex-set V and the edge set defined as follows. Two vertices v and w are connected by a directed edge of length ℓ > 0 if there is a centromeric read where w follows v at the distance ℓ units. If there are t different edges between v and w of the same length ℓ, we combine them into a single multiedge (v, w, ℓ) of multiplicity t. We further remove all multiedges with multiplicities below minCoverage = C*survivalRate*coverage (the default value C=0.4 and, thus, minCoverage=4 for our set of rare centromeric reads). Finally, we remove all conflicting parallel multiedges from the graph (multiedges connecting the same vertices but having different lengths) and all isolated vertices. The remaining vertices form a set of only 28,703 k-mers out of 391,361 initially constructed rare centromeric k-mers (below we refer to the remaining k-mers as “unique”). Even though, some of the remaining k-mers turned out to be rare rather than unique (Supplementary Fig. 1), they still appear to be valuable for assembly efforts.

Reconstructing the centromere (Fig. 1.6).

centroFlye_mono reconstructs the centromere sequence using an approach similar to the approach for resolving unbridged repeats in Flye³. Instead of using the divergent positions (like in Flye), it uses the unique centromeric k-mers to iteratively reconstruct the centromere.

Given a unit in a read, a bin of this unit is defined as the set of unique k-mers occurring in this unit. centroFlye represents each read as a sequence of bins (bin-sequence) that we refer to as readBin. Given two bins c and c’, we define shared(c,c’) as the number of shared unique k-mers in these bins. Given two bin-sequences of the same length x=x₁, … x_n and y=y₁, … y_n, their score is computed as Σ_i=1,n shared(x_i,y_i). Given bin-sequences x of length n and y of length m, their i-score (1≤ i≤ n) is defined as the score between x_i, … x_min(i+m,n) and the prefix y₁, …y_min(m,n-i+1) of y. The maxScore between x and y is defined as the maximum of i-scores over all possible values of i and an alignment of x and y that achieves the maxScore value is referred to as an optimal alignment.

An alignment of multiple reads (a contig) defines an alignment of their bin-sequences — a bin-sequence that we refer to as bin-contig (for multiple aligned units in this alignment, their combined bin is defined as the union of all individual bins). centroFlye_mono supports an operation of optimally aligning a new read against a bin-contig and updating the bin-contig to include a newly added read.

Fig. 1.6 illustrates the centroFlye_mono repeat resolution algorithm. First, all prefix reads are aligned based on their prefixes, represented as bin-sequences and combined into an initial bin-contig that starts at the unit position 0. Afterwards, centroFlye_mono selects a still unaligned read with a highest-scoring optimal alignment against the bin-contig (in case of ties, the read with the rightmost starting position of the optimal alignment is selected). If the score of this alignment exceeds stopThreshold, it adds this read to the growing bin-contig, otherwise it stops the contig extension (the default value stopThreshold = 10). In case centroFlye_mono incorporates nearly all reads in the growing contig-sequence (including suffix reads), we classify the centromere construction as successful and proceed to the polishing step (see Supplementary Note 4). Otherwise, we apply the same centromere construction procedure but this time starting from suffix rather than prefix reads. It may happen that the prefix-based centromere construction stops before completing the centromere but the suffix-based construction generates the entire centromere. If both prefix-based and suffix-based centromere reconstructions stop, we generate the suffix and prefix contig-sequences that do not span the entire centromere.

Note that at this step we do not obtain the cenX sequence, but rather the bin-sequence of the centromere and the starting unit positions inside the cenX for all aligned centromere reads. We can compare centroFlye assembly to other assemblies by mapping read bin-sequences to bin-sequences for these assemblies (see Results).

Polishing the reconstructed centromere sequence (Fig. 1.7).

Using reported starting unit positions for all centromeric reads, centroFlye_mono separately polishes each HOR unit of the (yet unknown) centromere separately. In the case of cenX, it selects unit of the median length from corresponding reads, uses it as a template, and applies four rounds of the polishing algorithm in Flye⁴⁵ (version 2.5). Polishing strategy implemented in TandemTools⁴⁰ can be used to further improve assembly quality.

Polishing results in a sequence of length 3,103,541 that includes 1510 units and a single insertion of a LINE repeat. It contains 39,530 unique 19-mers, i.e., 19-mers that appear only once in the assembly. Since ONT assemblies have high rates of homonucleotide indels, we further compressed all homonucleotide runs in the polished centromere, resulting in a compressed centromere that has only 26,333 unique 19-mers (Fig. 3, top right).

Assembly of cen6.

For cen6 assembly we used the Oxford Nanopore reads dataset generated by the T2T consortium (release 3) with 28,449,385 reads (367 Gb, 118x coverage) and N50 read length equal to 53 kb. This read-set includes 1,999,007 ultralong reads (longer than 50 kb) that result in ~62x coverage of the human genome. Below we describe various steps of centroFlye_mono (Fig. 2).

Recruitment of centromeric reads from cen6.

Using 18 cen6-specific monomers, we recruited 6,558 centromeric reads from cen6 (total length ~268 Mb). 1,621 out of these 6,558 reads represent ultralong reads that are most useful for centromere assembly (the longest read has length 530 kb).

Transforming reads into monoreads (Fig. 2.1).

NCRF⁴⁴ performs well in the case when the vast majority of a centromere is formed by canonical HORs. However, it generates a suboptimal decomposition into units when a read contains abnormal HOR units. StringDecomposer⁴⁶ addresses this limitation of NCRF by partitioning reads into monomers rather than HORs and generating monoreads in the monomer alphabet. centroFlye_mono uses StringDecomposer to transfrom the read-set Reads into a monoread-set Monoreads.

StringDecomposer fails to unambiguously translate some regions in a read into monomers either due to locally high error-rate in a read, or a retrotransposon insertion, or a still unknown monomer for a given chromosome. It represents each such region as a run of gap-symbols ‘?’ repeated GapMultiplicity times, where GapMultiplicity is defined as the length of this region divided by the mean nucleotide length of the input monomers.

For cen6, the average (maximum) monoread length is 238 (3,195). The total length of all cen6 monoreads is 1,562,933. The total number of gap-symbols across all reads is 34,303 (2.2%) and the total number of gap-runs (contiguous sequences of gaps) is 7,375. This is a high error rate that makes the construction of the de Bruijn graph on mono-k-mers problematic (at least, for large k) and necessitates the error correction step.

Error correction of monoreads (Fig. 2.2).

Supplementary Note 6 describes how centroFlye_mono filters out poor-quality reads, trims the low quality ends of monoreads, and splits monoreads that have a large fraction of gap-symbols. This step reduces the total number of gap-symbols across all monoreads to 5,989 (0.4%) and the total number of gap-runs to 3,193.

Supplementary Note 6 describes how centroFlye_mono extracts HOR sequences from the remaining monoreads by constructing the de Bruijn graph on short and abundant mono-k-mers. On cen6 we extract two standard HORs: a mono-18-mer identical to D6Z1 (represented as ABCDEFGHIJKLMNOPQR in the monomer alphabet) and a mono-15-mer ABFGHIJKLMNOPQR that differs from D6Z1 by the deletion of a mono-3-mer CDE (Supplementary Note 6). We say that a mono-t-mer fixes a run of t gap-symbols in a monoread if substituting this run by the mono-t-mer increases the number of standard HORs in the monoread. For each run of t gap-symbols in a monoread, centroFlye_mono attempts to find a mono-t-mer that fixes it and error-corrects the monoread by substituting the gap-run by the found mono-t-mer. Such HOR-based error-correction reduces the total number of gap-symbols across all monoreads to 2,505 (0.2%) and number of gap-runs to 948.

Constructing iterative de Bruijn graph of monoreads (Fig. 2.4).

The choice of the k-mer size affects the construction of the de Bruijn graph. Smaller values of k collapse more repeats, making the graph more tangled. Larger values of k fail to detect overlaps between reads, making the graph more fragmented. Also, since monoreads have gaps, increasing k becomes problematic when one constructs the de Bruijn graph on mono-k-mers (Fig. 2.3). 222,639 out of 249,119 (~89%) mono-400-mers in reads are gap-free after error-correction.

The iterative de Bruijn graph^32,33 incorporates information about mono-k-mers for multiple values of k into a single graph to reduce fragmentation in low-coverage regions and reduce repeat collapsing in high-coverage regions. While the de Bruijn graph DB_k(Reads) is constructed based on all k-mers in the read-set Reads, the iterative de Bruijn graph IDB_k(Reads) is recursively constructed based on a larger set of k-mers that extends all k-mers in Reads by adding all k-mers that are spelled by valid paths in the graph IDB_k-1(Reads). Below we define the concept of a valid path.

A vertex in a path is called an internal vertex if it is neither the initial nor the terminal vertex of this path. A vertex is called a 1-out (1-in) vertex if it has outdegree 1 (indegree 1). A path in a directed graph is called a 1-out (1-in) path if all its internal vertices are 1-out (1-in) vertices. For each edge e, there is a single longest 1-in path ending in e (referred to as (e_init, …, e)) and a single longest 1-out path starting at e (referred to as (e,…, e_term)). We refer to the path (e_init, …, e,…, e_term) as the valid path for the edge e to reflect that each traversal visiting all edges of the graph contains each valid path as a sub-path. We further refer to a string spelled by a valid path as a pseudoread and consider the set of all pseudoreads (one for each edge of the graph). Even though there may be no reads containing a given pseudoread, one can safely add all pseudoreads to the set of real reads since each such pseudoread represents a substring of the genome³³.

Given a parameter k, the graph IDB_k(Monoreads) on mono-k-mers is recursively defined based on the graph IDB_k-1(Monoreads). A mono-k-mer is called frequent if it appears at least minMultiplicity times in Monoreads. We define minMultiplicity as Coverage•MonoKmerSurvivalRate•C with default C=0.2. Specifically, we consider the set of all frequent mono-k-mers in Monoreads combining with all mono-k-mers in all pseudoreads and define IDB_k(Monoreads) as the de Bruijn graph constructed on these mono-k-mers. Each non-branching path is compressed into a single edge. The length of this edge is defined as the length of the path and its coverage is defined as the median multiplicity of mono-k-mers (edges) in the path. To initialize the construction of the iterative de Bruijn graph, we define IDB_k(Monoreads) as the de Bruijn graph on all frequent mono-k-mers in Monoreads for a small value of k (the default k=100) and iterate till a large value of k denoted as K (the default K=400). Supplementary Note 6 presents the graph IDB₄₀₀(Monoreads) for cen6.

Assembling monocentromere by scaffolding (Fig. 2.5).

An edge in the graph IDB_k(Monoreads) is called long if it spells a string of length at least MinLength (default value MinLength = 1000). An edge is called unique if its coverage does not exceed the average coverage of the genome (Supplementary Note 7). centroFlye_mono attempts to scaffold long unique edges that are likely traversed just once by the genome.

centroFlye_mono maintains an alignment of each centromeric read to the graph IDB_K(Monoreads) during its construction. A monoread connects a long unique edge e with a long unique edge e’ if it starts in e and ends in e’. Each such monoread R represents a concatenate of prefix_e(R) (the prefix of R mapping to e), middle_e,e’(R) (an internal segment of R that does maps neither to e nor to e’) and suffix_e’(R) (the prefix of R mapping to e’). We define offset_e,e’(R) as the length of middle_e,e’(R). We say that a long unique edge e precedes a long unique edge e’ if there are at least MinConnection reads connecting e with e’ and offsets of these reads are the same. We construct the scaffolding graph Scaffold_K(Monoreads) by maintaining all long unique edges in IDB_K(Monoreads), removing all other edges, and adding scaffolding edges that connect long unique edges e and e’ if e precedes e’. Each scaffolding edge is labeled by the consensus of strings middle_e,e’(R) taken over all monoreads R that connect e and e’. Paths in the scaffolding graph are referred to as scaffolds. centroFlye_mono further extends each scaffold from both sides by two reads that map to the prefix and suffix of each scaffold and extend this prefix and suffix as far as possible.

centroFlye_mono generated two scaffolds of length 11,156 and 5,582 monomers. There are no centromeric reads that connect long and unique edges of these scaffolds. The region of cen6 in-between consists of a long recent segmental duplication that results in a complex traversal of IDB₄₀₀(Monoreads). However, the extensions of these long edges with reads (entering the duplication from both sides) are overlapping in a single vertex. We thus concluded that these two scaffolds are joined via this vertex, resulting in a single path that is traversed by cen6 (further validation is required to rule out a possibility that this vertex is not duplicated in this path).

Translating monocentromere to the nucleotide alphabet (Fig. 2.6).

centroFlye_mono greedily partitions monocentromere into longest substrings such that no monomer is repeated more than once in each of substrings (we refer to these substrings as pseudo-units). Alignments of each centromeric read to the graph IDB_K(Monoreads) imply alignments of these reads to the monocentromere. centroFlye_mono uses these alignments to separately polish each of 962 identified pseudo-units on cen6 separately. The assembly can be further polished using TandemMapper from the TandemTools package⁴⁰.

Data availability

centroFlye centromere 6 and X assemblies and all supporting data is available at Zenodo: https://doi.org/10.5281/zenodo.3593460. The ONT reads that were generated by the T2T consortium are available at https://github.com/nanopore-wgs-consortium/CHM13.