Robust Estimation of Heterogeneous Treatment Effects: An Algorithm-based Approach

Abstract

Heterogeneous treatment effect estimation is an essential element in the practice of tailoring treatment to suit the characteristics of individual patients. Most existing methods are not sufficiently robust against data irregularities. To enhance the robustness of the existing methods, we recently put forward a general estimating equation that unifies many existing learners. But the performance of model-based learners depends heavily on the correctness of the underlying treatment effect model. This paper addresses this vulnerability by converting the treatment effect estimation to a weighted supervised learning problem. We combine the general estimating equation with supervised learning algorithms, such as the gradient boosting machine, random forest, and artificial neural network, with appropriate modifications. This extension retains the estimators’ robustness while enhancing their flexibility and scalability. Simulation shows that the algorithm-based estimation methods outperform their model-based counterparts in the presence of nonlinearity and non-additivity. We developed an R package, RCATE, for public access to the proposed methods. To illustrate the methods, we present a real data example to compare the blood pressure-lowering effects of two classes of antihypertensive agents.

1. Introduction

The practice of precision medicine relies on a sound causal understanding of treatment effects varying with patient characteristics. Estimating such effects, known as the heterogeneous treatment effects, from observational data is typically done within the Neyman-Rubin causal framework with appropriate assumptions (Sekhon, 2008). Popular approaches include the Quality or Q-learning that directly regresses the outcomes on patient characteristics (Watkins and Dayan, 1992; Watkins, 1989) and the Advantage or A-learning that models the contrasts among treatments (Murphy, 2003; Robins, 2004).

Despite the general applicability of these estimation methods, practical challenges abound: (1) Few existing estimators are designed to deal with data irregularities and high dimensionality. (2) Model-based methods remain vulnerable to model misspecification. (3) Few software packages are available for practical use in an off-the-shelf fashion and can handle the above issues. The lack of ready-made robust analytical tools has hindered the practical use of these methods because practitioners are rarely in a position to implement and test sophisticated causal inference methods.

Efforts have been made to alleviate the impact of data irregularities. For example, Xiao et al. (2019) extended the L₂-based R-learner (Nie and Wager, 2017), a method under the general A-learning umbrella, to the pinball loss function. More recently, our research team has put forward a general estimating equation for robust estimation of heterogeneous treatment effects, supported by strong theoretical and empirical evidence (Li et al., 2021). This estimating equation unifies many of the existing methods, including the R-learner (Nie and Wager, 2017), inverse propensity weighting (Hirano et al., 2003; Horvitz and Thompson, 1952), various modified outcome and covariate methods (with and without efficiency augmentation) (Chen et al., 2017; Tian et al., 2014), and the augmented inverse propensity weighting method (Robins and Rotnitzky, 1995). We showed that under fairly general regularity conditions, the robust estimators ascertained from the general estimating equation are asymptotic normal to allow for valid inference. Despite its broad coverage and good theoretical properties, the general estimating equation estimators are not robust against model misspecifications, nor are they easy to implement in practical data analyses.

This paper extends our previous work by combining the A-learner from the general estimating equation with supervised learning algorithms to further enhance its robustness again model misspecifications. This modification also frees analysts from the tedious and error-prone work of model building. We implement the causal inferences tools in the form of an R package - RCATE, short for Robust Estimation of the Conditional Average Treatment Effects, for a scalable solution to heterogeneous treatment estimation.

2. Methods

2.1. Notation and assumptions

Let T be a binary variable for treatment assignment: T = 1 if a patient is in the treatment group, and T = −1 otherwise. We define Y⁽¹⁾ and Y⁽⁻¹⁾ as the potential outcomes under treatments T = 1 and T = −1, respectively. Here, Y⁽¹⁾ and Y⁽⁻¹⁾ are assumed to be univariate and continuous. Let X be the p-dimensional pre-treatment covariates. In an observational study, one observes T, X, and Y = I(T = 1)Y⁽¹⁾ + I(T = −1)Y⁽⁻¹⁾, where I(·) is an indicator function. We assume that the data ${\left\{\left(Y_i,T_i,{\mathbf{X}}_i\right)\right\}}_{i=1}^n$ are independent and identically distributed (i.i.d.). The estimation target is the treatment effect τ₀(x), commonly known as the conditional average treatment effect (CATE)

$${\tau }_0(\mathbf{x})=E\left[Y^{(1)}-Y^{(-1)}\mid \mathbf{X}=\mathbf{x}\right]=E[Y\mid \mathbf{X}=\mathbf{x},T=1]-E[Y\mid \mathbf{X}=\mathbf{x},T=-1],$$

where the last part follows from the ignorability assumption below. With a binary treatment indicator, one can always express the conditional mean outcome as $E(Y\mid \mathbf{X},T)=b_0(\mathbf{X})+\frac{T}{2}{\tau }_0(\mathbf{X})$, with $b_0(\mathbf{x})=\frac{1}{2}\left(E\left[Y^{(1)}\mid \mathbf{X}=\mathbf{x}\right]+E\left[Y^{(-1)}\mid \mathbf{X}=\mathbf{x}\right]\right)$. This leads to a general interaction model

$$Y_i=b_0\left({\mathbf{X}}_i\right)+\frac{T_i}{2}{\tau }_0\left({\mathbf{X}}_i\right)+{\epsilon }_i.$$ (1)

We further define μ(x) = E[Y|X = x], μ⁽¹⁾(x) = E[Y|X = x, T = 1], and μ⁽⁻¹⁾(x) = E[Y|X = x, T = −1].

To estimate τ₀(X_i), we operate under the following assumptions: (1) Ignorability — Treatment assignment T_i is independent of the potential outcomes $(Y_i^{(1)},Y_i^{(-1)})$ given the covariates X_i, i.e., $\{Y_i^{(1)},Y_i^{(-1)}\text{⫫}{T}_i\mid {\mathbf{X}}_i\}$; (2) Positivity — The propensity score is strictly between 0 and 1, i.e., p(x) := P(T = 1|X = x) ∈ (0, 1); (3) Stable Unit Treatment Values Assumption (SUTVA) – the potential outcome in one individual is only affected by the treatment he receives; (4) Conditional Independence Error – The error is independent of the treatment assignment, conditional on the covariates, i.e., {ε_i ⫫ T_i|X_i}. We further assume that the conditional expectation of the error exists. The commonly seen assumption of E[ε] = 0 is sufficient but not necessary.

2.2. The existing methods

There is a sizable literature on the estimation of CATE using observational data. Caron et al. (2020) and Zhang et al. (2020) provided state-of-the-art reviews of the methods for CATE estimation. We summarize the existing methods in Table 1, along with the available analytical software. Importantly, most of these methods are based on the L₂-loss function, whose performance deteriorates with data irregularity.

Table 1:

Summary of existing popular CATE estimation algorithms

Base-learner/Algorithm	Description	Pros(+) and Cons(−)	Available R packages
The single-learner (or S-learner)	Fits a single-model for the outcome with the covariates and treatment assignment indicator.	(+) If the treatment effect is simple, then pooling the data together will be beneficial. (−) Performs bad if the treatment effect is strongly heterogeneous and the response surfaces of two groups are very different.	rlearner causalToolbox
The two-learner (or T-learner)	Fits two models for the outcome of two treatment groups separately with the covariates.	(+) Performs well if the treatment effect is strongly heterogeneous and the response surfaces of two groups are very different. (−) Uses the data inefficiently.	rlearner causalToolbox
The X-learner (Künzel et al., 2019)	A three step approach to crossover the information in the control and treated subjects.	(+) Has the advantages of both S and T-learner. (−) The three-step estimator increases the risk of over-fitting and the difficulty in tuning parameter.	rlearner causalToolbox
Inverse propensity score weighting (IPW)	Transforms the outcome by inverse propensity score weighting, then the conditional expectation of the transformed outcome is the treatment effect.	(+) After transformation, the IPW provides the flexibility in choosing off-the-shelf supervised learning algorithms. (−) Relies on the accurate estimation of the propensity score.
Augmented inverse propensity score weighting (AIPW)	Augmented IPW is robust to mis-specified mean or propensity score model.	(+) In addition to the advantage of IPW, AIPW has the property of double robustness.	RCATE
The R-learner (RL)	Decomposes the outcome by subtracting the mean model and gets an estimating equation.	(+) In addition to the advantage of IPW, R-learner has quasi-oracle property.	rlearner RCATE
The modified covariate method with efficiency augmentation (MCM-EA)	Transforms the covariates to get an estimating equation.	(+) Same as IPW. (−) Relies on the accurate estimation of mean and propensity score.	RCATE
The Q-learner	Fits the interaction model and the slope is the treatment effect function.	(+) No nuisance parameter need to be estimated. (−) Lacks of flexibility in algorithm choosing and sensitive to model mis-specification.
Causal tree (Athey and Imbens, 2016)	Uses regression tree that splits by maximizing the difference between treatment effects in child nodes to fit the outcome.	(+) Easy to interpret and provides the grouping of subjects. (−) Suffers from the problem of high variance.	causalTree
Causal forest (Athey et al., 2019)	Uses randomly selected subsample and covariates to build causal trees, then aggregate the results.	(+) Addresses the high variance problem. (−) Lose the interpretability.	grf
Causal boosting (Powers et al., 2018)	An adaption of gradient boosting algorithm with causal trees as weak-learner.	(+) Well-tuned causal boosting outperforms the causal forest. (−) Takes longer to train than causal forest and could overfit the training data.	causalLearning
Causal MARS (Powers et al., 2018)	Fits two multivariate adaptive regression spline models in parallel in two arms of the data. In each step, it chooses the same basis function to add to each model.	(+) Alleviates the bias problem of tree-based algorithms because they use the average treatment effect within each leaf as the prediction for that leaf.	causalLearning

The estimating equation that we proposed (Li et al., 2021), while not covering all methods in Table 1, does accommodate many loss functions, including the L₁-loss, Huber loss, and Bi-square loss, and thus greatly enhancing the estimators’ robustness against data irregularities. In the next section, we briefly review this formulation and the methods it covers.

2.3. A unified estimating equation for CATE

We previously described the general estimating equation that covers many of the existing methods for CATE estimation. An important feature of the estimating equation is that it readily accommodates the L₁ loss function so that robust estimation can be derived; see Li et al. (2021) for detailed derivation and theoretical development. Briefly, we consider the following estimating equation

$$\underset{\tau (\cdot )\in ℱ}{\min }\frac{1}{n}\sum _{i=1}^{n}w\left({\mathbf{X}}_i,T_i\right)M\left(Y_i-g\left({\mathbf{X}}_i\right)-c\left({\mathbf{X}}_i,T_i\right)\tau \left({\mathbf{X}}_i\right)\right),$$ (2)

where $ℱ$ is the treatment effect function space subject to predefined assumptions such as smoothness, M(·) is a user-specified loss function, and the two weight functions w(x, t) and c(x, t) are subject to the following constraints:

$$\mathrm{C}1.p\left(\mathbf{x}\right)w\left(\mathbf{x},1\right)c\left(\mathbf{x},1\right)+\left(1-p\left(\mathbf{x}\right)\right)w\left(\mathbf{x},-1\right)c\left(\mathbf{x},-1\right)=0;$$

$$\mathrm{C}2.c\left(\mathbf{x},1\right)-c\left(\mathbf{x},-1\right)=1;$$

$$\mathrm{C}3.w\left(\mathbf{x},t\right)c\left(\mathbf{x},t\right)\ne 0.$$

Equation (2) covers many existing popular methods for heterogeneous treatment effect estimation, including the modified covariate methods (MCM) (Chen et al., 2017; Tian et al., 2014), MCM with efficiency augmentation (MCM-EA) (Chen et al., 2017; Tian et al., 2014), inverse propensity score weighting (IPW) (Hirano et al., 2003; Horvitz and Thompson, 1952), augmented inverse propensity score weighting (AIPW) (Robins and Rotnitzky, 1995), and the R-learner (RL) (Nie and Wager, 2017). In Table 2, we list the functions c, w, and g that meet the constraints for popular A-learning methods.

Table 2:

Parameters of some popular methods in the framework

Method	w(Xi, Ti)	g(Xi)	c(Xi, Ti)
MCM	{Tip(Xi) + (1 − Ti)/2}−1	0	$\frac{T_i}{2}$
MCM-EA	{Tip(Xi) + (1 − Ti)/2}−1	μ(Xi)	$\frac{T_i}{2}$
RL	1	μ(Xi)	{Ti − 2p(Xi) + 1}/2
IPW	${\left\{\frac{T_i-2p\left({\mathbf{X}}_i\right)+1}{2p\left({\mathbf{X}}_i\right)\left(1-p\left({\mathbf{X}}_i\right)\right)}\right\}}^2$	0	$\frac{2p\left({\mathbf{X}}_i\right)\left(1-p\left({\mathbf{X}}_i\right)\right)}{T_i-2p\left({\mathbf{X}}_i\right)+1}$
AIPW	${\left\{\frac{T_i-2p\left({\mathbf{X}}_i\right)+1}{2p\left({\mathbf{X}}_i\right)\left(1-p\left({\mathbf{X}}_i\right)\right)}\right\}}^2$	(1 − p(Xi))μ1(Xi)+ p(Xi)μ−1(Xi)	$\frac{2p\left({\mathbf{X}}_i\right)\left(1-p\left({\mathbf{X}}_i\right)\right)}{T_i-2p\left({\mathbf{X}}_i\right)+1}$

An important appeal of the general formulation is its flexibility in specifying M, a feature that enhances the robustness against various forms of data irregularities through the use of L₁ and Huber loss functions. Here, we used the L₁-loss for illustration purpose. With the L₁-loss and under the above conditions, we have

$${\tau }_0(\cdot )=\arg \underset{\tau (\cdot )}{\min }E\left[w\left({\mathbf{X}}_i,T_i\right)\cdot \left|Y_i-g\left({\mathbf{X}}_i\right)-c\left({\mathbf{X}}_i,T_i\right)\tau \left({\mathbf{X}}_i\right)\right|\mid {\mathbf{X}}_i\right].$$ (3)

In the present research, we estimate τ(X) using modified supervised learning algorithms, which side-step the need to specify τ, and thus enhancing the method’s flexibility and scalability without sacrificing its robustness against data irregularities.

2.4. Supervised learning algorithms for robust CATE Estimation

Through a transformation, CATE estimation in (3) under the L₁-loss function can be seen as an optimization problem of ordinary least absolute deviation (LAD),

$$\widehat{\tau }(\cdot )=\arg \underset{\tau (\cdot )\in ℱ}{\min }\frac{1}{n}\sum _{i=1}^n{w}_i^{*}\left({\mathbf{X}}_i,T_i\right)\mid Y_i^{*}-\tau \left({\mathbf{X}}_i\right))\mid ,$$ (4)

where $Y_i^{*}=\frac{Y_i-g\left({\mathbf{X}}_i\right)}{c\left({\mathbf{X}}_i,T_i\right)}$ and $w_i^{*}\left({\mathbf{X}}_i,T_i\right)=w_i\left({\mathbf{X}}_i,T_i\right)\left|c\left({\mathbf{X}}_i,T_i\right)\right|$. We now show how to adapt three supervised learning algorithms for this purpose.

Depending on the structured assumptions one chooses for $ℱ$, one can select an appropriate learning algorithm for estimation, while taking care of the high dimensionality in X. In Section 3, we compare the L₁ and L₂-based algorithms. For the L₂-based methods, the transformed weight is $w_i^{*}\left({\mathbf{X}}_i,T_i\right)=w_i\left({\mathbf{X}}_i,T_i\right)c{\left({\mathbf{X}}_i,T_i\right)}^2$.

With the objective function in (4), different supervised learning algorithms can be used to estimate CATE - the optimization becomes a weighted supervised learning problem, where $Y_i^{*}$ and $w_i^{*}$ are the new outcome and new weight of each sample. The nuisance quantities in $Y_i^{*}$ and $w_i^{*}$ need to be pre-estimated and plugged in. Here we use L₁-based gradient boosting machine (GBM) with Y|T = −1, Y|T = 1, Y as outcomes to estimate μ⁽⁻¹⁾(x), μ⁽¹⁾(x), and μ(x). Note that μ⁽¹⁾(x) and μ⁽⁻¹⁾(x) are only needed for AIPW. And we use L₂-based GBM with D = (T + 1)/2 to estimate p(x). Any supervised learning algorithm with a weighted L₁ loss can be used to optimize (4) for robust CATE estimation. In this section, we describe three different algorithms for this purpose. The algorithms we describe are based on Random Forest (RF), GBM, and artificial neural network (ANN). The common process underlying these algorithms is graphically depicted in the following figure.

To achieve robust estimates of τ, we modified the existing supervised learning algorithms by incorporating the L₂-loss function. For example in RF, we used a weighted LAD splitting rule and the mean-of-medians to aggregate the trees, as opposed to the L₂-loss function and mean-of-means in the standard RF. Similarly in GBM, we used the L₁-loss to compute the working response and we calculated the weighted medians for prediction of the terminal nodes. In ANN, we used weighted LAD in back-propagation, and an L₁ regularization in high-dimensional situations to ascertain the sparse weights; here we used the adaptive moment estimation (Adam) to avoid being stuck at a local optimum (Kingma and Ba, 2014). We describe the algorithmic details in the following subsections.

2.4.1. A Robust Random Forest Learner

We first use RF for robust estimation of CATE. The building blocks of random forests are regression trees (Breiman et al., 1984). The tree structure comes from the recursively partitioning of the sample by covariates to minimize heterogeneity in the outcomes. The partition that minimizes the heterogeneity in child nodes is chosen, so that variables reducing heterogeneity most have the best chance of being selected than the background noise variables (Biau, 2012). Binary splits lead to trees, and then aggregated results within the terminal nodes are used for prediction. The random forest creates a more stable structure and reduces the variance by combining a large number of de-correlated regression trees (Breiman, 2001).

The standard regression trees minimize the mean squared error (MSE) in child nodes (i.e., $MSE={\sum }_{i\in L_l}{\left(y_i-{\overline{y}}_l\right)}^2+{\sum }_{i\in L_r}{\left(y_i-{\overline{y}}_r\right)}^2$, where ${\overline{y}}_l$ and ${\overline{y}}_r$ are the average values within the left and right child nodes) (Hastie et al., 2009). And robust random forests for regression have been studied to gain robustness against outliers, including using mean-of-medians (Meinshausen and Ridgeway, 2006) or median-of-means as estimators, and the LAD-based splitting rule (Roy and Larocque, 2012). Empirical studies have demonstrated that these modifications offer more protection against outliers than the standard RF.

The robust RF-based CATE estimation splits the samples by using the weighted LAD (WLAD) rule, a variant of the LAD rule. The WLAD rule is

$$WLAD=\sum _{i\in L_l}{w}_i^{*}|y_i^{*}-{\tilde{y}}_l^{{*}^{\prime }}|+\sum _{i\in L_r}{w}_i^{*}|y_i^{*}-{\tilde{y}}_r^{{*}^{\prime }}|,$$ (5)

where ${\tilde{y}}_l^{{*}^{\prime }}$ and ${\tilde{y}}_r^{{*}^{\prime }}$ are the leaf node medians to increase robustness and $w_i^{*}$ is the transformed weight of each observation. For prediction, we use the mean-of-medians that is consistant with the WLAD rule (Meinshausen and Ridgeway, 2006) instead of the median of means as advocated by Roy and Larocque (2012).

Algorithm 1: Robust RF-based CATE estimating algorithm

Input: Data ${\left\{\left(Y_i,T_i,{\mathbf{X}}_i\right)\right\}}_{i=1}^n$, number of trees T, fraction of features used in splitting p_fraction ∈ (0, 1), minimum node size k, and bootstrap sample size N.

Estimate nuisance quantities p(x), μ(x), μ⁽¹⁾(x), μ⁽⁻¹⁾(x) using (robust) GBM;

Calculate $w_i^{*}$ and $y_i^{*}$ according to Table 2 and Formulation (4);

for t in 1,…,T do

1. Randomly select N observations with replacement from the dataset as the bootstrap sample and randomly select a subset of variables with size p_fraction × p;

2. Fit a regression tree by repeating following steps until we reach the minimum node size k:

   b.1 Find the variable and the cutoff value that best split the data into two child nodes based on (5);

   b.2 Split the current node into two child nodes;

3. Calculate the median of the transformed outcomes in each terminal node as CATE estimator;

end

Output: Mean-of-medians as the final CATE estimation $\widehat{\tau }(\mathbf{x})$ and splitting criterion of trees.

The tuning parameters T, p_fraction, k, and N can be selected by cross validation.

2.4.2. The robust gradient boosting machine learner

Gradient boosting machine is a supervised learning technique that produces a prediction model $\widehat{f}(\mathbf{x})$ in the form of sequential weak-learners, typically regression trees, so that it performs better in high-dimensional settings (Friedman et al., 2000; Friedman, 2001, 2002). GBM builds the model in a step-wise fashion by allowing optimization of a differentiable loss function Ψ(y, f). The principle idea behind this algorithm is to construct weak-learners that are maximally correlated with the negative gradient of the loss function, associated with the whole ensemble.

Friedman’s GBM algorithm initializes $\widehat{f}(\mathbf{x})$ to be a constant. Then, in each iteration, it computes the negative gradient as the working response

$$z_i=-{\frac{\partial }{\partial f\left({\mathbf{x}}_i\right)}\mathrm{\Psi }\left(y_i,f\left({\mathbf{x}}_i\right)\right)|}_{f\left({\mathbf{x}}_i\right)=\widehat{f}\left({\mathbf{x}}_i\right).}$$

A regression model g(x) is fitted to predict z from the covariates x. Finally, it updates the estimate of f(x) as $\widehat{f}(\mathbf{x})\leftarrow \widehat{f}(\mathbf{x})+\lambda g(\mathbf{x})$, where λ is the step size. Friedman also proposed the LAD-TreeBoost algorithm (Friedman, 2001), a variation of GBM, which is highly robust against outliers. Ridgeway (2007) later extended the LAD-TreeBoost algorithm to a weighted version.

In the proposed robust GBM for CATE estimation, we further extended Ridgeway’s algorithm by combining it with the unified CATE estimation formulation as follows:

Algorithm 2: Robust GBM-based CATE estimating algorithm

Input: Data ${\left\{\left(Y_i,T_i,{\mathbf{X}}_i\right)\right\}}_{i=1}^n$, number of trees T, fraction of observations used in splitting p_sample ∈ (0, 1), interaction depth c, and step size λ.

Estimate nuisance quantities p(x), μ(x), μ⁽¹⁾(x), μ⁽⁻¹⁾(x) using (robust) GBM;

Calculate $w_i^{*}$ and $y_i^{*}$ according to Table 2 and Formulation (4);

Initialize $\widehat{\tau }(\mathbf{x})$ to be a constant,$\widehat{\tau }(\mathbf{x})=media{n}_{w^{*}}\left(y^{*}\right)$;

for t in 1,…,T do

1. Compute the negative gradient as the working response $z_i=-sign\left(y_i^{*}-\widehat{\tau }\left({\mathbf{x}}_i\right)\right)$;

2. Randomly select p_sample × n observations without replacement from the dataset;

3. Fit a regression tree to predict z_i using covariates x_i with interaction depth c and the number of leaf nodes K;

4. Compute the optimal predictions for feature x as ${\rho }_k(\mathbf{x})=argmi{n}_{\rho }{\sum }_{{\mathbf{x}}_i\in S_k}\mathrm{\Psi }\left(y_i^{*},\widehat{\tau }\left({\mathbf{x}}_i\right)+\rho ,w_i^{*}\right)$, where Ψ(y, x, w) = w|y − x| and k indicates the index of the terminal node S_k into which an observation with feature x would fall;

5. Update $\widehat{\tau }(\mathbf{x})$ as $\widehat{\tau }(\mathbf{x})\leftarrow \widehat{\tau }(\mathbf{x})+\lambda {\rho }_k(\mathbf{x})$, where λ is step size.

end

Output: Splitting criterion and CATE estimates as the resulted $\widehat{\tau }(\mathbf{x})$ from the above iteration.

For robust estimation, the terminal node estimate is the weighted median $media{n}_{w^{*}}(z)$, defined as the solution ρ to the equation $\frac{\sum w_i^{*}I\left(y_i^{*}\le \rho \right)}{\sum w_i^{*}}=\frac{1}{2}$. Tuning parameters T, λ, c, and K can be selected via cross validation.

2.4.3. A robust artificial neural network learner

Artificial neural network (ANN) is a computer program designed to simulate the way the human brain processes information (Goodfellow et al., 2016). A no-hidden-layer ANN with identity activation function is similar to linear regression in its modeling structure. But an ANN with multiple hidden layers offers more enhanced modeling flexibility. A feed-forward neural network with two hidden layers can be written as g(x) := f³(W³f²(W²f¹(W¹x))), where $W^l=(w_{jk}^l)$ are the weights between layer l − 1 and l, and $w_{jk}^l$ is the weight between the k-th node in layer l − 1 and the j-th node in layer l, and f^l is the activation function at layer l.

Multi-layer networks use a variety of techniques to learn the weights. The most popular approach is backpropagation (Rumelhart et al., 1986). In training, the loss of the model is defined based on the difference between the outcome y and the predicted output $\widehat{y}$. The most popular loss function is the Root Mean Squared Error (RMSE) (i.e.,$\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}$). However, numerous studies have shown that the presence of outliers poses a serious threat to the standard least squares analysis (Liano, 1996). The L₁-loss provides an effective remedy that can be applied to ANN (i.e.,$\frac{1}{n}{\sum }_{i=1}^n\left|y_i-{\widehat{y}}_i\right|$). An empirical study shows that L₁-based estimator had an improved performance than that of the L₂-based algorithm when outliers exist (El-Melegy et al., 2009).

As typical for CATE estimation, the activation functions of the hidden layers are rectified linear activation unis (ReLUs) and the last activation function is the identity function (Nair and Hinton, 2010). ReLU is a piecewise linear function that outputs the input directly if it is positive; otherwise, it outputs zero. Models that uses ReLUs are easier to train and often have better performance.

To ensure robustness, we propose to use the weighted Mean Absolute Error (MAE) $\frac{1}{n}{\sum }_{i=1}^n{w}_i^{*}\left|y_i^{*}-{\widehat{y}}_i^{*}\right|$ as the loss function, where w* and y* are the transformed weight and outcome in the unified formulation (4). We use the adaptive moment estimation (Adam), a gradient-based optimization algorithm, which runs averages of both the gradients and the second moments of the gradients (Kingma and Ba, 2014), to train the ANN. We add an L₁ regularization term λ∥W∥₁ to the loss function in high-dimensional settings in the first layer to achieve sparsity by driving some weights to zero (Feng and Simon, 2017; Girosi et al., 1995), where λ is the tuning parameter.

The algorithm is as follows:

Algorithm 3: Robust ANN-based CATE estimating algorithm

Input: Data ${\left\{\left(Y_i,T_i,{\mathbf{X}}_i\right)\right\}}_{i=1}^n$, number of iterations T, batch size $ℬ$, Adam parameters β₁, β₂, η, and ε, and L₁ regularization parameter λ in high-dimensional case.

Estimate nuisance quantities p(x), μ(x), μ⁽¹⁾(x), μ⁽⁻¹⁾(x) using (robust) GBM;

Calculate $w_i^{*}$ and $y_i^{*}$ according to Table 2 and Formulation (4);

Initialize an ANN with weights W, the decaying average of past gradients m to a zero vector, and the decaying average of past squared gradients v to a zero vector;

for t in 1,…,T do

1. Sample a mini-batch of data $\left\{y_i^{*},{\mathbf{x}}_i,w_i^{*}\right\}$ without replacement with size $ℬ$;

2. Compute the negative gradients g^(t) based on weighted MAE;

3. Update m and v by m^(t) = β₁m^(t−1) + (1 − β₁)g^(t),$v^{(t)}={\beta }_2{v}^{(t-1)}+\left(1-{\beta }_2\right)g^{{(t)}^2}$;

4. Compute bias correction terms ${\widehat{m}}^{(t)}=\frac{m^{(t)}}{1-{\beta }_1^t}$,${\widehat{v}}^{(t)}=\frac{v^{(t)}}{1-{\beta }_2^t}$;

5. Update the weights by $W^{(t)}=W^{(t-1)}-\eta \frac{{\widehat{m}}^{(t)}}{\sqrt{{\widehat{v}}^{(t)}}+\epsilon }$.

end

Output: Weights W in the ANN and the resulted $\widehat{\tau }(\mathbf{x})$ represented by the network.

Key advantages of the algorithm-based CATE estimators, in comparison with their model-based counterparts, are their automated implementation and scalability, as well as their accommodation of the non-additive effects and the high-dimensionality of X. For different algorithm-based CATE learners, we summarize the advantages and disadvantages in Table 3. Generally speaking, RF is easier to tune and it performs well in low dimensional cases. But a well-tuned GBM tends to outperforms RF in a high-dimensional data situation. ANN usually outperforms GBM and RF for image and text data because ANN is more flexible. For CATE estimation, however, when we have structured non-image or non-text data, the representation problem is easier to solve, and ANN might not offer added advantages.

Table 3:

Supervised learning algorithms for CATE estimation

Algorithm	Advantages	Disadvantages	Main Hyperparameters
Random Forests	Hard to overfit, easy to tune, good for parallel computing	Model can get large	Number of trees, number of features used in splitting
GBM	High-performing in high-dimensional case	Harder to tune than RF, take longer to train than RF	Number of trees, depth of trees, learning rate
Neural Network	Can handle extremely complex task	Hard and slow to train	Number of neurons in the hidden layer, number of epochs, learning rate

2.4.4. An R package for implementation

To make the proposed algorithms more accessible, we implemented the three CATE-learning algorithms in an R package RCATE. Each of the algorithms can be combined with MCM-EA, RL, and AIPW to achieve robust CATE estimation. For input data, we only require specification of the outcome, treatment assignment, and pre-treatment covariates. There is no need for users to estimate the nuisance quantities. A more detailed description of the R package RCATE and example code are provided in Appendix A.

3. Simulation Studies

3.1. Design and implementation

We conducted three sets of simulations to evaluate the performance of the proposed methods.

Simulation Study 1:

We compared the additive-model-based and algorithm-based learners under both L₁ and L₂ loss functions when the true treatment effect model involved interactions, i.e., non-additive.

Simulation Study 2:

We compared the proposed L₁-based algorithms with other machine learning algorithms in high-dimensional settings.

Supplemental Simulation Study (S):

We compared the algorithm-based robust estimators against model-based ones when the true treatment effect models were indeed additive; see details in Appendix B.

The methods considered in each of the three simulation studies are described in Table 4, where the numbers in the parentheses indicate the specific simulation studies.

Table 4:

Methods considered in the simulation studies. Numbers in the parentheses indicate the specific simulation studies in which the methods were assessed.

Methods under the Unified Formulation				Other Candidate Methods
	MCM-EA	RL	AIPW	Method
Robust RF	(1)(2)(S)	(1)(2)(S)	(1)(2)(S)	Robust QL	(1)
Robust GBM	(1)(2)(S)	(1)(2)(S)	(1)(2)(S)	Causal BART	(2)
Robust ANN	(1)(2)(S)	(1)(2)(S)	(1)(2)(S)	Causal Boosting	(2)
RF	(1)	(1)	(1)	Causal Forest	(2)
GBM	(1)	(1)	(1)	Causal MARS	(2)
ANN	(1)	(1)	(1)	X-learner+RF	(2)
Robust GAM	(1)(S)	(1)(S)	(1)(S)

We designed the simulation settings followed the structure of the real data in Section 4. The binary treatment levels (i.e., T ∈ {−1, 1}) and continuous outcome were used throughout. And we set the number of replications to R = 1, 000 and the size of the validation set to n_ν = 1, 000.

We assessed the performance of these methods using mean squared error (MSE), mean absolute error (MAE), and coverage probability (CP). The MSE and MAE were defined as follows:

$$MA{E}_v=\frac{1}{R}\sum _{r=1}^R\left|{\widehat{\tau }}^{(r)}\left({\mathbf{x}}_v\right)-{\tau }_0\left({\mathbf{x}}_v\right)\right|,MS{E}_v=\frac{1}{R}\sum _{r=1}^R{[{\widehat{\tau }}^{(r)}\left({\mathbf{x}}_v\right)-{\tau }_0\left({\mathbf{x}}_v\right)]}^2,$$

where x_v is the v-th observation from the validation set, ${\widehat{\tau }}^{(r)}(\mathbf{x})$ is the estimator of τ(x) based on the r-th data replicate. We summarized the performance over the whole validation set by taking the average (i.e.,$\overline{MSE}=\frac{1}{n_v}{\sum }_{v=1}^{n_v}MS{E}_v$). For simplicity, we reported MSE and MAE.

We calculated the CP as the proportion of the times that 95% bootstrap percentile intervals contained the true value of interest, out of the total number of simulating iterations (R = 1, 000), i.e.,

$$CP=\frac{1}{R}\sum _{i=1}^{R}I(\text{C}.\text{I}.\text{covers}\text{the}\text{true}\text{value}),$$

The tuning parameters were summarized in Appendix B.

3.1.1. Simulation 1: ML vs. model-based methods when τ₀ is not additive

We generated the outcome from the following model

$$Y_i=b_0\left({\mathbf{X}}_i\right)+\frac{T_i}{2}{\tau }_0\left({\mathbf{X}}_i\right)+{\epsilon }_i,{\epsilon }_i~\left(1-p_o\right)N(0,1)+p_{o}P.$$

We used two different error distributions P = N(0, 100) and $P=Laplace(0,\sqrt{50})$. The covariates were continuous variables (X_i ~ N₁₀(0, 1)). The treatment assignment followed a logistic model

$$D_i\mid {\mathbf{X}}_i~Bernoulli\left(p\left({\mathbf{X}}_i\right)\right),T_i=2D_i-1,logit\left(p\left({\mathbf{X}}_i\right)\right)=X_{i1}-X_{i2}.$$

Functions b₀(X_i) and τ₀(X_i) in the response surface were

$$b_0\left({\mathbf{X}}_i\right)=100+4X_{i1}+X_{i2}-3X_{i3},$$

$${\tau }_0\left({\mathbf{X}}_i\right)=6sin\left(2X_{i1}\right)+3\left(X_{i2}+3\right)X_{i3}+9tanh\left(0.5X_{i4}\right)+3X_{i5}\left(2I\left(X_{i4}\right)-1\right),$$

where the true treatment effect function included an interaction term, and thus violating the additive model assumption.

We compared all methods indicated by “(1)” in Table 4 while altering two design factors: The proportions of outliers p_o and the outlier generating mechanisms: (1) p_o ∈ {0, 0.05, 0.1, 0.15, 0.2, 0.3, 0.5}, n = 1000, and P = N(0, 100), and (2) p_o ∈ {0, 0.05, 0.1, 0.15, 0.2, 0.3, 0.5}, n = 1000, and $P=Laplace(0,\sqrt{50})$.

We reported the MSE and MAE of the CATE estimators graphically in Figure 1. The figure showed that all L₁-based algorithms outperformed the L₂-based ones. Advantage of the robust algorithms, as measured by MSE and MAE, increased with the proportion of outliers. Because the true treatment effect function was non-additive, when p_o < 0.2, the proposed machine learning algorithms outperformed additive models in MSE and CP; CPs were summarized in tabular form in Appendix Table B.3. The performance of robust GAMs was better than robust QL when the proportion of outliers was close to the breakdown point of LAD regression, i.e., p_o = 0.5.

Figure 1:

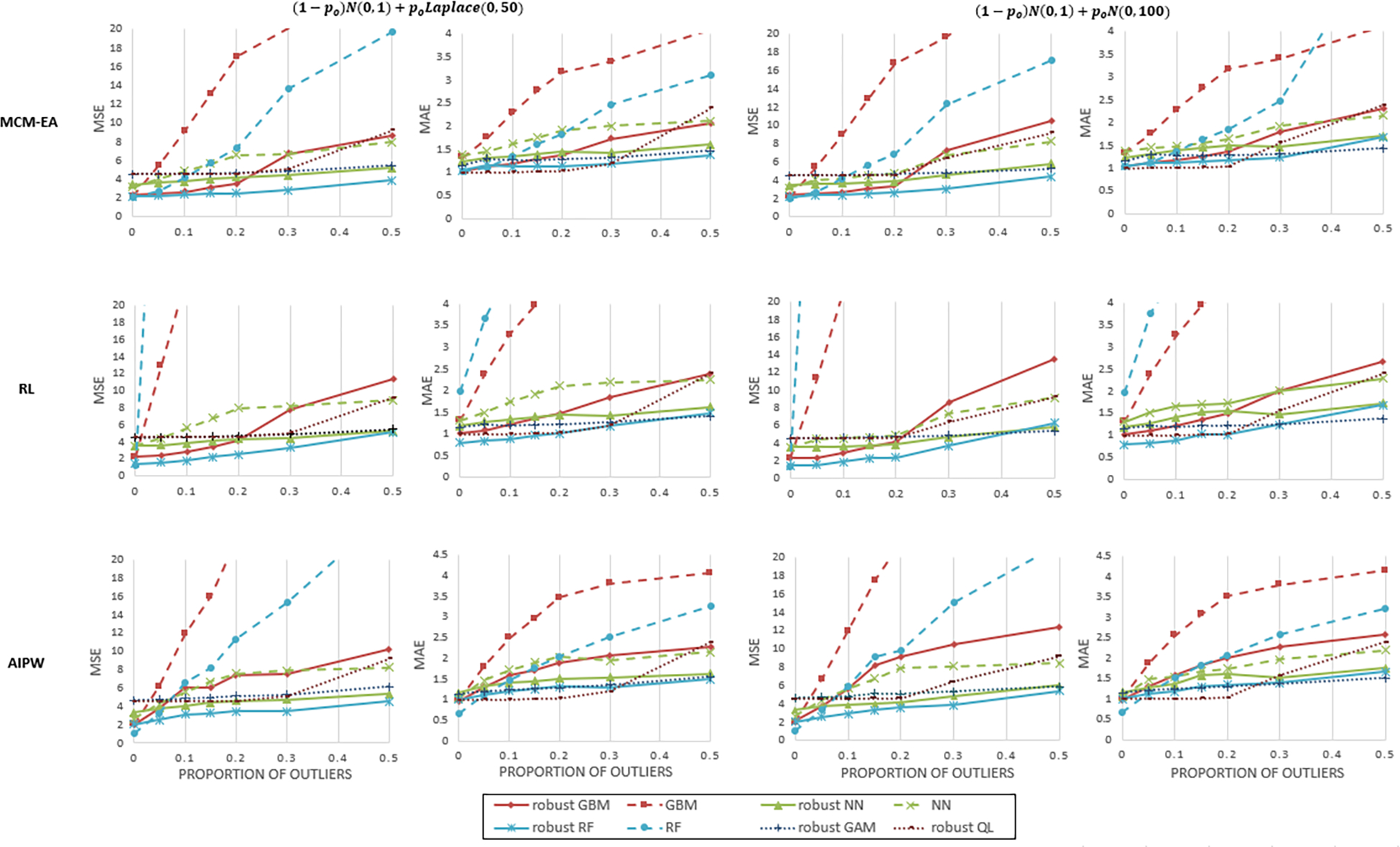
Results of Simulation Study 1 - MSE and MAE of different methods under various proportions of outliers and error generating mechanisms. The robust GBMs were indicated by red solid lines, the robust RFs were indicated by blue solid lines, the robust ANNs were indicated by green solid lines. The GBMs, RFs, and ANNs were indicated by dashed red, blue, and green lines. The robust GAMs were indicated by blue dotted line, and robust QL was indicated by brown dotted line.

There were little practical differences among the robust GBM, robust ANN and robust RF when combined with MCM-EA and R-learning. But the robust GBM didn’t work well together with AIPW transformation because AIPW tended to generate transformed weights with a large variability, and GBM was more likely to overfit when the data were noisy (Park and Ho, 2019).

3.1.2. Simulation 2: Performance in high-dimensional settings

Here, we only considered the methods that performed well in Simulation Study 1, and we focused on the methods’ performance in high-dimensional settings and when outliers existed.

We generated data sets with the same outlier distributions P, baseline function, and propensity score function as in Simulation Study 1. And we fixed the proportion of outliers at 0.15, sample size at n = 1, 000, and the data dimension at p ∈ {100, 2000}.

The true treatment effect functions when p = 100 and p = 2000 were

$$\begin{array}{l}{\tau }_0\left({\mathbf{X}}_i\right)=6sin\left(2X_{i1}\right)+3\left(X_{i2}+3\right)X_{i3}+9tanh\left(0.5X_{i4}\right)+3X_{i5}\left(2I\left(X_{i4}\right)-1\right)+\\ 3X_{i6}+2X_{i7}+X_{i8}-2X_{i9}-4X_{i10},\end{array}$$

and

$$\begin{array}{c}{\tau }_0\left({\mathbf{X}}_i\right)=6sin\left(2X_{i1}\right)+3\left(X_{i2}+3\right)X_{i3}+9tanh\left(0.5X_{i4}\right)+3X_{i5}\left(2I\left(X_{i4}\right)-1\right)+\\ \sum _{j=6}^{50}{\beta }_j{X}_{ij},{\beta }_j~Unif(-2,2),\end{array}.$$

Figure 2 (A) and (C) showed that when p = 100, the robust GBM and robust ANN combined with AIPW and MCM-EA outperformed all other methods when outliers exist. Among the existing algorithms, causal MARS had the best performance. The performance of robust RF and robust ANN combined with RL tied with that of the causal MARS. The boosting algorithms generally performed better than RFs, because a single deep tree tended to struggle to reduce bias on high dimensional data, so did the forests. When we increased the dimension to p = 2000 Figure 2 (B) and (D) showed that the robust GBMs had the best performance when the data dimension was much larger than the sample size.

Figure 2:

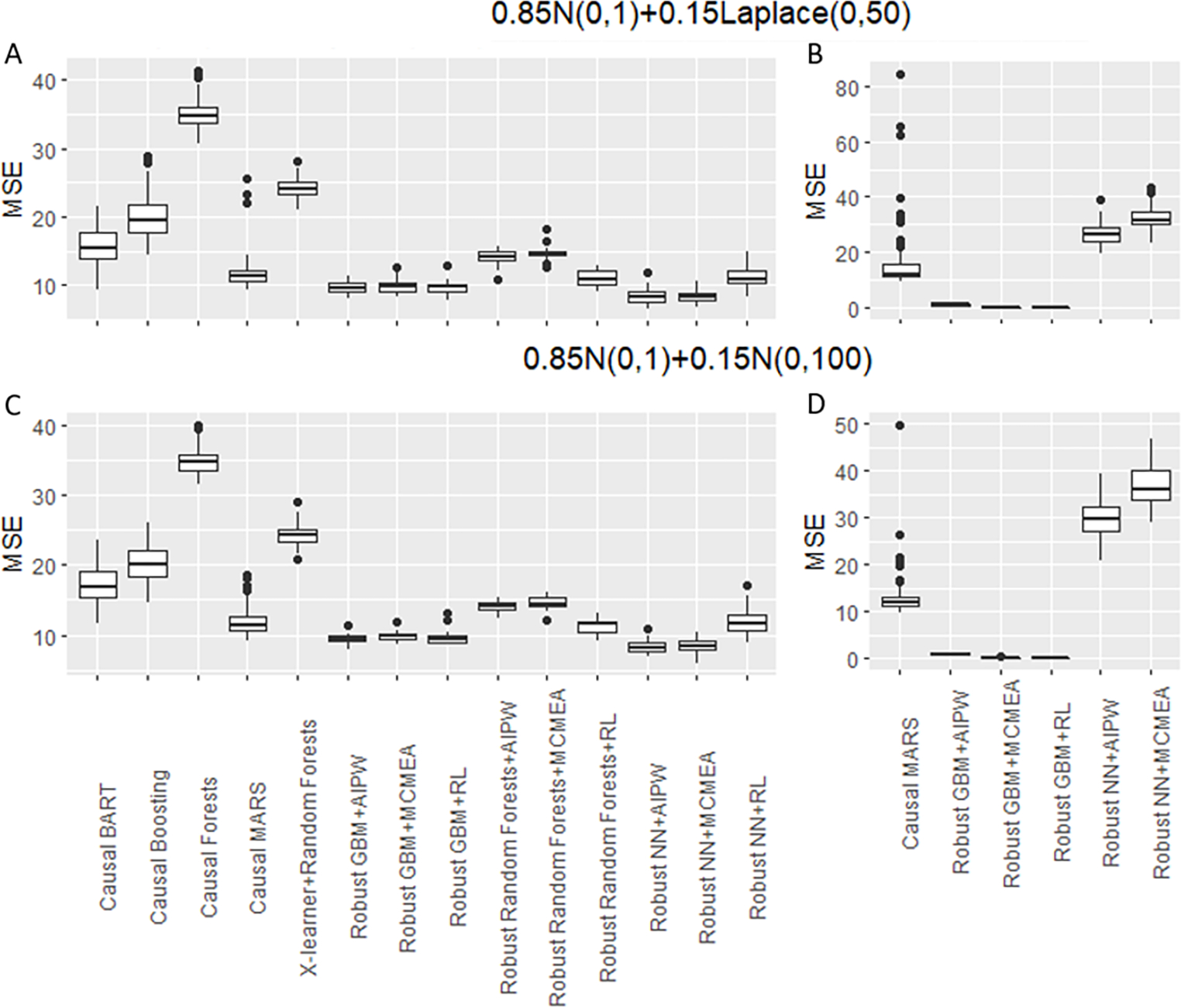
Simulation Study 2 - Mean squared error (MSE) of different algorithms when outliers exist. Figures A and C show the results when p = 100, Figures B and D show the results when p = 2000.

We additionally compared the computational speed of the proposed algorithms and additive models under difference sample sizes and dimensions of data. The robust RF was implemented in R, so that the speed was relatively slow and was not included in the comparisons here. The CPU time was collected on a personal computer with Intel Core i7–7700 CPU @3.60Ghz and 32 GB RAM. Table 5 showed that the robust GBM was the most efficient algorithms among all those considered in the comparison. Its advantage was most prominent when the sample size or dimension was high.

Table 5:

Comparison of the CPU time (s) of RF/GBM/ANN and additive model

Dimension	Algorithm	n = 1000	n = 3000	n = 5000	n = 8000
p = 10	Random Forests	0.30	1.67	3.34	7.41
	GBM	0.28	0.79	1.29	2.13
	Robust GBM	0.29	0.99	1.63	2.58
	ANN	4.72	12.87	21.43	35.89
	Robust ANN	4.51	12.63	20.90	35.25
	Robust GAM	1.65	18.94	38.23	86.18
p = 100	Random Forests	2.54	12.99	28.71	60.51
	GBM	2.27	6.64	11.33	18.75
	Robust GBM	2.29	7.13	12.13	19.02
	ANN	5.24	14.29	25.05	39.13
	Robust ANN	5.24	14.22	24.63	42.04
	Robust GAM	33.65	243.24	N/A	N/A

4. Real data application

To illustrate the use of the proposed algorithms, we assessed the treatment effects of two different antihypertensive therapies by analyzing recorded clinical data set from the “All of Us” research program. Sponsored by NIH, the program collected research data from multiple sources, including health surveys, health records, and digital health technologies (All of Us Research Program Investigators, 2019). Research data are publicly accessible at https://workbench.researchallofus.org/ through web-based Jupyter Notebook.

In this analysis, we compared the monotherapeutic effects of angiotensin-converting-enzyme inhibitors (ACEI) and thiazide diuretics on systolic blood pressure (SBP). We considered those receiving thiazide as in treatment group A (n = 504), and those receiving ACEI as in group B (n = 1040). The primary outcome of interest is the clinically recorded SBP in response to these therapies. Covariates of interest included the demographic and clinical characteristics of the participants; see Table 6.

Table 6:

Demographic and Clinical Characteristics of Study Subjects

Variable	Thiazide diuretic (n=504)	ACEI (n=1040)	p-value
	mean (sd)
Systolic BP (mmHg)	134.19 (17.22)	133.97 (21.61)	0.838
Pre-treatment Systolic BP (mmHg)	140.17 (18.46)	138.46 (21.96)	0.131
Age (year)	54.10 (12.19)	54.08 (11.94)	0.975
BMI	38.97 (9.26)	37.57 (33.09)	0.350
Potassium (mmol/L)	4.06 (0.45)	4.03 (0.47)	0.375
Sodium (mmol/L)	139.06 (2.78)	138.60 (3.08)	0.005*
Cholesterol in LDL (mg/dL)	111.44 (42.24)	111.15 (53.06)	0.914
Cholesterol in HDL (mg/dL)	47.51 (13.89)	45.32 (16.68)	0.011*
Albumim (g/dL)	11.21 (14.09)	20.00 (17.24)	<0.001*
Triglyceride (mg/dL)	171.03 (114.82)	181.31 (188.53)	0.260
Hemoglobin A1c (%)	7.25 (2.03)	7.25 (1.99)	0.993
Glomerular filtration rate (ml/min/1.73m2)	58.49 (18.56)	63.12 (18.04)	<0.001*
	n (percentage)
Female	324 (64.3)	589 (56.6)
Male	174 (34.5)	425 (40.9)	0.008*
Not answered	6 (1.2)	26 (2.5)
Black	113 (22.4)	366 (35.2)
White	279 (55.4)	415 (39.9)	<0.001*
More than one race or not answered	112 (22.2)	259 (24.9)
Hispanic	91 (18.1)	215 (20.7)	0.254

We expressed the treatment effect as a function of the patient characteristics x

$${\tau }_0(\mathbf{x})=E\left[Y^{(B)}-Y^{(A)}\mid \mathbf{X}=\mathbf{x}\right],$$

where Y^(A) and Y^(B) represented the potential outcome of the two treatment groups. Since the treatment effect of a therapy is measured by its ability to lower SBP, a positive $\widehat{\tau }(\mathbf{x})$ indicates a superior effect of the thiazide diuretics, for a given x. An important covariate is the baseline SBP.

In this analysis, we included individuals that were only on thiazide diuretic or ACEI for at least a month. Their first SBP within three months after the initiation of thiazide or ACEI was used as the outcome. The pre-treatment characteristics were measured within three months before the initiation of thiazide or ACEI, and they were presented in Table 6. Missing lab values were imputed by multiple imputation (Rubin, 2004).

Preliminary data examination showed that the observed outcome was right-skewed. See Figure 3. The Shapiro–Wilk’s test confirmed that the SBP was not normally distributed (thiazide diuretic: W = 0.9739, p = 8.011e − 08; ACEI: W = 0.9763, p = 5.422e − 12). We, therefore, used the L₁-based algorithms to analyze the data. Here the weighted supervised learning algorithms were used to accommodate the possible complex treatment effect function.

Figure 3:

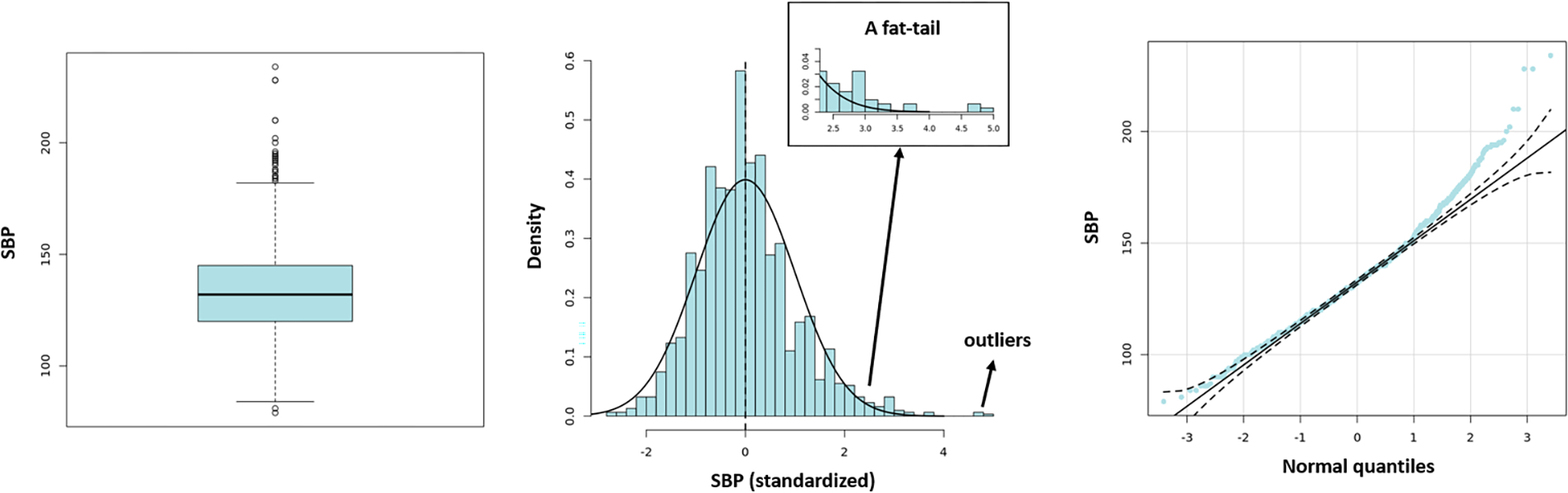
Heavy-tailed and Skewed Systolic Blood Pressure Distribution.

A closer examination of the patient characteristics revealed that patients on thiazide had higher sodium and high density lipid (HDL) levels, lower albumin level and glomerular filtration rate (GFR), and more likely to be female. Using GBM, we examined the mean function of SBP $\widehat{\mu }(\mathbf{x})$, ${\widehat{\mu }}^{(1)}(\mathbf{x})$, ${\widehat{\mu }}^{(-1)}(\mathbf{x})$ and the propensity of patient receiving ACEI $\widehat{p}(\mathbf{x})$. The estimated propensity score distributions were clearly different for the two treatment groups, whereas the mean functions were similar. See Figure 4. The different propensity score distributions of the two groups clearly showed the non-random nature of treatment assignment, and that a naive comparison should not be trusted.

Figure 4:

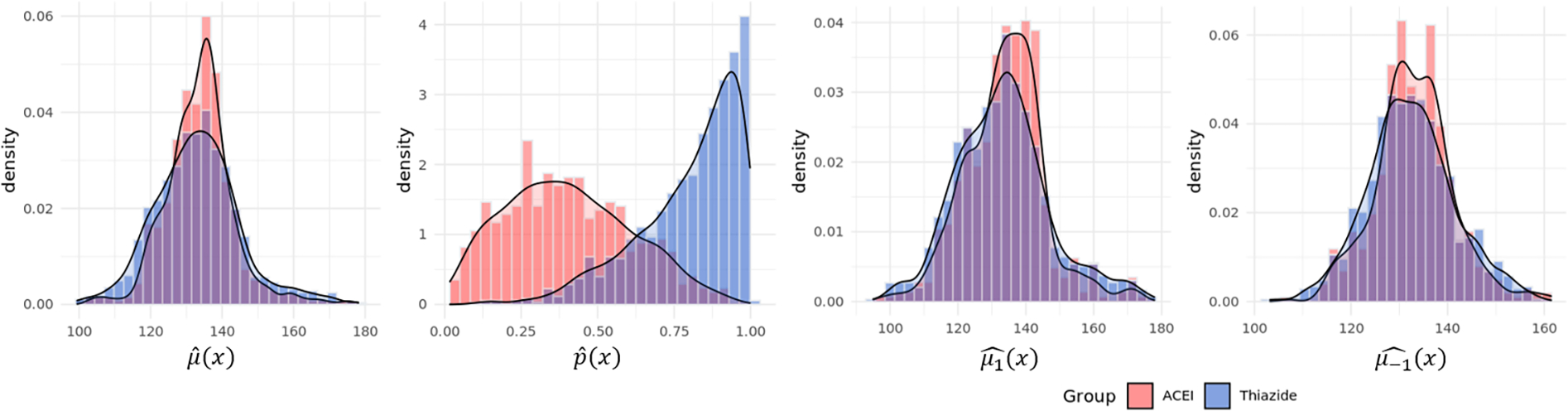
Data example: Estimated nuisance parameters by treatment group.

We then analyzed the data with the proposed algorithms: the robust RF and robust GBM combined with MCM-EA and R-learning. We use these four methods to estimate the CATE. Estimated treatment effects conditioning on pre-treatment SBP were shown graphically in Figure 5. To plot these marginal effects, we fixed the continuous covariates at their mean values, and categorical covariates at their mode levels.

Figure 5:

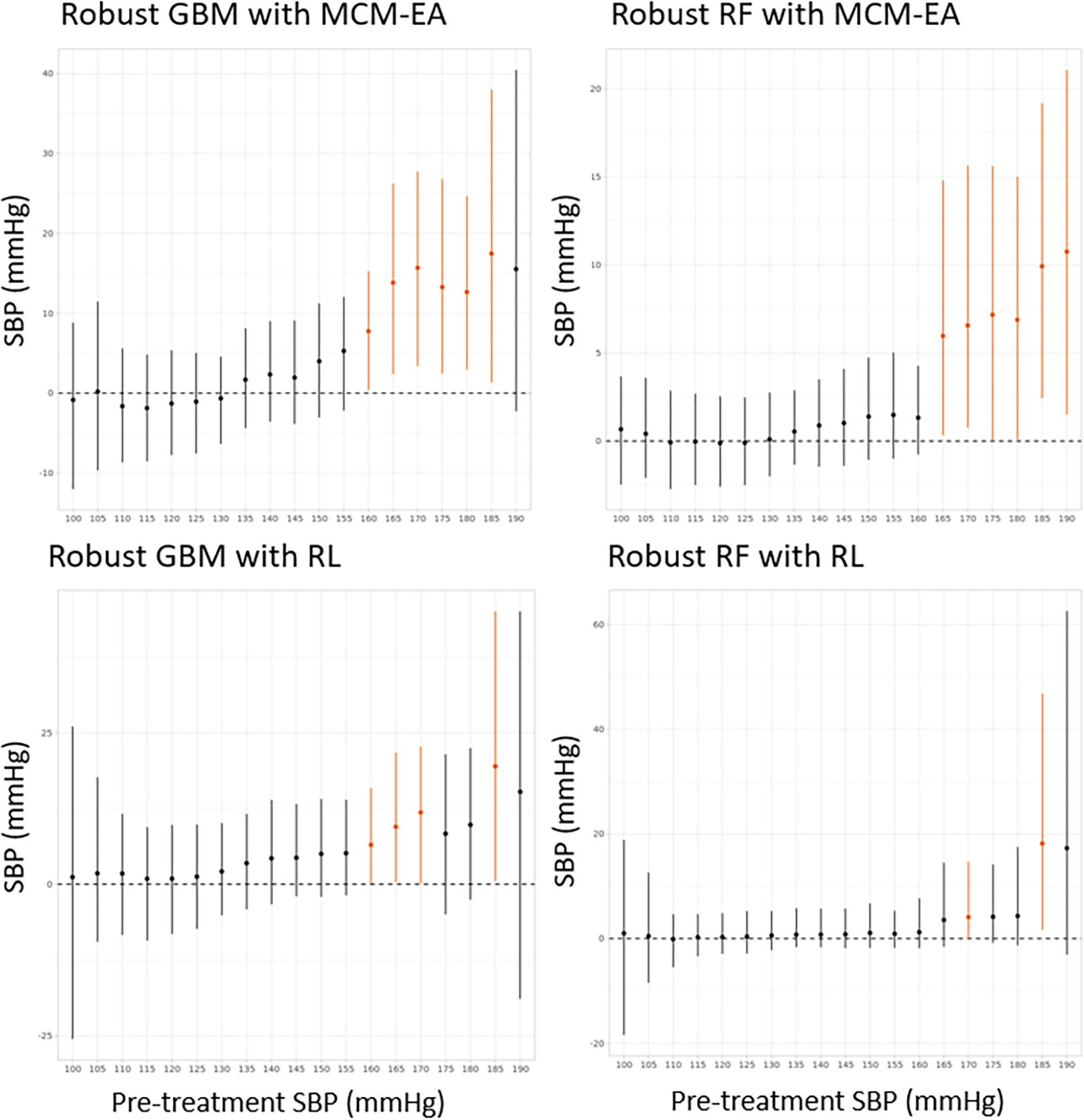
Data example: Marginal treatment effect of pre-treatment SBP. If the empirical 95% pointwise C.I. does not cover zero, the interval segment is colored in orange.

Results showed that the SBP lowering effects of thiazide diuretics and ACEI were similar when the pre-treatment SBP were below 160 mmHg. But for individuals with baseline SBP greater than 160 mmHg, diuretics tended to have a stronger SBP-lowering effect. This observation was largely consistent with the findings of the Antihypertensive and Lipid-Lowering Treatment to Prevent Heart Attack Trial (ALLHAT), which showed a comparable effect of thiazide-like diuretic chlorthalidone and ACEI lisinopril (The ALLHAT Officers and Coordinators for the ALLHAT Collaborative Research Group, 2002). Diuretics reduce blood pressure through their natriuretic actions – increase urinary excretion of sodium and reduce extracellular fluid volume (ECFV). It works particularly well in patients with greatly expanded ECFV, and thus explaining the greater SBP reduction in patients with higher pre-treatment SBP (Duarte and Cooper-DeHoff, 2010).

To verify the conditional independence error assumption, we performed the invariant residual distribution test (IRD-test), invariant environment prediction test (IEP-test), invariant conditional quantile prediction test (ICQP-test), invariant targeted prediction test (ITP-test) (Heinze-Deml et al., 2018). The conditional independence error assumption held for both proposed methods at the significant level of 0.05.

5. Discussion

The practice of precision medicine relies on a sound understanding of the causal effects of specific treatments in patients with different characteristics. By expressing the treatment effect as a function of patient characteristics, the heterogeneous treatment effect provides a useful quantification of the unknown causal effect. Among the existing methods for estimating heterogeneous treatment effects, few have considered the conditions of the data from which the estimates are derived - outliers and other forms of data irregularities could severely undermine the validity of the causal estimation. We described a general estimating equation that produces robust estimates against such data irregularities in recent work. However, the method requires the correct specification of the treatment effect function. From a practical perspective, such a requirement represents a significant constraint. Even when flexible additive models are used to accommodate the potential nonlinear effects, there is no assurance that such an additive structure would be adequate. To address this issue, we introduced a set of modified machine learning algorithms for treatment effect estimation. We also presented the necessary computational tools for practical data analysis.

When implemented within the framework of the previously proposed estimating equation for heterogeneous causal effects, we show that supervised learning algorithms could significantly reduce the risk of model misspecification without losing the method’s robustness. In a sense, the work presents a data-driven analytical approach that reduces the users’ burden of model specification while retaining good theoretical properties of the general estimating equation. A critical ingredient of this approach is the use of machine learning techniques to optimize the objective function. Simulation results confirmed that the new procedures’ good performance. As a result of this development, we improved the general estimating equation’s scalability in real data applications, making the methods more readily usable in practical data analysis.

Table 7:

Conditional independence test results (p-value)

Method	IRD-test	IEP-test	ICQP-test	ITP-test
Robust RF + MCM-EA	0.17	0.50	1.00	0.38
Robust RF + RL	0.22	0.54	0.95	0.49
Robust GBM + MCM-EA	0.06	0.57	0.69	0.29
Robust GBM + RL	0.29	0.50	0.32	0.55