Abstract
A Ruddlesden–Popper 2D perovskite PEA2PbX4 (X = I, Br, and Cl) is proposed for metasurface applications. Density functional theory is used to analyze the optical, electrical, mechanical properties, moisture and thermodynamic stability of PEA2PbX4. The refractive index of PEA2PbX4 varies with the halides, resulting in 2.131, 1.901, and 1.842 for X = I, Br, and Cl, respectively. Mechanical properties with Voigt-Reuss-Hill approximations indicate that all three materials are flexible and ductile. Based on the calculations of formation energy and adsorption of water molecules, PEA2PbI4 has superior thermodynamic and moisture stability. We present a novel metasurface based on 2D-PEA2PbI4 and analyze symmetry protected-bound states in the continuum (sp-BIC) excitation. The proposed structure can excite multiple Fano quasi-BICs (q-BICs) with exceptionally high Q-factors. We verify the group theoretical analysis and explore the near-field distribution and far-field scattering of q-BICs. The findings indicate that x-polarized incident waves can excite magnetic toroidal dipole-electromagnetic-induced transparency-BIC and magnetic quadrupole-BIC, while y-polarized incident waves can excite electric toroidal dipole-BIC and electric quadrupole-BIC. The influence of meta-atom and substrate losses, array size limitations, and fabrication tolerances are also discussed. The proposed structure can be employed for applications in the THz region, such as polarization-dependent filters, bidirectional optical switches, and wearable photonic devices.
Subject terms: Nanoscience and technology, Optics and photonics
Introduction
Terahertz (THz) technology is quite useful for screening security, and sensing without damaging or ionizing matter, as THz waves have properties such as low photon energy and strong penetrability1. Unfortunately, the weak interaction between light and matter in the THz region has hindered the development of THz technology due to the lack of powerful radiation sources2,3. However, by using resonant metasurfaces, it may be possible to overcome the challenges encountered in various THz research and improve the technology for diverse applications.
Metasurfaces possess resonances with a high-quality (Q) factor and concentrate light on a subwavelength scale, which makes them ideal for various applications, such as sensors, lasers, and nonlinear optics4–7. There have been numerous studies conducted on metasurface benefits in these fields. The conventional approach to achieving a high-Q resonance with an asymmetric spectral line shape is through effective design mechanisms that rely on Fano resonance. This type of resonance results from interference between a continuum state and a discrete state. A novel idea known as bound states in the continuum (BIC) has been put forth for structures lacking in-plane or out-of-plane inversion symmetry8. This concept highlights a correlation between the Q-factor of resonances and structural asymmetry, which can effectively be represented by an inverse-square law9. Symmetry-protected (sp) BIC arises due to the disallowed coupling between structures' eigenmodes and incident waves, owing to their mismatched symmetries. This leads to the formation of a localized state embedded within the continuum. The BIC ideally demonstrates an infinite Q value in a structure where symmetry is preserved. This renders it unobservable in the spectrum because of its zero spectral linewidth10. Asymmetry parameters can be used to engineer a quasi (q)-BIC mode with a finite linewidth and Q value. This approach offers a convenient means of accessing resonances with exceptionally high Q-factors11.
“The metamaterial absorbers (MMAs) are used to ensure high absorption of photons, which is required for absorbing a broad range of solar energy12–14. These MMAs are typically polarization-insensitive and maintain stable absorption levels even when subjected to mechanical stress or changes in incident angle. As a result, they can be widely utilized in a range of optical devices including sensors, solar cells, imaging tools, and detectors15.”
Metasurfaces composed of materials with high dielectric coefficients and low losses, are utilized to amplify the interaction between matter and light16. However, in the THz range, only a limited number of materials possess such properties. Among the dielectric metasurfaces described in the literature, silicon17,18 and lithium tantalate19,20 are frequently employed due to their desirable characteristics. Although there have been advancements in the THz region, it is still critical to introduce and examine novel materials. Furthermore, flexible metastructures are constructed by depositing metals on flexible substrates21. This approach results in significant radiation losses and a decrease in the Q-factor. Consequently, exploring the potential of employing new and flexible dielectric materials as an alternative to metals in the metastructure becomes crucial.
Ruddlesden–Popper quasi-two-dimensional (2D) perovskites can be described by the chemical formula (L)2(A)n−1BX3n+1, where L is a large monovalent cation (i.e., aliphatic or aromatic alkylammonium), A represents a small cation (such as formamidinium, methylammonium, or cesium), B indicates a divalent cation (i.e., tin and lead), X represents a halide anion (such as iodine (I), bromine (Br) and chlorine (Cl)), and n is the number of lead halide octahedral layers. For n = 1, the perovskite structure is pure 2D with formula L2BX4, and for n = ∞, it becomes analogous to bulk or three-dimensional (3D) perovskite with formula ABX322. Recently, 3D perovskites have been utilized in sensing applications23–25.
The 2D perovskites exhibit unique and remarkable structural and physical properties, such as low cost, ease of fabrication, direct and tunable bandgap, a soft and dynamic structure, and a relatively high nonlinear refractive index. Unlike 3D perovskites, the flexibility of the organic layer in 2D perovskites further contributes to their softness, along with the Van der Waals interface. In addition, 2D perovskite materials exhibit higher environmental and chemical stability compared to their 3D counterparts26. In the 2D perovskite material PEA2PbX4 (X = I, Br, and Cl), Phenethylammonium (PEA) with the chemical formula C6H5(CH2)2NH3 is used as the large cation. These aromatic cations exhibit hydrophobic characteristics typical of bulky aromatic cations. Consequently, they not only improve the material's environmental stability but also can influence its mechanical properties. In layered 2D halide perovskites based on PEA, moisture stability is generated by the hydrophobic nature of aromatic organic ammonium spacer cations. In general, perovskite materials, especially 2D perovskite (i.e., PEA2PbX4), have more flexibility than silicon because they have smaller elastic moduli27,28. PEA2PbX4 has recently been used in many optoelectronic fields due to its outstanding properties, such as moisture stability, photostability, and π-π interaction29, and we want to introduce and study it in the THz region for the first time to the best of our knowledge.
In the present work, we employ first-principles density functional theory (DFT) analysis to examine the mechanical, optical, electrical, and stability characteristics of PEA2PbX4 (X = I, Br, and Cl) to investigate their potential use in THz applications. The results indicate that PEA2PbI4 is significantly more thermodynamically stable than PEA2PbBr4 and PEA2PbCl4, and is some orders of magnitude more stable than 3D perovskites. The DFT calculation is used to assess the shear modulus, Poisson's ratio, Young's modulus, and bulk modulus of these compounds. The elastic moduli calculated by the Voigt-Reuss-Hill approximations indicate that these compounds have both ductility and mechanical stability. Moreover, for the first time, we demonstrate the moisture stability of PEA2PbX4 by calculating the adsorption energy of water molecules. We find that these materials have a high dielectric constant, near-zero loss in the THz region, thermodynamic stability, moisture resistance, and flexibility.
Following that, we introduce a novel kind of metastructure that uses periodic circular slot rings in a Ruddlesden–Popper quasi-2D perovskite layer (PEA2PbI4), which has not been reported yet to the best of our knowledge. By introducing an offset distance of the inner ring from the center, the symmetry of the structure is disrupted, which opens a zero-order channel, enabling the conversion of the dark modes to q-BIC states with a finite linewidth. After conducting an extensive mathematical examination utilizing group theory and finite element eigenfrequency calculations, we prove that the proposed metastructure can excite multiband high-quality q-BICs, such as the magnetic toroidal dipole (MTD) and electric toroidal dipole (ETD), which exhibit specific symmetry properties. By calculating the far-field radiations from the multipole decomposition method and near-field analysis with finite element frequency domain calculations, a thorough study is conducted on the q-BIC characteristics. The analysis of symmetry is beneficial in determining which BICs can be excited based on the polarization of the incident wave. Moreover, when the broad mode is coupled to the q-BIC, the Fano peak of low bandwidth transparency is visible. The Q value of electromagnetic-induced transparency-BIC resonance can be regulated by adjusting the offset distance. This work presents a valuable reference for developing applications in the THz region such as polarization-dependent switches, multi-channel wearable biochemical sensing, notch polarization-dependent filters, and non-linear optics.
Materials and methods
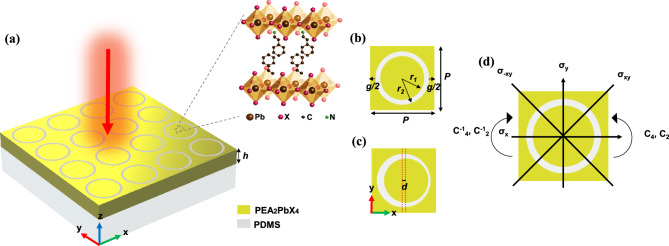
The schematic crystal structure of PEA2PbX4 (X = I, Br, and Cl) is depicted in Fig. 1a. Table S1 presents crystal data for room temperature structures.
Figure 1.
Schematic of (a) the proposed structure, (b) symmetric UC, (c) asymmetric UC, and (d) bases of UC’s symmetry.
Optical properties
The first-principle analysis based on DFT is used to compute the complex refractive index (RI) of PEA2PbX4 (X = I, Br, and Cl). The dielectric function, denoted as ε(ω) = ε1(ω) + iε2(ω), can be expressed as a complex quantity with a real part ε1(ω) and an imaginary part ε2(ω). To obtain optical properties, the imaginary part of the dielectric function is computed using the momentum matrix elements that correspond to the unoccupied and occupied wave functions in agreement with the selection rules, and is expressed as30:
| 1 |
where ħω is the photon energy, e represents the electronic charge, ε0 is the dielectric constant in vacuum, Ω is the volume of a unit cell, u is the unit vector along the polarization of the incident electric field, and ψkv and ψkc are wave functions for valence and conduction band electrons at a certain wave number, respectively. By employing the Kramers–Kronig relations, it is possible to extract the real component of the dielectric function from the imaginary component. The relation between complex dielectric function and complex RI is30:
| 2 |
| 3 |
where k and n are the imaginary and real parts of the refractive index, respectively (see Sect. S1).
Thermodynamic stability
The formation energy (FE) of quasi-2D perovskite () is defined as31:
| 4 |
where E is the total energy of the component material. For pure 2D perovskites (n = 1), the equation is modified as:
| 5 |
More negative formation energies directly correlate with a higher level of thermodynamic stability in the system31.
Mechanical properties
The mechanical properties of perovskites are critical for the analysis of ductility and flexibility in various applications. The mechanical properties are calculated using the stress–strain method to compute the elastic constant elements (Cij). From Hooke's law, the stress (σi) and strain (ϵj) in Voigt notation are related as32:
| 6 |
The shear modulus (G), bulk modulus (B), Young’s modulus (E), and Poisson’s ratio (τ) are calculated by DFT analysis. Employing Voigt (BV, GV, EV, νV) and Reuss (BR, GR, ER, νR) approximations, we can define the relations of elastic moduli by33–36:
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
The inverse of the elastic constant (Cij) is denoted as Sij. The Hill approximation (BH, GH, EH, νH) is the average of the Voigt and Reuss methods36:
| 15 |
Pugh's ratio refers to the ratio of the bulk modulus to the shear modulus (B/G). If the ratio of B/G is above 1.75, the material is characterized as ductile; otherwise, it is considered brittle. Another parameter for separating ductile from brittle materials is Poisson’s ratio. Ductility is observed in materials with a Poisson's ratio greater than 0.26, whereas materials with a Poisson's ratio of 0.26 or lower exhibit brittleness. Generally, materials with a higher Poisson’s ratio are more ductile37.
Moisture stability
The adsorption energy of water on perovskites is calculated by38:
| 16 |
where Eadsorbate presents the total energy of adsorbate (i.e., water molecules), Esub is the total energy of the isolated substrate system (i.e., perovskite surface), and Eadsorbate/sub is the total energy of adsorption system (i.e., water on the perovskite surface). For the negative value of Eads, perovskite has hydrophilicity. On the other hand, for a positive Eads value, perovskite has hydrophobicity.
Structure design and symmetry analysis
The proposed metastructure comprises a PDMS substrate (n = 1.4) with a thin layer of Ruddlesden–Popper perovskite on top, which has a periodic arrangement of slot rings (Fig. 1a). The symmetric and asymmetric unit cells (UC) are illustrated in Fig. 1b and c, respectively, and are characterized by certain structural features such as the inner and outer radii of the rings (r1 = 67.5 µm and r2 = 75 µm), the gap between adjacent rings (g = 31.25 µm), the thickness of the perovskite layer (h = 72.5 µm), and the period of the UC (P = 181.25 µm). By adjusting the inner ring position, an asymmetric structure is achieved. The offset distance of the inner ring from the center is denoted by d. Typically, the lithography process affects mainly the roughness and uniformity of the structure while the position of the rings remains fixed. This allows precise control over the asymmetry parameter during experimentation. This approach does not change the volume of the material portion of the metasurface, resulting in a minor shift in resonance frequency that is mainly caused by variations in the coupling between neighboring rings. Overall, this method results in a relatively stable resonance frequency for q-BICs. To determine the optical characteristics of the metastructure, the finite element method is utilized. Floquet-Bloch periodic boundary conditions are used along the x–z and y–z planes. Additionally, two perfectly matched layers are positioned at a specified distance from the structure along the z-axis and are supported by scattering boundary conditions.
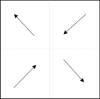
The unperturbed structure's UC is depicted in Fig. 1d, displaying a 2D group of geometrical symmetry denoted as C4v in Schoenfies notation39. Table 1 shows the four dark modes with irreducible representations (IRREPs) A1, A2, B1, and B2, and two degenerate bright modes (E), which are supported by the C4v symmetric group. Table 2 displays the resonant frequencies and field profiles associated with each mode. It should be noted that we use PEA2PbI4 in eigenfrequency calculations; the reason for this will be explained in the next sections. Four dark modes (i.e., real eigenfrequency) have different symmetries compared to the incident electric field and cannot be excited by it, as they belong to different IRREPs40. Because their components are orthogonal to that of the electric field and cannot be activated by incident waves. The arrow plots presented in Table 2 provide a visual representation indicating that these dark modes lack a total electric dipole moment in the x–y plane, thereby making them incapable of being coupled with the excited plane wave. Additionally, IRREPs E (E11, E12) describe two more orthogonal modes (Dy and Qx), while the other elements (E21, E22) specify two more orthogonal modes (Dx and Qy). When subjected to a 90-degree rotation, Dx and Qy transform into Dy and Qx, respectively. This establishes the polarization-independence of E modes.
Table 1.
IRREPs of group C4v.
| C4v | e | C2 | C4 | C-14 | σx | σy | σxy | σ-xy | Mode type |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Radial |
| A2 | 1 | 1 | 1 | 1 | − 1 | − 1 | − 1 | − 1 | Circular |
| B1 | 1 | 1 | − 1 | − 1 | 1 | 1 | − 1 | − 1 | Quadrupole |
| B2 | 1 | 1 | − 1 | − 1 | − 1 | − 1 | 1 | 1 | Quadrupole |
| E | 2 | − 2 | 0 | 0 | 0 | 0 | 0 | 0 | Dipole/quadrupole |
Table 2.
Eigenfrequencies of the proposed structure with C4v symmetry.
| IRREP | Mode schematic | Electric field profile | Magnetic field profile | Mode type |
|---|---|---|---|---|
|
A1 fres = 0.99240 THz |
 |
 |
 |
Radial mode |
|
A2 fres = 0.88074 THz |
 |
 |
 |
Circular mode |
|
B1 fres = 1.00258 THz |
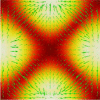
 |
 |
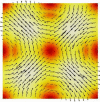 |
Quadrupole mode |
|
B2 fres = 0.98245 THz |
 |
 |
 |
Quadrupole mode |
|
E11, E12 fres1 = 0.993 + 0.0004i THz fres2 = 0.8999 + 0.0006i THz |
 |
 |
 |
Dipole and quadrupole mode (Dx and Qy) |
 |
 |
 |
||
|
E21, E22 fres1 = 0.993 + 0.0004i THz fres2 = 0.8999 + 0.0006i THz |
 |
 |
 |
Dipole and quadrupole mode (Dy and Qx) |
 |
 |
 |
To excite the dark resonances, it is necessary to reduce the symmetry of the UC. However, reducing the symmetry from C4v to C2v will not excite the dark modes. This conclusion is supported by Table S3 and Fig. S3 which display the IRREPs and electric field profiles of the C2v group, and Table S4, which outlines the process of symmetry degeneration from C4v to lower groups. However, it is possible to excite the dark resonances by reducing the symmetry of C4v to Cs. The IRREPs of Cs are presented in Table 3. This reduction allows the existence of corresponding electric field components. In this case, according to Table S4, A1 and B1 (A2 and B2) of C4v are reduced to A (B) of Cs.
Table 3.
IRREPs of group Cs.
| Cs | e | σx |
|---|---|---|
| A | 1 | 1 |
| B | 1 | − 1 |
The symmetries of distinct non-degenerate modes correspond to different incident wave polarizations, resulting in polarization-dependent BIC modes even for the same perturbation type. As explained in Sect. S4 and shown in Fig. S4, BIC modes A1 and B1 of C4v can be excited by an x-polarized plane wave, whereas BIC modes A2 and B2 can be excited by y-polarization, which indicates the possibility of selectively exciting BIC modes. Therefore, BICs are polarization-dependent.
Results and discussions
Material property studies
Complex RIs of PEA2PbX4 are shown in Fig. 2a–c. These materials exhibit neither dispersion nor loss in the THz region, making them suitable for employment in this spectral range. It is worth mentioning that the RI decreases as the halide changes from iodine to bromine and then to chlorine. This is because of the increase in the bandgaps (see Fig. S5).
Figure 2.
Complex RI curves vs. frequency for (a) PEA2PbI4, (b) PEA2PbBr4, and (c) PEA2PbCl4.
Table 4 presents the mechanical properties of PEA2PbX4 using the Voigt-Reuss-Hill approximations. The table shows that all three structures are mechanically stable (see Sect. S2) and ductile with B/G > 1.75 or ν > 0.26 according to DFT calculations. The bulk, shear, and Young’s moduli exhibit an increase when the halogen atom changes from I to Br and then to Cl. This indicates that PEA2PbI4 is more flexible compared to PEA2PbBr4 and PEA2PbCl4. Notably, silicon and GaAs have very high Young's modulus values of 174.8 GPa and 87 GPa, respectively, making them stiffer than PEA2PbX4, which exhibits Young's modulus range of 12–22 GPa41. Therefore, PEA2PbX4-based metasurfaces can be used in wearable photonic devices. In addition, the relatively low bulk modulus of all three structures suggests their inherent softness, enabling easy transformation into thin films. This characteristic is particularly crucial for photonic applications.
Table 4.
Mechanical properties of PEA2PbX4.
| Approach | PEA2PbI4 | PEA2PbBr4 | PEA2PbCl4 | |
|---|---|---|---|---|
| Voigt | 12.024 | 13.625 | 14.173 | |
| 7.050 | 7.058 | 7.125 | ||
| 17.692 | 18.056 | 18.307 | ||
| 1.705 | 1.930 | 1.989 | ||
| 0.254 | 0.279 | 0.284 | ||
| Type of material | Brittle | Ductile | Ductile | |
| Reuss | 11.354 | 13.459 | 13.942 | |
| 5.473 | 6.822 | 6.755 | ||
| 14.146 | 17.509 | 17.447 | ||
| 2.074 | 1.972 | 2.063 | ||
| 0.292 | 0.283 | 0.291 | ||
| Type of material | Ductile | Ductile | Ductile | |
| Hill | 11.689 | 13.542 | 14.058 | |
| 6.261 | 6.940 | 6.940 | ||
| 15.939 | 17.782 | 17.878 | ||
| 1.866 | 1.951 | 2.024 | ||
| 0.272 | 0.281 | 0.288 | ||
| Type of material | Ductile | Ductile | Ductile | |
Table 5 investigates the thermodynamic stability of PEA2PbX4 by calculation of the formation enthalpy energy for its component materials. As can be seen, PEA2PbI4 has a more negative value of formation enthalpy energy. This material is about 2 times more stable than PEA2PbBr4 and PEA2PbCl4, respectively, and is some orders of magnitude more stable than 3D perovskites42.
Table 5.
Formation enthalpy energies of PEA2PbX4.
| 2D perovskite | E(PEA2PbX4) (eV) | 2*E(PEAX) (eV) | E(PbX2) (eV) | FE (eV) |
|---|---|---|---|---|
| PEA2PbI4 | − 12,655.514 | − 8076.481 | − 4574.344 | − 4.689 |
| PEA2PbBr4 | − 26,157.016 | − 16,577.434 | − 9575.247 | − 4.335 |
| PEA2PbCl4 | − 26,839.994 | − 16,919.679 | − 9915.109 | − 4.506 |
Table 6 shows the adsorption energy of water molecules on PEA2PbX4 (see Sect. S3). The proposed materials exhibit better hydrophobicity than most perovskites, making them more moisture-stable43. PEA2PbI4 adsorbs water molecules approximately four times less than conventional 3D perovskites44. Among the proposed materials, PEA2PbI4 exhibits the highest stability, whereas PEA2PbBr4 shows the lowest stability against moisture. Therefore, adsorption energy and formation energy are directly correlated, and materials that have higher thermodynamic stability also tend to have better moisture stability45.
Table 6.
Adsorption energy for PEA2PbX4.
| 2D perovskite | Ewater/perovskite (eV) | Eperovskite (eV) | Ewater (eV) | Eads (eV) |
|---|---|---|---|---|
| PEA2PbI4 | − 13,123.759 | − 12,654.890 | − 468.804 | − 0.065 |
| PEA2PbBr4 | − 26,624.216 | − 26,155.335 | − 0.077 | |
| PEA2PbCl4 | − 27,307.211 | − 26,838.479 | − 0.072 |
Based on the above results, we chose PEA2PbI4 for the metastructure due to its higher RI in the THz region, superior thermodynamic stability compared to PEA2PbBr4 and PEA2PbCl4, better moisture stability, and ductile nature.
Wave propagation studies and mode analysis
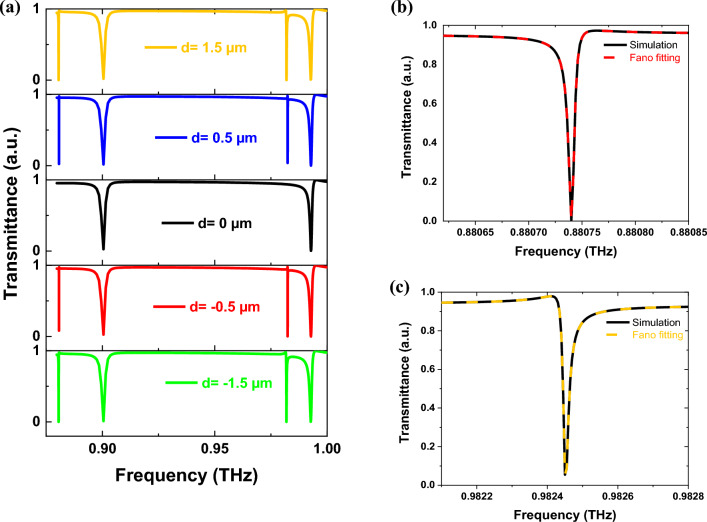
If d = 0, the structure exhibits C4v symmetry, and its transmittance spectrum for x and y polarizations is depicted in Figs. 3a and 4a, respectively. For both polarizations, two bright modes belonging to IRREP E are observed. Since q-BICs do not exist at d = 0, there is no energy leakage from the bound states to the zero-order channel. Furthermore, these modes are positioned at identical frequencies under both x and y polarizations, with their fields rotating 90 degrees from each other, highlighting their degeneracy (see Fig. S6). By adding an offset, it becomes possible to couple x-polarized waves with A1 and B1, and y-polarized waves with A2 and B2. This has been identified in the group theory analysis in “Structure design and symmetry analysis” section. As a consequence, the excitation of multiband q-BICs is selectively achieved depending on the polarization of the incident waves. In addition, symmetry breaking leads to the emergence of a transmission peak (mode A1) within the near-zero transmittance valley of the non-BIC mode under x-polarization. The resonant frequency of A1 is almost identical to that of the bright mode, producing an electromagnetic-induced transparency (EIT) effect. Moreover, the resonance peaks of q-BIC become broader as d moves away from zero. The typical Fano formula is utilized for fitting the Fano resonance curves of q-BICs46:
| 17 |
where ω0 is the resonant frequency, a1, a2, and b are the constants, and γ is the total rate of damping that characterizes the Q-factor () of the q-BICs. Figures 3b, c and 4b, c illustrate the fitting results for the four q-BICs at d = 0.5 µm. The Q-factors at d = 0.5 µm are 1.2 104, 5 105, 4.7 105, and 4 104 for A1, B1, A2, and B2, respectively.
Figure 3.
(a) The transmittance spectrum under x-polarization with various d, (b) Fano fitting of A1 at d = 0.5, and (c) Fano fitting of B1 at d = 0.5.
Figure 4.
(a) The transmittance spectrum under y-polarization with various d, (b) Fano fitting of A2 at d = 0.5, and (c) Fano fitting of B2 at d = 0.5.
The absence of clutter modes in the transmittance spectrum prevents interference with resonant states in the desired frequency range while maintaining high Q-factor q-BIC modes. Furthermore, all modes in this frequency range exhibit a spectral contrast ratio and modulation depth of approximately 100%. The spectral contrast ratio is defined as [(Ton − Toff)]/[(Ton + Toff)] × 100% and modulation depth is defined as [(Ton − Toff)/Ton] × 100%, where Toff and Ton represent the minimum and maximum transmittance, respectively47. These remarkable modulation depths and spectral contrast ratios significantly improve detection accuracy and switching efficiency in sensor and switch applications.
To provide an intuitive representation of the resonances, we analyze the near-field distributions of the displacement current, electric, and magnetic field within the UC shown in Fig. 5. In mode A1, the head-to-tail configuration of magnetic moments is quite evident. The presence of current loops in the plane perpendicular to it provides clear indications of the magnetic toroidal dipole (MTD) mode (also see Fig. S7a). This mode can be considered as the combined result of both intra-UC and inter-UC moments. Non-parallel magnetic moments are evident in mode B1, which represents a magnetic quadrupole (MQ). In the case of A2, the field map reveals a clear vortex of displacement currents threading through the inner ring. Additionally, magnetic moments take the form of a vortex within the plane perpendicular to the current. This configuration enables easy recognition of an electric toroidal dipole (ETD) (also see Fig. S7b). Mode A2 can also be considered as the combined result of both intra-UC and inter-UC moments. Finally, in B2, an electric quadrupole (EQ) mode can be identified by antiparallel electric moments. The fourth column in Fig. 5 displays a 3D representation of the electric field. The displacement current is represented by gray arrows, while the magnetic field is depicted by black arrows.
Figure 5.
The color maps of displacement currents, electric, and magnetic fields, as well as vector distributions in the x–y plane for (a) A1, (b) B1, (c) A2, and (d) B2. The fourth column displays a 3D representation of the electric field.
To perform a more comprehensive investigation of q-BIC properties, we utilize the Cartesian multipole decomposition technique (see Sect. S7)48. During this process, we integrate the displacement current density within the UC, to gain insight into the distribution of the electromagnetic source in the far-field. According to Fig. 6, the dominant multipole components in A1, B1, A2, and B2 are MTD, MQ, ETD, and EQ, respectively. These results are completely consistent with Fig. 5.
Figure 6.

The contributions of q-BICs to scattering power.
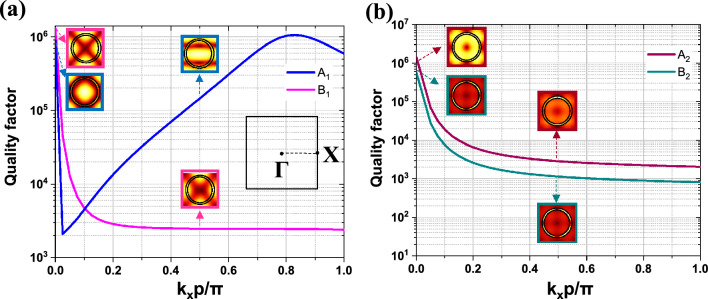
The verification of the four q-BIC modes' symmetry-protected nature is supported by an eigenvalue analysis of a part of their band diagram. In this analysis, the kx component of the periodic boundary condition sweeps from 0 to π/p (Γ to X in the first Brillouin zone). As shown in Fig. 7a and b, while all four modes theoretically have ultra-high Q-factors at the Γ point in the first Brillouin zone, their values decrease sharply from the Γ point, demonstrating their symmetry protected-bound state in the continuum (sp-BIC) nature. Moreover, in Fig. 7a, we observe a high Q-factor at kx = 0.8π/p, which corresponds to off Γ-BIC and lies beyond the scope of this work. The electric field profile of the modes at kx = 0 and kx = 0.5π/p can be observed in the insets of Fig. 7a and b. It is evident that the nature of each mode remains unchanged despite varying kx, however, the Q-factors differ.
Figure 7.
The Q values of (a) A1 and B1, and (b) A2 and B2 along the path from Γ to X in the first Brillouin zone.
We now examine how the Q value of the q-BICs is influenced by the offset distance of the inner ring from the center, as illustrated in Fig. 8. The results reveal that the Q-factor of the q-BICs exhibit remarkably high sensitivity to changes in d. When d deviates from 0, we observe an exponential decrease in the Q-factor (Q ∝ d−2). For instance, at d = 0.5 µm, the Q-factor is significantly higher compared to that of d = 1 or − 1 µm, with a difference of nearly four orders of magnitude. This exponential decline in the Q-factor of the q-BICs agrees well with findings from previous studies where an increase in the asymmetry parameter resulted in a similar trend49,50. Consequently, manipulation of the Q value of q-BIC modes can be realized with asymmetric parameters.
Figure 8.
Q values of (a) A1, (b) B1, (c) A2, and (d) B2 as a function of the inner ring’s offset distance from the center.
Considerations of fabrication non-idealities
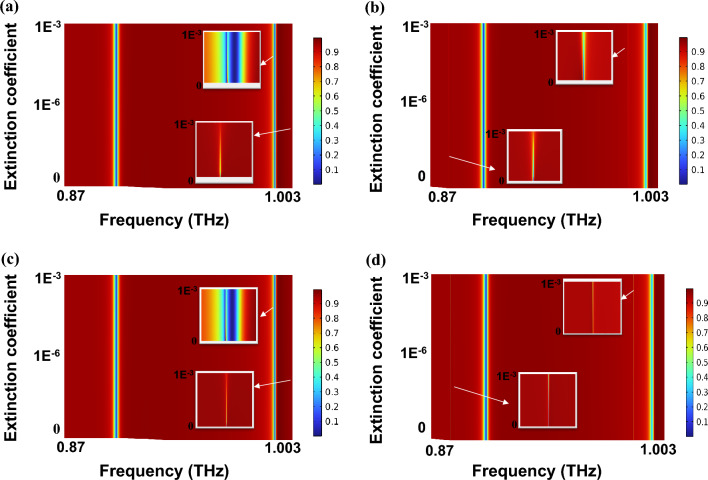
PEA2PbI4 has extremely low absorption losses in the THz region. However, in the real fabrication process, surface roughness and defects can lead to absorption and scattering losses, which are major concerns when designing the metasurface. These losses are considered by adding the imaginary part of the PEA2PbI4 refractive index (k) (i.e., the extinction coefficient) as nPEA2PbI4 = n-jk. Figure 9a and b and their insets show that for d = 0.5 µm as the k of PEA2PbI4 rises, particularly when k approaches 10–3, there is a noticeable increase in the full width at half maximum (FWHM) of q-BICs and a reduction in transmittance intensity. However, the transmittance spectrum remains largely unaffected when k 10−8. Meanwhile, the FWHM of non-BICs does not change, and all resonance frequencies exhibit no shifts. The impact of meta-atom losses is more pronounced on reflectance curves compared to transmittance curves (see Fig. S8). The results in Fig. 9c and d show that substrate losses have a notably smaller impact than meta-atom losses. Consequently, the observed variations in Q-factor and transmittance intensity of q-BICs are relatively minor.
Figure 9.
Evolution of the transmittance spectra versus meta-atom’s extinction coefficient for (a) x-polarized incident wave, (b) y-polarized incident wave at d = 0.5 µm, the evolution of the transmittance curves versus substrate’s extinction coefficient for (c) x-polarized incident wave, and (d) y-polarized incident wave at d = 0.5 µm.
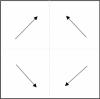
In the experiment, the actual Q-factor can be limited by the finite size of the array51. Periodicity among meta-atoms suppresses radiative loss through near-field coupling. To investigate the near-field coupling among the meta-atoms, we simulate how the resonance evolves for different array sizes (the number of UCs in the metastructure). The results for A1 are presented in Fig. 10. The electric field magnitude rises in proportion to the size of the array. Moreover, the central rings of the array demonstrate a greater level of field compared to those located at the edges. When a 27 × 27 array size is employed, the Q-factor of metastructure is very close to that of an infinite array. To achieve a Q value comparable to that of an infinite structure, the minimum array sizes for modes B1, A2, and B2 are 15 × 15, 17 × 17, and 25 × 25, respectively (not shown here).
Figure 10.
Electric Field Profiles of A1 in finite-sized arrays: 1 × 1, 3 × 3, 5 × 5, 7 × 7, and 9 × 9. The table displays the A1 Q value in different array sizes.
To examine the impact of fabrication process tolerance on the q-BICs of the proposed structure, we conducted investigations into the Q-factor and resonance frequency of the modes within a 5% range of change in the structure parameters. Based on the findings presented in Table 7, it can be observed that when the parameters of the metastructure undergo a 5% change, the Q-factors of q-BICs remain in the same order. Consequently, in practical scenarios, one can expect to observe high Q-factors. To discuss the red and blue shift of the modes we can refer to the dielectric resonator's Mie resonance frequency explained as52:
| 18 |
where V (x, y, z) is related to the size of the resonator, while μ and ε represent its permeability and permittivity, respectively. In addition, θ is a constant value that applies to a specific resonance. The rise (fall) in height, radius, and period can cause the device volume V (x, y, z) to increase (decrease), and as a result, the resonant frequency redshifts (blueshifts). Therefore, the shift in resonance frequencies caused by the aforementioned parameters is consistent with the Mie theory.
Table 7.
The effect of fabrication tolerance on resonance frequencies and Q-factor.
| Fabrication tolerance | fres (P/h/r) THz | fres (P/h/r-5%) THz | fres (P/h/r + 5%) THz | Q-factor (P/h/r) | Q-factor (P/h/r − 5%) | Q-factor (P/h/r + 5%) | |
|---|---|---|---|---|---|---|---|
| P 5% | A1 | 0.99240 | 1.0267 | 0.95879 | 1.2 104 | 1.1 104 | 2.2 104 |
| B1 | 1.00258 | 1.04608 | 0.96358 | 4.7 105 | 4.6 105 | 4.8 105 | |
| A2 | 0.88074 | 0.92089 | 0.84353 | 5 105 | 3.8 105 | 5.6 105 | |
| B2 | 0.98245 | 1.02438 | 0.93312 | 4 104 | 2.7 104 | 5 104 | |
| h 5% | A1 | 0.99240 | 1.00049 | 0.97023 | 1.2 104 | 1 104 | 4 104 |
| B1 | 1.00258 | 1.01158 | 0.98600 | 4.7 105 | 4.5 105 | 5.2 105 | |
| A2 | 0.88074 | 0.88404 | 0.87188 | 5 105 | 3.8 105 | 4.6 105 | |
| B2 | 0.98245 | 0.98635 | 0.97925 | 4 104 | 4 104 | 4.1 104 | |
| r1, r2 5% | A1 | 0.99240 | 1.0240 | 0.9623 | 1.2 104 | 1 104 | 104 |
| B1 | 1.00258 | 1.0459 | 0.9585 | 4.7 105 | 4.5 105 | 4.8 105 | |
| A2 | 0.88074 | 0.92774 | 0.83674 | 5 105 | 105 | 5.3 105 | |
| B2 | 0.98245 | 1.02445 | 0.94095 | 4 104 | 104 | 104 | |
Conclusion
In summary, we use DFT calculations with the CASTEP module to obtain electrical, mechanical, and optical properties, as well as the moisture and thermodynamic stability of 2D perovskite PEA2PbX4 (X = I, Br, and Cl). By comparing the results among PEA2PbI4, PEA2PbBr4, and PEA2PbCl4, we find that PEA2PbI4 has a higher refractive index in the THz range. In addition, DFT calculations show that all three materials are ductile and flexible. The formation energy calculations indicate that PEA2PbI4 is thermodynamically more stable due to its higher negative value. Moreover, the surface adsorption energy of water on perovskite reveals that PEA2PbI4 exhibits higher hydrophobicity, making it more moisture stable than the other two materials. We propose and analyze the excitation of sp-BICs in a novel PEA2PbI4-based metasurface, where multiple Fano q-BICs with ultra-high Q-factors can be excited. We employ group theory to justify the excitation of BICs and their polarization dependence. Through eigenfrequency and frequency domain simulations, we validate the group theoretical analysis and investigate the near-field distribution as well as the far-field scattering of q-BICs. Based on the results, we can conclude that MTD-EIT-BIC and MQ-BIC can be excited by x-polarized, and ETD-BIC and EQ-BIC by y-polarized incident waves. The effects of meta-atom losses, substrate losses, the finite size of the array, and fabrication tolerance are also investigated. The proposed metasurface with multiple Fano resonances and high efficiency is promising for different photonic applications such as polarization-dependent filters, switches, and wearable sensors.
Supplementary Information
Author contributions
S.B.S.: Conceptualization, Investigation, Writing–original draft, Writing–review and editing S.S.: Conceptualization, Investigation, Writing–original draft, Writing–review and editing V.A.: Conceptualization, Supervision, Project administration, Funding acquisition, Writing–review, editing and Resources S.M.H.: Conceptualization, Consultation, review and editing.
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-023-49224-9.
References
- 1.Fischer BM, et al. Terahertz time-domain spectroscopy and imaging of artificial RNA. Opt. Express. 2005;13(14):5205–5215. doi: 10.1364/OPEX.13.005205. [DOI] [PubMed] [Google Scholar]
- 2.Wang R, et al. Electric Fano resonance-based terahertz metasensors. Nanoscale. 2021;13(44):18467–18472. doi: 10.1039/D1NR04477J. [DOI] [PubMed] [Google Scholar]
- 3.Gupta M, Singh R. Terahertz sensing with optimized Q/Veff metasurface cavities. Adv. Opt. Mater. 2020;8(16):1902025. doi: 10.1002/adom.201902025. [DOI] [Google Scholar]
- 4.Maksimov DN, et al. Refractive index sensing with optical bound states in the continuum. Opt. Express. 2020;28(26):38907–38916. doi: 10.1364/OE.411749. [DOI] [PubMed] [Google Scholar]
- 5.Liu H, et al. Dirac semimetal and an all dielectric based tunable ultrasensitive terahertz sensor with multiple bound states in the continuum. Opt. Express. 2022;30(26):46471–46486. doi: 10.1364/OE.478457. [DOI] [PubMed] [Google Scholar]
- 6.Ning T, et al. Ultimate conversion efficiency of second harmonic generation in all-dielectric resonators of quasi-BICs in consideration of nonlinear refraction of dielectrics. Opt. Express. 2021;29(11):17286–17294. doi: 10.1364/OE.427355. [DOI] [PubMed] [Google Scholar]
- 7.Saadatmand SB, et al. Graphene-based integrated plasmonic sensor with application in biomolecule detection. JOSA B. 2023;40(1):1–10. doi: 10.1364/JOSAB.472734. [DOI] [Google Scholar]
- 8.Han S, et al. Extended bound states in the continuum with symmetry-broken terahertz dielectric metasurfaces. Adv. Opt. Mater. 2021;9(7):2002001. doi: 10.1002/adom.202002001. [DOI] [Google Scholar]
- 9.Zanotto S, et al. Optomechanical modulation spectroscopy of bound states in the continuum in a dielectric metasurface. Phys. Rev. Appl. 2022;17(4):044033. doi: 10.1103/PhysRevApplied.17.044033. [DOI] [Google Scholar]
- 10.Azzam SI, Kildishev AV. Photonic bound states in the continuum: From basics to applications. Adv. Opt. Mater. 2021;9(1):2001469. doi: 10.1002/adom.202001469. [DOI] [Google Scholar]
- 11.Doeleman HM, et al. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photon. 2018;12(7):397–401. doi: 10.1038/s41566-018-0177-5. [DOI] [Google Scholar]
- 12.Shuvo MMK, et al. Polarization and angular insensitive bendable metamaterial absorber for UV to NIR range. Sci. Rep. 2022;12(1):4857. doi: 10.1038/s41598-022-08829-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shuvo MMK, et al. A wide-angle, enhanced oblique incidence, bend-able metamaterial absorber employed in visible region with a sun shape resonator. IEEE Access. 2021;9:126466–126480. doi: 10.1109/ACCESS.2021.3111813. [DOI] [Google Scholar]
- 14.Shuvo MMK, et al. Wide-angle broadband polarization independent bend-able nano-meta absorber employed in optical wavelength. Opt. Mater. 2022;126:112174. doi: 10.1016/j.optmat.2022.112174. [DOI] [Google Scholar]
- 15.Mahmud S, et al. A multi-band near perfect polarization and angular insensitive metamaterial absorber with a simple octagonal resonator for visible wavelength. IEEE Access. 2021;9:117746–117760. doi: 10.1109/ACCESS.2021.3106588. [DOI] [Google Scholar]
- 16.Liao Z, et al. Guiding-mode-assisted double-BICs in an all-dielectric metasurface. Opt. Express. 2022;30(14):24676–24688. doi: 10.1364/OE.463340. [DOI] [PubMed] [Google Scholar]
- 17.Wang P, et al. Ultra-high-Q resonances in terahertz all-silicon metasurfaces based on bound states in the continuum. Photon. Res. 2022;10(12):2743–2750. doi: 10.1364/PRJ.470657. [DOI] [Google Scholar]
- 18.Seyedeh Bita Saadatmand, V. A., & Hamidi, S. M. Quasi-BIC based all-dielectric metasurfaces for ultra-sensitive refractive index and temperature sensing. Sci. Rep.13, (2023) [DOI] [PMC free article] [PubMed]
- 19.Wang Y, et al. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics. 2021;10(4):1295–1307. doi: 10.1515/nanoph-2020-0582. [DOI] [Google Scholar]
- 20.Saadatmand, S.B., Ahmadi, V. & Hamidi, S. M. Resonant field enhancement in all-dielectric metastructures supporting THz bound states in the continuum. in 2022 6th International Conference on Millimeter-Wave and Terahertz Technologies (MMWaTT). 2022. IEEE.
- 21.Walia, S., et al. Flexible metasurfaces and metamaterials: A review of materials and fabrication processes at micro-and nano-scales. Appl. Phys. Rev.2(1), (2015).
- 22.Mao L, Stoumpos CC, Kanatzidis MG. Two-dimensional hybrid halide perovskites: principles and promises. J. Am. Chem. Soc. 2018;141(3):1171–1190. doi: 10.1021/jacs.8b10851. [DOI] [PubMed] [Google Scholar]
- 23.Chemerkouh MJHN, Saadatmand SB, Hamidi SM. Ultra-high-sensitive biosensor based on SrTiO3 and two-dimensional materials: Ellipsometric concepts. Opt. Mater. Express. 2022;12(7):2609–2622. doi: 10.1364/OME.457983. [DOI] [Google Scholar]
- 24.Saadatmand, S.B., et al., Design and analysis of highly sensitive plasmonic sensor based on two-dimensional inorganic Ti-MXene and SrTiO3 interlayer.IEEE Sens. J. (2023).
- 25.Saadatmand SB, et al. Plasmonic heterostructure biosensor based on perovskite/two dimensional materials. Optik. 2023;290:171328. doi: 10.1016/j.ijleo.2023.171328. [DOI] [Google Scholar]
- 26.Blancon J-C, et al. Semiconductor physics of organic–inorganic 2D halide perovskites. Nat. Nanotechnol. 2020;15(12):969–985. doi: 10.1038/s41565-020-00811-1. [DOI] [PubMed] [Google Scholar]
- 27.Yang S, et al. Functionalization of perovskite thin films with moisture-tolerant molecules. Nature Energy. 2016;1(2):1–7. doi: 10.1038/nenergy.2015.16. [DOI] [Google Scholar]
- 28.Chen Y, et al. 2D Ruddlesden–Popper perovskites for optoelectronics. Adv. Mater. 2018;30(2):1703487. doi: 10.1002/adma.201703487. [DOI] [PubMed] [Google Scholar]
- 29.Alidaei M, et al. Stability improvement of perovskite solar cell using photoswitchable and moisture resistant dual-function interfacial layer. J. Alloys Compd. 2022;903:163891. doi: 10.1016/j.jallcom.2022.163891. [DOI] [Google Scholar]
- 30.Palik, E.D., Handbook of Optical Constants of Solids. Vol. 3. (Academic Press, 1998).
- 31.Yang Y, et al. Origin of the stability of two-dimensional perovskites: A first-principles study. J. Mater. Chem. A. 2018;6(30):14949–14955. doi: 10.1039/C8TA01496E. [DOI] [Google Scholar]
- 32.Giustino, F., Materials Modelling Using Density Functional Theory: Properties and Predictions. (Oxford University Press, 2014).
- 33.Wu Z-J, et al. Crystal structures and elastic properties of superhard Ir N 2 and Ir N 3 from first principles. Phys. Rev. B. 2007;76(5):054115. doi: 10.1103/PhysRevB.76.054115. [DOI] [Google Scholar]
- 34.Voigt, W., Lehrbuch der kristallphysik: Teubner-Leipzig (Macmillan New York, 1928).
- 35.Reuss A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929;9:49–58. doi: 10.1002/zamm.19290090104. [DOI] [Google Scholar]
- 36.Hill R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A. 1952;65(5):349. doi: 10.1088/0370-1298/65/5/307. [DOI] [Google Scholar]
- 37.Feng, J., Mechanical properties of hybrid organic-inorganic CH3NH3BX3 (B= Sn, Pb; X= Br, I) perovskites for solar cell absorbers. APL Mater.2(8), (2014).
- 38.Li Q, et al. Compositional effect on water adsorption on metal halide perovskites. Appl. Surf. Sci. 2021;538:148058. doi: 10.1016/j.apsusc.2020.148058. [DOI] [Google Scholar]
- 39.Bradley, C. and A. Cracknell, The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups. (Oxford University Press, 2010).
- 40.Algorri J, et al. Analogue of electromagnetically induced transparency in square slotted silicon metasurfaces supporting bound states in the continuum. Opt. Express. 2022;30(3):4615–4630. doi: 10.1364/OE.446720. [DOI] [PubMed] [Google Scholar]
- 41.Spanopoulos I, et al. Uniaxial expansion of the 2D Ruddlesden–Popper perovskite family for improved environmental stability. J. Am. Chem. Soc. 2019;141(13):5518–5534. doi: 10.1021/jacs.9b01327. [DOI] [PubMed] [Google Scholar]
- 42.Quan LN, et al. Ligand-stabilized reduced-dimensionality perovskites. J. Am. Chem. Soc. 2016;138(8):2649–2655. doi: 10.1021/jacs.5b11740. [DOI] [PubMed] [Google Scholar]
- 43.Smith IC, et al. A layered hybrid perovskite solar-cell absorber with enhanced moisture stability. Angew. Chem. Int. Ed. 2014;53(42):11232–11235. doi: 10.1002/anie.201406466. [DOI] [PubMed] [Google Scholar]
- 44.Hu J, et al. First-principles calculations of graphene-coated CH3NH3PbI3 toward stable perovskite solar cells in humid environments. ACS Appl. Nano Mater. 2020;3(8):7704–7712. doi: 10.1021/acsanm.0c01301. [DOI] [Google Scholar]
- 45.Soe CMM, et al. Structural and thermodynamic limits of layer thickness in 2D halide perovskites. Proc. Natl. Acad. Sci. 2019;116(1):58–66. doi: 10.1073/pnas.1811006115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang L, et al. Multiple Fano resonances excitation on all-dielectric nanohole arrays metasurfaces. Opt. Express. 2021;29(10):14905–14916. doi: 10.1364/OE.419941. [DOI] [PubMed] [Google Scholar]
- 47.Guo L, et al. Toroidal dipole bound states in the continuum in all-dielectric metasurface for high-performance refractive index and temperature sensing. Appl. Surf. Sci. 2023;615:156408. doi: 10.1016/j.apsusc.2023.156408. [DOI] [Google Scholar]
- 48.Zhou C, et al. Optical radiation manipulation of Si–Ge2Sb 2 Te 5 hybrid metasurfaces. Opt. Express. 2020;28(7):9690–9701. doi: 10.1364/OE.389968. [DOI] [PubMed] [Google Scholar]
- 49.Yang, F., et al. Bending sensing based on quasi bound states in the continuum in flexible terahertz metasurface.Adv. Opt. Mater. 2300909.
- 50.Wang L, et al. Tuning symmetry-protected quasi bound state in the continuum using terahertz meta-atoms of rotational and reflectional symmetry. Opt. Express. 2022;30(13):23631–23639. doi: 10.1364/OE.454739. [DOI] [PubMed] [Google Scholar]
- 51.Cai Y, et al. Symmetric metasurface with dual band polarization-independent high-Q resonances governed by symmetry-protected BIC. Opt. Lett. 2021;46(16):4049–4052. doi: 10.1364/OL.432117. [DOI] [PubMed] [Google Scholar]
- 52.Liu X, et al. Dual band metamaterial perfect absorber based on Mie resonances. Appl. Phys. Lett. 2016;109(6):062902. doi: 10.1063/1.4960802. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.