The Novel Hybrid Lattice Structure Approach Fabricated by Laser Powder Bed Fusion and Mechanical Properties Comparison

Abstract

Aluminum-based cellular structures are gaining a huge traction in several applications, including lightweight aircraft, military equipment, and heat exchangers. With additive manufacturing, the fabrication of complex periodic cellular structures with any unit cell form, size, and volume fraction has become a lot easier, allowing for more investment, research, and attention from both academia and industry. The aim of the research was to assess the manufacturability and performance of AlSi10Mg periodic cellular structures generated using the laser powder bed fusion process. Re-entrant and triply periodic and minimum surface (TPMS) gyroid cells were hybridized into a single cellular structure having identical volume fraction. Because of distinct mechanical properties of TPMS and re-entrant types, these cells were selected and assembled in various patterns to study their manufacturability, deformation behavior, energy absorption, and compressive strength. This work demonstrates good geometric agreement between the manufactured hybrid lattice structures and computer-aided design models. Hybridized structures with several repeated layers of TPMS gyroid and re-entrant cells can result in superior compressive strength and energy absorption than those with only few large layers.

Introduction

Lightweight cellular materials with interdispersed voids can provide high-strength, low-density, effective impact absorption, and thermal and acoustic insulation, making them highly suitable for advanced and multifunctional engineering products for automobile, aerospace, and medical industries.^1–4 The arrangement of cells in cellular structures can be stochastic or periodic. Although stochastic porous structures have a random distribution of open or closed voids, periodic cellular structures have regular and organized cell shapes that provide greater strength, stiffness, energy absorption, and high heat transmission.^4–6

The introduction of the laser powder bed fusion (LPBF) technology, an additive manufacturing (AM) process, has enabled the creation of fully dense cellular metal structures much easier than time- and cost-consuming conventional processes, such as casting.⁷ Complex cellular structures with enhanced functionality may be constructed using AM's infinite design flexibility to satisfy advanced needs and applications.⁸ AM can create three-dimensional high-resolution objects of nearly any shape from computer-aided design (CAD) models, and it has been widely used in recent years to build cellular structures with regulated internal structures and sophisticated exterior shapes.^9–11

Aluminum alloy cellular structures are widely used in a variety of applications, including automobile body constructions, highway sound insulation, heat exchangers, and light weight conformal pressure tanks.¹² Given their good damage tolerance, energy-absorbing capability, and cost-effective performance, Al alloy materials can offer 10 times strength and 50% less weight than parts made of steel.¹³

Some researchers investigated the manufacturability and mechanical properties of cellular structures made of aluminum alloys of various types and cell topologies,¹⁴ manufactured LPBF AlSi10Mg lattice structures with vertical and inclined strut boundaries to compare their microstructured heterogeneities in terms of porosities. The microstructure and compression behavior of LPBF AlSi10Mg diamond¹⁵ and gyroid^16,17 structures with varying volume fractions (5–20%) and unit cell sizes (3–7 mm) have also been investigated. They utilized the Gibson–Ashby model to analyze the compression strength, which was found decreasing with the unit cell size and increasing with the volume fraction. Zhou et al¹⁸ developed a 60% lighter AlSi10Mg phase change thermal controller for the spacecraft using an LPBF process, and found their thermal capacity to enhance by 50% than the traditional ones of the same volume,¹⁹ developed a BCC and BCCZ type sandwich panels using LPBF technique and AlSi10Mg material.

The objective was to evaluate the impact of geometrical imperfections both numerically and experimentally on the overall mechanical performance and energy absorption capability. Ngnekou et al²⁰ constructed LPBF AlSi10Mg specimens at 0° and 90° to assess the effect of microstructural anisotropy on fatigue characteristics. Using a Kitagawa type diagram, the authors discovered that the defect size is a major contributor of fatigue damage start. Meyer et al²¹ recently examined the fabrication of inclined LPBF AlSI10Mg filigree lattice struts at 45°–30°. They discovered that the inclination angles of specified struts have a significant impact on the overall mechanical performance of lattice materials. Likewise, Li et al²² investigated the impact of various construction angles (0°, 15°, 30°, 45°, 60°, 75°, and 90°) on the microstructure and mechanical characteristics of AlSi10Mg alloys. The construction angle was discovered to influence the melt-pool and grain morphology in the strut region. As a consequence, samples made at 45° had the maximum hardness, whereas those made at 60° had excellent strength and flexibility.

A chiral is a biomaterial-inspired cellular structure that cannot be superimposed on its mirror counterpart. The unique feature of a chiral structure is its stiff node that rotates during the in-plane compression force, allowing its ligaments to flex. Because of their diverse mechanical behavior, chiral metamaterials display negative Poisson's ratio, negative stiffness, energy dissipation, and acoustic absorption.^23–25 As previously stated, chiral structures are also damaged by process-induced defects such as subsurface porosity and semi-attached partly fused powder particles of the LPBF method, which contribute considerably in their poor mechanical response.²⁶

Recently many research investigations have placed major emphasis on improving lattice properties in terms of specific strength, stiffness, and energy absorption.^19,27,28 Because each cell has a different behavior depending on its design, hybrid arrangements can dramatically change how well a cell performs in terms of strength and stiffness. By adjusting, combining, or modifying their architecture, metamaterials with hybrid arrangement having superior physical and mechanical properties may be created.^29–31 For example, combining several unit cell layouts has resulted in improved mechanical performance³² and higher energy absorption.³³ By creating a hybrid lattice structure from the octet and rhombic dodecahedron cells,³⁴ we were able to combine the advantages of stretching- and bending-dominated characteristics. Their experimental and analytical findings demonstrated a superior strength and energy absorption capabilities in hybrid lattice structures.

Harris et al³⁵ introduced a lattice wall to a honeycomb structure to form a hybridized geometry. They found the hybrid lattice-walled honeycomb structure superior in specific strength, specific energy absorption, and energy absorption efficiency than previously reported AM lattices. Inspired by natural biology,³⁶ we used computational and experimental methods to examine and evaluate load bearing capabilities and deformation modes using several lattice forms (BCC, FCC, BFCC, and BFVC). Numerous additional researches have also shown that hybrid lattice structures demonstrate greater elastic rigidity and compressive strength compared with the majority of existing cellular forms.^37,38

Both triply periodic and minimum surface (TPMS) and chiral structures have demonstrated excellent mechanical performance and manufacturability in prior investigations on the LPBF.^3,12,39 This study aims to develop a novel method to fabricate periodic cellular lattice structures using two distinct cell types. By mixing the auxetic re-entrant and TPMS gyroid lattice forms with varying volume percentages, a hybrid structure was created to improve the mechanical and energy absorption capacities. Five distinct test samples were designed and constructed to assess the overall compression strength of their hybrid configuration design. Various physical and mechanical characteristics were observed and presented to maximize the stiffness/strength to weight ratio.

The Experimental

Lattice design and manufacturing

In this work, hybrid lattice geometries were created by combining re-entrant and TPMS gyroid lattice structures. The outstanding performance of each lattice type has already been documented in several studies; the goal here was to build their hybrid form to profit from their combined advantage, as well as to observe their design feasibility and create the appropriate mechanical response.

This study involves the manufacturing and compression testing stages of two conventional (m1, m2) and three hybrid (m3, m4, m5) lattice configurations. For the performance comparison between standard lattice types and the proposed new hybrid lattice forms, samples m1 and m2 representing the standard re-entrant honeycomb and TPMS gyroid structures, respectively, were used. Two standard CAD modules were used for the creation of lattice shapes. Although the re-entrant honeycomb structure was constructed using Catia V5^©, the TPMS gyroid lattice structure was created using the ANSYS Spaceclaim^© package. For hybrid lattice forms, ANSYS was used to create a mix of re-entrant and TPMS forms based on their respective volume fractions.

To scale and refine the *.stl files for the analysis of all the lattice structures, Magics software (Materialise, Belgium) was adopted. At least three copies of each sample type with overall dimensions of 20 × 20 × 60 mm³ were made, and an average value was chosen. The studied lattice structures were built on the EOSINT-M290 (EOS GmbH, Germany), with AlSi10Mg feedstock material, which is lightweight and features high mechanical strength. Based on preliminary optimization, the laser processing parameters were chosen, as given in Table 1.

Table 1.

Laser Powder Bed Fusion Production Parameters for AlSi10Mg

Laser power	Scan speed	Hatch distance	Layer thickness
370 W	1300 mm/s	0.19 mm	30 μm

Preheat temperature	Laser intensity	Scanning strategy
35°C	49.93 J/mm3	x-rotation

Laser type	Atmosphere	Global beam offset	Part beam offset
Ytterbium fiber	Argon	0.1 mm	0.02 mm

The total volume for each suggested lattice type was maintained at 10.95 cm³. As previously stated, models m1 and m2 were exclusively made up of re-entrant honeycomb and TPMS gyroid unit cells, respectively. Model m3 was composed of re-entrant cells, which accounted for ∼65% of the total volume, with the remainder occupied by the TPMS gyroid lattice type. The TPMS gyroid filled the core region, whereas the re-entrant occupied the outside surface.

Model m4 was created with their alternative cell layouts to achieve an equal percentage of the two lattice types, as indicated in Table 1. In a total of 10.95 cm³, ∼46% of re-entrant and 54% of TPMS gyroid total cell volume was presented. Model m5 was likewise constructed with frequent intervals of both lattice types, resulting in 79% re-entrant volume and 21% TPMS gyroid volume, with the re-entrant area remaining somewhat thicker than the TPMS gyroid.

To keep the total volume of all lattice structure to 10.95 cm³, the gyroid wall thickness was altered for each hybrid case. Table 2 describes the design parameters of the lattice models chosen in this study.

Table 2.

Design Parameters for the Proposed Lattice Structures

	m1	m2	m3	m4	m5
Total volume	10.95 cm3	10.95 cm3	10.95 cm3	10.95 cm3	10.95 cm3
Re-entrant wall thickness	0.5 mm	—	0.5 mm	0.5 mm	0.5 mm
Gyroid wall thickness	—	0.52 mm	0.43 mm	0.6 mm	0.24 mm
Gyroid length	0.65 mm	—	0.65 mm	0.65 mm	0.65 mm
Re-entrant: Re	Re:%100	Re:%0	Re:%65	Re:%46	Re:%79
TPMS gyroid: Gy	Gy:%0	Gy:%100	Gy:%35	Gy:%54	Gy:%21

TPMS, triply periodic and minimum surface.

LPBF production with AlSi10Mg (Table 3), compression tests

Table 3.

Material Properties of AlSi10Mg^38,40

Density (ISO3369)	Yield strength (vert.) ISO 6892-1	Yield strength (hor.) ISO 6892-1
≥2.67 g/cm3	230 MPa	270 MPa

Tensile strength (vert.) ISO 6892-1	Tensile strength (hor.) ISO 6892-1	Particle size distribution
460 MPa	450 MPa	25–70 μm

Average defect percentage as manufactured	Elongation at break (vert.) ISO 6892-1	Elongation at break (hor.) ISO 6892-1
%0.04	%6.3	%10.2

According to the standard of compression tests for porous and cellular metals (ISO 13314:2011), compression tests were performed using a universal test machine (ALSA 100 kN^®, Turkey) with a 100 kN load cell for all lattice types. Each test was performed with three replications at a fixed deformation rate of 1 mm/min. A video camera was simultaneously utilized to capture the deformation behavior of samples during the compression test. Zeiss Axio Lab A1 optical microscope (OM) was used to take the images. The images from the scanning electron microscopy (SEM) were taken on a Hitachi SU3500 T2 device.

Results and Discussion

Analysis of built structures

The designed and the as-built lattice models, re-entrant and TPMS, are given in Tables 4 and 5, demonstrating high repeatability of LPBF lattices from the CAD geometry without visible faults or broken cells. The fabricated structures demonstrated a continuous network through beam-like struts and the intertwined voids. A visual inspection of the hybrid lattices reveals no flaws or broken cells inside the lattice structures, demonstrating the LPBF ability to produce complex AlSi10Mg cellular lattice components with a wide range of unit cell topology, size, form, and pattern.

Table 4.

Lattice Models with Their Different Design Arrangements

CAD, computer-aided design.

Table 5.

Re-Entrant and Triply Periodic and Minimum Surface Cell Images and Measurements

LPBF, laser powder bed fusion.

Owing to the high heat induction during the scanning process, re-entrant cell geometry can be seen partly welding to the strut of the adjacent cell. Given the small gap between the vertical struts, their welding owing to the excessive melting is a common LPBF phenomenon. On the contrary, smooth topology of the TPMS model with designed porosity, their structures appeared regular. Furthermore, the produced lattices had somewhat larger strut dimensions than the design CAD model. Semi-attached partly molten particles on strut surfaces, surface roughness, and the stair-stepped effect are all responsible for such dimensional mismatches.

All the other design parameters for hybrid or standard lattice forms remain the same, with the exception of gyroid wall thickness. The standard wall thickness for the gyroid model, m2, was 0.52 mm. The wall thickness for the gyroid lattice changes depending on the arrangement of the gyroid and re-entrant lattices, such that the wall thickness grows with the total volume fraction of gyroid inside the designed lattice structure.

Longer struts of re-entrant honeycomb lattices are known to be undesirable owing to poor manufacturability.¹⁵ During the LPBF process, the long overhang region slags, causing the lattice to distort. The incorporation of gyroid TPMS can offer much needed stability to re-entrant honeycombs, particularly in the middle. Moreover, the stress concentration can be high in re-entrant structures owing to swift change in strut angles. On the contrary, TPMS gyroid cells are self-supporting that enable their fabrication with increasingly bigger cell sizes. As a result, the inclusion of TPMS gyroids in the midsection of models m4 and m5 is expected to stabilize the hybrid lattice structure.

Strut microstructure

Images of the strut cross-section were acquired using an OM in both the vertical and horizontal planes, as given in Table 6. Although the arc-shaped cross section of the melt pool on the vertical plane is more than the layer thickness, the length of its ellipsoidal form on the horizontal plane is considerably longer than the laser spot size. Melt pools were discovered partially overlapping in both planes because of the high incident energy density, inducing the previously solidified region to remelt, resulting in a dense strut.

Table 6.

Scan Electron Microscopy Images of Re-Entrant, Triply Periodic and Minimum Surface Cells and Hybrid Zone

SEM images reveal a nearly dense strut geometry with fewer nonhomogeneously dispersed spherical and irregular pores. Micropores in LPBF components can occur owing to the poor selection of laser processing parameters. Furthermore, investigations have shown that residual oxygen can promote aluminum oxidation, resulting in the development of cracks and pores across the microstructure of LPBF AlSi10Mg alloys.^41,42 The core of the melt pool exhibits an extremely fine cellular dendritic microstructure composed of a fibrous Si phase network inside a cellular cells/dendrites of α-Al matrix. The melt pool boundary area, on the contrary, was discovered to contain a coarser cellular/dendritic microstructure.

Mechanical properties

The cell topology of auxetic lattice structures is quite different from those of TPMS gyroid. The unique advantages of these two lattice types have been covered in many previous studies, making them one of the most sought after research topics. However, the comparison between the two is seldom presented. As a result, this study was undertaken to evaluate and compare their respective behavior. During the compression test process, video recordings were made for the purpose of visually determining the instantaneous deformation rates of lattice forms depending on time and pressure parameters. Photographs taken at intervals of 0, 10, 15, 20, and 25 mm are provided in Table 7, and the deformation stages between lattice forms were visually tabulated.

Table 7.

Compression Test Stages at 0, 10, 15, 20, and 25 mm of m1–m2–m3–m4–m5 Lattice Models

Compared with the other studies,^16,43 the height of the present model is relatively high, causing a significant variation in their overall deformation behavior. The typical auxetic behavior was not observed in this study. The re-entrant lattice geometry, model m1, can be seen bending to the side owing to the collapse of the top and middle vertical strut boundaries. The vertical strut toward the top bends to the right, whereas those in the center bend to the left, causing the entire lattice structure to bend to the left. As the upper layers densified, additional strut boundaries on the bottom side bend to the left, causing the structure to bend even further to the left. Bending continues until the structure begins to disengage from the weekly bonded vertical strut boundaries on both the top and bottom.

The TPMS gyroid form demonstrated distinct deformation behavior compared with the re-entrant auxetic structure. The cells seemed to break off from the bottom left, most likely as a result of brittle fracture of the cell walls, as evidenced by crack propagation across the lattice. The fracture is most likely the result of an existing fault, such as an interior pore or surface imperfection. The crack path of the individual cell was hard to determine because they broke into multiple pieces. Overall, fracture propagation in the TPMS gyroid was seen to follow a diagonal pattern, resulting in lattice structure bending to the crack side. The creation of a diagonal shear band 45° to the loading direction has previously been seen in various LPBF lattice types.^25,28,29

In hybrid lattice geometries, the deformation behavior was a combination of both lattice types. In the case of model m3, the lattice deformation was initiated by the displacement of the vertical strut boundaries of the re-entrant lattice section, whereas the TPMS gyroid section was unaffected. The top and bottom re-entrant sections can be observed deforming into a dense structure, whereas the TPMS part remained undeformed until the compression test was completed. The densified re-entrant section, together with the more stable TPMS gyroid structure, was found to be less stable than model m2, exhibiting early deformation during the compression test.

The deformation behavior of model m4, which consists of repeating layered cells of both lattice types, was also discovered to first begin in the re-entrant structure, followed by their total densification. Later, similar to model m2, the gyroid section can be observed ripping diagonally into many pieces. However, unlike model m2, the deformation was rapid, indicating low compression stability similar to model m3.

Model m5 is made up of even more repeating units of two lattice types, resulting in exceedingly thin individual layer thicknesses compared with earlier hybrid structures. Its deformation behavior, as viewed through the camera, is roughly identical to that of model m4, but less deforming. Model m5 appeared to resist compression stress as compared with models m3 and m4, which deformed when the compression stage was just 10 mm. Furthermore, when compared with model m2, model m5 maintained a practically undeformed form at 15 mm of the compression test stage, in contrast to the excessively bending and diagonally shredded m2 model. Model m5 deformed similarly to model m4 at 20 mm of the compression stage, with a re-entrant cell layer deforming first, leading the structure to bend to the right. The re-entrant layer toward the bottom collapsed as the layer densified, giving support to other neighboring layers, causing the structure to bend to the left. Model m5 had a more stable deformation behavior than the other proposed geometries, indicating that it could sustain compression better than the others.

Figure 1 provides the compressive stress–strain curves of the deformed LPBF lattice structures obtained from the compression testing. The compressive stress–strain curve of all lattice structures showed multiple collapsed zones, beginning with an elastic region and progressing through a long plateau region to an onset densification region before the structure is fully crushed.

FIG. 1.

(a and b) Experimental stress–strain response of cellular core in compression.

The strut walls begin to flex during the elastic region. As the compressive force progresses to the plastic zone, struts begin to fail because of shearing and breaking at a 45° angle to the applied load direction. Because of the layered topology of cells in a lattice structure, individual deformation and fracture behavior cause stress variations during a plastic region. The bulk of the fracture occurred at the strut joints, where compressive forces caused the strut to rotate locally. Although strut deformations cause strength loss during the collapse, fractured cells resist the applied load, producing a small increase in stress levels. As all the cells collapse, the structure reaches a densification limit, where it behaves similar to the dense structure. A modest strain causes a very large increase in stress levels at this point.

The stress–strain curve for the re-entrant lattice structure can be seen collapsing after attaining a low stress values of ∼23 MPa. As the first layer of re-entrant cells collapse, the stress level drops by 97.5% to an extremely low value of 0.58 MPa. The stress fluctuation keeps on changing repeatedly within these two extreme values until the densification strain of 33% is reached. On the contrary, the TPMS gyroid lattice structure exhibits a distinctive deformation behavior with 45° shear band failure. After an elastic stage, the stress level reached was ∼102 MPa, which is maximum among the examined structure. When the first layer collapses, the stress drops to 64 MPa, showing a drop of only 37% in stress values. The densification strain for the TPMS gyroid lattice structure was observed at 62%.

As observed from Table 7, only re-entrant cells of model m3 collapsed, whereas the TPMS gyroid cells at the center remain largely unaffected until the onset of structural densification observed at the compression test stage of 25 mm. Similar is the case for model m4 where only re-entrant cells were found to collapse more than the TPMS gyroid cells, revealing the weak resistance of re-entrant cells to the applied load. Although the peak stress during the compression of model m4 remained lower than that of the TPMS gyroid, the stress level continue to rise owing to the presence of TPMS cells within the lattice structure. In contrast to models m3 and m4, the compressive stress–strain curves of hybrid lattice structure m5 displayed a mix of both re-entrant and TPMS gyroid deformation behavior (Fig. 1). Although the stress level after the elastic region remained lower owing to the weaker re-entrant cells, the repeated embedding of the TPMS cells raises the maximum stress level. Their presence also delayed the densification stage to almost 60%, making the structure to resist external loading more than the other hybrid structures and model m1.

Energy absorption

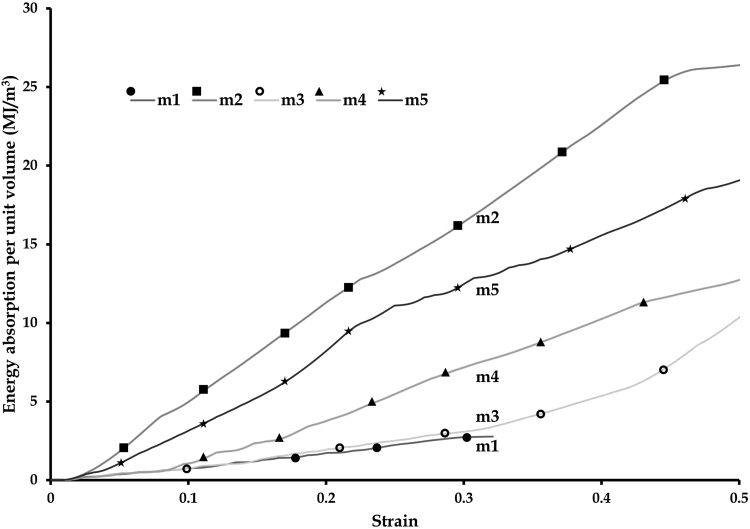
The propensity of lattice structures to absorb energy provides useful insight for areas involving impact and energy absorbing applications. The area underneath the compressive stress–strain curves was used to compute the energy absorption capabilities of all lattice structures. The total cumulative values of calculated energy per unit volume (Wv) up to the densification state of model, m1, and 50% strain for all the other models are given in Table 8. The energy absorption by the re-entrant model m1 was the least, whereas that of model m2 was the largest. More uniform distribution of TPMS gyroid cells leads to more efficient energy absorption across the hybrid models.

Table 8.

Energy Absorption Properties of Lattice Structures

Lattice models	Energy absorption per unit volume (MJ/m3)
Re-entrant, m1	2.77
TPMS gyroid, m2	26.39
m3	10.34
m4	12.74
m5	19.07

After attaining the peak of compression stress in model m1, the structure enters the plateau domain with a low level of plateau stress against the applied load, causing lower energy absorption. The structure enters a densification stage before the 50% compression strain, such that the total energy absorbed at 30% strain was ∼2.77 MJ/m³. In contrast, the TPMS gyroid lattice structure displayed the maximum capability to absorb energy (26.39 MJ/m³) among all the lattice models. The increased absorbed energy was closely tied to the deformation behavior of the TPMS gyroid structure, which demonstrated quite a high resistance to the applied load, as given in Figure 1.

When it comes to hybrid lattice structures with the same overall volume fraction, the positioning and the arrangement of TPMS gyroid lattice cells played a major role in advancing the deformation characteristics of the lattice model. Figure 2 indicates that the more repeated TPMS cell layers between the re-entrant cells, the greater the rise in the energy absorption behavior of hybrid models. The total cumulative energy absorbed for models m3, m4, and m5 were found to be 10.34, 12.74, and 19.07 MJ/m³, respectively.

FIG. 2.

Cumulative energy absorption per unit volume vs. compressive strain curves of different models.

Conclusion

This study demonstrated the effective 3D printing of hybrid lattice structures. Under compression loads, the mechanical performance of all proposed hybrid lattice structures was compared with that of uniform re-entrant and TPMS gyroid lattice structures of the same volume. The experimental testing conducted in this study led to the following results.

• The OM and SEM images illustrate that LPBF technique is capable of producing hybrid lattice structures with high repeatability in AlSi10Mg. Moreover, the surface morphology of the created geometries demonstrates that semi-attached powder particles, structural porosity, and a step-stair effect can substantially change strut size from the predesigned CAD model.

• The experimental compression results reveal that the TPMS gyroid lattice structure deforms distinctly from the re-entrant type under compressive stresses. The TPMS gyroid lattice structure collapsed diagonally at roughly 45°, whereas the re-entrant exhibited strut bending under increasing compressive load. The compressive stress fluctuation in the plateau area was notably different from that of the re-entrant lattice in the TPMS gyroid lattice structure.

• The model m5 with homogeneously repeated re-entrant and TPMS gyroid layers displayed the highest energy absorption of all the proposed hybrid structures. The compression stress–strain curve demonstrates its different deformation features from the other hybrid types, with collapsing behavior of both re-entrant and TPMS gyroid lattice structures. Model m2 with uniform TPMS gyroid topology, on the contrary, continues to have the highest stress reach and the highest energy absorption among all the models, whereas re-entrant model m1 has the lowest of the two values.

Authors' Contributions

H.M.K.: The idea of hybrid use of lattice forms, abstract, introduction, result and discussion, conclusion sections authorship; C.İ.Ç.: Introduction, design, LPBF production sections authorship, design and table studies; M.E.B.: Gyroid form creation and compression tests, graphic work.

Author Disclosure Statement

The authors whose names are listed immediately below certify that they have no affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers' bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or nonfinancial interest (such as personal or professional relationships, affiliations, knowledge, or beliefs) in the subject matter or materials discussed in this article.

Funding Information

This study was prepared within the scope of “ALUTEAM-Aluminum Test Training and Research Center,” carried out by Fatih Sultan Mehmet Vakif University.