Generalized vehicle routing problem: Contemporary trends and research directions

Abstract

Generalized Vehicle Routing Problem (GVRP) is a challenging operational research problem which has been widely studied for nearly two decades. In this problem, it is assumed that graph nodes are grouped into a number of clusters, and serving any node of a cluster eliminates the need to visit the other nodes of that cluster. The general objective of this problem is to find the set of nodes to visit and determine the service sequence to minimize the total traveling cost. In addition to these general conditions, GVRP can be formulated with different assumptions and constraints to practically create different sub-types and variants. This paper aims to provide a comprehensive survey of the GVRP literature and explore its various dimensions. It first encompasses the definition of GVRP, similar problems, mathematical models, classification of different variants and solution methods developed for GVRPs, and practical implications. Finally, some useful suggestions are discussed to extend the problem. For this review study, Google Scholar, Scopus, Science Direct, Emerald, Springer, and Elsevier databases were searched for keywords, and 160 potential articles were extracted, and eventually, 45 articles were judged to be relevant.

1. Introduction

Vehicle Routing Problem (VRP) is one of the most widely discussed and studied problems in the field of logistics and transportation (Su et al., 2021; Figueroa–Garcia et al., 2022). This problem concerns the challenge of assigning customers to vehicles and also determines the sequence in which customers must be visited so that a predefined objective function is optimized [1]. VRP was first introduced by Dantzig and Ramser [2], and since then researchers have introduced many variants of this problem. Several classifications of VRPs have been proposed by Toth and Vigo [3], Cordeau and Laporte [4], and Golden, Raghavan and Wasil [5]. Indeed, there are many different classes of VRP, which differ in terms of fleet type and characteristics, fleet mix, cargo type, travel time, number of depots, organizational rules, service request type, and objective function [6].

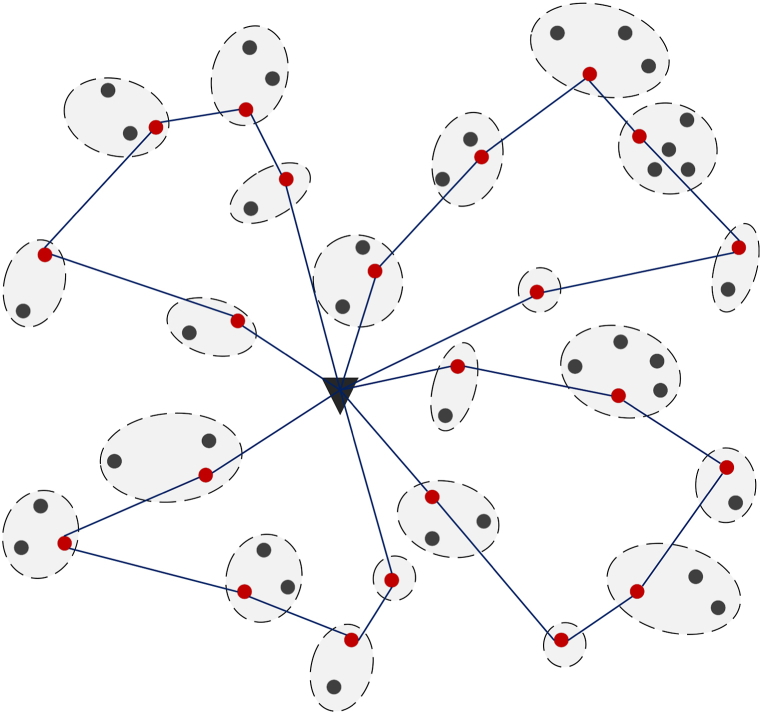
Similar to the Traveling Salesman Problem (TSP), classic VRP assumes that all vertices of the graph must be visited or in other words, all customers must be served by vehicles. Several variants of VRP have relaxed or eliminated this assumption, making it optional to visit all vertices. As shown in Fig. 1, GVRP, VRPP, School Bus Routing Problem (SBRP), and Multi-vehicle Covering Tour Problem (m-CTP) belong to this group of VRPs. In these problems, the classic assumption of needing to serve all customers is slightly changed. These changes are briefly discussed below.

Fig. 1.

Variants of VRP without any obligation to visit all vertices.

One of the variants of VRP where it is not mandatory to visit all vertices is the Vehicle Routing Problem with Profit (VRPP). In this problem, visiting each vertex of the graph generates a certain amount of profit. In other words, visiting each vertex has a certain score and the scores earned by visiting different vertices will be summed up to a total score, which determines the profit. However, this process is also subject to certain constraints like maximum available time, maximum travel distance, etc. [7]. Some refer to this type of VRP as “prize collection” problem [8]. These problems can be divided into two groups based on the number of vehicles: (i) the problems wherein there is only one vehicle, which are called Orienteering Problems; (ii) the problems with more than one vehicle, which are known as Team Orienteering Problems. More detailed descriptions and analyses of these problems can be found in Gunawan, Lau and Vansteenwegen [9] and Vansteenwegen, Souffriau and Van Oudheusden [7].

Another variant of VRP where it is not required to visit all vertices is m-CTP [10]. In this problem, there are a number of nodes (|V|) that vehicles can potentially visit and a number of nodes (|W|) that need to be served. Each node $w\in W$ is associated (linked) with one or more nodes $v\in$ V. The purpose of this problem is to find m tours with the lowest cost whereby all nodes in set W are covered by visiting the nodes in set V. In other words, the goal is to satisfy the demand of each point in set W by making deliveries to one of its linked nodes such that the total cost is minimized [10].

Another problem where there is no need to visit all vertices is the SBRP (Perez et al., 2022). SBRP is a practical problem that concerns the challenge of offering low-cost but safe and reliable transportation services to schools. This problem was first explored by Newton and Thomas [11], but over the years, several different types of SBRP have been proposed and formulated. One of these is the Bus Stop Selection Problem, where the location of bus stops must be selected from among a number of potential nodes such that they can be easily and cheaply accessed. In some studies, this problem has been formulated with some additional constraints. This problem and its variants have been thoroughly discussed by Ellegood, Solomon, North and Campbell [12].

Generalized Vehicle Routing Problem (GVRP) is another type of VRP where it is not necessary to visit all customers [13]. In this problem, customers are clustered based on their nature, characteristics, condition, etc., and visiting one customer in a cluster eliminates the need to visit other customers in that cluster. In other words, visiting only one customer from a cluster satisfies the service constraint for that cluster. In this problem, all customers of each cluster have the same demand and all vehicles have capacity constraints. The objective function of this problem minimizes the distance/cost of visiting customers. A graphical representation of GVRP is illustrated in Fig. 2.

Fig. 2.

A graphical representation of GVRP.

Moreover, researchers have recently introduced a new type of VRP called the Selective Vehicle Routing Problem (SVRP) [14], which is very similar to GVRP but offers an even more generalized form of this problem. While GVRP is based on the assumption that clusters are mutually exclusive, SVRP makes no such assumption. Similar to GVRP, SVRP assumes that each cluster has to be visited only once. It also defines the demand of each cluster as the total demand of all vertices of that cluster. Therefore, in SVRP, there is no need to visit other nodes once the common nodes of clusters are visited. Despite being similar to GVRP, SVRP is certainly a new type of this problem. To the best of our knowledge, so far, this problem has been discussed in only two articles [14,15].

This paper is mainly focused on GVRP. To the best of our knowledge, the only study that briefly investigates GVRP has been a 2010 paper by Baldacci, Bartolini and Laporte [16], which has concentrated on applications and modeling approaches. Considering the multitude of articles published in this area since 2010, the literature can benefit from a new review study on the subject. Furthermore, as mentioned, no review study in this field has covered all aspects of the subject in detail, an issue that this paper aims to amend. Thus, this article attempts to cover all aspects of GVRP as comprehensively as possible, offer useful insights for the classification of previous works in the area, and illuminate the path for future research by highlighting under-studied and overlooked aspects.

For this review study, all articles that have cited the article where GVRP was originally introduced [13] were examined. Furthermore, Google Scholar, Scopus, Science Direct, Emerald, Springer, and Elsevier databases were searched for keywords “Generalized vehicle routing problem”, “GVRP”, “Selective Vehicle Routing Problem”, “Delivery Option” and “Roaming Delivery locations” to identify potentially relevant articles. This search revealed 151 potentially relevant articles, which were independently reviewed by at least two members of the research team. Disagreements between the two reviewers about the relevance or classification of articles were settled by a third reviewer. Ultimately, 41 of these 151 articles were judged to be relevant. The frequency of these publications by year is shown in Fig. 3.

Fig. 3.

Frequency of GVRP publications by year.

The identified articles were then reviewed and classified from the perspective of mathematical models, assumptions, solution methods, and practical applications. In the rest of this article, Section 2 presents the definition of GVRP and discusses the variety of approaches used to model this problem, Section 3 classifies the reviewed articles based on how they have modified the problem and their assumptions, Section 4 describes the variety of methods employed to solve the problem and also the data used in this area, Section 5 discusses the potential applications of GVRP, and finally, Section 6 concludes the paper and suggests some directions for future research.

2. Generalized vehicle routing problem

The GPRV is an extension of VRP that is defined as follows. Consider the directed graph $G=\left(N,A\right)$ where $A=\left\{\left(i,j\right)|i,j\in N;i\ne j\right\}$ is the set of arcs and $N=\left\{\mathrm{0,1,2},...,n\right\}$ is the set of vertices (nodes), with 0 denoting the depot. The cost of traversing each edge $\left(i,j\right)\in A$ is denoted by $c_{ij}$. Set $N$ is partitioned into a number of mutually exclusive nonempty subsets, such that $N_0=\left\{0\right\}$ only contains the depot and other vertices are placed in different clusters. In this problem, the demand of each cluster is equal to the demand of all customers in that cluster. Moreover, vehicles are assumed to have a limited capacity. With these assumptions, GVRP involves finding the set of shortest tours starting from and ending in the depot such that at least one customer from each cluster is visited and the total demand satisfied in each tour does not exceed the vehicle capacity. Since VRP is NP-Hard [17], GVRP will also be an NP-Hard problem, because it turns into classic VRP if there is only one vertex in each cluster.

GVRP was first introduced by Ghiani and Improta [13], who transformed it into a Capacitated Arc Routing Problem (CARP) so that it can be treated by arc routing algorithms. Since then, GVRP has been the subject of several studies, which have proposed various models and formulations for this problem. These include the polynomial formulation developed by Kara and Bektas [18], in which they defined some constraints for the amount of cargo that can be carried by each vehicle. In another work, Pop, Matei, Sitar and Chira [19] offered an Integer Programming (IP) model for GVRP. Bektaş, Erdoğan and Røpke [20] proposed and compared four new models for GVRP. The first model of Bektaş, Erdoğan and Røpke [20] is a single commodity model formulated by considering the flow between nodes. The second model is similar to the first model, except that it is based on the flow between clusters rather than nodes; a change that significantly reduces the number of variables. The third model takes a variable reduction approach based on the idea of removing the auxiliary variables used in vehicle capacity or route continuity constraints of GVRP so that the model is made exclusively of natural variables. However, while this approach significantly reduces the number of variables, it leads to an exponential increase in the number of constraints. Finally, the fourth model applies a formulation that is based on an undirected graph. This model has a variable tasked with counting the number of times each edge is visited, which can be greater than only if the edge is adjacent to the depot. After comparing these four formulations analytically and experimentally, Bektaş, Erdoğan and Røpke [20] reported that the fourth model provides far better results than the other models. In an article by Pop and Pop-Sitar [21], they presented an IP model for GVRP and a method to turn it into a classical vehicle routing problem. In another work, Pop, Kara and Marc [22] proposed two integer linear programming models developed with two different approaches. The first model, which uses a node-based approach, is somewhat similar to the model proposed by Kara and Bektas [18], but performs better in providing a lower bound for the problem. The second model utilizes a flow-based approach. These researchers also proposed some models for Generalized Traveling Salesman Problem (GTSP) and Generalized Multiple Traveling Salesman Problem (GMTSP) by using the flow-based approach and manipulating problem assumptions, and also developed a model for Capacitated Vehicle Routing Problem (CVRP) by adding constraints to these formulations. Hà, Bostel, Langevin and Rousseau [23] employed the first model of Bektaş, Erdoğan and Røpke [20] to develop a new formulation for GVRP. In this formulation, the number of vehicles is considered as a decision variable, and an integer variable is used to count the number of times each edge is visited.

Detailed information about the general models developed for GVRP is given in Table 1. This table provides a list of articles that have presented a mathematical model for the classical GVRP and the modeling approaches that they have employed for this purpose.

Table 1.

Modeling approaches.

Reference	Year	Modeling Approach
[18]	2003	Flow-based formulation
[19]	2010	Node-based formulation
[20]	2011	Single-commodity formulation,
		Compact single-commodity formulation,
		Directed formulation,
		Undirected formulation
[21]	2011	Node-based formulation
[22]	2012	Node-based formulation
		Flow-based formulation
[23]	2014	Flow-based formulation

3. Classification

The previous section provided a definition of GVRP and a short review of the modeling approaches used for this problem. In this section, the GVRP-related articles (those that were judged to be relevant according to the method described in Section 2 are classified based on their assumptions and the main features they have considered for the problem. Since the introduction of GVRP, researchers have extended and modified this problem in various ways. In the following, we provide a general classification of these extensions and modifications based on their key aspects. These extensions and modifications can be divided into seven classes based on what assumptions they have employed in their formulations: (i) Time windows, (ii) Split delivery, (iii) Pickup and delivery, (iv) Multi-level, (v) Stochastic, (vi) Flexible Fleet size, and (vii) Multi-objective. The frequency of research studies in each class is shown in Fig. 4. As the figure indicates, the most popular type of extension/modification in the GVRP literature is the use of time windows and stochastic variables. A closer examination of the formulations with time windows reveals that the most frequently discussed problem of this class is GVRP with Roaming Delivery Options. A description of these classes and the works published in each area is provided below.

Fig. 4.

Frequency of articles on different classes of GVRP.

3.1. Time windows

Incorporating time windows into the formulations of VRPs makes them more realistic. Researchers have proposed multiple types of time windows for VRPs, the most important of which are soft time windows and hard time windows. In hard time windows, customers must be strictly served within the defined time interval. In soft time windows, customers can be served outside the defined time interval but this imposes a penalty on the objective function. Soft and hard time windows have been incorporated into a wide range of GVRP formulations. The time window was first considered by Moccia, Cordeau and Laporte [24] in the GVRP. Raucq, Sörensen and Cattrysse [25] incorporated the notion of time windows into the waste collection problem. They defined a time window for each customer and formulated the objective function as the minimization of the total duration, which consists of transport times (time needed to move between nodes), service times, waiting times, and handling time in the depot. Nguyê~ n, Bektaş, Cherrett, McLeod, Allen, Bates, Piotrowska, Piecyk, Friday and Wise [26] considered the notion of time windows in the problem of delivery of postal packages. In this article, it was assumed that the postman must park the vehicle near the delivery point and walk a distance before delivering a package, and therefore it is necessary to pick one of the parking spots from among available options. Los, Spaan and Negenborn [27] formulated a model for the pickup and delivery problem with multiple locations. This model optimally selects one pickup point and one delivery point from a range of customer locations according to the defined time window.

After the introduction of time windows to GVRP, many researchers tried to expand the scope of GVRPs by adding time windows of different forms to their formulations. Some researchers proposed the idea that delivery options may change over time. The idea that delivery locations may vary with time was first introduced by Reyes, Savelsbergh and Toriello [28]. In their model, the customer's vehicle parks in different locations based on a predefined travel itinerary and the ordered goods must be delivered to one of these locations. Since the customer remains in each location only for a certain period of time and the location gets useless once the customer moves away, the time window of this problem is of hard type. In this problem, parking locations can be considered as a cluster, from which one location must be selected for delivery according to the time window. The introduction of this idea led to the emergence of a new family of VRPs called the Vehicle Routing Problem with Roaming Delivery Locations (VRPRDL), which became a popular subject of research in this area. In a study by Ozbaygin, Karasan, Savelsbergh and Yaman [29], they proposed an IP model for cost minimization in VRPRDL. Sampaio, Kinable, Veelenturf and Van Woensel [30] introduced stochastic travel times to VRPRDL, turning it into a two-stage stochastic optimization problem. In this VRPRDL, the stochastic nature of travel times affects not only the vehicles but also the customer locations, making it extremely important to manage these times. He, Qi, Zhou and Su [31] developed the roaming delivery problem into the last mile delivery problem with stochastic travel times. To make the model more realistic, they considered how travel times can be affected by factors such as weather conditions and road congestion. Ozbaygin and Savelsbergh [32] developed a model for dynamic VRPRDL, where customers' travel itineraries may change over the planning horizon. They stated that various factors may change customers' itinerary. For example, a customer who has a meeting at work from 3 to 4 p.m. may want to return home immediately if the meeting is canceled. Thus, he will not be able to receive any package at the workplace after 3 p.m., a change that will make the delivery plan impossible to implement. In a study by Dumez, Lehuédé and Péton [33], they considered a VRPRDL where customers have certain preferences for receiving delivery at different locations with different time windows. In this problem, it was assumed that customers set a preference for each delivery option. They developed a mathematical Mixed-Integer Programming (MIP) model for this problem, where the objective function was to minimize the travel cost [34]. considered electronic vehicles in the VRPRDL and extended the GVRP. In this problem, the vehicles are allowed to recharge their batteries en-route.

3.2. Split delivery

In classic VRP, the demand of each customer will be delivered in one visit by one vehicle. VRP with split deliveries is an extension of classic VRP that lacks the aforementioned assumption. In other words, it assumes that the demand of each customer can be split into multiple parts, each of which can be delivered separately by different vehicles. Using this approach usually leads to better results in cases where customer demand is large or near the capacity of vehicles [35]. Moumou, Rhofir and Allaoui [36] introduced the notion of split deliveries to GVRP and formulated an IP model for this problem. In this model, customer demand can be delivered in different locations. In other words, demand can be split and delivered at different nodes of each cluster.

3.3. Pickup and delivery

In VRP with pickup and delivery, customers have two types of demand, one for picking up and the other for delivering goods. The delivery part of this operation may encounter several problems, one of which is that customers may not be present to receive the delivery [37]. Various solutions have been proposed to solve this problem. One of these solutions is to visit the customers in the time window they have specified. It might also be beneficial to set multiple locations for the pickup and delivery of goods. Furthermore, customers or distributors may give higher priority to the distribution and delivery of goods at certain locations or at certain times. Therefore, one can define a series of preferences for different options. Introducing such preferences to the operation will result in different service levels. The problem of pickup and delivery vehicle routing with different pickup and delivery options was the subject of a study by Los, Spaan and Negenborn [27]. In this study researchers considered a set of possible pickup and delivery nodes for each customer, thereby turning the said problem into a GVRP with pick-up and delivery, and then formulated an ILP model for the transformed problem. In this problem, it is necessary to select one point for delivery and one point for pickup from a set of locations available for each customer. They also considered the preferences of customers for different locations. To apply these preferences to the objective function, they defined a coefficient for converting customer dissatisfaction into a penalty term. Raucq, Sörensen and Cattrysse [25] added the notion of pickup and delivery to the waste collection problem. They assumed that waste management companies transfer empty waste containers from a number of depots to a number of industrial units. Once the containers are filled, the companies collect the containers and haul them back to the waste management depots. In this problem, it is necessary to select one point for pickup and one point for delivery from among the existing warehouses.

3.4. Multi-level GVRP

With the growing need for distribution and delivery of goods in large cities, multilevel distribution has become a more important part of transportation planning, logistics and supply chain management. One of the major types of multi-level distribution is the two-echelon distribution, where the goods coming from one or more main depots are delivered to customers after going through a network of satellite warehouses. In a study by Zhou, Baldacci, Vigo and Wang [38], they introduced the two-echelon format of GVRP for a multi-depot network. In this problem, routing at the first level determines how goods are transferred from depots to satellites, and routing at the second level determines how they are delivered from satellite to customers. Considering multiple delivery options for customers at the second level of this problem turns it into a GVRP. The objective function of the problem formulated in this study was the minimization of traveling cost, connection cost, and handling cost, where traveling cost and connection cost are the costs arising from distribution, and handling cost is the cost of unloading cargo at the first-level and loading cargo at the second-level.

3.5. Stochastic GVRP

A stochastic VRP is a VRP with a stochastic problem parameter. It is possible to consider three states for the stochastic parameters of this problem. The first state is the stochastic demand size, which means the demand size may change at the time of delivery. The second state is the stochastic customers, which means some orders may be canceled and some new orders may be placed in the course of delivery operation. The third state is the stochastic graph network. In this state, the travel time on some edges may be affected by factors like traffic congestion or part of the network may become temporarily or permanently unavailable because of incidents like a car crash or an earthquake.

One of the problems of interest to researchers in the field of stochastic routing is the Generalized Vehicle Routing Problem with Stochastic Demand (GVRPSD). GVRPSD can be described as a combination of GVRP and VRPSD. In this problem, the nodes are divided into a number of clusters whose demand is not known for certain. This problem was first introduced by Biesinger, Hu and Raidl [39]. In this problem, customer demand may be higher or lower than expected. If customer demand exceeds expectations, then the vehicle will run out of cargo before the tour ends and will have to return to the depot to restock. This restocking can be done in two ways. The first way, which is known as the standard restocking strategy, is to instruct the vehicle to return for restocking only after it runs out of cargo. The second way, which is known as the preventive restocking strategy, is to allow the vehicle to return for restocking before it runs out of cargo. Biesinger, Hu and Raidl [39] used the preventive strategy, stating that it tends to be more efficient in terms of travel time. The assumptions of Biesinger, Hu and Raidl [39] have also been taken into account in two other studies [40,41], which have attempted to achieve better solutions by using different solution methods. Sampaio, Kinable, Veelenturf and Van Woensel [30] formulated a model for a two-stage stochastic optimization problem. In this study, they considered travel times to be a stochastic function of factors like weather conditions, accidents, vehicle problems, etc., and modeled the problem with a stochastic approach. In another study, He, Qi, Zhou and Su [31] also considered travel times to be stochastic and formulated the problem as a two-stage stochastic model with the objective of minimizing travel time.

3.6. Flexible fleet size

In VRP with Flexible Fleet Size, the number of vehicles is not known in advance and instead is treated as a decision variable that can be altered for cost minimization purposes. In several articles, GVRP has been extended with this assumption. In one of these articles, Hà, Bostel, Langevin and Rousseau [23] explored this approach and developed a model for this problem. The model presented in this article is based on the model of Bektaş, Erdoğan and Røpke [20], except that it has defined the number of vehicles as a decision variable. The objective function of this model is the minimization of the cost of visiting the vertices of the graph. In this model, all vehicles are identical, forming a homogeneous fleet. Afsar, Prins and Santos [42] introduced a model for GVRP with a flexible fleet size for crisis logistics. This model is also for a homogeneous fleet consisting of vehicles of the same type. In this model, graph vertices, which researchers refer to as “active point”, are placed in different clusters, the demand of each cluster is the sum of the demands of all nodes within that cluster, and the objective is to satisfy the demand of every cluster through the shortest possible tour.

A summary of the characteristics of the reviewed articles is provided in Table 2. The characteristics outlined in this table include the year of publication, the class of the problem, the considered fleet mix, objective function, and problem constraints, whether the article provides a mathematical model, and general information about the solution method employed in the article. More detailed information about the solution methods is presented in the next section.

Table 2.

Problems Classification and characteristics of GVRP publications.

Reference	Year	Class	Fleet mix	Objective Function	Constraints	Mathematical model	Solution Approach
							Exact	Heuristic	Metaheuristic
[24]	2012	Time window	HO	C	Cap, TW, MTT				✓
[42]	2014	Flexible fleet size	HO	D	Cap		✓		✓
[23]	2014	Flexible fleet size	HO	C	Cap	✓	✓		✓
[39]	2015	Stochastic	HO	D	Cap			✓	✓
[40]	2016	Stochastic	C	C, ResC	Cap	✓	✓
[28]	2017	Time window	HO	TC	Cap, TW, MTT	✓		✓
[29]	2017	Time window	HO	TC	Cap, TW, MTT	✓	✓
[38]	2018	Multi-level	HO	TC, HC, CC	Cap, MTT			✓	✓
[41]	2018	Stochastic	HO	TC, ResC	Cap				✓
[27]	2018	Pickup and delivery, Time window	HO	TC, CD	Cap, TW	✓		✓	✓
[36]	2019	Split delivery	HO	D	Cap	✓		✓
[30]	2019	Time window, Stochastic	HO	TC, RecC	Cap, TW, MTT	✓		✓
[25]	2019	Pickup and delivery, Time window	HO	Du	Cap, TW	✓		✓
[26]	2019	Time window		Du	TW	✓
[32]	2019	Time window	HO	TC	Cap, CCap, TW, MTT		✓
[31]	2020	Time window, Stochastic	HO	Du, RecC	Cap, TW	✓		✓	✓
[33]	2021	Time window	HO	TC	Cap, CCap, TW, SL	✓			✓
[34]	2022	Time window	HO	D	Cap, TW, Ch	✓		✓	✓

Objectives [TC: Traveling Cost, D: Distance, Du: Duration, HC: Handling Cost, ResC: Restocking cost, RecC: Recourse Cost, GTC: Ground Transportation Cost, MTC: Maritime Transportation Cost, CD: Customer Dissatisfaction, P: Penalty for parcels not delivered, VFC: Vehicle Fixed Cost, CC: Connection Cost, Battery charge constraint].

Constraints [Cap: Capacity, CCap: Customer Capacity, TW: Time Windows, MTT: Maximum Travel Time, SL: Satisfaction Level, Ch: Charging constraint].

Fleet Mix [HO: Homogeneous].

4. Solution approaches

Researchers have proposed various methods for solving GVRPs. This section is focused on the articles in which the mathematical model has been treated through a solution method other than commercial solvers. These solution methods are divided into three categories: exact, heuristic, and metaheuristic methods. As shown in Fig. 5, metaheuristic methods have been more popular than other methods. Among the reviewed articles, twenty-four have utilized metaheuristic methods, twelve have employed heuristic methods, and eight have used exact methods to solve their problems. Furthermore, Fig. 5 clearly depicts that the tendency to choose metaheuristic methods has increased over the past years.

Fig. 5.

Frequency of the use of different solution methods in the GVRP literature.

In the following subsections, the reviewed articles have been discussed separately based on whether they have used exact, heuristic, or metaheuristic methods.

4.1. Exact methods for GVRP

In some articles, GVRP models have been treated with exact methods. Among these methods, branch-and-cut-based algorithms have been remarkably popular. For example, Bektaş, Erdoğan and Røpke [20] employed the branch-and-cut algorithm to solve their problems. However, before starting the branch-and-cut algorithm, they utilized the Large Neighborhood Search (LNS) algorithm to determine the upper bounds. This paper also introduced three new datasets for evaluating algorithms. Hà, Bostel, Langevin and Rousseau [23] used a branch-and-cut algorithm as well as a hybrid algorithm to treat GVRP with flexible fleet size and then used datasets of Bektaş, Erdoğan and Røpke [20] to test the algorithms. Bulhões, Ha, Martinelli and Vidal [43] also used the branch-and-cut algorithm to solve their model. Because of the absence of a suitable database, they conducted their evaluations with two datasets developed for classical CVRP and Prize Collection VRP [43,44]. Reihaneh and Ghoniem [45] added pricing to the branch-and-cut algorithm and developed a Branch, Cut and Price (BCP) algorithm to tackle their problem. These researchers also used the dataset of Bektaş, Erdoğan and Røpke [20] for their evaluations. The results of this study showed that the developed BCP algorithm somewhat complements the BC algorithm proposed by Bektaş, Erdoğan and Røpke [20], as the problems that are difficult to solve with the BC algorithm can be easily treated with the BCP algorithm and vice versa. In the article of Ozbaygin, Karasan, Savelsbergh and Yaman [29], they used the branch-and-price algorithm to solve their model. They used two sets of data to test the numerical results. The first is a modified set of Reyes, Savelsbergh and Toriello [28] and the second is a new dataset. In another study, Ozbaygin and Savelsbergh [32] designed an enhanced version of the branch-and-price method used in their previous study [29]. The data used in this second study were also derived from Ozbaygin, Karasan, Savelsbergh and Yaman [29].

Another group of articles that have used the exact solution methods includes the study of Afsar, Prins and Santos [42], where they utilized the column generation method to treat their model and used five datasets to test their algorithm. Out of these five datasets, four were derived from previous studies and one was developed by Afsar, Prins and Santos [42] specifically for their model. Biesinger, Hu and Raidl [40] used the L-shaped method to tackle GVRP with stochastic demands. In this paper, researchers added specific and general cuts to the algorithm and compared the results. They used the datasets of Bektaş, Erdoğan and Røpke [20] to test the algorithm. The results demonstrated that better results will be obtained by using specific and general cuts simultaneously rather than applying only specific cuts.

Detailed information about the articles that have used the exact solution methods to treat GVRPs is provided in Table 3. The information provided in this table includes the names of the authors, the year of publication, the problem class, the solution method, and the dataset used in the article.

Table 3.

Exact methods used to solve GVRP.

Reference	Year	Class	Method	Instances
[20]	2011		Branch-and-cut algorithm	New instances
[23]	2014	Flexible Fleet size	Branch-and-cut algorithm	Bektaş, Erdoğan and Røpke [20]
[42]	2014	Flexible Fleet size	Column generation	Pop, Zelina, Lupşe, Sitar and Chira [46], Araque, Kudva, Morin and Pekny [47], Solomon [48], Bektaş, Erdoğan and Røpke [20], New instances
[40]	2016	stochastic	L-shaped method	Bektaş, Erdoğan and Røpke [20]
[29]	2017	time window	Branch-and-price algorithm	Reyes, Savelsbergh and Toriello [28], New instances
[43]	2018		Branch-and-price algorithm	Modified instances of Augerat, Naddef, Belenguer, Benavent, Corberan and Rinaldi [49], Modified instances of Archetti, Bianchessi and Speranza [44]
[45]	2018		BCP algorithm	Bektaş, Erdoğan and Røpke [20]
[32]	2019	time window	Branch-and-price algorithm	Ozbaygin, Karasan, Savelsbergh and Yaman [29]

As shown in Table 3, a majority of articles that have used an exact solution method have used branch-and-price and/or branch-and-cut methods. Out of the eight articles that fall in this category, three have used the branch-and-price method, two have used the branch-and-cut method, and one has used a combination of these two methods.

4.2. Heuristic algorithms for GVRP

Researchers have also developed a variety of heuristic methods for solving GVRPs. In the study of Ghiani and Improta [13], they turned GVRP into a form of CARP and treated it with the heuristic algorithm called CARPET, which has been proposed by Hertz, Laporte and Mittaz [50] for arc routing problems. To test the numerical results, these researchers used the dataset of Araque, Kudva, Morin and Pekny [47], which consisted of 50 nodes divided into 25 clusters by the authors. Bautista, Fernández and Pereira [51] proposed two heuristic algorithms for the municipal waste collection problem: a savings-based algorithm and an algorithm based on the Nearest Neighbor (NN) algorithm. They introduced three local search operators to improve the solutions. Two of these operators can be used specifically for searching the intra-route space, and one of them can be used for searching both inter-route and intra-route spaces. While intra-route operators change the route of a single vehicle, inter-route operators try to create new solutions by changing customers or changing edges in a multi-tour route. Pop, Zelina, Lupşe, Sitar and Chira [46] tried several heuristic algorithms to tackle GVRP and created two algorithms based on the NN algorithm and the Clarke & Wright (CW) algorithm for this purpose. They also introduced four local search operators for improving the solutions and used the Local-Global approach to solve their problem. In another study, Horvat-Marc [52] introduced seven local search operators, two intra-route and five inter-route, for this problem. Biesinger, Hu and Raidl [39] used the farthest insertion algorithm to generate an initial solution, which was then hybridized with Variable Neighborhood Search (VNS) algorithm to treat the problem. Reyes, Savelsbergh and Toriello [28] employed a heuristic approach to solve VRPRDL. In their algorithm, an insertion strategy is used to create an initial solution, which is then improved with an improvement heuristic. This improvement algorithm uses three strategies: (i) Greedy destroy and greedy recreate, (ii) Randomized greedy destroy and randomized greedy recreate, and (iii) Random destroy and greedy recreate rule [34]. proposed an insertion-based heuristic algorithm to create an initial solution. In this algorithm, the nearest delivery location of each customer to the depot is determined. Then, among selected locations, the farthest location to the depot is considered for initializing the route. Then other locations are inserted according to the cheapest insertion rule.

Zhou, Baldacci, Vigo and Wang [38] developed a three-phase heuristic algorithm for solving a multi-level GVRP. In the first phase of this algorithm, a set of second-level routes is constructed; in the second phase, the created routes are improved with delivery options taken into account; and finally, in the third phase, the second-level routes are determined according to the routes built for the first level.

Researchers have also developed various heuristic algorithms for solving other types of GVRP. Moumou, Rhofir and Allaoui [36] proposed a heuristic algorithm for GVRP with split delivery and used the dataset of Ghiani and Improta [13] to test their numerical results. Their results revealed that the designed algorithm exhibits good performance within a reasonable time. Orenstein, Raviv and Sadan [53] developed two heuristic algorithms, one based on the CW algorithm and the other based on the Petal heuristic, for the Flexible Parcel delivery problem. Raucq, Sörensen and Cattrysse [25] treated their waste collection problem with a Column generation-based method, in which the insertion algorithm of Solomon [48] was implemented to create an initial solution. They evaluated the performance of their method in a case study in Belgium. He, Qi, Zhou and Su [31] developed an insertion-based algorithm for generating an initial solution for their model. This algorithm randomly picks a customer from the list of unselected customers and inserts it in the best possible place on the tour with a greedy approach.

Sampaio, Kinable, Veelenturf and Van Woensel [30] developed a heuristic method for solving VRPRDL with stochastic travel times, which is a combination of the local search of Reyes, Savelsbergh and Toriello [28] with the sample average approximation (SAA). SAA is a framework proposed by Kleywegt, Shapiro and Homem-de-Mello [54] for solving stochastic (discrete) optimization problems based on the Monte Carlo simulation. Sampaio, Kinable, Veelenturf and Van Woensel [30] showed that their approach results in 30 % time saving compared to the exact solution method. They also demonstrated that allowing flexibility in deliveries leads to 18 % cost-saving on average.

Table 4 provides an overview of the heuristic algorithms used for various types of GVRP in the literature. The first and second columns of this table give the names of the authors and the year of publication of the articles. In the rest of the table, the heuristic algorithms are divided into three categories. The first category is construction algorithms, the varieties of which are listed below in Table 4. The second category is improvement algorithms, which are divided into two subcategories. Other heuristic algorithms that researchers have used to solve GVRPs are listed in the last column.

Table 4.

Heuristic algorithms details.

Reference	Year	Construction			Improvement		Other algorithms
		Saving	Insertion	Nearest neighbor	Intra-route operators	Inter-route operators
[13]	2000						CARPET
[51]	2008		✓	✓	SN, RN, 3-Ex	RN
[46]	2011	✓		✓		SC, SE, SR, SM
[52]	2012				2-PM 3-OM	1-PM, 3-PM, 2-OM, Or-OM, C-EM
[39]	2015		✓
[28]	2017		✓				Greedy destroy, Greedy recreate
[38]	2018						3-Phase heuristic
[36]	2019	✓
[53]	2019	✓					Petal heuristic
[25]	2019		✓
[30]	2019						A Scenario-based SAA heuristic
[31]	2020		✓
[34]	2022		✓

SN: Substitution Neighborhood, 3-Ex: 3-Exchange Neighborhood,: SE String Exchange.

RN: Reinsertion Neighborhood, SC: String Cross, SR: String Relocation.

SM: String mix, 1-PM: One-Point Move, 2-PM: Two-Point Move.

3-PM: Three-Point Move, 2-OM: Two-Opt Move, 3-OM: Three-Opt Move.

Or-OM: Or-Opt Move, C-EM: Cross-Exchange Move.

As shown in Table 4, among construction algorithms, insertion-based algorithms are used more frequently than other types. Improvement-based heuristic algorithms have been used in only three papers.

4.3. Metaheuristics for GVRP

The most frequently used group of solution methods in the GVRP literature are metaheuristic algorithms. Researchers have utilized these algorithms to tackle GVRPs of different classes. In the class of GVRPs with time windows, Moccia, Cordeau and Laporte [24] developed a Tabu Search (TS)-based approach for solving their problem. This algorithm was tested with the problem instances of Bektaş, Erdoğan and Røpke [20] and the results were compared with the results of the LNS algorithm developed by Bektaş, Erdoğan and Røpke [20], which showed the superiority of the Iterated Tabu Search (ITS) algorithm. Furthermore, these researchers introduced new instances for GVRPTW and treated them with the ITS algorithm. He, Qi, Zhou and Su [31] designed a metaheuristic algorithm for solving VRPRDL with stochastic travel times. They applied the SAA method as a sampling scheme in combination with a metaheuristic algorithm. The designed solution method consists of two phases. In the first phase, an initial solution is generated by a random greedy heuristic. In the second phase, the results are improved by a Hybrid Iterated Greedy metaheuristic with Route Re-optimization and Simulated Annealing (HIGRR-SA) in combination with SAA. These researchers used the dataset of Reyes, Savelsbergh and Toriello [28] to evaluate their method. Dumez, Lehuédé and Péton [33] utilized VNS to tackle the problem. In this study, five destroy operators and four recreate operators were introduced to the literature. These researchers also equipped their solution method with a post-optimization phase operating based on a Set Partitioning approach. They tested the performance of their algorithm with the datasets of Ozbaygin, Karasan, Savelsbergh and Yaman [29] and Reyes, Savelsbergh and Toriello [28] and also introduced three new groups of problem instances [34]. implemented a hybrid algorithm called VNS/GTS. In this algorithm, the neighborhood search is employed in the shaking phase and the Granular Tabu Search (GTS) is used as the local search method. They used a strategy to allow the infeasible solution by penalizing the objective function according to the amount of infeasibility. To test the efficiency of the VNS/GTS algorithm, they modified two datasets introduced by Refs. [28,29] according to their problem and added electronic vehicle-related parameters.

Biesinger, Hu and Raidl [41] developed a Genetic Algorithm with Solution Archive (GASA) for solving GVRP with stochastic demand. In this method, a variable neighborhood descent algorithm with four different neighborhood structures was also employed to intensify the search. Given the importance of initial solutions in Genetic Algorithms (GAs), these researchers used three strategies for generating the initial population: a quality-oriented strategy, a diversity-oriented strategy, and a combination of both. Finally, they evaluated the performance of their algorithm with the dataset of Hà, Bostel, Langevin and Rousseau [23]. Biesinger, Hu and Raidl [39] applied the VNS algorithm to treat GVRP with stochastic demands. In this work, the initial solutions were obtained through two methods: using the farthest insertion algorithm and relaxing the constraints of GTSP. They utilized three neighborhood structures to search the solution space: 1-shift, 2-opt, and or-opt. In the end, they evaluated the performance of their algorithm with the dataset of Bektaş, Erdoğan and Røpke [20].

In the category of GVRPs with flexible fleet size, Afsar, Prins and Santos [42] employed the Iterated Local Search (ILS) algorithm to solve their problem. They developed two versions of the ILS algorithm. In the first version, which they called Multi-Start ILS (MS-ILS), they just added a few components (e.g., a reinitialization procedure) to the algorithm. In the second version, called Relaxed-ILS (R-ILS), they modified the ILS algorithm to also accept a number of bad solutions in each iteration. Hà, Bostel, Langevin and Rousseau [23] used a hybrid method consisting of Greedy Randomized Adaptive Search (GRASP) and Evolutionary Local Search (ELS) to tackle their model for GVRP with flexible fleet size. They also evaluated the performance of their algorithm with the problem instances of Bektaş, Erdoğan and Røpke [20]. This evaluation showed that the algorithm offers good performance in a reasonable time.

Zhou, Baldacci, Vigo and Wang [38] developed a hybrid algorithm called Hybrid Genetic Search Algorithm with Adaptive Diversity Control (HGSADC) to tackle a two-echelon GVRP with customer preferences. This algorithm was implemented in a real problem instance in Chongqing city. These researchers also introduced several new instances for their problem and assessed the performance of their algorithm in solving these instances.

Metaheuristic algorithms have also been applied to other variants of GVRP. Bautista, Fernández and Pereira [51] employed two metaheuristic algorithms based on Ant Colony System (ACS) to solve their model. These two algorithms are different in their construction phase, one using the NN algorithm and the other using the nearest insertion-based algorithm for this purpose. The proposed algorithm was employed for a case study in Sant Boi de Llobregat, Spain. Pop, Pintea, Zelina and Dumitrescu [55] also employed an Ant Colony Optimization (ACO) algorithm to treat their model. In this work, the NN algorithm was used to generate initial solutions. These researchers utilized seven TSPLIB library benchmarks to measure the performance of their algorithm. However, since these data are not clustered, they applied the algorithm of Fischetti, Salazar González and Toth [56] to cluster them. In another study, Pop, Matei, Sitar and Chira [19] applied a GA to solve their GVRP. The results of this study represented that the GA outperforms the ACO that they employed in their previous work [55]. Next, Pop, Matei and Sitar [57] developed a solution method for the problem by combining the GA with the local-global approach. They showed that their algorithm outperforms previous methods by testing it on the data available at Vehicle Routing Data Sets. In another study, Pop, Matei and Valean [58] used the combination of local-global search and the GA to tackle another GVRP. They employed two datasets to test their algorithm, one similar to the dataset used by Refs. [19,55] and another based on the CVRP library (Vehicle Routing Data Sets). This study also employed the clustering method of Fischetti, Salazar González and Toth [56] to cluster the nodes. Pop, Fuksz and Marc [59] also utilized a VNS algorithm where the initial solution is generated by a savings-based method to tackle the suggested GVRP. In this study, two groups of neighborhood structures were used to search the solution space: intra-route and inter-route. Intra-route operators included 2-opt, 3-opt, and Or-opt, and inter-route operators were 1-0 Exchange, 1-1 Exchange, 1–2 Exchange, Relocate, and Cross-exchange. The algorithm was tested on the problem instances of [19,55] and also those provided at Vehicle Routing Data Sets. Comparison with GA [19] and ACS [55] revealed the good performance of the algorithm in terms of solution quality and solution time. The designed VNS algorithm was also compared with the Adaptive Large Neighborhood Search (ALNS) algorithm [16] and the incremental TS [24] in terms of performance in solving small and medium-sized instances. This comparison demonstrated a good performance of the algorithm compared to these methods.

Bräysy, Martínez, Nagata and Soler [60] applied a Memetic Algorithm (MA) to treat their problem. MA is a population-based algorithm for searching the solution space that uses a combination of evolutionary methods with local search for this purpose. Bräysy, Martínez, Nagata and Soler [60] tested the performance of their MA on three sets of instances. Prins, Afsar and Santos [61] designed an ILS algorithm to solve the problem. This method involves using a heuristic based on the Geometric Sweep Algorithm (GSA) to generate an initial tour and then using swap, relocation, and 2-opt operators for local search. These researchers used two datasets, one from the article of Afsar, Prins and Santos [42] and the other from the article of Pop, Zelina, Lupşe, Sitar and Chira [46], to evaluate the performance of their algorithm.

Pintea, Chira, Dumitrescu and Pop [62] employed an algorithm called the Sensitive Ant Model (SAM) to tackle GVRP. The SAM's general approach to the solution procedure is similar to that of the ACS approach used by Pop, Pintea, Zelina and Dumitrescu [55]. These researchers tested the performance of their method with the dataset of Pop, Pintea, Zelina and Dumitrescu [55], which showed the good performance of SAM in solving the problem. However, while SAM improved the results of ACS, it had longer solution times in some cases.

Navidadham, Arbabsadeghi, Bayat and Didehvar [63] proposed a hybrid solution method consisting of a TS algorithm and Parallel Universes Algorithm (PUA) for the problem. Bulhões, Ha, Martinelli and Vidal [43] developed a hybrid algorithm based on the GA with population management to solve the problem. In this algorithm, which is called Hybrid Genetic Search (HGS), the initial solution is generated randomly, the characteristics of the algorithm are adjusted according to the characteristics of each problem, and a novel penalty mechanism is implemented to balance service levels and costs. Wisittipanich and Ananthapanyasut [64] designed an algorithm based on Particle Swarm Optimization (PSO) to treat the problem. This method also involves generating an initial solution at random. These researchers also used the swap strategy to improve the local search and reach better solutions. The developed algorithm was employed in a case study in Chiang Mai city, Thailand. Effendy & Yap [71] used a method to solve the SBRP in an efficient time. They focused on solving practical problems that the number of passengers is not known well. In this case, solving the problem in a short time is necessary, so they developed a local search framework to treat the problem in which efficient run time had a higher priority than optimality. They applied remove, replace, and implode operators to search the solution space. The performance of the algorithm is evaluated on a real case study dataset.

The list of articles that have metaheuristic methods to solve GVRPs is provided in Table 5. In this table, the first and second columns give the names of the authors and the year of publication of the articles, the third column shows which class of the problem they have treated, the fourth column displays the type of metaheuristic they have used, and finally, the last column represents the dataset(s) they have employed to evaluate the method.

Table 5.

Details of GVRP metaheuristic algorithms.

Reference	Year	Class	Metaheuristic	Instances
[51]	2008		ACS	Case study
[55]	2009		ACS	Modified TSPLIB
[19]	2010		GA	Pop, Pintea, Zelina and Dumitrescu [55]
[58]	2011		GA	Pop, Pintea, Zelina and Dumitrescu [55]
[60]	2011		MA	Pessoa, De Aragao and Uchoa [65], Soler, Martínez and Micó [66], New instances
[61]	2012		ILS	Afsar, Prins and Santos [42]
[24]	2012	Time Window	Incremental TS	Bektaş, Erdoğan and Røpke [20], Cordeau and Laporte [4], New instances
[62]	2012		SAM	Pop, Pintea, Zelina and Dumitrescu [55]
[57]	2013		GA	Pop, Pintea, Zelina and Dumitrescu [55]
[42]	2014	Flexible Fleet Size	ILS	Pop, Zelina, Lupşe, Sitar and Chira [46], Araque, Kudva, Morin and Pekny [47], Solomon [48], Vehicle Routing Data Sets
[23]	2014	Flexible Fleet Size	GRASP, ELS	Bektaş, Erdoğan and Røpke [20]
[59]	2014		VNS	Pop, Pintea, Zelina and Dumitrescu [55], Vehicle Routing Data Sets
[39]	2015		VNS	Bektaş, Erdoğan and Røpke [20]
[63]	2015		TS, PUA	Unknown
[38]	2018	Multi-Level	GA	Case study, New instances based on Crainic, Mancini, Perboli and Tadei [67]
[41]	2018	Stochastic	GA	Hà, Bostel, Langevin and Rousseau [23]
[43]	2018		GA	Modified instances of Augerat, Naddef, Belenguer, Benavent, Corberan and Rinaldi [49], Modified instances of Archetti, Bianchessi and Speranza [44]
[27]	2018	Pickup and delivery, Time window	ALNS	New instances
[64]	2019		PSO	Case study
[31]	2020	Time Window	HIGRR-SA	Reyes, Savelsbergh and Toriello [28]
[33]	2021	Time Window	VNS	Ozbaygin, Karasan, Savelsbergh and Yaman [29], Reyes, Savelsbergh and Toriello [28]
[71]	2022		LSA	Case study
[34]	2022	Time Window	VNS/GTS	New instances

As illustrated in Table 5, 20 articles have used metaheuristic algorithms to tackle the problem. As the last column of this table indicates, the most frequently employed dataset among these articles is the dataset of Pop, Pintea, Zelina and Dumitrescu [55]. In three of these articles, metaheuristic algorithms have been used to solve a real problem. Overall, researchers have utilized 12 different metaheuristic methods to treat GVRPs. These methods are shown in Fig. 6. Accordingly, GA, VNS, and ACO have been more popular than other algorithms in this group.

Fig. 6.

Distribution of metaheuristic algorithms for GVRP.

5. Practical implications

Researchers have proposed a wide range of applications for GVRPs. These applications can be divided into two categories: practical and theoretical. Theoretical applications refer to how a range of problems such as TSP with profits, some VRPs, and automated guided vehicle routing problems can be converted into GVRP. The theoretical applications of GVRP have been thoroughly discussed by Baldacci, Bartolini and Laporte [16]. In this section, we investigate the practical applications of GVRPs.

One potential application of GVRP is in the planning of municipal waste collection, which is one of the most challenging problems of urban management. This problem involves designating a point for waste collection from each area (i.e. a point where people living in that area will leave their trash) and then planning the process whereby garbage trucks collect waste from these nodes. This application for GVRP was proposed by Bautista, Fernández and Pereira [51].

Another application of GVRP is in the pickup and delivery of postal packages. Laporte, Chapleau, Landry and Mercure [68] were the first to turn the problem of transporting postal packages into a GVRP. They formulated this problem for urban areas and tackled it by the use of clustering techniques. In this formulation, some delivery nodes were decomposed into two nodes because of their location, which could have an impact on the routing of vehicles. For example, a place on the corner of a street block can be accessed from two sides and thus visited through two routes: the straight route, and the route that is perpendicular to the first one. In this case, solving the problem will give the sequence of visits, but will not specify the exact route on which they occur. To solve this problem, the corner point can be decomposed into two nodes, only one of which is allowed to be selected. With this approach, not only the sequence of visits but also the route by which corner nodes must be visited can also be determined.

GVRPs can also have some military applications, for example in planning attacks on ground targets with military aircrafts. Quttineh, Larsson, Lundberg and Holmberg [69] proposed such a military application for GVRP. In their problem, it is assumed that each target is an area and shooting any point in an area is like shooting the target. Thus, each area can be considered a cluster, and the nodes in that area represent the nodes belonging to that cluster. Therefore, to fire at the target, it is necessary to select one of all nodes inside the cluster.

One of the applications that have received much attention from researchers is the distribution of goods in what is called last mile logistics. Researchers have proposed various ways of applying GVRP to this area. One of these ways is to consider different delivery options. In this application, each customer proposes several locations for the delivery of their goods. Making a delivery at any of these locations will mean that the customer is served. Moreover, customers may propose several options as to when they prefer to receive their goods. In that case, delivery locations may vary with time. In this problem, delivery options are considered as a cluster, and visiting one point of a cluster eliminates the need to visit other parts of that cluster. Orenstein, Raviv and Sadan [53] proposed another way of applying GVRP to last mile logistics. They designed a problem in which each customer specifies a number of service nodes where their goods can be delivered. However, in this problem, the goods are not delivered directly to the customer and instead, the customer must pick up the goods from the service point. Service nodes can be close to the customer's home, workplace, shopping malls, etc. If customers are flexible and offer more than one service point, delivery can be done at lower costs and in shorter timespans.

Another application of GVRP is in drug distribution [20]. In this application, it is assumed that drug shipments must be sent to a number of regions, each comprised of multiple cities. However, it is enough to deliver the shipments to only one city in each region, since they can be redistributed to other cities in that region from that destination. The same logic can also be applied to maritime transport, where each region comprises several ports and it is enough to select only one port from each region for delivering shipments.

GVRP can also be utilized in the planning and scheduling of bus routing [24]. This is very similar to the school bus routing problem. Moccia et al. [24] considered this problem in such a way that a number of nodes is given as potential bus stops. Each employee must select a point for boarding the bus. There is no preference relationship between stops and they are all considered as nodes of a cluster. Once the stops for all employees are specified, it is necessary to plan the routes accordingly. In this problem, the objective is to minimize the distance traveled by vehicles without violating the constraints introduced in the problem, such as those concerning time windows. Effendy & Yap [71] developed the application of the bus routing problem by considering two objective functions. In this problem, passengers choose several location options. These options can be the passenger's home or a station close to it. In this problem, two objective functions are considered. First total bus driving distance and second the total passengers' walking distance.

Another application of GVRP is in operations planning during crises and natural disasters [42]. Some crises and natural disasters cause the roads to become blocked or temporarily inaccessible. In these situations, affected areas need to receive resources such as medical help, water, food, medicine, and essential items by helicopter. For this purpose, affected areas need to be classified into multiple zones, and then for each zone, a nearby airport must be chosen to receive and redistribute resources so that rescue and relief operations can progress as fast as possible.

GVRP can also benefit the field of urban transportation management [60,70], especially for cities where there are several traffic restrictions and it is essential to consider these traffic rules when solving the routing problem. Furthermore, in problems that involve large vehicles, it is important to consider the limitations on the movement of these vehicles (e.g. left turns and U-turns). Considering these details in the routing operation can turn a simple VRP into a GVRP, where edges and vertices that need to be served are broken down into different nodes and the costs and penalties for moving between these nodes must be incorporated into the graph analysis.

6. Conclusions and future lines of research

Over the past two decades, numerous studies have been conducted on GVRP and its applications. During this time, researchers have proposed many different variants and extensions of GVRP and have modeled a wide range of practical problems as GVRP or its variants. However, to the best of the authors’ knowledge, the literature does not contain a comprehensive review of the articles published in this field. In this paper, articles related to the subject of GVRP and its applications were reviewed. The reviewed articles were divided into seven classes of 1- Time windows, 2- Split delivery, 3- Pickup and delivery, 4-Multi-level, 5- Stochastic, 6- Flexible Fleet size, and 7- Multi-objective based on the assumptions they have used in their formulations, and the articles in each class were separately examined. The reviewed articles were also classified in terms of the methods they have employed to treat their problems. Finally, the datasets that the articles employed to evaluate their solution methods were reviewed and categorized.

Our review of the literature suggests that, despite the multitude of works done in the field of GVRP over the past two decades, this could still be an attractive line of research, as future studies can still explore many different dimensions of the problem. Suggestions for future research can be classified into five categories, namely considering other types of VRP, expanding objective functions, introducing the notion of uncertainty to the problem, designing solution methods, and finally extending new datasets for the problem. These potential lines of research are discussed below.

• (I)Other classes (variants): Since the introduction of VRP, researchers have defined many different variants of this problem. In this sense, VRP can be considered a highly diverse problem. However, as the classifications provided in Section 3 showed, previous studies have not provided as many operational variants for GVRP. For example, GVRP can be further expanded by producing functionally relevant equivalents of multi-depot VRP, VRP with backhauls, periodic VRP, open VRP, and VRP with 2D and 3D loading in the GVRP framework. This problem can also be expanded by adding assumptions in relation to the site dependence of vehicles, heterogeneity of fleet, time dependence, etc. Another good idea for future research is to expand the problem for operations that use electric and hybrid vehicles.
• (II)Objective functions: After reviewing the GVRP literature, we can conclude that the articles in this field have not paid much attention to their objective functions. As with VRP, it is possible to produce a great variety of objective functions for this problem. For example, one can consider the balance of vehicles in terms of load or travel distance in the objective function. Another suggestion could be to consider driver-customer relationships, in the sense that customer satisfaction may be affected by how frequently they are served by a particular driver. Another practical idea could be to prioritize the nodes of each cluster. On the other hand, customer satisfaction can be influenced by the place the delivery is made and this can be modeled with the help of a multi-objective formulation [72]. Another idea is to define several objective functions for GVRP to make it more sustainable [73]. Despite the potential benefits of this approach in terms of offering multiple options for expanding the formula, it has not received much attention in previous works.
• (III)Uncertainty: Uncertainty is an integral part of all real-world problems [[74], [75], [76], [77], [78]]. To the best of the authors' knowledge, articles in the GVRP literature have so far only considered the potential for uncertainty in customer demand and delivery network conditions. Given the potential application of GVRP in the field of rescue and relief delivery in crisis situations, it might be beneficial to explore different modes of uncertainty that can affect such a problem. For example, future studies can expand GVRP by considering not only stochastic customers but also the possibility of vehicle breakdowns, the possibility of encountering fuzzy or missing information about some problem parameters, and the possibility of disruption in the operations.
• (IV)Solution methods: While researchers have developed a variety of solution methods for different types of GVRP, there is no consensus as to which is the best way to solve the various variants of this problem. Therefore, the field can benefit from a fair examination and comparison of different methods developed for different GVRPs. It might also be beneficial to try creative methods of using heuristic/metaheuristic methods to apply general adjustments to solution procedures [[79], [80], [81]].
• (V)Datasets: With the growth of cities and online businesses, real-world routing problems are becoming progressively larger. Therefore, the field can benefit from new datasets with a realistically large number of customers, such as 1000 to 10,000.

Data availability statement

Google Scholar, Scopus, Science Direct, Emerald, Springer, and Elsevier databases were employed to collect the required data.

Additional information

No additional information is available for this paper.

CRediT authorship contribution statement

Ali Aghadavoudi Jolfaei: Resources, Software, Visualization, Writing - original draft. Mahdi Alinaghian: Formal analysis, Supervision, Validation, Writing - review & editing. Roghayeh Bahrami: Formal analysis, Resources, Software, Writing - original draft. Erfan Babaee Tirkolaee: Conceptualization, Investigation, Validation, Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.