Abstract
Simulations of cancer cell transport require accurately modeling mm-scale and longer trajectories through a circulatory system containing trillions of deformable red blood cells, whose intercellular interactions require submicron fidelity. Using a hybrid CPU-GPU approach, we extend the advanced physics refinement (APR) method to couple a finely-resolved region of explicitly-modeled red blood cells to a coarsely-resolved bulk fluid domain. We further develop algorithms that: capture the dynamics at the interface of differing viscosities, maintain hematocrit within the cell-filled volume, and move the finely-resolved region and encapsulated cells while tracking an individual cancer cell. Comparison to a fully-resolved fluid-structure interaction model is presented for verification. Finally, we use the advanced APR method to simulate cancer cell transport over a mm-scale distance while maintaining a local region of RBCs, using a fraction of the computational power required to run a fully-resolved model.
Keywords: cancer cells, red blood cells, multiphysics, computational fluid dynamics, multiscale modeling, heterogeneous architecture
1. INTRODUCTION
Metastasis, a multifaceted process that drives the spread of cancer, is the underlying cause of over 90% of cancer-related mortalities [1]. Despite extensive research efforts, predicting the precise location of secondary tumor sites remains challenging due to the transport process’s complexity and wide-ranging scales. Gaining a better understanding of the factors that govern the movement of circulating tumor cells (CTCs) through the bloodstream could potentially facilitate early detection of secondary tumors and targeted treatment of CTCs in the bloodstream [2]. Given that tracking cancer cells in vivo on a patient-specific basis is not feasible, computational models that account for intercellular interactions and the movement of cells over systemic length scales are needed. Human blood is approximately 55% plasma and 45% blood cells (RBCs) by volume [3]. Plasma is the liquid component of blood, mainly containing water, and is used to transport cells and other microparticles, while RBCs are used to transport oxygen. Because of their high concentration in the blood, interactions with surrounding RBCs must be included to accurately model a CTC’s movement through the bloodstream. Direct simulation of large portions of the circulatory system at submicron resolution is fundamentally intractable due to the large number of fluid points and blood cells required since the average human body contains 5 liters of blood and 25 trillion RBCs. Instead, new methods must be developed.
To model cellular transport phenomena, we build upon a previously published adaptive physics refinement (APR) method [4]. This technique utilizes a multiphysics modeling scheme by coupling a submicron resolution fluid-structure interaction region where cellular interactions are explicitly modeled to a coarsely resolved fluid. We refer to the high-resolution region in which cellular-scale dynamics are modeled explicitly as the “window”, chosen to encompass a cell or region of interest [5]. By resolving cell dynamics only within the window, the technique can capture fluid-structure interactions where they are needed to minimize overall computational cost. The work described in Ref. [4] introduces methods for coupling two volumes at differing lattice resolutions, distributing the computational workload effectively between GPU and CPU, and developing a method to move the window while simulating a single cell inside the window.
The final and most crucial step is filling the window containing the cancer cell with red blood cells and allowing it to move with the cancer cell through the bloodstream. This brings multiple new algorithmic challenges: (I) Adaptive physics refinement: the problem requires not just coupling two varying grid resolutions, but also different physics-based models. Within the window, cells are explicitly modeled within a fluid whose viscosity is that of blood plasma whereas outside the window, a higher-viscosity uniform fluid approximates whole blood. Typical adaptive mesh refinement methods couple regions of the same fluid at different resolutions [6, 7], but in this case, a convergent and robust coupling method between two fluids of different viscosity is required. (II) Solving a time-evolving density problem: although the window is centered around a CTC, as it moves through the system the volume fraction, or hematocrit (Ht), of RBCs within the window must be maintained without restricting their movement or biasing the trajectory of the cancer cell. Unlike traditional systems of particle flow that can rely on boundary conditions or simplified geometries, flow through a human arterial geometry requires unique algorithms to maintain cell density. In addition, the method must not only maintain a target cell density, but the cells must all be equilibrated with the flow surrounding the CTC to mimic in vivo conditions. Simply dropping in undeformed cells near the CTC would almost certainly have an unphysical effect on the intercellular interactions. (III) Moving the window: shifting the finely resolved region as it moves through complex vasculatures while retaining the dynamics of the CTC and neighboring RBCs in order to maintain the structure of nearby equilibrated cells so that any non-physical effects due to the window shift or insertion of new cells are neutralized.
In this paper, we present the first implementation of an adaptive physics circulatory modeling code capable of dynamically tracking a circulating tumor cell through a realistic human arterial geometry while maintaining a realistic environment of deformable red blood cells around it throughout the simulation. We describe an addition to the previous APR framework that allows for different viscosity fluids in the window and bulk regions. We propose and demonstrate a new method for maintaining a target density of red blood cells within the window, allowing cells to move freely in and out of the window from any direction. Our approach ensures any new cells entering the window are fully equilibrated before have a chance to interact with the CTC. Algorithms to preserve the general structure of deformed RBCs surrounding the CTC, optimally re-use deformed RBC shapes, and limit re-initialization as the window moves are presented as well.
To demonstrate the capabilities of our extended model, we present verification studies of the variable viscosity component against analytical results. We demonstrate that three different target hematocrits can be maintained using our new cell repopulation and equilibration algorithms. We compare the radial motion of CTCs using explicit fluid-structure (eFSI) and APR methods and show that the latter gives nearly identical results while using significantly fewer computational resources. We perform a feasibility demonstration using the full upper body vasculature in Figure 1 on 256 nodes of the Summit supercomputer. Finally, we present results from a previously-impossible study of brain cancer metastasis, where a CTC at full submicron cellular resolution surrounded by an explicit, deformable RBC environment moves thousands of microns through a complete cerebral geometry using just hundreds of node-hours on a single-node AWS cloud instance.
Figure 1:
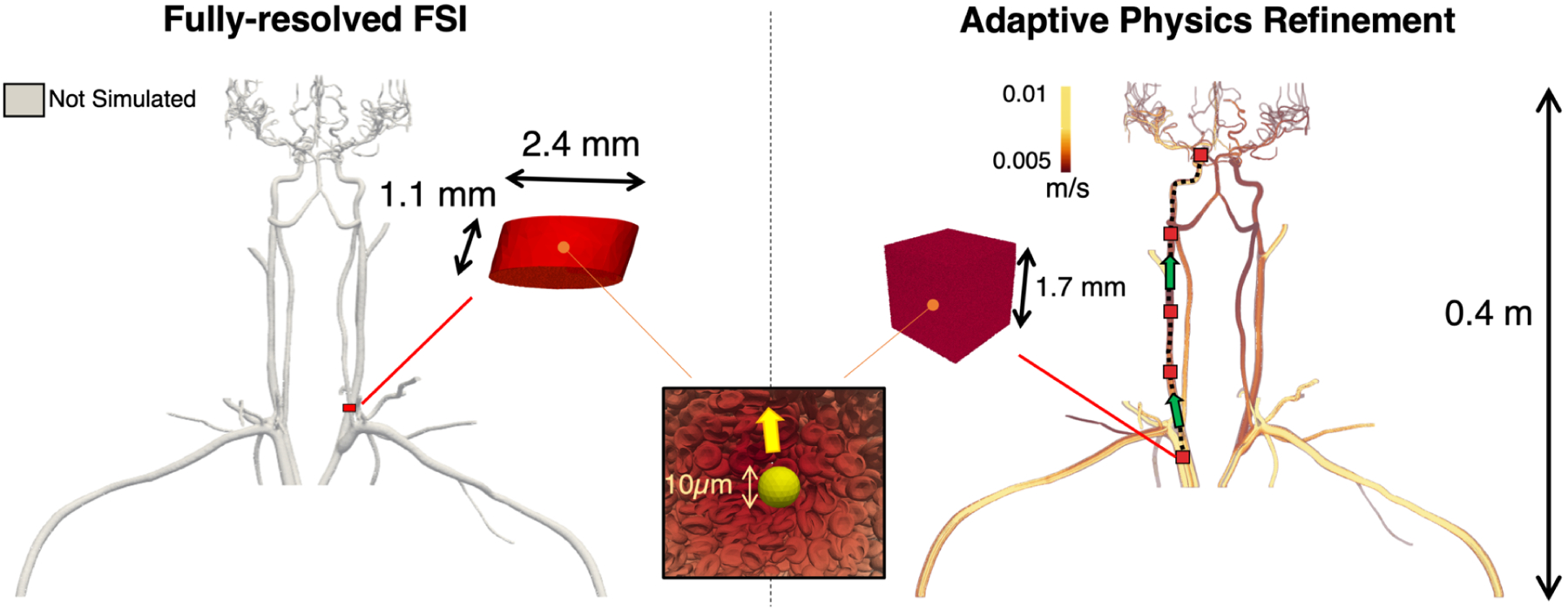
Use of the Adaptive Physics Refinement (APR) model within an upper body vasculature enables up to 4 orders of magnitude increase in total simulated fluid volume accessible to cellular resolution. Using 256 nodes on Summit (1.5k GPUs and 10.8k CPUs), the APR simulation, shown on the right, has the ability to track a cancer cell through the upper body geometry, a volume of 41.0 mL, using a local finely resolved window. This window can travel through the vessel, depicted by the red boxes moving along the dashed black line in the direction of the green arrows, opening up the entire volume to a submicron, cell-resolved mesh. By comparison, the left image displays the theoretical volume simulated using a fully-resolved fluid structure interaction, which can only capture a stationary region at submicron resolution totaling a volume of 4.91 × 10−3 mL using the same compute resources. While the length scale of the fully resolved FSI model is in millimeters, the APR technique extends into meters, making it the first computational method that can track an individual cancer cell across system-scale distances while resolving submicron 3D cellular interactions.
2. METHODS AND ALGORITHMS
The coupled multiphysics model is developed within HARVEY, a lattice Boltzmann method (LBM)-based massively parallel computational fluid dynamics solver [8–11]. The bulk blood flow simulation performed on the CPUs uses the LBM, while the cell-resolved window calculations reside on the GPUs, where the LBM is augmented by an efficient fluid-structure interaction (FSI) algorithm to account for deformable cells. The details behind each of these components, as well as new algorithmic developments and optimizations, are described in the subsections below.
2.1. Lattice Boltzmann Method
LBM is a deterministic, mesoscopic approach that numerically solves the Navier-Stokes equations by modeling fluid with a particle distribution function. A fixed Cartesian lattice is used to discretize space and velocity, where the probability function determines the probability of finding a particle at lattice point and time with a discrete velocity [12]. The evolution of the particles with an external force field is governed by:
| (1) |
where, is the Maxwell-Boltzmann equilibrium distribution and is the external force field at unit lattice spacing and time step. We employ a D3Q19 velocity discretization model with the BGK collision operator, , where is the relaxation time which determines the relaxation of towards the equilibrium distribution function . The kinematic viscosity, is linked to by with a lattice speed of sound , at unit spatial and temporal steps. At the walls, no-slip condition is enforced using the halfway bounce-back boundary conditions is applied.
2.2. Cell Finite Element Model
Each cell is modeled as a fluid-filled membrane represented by a Lagrangian surface mesh composed of triangular elements. The membrane model includes both elasticity and bending stiffness [13]. The shear and dilational elastic responses of the membrane are governed by the Skalak constitutive law, where the elastic energy is computed as:
| (2) |
for strain invariants , shear elastic modulus , and area preservation constant [14]. For the FEM membrane force calculations, Loop subdivison approach is applied [15]. The membrane’s resistance to bending is implemented using Helfrich formulation [16] following:
| (3) |
where is the bending modulus, and are the mean and spontaneous curvatures, respectively, and is the entire surface area of the cell. A surface force density is calculated at each element by computing the surface gradient of the sum of these stresses and applied on to the vertices. Overall, this method has been shown to accurately resolve complex non-linear 3D deformations of biological cells [17, 18].
2.3. Immersed Boundary Method
To account the interaction of the cell with the ambient fluid, the Lagrangian grid of the FEM cell model is coupled to the Eulerian grid of LBM by applying the immersed boundary method [19]. Three components of immersed boundary method are implemented here with the following sequence: interpolation, updating, and spreading. At first, to determine the cell membrane deformation, Lagrangian membrane velocity is interpolated from the Eulerian velocity with a three-dimensional Dirac delta function considering while unit spacing as follows:
| (4) |
where X is the vertex location of the Lagrangian grid and x is the fluid lattice location in the Eulerian grid. A cosine function is used to approximate for unit spacial steps of the Eulerian grid with a four point support [19].
Next, we update the position of the cell vertex with a no-slip condition assuming unit timesteps:
| (5) |
Lastly, the forces calculated at each Lagrangian vertex are spread on to the surrounding Eulerian grid using the same delta function:
| (6) |
2.4. Algorithmic Advances to Capture Cell-Laden Flow with APR
In this section, we describe the main components of the APR algorithm and its extension to include RBCs: (I) multi-resolution/multi-viscosity bulk-fine coupling, (II) maintaining cellular hematocrit for physiologically deformed RBCs, and (III) moving the window and all the cells inside, as well as CPU-GPU optimizations. The underlying principle of the approach involves maintaining a stationary window while the CTC travels through it. To achieve this, a multi-resolution/multi-viscosity algorithm links the bulk and window simulations and regulates the cell density on the window. When the CTC reaches a predetermined distance from the window’s edge, the window undergoes a displacement to a new location centered on the CTC’s position. The process is repeated until the CTC reaches the end of its trajectory.
2.4.1. Multi-resolution Lattice Boltzmann with Variable Viscosity.
In the previous work regarding the APR algorithm, Puleri et. al. developed a multi-resolution approach that efficiently coupled a fine window region having sub-micron resolution with a coarser bulk fluid along with coupling the different physics-based models corresponding to each of the regions. Details about this multi-resolution coupling for maintaining stress continuity can be found in [4]. Since the earlier work did not model RBCs within the window region, it allowed the fine and the coarse lattices to have a consistent viscosity throughout corresponding to the viscosity of whole blood. For the previous APR algorithm, it was enough to consider the coupling related to multi-resolution and did not require a multi-viscosity approach. However, once RBCs are introduced within the window region the viscosities between fine and coarse lattices change. Now only the coarse bulk will represent the whole blood whereas for the window the fluid will have a viscosity identical to that of plasma due to the presence of RBCs. Thus, building upon the previous APR algorithm, for modeling RBCs explicitly within the window region we consider a discontinuity in the physical kinematic viscosity such that, , where c and f respectively correspond to the coarse and fine lattices. The variable represents the ratio in viscosities between the fine lattice and the coarse lattice, determined based on values reported in the literature. Again since in LBM the kinematic viscosity is tied with the relaxation time , we relate the relaxation times of the fine and the coarse lattices by:
| (7) |
where is the ratio of coarse to fine lattice spacing.
2.4.2. Ensuring Physiologically Deformed Cells and Maintaining Cell Density.
For capturing the proper interaction of RBCs and CTC within the window it is crucial that we allow the CTC to interact with deformed RBCs depicting a more physiologically relevant scenerio as RBCs tend to deform in the blood flow. Next, it is important that we maintain a desired hematocrit within the moving window throughout the simulation. Addressing both of these concerns we partition the window into three regions: insertion, on-ramp, and window proper as shown in Figure 3A.
Figure 3:
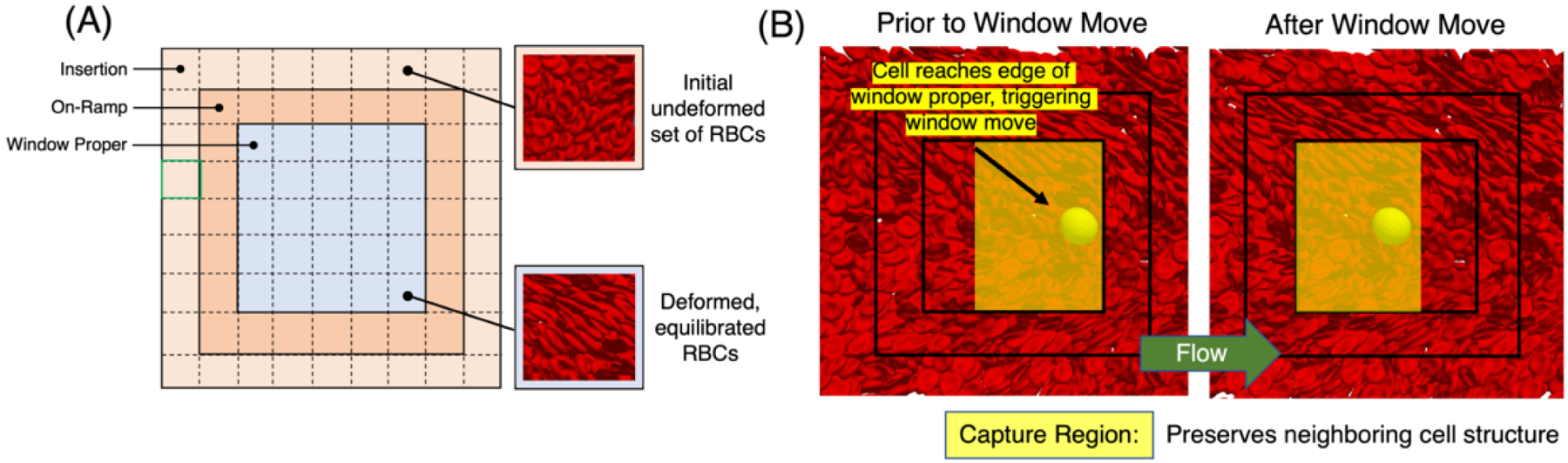
Overview of window components associated with maintaining cell density. (A) Window anatomy delineating insertion, on-ramp, and window proper regions. New RBCs are added into the insertion region once the hematocrit drops below a threshold. These cells travel through the on-ramp region to equilibrate with the flow before reaching the window proper region. Dashed lines depict subregion cubes used for initial placement and monitoring cell density in the insertion region. Also shown is a pre-defined RBC tile used to populate each of the subregion cubes. (B) Depiction of the algorithm to move the window using a representative example. The left-most figure depicts the CTC position near the boundary which triggers a window move. The capture region is marked in translucent blue, labeling the section of cells that are maintained when the window is moved, minimizing the re-instantiation of new undeformed RBCs each time. The right-most figure depicts the configuration at the the end of the window move, with the yellow arrow giving the general flow direction.
The insertion region, located at the outermost layer of the window, is used to maintain a desired density by adding undeformed RBCs to the simulation. To place cells and monitor their density in the insertion region, the domain is divided into cubic subregions. A procedure is developed to randomly place a cube of the same size as a free subregion, with a randomly selected centroid and orientation from a pre-defined tile of RBCs with a specified density. Overlapping cells are removed using an efficient algorithm that detects overlaps by identifying nearby cells at each vertex of the tested cell, using a background uniform subgrid. The algorithm can run on multiple MPI tasks, and maintain consistency across task counts by preferentially removing overlapping cells based on global IDs. Throughout the simulation, the density of cells in each injection subregion is monitored by tracking the number of RBCs in that subregion based on their centroid. If the number of cells falls below a predefined threshold, new undeformed RBCs are added to the injection subregion to maintain the desired density. Re-populating an injection subregion is similar to the initial placement of cells, except that no new cells are added if they overlap with existing cells in the simulation.
The on-ramp region acts as a transition layer, allowing cells to equilibrate with the background flow before entering the window proper region. The outer two regions also provide ample time for the RBCs to deform in the flow before entering into the window proper region where it interacts with the CTC making the interaction more physiologically relevant. In the window proper region the RBCs further deform and interacts with the CTC. Cells that leave the window are removed once they cross the outer boundary. It is worth noting that the primary flow direction may vary, and some parts of the insertion region can also serve as cell exit points.
2.4.3. Moving the Region with Explicitly Resolved Cells.
Previously for tracking the trajectory of a single CTC in large geometries with APR, the CTC was allowed to move through the window simulation domain until it reached a specific distance from the window boundary. Once the CTC reached that distance the window was moved to a new position and the communication between the fine and coarse lattices was re-established, details of which can be found in Ref. [4].
We use a similar approach to the one described earlier to move the window in a simulation of a cell-laden fluid. However, before moving the window, we first sort the RBCs in the simulation into the capture and fill regions. The capture region surrounds the CTC, and the RBCs in this region are kept in place as the window moves. To ensure that the CTC will be centered in the window at the end of the move and that the capture region boundary will align with the insertion region boundary, we carefully select the dimensions of the capture region. The fill region, on the other hand, occupies the remaining volume in the window up to the boundary of the insertion region and complements the capture region at the new window position.
To illustrate this new technique, the left-most image in Figure 3B first depicts a CTC position near the boundary, triggering a window move. Next, the capture region for this example is shown in this figure, and RBCs within each are identified. Next, RBCs in both the capture and fill regions are deep copied, with the copy placed into the fill region group. The fill region RBCs are then shifted to their new location, effectively filling the remainder of the window to the insertion region boundary. Finally, the insertion regions are re-populated, marking the window move’s end.
2.4.4. Hybrid CPU-GPU Implementation.
Following the initial implementation of the APR approach, the simulation workload is partitioned such that the bulk fluid is assigned to the CPU while the fluid and cells in the finely resolved region are allocated to the GPU. This method maximizes the use of the heterogeneous architecture available on the Summit supercomputer. The code was developed in C++ and compiled using the IBM XL compiler (v16.1.1), Spectrum MPI (v10.4.0.3), and CUDA 11. For the simulations presented in this study, all 42 cores across the dual sockets of POWER9 CPUs on Summit were used, with 42 tasks per node, 36 assigned to the bulk fluid and 6 to the window region. Further details about the computational design for CPU-GPU architectures are available in Ref. [4].
2.4.5. Cell-related Optimizations.
Cell Memory Management.
During the window simulation, deformable cells leave the simulated domain and are added as needed to maintain the desired cell density (as described in Section 2.4.2). Additionally, cells continuously enter and exit neighboring computational tasks. However, a straightforward approach to managing cell migration between tasks would require frequent memory allocation and de-allocation during the simulation, which could have a negative impact on performance. To address this issue, we allocated all the necessary memory for cells, with additional space for other cells, at the beginning of the simulation. Additionally, the buffers related to the memory of a single cell were shifted to accommodate cell addition or deletion from a task, which helped to optimize the memory pooling process.
Reducing Cell Communication.
For proper parallelization of the immersed boundary spreading operation, each MPI task requires updated cell forces for all cells within its domain. These forces can be computed on owned cells and then communicated to other tasks with these cells in their halos, or a task can compute updated cell forces for all owned and halo cells within its domain. To reduce the amount of communication and improve performance, this study utilizes the latter approach, in which each task computes updated cell forces for all cells within its domain, even those in its halos. This approach requires the recomputation of forces on the GPU, but it ultimately reduces the communication needed.
Vertex Re-ordering for FEM Calculations.
With FEM computations, the spatial locality of the mesh vertex ordering is an important consideration. Each element accesses data from twelve surrounding vertices when calculating the element stress. Thus improved efficiency concerning memory accesses can be achieved via the vertex ordering in the connectivity arrays. The reverse Cuthill-McKee (RCM) ordering algorithm [20] has been shown to improve locality in a manner well suited for FEM applications, and we use RCM in the present work to optimally order our deformable cell mesh connectivity arrays.
3. RESULTS & DISCUSSION
We ensure the accuracy of our algorithm by performing three different verification tests. In Section 3.1, we first consider fluid-only simulations to focus on variable viscosity components and compare them against analytical solutions for the velocity field within given geometries. Using these components, in Section 3.2, we then consider cell-resolved window simulations and validate both the ability to maintain a desired hematocrit as well as the general multiphysics capability through comparison with experiment. Next, in Section 3.3 we use the moving window to track a CTC interacting with RBCs and compare it with that of eFSI. In Section 3.4 we analyze the performance of the APR approach on Summit. Finally, in Sections 3.5 and 3.6 we show the application of this method in simulating large vasculatures with cellular resolution.
3.1. Linking Regions of Varying Viscosity Using Multi-fluid Shear Simulations
We verified the variable viscosity component of the method by considering a shear flow with three fluid layers, as depicted in Figure 4. This configuration facilitates comparison with an analytical solution for the velocity field and thus provides a direct means of focusing on the variable viscosity component of the method. For the simulation setup, we considered an overall cubic domain with an edge length . Within the overall domain, each fluid layer, denoted as Regions 1–3 in Figure 4A, has a height of along the -axis, with Regions 1 and 3 having the same viscosity which is greater than that of Region 2. A finely resolved rectangular window is placed around the boundaries of Region 2. This viscosity contrast is quantified by , where the subscripts refer to the Region number. Shear flow is imposed by applying a zero-velocity boundary condition at the plane as defined in Figure 4B, and a velocity in the direction at the plane Velocity boundary conditions are applied at the remaining faces in accordance with the profile for given values. The window is placed such that the boundaries are aligned with the region boundaries, rendering the viscosity contrast between the window and bulk domains equal to .
Figure 4:
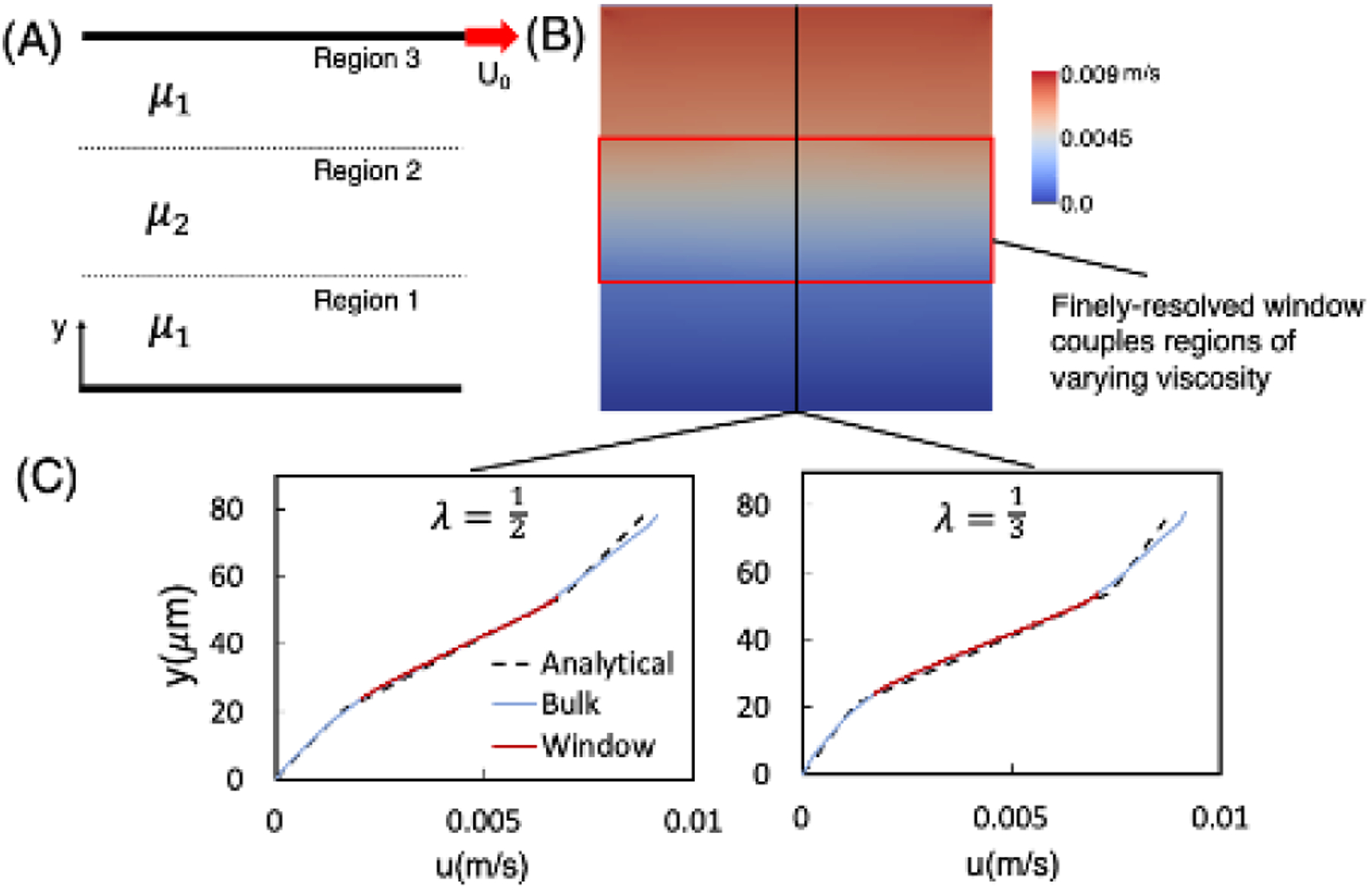
Verification of the variable viscosity capability of our method. (A) Simulation schematic depicting the variable viscosity shear flow configuration, with the bottom stationary plane, the top plane moving with velocity in the direction shown, and three regions as labeled. (B) Contours give the fluid velocity corresponding to a representative profile. Regions 1 and 3 have the same viscosity which is greater than that of Region 2 , and the viscosity contrast is . A finely resolved window (red) is placed the center of the domain with top/bottom boundaries aligned with the region boundaries as shown. (C) Velocity profiles as a function of position and passing through the window. Results are shown for and . The dashed black line gives the solution per Eq. 8, the solid blue line gives the velocity profile through the bulk domain, and the solid red line gives the profile through the window domain.
For the LBM parameters, we considered a of approximately 1, with the corresponding determined from Equation 7. We note that for variable viscosity simulations, the will be reduced relative to single-viscosity simulations since , as is evident from Equation 7. This permits using a relatively more significant value, or relatively larger values than would be acceptable for a single-viscosity simulation.
Simulations are performed for , chosen to span values representative of the viscosity contrast between blood modeled as a bulk fluid and plasma [21, 22]. For each value we considered the same resolution ratios of 2, 5, and 10 to determine the accuracy over multiple scenarios. Simulation results for the velocity profile as a function of position passing through the window domain are compared against the analytical solution for the velocity profile through Region , which can be derived as:
| (8) |
with and given by:
along with , and . In Figure 4C we plot the simulation velocity profile as a function of position for each . Specifically shown are results for the cases, along with the analytical profile given by Equation 8. The velocity linearly increases with a slope proportional to the viscosity of each region. Table 1 displays all of the bulk and window errors for each resolution and viscosity combination. Strong agreement between the two is evident for each value, ranging from 1–4%, thus demonstrating the accuracy of the coupling of varying viscosities between bulk and window using this method.
Table 1:
Simulation error norms for variable viscosity shear flow, based on comparison with Equation 8. Results are given for each viscosity ratio and resolution ratio considered, and are broken out in terms of that in the bulk and window regions.
| n | λ = 1/2 | λ = 1/3 | λ = 1/4 | |||
|---|---|---|---|---|---|---|
| bulk | window | bulk | window | bulk | window | |
| 2 | 0.0099 | 0.0178 | 0.0099 | 0.0306 | 0.0101 | 0.0385 |
| 5 | 0.0097 | 0.0179 | 0.0096 | 0.0308 | 0.0097 | 0.0389 |
| 10 | 0.0096 | 0.0183 | 0.0095 | 0.0310 | 0.0098 | 0.0387 |
3.2. Verification of Cell Repopulation Algorithms and Effective Viscosity for APR Window
The presence of red blood cells (RBCs) in blood flow increases the fluid viscosity compared to the plasma in which they are suspended. The accuracy of viscosity prediction in simulation methods is crucial for determining critical hemodynamic factors, such as wall shear stress, pressure differentials, flow distribution, and fluid velocity gradients, all affecting individual cell dynamics and interactions. In this section, we present a verification of the multiphysics capability of our method by examining flow through a straight tube with a cell-resolved window positioned at the center (Figure 5A). In addition, we compared the predicted viscosity of the simulation across a range of physiological hematocrit values with an experimental correlation [21]. These comparisons provide a comprehensive means of validating the accuracy of the relevant physics captured by the method, as well as the method’s ability to maintain desired hematocrit over time.
Figure 5:
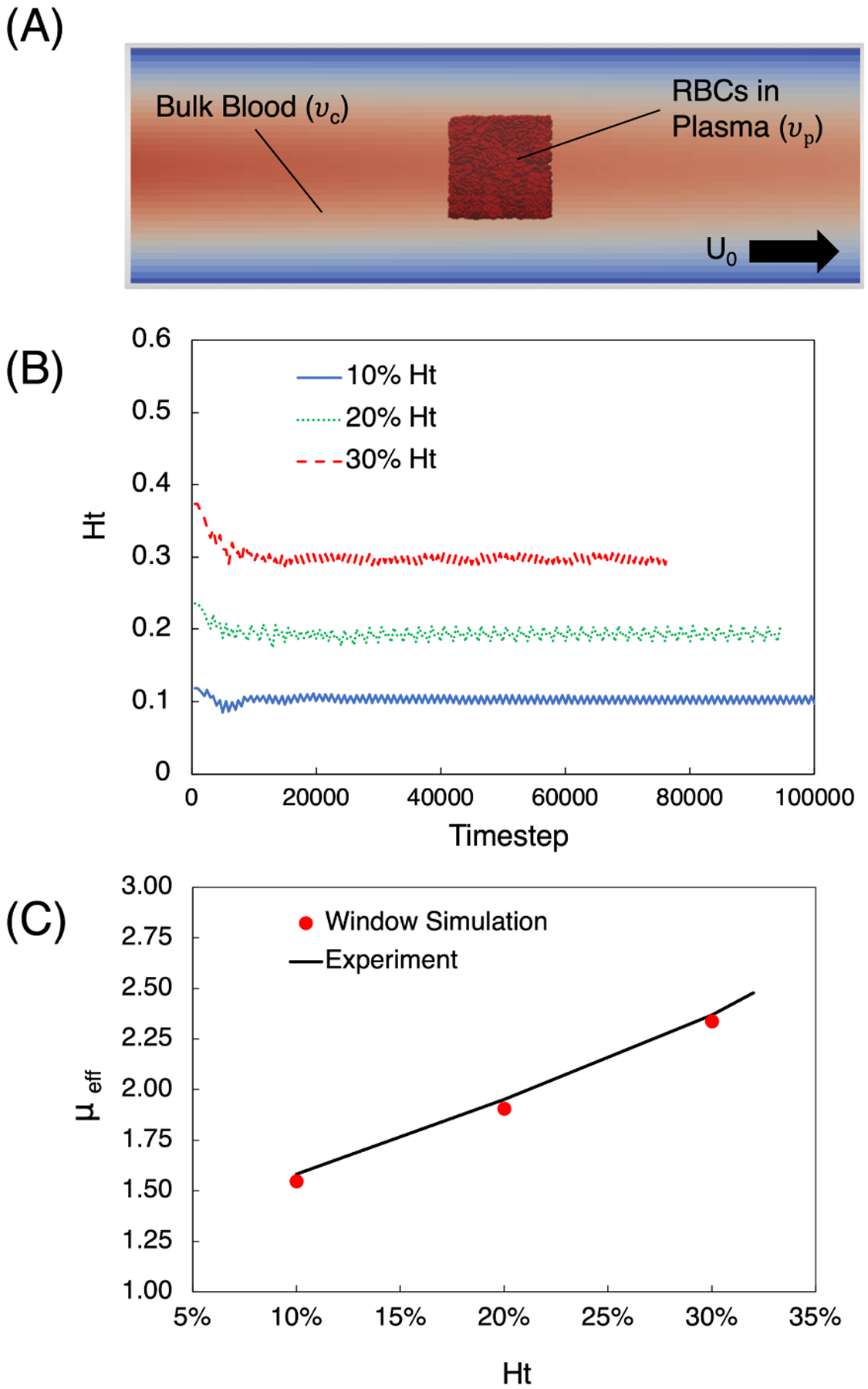
Cell resolved window simulation and comparison with experiment. (A) Schematic depicting the simulation setup, with the cell-resolved window placed a the center of a tube of diameter . Outside the window the fluid represents bulk blood flowing in the direction of the black arrow. (B) Hematocrit versus time for the 10% – 30% cases, demonstrating the ability of the method to maintain the desired value. (C) Effective viscosity predicted by the window simulation as a function of hematocrit, compared against the experimental correlation[21] given by Eq. 9.
A well-known experimental correlation established by Pries et al. [21] demonstrates the dependence of blood viscosity on vessel diameter and hematocrit.
| (9) |
with:
| (10) |
where is the relative apparent viscosity for blood in a vessel of diameter in . is the discharge hematocrit, which is related to the tube hematocrit via the Fahraeus effect, fitted by [23]:
| (11) |
To capture realistic red blood cell counts, we performed simulations with hematocrit values of 10%, 20%, and 30% with the configuration depicted in Figure 5A. We considered a tube of diameter , a cell-resolved window with side length , and a flow rate of 5.7 ml/hr corresponding to an effective shear rate of 250 s−1. Fluid outside the window is taken to be blood modeled as a bulk fluid, with viscosity determined from Eq. 9 for the associated hematocrit maintained in the window. Fluid inside the window represents plasma with a viscosity of 1.2 cP [22] and a shear elastic modulus for the RBCs to be [24], which corresponds to a healthy stiffness value. We considered the lattice spacing in the flow domain to have a resolution of in the bulk region and in the window region, leading to a resolution ratio of .
Results are presented in Figures 5B, C for each of the cases considered, corresponding to the aforementioned hematocrit values. In Figure 5B the window hematocrit is plotted versus time for each of the values considered. Each simulation is started from an initial zero-velocity condition, and the effect of the initial transient associated with the flow equilibrating can be seen in each of the curves. Each domain is initially packed with a Ht higher than desired, but quickly equilibrates as cells pass through the window. Small fluctuations can also be seen here as a result of the repopulation of window injection method to maintain the desired hematocrit. This repopulation occurs when the hematocrit in a particular injection subregion drops below a prescribed threshold in order to minimize the injection frequency.
For each simulation case we determined the effective viscosity using the predicted simulation pressure drop in conjunction with Poiseuille’s law:
| (12) |
where is the volumetric flow rate, is the tube radius, and is the length. For each of the three hematocrit values, in Figure 5C we plotted the effective viscosity predicted by the simulation alongside the experimental correlation from Eq. 9. For each case we observe strong agreement between the two, which importantly demonstrates the accuracy of the method in resolving the primary effects of RBCs on the hemodynamic characteristics. Thus, the observed agreement demonstrates the ability of the method to accurately capture the flow physics.
3.3. Comparison of APR and eFSI Cancer Cell Trajectory in an Expanding Channel
In order to assess the performance of the APR technique in recovering CTC trajectory, we conducted eFSI and APR simulations in an expanding microfluidic channel. This type of channel is commonly used to investigate cellular motion towards vessel walls and offers valuable insights into the effects of hemodynamics on cell margination [25]. Unlike a straight-line vessel, an expanding channel results in a change in radial distance from the centerline of the channel due to the underlying fluid profile. This study provides a means to validate the accuracy of the APR method in capturing cell motion and and provides a method of comparison to its eFSI counterpart.
The expanding microchannel is depicted in Figure 6, with the eFSI and APR initializations shown in A and B, respectively. The channel expands from 200 μm to 400 μm at and has a length of 2000 μm. For the CTC, we use a shear elastic modulus of , which is representative of the known increased stiffness relative to RBCs [26]. The CTC is initially placed with a radial offset of 25 μm at , and an inlet velocity of 0.1 m/s is used to drive the flow. It has been numerically shown that a submicron resolution is required to accurately capture the deformation of cells [27], thus we choose a lattice grid spacing for the window and the bulk flow component as and , respectively, leading to a lattice resolution ratio of . The bulk is treated as whole blood while the window contains plasma, with kinematic viscosities of 4 cP and 1.2 cP, respectively. The window is initialized with a 120 μm edge length: 20 μm injection, 20 μm on-ramp, and 40 μm window proper side lengths. Both sets of simulations are generated at the same hematocrit.
Figure 6:
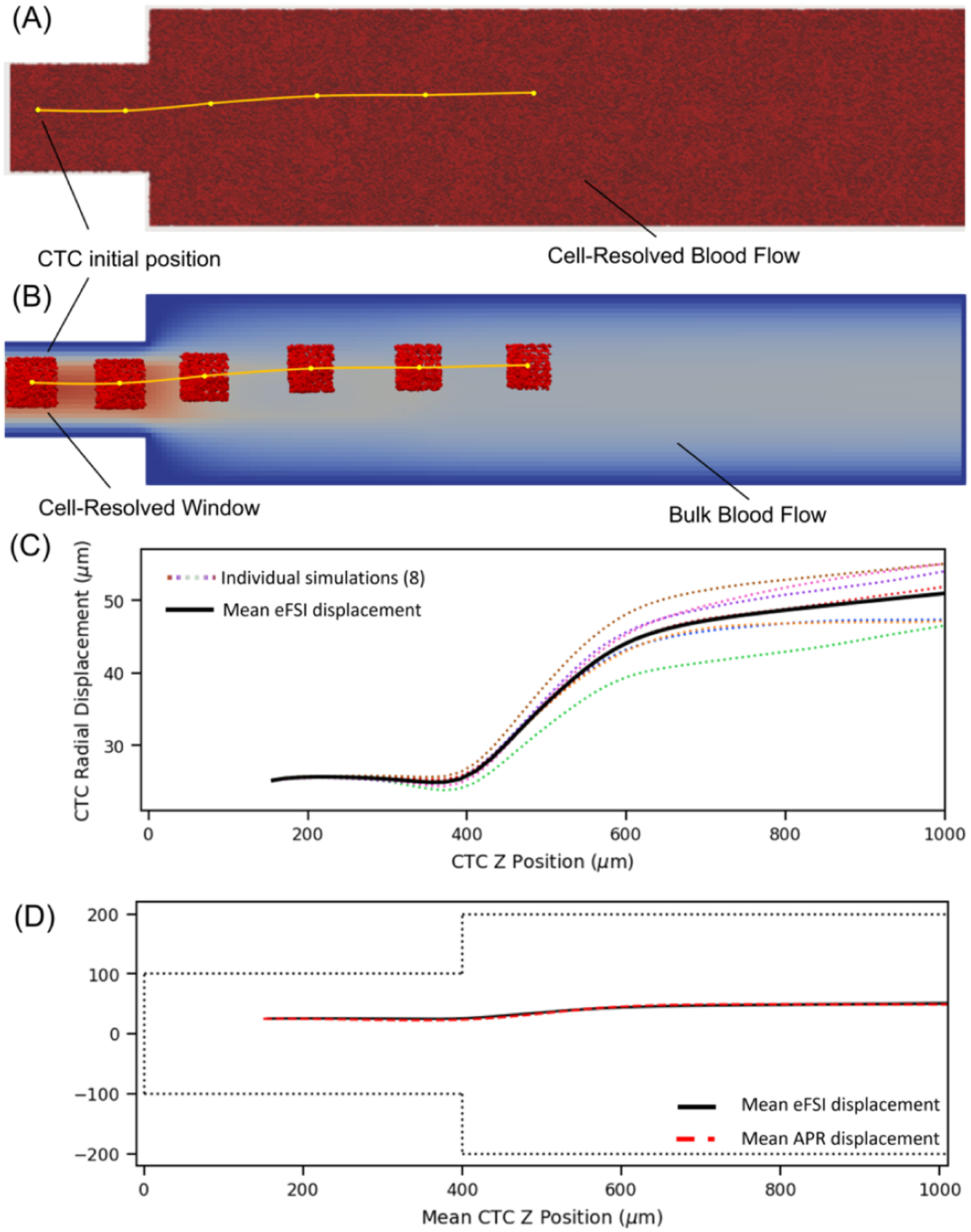
Comparison of APR vs eFSI in the expanding channel domains. Visualizations of (A) fully resolved eFSI simulation where the entire domain is at a 0.5 grid spacing filled with RBCs compared to (B) an APR window centered on the CTC where the window domain has a lattice spacing of 0.5 connected to bulk whole blood. (C) Distribution of eFSI results for CTC motion, showing that differing initial RBC positions can affect CTC trajectory. (D) Comparison between eFSI and APR showing similar CTC trajectories.
We note that the positions and orientation of neighboring RBCs can influence the motion of the CTC, leading to changes in trajectory even at the same hematocrit, shown in previous simulation work [28]. Thus to capture general behavior, we set up 8 eFSI and APR simulations with varying RBC positions. The distribution of eFSI trajectories is presented in Figure 6C.
Figure 6D illustrates the motion of the CTC as it moves along the axis, showing that the APR model is able to capture the similar trajectories as eFSI. The eFSI value marginates slightly earlier, but both reach a similar radial location as the cell progresses past the expansion. Due to the influence of varying RBC locations, we expect that the two lines will not match up exactly, similar to how two sets of RBCs are unlikely to return identical results; however, we are able to show that the APR model captures the general behavior.
Finally, we compared the computational savings of utilizing the APR model over the eFSI method. Both sets of simulations were performed on the Summit supercomputer. The APR simulations were run on 6 nodes with approximately 5.3 × 103 RBCs over 36 hours, utilizing 36 GPUs and 252 CPUs. The eFSI versions ran on 22 nodes with approximately 4.5 × 105 RBCs over 120 hours of wall time for the CTCs to reach the equivalent distance as in the APR model. With these configurations, the APR method saved over 10x compute time in terms of node-hours.
3.4. Scaling Performance on Summit Supercomputer
In Figure 7 we assessed strong scaling using a cube with side length 10.5 mm. A window of side length 0.65 mm (injection: 0.05 mm, on-off: 0.02 mm, proper: 0.51 mm) is placed in the center of the geometry with a resolution ratio of 10, leading to approximately 1M RBCs placed inside. We utilized 32 to 256 nodes on the Summit Supercomputer with a breakdown of 42 tasks per node: 36 on CPUs and 6 on GPUs. We observe good strong scaling with more resources where moving from 32 nodes to 512 nodes showed a speedup of over 6x. We theorize that the speedup starts the breakdown at higher node counts because of the increase in halo data needed to be transferred between neighboring tasks. The volume that each task owns and performs computations within scales down, but performing operation related to the immersed boundary method requires several lattice points in each direction from each neighboring tasks. We expect the halo operations to dominate run time when the task count is significantly increased for this problem size. Thus it is important to choose a proper task count for further simulations that leaves each task’s domain with local computations such that the majority of run time is not spent on neighbor/halo data.
Figure 7:
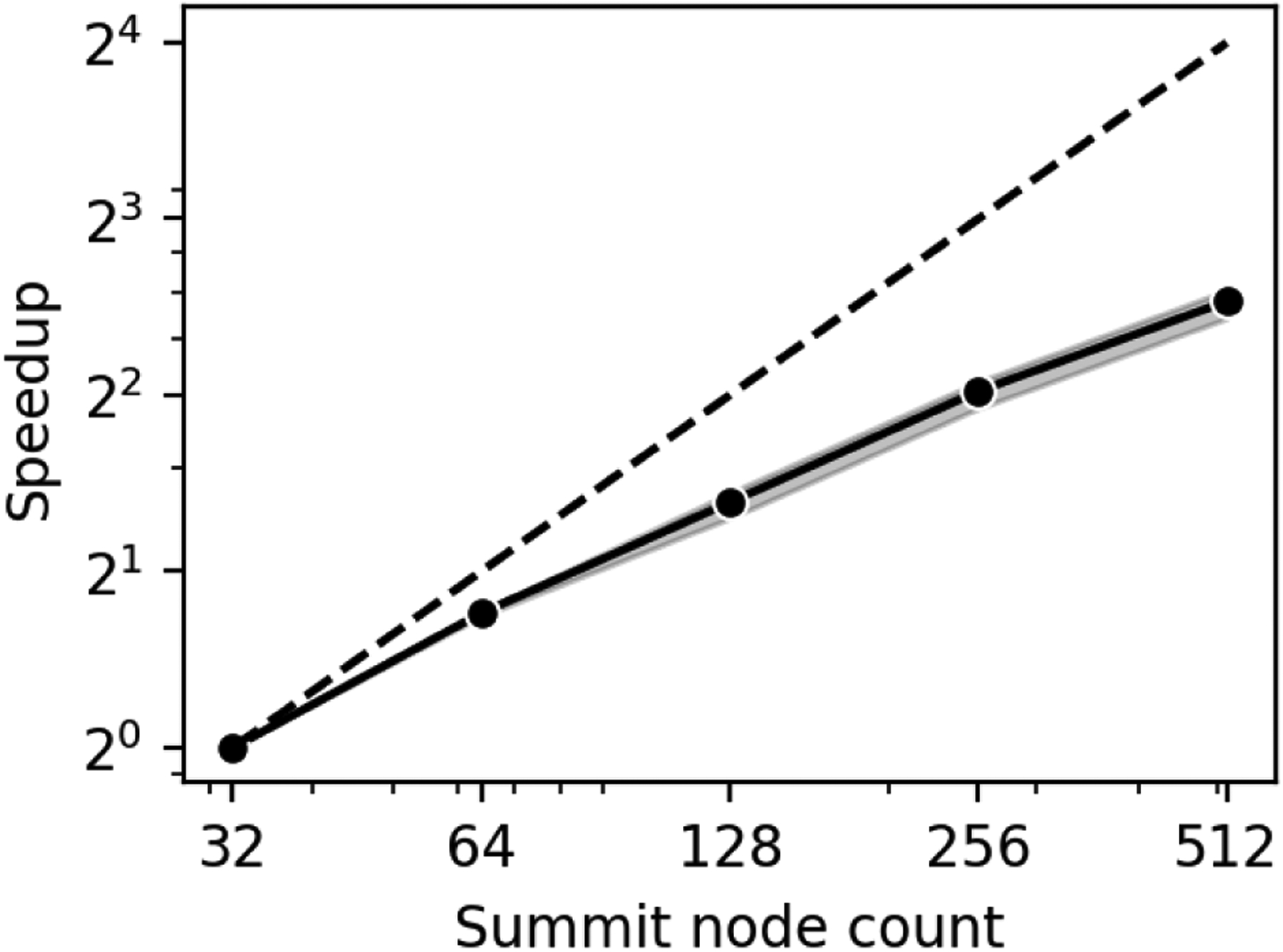
Strong scaling of the coupled window and bulk simulation on Summit using a simplified cubic geometry. A 6x speedup is observed from 32 to 512 nodes.
For the weak scaling in Figure 8, we performed simulations using 1 to 256 nodes on Summit where the number of nodes are increased proportionately with the problem size. This is accomplished by growing the cube and the window while maintaining the volume ratio between the two, asserting that the amount of work on each task is approximately the same. To account for run-to-run variance arising from the interference of other jobs’ communication traffic each case was repeated 10 times where in each simulation roughly 17 × 106 fluid points were maintained per node with 9.1 × 106 bulk fluid points per node and 8.0 × 106 window fluid points per node. A grid spacing of 10 μm in the bulk region and 0.5 μm in the window region was maintained. Around 2400 cells were placed in the simulations with 1 node, linearly scaling up to 6 × 105 cells in the 256-node simulations.
Figure 8:
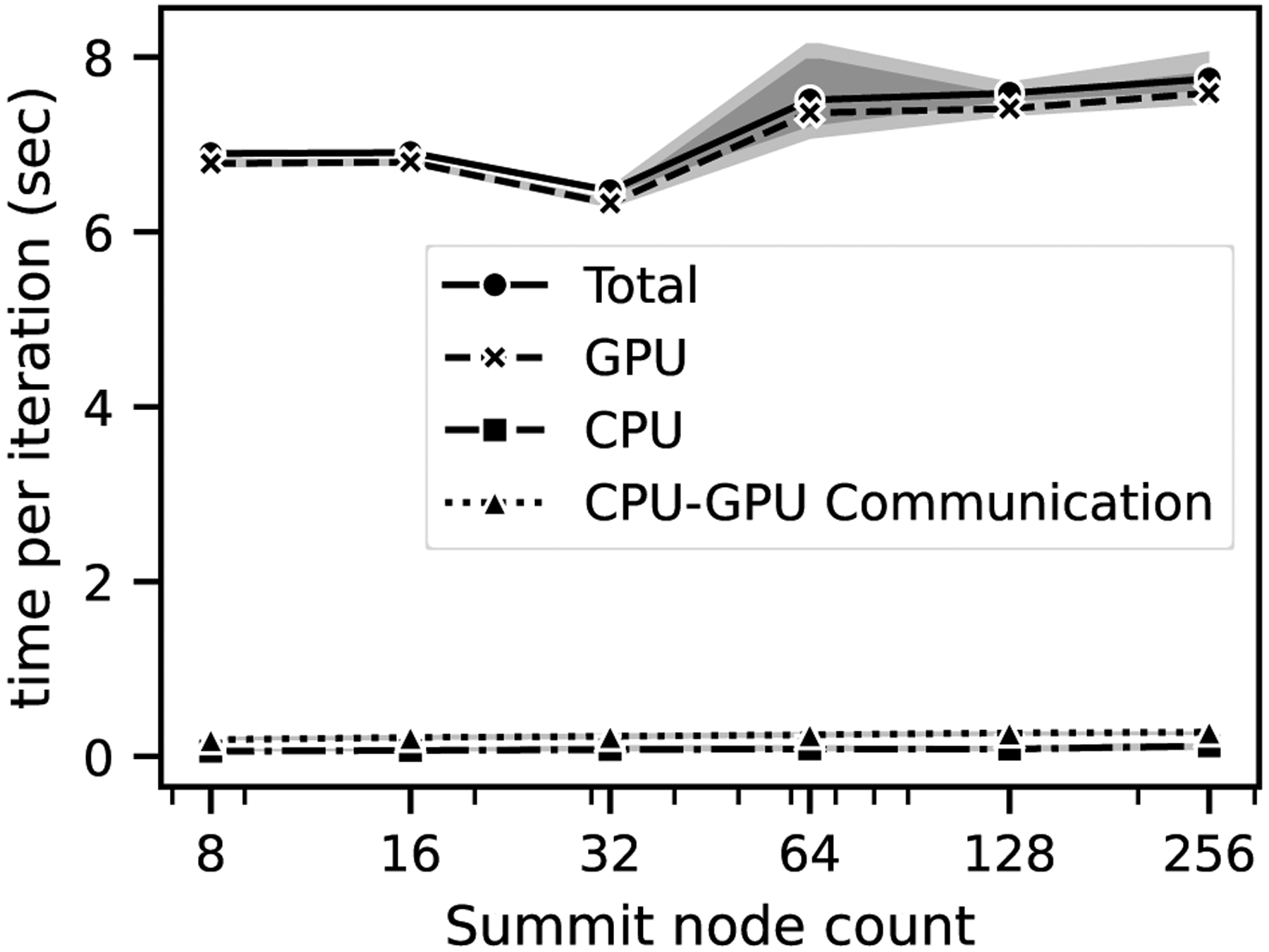
Weak scaling of the coupled window and bulk simulation on Summit. Excellent performance scaling is observed at 8 nodes and above, where full communication volume is reached compared to the 1 to 4 node cases.
We note that the lower node count simulations at 1 to 4 exhibited faster run times, leading to comparatively lower efficiency at the higher node counts. We hypothesize that the communication overhead was not fully realized at the lower node counts from 1 to 4 as each rank did not hit the expected threshold number of neighbors, which resulted in a lower simulation time. At 8 nodes and above, full communication volume was reached, and we observed that the communication per task leveled off which resulted in a more consistent runtime and efficiency at 8+ nodes showed in Figure 8. The efficiency was observed to be 90% for all the cases above 8 nodes which indicated good parallel performance in weak scaling. A breakdown of CPU, GPU timings along with the communication between them showed that for all the cases, most of the total time was spent on the GPUs solving the cellular dynamics within the window and the run-to-run variation arose mainly from the GPUs.
3.5. APR Feasibility Demonstration in Upper Body Vascular Model
To demonstrate the APR model’s large-scale simulation capabilities, we performed a simulation with the upper body vasculature, as visualized in Figure 1. The window domain is set up as a cube with a side length of 1.7 mm (window proper: 1.5 mm, on-ramp: 0.05 mm, injection: 0.05 mm). The domain is filled at 40% Ht, reaching over 20M RBCs. The window fluid domain is treated as a plasma with viscosity of 1.2 cP and a submicron grid spacing of 0.75 μm, and is coupled to the bulk domain which is modeled as whole blood at a 15 μm lattice resolution and viscosity of 4 cP. The simulation is run on 256 nodes on the Summit supercomputer using 1536 v100 GPUs and 10752 Power9 CPUs, with a 6:1 ratio of bulk to window tasks. We find that using this method, we are able to simulate a full volume of 41.0 mL. By comparison, a fully-resolved model at the same fine resolution would only fit 4.98 × 10−3 mL of fluid filled with RBCs using the same compute resources. These fluid volume APR and the eFSI models can simulate are compiled into Table 2.The fully resolved FSI model has a length scale in millimeters, whereas the APR technique can span meters, thus making the APR model a viable method for tracking CTC trajectory over large length scales in the human body while resolving submicron 3D cellular deformations and interactions.
Table 2:
Approximate fluid volume simulated versus resources used for upper body vascular geometry using APR vs small chunk using eFSI. Using the same resources, APR allows the CTC to access significantly larger fluid volumes within a simulation, and thus can capture longer trajectories.
| Model | Δx (μm) | Resource Count | Fluid Volume |
|---|---|---|---|
| APR (window) | 0.5 | 1536 GPUs | 4.91 × 10−3 mL |
| APR (bulk) | 15 | 10752 CPUs | 41.0 mL |
| eFSI | 0.5 | 256 nodes | 4.98 × 10−3 mL |
3.6. Investigating Cancer Dynamics in Full Cerebral Geometry on Cloud Resources
Section 3.5 shows the memory efficiency of the APR algorithm in dealing with cellular resolution. Utilizing this memory efficiency, we aim to target a previously intractable real-world application where we track a cancer cell through a patient-derived cerebral vasculature. Considering a lower bound of 408 bytes of data per fluid point and 51 kilobytes per RBC (using 3 subdivision steps of an initially icosahedral mesh, leading to 1280 elements and 642 vertices), if we wanted to address this problem with a traditional eFSI approach, we would require a total of 9.2 PB of memory. Table 3 summarizes a breakdown of the memory usage for both the eFSI and the APR approaches which shows that APR can handle this problem by using under 100 GB of memory instead of 9.2 PB.
Table 3:
Estimated resource requirements for cerebral geometry using APR vs eFSI. At this grid spacing and resolution ratio, the total estimated memory needed is 5 orders of magnitude smaller using APR. Thus an APR simulation can fit on a single node while the eFSI model would be unable to fit on a single system.
| Model | Δx (μm) | Fluid Pts | Fluid Memory | Num RBCs | RBC Memory |
|---|---|---|---|---|---|
| APR (window) | 0.75 | 1.76 × 107 | 7.2 GB | 2.9 × 104 | 1.48 GB |
| APR (bulk) | 15 | 1.58 × 108 | 64.4 GB | - | 0 |
| eFSI | 0.75 | 1.47 × 1013 | 6.0 PB | 6.3 × 1010 | 3.2 PB |
Exploiting this memory efficiency, we used a single node of virtual machines on AWS with eight NVIDIA Tesla V100 GPUs and 48 Intel Xeon Platinum 8175M CPUs for simulating a cancer cell in the cerebral geometry with a cell-resolved window as depicted in Figure 8. The upper left inset shows a fluid-only simulation for capturing the bulk blood flow at a 100 μm resolution. The main panel showcases the APR approach where we model a window of side length 200 μm and approximately 30,000 RBCs, corresponding to roughly 35% RBC volume fraction, which is representative of physiological hematocrit levels observed in such vasculatures. The APR allows us to have a CPU-based bulk blood flow component at lattice spacing of 15 μm, while for the GPU-based window, a sub-micron lattice spacing of 0.75 μm is utilized. This window resolution is an order of magnitude smaller than the length scale of an individual RBC, which is important to accurately capture the fluid flow field that conveys the cells and in turn, accurately resolves the complex deformation of the individual cells. The image in the lower right shows the deformed CTC and surrounding RBCs, with contours on the RBC surfaces giving forces determined by the FEM in response to deformation.
The solid yellow line depicts the trajectory of the CTC tracked by the moving window, traversing 1.5 mm per day over the course of 96 node-hours. The dotted yellow line represents the predicted motion of the cell if the simulation were to run for 500 node-hours. Thus, using the APR method enables CTC traversal thousands of times its diameter, allowing body-scale simulations using only a fraction of the node-hours a traditional eFSI would utilize, making these large length scale simulations computationally tractable.
4. CONCLUSION
In this study, we have made significant strides in simulating cancer cell transport by incorporating explicit red blood cells in the hybrid CPU-GPU APR framework. This method can capture cellular trajectory at much larger distances than previously possible, enabling accurate tracking of cancer cells through large portions of the human vasculature.
We demonstrate that the new model can couple regions of varying viscosity, representing whole blood in the bulk and plasma in the window, while effectively maintaining a target volume fraction of red blood cells and effective viscosity within the window over time. Moreover, we demonstrate the efficacy of the APR model in recovering the average radial trajectory of CTCs with significantly lower computational cost than the conventional eFSI method. The scalability of our approach is also proven, with good strong and weak scaling behaviors observed on the Summit supercomputer. To further illustrate the capability of our approach, we conduct a capability demonstration using APR within an upper body geometry, which makes previously-intractable systems accessible with modest HPC resources. Finally, we show ongoing results on a brain cancer metastasis study, where we track a CTC over mm-scale lengths within a cerebral vasculature using a single AWS compute node.
By incorporating RBCs at realistic hematocrit with the APR method, we move towards the digital realization of increasing physiologically accurate systems. We show how this approach overcomes the challenges of integrating a submicron-scale resolution required to resolve cellular interactions with a system-level model of the whole body. By making large-scale transport simulations computationally viable, this approach opens up new opportunities for understanding cellular-scale biophysical mechanisms in hemodynamics and cancer metastasis, allowing for more accurate predictions about how the disease spreads and further insight towards treatment.
Figure 2:
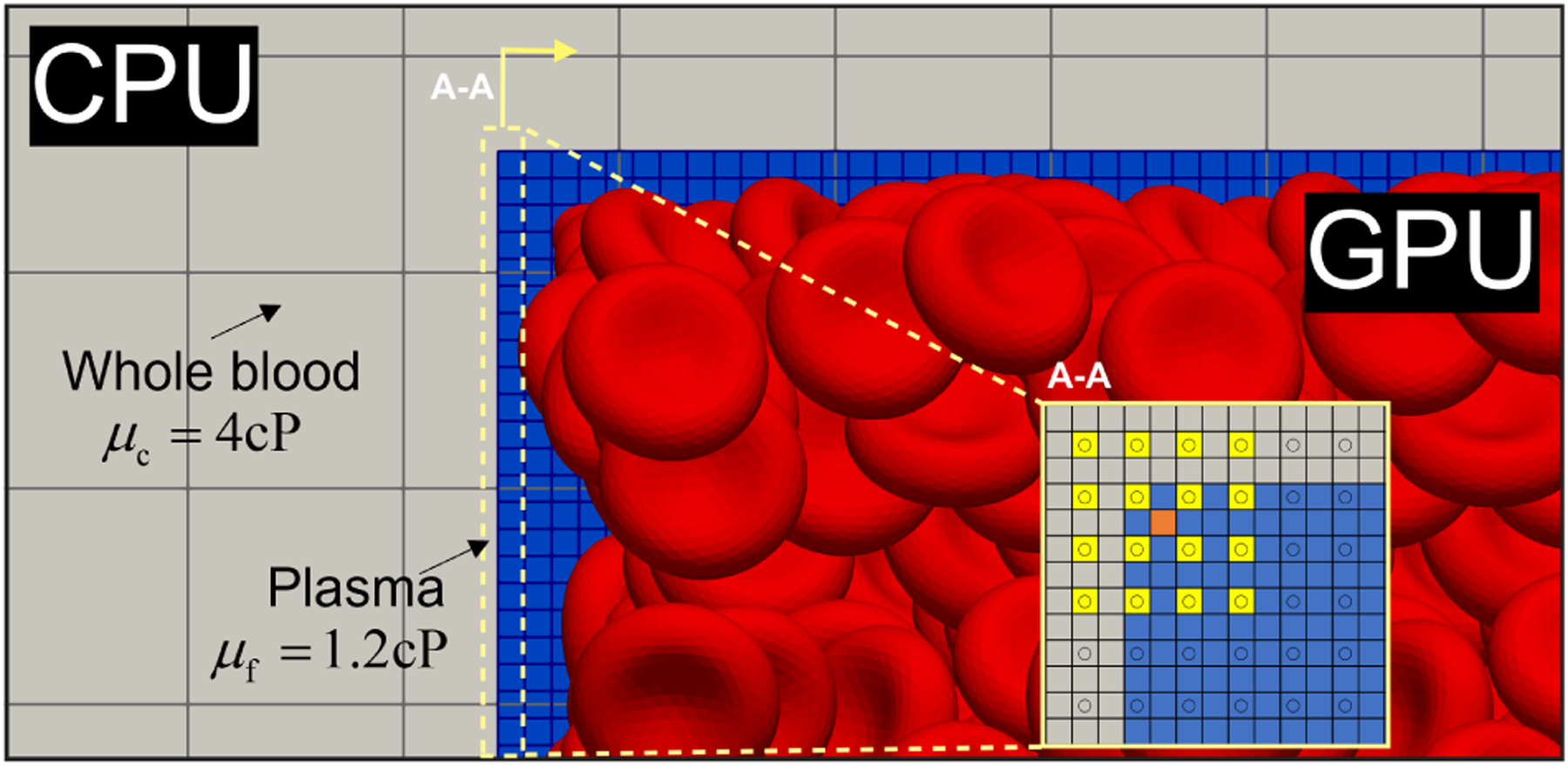
The APR model accounts for both varying resolutions and viscosities at the interface, illustrated here. The gray region depicts the coarsely resolved bulk domain as whole blood while the blue region represents the finely resolved window domain as a suspension of RBCs in plasma. The inset shows an orthogonal perspective of the interface between the fine and coarse lattices, with an example interpolation of the orange square from the yellow square support.
Figure 9:
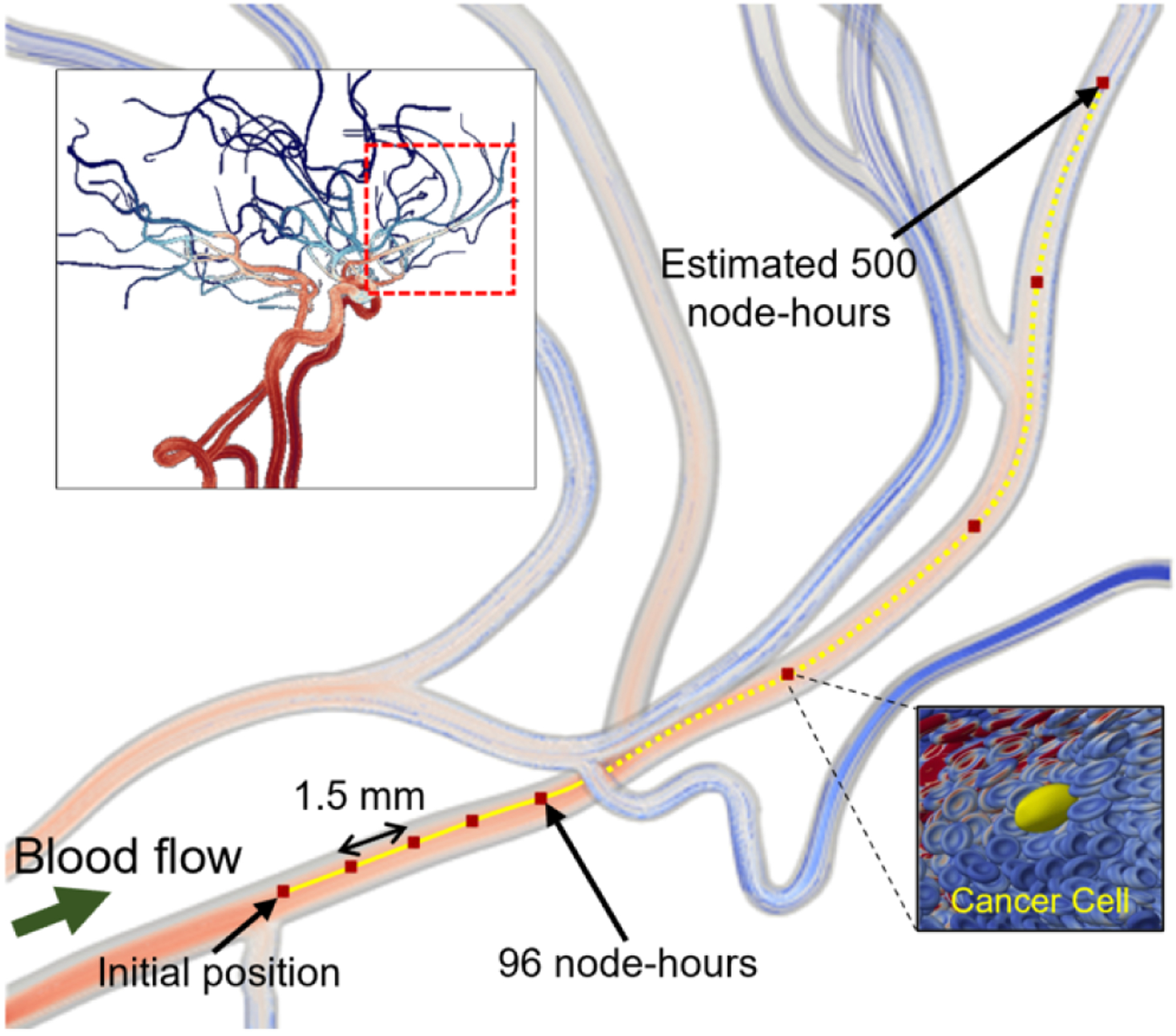
The APR method makes submicron fidelity simulations of CTC trajectory over mm-length scales tractable. We perform an APR simulation of cancer cell transport through a cerebral vasculature on AWS, using one node of VMs with eight NVIDIA Tesla V100 GPUs and 48 Intel Xeon Platinum 8175M CPUs. The upper-left panel provides streamlines through a patient-derived cerebral vasculature. The main panel provides a zoomed-in view of the window the location encompassed by the red dashed box in the upper-left panel. The solid yellow line traces the cancer cell trajectory as it is transported at a rate of 1.5 mm per simulation day, with the dashed yellow line predicting 500 node-hours to travel the entire length of the zoomed-in vessel. The lower-right panel shows the deformed CTC in yellow and its surrounding RBCs.
CCS CONCEPTS.
Applied computing → Biological networks; • Computing methodologies→ Multiscale systems; Massively parallel and high-performance simulations.
ACKNOWLEDGMENTS
The authors would like to thank Cyrus Tanade, Ayman Yousef, and Nusrat Sadia Khan for their helpful feedback through the writing and stages of this project.
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a nonexclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan). Research reported in this publication was supported by National Institutes of Health under Award Number U01-CA253511 and NSF Career Award 1943036. Computing support for this work came from the DOE IN-CITE program and the Lawrence Livermore National Laboratory (LLNL) Institutional Computing Grand Challenge program.
Appendix: Artifact Description/Artifact Evaluation
ARTIFACT IDENTIFICATION
This study presents a novel extension to an advanced physics refinement model. The extension incorporates red blood cells to enable accurate tracking of cell dynamics during the movement of cancer cells in the bloodstream. We used HARVEY, a massively parallel fluid dynamics solver, to obtain the simulation results presented in this study. HARVEY is generally available under a proprietary research license from Duke University. This license has a provision for a free license for academic use. For access, contact the Duke Office of Licensing and Ventures.
Computing platforms:
Most simulations utilize the Summit supercomputer at Oak Ridge National Laboratory, where each node contains 2 22-core POWER9 CPUs and 6 NVIDIA V100 GPUs connected via NVLink, capable of a 25GB/s transfer rate.
The final simulation with the cerebral geometry (results shown in Figure 8) is run using an Amazon Web Services EC2 instance with 8 NVIDIA Tesla V100 GPUs and 48 Intel Xeon Platinum 8175M CPUs connected via NVLink. These contain 256 GB of GPU memory and 768 GB of CPU memory, with a network bandwidth of 100 Gbps.
All artifacts can be found here: http://doi.org/10.7924/r42233d04
REPRODUCIBILITY OF EXPERIMENTS
Experimental workflow, general summary: Each set of simulations are performed using HARVEY. The simulation domain is specified using a geometry in the form of an OFF file. Input parameters, including fluid velocity, hematocrit, viscosity ratio between finely-resolved window and bulk fluid, and others, are all specified in the text for each specific figure. The software outputs several metrics, including the fluid profile in both regions, the trajectory of the cancer cell, current hematocrit, and the calculated pressure drop.
Upper body simulations. Figure 1 Two sets of simulations are performed in the upper body vasculature. First, an eFSI branch of the HARVEY codebase is used to run a small subsection of the upper body geometry on 24.5k GPUS on Summit, shown on the left side of the Figure. The relevant inputs and output cell data are in the upperbody_efsi folder. Next, a simulation is performed within a high-resolution domain, referred to as the APR window, to demonstrate the length scale it enables; this is done on 1.5k GPUS and 10.8k CPUs on Summit. Cell data and upper body geometry are located in upperbody_apr folder.
Shear flow validation. Figure 4 Simulations are performed in a rectangular prism with shear flow. Three viscosity contrasts (1/2, 1/3, 1/4) are used with three resolution ratios (n = 2, 5, 10). Each simulation is run on one node with 32 tasks evenly split among the APR window and bulk fluid. Fluid results and input geometry are placed in the folder shearflow. The fluid profile in each region is output into a CSV file with the velocity at each fluid node. An analytical solution is calculated using equation (8). A python script is used to extract fluid velocities along a slice in the x-z plane, located at shearflow/analysis_script/shearflowErrorTest2.py. We plot the analytical versus simulation results and generate the error difference between the analytical versus the bulk and finely-resolved regions in the spreadsheet shear_figures.xlsx.
Hematocrit maintenance and effective viscosity. Figure 5 Three simulations at varying hematocrit (10%, 20%, 30%) are performed using a tube of diameter 200 μm and a cell-resolved window with side length 100 μm, each run on 2 nodes with 84 tasks evenly distributed among the APR window and bulk fluid. Plots are generated from the simulation outputs of hematocrit versus time. The simulation effective viscosity is calculated using equation (12) with the pressure drop output while the experimental correlation is calculated using equation (9). Results and the geometry are placed in the folder hctvisctests.
Cancer cell trajectory. Figure 6 Comparison of CTC motion in a fully-resolved model with red blood cells in the entire domain versus the proposed APR method with only a small window containing red blood cells. The CTC is tracked in each simulation and the xyz coordinates are extracted for the visualization. The eFSI simulations are performed on 64 nodes using 384 GPUs while the APR runs are performed on 8 nodes with 48 GPUs and 336 CPUs, both on Summit. Radial displacement is calculated by distance to the channel’s centerline. Cell trajectory results and the expansion channel geometry are placed in the folder ctctrajectory.
Scaling results. Figure 7 Strong and weak scaling problems are considered. For strong scaling, we use a cube with side length 10.5 mm and a window of side length 0.65 mm in the center of the geometry with a resolution ratio of 10. Node count is varied from 64 to 256. Simulations are run for 100 timesteps and an average wall time per step is calculated. Speedup is presented as a ratio of run time compared to the base 64 node case. For weak scaling runs, we scale the cube volume by the number of nodes in order to maintain the fluid volume per node as constant from 1 to 256 nodes. Efficiency is calculated in comparison to the baseline 8 node count, as explained in the text. Timing data can be found in the folder scaling.
Cerebral CTC tracking simulation. Figure 8 Simulation of a CTC in a window in the cerebral geometry is performed on a single AWS cloud node with 56 tasks distributed in a 6:1 ratio among the CPUs and GPUs, respectively. Memory footprints are calculated using the estimated values specified in the text. CTC trajectory and the vascular geometry can be found in the folder cerebral.
ARTIFACT DEPENDENCIES REQUIREMENTS
N/A
ARTIFACT INSTALLATION DEPLOYMENT PROCESS
N/A
Contributor Information
Sayan Roychowdhury, Duke University, Durham, NC, USA.
Peter Balogh, Duke University, Durham, NC, USA.
Samreen T. Mahmud, Duke University, Durham, NC, USA
Daniel F. Puleri, Duke University, Durham, NC, USA
Aristotle Martin, Duke University, Durham, NC, USA.
John Gounley, Oak Ridge National Laboratory, Oak Ridge, TN, USA.
Erik W. Draeger, Lawrence Livermore National Laboratory, Livermore, CA, USA
Amanda Randles, Duke University, Durham, NC, USA.
REFERENCES
- [1].Wirtz Denis, Konstantopoulos Konstantinos, and Searson Peter C. The physics of cancer: the role of physical interactions and mechanical forces in metastasis Nature Reviews Cancer, 11(7):512–522, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Mitchell Michael J, Wayne Elizabeth, Rana Kuldeepsinh, Schaffer Chris B, and King Michael R. Trail-coated leukocytes that kill cancer cells in the circulation. Proceedings of the National Academy of Sciences, 111(3):930–935, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Sharma Ragav and Sharma Sandeep. Physiology, blood volume. 2018. [PubMed]
- [4].Puleri Daniel F, Roychowdhury Sayan, Balogh Peter, Gounley John, Draeger Erik W, Ames Jeff, Adebiyi Adebayo, Chidyagwai Simbarashe, Hernández Benjamín, Lee Seyong, et al. High performance adaptive physics refinement to enable large-scale tracking of cancer cell trajectory. In 2022 IEEE International Conference on Cluster Computing (CLUSTER), pages 230–242. IEEE, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Herschlag Gregory, Gounley John, Roychowdhury Sayan, Draeger Erik W, and Randles Amanda. Multi-physics simulations of particle tracking in arterial geometries with a scalable moving window algorithm. In 2019 IEEE International Conference on Cluster Computing (CLUSTER), pages 1–11. IEEE, 2019. [Google Scholar]
- [6].Wang Peng, Abel Tom, and Kaehler Ralf. Adaptive mesh fluid simulations on gpu. New Astronomy, 15(7):581–589, 2010. [Google Scholar]
- [7].Calder Alan C, Curts BC, Dursi LJ, Fryxell Bruce, Henry Greg, MacNece P, Olson Kevin, Ricker P, Rosner Robert, Timmes Francis X, et al. High-performance reactive fluid flow simulations using adaptive mesh refinement on thousands of processors. In SC’00: Proceedings of the 2000 ACM/IEEE Conference on Supercomputing, pages 56–56. IEEE, 2000. [Google Scholar]
- [8].Randles Amanda Peters, Kale Vivek, Hammond Jeff, Gropp William, and Kaxiras Efthimios. Performance analysis of the lattice Boltzmann model beyond Navier-Stokes. In Parallel & Distributed Processing (IPDPS), 2013 IEEE 27th International Symposium on, pages 1063–1074. IEEE, 2013. [Google Scholar]
- [9].Randles Amanda, Draeger Erik W, and Bailey Peter E. Massively parallel simulations of hemodynamics in the primary large arteries of the human vasculature. j Comp Sci, 9:70–75, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Gounley John, Draeger Erik W, and Randles Amanda. Immersed Boundary Method Halo Exchange in a Hemodynamics Application. LNCS, pages 441–455, 2019. doi: 10.1007/978-3-030-22734-0_32. [DOI] [Google Scholar]
- [11].Ames Jeff, Puleri Daniel F, Balogh Peter, Gounley John, Draeger Erik W, and Randles Amanda. Multi-gpu immersed boundary method hemodynamics simulations. journal of Computational Science, page 101153, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Chen Shiyi and Doolen Gary D. Lattice Boltzmann method for fluid flows. Ann Rev Fluid Mech, 30(1):329–364, 1998. [Google Scholar]
- [13].Gounley John, Draeger Erik W, and Randles Amanda. Numerical simulation of a compound capsule in a constricted microchannel. Procedia Comput Sci, 108: 175–184, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Walter J, Salsac A-V, Barthès-Biesel D, and Le Tallec P. Coupling of finite element and boundary integral methods for a capsule in a Stokes flow. International journal for Numerical Methods in Engineering, pages n/a-n/a, 2010. ISSN 00295981. doi: 10.1002/nme.2859. [DOI] [Google Scholar]
- [15].Cirak Fehmi, Ortiz Michael, and Schroder Peter. Subdivision surfaces: a new paradigm for thin-shell finite-element analysis. Int j Numer Methods Eng, 47(12): 2039–2072, 2000. [Google Scholar]
- [16].Zhong-Can Ou-Yang and Helfrich Wolfgang. Bending energy of vesicle membranes: General expressions for the first, second, and third variation of the shape energy and applications to spheres and cylinders. Physical Review A, 39(10):5280, 1989. [DOI] [PubMed] [Google Scholar]
- [17].Balogh Peter and Bagchi Prosenjit. A computational approach to modeling cellular-scale blood flow in complex geometry. j Comp Phys, 334:280–307, 2017. [Google Scholar]
- [18].Pepona Marianna, Gounley John, and Randles Amanda. Effect of constitutive law on the erythrocyte membrane response to large strains. Computers & Mathematics with Applications, 132:145–160, 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Peskin Charles S. The immersed boundary method. Acta Numerica, 11:479–517, 2002. [Google Scholar]
- [20].Liu Wai-Hung and Sherman Andrew H. Comparative analysis of the cuthillmckee and the reverse cuthill–mckee ordering algorithms for sparse matrices. SIAM Journal on Numerical Analysis, 13(2):198–213, 1976 [Google Scholar]
- [21].Pries Axel R, Neuhaus D, and Gaehtgens P. Blood viscosity in tube flow: dependence on diameter and hematocrit. American journal of Physiology-Heart and Circulatory Physiology, 263(6):H1770–H1778, 1992. [DOI] [PubMed] [Google Scholar]
- [22].Fung Yuan-cheng. Biomechanics: circulation. Springer Science & Business Media, 2013. [Google Scholar]
- [23].Pries Axel R, Secomb Timothy W, Gaehtgens P, and Gross JF. Blood flow in microvascular networks. experiments and simulation. Circulation research, 67(4): 826–834, 1990. [DOI] [PubMed] [Google Scholar]
- [24].Skalak R, Tozeren A, Zarda RP, and Chien S. Strain Energy Function of Red Blood Cell Membranes. Biophysical journal, 13(3):245–264, 1973. ISSN 00063495. doi: 10.1016/S0006-3495(73)85983-1. URL http://dx.doi.org/10.1016/S0006-3495(73)85983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Jain Abhishek and Munn Lance L. Determinants of leukocyte margination in rectangular microchannels. PloS one, 4(9):e7104, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Shaw Bagnall Josephine, Byun Sangwon, Begum Shahinoor, Miyamoto David T, Hecht Vivian C, Maheswaran Shyamala, Stott Shannon L, Toner Mehmet, Hynes Richard O, and Manalis Scott R. Deformability of tumor cells versus blood cells. Scientific reports, 5(1):1–11, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Krüger Timm, Holmes David, and Coveney Peter V. Deformability-based red blood cell separation in deterministic lateral displacement devices—a simulation study. Biomicrofluidics, 8(5):054114, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Roychowdhury Sayan, Gounley John, and Randles Amanda. Evaluating the influence of hemorheological parameters on circulating tumor cell trajectory and simulation time. In Proceedings of the Platform for Advanced Scientific Computing Conference, pages 1–10, 2020. [Google Scholar]


