High Performance Adaptive Physics Refinement to Enable Large-Scale Tracking of Cancer Cell Trajectory

Abstract

The ability to track simulated cancer cells through the circulatory system, important for developing a mechanistic understanding of metastatic spread, pushes the limits of today’s supercomputers by requiring the simulation of large fluid volumes at cellular-scale resolution. To overcome this challenge, we introduce a new adaptive physics refinement (APR) method that captures cellular-scale interaction across large domains and leverages a hybrid CPU-GPU approach to maximize performance. Through algorithmic advances that integrate multi-physics and multi-resolution models, we establish a finely resolved window with explicitly modeled cells coupled to a coarsely resolved bulk fluid domain. In this work we present multiple validations of the APR framework by comparing against fully resolved fluid-structure interaction methods and employ techniques, such as latency hiding and maximizing memory bandwidth, to effectively utilize heterogeneous node architectures. Collectively, these computational developments and performance optimizations provide a robust and scalable framework to enable system-level simulations of cancer cell transport.

I. Introduction

Cancer is the attributed cause of death in one in four cases in the United States [1] and metastasis, a complex multistep process leading to the spread of tumors, is responsible for more than 90% of these deaths [2]. While we know that circulating tumor cells arrest in non-random patterns and that biophysical properties influence their movement, the effect of different mechanical properties of the cell and microenvironment on preferential arrest remain poorly understood. In silico models designed to model cellular transport in complex 3D topologies provide a unique ability to isolate the influence of specific cell properties and extract a variety of metrics that cannot be directly measured through in vivo or in vitro methods. To properly simulate metastatic dissemination, computational methods need to capture arterial length scales orders of magnitude larger than the size of the cell. However, direct numerical simulation that relies on sub-micron resolution is intractable for all but the smallest systems.

To effectively model cancer cell transport, we have developed an adaptive physics refinement (APR) technique. The APR integrates multiphysics modeling by limiting the region in which cellular-scale dynamics are realized to the volume surrounding a cell of interest—termed the “window,” after initially exploring the concept in [3]. Resolving cell dynamics only in the window has the benefits of capturing fluid-structure interaction that could not be explained purely through hemodynamics, reducing the amount of computationally expensive high-resolution mesh, and limiting the locations in which fluid-structure interaction is needed. The APR window is required to adaptively follow the cell of interest because the distances a cell can meaningfully travel are larger than the window itself. We tailored the APR algorithm to the problem of tracking cancer cells because the region requiring a more refined resolution is defined by a moving location and not by an error estimation (e.g., [4]) which informs refinement during the simulation itself. Additional benefits are afforded because the adaptive window can be defined at the start of the simulation. Therefore, the APR scheme is designed for modern heterogeneous systems whereby the window is distributed on all GPUs and the coarsely-resolved regions can use the remaining processor cores.

The limited scope of past modeling to small sub-regions or short time domains is due in part to the computational challenge associated with modeling large-scale cellular behavior using conventional modeling frameworks, which we refer to as explicit fluid-structure interaction models (eFSI). Current state-of-the-art eFSI (details of which can be found in [5]) are limited to sub-mm cubed domains when simulating the resolutions necessary to capture the cell’s viscoelastic properties, making it impossible to quantify the effects of individual cell mechanical properties on long-term cell fate and overall trajectory. To overcome this fundamental limitation, we introduce the APR technique to provide system scale modeling at cellular resolution within a localized region of interest. The state-of-the art eFSI model is built upon and could be considered a subset of the APR approach. The APR method, as shown in Figure 1, defines a high-resolution FSI window that follows an assigned cell as it flows through a target geometry. The window size and FSI algorithm are chosen to accurately capture the environment around the target cell, with the surrounding lower-resolution fluid used to enable accurate window motion. Compared with eFSI, the APR framework drastically reduces the overall computational cost, making it feasible to analyze cell transport over anatomically-relevant length scales (cm to m).

Fig. 1.

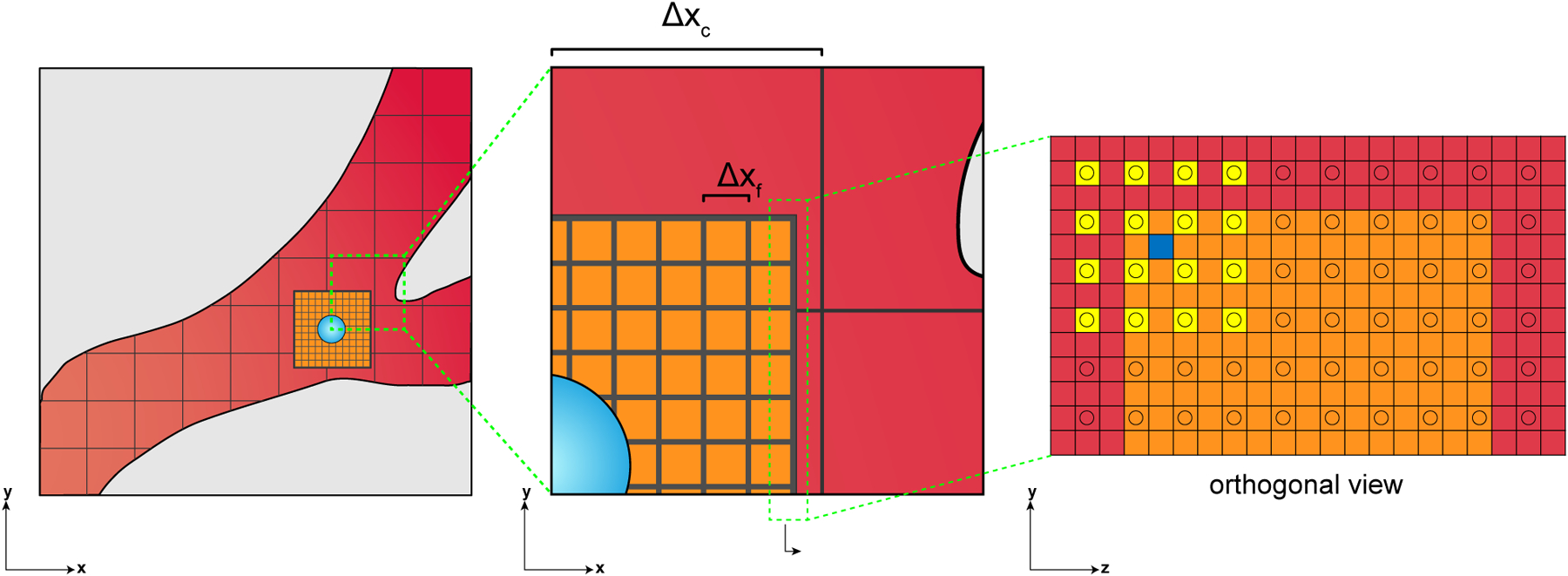
Left: APR model overview depicting the coupling between the the finely resolved fluid-structure interaction within the window (orange) to a coarsely-resolved bulk fluid domain (red). Middle: a closer view of the multi-resolution interface between the fine and coarse regions. Right: an orthogonal perspective of the interface between the fine and coarse lattices, with an example interpolation to the blue square from the support of the yellow squares. Lattice points for each domain are located at the centroids of the grid made by the black lines, where Δx_c and Δx_f refer to the lattice resolution of the coarse and fine grids, respectively. The resolution ratio, n = Δx_c/Δx_f, between the bulk and the window has been reduced for display purposes.

Building a coupled multiphysics capability to be broadly used for circulatory modeling requires addressing multiple algorithmic challenges due to 1) multi-resolution coupling: the sub-micron resolution fluid in the window must be accurately coupled to the coarser fluid in the bulk for the proposed moving window approach to be feasible; 2) adaptive physics refinement: the posed problem requires not just coupling varied grid resolutions, but different physics-based models. Within the window, different explicit cell models may be used depending on the system and flow, whereas outside the window we only solve fluid dynamics equations; and 3) resource allocation: in addition to the challenges of efficiently distributing the 3D geometries across many compute elements, balancing both compute and memory requirements of the window and the bulk regions between CPU and GPU requires careful management.

We address these challenges by introducing a hybrid CPU-GPU, multiphysics technique innovating upon our previously established moving window paradigm [3] by 1) introducing a multi-block scheme to couple the coarse and fine lattices, 2) creating a framework for splitting scales between a tightly coupled CPU-based bulk model and a GPU-based window model, 3) developing algorithms to move the window, and 4) efficiently distributing work between the host and device on a heterogeneous accelerator-based machine such as the Summit supercomputer while maximizing overlap of communication and computation. As demonstrated in our results, the APR method we present radically increases the potential domain sizes for multiphysics modeling to enable new classes of problems to be tackled with in silico methods.

II. Methods and Algorithmic Developments

After decades of innovation [4], [6]–[8], there are now many numerical approaches one can use to design a multiphysics code with varying degrees of sophistication. The APR method presented in this paper represents one such approach that is tailored to the specific needs of circulatory modeling. A key feature is the use of a single, moving region of interest in which the numerical accuracy required remains constant throughout the simulation. Such specialization has several advantages. For example, this numerical decomposition creates two well-contained domains (see Fig. 1) with a sharp interface, thereby creating a natural decomposition of computationally-intense window tasks mapped onto GPUs and lower-resolution fluid tasks mapped onto CPUs with manageable communication across the fully-coupled interface. High GPU utilization can be maintained throughout the simulation thanks to the fixed window size. As the simulation evolves, the cell of interest can accurately traverse a large branching geometry without a priori assumptions about its ultimate destination.

We have previously established the window paradigm in Herschlag et al., whereby the modeling of cell-resolved flow is restricted to a small region around the cell [3]. The focus on that work was on maintaining the requisite hematocrit (red blood cell volume fraction) for biological blood flow and partitioning the simulation domain into regions where different physics are resolved so as to reduce the total number of cells explicitly modeled. In this manuscript, we significantly advance the adaptive window method by developing a multi-resolution scheme which adapts to the motion of the tracked cancer cell. Our scheme uses the nature of the problem itself, tracking deformable cells of interest, to drive the adaptive resolution as the level of detail is not driven by the fluid itself, but by the cells within the fluid. This new expression of the problem brings with it challenges, which we have overcome, regarding the distribution of work between the finely-resolved window domain, the two-way coupling of physics, and the methods required to move the window as the cell’s trajectory evolves. An additional computational difference is which domain is accelerated on GPUs.

Within the following subsections we outline the components of the APR method. A diagram providing a depiction of the overall algorithm is shown in Fig. 2. The coupled multiphysics model is developed within a lattice Boltzmann method (LBM)-based massively parallel computational fluid dynamics solver [5], [9]–[11]. The existing GPU-accelerated FSI model was further optimized for Summit, a 200 petaFLOPS heterogeneous supercomputer at the Oak Ridge Leadership Computing Facility [12]. We additionally augmented the adaptive multiphysics algorithm pioneered in [3] with the layer of the multi-block/multi-resolution interface between the cell-resolved domain and the bulk flow domain. To integrate the fine-window simulation with the coarse-bulk, we implemented and extended a multi-resolution algorithm previously developed in the literature [13]–[16]. In those previous multi-block approaches, the finely-resolved domain was primarily static and here we show a novel way of changing the domain as the transient system simulated advances. The details of these components, as well as new algorithmic developments, optimizations, and our process for validating the implementation are described in the subsections below.

Fig. 2.

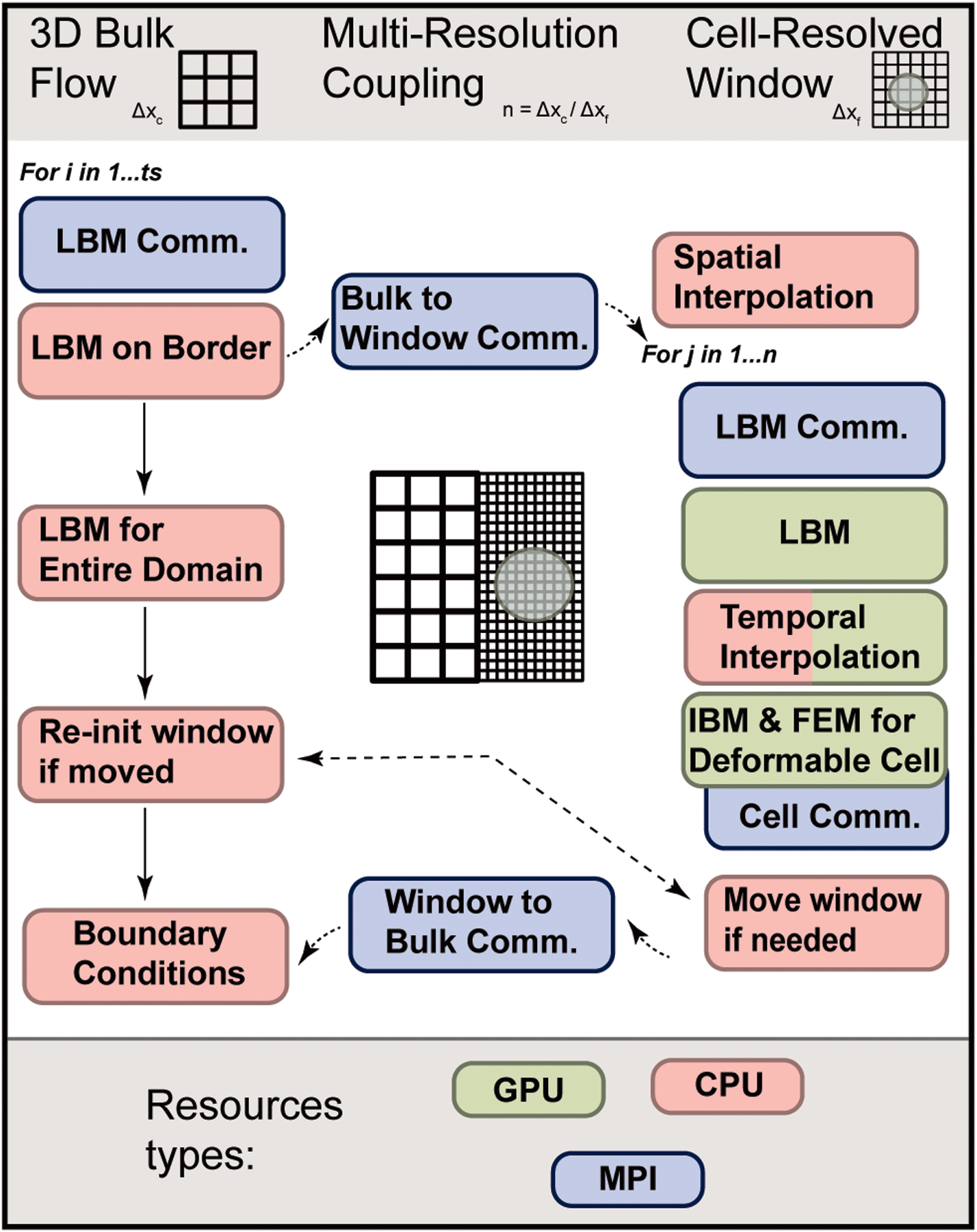
Diagrammatic depiction of the overall algorithm for one bulk time step. Operations have been batched into a single category for simplicity. The shown structure reflects optimizations to best overlap compute-intensive simulation time steps on the GPU/window with the CPU/bulk. The only synchronization points between the window and bulk parts of the APR model are the bulk-to-window, window-to-bulk communication routines, and checking/re-initialization if the window moves.

A. Lattice Boltzmann Method

The LBM is a mesoscopic approach for numerically solving the Navier-Stokes equations, in which the fluid is represented as set of particles moving between lattice nodes in discrete time steps [17]. The lattice Boltzmann equation governs the evolution of a particle distribution function f_i(x,t), which gives the probability of particles residing at lattice point x and time t with a discrete velocity c_i. Using the Bhatna-gar–Gross–Krook (BGK) collision operator, this equation in the presence of an external force field is:

$$f_i\left(\mathbf{\text{x}}+{\mathbf{\text{c}}}_i,t+1\right)=\left(1-\frac{1}{\tau }\right)f_i(\mathbf{\text{x}},t)+\frac{1}{\tau }{f}_i^{eq}(\mathbf{\text{x}},t)+F_i(\mathbf{\text{x}},t)$$ (1)

for an external force distribution F_i, equilibrium distribution $f_i^{eq}$, and relaxation time τ. This equation encapsulates the two core components of the LBM time step – collision and streaming – which are implemented as a single unified kernel in code. We employ the D3Q19 velocity discretization model, as well as the method of Guo et al. [18] to incorporate the external force field into the distribution. No-slip conditions on rigid walls are enforced using the halfway bounce-back boundary conditions at the vessel walls.

B. Cell Finite Element Model

Cancer cells are represented as fluid-filled membranes discretized by a Lagrangian surface mesh of triangular elements. The membrane model includes both elasticity and bending stiffness [19]. The shear and dilational elastic responses of the membrane are governed by the Skalak constitutive law, where the elastic energy W_s is computed as: $W_s=\frac{G_s}{4}\left(I_1^2+2I_1-2I_2+C{I}_2^2\right)$ for strain invariants I₁, I₂, shear elastic modulus G_s, and area preservation constant C [20]. Loop subdivision [21] provides the basis for the finite element method (FEM) membrane force calculations, which determine elemental strains based on 12 surrounding elements. Details on the finite element method used can be found in previous works, such as [22] and [23]. The Helfrich formulation [24] is used to model resistance to bending based on membrane curvature following: $W_b=\frac{E_b}{2}{\int }_S{\left(2\kappa -c_0\right)}^2$, where E_b is the bending modulus, κ and c₀ are the mean and spontaneous curvatures, respectively, and S is the entire surface area of the cell. The resultant membrane forces are calculated every timestep in the same simulation code and used for the spreading routine in the immersed boundary coupling. Overall, this method has been shown to accurately resolve complex non-linear 3D deformations of biological cells [25] and was recently accelerated on GPUs [5].

C. Immersed Boundary Method

The immersed boundary method (IBM) [26] is used to couple the FEM-calculated forces in cell membranes to the background fluid with which they flow and has been previously demonstrated to capture cancer cell trajectory (e.g., [27]). First, a cell vertex’s velocity V is interpolated from the velocities v of surrounding fluid points x using:

$$V(X,t)=\sum _{x}v(x,t)\delta (x-X(t))$$ (2)

We use a cosine-approximated 3D discrete delta function (δ) with four-point support in each dimension, as described in [11]. Using these velocities, the positions of the cell vertices are updated using Euler integration,

$$X(t+1)=X(t)+V(t)\Delta t$$ (3)

a process referred to in the subsequent sections as advection. The elemental deformation associated with these position changes are determined with the FEM as above, and the resulting forces G at each cell vertex X are spread back to the surrounding fluid points x as:

$$g(x,t)=\sum _{X}G(X,t)\delta (x-X(t))$$ (4)

In the subsequent sections, the algorithms and operations associated with equations 2 and 4 are respectively referred to as interpolation and spreading.

D. Innovations and Implementation of APR Algorithm

When modeling biological cells in the circulatory system, one of the main computational expenses comes from the fluid resolution needed to accurately recapitulate the flows of deformable cells within the circulatory system. As the required resolution drives computational cost, there is a motivation to limit it to targeted regions of interest. Moreover, the relationship between the resolution and time step in the LBM (further detailed in Sec. II-D1) leads to a greater computational burden and inherent complexity as multiple time steps are needed within the window for every bulk fluid time step. Therefore, it was paramount that the bulk and window domains of the simulation be concurrently advancing and that the window be accelerated by the high bandwidth and computational power available on GPUs in modern heterogeneous systems (see Sec. II-E). Our solution to address these challenges is the APR method. The originality of the overall concept presented herein is a moving, finely-resolved domain centered on the cell of interest which is fully coupled to the surrounding lower-resolution environment. The combination of the multiresolution scheme presented in Sec. II-D1 coupled with an enhanced version of the window tracking algorithm (Sec. II-D2) provides a tailored multi-physics adaptive model to track cells across a range of vessel sizes.

1). Multi-Resolution Lattice Boltzmann:

To simultaneously model both macro- and micro-scale blood flows present in the body, we implemented a multi-block LBM (multi-resolution) scheme for efficient computation. Specifically, we extended a scheme developed in 2D [13], [14] and adapt it to 3D similar to Yu et al. and others [15], [16]. However, one of the main differences between our implementation of the ‘traditional’ multi-resolution LBM algorithms and previous literature is that we maintain the underlying physics of the static multi-block methods previously described and significantly expand this approach to derive an adaptive algorithm through the coupling with the adaptive multi-physics moving window algorithm so that the model adapts over time given the transient nature of the problem being studied.

Following Peng et al. [14], we consider a multi-block scheme which couples a coarse lattice to a fine lattice. Given the continuity in density and momentum between the coarse and fine grids, the equilibrium distribution functions of each lattice are equal [13]:

$$f_i^{\text{eq,c}}=f_i^{\text{eq,f}}=f_i^{\text{eq }}.$$ (5)

For the non-equilibrium part of the distribution functions $f_i^{\text{neq }}=f_i-f_i^{\text{eq }}$, the stress continuity is maintained across the interface by the relation:

$$f_i^{\text{neq,c}}=n\frac{{\tau }_{\text{c}}}{{\tau }_{\text{f}}}{f}_i^{\text{neq,f}}$$ (6)

where the subscripts c and f refer to the coarse and fine lattices, respectively, and n gives the ratio of coarse to fine lattice spacing. Following this, the relaxation times of the coarse and fine lattices are related by:

$${\tau }_{\text{f}}=\frac{1}{2}+n\left({\tau }_{\text{c}}-\frac{1}{2}\right)$$ (7)

In contrast to the relationship between the fine and coarse grid used by [28] and [14], which scales the post-collision distribution functions, we use the method developed by [29] which scales the “incoming” LBM distribution functions. Combining Eqs. 5 and 6, we are able to express a direct relationship between the coarse and fine lattice LBM distributions. Specifically, the coarse-to-fine and fine-to-coarse transfers at coincident lattice points between the two resolutions can be written as:

$$\begin{gathered} f_i^{\text{c}}=f_i^{\text{eq}}+\frac{n{\tau }_{\text{c}}}{{\tau }_{\text{f}}}{f}_i^{\text{neq,f}} \\ {f}_i^{\text{f}}=f_i^{\text{eq }}+\frac{{\tau }_{\text{f}}}{n{\tau }_{\text{c}}}{f}_i^{\text{neq,c}}. \end{gathered}$$ (8)

For points on the fine lattice that are not coincident with the coarse lattice, a spatial interpolation is required; we use a Catmull-Rom spline to maintain C¹ continuity [30]:

$$f_i(\mathbf{\text{x}})=a_j+b_j\mathbf{\text{x}}+c_j{\mathbf{\text{x}}}^2+d_j{\mathbf{\text{x}}}^3$$ (9)

with coefficients determined based on derivative continuity. Similarly, a bicubic spline interpolation is used where a fine lattice point is not aligned with two dimensions of the coarse lattice—an illustration of which is shown on the right-hand side of Fig. 1.

A consequence of the different spatial resolutions is a discrepancy in the physical time step size, related by Δt_c = nΔt_f. Therefore, the window and bulk parts of the simulation must synchronize every bulk time step, which corresponds to n window time steps (see Fig. 2 for an overview). The data transferred at the synchronization from the coarse grid is then advanced via temporal interpolation to the same fractional time step (from the coarse perspective) upon which the fine grid operates. To achieve the temporal interpolation at the interface points, we employ a Lagrange interpolating polynomial [14]:

$$f_i(\mathbf{\text{x}})=\sum _{j=1}^3{\left(\prod _{k=1}^3\frac{\mathbf{\text{x}}-{\mathbf{\text{x}}}_k}{{\mathbf{\text{x}}}_j-{\mathbf{\text{x}}}_k}\right)}_{j\ne k}$$ (10)

The multi-resolution interface coupling the bulk domain to the window domain with cells is shown in Fig. 1 along with a representative interpolation stencil. To enable the parallel implementation of this algorithm, when an unaligned lattice point on the edge of the fine grid attempts to interpolate from the coarse grid, an overlap of one point into the coarse grid must be available to the MPI rank for a given part of the fine lattice. The interface between the fine and coarse lattice is spread across MPI ranks with multiple fine MPI ranks being neighbors of coarse tasks and multiple coarse MPI ranks being neighbors with fine MPI ranks.

2). Moving the Window:

As the cell traverses the window and reaches a prescribed distance from the boundary, the window is moved to a new location centered on the cell. For the present work, we trigger a window move when the cell centroid crosses into a designated region near the edge of the window domain which can be controlled by the user. The objective is to move the window prior to the cell experiencing any possible edge-effects as it nears the boundaries between domains. The communication scheme between fine and coarse lattice tasks must be re-initialized every time the window moves as the fine lattice points will then border new coarse lattice points.

When the window moves, the Eulerian data within the window must be updated to represent the fluid dynamics of the new window location. This window shifting and reconnection to the bulk-simulation requires a combination of two newly devised steps which have not previously been developed in literature. Indeed, the work of [3] did not need to consider the differences in momentum between the window and bulk domains. First, lattice data at the intersection between both the pre- and post-move window bounding boxes must be translated, highlighted in white in Fig. 3. The lattice or fluid data referenced includes not only the latice Boltzmann distribution values, but also the body force values present at each location in the domain. Fluid data in this white-shaded volume only need to be moved to their new relative location in the window and therefore are communicated via MPI to tasks which manage the respective section of the finely-resolved domain. Next, we need to account for new fluid points in the non-overlapping portion of the post-move window that did not exist in the pre-move window, highlighted in red in Fig. 3. We generate these fine grid fluid points by interpolating from the coarsely resolved bulk domain using tricubic interpolation. This new interpolation step is required as the lattice distribution functions in the bulk domain at a coarser resolution are essentially in a different unit space from the fine domain. Therefore, the Eulerian data must first be transformed using Eq. 8 and then interpolated onto all of the new lattice points on the finely resolved grid.

Fig. 3.

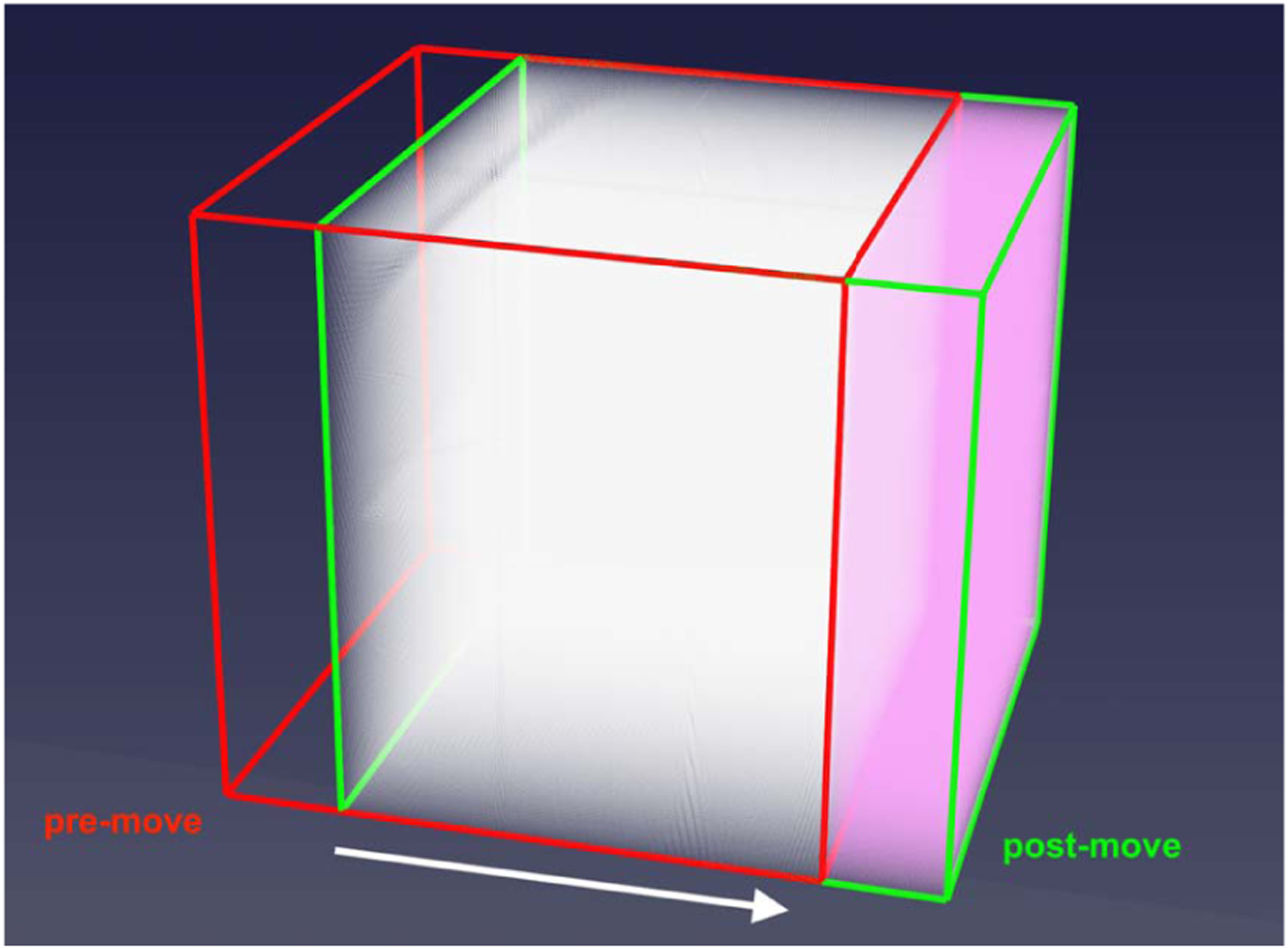
Depiction of the parts of the window to be updated with the red and green bounding boxes showing the pre- and post-move bounding boxes. The shaded white area shows points which exist in both window locations, while the shaded pink area shows the non pre-existing points which are interpolated from the bulk domain. The arrow indicates the direction of window movement.

E. Computational Design for Heterogeneous Architectures

To maximize use of heterogeneous CPU-GPU supercomputing architectures, we assigned the bulk fluid computation to the CPU and the window computation to the GPU, synchronizing the execution between the two, as necessary. The bulk fluid computation has characteristics such as a comparatively smaller workload when compared to the window and irregular control flow that make it a good fit for the CPU. The window computation, where the 3D deformation and dynamics of the tracked cell are fully resolved, has characteristics such as fine-grained parallelism, regular control flow, and limited data dependency between kernel launches that match well with the GPU. Additionally, as the window maintains its size during each move, the data arrays allocated on the GPU at the beginning of the simulation can be maintained throughout with only arrays representing the multi-resolution interface needing to be updated during each move. By partitioning the computation in this way, we also reduce the cost of data reorganization and data transfers among the CPUs and GPUs. More details can be found in Sec. II-E3.

Here, we divided the workload such that the the window computations were distributed among all GPUs while the bulk fluid used the remaining CPU resources. This is in contrast to previous work, where in [3] there was a uniform resolution between the bulk and window domains and, naturally, it followed to put the larger fraction of the computational load on GPUs. However, as one of the major advances in our work is the multi-block aspect which allows for a resolution difference between the bulk and the window, a similarly sized window would have n³ more fluid points, making the GPU more effective for window computations. Moreover, given the time scaling outlined in Sec. II-D1 (Δt_f = nΔt_c), there is more work given the additional timesteps needed in the window when compared to the bulk—even if the number of simulated points in both domains were the same. The window also has the added burden of calculating the IBM and FEM updates for the cell(s) in the window. In this work we focused on a single cell in the window in order to emphasize the multiscale physics and balance the computational workload.

Simulations for performance analysis were performed on the Summit supercomputer at Oak Ridge National Laboratory, the second fastest supercomputer on the TOP500 list (as of November 2021), and implementation details provided in the subsequent sections (II-E1, II-E2). Other development simulations were performed on the Lassen supercomputer at Lawrence Livermore National Laboratory. Both systems utilize a heterogeneous architecture with powerful nodes accelerated by dual CPU sockets and four to six GPUs. The same CPU and GPU architectures are used on both systems.

1). GPU Acceleration Within Window:

All compute-intensive operations of the window simulation (i.e., LBM, IBM, and FEM) are executed on the GPUs, which for simulations performed on the Summit supercomputer use all six NVIDIA V100s per node. Device code was implemented in CUDA. Work related to inter-node communication and the multi-resolution coupling such as the coarse to fine spatial interpolation, fine to coarse communication, and temporal interpolation (see Sec. II-D1) is performed on the host as the data is received from neighboring MPI ranks.

For the fluid component of the cell-resolved simulation, kernels are launched with each thread acting upon a single LBM point. The thread computes the collision update for the given LBM point and then writes the streamed particle distributions to its neighboring LBM points. The collide and stream operations are performed in a fused kernel so as to decrease reads and writes to main memory [31].

For the deformable cell component of the simulation, kernels are launched on either cell vertices or elements. The immersed boundary interpolation, spreading, and advection kernels are launched with each thread working on a particular vertex residing on the current MPI task. The finite element force calculation kernel is launched on all elements ‘owned’ by an MPI rank with the updated force being written to the constitutive vertices of a given element. To optimize performance on the GPU, all buffers relating to the fluid and the deformable cells have been arranged in the structure of arrays (SoA) format. This memory layout enables overlapped memory accesses of data buffers such as the LBM distribution data, fluid body forces, cell positions, cell velocities, and cell forces. As the amount of memory available on GPUs is significantly less than CPUs, we aimed to store the minimum amount of data needed to perform updates. At a minimum, each fluid point requires 408 bytes to store two copies of the 19 discrete velocities, a force vector, the indirect streaming stencil consisting of 19 ints, and its indirect array location. IBM cells are discretized by 642 vertices comprising 1, 280 elements per cell. Therefore, each cell requires a minimum of 51 kilobytes to store vectors of forces, velocities, positions, and other supporting data.

Details on optimizations made such as buffer packing to enable contiguous memory transfers and partial updates to overlap communication and computation are in Sec. II-F.

2). Per-Node Resource Allocation:

The bulk fluid is where inter-task communication, the systemic-scale bulk LBM simulation, and the window-to-bulk coupling are implemented. For all performance results reported, the code makes use of all 42 cores across the dual sockets of POWER9 CPUs on Summit. Specifically, 42 MPI ranks per node were used, with 36 tasks assigned to the bulk fluid region and 6 MPI ranks to the window region. Code was implemented in C++ and compiled on Summit using the IBM XL compiler (v16.1.1), Spectrum MPI (v10.4.0.3), and CUDA 11.

3). MPI Rank Decomposition of APR Method:

When developing the paradigm for allocation of resources, the main parallelization choice was whether to have the window and bulk threads be within a parent MPI rank or whether MPI ranks would be decomposed into window and bulk MPI ranks. There would be very little shared information between a window and bulk process residing on the same socket or node due to the fact that the smaller real dimensions of the window and the movement of the window mean that processes of the window that are spatially adjacent to a bulk process would be spread across the entirety of the simulation. Therefore, in practice, depending on the problem size, a relatively small portion of the bulk simulation will be required to communicate with the window simulation tasks. Here, we implement the latter design choice of using MPI subcommunicators to decompose the window and bulk tasks. This MPI-based decomposition allows for more flexibility when allocating computational resources on a fractional basis between the window and bulk versus an on-node parallelization that decomposes the two simulations among threads within a given process. To determine the division of resources, the user must specify the fraction of MPI ranks to devote to the window.

The bulk fluid part of the simulation is set up by first voxelizing its domain given an input triangular mesh describing the surface of the geometry to be modeled. The window part of the simulation is set up by defining a high resolution rectangular box, corresponding to a desired window size, within the bulk domain. Since the window part of the simulation is always shaped as a rectangular prism, we use a simple geometrical algorithm to break down the window evenly into equally sized subproblems based on the proportion of total MPI ranks devoted to the window in the simulation. The window is initially divided into three pieces and then subsequently divided in half on the longest dimensions so that the window is as close to ideally balanced as possible to the three GPUs available per socket on Summit. It is assumed that work is evenly spatially distributed across all window MPI ranks. This assumption is justified for the simulation due to the uniform resolution of the Cartesian LBM grid. The bulk part of the simulation is separately load balanced on its respective MPI subcommunicator using a recursive bisection algorithm described in [32].

To determine which tasks communicate across the boundary between the coarsely-resolved bulk and the finely-resolved window MPI ranks we communicate the bounds of the window at the start of the simulation and every time the window moves. Checks for window moves are done at a user-controlled frequency to amortize collective operations. Once the window and bulk tasks have determined neighbor relations, tasks that are adjacent to the multi-resolution boundary update their communication partners and the window MPI ranks re-use the same initially allocated CPU and GPU buffers to execute the multi-resolution operations. Synchronization between bulk and window MPI ranks spatially adjacent to each other occurs during the coarse to fine and fine to coarse multi-resolution coupling operations as illustrated in Fig. 2.

F. Concurrency and Buffer Packing for Optimal Performance

1). Overlap Between Bulk and Window time steps:

A diagrammatic depiction of the overall algorithm for our method over one bulk time step is provided in Fig. 2. Due to the nature of LBM and the relationship between physical time step size and physical spacing between lattice points, n = Δt_c/Δt_f window time steps correspond to one bulk time step. Thus, care must be taken in designing this overall algorithm to optimally balance the window/bulk components. We therefore optimized our algorithm to best overlap compute-intensive simulation time steps on the GPU/window with the CPU/bulk.

As shown in Fig. 2, we first execute the LBM in the region encapsulating the border between window and bulk. Essentially, this setup splits part of the time step so that the streaming discrete velocities from the bulk to the window are transmitted at the beginning of the bulk time step. By partially updating the domain, the rest of the fluid in the bulk domain can be updated simultaneously while the window completes its operations to finally compute the requisite discrete velocities in the other direction to complete the two-way coupling between the window and bulk domains. The communication from coarse to fine prior to updating the majority of the bulk domain aligns the barrier between window and bulk so that they only need to synchronize every time step for the bulk and every n time steps for the window, thereby facilitating overlapping window/bulk computations. Without the partial update of points that the window task depends upon, the overall time for a time step would be the sum of the bulk and window, rather than the maximum. The bulk and window calculations subsequently proceed in parallel, at the end of which distribution functions are transferred from the fine window grid to inform the bulk simulation at the end of the time step.

2). Optimizing Communication Through Buffer Packing:

Communication between MPI ranks requires first moving data between the host and device. Inefficient device-host transfers are significant potential bottlenecks as even modern interconnects such as NVLink have low bandwidth relative to HBM2 and DDR. In our case, communicated data is not coalesced and is laid out differently on the host and device. The host uses an array of structures (AoS) layout for ease of development while utilizing the sophisticated caching and lower latency on cache misses available on CPUs. The device uses an SoA format described above as it facilitates adjacent threads operating on contiguous data. Our communication routines transfer a high volume of data on the order of hundreds of MB per node and thus achieving high bandwidth is crucial to application performance. A naïve solution of making many small transfers results in low transfer bandwidth and high latency. Asynchronous small data transfers launched in parallel are also costly because they cannot be overlapped easily with computation, they stall dependent intranode communication, and they compete for DDR bandwidth with the memory bound CPU bulk simulation.

To optimize transfer performance, we pack data into contiguous buffers before copying between the device and host—an approach shown to dramatically reduce data movement in GPU accelerated MPI applications [33]. Custom GPU kernels pack data to enable large, contiguous high bandwidth copies to page-locked CPU memory. Similarly, data received from MPI communication is packed before a host-device copy and unpacked with a GPU kernel. One trade-off of this approach is the additional memory on the device-side required for the packed buffer, though the buffer size is small in comparison to other data structures as communicated data is proportional to surface area while owned data is proportional to volume. Another trade-off is the overhead associated with packing and unpacking; however, this overhead is far outweighed by improved achieved transfer bandwidths that cut overall application run time in half.

The data vectors that are on device were allocated using CUDA’s unified memory which aided in the ease of development and in reducing the complexity of initialization routines. However, we found that manually triggering host-device transfers prior to inter-node communication using cudaMemcpy resulted in faster performance for computational routines. We hypothesize that this performance improvement is due to the manual memory transfers obviating the need for any latency in computational kernels while waiting for hardware to migrate the required data.

III. Results and Discussion

We systematically establish the accuracy of our method by validating the individual components of the algorithm. Then, we present scaling results for the APR model on the Summit supercomputer. Finally, we choose a realistic microvessel network as an example and provide a memory cost breakdown, focusing on the bandwidth saving due to the APR algorithm.

A. Validation of Multi-Resolution and Multi-Physics

To validate the APR algorithm, we first focused on a fluid-only simulation and compare against an analytical solution for the velocity field within a complex geometry to isolate and validate the multi-resolution component. We then demonstrate that the mapped out trajectories of a circulating tumor cell (CTC) through an expanding microchannel using both APR and eFSI are consistent. These experiments confirm the ability of the APR method to accurately capture both the fluid profile and the path of a single cell without requiring the resources of a fully cell-resolved simulation, thereby enabling simulations that would not be tractable without our APR approach.

1). Validating Fluid dynamics Component of APR Simulation:

To first validate the coupling of different resolution grids, we considered flow through a helical tube of circular cross-section within which a finely resolved window is placed. The helix geometry facilitates comparison with an analytical solution and, importantly, one in which all three velocity components are non-zero—thus providing a sufficiently robust validation. Furthermore, such a circuitous vessel is representative of the vascular geometric complexity which occurs in physiology. We have also conducted comparisons of the APR algorithm with analytical solutions for Poiseuille flow and Womersley flow, representing both steady state and oscillatory flow states common in the vasculature. In contrast to [3], fluid dynamics validation is required as the APR method uses multiple resolutions. Previous multi-block methods have typically used resolution ratios of n = 2 or 4 at the sharp interface between grids (e.g., [13], [14], [35]), while we tested up to n = 20 across the interface in the following section.

Fig. 4a provides a general schematic of the helix geometry. A helix with geometric parameters ϵ = γ = 0.05 and an axial length traversing one turn was used, where ϵ is the dimensionless curvature and γ is the dimensionless torsion. The flow was characterized by Re = U₀a/ν = 50, and the helix cross-section is set to have radius a = 50 μm. We imposed an inlet flow rate corresponding to a Poiseuille flow with U₀ = 2 m/s and a kinematic viscosity of 2.0×10⁶ m/s². These parameters were chosen to result in a cross-sectional secondary flow field with non-negligible asymmetry to amplify the 3D nature of the flow. For the finely resolved window, we used resolution ratios n = 2, 5, 10, and 20 for a fixed bulk resolution. The window has a side length of 30 μm, and was placed on the helix centerline midway across the axial distance spanned by the geometry. For the LBM simulation parameters, we used a coarse grid relaxation time (τ_c) of 0.525 and a corresponding fine-grid relaxation time (τ_f) determined from Eq. 7 for each of the resolution ratios. This τ_c value was chosen such that τ_f ≤ 1, maintaining LBM’s accuracy [36].

Fig. 4.

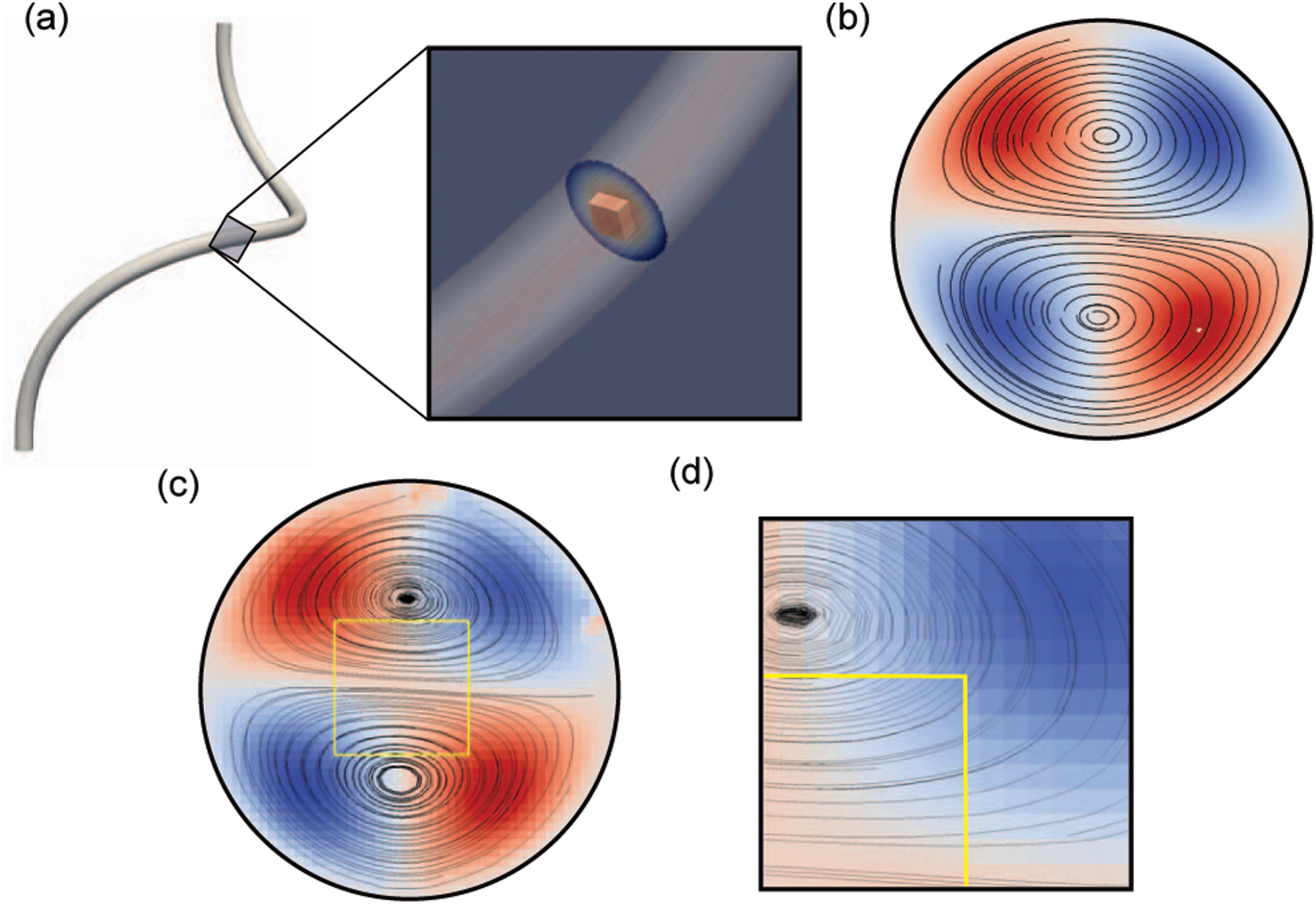
Demonstration of multi-resolution validation using flow through a helix of circular cross-section. (a) General schematic of the helix geometry with an inset of simulation results for depicting fluid streamlines through the bulk region and the finely resolved window. (b) Analytical solution [34] for the secondary flow field. (c) Simulation streamlines for the secondary flow field, through both the bulk and window regions, with contours giving the axial velocity component in this plane. The yellow box depicts the region of the window with a 10:1 resolution ratio and a 2 μm bulk resolution. (d) A zoomed-in version of subfigure (c) showing the smooth secondary flow field between the window in the yellow box and the bulk outside of the box. The differences in resolution are visible through the node size in the bulk domain.

Simulation results are provided in Fig. 4 and Table I for each of the cases. The inset in Fig. 4a provides streamlines through the geometry and illustrates the placement of the window within the helix and the general flow configuration. Fig. 4c depicts the secondary flow field at a cross-section which intersects the window for a representative case, with streamlines shown within both the bulk and window regions to illustrate the recirculation patterns predicted by the simulation. Both the contours of the axial velocity component in this plane and the streamlines are in good qualitative agreement with the analytical result shown in Fig. 4a.

TABLE I.

Simulation L₂ error norms e for flow through a helix based on comparison to analytical solutions.

Resolution ratio (n)	e bulk	e wind
2	0.0288	0.01013
5	0.0288	0.00993
10	0.0288	0.00997
20	0.0288	0.00995

We quantified the simulation accuracy for each case by computing the L₂ norms based on comparison to published analytical solutions for helical flow [34]. We defined our L2 norm in Eq. 11, with the error e across points i in the slice. Where u_s(i) is the simulated velocity vector at location i, and u_a(i) is the analytical velocity vector at location i, and Ω represents the domain of a slice. All vector squares were taken as dot products (e.g., u² = u · u).

$$e={\left[\frac{{\sum }_{i\in \Omega }{\left(u_s(i)-u_a(i)\right)}^2}{{\sum }_{i\in \Omega }{u}_a^2}\right]}^{1/2}$$ (11)

These values are provided in Table I, broken out in terms of the bulk and window regions, with good overall agreement demonstrated by values ranging from approximately 1–3%. As bulk resolution is fixed and the accuracy within the window domain is gated by the accuracy of the bulk simulation, convergence with increasing n is not expected. Rather, these error values remaining consistent indicates that the multi-block coupling scheme remains both accurate and stable even for large resolution ratios between the window and bulk. This accuracy and stability persists despite large n. Overall, we demonstrated that the APR model falls within 3% of the analytical solution for multiple resolution ratios, which validates accurate fluid dynamics modeling in complex geometries using the APR algorithm.

2). CTC Tracking Using APR Predicts the Same Trajectory as a Fully Resolved Simulation:

Next, we utilized the APR method to track the trajectory of a CTC through an expanding channel and compare it with that of a fully resolved simulation. Expanding microfluidic channels have been used to study the motion of cells towards the channel walls [37], aiding in understanding the role of hemodynamics on the likelihood of cell margination. The underlying fluid profile in an expansion leads to a change in radial distance away from the center line of the channel, rather than letting the cell travel in a straight line down a simple vessel. This validation was used to confirm whether the APR model can accurately capture the motion of the cell compared to its eFSI counterpart.

Fig. 5a shows a general schematic of the expanding microchannel. The channel has a length of 2000 μm with a width that expands from 200 μm to 400 μm at the z = 400 μm mark. For boundary conditions, we input an inlet velocity of 0.1m/s. We generated a window with side length 120 μm with the underlying fluid modeled as blood plasma with a viscosity of 1.2×10⁻⁶m²/s. The window utilized a lattice grid spacing of Δx_f =0.5 μm and the CPU-based bulk flow component used a lattice grid spacing of Δx_c =2.5 μm, leading to a lattice resolution ratio of n = 5. This window resolution is an order of magnitude smaller than the length scale of an individual cell, which is important to most accurately capture the fluid flow field which conveys the CTC and in turn accurately resolve the complex deformation of the cell.

Fig. 5.

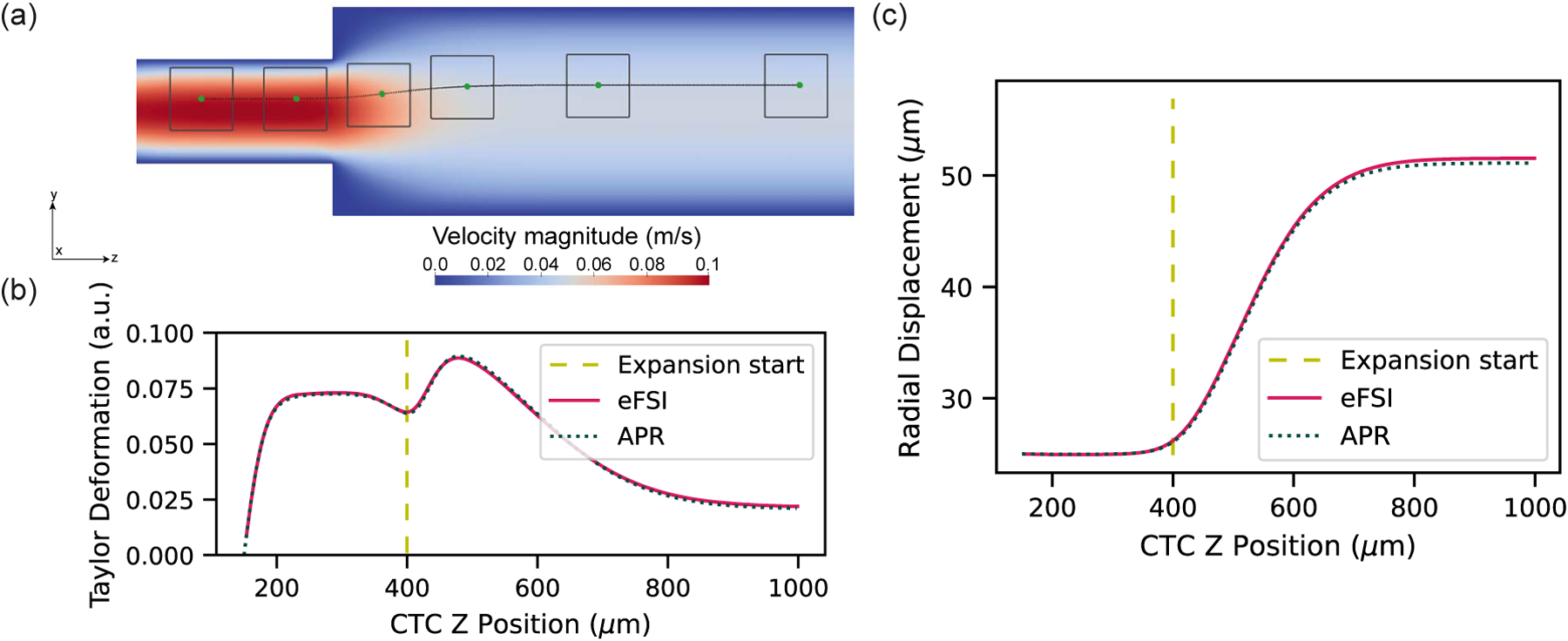
(a) Visualization consisting of time series where the cell in the window is moving across the expansion channel. The background pseudocolor represents an instantaneous velocity profile in the center of the geometry as computed by the coarsely resolved bulk domain part of the simulation. (b) A comparison of the deformation measured in the CTC as computed by the APR and eFSI models. The Taylor deformation parameter calculated as a the following ratio D = (A − B)/(A + B), where A and B are the major and minor axis lengths, respectively. (c) A comparison of CTC trajectory in an expansion geometry using the APR vs eFSI models. The radial displacement of the cell with respect to the centerline using the APR model is within 1% of the displacement using the eFSI model. The vertical yellow line in both (b) and (c) represents the axial location of the expansion in the channel.

A visualization of the CTC moving over time and the corresponding window updating its position are shown at several timepoints in Fig. 5a. Quantitative results in terms of CTC deformation and radial displacement from the centerline of the channel are presented in Fig. 5a and Fig. 5b for the APR and eFSI models. For reference, the gold line indicates the location of the sudden expansion in width. The trajectories from both eFSI and the APR model showed strong agreement as they overlap for most of the simulation and difference in the asymptotic trajectories of less than 1%, validating the APR model’s ability to accurately capture the motion of a single cell through a geometry.

To determine the comparative computational costs of a large eFSI model, we measured the time to solution for simulating CTC traversal in an expansion channel. We found that the APR and eFSI CTC tracking simulations used 22.7 and 287.9 nodehours using six GPUs per node on Summit, respectively. Both simulations were run on 22 nodes and used GPU acceleration with different configurations specific to the models used. We extracted times spent calculating the fluid-structure interaction of the deformable CTC with the surrounding fluid over the course of the parallel simulation. These results emphasize how the APR model can significantly decrease the computational expense of large-scale cell-tracking studies and open new simulation paradigms for longer length- and time-scale runs.

B. Scaling the APR Model to 512 Nodes (3,072 V100 GPUs)

We completed strong and weak scaling tests on the Summit supercomputer to assess the APR performance. A high-resolution (0.5 μm) cubic window containing a single circulating tumor cell centered within a coarse (10 μm) cubic domain was used. This simplified geometry allowed for straightforward scaling and analysis of the APR implementation free of load imbalance across a range of system sizes.

For both the strong and weak scaling results, resource allocation divided each Summit node on a per-CPU and per-GPU basis. Specifically, we assign one MPI rank per CPU core, using all cores rather than just one per GPU. For Summit, with 42 CPU cores across two sockets, this corresponds to 36 cores per node allocated to the bulk (coarse) fluid and 6 cores along with all 6 V100 GPUs per node allocated to the high-resolution window. Additionally, we repeated each strong and weak scaling run ten times to capture variability we observed in system performance.

The strong scaling results are shown in Figure 6. Two system sizes were run, starting from inputs designed to maximize memory usage for 1 and 16 Summit nodes. The smaller system contained 418M fluid points in the bulk and 141M fluid points in the window, while the larger system contained 6.7B fluid points in the bulk and 2.3B fluid points in the window. The largest run consisted of 10, 752 MPI ranks and used 1, 536 GPUs on 256 nodes of Summit. Both systems showed reasonable strong scaling performance with a relative speedup between six and seven times given a 16-fold increase in resources. This is consistent with previous observations of memory-bound code on GPUs [38], [39], which are less sensitive to GPU occupancy than compute-bound applications. The timing variability increased with job size, but overall were smaller than seen in the weak scaling results.

Fig. 6.

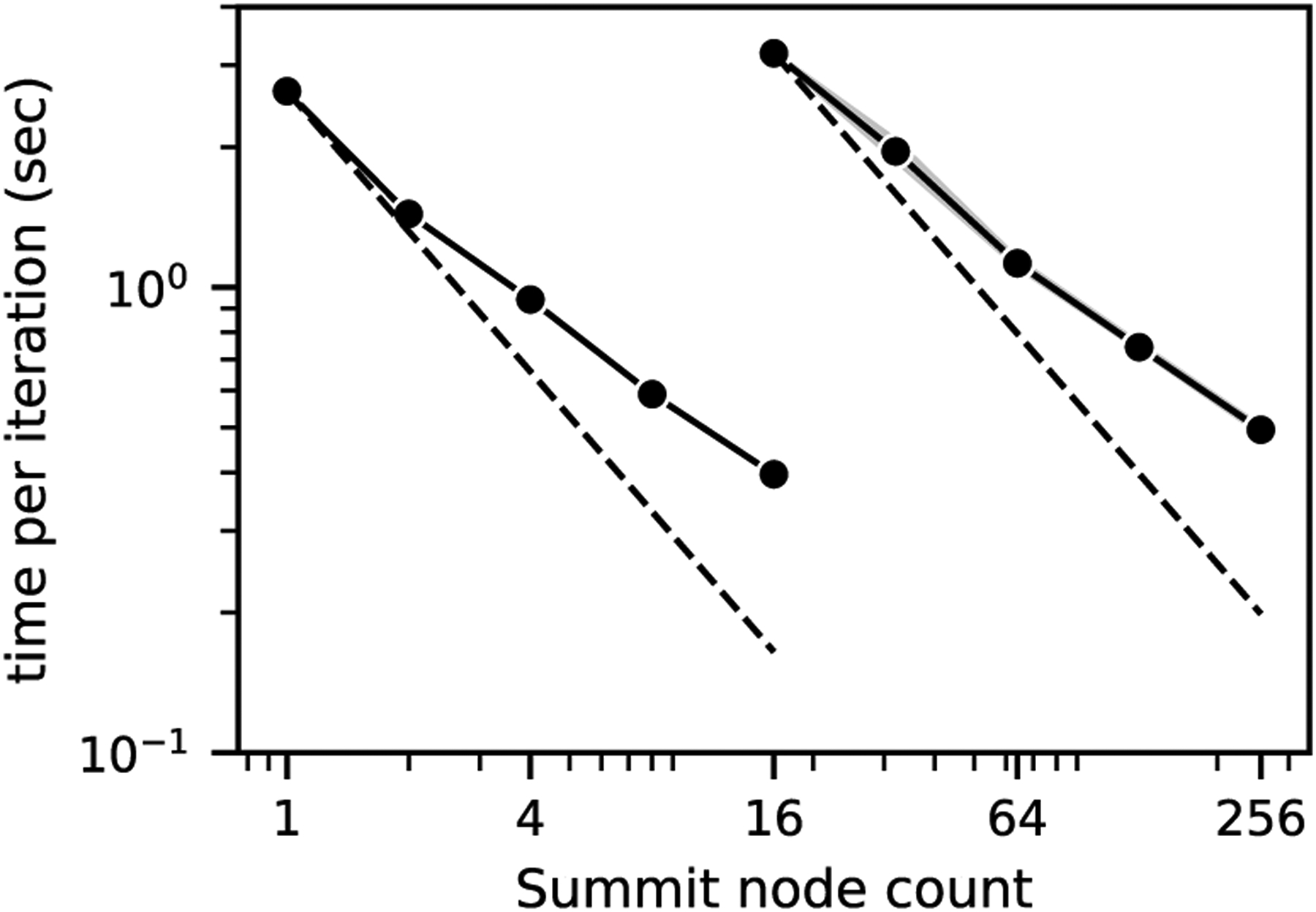
Strong scaling of the coupled window and bulk simulation on Summit, using simplified geometries. The left curve is for a system with a cubic bulk domain side length of 7.5 mm and a cubic window domain side length of 0.26 mm—corresponding to 4.2×10⁸ and 1.4×10⁸ fluid points in the bulk and window, respectively. The right curve is for a larger system with a cubic bulk domain side length of 18.9 mm and a cubic window domain side length of 0.66 mm—corresponding to 6.7 × 10⁹ and 2.3 × 10⁹ fluid points in the the bulk and window, respectively. The dashed line represents ideal scaling and the shaded area represents the 95% confidence interval of ten repeated runs.

Weak scaling results are shown in Figure 7, run with 5.6 × 10⁸ fluid points per node (4.2 × 10⁸ bulk, 1.4 × 10⁸ window), from 1 to 512 Summit nodes. We observed weak scaling efficiency over 75% out to 64 nodes and above 60% at 256 and 512 nodes. We also saw significant run-to-run performance variability emerge, ranging from a coefficient of variation (standard deviation normalized by the mean) of 0.5% to up to 19%. Variability was under 12% for runs smaller than 32 nodes and was bigger at nodecounts above 16 nodes. We attributed this to interference from other jobs’ communication traffic, as the increased time is observed almost entirely in communication routines. To minimize the impact of this contention on our ability to accurately assess the scalability of our implementation, we executed multiple runs at different times and present the average results over ten repetitions in Figure 7. Our approach reflects the reality of running on a shared resource.

Fig. 7.

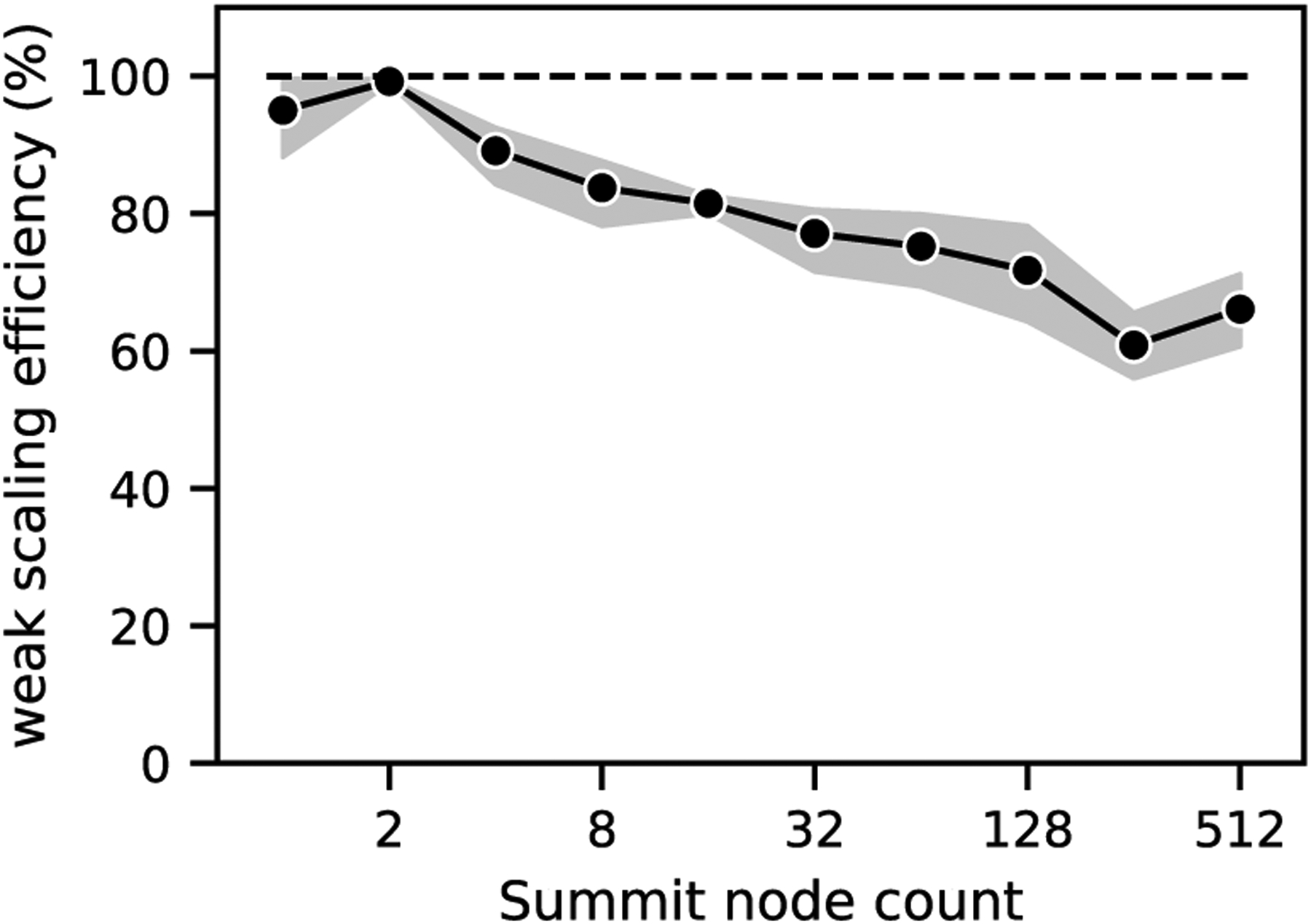
Weak scaling of the coupled window and bulk simulation on Summit, using simplified geometries. The bulk region had 4.2 × 10⁸ fluid points per node, the window region had 1.4 × 108 fluid points and one CTC. The dashed line represents ideal scaling and the shaded area represents the 95% confidence interval of ten repeated runs.

C. Memory Savings Due to Application of APR

To quantify the increase in fluid volume that can be captured at cellular resolution on a fixed resource provided by APR over state of the art eFSI models, we compared the maximum volume that could be captured on a range of node counts, as shown in Fig. 8. Using 256 nodes of Summit—corresponding to 24.5TB of GPU memory, the APR method achieves a simulated domain size of > 100 mL, whereas eFSI is limited to approximately 10⁻² mL simulated volume.

Fig. 8.

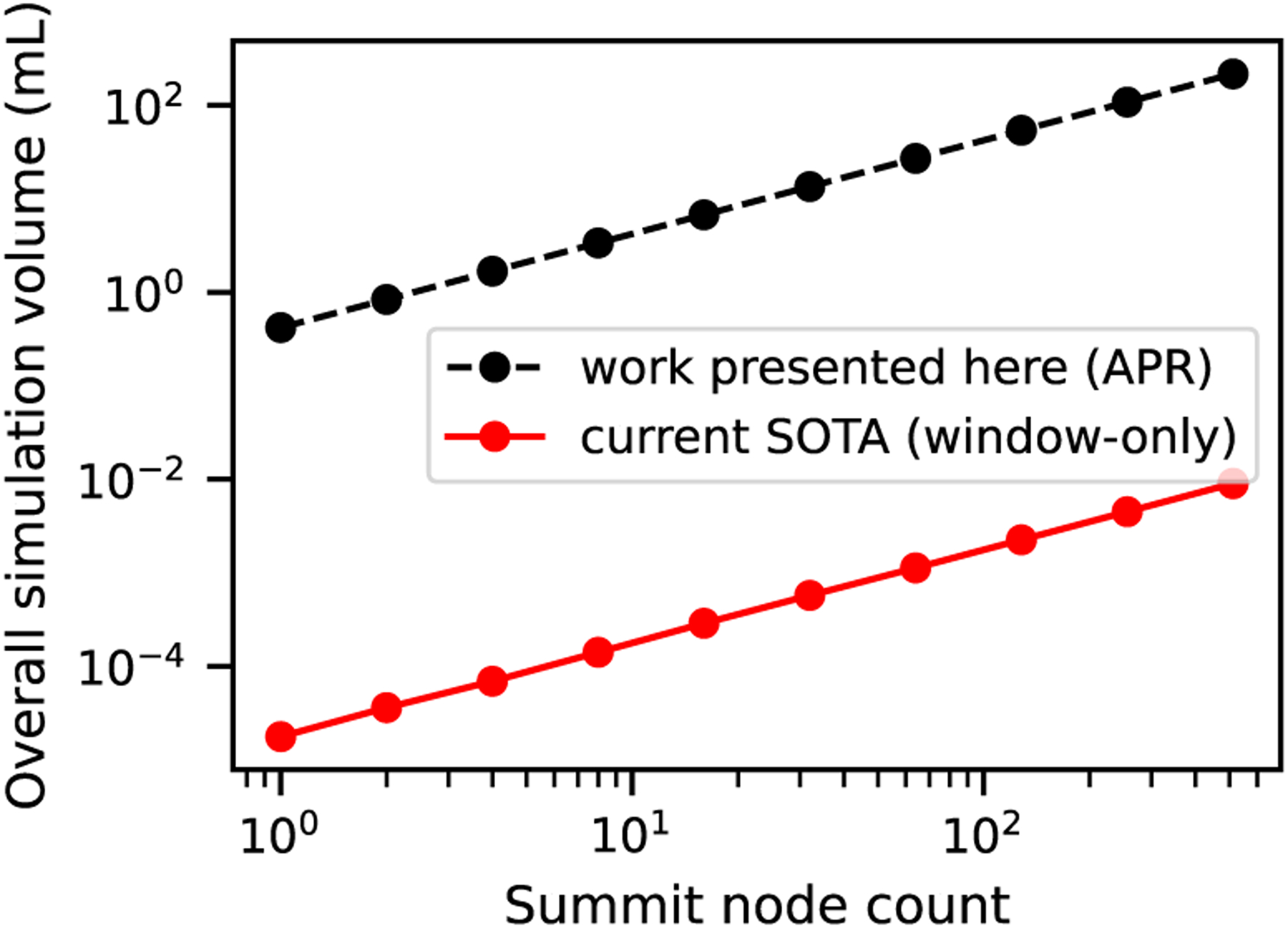
Effective simulation volumes enabled through APR technique presented in this work, compared with state of the art (SOTA). Numbers are derived from successful weak scaling experimental setups.

Therefore, by using APR we were able to expand the available volume that can be traversed by the cell of interest by four orders of magnitude. Through these advancements, we bring the vessel sizes that can be simulated with cell-resolved flow from vessels on the order of fractions of microns to vessels on the order of centimeters.

To further explore the impact of the APR memory savings, we investigated its use for creating “digital twins” of microfluidic and bioprinted devices. Using an example bioprinted vascular bed from literature [40], we demonstrated that the eFSI approach would require 235 nodes on Summit (over 22 TB), while the APR model would require only 1 node (250 GB of memory). The vessel dimensions are approximately 18mm from end-to-end with a volume of 6.9mm³. Dimensions for the finely-resolved grid are 0.45mm by 0.45mm by 0.05mm, accounting for 0.1% of the total volume.

Comparisons of the theoretical memory and resource usage for the APR and eFSI models for the bioprinted vascular bed are shown in Table II. Resources are presented in terms of DRAM and HBM found on each compute node on the Summit supercomputer. The number of fluid points were calculated for the APR window and bulk components at resolutions Δx_f = 0.5 μm and Δx_c = 2.5 μm, while the eFSI model assumed a cell-resolved grid spacing of 0.5 μm throughout the entire domain. A lower bound of 408 bytes per fluid point was utilized for these memory and resource calculations, based on the breakdown described in Sec. II-E1.

TABLE II.

Estimated memory usage and resources allocated for the double branching microvessel shows that using the APR model shrinks the problem size from 235 nodes to one node on Summit.

Model	Fluid Resolution	Num Fluid Pts	Memory	Resources
APR (window)	0.5 μm	8.1 × 107	33.0 GB	3 NVIDIA V100 GPUs (fits on 1 node)
APR (bulk)	2.5 μm	4.4 × 108	183.0 GB	2 IBM Power9 CPUs (fits on 1 node)
eFSI	0.5 μm	5.5 × 1010	22.5 TB	1406 NVIDIA V100 GPUs (fits on 235 nodes)

Continuing with the aforementioned asymmetric bioprinted vessel, we additionally simulated a window within the geometry on 32 nodes of Lassen with a speed of 0.19 seconds per coarse time step. Fig. 9 shows the fluid streamlines and starting cell state after the fluid had equilibrated. These results highlight the length scales within one simulation from a cell of 12 μm in diameter to a vessel on the order of 18mm.

Fig. 9.

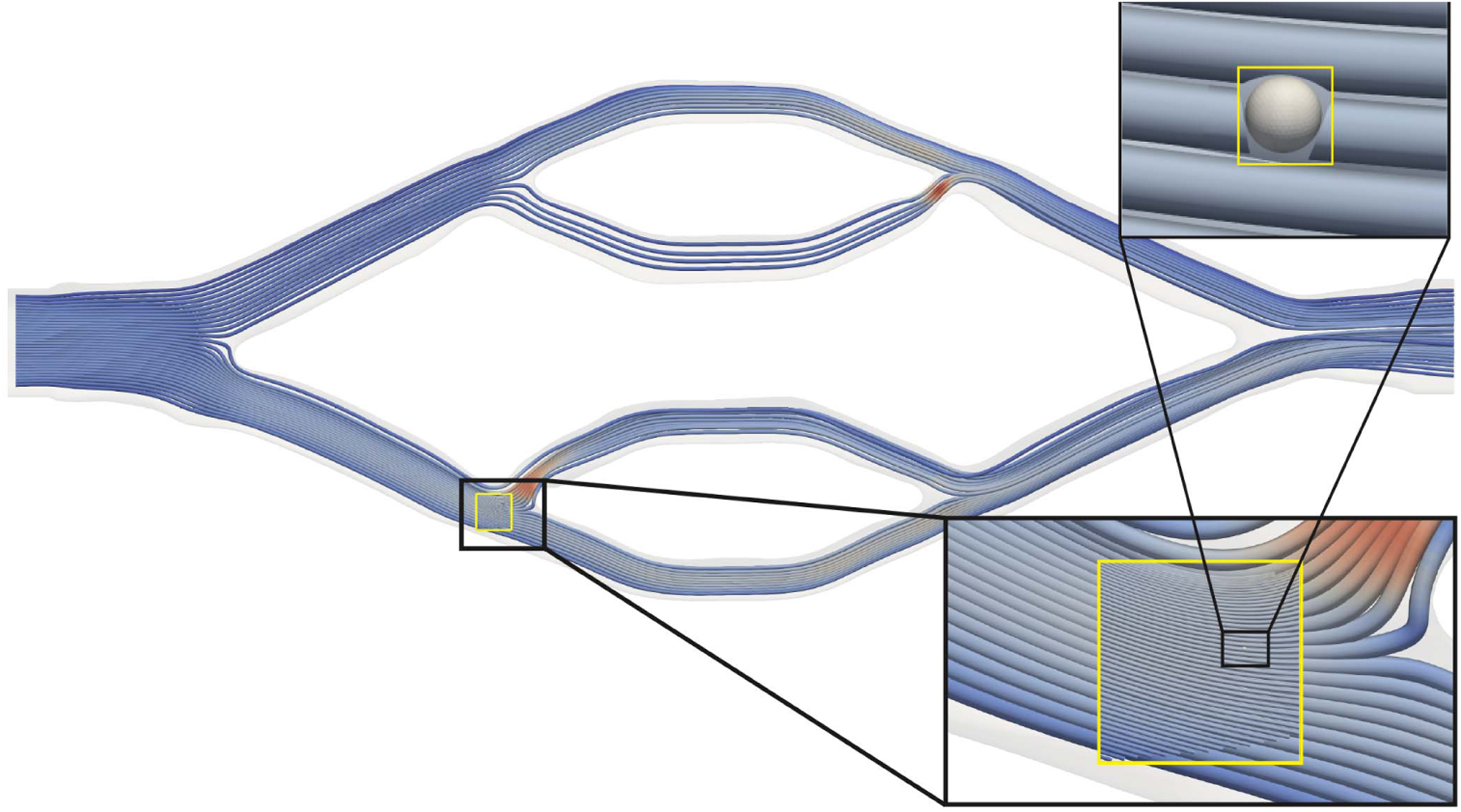
Simulation of a large, asymmetric bioprinted vascular bed (via [40]) using the APR algorithm. Streamlines in the window at 4.0 × 10⁵ fine time steps, corresponding to 8.0 × 10⁴ coarse time steps in the bulk are visualized. The cell is also presented at the same time—which is when it was inserted into the simulation. The two insets progressively zoom to the simulated cell. The top-right inset shows the simulated cell with a cut-away from the nearby streamlines.

IV. Conclusion and Discussion

Current eFSI models are computationally limited to modeling small sub-regions and brief time domains. The presented APR method provided an order of magnitude reduction in compute costs to provide a three-fold benefit: 1) cellular resolution at previously intractable volumes, which will facilitate new research in the areas of cancer biology and microfluidic device design, among others; 2) extension of the time domain that can be modeled by moving the requirement from full leadership-scale cluster runs to single node resources that can be more readily dedicated for long simulation durations; and 3) empowering searches of a very large number of cell types or properties to quantify their impact on cell transport.

In this work, we introduced the APR method and demonstrated its accuracy at capturing both the fluid and cellular components. By specifically designing the method to take advantage of heterogeneous architectures, communication times were minimized and data movement optimized. To achieve these goals, we addressed several algorithmic challenges. We coupled the sub-micron cell-resolved window to the coarser bulk domain to bridge the disparity in relevant length scales. The multi-resolution capability was transformed to an adaptive model which conforms to the problem by tracking, moving, and updating the fine resolution domain over the course of simulation. The problem of resource allocation was ameliorated by balancing the compute and memory requirements of the fully-coupled APR model with careful splitting of simulation resources based on the problem sizes encountered.

Designs for next generation microfluidic devices as well as questions regarding cellular interaction and the role of clusters in cancer metastasis would benefit from the APR approach which is designed from the ground up to improve time-to-solution, volume modeled, resolution captured, and per-node throughput for fluid-structure interaction models. In order to establish the validity of the framework, we focused this work on the introduction of the adaptive physics refinement itself and systematically tested the multi-resolution coupling, the heterogeneous parallelization scheme, and algorithms to efficiently move the window without introducing erroneous forces or momentum under the representative use case of a single CTC moving in a large complex geometry. We expect this crucial work to set the stage for future studies leveraging APR to capture multiple cell interactions at the centimeter or even meter scale.