Developments in describing equilibrium phase transitions of multivalent associative macromolecules

Abstract

Biomolecular condensates are distinct cellular bodies that form and dissolve reversibly to organize cellular matter and biochemical reactions in space and time. Condensates are thought to form and dissolve under the influence of spontaneous and driven phase transitions of multivalent associative macromolecules. These include phase separation, which is defined by segregation of macromolecules from the solvent or from one another, and percolation or gelation, which is an inclusive networking transition driven by reversible associations among multivalent macromolecules. Considerable progress has been made to model sequence-specific phase transitions, especially for intrinsically disordered proteins. Here, we summarize the state-of-the-art of theories and computations aimed at understanding and modeling sequence-specific, thermodynamically controlled, coupled associative and segregative phase transitions of archetypal multivalent macromolecules.

Introduction

Biomolecular condensates are cellular bodies that concentrate distinct classes of proteins and nucleic acids into assemblies that span a range of stoichiometries [1,2]. Condensates provide spatial and temporal control over cellular matter and synergistic biochemical reactions [1,3].

Phase separation of macromolecular solutions is proposed to be the defining mechanism for condensate formation [2,4,5]. Macromolecular solutions are mixtures of different types of macromolecules dissolved in a complex solvent. The overall free energy of the macromolecular solution can be parsed as a sum of two terms viz., (i) the free energy of mixing and (ii) the free energies of reversible associations among macromolecules [6,7]. Phase separation is defined by segregation of macromolecules from an incompatible solvent or from other incompatible macromolecules [8]. As a result, phase separation, which is a segregative transition, gives rise to two or more compositionally distinct phases that coexist with one another.

Macromolecules are also characterized by reversible associations mediated by non-covalent interactions among specific types of cohesive motifs. These include hydrogen bonds, a hierarchy of electrostatic interactions, and interactions among aromatic and / or hydrophobic groups [9]. Above a system-specific threshold concentration, known as the percolation threshold, multivalent associative macromolecules (MAMs) can form system-spanning networks [10]. This process is a continuous, associative transition known as percolation [8,9]. On its own, percolation does not give rise to distinct coexisting phases, but instead it generates a single, highly connected network known as a gel.

Biologically relevant solutions of MAMs include different types of macromolecules in a solvent. In such systems, associative and segregative transitions will be coupled to one another. Accordingly, a solution of MAMs can undergo coupled associative and segregative phase transitions, which we refer to as COAST. The extent and nature of the coupling between associative and segregative phase transitions will be governed by the architectures of macromolecules [11], the hierarchical networks of associative interactions [12], and the mutual (in)compatibility of macromolecules with one another and with the solvent [13]. COAST-like processes include phase separation coupled to percolation [14], complex coacervation [15], and polymerization induced phase separation [16].

The distinction between segregative and associative phase transitions introduced above is different from a recent definition introduced by Minton [17]. They defined phase separation driven by attractive interactions vs. repulsive interactions as being associative vs. segregative, respectively. In a ternary mixture of a pair of macromolecules in a solvent, one can map the phase boundary in a plane defined by the volume fractions of a pair of macromolecules. According to Minton, associative phase separation is defined by tie lines that are parallel to the diagonal. Conversely, segregative phase separation would be defined by tie-lines that are parallel to either the abscissa or ordinate. However, in complex mixtures such as ternary or n-nary mixture of macromolecules in a solvent, the slopes of tie lines will be governed by the interplay between solvent-mediated homotypic and heterotypic interactions between macromolecules, and the mutual (in)compatibility of macromolecules with the solvent and with one another. As noted by Tanaka [6,9], the effective two-body interactions, which capture the two types of free energies that prevail in macromolecular solutions, can be parsed into a solvation term that drives segregative transitions and an associative term that drives networking. Therefore, COAST-like processes in solutions of MAMs derive from the combination of macromolecular and solvent (in)compatibility, which contributes to the free energy of mixing, and reversible associations, which contribute to percolation. For simplicity, we shall use the term condensation to refer to the totality of COAST-like processes that are operative in a solution of MAMs.

Our growing understanding of spontaneous condensation is being driven by the mapping of MAMs onto rigid or flexible molecules with multiple cohesive motifs (stickers) that are interspersed, either spatially or along the linear sequence, by regions known as spacers [12]. In the simplest descriptions, stickers contribute reversible crosslinks and spacers modulate the cooperativity of sticker-sticker interactions whilst contributing to solubility as well [12,18,19].

Here, we present an overview that highlights key contributions to the recent literature on condensation of MAMs. Our contribution is inherently limitations because it sacrifices deep discussions of the relevant physical concepts. The hope is that the citations of key papers from the recent literature will spur interest and prompt deep dives into the relevant topics.

Theoretical foundations of macromolecular condensation

Flory-Huggins (FH) theories [8,20] are useful starting points for describing phase separation in polymer solutions and polymer blends. The theories rest on a mean field description for the free energy of mixtures of macromolecules in a solvent. In a binary mixture, there exists a saturation concentration of polymers above which the free energy of the system is minimized by separation into coexisting dilute and dense phases (Figure 1A). A key determinant of the saturation concentration is the effective two-body interaction parameter that quantifies the balance of polymer-solvent, polymer-polymer, and solvent-solvent interactions.

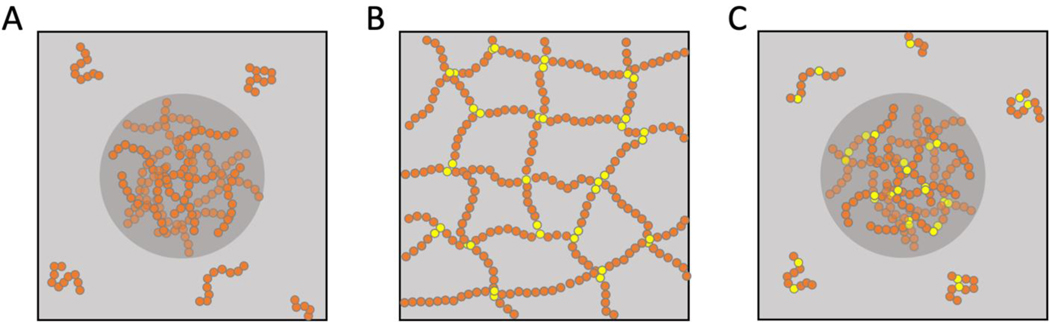
Figure 1. Condensation of multivalent associative macromolecules showing segregative phase separation, associative percolation, and the coupling between the two processes.

Schematics are shown for flexible polymers, but they apply to rigid multivalent macromolecules as well [12]. (A) In a binary mixture comprising a polymer (orange) in a solvent (gray background), can undergo phase separation, which is a segregative transition. This leads to the formation of two distinct coexisting phases delineated by a phase boundary. Chemical potentials of the polymer and solvent as well as the osmotic pressure are equalized across the phase boundary. (B) Multivalent associative macromolecules (MAMs in the main text) feature functional groups or cohesive motifs (shown in yellow). These cohesive motifs are known as stickers, and they form reversible (non-covalent) physical crosslinks. Above a system-specific percolation threshold, which is defined by the valence, interaction strengths, and bond volumes of stickers, the system of MAMs undergoes percolation, which is a continuous associative, networking transition. Note that percolation is an inclusive transition that does not create solvent-rich and MAM-rich coexisting phases. Instead, the solvent is incorporated into the system-spanning network. (C) In a solution of MAMs that feature stickers (yellow) and spacers (orange), phase separation will be coupled to percolation. This gives to a dense, MAM-rich phase, known as a condensate, that is defined by a percolated network of MAMs.

In contrast to FH theories, Flory-Stockmayer (FS) theories [10,21] describe the networking of polymers with reactive groups. This enables polymers to be topologically connected via reversible physical crosslinks into system-spanning networks (Figure 1B). The term percolation is used to describe associative phase transitions that lead to system-spanning networks of MAMs. The study of phase transitions of MAMs, which combines contributions from the physics of patchy colloids [22] and the physics of associative polymers [23,24], has highlighted the importance of the coupling between phase separation, driven by solubility considerations, and percolation, driven by networks of associative interactions (Figure 1C).

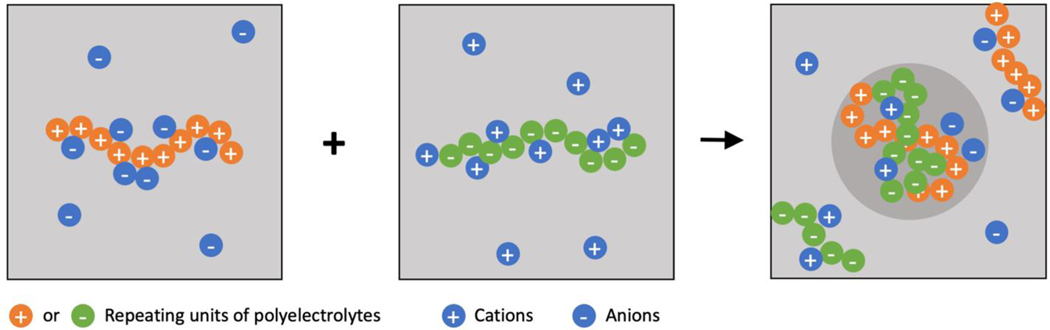
Complex coacervation is another example of condensation (Figure 2). This involves the association of oppositely charged polymers that segregate into polymer-rich and solvent-rich phases. Modern theories [25,26] are being developed to reevaluate the assumptions that go into mean field descriptions for complex coacervation [15]. Particular attention is being paid to the importance of solution ions, linear charge density, and sequence effects [27]. Field-theoretic methods, where a single chain interacts with a phantom field created by other macromolecules and the complex solvent, are being brought to bear to understand several aspects of complex coacervation in polyelectrolytic and polyampholytic systems [28–30].

Figure 2. Oppositely charged MAMs, which can be flexible polyelectrolytes or colloidal macroions, undergo complex coacervation.

The association of oppositely charged MAMs initiates phase separation, which is the driven, in part by the release of counterions from the oppositely charged macromolecules.

Adaptations and generalizations of FH and FS theories for biomolecular condensates

Chan and coworkers modified the FH theory to include the effects of associations via aromatic stickers [31]. They also included sequence correlations to model the coupling between electrostatic interactions and the linear patterning of oppositely charged residues [32,33]. Lin and Chan showed that the critical temperature is inversely correlated with the radii of gyration of polyampholytic disordered proteins in the dilute phase [34].

Intrinsically disordered prion-like low complexity domains (PLCDs) are exemplars of linear MAMs. These systems are key components of several biomolecular condensates including stress granules. Martin et al., measured the coexistence curves for the PLCD from the protein hnRNP-A1 [35]. The measured coexistence curves of these finite-sized heteropolymers could be fit using a modification of the FH theory that includes contributions from three-body interactions. Specific sequence features, namely the non-random and uniform distribution of aromatic stickers along the linear sequence allowed Martin et al., to use the FH theory for homopolymers to describe the measured phase boundaries for PLCDs [35]. The uniform distribution of aromatic stickers is a conserved feature of PLCDs, although exceptions such as the PLCD from the protein Velo1 highlight how evolution coopts exceptions to enable different types of functions [18].

Generalization of FH theory to multicomponent systems has proven to be effective for demonstrating how stoichiometric ratios contribute to the saturation of dilute phases when there is a blend of homotypic and heterotypic interactions among MAMs [36,37]. In this case, attention must be paid to the slopes of tie lines [38] to avoid naïve expectations that every MAM will have an intrinsic and fixed saturation concentration.

The Gibbs phase rule sets an upper limit of n+1 coexisting phases for fixed temperature and pressure in a system with n macromolecules plus a solvent. Jacobs and Frenkel [39] and Jacobs separately [40] generalized the FH theory to show that there are two limiting scenarios that result from the variance of pairwise interaction energies among MAMs. Low variance gives rise to a single condensed phase comprising all the macromolecules coexisting with a dilute, macromolecule deficient phase. Conversely, a high variance of interaction energies gives rise to the limiting scenario that matches the expectations from Gibbs phase rule.

Zwicker and Laan [41] analyzed what it would take to achieve compositionally distinct condensates that coexist with one another. They showed, using an evolutionary algorithm, designed to achieve the coexistence of condensates, that pairwise two-body interactions can be encoded to yield desired objective of compositionally distinct, coexisting condensates.

Phase separation coupled to percolation and generalized models for percolation

For linear MAMs, the excluded volumes of linkers determine the extent of coupling between phase separation and percolation [12]. This highlights the key contributions of chain-solvent interactions as drivers of segregative transitions and their coupling with associative transitions. The bond fluctuation model has been codified into a lattice engine, known as LaSSI, that enables simulations of phenomenological, architecture-specific, and sequence-specific condensation transitions for macromolecules with different sticker-and-spacer architectures [38].

Schmit and coworkers developed quasi-analytical approaches to capture the effects of molecular topologies of finite-sized macromolecules. They modeled polymerization induced phase separation, as well as binding induced phase separation coupled to percolation [42,43]. These models highlight the importance of molecular structures and fluctuations about these structures for determining the nature of interactions that drive phase transitions, and the internal organization of molecules within condensates.

Choi et al., recently generalized the FS theory to allow for multiple sticker types [44]. They also showed that three body interactions and corrections to entropic contributions can have a profound impact on the percolation threshold. This formalism was adapted by Bremer et al., [45] to uncover the role of Arg residues as auxiliary stickers and Lys residues as suppressors of phase separation coupled to percolation in PLCDs.

Wingreen and colleagues have investigated the phase behaviors of rigid multivalent macromolecules using numerical and analytical approaches based on percolation models [46]. They showed that if the sticker valence of rigid MAMs interacting via heterotypic interactions matches a magic number, then percolation is suppressed through the formation of clusters of precise stoichiometries.

Dynamical arrest in condensates that form via phase separation coupled to percolation

Wingreen and colleagues have also shown that as the valence of stickers approaches magic number ratios, the internal dynamics of molecules within clusters that approximate condensates are slowed when compared to valencies that are farther removed from the magic number ratios [47]. These results were cast in different, albeit complementary light, by Ranganathan and Shakhnovich [48]. They adapted a stickers-and-spacers architecture and performed off-lattice Langevin dynamics simulations to model condensate growth. Their simulations showed an intricate interplay between the timescales for molecular diffusion (t_D) and the timescales associated with the making and breaking of physical crosslinks (t_bond). When t_bond becomes considerably longer than t_D, the growth of clusters is arrested. This suggests designable and evolvable routes to controlling condensate size through the dynamical interplay between the distinct timescales associated with crosslinking and molecular transport.

Dynamical arrest has also been observed in protein-RNA mixtures that show reentrant phase behaviors. Systematic assessments using different protein-RNA mixtures led to the suggestion that hollow condensates might be globally stable phases [49]. However, the recent work of Feric et al., [50] which recapitulated the formation of hollow condensates in a five-component mixture or protein, DNA, and newly transcribed molecules, shows clear evidence that vesicle-like hollow condensates are metastable, dynamically arrested phases. Instead, spatially organized, non-hollow condensates are the equilibrium morphologies of condensates that are intended to be mimics of mitochondrial nucleoids [50].

Condensates are viscoelastic materials [51]. Such materials should be characterized by spatially inhomogeneous organization of the underlying MAMs. This feature has been demonstrated by two recent computations. Using graph-theoretic analyses, Shillcock et al., [52] and Farag et al., [53] converged upon distinctive, networked organization of model MAMs and several PLCD variants within condensates. Further, at least three separate studies have demonstrated that the conformations of disordered proteins within condensates are distinct from the conformations in dilute phases. Specifically, the networking of MAMs within condensates causes chain expansion that appears to be a robust and reproducible observation across different systems [52–54]. These conformational features within condensates are likely to be seeds of solidification transitions, which involve conversion to beta strands [55], and to fibril formation via first-order phase transitions [56].

Connecting single chain conformational and phase equilibria of disordered proteins

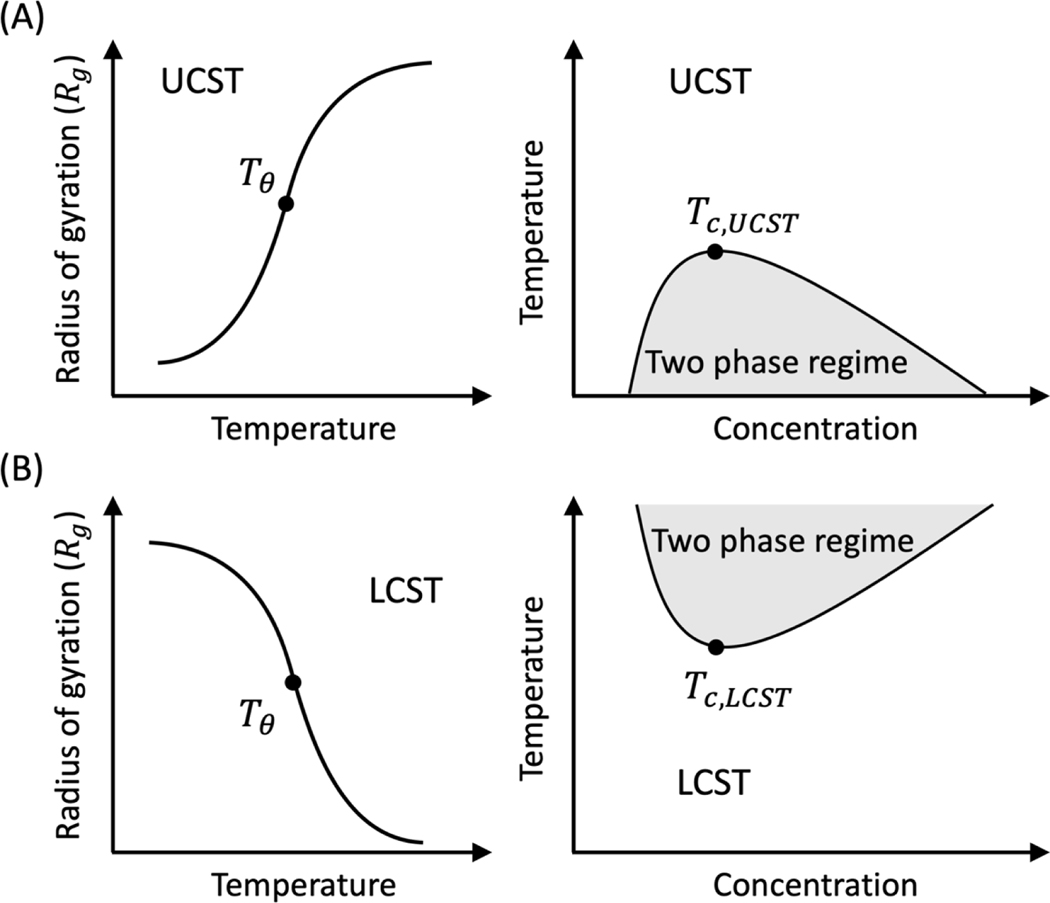
The Gaussian cluster theory (GCT) of Raos and Allegra [57] provides a clear route to formalize the connection between single-chain coil-to-globule transitions and phase separation [58] for homopolymers. In the GCT, the same two- and three-body interaction coefficients are used to describe the free energy of a single polymer and for clusters of polymers in a solvent. Zeng et al., adapted the GCT to extract two- and three-body interaction coefficients from simulations of single chain coil-to-globule transitions [59]. They showed that the GCT could be deployed across a variety of systems – not just homopolymers. The two- and three-body interaction coefficients were combined with the GCT to compute full phase diagrams, including coexistence curves (binodals) and instability boundaries (spinodals). Zeng et al., showed that the GCT can be deployed for modeling and designing sequences showing phase transitions with either upper or lower critical solution temperatures [60] (Figure 3). Chou and Aksimentiev [61] showed that the binodals computed using the Zeng et al., adaptation of the GCT matched those computed using the simulation paradigm of Dignon et al., [62].

Figure 3. Single-chain coil-to-globule transition of flexible MAMs such as intrinsically disordered proteins (IDPs) is connected to their phase behavior.

(A) For IDPs with an upper critical solution temperature (UCST), a single chain adopts compact conformations below a system-specific transition temperature 𝑇_𝜃 and expanded conformations above 𝑇_𝜃. Below 𝑇_𝜃, phase separation via intermolecular interactions is driven by the same set of interactions that drive chain compaction in the single chain limit. (B) For IDPs with a lower critical solution temperature (LCST), a single chain adopts compact conformations above a system-specific transition temperature 𝑇_𝜃 and expanded conformations below 𝑇_𝜃. Above 𝑇_𝜃, phase separation via intermolecular interactions is driven by the same set of interactions that drive chain compaction in the single chain limit. In panels (A) and (B), the temperatures T_c,UCST and T_c,LCST are the critical temperatures for UCST- and LCST-type of phase separation, respectively. Notice that T_θ > T_c,UCST for the system showing UCST-type phase separation, and T_θ < T_c,LCST for the system showing LCST-type of phase separation. This reflects the continuous nature coil-to-globule transitions, with T_θ being a tricritical point. The theta temperatures approach the critical temperatures for infinitely long polymers.

The deployment of the GCT is promising because it points the way toward leveraging information gleaned from computationally tractable simulations of single chain conformational equilibria for computing full phase diagrams for linear MAMs. Generalizations of the GCT will be of interest for understanding the coupling between conformational and condensation transitions in complex mixtures of MAMs and for the design of novel protein sequences with bespoke thermoresponsive phase behaviors [60].

The differential impact of scaffolds vs. ligands

Condensates comprise a heterogeneous mixture of MAMs. Scaffolds drive the formation of condensates. These are likely to be MAMs with the highest valence of stickers and spacers with the lowest excluded volume. In contrast, ligands are likely to have lower valence of stickers. They could also have an excluded volume that weakens the driving forces for phase separation.

Using a patchy colloid model for rigid associative macromolecules, Zhou and coworkers have performed a series of simulations to query the impacts of scaffolds vs. ligands on the coupling of phase separation and percolation [63,64]. The patchy colloid model, a mainstay for rigid MAMs, has also found usage in the work of Espinosa et al., [65]. Their analyses highlighted the network structures of condensates, demonstrating a direct connection between the extent of networking and the stability of the condensates. Additionally, high-valence particles were shown to have a larger effect on the phase behavior of multicomponent systems than low-valence particles.

The impact of site-specific binding of ligands on the phase equilibria of linear multivalent systems was investigated by Ruff et al., [66]. They extracted rules regarding the effects of different ligands as modulators of phase separation. Interest in the effects of ligands on the phase transitions of MAMs [67] has activated interest in the polyphasic linkage formalism of Wyman and Gill [68].

The importance of and distinct approaches for coarse graining

Phase transitions arise due to the collective effects of MAM-solvent, inter-MAM interactions, and solvent-solvent interactions. Detecting the onset of a phase transition requires simulations performed at a series of different concentrations of MAMs and solution conditions. The necessity of these computational titrations highlights the primacy of solvent effects on driving segregative transitions. And yet, it is computationally expensive to include solvent effects whilst gaining access to the collective effects of O(10²) or more MAMs. Instead, one must resort to computations that rely on coarse grained models.

The development and deployment of coarse-grained models that capture the phenomenology of a specific process are useful and have a proven track record in the physical literature. Such approaches can be deployed to ask “what if” questions, and these approaches can yield important insights regarding condensation [18,31,33,41–43,46–48,56,63–65,69–77].

Beyond phenomenology, there are two categories of models namely, transferable and learned models. Both approaches can be systematized to allow for resolution-specific questions to be asked and answered. And while it is easy to get caught up in arguments about the superiority of one approach over the other, it is worth noting that every model is an abstraction. Accordingly, knowing the limitations of an approach is just as important as knowing the advantages.

A popular approach for simulating the phase behaviors of IDPs / IDRs as autonomous units is the methodology pioneered by Mittal and coworkers [28,58,62,78,79]. This method uses potentials that emphasize the relative hydrophobicities of different amino acids, each represented as a single bead [80–84]. A series of concentration- and temperature-dependent molecular dynamics simulations, performed in confined geometries, with ca. 40–50 molecules, are used to map coexistence curves and interrogate the properties of dense phases [84,85]. There has been a surge of interest, with improvements being proposed to the underlying potentials that account for more sophisticated nuances of spatial ranges of interaction potentials, and the relative strengths of these potentials [81,84]. The effects of electrostatic interactions [73] have been incorporated using Yukawa potentials [86]. Insights have been extracted regarding the nature of interactions within dense phases, and these have been used to challenge the stickers-and-spacers framework [87]. The MARTINI model, readily accessible via packages such as GROMACS, has also been deployed to study specific types of MAMs [88].

A different approach, inspired by the paradigm of systematic coarse-graining, pioneered by Voth and coworkers [89], leads to systems-specific coarse-grained models by learning from higher resolution simulations and / or experiments. This method, coupled to a Gaussian process Bayesian optimization learning paradigm [90], has been used to develop a residue-specific model for lattice-based simulations of PLCDs [53]. While this model is interoperable across PLCDs that share compositional biases, it cannot be deployed without additional learning, to other IDP archetypes [53]. Whether this is a weakness, or a strength is a matter of debate. It is worth noting, however, that transferable models can get the right answers for the wrong reasons. A case in point is the choice one must make in transferable models regarding the relative strengths of Arg-π interactions vs. π-π interactions [84]. While data suggest that Arg-π interactions are stronger than π-π interactions in molecules such as full-length FET family proteins [91], data for PLCDs [45] or IDRs with PLCD-like compositions [87] support the opposite conclusions. This highlights the context dependence of sticker-sticker interaction strengths. This is a challenge on two fronts: Learned models must be bespoke whereas transferable models must make a choice. For the latter, getting the right phase behaviors then depends either on the serendipity of compositional biases or on a balancing of the relative interaction strengths, whereby all sequence contexts enable appropriate cancellation of errors. Recent theoretical advances suggest that a way to bridge the divide between transferable and learned models is for both paradigms to consider the contributions of context-dependent, three-body interactions [44,45].

Another important consideration in the design of coarse-grained simulations is the issue of finite size. Off-lattice simulations typically deploy ca. 40–50 molecules. This gives rise to dense phase clusters that coexist with an ultra-dilute vapor. While this is useful for comparative mapping of phase boundaries, there are challenges that cannot be ignored. Some of these have been discussed by Nilsson and Irback [92] and by Choi et al., [38]. Two specific challenges pertain to the modeling of pre-percolation clusters that form in sub-saturated solutions, [93] and to the analysis of interfaces between coexisting phases [53]. Gaining access to accurate descriptions of these features require O(10⁴) – O(10⁵) molecules at least [53]. Working around the limitations of finite sizes is relatively easy for lattice models, but problematic off a lattice. However, lattice models have their own set of problems, not the least of which is the use of a lattice and interactions based purely on contact potentials. These issues highlight the tradeoffs one must make in designing coarse-grained models. Invariably, the model one chooses in terms of resolution, sampling method, and the space to be sampled will be contingent upon the question one seeks to answer.

Overall, there is emerging maturity and convergence in terms of modeling of IDPs and even mixtures of IDPs, which are the simplest exemplars of MAMs. However, the challenge of modeling nucleic acids, specifically the ion- and solvent-mediated effects, the effects of heterotypic protein-nucleic acid interactions, and the effects of hybrid architectures featuring folded and disordered domains within RNA and protein molecules, remains a pressing challenge. Likewise, integrating the analysis of simulation results with the development of novel theoretical approaches for the modeling of spontaneous condensation is a fundamental challenge for theory and computation alike.