Abstract
To mitigate the adverse effects of fossil fuel-based energy, mankind is in constant search of clean and cost-effective sources of energy, such as solar energy. The economic viability of a power plant to harness solar energy mostly depends on the efficiency of solar panels. Investigations over the years show that the solar panel efficiency significantly depends on the different meteorological parameters. Therefore, there is an imminent need for a correlation explaining the relations between the efficiency and different meteorological parameters. In this study, an effort has been made to analyze the effects of various meteorological parameters on the efficiency and subsequently propose a correlation between them. Initial investigations reveal that the optimal tilt angle for the maximum power output is 26°. The study demonstrates that efficiency is directly proportional to solar intensity and wind speed while being inversely proportional to temperature, humidity, and dew point temperature. Regression analysis of a data set comprising 100 data sets establishes a strong correlation between efficiency and five meteorological parameters: temperature, humidity, wind speed, solar intensity, and dew factor. The calculated efficiencies using the developed correlation deviate from the experimental values, with absolute errors ranging from 0.08 to 1.20%. The findings provided valuable insights for optimizing solar power plant performance by understanding the relationship between efficiency and meteorological parameters.
1. Introduction
Fossil fuel consumption for meeting energy needs has led to environmental consequences such as global warming and air pollution. To mitigate climate change and air pollution, the adoption of clean and renewable energy sources has become imperative. Solar energy, in particular, has gained significant attention as a viable renewable energy option due to its environmental benefits. Consequently, extensive research is being conducted to explore various aspects of harnessing solar power.1−3 The efficiency of solar panels plays a crucial role in determining the economic viability of a solar photovoltaic (PV) power plant, as it directly converts solar energy into electrical energy. This efficiency is influenced by multiple factors, including solar intensity, temperature, wind speed, rainfall, humidity, dew point, and cloud cover. Consequently, investigating the impact of these factors on solar panel efficiency has become a key area of interest for researchers.
Kazem et al.4,5 conducted a study examining the impact of solar radiation on PV systems in Oman. They explored various configurations and assessed their technical and financial viability. The study highlighted that despite the challenges posed by high temperatures, Oman’s abundant solar radiation, long days, and peak hours make it a promising location for investing in PV systems. Yousif et al.6 also conducted a feasibility study on the solar power production potential of Oman. Song et al.7 investigated the impact of PM2.5 pollution on the solar energy availability in Hong Kong. The study reveals that PM2.5 pollution negatively impacts solar energy availability and PV system performance. With PM2.5 exceeding 33.5 μg/m3, a global horizontal irradiance reduction of over 5% is observed. Crystalline and thin-film PV systems experience energy losses up to 7.00 and 9.73%, respectively, suggesting a significant impact of PM2.5 on solar-cell performance. Additionally, Singh and Ravindra8 conducted theoretical investigations on the effect of temperature on the performance parameters of solar cells, including current density, voltage, fill factor, and efficiency, in the temperature range of 273–523 K. They observed that as temperature increases, reverse-current increases while voltage, fill factor, and efficiency decrease. Makrides et al.9 examined the impact of temperature on various solar technologies in Cyprus. They found that different solar-cell types exhibited varying thermal losses, with monocrystalline silicon, multicrystalline silicon, and thin-film technologies experiencing average thermal losses of 8, 9, and 5%, respectively. Kaldellis et al.10 conducted an experimental study in Greece, investigating the influence of temperature and wind speed on the performance of PV modules. Furthermore, Ebhota and Tabakov11 investigated the effects of temperature variation (10–50 °C) on different types of PV modules. Their comparative study revealed that copper indium gallium selenide PV cells had a higher performance ratio compared with crystalline silicon PV cells. Chakraborty et al.12 investigated the effects of different meteorological parameters on solar PV by using machine learning in eastern India. Different Ensemble ML models, including Bagging, Boosting, Stacking, and Voting, were used for the purpose. The machine learning algorithm is verified by the field data of a 10 kWp solar PV power plant. With a test-bed framework for data mining and model selection, it achieves a high prediction accuracy of up to 96% for selected models, demonstrating potential applicability for large-scale solar PV power plants. Aoun13 evaluated five different mathematical models which estimate the temperature of a monocrystalline PV module. These models take solar radiation and ambient temperature as inputs. Based on the type of data source, the analysis is carried out for three different groups. It has been reported that the models demonstrate consistent performance throughout the year, with mean square errors ranging from 0.45 to 5.7 °C. Superior results were achieved during the hot months (April to October). Ghazy et al.14 proposed a novel hybrid PV module and adsorption desalination system wherein electrical energy production and desalination occur simultaneously. Their model exploits the concept of utilizing the cool water generated during desalination as a coolant for the PV module, thereby enhancing its performance in hot weather regions. Mehmood et al.15 assessed the integration of solar PV energy into residential sectors, emphasizing a holistic feasibility analysis. Using statistical and information-gain ratio methods, we quantify trade-offs and synergies among different design parameters. The findings indicate that linking the solar PV system to the power grid yields a significant effect, whereas connecting it to a battery storage system demonstrates greater competitiveness. Additionally, the influence of other meteorological parameters, such as humidity, on the performance of PV cells has also been considered by several researchers.
Gwandu and Creasey16 conducted an experimental investigation to examine the effects of humidity on the performance of monocrystalline silicon PV modules. They found a nonlinear relationship between humidity and solar radiation. Similarly, Panjwani and Narejo17 reported a detrimental effect of humidity on the power output of PV modules, estimating a loss of approximately 15–30% in PV power. Mekhilef et al.18 assessed the impact of dust accumulation, humidity, and air velocity on the efficiency and overall performance of PV cells. They observed an increase in efficiency with higher wind speeds due to the decreased relative humidity. However, excessive wind speeds can cause dust lifting and dispersion, leading to a reduction in the cell efficiency. They also noted that air velocity, dust, and humidity all significantly influence PV cell performance. Ghazi and Ip19 conducted experimental studies and reported that dust coverage, humidity, rain, and snow can significantly reduce the efficiency of PV modules. Sohani et al.20 investigated the impact of temperature, humidity, wind speed, and solar radiation on the photocurrent and thermal voltage of a diode. They found that solar radiation has the greatest impact on the photocurrent, while temperature has the greatest impact on the voltage of the diode. Additionally, they highlighted that CO2 emissions are more sensitive to photocurrent compared to voltage. Recently, Akonjom and Njok21 investigated the impact of meteorological parameters on PV performance. Employing precise instruments, it identifies optimal humidity levels (67–47%) for voltage stability and favorable temperature conditions (rarely exceeding 40 °C), supporting 90% efficiency. The region’s altitude and early high solar power levels (800 W/m2 at 9:00 am) recommend it as a promising site for solar energy farms.
Hussein et al.22 conducted an investigation and found that south-facing PV panels with tilt angles between 20 and 30° exhibit the highest power output. Jamil et al.23 also conducted a study on the optimal tilt angles for south-facing PV modules and discovered that these angles are greater during the winter compared to the summer. They reported an annual optimum angle of 27.62° for Aligarh, India, and 27.95° for Delhi, India. Bhattacharya et al.24 conducted experimental research to establish a correlation between various meteorological parameters and the efficiency of PV modules. Through the analysis of 30 sets of data, they established correlations between efficiency and different meteorological parameters such as temperature, radiation, wind speed, and humidity. Bahanni et al.25 conducted a comparative study of different PV cell technologies in two cities in Morocco and evaluated the effects of meteorological parameters on PV cell performance. They concluded that among monocrystalline, amorphous, and polycrystalline PV cells, polycrystalline cells performed the best regardless of location. They also observed that El Jadida, despite having a lower solar intensity than BeniMellal, had a higher production capacity, indicating the significant influence of meteorological parameters on PV cell productivity. Iqbal et al.26 investigated the power loss caused by temperature, humidity, dew point, and heat index at three different locations: rooftop, parking area, and ground level. They reported that the highest power loss occurred at the ground level, followed by the rooftop and parking areas in sequential order.
Based on the reviewed literature, it is evident that existing studies on PV cell performance primarily focus on assessing the feasibility of specific locations for solar energy harnessing,4−6 determining the optimal tilt angle for maximum output,22,23 comparing the performance of different PV cell technologies,9,25 and investigating the effects of various meteorological parameters on PV cell performance. The meteorological parameters considered include solar intensity,4,5 ambient temperature,4−11 humidity,16−21 wind speed,10,18,20 and dew point.26 However, among these studies, only Bhattacharya et al.24 developed a correlation to predict PV module efficiency using meteorological data such as temperature, humidity, and solar radiation. Nevertheless, they did not consider dew point temperature, an important parameter for evaluating solar panel performance,26 and their correlation was based on a limited number of data points. Therefore, it is necessary to revisit and improve this correlation by including dew point temperature as an independent variable and incorporating a larger data set. In light of these considerations, this study aims to develop a correlation between PV module efficiency and various meteorological parameters, including ambient temperature, humidity, solar intensity, wind speed, and dew point, through regression analysis of experimental data. Additionally, an investigation into determining the optimal tilt angle for maximum power output is conducted. The experimental setup details and outcomes are discussed in subsequent sections.
2. Experimental Setup and Experimentation
The study presented here presents an analytical correlation aimed at predicting the efficiency of a solar panel. This correlation takes into account various factors, including solar intensity, wind speed, humidity, ambient temperature, and the dew point. These meteorological data are relevant to the specific weather and climate conditions of the research location, which, in this case, is the Dibrugarh University campus in Dibrugarh, Assam, India. The coordinates of the location are approximately 27.4495°N latitude and 94.9119°E longitude. The weather in this area is characterized by hot and humid conditions, with summer temperatures reaching around 40 °C, and cold and dry conditions in winter, with maximum temperatures around 22 °C.
An anemometer, a solar power meter, and a dew point meter were among the tools used to gather the necessary meteorological data. The solar power meter monitored solar power, while the anemometer measured wind speed. The dew point meter was used to gauge humidity, ambient temperature, and dew point temperature. Table 1 contains the specific details of these instruments.
Table 1. List of the Key Instruments with Specifications.
| sl. no. | name of instrument | specification |
|---|---|---|
| 1. | digital anemometer | wind speed range: 0–140 km/h |
| 2. | solar power meter | maximum radiation: 1999 W/m2 or 634 BTU/(Ft2 h) |
| resolution: 1 W/m2; 1 BTU/(Ft2 h) | ||
| accuracy: ±10 W/m2 | ||
| 3. | dew point meter | temperature range: 20–60 °C |
| temperature accuracy: ±1 °C (0–45 °C), ±1.5 °C (45–60 °C) | ||
| humidity range: 0–100% RH | ||
| humidity accuracy: ±3% (20–80%), ±4% (0–20%, 80–100%) | ||
| wet bulb temperature range: −20 to 60 °C | ||
| wet bulb temperature accuracy: ±1 °C (0–45 °C), ±1.5 °C (45–60 °C) | ||
| dew point range: −50 to 60 °C | ||
| dew point accuracy: ± 1 °C (0–45 °C), ± 1.5 °C(−50 to 0 °C, 45–60 °C) | ||
| resolution: 0.1 °C | ||
| 4. | mini inclinometer | measuring range: 4 × 90° |
| resolution: 0.05° | ||
| accuracy: ± 0.2° | ||
| repeatability: 0.1° |
In addition, a 100 W solar panel with dimensions of 0.620 × 0.755 m was utilized for the investigation. Table 2 contains the panel’s detailed information. The solar panel was installed on an iron frame (Figure 1) to allow for various orientations because the experiment was primarily concerned with examining the effects of varied tilt degrees. The panel and frame were put in place on a two-story building’s south-facing roof (9.15 m in height). The solar panel’s alignment was fixed using an inclinometer, which is visible in the figure put over it.
Table 2. Specifications of the Solar Panel Considered in the Present Study.
| maximum power | 100.00 W |
| maximum voltage | 20.00 V |
| maximum current | 5.0 A |
Figure 1.

Solar panel test rig installed on the roof of a two-story building.
The experimental solar panel efficiency was then determined by using the methodology listed below.
| 1 |
Here, ηp is the solar panel efficiency, Pp is the power, Ap is the surface area of the panel, and Ip is the solar intensity. Here, the power of the solar panel is the product of voltage and current, which are measured with the help of a multimeter. Likewise, the solar intensity is measured with the help of a solar power meter.
3. Results and Discussion
In the present work, experiments are performed to analyze the effect of tilt angle and variation of efficiency with different meteorological parameters. Further, a correlation is established between the efficiency of the solar panel and various meteorological parameters. The outcomes of these experiments are discussed in detail in the following subsections.
3.1. Effect of Tilt Angle
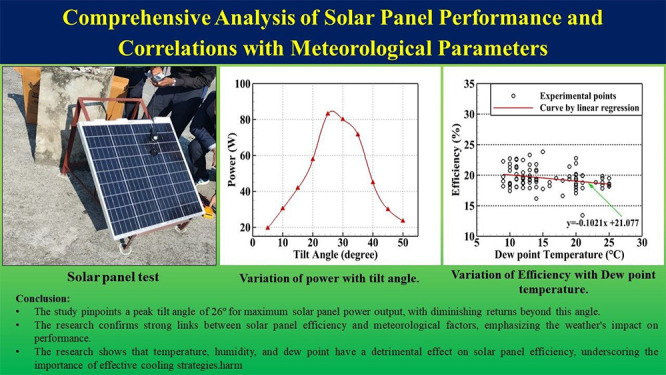
Before the detailed investigation, a study was carried out to detect the optimum angle for maximum power output. For this purpose, the tilt angle of the solar panel is varied in multiples of 5 from 5° to 50°. The voltage and current for each angle are recorded for 5 consecutive days (20–24 December 2021). The average power output obtained at different tilt angles is shown in Figure 2. It can be seen that initially, the power output increases with an increase in tilt angle. However, after an optimum level is reached, it starts to decrease. It is observed that the maximum power output is 84.64 W for a tilt angle of 26°. This is in accordance with the results claimed by Jamil et al.,23 where they have reported that the maximum power output is achieved at around 27° in India. Therefore, the tilt angle is fixed at 26° for a further detailed study.
Figure 2.
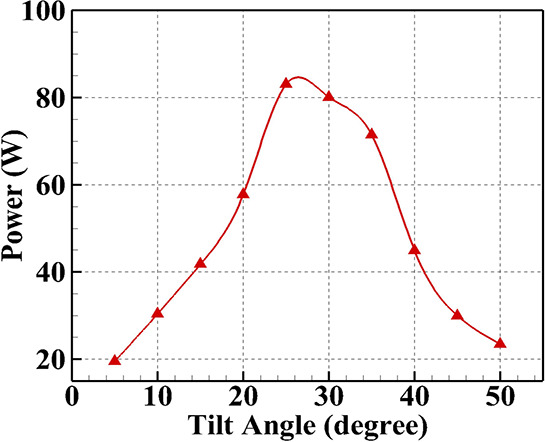
Variation of power with the tilt angle.
3.2. Effect of Meteorological Parameters
The efficiency analysis of the solar panel based on various meteorological parameters was carried out. The parameters considered were solar intensity, ambient temperature, humidity, wind speed, and dew point. The study was conducted over 100 days, between January 3, 2022 and April 25, 2022. The different meteorological data obtained from experimental measurements are given in Table A1. The location, tilt angle, and orientation of the solar panel were kept constant.
Table A1.
| date | solar intensity (W/m2) | ambient temperature (°C) | humidity (%) | wind speed (km/h) | dew point temperature (°C) |
|---|---|---|---|---|---|
| 1/3/2022 | 863 | 24 | 41 | 6 | 10 |
| 1/4/2022 | 910 | 22 | 46 | 5 | 10 |
| 1/5/2022 | 970 | 20 | 68 | 7 | 11 |
| 1/10/2022 | 780 | 19 | 45 | 6 | 11 |
| 1/11/2022 | 676 | 19 | 82 | 6 | 16 |
| 1/13/2022 | 115 | 15 | 93 | 7 | 14 |
| 1/14/2022 | 358 | 18 | 77 | 6 | 14 |
| 1/15/2022 | 920 | 21 | 68 | 6 | 15 |
| 1/16/2022 | 707 | 19 | 72 | 4 | 14 |
| 1/17/2022 | 724 | 19 | 59 | 6 | 11 |
| 1/18/2022 | 770 | 20 | 48 | 6 | 11 |
| 1/19/2022 | 980 | 21 | 52 | 6 | 11 |
| 1/20/2022 | 132 | 18 | 63 | 6 | 11 |
| 1/21/2022 | 140 | 16 | 87 | 6 | 14 |
| 1/22/2022 | 290 | 16 | 82 | 6 | 13 |
| 1/23/2022 | 260 | 15 | 82 | 7 | 12 |
| 1/24/2022 | 326 | 15 | 93 | 6 | 14 |
| 1/25/2022 | 679 | 16 | 82 | 7 | 13 |
| 1/26/2022 | 660 | 16 | 87 | 7 | 14 |
| 1/27/2022 | 550 | 14 | 93 | 6 | 13 |
| 1/28/2022 | 658 | 16 | 63 | 6 | 9 |
| 1/29/2022 | 600 | 14 | 76 | 6 | 10 |
| 1/30/2022 | 820 | 20 | 48 | 6 | 9 |
| 1/31/2022 | 700 | 18 | 48 | 6 | 9 |
| 2/1/2022 | 780 | 21 | 52 | 3 | 11 |
| 2/2/2022 | 700 | 20 | 55 | 7.5 | 11 |
| 2/3/2022 | 730 | 15 | 82 | 3.7 | 12 |
| 2/4/2022 | 879 | 20 | 55 | 6.4 | 11 |
| 2/5/2022 | 324 | 20 | 68 | 5 | 14 |
| 2/6/2022 | 840 | 24 | 40 | 5.3 | 10 |
| 2/8/2022 | 458 | 18 | 52 | 6.4 | 12 |
| 2/9/2022 | 956 | 21.5 | 52 | 5 | 11 |
| 2/10/2022 | 964 | 24 | 40 | 2 | 10 |
| 2/11/2022 | 891 | 22 | 43 | 5 | 10 |
| 2/12/2022 | 948 | 26 | 35 | 5.4 | 9 |
| 2/13/2022 | 876 | 26 | 36 | 6 | 10 |
| 2/14/2022 | 652 | 21.7 | 59 | 3.9 | 12 |
| 2/15/2022 | 805 | 24 | 46 | 2 | 12 |
| 2/16/2022 | 780 | 21.5 | 68 | 4 | 14 |
| 2/17/2022 | 220 | 17.8 | 77 | 3.9 | 12 |
| 2/18/2022 | 948 | 26 | 35 | 5.4 | 9 |
| 2/19/2022 | 876 | 26 | 36 | 6.1 | 10 |
| 2/20/2022 | 652 | 21.7 | 59 | 3.9 | 12 |
| 2/21/2022 | 805 | 24 | 46 | 2 | 12 |
| 2/22/2022 | 780 | 21.5 | 68 | 4 | 14 |
| 2/23/2022 | 607 | 28 | 41 | 3.8 | 12 |
| 2/24/2022 | 803 | 30 | 36 | 3 | 13 |
| 2/25/2022 | 809 | 31 | 33 | 1.8 | 14 |
| 2/26/2022 | 804 | 32 | 39 | 1.8 | 13 |
| 2/27/2022 | 700 | 31 | 36 | 3.4 | 13 |
| 2/28/2022 | 640 | 31 | 52 | 4.1 | 10 |
| 3/1/2022 | 650 | 31 | 52 | 2 | 10 |
| 3/2/2022 | 650 | 25 | 52 | 3.9 | 11 |
| 3/3/2022 | 694 | 26.5 | 50 | 4.3 | 12 |
| 3/4/2022 | 600 | 26 | 52 | 3.7 | 10 |
| 3/7/2022 | 115 | 23 | 91 | 2 | 17 |
| 3/8/2022 | 105 | 22 | 92 | 3.5 | 18 |
| 3/9/2022 | 109 | 22.3 | 91 | 3 | 16 |
| 3/10/2022 | 230 | 22.8 | 65 | 3.9 | 15 |
| 3/11/2022 | 240 | 25 | 50 | 3.4 | 13 |
| 3/12/2022 | 109 | 22.3 | 91 | 2.3 | 16 |
| 3/13/2022 | 148 | 23 | 91 | 3.8 | 18 |
| 3/15/2022 | 700 | 28 | 56 | 4.8 | 19 |
| 3/16/2022 | 712 | 30 | 29 | 2.8 | 13 |
| 3/17/2022 | 650 | 28 | 39 | 3 | 13 |
| 3/18/2022 | 600 | 28 | 41 | 3 | 13 |
| 3/19/2022 | 722 | 29 | 53 | 2.3 | 21 |
| 3/22/2022 | 398 | 26 | 60 | 2 | 25 |
| 3/23/2022 | 630 | 28 | 61 | 3 | 20 |
| 3/24/2022 | 398 | 27 | 57 | 3.5 | 20 |
| 3/25/2022 | 398 | 29.7 | 54 | 1.8 | 20 |
| 3/26/2022 | 670 | 30 | 49 | 3.4 | 19 |
| 3/27/2022 | 600 | 27 | 52 | 2.4 | 20 |
| 3/29/2022 | 350 | 22 | 80 | 5 | 21 |
| 3/30/2022 | 240 | 22 | 93 | 3.1 | 21 |
| 3/31/2022 | 300 | 24 | 86 | 4 | 20 |
| 4/1/2022 | 758 | 28 | 61 | 4.3 | 20 |
| 4/2/2022 | 600 | 27 | 58 | 3 | 20 |
| 4/3/2022 | 663 | 28 | 51 | 2 | 20 |
| 4/4/2022 | 350 | 23 | 61 | 3.8 | 21 |
| 4/5/2022 | 800 | 31 | 50 | 2 | 20 |
| 4/6/2022 | 398 | 23 | 50 | 4 | 20 |
| 4/7/2022 | 785 | 31 | 51 | 3 | 20 |
| 4/8/2022 | 725 | 29 | 51 | 3 | 21 |
| 4/9/2022 | 750 | 31 | 50 | 2 | 19 |
| 4/10/2022 | 717 | 32 | 48 | 1.8 | 19 |
| 4/11/2022 | 666 | 33 | 55 | 1.5 | 24 |
| 4/12/2022 | 790 | 34 | 46 | 1.8 | 20 |
| 4/13/2022 | 341 | 27 | 83 | 3.1 | 24 |
| 4/15/2022 | 388 | 27 | 63 | 2 | 24 |
| 4/16/2022 | 244 | 27 | 70 | 2.8 | 24 |
| 4/17/2022 | 115 | 26.7 | 94 | 3.1 | 25 |
| 4/18/2022 | 109 | 27 | 96 | 2.8 | 25 |
| 4/19/2022 | 109 | 27.1 | 100 | 2.4 | 25 |
| 4/20/2022 | 110 | 27 | 100 | 2.8 | 25 |
| 4/21/2022 | 109 | 26.3 | 100 | 1.2 | 25 |
| 4/22/2022 | 115 | 25.8 | 94 | 3.1 | 25 |
| 4/23/2022 | 140 | 26 | 100 | 2.5 | 25 |
| 4/24/2022 | 354 | 29 | 67 | 1.4 | 23 |
| 4/25/2022 | 349 | 28 | 68 | 1.8 | 24 |
By measuring the current and voltage and using eq 1 to determine the experimental efficiency, the efficiency of the solar panel was evaluated. The relationship between solar panel efficiency and solar intensity—the quantity of solar radiation or sunlight that reaches the panel surface—should be taken into account. The relationship between the efficiency and solar intensity is shown in Figure 3a. The data shows a positive association, showing that as solar intensity rises, so does solar panel efficiency. This link is further supported by the regression line equation y = 0.0027x + 17.955, which has a positive coefficient (0.0027) and shows that the efficiency of the solar panel rises by 0.0027 for every unit increase in solar intensity. This connection can be explained by the fact that solar panels that receive more energy from higher sun intensities can produce more electricity.
Figure 3.
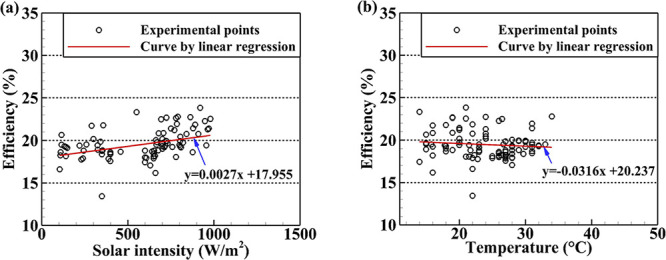
Variation of efficiency with (a) solar intensity and (b) temperature.
Additionally, Figure 3b shows how the efficiency changes with temperature. The plot shows that a rise in temperature has a negative impact on the effectiveness of the panel. The regression line equation y = −0.0316x + 20.237, which has a negative coefficient, provides additional evidence for this result (−0.0316). This implies that the efficiency of the solar panel drops by 0.0316 for every unit increase in temperature. This is in accordance with the previous findings.8,10 This decrease in efficiency with increase in temperature can be justified by the fact that, as temperature rises, the voltage drops,10 resulting in a drop in power output. As a result, the efficiency falls.
Subsequently, the effect of the humidity on efficiency is analyzed. According to the investigation, humidity levels cause a drop in PV panel efficiency (Figure 4a). The regression line equation y = −0.021x + 20.797 shows that this is the case. Efficiency and humidity have a negative association, as seen by the negative coefficient (−0.021). A similar detrimental effect of rise in humidity on the solar panel efficiency has also been reported by Panjwani and Narejo.17 The performance of solar panels can be impacted in a number of ways by higher humidity levels. An important factor is the increased cloud cover brought on by excessive humidity. The overall solar intensity is decreased when clouds prevent some of the sun’s rays from reaching the solar panel. Reduced solar intensity results in less energy being produced, which, in turn, reduces the efficiency of the panel. Again, high humidity levels might also make it more likely that dust and debris accumulate on the surface of the solar panels. This buildup may prevent sunlight from reaching the solar cells, which would decrease efficiency. Furthermore, higher humidity may have an impact on how the solar panel manages its thermal environment. Higher operating temperatures can result from less heat dissipation efficiency caused by moisture in the air. The performance and efficiency of the solar panel may suffer at high temperatures. Overall, humidity indirectly impacts the efficiency of the solar panel by affecting solar intensity, dust collection, and heat dissipation, even though it may not directly alter the electrical characteristics of the solar panel.
Figure 4.
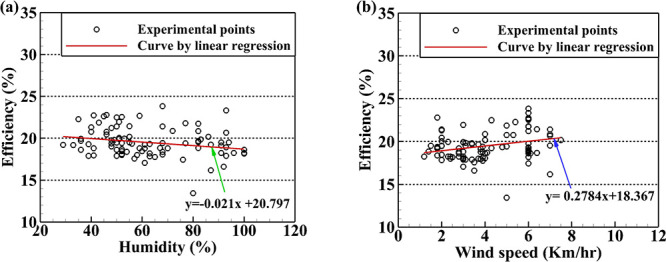
Variation of efficiency with (a) humidity and (b) wind speed.
Additionally, the data reveal that as wind speed increases, the efficiency of the PV panel increases (Figure 4b). The regression line equation y = 0.2784x + 18.367 shows that this is the case. Efficiency and wind speed have a positive association, as seen by the positive coefficient (0.2784). This positive effect on efficiency due to higher wind speeds is attributed to the fact that the higher wind speed aids in more efficient heat dissipation, keeping the solar panel from overheating,10 resulting in higher efficiency. In addition, stronger winds can move debris off the panel and maintain the surface clean. Therefore, more sunlight can enter the solar cells through a cleaner panel, thereby increasing efficiency.
In summary, higher wind speeds generally improve PV panel efficiency by assisting with cooling, cleaning the surface, and boosting convective cooling. However, it is essential to maintain wind speeds within a safe and ideal range for the solar panel system to operate as intended.
The temperature at which air becomes saturated and condenses is known as the dew point. It serves as a gauge of the amount of moisture in the atmosphere. The efficiency of PV panels can be impacted in a number of ways by environmental moisture levels, which are indicated by an increase in the dew point temperature. According to the analysis (see Figure 5), the efficiency of the PV panel drops as the dew point temperature rises. The regression line equation y = −0.1021x + 21.077 serves as an illustration of this, where the negative coefficient (−0.1021) denotes a negative association between efficiency and dew point temperature.
Figure 5.
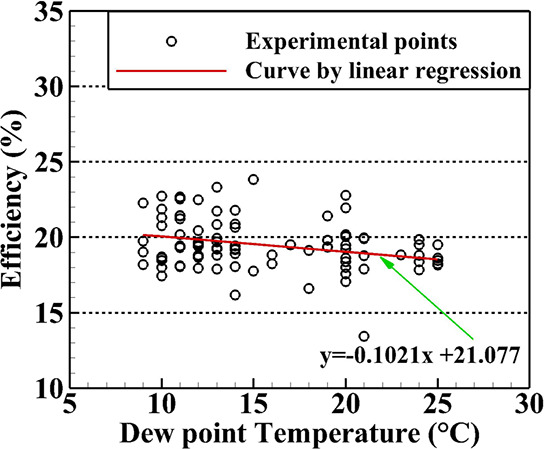
Variation of efficiency with the dew point temperature.
This decrease in the efficiency with the increasing dew point temperature can be explained by the fact that an increase in air moisture can cause dew or condensation to form on the surface of solar panels. The amount of sunlight that reaches the solar cells is decreased by this moisture layer, effectively lowering the solar intensity and lowering the power production and efficiency of the panel. Again, condensation can cause water droplets to develop on the surface of the solar panels, which can block sunlight from entering the solar cells. The solar panel’s efficiency is reduced as a result of the light scattering and absorption caused by these droplets. Additionally, a solar panel’s ability to manage its temperature environment may be impacted by the air’s increased moisture content. This moisture decreases the heat dissipation, thereby raising the operating temperature of the panel. This increase in temperature of the panel in turn reduces the efficiency of the panel.8,10
Overall, a rise in dew point temperature—a sign of more moisture in the air—has a negative impact on how effective PV panels are. Reduced sun intensity, condensation formation, light scattering and absorption, and hampered heat dissipation are the results. To minimize the detrimental effects of dew or condensation on the system’s effectiveness, proper maintenance and cleaning of the solar panel surfaces are necessary.
The above findings provide insights into the impact of meteorological parameters on the efficiency of the solar panel, confirming previous observations and highlighting the importance of considering these factors in optimizing the solar panel performance.
3.3. Assessment Correlation of Meteorological Parameters over Efficiency
The above sections highlight how efficiency is dependent on different meteorological parameters. The efficiency is directly proportional to a few meteorological parameters and indirectly proportional to the remaining parameters. Because of these, employing the data sets mentioned in the above section, a linear regression analysis is performed to find a correlation between the efficiency and these important meteorological parameters. Considering efficiency as the dependent variable and the rest as independent variables, the relationship can be defined as
| 2 |
where T, H, W, S, and D represent temperature, humidity, wind speed, solar intensity, and dew point, respectively and a0, a1, a2, a3, a4, and a5 are constants. Furthermore, these constants can be evaluated by the following system of equations based on the assumption of linear regression.
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
Here, n represents the number of sampling points, and as the data were collected for 100 days, hence n = 100 for the present study. Now, putting the values of η, T, H, W, S, and D recorded from the experiments in eqs 3–8, these equations transformed into the following matrix form.
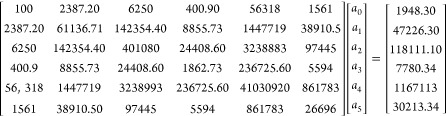 |
These systems of linear equations can be solved by any of the standard numerical methods, such as Gauss elimination, Gauss-Seidel, and Jacobi iteration methods. The present study chose the Gauss elimination method because of its simplicity. Solving the above system of equations, the values of a0, a1, a2, a3, a4, and a5 are found to be −2.30054, 0.413065, 0.109577, 0.882282, 0.005034, and −0.08313, respectively. Therefore, the relations between efficiency and different meteorological parameters can be given by
| 9 |
3.4. Error Analysis
To validate the correlation between efficiency and various meteorological parameters described in the previous section, a data collection was conducted on May 14–30, 2022. Ten sets of data were collected, including temperature, humidity, wind speed, solar intensity, dew point, and current and voltage output. By using eq 1, the experimental efficiency was calculated by multiplying the measured current and voltage values. Additionally, eq 9 was employed to calculate the expected efficiency using the recorded meteorological parameter values as inputs. A comparison between the calculated and experimental efficiencies was performed to assess the accuracy of the correlation, and the results are presented in Figure 6. The figure demonstrates an excellent match between the experimental and calculated efficiencies, indicating a strong correlation between the meteorological parameters and the efficiency of the solar panel.
Figure 6.
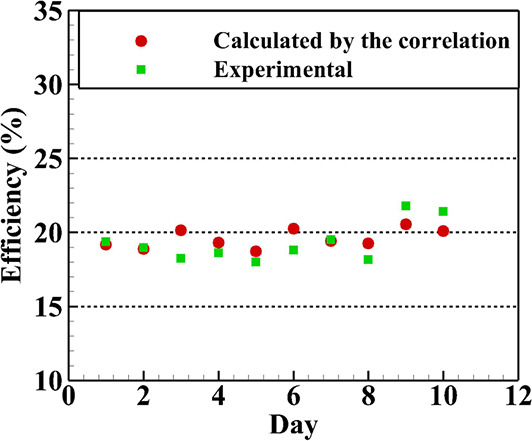
Comparison between the calculated and experimental efficiency.
Table 3 further supports this conclusion by listing the absolute errors between the calculated and experimental efficiencies. The low absolute error values reinforce the proposed correlation’s effectiveness in predicting the solar panel’s efficiency using various meteorological data as inputs. Based on these findings, it can be concluded that the correlation established between the efficiency and the different meteorological parameters can reliably predict the efficiency of a solar panel. By utilizing the relevant meteorological data as inputs, this correlation provides a practical method for estimating the performance of a solar panel in terms of its efficiency.
Table 3. Error between the Calculated and the Experimental Efficiency.
| day | solar intensity (W/m2) | current (amp) | voltage (V) | power (W) | experimental efficiency (%) | calculated efficiency (%) | absolute error |
|---|---|---|---|---|---|---|---|
| day 1 (15/5/2022) | 717 | 4.14 | 15.7 | 65.00 | 19.37 | 19.17 | 0.20 |
| day 2 (16/5/2022) | 690 | 3.95 | 15.5 | 61.23 | 18.96 | 18.88 | 0.08 |
| day 3 (20/5/2022) | 710 | 4.12 | 15.7 | 64.68 | 19.47 | 20.15 | –0.68 |
| day 4 (21/5/2022) | 764 | 4.50 | 16.3 | 73.35 | 20.51 | 19.31 | 1.20 |
| day 5 (22/5/2022) | 600 | 3.20 | 15.8 | 50.56 | 18.01 | 18.72 | –0.71 |
| day 6 (23/5/2022) | 570 | 3.30 | 15.2 | 50.16 | 18.80 | 19.44 | –0.64 |
| day 7 (26/5/2022) | 698 | 3.99 | 15.5 | 61.85 | 18.93 | 19.41 | –0.48 |
| day 8 (27/5/2022) | 730 | 4.30 | 15.7 | 67.51 | 19.76 | 19.26 | 0.50 |
| day 9 (28/5/2022) | 736 | 4.29 | 17.1 | 73.36 | 21.30 | 20.56 | 0.74 |
| day 10 (29/5/2022) | 750 | 4.50 | 16.1 | 72.45 | 20.64 | 20.10 | 0.54 |
4. Conclusions
This study analyzes the performance of a solar panel over a four-month period, considering meteorological parameters like temperature, humidity, wind speed, dew point, and solar intensity. It examines the effect of the tilt angle on efficiency and establishes correlations between efficiency and meteorological factors. By recording current, voltage, and meteorological data, we investigated the relationship between these variables and solar panel efficiency. Results show the positive influence of solar intensity and wind speed, while the temperature, humidity, and dew point negatively affect efficiency. The proposed correlations accurately predict efficiency and contribute to optimizing the solar panel performance in real-world applications.
The study found an optimal tilt angle of 26° that maximizes the power output. Beyond this angle, the power output begins to decrease.
The regression analysis of the research establishes clear and strong correlations between the efficiency of the solar panel and the considered meteorological parameters.
The analyzed data sets were used to evaluate the performance in comparison with the experimental data, demonstrating a strong qualitative and quantitative validation of the proposed correlations.
Higher solar intensity leads to increased power generation, while greater wind speed enhances cooling and improves overall efficiency.
The study reveals the negative influence of temperature, humidity, and dew point on the efficiency of the solar panel.
The proposed correlations provide valuable insights for optimizing the efficiency of solar panels in practical applications. By considering the meteorological parameters, it becomes possible to predict and enhance the panel’s efficiency, improving its overall performance and power output. Furthermore, a thorough analysis may be needed at other geographic locations before field applications.
Acknowledgments
The authors thank their respective institutions for supporting this research and Mattu University, Ethiopia, for their extended support in this publication process.
Appendix
Different meteorological data obtained from experimental measurements are given in Table A1.
Data Availability Statement
The data used to support the findings of this study are included in the article. Should further data or information be required, these are available from the corresponding author upon request.
The authors declare no competing financial interest.
References
- Han X.; Wang Y.; Zhu L.; Xiang H.; Zhang H. Mechanism study of the electrical performance change of silicon concentrator solar cells immersed in de-ionized water. Energy Conversion and Management 2012, 53 (1), 1–10. 10.1016/j.enconman.2011.08.011. [DOI] [Google Scholar]
- Wu X.; Yang C.; Han W.; Pan Z. Integrated design of solar photovoltaic power generation technology and building construction based on the Internet of Things. Alexandria Engineering Journal 2022, 61 (4), 2775–2786. 10.1016/j.aej.2021.08.003. [DOI] [Google Scholar]
- Yao W.; Kong X.; Xu A.; Xu P.; Wang Y.; Gao W. New models for the influence of rainwater on the performance of photovoltaic modules under different rainfall conditions. Renewable Sustainable Energy Rev. 2023, 173, 113119 10.1016/j.rser.2022.113119. [DOI] [Google Scholar]
- Kazem H. A.; Khatib T. Techno-Economical Assessment of Grid Connected Photovoltaic Power Systems Productivity in Oman. Sustainable Energy Technologies and Assessments 2013, 3, 61–64. 10.1016/j.seta.2013.06.002. [DOI] [Google Scholar]
- Kazem H. A.; Khatib T.; Sopian K.; Elmenreich W. Performance and Feasibility Assessment of a 1.4 kW Roof Top Grid-Connected Photovoltaic Power System under Desertic Weather Conditions. Energy and Building 2014, 82, 123–129. 10.1016/j.enbuild.2014.06.048. [DOI] [Google Scholar]
- Yousif J. H.; Al-Balushi H. A.; Kazem H. A.; Chaichan M. T. Analysis and forecasting of weather conditions in Oman for renewable energy applications. Case Stud. Therm. Eng. 2019, 13, 100355. 10.1016/j.csite.2018.11.006. [DOI] [Google Scholar]
- Song Z.; Wang M.; Yang H. Quantification of the Impact of Fine Particulate Matter on Solar Energy Resources and Energy Performance of Different Photovoltaic Technologies. ACS Environmental Au 2022, 2 (3), 275–286. 10.1021/acsenvironau.1c00048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh P.; Ravindra N. M. Temperature Dependence of Solar Cell Performance—an Analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. 10.1016/j.solmat.2012.02.019. [DOI] [Google Scholar]
- Makrides G.; Zinsser B.; Phinikarides A.; Schubert M.; Georghiou G. E. Temperature and Thermal Annealing Effects on Different Photovoltaic Technologies. Renewable Energy 2012, 43, 407–417. 10.1016/j.renene.2011.11.046. [DOI] [Google Scholar]
- Kaldellis J. K.; Kapsali M.; Kavadias K. A. Temperature and wind speed impact on the efficiency of PV installations. Experience obtained from outdoor measurements in Greece. Renewable Energy 2014, 66, 612–624. 10.1016/j.renene.2013.12.041. [DOI] [Google Scholar]
- Ebhota W. S.; Tabakov P. Y. Influence of photovoltaic cell technologies and elevated temperature on photovoltaic system performance. Ain Shams Eng. J. 2023, 14 (7), 101984 10.1016/j.asej.2022.101984. [DOI] [Google Scholar]
- Mehmood A.; Ren J.; Zhang L. Achieving energy sustainability by using solar PV: System modelling and comprehensive techno-economic-environmental analysis. Energy Strategy Reviews 2023, 49, 101126 10.1016/j.esr.2023.101126. [DOI] [Google Scholar]
- Chakraborty D.; Mondal J.; Barua H. B.; Bhattacharjee A. Computational solar energy – Ensemble learning methods for prediction of solar power generation based on meteorological parameters in Eastern India. Renewable Energy Focus 2023, 44, 277–294. 10.1016/j.ref.2023.01.006. [DOI] [Google Scholar]
- Ghazy M.; Ibrahim E. M. M.; Mohamed A. S. A.; Askalany A. A. Experimental investigation of hybrid photovoltaic solar thermal collector (PV/T)-adsorption desalination system in hot weather conditions. Energy 2022, 254, 124370 10.1016/j.energy.2022.124370. [DOI] [Google Scholar]
- Aoun N. Methodology for predicting the PV module temperature based on actual and estimated weather data. Energy Conversion and Management: X 2022, 14, 100182 10.1016/j.ecmx.2022.100182. [DOI] [Google Scholar]
- Gwandu B. A. L.; Creasey D. J. Humidity: a factor in the appropriate positioning of a photovoltaic power station. Renewable Energy 1995, 6 (3), 313–316. 10.1016/0960-1481(95)00073-S. [DOI] [Google Scholar]
- Panjwani M. K.; Narejo G. B. Effect of humidity on the efficiency of a solar cell (photovoltaic) International Journal of Engineering Research and General. Int. J. Eng. Res. Gen. Sci. 2014, 2 (4), 499–503. [Google Scholar]
- Mekhilef S.; Saidur R.; Kamalisarvestani M. Effect of dust, humidity and air velocity on efficiency of photovoltaic cells. Renewable and Sustainable Energy Reviews 2012, 16, 2920–2925. 10.1016/j.rser.2012.02.012. [DOI] [Google Scholar]
- Ghazi S.; Ip K. The effect of weather conditions on the efficiency of PV panels in the southeast of UK. Renewable Energy 2014, 69, 50–59. 10.1016/j.renene.2014.03.018. [DOI] [Google Scholar]
- Sohani A.; Sayyaadi H.; Miremadi S. R.; Samiezadeh S.; Doranehgard M. H. Thermo-electro-environmental analysis of a photovoltaic solar panel using machine learning and real-time data for smart and sustainable energy generation. J. Cleaner Prod. 2022, 353, 131611 10.1016/j.jclepro.2022.131611. [DOI] [Google Scholar]
- Akonjom N. A.; Njok A. O. Effect of Meteorological Parameters on the Performance of Photovoltaics Installed under the Guinea Savannah Atmosphere in Ogoja, Cross Rivers State, Nigeria. Journal of Applied Sciences and Environmental Management 2022, 26 (7), 1299–1306. 10.4314/jasem.v26i7.17. [DOI] [Google Scholar]
- Hussein H. M. S.; Ahmad G. E.; El-Ghetany H. H. Performance evaluation of photovoltaic modules at different tilt angles and orientations. Energy Conversion and Management 2004, 45 (15–16), 2441–2452. 10.1016/j.enconman.2003.11.013. [DOI] [Google Scholar]
- Jamil B.; Siddiqui A. T.; Akhtar N. Estimation of solar radiation and optimum tilt angles for south-facing surfaces in Humid Subtropical Climatic Region of India. Engineering Science and Technology, an International Journal 2016, 19 (4), 1826–1835. 10.1016/j.jestch.2016.10.004. [DOI] [Google Scholar]
- Bhattacharya T.; Chakraborty A. K.; Pal K. Statistical Analysis of the Performance of Solar Photovoltaic Module with the Influence of Different Meteorological Parameters in Tripura, India. International Journal of Engineering Research. 2015, 4 (3), 137–140. 10.17950/ijer/v4s3/312. [DOI] [Google Scholar]
- Bahanni C.; Adar M.; Boulmrharj S.; Khaidar M.; Mabrouki M. Performance comparison and impact of weather conditions on different photovoltaic modules in two different cities. Indonesian Journal of Electrical Engineering and Computer Science 2022, 25 (3), 1275–1286. 10.11591/ijeecs.v25.i3.pp1275-1286. [DOI] [Google Scholar]
- Iqbal S.; Khan S. N.; Sajid M.; Khan J.; Ayaz Y.; Waqas A. Impact and performance efficiency analysis of grid-tied solar photovoltaic system based on installation site environmental factors. Energy Environ. 2022, 34, 2343–2363. 10.1177/0958305X221106618. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used to support the findings of this study are included in the article. Should further data or information be required, these are available from the corresponding author upon request.


