Increasing volatility of reconstructed Morava River warm-season flow, Czech Republic

Abstract

Study region

The Morava River basin, Czech Republic, Danube Basin, Central Europe.

Study focus

Hydrological summer extremes represent a prominent natural hazard in Central Europe. River low flows constrain transport and water supply for agriculture, industry and society, and flood events are known to cause material damage and human loss. However, understanding changes in the frequency and magnitude of hydrological extremes is associated with great uncertainty due to the limited number of gauge observations. Here, we compile a tree-ring network to reconstruct the July–September baseflow variability of the Morava River from 1745 to 2018 CE. An ensemble of reconstructions was produced to assess the impact of calibration period length and trend on the long-term mean of reconstruction estimates. The final estimates represent the first baseflow reconstruction based on tree rings from the European continent. Simulated flows and historical documentation provide quantitative and qualitative validation of estimates prior to the 20th century.

New hydrological insights for the region

The reconstructions indicate an increased variability of warm-season flow during the past 100 years, with the most extreme high and low flows occurring after the start of instrumental observations. When analyzing the entire reconstruction, the negative trend in baseflow displayed by gauges across the basin after 1960 is not unprecedented. We conjecture that even lower flows could likely occur in the future considering that pre-instrumental trends were not primarily driven by rising temperature (and the evaporative demand) in contrast to the recent trends.

Highlights

• •Tree rings are used to reconstruct Morava River baseflow since 1745 CE.
• •Hydrological model output help validate pre-calibration estimates.
• •Negative trends in baseflow have reoccurred during the past 250 years.
• •Climate change may amplify extreme low flows beyond the natural variability.

1. Introduction

Hydroclimatic variability is becoming a concern for European risk and resources management, as the continent has experienced severe droughts and floods in recent decades (e.g., Bastos et al., 2020; Dietze and Ozturk, 2021; Rakovec et al., 2022). Some of these events appear to be unusual in the context of 20th-century meteorological and hydrological instrumental data (Hanel et al., 2018, García-Herrera et al., 2019; Moravec et al., 2019), and perhaps even for the past 500 years (Blöschl et al., 2020). Higher temperatures can directly or indirectly influence the occurrences of droughts, and drought frequency and magnitude are projected to increase through the current century (Dai, 2011, Ruosteenoja et al., 2018, IPCC, 2021). Rising temperatures can also affect flooding (Alfieri et al., 2015) but projections of future flood risks are not spatially or seasonally homogeneous across Europe (Stahl et al., 2010, Blöschl et al., 2019, Tarasova et al., 2023). A limiting factor to such projections is the relatively short instrumental records, which add uncertainty to the analysis of trend and low-frequency variability (Kundzewicz et al., 2017).

The Czech Republic is not immune to the changes brought on by warmer temperatures in recent decades (Zahradníček et al., 2021). Perhaps of equal importance is the variability in precipitation. The negative trend in annual precipitation totals recorded since the beginning of the 20th century in the eastern Czech Republic may be of greater magnitude than anywhere else in Europe (Ionita and Nagavciuc, 2021), but seasonal and annual precipitation totals appear to have been approximately stable since the 1960s (Brázdil et al., 2021). Increasing temperatures, which drive increased summer evapotranspiration and decreased snowpack, combined with decreasing (or stable) precipitation act in the same direction to produce lower summer flows in Czech watercourses (Kašpárek and Kožín, 2022, Peña-Angulo et al., 2022, Fischer et al., 2023). Similar changes have also been recorded for the occurrence and magnitude of extreme low flows in rivers (Ledvinka, 2015). Furthermore, human water withdrawals are expected to increase and projected climatic changes will produce unsustainable demands on existing water resources in the eastern Czech Republic (Potopová et al., 2022).

Tree-ring records have been used extensively to reconstruct streamflow variability prior to the period of instrumental measurements, with a historical focus on watersheds in the United States (e.g., Meko et al., 2007; Maxwell et al., 2017; Stagge et al., 2018), but also rapidly to include many other regions globally (Karanitsch-Ackerl et al., 2019, Nguyen et al., 2021, Khan et al., 2022, Nagavciuc et al., 2023). Traditional streamflow reconstruction approaches have focused on total streamflow, using an approach analogous to temperature and precipitation reconstruction. However, streamflow is distinct because some of the flow generating processes, like surface runoff, do not directly contribute to the soil moisture that acts as a limiting factor for tree growth, and thus the tree-ring chronology. As a result, it has been hypothesized that specific components of streamflow are more strongly correlated with tree-ring width variability (Torbenson and Stagge, 2021). This approach has found support for a focus on the reconstruction of baseflow, a slower changing component of streamflow that excludes surface runoff processes (Maxwell et al., 2022, Torbenson et al., 2023a). Flow separation into baseflow and stormflow as a method for hydrologic reconstruction from tree rings has not yet been used for any European catchments despite its potential for more stable and accurate estimates.

Here we present an analysis of the instrumental baseflow of the Morava River (in the eastern part of the Czech Republic) for a late summer window (July-September; JAS) since 1921 and produce a suite of interannual reconstructions of the same seasonal target extending back to 1745 CE. We quantitatively assess how methodological choices impact the validity of reconstructions and the potential bias introduced from calibrating on instrumental data that contain continuous trend. A final reconstruction from 1745 to 2018, is compared with measured precipitation totals and documentary evidence before the calibration period for further validation. The resulting reconstruction is used to test how well the trend and return intervals of the instrumental period represent long-term variability of flow in the Morava River basin.

2. Data and methods

2.1. Study region: the Morava River

The Morava River is the largest waterway in the eastern Czech Republic (Kadlec et al., 2009), with a catchment of 26,658 km². Its headwaters are found in the Jeseník Mountains, near the Polish border, and the river flows north to south through a diverse landscape that includes considerable stretches of floodplain forests. Major tributaries include the Bečva and the Thaya rivers (with the Svratka River being the largest tributary of the Thaya). The Morava marks a natural boundary between the Czech Republic and Slovakia. It makes up much of the Austria-Slovakia border, before meeting the Danube with a mean annual discharge of 110 m³/s. Seasonal high flows occur in March-April and low flows in August-September.

The basin has experienced different human impacts influencing general flow patterns during the past three centuries. For example, from the mid-19th century to 2000 CE, the percentage of the area used for agriculture decreased (from 52.1% to 43.9%), while the forested area slightly increased (from 28.6% to 32.2%) (Brázdil et al., 2012b). Between 1912 and 1996, twelve reservoirs were built on tributaries of the Morava above the Strážnice gauge, with a total storage volume greater than 50 × 10⁶ m³ (Brázdil et al., 2011b). The river also experienced various channel modifications, particularly in the form of channel straightening and the creation of the Baťa Shipping Canal, built in 1934–1938, to make the river navigable (Brázdil et al., 2011a). However, unlike many other rivers in central Europe, the Morava River has not experienced a strong trend in increasing sedimentation rates in the past 400 years (Grygar et al., 2011).

2.2. Streamflow data and flow separation

Records of daily resolved streamflow from 70 instrumental gauges within the Morava River basin were obtained from the Czech Hydrometeorological Institute. The streams range from 0.05 to 58 m³/s in mean annual discharge and drainage areas range from 4 to 9144 km². All records cover a common period of 1961–2020 CE. Daily resolved data for the Strážnice gauge, the target of the reconstruction exercise and the gauge recording the highest annual flows of the available 70 Morava River gauges, are available for 1921–2020. The influence of human activity on flow was quantified through double-mass analysis (Kohler, 1949, Cook and Jacoby, 1983) for the period 1921–2018, using drainage area precipitation data to estimate cumulative flow.

Baseflow and stormflow were separated from daily-resolved streamflow data and averaged to produce monthly resolution baseflow and stormflow series. The HYSEP sliding interval method (Sloto and Crouse, 1996) was applied using the approach developed by Lorenz (2017). The width of the sliding window length (2 N) represents twice the number of days that is assumed for surface runoff effects on streamflow to end following a storm event (Pettyjohn and Henning, 1979). The empirical relationship provided by Lorenz (2017) of N = 0.83 × A^0.2 was applied at each gauge, where A is the drainage area in km². The resulting travel times range from 1 to 5 days for the gauges studied. Several approaches to flow separation exist but the HYSEP sliding interval method has proven simple and reliable (Eckhardt, 2008, Gonzales et al., 2009, Partington et al., 2012). Any uncertainty stemming from the flow separation is assumed to be negligible compared to the uncertainty associated with the reconstruction models (Torbenson and Stagge, 2021). In addition to the flow constituent timeseries, a baseflow index (BFI; Stoelzle et al., 2020) was calculated for all gauges as the proportion of total streamflow associated with baseflow.

2.3. Tree-ring chronology and predictor selection

Total tree-ring width (TRW) collections publicly available (e.g., through the International Tree-Ring Data Bank (ITRDB); Zhao et al., 2019) and of previously published studies were compiled from the Morava River basin and its surroundings (12.75–22.95ºE and 47.95–54.15ºN). To ensure a robust comparison with flow variables, a minimum end date of 2011 was enforced. Only collections that contained the raw measurements of individual series were considered. Series from each collection were detrended to remove age-related changes in interannual variability (Cook, 1985). The TRW measurements were power transformed, and an age-dependent spline (n = 66% of the series length) was fitted to each series (Cook and Peters, 1981). Indices were calculated as residuals from the fitted curves and a master chronology was calculated through a mean of these indices. In addition to the TRW predictors, two annually resolved stable oxygen (δ¹⁸O) and carbon (δ¹³C) isotope chronologies from living, historical, and archaeological oak wood from the study region were included in the analysis (Urban et al., 2021). The isotope series have previously been used to produce reconstructions of drought (Büntgen et al., 2021a) and separately of atmospheric moisture and temperature (Torbenson et al., 2023b).

Chronologies were screened against Morava River flow (baseflow, stormflow, and streamflow) data from the Strážnice gauge for varying window lengths of seasonal flow (from 1 to 3-month length during what is generally considered a main growing season (April-October)). Any tree-ring record that displayed correlation with the flow data above specific thresholds (r > 0.29 with p < 0.05; and r > 0.365 with p < 0.01 for 1921–2011) was considered as a potential predictor chronology. A Principal Components Analysis (PCA; Jolliffe, 2002) was performed on the pool of predictor chronologies to extract the common signals of tree-ring variability in the subset of significantly correlated tree-ring chronologies. The screening of predictor chronologies was performed on a short (1961–2011) and long (1921–2011) period, to assess the potential impact of trends within the target flow variable on the calibration and subsequent pre-calibration estimates.

2.4. Model calibration

Principal components (PCs) from the network of chronologies screened against July-September (JAS) baseflow at Strážnice were used for a forward stepwise regression model. In addition to PC predictors based on chronologies displaying positive correlations with baseflow, a negative predictor (the regional δ¹⁸O chronology) was also used in the analysis. Calibration models were produced using all chronologies included in the PCA, and only chronologies with positive correlations. For the latter, the δ¹⁸O chronology was entered into the regression separately with a flipped sign to account for its negative correlation with flow. The transfer function (1) used for the calibration follows as:

$$Y_i=K+{\mathit{PC}1}_i+{\mathit{PC}2}_i+\dots {\mathit{PCn}}_i-({\mathrm{\delta }}^{18}\mathrm{O})$$ (1)

where Y_i is the estimated Morava River baseflow for the year i, K is the scale factor, PC1 to PCn are the principal components of the screened tree-ring chronologies, and δ¹⁸O is the negative predictor. Calibrations were produced allowing for one, two, three, and n PCs (where n is the maximum number of screened chronologies entered into the PCA). The inclusion of PCs was based on the Akaike Information Criterion (AIC; Bozdogan, 1987). Calibration models for 20 different predictor configurations were produced, each made up of five models using: (i) a short calibration period and low correlation threshold (SL); (ii) a short calibration period and high correlation threshold (SH); (iii) a long calibration period and low correlation threshold (LL); (iv) and a long calibration period and high correlation threshold (LH).

For the final reconstruction model, based on the calibration that was deemed the most robust, several nested models were produced using ever decreasing numbers of predictor chronologies as individual chronologies become unavailable in the distant past. The first (shortest) nest, for which the most tree-ring chronologies were available, spans 1848–2011. The second nest, for which all chronologies except one were available, spans 1805–2011. The procedure was repeated for each drop in the number of chronologies to maximize the predictor coverage and length of reconstruction estimates back in time. In addition, the same approach moving forward from 2011 was taken to produce calibration models until 2018. A quantile mapping bias correction was applied to each of the reconstruction nests (Robeson et al., 2020), using the full possible overlap of reconstructed and instrumental data (i.e., 1921–2011 or 1921–2018) as reference periods.

Rather than splicing together nests as is often done in dendroclimatic reconstructions (e.g., Maxwell et al., 2011; Torbenson and Stahle, 2018), the final reconstruction represents a mean of estimates from all nests that cover a given year. Prediction intervals were calculated for the full reconstruction and represent uncertainty associated with the annual estimates (Olive, 2007). The spread of nests was also used to qualitatively assess robustness.

2.5. Precipitation, drought, and flood data for reconstruction validation

Instrumental JAS baseflow at Strážnice was compared to monthly and seasonal precipitation totals from the E-OBS network (Cornes et al., 2018) for the period 1961–2018 to assess the strongest precipitation driver of the reconstruction target. The same was done for the reconstructed timeseries. The seasonal configuration of the highest correlation was then used as a benchmark for the pre-calibration verification of reconstruction estimates. Three different types of timeseries expressing hydroclimatic variability were used for comparison and validation of the reconstructed baseflow prior to 1921:

(1) Precipitation totals for Moravia, 1803–2020: Series of monthly precipitation totals were calculated as the median from stations with long-term homogenized precipitation series extending back to 1803 which were adjusted to areal precipitation means of Moravia after 1961 (Brázdil et al., 2012a).

(2) Drought indices for the Czech Republic, 1501–2016: Reconstructed monthly Central European temperature series (Dobrovolný et al., 2010) and seasonal Czech precipitation series (Dobrovolný et al., 2015), both based on documentary and instrumental data, were used to calculate seasonal and annual Standard Precipitation Index (SPI), Standard Precipitation Evapotranspiration Index (SPEI), and Palmer Drought Severity Index (PDSI) for the territory of the Czech Republic since 1501 CE (Brázdil et al., 2016).

(3) Flood series for the Morava River, 1691–2010: Flood series for the Morava River consist of the year and month of the flood occurrence. The different versions were produced from various documentary data (before 1881 floods represent cases when the Morava River left its bed and flooded surroundings), water level measurements (of different stations for 1881–1920), and discharge measurements (from the Strážnice station since 1921). Three datasets based on documentary evidence were available: (a) floods of the middle part of the Morava River for 1691–1880 (Brázdil et al., 2011b); (b) floods between the Thaya tributary and Kroměříž complemented by taxation records for 1711–1920 (Brázdil et al., 2014); and (c) compiled flood series from (a) and (b) for 1691–2010.

Reconstructions were correlated with the above (1,2) series over various periods prior to 1961 as validation of the baseflow reconstruction and to ensure that the meteorological drivers of baseflow remained consistent throughout the reconstruction period. Areal means of the hydrometeorological series (1,2), in relationship to the calibration period, were also compared to the different calibration model estimates to assess any possible offsets resulting from trend during the calibration period. Additionally, qualitative testing of co-occurrences between summer floods/droughts (3) and high/low reconstruction estimates was performed as further validation of the reconstruction.

2.6. Flow simulation for reconstruction evaluation

The mesoscale Hydrological Model (mHM; Samaniego et al., 2010; Kumar et al., 2013) was used to simulate discharge at Strážnice as an additional source of verification. The mHM was calibrated using daily observations of the catchment outlet, using a 101-year calibration period (1920–2020), with 200 iterations of the Dynamically Dimensioned Search algorithm (Tolson and Shoemaker, 2007). The model was forced using CRU TS4.1 (Harris et al., 2020) meteorological data for 1901–2021 and Casty et al. (2007) data for 1772–1900 (as described by Rakovec et al., 2022). Model performance was assessed (compared with the instrumental flow data) for 1921–2021 and indicated a very strong ability to capture interannual variability, but also seasonal hydrology and long-term changes (Supplementary Figure 1). In addition to correlations between reconstructed and simulated JAS baseflow, the residuals from the two series were compared to other components of the mHM output. These comparisons include the assessment of potential stormflow signals in the reconstruction.

2.7. Trend and return interval analyses

JAS baseflow, stormflow, streamflow, and BFI were tested for linear trend at all 70 gauges for the common 1961–2018 period. A modified Mann-Kendall test was applied to account for possible positive autocorrelation (Kendall, 1975, Hamel and Rao, 1998). For the Strážnice gauge, the same procedure was repeated for the full period of calibration (1921–2018) for both instrumental and reconstructed baseflow. The trends were also tested for different pre-calibration periods of the reconstruction.

Empirical return intervals were calculated for instrumental and reconstructed JAS baseflow for the 1921–2018 calibration period and the entire reconstruction period. Additionally, the same values of baseflow were fitted with a generalized extreme value distribution (GEV; Kotz and Nadarajah, 2000). The fits were used to estimate continuous return intervals for the three subsets of baseflow values.

3. Results

3.1. Flow constituents

The baseflow of the Morava River at Strážnice peaks in April and reaches its lowest levels in late summer and early fall (Fig. 1a). Baseflow and stormflow make up similar proportions of the total JAS streamflow (51.3% and 48.7% respectively), and both components are highly correlated with total streamflow (r = 0.792 and 0.949, respectively) for the period 1921–2018 (Fig. 1b). The inter-correlation between baseflow and stormflow is considerably weaker, with either constituent explaining about 30% of the variance in the other (r = 0.560). Similar values for contributions and correlations of baseflow/stormflow are recorded for gauges across the basin. The double-mass test suggests that the relationship between precipitation over the drainage area and Morava River flow at Strážnice has remained relatively constant over the 1921–2018 period (Supplementary Figure 2).

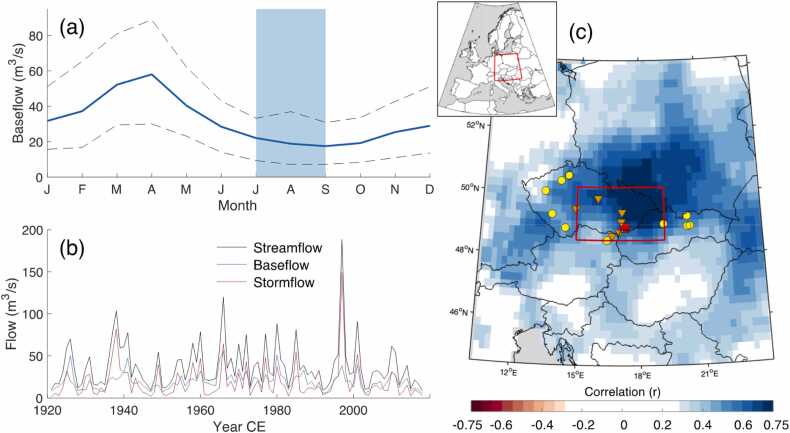
Fig. 1.

(a) Baseflow climatology of the Morava River at Strážnice for 1921–2018, with dashed lines representing the 5th and 95th percentiles. (b) Timeseries of instrumental JAS streamflow, baseflow, and stormflow at Strážnice. (c) Mapped correlations of July-September (JAS) baseflow at Strážnice (red marker) and gridded April-August precipitation data from the E-OBS network (Cornes et al., 2018) for 1950–2018. The red box outlines a general region of the Morava River catchment. Yellow circles indicate the location of the tree-ring records used in the final reconstruction, orange triangles the location of stable isotope materials. Red square indicates the location of the Strážnice gauge.

The highest correlation between JAS baseflow at Strážnice and seasonal precipitation totals (as averaged for data from E-OBS gridpoints within the basin boundary) can be found for April-to-August (A5A). This relationship follows logically, as precipitation anomalies from the preceding spring and concurrent summer propagate through soil moisture and groundwater to generate anomalies in late summer baseflow. Around the headwaters of the Morava, on the border between the Czech Republic and Poland, correlations between A5A precipitation totals and JAS baseflow exceed 0.75 (Fig. 1c). The reconstruction target (JAS baseflow) contains statistically significant autocorrelation (AC1 = 0.344 for 1921–2018; Supplementary Figure 3); however, no such significant autocorrelation is recorded for regional A5A precipitation for the same period (e.g., in the Morava mean used for the pre-calibration verification (Brázdil et al., 2012a)). This difference suggests some hydrologic “memory” effects in the watershed, likely due to groundwater, that are not present in the precipitation record.

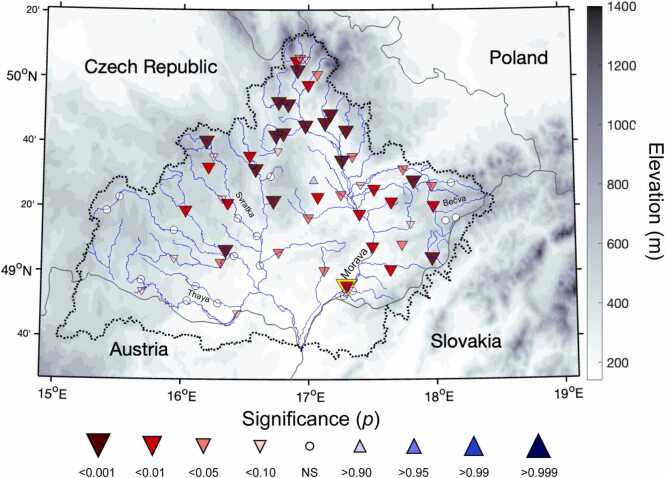
A statistically significant decrease in JAS baseflow since 1961 is recorded across most of the sub-basins (Fig. 2). These trends are the strongest in the northern part of the watershed, near the headwaters, while weaker (and non-significant) trends are mainly located in the southwest. This spatial pattern may, in part, stem from elevation. JAS baseflow at Strážnice displays a statistically significant (p < 0.01) trend for 1961–2018. The negative trend is weaker for 1961–2011 (p = 0.097), due to six of the seven following years (2012–2018) being below the long-term mean. Streamflow also displays generally negative trends for many gauges within the basin, but considerably weaker, and few gauges record statistically significant negative trend for stormflow (Supplementary Figure 4). At the Strážnice gauge, neither stormflow nor streamflow trends are significantly negative for 1961–2011 or 1961–2018.

Fig. 2.

Significance of linear trend (Mann-Kendall test) in JAS baseflow for 70 gauges in the Morava River basin (dotted black line), calculated for the period 1961–2018. Strážnice is indicated by a yellow outline.

3.2. Chronology screening and model calibration

The number of selected chronologies varies depending on the significance of the correlation threshold (p < 0.05 or p < 0.01) and the period of comparison (1921–2011 or 1961–2011). Six and ten tree-ring records passed the screening for the stricter and looser thresholds, respectively for the long calibration period (LL and LH), while for the shorter period, six and eight records were selected (SL and SH, Table 1). Of the twelve TRW chronologies that passed the correlation criteria for at least one screening configuration, nine were Pinus sylvestris (the other species used in the reconstruction are Quercus robur and Picea abies). Three of the chronologies met the screening threshold only for a single predictor pool, while four were selected for all four pools. The tree-ring stable isotope records passed the screening threshold for all four model groups (SL, SH, LL, and LH defined in Section 2.4). Many of the chronologies selected are located outside the drainage area of the Morava River and their connection to baseflow is likely tied to the spatial autocorrelation in precipitation (Fig. 1c).

Table 1.

Tree-ring chronologies that were used as predictors in the reconstruction of Morava River JAS baseflow at Strážnice. PCAB = Picea abies, PISY = Pinus sylvestris, QURO = Quercus robur, QUSP = Quercus robur and Q. petraea. AC1 = serial correlation at 1 year lag, rbar = mean inter-series correlation. LH/LL/SH/SL indicate the inclusion of the chronology in the long/high, long/low, short/high, and short/low calibration, respectively.

Site name	Species	Lat.	Lon.	Start	End	AC1	rbar	LH	LL	SH	SL	ITRDB#	Study / PI
Kostelec Jih	PISY	50.56	14.46	1778	2019	0.655	0.290		x	x	x	czec008	Mašek et al. (2021)
Kostelec Sever	PISY	50.57	14.45	1785	2017	0.642	0.292				x	czec009	Mašek et al. (2021)
Weinviertel	QUSP	48.50	16.40	1748	2011	0.337	0.309	x	x	x	x	aust113	Karanitsch-Ackerl et al. (2019)
Dívčí Kámen	PISY	48.89	14.36	1768	2019	0.503	0.368	x	x			czec013	Treml et al., 2021
Prácheň	PISY	49.32	13.68	1804	2019	0.549	0.254	x	x	x	x	czec020	Treml et al., 2021
Rabštejn	PCAB	50.04	13.30	1847	2018	0.247	0.565	x	x	x	x	czec021	Treml et al., 2021
Rabštejn	PISY	50.04	13.30	1751	2018	0.482	0.352	x	x	x	x	czec022	Treml et al., 2021
Myslivna	QURO	50.39	14.07	1831	2015	0.468	0.375		x			czec029	Tumajer and Treml (2016)
Letanovský Mlýn	PISY	48.95	20.44	1840	2019	0.392	0.325		x			svk010	Treml et al., 2021
Pálenica	PISY	49.26	20.32	1752	2020	0.479	0.295		x	x	x	svk012	Treml et al., 2021
Tmavá	PISY	49.02	19.16	1745	2018	0.471	0.294	x	x		x	svk015	Treml et al., 2021
Tři Kopy	PISY	48.94	20.31	1696	2019	0.652	0.272		x			svk016	Treml et al., 2021
Czech δ13C	QURO	N/A	N/A	0	2018	0.727	0.234	x	x	x	x	N/A	Büntgen et al. (2021a)
Czech δ18O	QURO	N/A	N/A	0	2018	0.510	0.281	x	x	x	x	N/A	Büntgen et al. (2021a)

Overall, the shorter (1961–2018) calibration periods produce stronger calibration statistics. For example, the predictor pool with a correlation threshold of p < 0.01 that allows for a negative stable isotope predictor and four PCs in the regression explains 64% of the variance of the instrumental JAS baseflow (Table 2). Conversely, a model with the same predictor variables for the 1921–2018 calibration period explains 51% of the variance. This decrease in explained variance is generally observed for all potential pairings (i.e., no change in predictor selection/configuration except for the calibration period length) that allow for a negative predictor. However, because models of both calibration periods share many predictor chronologies, the interannual agreement between model estimates remains high (Fig. 3a).

Table 2.

Common calibration and verification statistics for the 20 reconstruction models produced. lm = linear model, NEG = negative predictor, DW = Durbin-Watson test, 1921–60 diff. = mean difference against the instrumental flow data. The LH model used for the final reconstruction is underlined.

SH	1961–2011
# of preds.	Adj. r2	DW	1921–60 r2	1921–60 diff.
1 (lm)	0.484	* (1.324)	0.592	+ 37.652
2	0.551	ns (1.534)	0.560	+ 42.039
3	0.589	ns (1.724)	0.649	+ 34.681
n	0.644	ns (1.934)	0.687	+ 26.417
n + NEG	0.615	ns (1.876)	0.434	+ 31.014
SL
# of preds.	Adj. r2	DW	1921–60 r2	1921–60 diff.
1 (lm)	0.484	* (1.325)	0.593	+ 37.581
2	0.552	ns (1.535)	0.561	+ 41.980
3	0.588	ns (1.772)	0.654	+ 34.195
n	0.700	ns (1.789)	0.663	+ 30.592
n + NEG	0.615	ns (1.876)	0.434	+ 31.014
LL	1921–2011
# of preds.	Adj. r2	DW	1921–60 r2	1921–60 diff.
1 (lm)	0.233	* ** (1.044)	0.363	+ 11.210
2	0.233	* ** (1.044)	0.363	+ 11.210
3	0.412	* * (1.370)	0.506	+ 7.390
n	0.441	* * (1.447)	0.523	+ 6.374
n + NEG	0.454	* * (1.493)	0.529	+ 6.865
LH
# of preds.	Adj. r2	DW	1921–60 r2	1921–60 diff.
1 (lm)	0.230	* ** (1.044)	0.357	+ 11.171
2	0.230	* ** (1.044)	0.357	+ 11.171
3	0.399	* * (1.367)	0.483	+ 7.245
n	0.512	ns (1.674)	0.640	+ 6.905
n + NEG	0.507	* (1.595)	0.644	+ 6.954

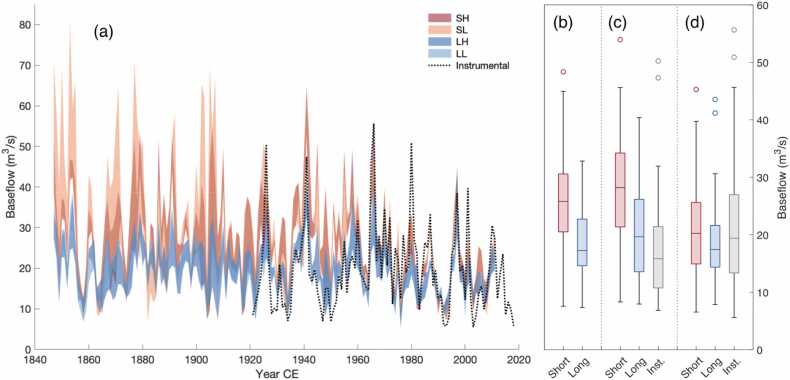
Fig. 3.

(a) Ranges of reconstruction estimates based on the four groups of predictors are plotted for the shortest nest (1848–2011). The reconstruction estimates of the strongest calibration model for each calibration length (red/blue) and the instrumental values (gray) are summarized for the periods 1848–1920 (b), 1921–1960 (c), and 1961–2011 (d). For explanations of SH, SL, LH, and LL see 2.4.

Allowing the negatively correlated predictor (i.e., the regional oak δ¹⁸O series) to enter the PCA versus it being a separate predictor in the stepwise regression appears to have a more significant influence on the short (SL and SH) calibration models (Table 2), likely due to the significant trend in both variables. However, the most apparent difference between the short (SH and SL) and long (LH and LL) calibration models are the pre-calibration estimate means (Fig. 3b). For the most replicated nest (i.e., 1848–2011), the shorter calibration models produce estimates of significantly higher values for the pre-calibration period. The SL model has the highest values, which is also apparent in the 1921–1960 period (Table 2). For 1848–1920, the SL and SH models on average produce baseflows estimates 36% and 32% higher than the LL and LH models, respectively.

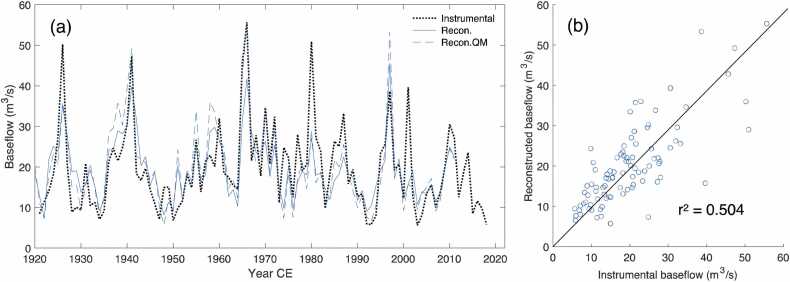
Because of the above differences in mean baseflow, the reconstruction estimates discussed below are those from the long calibration model with a high correlation threshold (LH; Fig. 4a), allowing for the δ¹⁸O series to be used in the PCA. This final reconstruction explains 51.2% of the variance of instrumental JAS baseflow in the most replicated nest and, when bias corrected through quantile mapping, still produces an r² = 0.504 against the target data for 91 years (Fig. 4b). The correction shifts values of underpredicted high flows (e.g., 1966; Fig. 4a) and has a slightly more even distribution of residuals. The bias-corrected reconstruction displays similar variance for the pre-calibration period as it does for the calibration period (Fig. 5), however, more years of extremes (< 5th and >95th percentile, relative to the number of years) are present after 1921. The nests show higher agreement from 1804 onwards, indicating the relative importance of the P. sylvestris chronology from Prácheň, the Czech Republic (Table 1; Treml et al., 2022).

Fig. 4.

(a) The time series comparison between instrumental and reconstructed JAS Morava River baseflow. The bias corrected reconstruction (QM) is also plotted. (b) The relationship between instrumental and bias corrected reconstructed baseflow.

Fig. 5.

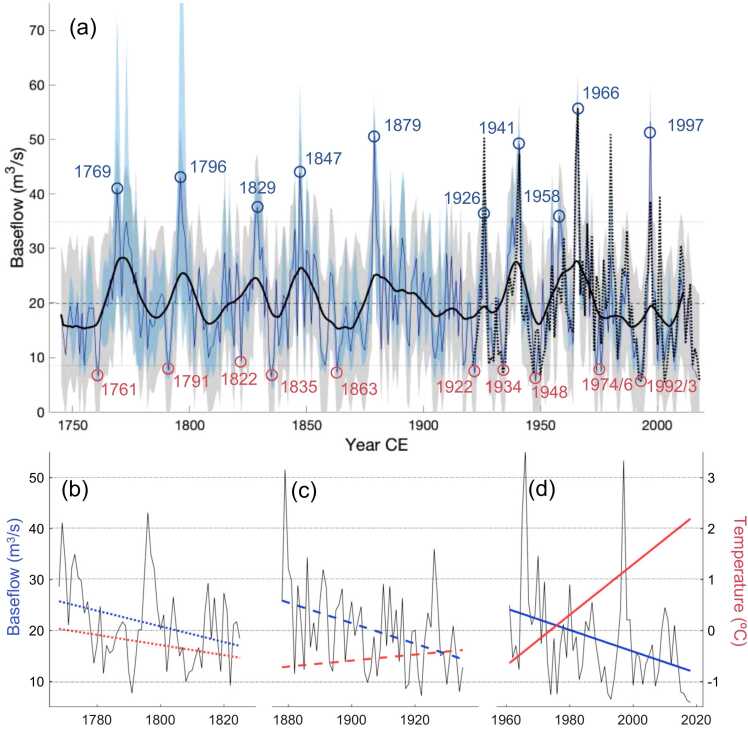
(a) Reconstructed (blue) and instrumental (dotted black) Morava River baseflow for July-September at Strážnice. The dashed line represents the instrumental mean for the calibration period (1921–2018) and the dotted horizontal lines show the 5th and 95th percentile of the full reconstruction (1745–2018). Gray shading indicates the prediction interval (95%), and blue shading indicates the spread of estimates of the different nests. Years of extreme high and low baseflows (Table 3) are highlighted. (b-d) Reconstructed baseflow is plotted in black for three 58-year periods with significant negative trend (blue). Linear fits of JJA temperature (of Dobrovolný et al., 2010 and Brázdil et al., 2022) for the same period are plotted in red. Note that the three periods are not covering the full reconstructed period of (a).

3.3. Reconstruction verification

Many of the reconstructed years of high or low flow align well with documentary evidence of extremes (Table 3). Two years during the calibration period stand out as extreme highs in the reconstruction, 1966 and 1997 - both years of July flooding on the Morava River. In general, years of high reconstructed baseflows correspond to extreme spring or summer precipitation totals, followed by flooding in Moravia (Bečva, Thaya, Morava, and Svratka rivers) and south Silesia (Opava and Odra rivers). In three of the most extreme high flow years (1829, 1941, and 1966), documentary sources also describe preceding winter floods. The lowest calibration-period year of flow in the reconstruction is 1948, followed by 1993 and 1976 (all years of extreme drought in the Czech Republic; Brázdil et al., 2009). The lowest flows estimated for the 19th and late 18th centuries also have corresponding mentions of drought. Low baseflow appears to be part of a preceding-year or multi-year event of drier conditions for some of these years.

Table 3.

Years with reconstructed JAS baseflow values below (above) the 5th (95th) percentile prior to 2012 and corresponding information in documentary sources/instrumental data from the Czech Lands (Brázdil et al., 2011b, Brázdil et al., 2012b, Brázdil et al., 2014, Brázdil et al., 2021).

Year	Historical events from documentary and other sources
Extreme high baseflow
1769	August flood (Morava River). Rainy from spring to autumn.
1796	Very rainy June, rainy July.
1829	March flood (Bečva River), June flood (Thaya, Opava and Svratka rivers). Summer flood (Morava River). Rainy summer.
1847	June flood (Bečva, Morava and Opava rivers). Rainy July.
1879	June flood (Thaya, Odra, Opava, Morava and Svratka rivers).
1926	June flood (Thaya, Odra, Opava, Morava and Svratka rivers). Frequent landslides.
1941	March–April flood (Thaya, Morava and Svratka rivers), June flood (Thaya River).
1958	Late June–July flood (Odra and Morava rivers; the Elbe and northern Bohemia rivers).
1966	February (Morava River) and July floods (Morava and Svratka rivers).
1997	Precipitation extremes in July 1997 and “millennial” flood in Moravia. Frequent landslides.
Extreme low baseflow
1761	Dry April, warm and dry summer. Bad harvest due to drought.
1791	Preceded by extremely dry year 1790 in Moravia. Dry summer 1791.
1822	Dry in spring and summer, particularly from May to July, bad harvest of cereals.
1835	The second dry year after extremely dry 1834. Bark beetle calamity.
1863	Drought from May to August. Lack of water, bad harvest.
1922	Preceded by extremely dry year 1921 (March, May–September, November).
1934	Part of dry years 1932–1934 (reported as “the longest and most critical dry period in the 20th century”).
1948	Preceded by the extremely dry year 1947 (April–June, August–October) with bad harvest of cereals.
1974–1976	Preceded by the very dry 1969–1973 period.
1992–1993	Part of the very dry 1989–1993 period. Beginning of bark beetle calamity.

The year of greatest overestimation in the reconstruction is 1997 and it coincides with the largest instrumental stormflow value. The eastern Czech Republic experienced the worst flood on record, referred to as a “millennial flood” of the Morava (Matějíček and Hladný, 1999) with some 60 deaths recorded (Brázdil et al., 2019). It is worth noting that 1997 is the sixth highest JAS baseflow recorded at Strážnice since 1921. The greatest underestimations of baseflow are recorded for 2001 and 1980, the latter being the year of highest flow in the instrumental data (but for which the reconstruction still estimates flow in the 85th percentile).

The qualitative comparisons are further supported by correlations between the baseflow reconstruction and regional precipitation data that exist prior to the calibration period. Instrumental JAS baseflow is correlated at r = 0.729 (p < 0.001) with April-August precipitation totals for 1921–2011 (the seasonal window identified as the strongest gridded data; Fig. 1). The reconstructed JAS baseflow displays similar magnitude of correlation for the same period (r = 0.659; p < 0.001). The reconstruction and instrumental data also share similar autocorrelation structures (Supplementary Figure 3). Finally, the reconstruction is correlated at r = 0.607 with instrumental stormflow (1921–2011), of similar magnitude and not statistically different to the instrumental baseflow data (Fisher’s t-test; Fisher, 1921).

For 1803–1920, Moravian A5A precipitation totals and reconstructed JAS baseflow are correlated at r = 0.486 (p < 0.001), suggesting a stable relationship with the driving hydroclimatic forcing data. Correlations between simulated and reconstructed JAS baseflow are also positively and significantly correlated (r = 0.361, p < 0.001) for the longest pre-calibration overlap (1772–1920). When confined to a shorter period (1828–1920), for which the simulated baseflow retains similar variance to the calibration period, the correlation is r = 0.460. For the period 1772–2018 (1828–2018), the two timeseries are correlated at r = 0.554 (r = 0.636). The internal baseflow component of the mHM hydrologic model output and HYSEP-separation of full simulated flow display very similar correlations with the reconstruction. Many other proxy-based reconstructions from the region share predictors with the baseflow estimates presented here but the Büntgen et al. (2011) drought reconstruction from southern Moravia uses a chronology from a species (and genus) not entered in the predictor pool. Correlations for the longest pre-calibration (1745–1920) and full (1745–1932) periods between this Abies alba-based drought record and the JAS baseflow reconstruction are 0.613 and 0.623, respectively.

3.4. Trend and return intervals

The negative trend displayed by instrumental JAS baseflow at Strážnice (p = 0.097 for 1961–2011), is similarly captured by the most replicated reconstruction nest (p = 0.033), as well as for the 1961–2018 period (p < 0.01 for both instrumental (Fig. 2) and reconstructed series (Fig. 5d)). Two identical-length periods of a similar negative trend are observed in the pre-calibration period: 1768–1825 (p < 0.001; Fig. 5b) and 1878–1935 (p < 0.01; Fig. 5c). The lowest 20-year mean of the reconstruction is the most recent 20 years (14.039 m³/s; 1999–2018) but 1856–1875 display similar deficits (14.992 m³/s) and is the most extreme multidecadal period of the most replicated nest (1847–2011). The differences in JJA temperature trends for the three periods, based on Dobrovolný et al. (2010) and Brázdil et al. (2022) documentary temperature records, are also worth noting.

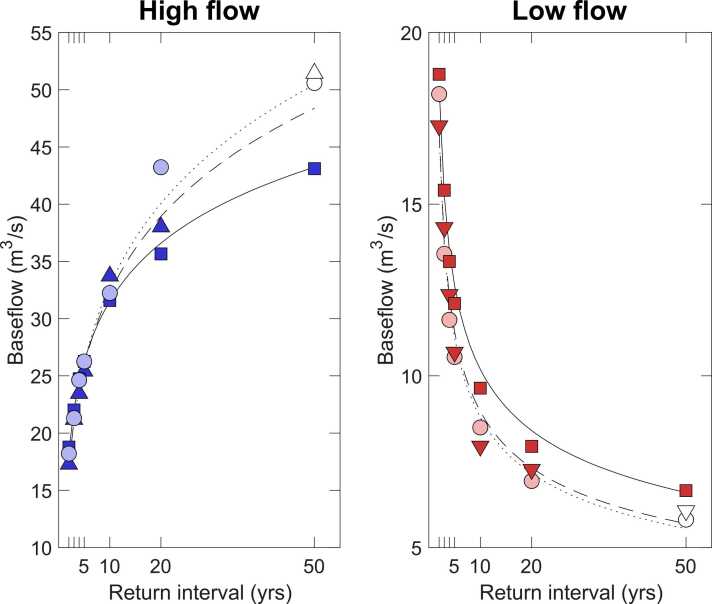
The return intervals for instrumental and reconstructed baseflow in the overlapping period (1921–2018) are highly similar (Fig. 6), with 20-year high flows having the largest discrepancy. Flows for the full reconstruction period are less extreme at all intervals and for both signs (high and low). The largest differences between the full and calibration period return intervals in the reconstructed data are recorded for the 50-year high flows and 10-year low flows. The GEV distributions display general good fits for all data.

Fig. 6.

Return intervals calculated empirically for instrumental data (circles) for 1921–2018, reconstructed data (triangles) for 1921–2018, and reconstructed data (squares) for 1745–2018. White markers indicate return intervals for which the return period is greater than one-third of the length of the record analyzed. The GEV fits are plotted as dotted (instrumental), dashed (reconstructed, 1921–2018), and solid (reconstructed, 1745–2018) lines.

4. Discussion

The Morava River basin is experiencing the strongest trends towards drier conditions in the Czech Republic (Fiala et al., 2010, Trnka et al., 2015). Summer temperatures in the region are increasing (Zahradníček et al., 2021) and the estimated contribution of warming to decreases in flow over the past 30 years is also greater for the Morava River than for any of the other major Czech watercourses (Kašpárek and Kožín, 2022). Discharges are decreasing, as is evident in JAS flow data across the watershed, and the negative trend is mainly driven by baseflow variability (Fig. 2; Supplementary Figure 4). As a result, the relative component of fast-moving water is increasing.

Despite experiencing the lowest annual discharge during high summer (Fig. 1a), the highest frequency of flooding on the Morava occurs in July (Brázdil et al., 2012b). Summer floods tend to be the result of heavy multi-day precipitation events. These events are often associated with Mediterranean cyclones advancing over central Europe (Mudelsee et al., 2004), which may have a greater impact over the headwaters of the Morava River basin than elsewhere in the Czech Republic (Kyselý and Picek, 2007). Sub-daily heavy precipitation displays a positive trend from stations within the basin (between 1961 and 2011; Hanel et al., 2016), which may increase the risk of warm-season flooding. These findings are in line with general projections of increased extreme precipitation variability for much of Europe (Robinson et al., 2021).

Baseflow during such events act as a floor for flood magnitude/extent, perhaps best exemplified by the extremes of 1966 and 1997. These flood events were the results of compound drivers: sustained high seasonal baseflow combined with acute, intense storm events. Therefore, understanding the long-term natural variability of baseflow is essential for water resources (low flow/drought) and risk (high flow/flooding) management. Tree rings, which may have a stronger correlation with baseflow than with total streamflow, offer a unique glimpse into the past that can provide a more robust baseline for future scenarios. The estimates of JAS baseflow at Strážnice in this paper represent the first baseflow reconstruction from tree-ring proxies on the European continent.

4.1. Calibration choices and reconstruction uncertainties

Choices made prior to and during calibration can significantly impact the resulting estimates in dendroclimatic reconstruction studies (Esper et al., 2005, Büntgen et al., 2021b). Although what is generally considered good practices have been established (e.g., Cook and Kairiukstis, 1990), some decisions need to be reconsidered based on local and study-specific conditions. Of special concern for Morava baseflow is the negative trend that has been present for many of the instrumental gauges in the basin since 1961 (Fig. 2). Because the trend alone explains > 7% (>12%) of the variance in JAS baseflow at Strážnice for 1961–2011 (1961–2018), proxy records unrelated to baseflow (or hydroclimate) but with the trend of the same direction may be selected as predictors. The short calibration models (SL and SH) appear to capture the interannual variability of JAS baseflow for the 1921–1960 verification period, however, the SL and SH long-term means are higher than both LL/LH estimates and instrumental data for the same period. The difference in long-term means between SL/SH and LL/LH persists further back in time and is in the order of 30% for the period 1848–1920. The comparison with mHM simulated flows for the same period indicates that the longer calibration models are better at capturing the mean and variance of expected flows.

It is not only in the long-term means that the calibration model groups differ in estimates. Among pre-calibration years for which the models display a large range of estimates, the year 1906 stands out (Fig. 3a). The LL/LH calibration models are, on average, estimating flows far below the 20th century mean but some short calibration models indicate the highest flow for a 50-year surrounding period. Rather than representing the long-term variability (for which all models show high interannual agreement), 1906 is a clear example of uncertainty pertaining to an individual year. Different drought variables, such as PDSI and SPEI, may shed light on some of these differences. June–August PDSI was high (1.367), but JJA SPEI was slightly below the mean (−0.217) in 1906 (Brázdil et al., 2016). This divergent result is expected, if some predictors are mainly limited by long-term soil moisture memory but others are driven by hydroclimatic variability within a shorter window. The differences could also be a result of the individual chronologies and their responses to spatial differences in precipitation – reduced growth in 1906 is notably pronounced in tree-ring records from the western Czech Republic. For comparison, the range of estimates is much narrower during 1910 (wet in both JJA PDSI and SPEI) and 1911 (dry in both JJA PDSI and SPEI).

Anthropogenic impact on flows (e.g., damming, releases, withdrawals, rerouting, and land-use change and managements) can also influence the uncertainties in the reconstructions as the instrumental record contains variability not part of the proxy signal (Torbenson and Stagge, 2021). Hydrological model output data offer an alternative verification of reconstruction estimates, not only prior to calibration (in the case of comparison of means described above) but also as a control in non-natural flow settings. The high agreement between mHM simulated flow and instrumental observations, as well as between mHM and reconstructed flow, indicates that these sources of uncertainty are minor - especially compared to the proxy signal uncertainties. Ultimately, all paleoclimate reconstruction approaches come with associated uncertainties. Documentary evidence act as additional validation of the pre-calibration estimates. We therefore consider the final reconstruction as a robust and conservative estimate of the natural variability of warm-season Morava River baseflow over the past 275 years. As such, it allows to put the instrumental data in a long-term perspective and assess how representative year-to-year changes and extremes experienced in recent decades are.

4.2. Instrumental July-September baseflow variability in a 275-year context

The highest and lowest estimated JAS baseflows since 1745 CE both occur in the calibration period (1966 and 1948, respectively). The summer flood year of 1966 also displays the highest baseflow of the full instrumental data, 185% higher than the 1921–2018 mean. The baseflow reconstruction overestimates the volume of flow for 1997 (the 2nd highest full reconstruction estimate) but eight other years in the reconstruction exceed the instrumental flows of 1997. Many of these highs coincide with summer flood events in the eastern Czech Republic (Table 3). It is worth noting that of these eight years, only four occurred prior to 1921. Similarly, for estimates below the reconstruction 5th percentile, ten of the fourteen years fall during the calibration period.

The frequency of individual year extremes in recent times is also reflected in the calculated return intervals. Direct comparisons between instrumental and reconstructed return intervals may be obscured by differences in variance (as the reconstruction only explains a limited amount of the instrumental data and anything else is assumed to be random) but comparisons between reconstructed intervals for different periods do not suffer from this problem. The full reconstruction period (1745–2018) displays lower high flow and higher low flows beyond the high frequency (<10 years) interval than the calibration period (1921–2018; Fig. 6). The differences are especially pronounced for high flows of 50-year return intervals (25% higher for the 1921–2018 reconstruction estimates). However, return intervals beyond 30 years for the calibration period have large associated uncertainties (Koutsoyiannis and Montanari, 2007), and should be used cautiously. Overall, the baseflow reconstruction indicates an increase in the magnitude of extremes during the 20th and early 21st century. This suggestion is supported by the fully independent output from the mHM simulation, which also displays the most extreme high and low flows after 1900. The lack of extreme high summer flows during the 19th century is also in line with European-wide patterns of flooding (e.g., Blöschl et al., 2020), however, it is worth noting that the baseflow reconstruction is not targeting full streamflow and should rather be seen as an increased risk factor for potential floods.

The negative trend displayed by the instrumental baseflow data since 1961 has become more intense in the most recent 10 years. The comparison presented here ends in 2018 due to the temporal coverage of tree-ring predictors, however, the severe drought of 2018–2020 has undoubtedly exacerbated the ongoing trend even further (Rakovec et al., 2022, Fischer et al., 2023). Nonetheless, the reconstruction indicates that similar decreases in flow for 50 + year periods have occurred in the relatively recent past. The statistically significant trend for the 51 (or 58) years following the late 1870s suggests that the magnitude of hydrological change experienced in the recent six decades is not unprecedented. Similarly, baseflow decreased significantly following the late 1760s. If the current trend is driven (in part) by warming temperatures that were not in play during the late 18th or 19th centuries (Fig. 5b-d), it is possible that the hydrological bottom has not been reached and that the current and/or future trend could be worse within the bounds of natural variability.

Overall, the reconstructed timeseries appears to suggest that the Morava River has experienced more frequent high and low flows since 1921. The average 10- and 20-year high flows are of greater magnitude than for the period 1745–2018, despite a strong negative trend in JAS baseflow since the 1960s. Možný et al. (2020) suggested that average pan evaporation demands in the eastern Czech Republic have increased by almost 20% over the past two decades compared to a 1971–2000 base period and may increase by another 25% by 2060. These changes have mainly been, and are expected to be, driven by summer conditions and are likely to further stress water resources management in an already pressed region (Hanel et al., 2012, Potopová et al., 2022).

4.3. Future perspectives

Long-term trends and the range of natural variability in flow remain an important research objective for the paleoclimatic community (St. George et al., 2020). In Europe, the high-quality documentary records of streamflow and extreme events (e.g., Glaser et al., 2010; Brázdil et al., 2012b; Blöschl et al., 2020) can help extend the relatively short instrumental record and provide significant insights on the topic. However, documentary records vary in quality and spatiotemporal resolution, and different hydrological components of streamflow are difficult to assess from such evidence alone.

The comparison with simulated flows provides independent validation, not only for the reconstruction but also for the mHM model. Hydrological model output is rarely used in dendroclimatic reconstructions of flow (but see Saito et al., 2008; Gangopadhyay et al., 2015) and our results highlight the possibilities to further combine the two approaches. Simulated data have the advantage of potentially eliminating the human influence on flow in basins where the naturalization of flows is difficult (e.g., Dang et al., 2020a; Dang et al., 2020b). Although our reconstruction target undoubtedly contains some influence from human activities, 20th century modifications to the Morava were relatively limited (with no reservoirs built on the main channel) compared to other Czech water courses (Brázdil et al., 2011b). Future studies should explore the relationship between simulated streamflow (and components of streamflow) and proxy records further. The routing of water in models could also help the interpretation of climate signals in various tree-ring variables.

Finally, the importance of underlying tree-ring chronologies in reconstruction exercises cannot be stressed enough. Many of the predictors used here come from studies that did not explicitly target trees with a baseflow signal (e.g., Tumajer and Treml, 2016; Treml et al., 2022), yet hold invaluable information on past hydrological variability. The spread of reconstruction nests for 1796, one of the highest years of estimated baseflow prior to the calibration period, is the highest of estimated extreme years. Extension of current chronologies back in time could vastly improve reconstruction estimates. Combining multiple variables, such as TRW combined with isotopes, has also shown improved signals of drought (Freund et al., 2023) and streamflow (Nguyen et al., 2022). The baseflow reconstruction presented here indicates the usefulness of tree-ring stable isotopes, and other tree-ring variables (such as densities, earlywood, and latewood widths) may increase the explanatory variance of future reconstructions.

5. Conclusions

Trees from the region surrounding the Morava River record information on late summer hydrological variability in their ring-widths and isotopic composition. We show that the reconstruction of warm-season baseflow in Europe is not only possible but represents a viable paleoclimatic alternative with results relevant to water management and complementary to the information gained from pre-instrumental documentary sources. The reconstruction presented here captures significant variance and magnitude of interannual changes in the instrumental data during the calibration period. Years of estimated extreme flow prior to the 1920s are corroborated by documentary evidence of hydrological events in the region. Furthermore, simulated Morava River flows at Strážnice prior to the calibration period are in agreement with reconstructed values. The 20th and 21st century instrumental data includes extreme flows of both signs that are not eclipsed in earlier estimates, but the trend recorded since the 1960s is rivaled by pre-calibration periods. These findings indicate that the current volatility of July-September baseflow is unprecedented in the past 275 years, which represents an elevated risk of both water scarcity and late summer flooding.

CRediT authorship contribution statement

Max Torbenson: conceptualization, methodology, formal analysis, writing – original draft. Rudolf Brázdil: investigation, formal analysis, writing – original draft. James Stagge: methodology, validation. Jan Esper: supervision, investigation. Ulf Büntgen: investigation. Adam Vizina: validation, investigation. Martin Hanel: validation, investigation. Oldrich Rakovec: methodology, formal analysis, validation, investigation, software. Milan Fischer: investigation, validation. Otmar Urban: resources, data curation. Václav Treml: investigation, data curation. Frederick Reinig: investigation. Edurne Martinez del Castillo: investigation. Michal Rybníček: investigation, data curation. Tomáš Kolář: investigation, data curation. Miroslav Trnka: methodology, supervision, project administration. All authors contributed to the writing – reviewing and editing.

Declaration of Competing Interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Max Torbenson reports financial support was provided by European Research Council. Jan Esper, Ulf Buentgen reports financial support was provided by European Research Council. Michal Rybnicek, Tomas Kolar reports financial support was provided by Czech Grant Agency. James Stagge reports financial support was provided by National Science Foundation. Miroslav Trnka, Jan Esper, Ulf Buentgen, Milan Fischer reports financial support was provided by Ministry of Education Youth and Sports of the Czech Republic.

Appendix A. Supplementary material

Supplementary material

.

Data Availability

All data used as reconstruction predictors are available through the NOAA Paleoclimatology website.