Abstract
The extent and patterns of linkage disequilibrium (LD) determine the feasibility of association studies to map genes that underlie complex traits. Here we present a comparison of the patterns of LD across four major human populations (African-American, Caucasian, Chinese, and Japanese) with a high-resolution single-nucleotide polymorphism (SNP) map covering almost the entire length of chromosomes 6, 21, and 22. We constructed metric LD maps formulated such that the units measure the extent of useful LD for association mapping. LD reaches almost twice as far in chromosome 6 as in chromosomes 21 or 22, in agreement with their differences in recombination rates. By all measures used, out-of-Africa populations showed over a third more LD than African-Americans, highlighting the role of the population's demography in shaping the patterns of LD. Despite those differences, the long-range contour of the LD maps is remarkably similar across the four populations, presumably reflecting common localization of recombination hot spots. Our results have practical implications for the rational design and selection of SNPs for disease association studies.
Recently, there has been tremendous interest in empirically establishing the patterns of allelic association, also known as linkage disequilibrium (LD), among polymorphic variants of the human genome. When two alleles at adjacent loci co-occur in a chromosomal segment more often than expected if they were segregating independently in the population, the loci are in linkage disequilibrium (Weir 1996). The profile of LD depends on the age of the mutations, genetic drift, and the demographic history of a given population. It is also eroded by recombination (Jeffreys et al. 2001) and gene conversion (Ardlie et al. 2001). The extent of LD across genomic regions is a crucial parameter for defining the statistical power of association studies utilizing single-nucleotide polymorphisms (SNP) as surrogate genetic markers (Schork 2002), and for guiding the selection and spacing of such polymorphisms to create marker maps useful in candidate gene, candidate region, and eventually whole-genome association studies (De La Vega et al. 2002).
The surveys of LD performed to date with SNPs have been generally limited to small samples of the genome (Gabriel et al. 2002) or to single populations (Tsunoda et al. 2004) or chromosomes (Patil et al. 2001; Dawson et al. 2002; Phillips et al. 2003). Previous studies in a small number of loci have shown marked differences in the extent of LD observed between African and non-African populations (Kidd et al. 1998; Service et al. 2001). Service et al. (2001) performed a genome-wide survey of background LD with microsatellites in a population isolate showing LD extending on a cM range and suggesting that a population's demographic history contributes significantly to the observed patterns of LD. A large project to genotype hundreds of thousands of SNPs across the genome in four major populations is underway (The International HapMap Consortium 2003); at the time of this writing, full analysis is pending completion of the genotyping. Therefore, it remains to be examined in detail how LD differs among population groups and between distinct chromosomes.
With the aim of developing a SNP map for candidate-gene and candidate-region association studies useful across multiple populations, we identified SNPs with a median spacing of less than 8.4 kb covering almost the entire length (>211 Mb) of three human autosomes: chromosomes 6, 21, and 22 (see Supplemental Table 1). We developed a set of 5′ nuclease assays that are available (De La Vega et al. 2002) to genotype 24,940 SNPs selected from the Celera Human RefSNP database (Kerlavage et al. 2002) (v 3.6) in 180 DNA samples from African-American, Caucasian (European-American), Chinese, and Japanese unrelated individuals.
Results
Construction and analysis of metric LD maps
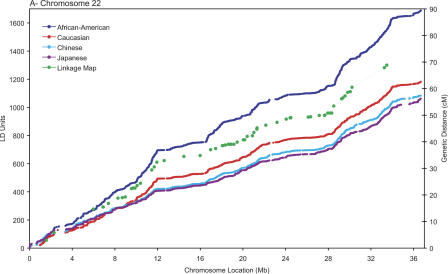
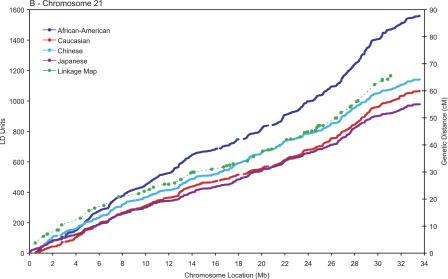
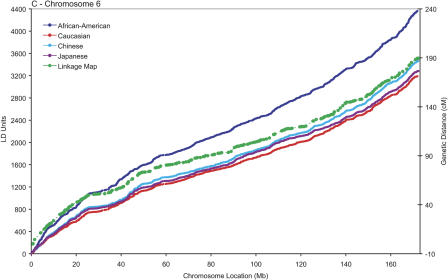
A useful methodology to describe the fine variations in the patterns of LD across the axes of the chromosomes involves calculating the metric linkage disequilibrium units (LDUs) between pairs of SNPs described by Maniatis et al. (2002). The LDU scale, which has additive distances and locations monotonic with physical and genetic maps (Zhang et al. 2002), provides a coordinate system whose scale is proportional to the regional differences in the strength of LD, in a fashion analogous to the recombination maps constructed in cM used to guide linkage studies (Kong et al. 2002). Figure 1 shows the metric LD map of the three chromosomes plotted against physical location of the SNPs. A pattern of “plateaus,” which correspond to regions of high LD, and “steps,” which correspond to regions of increased recombination (Zhang et al. 2002), is evident. Also plotted in the figure are the genetic locations, on the cM scale, and the physical locations of the markers used in construction of the high-resolution linkage map described by Kong et al. (2002), revealing that the steps and plateaus of the LD map are mostly in concordance with the hot and cold spans of recombination. On a large scale, multi-megabase segments with fewer than 100 LDUs can be observed even close to the telomeres in the small acrocentric chromosomes, but not in the large mesocentric chromosome 6, suggesting that elevated recombination rates may not be ubiquitous near all telomeres (Baird et al. 2000). As reported by Stenzel et al. (2004) in a study with larger sample size of European descent, a particularly large “cold span” is observed near the MHC region in chromosome 6p (31.2–34.6 Mb; Fig. 1C). It is also noteworthy that a cold span is found across the centromere of chromosome 6 (around 60 Mb), which is consistent with the notion that recombination is suppressed in this region (Sun et al. 2004).
Figure 1.
Population-specific metric LD maps of the three chromosomes. (A) Chromosome 22; (B) chromosome 21; (C) chromosome 6. SNP locations in LDUs (left vertical axis) and physical coordinates in Mb (horizontal axis) for African-American (blue); Caucasians (red); Chinese (turquoise); Japanese (purple). The location of the markers' part of the high-resolution linkage map of Kong et al. (2002) in the physical and the genetic maps is shown in green (cM scale, right vertical axis).
A remarkable property of the LDU maps for the four populations studied is that their overall contour is rather similar— most of the differences are found in the magnitude of the steps in regions of low LD/high recombination. The close correspondence between long-range LD patterns in these populations, as is evident from the many shared plateau and step regions, presumably reflects the common distribution of underlying recombination hot spots across populations (Kauppi et al. 2003). In finer scale, chromosomal segments with extensive LD and low haplotype diversity (i.e., haplotype “blocks”; Gabriel et al. 2002) can be identified as plateaus in the LD map where the increase in LDUs is very small or zero (Tapper et al. 2003). The latter block definition, although arbitrary, is more robust than those based on heuristics that typically yield ambiguous boundaries (Gabriel et al. 2002; compare with Schwartz et al. 2003). Table 1 describes the mean sizes and number of LD blocks (ΔLDU = 0) and the mean LDU length of the inter-block regions. The block sizes in the African-American sample are consistently smaller. This suggests that because of the increased length of the population history, reflecting African origin, more recombination events have accumulated and blocks have been consequently split. Supporting this suggestion, we observe that the African-American population generally has more blocks than the other three populations. However, there are substantial differences across the three chromosomes and four populations with, for example, only 488 blocks in the Japanese population for chromosome 22, where there are 875 in African Americans. The differences between the same populations for chromosome 6 are, in contrast, relatively minor. The extent to which sample size differences and marker density influence the fine-scale structure of the maps is not entirely clear, but the trends observed are consistent with those expected given differences in length of population history and, consequently, historical recombination intensity. Increased length of population history and recombination intensity is likely to account for the overall increased step height in African Americans, although this is not true for chromosome 22 where African American, Chinese, and Japanese samples show similar mean step heights. Cumulatively, blocks of relatively high LD (LDU < 0.3) account for up to 54% of the chromosome span in the out-of-Africa populations, and up to 44% in African-Americans, with 15%–18% of the chromosome segments being in recombination cold spans in all populations.
Table 1.
Statistics of blocks and steps in the LDU maps
| Chromosome | Population | Mean blockasizes (kb) | Number of blocks | Mean step sizes (LDU) |
|---|---|---|---|---|
| 6 | African-American | 23.0 | 2110 | 2.1 |
| Caucasian | 28.6 | 1965 | 1.6 | |
| Chinese | 33.8 | 2076 | 1.7 | |
| Japanese | 35.6 | 2045 | 1.6 | |
| 21 | African-American | 14.1 | 747 | 2.1 |
| Caucasian | 17.3 | 751 | 1.4 | |
| Chinese | 20.3 | 664 | 1.7 | |
| Japanese | 21.3 | 651 | 1.5 | |
| 22 | African-American | 5.6 | 875 | 1.9 |
| Caucasian | 19.6 | 827 | 1.4 | |
| Chinese | 24.4 | 516 | 2.1 | |
| Japanese | 26.9 | 488 | 2.2 |
Block defined as continuous region with ΔLDU = 0
The extrapolation of the LDU length of the genome is interesting because LD maps are formulated such that one LDU corresponds to the “swept radius,” which is the physical distance within which LD is likely to be useful for positional cloning (Morton et al. 2001). Therefore, the LDU length offers a lower limit of the number of SNPs required to cover the genome when spaced evenly on the LD map. Table 2 gives the LDU map lengths for the three chromosomes and four populations. The total LDU lengths of a chromosome in the out-of-Africa populations are always lower than in the African-American population and consistent with other metrics of LD. In all populations the total number of LDUs is proportionally lower in chromosome six than in chromosomes 21 and 22, where the LDUs per Mb increase over 80% with respect to the large chromosome. The LDU length of the genome has been extrapolated from each chromosome, and for all three together from the LDU/cM ratio, using figures from Kong et al. (2002). The genome-wide estimate of LDUs calculated for each population is remarkably consistent across the chromosomes, with a mean of 88,957 for African-Americans and between 59,342 to 64,049 for the other three populations. These results suggest that the African-American whole-genome LD map is 30% longer, again reflecting the longer population history of African ancestry. Furthermore, these analyses suggest that a whole-genome scan would need to type SNPs in about 60,000 LD units in Caucasians and 85,000 in African-Americans. The total number of SNPs required will be some multiple of these figures because it will be important to perform scans using SNPs over a series of allele frequencies in order to capture ranges of haplotype diversity.
Table 2.
Metric LD map lengths
|
Chromosomal map lengths (LDUs)
|
Extrapolated genome-wide map lengths (LDUs)a
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Chromosome | African-American | Caucasian | Chinese | Japanese | Mb | cM | African-American | Caucasian | Chinese | Japanese |
| 6 | 4362 | 3190 | 3464 | 3283 | 171.7 | 189.6 | 83,168 | 60,822 | 66,046 | 62,595 |
| 21 | 1560 | 1066 | 1141 | 979 | 33.2 | 61.9 | 91,105 | 62,255 | 66,636 | 57,174 |
| 22 | 1688 | 1183 | 1084 | 1062 | 35.0 | 65.9
|
92,597
|
64,894
|
59,464
|
58,257
|
| Mean: | 88,957 | 62,657 | 64,049 | 59,342 | ||||||
Assuming the genome has 3615 cM (Kong et al. 2002)
Correlation of LD with sequence features
We investigated the correlation between LDUs and sequence descriptors looking for predictors of LD distance: GC content, density of SNPs discovered by random shotgun sequencing (Venter et al. 2001), repetitive elements (LINEs and SINEs), CpG islands, and the recombination rate estimated by the map of Kong et al. (2002). We calculated Pearson correlations across a variety of bin sizes ranging from 50 kb to 5 Mb. The results of this analysis show that at a large scale (bin sizes of 1–5 Mb) the recombination rate strongly correlates with LDUs (Pearson correlation r ≥ 0.8 at 2 Mb bins, p < 0.001, see Table 3), whereas at a short scale the correlation decreases (see Supplemental Figure 2). The latter fact could be interpreted to mean that at short scale, gene/loci demographic history and drift dominate (Reich et al. 2002), however this could simply be due to the resolution limit of the linkage map of Kong et al. (2002)—about 1cM. Shotgun SNP density, which here is used as a proxy for nucleotide diversity, is the second strongest correlating metric with Pearson's coefficients ranging from 0.55–0.78. In addition, we observe a correlation of LDU with GC content (r = 0.16–0.48). The previous two observations appear to be secondary to correlations between recombination and diversity (Lercher and Hurst 2002) and recombination and GC content (Montoya-Burgos et al. 2003), supporting the notion that recombination can be mutagenic (Strathern et al. 1995). SINEs, LINEs, and the density of CpG islands do not appear to be consistently correlated with LD. Since the presence of outliers can affect the Pearson correlation values, we also performed Spearman rank correlations (values in parenthesis on Table 3) without obtaining significant differences with the Pearson correlation results. Recombination per se explains 66%–74% of the variance of LDUs, whereas including all six descriptors only increases the explained variance up to 87% (Table 4), a modest increase. Therefore, the smaller correlation values obtained for the descriptors other than recombination might be the result of finer-scale variation in the recombination rate than the resolution of the map of Kong et al. (2002) can measure. Most of the correlations obtained with LDUs can be replicated utilizing sliding windows of averaged |D′| or r2 (Table 3), but they are always smaller (and, as expected, of inverse sign). The latter suggests that LDUs are more effective reporters of local variance of LD and historical recombination than simple averages of D′ and r2, and potentially a more suitable metric with which to position markers and develop standard SNP maps. Furthermore, because of its high correlation with recombination rate, the LD map could be potentially used to increase the resolution of the genetic map, predicting with good confidence genetic distances at intervals of less than 1 cM.
Table 3.
Correlations of different metrics of LD with sequence descriptors of chromosomal segments
| Chromosome | Recombination (cM/Mb) | Polymorphism density | GC content | LINES density | SINES density | CpG islands |
|---|---|---|---|---|---|---|
| Correlationsawith LDU | ||||||
| Chr. 6 | 0.82 (0.81) | 0.48 (0.42) | 0.33 (0.4) | –0.37 (–0.43) | 0.32 (0.41) | 0.23 (0.36) |
| Chr. 21 | 0.88 (0.77) | 0.77 (0.69) | 0.50 (0.31) | –0.26 (–0.16) | 0.001 (0.07) | 0.43 ((0.31) |
| Chr. 22 | 0.92 (0.9) | 0.69 (0.66) | 0 (0.06) | 0.22 (0.12) | –0.45 (–0.45) | –0.38 (–0.38) |
| Correlationsawith |D′| | ||||||
| Chr. 6 | –0.68 (–0.73) | –0.35 (–0.34) | –0.24 (–0.33) | 0.33 (0.42) | –0.30 (–0.37) | –0.09 (–0.26) |
| Chr. 21 | –0.79 (–0.7) | –0.57 (–0.49) | –0.36 (–0.22) | 0.04 (–0.1) | 0.03 (0.001) | –0.36 (–0.21) |
| Chr. 22 | –0.75 (–0.78) | –0.63 (0.63) | 0.13 (0.04) | –0.19 (–0.18) | 0.58 (0.43) | 0.34 (0.47) |
| Correlationsawith r2 | ||||||
| Chr. 6 | –0.62 (–0.72) | –0.37 (0.43) | –0.30 (–0.42) | 0.39 (0.45) | –0.37 (–0.48) | –0.14 (–0.28) |
| Chr. 21 | –0.81 (–0.79) | –0.45 (0.38) | –0.36 (–0.32) | 0.15 (0.1) | –0.10 (–0.12) | –0.29 (–0.27) |
| Chr. 22 | –0.79 (–0.79) | –0.69 (0.67) | 0.1 (0.01) | –0.22 (–0.2) | 0.6 (0.48) | 0.37 (0.44) |
Note. The correlations are reported for 2-MB bins generated as described in Methods for the Caucasian samples. Similar results were obtained for the other populations studied. All correlations above 0.2 are significant with p < 0.001 derived by bootstrapping. Density of SNPs, LINES, SINES, and GpC islands is calculated as number of features per window.
Pearson correlation (Spearman rank correlation)
Table 4.
Fraction of the LDU variance explained by sequence descriptors
| Chromosome | Recombination (cM/Mb) | All (six) descriptors | All (five) descriptors except recombination | Polymorphism densitya | GC content | LINES densitya | SINES densitya | CpG islandsa |
|---|---|---|---|---|---|---|---|---|
| 6 | 0.673 | 0.725 | 0.431 | 0.232 | 0.110 | 0.137 | 0.102 | 0.054 |
| 21 | 0.766 | 0.890 | 0.744 | 0.590 | 0.249 | 0.068 | 0.000 | 0.186 |
| 22 | 0.840 | 0.917 | 0.548 | 0.472 | 0.000 | 0.047 | 0.206 | 0.141 |
The correlations are reported for 2-MB bins generated as described in Methods for the Caucasian samples. Similar results were obtained for the other populations studied.
Density calculated as number of features per window
Breakdown of LD with physical distance
Table 5 summarizes the half-length of the decay of LD: the distance over which LD decays to half of its maximum value to the asymptotic value (see Supplemental Figure 1A,B, for a plot of the decay of |D′| and r2 depending on the physical distance between markers). Chromosome 6 exhibits from 26% to 58% slower decay of LD with distance as compared with the smaller chromosomes. The metric |D′| commonly shows greater differentials than r2. Another metric of the decay of LD is the chromosome-wide swept radius (Morton et al. 2001), which is equivalent to the average kb distance of one LDU. As shown in Table 5, this metric yields greater differences between the chromosomes in terms of decay of LD: The estimated swept radii are over 53% longer for chromosome 6 than for chromosomes 21 and 22. Thus, the overall extent of LD for the three chromosomes follows the comparative ranking: 6 ≫ 21 ≈ 22, which is consistent with the known genetic lengths of these chromosomes. Since the number of recombination events per meiosis is rather similar across chromosomes, the large differences in their lengths are expected to result in lower overall recombination rates (Kong et al. 2002) and thus slower breakdown of LD in the larger chromosomes. Here we show that potentially useful LD extends up to 50–56 kb in chromosome 6 for the out-of-Africa populations (Caucasian, Chinese, and Japanese), whereas the African-Americans exhibit at least 25% smaller swept radius. In the smaller chromosomes this reduction is even larger, at least over 40%, where useful LD extends over 30 kb out-of-Africa, but only to 22 kb in African-Americans. When the decay of common pairwise metrics of LD is plotted versus the genetic distance of the markers expressed in LDUs, the curves show no significant differences between chromosomes or populations (see Supplemental Figure 1C,D). The later is expected as the LD map already normalizes the LD pattern between populations and loci. The half-length of decay in this coordinate system provides a rough equivalence between the LDUs and the pairwise metrics (|D′| half-length ≈ 0.7 LDUs; r2 half-length ≈ 0.3 LDUs) and supports the suggestion (Morton et al. 2001) that beyond one LDU, the intensity of LD would be too weak to provide sufficient power for association mapping under most genetic models.
Table 5.
Chromosome-wide SNP and LD summary statistics
| Population | Statistic | Chr 6 | Chr 21 | Chr 22 | ||
|---|---|---|---|---|---|---|
| African-American | No. of SNPs | 9129 | 3418 | 3688 | ||
| SNP spacing on covered segments (kb)a | ||||||
| Mean | 10.1 | 7.9 | 7.3 | |||
| Median | 6.9 | 4.5 | 4 | |||
| Minor allele frequency | ||||||
| Mean | 0.29 | 0.3 | 0.29 | |||
| Median | 0.28 | 0.3 | 0.29 | |||
| Decay of LD (kb) | ||||||
| |D′| half length | 28.9 | 19 | 18.2 | |||
| r2 half length | 16.4 | 11.8 | 9.9 | |||
| Swept radius | 41 | 22.1 | 21.8 | |||
| Caucasian | No. of SNPs | 9274 | 3551 | 3931 | ||
| SNP spacing on covered segments (kb)a | ||||||
| Mean | 9.9 | 7.6 | 7 | |||
| Median | 6.7 | 4.1 | 3.7 | |||
| Minor allele frequency | ||||||
| Mean | 0.31 | 0.31 | 0.31 | |||
| Median | 0.31 | 0.32 | 0.32 | |||
| Decay of LD (kb) | ||||||
| |D′| half length | 46 | 29.5 | 29.3 | |||
| r2 half length | 26.7 | 19.2 | 19.3 | |||
| Swept radius | 56.3 | 31.2 | 30.9 | |||
| Chinese | No. of SNPs | 10,916 | 3567 | 3496 | ||
| SNP spacing on covered segments (kb)a | ||||||
| Mean | 11.7 | 8.2 | 7.7 | |||
| Median | 8.3 | 5.8 | 4.7 | |||
| Minor allele frequency | ||||||
| Mean | 0.3 | 0.3 | 0.3 | |||
| Median | 0.3 | 0.3 | 0.3 | |||
| Decay of LD (kb) | ||||||
| |D′| half length | 41.7 | 31.2 | 31.8 | |||
| r2 half length | 27.5 | 20.4 | 21.8 | |||
| Swept radius | 50.2 | 31.3 | 31.6 | |||
| Japanese | No. of SNPs | 10,825 | 3536 | 3483 | ||
| SNP spacing on covered segments (kb)a | ||||||
| Mean | 11.8 | 8.3 | 7.8 | |||
| Median | 8.4 | 5.9 | 4.6 | |||
| Minor allele frequency | ||||||
| Mean | 0.3 | 0.3 | 0.31 | |||
| Median | 0.31 | 0.31 | 0.3 | |||
| Decay of LD (kb) | ||||||
| |D′| half length | 44 | 32.8 | 34 | |||
| r2 half length | 28.9 | 21.1 | 21.1 | |||
| Swept radius | 53.1 | 34.6 | 33 | |||
Covered segments are defined as intervals where inter-SNP distances are ≤50 Kb
Discussion
Until recently, patterns of LD have been studied in small random samples of the genome (Daly et al. 2001; Gabriel et al. 2002), or in a few single chromosome studies (Dawson et al. 2001; Patil et al. 2001; Phillips et al. 2003), and mostly only for a single population (Tsunoda et al. 2004) or cosmopolitan sample aggregates (Patil et al. 2001). These investigations, although they provide an important contribution to our understanding of the underlying structure of LD in the human genome, have not allowed for a large-scale comparison of the differences in the strength and distribution of LD between major human populations. Here we have presented more-extensive studies of the patterns of LD for two previously studied chromosomes and, to our knowledge, the first high-resolution LD study of a large mesocentric chromosome (chromosome 6).
The partly cumulative effect of numerous population bottlenecks has had an important impact on the patterns of LD that we see today. Migration out of Africa approximately 100,000 years ago (Stringer and Andrews 1988) had, presumably, the greatest influence, but other bottlenecks of smaller magnitude have taken place over many generations. African-Americans, a population derived mainly from West Africans, show reduced LD decay distances and longer LDU maps. The samples of European ancestry, as well as the Asian populations show significantly shorter LDU maps and more extensive LD, presumably the result of acute population bottlenecks. Zhang et al. (2004a) defined the `effective bottleneck time' (EBT) by analogy with effective population size. The LDU/Morgan ratio estimates the effective number of generations over which LD has been declining consistent with the extent of LD we observe today. From the LD maps for the three chromosomes given here (Table 2), and assuming 25 years per generation, the EBT for the Caucasian population is 43,325 years (range for three chromosomes 42,050–44,879), the Chinese population has 44,300 years (range 41,123–46,075) and the Japanese population 41,039 years (range 39,550–43,300). It is noteworthy that these times are less than half of the time to the presumed out-of-Africa event (Stringer and Andrews 1988), consistent with the compound effect of subsequent bottlenecks in creating LD. To the extent that these three populations share a common history, the EBT ranges are all overlapping. By contrast the EBT for the African-American sample is 61,525 years (range 57,041–64,036), which reflects the very different demographic history. The African-American population is somewhat admixed (Collins-Schramm et al. 2002) and thus a native African population might show even longer LD maps and EBT. However, because of the ascertainment bias to SNPs of high heterozygosity across multiple populations in our study, it is unlikely that admixture effects are strongly influencing our results. It will be of interest to examine other populations with partial or complete African ancestry to determine the impact of recent admixture on the EBT.
Tapper et al. (2003) have constructed LD maps of chromosome 22 for the data of Dawson et al. (2002). LDU map lengths in UK-unrelated and CEPH samples are very similar, being in the range 818 LDUs to 841 LDUs over 62.8 cM, implying a genome of approximately 48,000 LDUs in these populations. This is somewhat shorter than that seen in our current analysis; the discrepancy may be due to the lower resolution of the Dawson et al. (2002) map, where the SNP density may be insufficient to precisely estimate the length of the map, in particular in areas of high recombination. In contrast to haplotype block boundaries, additivity of LDU maps has been shown recently for a range of SNP densities (2–10 kb mean interval size on chromosome 20) (Ke et al. 2004). However, additivity must be lost locally below critical SNP densities that depend to a large extent on recombination intensity. We were able to reproduce the two large recombination cold spans observed in the data of Dawson et al. (2001) (Tapper et al. 2003) (Fig. 1). Moreover, we were able to identify a third region with extensive LD close to the q-telomere of chromosome 22 in both populations, as well as other smaller recombination cold spans. Dawson et al. (2001) previously reported a correlation between the strength of LD and recombination. We observe a much stronger positive correlation between LDU and recombination rate, but we are unable to find a consistent correlation between LD and repetitive elements similar to those reported by these authors.
The gross-scale variation in local recombination rate is probably responsible for much of the consistency of the LDU maps across populations. Differences are mostly in the overall map length, as suggested by Maniatis et al. (2002), and suggest the possibility of developing a `standard' LD map that is efficient for association mapping in all populations if suitably scaled (Zhang et al. 2002). These scaling factors could be obtained from studies in more populations and would reflect different population history lengths. Nevertheless, Kauppi et al. (2003) have shown that in spite of a common distribution of recombination hot spots in the MHC class II region, haplotype composition in the cold spans is considerably divergent between populations. This is corroborated by the results of others (Crawford et al. 2004; Liu et al. 2004) and by an analysis of haplotype frequencies in LD blocks of the data sets of the present study (F. De La Vega, H. Isaac, C. Scafe, and E. Spier, unpubl.) showing a significant proportion of unshared haplotypes between African-Americans and out-of-Africa populations, in spite of the similar shape of the LD maps. Therefore, our results do not necessarily imply that the similarity in the LD maps translates to an identical choice of optimal markers for association studies in different populations. Subsets of markers that attempt to capture the haplotype diversity of the genomic regions may need to be somewhat different between populations, even if the LD map can be extremely useful to guide their selection, for example, by determining sensible neighborhoods to select haplotype-tagging SNPs (Halldórsson et al. 2004). However, the relevance of selecting markers that preserve haplotype diversity in terms of the power of an association study remains controversial (Zhai et al. 2004; Zhang et al. 2004b).
The role of LD maps in disease mapping is twofold. Firstly, LD maps indicate regions of LD breakdown within which higher SNP densities may be required for identification of some causal polymorphisms. Designing studies assuming a constant or average level of LD across the genome is clearly flawed (Schork 2002). Instead, marker selection, statistical power, and sample size estimations could now be based on the empirically determined LD map of the population of interest. Zhang et al. (2004b) have argued for a multi-stage design where an initial screen at relatively low SNP density is followed by a higher SNP density scan to fully elucidate relationship(s) with the disease phenotype. For the initial screen and for the addition of further SNPs, uniform spacing on the LD scale is optimal. Many studies have associated autoimmune disease phenotypes to the MHC region of chromosome 6p (Horton et al. 2004). The availability of a detailed LD map of this region, showing that LD extent is not constant across the entire MHC span (Stenzel et al. 2004), should allow for better design and interpretation of association studies in this region. For example, the PSORS1 locus on 6p21 has been implicated with psoriasis by linkage (Leder et al. 1998). Our map shows extensive LD across the locus implying that the power to detect association should be high, which is consistent with the studies performed to date (Nair et al. 2000; Veal et al. 2002). Our results also suggest that, everything else being equal, studies in larger chromosomes would have more power, and studies in African-Americans will require about 30% more markers and/or larger sample size. Previous surveys of LD on population isolates have shown that “background” LD extends over large genetic distances (Service et al. 2001). Thus, younger population isolates should exhibit significantly shorter LD maps, making these populations an ideal target for testing the feasibility of whole-genome association studies. The second major role of LD maps is in multi-locus analysis where the LD map has the equivalent function for association mapping as the linkage map for multipoint analysis of major genes. Maniatis et al. (2005) demonstrated huge increases in power and a much reduced confidence interval when localizing a causal polymorphism on an underlying LDU map rather than a physical (kb) map. This dual role for the LDU map is, of course, applicable for association mapping studies in general and not just for the chromosomes we describe here.
In summary, our results illustrate the interplay between recombination and demography as the major forces shaping the patterns of LD in the human genome. While demography strongly impacts the overall extent of LD manifested in the LD map lengths, an underlying pattern of recombination appears to dominate at the chromosomal scale, defining the major features of the LD maps.
Methods
SNP ascertainment
All SNP data was obtained from the Celera Human RefSNP database (version 3.6), part of the Celera Discovery System (Kerlavage et al. 2002). This version of the database included about 2.4 million Celera SNPs, as well as 2.2 million publicly available SNPs uniquely mapped to the Celera Human Genome assembly, release 27. We developed a “triage” process for selecting SNPs that requires evidence of two independent discoveries of the minor allele (De La Vega et al. 2002). See Supplemental Methods for details.
Table 5 shows the statistics of the number of SNPs typed per chromosome and population, their minor allele frequency, and the SNPs density across “covered segments”—contiguous segments where inter-SNPs distances are ≤50 kb (see Supplemental Table 1). The chromosomal regions not covered in our study include heterochromatin, highly repetitive regions, and duplicated regions, where it is difficult to develop genotyping assays. The mean (7–1.8 kb) and median (3.7–8.4 kb) SNP spacing indicate that we achieved a high-resolution coverage of the chromosomes. All SNPs genotyped successfully in our study are listed in Supplemental Table 2.
DNA samples
The African-American and Caucasian DNA samples, 45 each, were obtained from the Coriell Institute/National Institute of General Medical Sciences Human Variation Panels (http://locus.umdnj.edu/ccr/). Supplemental Table 3 lists the Coriell IDs for these samples. The Chinese samples were obtained from 45 Han Chinese patients enrolled in a cohort study of individuals at risk for nasopharyngeal carcinoma in Guanxi Province, China. An additional set of 45 Japanese DNA samples were obtained from unrelated healthy Japanese volunteers at the University of Tokushima, Japan. All the samples were collected with proper informed consent and IRB approval (see Supplemental Methods).
Assay development and genotyping
We used a high-throughput assay design pipeline to develop 5′ nuclease allelic discrimination assays used in the TaqMan Custom SNP Genoptyping Assay design service (Applied Biosystems, Foster City, CA). After the design of primers and TaqMan probes, a computational quality-control step was performed to ensure uniqueness of the predicted amplicons in the genome assembly. This allowed us to eliminate potentially problematic SNP targets that may arise from repeated genomic regions, pseudo-SNPs, and other possible assembly artifacts (Heil et al. 2002).
Genotyping was performed with commercially available TaqMan Validated SNP Genotyping Assays from Applied Biosystems (http://myscience.appliedbiosystems.com), following the standard protocol suggested by the manufacturer (see the Supplemental Methods for more detail). The average genotyping error rate in our production lab was estimated at about 0.1% by routinely running duplicate control plates. The genotypes for the samples typed in the study are available for download within the SNPbrowser Software provided freely by Applied Biosystems (http://www.allsnps.com/snpbrowser/), from which they can be easily exported. Genotypes and SNP records are also available from dbSNP (Sherry et al. 2001) under the submitter handle “ABI,” and from the PharmGKB database (Hewett et al. 2002) under project code “LDCHRS.”
Construction of metric LD maps
The LDMAP program (http://cedar.genetics.soton.ac.uk/pub/PROGRAMS/LDMAP; Maniatis et al. 2002) was used to construct LD maps from phase-unknown diplotypes describing the variation in the extent of LD between adjacent SNPs expressed in LDUs. LDMAP estimates a Malécot ε parameter in each map interval. The length of the ith interval is εidi LDUs, where εi is the Malécot parameter, and di is the length of the interval on the physical map in kb. A chromosome has Σεidi LDUs. The model is formulated such that one LDU equals one swept radius so that equal spacing of SNPs on the LDU scale is required for coverage of a region.
Correlation with chromosomal features
The average values of LD were computed for equally sized base-pair bins, uniformly spaced at 100 Kb intervals along each of the three chromosomes. This computation was repeated for the different measures of LD. The average values of each of six commonly known chromosomal descriptors were also computed for the same base-pair bins (recombination rate; GC content; SNP density; density of LINEs, SINEs, and CpG islands) from the Celera Human Genome assembly, release 27. The Pearson and Spearman's rank correlations between the LD measures and each descriptor were calculated (Mendenhall et al. 1986) and its significance was assessed calculating p-values obtained by bootstrapping. A linear minimum squared error model was also computed to predict each of the LD measures using each of the descriptors individually, or using all of the descriptors combined, or using all of the descriptors excluding the recombination rate. See the Supplemental Methods section for more details.
Acknowledgments
We are indebted to Leila Smith; Helen Belcastro; Annie Titus; Joanna Curlee; the production genotyping, LIMS, and IT teams of Services Development and Delivery; and the Global Oligo Operations teams of Applied Biosystems for their support in the generation of the data used in this paper. Thanks are also due to Mark Adams, Sam Broder, David Dailey, Penny Dong, Nelson Freimer, Derek Gordon, Kenneth Kidd, Kit Lau, Adam Lowe, Newton Morton, Michael Rhodes, Stefan Schreiber, Sue Service, John Sninsky, and Trevor Woodage for many helpful discussions and/or comments on the text and to Mignon Fogarty for assistance with the manuscript. The development of LDMAP was supported by the Medical Research Council, UK.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.3241705. Article published online before print in March 2005. Freely available online through the Genome Research Immediate Open Access option.
Footnotes
[Supplemental material is available online at www.genome.org.]
References
- Ardlie, K., Liu-Cordero, S.N., Eberle, M.A., Daly, M., Barrett, J., Winchester, E., Lander, E.S., and Kruglyak, L. 2001. Lower-than-expected linkage disequilibrium between tightly linked markers in humans suggests a role for gene conversion. Am. J. Hum. Genet. 69: 582-589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baird, D.M., Coleman, J., Rosser, Z.H., and Royle, N.J. 2000. High levels of sequence polymorphism and linkage disequilibrium at the telomere of 12q: Implications for telomere biology and human evolution. Am. J. Hum. Genet. 66: 235-250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins-Schramm, H.E., Phillips, C.M., Operario, D.J., Lee, J.S., Weber, J.L., Hanson, R.L., Knowler, W.C., Cooper, R., Li, H., and Seldin, M.F. 2002. Ethnic-difference markers for use in mapping by admixture linkage disequilibrium. Am. J. Hum. Genet. 70: 737-750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford, D.C., Carlson, C.S., Rieder, M.J., Carrington, D.P., Yi, Q., Smith, J.D., Eberle, M.A., Kruglyak, L., and Nickerson, D.A. 2004. Haplotype diversity across 100 candidate genes for inflammation, lipid metabolism, and blood pressure regulation in two populations. Am. J. Hum. Genet. 74: 610-622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daly, M.J., Rioux, J.D., Schaffner, S.F., Hudson, T.J., and Lander, E.S. 2001. High-resolution haplotype structure in the human genome. Nat. Genet. 29: 229-232. [DOI] [PubMed] [Google Scholar]
- Dawson, E., Chen, Y., Hunt, S., Smink, L.J., Hunt, A., Rice, K., Livingston, S., Bumpstead, S., Bruskiewich, R., Sham, P., et al. 2001. A SNP resource for human chromosome 22: Extracting dense clusters of SNPs from the genomic sequence. Genome Res. 11: 170-178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson, E., Abecasis, G.R., Bumpstead, S., Chen, Y., Hunt, S., Beare, D.M., Pabial, J., Dibling, T., Tinsley, E., Kirby, S., et al. 2002. A first-generation linkage disequilibrium map of human chromosome 22. Nature 418: 544-548. [DOI] [PubMed] [Google Scholar]
- De La Vega, F.M., Dailey, D., Ziegle, J., Williams, J., Madden, D., and Gilbert, D.A. 2002. New generation pharmacogenomic tools: A SNP linkage disequilibrium map, validated SNP assay resource, and high-throughput instrumentation system for large-scale genetic studies. Biotechniques Suppl. 48-50, 52, 54. [PubMed]
- Gabriel, S.B., Schaffner, S.F., Nguyen, H., Moore, J.M., Roy, J., Blumenstiel, B., Higgins, J., DeFelice, M., Lochner, A., Faggart, M., et al. 2002. The structure of haplotype blocks in the human genome. Science 296: 2225-2229. [DOI] [PubMed] [Google Scholar]
- Halldórsson, B.V., Bafna, V., Lippert, R., Schwartz, R., De La Vega, F.M., Clark, A.G., and Istrail, S. 2004. Optimal haplotype block-free selection of tagging SNPs for genome-wide association studies. Genome Res. 14: 1633-1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heil, J., Glanowski, S., Scott, J., Winn-Deen, E., McMullen, I., Wu, L., Gire, C., and Sprague, A. 2002. An automated computer system to support ultra high throughput SNP genotyping. Pac. Symp. Biocomput. 7: 30-40. [DOI] [PubMed] [Google Scholar]
- Hewett, M., Oliver, D.E., Rubin, D.L., Easton, K.L., Stuart, J.M., Altman, R.B., and Klein, T.E. 2002. PharmGKB: the Pharmacogenetics Knowledge Base. Nucleic Acids Res. 30: 163-165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horton, R., Wilming, L., Rand, V., Lovering, R.C., Bruford, E.A., Khodiyar, V.K., Lush, M.J., Povey, S., Talbot Jr., C.C., Wright, M.W., et al. 2004. Gene map of the extended human MHC. Nat. Rev. Genet. 5: 889-899. [DOI] [PubMed] [Google Scholar]
- The International HapMap Consortium. 2003. The International HapMap Project. Nature 426: 789-796. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A.J., Kauppi, L., and Neumann, R. 2001. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat. Genet. 29: 217-222. [DOI] [PubMed] [Google Scholar]
- Kauppi, L., Sajantila, A., and Jeffreys, A.J. 2003. Recombination hotspots rather than population history dominate linkage disequilibrium in the MHC class II region. Hum. Mol. Genet. 12: 33-40. [DOI] [PubMed] [Google Scholar]
- Ke, X., Hunt, S., Tapper, W., Lawrence, R., Stavrides, G., Ghori, J., Whittaker, P., Collins, A., Morris, A.P., Bentley, D., et al. 2004. The impact of SNP density on fine-scale patterns of linkage disequilibrium. Hum. Mol. Genet. 13: 577-588. [DOI] [PubMed] [Google Scholar]
- Kerlavage, A., Bonazzi, V., di Tommaso, M., Lawrence, C., Li, P., Mayberry, F., Mural, R., Nodell, M., Yandell, M., Zhang, J., et al. 2002. The Celera Discovery System. Nucleic Acids Res. 30: 129-136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidd, K.K., Morar, B., Castiglione, C.M., Zhao, H., Pakstis, A.J., Speed, W.C., Bonne-Tamir, B., Lu, R.B., Goldman, D., Lee, C., et al. 1998. A global survey of haplotype frequencies and linkage disequilibrium at the DRD2 locus. Hum. Genet. 103: 211-227. [DOI] [PubMed] [Google Scholar]
- Kong, A., Gudbjartsson, D.F., Sainz, J., Jonsdottir, G.M., Gudjonsson, S.A., Richardsson, B., Sigurdardottir, S., Barnard, J., Hallbeck, B., Masson, G., et al. 2002. A high-resolution recombination map of the human genome. Nat. Genet. 31: 241-247. [DOI] [PubMed] [Google Scholar]
- Leder, R.O., Mansbridge, J.N., Hallmayer, J., and Hodge, S.E. 1998. Familial psoriasis and HLA-B: Unambiguous support for linkage in 97 published families. Hum. Hered. 48: 198-211. [DOI] [PubMed] [Google Scholar]
- Lercher, M.J. and Hurst, L.D. 2002. Human SNP variability and mutation rate are higher in regions of high recombination. Trends Genet. 18: 337-340. [DOI] [PubMed] [Google Scholar]
- Liu, N., Sawyer, S.L., Mukherjee, N., Pakstis, A.J., Kidd, J.R., Kidd, K.K., Brookes, A.J., and Zhao, H. 2004. Haplotype block structures show significant variation among populations. Genet. Epidemiol. 27: 385-400. [DOI] [PubMed] [Google Scholar]
- Maniatis, N., Collins, A., Xu, C.F., McCarthy, L.C., Hewett, D.R., Tapper, W., Ennis, S., Ke, X., and Morton, N.E. 2002. The first linkage disequilibrium (LD) maps: Delineation of hot and cold blocks by diplotype analysis. Proc. Natl. Acad. Sci. 99: 2228-2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maniatis, N., Morton, N.E., Gibson, J., Xu, C.F., Hosking, L.K., and Collins, A. 2005. The optimal measure of linkage disequilibrium reduces error in association mapping of affection status. Hum. Mol. Genet. 14: 145-153. [DOI] [PubMed] [Google Scholar]
- Mendenhall, W., Scheaffer, R.L., and Wackerly, D.D. 1986. Mathematical statistics with applications. Duxbury Press, Boston, MA.
- Montoya-Burgos, J.I., Boursot, P., and Galtier, N. 2003. Recombination explains isochores in mammalian genomes. Trends Genet. 19: 128-130. [DOI] [PubMed] [Google Scholar]
- Morton, N.E., Zhang, W., Taillon-Miller, P., Ennis, S., Kwok, P.Y., and Collins, A. 2001. The optimal measure of allelic association. Proc. Natl. Acad. Sci. 98: 5217-5221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair, R.P., Stuart, P., Henseler, T., Jenisch, S., Chia, N.V., Westphal, E., Schork, N.J., Kim, J., Lim, H.W., Christophers, E., et al. 2000. Localization of psoriasis-susceptibility locus PSORS1 to a 60-kb interval telomeric to HLA-C. Am. J. Hum. Genet. 66: 1833-1844. [Erratum appears in Am. J. Hum. Genet. 2002 Apr:70(4): 1074]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil, N., Berno, A.J., Hinds, D.A., Barrett, W.A., Doshi, J.M., Hacker, C.R., Kautzer, C.R., Lee, D.H., Marjoribanks, C., McDonough, D.P., et al. 2001. Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294: 1719-1723. [DOI] [PubMed] [Google Scholar]
- Phillips, M.S., Lawrence, R., Sachidanandam, R., Morris, A.P., Balding, D.J., Donaldson, M.A., Studebaker, J.F., Ankener, W.M., Alfisi, S.V., Kuo, F.S., et al. 2003. Chromosome-wide distribution of haplotype blocks and the role of recombination hot spots. Nat. Genet. 33: 382-387. [DOI] [PubMed] [Google Scholar]
- Reich, D.E., Schaffner, S.F., Daly, M.J., McVean, G., Mullikin, J.C., Higgins, J.M., Richter, D.J., Lander, E.S., and Altshuler, D. 2002. Human genome sequence variation and the influence of gene history, mutation and recombination. Nat. Genet. 32: 135-142. [DOI] [PubMed] [Google Scholar]
- Schork, N.J. 2002. Power calculations for genetic association studies using estimated probability distributions. Am. J. Hum. Genet. 70: 1480-1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, R., Halldórsson, B.V., Bafna, V., Clark, A.G., and Istrail, S. 2003. Robustness of inference of haplotype block structure. J. Comput. Biol. 10: 13-19. [DOI] [PubMed] [Google Scholar]
- Service, S.K., Ophoff, R.A., and Freimer, N.B. 2001. The genome-wide distribution of background linkage disequilibrium in a population isolate. Hum. Mol. Genet. 10: 545-551. [DOI] [PubMed] [Google Scholar]
- Sherry, S.T., Ward, M.H., Kholodov, M., Baker, J., Phan, L., Smigielski, E.M., and Sirotkin, K. 2001. dbSNP: The NCBI database of genetic variation. Nucleic Acids Res. 29: 308-311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stenzel, A., Lu, T., Koch, W.A., Hampe, J., Guenther, S.M., De La Vega, F.M., Krawczak, M., and Schreiber, S. 2004. Patterns of linkage disequilibrium in the MHC region on human chromosome 6p. Hum. Genet. 114: 377-385. [DOI] [PubMed] [Google Scholar]
- Strathern, J.N., Shafer, B.K., and McGill, C.B. 1995. DNA synthesis errors associated with double-strand-break repair. Genetics 140: 965-972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stringer, C.B. and Andrews, P. 1988. Genetic and fossil evidence for the origin of modern humans. Science 239: 1263-1268. [DOI] [PubMed] [Google Scholar]
- Sun, F., Oliver-Bonet, M., Liehr, T., Starke, H., Ko, E., Rademaker, A., Navarro, J., Benet, J., and Martin, R.H. 2004. Human male recombination maps for individual chromosomes. Am. J. Hum. Genet. 74: 521-531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tapper, W.J., Maniatis, N., Morton, N.E., and Collins, A. 2003. A metric linkage disequilibrium map of a human chromosome. Ann. Hum. Genet. 67: 487-494. [DOI] [PubMed] [Google Scholar]
- Tsunoda, T., Lathrop, G.M., Sekine, A., Yamada, R., Takahashi, A., Ohnishi, Y., Tanaka, T., and Nakamura, Y. 2004. Variation of gene-based SNPs and linkage disequilibrium patterns in the human genome. Hum. Mol. Genet. 13: 1623-1632. [DOI] [PubMed] [Google Scholar]
- Veal, C.D., Capon, F., Allen, M.H., Heath, E.K., Evans, J.C., Jones, A., Patel, S., Burden, D., Tillman, D., Barker, J.N., et al. 2002. Family-based analysis using a dense single-nucleotide polymorphism-based map defines genetic variation at PSORS1, the major psoriasis-susceptibility locus. Am. J. Hum. Genet. 71: 554-564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venter, J.C., Adams, M.D., Myers, E.W., Li, P.W., Mural, R.J., Sutton, G.G., Smith, H.O., Yandell, M., Evans, C.A., Holt, R.A., et al. 2001. The sequence of the human genome. Science 291: 1304-1351. [DOI] [PubMed] [Google Scholar]
- Weir, B.S. 1996. Genetic Data Analysis II. Sinauer Associates, Sunderland, MA.
- Zhai, W., Todd, M.J., and Nielsen, R. 2004. Is haplotype block identification useful for association mapping studies? Genet. Epidemiol. 27: 80-83. [DOI] [PubMed] [Google Scholar]
- Zhang, W., Collins, A., Maniatis, N., Tapper, W., and Morton, N.E. 2002. Properties of linkage disequilibrium (LD) maps. Proc. Natl. Acad. Sci. 99: 17004-17007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, W., Collins, A., Gibson, J., Tapper, W.J., Hunt, S., Deloukas, P., Bentley, D.R., and Morton, N.E. 2004a. Impact of population structure, effective bottleneck time, and allele frequency on linkage disequilibrium maps. Proc. Natl. Acad. Sci. 101: 18075-18080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, W., Collins, A., and Morton, N.E. 2004b. Does haplotype diversity predict power for association mapping of disease susceptibility? Hum. Genet. 115: 157-164. [DOI] [PubMed] [Google Scholar]
Web site references
- http://locus.umdnj.edu/ccr/; Coriell Institute, for details of the NIGMS Human Variation Panels used in this study.
- https://myscience.appliedbiosystems.com/; Applied Biosystems' myScience research environment, for the TaqMan Validated SNP Genotyping Assays used in this study.
- http://cedar.genetics.soton.ac.uk/pub/PROGRAMS/LDMAP; LDMAP Program.
- http://www.allsnps.com/snpbrowser/; SNPbrowser Software, to obtain the genotypes used in this study.